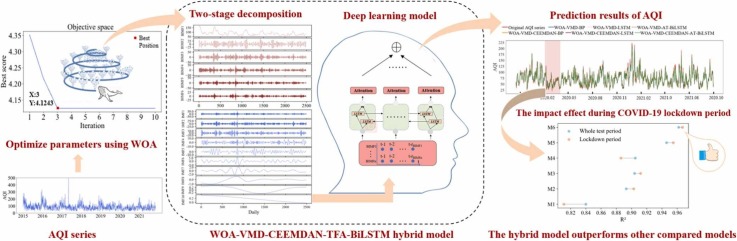
Abstract
Accurate and dependable air quality forecasting is critical to environmental and human health. However, most methods usually aim to improve overall prediction accuracy but neglect the accuracy for unexpected incidents. In this study, a hybrid model was developed for air quality index (AQI) forecasting, and its performance during COVID-19 lockdown was analyzed. Specifically, the variational mode decomposition (VMD) was employed to decompose the original AQI sequence into some subsequences with the parameters optimized by the Whale optimization algorithm (WOA), and the residual sequence was further decomposed by the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN). On this basis, a deep learning method bidirectional long short-term memory coupled with added time filter layer and attention mechanism (TFA-BiLSTM) was employed to explore the latent dynamic characteristics of each subsequence. This WOA-VMD-CEEMDAN-TFA-BiLSTM hybrid model was used to forecast AQI values for four cities in China, and results verified that the accuracy of the hybrid model outperformed other proposed models, achieving R2 values of 0.96–0.97. In addition, the improvement in MAE (34.71–49.65%) and RMSE (32.82–48.07%) were observed over single decomposition-based model. Notably, during the epidemic lockdown period, the hybrid model had significant superiority over other proposed models for AQI prediction.
Keywords: Air quality index, COVID-19, Two-stage decomposition, Long short-term memory, Attention mechanism
Graphical Abstract
1. Introduction
Nowadays, rapid global economic development increases the problem of atmospheric pollution and has caused widespread concerns around the world. Severe atmospheric pollution had a plethora of negative consequences for economic activity and human health (Ma et al., 2020). The air quality index (AQI) is a comprehensive measure to evaluate the air pollution level and reflect the air quality. It is calculated using six pollutants, including PM2.5, PM10, SO2, NO2, O3 and CO. The concentration of each pollutant corresponds to one individual air quality index (IAQI), which can be obtained through the specification table in the ambient air quality standards (GB3095–2012) (Wu and Lin, 2019). Among these six pollutants, the pollutant with the highest IAQI is identified as the primary pollutant and its IAQI value is directly considered as the AQI value. AQI has become a critical measure of air quality in China, and it is a widely accepted health indicator: a higher number indicates a greater danger to health and emphasizes the significance of preventative measures. Therefore, it is critical to employ an accurate AQI forecast approach to avoid severe accidents caused by air pollution.
There are two basic groups of forecasting methods: statistics and machine learning. Statistical approaches, such as the autoregressive integrated moving average (ARIMA) model, were used to forecast air quality and showed that the prediction accuracy still needed to be improved (Díaz-Robles et al., 2008). When dealing with the air pollution nonlinear problems, statistics-based models were incapable of effectively capturing the rule of nonlinear changes, resulting in a significant level of prediction error. In order to overcome this limitation, researchers began to develop nonlinear methods. As the development of machine learning, deep learning techniques such as long short-term memory (LSTM) were capable of successfully learning complex temporal properties and capturing time dependency, improving prediction accuracy (Zhou et al., 2019). Bidirectional LSTM (BiLSTM), a novel form of LSTM, has been popular in regression situations recently. By incorporating forward and backward LSTM layers into the design, BiLSTM can utilize future data. This structure enables the model to store both historical and future data. As a result, BiLSTM outperforms unidirectional neural network models when it comes to processing data with time series characteristics. The BiLSTM network has been used to deal with complex regression issues in recent years, such as wind speed forecasting (Liu and Chen, 2019), solar radiation prediction (Heidari and Khovalyg, 2020) and electricity price forecasting (Cheng et al., 2019). Moreover, as an important development of deep learning, attention mechanism can make models selectively focus on data carrying more information, which has been widely used in many fields (Heidari and Khovalyg, 2020). However, in air quality forecasting, the benefit of BiLSTM coupled with attention mechanism has not been proved. Moreover, as an important input setting of BiLSTM, the value of time steps determines how many observations in the past will profoundly influence the prediction results. In the majority of studies, however, the value of time steps was obtained empirically or experimentally, and the results obtained in this way were often time-consuming, labor-intensive and poor universal. Consequently, it is required to optimize the method to determine the length of time steps.
Due to the uncertainty of meteorological conditions and human activities, the AQI time series exhibited a high degree of unpredictability, complex nonlinearity, and multiscale variability (Janarthanan et al., 2021). Therefore, appropriate data preprocessing technologies should be used to extract information from the original time series to increase forecast accuracy. For example, Singla et al. (2022c) proposed an advanced ensemble model combining BiLSTM and wavelet transform (WT) to forecast the solar time series, which was proved to be the best forecasting model for 24-h ahead solar forecasts. Another data preprocessing method, variational mode decomposition (VMD) could also be applicable to the original AQI time series analysis with high precision, rapid convergence, and a high level of noise resilience. The choice of two critical parameters, the penalty factor α and the decomposition level K, is very important for VMD performance, but it is difficult to select proper parameters effectively. Mirjalili and Lewis (2016) introduced whale optimization algorithm (WOA) as a revolutionary meta-heuristic optimization approach. Numerous researches and practical findings have suggested that it performed well in global optimization and might be efficiently used to tackle the problem of self-adaptive parameter selection. Furthermore, the residual sequence generated by VMD contained many high-frequency components and had strong randomness, which might impede the improvement of modelling performance (Shi et al., 2021). This problem could be resolved by additional decomposition of the high-frequency residual sequence (Singla et al., 2022a). A complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) proposed by Torres et al. (2011) could effectively deal with the high-frequency residual sequence by breaking them down into a number of more stationary sub-modes (Peng et al., 2021). Through such a secondary decomposition, more hidden information would be further extracted, which helped to improve the model effectiveness (Fijani et al., 2019). The two-stage decomposition using WOA-VMD and CEEMDAN is expected to extract the time characteristic information and reduce the complexity of the original sequence effectively. However, it has not been utilized in air quality prediction so far.
Although extensive methods have been attempted to improve overall prediction accuracy of models, the improvement on accuracy for unexpected incidents is still limited. It was generally considered that unexpected incidents would impact the prediction performance of machine learning models (Hu et al., 2022). The coronavirus disease (COVID-19) pandemic was one of the most significant global public health emergencies in recent centuries (Berber et al., 2021). The threat of COVID-19 spread caused health emergencies, resulting in severe control measures and restrictions around the world. As a result of the lockdown, enormous declines in industrial activity and automobile use, which are two of the primary causes of air pollution, have been observed. Studies have shown that extraordinary measures during the COVID-19 period significantly impacted air quality (Ravindra et al., 2022). Al-qaness et al. (2021) built a more advanced version of the adaptive neuro-fuzzy inference system to forecast air quality in Wuhan City, China, and investigated the influence of COVID-19 lockdown on air quality. González-Pardo et al. (2022) predicted business-as-usual air pollutant levels in 2020 using meteorological variables. As an emergency, the COVID-19 lockdown is likely to affect the performance of air quality prediction, but its relative information is still very little.
This study built a deep learning model using BiLSTM method coupled with added time filter layer and attention mechanism (TFA-BiLSTM) to forecast air quality of four cities in China. The two-stage decomposition including WOA-VMD and CEEMDAN was proposed to preprocess the original AQI sequence, so as to increase the prediction accuracy. Effects of the COVID-19 lockdown on air quality of the four cities and prediction performance of the hybrid model were analyzed.
2. Methodology
2.1. Two-stage decomposition method
2.1.1. VMD
VMD is a recently developed quasi-orthogonal signal processing technique for achieving component separation in non-recursive signal processing (Dragomiretskiy and Zosso, 2014). In essence, VMD completes the determination of modal bandwidth by solving the search-constrained variational problem. Thus, possible characteristics might be successfully mined by variable frequency domain segmentation of the data (Dong and Zhang, 2021). The VMD iteratively searches for the best solution of a variational mode with a preset number of modes K to get the frequency center and modal function of the K components of the band-limited intrinsic modal function (BIMF). The details are shown in Part S1 in the Supplementary Information.
2.1.2. CEEMDAN
The CEEMDAN method is an adaptive, data-driven and completely non-recursive algorithm which decomposes the original data into intrinsic mode function (IMF) representing different scale characteristics. In comparison to traditional empirical mode decomposition (EMD) methods, it has the ability to lessen some of the computation strain and increase decomposition efficiency with the addition of a limited amount of adaptive white noise. It decomposes nonstationary signals according to their extreme-scale properties, increasing their sensitivity to severe residual sequence fluctuations and assuring feature fitting and convergence of prediction models (Gao et al., 2020). The details are shown in Part S2 in the Supplementary Information.
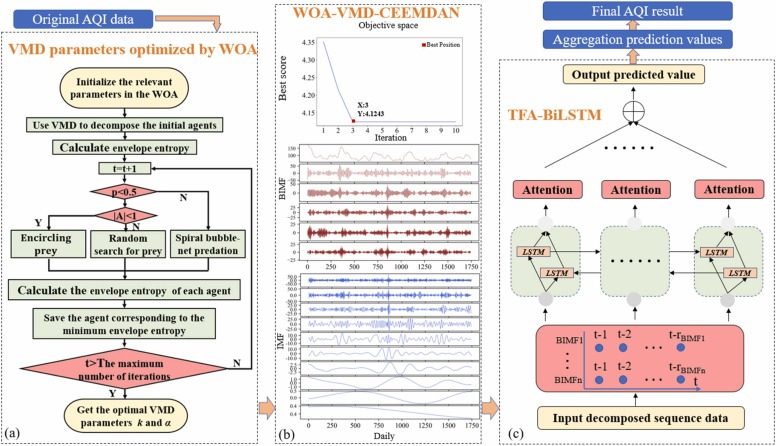
2.2. VMD optimization
2.2.1. Whale optimization algorithm
Mirjalili and Lewis (2016) suggested a new metaheuristic population optimization method based on the foraging behavior of humpback whales, named whale optimization algorithm (WOA). This algorithm addresses optimization issues by replicating the humpback whale's distinctive bubble-net foraging behavior, which consists of three stages: surrounding prey, spiral bubble-net predation, and searching for prey. The detailed explanation can be found in Part S3 in the Supplementary Information.
2.2.2. Proposed parameter-adaptive VMD based on WOA
As shown in the principle of VMD, the quadratic penalty factor α and the modal component number K are crucial to the decomposition results. However, manually adjusting parameters is time-consuming. In order to optimize VMD parameters, WOA was used and envelope entropy was selected as fitness function to evaluate the parameters (Zhou et al., 2021). The envelope entropy is a measure of the signal's sparsity. Generally, when the BIMF has more noise and less characteristic information, the signal's sparsity is weak, resulting in greater envelope entropy. The detailed calculation steps are shown in Part S3.
Then, the parameter-adaptive VMD with WOA algorithm employs the following optimization steps:
Step1: Initialize the pertinent parameters, including whale population (10), the maximum number of iterations (20), and the range of iterations for K [3,8] and α [1000,4500].
Step2: Utilize VMD to get the modes and compute the envelope entropy of each mode.
Step3: Conduct the specified times of iterations to update the optimal search agent. If the optimization condition is fulfilled, update the optimum agent of whales and the least fitness value using the associated update formula.
Step4: The iterations have come to an end, and the method outputs the optimal parameter combination (K, α).
The optimization algorithm flow is shown in Fig. 1a. and the details are shown in Part S3.
Fig. 1.
The overall structure of the hybrid model for AQI prediction.
2.3. Bidirectional LSTM network with time filter layer and attention mechanism
As a modified recurrent neural network (RNN) model, The LSTM network solves the long-term dependency problem by introducing a new memory unit and the gate structure (Hochreiter and Schmidhuber, 1997). Graves and Schmidhuber (2005) proposed the bidirectional long short-term memory (BiLSTM) as an alternative to the traditional one-directional LSTM, which uses solely backward propagation to obtain prior knowledge in historical variables when processing data. BiLSTM is a deformation structure of LSTM that combines forward and backpropagation LSTM layers and can extract past and future temporal characteristics of samples concurrently to generate better prediction results than LSTM (Saeed et al., 2020). The detailed implementation steps of BiLSTM are shown in Part S4 in the Supplementary Information.
The value of the time step determines how many lagged observations will be input into the BiLSTM to forecast the future feature changes. This study adopted a time filter layer between the input layer and the BiLSTM layer of the ordinary BiLSTM, which determined the length of the time step by calculating the autocorrelation value of the sequence, so as to optimize the highly correlated lags efficiently. The function can be expressed as Eq. (1).
| (1) |
where and are the inputs and outputs of the time filter layer, and is the activation function. and are the weights and constants and would be pre-set as unit vectors and zero vectors, respectively. The sample inputs at time t are simply the time series of the variables as shown in Eq. (2).
| (2) |
where n is the number of different time-series variables, and r represents the input time lag.
The specialty of the time filter layer lies in the activation function, which can be expressed using Eq. (3).
| (3) |
where * represents the element-wise product, (∙)T represents the matrix transpose, and I R is the correlation identifier, which is given by Eq. (4).
| (4) |
where represents the correlation threshold, I(∙) represents the indicator function. When , = 1, When , = 0. R is the correlation matrix, which is defined by Eq. (5).
| (5) |
where is the autocorrelation value at time t-r for the n th time series. After the outputs of the time filter layer are given, they are input to the BiLSTM layer.
Attention allows a neural network to concentrate on the most relevant inputs to the current outputs, which has a track record of success across a broad range of tasks (Lin et al., 2022, Yoon et al., 2021). This study adds the attention mechanism to the BiLSTM, which determined the correlation between the output state and the candidate state, so as to optimize the model performance. The output of the attention layer in the attentive BiLSTM network at time t can be formed according to the following (6), (7), (8).
| (6) |
| (7) |
| (8) |
where represents the attention probability distribution value determined by the output vector of BiLSTM layer at time t; u and w are weight coefficients; b is the bias coefficient.
2.4. Prediction models
A hybrid model was developed for air quality prediction, combing time filter layer and attention-mechanism based BiLSTM (TFA-BiLSTM) and the two-stage decomposition with WOA-VMD and CEEMDAN, which was named as WOA-VMD-CEEMDAN-TFA-BiLSTM. The overall structure and flowchart of the hybrid model was shown in Fig. 1. In order to ascertain the prediction performance of the hybrid model, another two commonly used models were selected for comparison, including the back-propagation (BP) artificial neural network and traditional BiLSTM. Moreover, primary decomposition (WOA-VMD) was also combined to each model for comparison, in order to verify the function of two-stage decomposition (WOA-VMD-CEEMDAN).
2.5. Performance evaluation indices
The mean absolute error (MAE), root mean square error (RMSE), and coefficient of determination (R2) were chosen as model evaluation criteria, which were calculated as follows:
| (9) |
| (10) |
| (11) |
where is the actual data at time i, is the mean of the actual data, and is the corresponding predictive data.
The deviations between observed and forecast values were measured using MAE and RMSE, and the criteria is smaller, the better the performance. To characterize the model's fit to the data and its prediction performance, R2 was utilized to identify and analyze the variance of dependent variables, and it was considered as the standard of validity and accuracy of model prediction.
The coefficient of variation (CV) was used to measure the degree of dispersion, which was calculated as Eq. (12).
| (12) |
where is the actual data at time i and is the mean of the actual data.
Moreover, the impact effect, which was commonly used in macroeconomics, was introduced in this study. It was used to evaluate the short-term impact of COVID-19 lockdown on air quality and prediction performance of models. The degree of impact effect on air quality was measured by the difference percentage of AQI and its CV.
For investigating the significant differences between the models statistically, the Harvey, Leybourne, and Newbold (HLN) test was used, which was a small-sample variant of the Diebold-Mariano (DM) test (Harvey et al., 1997). The significant deference could be analyzed through the comparison between the HLN test result and , which was the two-tailed critical value for the standard normal distribution. The details are provided in Part S5 in the Supplementary Information.
In order to measure the performance of the model more comprehensively, sensitivity and scalability experiments were performed on the proposed model. Index of agreement (IA) and directional change (DC) were used to analyze the sensitivity of the model (Singla et al., 2022b). The details are provided in Part S6 in the Supplementary Information. Finally, scalability was analyzed by changing the size of the training and test sets of the hybrid model.
3. Results
3.1. Study areas and data description
This study utilized AQI data from January 2015 to November 2021 of four cities (Wuhan, Zhengzhou, Shijiazhuang and Xingtai) in China to verify the efficacy of proposed models. AQI series and air pollutants concentrations including PM2.5, PM10, SO2, NO2, O3 and CO, are retrieved from the website of China Air Quality Online Monitoring and Analysis Platform (https://www.aqistudy.cn/). The first 70% of the daily data (2015–2019) were utilized for model training, and the rest was utilized to validate the suggested models' performance. It is worth mentioning that these four cities were affected by the outbreak of COVID-19 and experienced the nationwide lockdown during the period of 1st Feb 2020–31 st Mar 2020. Therefore, the AQI data of these four cities during the lockdown period were also selected to investigate the performance of the proposed hybrid model under sudden event. The statistical information of AQI data is listed in Table S1.
Due to the different geographical location of these cities, their AQI values showed different variation range. The three cities, Zhengzhou, Shijiazhuang and Xingtai located in the northern China had similar air quality characteristics. However, the southern city, Wuhan had obviously lower mean AQI value. This might be due to the much higher consumption of coal in northern cities for power generation and winter heating, which contributed to air pollution.
Due to the measurement error, sensor failure, and data transmission error, the raw dataset contains some missing values and outliers. To address these issues, several pre-processing methods are used in this paper. The missing values were filled using interpolation methods. Data points that differ significantly from surrounding observations are considered outliers and are analyzed and removed using smoothing and thresholding methods.
3.2. Two-stage decomposition for AQI data of different study areas
For the AQI data oscillatory mixing on several scales, two-stage decomposition was utilized to get better prediction performance. VMD was firstly used to decompose the time series. Since the development of VMD performance was limited by the choice of penalty factor α and decomposition level K, the VMD were optimized by WOA to efficiently select proper parameters α and K. When the envelope entropy decreased to the lowest value, which was considered as the global optimal value during the fitness demonstration, the corresponding ideal parameter combination (K, α) was obtained. Then, the original AQI sequence was decomposed into several subsequences that showed a variety of patterns, trends, and variations at each time scale of AQI using the optimized K and α. These patterns and characteristics have been proven to be more advantageous for prediction models than the original sequence in capturing data properties (Wu and Lin, 2019). Then, CEEDMAN was introduced further to adaptively decompose the residual of VMD decomposition result, which can be decomposed into a sequence of more stationary sub-modes. The two-stage decomposition results are shown in Fig.S3. Taking the AQI series of Wuhan as an example, the global optimal value was 4.1243 in the fitness curve, and under this situation the ideal K and α were 6 and 3960 respectively. The AQI sequence was decomposed into 6 subsequences by VMD and the residual sequence was decomposed into 9 subsequences by CEEDMAN further. Similarly, the AQI data sequences of other cities were also decomposed.
3.3. Forecasting performance with two-stage decomposition method
In order to assess the efficacy of the suggested the quadratic decomposition algorithm, the daily variations of AQI of four cities in China were characterized using the single (WOA-VMD) and two-stage (WOA-VMD-CEEMDAN) decomposition models. Fig. 2 shows the error evaluation results of AQI prediction for the four cities. To achieve optimal model performance, the hyperparameters of each component were fine-tuned. Specifically, in this investigation, the grid search method was employed to optimize all hyperparameters in the BiLSTM method. A summary of the hyperparameter settings for each component can be found in Table S4.
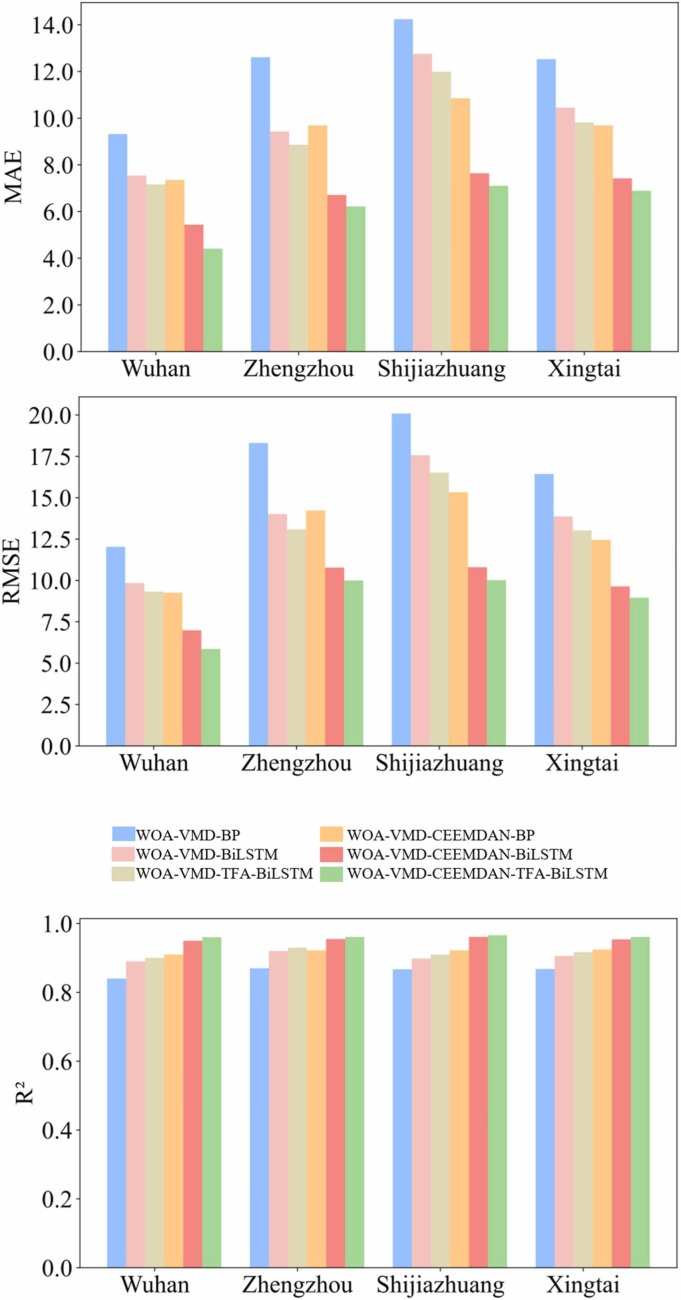
Fig. 2.
Error evaluation results of AQI prediction in the four cities in China.
The average MAE, RMSE and R2 values of the models with single decomposition were 10.56, 14.51 and 0.89, respectively. The two-stage decomposition improved predicting performance of models with average MAE, RMSE, and R2 values of 7.44, 11.81, and 0.95, respectively. Using MAE as an example, the average prediction error of models was decreased by 29.55% after combining CEEMDAN decomposition. As shown in Fig. 3, the prediction curves derived from the models using the two-stage decomposition fit the observed data better, successfully matching the shifting trend in the AQI. For BP model, the MAE and RMSE values were respectively lowered by 22.91% and 23.34% using two-stage decomposition, while the R2 value increased by 6.37%. Regarding to the BiLSTM model, WOA-VMD-CEEMDAN improved the MAE, RMSE, and R2 by 32.34%, 30.10% and 5.53%, respectively. For TFA-BiLSTM, the corresponding improvements were 34.99%, 32.90% and 5.25%, respectively. Overall, compared with the single decomposition, WOA-VMD-CEEMDAN based models showed better performance on predicting AQI of all the four cities ( Fig. 4). This indicates that the two-stage decomposition could more effectively extract the multiscale periodicity and nonlinearity of AQI series, achieving lower prediction bias.
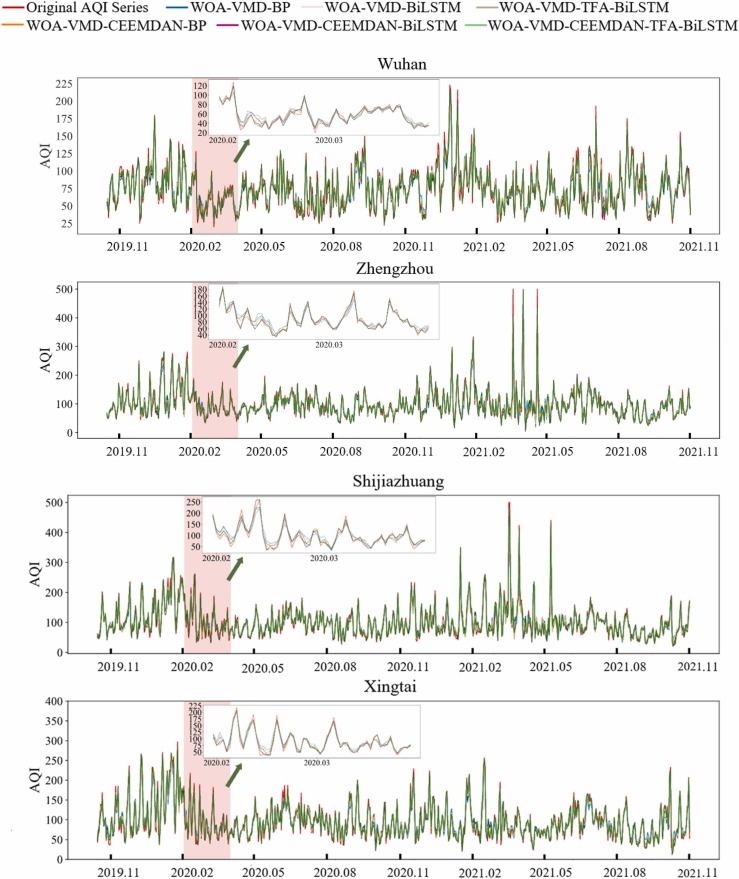
Fig. 3.
Prediction results of AQI in the four cities in China. (The shaded areas represent the studied COVID-19 lockdown periods.).
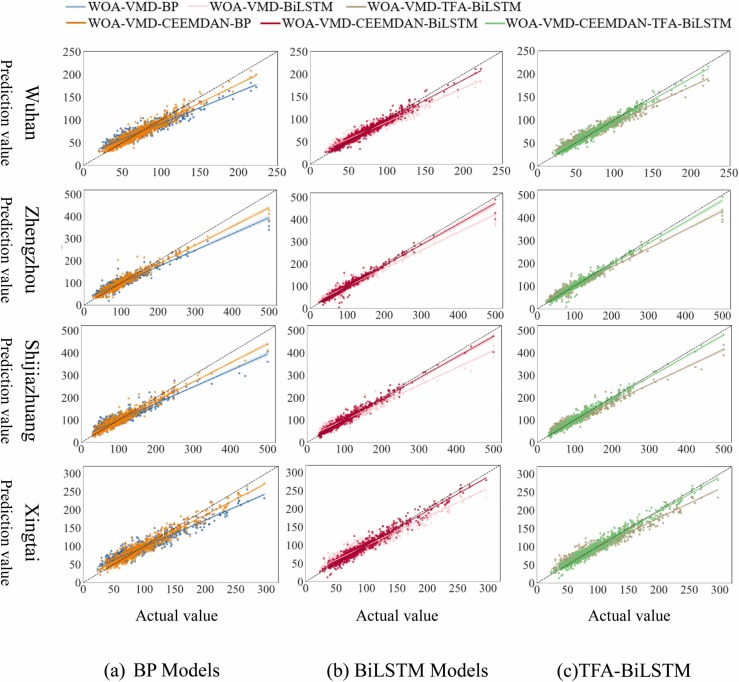
Fig. 4.
Scatterplots of the (a) BP, (b) BiLSTM, (c) TFA-BiLSTM modelling results, and AQI measurements in the four cities in China.
Besides, for comparison, three basic standalone models, BP, support vector machines (SVM) and random forests (RF) were also used to predict AQI of Wuhan city. Results show that the R2 values were 0.56–0.63, and the MAE and RMSE values were 19.92–21.56 and 26.67–28.86, respectively (Table S5). This suggests that the standalone models could not provide satisfactory prediction accuracy for AQI, and data decomposition was very important.
3.4. Forecasting performance of TFA-BiLSTM model
To evaluate the validity of the TFA-BiLSTM model, the performance of TFA-BiLSTM was compared with the other two proposed predictor models.
As shown in Fig. 2, the average MAE and RMSE of TFA-BiLSTM based models were 7.81 and 10.85, respectively, which were 27.62% and 26.54% lower than those of BP based models. Furthermore, the average R2 value of 0.94 for TFA-BiLSTM was much higher than BP (average R2 = 0.85). This indicated that the AQI prediction accuracy of the TFA-BiLSTM was obviously better than the BP based models. For the BiLSTM models, which also used memory units to deal with long-term dependence, a good level of R2 was achieved, with a value of 0.93. However, their average MAE (8.42) and RMSE (11.69) were both larger than those of TFA-BiLSTM, which suggested that BiLSTM coupled with added time filter layer and attention mechanism could improve the performance further. These results confirmed that the TFA-BiLSTM model could incorporate the merits of time filter layer, bidirectional LSTM layers and attention mechanism, and thus had lower AQI bias and stronger model robustness.
3.5. Forecasting results during the lockdown period of COVID-19
Due to the COVID-19 outbreak, China had ever been obliged to lockdown some cities and place restrictions on transportation, industry, and social activities, leading to a significant reduction of anthropogenic emissions, which would affect the air quality (Yumin et al., 2021). The four cities of this study have experienced the lockdown during the period of 1st Feb 2020–31 st Mar 2020. The forecasting accuracy of proposed models during the lockdown period was studied, with the prediction during the whole test period (October 2019 to October 2021) for comparison, and the results are shown in Fig. 5.
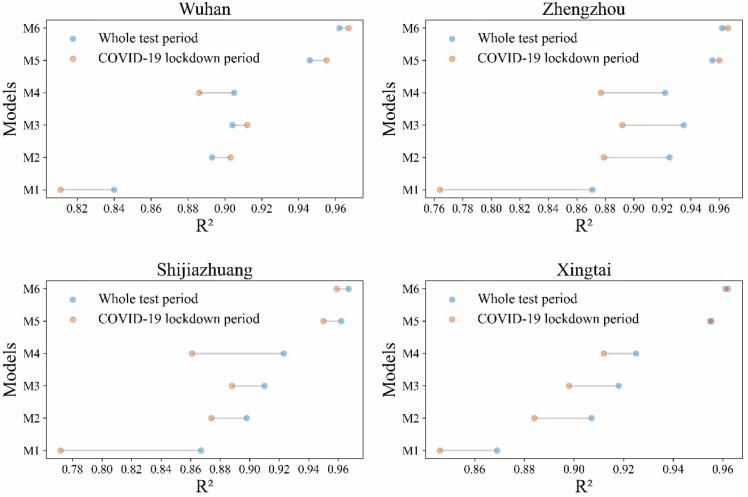
Fig. 5.
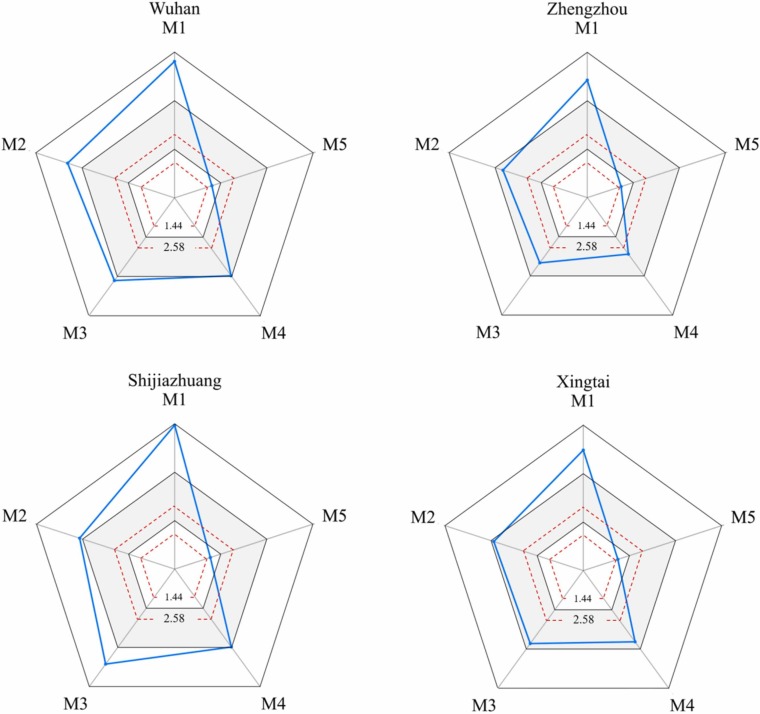
Comparison of models performance between the COVID-19 lockdown period and the whole test period. (M1: WOA-VMD-BP, M2: WOA-VMD-BiLSTM, M3: WOA-VMD-TFA-BiLSTM, M4: WOA-VMD-CEEMDAN-BP, 5: WOA-VMD-CEEMDAN -BiLSTM, M6: WOA-VMD-CEEMDAN-TFA-BiLSTM).
The R2 of AQI prediction models during the whole test period were in the range of 0.84–0.96, 0.87–0.96, 0.86–0.96 and 0.87–0.96 for Wuhan, Zhengzhou, Shijiazhuang and Xingtai, respectively, with the respective average values of 0.91, 0.95, 0.92 and 0.93. In comparison, the corresponding R2 values during COVID-19 lockdown period was 0.81–0,96, 0.76–0.96, 0.77–0.94 and 0.84–0.96, and the corresponding average values were 0.89, 0.89, 0.88 and 0.88, respectively. Unexpected events were usually assumed to have an effect on the predictive performance of machine learning models (Hu et al., 2022), and results in this study suggested that the prediction accuracy during the COVID-19 lockdown period was lower than the whole test period.
As shown in Fig. 5, the predictive accuracy of BP-based models was significantly lower during the closed management period especially in Zhengzhou and Shijiazhuang. It indicated that the generalization ability of the BP was poor and could not fully capture the time characteristics in the sequence information that also proven by other reports (Dong and Zhang, 2021). It should be noted that the prediction accuracy of the BiLSTM and TFA-BiLSTM models with two-stage decomposition for the AQI data during the lockdown period was close to that during the whole test period.
No matter which benchmark model was used, the two-stage decomposition technique was always more helpful for the prediction accuracy of AQI than the single decomposition during the lockdown period. These results proved that the suggested quadratic decomposition algorithm could combine the benefits of VMD and CEEMDAN to create smoother subseries, and hence improving the accuracy and reliability of forecasting models. With the best coefficient of determination (R2) and superior AQI series prediction throughout the COVID-19 lockdown period, the hybrid WOA-VMD-CEEMDAN-TFA-BiLSTM model outperformed the other proposed models.
4. Discussion
4.1. Two-stage decomposition improves the forecasting accuracy
Previously, the machine learning models were trained directly using the original sequences (Suárez Sánchez et al., 2011, Yeganeh et al., 2012). In order to increase the prediction accuracy, recent studies tried to preprocess the original data before inputting into the model (Yang et al., 2020). In this study, the AQI prediction performance of all the three proposed models reached an acceptable level after single-stage (WOA-VMD) decomposition, with R2 values of 0.84–0.93 (Fig. 2). Yang et al. (2020) also found that the carbon prices prediction accuracy was improved by EMD decomposition for BiLSTM model, with a mean accuracy increase by 22.22%. In addition to reducing the prediction error, the decomposition approach also corrected the temporal lag generated by the original model, making it more accurate with a MAE decrease by 40.82% (Huang et al., 2021). Extensive reported results have proven that the decomposition of original data played an important role in facilitating machine learning.
In this study, although the WOA-VMD could effectively reduce the instability of the sequence and obtained acceptable accuracy for models, there were still many high-frequency components and substantial unpredictability in the VMD residual sequence, which required further processing. By using CEEMDAN to deconstruct the residual sequence further, more regular subsequences were extracted and time-series features concealed in the residual sequence could be mined. Consequently, the AQI prediction accuracy for the four cities by all the three machine learning models was increased, achieving higher R2 values of 0.91–0.97 (Fig. 2). Also, the predicted AQI values by models using two-stage decomposition were closer to the actual data (Fig. 4). These results reasonably confirmed that WOA-VMD-CEEMDAN could create smoother subseries and thus effectively improve the AQI forecasting accuracy.
4.2. Deep learning guarantees the forecasting reliability
As a comprehensive index reflecting the level of air quality, AQI is inextricably linked to historical concentrations and its data are represented in the time scale patterns. The subsequence obtained by decomposition contains much time information (Cao et al., 2019), so that traditional machine learning models may have limits in processing time series data. In this study, both BiLSTM-based and TFA-BiLSTM-based models could deal with the long-term dependence of data with distinct temporal characteristics utilizing memory units (Chen et al., 2021), and thus they performed much better than BP-based model, whether using WOA-VMD or WOA-VMD-CEEMDAN decomposition (Fig. 2).
Previous studies have shown that when processing data with time series features, BiLSTM outperforms unidirectional LSTM models (Sun et al., 2018). In addition, as a newly designed neural network layer, the time filter layer can assist in eliminating noise inputs, hence contributing to improved precision. Moreover, attention mechanism can put more emphasis on key input data while suppressing less important ones during weight computation. By introducing both forward and backward LSTM layers and coupling with the time filter layer and attention mechanism, the TFA-BiLSTM can preserve both past and future information while selectively paying attention to more important information. It has been proven to have great potential in the field of well measurement forecasting (Shan et al., 2021). In this study, TFA-BiLSTM-based models outperformed BiLSTM-based models with lower bias and higher accuracy (Fig. 2). Therefore, the hybrid model, which utilized TFA-BiLSTM as a predictor, demonstrated best performance, with a highest R2 of 0.97 combing with WOA-VMD-CEEMDAN. Compared to single decomposition-based models, the hybrid model improved the prediction accuracy by 34.71–49.65% in MAE and 32.82–48.07% in RMSE.
4.3. Sensitivity and scalability analysis
In order to evaluate the sensitivity and scalability of the proposed hybrid model (WOA-VMD-CEEMDAN-TFA-BiLSTM) for air quality prediction, a detailed analysis was conducted using various metrics. The sensitivity of each model to discrepancies between forecasted and actual values is demonstrated in Table S6 through the presentation of the corresponding IA values for each season. IA serves as an evaluative metric for quantifying the extent of forecasting discrepancies exhibited by each model. The resulting IA values range from 0 to 1, wherein 1 signifies a perfect alignment while 0 denotes a lack of concurrence. In essence, IA signifies the model's responsiveness to disparities between predicted and actual values. As revealed in Table S6, compared to other models, the proposed model achieved highest IA values close to 1 (average IA = 0.990). The IA values of the proposed model were relatively lower in winter compared to other seasons, but still higher than the winter values of other models. The TFA-BiLSTM-based model had higher IA values than the other two predictors in all seasons from the perspective of the model structure. Additionally, the dual-stage decomposition based models generally had higher IA values compared to the single-stage decomposition models. Winter was the most challenging season for all models as they had lower IA values, reflecting the difficulty in capturing AQI changes during this season. In contrast, most models achieved larger IA values in summer due to the more stable air quality, allowing for better prediction with less fluctuation (Zhang and Gong, 2018).
Furthermore, directional change (DC) was employed to assess the accuracy of the predicted direction of air quality changes. This criterion represents an additional measure employed to assess the predictive capabilities of the proposed model, offering valuable insights into the directionality of forecasted movements, including identification of turning points. A higher value of DC indicates superior performance, thereby designating the model as the most optimal choice for achieving accurate forecasts. DC analysis is particularly useful when the direction of change is more important than the magnitude of the predicted and actual values, such as in air quality forecasting. As shown in Table S7, the proposed model outperformed other models in terms of DC, indicating that the proposed model was able to capture credible turning points or movements in the forecast results. Take Wuhan as an example, the proposed model achieved a DC value of 98.991, with an improvement of up to 85.59% compared to other methods. These higher DC values can be interpreted as more credible forecast results. The obtained results provided evidence that the proposed model was suitable for forecasting air quality changes and could be applied in practical applications. In addition, the scalability of the proposed model was explored by modifying the size of both the training and test sets, and by comparing the model's performance pre- and post-adjustment. Table S8 demonstrates that the predictive capabilities of the proposed model remained relatively consistent when the training and test set sizes varied within a reasonable range. The observed fluctuations in the R2 values were within a 2% threshold, indicating the proposed method exhibits robust scalability.
4.4. The outbreak of COVID-19 influences the model performance
4.4.1. The impact effect of COVID-19 lockdown on air quality
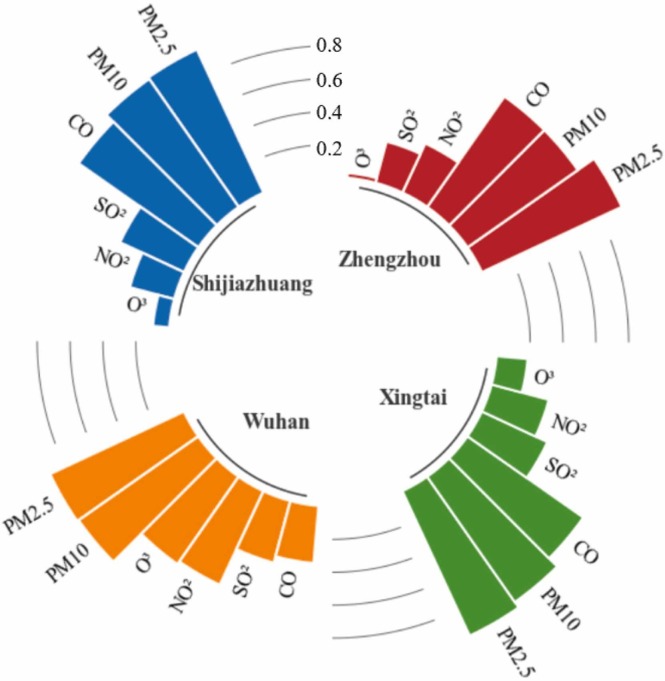
The values of AQI and six relevant pollutants (PM2.5, PM10, SO2, NO2, O3 and CO) during the COVID-19 lockdown period in the four cities were used to analyze the impact effect of COVID-19 on air quality. The correlation coefficient between AQI and air pollutant factors in the study areas was shown in Fig. 6 and the detailed heat map was shown in Fig.S4. The top three correlation corresponding features were used to analyze the impact on AQI. The absolute value of correlation coefficient of 0.8–1.0 was considered as very strong (Wuensch and Evans, 1996). As shown in Fig. 6, the AQI values in the four cities were highly correlated with both PM2.5 and PM10, suggesting that these two pollutant factors have the greatest influence on the AQI values.
Fig. 6.
The correlation coefficients between AQI and air pollutant factors in the four cities in China.
The top three relevant pollutants during the COVID-19 lockdown period were compared with the data in the corresponding period with previous two years (Table S2). Close values of pollutants concentrations were observed in 2018 and 2019, when there were no COVID-19 outbreaks. The concentration of the PM2.5 in Wuhan, Zhengzhou, Shijiazhuang and Xingtai during the COVID-19 lockdown period decreased by 36.55%, 35.01%, 31.97% and 39.62% in average, and PM10 averagely decreased by 40.01%, 27.57%, 34.09% and 38.88%, respectively. These two kinds of air particulate matters (PM) are considered to be one of the most frequent and vital components of air pollution, which mainly come from industrial production, combustion of fossil raw materials (automobile exhaust, thermal power generation, coal combustion) and the dust from urban infrastructure (Zhao et al., 2021). During the COVID-19 lockdown period, traffic control, industrial unnecessary production and infrastructure construction stopped, resulting in a significant decrease in air pollutants emission and thus the lower pollutant index levels.
In addition, there was a high degree of correlation between CO and AQI in Zhengzhou, Shijiazhuang and Xingtai, where the CO concentration decreased by 26.11%, 18.83% and 18.41% in average, respectively. The CO mainly comes from incomplete combustion of fossil fuel and automobile exhaust (Yumin et al., 2021). During the period of city lockdown, it was winter in the northern area, and the three cities have central heating. Compared with PM, the lower decline percentage of CO might be due to the fuel combustion for central heating. The heat map of the correlation coefficient (Fig.S4) showed that CO had a high correlation with PM, indicating that part of their change source was consistent, which was likely to be vehicle exhaust emissions. Therefore, it was speculated that the decrease of CO level during the lockdown period might be due to the less vehicles travelling, which was also mentioned in other reports (Yang et al., 2022).
It should be noted that the third correlation corresponding factor with AQI in Wuhan was O3. Although air pollutants such as PM2.5, PM10 and CO, decreased during the epidemic, the O3 concentration showed an upward trend with an increase by 24.29% in average. Further analysis showed that NO2 in Wuhan decreased by 51.2% over the same period in the previous two year. It was reported that the reduction of NO2 concentration would weaken the titration effect of nitrogen oxides so as to reduce the consumption of O3, resulting in the increase of O3 (Sicard et al., 2020). Ordóñez et al. (2020) analyzed the O3 change during the COVID-19 lockdown period in Europe and found that the O3 increase were dominated by the meteorology. Compared with the corresponding period in previous years, the precipitation in Wuhan decreased by 31% and the sunshine duration increased by over 100% during the lockdown period, which promoted photochemical synthesis and O3 buildup. The above-discussed reasons might lead to the magnification of local O3 pollution during the COVID-19 lockdown period.
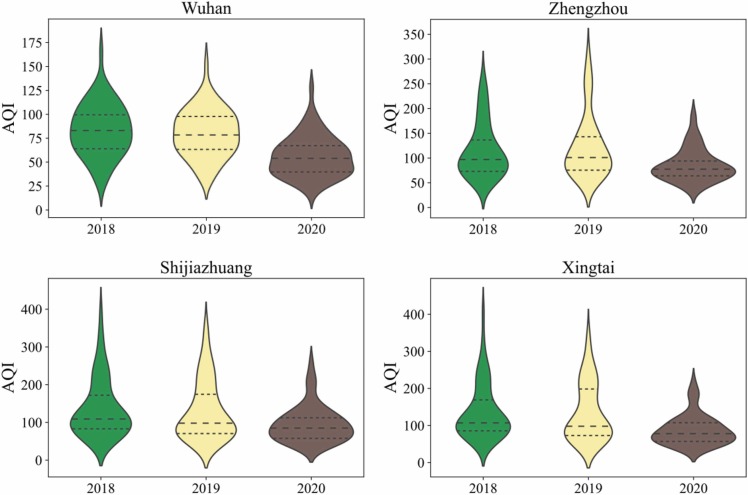
With the changes of relevant pollutants discussed above, the AQI values varied during the lockdown period accordingly. Fig. 7 showed the AQI data distribution during the COVID-19 lockdown period and the corresponding periods in previous two years, and the average value and CV were summarized in Table S3. The AQI in Wuhan, Zhengzhou, Shijiazhuang and Xingtai during lockdown days averagely decreased by 31.76%, 26.66%, 25.71% and 33.95%, respectively. Also, the CV of AQI values in these four cities decreased by 16.58%, 41.06%, 24.96% and 20.37%, respectively, suggesting the degree of dispersion for AQI data decreased. These findings indicated that the COVID-19 lockdown had an obvious impact effect on air quality considering the apparent decrease in AQI value and its dispersion degree.
Fig. 7.
AQI data distribution during the COVID-19 lockdown period in 2020 and the corresponding periods in previous two years (the line inside the violins represents quartile.).
4.4.2. The hybrid model outperforms other proposed models during the COVID-19 lockdown period
The impact effect of the COVID-19 lockdown on the air quality resulted in a different AQI data distribution from the other periods without epidemic, which led to the differences in AQI prediction accuracy during COVID-19 (Fig. 5). As discussed above, the hybrid model, WOA-VMD-CEEMDAN-TFA-BiLSTM, had highest prediction accuracy during both the whole test period and COVID-19 lockdown period. In order to further analyze the effectiveness of the hybrid model in the face of the impact effect of the epidemic, the HLN test was employed to discuss its superiority over other proposed models. Fig. 8 showed the results of the HLN test using mean absolute percent error function for the four study cities. Notably, the results of HLN test between the hybrid model and all the proposed comparison models were greater than 2.58, except the WOA-VMD-CEEMDAN-BiLSTM (1.51–1.66), indicating that the hybrid model was significantly superior to the WOA-VMD-CEEMDAN-BiLSTM under the confidence level of over 85% and significantly outperforms other proposed models under the 99% confidence level. Therefore, the proposed hybrid model had the most satisfactory performance, which further verified that it had obvious superiority for AQI prediction during the lockdown period.
Fig. 8.
HLN test results of predicted AQI values during COVID-19 lockdown period for the four cities in China. ( = 2.58, = 1.44, M1: WOA-VMD-BP, M2: WOA-VMD-LSTM, M3: WOA-VMD-TFA-BiLSTM, M4: WOA-VMD-CEEMDAN-BP, M5: WOA-VMD-CEEMDAN-BiLSTM).
5. Conclusions
A hybrid model was developed to obtain the accurate and reliable prediction of air quality based on AQI data of four study cities. The two-stage decomposition was employed for time series data preprocessing, using WOA-VMD to generate subsequences and CEEMDAN to further decomposing the residual sequence. Results demonstrated that compared to the single decomposition, the two-stage decomposition approach was capable of efficiently extracting temporal characteristic information and improving the prediction accuracy and stability. The TFA-BiLSTM based model outperformed other neural networks with higher forecasting reliability. Combing two-stage decomposition and TFA-BiLSTM, the hybrid WOA-VMD-CEEMDAN-TFA-BiLSTM model achieved best performance for AQI prediction.
Since all of the four study cities experienced COVID-19 lockdown in 2020, the impact effect of lockdown on the air quality in study cities was analyzed. Among the air pollution factors with high correlation with AQI, the air particulate matters (PM2.5, PM10) and CO concentration decreased significantly during the COVID-19 lockdown period, while O3 concentration increased. Also, both AQI data and its dispersion degree decreased during this period. According to HLN test, it was verified that the hybrid model had obvious superiority over other proposed models for AQI prediction in the face of the impact effect of the COVID-19 lockdown.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
The authors appreciate the supports from the Major Science and Technology Program for Water Pollution Control and Treatment, China (Project No. 2017ZX07106004).
Footnotes
Supplementary data associated with this article can be found in the online version at doi:10.1016/j.psep.2023.06.021.
Appendix A. Supplementary material
Supplementary material
.
References
- Al-qaness M.A.A., Fan H., Ewees A.A., Yousri D., Abd Elaziz M. Improved ANFIS model for forecasting Wuhan City Air Quality and analysis COVID-19 lockdown impacts on air quality. Environ. Res. 2021;194 doi: 10.1016/j.envres.2020.110607. [DOI] [PubMed] [Google Scholar]
- Berber E., Sumbria D., Çanakoğlu N. Meta-analysis and comprehensive study of coronavirus outbreaks: SARS, MERS and COVID-19. J. Infect. Public Health. 2021;14:1051–1064. doi: 10.1016/j.jiph.2021.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao J., Li Z., Li J. Financial time series forecasting model based on CEEMDAN and LSTM. Phys. A Stat. Mech. its Appl. 2019;519:127–139. doi: 10.1016/j.physa.2018.11.061. [DOI] [Google Scholar]
- Chen Y., Dong Z., Wang Y., Su J., Han Z., Zhou D., Zhang K., Zhao Y., Bao Y. Short-term wind speed predicting framework based on EEMD-GA-LSTM method under large scaled wind history. Energy Convers. Manag. 2021;227 doi: 10.1016/j.enconman.2020.113559. [DOI] [Google Scholar]
- Cheng H., Ding X., Zhou W., Ding R. A hybrid electricity price forecasting model with Bayesian optimization for German energy exchange. Int. J. Electr. Power Energy Syst. 2019;110:653–666. doi: 10.1016/j.ijepes.2019.03.056. [DOI] [Google Scholar]
- Díaz-Robles L.A., Ortega J.C., Fu J.S., Reed G.D., Chow J.C., Watson J.G., Moncada-Herrera J.A. A hybrid ARIMA and artificial neural networks model to forecast particulate matter in urban areas: The case of Temuco, Chile. Atmos. Environ. 2008;42:8331–8340. doi: 10.1016/j.atmosenv.2008.07.020. [DOI] [Google Scholar]
- Dong L., Zhang J. Predicting polycyclic aromatic hydrocarbons in surface water by a multiscale feature extraction-based deep learning approach. Sci. Total Environ. 2021;799 doi: 10.1016/j.scitotenv.2021.149509. [DOI] [PubMed] [Google Scholar]
- Dragomiretskiy K., Zosso D. Variational mode decomposition. IEEE Trans. Signal Process. 2014;62:531–544. doi: 10.1109/TSP.2013.2288675. [DOI] [Google Scholar]
- Fijani E., Barzegar R., Deo R., Tziritis E., Konstantinos S. Design and implementation of a hybrid model based on two-layer decomposition method coupled with extreme learning machines to support real-time environmental monitoring of water quality parameters. Sci. Total Environ. 2019;648:839–853. doi: 10.1016/j.scitotenv.2018.08.221. [DOI] [PubMed] [Google Scholar]
- Gao B., Huang X., Shi J., Tai Y., Zhang J. Hourly forecasting of solar irradiance based on CEEMDAN and multi-strategy CNN-LSTM neural networks. Renew. Energy. 2020;162:1665–1683. doi: 10.1016/j.renene.2020.09.141. [DOI] [Google Scholar]
- González-Pardo J., Ceballos-Santos S., Manzanas R., Santibáñez M., Fernández-Olmo I. Estimating changes in air pollutant levels due to COVID-19 lockdown measures based on a business-as-usual prediction scenario using data mining models: A case-study for urban traffic sites in Spain. Sci. Total Environ. 2022;823 doi: 10.1016/j.scitotenv.2022.153786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graves A., Schmidhuber J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005;18:602–610. doi: 10.1016/j.neunet.2005.06.042. [DOI] [PubMed] [Google Scholar]
- Harvey D., Leybourne S., Newbold P. Testing the equality of prediction mean squared errors. Int. J. Forecast. 1997;13:281–291. doi: 10.1016/S0169-2070(96)00719-4. [DOI] [Google Scholar]
- Heidari A., Khovalyg D. Short-term energy use prediction of solar-assisted water heating system: Application case of combined attention-based LSTM and time-series decomposition. Sol. Energy. 2020;207:626–639. doi: 10.1016/j.solener.2020.07.008. [DOI] [Google Scholar]
- Hochreiter S., Schmidhuber J. Long short-term memory. Neural Comput. 1997;9:1735–1780. doi: 10.1162/neco.1997.9.8.1735. [DOI] [PubMed] [Google Scholar]
- Hu C., Zhang J., Yuan H., Gao T., Jiang H., Yan J., Wenzhong Gao D., Wang F.Y. Black swan event small-sample transfer learning (BEST-L) and its case study on electrical power prediction in COVID-19. Appl. Energy. 2022;309 doi: 10.1016/j.apenergy.2021.118458. [DOI] [Google Scholar]
- Huang G., Li X., Zhang B., Ren J. PM2.5 concentration forecasting at surface monitoring sites using GRU neural network based on empirical mode decomposition. Sci. Total Environ. 2021;768 doi: 10.1016/j.scitotenv.2020.144516. [DOI] [PubMed] [Google Scholar]
- Janarthanan R., Partheeban P., Somasundaram K., Navin Elamparithi P. A deep learning approach for prediction of air quality index in a metropolitan city. Sustain. Cities Soc. 2021;67 doi: 10.1016/j.scs.2021.102720. [DOI] [Google Scholar]
- Lin J., Ma J., Zhu J., Cui Y. Short-term load forecasting based on LSTM networks considering attention mechanism. Int. J. Electr. Power Energy Syst. 2022;137 doi: 10.1016/j.ijepes.2021.107818. [DOI] [Google Scholar]
- Liu H., Chen C. Multi-objective data-ensemble wind speed forecasting model with stacked sparse autoencoder and adaptive decomposition-based error correction. Appl. Energy. 2019;254 doi: 10.1016/j.apenergy.2019.113686. [DOI] [Google Scholar]
- Ma J., Li Z., Cheng J.C.P., Ding Y., Lin C., Xu Z. Air quality prediction at new stations using spatially transferred bi-directional long short-term memory network. Sci. Total Environ. 2020;705 doi: 10.1016/j.scitotenv.2019.135771. [DOI] [PubMed] [Google Scholar]
- Mirjalili S., Lewis A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016;95:51–67. doi: 10.1016/j.advengsoft.2016.01.008. [DOI] [Google Scholar]
- Ordóñez C., Garrido-Perez J.M., García-Herrera R. Early spring near-surface ozone in Europe during the COVID-19 shutdown: Meteorological effects outweigh emission changes. Sci. Total Environ. 2020;747 doi: 10.1016/j.scitotenv.2020.141322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng T., Zhang C., Zhou J., Nazir M.S. An integrated framework of Bi-directional long-short term memory (BiLSTM) based on sine cosine algorithm for hourly solar radiation forecasting. Energy. 2021;221 doi: 10.1016/j.energy.2021.119887. [DOI] [Google Scholar]
- Ravindra K., Singh T., Vardhan S., Shrivastava A., Singh S., Kumar P., Mor S. COVID-19 pandemic: What can we learn for better air quality and human health? J. Infect. Public Health. 2022;15:187–198. doi: 10.1016/j.jiph.2021.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saeed A., Li C., Danish M., Rubaiee S., Tang G., Gan Z., Ahmed A. Hybrid bidirectional lstm model for short-term wind speed interval prediction. IEEE Access. 2020;8:182283–182294. doi: 10.1109/ACCESS.2020.3027977. [DOI] [Google Scholar]
- Shan L., Liu Y., Tang M., Yang M., Bai X. CNN-BiLSTM hybrid neural networks with attention mechanism for well log prediction. J. Pet. Sci. Eng. 2021;205 doi: 10.1016/j.petrol.2021.108838. [DOI] [Google Scholar]
- Shi G., Qin C., Tao J., Liu C. A VMD-EWT-LSTM-based multi-step prediction approach for shield tunneling machine cutterhead torque. Knowl. -Based Syst. 2021;228 doi: 10.1016/j.knosys.2021.107213. [DOI] [Google Scholar]
- Sicard P., De Marco A., Agathokleous E., Feng Z., Xu X., Paoletti E., Rodriguez J.J.D., Calatayud V. Amplified ozone pollution in cities during the COVID-19 lockdown. Sci. Total Environ. 2020;735 doi: 10.1016/j.scitotenv.2020.139542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singla P., Duhan M., Saroha S. A dual decomposition with error correction strategy based improved hybrid deep learning model to forecast solar irradiance. Energy Sources, Part A: Recovery, Util., Environ. Eff. 2022;44(1):1583–1607. [Google Scholar]
- Singla P., Duhan M., Saroha S. A hybrid solar irradiance forecasting using full wavelet packet decomposition and bi-directional long short-term memory (BiLSTM) Arab. J. Sci. Eng. 2022;47(11):14185–14211. [Google Scholar]
- Singla P., Duhan M., Saroha S. An ensemble method to forecast 24-h ahead solar irradiance using wavelet decomposition and BiLSTM deep learning network. Earth Sci. Inform. 2022;15(1):291–306. doi: 10.1007/s12145-021-00723-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suárez Sánchez A., García Nieto P.J., Riesgo Fernández P., del Coz Díaz J.J., Iglesias-Rodríguez F.J. Application of an SVM-based regression model to the air quality study at local scale in the Avilés urban area (Spain) Math. Comput. Model. 2011;54:1453–1466. doi: 10.1016/j.mcm.2011.04.017. [DOI] [Google Scholar]
- Sun Q., Jankovic M.V., Bally L., Mougiakakou S.G. Predicting Blood Glucose with an LSTM and Bi-LSTM Based Deep Neural Network. 2018 14th Symp. Neural Netw. Appl. NEUREL. 2018;2018:12–16. doi: 10.1109/NEUREL.2018.8586990. [DOI] [Google Scholar]
- Torres M.E., Colominas M.A., Schlotthauer G., Flandrin P. A complete ensemble empirical mode decomposition with adaptive noise. ICASSP, IEEE Int. Conf. Acoust. Speech Signal Process. - Proc. 2011:4144–4147. doi: 10.1109/ICASSP.2011.5947265. [DOI] [Google Scholar]
- Wu Q., Lin H. A novel optimal-hybrid model for daily air quality index prediction considering air pollutant factors. Sci. Total Environ. 2019;683:808–821. doi: 10.1016/j.scitotenv.2019.05.288. [DOI] [PubMed] [Google Scholar]
- Wuensch K., Evans J. Straightforward Statistics for the Behavioral Sciences. J. Am. Stat. Assoc. 1996;91:1750. doi: 10.2307/2291607. [DOI] [Google Scholar]
- Yang M., Chen L., Msigwa G., Tang K.H.D., Yap P.S. Implications of COVID-19 on global environmental pollution and carbon emissions with strategies for sustainability in the COVID-19 era. Sci. Total Environ. 2022;809 doi: 10.1016/j.scitotenv.2021.151657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang S., Chen D., Li S., Wang W. Carbon price forecasting based on modified ensemble empirical mode decomposition and long short-term memory optimized by improved whale optimization algorithm. Sci. Total Environ. 2020;716 doi: 10.1016/j.scitotenv.2020.137117. [DOI] [PubMed] [Google Scholar]
- Yeganeh B., Motlagh M.S.P., Rashidi Y., Kamalan H. Prediction of CO concentrations based on a hybrid Partial Least Square and Support Vector Machine model. Atmos. Environ. 2012;55:357–365. doi: 10.1016/j.atmosenv.2012.02.092. [DOI] [Google Scholar]
- Yoon N., Kim J., Lim J.L., Abbas A., Jeong K., Cho K.H. Dual-stage attention-based LSTM for simulating performance of brackish water treatment plant. Desalination. 2021;512 doi: 10.1016/j.desal.2021.115107. [DOI] [Google Scholar]
- Yumin L., Shiyuan L., Ling H., Ziyi L., Yonghui Z., Li L., Yangjun W., Kangjuan L. The casual effects of COVID-19 lockdown on air quality and short-term health impacts in China. Environ. Pollut. 2021;290 doi: 10.1016/j.envpol.2021.117988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X., Gong Z. Spatiotemporal characteristics of urban air quality in China and geographic detection of their determinants. J. Geogr. Sci. 2018;28:563–578. [Google Scholar]
- Zhao X., Wang G., Wang S., Zhao N., Zhang M., Yue W. Impacts of COVID-19 on air quality in mid-eastern China: An insight into meteorology and emissions. Atmos. Environ. 2021;266 doi: 10.1016/j.atmosenv.2021.118750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou X., Li Y., Jiang L., Zhou L. Fault feature extraction for rolling bearings based on parameter-adaptive variational mode decomposition and multi-point optimal minimum entropy deconvolution. Meas. J. Int. Meas. Confed. 2021;173 doi: 10.1016/j.measurement.2020.108469. [DOI] [Google Scholar]
- Zhou Y., Chang F.J., Chang L.C., Kao I.F., Wang Y.S. Explore a deep learning multi-output neural network for regional multi-step-ahead air quality forecasts. J. Clean. Prod. 2019;209:134–145. doi: 10.1016/j.jclepro.2018.10.243. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material