Generalizing deep learning brain segmentation for skull removal and intracranial measurements

Abstract

Total intracranial volume (TICV) and posterior fossa volume (PFV) are essential covariates for brain volumetric analyses with structural magnetic resonance imaging (MRI). Detailed whole brain segmentation provides a noninvasive way to measure brain regions. Furthermore, increasing neuroimaging data are distributed in a skull-stripped manner for privacy protection. Therefore, generalizing deep learning brain segmentation for skull removal and intracranial measurements is an appealing task. However, data availability is challenging due to a limited set of manually traced atlases with whole brain and TICV/PFV labels. In this paper, we employ U-Net tiles to achieve automatic TICV estimation and whole brain segmentation simultaneously on brains w/and w/o the skull. To overcome the scarcity of manually traced whole brain volumes, a transfer learning method is introduced to estimate additional TICV and PFV labels during whole brain segmentation in T1-weighted MRI. Specifically, U-Net tiles are first pre-trained using large-scale BrainCOLOR atlases without TICV and PFV labels, which are created by multi-atlas segmentation. Then the pre-trained models are refined by training the additional TICV and PFV labels using limited BrainCOLOR atlases. We also extend our method to handle skull-stripped brain MR images. From the results, our method provides promising whole brain segmentation and volume estimation results for both brains w/and w/o skull in terms of mean Dice similarity coefficients and mean surface distance and absolute volume similarity. This method has been made available in open source (https://github.com/MASILab/SLANTbrainSeg_skullstripped).

1. Introduction

Whole brain segmentation from structural magnetic resonance imaging (MRI) is essential in understanding the human brain with quantitative volumetry. TICV is the total volume of gray matter, white matter and cerebrospinal fluid (CSF) and meninges [1], which has been widely used as a covariate in regional and whole brain volumetric analyses [2–8]. The PFV is essential in investigating the clinical conditions of the cerebellum [9–11]. Therefore, achieving TICV and PFV estimation and whole brain segmentation in a single pipeline would be an interesting topic. Furthermore, for privacy protection, the skull is increasingly removed in neuroimaging data. Hence, it is also appealing to design a pipeline for skull-stripped brains.

The manual delineation of the cranial vault and brain sub-regions is the gold standard for measuring volume. However, manual delineation of large-scale cohorts is computationally demanding. Atlas-based segmentation is one of the most popular segmentation approaches due to high accuracy [12–14]. This technique propagates labels from atlases to a previously unseen image using deformation field. However, atlas-based segmentation is a highly time-consuming task that limits its application to large-scale cohorts [12,15]. To achieve more efficient segmentation and to utilize the large-scale cohorts, deep learning-based brain segmentation methods have been widely developed [16–26]. One common way to address whole brain segmentation is to label all brain structures with a 3D segmentation network, for example, 3D U-Net [16] or V-Net [17]. However, a full-resolution whole brain segmentation with over 100 labels is still challenging due to hardware constraints and limited availability in training data. Huo et al., overcame this limitation by proposing a tile-based method called 3D spatially localized atlas network tiles (SLANT), which segmented T1-weighted brain MRIs into 132 sub-regions [27]. To avoid GPU memory restriction, SLANT used 3D subspaces with separate U-Nets to predict individual tiles. Huo et al. also used 5111 multi-site scans as auxiliary data to pre-train each U-Net [27]. Although many previous works could handle whole brain segmentation task [19,21,22,25], they mainly focus on brain segmentation without estimating TICV and PFV.

In terms of TICV estimation, one type of approaches directly uses skull-stripping techniques for TICV estimation, by taking the total volume of the CSF and brain tissues as TICV. For example, the brain extraction tool (BET) and the brain surface extractor (BSE) achieved accurate TICV estimation using proton density (PD) images [28]. However, in some modalities, the low contrast between CSF and skull (such as in T1-weighted images) might result in less accurate TICV estimation. Some previous efforts have been made to address this problem [29–38]. Among them, three popular methods are integrated in FreeSurfer [39], FSL [38] and Statistical Parametric Mapping (SPM12) [40], which are well validated and widely accepted TICV estimation software packages. However, they do not estimate TICV by directly segmenting the intracranial cavity and counting the voxels inside skull, which is a natural way of calculating TICV. Therefore, they might not be applied to skull-stripped brains and estimate PFV. Recently, Huo et al. proposed a non-local spatial STAPLE label fusion (NLSS)-based simultaneous TICV and PFV estimation method from a single MR T1w image [41]. In their work, TICV and PFV labels are added to the widely used BrainCOLOR atlases [42,43]. However, their methods mainly focus on volume estimation without whole brain segmentation.

In this work, we generalize deep learning brain segmentation for skull removal and intracranial volume measurements. The proposed method uses the modified BrainCOLOR atlases with manually traced whole brain as well as TICV and PFV labels from [41] as the training data. However, the number of modified BrainCOLOR atlases is limited for deep learning. With the limited data, directly training a 3D deep learning network for whole brain segmentation with TICV and PFV labels is difficult. To overcome this problem, a transfer learning-based method is introduced to estimate TICV and PFV during whole brain segmentation in this work. Specifically, we use 5111 auxiliary scans with only whole brain labels to pre-train the U-Net tiles. After pre-training, we get reasonable model parameters for whole brain segmentation. Then we add two additional output channels for TICV and PFV labels to the pre-trained tiles and use the modified BrainCOLOR atlases to fine-tune the pre-trained networks. The main contributions of this work are: (1) To our knowledge, this is a relatively new work to achieve TICV and PFV estimation during whole brain segmentation with over 100 labels in a single pipeline. (2) We generalize the whole brain segmentation as well as TICV and PFV estimation on both skull-stripped and non-skull-stripped brains.

2. Methods

In this section, we present a new pipeline that generalizes SLANT [27] for intracranial volume measurements. Here, we combined whole brain segmentation and TICV estimation together in a single pipeline for both skull-stripped and non-skull-stripped brains. We proposed two versions of SLANT in this section, which are non-skull-stripped SLANT (nssSLANT) and skull-stripped SLANT (ssSLANT). The detailed procedures of ssSLANT and nssSLANT are introduced in this section. In Section 2.1, we introduce the preprocessing including registration to MNI305 space, N4 bias field correction, intensity normalization and skull-stripping method. In Section 2.2, we introduce the details of U-Net tiles and transfer learning procedure proposed in this work. Section 2.3 gives the description of majority voting and inverse registration of segmentation from MNI305 space to target space.

2.1. Preprocessing and Skull-stripping

The input of our pipeline is a single 3D T1w MRI whose dimensions might be variable. Therefore, the first step in our method is an affine registration from the target image to the MNI305 template [44] using NiftyReg [45]. Then, an N4 bias field correction [46] is performed to alleviate the bias from the imaging procedure. Since the intensities of acquired scans varies across different scanners, intensity normalization is introduced to reduce the effect caused by various intensities across different scans as in [27]. Moreover, we generalize the original SLANT to skull removal brains by including skull-stripping procedure. To remove skull, we first inflated the whole brain label as a brain mask and then multiplied the raw T1 image with its corresponding mask. After multiplication, the skull is filtered out. The whole skull-stripping procedure is shown in Fig. 1. In nssSLANT and ssSLANT, the preprocessing procedure is the same, except for the skull removal step. In nssSLANT, skull-stripping step is not required.

Fig. 1.

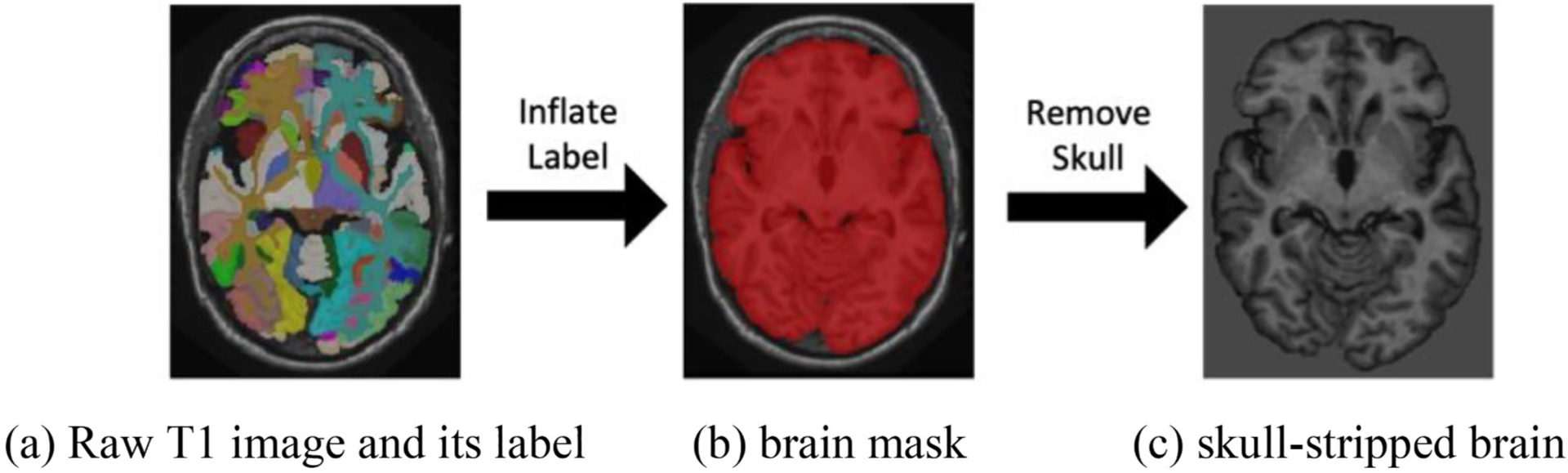
The whole procedure of skull-stripping. (a) The raw T1 image and its corresponding manually traced label image. (b) The brain mask is obtained by inflating the label image. (c) The skull-stripped image is obtained by multiplying brain mask with raw T1 image.

2.2. U-Net-based segmentation with transfer learning

After the preprocessing step, both skull-stripped and non-skull-stripped brain volumes are mapped to MNI305 space, which has 172 × 220 × 156 voxels with 1 mm isotropic resolution. We then trained UNet with the preprocessed brain volumes. Due to limited memory capacity of GPU, U-Net tiles were trained similarly as SLANT. In [27], the authors show that 27 tiles lead to better results compared with 8 overlapped tiles. Hence, in our pipeline, the entire images are divided into 27 overlapped subspaces. Let j, (j = 1,…,27) denotes the indices of subspaces and P_j denotes the jth subspace with the size of (d_x,d_y,d_z). The corner coordinate of each tile is denoted as (x_j,y_j,z_j). Therefore, the jth tile is denoted as P_j = [x_j : (x_j+d_x),y_j : (y_j+d_y),z_j : (z_j+d_z)]. In this paper, each subspace covered 96 × 128 × 88 voxels and we trained 27 U-Net tiles for 27 subspaces respectively.

Our goal is to estimate TICV and PFV during whole brain segmentation. However, forty-five modified BrainCOLOR atlases with TICV and PFV labels are available, which is limited. In order to enhance the segmentation capability with limited data, we introduce transfer learning into our pipeline. The whole procedure of transfer learning is shown in Fig. 2. We have pre-training and fine-tuning stage for segmentation. Note that, Fig. 2 only shows the procedure of ssSLANT. In terms of nssSLANT, the skull-stripping step is excluded. Meanwhile, the remainder procedure is the same.

Fig. 2.

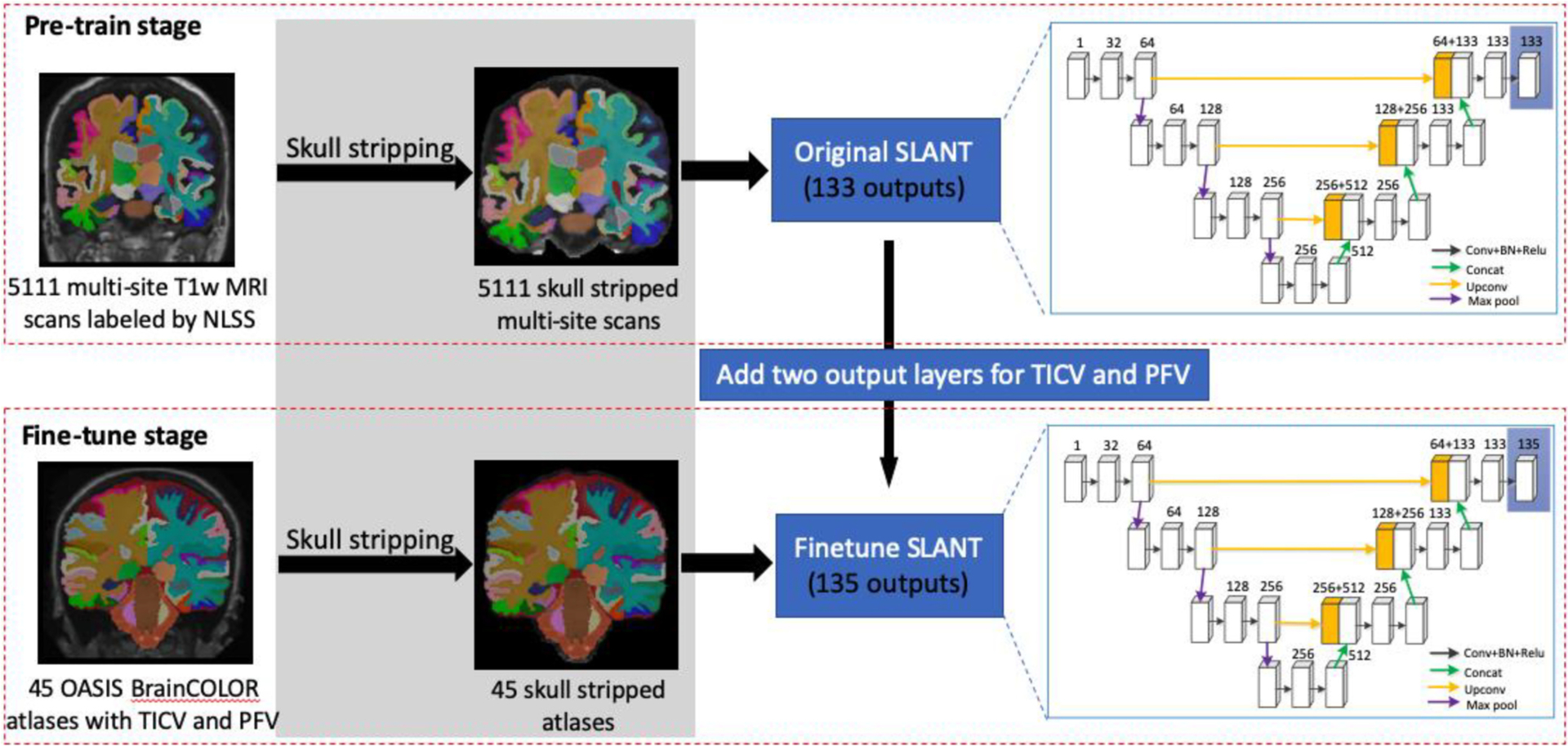
The whole procedure of transfer learning on ssSLANT (skull-stripped SLANT). The gray part (skull-stripping step) is excluded in nssSLANT. In the pre-training stage, the original SLANT is trained on 5111 skull-stripped brains with a whole brain labeling obtained from multi-atlas segmentation. Next, in order to achieve TICV and PFV estimation, additional two output layers are added to the original SLANT for TICV and PFV. The parameters of new added layers are randomly initialized. Then, OASIS BrainCOLOR atlases with TICV and PFV labels are used to fine-tune the pre-trained SLANT with 135 outputs (including background). The procedure of nssSLANT is the same, except for the skull-stripping step.

In the pre-training stage, we pre-trained each tile with 5111 auxiliary scans with 132 brain structure labels (no TICV and PFV labels). As in the original SLANT, the pre-training dataset with 5111 auxiliary scans is obtained using NLSS-based multi-atlas segmentation pipeline [47] on initially unlabeled MRIs. After pre-training, each network tile could segment the whole brain into 132 structures except for TICV and PFV. The original SLANT has 133 output channels which predict 132 brain structures and background individually. However, the 132 brain structures segmentation is not precise enough by using NLSS segmentation results as ground truth. In order to obtain more precise segmentation results of 132 structures as well as estimate TICV and PFV jointly, we transferred parameters in pre-trained U-Net tiles to new U-Net tiles with two additional output channels. Specifically, in addition to the original 132 output channels, we added two more output channels in the last layer for TICV and PFV prediction in our pipeline. The weights for these two channels were randomly initialized. The new SLANT in this paper could predict 132 brain structures as well as TICV and PFV.

In the fine-tuning stage, we refined parameters of each tile with modified BrainCOLOR atlases (132 brain structures with TICV and PFV labels). The fine-tuning dataset which consists of 45 modified BrainCOLOR atlases with TICV and PFV labels is obtained from [41]. In [41], TICV and PFV labels are added to the widely used BrainCOLOR atlases which consists of 45 T1-weighted (T1w) MRI scans from Open Access Series on Imaging Studies (OASIS) dataset [48] with BrainCOLOR labeling protocol [43]. The fine-tuning with modified BrainCOLOR atlases not only improved segmentation accuracy but also estimated TICV and PFV simultaneously. As shown in Fig. 2, during the fine-tuning stage, we added two additional output layers to U-Net and kept other parameters fixed. Network tiles were trained without freezing any layers. The parameters of new added layers were randomly initialized.

2.3. Majority voting

As mentioned above, segmentation was performed on 27 overlapped image subspaces using 27 U-Net tiles. In the overlapped region, each voxel has more than one label. In order to fuse h labels for a single voxel, majority voting was employed after U-Net-based segmentation in our pipeline. After majority vote, the final segmentation result of voxel i is given by

$$S_{MNI}(i)=\underset{l\in \{0,1,\dots ,L-1\}}{\text{argmax}}\frac{1}{h}\sum _{n=1}^{h}p\left(l\mid S_n,i\right)$$ (1)

where L is the total number of labels, and h denotes the total number of overlapped subspaces at voxel i. p(l|S_n, i) = 1 if S_n(i) = l, and 0, otherwise. In the majority voting, outliers in each subspace are reduced by label fusion. The final segmentation S_MNI is in the MNI space. An inverse transformation was employed to register segmentation result S_MNI in MNI305 space back to the original space.

3. Results

In this work, we extended the original SLANT to total intracranial and posterior fossa volume estimation. In this section, we show that the proposed ssSLANT and nssSLANT methods can estimate TICV and PFV promisingly in both skull-stripped and non-skull-stripped brains. Simultaneously, our methods can also achieve whole brain segmentation.

3.1. Data

The large-scale pre-training dataset contains 5111 MRI T1w 3D volumes, which is obtained from multiple sites. The 5111 MRIs are segmented into 132 ROIs by NLSS [47].

The fine-tuning dataset consists of 45 T1w MRIs from Open Access Series on Imaging Studies (OASIS) dataset [48]. Each T1w MRI in the fine-tuning dataset has 134 ROIs including 132 brain structures as well as TICV and PFV labels. The 132 brain structures are manually traced by the BrainCOLOR labeling protocol [43]. The TICV and PFV labels are added to BrainCOLOR protocol by Huo et al. [41].

3.2. Evaluation metrics

We mainly employed Dice similarity coefficients (DSC) (a ratio from 0 to 1, higher is better) to evaluate the performance of our methods in this work. DSC is calculated as the ratio between the intersection and union of the segmented volume H and ground truth volume G:

$$\mathit{\text{DSC}}=\frac{2|H\cap G|}{\left|H\right|+\left|G\right|}.$$ (2)

Distance measurements are complimentary metrics to evaluate the performance of our method. Specifically, we use M and A to denote the vertices on the manual segmentation and automatic segmentation. The mean surface distance (MSD) (a ratio larger than 0, lower is better) between M and A is:

$$\mathit{\text{MSD}}(M,A)=\underset{m\in Ma\in A}{\text{avg}inf}d(M,A)$$ (3)

where avg presents the average and inf presents the infimum. The above DSC and MSD are used to evaluate the segmentation accuracy. Besides the segmentation accuracy, in this work, we also aim at conducting volumetric analyses. In particular, we employed the absolute volume similarity (ASIM) (a ratio from −1 to 1, higher is better) to evaluate the volumetric similarity between the proposed method and the ground truth. ASIM is given by:

$$\mathit{\text{ASIM}}=1-\frac{\left|V_1-V_2\right|}{0.5\left(V_1+V_2\right)}$$ (4)

where V₁ and V₂ are the volume of manual segmentation and automatic segmentation, respectively. The differences between methods were evaluated by t-test using false discovery rate (FDR) [49] at q = 0.05 and the difference was significant means p < 0.05 in this paper.

3.3. Experimental settings

The performance and effectiveness of the original SLANT compared with several baselines are shown in [27]. In order to evaluate the performance of SLANT for skull-stripped brains and volume estimation, in this work, we compared the qualitative and quantitative performance of ssSLANT and nssSLANT on segmentation accuracy and volume estimation. After preprocessing for both pre-training and fine-tuning datasets, all brain volumes were mapped to the MNI 305 standard space. For each U-Net tile, the input resolution was 96 × 128 × 88 and the input channel was 1. The output channel was 133 in the pre-training stage and 135 in the fine-tuning stage. The optimizer was Adam and the learning rate was set to 0.0001. The experiments were performed on an NVIDIA Titan GPU with 12 GB memory. For pre-training using 5111 scans, the number of epochs was set to six and each epoch took four hours. As mentioned in [27], the best pre-training performance is from epoch 5. Therefore, we used the same initial parameters for fine-tuning. The fine-tuning epoch was set to 35 in this work. We reported the mean DSC, MSD and ASIM taken over five-fold cross-validation. The cross validation was performed on 45 modified BrainCOLOR atlases with TICV and PFV during the fine-tuning stage.

3.4. Whole brain segmentation

In this section, we evaluate the whole brain segmentation results of ssSLANT and nssSLANT. Qualitative results of whole brain segmentation with the sagittal, coronal and axial views are shown in Fig. 3. The proposed method achieves simultaneous brain structures, TICV and PFV labeling. Hence, in Fig. 3, we show both 132 brain structures, TICV and PFV labels simultaneously. Most details in the manual tracing are well preserved by ssSLANT and nssSLANT. The boundaries of the automatic segmentations are smooth. In order to inspect the segmentation for each ROI. Fig. 4 shows the comparison of the mean DSC across all folds for each ROI. The name of each ROI in BrainCOLOR protocol is listed in the table in the supplementary material. From Fig. 3 and Fig. 4, nssSLANT and ssSLANT show comparable performance on whole brain segmentation. After removing the skull, SLANT could still achieve promising whole brain segmentations. Table 1 shows the detailed median, mean and standard deviation of DSC and MSD. The mean values are computed across all folds and all ROIs. From Table 1 we can see that the ssSLANT and nssSLANT show comparable whole brain segmentation performance in terms of mean and median DSC and MSD. We conducted t-test using false discovery rate (FDR) [49] over all 132 ROIs at q = 0.05. No significant difference (p > 0.05) is observed between the two methods, which suggests that removing skull has no significant influence on segmentation results.

Fig. 3.

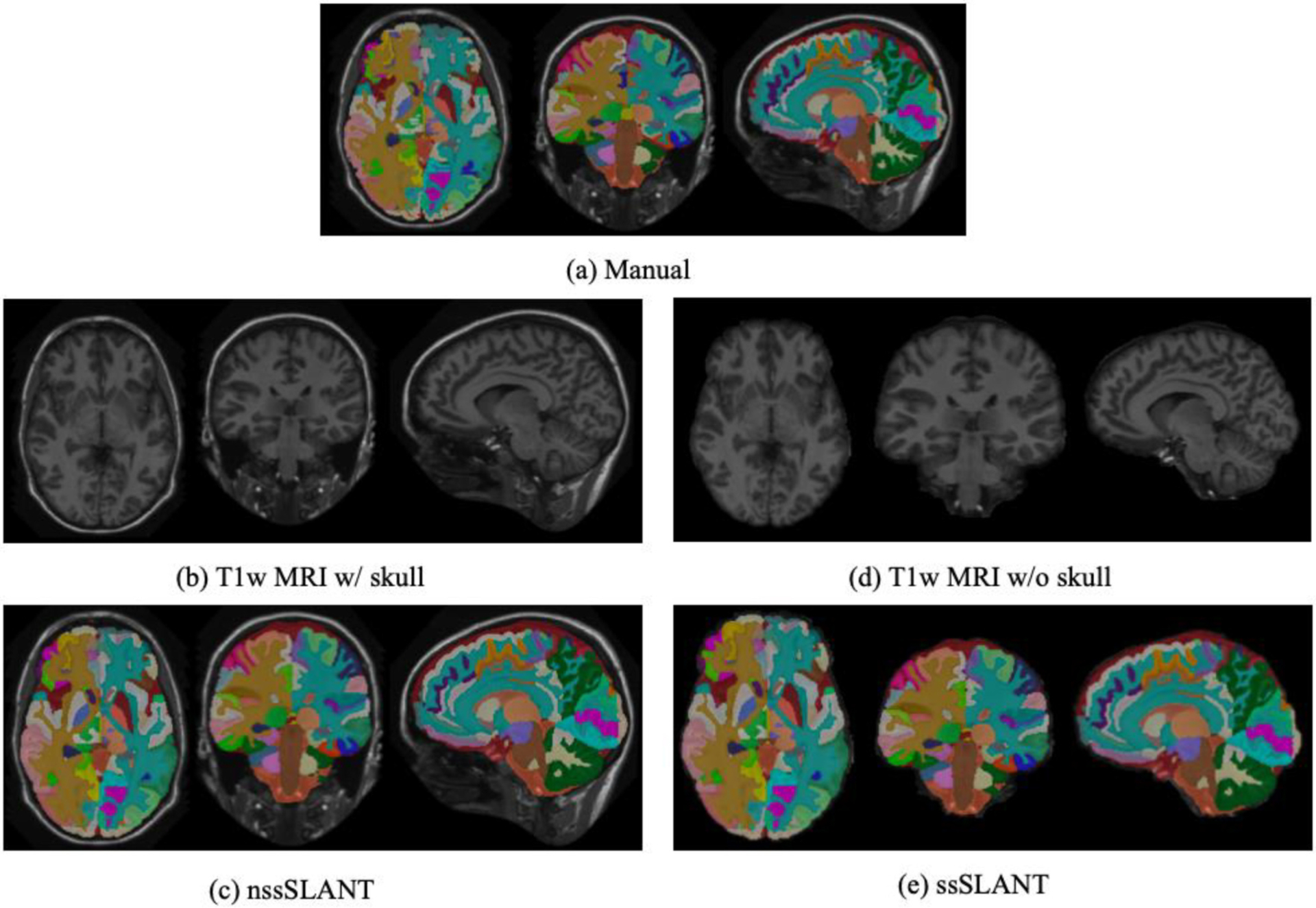
Qualitative results of nssSLANT and ssSLANT methods with three views for whole brain as well as TICV and PFV labels. Most details in the manual tracing are well preserved by ssSLANT and nssSLANT. The boundaries of the automatic segmentations are smooth. From (c) and (e), nssSLANT and ssSLANT show comparable performance.

Fig. 4.

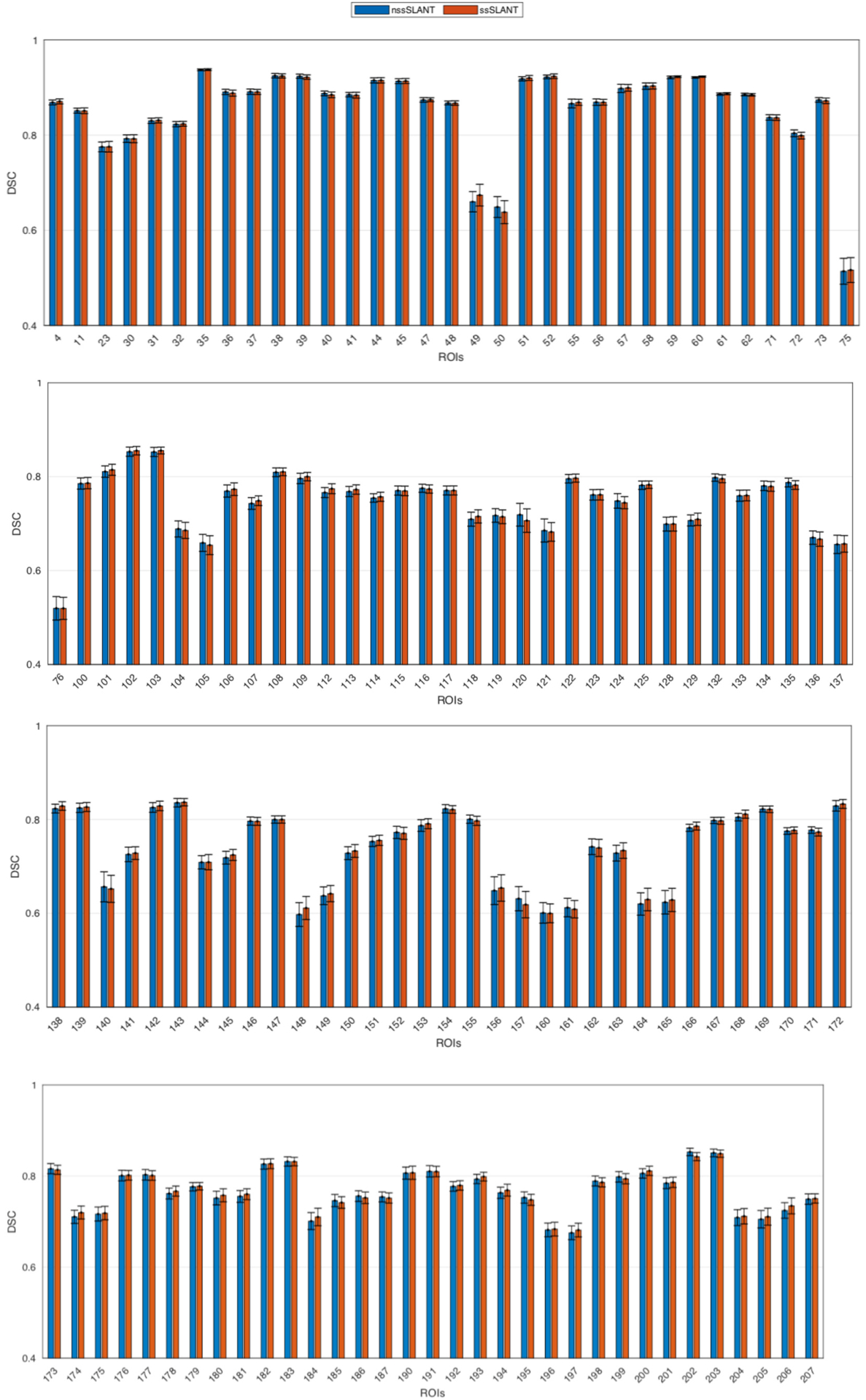
Quantitative results of nssSLANT and ssSLANT methods on whole brain segmentation (132 ROIs). The mean DSC between ground truth and our methods across all folds are shown as bar graph. No significant difference is observed between the two methods, which suggests that removing skull has no significant influence on segmentation results.

Table 1.

Mean and median DSC and MSD (mm) across all ROIs. The proposed ssSLANT and nssSLANT methods show comparable whole brain segmentation performance in terms of mean and median DSC and MSD, with no significant difference.

Methods	DSC		MSD
	Mean±std	Median	Mean±std	Median
nssSLANT	0.782±0.014	0.785	0.919±0.067	0.915
ssSLANT	0.778±0.043	0.789	0.944±0.031	0.947

3.5. TICV and PFV estimation

In this section, we investigate the volume estimation performance of ssSLANT and nssSLANT. In order to evaluate the labeling results of total intracranial cavity and posterior fossa, we combined all white matter, gray matter structures, cerebrospinal fluid, and meninges as total intracranial cavity and combined brainstem and cerebellum as posterior fossa. The combined labeling results are shown in Fig. 5. From Fig. 5, ssSLANT and nssSLANT show promising labeling results compared with the manual labeling. The proposed methods can delineate the TICV and PFV preciously. We compared the TICV and PFV labeling performance of our method with the existing methods including FreeSurfer (FS), SPM12, majority vote (MV) and NLSS in Table 2–3 using DSC and MSD metrics. We observed significant difference between the previous methods (FS, SPM12, MV and NLSS) and the proposed methods on DSC and MSD. Meanwhile, ssSLANT and nssSLANT show no significant difference on DSC and MSD, in terms of TICV and PFV labeling results.

Fig. 5.

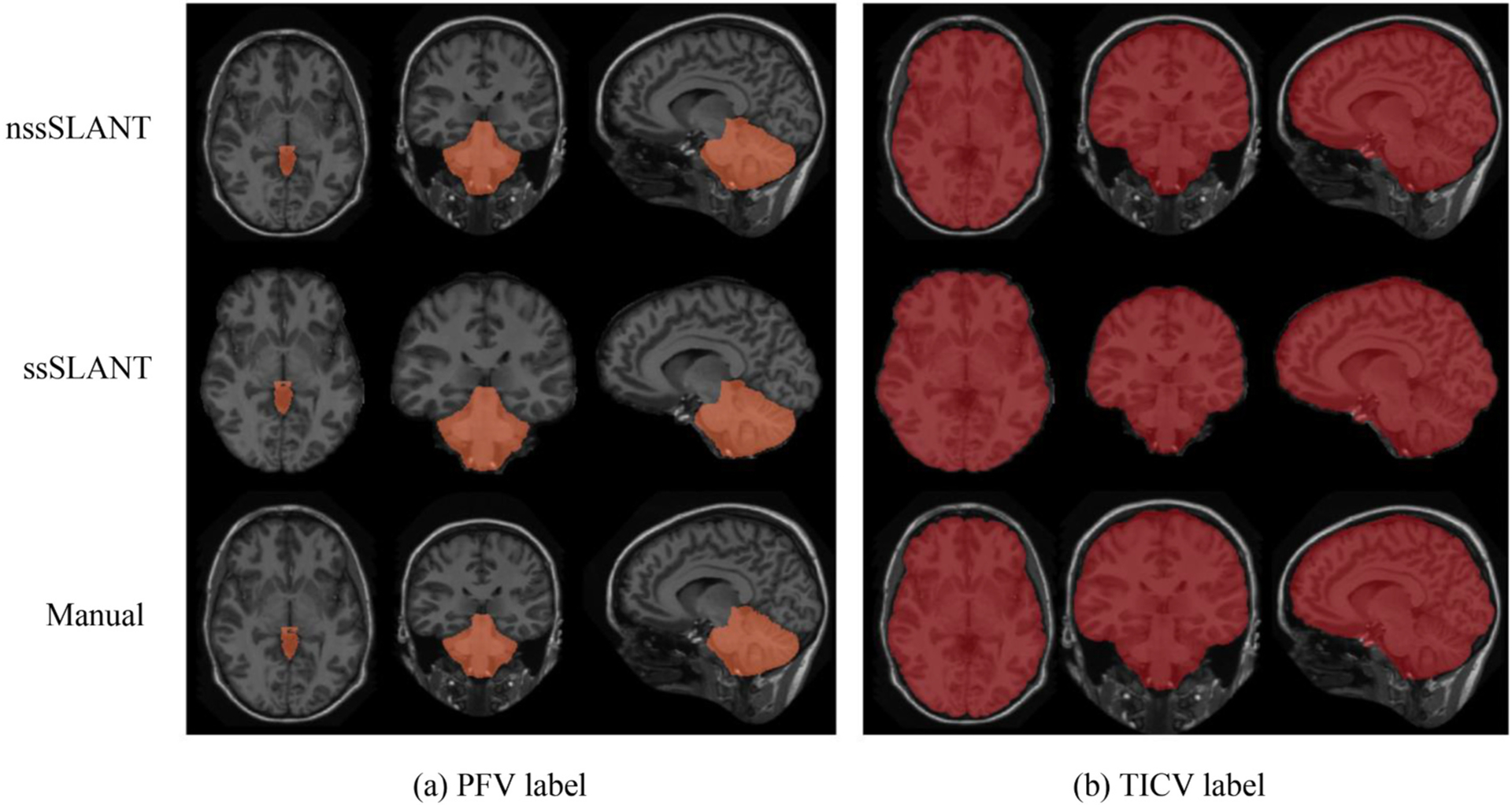
Qualitative results of nssSLANT and ssSLANT with three views for TICV and PFV labeling. The first two rows show nssSLANT and ssSLANT volume labeling results, respectively. The third row shows the manual labeling. Compared with the manual labeling, our methods show promising performance.

Table 2.

Comparison results on TICV segmentation. Our methods outperform existing methods in terms of mean DSC and MSD. It is worth noting that FreeSurfer and SPM12 do not generate hard total intracranial segmentation. Therefore, the results of FS and SPM12 on DSC and MSD are N/A. The statistical analyses were conducted between the previous methods and the proposed methods.

Methods	FreeSurfer	SPM12	MV*	NLSS*	nssSLANT	ssSLANT
DSC	N/A	N/A	0.977	0.983	0.987	0.989
MSD	N/A	N/A	0.968	0.743	0.491	0.489

The methods with significant difference (p < 0.05) are marked with ‘*’. All benchmarks are run on brain with skull.

Table 3.

Comparison results on PFV segmentation. Our methods outperform existing methods in terms of mean DSC and MSD. The statistical analyses were conducted between the previous methods and the proposed methods.

Methods	FreeSurfer	SPM12	MV*	NLSS*	nssSLANT	ssSLANT
DSC	N/A	N/A	0.960	0.968	0.975	0.977
MSD	N/A	N/A	0.847	0.675	0.554	0.542

The methods with significant difference (p < 0.05) are marked with ‘*’. The statistical analysis is not conducted on FS and SPM12 in this Table, since they do not provide hard posterior fossa segmentation. All benchmarks were run on brain with skull.

In the volume analysis, we compare our method with existing methods including FS, SPM12, MV and NLSS in Table 4. In addition to DSC and MSD metrics for segmentation accuracy in Table 2–3, we show ASIM value for volume analysis in Table 4. None of FS and SPM12 estimates TICV by counting the voxels inside skull, while our method estimated the volume by counting voxels. Therefore, FS and SPM12 do not work on skull-stripped brains and estimate PFV. From Table 4, we can see that our methods show better performance on volume estimation, compared with widely used FS, SPM12 packages and typical label fusion methods (MV and NLSS). Furthermore, after statistical analysis, nssSLANT and ssSLANT show no significant difference on ASIM for volume estimation. This suggests that the proposed pipeline could provide reliable TICV and PFV estimation for both skull-stripped brain and non-skull-stripped brains. We also observed significant difference between the previous methods (FS, SPM12, MV and NLSS) and the proposed methods on ASIM.

Table 4.

Comparison results on ASIM. Our methods outperform existing methods in terms of mean ASIM. The statistical analyses were conducted between the previous methods and the proposed methods.

Methods	FreeSurfer*	SPM12*	MV*	NLSS*	nssSLANT	ssSLANT
TICV	0.941	0.964	0.976	0.986	0.991	0.991
PFV	N/A	N/A	0.975	0.984	0.992	0.993

The methods with significant difference (p < 0.05) are marked with ‘*’. The statistical analysis is not conducted on FreeSurfer and SPM12 in terms of PFV, since they do not provide PFV estimation. All benchmarks are run on brain with skull.

4. Discussion

In this work, we proposed a simultaneous whole brain segmentation and volume estimation method for both skull-stripped and non-skull-stripped brains. Different from some existing methods, the proposed method estimates TICV and PFV by counting the voxels. Therefore, it could be applied in skull-stripped scenarios. The proposed method is quantitatively evaluated using DSC, MSD and ASIM for segmentation and volume estimation. The proposed method is compared with Free-Surfer, SPM12 and atlas-based methods for volume estimation.

After removing skull, the performance of segmentation and volume estimation have no significant changes (Tables 1–4). The details of whole brain segmentation and volume segmentation are well preserved for isolated brains (Figs. 3 and 5). Compared with other brain segmentation and total intracranial volume estimation methods: (1) Our method achieves simultaneous brain segmentation and total intracranial volume estimation. (2) Our method could be applied for both brains w/and w/o the skull with no significant differences. (3) Our method shows significant differences with other previous methods.

4.1. Simultaneous segmentation and volume estimation

Several previous studies focus on either brain segmentation or volume estimation. We combine the two tasks in a single pipeline. We compared our method to previous volume estimation methods in Table 2–4. None of FS and SPM12 estimates TICV by segmenting the intracranial cavity and counting the voxels. Therefore, FS and SPM12 do not estimate PFV and do not work on skull-stripped brains.

Atlas-based methods such as MV and NLSS not only provide TICV estimation, but also estimate PFV simultaneously. Meanwhile, atlas-based methods show higher accuracy in TICV estimation than FS and SPM12. However, they still show significant difference with our methods in terms of volume estimation (Table 2–4). Also, previous atlas-based methods do not focus on both segmentation and volume estimation tasks in a single pipeline. Furthermore, one of the major limitations of atlas-based methods is the high computational consumption. Hence, atlas-based methods usually utilize a small number of atlases, which may hinder higher accuracy. In order to utilize the large number of labeled training data, we proposed a deep learning-based method in this work.

4.2. Containerized implementation

Our pipeline consists of several steps including preprocessing, segmentation and label fusion etc. In order to make it easy for researchers to obtain results, we containerized the implementation using singularity technique (https://singularity.lbl.gov/). In this way, our pipeline could be deployed on any T1w scans with one command line. The singularity containers and command lines for both nssSLANT and ssSLANT could be found in https://github.com/MASILab/SLANTbrainSeg_skullstripped.

4.3. Robustness and generalization

In this work, the pre-training datasets contains 5111 multi-site scans which are from different gender, age (5–96 years) and health states (Attention Deficit Hyperactivity Disorder and Alzheimer’s disease) [27]. The fine-tuning data are from OASIS dataset which contains subjects aged 18–96 and subjects over the age of 60 have been clinically diagnosed with mild to moderate Alzheimer’s disease. Forty-five modified BrainCOLOR atlases with TICV and PFV labels are used as fine-tuning data and we report the results taken over five-fold cross-validation. We do not test our method on infants or newborns, because the manually traced ground truth is not available currently on them. Testing with different cohorts might better prove the generalization of the proposed pipeline. Our future work would be to test the robustness of our method on various cohorts.

5. Conclusion

In this work, we generalize deep learning whole brain segmentation for skull removal brain and intracranial measurements. The whole pipeline consists of three stages: preprocessing, U-Net-based segmentation and postprocessing. In the preprocessing stage, the target images are registered to the MNI305 space using affine transformation. Then, an N4 bias field correction is employed to reduce the bias during the imaging procedure. Finally, intensity normalization is introduced to reduce the effect caused by various intensities across different scans. In the U-Net-based segmentation stage, we crop the preprocessed image into 27 subspaces and train 27 U-Net tiles. We pre-train each tile with 5111 images from multi-site and then fine-tune them with 45 modified OASIS BrainCOLOR atlases with TICV and PFV labels. In the postprocessing stage, we use majority voting to fuse the segmentation results of all 27 tiles to a single segmentation. Then we inverse register the segmentation from MNI305 space to original space. Finally, we obtain the automatic segmentation results in target space. The overall pipeline is shown in Fig. 2. We not only get the whole brain segmentation, but also achieve TICV and PFV estimation in a single pipeline (Figs. 3 and 5). We also take isolated brain into consideration and get promising results, compared to the existing methods (FreeSurfer, SPM12 and atlas-based methods) in Table 1–4.