Abstract
Background
Although digital mobility outcomes (DMOs) can be readily calculated from real-world data collected with wearable devices and ad-hoc algorithms, technical validation is still required. The aim of this paper is to comparatively assess and validate DMOs estimated using real-world gait data from six different cohorts, focusing on gait sequence detection, foot initial contact detection (ICD), cadence (CAD) and stride length (SL) estimates.
Methods
Twenty healthy older adults, 20 people with Parkinson’s disease, 20 with multiple sclerosis, 19 with proximal femoral fracture, 17 with chronic obstructive pulmonary disease and 12 with congestive heart failure were monitored for 2.5 h in the real-world, using a single wearable device worn on the lower back. A reference system combining inertial modules with distance sensors and pressure insoles was used for comparison of DMOs from the single wearable device. We assessed and validated three algorithms for gait sequence detection, four for ICD, three for CAD and four for SL by concurrently comparing their performances (e.g., accuracy, specificity, sensitivity, absolute and relative errors). Additionally, the effects of walking bout (WB) speed and duration on algorithm performance were investigated.
Results
We identified two cohort-specific top performing algorithms for gait sequence detection and CAD, and a single best for ICD and SL. Best gait sequence detection algorithms showed good performances (sensitivity > 0.73, positive predictive values > 0.75, specificity > 0.95, accuracy > 0.94). ICD and CAD algorithms presented excellent results, with sensitivity > 0.79, positive predictive values > 0.89 and relative errors < 11% for ICD and < 8.5% for CAD. The best identified SL algorithm showed lower performances than other DMOs (absolute error < 0.21 m). Lower performances across all DMOs were found for the cohort with most severe gait impairments (proximal femoral fracture).
Algorithms’ performances were lower for short walking bouts; slower gait speeds (< 0.5 m/s) resulted in reduced performance of the CAD and SL algorithms.
Conclusions
Overall, the identified algorithms enabled a robust estimation of key DMOs. Our findings showed that the choice of algorithm for estimation of gait sequence detection and CAD should be cohort-specific (e.g., slow walkers and with gait impairments). Short walking bout length and slow walking speed worsened algorithms’ performances.
Trial registration ISRCTN – 12246987.
Supplementary Information
The online version contains supplementary material available at 10.1186/s12984-023-01198-5.
Keywords: Real-world gait, Algorithms, DMOs, Validation, Wearable sensor, Walking, Cadence, SL, Digital health, Accelerometer
Introduction
The adverse consequences of physical mobility loss and the importance of preserving mobility to ensure healthy ageing are undeniable [1, 2]. For this reason, a variety of behavioural, nutritional, and pharmacological interventions aim to improve mobility in general, and more specifically target the preservation of an individual’s ability to walk independently and safely both within and outside their homes [3–6]. Evaluating the effectiveness of interventions by quantifying an improved gait pattern, however, remains a challenge when relying on traditional tools such as patient-reported outcomes or supervised gait tests in clinic or lab, as these typically lack ecological validity [7].
Therefore, there is a need for the development of accurate, reliable, and sensitive tools for the quantification of gait and mobility in real-life [8, 9]. Digital health technology, including body-worn or wearable devices, offers a way forward by providing digital outcomes to remotely measure and monitor gait [10, 11], a fundamental component of mobility [12, 13]. Nonetheless, due to several persisting challenges in this field, current tools and techniques are still in their infancy. These challenges need to be addressed before digital mobility outcomes can be confidently adopted in clinical trials and as part of standard healthcare, including a variety of technical, clinical, and regulatory aspects [9, 14].
Exciting technical advances in algorithms and data processing techniques have led to the deployment of a plethora of algorithms to extract digital mobility outcomes from gait data recorded using inertial measurement units embedded within wearable devices [15–17]. Even so, significant ongoing challenges exist, in particular establishing the technical validity of these algorithms. A thorough validation process must account for complex factors that simultaneously arise from multiple sources influencing digital mobility outcome measures, including disease characteristics, patient specific habits, and the context in which walking is recorded (i.e. indoors, outdoors, public vs. private domain) [18–20]. All these factors concur to potentially limit the generalizability of validation data recorded during traditional gait protocols such as those administered within a controlled clinical or laboratory setting in which participants are asked to walk along a straight path or just a few daily life activities are simulated [21, 22]. Only recently, ad-hoc wearable devices have been developed, which finally allow moving the validation to more complex and realistic real-life scenarios [19, 23]. However, published validation studies generally only target a subset of specific digital mobility outcomes as calculated from one or a reduced number of algorithms and/or include only a few cohorts, hence providing partial information about generalizability of the results [22, 24].
The aim of this paper is to identify, compare and rank the most promising algorithms that quantitatively characterize gait with digital mobility outcomes from continuous real-life monitoring in a diverse group of patients who present with different mobility challenges. Here we focus on detection of gait sequences (i.e., identified walking bouts), individual steps, and estimation of cadence and stride length from a single wearable device positioned on the lower back, an ergonomically easy-to-use position near the centre of mass, which is well accepted by participants [25, 26]. To establish generalizability, we independently compare algorithms in six cohorts: healthy older adults, Parkinson’s disease, multiple sclerosis, proximal femoral fracture, chronic obstructive pulmonary disease and congestive heart failure. Specifically, we aim to:
Identify, compare and rank the best performing (i.e., most accurate and reliable) algorithms for each cohort;
Describe the performance of the identified best algorithms;
Analyse the influence of walking speed and walking bout duration on the algorithm performance;
Provide recommendations to implement and select algorithms for real-world gait analysis tailored to different patient cohorts.
Methods
Participants
A convenience sample of 108 participants were recruited to represent five disease cohorts (chronic obstructive pulmonary disease, Parkinson’s disease, multiple sclerosis, proximal femoral fracture, and congestive heart failure), as well as healthy older adults, encompassing a broad range of mobility levels. Participants were recruited in five sites: The Newcastle upon Tyne Hospitals NHS Foundation Trust, UK and Sheffield Teaching Hospitals NHS Foundation Trust, UK (ethics approval granted by London – Bloomsbury Research Ethics committee, 19/LO/1507); Tel Aviv Sourasky Medical Center, Israel (ethics approval granted by the Helsinki Committee, Tel Aviv Sourasky Medical Center, Tel Aviv, Israel, 0551-19TLV), Robert Bosch Foundation for Medical Research, Germany (ethics approval granted by the ethical committee of the medical faculty of The University of Tübingen, 647/2019BO2), University of Kiel, Germany (ethics approval granted by the ethical committee of the medical faculty of Kiel University, D438/18). All participants gave written informed consent to take part in the study. Inclusion and exclusion criteria and details about the technical validation study experimental protocol are described in [19].
Experimental protocol
Participants were monitored for 2.5 h as they went about their usual activities in their habitual environment (home/work/community/outdoor). To ensure diversity of walking activity, participants were also asked to perform some specific tasks: outdoor walking; walking up and down a slope and stairs; and moving from one room to another. Participants wore a single McRoberts Dynaport MM+ wearable device (sampling frequency 100 Hz, triaxial acceleration range: ± 8 g/resolution: 1 mg, triaxial gyroscope range: ± 2000 degrees per second (dps)/resolution: 70 mdps), secured to the lower back with an elasticated belt and Velcro fastening. A reference system was used to establish the accuracy of algorithms and was comprised of a multicomponent system of INertial modules, DIstance Sensors and Pressure insoles (INDIP) [19, 23, 27]. The INDIP system and the associated algorithms to estimate digital mobility outcomes have been validated in previous studies in healthy and pathological cohorts (e.g., hemiparetic, Parkinson’s disease, Huntington’s disease and mild cognitive impairment) and in this study participants [23, 28–32]. The INDIP and the single wearable device on the lower back were synchronized using timestamps referred to a common clock [19].
Pre-selection of algorithms for further validation and ranking
In this paper we focused on key metrics of real-world walking that form the basis from which a variety of digital mobility outcomes, including walking speed, can then be quantified. These are: gait sequence detection, foot initial contact detection, cadence and stride length estimation. For each metric, we identified published algorithms from laboratory-based or semi-structured protocols [8, 33]. This yielded 14 for gait sequence detection, 21 for initial contact detection, 23 for cadence and 18 for stride length estimation. For each digital mobility outcome, a shortlist of up to four most promising algorithms was selected based on initial testing in pre-existing data from older adults and pathological cohorts, including Parkinson’s disease [28, 34–36], multiple sclerosis [37, 38], stroke & chorea [28, 39]. Algorithms’ selection was based on the ranking methodology proposed in Bonci et al. [24]. The final subset of optimized algorithms (including detailed descriptions of implementation) are summarized in Table 1 and briefly outlined below.
Table 1.
Description of algorithms for each metric: gait sequence detection (GSD), initial contact event detection (ICD), cadence estimation (CAD) and stride length estimation (SL)
| Metric | Name | Description | Input | Output | Language | References |
|---|---|---|---|---|---|---|
| Gait sequence detection | GSDA | Based on a frequency-based approach, this algorithm is implemented on the vertical and anterior–posterior acceleration signals. First, these are band pass filtered to keep frequencies between 0.5 and 3 Hz. Next, a convolution of a 2 Hz sinewave (representing a template for a gait cycle) is performed, from which local maxima will be detected to define the regions of gait |
acc_v: vertical acceleration acc_ap: anterior–posterior acceleration WinS = 3 s; window size for convolution OL = 1.5 s; overlap of windows Activity_thresh = 0.01; Motion threshold Fs: sampling frequency |
Start: beginning of N gait sequences [s] relative to the start of a recording or a test/trial. Format: 1 × N vector End: termination of N gait sequences [s] relative to the start of a recording or a test/trial. Format: 1 × N vector |
Matlab® | Iluz, Gazit [40] |
| GSDB | This algorithm, based on a time domain-approach, detects the gait periods based on identified steps. First, the norm of triaxial acceleration signal is low-pass filtered (FIR, fc=3.2Hz), then a peak detection procedure using a threshold of 0.1 [g] is applied to identify steps. Consecutive steps, detected using an adaptive step duration threshold are associated to gait sequences. |
acc_norm: norm of the 3D-accelerometer signal Fs: sampling frequency th: peak detection threshold: 0.1 (g) |
Start: beginning of N gait sequences [s] relative to the start of a recording or a test/trial. Format: 1 x N vector End: termination of N gait sequences [s] relative to the start of a recording or a test/trial. Format: 1 x N vector |
Matlab® | Paraschiv-Ionescu, Newman [41] | |
| GSDc | This algorithm utilizes the same approach as GSDB the only difference being a different threshold for peak detection of 0.15 [g] |
acc_norm: norm of the 3D-accelerometer signal Fs: sampling frequency th: peak detection threshold: 0.15 (g) |
Start: beginning of N gait sequences [s] relative to the start of a recording or a test/trial. Format: 1 × N vector End: termination of N gait sequences [s] relative to the start of a recording or a test/trial. Format: 1 × N vector |
Matlab® | Paraschiv-Ionescu, Newman [41] | |
| Initial Contact Detection | ICDA | Algorithm implemented on a pre-processed vertical acceleration signal. This is first detrended and then low-pass filtered (FIR, fc = 3.2 Hz). The resulting signal is numerically integrated (cumtrapz) and differentiated using a Gaussian continuous wavelet transformation (CWT, scale 9, gauss2). The initial contact events are identified as the positive peaks between zero-crossings |
acc_v: the acceleration in the vertical axis Fs: sampling frequency GS: array of gait sequences |
ICs: detected N initial contacts [s] relative to the beginning of the recording or the test/trial. Format: 1 × N vector GaitSequenceRefined_Start: refinement of the beginning of the gait sequences provided from the Gait sequence detection step; it starts one second before the first detected IC GaitSequenceRefined_End: refinement of the termination of the gait sequences provided from the Gait sequence detection step; it finishes one second after the last detected IC |
Matlab® |
McCamley, Donati [42] Paraschiv-Ionescu, Newman [41] Paraschiv-Ionescu, Soltani [16] |
| ICDB | Algorithm implemented on a pre-processed anterior–posterior acceleration signal. This is first detrended and then low-pass filtered at 10 Hz with a second-order Butterworth filter. The resulting signal is numerically integrated (cumtrapz) and differentiated using an estimated wavelet scale [43] and a Gaussian first-order (gaus1) wavelet. The initial contact events are identified with a peak detection function (findpeaks) |
acc_ap: the acceleration in the anterior–posterior axis Fs: sampling frequency GS: array of gait sequences |
ICs: detected N initial contacts [s] relative to the beginning of the recording or the test/trial. Format: 1 × N vector GaitSequenceRefined_Start: refinement of the beginning of the gait sequences provided from the Gait sequence detection step; it starts one second before the first detected IC GaitSequenceRefined_End: refinement of the termination of the gait sequences provided from the Gait sequence detection step; it finishes one second after the last detected IC |
Matlab® |
McCamley, Donati [42] Abry [43] Pham, Elshehabi [44] |
|
| ICDC |
This algorithm is an optimized version of algorithm ICDA. In this case, the pre-processing of the acceleration signal is selected according to the degree of gait impairment, assessed with the symmetry index (ref) ∙ If estimated symmetry index > 0.5 the pre-processing of acceleration includes, in the following order: detrending and low-pass filtering (FIR, fc = 3.2 Hz), numerical integration (cumtrapz) and differentiation using Gaussian continuous wavelet transformation (CWT, scale 9, gauss2); ∙ If estimated symmetry index is in the range [0.25–0,5] the pre-processing includes an additional smoothing using moving average after CWT (smoothdata) ∙ If estimated symmetry index < 0.25, i.e., very impaired gait, the pre-processing includes two successive moving average after CWT, to efficiently smooth the signal |
acc_v: the acceleration in the vertical axis Fs: sampling frequency GS: array of gait sequences |
ICs: detected N initial contacts [s] relative to the beginning of the recording or the test/trial. Format: 1 × N vector GaitSequenceRefined_Start: refinement of the beginning of the gait sequences provided from the Gait sequence detection step; it starts one second before the first detected IC GaitSequenceRefined_End: refinement of the termination of the gait sequences provided from the Gait sequence detection step; it finishes one second after the last detected IC |
Matlab® |
McCamley, Donati [42] Paraschiv-Ionescu, Newman [41] Paraschiv-Ionescu, Soltani [16] |
|
| ICDD |
This algorithm is implemented on the norm of the 3D acceleration signals A sliding window summing technique is utilized to reduce the noise of the norm signal. Next, a differential technique on the acceleration is used to eliminate the effect of gravity, as a high pass filter. Finally, zero-crossings on the positive slope are detected, which determine the initial contact time events |
acc_norm: norm of the 3d-accelerometer signal Fs: sampling frequency GS: array of gait sequences |
ICs: detected N initial contacts [s] relative to the beginning of the recording or the test/trial. Format: 1 × N vector GaitSequenceRefined_Start: refinement of the beginning of the gait sequences provided from the Gait sequence detection step; it starts one second before the first detected IC GaitSequenceRefined_End: refinement of the termination of the gait sequences provided from the Gait sequence detection step; it finishes one second after the last detected IC |
Matlab® | Shin and Park [45] | |
| Cadence | CADA | This algorithm is the same as ICDA. From the initial contact events estimated, the step periodicity is derived and the CAD is calculated |
acc_v: the acceleration in the vertical axis Fs: sampling frequency GS: array of gait sequences |
output_CAD: a vector structure containing: output_CAD(N).start: start of N-th GS [s] output_CAD(N).stop: stop of N-th GS [s] output_CAD(N).cadSec: Estimated CAD-per-sec [steps/min] of N-th GS output_CAD(N).cadMean: mean of CAD [steps/min] estimated for N-th GS output_CAD(N).cadSTD: std of CAD [steps/min] estimated for N-th GS output_CAD(N).steps: number of steps of N-th GS |
Matlab® |
McCamley, Donati [42] Paraschiv-Ionescu, Newman [41] Paraschiv-Ionescu, Soltani [16] Soltani, Aminian [17] |
| CADB | This algorithm first implements a pre-processing of the 3D acceleration norm, including low-pass filtering (FIR, fc = 3.2 Hz), detrending, smoothing using Savitsky–Golay filter (order = 7, frame length = 21) and Gaussian smoothing and finally a continuous wavelet transformation (CWT, scale 10, ‘gaus2’) to enhance the relevant steps-related features in acceleration signal. The pre-processed signal is then further processed using morphological filters, according to methods described in Lee, You [46]. Finally, the timing of steps, used to estimate step/stride frequency are detected as maxima between zero-crossings |
acc_norm: norm of the 3D-accelerometer signal Fs: sampling frequency GS: array of gait sequences |
output_CAD: a vector structure containing: output_CAD(N).start: start of N-th GS [s] output_CAD(N).stop: stop of N-th GS [s] output_CAD(N).cadSec: Estimated CAD-per-sec [steps/min] of N-th GS output_CAD(N).cadMean: mean of CAD [steps/min] estimated for N-th GS output_CAD(N).cadSTD: std of CAD [steps/min] estimated for N-th GS output_CAD(N).steps: number of steps of N-th GS |
Matlab® |
Lee, You [46] Paraschiv-Ionescu, Soltani [16] Soltani, Aminian [17] |
|
| CADC | This algorithm is the same as ICDD. From the initial contact events estimated, the step periodicity is derived and the CAD is calculated |
acc_norm: norm of the 3D-accelerometer signal Fs: sampling frequency GS: array of gait sequences |
output_CAD: a vector structure containing: output_CAD(N).start: start of N-th GS [s] output_CAD(N).stop: stop of N-th GS [s] output_CAD(N).cadSec: Estimated CAD-per-sec [steps/min] of N-th GS output_CAD(N).cadMean: mean of CAD [steps/min] estimated for N-th GS output_CAD(N).cadSTD: std of CAD [steps/min] estimated for N-th GS output_CAD(N).steps: Number of steps of N-th GS |
Matlab® |
Shin and Park [45] Soltani, Aminian [17] |
|
| Stride length | SLA |
Biomechanical model which includes: – The implementation of the inverted pendulum model – Double integration of the acceleration in the vertical axis – Detrending and removal of integration drift: high pass filtering of vertical acceleration (fc = 0.1 Hz) and integrated vertical acceleration (fc = 1 Hz) – Correction factors based on the calibration factor “k”. Note that the tuning coefficients are optimized by training |
acc_v: the acceleration in the vertical axis (orientation corrected) Fs: sampling frequency GS: array of gait sequences ICs: initial contacts [s] Leg length [cm] Calibration factors “k” (k = 4.739 for all cohorts) |
output_sl: a vector structure containing: output_sl(N).start: start of N-th GS [s] output_sl(N).stop: stop of N-th GS [s] output_sl(N).slSec: Estimated SL-per-second [m] of N-th GS output_sl(N).slMean: mean of SL [m] estimated for N-th GS output_sl(N).slSTD: std of SL [m] estimated for N-th GS output_sl(N).distance: covered distance [m] of N-th GS output_sl(N).warnMes: shows if there is a warning for N-th GS (1 means yes) |
Matlab® |
Zijlstra and Hof [47] Zijlstra and Zijlstra [48] Soltani, Aminian [17] |
|
SLB *SLB |
This algorithm is the same as SLA. For all cohorts, the same factor “k” is used, whereas for the MS cohort, a special factor is implemented (*SLB) |
acc_v: the acceleration in the vertical axis (orientation corrected) Fs: sampling frequency GS: array of gait sequences ICs: initial contacts [s] Leg length [cm] Calibration factors “k” (k = 4.99 for all cohorts except MS, for which k = 4.587) |
output_sl: a vector structure containing: output_sl(N).start: start of N-th GS [s] output_sl(N).stop: stop of N-th GS [s] output_sl(N).slSec: Estimated SL-per-second [m] of N-th GS output_sl(N).slMean: mean of SL [m] estimated for N-th GS output_sl(N).slSTD: std of SL [m] estimated for N-th GS output_sl(N).distance: covered distance [m] of N-th GS output_sl(N).warnMes: shows if there is a warning for N-th GS (1 means yes) |
Matlab® |
Zijlstra and Hof [47] Zijlstra and Zijlstra [48] Soltani, Aminian [17] |
|
| SLC |
Based on the intensity of the vertical acceleration signal, this algorithm estimates the step length according to the following formulas, which represent the relation between the measured vertical acceleration, as a mean absolute value during a step cycle, and the samples within the step (ic = initial contact time event, k = calibration factor 1, p = calibration factor 2). Note that in this section, variables k and p are the tuning coefficients, optimized by machine-learning training
|
acc_v: the acceleration in the vertical axis (orientation corrected) Fs: sampling frequency GS: array of gait sequences ICs: initial contacts [s] Leg length [cm] Calibration factors “t” and “p” (t = 0.93, p = foot length) |
output_sl: a vector structure containing: output_sl(N).start: start of N-th GS [s] output_sl(N).stop: stop of N-th GS [s] output_sl(N).slSec: Estimated SL-per-second [m] of N-th GS output_sl(N).slMean: mean of SL [m] estimated for N-th GS output_sl(N).slSTD: std of SL [m] estimated for N-th GS output_sl(N).distance: covered distance [m] of N-th GS output_sl(N).warnMes: shows if there is a warning for N-th GS (1 means yes) |
Matlab® |
Kim, Jang [49] Zhao, Zhang [50] Soltani, Aminian [17] |
|
| SLD |
This algorithm is based on the double integration of the anterior–posterior acceleration signal It integrates the signal and corrects the drift based on the combination of two methods: – The inverted pendulum model, as for SLA – The geometrical acceleration-intensity-based model, which assumes the following:
Note that in this section, variables k, t and p are the tuning coefficients, optimized by machine-learning training |
acc_ap: the acceleration in the anterior–posterior axis (orientation corrected) Fs: sampling frequency GS: array of gait sequences ICs: initial contacts [s] Leg length [cm] Calibration factors “t”, “p” (t = 0.85, p = foot size) |
output_sl: a vector structure containing: output_sl(N).start: start of N-th GS [s] output_sl(N).stop: stop of N-th GS [s] output_sl(N).slSec: Estimated SL-per-second [m] of N-th GS output_sl(N).slMean: mean of SL [m] estimated for N-th GS output_sl(N).slSTD: std of SL [m] estimated for N-th GS output_sl(N).distance: covered distance [m] of N-th GS output_sl(N).warnMes: shows if there is a warning for N-th GS (1 means yes) |
Matlab® |
Zijlstra and Hof [47] Zijlstra and Zijlstra [48] Weinberg [51] Soltani, Aminian [17] |
Gait sequence detection (GSD) This metric identifies sections of the raw signal which correspond to walking/gait. Three algorithms were selected: GSDA [40], GSDB [16] and GSDC [41].
Initial contact detection (ICD) This metric detects the foot initial contact within each gait sequence. Four algorithms were selected: ICDA [16, 41, 42], ICDB [44], ICDC [16, 41, 42] and ICDD [45].
Cadence estimation (CAD) This metric identifies strides as a cyclic pattern from which cadence [number of steps within a minute (min)] is estimated in each walking bout [17]. Three algorithms were selected: CADA [41, 42, 44], CADB [16, 46] and CADC [17, 45]. Cadence (steps/min) was derived from identified strides as follows:
| 1 |
where are the different walking bouts and Stride Frequency is evaluated as:
| 2 |
where are the different walking bouts, is the number of strides (including right and left steps) in the relevant – walking bout, is the duration [seconds] of the k – stride in the relevant walking bout
Stride length estimation (SL) This metric quantifies stride length, evaluated as the distance between two non-consecutive initial contacts. Four algorithms were selected based either on biomechanical or machine-learning models: SLA [47, 48], SLB [47, 48], SLC [49, 50] and SLD [17, 51].
Data and statistical analyses for validation and ranking of algorithms.
All calculations and statistical analysis were performed using Matlab® R2021a (Mathworks, Natick, MA).
Performance measures to describe and establish algorithm validity
To ensure objective comparison between systems (INDIP and wearable device), walking bouts detected by the INDIP were given as a standardized input to all algorithms except for gait sequence detection where the full wearable device recording was given as input. A walking bout was defined as a walking sequence containing at least two consecutive strides of both feet (e.g., R–L–R–L–R–L or L–R–L–R–L–R, with R/L being the right/left foot contact with the ground) [18]. Criteria for inclusion of a stride were: (a) duration of 0.2–3 s, and (b) a minimum length of 0.15 m. A resting period/break of 3 s or more identified consecutive walking bouts [18], thus each walking bout could include resting periods/breaks ≤ 3 s. Each metric was determined by the algorithms implemented on the single wearable device and by the INDIP.
Algorithm validation was established independently for each cohort by comparing digital mobility outcomes obtained from the selected algorithms applied to the wearable device with those from the INDIP using the following set of performance measures to describe and establish validity:
| 3 |
| 4 |
| 5 |
| 6 |
where TP = True Positive events, TN = True Negative events, FP: False Positive events, FN: False Negative events.
Intra class correlation coefficient (ICC(2,1)) [52] was calculated to assess the association between the digital mobility outcomes of the two systems using all walking bouts collected from each cohort separately. Based on ICC estimates, values less than 0.5, between 0.5 and 0.75, between 0.75 and 0.9, and greater than 0.9 were deemed to be indicative of poor, moderate, good, and excellent agreement, respectively [53].
Absolute agreement was assessed by quantifying (i) absolute error, (ii) bias, and (iii) Limits of Agreement [54] between the wearable device and reference system digital mobility outcomes calculated for each walking bout.
Relative errors between the wearable device and INDIP digital mobility outcomes were determined for each walking bout.
Mean and 95% confidence intervals of all digital mobility outcomes were evaluated at a cohort level (i.e., quantified using all walking bouts across all participants belonging to that specific cohort). Subsets of relevant measures were then used for the different digital mobility outcomes and evaluated as detailed below.
For gait sequence detection algorithms, each window of 0.1 s from the complete 2.5-h recording was classified (see Fig. 1) as either true positive, false positive, true negative or false negative and accuracy, sensitivity, specificity, positive predictive value were calculated. These measures were evaluated for each 2.5-h assessment. In addition, absolute errors and ICC(2,1) for the total accumulated duration of all gait sequences identified in a 2.5-h recording was assessed and compared between the two systems, for each participant.
Fig. 1.
Example of identification of False Positive (FP), False Negative (FN), True Positive (TP) and True Negative (TN) for the Gait Sequence Detection (GSD) algorithms, of each window (0.1 s). Events classified from the comparison of each individual window between the INDIP reference system (RS) and the single wearable device (WD) for the detection of gait sequences. Each window of the WD and RS outputs are depicted as a rectangle, where white rectangles represent windows of non-gait sequences, and grey rectangles denote windows of a detected gait sequence
In the case of initial contact detection, we defined each initial contact event within a walking bout as a true positive, false positive and false negative by comparing the initial contact events detected by the wearable device to the events detected by the INDIP within a tolerance window of 0.5 s (centred around the event identified by the INDIP, see Fig. 2), representative of a step duration [55]. This approach has been previously used and was adopted to take into account the potential mismatch on the event time between the INDIP and the wearable device [56]. To assess initial contact detection, true negative events were not evaluated, since true negative would correspond to all non-initial contact events identified as such by both systems.
Fig. 2.
Example of performance analysis for initial contact detection (ICD) algorithms. The figure shows Initial contacts events identified by the reference system (IC-RS, depicted in black solid line) and initial contacts events identified by the single wearable device (IC-WD, depicted in orange dotted line). False Negatives, False Positive and True Positive events are defined with respect to the selected temporal tolerance window of 0.5 s (in grey) centred around the IC-RS. a Shows the identification of False Negative events (i.e., initial contact identified by the reference system but not identified by the single wearable device within the tolerance window) and False Positive events (i.e., initial contact wrongly identified by the single wearable device because although identified, it is outside the tolerance window). b Shows the identification of True Positives events (i.e., initial contact events correctly identified by the single wearable device) and example of other cases for identification of False Positive events (i.e., initial contact wrongly identified by the single wearable device). Note that the initial contact event, identified by the single wearable device, nearest to the true event (identified by the INDIP) will be considered a True Positive, and the rest of the identified events, False Positives. The figure also shows in blue how absolute errors are calculated only from True Positive events
For initial contact detection, we utilised the following measures: sensitivity, positive predictive values, absolute errors (which were estimated for each true positive initial contact (see Fig. 2)) and relative error (estimated by dividing all absolute errors, within a walking bout, by the average step duration estimated by the INDIP [55]).
For cadence and stride length algorithms, the measures used were: relative errors, absolute errors and ICC(2,1).
Ranking algorithms using performance measures
A simplified version of the ranking methodology described in Bonci et al. [24] was applied to compare algorithm performance using a decision matrix. This was based on the weighted combination of performance measures described above assessing agreement between the single wearable device and the INDIP system (classified as benefit or cost). Performance measures considered as benefits were: accuracy, sensitivity, specificity, positive predictive value and ICC(2,1) [52]. Performance measures considered as costs were absolute and relative errors. Each measure was weighted based on its relative importance to the algorithm’s validity assessment (see Bonci et al. [24] and Additional file 1 for further detail regarding the specific performance measures and assigned weights for gait sequence detection, initial contact detection, cadence and stride length algorithms). This information was combined to determine a performance index (0 = worst, 1 = best), calculated as a weighted mean of the selected benefit and/or cost analysis, which was subsequently used to compare and rank the algorithm performances, and thus, to select the top performing algorithms for each cohort independently.
Influence of walking speed and walking duration on the algorithms’ performance
The performance of initial contact detection, cadence and stride length top-selected algorithms was then assessed considering the impact that walking bout walking speed values (calculated as the average stride speed by the INDIP system) and walking bout durations had on the relative error of each digital mobility outcome (i.e., step duration, cadence and stride length). Specifically, median relative errors for each digital mobility outcome were quantified evaluating all the walking bouts characterized by specific walking speed and walking bout duration ranges; including errors observed in consecutive walking speed windows of 0.05 m/s [57] and in consecutive walking bout duration windows of 2 s. For each digital mobility outcome, the resulting median errors were then employed in a best-fit approach to determine their association between the relative errors and walking speed or walking bout duration, respectively. In the best-fit approach, median error values were also weighted according to the relevant number of observations in a given window with respect to the total number of observations.
Results
Participant clinical and demographic characteristics per cohort are presented in Table 2.
Table 2.
Demographic and clinical characteristics of the participants
| Characteristic (unit of measure) or [range] | HA (n = 20) | CHF (n = 12) | COPD (n = 17) | MS (n = 20) | PD (n = 20) | PFF (n = 19) |
|---|---|---|---|---|---|---|
| Number of walking bouts included in the analyses (n) | 1343 | 416 | 1031 | 795 | 681 | 684 |
| Age (years) | 71.7 ± 5.8 | 69.1 ± 11.7 | 69.4 ± 9.1 | 48.7 ± 9.7 | 69.8 ± 7.2 | 80.0 ± 8.5 |
| Height (cm) | 1.66 ± 0.10 | 1.74 ± 0.10 | 1.69 ± 0.07 | 1.71 ± 0.13 | 1.73 ± 0.07 | 1.69 ± 0.08 |
| Weight (kg) | 75.1 ± 11.8 | 84.5 ± 16.8 | 73.7 ± 14.2 | 84.0 ± 22.9 | 78.2 ± 14.4 | 68.4 ± 16.0 |
| Gender: % females [females n, males n] | 45% [9, 11] | 33% [4, 8] | 47% [8, 9] | 45% [9, 11] | 20% [4, 16] | 58% [8, 11] |
| WS during the 2.5-h assessment (mean and [range]) (m/s) | 0.59 [0.12, 1.63] | 0.72 [0.14, 1.46] | 0.60 [0.11, 1.36] | 0.58 [0.15, 1.60] | 0.60 [0.10, 1.44] | 0.54 [0.14, 1.29] |
| Walking Aid use: % of users [n] | 5% [1] | 25% [3] | 6% [1] | 25% [5] | 30% [6] | 68% [13] |
| MoCA [0–30] | 27.7 ± 2.6 | 27.1 ± 2.9 | 24.6 ± 3.4 | 26.7 ± 3.1 | 24.6 ± 4.0 | 24.1 ± 4.2 |
| LLFDI [0–100] | 73.53 ± 14.22 | 67.29 ± 21.35 | 59.07 ± 7.96 | 57.34 ± 10.66 | 60.26 ± 12.51 | 52.59 ± 16.61 |
| Hoehn & Yahr stage (n) |
H&Y I: 4 H&Y II: 11 H&Y III: 5 |
|||||
| MDS-UPDRS III [0–132] | 28.4 ± 13.6 | |||||
| EDSS [0–6] | 3.5 ± 1.7 | |||||
| SPPB [0–12] | 6.2 ± 3.9 | |||||
| CAT Score [0–40] | 16.6 ± 8.9 | |||||
| FEV1 (litres) | 1.6 ± 0.6 | |||||
| 6MWT distance (m) | 370.7 ± 115.6 | 357.6 ± 88.5 | ||||
| KCCQ-12 Score [0–100] | 80.5 ± 20.2 |
Values are presented as mean ± standard deviation, unless otherwise stated
CAT chronic obstructive pulmonary disease (COPD) Assessment Test; EDSS Expanded Disability Status Scale; FEV1 Forced Expiratory Volume in 1 Second; KCCQ-12 Kansas City Cardiomyopathy Questionnaire-12; LLFDI Late Life Function and Disability Instrument; MDS-UPDRS III Movement Disorder Society Unified Parkinson’s Disease Rating Scale Part III; MoCA Montreal Cognitive Assessment; SPPB Short Physical Performance Battery; 6MWT 6 Minute Walking Test; HA healthy adults; PD Parkinson’s disease; MS multiple sclerosis; COPD chronic obstructive pulmonary disease; CHF congestive heart failure; PFF proximal femoral fracture
The cohorts covered a wide range of mobility levels: the walking speed measured by the INDIP system during the 2.5-h assessment ranged from an average of 0.54 m/s (proximal femoral fracture) to 0.72 m/s (congestive heart failure), with a minimum measured walking speed of 0.10 m/s (in Parkinson’s disease) and a maximum of 1.63 m/s (in healthy older adults) (Table 2).
Nine participants (8%: three with chronic heart failure, two with multiple sclerosis, one with Parkinson’s disease and three proximal femoral fracture participants) were excluded from subsequent analysis due to data unavailability.
Gait sequence detection
Performance measures and ranking
We report in Table 3 the gait sequence detection algorithms main peformance measures (All performance measures are considered for the evaluation of the performance index are shown in the Additional file 1: Table).
Table 3.
Gait sequence detection (GSD) performance measures; gait sequence total duration obtained from the INDIP and the single wearable device, absolute error, bias and limits of agreement (LoA) and intra class correlation (ICC(2,1)) for comparison between systems, and overall performance index for the GSD algorithms. Values are expressed as mean and 95% confidence intervals (CI) for each cohort. In italic and boldface recommended algorithms. Underlined performance index indicates top-ranked algorithm for the specific cohort of that row
| Cohort | Gait sequence detection | Gait sequence total duration | Performance index | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sensitivity | Positive predictive value | Accuracy | Specificity | INDIP mean and CI [s] | Single wearable device mean and CI [s] | Bias and LoA [s] | Absolute error [s] | ICC (2,1) | ||
| GSDA | ||||||||||
| HA | 0.84 [0.77, 0.92] | 0.81 [0.75, 0.88] | 0.94 [0.93, 0.96] | 0.96 [0.95, 0.97] | 1640.0 [1273.4, 2006.6] | 1708.5 [1316.3, 2100.7] | 68.5 [− 710.6, 847.5] | 215.7 [57.7, 373.7] | 0.88 [0.73, 0.95] | 0.819 |
| CHF | 0.85 [0.68, 1.01] | 0.81 [0.72, 0.90] | 0.95 [0.92, 0.98] | 0.96 [0.94, 0.99] | 1545.4 [421.1, 2669.6] | 1595.4 [395.2, 2795.6] | 50.0 [− 689.5, 789.5] | 242.0 [39.6, 444.4] | 0.98 [0.91, 0.99] | 0.853 |
| COPD | 0.85 [0.81, 0.88] | 0.75 [0.68, 0.82] | 0.95 [0.93, 0.97] | 0.96 [0.95, 0.98] | 1004.8 [829.2, 1180.4] | 1151.6 [955.7, 1347.6] | 146.8 [− 369.1, 662.8] | 176.5 [51.5, 301.5] | 0.68 [0.32, 0.87] | 0.822 |
| MS | 0.92 [0.87, 0.97] | 0.75 [0.66, 0.84] | 0.95 [0.92, 0.98] | 0.95 [0.92, 0.98] | 1119.5 [736.9, 1502.2] | 1452.0 [990.4, 1913.6] | 332.5 [− 883.9, 1548.8] | 358.5 [57.7, 659.4] | 0.68 [0.34, 0.87] | 0.735 |
| PD | 0.86 [0.78, 0.94] | 0.81 [0.71, 0.91] | 0.96 [0.95, 0.98] | 0.97 [0.96, 0.99] | 1121.8 [626.5, 1617.1] | 1177.3 [656.2, 1698.5] | 55.6 [− 402.4, 513.6] | 139.1 [45.8, 232.4] | 0.98 [0.94, 0.99] | 0.852 |
| PFF | 0.71 [0.54, 0.89] | 0.74 [0.61, 0.88] | 0.95 [0.92, 0.97] | 0.97 [0.96, 0.99] | 954.4 [599.5, 1309.4] | 975.7 [589.8, 1361.6] | 21.3 [− 365.3, 407.9] | 144.4 [72.1, 216.7] | 0.96 [0.89, 0.99] | 0.770 |
| GSDB | ||||||||||
| HA | 0.86 [0.82, 0.90] | 0.85 [0.79, 0.92] | 0.95 [0.94, 0.96] | 0.97 [0.96, 0.98] | 1645.8 [1258.1, 2033.5] | 1657.4 [1283.5, 2031.3] | 11.6 [− 592.4, 615.6] | 170.5 [48.1, 292.8] | 0.93 [0.83, 0.97] | 0.727 |
| CHF | 0.91 [0.88, 0.94] | 0.82 [0.71, 0.92] | 0.96 [0.94, 0.98] | 0.96 [0.94, 0.99] | 1545.4 [421.1, 2669.6] | 1689.6 [557.8, 2821.5] | 144.3 [− 331.8, 620.4] | 176.1 [19.8, 332.3] | 0.99 [0.95, 1.00] | 0.792 |
| COPD | 0.84 [0.81, 0.88] | 0.80 [0.77, 0.82] | 0.96 [0.95, 0.97] | 0.97 [0.97, 0.98] | 1004.8 [829.2, 1180.4] | 1058.4 [865.5, 1251.4] | 53.6 [− 120.3, 227.6] | 71.9 [34.0, 109.8] | 0.96 [0.90, 0.99] | 0.814 |
| MS | 0.91 [0.87, 0.95] | 0.75 [0.65, 0.85] | 0.95 [0.92, 0.98] | 0.95 [0.92, 0.98] | 1119.5 [736.9, 1502.2] | 1416.3 [947.8, 1884.8] | 296.8 [− 911.6, 1505.2] | 323.1 [23.5, 622.6] | 0.70 [0.38, 0.88] | 0.655 |
| PD | 0.84 [0.76, 0.92] | 0.83 [0.73, 0.93] | 0.96 [0.95, 0.97] | 0.98 [0.96, 0.99] | 1121.8 [626.5, 1617.1] | 1145.9 [629.1, 1662.6] | 24.1 [− 450.9, 499.0] | 167.9 [85.1, 250.8] | 0.97 [0.94, 0.99] | 0.726 |
| PFF | 0.73 [0.60, 0.86] | 0.84 [0.76, 0.93] | 0.96 [0.95, 0.98] | 0.98 [0.97, 0.99] | 911.7 [569.4, 1254.0] | 861.1 [542.8, 1179.3] | − 50.7 [− 445.9, 344.6] | 141.4 [62.2, 220.6] | 0.95 [0.86, 0.98] | 0.771 |
| GSDC | ||||||||||
| HA | 0.77 [0.71, 0.83] | 0.91 [0.85, 0.98] | 0.95 [0.94, 0.96] | 0.99 [0.98, 1.00] | 1645.8 [1258.1, 2033.5] | 1409.3 [1034.8, 1783.7] | − 236.5 [− 848.7, 375.7] | 323.6 [220.1, 427.1] | 0.88 [0.73, 0.95] | 0.722 |
| CHF | 0.84 [0.79, 0.88] | 0.89 [0.82, 0.96] | 0.97 [0.95, 0.98] | 0.98 [0.97, 0.99] | 1545.4 [421.1, 2669.6] | 1466.6 [359.8, 2573.4] | − 78.7 [− 309.9, 152.4] | 113.1 [55.1, 171.1] | 1.00 [0.99, 1.00] | 0.811 |
| COPD | 0.73 [0.68, 0.78] | 0.89 [0.87, 0.91] | 0.96 [0.95, 0.97] | 0.99 [0.99, 0.99] | 1004.8 [829.2, 1180.4] | 825.2 [664.4, 986.1] | − 179.6 [− 420.7, 61.6] | 179.6 [116.3, 242.8] | 0.80 [0.53, 0.92] | 0.776 |
| MS | 0.83 [0.77, 0.90] | 0.83 [0.73, 0.93] | 0.96 [0.93, 0.98] | 0.97 [0.94, 1.00] | 1119.5 [736.9, 1502.2] | 1223.3 [794.0, 1652.5] | 103.8 [− 1100.0, 1307.5] | 246.9 [− 36.2, 530.0] | 0.72 [0.41, 0.89] | 0.693 |
| PD | 0.76 [0.65, 0.87] | 0.87 [0.76, 0.98] | 0.96 [0.95, 0.97] | 0.99 [0.98, 1.00] | 1121.8 [626.5, 1617.1] | 1000.4 [514.3, 1486.5] | − 121.4 [− 579.4, 336.5] | 192.3 [107.3, 277.3] | 0.97 [0.92, 0.99] | 0.726 |
| PFF | 0.60 [0.45, 0.75] | 0.89 [0.77, 1.01] | 0.94 [0.91, 0.97] | 0.99 [0.99, 1.00] | 954.4 [599.5, 1309.4] | 697.3 [439.9, 954.8] | − 257.1 [− 823.6, 309.4] | 272.4 [120.9, 423.9] | 0.78 [0.47, 0.92] | 0.687 |
HA healthy adults; PD Parkinson’s disease; MS multiple sclerosis; COPD chronic obstructive pulmonary disease; CHF congestive heart failure; PFF proximal femoral fracture; CI confidence intervals, LoA limits of agreement, ICC intra class correlation
Across all cohorts, performance measures for the three gait sequence detection algorithms were good to excellent (sensitivity ranged between 0.60 and 0.92, specificity between 0.95 and 0.99, accuracy between 0.94 and 0.97 and positive predictive value between 0.74 and 0.91 [41] (Table 3, Additional file 1: Table). The lowest sensitivity was observed for the most impaired cohort (proximal femoral fracture) for all algorithms.
The absolute error between the wearable device and the INDIP for the total accumulated duration of the detected gait sequences ranged from 71.9 to 358.5 s across the three algorithms which was approximately from 7 to 32% of the total duration estimated by the INDIP. Overall, except for the proximal femoral fracture cohort, GSDA and GSDB overestimated the total gait sequence duration, whereas GSDC underestimated it. The ICC(2,1) ranged from 0.68 to 1.00, with the lowest ICC(2,1) found for the multiple sclerosis cohort, in line with the largest disagreement, based on the largest limits of agreement [54], among all cohorts and the three algorithms.
Algorithm GSDA presented the overall best performance index for healthy older adults (0.819), congestive heart failure (0.853), chronic obstructive pulmonary disease (0.822), multiple sclerosis (0.735) and Parkinson’s disease (0.852) cohorts (see Additional file 1). Algorithm GSDB presented the highest performance indexes for the proximal femoral fracture cohort (0.771) and similar good performances for multiple sclerosis (0.655) and Parkinson’s disease (0.726).
Initial contact detection
Performance measures and ranking
Table 4 presents performance measures of initial contact detection algorithms, which were very similar for the four algorithms. Across algorithms and cohorts, sensitivity ranged from 0.76 to 0.83 and positive predictive values from 0.81 to 0.93, whilst relative errors ranged from 7.6 to 21.2%.
Table 4.
Initial contact detection (ICD) performance measures. Sensitivity, positive predictive value, absolute and relative errors, and overall performance index for the ICD algorithms. Values are expressed as mean and 95% confidence intervals (CI) for each cohort. In italic face: recommended algorithms. Underlined performance index indicates top-ranked algorithm for the specific cohort of that row
| Cohort | Initial contact detection | ||||
|---|---|---|---|---|---|
| Sensitivity | Positive predictive value | Absolute error [s] | Relative error [%] | Performance index | |
| ICDA | |||||
| HA | 0.80 [0.79, 0.81] | 0.91 [0.90, 0.92] | 0.06 [0.05, 0.06] | 8.0 [7.7, 8.3] | 0.804 |
| CHF | 0.79 [0.77, 0.80] | 0.89 [0.88, 0.91] | 0.07 [0.06, 0.07] | 10.9 [10.1, 11.8] | 0.771 |
| COPD | 0.81 [0.81, 0.82] | 0.93 [0.92, 0.94] | 0.07 [0.06, 0.07] | 9.1 [8.8, 9.3] | 0.790 |
| MS | 0.80 [0.79, 0.82] | 0.92 [0.91, 0.93] | 0.06 [0.06, 0.06] | 8.4 [8.1, 8.7] | 0.805 |
| PD | 0.79 [0.77, 0.80] | 0.90 [0.89, 0.91] | 0.06 [0.06, 0.06] | 8.3 [7.9, 8.6] | 0.798 |
| PFF | 0.80 [0.78, 0.81] | 0.89 [0.88, 0.90] | 0.05 [0.05, 0.06] | 7.6 [7.3, 7.9] | 0.818 |
| ICDB | |||||
| HA | 0.80 [0.79, 0.81] | 0.86 [0.85, 0.87] | 0.13 [0.13, 0.13] | 18.0 [17.8, 18.3] | 0.641 |
| CHF | 0.80 [0.78, 0.81] | 0.88 [0.86, 0.90] | 0.13 [0.13, 0.14] | 19.9 [19.3, 20.4] | 0.641 |
| COPD | 0.78 [0.77, 0.79] | 0.85 [0.84, 0.86] | 0.15 [0.15, 0.15] | 21.2 [20.9, 21.5] | 0.590 |
| MS | 0.75 [0.73, 0.77] | 0.81 [0.79, 0.83] | 0.14 [0.14, 0.15] | 19.8 [19.3, 20.4] | 0.595 |
| PD | 0.80 [0.78, 0.81] | 0.86 [0.84, 0.88] | 0.14 [0.14, 0.14] | 19.2 [18.9, 19.6] | 0.620 |
| PFF | 0.80 [0.79, 0.82] | 0.86 [0.85, 0.88] | 0.13 [0.13, 0.13] | 17.9 [17.5, 18.2] | 0.641 |
| ICDC | |||||
| HA | 0.82 [0.81, 0.83] | 0.86 [0.85, 0.88] | 0.06 [0.06, 0.07] | 8.9 [8.6, 9.2] | 0.795 |
| CHF | 0.81 [0.80, 0.82] | 0.87 [0.85, 0.88] | 0.07 [0.07, 0.08] | 11.1 [10.2, 11.9] | 0.771 |
| COPD | 0.83 [0.82, 0.83] | 0.90 [0.89, 0.91] | 0.07 [0.07, 0.07] | 9.7 [9.4, 9.9] | 0.786 |
| MS | 0.82 [0.81, 0.84] | 0.89 [0.87, 0.90] | 0.07 [0.06, 0.07] | 9.2 [8.8, 9.6] | 0.783 |
| PD | 0.80 [0.78, 0.81] | 0.84 [0.82, 0.86] | 0.07 [0.07, 0.07] | 9.4 [9.0, 9.8] | 0.766 |
| PFF | 0.80 [0.79, 0.82] | 0.81 [0.79, 0.82] | 0.07 [0.07, 0.07] | 9.6 [9.2, 10.0] | 0.759 |
| ICDD | |||||
| HA | 0.78 [0.77, 0.79] | 0.88 [0.87, 0.89] | 0.10 [0.10, 0.10] | 14.1 [13.8, 14.5] | 0.705 |
| CHF | 0.79 [0.78, 0.81] | 0.92 [0.91, 0.93] | 0.09 [0.09, 0.10] | 13.8 [13.4, 14.3] | 0.735 |
| COPD | 0.76 [0.75, 0.77] | 0.89 [0.88, 0.90] | 0.11 [0.11, 0.12] | 15.9 [15.5, 16.3] | 0.680 |
| MS | 0.78 [0.77, 0.80] | 0.89 [0.88, 0.91] | 0.10 [0.10, 0.11] | 14.4 [13.9, 15.0] | 0.706 |
| PD | 0.76 [0.75, 0.78] | 0.86 [0.84, 0.87] | 0.11 [0.11, 0.11] | 15.4 [15.0, 15.8] | 0.674 |
| PFF | 0.80 [0.78, 0.81] | 0.86 [0.85, 0.88] | 0.10 [0.09, 0.10] | 13.6 [13.1, 14.1] | 0.706 |
HA healthy adults; PD Parkinson’s disease; MS multiple sclerosis; COPD chronic obstructive pulmonary disease; CHF congestive heart failure; PFF proximal femoral fracture; LoA limits of agreement
Algorithm ICDA presented the highest overall performance index across all cohorts: healthy older adults (0.804), congestive heart failure (0.771), chronic obstructive pulmonary disease (0.790), multiple sclerosis (0.805), Parkinson’s disease (0.798) and proximal femoral fracture (0.818) reflecting the lowest absolute and relative errors, highest sensitivity, and positive predictive values.
Effect of walking speed and bout duration
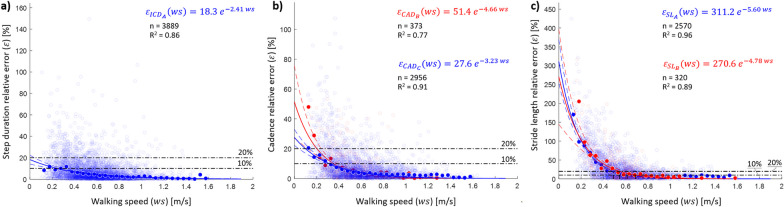
Relative errors for step duration, as extracted from the initial contacts, decreased with walking speed (R2 = 0.86), with errors lower than 10% reached for walking speeds > 0.25 m/s (Fig. 3a) [58]. Any value of walking bout duration showed median errors lower than 10%, but an overall error decrease was observed when the walking bout duration increased (R2 = 0.70, Fig. 4a). Overall, higher errors (> 50%) were observed only in the 0.9% of the detected walking bouts; these bouts were characterised by a short duration (8.37 ± 4.71 s) and slow walking speed (0.44 ± 0.24 m/s).
Fig. 3.
Effect of walking speed on the relative errors in a step duration, b CAD and c step length estimations. The empty shaded circles (n) represent the relative error for each walking bout when the selected algorithms are used (ICDA for all cohorts in blue; CADB for the congestive heart failure (CHF), chronic obstructive pulmonary disease (COPD), healthy adults (HA), multiple sclerosis (MS) and Parkinson’s disease (PD) cohorts in red; CADC for the proximal femoral fracture (PFF) cohort in blue; SLA for CHF, COPD, HA, PFF and PD in blue; and SLB for MS in red). The filled circles indicate the median relative errors quantified in consecutive walking speed (ws) windows of 0.05 m/s. The sizes of the filled circles have been calculated as the ratio between the number of empty shaded circles in a given walking speed window and the total number of empty shaded circles (i.e., all observations). The obtained exponential curves (represented in blue and red continuous lines) and equations are the result of a best-fit approach used to determine the association between walking speed and the calculated median errors; R2 values are also shown. The horizontal black dash-dotted lines visually indicate the relative error thresholds of 10 and 20%
Fig. 4.
Effect of walking bout duration on the relative errors () in a step duration, b cadence, and c step length estimations. For each parameter and the selected algorithms (ICDA for all cohorts; CADB for the congestive heart failure (CHF), chronic obstructive pulmonary disease (COPD), healthy adults (HA), multiple sclerosis (MS) and Parkinson’s disease (PD) cohorts; CADC for the proximal femoral fracture (PFF) cohort; SLA for CHF, COPD, HA, PFF and PD; and SLB for MS), the individual filled circles (n) represent the relative error for each WB, colour coded according to the walking speed measured for that specific bout. The empty grey circles indicate the median relative errors quantified in subsequent separate walking bout duration (wbd) windows of 2 s. Grey intensity represents the weight associated to the relevant observation, calculated as the ratio between the number of points in a given walking bout duration window and the total number of points, in the best-fit approach; a darker grey represents a larger weight. The black continuous lines and equations are the result of a best-fit approach used to determine the association between walking bout duration and the median errors; R2 values are also shown. The horizontal black dash-dotted lines visually indicate the relative error thresholds of 10% and 20%. For a clear visualization of the results, 95% of the walking bout duration have been reported
Cadence estimation
Performance measures and ranking
Performance measures of the cadence algorithms are presented in Table 5, reflecting a slight (4.6–7.2 steps/min) overestimation of cadence by the wearable device with respect to INDIP for all the cohorts with algorithms CADB and CADC (except for proximal femoral fracture with CADC, in which case there is a misestimation). The absolute error ranged from 5.2 to 9.3 steps/min, the relative error between 6.6% to 11.8% and ICC(2,1) ranged from 0.44 to 0.82 across the three algorithms.
Table 5.
Cadence (CAD) estimation performance measures. Cadence obtained from the INDIP and the single wearable device, bias, limits of agreement (LoA) and intra class correlation (ICC(2,1)) for comparison between systems, and overall performance index for the CAD algorithms. In italic and boldface recommended algorithms. Underlined performance index indicates top-ranked algorithm for the specific cohort of that row
| Cohort | Cadence | ||||||
|---|---|---|---|---|---|---|---|
| INDIP mean and CI [steps/min] | Single wearable device mean and CI [steps/min] | Bias and LoA [steps/min] | Absolute error [steps/min] | Relative error [%] | ICC (2, 1) | Performance index | |
| CADA | |||||||
| HA | 86.0 [85.1, 87.0] | 85.6 [84.4, 86.8] | − 0.4 [− 27.0, 26.2] | 8.6 [7.9, 9.3] | 10.5 [9.6, 11.5] | 0.65 [0.61, 0.69] | 0.538 |
| CHF | 91.2 [89.8, 92.5] | 89.8 [88.2, 91.5] | − 1.4 [− 30.7, 28.0] | 9.3 [8.2, 10.3] | 10.6 [9.5, 11.8] | 0.63 [0.57, 0.68] | 0.517 |
| COPD | 84.6 [83.7, 85.4] | 86.3 [85.2, 87.3] | 1.7 [− 17.5, 20.8] | 6.7 [6.2, 7.2] | 8.3 [7.6, 9.0] | 0.72 [0.68, 0.75] | 0.644 |
| MS | 84.6 [83.1, 86.1] | 85.7 [83.9, 87.5] | 1.1 [− 22.8, 25.0] | 8.2 [7.3, 9.2] | 10.1 [8.9, 11.3] | 0.71 [0.65, 0.75] | 0.594 |
| PD | 84.8 [83.4, 86.1] | 87.0 [85.4, 88.6] | 2.2 [− 24.9, 29.4] | 9.1 [8.1, 10.1] | 11.8 [10.4, 13.2] | 0.62 [0.56, 0.67] | 0.520 |
| PFF | 85.0 [83.4, 86.5] | 81.6 [79.9, 83.4] | − 3.3 [− 30.6, 23.9] | 8.9 [7.7, 10.0] | 10.4 [9.1, 11.7] | 0.60 [0.54, 0.67] | 0.529 |
| CADB | |||||||
| HA | 86.0 [85.1, 87.0] | 89.8 [88.9, 90.6] | 3.7 [− 16.3, 23.8] | 7.1 [6.6, 7.7] | 9.1 [8.3, 9.9] | 0.69 [0.65, 0.72] | 0.585 |
| CHF | 91.2 [89.8, 92.5] | 94.6 [93.5, 95.8] | 3.5 [− 14.0, 21.0] | 6.4 [5.8, 7.0] | 7.7 [6.9, 8.5] | 0.79 [0.76, 0.82] | 0.654 |
| COPD | 84.6 [83.7, 85.4] | 89.1 [88.3, 89.9] | 4.5 [− 10.4, 19.4] | 6.2 [5.7, 6.6] | 7.9 [7.2, 8.6] | 0.71 [0.67, 0.74] | 0.660 |
| MS | 84.6 [83.1, 86.1] | 88.5 [87.1, 89.9] | 3.9 [− 15.2, 23.0] | 7.0 [6.2, 7.8] | 9.0 [7.8, 10.2] | 0.72 [0.66, 0.76] | 0.633 |
| PD | 84.8 [83.4, 86.1] | 89.5 [88.4, 90.7] | 4.8 [− 14.3, 23.8] | 7.2 [6.5, 8.0] | 9.7 [8.5, 10.8] | 0.69 [0.63, 0.73] | 0.580 |
| PFF | 85.0 [83.4, 86.5] | 86.2 [85.0, 87.5] | 1.3 [− 20.9, 23.5] | 7.2 [6.3, 8.1] | 8.5 [7.5, 9.5] | 0.66 [0.60, 0.71] | 0.584 |
| CADC | |||||||
| HA | 86.0 [85.1, 87.0] | 87.4 [86.5, 88.3] | 1.4 [− 18.4, 21.2] | 6.4 [5.9, 6.9] | 8.1 [7.3, 8.8] | 0.74 [0.70, 0.76] | 0.653 |
| CHF | 91.2 [89.8, 92.5] | 92.2 [90.9, 93.5] | 1.0 [− 16.9, 19.0] | 5.8 [5.1, 6.4] | 6.6 [5.9, 7.3] | 0.82 [0.79, 0.84] | 0.720 |
| COPD | 84.6 [83.7, 85.4] | 86.6 [85.8, 87.4] | 2.0 [− 12.9, 17.0] | 5.2 [4.8, 5.6] | 6.6 [6.0, 7.2] | 0.77 [0.73, 0.79] | 0.693 |
| MS | 84.6 [83.1, 86.1] | 85.3 [83.9, 86.8] | 0.7 [− 18.8, 20.3] | 6.7 [5.9, 7.5] | 8.2 [7.2, 9.2] | 0.75 [0.70, 0.79] | 0.644 |
| PD | 84.8 [83.4, 86.1] | 87.1 [85.9, 88.4] | 2.3 [− 16.2, 20.9] | 6.4 [5.7, 7.1] | 8.2 [7.2, 9.2] | 0.76 [0.71, 0.79] | 0.653 |
| PFF | 85.0 [83.4, 86.5] | 82.0 [80.7, 83.3] | − 2.9 [− 31.5, 25.6] | 8.3 [7.0, 9.5] | 9.1 [7.9, 10.4] | 0.44 [0.35, 0.51] | 0.460 |
HA healthy adults; PD Parkinson’s disease; MS multiple sclerosis; COPD chronic obstructive pulmonary disease; CHF congestive heart failure; PFF proximal femoral fracture; CI confidence intervals, LoA limits of agreement, ICC intra class correlation
The highest absolute and relative errors, and the lowest ICC(2,1) were found for the proximal femoral fracture cohort. CADC had the highest performance index for healthy older adults (0.653), congestive heart failure (0.720), chronic obstructive pulmonary disease (0.693), multiple sclerosis (0.644), Parkinson’s disease (0.653). CADB presented the best performances for proximal femoral fracture (0.584) showing the lowest absolute error (7.2 steps/min), closest largest limits of agreement (− 10.1 to 24.2 steps/min), lowest relative error (8.5%) and highest ICC(2,1) (0.66). Overall good performances were also found for CADB for multiple sclerosis and Parkinson’s disease.
Effect of walking speed and bout duration
For both CADB and CADC, as walking speed increased, the relative error decreased (Fig. 3b), with speeds above 0.3 m/s resulting in an error below a 10% threshold [58]. Generally, the highest errors were observed for the shortest and slowest bouts (Fig. 4b). The walking bouts with higher errors [> 50%, n = 25 (0.8%)] had a mean duration of 8.88 s (std: 5.97 s) and slow walking speed values (0.28 ± 0.09 m/s).
Stride length estimation
Performance measures and ranking
Table 6 shows an overall overestimation of stride length by the wearable device with respect to the INDIP. The absolute error between the wearable device and the INDIP outcomes ranged from 0.15 to 0.33 m across all algorithms.
Table 6.
Stride length (SL) estimation performance measures. Stride length obtained from the INDIP and the single wearable device, bias, limits of agreement (LoA) and intra class correlation (ICC(2,1)) for comparison between systems, and overall performance index for the SL algorithms. In boldface: recommended algorithms. Underlined performance index indicates top-ranked algorithm for the specific cohort of that row
| Cohort | Stride length | ||||||
|---|---|---|---|---|---|---|---|
| INDIP mean and CI [m] | Single wearable device mean and CI [m] | Bias and LoA [m] | Absolute error [m] | Relative error [%] | ICC (2,1) | Performance index | |
| SLA | |||||||
| HA | 0.81 [0.79, 0.83] | 0.93 [0.91, 0.94] | 0.12 [− 0.24, 0.48] | 0.15 [0.14, 0.17] | 25.9 [23.2, 28.6] | 0.58 [0.53, 0.63] | 0.582 |
| CHF | 0.93 [0.90, 0.95] | 1.00 [0.98, 1.02] | 0.07 [− 0.34, 0.49] | 0.16 [0.15, 0.18] | 25.3 [22.4, 28.1] | 0.70 [0.65, 0.74] | 0.663 |
| COPD | 0.85 [0.83, 0.87] | 1.03 [1.02, 1.05] | 0.18 [− 0.20, 0.57] | 0.21 [0.19, 0.22] | 31.2 [28.0, 34.3] | 0.28 [0.21, 0.36] | 0.381 |
| MS | 0.82 [0.79, 0.85] | 1.02 [0.99, 1.04] | 0.19 [− 0.22, 0.61] | 0.21 [0.19, 0.24] | 34.1 [29.3, 38.8] | 0.41 [0.32, 0.50] | 0.462 |
| PD | 0.82 [0.79, 0.85] | 0.93 [0.90, 0.95] | 0.11 [− 0.31, 0.52] | 0.17 [0.15, 0.18] | 26.5 [23.0, 30.0] | 0.60 [0.54, 0.66] | 0.607 |
| PFF | 0.75 [0.73, 0.78] | 0.86 [0.84, 0.87] | 0.10 [− 0.32, 0.52] | 0.17 [0.15, 0.19] | 29.3 [25.2, 33.4] | 0.36 [0.26, 0.46] | 0.465 |
| SLB | |||||||
| HA | 0.81 [0.79, 0.83] | 0.97 [0.95, 0.98] | 0.16 [− 0.20, 0.52] | 0.18 [0.17, 0.19] | 29.6 [26.7, 32.5] | 0.52 [0.47, 0.57] | 0.546 |
| CHF | 0.93 [0.90, 0.95] | 1.04 [1.02, 1.07] | 0.12 [− 0.30, 0.53] | 0.17 [0.16, 0.19] | 27.4 [24.2, 30.5] | 0.66 [0.61, 0.71] | 0.604 |
| COPD | 0.85 [0.83, 0.87] | 1.08 [1.06, 1.09] | 0.23 [− 0.16, 0.62] | 0.24 [0.23, 0.25] | 35.8 [32.5, 39.1] | 0.20 [0.12, 0.27] | 0.345 |
| MS (*SLB) | 0.82 [0.79, 0.85] | 0.99 [0.96, 1.01] | 0.16 [− 0.24, 0.57] | 0.19 [0.17, 0.21] | 31.2 [26.7, 35.7] | 0.47 [0.38, 0.55] | 0.487 |
| PD | 0.82 [0.79, 0.85] | 0.97 [0.94, 0.99] | 0.15 [− 0.27, 0.56] | 0.19 [0.17, 0.20] | 29.7 [25.9, 33.4] | 0.55 [0.48, 0.62] | 0.537 |
| PFF | 0.75 [0.73, 0.78] | 0.89 [0.88, 0.91] | 0.14 [− 0.28, 0.56] | 0.18 [0.16, 0.20] | 32.2 [27.8, 36.6] | 0.31 [0.20, 0.40] | 0.448 |
| SLC | |||||||
| HA | 0.81 [0.79, 0.83] | 0.91 [0.90, 0.92] | 0.10 [− 0.31, 0.50] | 0.17 [0.16, 0.18] | 29.0 [26.2, 31.8] | 0.42 [0.36, 0.48] | 0.509 |
| CHF | 0.93 [0.90, 0.95] | 0.98 [0.96, 0.99] | 0.05 [− 0.47, 0.56] | 0.21 [0.19, 0.22] | 30.3 [26.9, 33.8] | 0.46 [0.39, 0.52] | 0.473 |
| COPD | 0.85 [0.83, 0.87] | 0.95 [0.94, 0.96] | 0.10 [− 0.32, 0.52] | 0.18 [0.17, 0.19] | 26.9 [24.2, 29.6] | 0.26 [0.19, 0.34] | 0.420 |
| MS | 0.82 [0.79, 0.85] | 0.95 [0.94, 0.97] | 0.13 [− 0.32, 0.58] | 0.20 [0.18, 0.22] | 32.6 [27.9, 37.3] | 0.22 [0.11, 0.32] | 0.387 |
| PD | 0.82 [0.79, 0.85] | 0.91 [0.89, 0.93] | 0.09 [− 0.35, 0.53] | 0.18 [0.17, 0.20] | 30.5 [26.7, 34.4] | 0.45 [0.37, 0.53] | 0.498 |
| PFF | 0.75 [0.73, 0.78] | 0.85 [0.84, 0.86] | 0.09 [− 0.36, 0.54] | 0.21 [0.19, 0.22] | 34.5 [30.7, 38.4] | 0.11 [0.00, 0.22] | 0.328 |
| SLD | |||||||
| HA | 0.81 [0.79, 0.83] | 0.88 [0.86, 0.90] | 0.07 [− 0.62, 0.76] | 0.28 [0.26, 0.30] | 41.9 [38.2, 45.5] | 0.14 [0.06, 0.21] | 0.250 |
| CHF | 0.93 [0.90, 0.95] | 0.90 [0.88, 0.93] | − 0.03 [− 0.84, 0.79] | 0.33 [0.30, 0.35] | 42.3 [38.1, 46.6] | 0.10 [0.01, 0.19] | 0.205 |
| COPD | 0.85 [0.83, 0.87] | 0.93 [0.91, 0.96] | 0.08 [− 0.63, 0.80] | 0.29 [0.27, 0.31] | 40.4 [36.9, 43.9] | 0.03 [− 0.05, 0.11] | 0.200 |
| MS | 0.82 [0.79, 0.85] | 0.92 [0.89, 0.96] | 0.10 [− 0.59, 0.78] | 0.28 [0.25, 0.30] | 41.3 [35.2, 47.4] | 0.15 [0.04, 0.26] | 0.250 |
| PD | 0.82 [0.79, 0.85] | 0.85 [0.82, 0.88] | 0.03 [− 0.73, 0.79] | 0.30 [0.28, 0.33] | 44.9 [39.3, 50.5] | 0.10 [0.00, 0.20] | 0.225 |
| PFF | 0.75 [0.73, 0.78] | 0.85 [0.81, 0.88] | 0.09 [− 0.67, 0.85] | 0.30 [0.27, 0.33] | 47.7 [42.0, 53.5] | − 0.04 [− 0.14, 0.07] | 0.172 |
Stride length obtained from the INDIP and the single wearable device, bias, limits of agreement (LoA) and intra class correlation (ICC(2,1)) for comparison between systems, and overall performance index for the SL algorithms. In italicface: recommended algorithms
HA healthy adults; PD Parkinson’s disease; MS multiple sclerosis; COPD chronic obstructive pulmonary disease; CHF congestive heart failure; PFF proximal femoral fracture; CI confidence intervals, LoA limits of agreement, ICC intra class correlation
The mean relative errors ranged from 25.3 to 34.1% for SLA, and similarly from 27.4 to 35.8% for SLB. These were larger for SLC (ranging from 29.0 to 34.5%) and for SLD (40.4 to 47.7%). The ICC(2,1) for SLA were the largest, ranging from 0.28 to 0.70, followed by SLB with a range from 0.20 to 0.66. The ICC(2,1) for SLC were below 0.5, and below 0.15 for SLD.
Overall, SLA presented the highest performance indexes for all cohorts excluding multiple sclerosis, with the following values: healthy older adults (0.582), congestive heart failure (0.663), chronic obstructive pulmonary disease (0.381), Parkinson’s disease (0.607), and proximal femoral fracture (0.465). In the multiple sclerosis cohort, SLB had the highest performance index (0.487).
Effect of walking speed and bout duration
Critical errors in the stride length estimate were observed for the slowest bouts, with values decreasing below 20% only for walking speed > 0.5 m/s and below 10% only for 0.6 m/s (Fig. 3c). Highest errors were also still associated with shortest and slowest bouts (Fig. 4c); specifically, the shortest bouts (≤ 10 s) had a mean error of 32.6%, while the longest ones (> 60 s) 9.3%. Overall, errors higher than 50% were observed in about 17% of the total number of walking bouts. These bouts were short (13.03 ± 10.53 s), with slow walking speed (0.36 ± 0.13 m/s) and short stride length values (0.45 ± 0.17 m).
Discussion
This is the first study presenting a comprehensive comparative assessment of a broad range of algorithms applied to a single wearable device, for estimating key digital mobility outcomes pertaining to gait (i.e., gait sequences, individual steps, cadence and stride length) in heterogeneous diseases and using data from the real world. In this work, we have described algorithms’ performances, selected the best algorithm for each digital mobility outcome and cohort, analysed the influence of walking speed and walking bout duration on their performance, and provided recommendations for their selection and implementation for real-world gait analysis.
Gait sequence detection
When comparing all gait sequence detection algorithms, concurrent validity was high, reflected by ICC(2,1) values and performance measures above 0.7, matching previous work [16, 41, 59]. Accuracy, specificity, and positive predictive values were very high for all gait sequence detection algorithms. Our results were comparable to previous work on a different population (post-stroke survivors) which reported similar sensitivity (0.92) and positive predictive value (0.84) of gait sequence detection algorithms implemented on data obtained from bilateral wearable devices on the feet [16]. The excellent results for specificity are similar or even higher than those reported previously in the literature 0.96 in Parkinson’s disease [59] and 0.93 in stroke survivors [16]. This is encouraging, as gait analysis relies on high specificity, which corresponds to a correct identification of gait sequences (high number of true positive events) while avoiding the misidentification of gait sequences (low number of false positive events). Avoiding incorrect identification of gait-sequences (as also reflected by positive predictive values) is preferable, to avoid the extraction of digital mobility outcomes from activities which are not directly representative of gait, such as shuffling or transitions [59].
When considering differences between algorithms, GSDA and GSDB tended to overestimate the total walking time (total gait sequence duration). This could potentially relate to different signal characteristics between the compared systems (low-back signals recorded with the wearable device may be different from feet signals [55] recorded with the INDIP). Slow gait, curved paths and short walking bouts with insufficient steady-pace phases for the spectral analysis could have also influenced the results, as the characteristics of the signals are more variable and the periods are less uniform than in steady-pace gait undertaken at faster speeds along straight paths [41].
Based on our findings collectively, we recommend using GSDB on cohorts with slower gait speeds and substantial gait impairments (e.g., proximal femoral fracture). This may be because this algorithm is based on the acceleration norm (overall accelerometry signal rather than a specific axis/direction (e.g., vertical), hence it is more robust to sensor misalignments that are common in unsupervised real-life settings. Moreover, the use of adaptive threshold, that are derived from the features of a subject’s data and applied to step duration for detection of steps belonging to gait sequences, allows increased robustness of the algorithm to irregular and unstable gait patterns. GSDA algorithm may be more suitable for cohorts with a faster gait speed and regular gait pattern (e.g., healthy older adults). This algorithm is based on a convolutional transformation (based on a gait cycle) of a single axis signal [40], potentially justifying its suitability to conditions characterised by more stable and regular gait patterns.
Initial contact detection
Overall, all algorithms investigated for initial contact detection presented excellent sensitivity and positive predictive values (all above 0.81) and relative errors below 21% in diverse cohorts of patients. These errors are in line with previous work, although slightly higher than those assessed in laboratory or controlled and supervised environments, ranging between 4 and 13% [28, 39, 55]. Positive predictive values resulted were larger than sensitivity (although sensitivity values were > 0.75). This could be due to a lower number of false positive events (wrongly identified initial contact events) with respect to true positive events; slightly lower sensitivity measures reflect a higher number of missed initial contact events. Similar to gait sequence detection, higher positive predictive values (higher numbers of correctly identified initial contacts) are preferable, as gait assessment based on incorrectly identified events could lead to invalid digital mobility outcome extraction and misleading clinical interpretation. Low relative errors (< 11%), found for ICDA and ICDC, for step duration across all cohorts based on similar approaches are very encouraging and concurs with previous work which reported errors between 4 and 13% from data collected in laboratory conditions [39, 60].
Accurate detection of steps is critical for estimation of a plethora of digital mobility outcomes like cadence, step symmetry, gait variability, etc., which might have relevant clinical value (e.g., for the differentiation of stages of neurodegenerative diseases [60]). In addition, step detection can be used to refine the identification of gait sequences [41], and thus, the definition of a walking bout, which highlights the importance of using a robust algorithm with high sensitivity and positive predictive value.
For all cohorts, we recommend the use of the ICDA for the identification of initial contact events, given the lowest absolute and relative errors (both in mean and standard deviation of step duration and initial contact time event) and best performance indexes. ICDA is an optimized implementation of the algorithm based on continuous wavelet transform and peak detection originally presented in [42], and is frequently used and reported in the literature for heel-strike or initial time contact event detection [39, 61]. This algorithm has been previously validated under different conditions, producing similar results in algorithm performance [44] even if tested under less challenging conditions (such as supervised lab/clinical settings). To increase robustness to the variety of impaired gait patterns, ICDA applies additional detrending and filtering before the continuous wavelet transform, then it detects the step-related peaks as maxima between zero-crossings (instead of using a predefined threshold for peak amplitude).
Cadence estimation
The excellent performances of cadence algorithms, reflected by low relative errors of < 12%, were in line with [17, 41, 45], or lower than previous results reported in the literature (13–14%) [16]. As based upon [53], moderate to excellent ICC(2,1) (> 0.70) were found in all cohorts except proximal femoral fracture, for the CADB and CADC algorithms. These results confirm the robustness of cadence estimation in all cohorts. Proximal femoral fracture data showed the lowest ICC(2,1) values but good performances for the other metrics. This may be partially explained by the high asymmetry and the slow speed that characterize the proximal femoral fracture cohort (all proximal femoral fracture patients walked at a speed of < 1.29 m/s) [62]. This and the use of walking aids may have impacted the wearable device signal quality (amplitude and shape) and hence challenged the processing techniques on which the algorithms are based (i.e., wavelet transformations for CADA and CADB [41, 42], and zero-crossings for CADC [45]).
The recommended algorithm for cadence estimation is dependent upon the mobility function of the cohort. Overall, CADC performances were excellent across all cohorts, especially for groups with higher gait speeds. CADB was more robust in the proximal femoral fracture cohort as reflected by the performance index. Therefore, we suggest the implementation of CADB in cohorts with compromised gait speed and symmetry (e.g., severe or advanced neurological diseases) for which a zero-crossing approach may not be so suitable.
It is worth mentioning that the methodology for initial contact events/step detection, used by initial contact detection and cadence algorithms, includes two main stages. The first is related to the processing of the wearable device acceleration signal in order to remove noise, artefacts and to enhance the step-related features (e.g., zero-phase low-pass filtering, detrending). Then, on the processed acceleration signal, the initial contacts/steps are detected using peak detection or zero-crossing approaches. The combination of the various techniques for these two stages allowed us to implement optimized versions of state-of-the art algorithms.
Although initial contact detection and cadence algorithms are based on similar approaches, our results are in line with previous findings showing that the use of a peak detection approach may be more suitable for identification of events (initial contact detection), whereas zero-crossing techniques result in more accurate identification of cyclic events and step segmentation, required for the cadence estimation. All in all, as observed by Panebianco et al. [61], this underlines that each principle is better tailored to each digital mobility outcome; i.e., a wavelet transformation with peak detection is better suited for initial contact detection, whereas the zero-crossing approach seems better suited for the cadence.
Stride length estimation
The performances of the stride length metrics are lower with respect to the other metrics presented in this work (e.g. cadence, initial contact detection), as reflected by relatively high absolute and relative errors, and low ICC(2,1). This could be due to the nature of the lower-back accelerometry signals recorded in real-world conditions, from which the stride length is calculated. Particularly, the estimation of the position of the centre of mass (by double integration of the acceleration) and the inverted pendulum models on which stride length algorithms are based, assumes straight walking trajectories. Moreover these methodological principles do not consider turns or non-straight walking trajectories (i.e. veering). All of these deviations from a purely symmetrical and straight walking pattern are frequently found in real-world recordings [36].
Among the four algorithms, our recommendation is to use SLA in all cohorts, given the lowest absolute, relative error and highest ICC(2,1), as summarized by the performance indexes. It must be noted that SLB was the best performer for the multiple sclerosis cohort, which is based on the same algorithm principle as SLA, but using a different correction factor implemented to estimate stride length [48]. All in all, SLA showed good performance and similar to SLB also for multiple sclerosis.
In general stride length algorithms tended to overestimate stride length between 0.07 and 0.16 m, this could be due to the correction factors that are implemented in both SLA and SLB [17]. Overall, the results highlight the better suitability of biomechanically-based algorithms, rather than those based solely upon machine-learning approaches. This is in line with the results observed on a previous study which implemented the same algorithms, trained on the same pre-available datasets [17]. This could be due to the fact that the biomechanically-based algorithms are less dependent on the intensity and morphology of the acceleration signals, and are highly influenced by the gait speed and irregularity of the gait patterns [17], which highlights a potential limitation in the generalization of the machine-learning based models when applied to external datasets. Future and novel machine-learning/deep-learning based models based on bigger datasets might produce better results.
The protocol used in the present study covered a comprehensive range of real-world scenarios. As such, results showed higher errors than those reported in previous studies: almost double with respect to [28] where results were evaluated from sensors on the shanks, and similar to [17] showing root mean square error between 0.04 and 0.18 m, where data was collected in the laboratory. This could potentially be due to the additional challenges involved in real-world and uncontrolled gait assessments presented in the current study, and the use of different data, i.e., based on a wearable device and on a different reference system for comparison. Moreover, to ensure a fair comparison of the algorithms, the walking bout (input) on which the algorithms were applied was defined and “imposed” by the reference system (INDIP). This could have potentially led to higher errors stemming from applying the algorithms to a wearable device signal with reduced amplitude and noisier characteristics with respect to the signal identified by the INDIP (sensors on the feet), especially for short and slow walking bout. All in all, our results highlight that future studies should focus on the development and optimization of stride length algorithms for increasing robustness of stride length estimation in order for this to be a useful (i.e., sensitive to change) digital mobility outcome that could be used in clinical interventional studies.
Effect of walking speed and walking bout duration on algorithms’ performances
Generally, the performances of all algorithms significantly worsened for walking speeds below 0.5 m/s, which is considered as a threshold between slow and medium speed walkers [2], confirming what is well established in the literature [17, 63, 64]. This may be explained by the fact that the signals recorded with the wearable device in slow walkers are characterized by a compromised amplitude, non-uniform gait cycles [64, 65], and variable and irregular gait patterns [17]. Likewise, the lowest performances observed within proximal femoral fracture, may be explained by the lower speed and irregular gait patterns of this cohort [62]. Accordingly, the choice of algorithms for digital mobility outcome extraction should consider its sensitivity to gait speed, given its proven confounding effect on gait analysis [66], and the population of interest.
Walking bout duration also significantly affected the performances of the cadence algorithms, with an overall significant reduction of the relative error observed for longer walking bouts when estimating both step duration and cadence. This trend was also likely magnified by the fact that the shortest bouts were also the slowest ones and confirms similar previous results [34]. This could also be due to the fact that the impact of breaks (start and stop) and/or mis-detected strides in short walking bouts may be much larger than in longer walking bouts when quantifying algorithms’ performances.
Individual relative errors for stride length were higher for short walking bouts (e.g., < 10 s), although the median error did not seem to be significantly affected by bout length. digital mobility outcomes estimated from short walking bouts, which have been reported as the majority (about 50%) in real-world conditions [21, 67], should have special consideration as, in agreement with previous work, these walking bouts were observed to be the slowest [67], and therefore more sensitive to higher error estimation.
General discussion
When considering the optimal location of the sensor, the signals recorded at the lower back are less robust than at other locations, such as the foot or shank, for the identification of initial contact events [61], although still more accurate than wrist data [68]. However, the lower back is among the most clinically favourable location for a single device, given its cost (one device), its location near to the centre of mass (which represents the overall human motion pattern), ergonomic conditions when worn attached to a belt or affixed to the skin, and its clinical value for fall risk, trunk stability and balance control, among others [21, 60, 69].
An advantage of real-world gait monitoring is the possibility of capturing a large number of diverse walking bouts and truly unsupervised gait performance in an ecologically valid environment [20]. However, the presence of contextual factors in a real-world context, which were not accounted for in this study, may have significantly influenced the performance of the algorithms. In particular, the presence of turns, the deviation from a straight path or other gait tasks (e.g., slope, presence of stairs or/and obstacles, crowdedness of space, visibility of trajectory), and the usage of various walking aids may have altered the gait pattern of the participant [20] and may partially explain the larger errors observed for stride length.
When comparing the performance between spatial and temporal digital mobility outcomes, the results indicate that the temporal characteristics (initial contact events, step duration, cadence) of gait, analysed with the proposed algorithms were more robust and valid than the spatial ones. This may be due to the fact that lower-back signals are better tailored to estimate particular events in the signal (i.e., initial contact events) and to assess its periodicity (i.e., cadence estimation) than to estimate displacements. These aspects should be considered when using the proposed algorithms, especially when interpreting findings for clinical applications and assessing minimal detectable changes in pathological gait. Moreover, it should be noted that given the biomechanical relationship between temporal and spatial features of gait, the identification of temporal estimates may directly impact on spatial calculations [48].
Limitations
The results presented here are derived from real-world data comparing outcomes from a single wearable device to a reference system, INDIP, that has been thoroughly characterized and validated in a laboratory context, against a stereophotogrammetric system [23]. We did not include validation of DMOs derived from the single wearable device against a laboratory-based reference system as the focus of this study was on real-world gait. It must be noted that a complete algorithm ranking methodology should not only consider the overall findings for each cohort (as in this study) but should also consider the performance of algorithms on stratified subgroups (e.g., based on gait speed: slow-medium-fast walkers). This can be done by assigning a higher weight to the slow walkers’ results, given that their corresponding signals are more challenging and yield higher errors, as observed in this study. In addition, the percentage of walking bouts, as well as participants, in which the algorithm successfully provided digital mobility outcomes estimates should be considered to scale the overall performance of algorithms [24]. Thus, a simplified, although comprehensive, implementation of the ranking methodology could be seen as a limitation of this study. Nonetheless, the purpose of this was to provide an overall recommendation on the algorithm that performed best for each digital mobility outcome assessed in challenging real-world environments [20]. We are aware that, using a 2.5-h window of activity in the real world for the validation purposes, we may not have captured change and higher variability in mobility that are due to fatigue or the cyclic nature of activity. We also suggest that the inclusion of laboratory assessments for the implementation of the ranking methodology could be relevant. Indeed, even if collected under controlled or semi-structured conditions, data from short and slow walking bouts, that are typical in lab-based settings, may add variability and challenge algorithm performance [19]. In addition, the effect of walking aid use on results has not been assessed in this study. Thus, future work assessing this aspect could be clinically relevant, given the potential impact that walking aids (and the variety of types of walking aids) have on the quality of the wearable device signals and reference data [17], and as a consequence, on the assessment of the algorithm’s performance.
Conclusions
This work was aimed at providing recommendations to implement and select algorithms for real-world gait analysis using lower-back worn sensors in patient cohorts with mobility impairments. We achieved this by comprehensively assessing and ranking algorithms’ performances, and we evaluated the effect of walking speed and walking bout duration on those performances.
The results highlighted good to excellent performances of the top algorithms in all cohorts. Particularly, algorithms for cadence and initial contact event detection were the most robust for all cohorts. Performances on gait sequence detection showed good performance measures, particularly when assessing sensitivity (> 0.70), positive predictive value (> 0.80), accuracy (> 0.95) and specificity (> 0.97). However, stride length estimation was the most challenging digital mobility outcome to estimate (with absolute error < 0.21 m). Relative errors for step duration and cadence generally decreased for longer walking bouts. Lower gait speeds (below 0.5 m/s) negatively influenced step duration, cadence and stride length estimates. We identified two top-performer algorithms for gait sequence detection [16] and cadence [45, 46], and a single best performer for initial contact detection [16] and stride length [47, 48]. The proximal femoral fracture cohort was the most challenging for algorithm performance.
In conclusion, the identified algorithms allow a robust estimation of digital mobility outcomes and gait characterization, with potential for improvement identified for stride length. Throughout this study we made recommendations for algorithm selection and implementation. Thus, our findings can be used to support future choices of the most suitable algorithms for real-world gait analysis, depending on type of cohort and research question. Finally, these results may inform future design of novel and more efficient gait analysis algorithms.
Supplementary Information
Additional file 1. Details of ranking methodology.
Acknowledgements
The authors would like to acknowledge all the members of the Mobilise-D WP2 work-package for continuous discussion and critical input. They are particularly grateful to the participants in the study for their time and enthusiastic contribution, especially during the pandemic.
Abbreviations
- CAD
Cadence estimation
- CI
Confidence intervals
- CHF
Congestive heart failure
- COPD
Chronic obstructive pulmonary disease
- d
Duration
- FP
False positive
- FN
False negative
- GSD
Gait sequence detection
- HA
Healthy adults
- ICC(2,1)
Intra-class correlation coefficient
- ICD
Initial contact detection
- INDIP
INertial modules, DIstance Sensors and Pressure insoles
- LoA
Limits of agreement
- MS
Multiple sclerosis
- PD
Parkinson’s disease
- PFF
Proximal femoral fracture
- SL
Stride length estimation
- TN
True negative
- TP
True positive
- WB
Walking bout
- WBD
Walking bout duration
- WD
Wearable device
- ws
Walking speed
- FIR
Finite impulse response filter
Author contributions
Study design: SDD, CM, LR, AC, AM. Data collection and pre-processing of the data: TB, FS, KS, LA, PB, SB, FS, MC, EB, EG, CH, LP, IA and LS. Patient recruitment and clinical oversight: BS, WM, CB, JMH, IV, EH, DM, AJY, LR. Algorithm development: AP-I, AS, MU, AK, EG, FK. Data management platform and analysis: HH, DS, CK, MU. Data analysis, statistical analysis and tables creation: MEM-A. Figures preparation: TB. Data interpretation: MEM-A, SDD, TB, LR, AC, CM. Drafting of the manuscript: MEM-A, SDD and CM. Intellectual contribution: MEM-A, SDD, TB, LR, AC, A-EC, SF, SK, JG-A, CM, AC, CK, AM, HS, KA, BE, BC, AK, BV, FK, LC, MF, MN, BV, AP-I. All authors have provided critical intellectual input during the revision of the manuscript. All authors read and approved the final manuscript.
Funding
This work was supported by the Mobilise-D project that has received funding from the Innovative Medicines Initiative 2 Joint Undertaking (JU) under Grant Agreement No. 820820. This JU receives support from the European Union’s Horizon 2020 research and innovation program and the European Federation of Pharmaceutical Industries and Associations (EFPIA). SDD, LR, AY were also supported by the Innovative Medicines Initiative 2 Joint Undertaking (IMI2 JU) project IDEA-FAST—Grant Agreement 853981. LA, LR, AY and SDD were also supported by the National Institute for Health Research (NIHR) Newcastle Biomedical Research Centre (BRC) based at The Newcastle upon Tyne Hospital NHS Foundation Trust, Newcastle University and the Cumbria, Northumberland and Tyne and Wear (CNTW) NHS Foundation Trust. LA, LR, AY and SDD were also supported by the NIHR/Wellcome Trust Clinical Research Facility (CRF) infrastructure at Newcastle upon Tyne Hospitals NHS Foundation Trust. This study was also supported by the National Institute for Health Research (NIHR) through the Sheffield Biomedical Research Centre (BRC, Grant Number IS-BRC-1215–20017). ISGlobal acknowledges support from the Spanish Ministry of Science and Innovation through the “Centro de Excelencia Severo Ochoa 2019–2023” Program (CEX2018-000806-S), and from the Generalitat de Catalunya through the CERCA Program. All opinions are those of the authors and not the funders. The content in this publication reflects the authors’ view, and neither IMI nor the European Union, EFPIA, NHS, NIHR, DHSC, or any associated partners are responsible for any use that may be made of the information contained herein.
Availability of data and materials
Representative data from the dataset and recommended algorithms presented in this study can be found on online repositories: Data can be found on Zenodo, 10.5281/zenodo.7547125. Algorithms can be found on GitHub, 10.5281/zenodo.7575872.
Declarations
Ethics approval and consent to participate
Participants were recruited in five sites: Tel Aviv Sourasky Medical Center, Israel (ethics approval granted by the Helsinki Committee, Tel Aviv Sourasky Medical Center, Tel Aviv, Israel, 0551-19TLV), Robert Bosch Foundation for Medical Research, Germany (ethics approval granted by the ethical committee of the medical faculty of The University of Tübingen, 647/2019BO2), University of Kiel, Germany (ethics approval granted by the ethical committee of the medical faculty of Kiel University, D438/18), The Newcastle upon Tyne Hospitals NHS Foundation Trust, UK and Sheffield Teaching Hospitals NHS Foundation Trust, UK (ethics approval granted by London – Bloomsbury Research Ethics committee, 19/LO/1507). All participants gave written informed consent prior to undergoing a clinic/laboratory-based session to record generic and disease-specific characterizations.
Consent for publication
NA.
Competing interests
A. Mueller and F. Kluge are employees of, and may hold stock in, Novartis. B. Eskofier reports consulting activities with adidas AG, Siemens AG, Siemens Healthineers AG, WSAudiology GmbH outside of the study. He is a shareholder in Portabiles HealthCare Technologies GmbH. In addition, Dr. Eskofier holds a patent related to gait assessment. H. Sillén is an employee of, and may hold stock in, AstraZeneca. M. Froelich is an employee of Grunenthal. L. Palmerini and L. Chiari are co-founders and own shares of mHealth Technologies (https://mhealthtechnologies.it/). L. Schwickert and C. Becker are consultants of Philipps Healthcare, Bosch Healthcare, Eli Lilly, Gait-up. M. Niessen is an employee of McRoberts. Jeff Hausdorff reports having submitted a patent for assessment of mobility using wearable sensors in 400 PD.
Footnotes
The original online version of this article was revised: the errors in Table 1, and in Discussion section has been corrected.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Change history
5/3/2024
A Correction to this paper has been published: 10.1186/s12984-024-01361-6
References
- 1.Van Kan GA, Rolland Y, Andrieu S, Bauer J, Beauchet O, Bonnefoy M, et al. Gait speed at usual pace as a predictor of adverse outcomes in community-dwelling older people an International Academy on Nutrition and Aging (IANA) Task Force. J Nutr Health Aging. 2009;13(10):881–9. doi: 10.1007/s12603-009-0246-z. [DOI] [PubMed] [Google Scholar]
- 2.Studenski S, Perera S, Patel K, Rosano C, Faulkner K, Inzitari M, et al. Gait speed and survival in older adults. JAMA. 2011;305(1):50–58. doi: 10.1001/jama.2010.1923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Handoll HH, Sherrington C, Mak JC. Interventions for improving mobility after hip fracture surgery in adults. Cochrane Database Syst Rev. 2011 doi: 10.1002/14651858.CD001704.pub4. [DOI] [PubMed] [Google Scholar]
- 4.Henderson EJ, Lord SR, Brodie MA, Gaunt DM, Lawrence AD, Close JC, et al. Rivastigmine for gait stability in patients with Parkinson’s disease (ReSPonD): a randomised, double-blind, placebo-controlled, phase 2 trial. Lancet Neurol. 2016;15(3):249–258. doi: 10.1016/S1474-4422(15)00389-0. [DOI] [PubMed] [Google Scholar]
- 5.Mirelman A, Rochester L, Maidan I, Del Din S, Alcock L, Nieuwhof F, et al. Addition of a non-immersive virtual reality component to treadmill training to reduce fall risk in older adults (V-TIME): a randomised controlled trial. Lancet. 2016;388(10050):1170–1182. doi: 10.1016/S0140-6736(16)31325-3. [DOI] [PubMed] [Google Scholar]
- 6.Taylor L, Parsons J, Taylor D, Binns E, Lord S, Edlin R, et al. Evaluating the effects of an exercise program (Staying UpRight) for older adults in long-term care on rates of falls: study protocol for a randomised controlled trial. Trials. 2020;21(1):1–11. doi: 10.1186/s13063-019-3949-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Atrsaei A, Corra MF, Dadashi F, Vila-Cha N, Maia L, Mariani B, et al. Gait speed in clinical and daily living assessments in Parkinson’s disease patients: performance versus capacity. NPJ Parkinsons Dis. 2021;7(1):24. doi: 10.1038/s41531-021-00171-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Polhemus A, Ortiz LD, Brittain G, Chynkiamis N, Salis F, Gaßner H, et al. Walking on common ground: a cross-disciplinary scoping review on the clinical utility of digital mobility outcomes. NPJ Digit Med. 2021;4(1):1–14. doi: 10.1038/s41746-021-00513-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rochester L, Mazzà C, Mueller A, Caulfield B, McCarthy M, Becker C, et al. A roadmap to inform development, validation and approval of digital mobility outcomes: the Mobilise-D approach. Digit Biomark. 2020;4(1):13–27. doi: 10.1159/000512513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mobbs RJ, Perring J, Raj SM, Maharaj M, Yoong NKM, Sy LW, et al. Gait metrics analysis utilizing single-point inertial measurement units: a systematic review. mHealth. 2022 doi: 10.21037/mhealth-21-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Breasail MÓ, Biswas B, Smith MD, Mazhar MKA, Tenison E, Cullen A, et al. Wearable GPS and accelerometer technologies for monitoring mobility and physical activity in neurodegenerative disorders: a systematic review. Sensors. 2021;21(24):8261. doi: 10.3390/s21248261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Deane KH, Flaherty H, Daley DJ, Pascoe R, Penhale B, Clarke CE, et al. Priority setting partnership to identify the top 10 research priorities for the management of Parkinson’s disease. BMJ Open. 2014;4(12):e006434. doi: 10.1136/bmjopen-2014-006434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Port RJ, Rumsby M, Brown G, Harrison IF, Amjad A, Bale CJ. People with Parkinson’s disease: what symptoms do they most want to improve and how does this change with disease duration? J Parkinsons Dis. 2021;11(2):715–724. doi: 10.3233/JPD-202346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Viceconti M, Hernandez Penna S, Dartee W, Mazzà C, Caulfield B, Becker C, et al. Toward a regulatory qualification of real-world mobility performance biomarkers in Parkinson’s patients using digital mobility outcomes. Sensors. 2020;20(20):5920. doi: 10.3390/s20205920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bouça-Machado R, Jalles C, Guerreiro D, Pona-Ferreira F, Branco D, Guerreiro T, et al. Gait kinematic parameters in Parkinson’s disease: a systematic review. J Parkinsons Dis. 2020;10(3):843–853. doi: 10.3233/JPD-201969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Paraschiv-Ionescu A, Soltani A, Aminian K, editors. Real-world speed estimation using single trunk IMU: methodological challenges for impaired gait patterns. In: 2020 42nd annual international conference of the IEEE Engineering in Medicine & Biology Society (EMBC). IEEE; 2020. [DOI] [PubMed]
- 17.Soltani A, Aminian K, Mazza C, Cereatti A, Palmerini L, Bonci T, et al. Algorithms for walking speed estimation using a lower-back-worn inertial sensor: a cross-validation on speed ranges. IEEE Trans Neural Syst Rehabil Eng. 2021;29:1955–1964. doi: 10.1109/TNSRE.2021.3111681. [DOI] [PubMed] [Google Scholar]
- 18.Kluge F, Del Din S, Cereatti A, Gaßner H, Hansen C, Helbostad JL, et al. Consensus based framework for digital mobility monitoring. PLoS ONE. 2021;16(8):e0256541. doi: 10.1371/journal.pone.0256541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mazzà C, Alcock L, Aminian K, Becker C, Bertuletti S, Bonci T, et al. Technical validation of real-world monitoring of gait: a multicentric observational study. BMJ Open. 2021;11(12):e050785. doi: 10.1136/bmjopen-2021-050785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Warmerdam E, Hausdorff JM, Atrsaei A, Zhou Y, Mirelman A, Aminian K, et al. Long-term unsupervised mobility assessment in movement disorders. Lancet Neurol. 2020;19(5):462–470. doi: 10.1016/S1474-4422(19)30397-7. [DOI] [PubMed] [Google Scholar]
- 21.Del Din S, Godfrey A, Galna B, Lord S, Rochester L. Free-living gait characteristics in ageing and Parkinson’s disease: impact of environment and ambulatory bout length. J Neuroeng Rehabil. 2016;13(1):46. doi: 10.1186/s12984-016-0154-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Del Din S, Kirk C, Yarnall AJ, Rochester L, Hausdorff JM. Body-worn sensors for remote monitoring of Parkinson’s disease motor symptoms: vision, state of the art, and challenges ahead. J Parkinsons Dis. 2021;11(s1):S35–S47. doi: 10.3233/JPD-202471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Salis F, Bertuletti S, Bonci T, Caruso M, Scott K, Alcock L, et al. A multi-sensor wearable system for the assessment of diseased gait in real-world conditions. Front Bioeng Biotechnol. 2023;11:518. doi: 10.3389/fbioe.2023.1143248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bonci T, Keogh A, Del Din S, Scott K, Mazzà C, Consortium M-D An objective methodology for the selection of a device for continuous mobility assessment. Sensors. 2020;20(22):6509. doi: 10.3390/s20226509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Micó-Amigo ME, Bonci T, Paraschiv-Ionescu A, Ullrich M, Kirk C, Soltani A, et al. Assessing real-world gait with digital technology? Validation, insights and recommendations from the Mobilise-D consortium. Res Square. 2022 doi: 10.21203/rs.3.rs-2088115/v1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Keogh A, Alcock L, Brown P, Buckley E, Brozgol M, Gazit E, et al. Acceptability of wearable devices for measuring mobility remotely: observations from the Mobilise-D technical validation study. Digit Health. 2023;9:20552076221150745. doi: 10.1177/20552076221150745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bertuletti S, Della Croce U, Cereatti A. A wearable solution for accurate step detection based on the direct measurement of the inter-foot distance. J Biomech. 2019;84:274–277. doi: 10.1016/j.jbiomech.2018.12.039. [DOI] [PubMed] [Google Scholar]
- 28.Trojaniello D, Cereatti A, Pelosin E, Avanzino L, Mirelman A, Hausdorff JM, et al. Estimation of step-by-step spatio-temporal parameters of normal and impaired gait using shank-mounted magneto-inertial sensors: application to elderly, hemiparetic, parkinsonian and choreic gait. J Neuroeng Rehabil. 2014;11(1):1–12. doi: 10.1186/1743-0003-11-152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bertoli M, Cereatti A, Trojaniello D, Avanzino L, Pelosin E, Del Din S, et al. Estimation of spatio-temporal parameters of gait from magneto-inertial measurement units: multicenter validation among Parkinson, mildly cognitively impaired and healthy older adults. Biomed Eng Online. 2018;17(1):1–14. doi: 10.1186/s12938-018-0488-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rossanigo R, Caruso M, Salis F, Bertuletti S, Della Croce U, Cereatti A, editors. An optimal procedure for stride length estimation using foot-mounted magneto-inertial measurement units. In: 2021 IEEE international symposium on medical measurements and applications (MeMeA). IEEE; 2021.
- 31.Salis F, Bertuletti S, Bonci T, Della Croce U, Mazzà C, Cereatti A. A method for gait events detection based on low spatial resolution pressure insoles data. J Biomech. 2021;127:110687. doi: 10.1016/j.jbiomech.2021.110687. [DOI] [PubMed] [Google Scholar]
- 32.Salis F, Bertuletti S, Scott K, Caruso M, Bonci T, Buckley E, et al., editors. A wearable multi-sensor system for real world gait analysis. In: 2021 43rd annual international conference of the IEEE Engineering in Medicine & Biology Society (EMBC). IEEE; 2021. [DOI] [PubMed]
- 33.Soltani A, Dejnabadi H, Savary M, Aminian K. Real-world gait speed estimation using wrist sensor: a personalized approach. IEEE J Biomed Health Inform. 2019;24(3):658–668. doi: 10.1109/JBHI.2019.2914940. [DOI] [PubMed] [Google Scholar]
- 34.Del Din S, Godfrey A, Rochester L. Validation of an accelerometer to quantify a comprehensive battery of gait characteristics in healthy older adults and Parkinson’s disease: toward clinical and at home use. IEEE J Biomed Health Inform. 2015;20(3):838–847. doi: 10.1109/JBHI.2015.2419317. [DOI] [PubMed] [Google Scholar]
- 35.Yarnall AJ, Breen DP, Duncan GW, Khoo TK, Coleman SY, Firbank MJ, et al. Characterizing mild cognitive impairment in incident Parkinson disease: the ICICLE-PD study. Neurology. 2014;82(4):308–316. doi: 10.1212/WNL.0000000000000066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rehman RZU, Klocke P, Hryniv S, Galna B, Rochester L, Del Din S, et al. Turning detection during gait: algorithm validation and influence of sensor location and turning characteristics in the classification of Parkinson’s disease. Sensors. 2020;20(18):5377. doi: 10.3390/s20185377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Storm FA, Nair K, Clarke AJ, Van der Meulen JM, Mazzà C. Free-living and laboratory gait characteristics in patients with multiple sclerosis. PLoS ONE. 2018;13(5):e0196463. doi: 10.1371/journal.pone.0196463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tamburini P, Storm F, Buckley C, Bisi MC, Stagni R, Mazzà C. Moving from laboratory to real life conditions: influence on the assessment of variability and stability of gait. Gait Posture. 2018;59:248–252. doi: 10.1016/j.gaitpost.2017.10.024. [DOI] [PubMed] [Google Scholar]
- 39.Trojaniello D, Ravaschio A, Hausdorff JM, Cereatti A. Comparative assessment of different methods for the estimation of gait temporal parameters using a single inertial sensor: application to elderly, post-stroke, Parkinson’s disease and Huntington’s disease subjects. Gait Posture. 2015;42(3):310–316. doi: 10.1016/j.gaitpost.2015.06.008. [DOI] [PubMed] [Google Scholar]
- 40.Iluz T, Gazit E, Herman T, Sprecher E, Brozgol M, Giladi N, et al. Automated detection of missteps during community ambulation in patients with Parkinson’s disease: a new approach for quantifying fall risk in the community setting. J Neuroeng Rehabil. 2014;11(1):1–9. doi: 10.1186/1743-0003-11-48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Paraschiv-Ionescu A, Newman CJ, Carcreff L, Gerber CN, Armand S, Aminian K. Locomotion and cadence detection using a single trunk-fixed accelerometer: validity for children with cerebral palsy in daily life-like conditions. J Neuroeng Rehabil. 2019;16(1):1–11. doi: 10.1186/s12984-019-0494-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.McCamley J, Donati M, Grimpampi E, Mazzà C. An enhanced estimate of initial contact and final contact instants of time using lower trunk inertial sensor data. Gait Posture. 2012;36:316–318. doi: 10.1016/j.gaitpost.2012.02.019. [DOI] [PubMed] [Google Scholar]
- 43.Abry P. Ondelettes et turbulences: multirésolutions, algorithmes de décomposition, invariance d’échelle et signaux de pression. Paris: Diderot multimédia éd; 1997.
- 44.Pham MH, Elshehabi M, Haertner L, Del Din S, Srulijes K, Heger T, et al. Validation of a step detection algorithm during straight walking and turning in patients with Parkinson’s disease and older adults using an inertial measurement unit at the lower back. Front Neurol. 2017;8:457. doi: 10.3389/fneur.2017.00457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Shin SH, Park CG. Adaptive step length estimation algorithm using optimal parameters and movement status awareness. Med Eng Phys. 2011;33(9):1064–1071. doi: 10.1016/j.medengphy.2011.04.009. [DOI] [PubMed] [Google Scholar]
- 46.Lee H, You J, Cho S, Hwang S, Lee D, Kim Y, et al. Computational methods to detect step events for normal and pathological gait evaluation using accelerometer. Electron Lett. 2010;46(17):1. doi: 10.1049/el.2010.0532. [DOI] [Google Scholar]
- 47.Zijlstra W, Hof AL. Assessment of spatio-temporal gait parameters from trunk accelerations during human walking. Gait Posture. 2003;18(2):1–10. doi: 10.1016/S0966-6362(02)00190-X. [DOI] [PubMed] [Google Scholar]
- 48.Zijlstra A, Zijlstra W. Trunk-acceleration based assessment of gait parameters in older persons: a comparison of reliability and validity of four inverted pendulum based estimations. Gait Posture. 2013 doi: 10.1016/j.gaitpost.2013.04.021. [DOI] [PubMed] [Google Scholar]
- 49.Kim JW, Jang HJ, Hwang D-H, Park C. A step, stride and heading determination for the pedestrian navigation system. J Glob Position Syst. 2004;3(1–2):273–279. doi: 10.5081/jgps.3.1.273. [DOI] [Google Scholar]
- 50.Zhao Q, Zhang B, Wang J, Feng W, Jia W, Sun M. Improved method of step length estimation based on inverted pendulum model. Int J Distrib Sens Netw. 2017;13(4):1550147717702914. doi: 10.1177/1550147717702914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Weinberg H. Using the ADXL202 in pedometer and personal navigation applications. Analog Devices AN-602 Application Note. 2002;2(2):1–6. [Google Scholar]
- 52.McGraw KO, Wong SP. Forming inferences about some intraclass correlation coefficients. Psychol Methods. 1996;1(1):30. doi: 10.1037/1082-989X.1.1.30. [DOI] [Google Scholar]
- 53.Koo TK, Li MY. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J Chiropr Med. 2016;15(2):155–163. doi: 10.1016/j.jcm.2016.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Giavarina D. Understanding Bland Altman analysis. Biochem Med. 2015;25(2):141–151. doi: 10.11613/BM.2015.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Micó-Amigo ME, Kingma I, Ainsworth E, Walgaard S, Niessen M, van Lummel RC, et al. A novel accelerometry-based algorithm for the detection of step durations over short episodes of gait in healthy elderly. J Neuroeng Rehabil. 2016;13(1):1–12. doi: 10.1186/s12984-016-0145-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Gadaleta M, Cisotto G, Rossi M, Ur Rehman RZ, Rochester L, Del Din S. Deep learning techniques for improving digital gait segmentation. In: Annual international conference of the IEEE Engineering in Medicine and Biology Society. Vol 2019. 2019. p. 1834–7. [DOI] [PubMed]
- 57.Bonci T, Salis F, Scott K, Alcock L, Becker C, Bertuletti S, et al. An algorithm for accurate marker-based gait event detection in healthy and pathological populations during complex motor tasks. Front Bioeng Biotechnol. 2022;10:868928. doi: 10.3389/fbioe.2022.868928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Urbanek JK, Roth DL, Karas M, Wanigatunga AA, Mitchell CM, Juraschek SP, et al. Free-living gait cadence measured by wearable accelerometer: a promising alternative to traditional measures of mobility for assessing fall risk. J Gerontol A. 2022 doi: 10.1093/gerona/glac013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ullrich M, Küderle A, Hannink J, Del Din S, Gaßner H, Marxreiter F, et al. Detection of gait from continuous inertial sensor data using harmonic frequencies. IEEE J Biomed Health Inform. 2020;24(7):1869–1878. doi: 10.1109/JBHI.2020.2975361. [DOI] [PubMed] [Google Scholar]
- 60.Micó-Amigo M, Kingma I, Faber G, Kunikoshi A, Van Uem J, Van Lummel R, et al. Is the assessment of 5 meters of gait with a single body-fixed-sensor enough to recognize idiopathic Parkinson’s disease-associated gait? Ann Biomed Eng. 2017;45(5):1266–1278. doi: 10.1007/s10439-017-1794-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Panebianco GP, Bisi MC, Stagni R, Fantozzi S. Analysis of the performance of 17 algorithms from a systematic review: influence of sensor position, analysed variable and computational approach in gait timing estimation from IMU measurements. Gait Posture. 2018;66:76–82. doi: 10.1016/j.gaitpost.2018.08.025. [DOI] [PubMed] [Google Scholar]
- 62.Taraldsen K, Thingstad P, Døhl Ø, Follestad T, Helbostad JL, Lamb SE, et al. Short and long-term clinical effectiveness and cost-effectiveness of a late-phase community-based balance and gait exercise program following hip fracture. The EVA-Hip randomised controlled trial. PLoS One. 2019;14(11):e0224971. doi: 10.1371/journal.pone.0224971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Byun S, Lee HJ, Han JW, Kim JS, Choi E, Kim KW. Walking-speed estimation using a single inertial measurement unit for the older adults. PLoS ONE. 2019;14(12):e0227075. doi: 10.1371/journal.pone.0227075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Quintero D, Lambert DJ, Villarreal DJ, Gregg RD, editors. Real-time continuous gait phase and speed estimation from a single sensor. In: 2017 IEEE conference on control technology and applications (CCTA). IEEE; 2017. [DOI] [PMC free article] [PubMed]
- 65.Hebenstreit F, Leibold A, Krinner S, Welsch G, Lochmann M, Eskofier BM. Effect of walking speed on gait sub phase durations. Hum Mov Sci. 2015;43:118–124. doi: 10.1016/j.humov.2015.07.009. [DOI] [PubMed] [Google Scholar]
- 66.Fukuchi CA, Fukuchi RK, Duarte M. Effects of walking speed on gait biomechanics in healthy participants: a systematic review and meta-analysis. Syst Rev. 2019;8(1):1–11. doi: 10.1186/s13643-019-1063-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Rehman RZU, Guan Y, Shi JQ, Alcock L, Yarnall AJ, Rochester L, et al. Investigating the impact of environment and data aggregation by walking bout duration on Parkinson’s disease classification using machine learning. Front Aging Neurosci. 2022 doi: 10.3389/fnagi.2022.808518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Kim DW, Hassett LM, Nguy V, Allen NE. A comparison of activity monitor data from devices worn on the wrist and the waist in people with Parkinson’s disease. Mov Disord Clin Pract. 2019;6(8):693–699. doi: 10.1002/mdc3.12850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Hubble RP, Naughton GA, Silburn PA, Cole MH. Wearable sensor use for assessing standing balance and walking stability in people with Parkinson’s disease: a systematic review. PLoS ONE. 2015;10(4):e0123705. doi: 10.1371/journal.pone.0123705. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional file 1. Details of ranking methodology.
Data Availability Statement
Representative data from the dataset and recommended algorithms presented in this study can be found on online repositories: Data can be found on Zenodo, 10.5281/zenodo.7547125. Algorithms can be found on GitHub, 10.5281/zenodo.7575872.