Abstract
Since the outbreak of COVID-19, it has seriously endangered the health of human beings. Computer automatic segmentation of COVID-19 X-ray images is an important means to assist doctors in rapid and accurate diagnosis. Therefore, this paper proposes a modified FOA (EEFOA) with two optimization strategies added to the original FOA, including elite natural evolution (ENE) and elite random mutation (ERM). To be specific, ENE and ERM can effectively speed up the convergence and deal with the problem of local optima, respectively. The outstanding performance of EEFOA was confirmed by experimental results comparing EEFOA with the original FOA, other FOA variants, and advanced algorithms at CEC2014. After that, EEFOA is implemented for multi-threshold image segmentation (MIS) of COVID-19 X-ray images, where a 2D histogram consisting of the original greyscale image and the non-local means image is used to represent the image information, and Rényi's entropy is used as the objective function to find the maximum value. The evaluation results of the MIS segmentation experiments show that, whether high or low threshold, EEFOA can achieve higher quality segmentation results and greater robustness than other advanced segmentation methods.
Keywords: Meta-heuristic algorithm, Fruit fly optimization algorithm, Multi-threshold image segmentation, COVID-19 X-ray images
1. Introduction
The Corona Virus Disease 2019 (COVID-19) outbreak in early 2020 has not yet been fully contained. The continued evolution and spread of coronavirus disease have caused enormous pressure on societies and healthcare systems in all countries [1], [2]. Faced with this critical situation, the efficient identification and detection of COVID-19 are crucial. The COVID-19 nucleic acid detection reagents have currently used in many countries, but their false negative rate is about 20%, and their sensitivity is poor. In recent years, lung X-ray (LXR) images have been extensively studied as an essential medical imaging technique suitable for COVID-19 detection [3], [4], [5]. Extensive literature observes that LXR image identification of suspected patients is the most reliable technique for the detection of COVID-19. Therefore, the accurate and efficient segmentation for LXR images of COVID-19 is an integral part of the successfully assisted diagnosis.
Image processing methods, however, gained increased momentum in progress of medical and applied information systems [6], [7], [8], [9]. Such methods witnessed increased momentum in medical systems [10]. The reason is that they can help doctors to understand patterns and raw data much easier and more efficient [11], [12], [13]. There are numerous methods for image segmentation, such as region-based segmentation [14], edge-based image segmentation [15], active contour model-based segmentation [16], Markov random field-based segmentation [17], graph theory-based segmentation methods [18], and so on. Thresholding segmentation gets much importance in recent years owing to its simplicity and robustness [19]. Based on the region of interest in the image, it can be broadly divided into multi-threshold and bi-threshold processing. Bi-threshold image segmentation (BIS) divides an image into two classes by employing a single threshold value. However, splitting an image into more than two regions of interest requires the usage of multi-threshold image segmentation (MIS) [20]. The eventual object of MIS is finding the optimal thresholds with the information in the histogram.
Broadly speaking, the methods for selecting the optimal thresholds can be divided into parametric and non-parametric. The parametric approach requires finding the parameters of the statistical distribution that each region obeys. Conversely, the non-parametric approach aims to find the optimal solution to a certain objective function, such as various entropy, including Renyi entropy [21], Shannon entropy [22], Tsallis entropy [23] and so on. To date, various new methods have been proposed to improve non-parametric methods. However, as the threshold value increases, these methods result in a complex and time-consuming operation of threshold segmentation. Several studies examined that meta-heuristic algorithms (MAs) have the unique advantage of solving complex problems, especially the ability of high-dimensional, big data and non-differentiable problems. Thus, many researchers have applied various MAs to optimize MIS methods in recent years.
MAs are computational intelligence-based mechanisms for solving complex optimization problems optimally or satisfactorily. Many algorithms have been developed in recent years, such as particle swarm optimization (PSO) [24], ant colony optimization (ACO) [25], differential evolution (DE) [25], artificial bee colony (ABC) [26], firefly algorithm (FA) [25], covariance matrix adaptation evolution strategy (CMA-ES) [27], whale optimization algorithm (WOA) [25], grey wolf optimization (GWO) [25], moth flame optimization (MFO) [25], bat algorithm (BA) [28], salp swarm algorithm (SSA) [25], sine cosine algorithm (SCA) [25], Harris Hawks optimization (HHO)1 [29], slime mould algorithm (SMA)2 [30], [31], the weighted mean of vectors (INFO)3 [32], Runge Kutta optimizer (RUN)4 [33], hunger games search (HGS)5 [34], rime optimization algorithm (RIME)6 [35], teaching–learning-based optimization (TLBO) [25], fruit fly optimization algorithm (FOA) [36] and others. In recent years, they have also been successfully used in a variety of areas, such as multi-objective problem [37], [38], optimization of machine learning model [39], combination optimization problems [40], bankruptcy prediction [41], [42], plant disease recognition [43], expensive optimization problems [44], [45], medical diagnosis [46], [47], [48], feature selection [49], [50], image segmentation [51], [52], economic emission dispatch problem [53], practical engineering problems [54], [55], scheduling problems [56], [57], [58], and solar cell parameter identification [59].
Among them, FOA is an optimizer that seeks the global optimal solution derived from the foraging behavior of fruit flies. Due to its strong versatility and high computational efficiency, have attracted considerable attention from researchers in different fields. But there is no perfect optimization algorithm, and the optimization algorithm should be improved to solve problems better. Therefore, numerous excellent algorithms were proposed, such as work in [60], introducing quasi-affine transformation evolutionary strategy to prevent premature convergence of FOA (QTFOA) and applying it to optimize the capacitated vehicle routing problem. To prevent FOA falls prematurely, [61] proposed an improved FOA to solve the transmission line tower junction optimization problem. To enhance the exploration and exploitation of FOA, [62] proposed BSSFOA based on bat sonar strategy and hybrid distribution and used it for feature selection. [63] proposed sine cosine-based FOA (SCA_FOA) and applied it to solve three engineering cases. [64] proposed an optimized FOA (MOFOA) using the outpost and multi-population mechanisms to optimize the SVM. [65] proposed CIFOA to improve the FOA’s convergence speed and search capability by introducing mutation strategy and chaos particle optimization, which was used for feature selection and parameter optimization for SVM.
Although these improved FOA variants have yielded decent success in various domains, as stated in No-Free-Lunch (NFL) [66], an optimization algorithm cannot have better performance on all problems. In other words, each optimization algorithm (e.g., FOA) needs to be altered according to the features of the problem. Therefore, this paper proposed an enhanced FOA (EEFOA) and applied it to the segmentation of COVID-19 X-rays.
The proposed EEFOA incorporates the elite natural evolution (ENE) and elite random mutation (ERM) mechanisms on the original FOA. ENE crosses and recombines the best individuals in the population to inherit excellent genes, accelerating the convergence speed. ERM mutates the best individual in the population to enhance the exploration ability of FOA in the later stage so as to jump out of local optimum (LO) effectively. To demonstrate the positive impact of the above two mechanisms on the original FOA, a mechanism comparison experiment was conducted on 30 benchmark functions of CEC2014 [67]. Further, to verify the superior performance of EEFOA, a series of CEC2014-based benchmark function experiments were performed, in which EEFOA was compared with the original FOA, seven well-known algorithms, 11 improved FOA variants, and nine state-of-art algorithms, respectively. The results of the comparison experiments were evaluated by mean (AVG), variance (STD), Wilcoxon signed-rank test (WSRT) [68], the Freidman test (FT) [69], and other data analysis methods.
In addition, the EEFOA-based MIS method utilizes a 2D histogram to represent image information and uses 2D Rényi's entropy as the objective function. Also, to test the proposed method's stability under multiple thresholds, the image segmentation experiments were carried out in this paper under multiple thresholds, with low thresholds (2, 4, 6) and high thresholds (10, 15, 20). Moreover, the comparison results of the image segmentation experiments are given by three evaluation criteria; they are Peak Signal Noise Ratio (PSNR) [70], Structural Similarity Index (SSIM) [71], and Feature Similarity Index (FSIM) [72]. And the experimental results were further analyzed by WSRT and FT.
In brief, the main contribution of this paper is as follows:
-
•
EEFOA is developed, in which ENE and ERM positively impact speeding up convergence and jumping out of the LO. Also, the EEFOA-based MIS method is proposed that gets the superior quality of image segmentation.
-
•
The outstanding performance of EEFOA is validated by comparing it with the original FOA and other competitive peers.
-
•
Segmentation experiments for COVID-19 X-ray images are performed, where the experimental results show that the EEFOA-based MIS method has much better segmentation quality and greater stability at different threshold levels.
-
•
EEFOA performs excellently on both the test functions and the COVID-19 X-ray image segmentation.
The remaining sections of this paper are planned as follows: Section 2 introduces the MIS. Section 3 illustrates the original FOA. Section 4 presented the developed EEFOA in detail. A series of comparison experimental results are presented in Section 5. Section 6 states some discussion of the proposed method in this paper. Finally, Section 7 summarizes the entire work of this paper and provides an outlook on future research plans.
2. Multi-threshold image segmentation
Image segmentation is the basis of computer vision and, at the same time, one of the most difficult problems in image processing. So-called image segmentation refers to the division of an image into a number of disjoint regions based on features such as grey scale, color, spatial texture, geometry, making these features appear consistent or similar within the same region and distinctly different between different regions [73].
2.1. Related works for muti-threshold image segmentation
Multi-threshold image segmentation sets multiple thresholds based on the greyscale of the image, which classifies each pixel of the image by comparing the greyscale of the image with the threshold, so as to segment the image into multiple regions. MIS is a pattern recognition categorization process. In recent years, MIS has attracted considerable attention due to its intuitive processing, simple calculation, and high operational efficiency, and many researchers have developed various MIS methods.
Mousavirad et al. [74] used DE to optimize the MIS method. Ning et al. [75] proposed a MIS method based on a hybrid WOA. Nama et al. [76] proposed the quasi-reflected slime mold algorithm (QRSMA) for image segmentation. Vijh et al. [77] presented a new hybrid algorithm (H-LOA_CSO) to enhance global search capabilities, which used for finding near-optimal thresholds for MIS methods. Qi et al. [78] developed XMACO to improve the performance of ACO to find the optimal value of Kapur's entropy. Aranguren et al. [79] proposed a robust meta-heuristic algorithm named LASHDE with the minimum cross entropy as the objective function to segment magnetic resonance brain images (MRBI). Renugambal et al. [80] Kapur’s entropy-based MIS method with the combination of water cycle algorithm and moth flame optimization for MRBI segmentation. Naji Alwerfali et al. [81] proposed a modified spherical search optimizer combined with Fuzzy entropy for MIS. Ding et al. [82] proposed a modified FOA (HACLFOA) by introducing a hybrid adaptive-cooperative learning strategy for image segmentation. Yue et al. [83] proposed combining the bat algorithm with invasive weed optimization for image segmentation. Jun et al. [84] proposed a 2D Otsu-based MIS method with the improved adaptive differential evolution algorithm (JADE) as the optimizer. Zhou et al. [85] utilize the moth swarm algorithm as an optimizer in combination with an MIS method. Kotte et al. [86] presented an adaptive wind-driven optimization algorithm to optimize image segmentation for brain MRI images.
Besides, the histogram-based MIS method is one of the standard segmentation methods. This method comprises one-dimensional (1D) histograms and two-dimensional (2D) histograms. However, the 1D histogram-based MIS method does not use the spatial location information of the image, and the segmentation results are easily disturbed by noise. Moreover, the smaller size of the image tends to cause serious mis-segmentation. Thus, Abutaleb [87] combined the original grayscale histogram with local averaging of pixels, and they proposed a 2D histogram-based MIS method. But the 2D histogram-based MIS method utilizes exhaustive enumeration to find the optimal threshold, leading to significant computational complexity. To combat this drawback, many researchers have successfully applied MAs to optimize the process of finding optimal thresholds.
Nevertheless, this traditional 2D histogram does not adequately take into consideration some details contained in the image, such as points and edges [88], [89]. Therefore, this paper employed an MIS method combining the non-local means (NL-means) 2D histogram and 2D Rényi's entropy for image segmentation. Fig. 1 shows the detailed MIS process based on the proposed method of this paper.
Fig. 1.
MIS’s flowchart on EEFOA-based 2D Rényi's entropy indicated by COVID-19 X-ray image A.
2.2. Non-local means for 2D histogram
The non-local means (NL-means) technique was developed by Buades [90], [91] et al. in 2015. NL-means is a new denoising technique that fully uses redundant information and preserves as many detailed features of the image as possible while denoising. Suppose and are the grayscale values of pixels and of image respectively, the NL-means of image can be calculated from the following equations:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where denotes the weight between pixel and . is the normalization constants. and stand for the local means. and are blocks of images centered on pixels and . Besides, represents the degree of filtering, is the standard deviation.
The NL-means 2D histogram is composed of the NL-means image and the grayscale image. In case the original grayscale image has a level and the image size is set to , then the corresponding NL-means image also has level and the image size is also . On this basis, and are combined to generate a plane; on that plane, is applied to express the frequency of occurrence of the corresponding pixel combination , where represents the grey scale value of pixel in and represents the grey scale value of pixel in . Thus, the final 2D histogram is obtained by the normalizing of Eq. (6):
| (6) |
Fig. 2 shows the 3D views of NL-means 2D histograms and their corresponding plan view.
Fig. 2.
The calculation process of NL-means and its corresponding plan view.
2.3. 2D Rényi's entropy
Rényi's entropy is a generalized form of Shannon entropy, introduced by Alfred Rényi in 1961. In contrast to the Shannon entropy, Rényi's entropy introduces an adjustable parameter , which makes it a more general and flexible measure of the amount of information. In this paper, is 0.5 and Rényi's is equal to Shannon entropy as converges to 1. As displayed in Fig. 2, the segmentation of image is performed at the gray levels , so it is segmented into classes . Therefore, the Rényi's entropy can be given by:
| (7) |
This paper employs Rényi's entropy as the objective function for the segmentation of the image to the maximum total entropy value by seeking the optimal threshold values, and uses EEFOA to optimize the process for selecting the best thresholds.
3. Fruit fly optimization algorithm (FOA)
The fruit fly optimization algorithm (FOA) [36] is a swarm intelligence algorithm proposed on the basis of careful observation and research on the foraging behavior of fruit flies. Fruit flies have keen senses and unique advantages in smell and vision. During the foraging process, the fruit fly first uses its powerful sense of smell to collect different odors to locate the food source quickly, then flies closer to it. Further, at a certain distance from the food source, individual fruit flies can detect the location of the food source and their companions through keen vision. By simulating the foraging process of Fruit flies described above, the Fruit Fly Optimization Algorithm can be divided into two stages: 1) Initialization, 2) Olfactory search phase, 3) Visual localization phase. The pseudo-code of the FOA is shown in Algorithm 1.
3.1. Initialization
In the initialization phase, the parameters and population position are initialized. The main parameters of the setting are as follows: fruit fly colony size (), the maximum number of evaluations (), the initial range of activity of the population () and flight distance (FR). In addition, the initial position of the fruit fly population is defined as:
| (8) |
| (9) |
where denotes a uniform value generated randomly between 0 and 1.
3.2. Olfactory search phase
In the olfactory search phase, the positions of the fruit fly population are updated around the optimal solution. In the first place, the individual fruit fly distance to find food is given based on random flight distances (FR) and current optimal locations (), which the calculation method is shown as follows.
| (10) |
| (11) |
Where , and the flight distances (FR) is generated randomly.
Besides, the distance from the food source to the origin () are defined according to the following formulation.
| (12) |
Then the taste concentration determination value () perceived by each individual Fruit Fly is inversely proportional to the distance from the food source to the origin (). And the taste concentration values () can be given by the taste concentration determination value ().
| (13) |
| (14) |
Finally, sifting the individuals with the best taste concentration values () in fruit fly populations, and record the corresponding location () of the individual.
| (15) |
3.3. Visual localization phase
In the visual localization phase, the history best taste concentration values () and current optimal locations are gradually updated based on the current best taste concentration values () and the corresponding location () according to the rules chosen by greed. If the value of is lower than , the will be updated with the , at meanwhile, fruit fly populations fly to optimal concentration locations, which can be described in the equations as follows:
| (16) |
| (17) |
| (18) |
Repeat olfactory search and visual localization of the two phases until the value of is the global optimal taste concentration values or the current iteration reaches the maximum number of evaluations ().
| Algorithm 1 Pseudo-code of FOA |
|---|
| Initialize parameters:; |
| Initialize the population randomly by Eqs. (8–13); |
| Calculate the fitness value by Eq. (14); |
| Retain the best individual by Eq. (15) and Eq. (16); |
| Update the position by Eq. (17) and Eq. (18); |
| whiledo |
| Update the population by ; |
| Correct the boundaries of the population ; |
| Calculate the fitness value by Eq. (14); |
| Retain the best individual by Eq. (15) and Eq. (16); |
| Update the position by Eq. (17) and Eq. (18); |
| ; |
| end while |
| return |
4. Proposed FOA-based method
4.1. The weakness of the FOA
FOA has been applied to various sectors due to its simple principle and easy implementation [92], [93], [94]. Nonetheless, FOA remains disadvantageous in some aspects, and the EEFOA proposed in this paper effectively mitigates the following disadvantages. While searching for the optimal solution, FOA tends to stagnate at the local optimal point, accompanied by a slow convergence rate. This search scheme will cause the algorithm to be incapable of further searches for a more optimal solution and end the search status early. Therefore, FOA often performs poorly when faced with high-dimensional, complex, or nonlinear optimization problems. Analysis of the update formula Eq. (5) and Eq. (6) of FOA reveals that each individual must be an integer. In other words, the search area of FOA is limited. A serious problem with FOA is that, as shown in Eq. (1), all individuals can only iterate around the global optimal solution and cannot explore other domains. There is a lack of communication among individuals in the population. Thus, individuals in a population should exchange with each other and try to adjust the exploration area with other instruments to enhance population diversity. In particular, when handling multimodal and composite functions, the above idea can effectively alleviate the LO problem of the algorithm.
4.2. Elite natural evolution (ENE)
The basic idea of elite natural evolution (ENE) is mimicking the crossover and mutation of genes. Crossover of the gene is the process by which chromosomes exchange some genes with each other in a certain way to form a new individual, and mutation of a gene refers to the variation of an individual that has a certain probability of occurring in a certain part. It is worth noting that gene crossover is mainly carried out with excellent genes which have outstanding chromosomes. In addition, it can be expressed as the following three procedures.
-
•
Elitist selection.
First of all, the top three best-performing individuals in the population were selected, namely , , and , separately. Besides, denotes the optimal individual. It is essential to mention that the fitness values of these individuals are stated as: .
-
•
Gene cross-recombination of elite chromosomes.
Assuming that , , and are 3 chromosomes, thus, each dimension of which can be considered as a gene. First, randomly select 50% genes of each of the , and chromosomes to combine, thereby obtaining a new chromosome. Then, [100 genes of and [100 genes of are randomly selected to generate a new chromosome . And it can be expressed as follows.
| (19) |
| (20) |
where shows the random selection from the elite chromosomes, and the symbol is the cross-combining randomly selected genomes to generate new chromosomes. is a variable parameter that determines the number of genes from and for crossover recombination.
-
•
Gaussian local mutation.
In the final step, the Gaussian mechanism is applied to , resulting in the creation of a new individual . It can be expressed as follows.
| (21) |
where stands for Gaussian distribution, in which . represents the individual who is currently mutated, accordingly, and is the individual that has undergone mutations.
Cross-recombination depends on the best individuals in the population to inherit excellent genes. This method can effectively speed up convergence. And in order to further involve their mutations, the Gaussian mechanism is applied; in this way, the individuals mutate locally, intending to prevent the population from getting trapped in LO.
4.3. Elite random mutation (ERM)
As another evolutionary direction, the main purpose of elite random mutation (ERM) is to mutate elite chromosomes instead of general chromosomes. This method can enhance the exploration ability in the later stage of the FOA algorithm so as to jump out of the LO effectively. And it can be expressed as the following steps.
-
•
Randomly mutated chromosome.
This step randomly generates a new chromosome in the search space according to the upper and lower bound, and at the same time, the generation process should also be guided by the optimal chromosome. The rationale behind this step is that excessive randomness runs the risk of slowing convergence. The formula for updating chromosomes is as follows:
| (22) |
| (23) |
where and are the upper and lower bounds of the search space, respectively, so that denotes the intermediate position of the search space. shows a value resulting from a Gaussian probability distribution, whereby the parameter , and . Notably, the difference between the 2 parameters, that is and is that the value fluctuates more at .
-
•
Gene cross-recombination.
In this step, the optimal chromosome is cross-combined with the newly generated chromosome , and the formulation of is defined as follows.
| (24) |
where shows the random selection from the chromosomes, and the symbol is the cross-combining of randomly selected genomes to generate new chromosomes. is a variable parameter that determines the number of genes in the and .
4.4. Parameter setting
The variable parameter occupies a vital position in the implementation of the EES mechanism, and its main role is to determine the proportion of genes involved in the mutation, thus effectively balancing the two stages of exploration and development. The larger value of mean that the more mutant genes are contained in the newly produced chromosomes, and conversely, the more elite genes, it can be formulated as follows:
| (25) |
| (26) |
where is the number of current evaluations, is the maximum number of evaluations. is a uniform random number in the range [0,1].
4.5. Modified FOA (EEFOA)
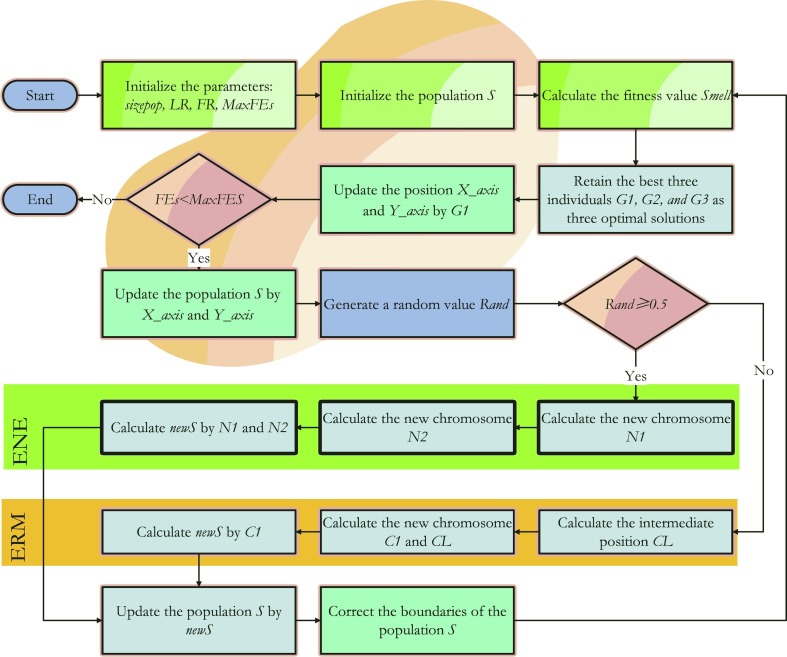
In order to further improve the performance of the FOA algorithm, the elite natural evolution (ENE) and elite random mutation (ERM) are introduced to the original FOA to alleviate its slow convergence issue and prevent it from dropping into the local best. The entire pseudo-code of the improved FOA can be viewed in Algorithm 2, and the flowchart is shown in Fig. 3 .
| Algorithm 2 Pseudo-code of EEFOA |
|---|
| Initialize parameters:; |
| Initialize the population by Eqs. (8–13); |
| Calculate the fitness value by Eq. (14); |
| Retain the best three individuals as three optimal solutions; |
| Update the position by ; |
| whiledo |
| Update the population by ; |
| Generate a random value ; |
| ifthen |
| // ENE |
| Calculate by Eq. (19); |
| Calculate by Eq. (20); |
| Calculate by and ; |
| Update the population by ; |
| else then |
| // ERM |
| Calculate by Eq. (23); |
| Calculate by Eq. (22) and ; |
| Calculate by ; |
| Update the population by ; |
| end |
| Correct the boundaries of the population ; |
| Calculate the fitness value by Eq. (14); |
| Retain the best three individuals as three optimal solutions; |
| Update the position by ; |
| ; |
| end while |
| return |
Fig. 3.
The flowchart of EEFOA.
5. Experiments and results
In this section, the positive effects of the introduced ENE and ERM were verified in the corresponding experiment by the benchmark functions of Table A1. In addition, to validate the superior performance of the proposed EEFOA, several experiments were conducted to compare EEFOA with FOA and some well-known algorithms, improved FOA variants, and state-of-art algorithms on 30 benchmark functions in CEC2014.
Stability analysis and structural validations are the bases of the studies with some mathematical background [95]. To preserve the fairness and validity of the experiments, all the algorithms involved in the experiments were performed in the same environment [96], [97], [98]. The population size was 30, and the maximum number of evaluations was 300,000. Notably, to reduce errors caused by the random operation, the final comparison results were the average of 30 independent runs of the algorithm.
The average (AVG) and variance (STD) of 30 independent runs were used to measure the algorithm's optimization capability and stability. The Wilcoxon signed-rank test (WSRT) [68] and Freidman test (FT) [69] as evaluation criteria were used to analyze the experimental results further.
Further, the excellent application of EEFOA in image segmentation has also been demonstrated by comparative experiments with other segmentation methods. To ensure the fairness of the experiment, all segmentation methods were carried out under identical conditions. The image size is set to 521 521, the number of iterations is 100, the population size is set to 20, and all algorithms are finalized as the average of 30 independent runs.
In the end, Peak Signal Noise Ratio (PSNR), Structural Similarity Index (SSIM), and Feature Similarity Index (FSIM) are used as assessment criteria for segmentation results and then further analyzed by AVG, STD and WSRT.
Finally, the experiment was performed on a desktop computer with an Intel(R) Core (TM) i7-6700 CPU @ 3.40 GHz 3.41 GHz, and all programs were coded on MATLAB 2020b.
5.1. The impact of ENE and ERM
In this subsection, four FOA variants were set up for mechanism comparison experiments based on these two mechanisms to demonstrate the effects of ENE and ERM on the original FOA. Table 1 gives the variants resulting from the above four combinations, where “0″ means that the corresponding mechanism is not introduced, and ”1″ means that the related mechanism is added.
Table 1.
Portfolio options for the introduction of mechanisms.
| Variants | EEFOA | FOA_N | FOA_R | FOA |
|---|---|---|---|---|
| ENE | 1 | 1 | 0 | 0 |
| ERM | 1 | 0 | 1 | 0 |
Table 2 shows the detailed analysis of experimental results evaluated by WRST and FT. WRST would compare algorithms' performance in each benchmark function and note that the analysis result is indicated by the symbol “+/-/=”. “+” means that EEFOA outperforms the current algorithm, “-” means that EEFOA underperforms the current algorithm, and “=” means that EEFOA and the current algorithm perform equally well. FT would calculate and rank algorithms' average performance in the benchmark function, denoted by ''Mean'' and ''Rank''. According to the results of WSRT, it can be found that EEFOA outperforms FOA on all benchmark functions. EEFOA performs better than FOA_N on 29 benchmark functions and is equal to it on 1 benchmark function. EEFOA outperforms FOA_R on 4 benchmark functions and is equal to it on 23 benchmark functions. EEFOA's overall performance is better among the 30 benchmark functions. As per the results of FT, it can be seen that the original FOA ranked last compared to the other variants, indicating that introducing all mechanisms had a positive effect on FOA. Also, EEFOA ranked first with the smallest mean value of 1.267, indicating that the simultaneous introduction of both mechanisms was the strongest optimization of FOA.
Table 2.
Comparison of various strategies for FOA.
| Methods | EEFOA | FOA_N | FOA_R | FOA |
|---|---|---|---|---|
| +/−/= | ∼ | 29/0/1 | 4/3/23 | 30/0/0 |
| Mean | 1.477 | 3.229 | 1.568 | 3.726 |
| Rank | 1 | 3 | 2 | 4 |
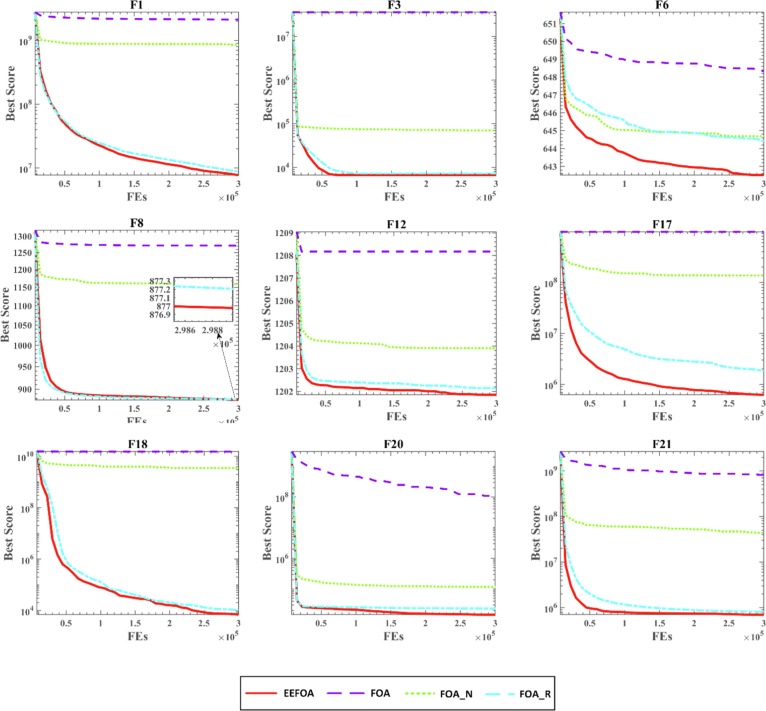
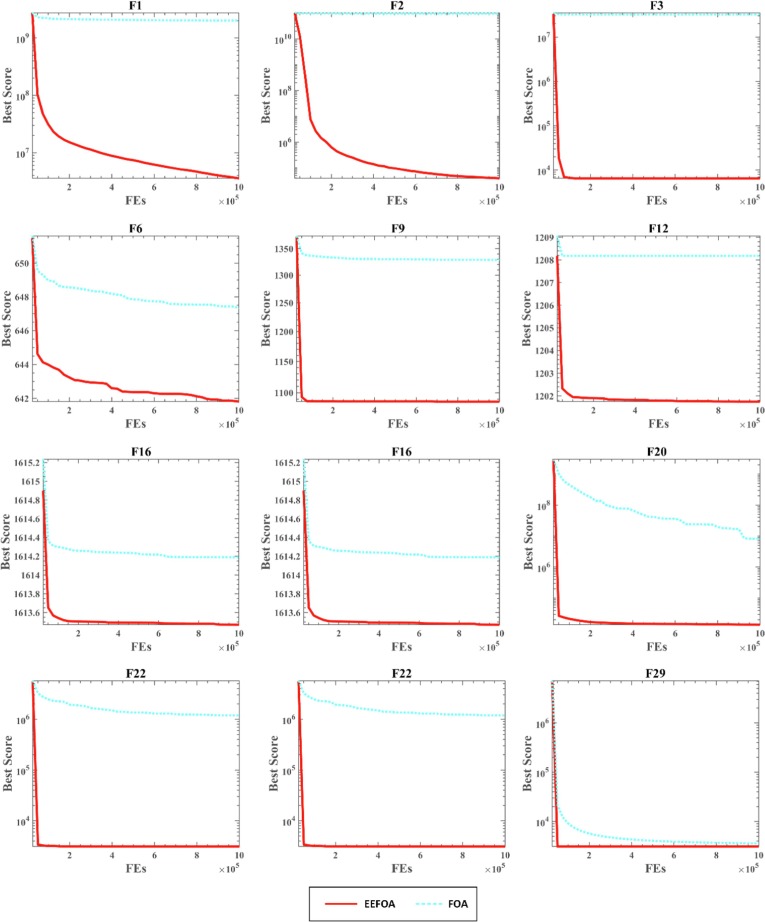
Fig. 4 presents the convergence curves of the optimum solutions of 30 independent runs. From the convergence curves of F6, F12, F17, F18, and F21, EEFOA converges faster than other FOA variants throughout the entire iteration cycle. The convergence curves of F6, F12, and F17 show that although EEFOA converges slowly in the early stage for partial functions, EEFOA eventually converges to a more optimal solution. From the above analysis, it is clear that EEFOA achieves significant improvements in terms of convergence speed and jumping out of the LO. Hence it can find a superior solution more quickly when solving optimization problems.
Fig. 4.
Convergence curves of FOA variants in dimension 30.
In all, both the ENE and ERM mechanisms can bring positive improvements to the performance of FOA, and the introduction of both mechanisms results in EEFOA that has the most robust performance and can effectively improve the convergence speed of the FOA and avoid local optima, thus improving the capability of solving complex optimization problems.
5.2. Performance optimization
5.2.1. The scalability test for EEFOA
It is critical to note the manner in which the reliability of a technique is impacted by its components and dimensions, as well as what occurs as we strengthen it [99], [100]. Therefore, the functions' dimension was set to 50, 100, and 200 in equal conditions, respectively, and the comparison experiments between EEFOA and the original FOA were carried out using 30 benchmark functions from CEC2014.
Table 3 gives the results of the comparison experiments for the three dimensions (50, 100, 200) and further analyzes WSRT and FT, which summarize the mean (AVG) and variance (STD) of solutions to the 30 benchmark functions solved by EEFOA and FOA, with the smaller AVG and STD bolded in EEFOA or FOA. A smaller AVG means the algorithm can explore a better solution in such functions, and a minor STD means more excellent stability. From the AVG of Table 3, it can be seen that whether the dimension is 50, 100, or 200, EEFOA's AVG is smaller than FOA in all benchmark functions. In sum, even if the complexity of the operation becomes more extensive, the performance of EEFOA in exploring the optimal solution is stronger than the original FOA. From the STD of Table 3, when the dimension is 50 and 100, EEFOA's STD is smaller than FOA in 24 benchmark functions; when the dimension is 200, EEFOA's STD is smaller than FOA in 25 benchmark functions. The above results indicate that EEFOA is more stable than FOA in most functions. Besides, according to the analysis of WSRT and FT, it can be found that EEFOA outperforms FOA on all benchmark functions in different dimensions. In other words, the overall performance of EEFOA has improved considerably compared to FOA when faced with functions of different dimensions.
Table 3.
Results of EEFOA and FOA in. 50-dimension, 100-dimension, and 200-dimension.
| Fun | Item | 50 |
100 |
200 |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EEFOA | FOA | EEFOA | FOA | EEFOA | FOA | |||||
| F1 | AVG | 6.6304E + 06 | 2.1176E + 09 | 3.5433E + 06 | 2.0184E + 09 | 8.8732E + 06 | 2.1137E + 09 | |||
| STD | 2.5971E + 06 | 1.1394E + 08 | 1.3633E + 06 | 5.9791E + 07 | 3.5533E + 06 | 1.0266E + 08 | ||||
| F2 | AVG | 7.4745E + 04 | 9.5930E + 10 | 3.8706E + 04 | 9.4860E + 10 | 1.6638E + 05 | 9.6726E + 10 | |||
| STD | 2.5411E + 04 | 4.7599E + 09 | 1.1572E + 04 | 4.1980E + 09 | 6.8419E + 04 | 4.1934E + 09 | ||||
| F3 | AVG | 6.4381E + 03 | 3.4372E + 07 | 6.4957E + 03 | 3.2007E + 07 | 6.4149E + 03 | 3.3240E + 07 | |||
| STD | 2.0248E + 02 | 6.4746E + 06 | 3.3240E + 02 | 1.0822E + 07 | 6.6830E + 01 | 8.8078E + 06 | ||||
| F4 | AVG | 4.9353E + 02 | 2.5411E + 04 | 4.8752E + 02 | 2.5589E + 04 | 5.0469E + 02 | 2.5604E + 04 | |||
| STD | 3.6515E + 01 | 1.2930E + 03 | 3.6231E + 01 | 1.3206E + 03 | 4.0580E + 01 | 9.2391E + 02 | ||||
| F5 | AVG | 5.2000E + 02 | 5.2119E + 02 | 5.2000E + 02 | 5.2116E + 02 | 5.2000E + 02 | 5.2118E + 02 | |||
| STD | 9.4352E-05 | 4.9013E-02 | 2.8948E-05 | 6.8934E-02 | 1.1627E-05 | 1.1492E-01 | ||||
| F6 | AVG | 6.4155E + 02 | 6.4777E + 02 | 6.4181E + 02 | 6.4734E + 02 | 6.4316E + 02 | 6.4863E + 02 | |||
| STD | 3.4340E + 00 | 9.7120E-01 | 3.5169E + 00 | 6.6941E-01 | 3.7005E + 00 | 9.4732E-01 | ||||
| F7 | AVG | 7.0021E + 02 | 1.6511E + 03 | 7.0013E + 02 | 1.6450E + 03 | 7.0035E + 02 | 1.6508E + 03 | |||
| STD | 8.9520E-02 | 1.3960E + 01 | 6.8060E-02 | 9.7219E + 00 | 1.0766E-01 | 1.4101E + 01 | ||||
| F8 | AVG | 8.7258E + 02 | 1.2738E + 03 | 8.6739E + 02 | 1.2705E + 03 | 8.7868E + 02 | 1.2726E + 03 | |||
| STD | 6.9606E + 00 | 8.3994E + 00 | 6.2489E + 00 | 9.7965E + 00 | 5.5604E + 00 | 1.0098E + 01 | ||||
| F9 | AVG | 1.0869E + 03 | 1.3352E + 03 | 1.0863E + 03 | 1.3285E + 03 | 1.0842E + 03 | 1.3335E + 03 | |||
| STD | 6.6261E + 00 | 2.6559E + 01 | 7.6820E + 00 | 2.5628E + 01 | 5.4980E + 00 | 2.4689E + 01 | ||||
| F10 | AVG | 3.0719E + 03 | 1.0325E + 04 | 3.0374E + 03 | 1.0317E + 04 | 3.0688E + 03 | 1.0409E + 04 | |||
| STD | 2.3694E + 02 | 2.2991E + 02 | 2.3575E + 02 | 2.1006E + 02 | 2.8794E + 02 | 2.3647E + 02 | ||||
| F11 | AVG | 5.5212E + 03 | 1.1291E + 04 | 5.2129E + 03 | 1.1212E + 04 | 5.4827E + 03 | 1.1261E + 04 | |||
| STD | 3.6369E + 02 | 3.5838E + 02 | 4.6763E + 02 | 3.0455E + 02 | 4.2924E + 02 | 2.7964E + 02 | ||||
| F12 | AVG | 1.2020E + 03 | 1.2082E + 03 | 1.2018E + 03 | 1.2082E + 03 | 1.2017E + 03 | 1.2081E + 03 | |||
| STD | 6.4340E-01 | 3.6117E-06 | 6.1358E-01 | 2.6062E-06 | 6.5852E-01 | 4.1872E-01 | ||||
| F13 | AVG | 1.3007E + 03 | 1.3102E + 03 | 1.3006E + 03 | 1.3100E + 03 | 1.3007E + 03 | 1.3103E + 03 | |||
| STD | 1.4721E-01 | 6.6035E-01 | 1.3806E-01 | 6.4764E-01 | 1.3448E-01 | 6.0599E-01 | ||||
| F14 | AVG | 1.4003E + 03 | 1.7204E + 03 | 1.4003E + 03 | 1.7162E + 03 | 1.4003E + 03 | 1.7273E + 03 | |||
| STD | 9.5222E-02 | 1.1215E + 01 | 4.2356E-02 | 8.8266E + 00 | 1.1638E-01 | 1.6598E + 01 | ||||
| F15 | AVG | 1.5791E + 03 | 5.2304E + 05 | 1.5771E + 03 | 5.3561E + 05 | 1.5766E + 03 | 5.4107E + 05 | |||
| STD | 6.4395E + 01 | 6.8522E + 04 | 6.1736E + 01 | 4.5147E + 04 | 6.9130E + 01 | 3.3981E + 04 | ||||
| F16 | AVG | 1.6135E + 03 | 1.6143E + 03 | 1.6135E + 03 | 1.6142E + 03 | 1.6135E + 03 | 1.6142E + 03 | |||
| STD | 2.0779E-01 | 2.6354E-01 | 1.0847E-01 | 2.7878E-01 | 8.7075E-02 | 1.2213E-01 | ||||
| F17 | AVG | 7.3890E + 05 | 9.7960E + 08 | 6.7523E + 05 | 9.7960E + 08 | 8.0129E + 05 | 9.6913E + 08 | |||
| STD | 7.4173E + 05 | 3.3298E-01 | 5.3941E + 05 | 1.2487E-01 | 7.3268E + 05 | 5.7374E + 07 | ||||
| F18 | AVG | 5.2678E + 03 | 1.5123E + 10 | 4.3841E + 03 | 1.4859E + 10 | 8.5669E + 03 | 1.4913E + 10 | |||
| STD | 3.0519E + 03 | 8.6022E + 08 | 2.8906E + 03 | 1.0958E + 09 | 5.9461E + 03 | 1.0011E + 09 | ||||
| F19 | AVG | 1.9255E + 03 | 2.5217E + 03 | 1.9258E + 03 | 2.5095E + 03 | 1.9222E + 03 | 2.5273E + 03 | |||
| STD | 1.7160E + 01 | 4.4909E + 01 | 1.9449E + 01 | 3.1337E + 01 | 1.0623E + 01 | 3.9137E + 01 | ||||
| F20 | AVG | 1.6810E + 04 | 6.8992E + 07 | 1.3912E + 04 | 8.1770E + 06 | 1.3264E + 04 | 1.0626E + 08 | |||
| STD | 6.5707E + 03 | 8.3044E + 07 | 5.9371E + 03 | 6.6192E + 06 | 2.9018E + 03 | 2.1632E + 08 | ||||
| F21 | AVG | 6.6250E + 05 | 7.1938E + 08 | 5.9648E + 05 | 4.9541E + 08 | 7.1578E + 05 | 8.2941E + 08 | |||
| STD | 3.6573E + 05 | 2.0260E + 08 | 3.0667E + 05 | 1.3182E + 08 | 3.6219E + 05 | 2.8354E + 08 | ||||
| F22 | AVG | 3.1790E + 03 | 1.0876E + 06 | 3.1150E + 03 | 1.1890E + 06 | 3.1655E + 03 | 1.2148E + 06 | |||
| STD | 1.4065E + 02 | 3.2514E + 05 | 8.1209E + 01 | 1.2855E + 06 | 1.2730E + 02 | 4.4651E + 05 | ||||
| F23 | AVG | 2.5000E + 03 | 2.5000E + 03 | 2.5000E + 03 | 2.5000E + 03 | 2.5000E + 03 | 2.5000E + 03 | |||
| STD | 0.0000E + 00 | 8.1294E-07 | 0.0000E + 00 | 3.0181E-07 | 0.0000E + 00 | 2.0835E-06 | ||||
| F24 | AVG | 2.6000E + 03 | 2.6000E + 03 | 2.6000E + 03 | 2.6000E + 03 | 2.6000E + 03 | 2.6000E + 03 | |||
| STD | 6.1416E-04 | 9.8513E-06 | 8.2106E-05 | 5.3156E-06 | 7.9746E-04 | 1.4736E-05 | ||||
| F25 | AVG | 2.7000E + 03 | 2.7000E + 03 | 2.7000E + 03 | 2.7000E + 03 | 2.7000E + 03 | 2.7000E + 03 | |||
| STD | 0.0000E + 00 | 1.5070E-08 | 0.0000E + 00 | 5.6377E-09 | 0.0000E + 00 | 3.2727E-08 | ||||
| F26 | AVG | 2.8000E + 03 | 2.8000E + 03 | 2.8000E + 03 | 2.8000E + 03 | 2.8000E + 03 | 2.8000E + 03 | |||
| STD | 0.0000E + 00 | 3.6239E-11 | 0.0000E + 00 | 1.7684E-11 | 0.0000E + 00 | 8.5446E-11 | ||||
| F27 | AVG | 2.9000E + 03 | 2.9000E + 03 | 2.9000E + 03 | 2.9000E + 03 | 2.9000E + 03 | 2.9000E + 03 | |||
| STD | 0.0000E + 00 | 1.3611E-07 | 0.0000E + 00 | 6.0457E-08 | 0.0000E + 00 | 3.3915E-07 | ||||
| F28 | AVG | 3.0000E + 03 | 3.0000E + 03 | 3.0000E + 03 | 3.0000E + 03 | 3.0000E + 03 | 3.0000E + 03 | |||
| STD | 0.0000E + 00 | 3.7495E-07 | 0.0000E + 00 | 1.1045E-07 | 0.0000E + 00 | 6.7094E-07 | ||||
| F29 | AVG | 3.1000E + 03 | 4.0297E + 03 | 3.1000E + 03 | 3.5650E + 03 | 3.1000E + 03 | 4.6491E + 03 | |||
| STD | 0.0000E + 00 | 1.1571E + 00 | 0.0000E + 00 | 3.9508E-01 | 0.0000E + 00 | 2.0574E + 00 | ||||
| F30 | AVG | 3.2000E + 03 | 3.2634E + 03 | 3.2000E + 03 | 3.2317E + 03 | 3.2000E + 03 | 3.3056E + 03 | |||
| STD | 0.0000E + 00 | 6.1360E-02 | 0.0000E + 00 | 3.0551E-02 | 0.0000E + 00 | 1.5949E-01 | ||||
| +/-/= | ∼ | 30/0/0 | ∼ | 30/0/0 | ∼ | 30/0/0 | ||||
| Mean | 1 | 2 | 1 | 2 | 1 | 2 | ||||
| Rank | 1 | 2 | 1 | 2 | 1 | 2 | ||||
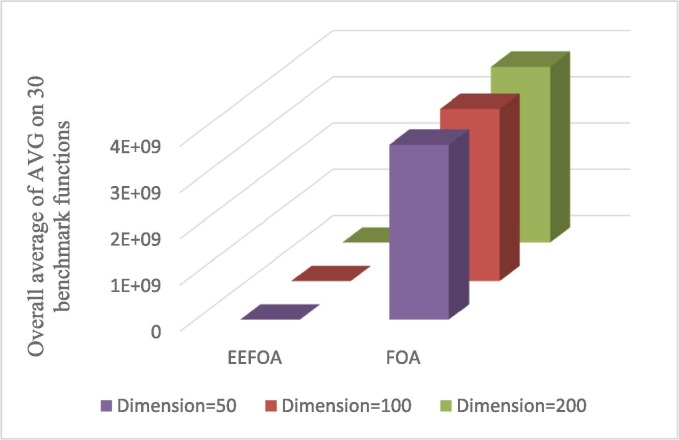
To further facilitate the observation of the analytical results in Table 3, Fig. 5, Fig. 6 give the overall average of the AVG and STD of the solutions for the 30 benchmark functions, respectively. As can be seen from Fig. 5, Fig. 6, there is a noticeable difference between FOA in contrast to EEFOA, which indicates that the proposed EEFOA has a significant development in terms of ability and stability to find optimal solutions.
Fig. 5.
Overall average of AVG on 30 benchmark functions of EEFOA and FOA.
Fig. 6.
Overall average of STD on 30 benchmark functions of EEFOA and FOA.
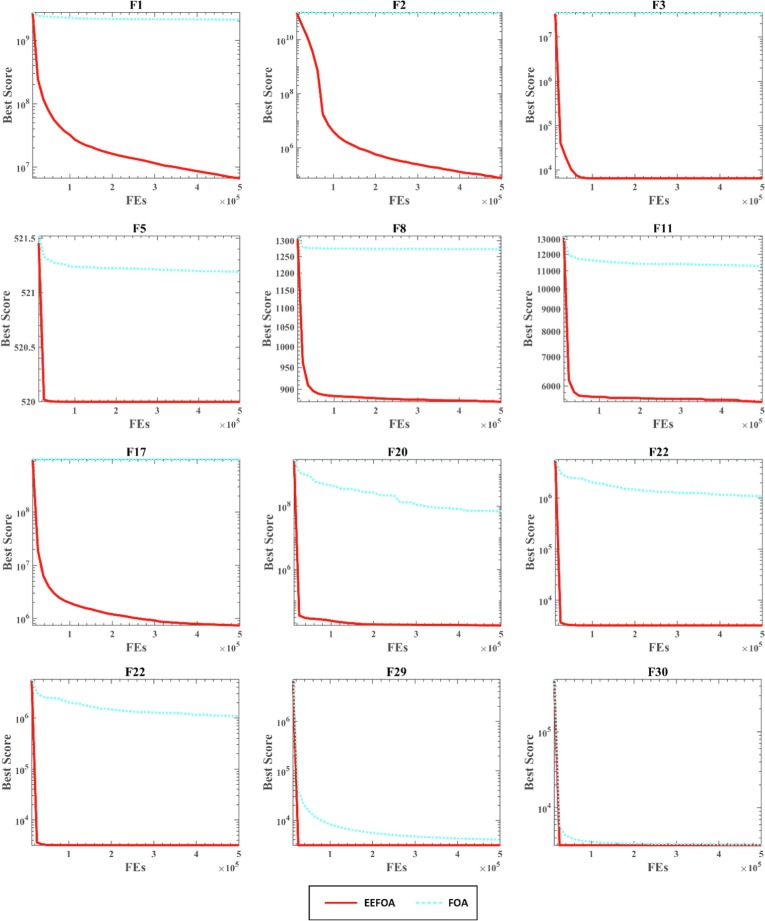
Fig. 7, Fig. 8, Fig. 9 show the convergence curves of EEFOA and FOA in different dimensions (50, 100, 200). The results of the convergence curves show that EEFOA is effectively improved over FOA in terms of convergence speed and convergence accuracy in various dimensions and alleviates the LO problem successfully.
Fig. 7.
Convergence curves of EEFOA and FOA in dimension 50.
Fig. 8.
Convergence curves of EEFOA and FOA in dimension 100.
Fig. 9.
Convergence curves of EEFOA and FOA in dimension 200.
In conclusion, the above findings show that, even with different function complexities, EEFOA is more performant and more stable than FOA. In addition, the convergence speed of EEFOA has been greatly improved, and it can effectively solve the LO problem. In other words, EEFOA is a successful and effective improvement over the original FOA.
5.2.2. Comparison with well-known algorithms
In this subsection, EEFOA was compared with seven traditional meta-heuristic algorithms, including WOA, GWO, MFO, BA, SCA, FA, and PSO, on 30 benchmark functions of CEC2014. Table A2 gives the experimental results of all algorithms on CEC2014, and represents the AVG and STD of 30 independent runs of each benchmark function. The accurate analysis of the AVG shows that EEFOA can achieve the smallest AVG value in most functions, which indicates that EEFOA has the most remarkable ability to obtain the optimal solution. Also, the experimental results of STD fully demonstrate that EEFOA is more stable than other comparative algorithms.
Table 4 stands for the evaluation results of EEFOA with other compared algorithms by WSRT and FT. According to the comparison results of Table 4, it can be found that EEFOA ranked first with the smallest mean value of 2.933. The smaller Mean value means the better performance of the algorithm, so the performance of EEFOA is significantly better than other comparison algorithms. In addition, the statistical results from WSRT show that EEFOA outperforms other algorithms in most functions. Thus, the proposed EEFOA is a competitive algorithm for solving most functions.
Table 4.
Comparison of EEFOA and well-known algorithms by WSRT.
| Methods | EEFOA | WOA | GWO | MFO | BA | SCA | FA | PSO |
|---|---|---|---|---|---|---|---|---|
| +/-/= | ∼ | 20/5/5 | 16/6/8 | 23/5/2 | 15/13/2 | 26/4/0 | 26/4/0 | 16/11/3 |
| Mean | 2.933 | 4.533 | 3.400 | 4.833 | 4.033 | 6.233 | 6.733 | 3.300 |
| Rank | 1 | 5 | 3 | 6 | 4 | 7 | 8 | 2 |
Table 5 represents the p-values given by WSRT. p-value lower than 0.05 means that EEFOA outperforms the corresponding algorithm. The bolded parts of Table 5 indicate values greater than 0.05, so it can be seen that almost all p-values are well below 0.05 (unbolded values), which indicates that the performance of EEFOA has a decisive advantage over the comparison algorithm.
Table 5.
The p-values of EEFOA versus well-known algorithms on WSRT.
| Fun | WOA | GWO | MFO | BA | SCA | FA | PSO |
|---|---|---|---|---|---|---|---|
| F1 | 1.7344E-06 | 1.9209E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 6.5833E-01 |
| F2 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 6.3391E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F3 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F4 | 1.9209E-06 | 2.3534E-06 | 1.7344E-06 | 4.1955E-04 | 1.7344E-06 | 1.7344E-06 | 1.1138E-03 |
| F5 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F6 | 3.5152E-06 | 1.7344E-06 | 1.7344E-06 | 3.1817E-06 | 2.6033E-06 | 1.7344E-06 | 1.7344E-06 |
| F7 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 4.4493E-05 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F8 | 1.7344E-06 | 3.8723E-02 | 4.7292E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F9 | 1.2866E-03 | 1.9209E-06 | 1.8910E-04 | 3.5152E-06 | 1.7344E-06 | 1.7344E-06 | 2.1630E-05 |
| F10 | 1.7344E-06 | 1.6503E-01 | 2.8786E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F11 | 4.6818E-03 | 1.7344E-06 | 2.5364E-01 | 4.1653E-01 | 1.7344E-06 | 1.7344E-06 | 6.0350E-03 |
| F12 | 2.7116E-01 | 4.7795E-01 | 1.7344E-06 | 2.2248E-04 | 1.4839E-03 | 7.7122E-04 | 5.3197E-03 |
| F13 | 1.0570E-04 | 5.2165E-06 | 2.5967E-05 | 5.2872E-04 | 1.7344E-06 | 1.7344E-06 | 2.3534E-06 |
| F14 | 8.7740E-01 | 3.5888E-04 | 1.7344E-06 | 6.5641E-02 | 1.7344E-06 | 1.7344E-06 | 2.8948E-01 |
| F15 | 8.7740E-01 | 1.0201E-01 | 3.5152E-06 | 6.3391E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F16 | 1.9209E-06 | 1.7344E-06 | 3.8822E-06 | 6.8923E-05 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F17 | 1.4936E-05 | 4.5281E-01 | 3.3269E-02 | 1.7344E-06 | 1.9209E-06 | 1.7344E-06 | 3.0650E-04 |
| F18 | 5.1931E-02 | 3.6094E-03 | 4.9916E-03 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F19 | 3.3269E-02 | 2.6230E-01 | 6.0350E-03 | 4.6818E-03 | 2.1266E-06 | 1.7344E-06 | 2.0671E-02 |
| F20 | 1.1973E-03 | 3.3886E-01 | 3.1817E-06 | 1.7344E-06 | 3.5009E-02 | 2.4308E-02 | 1.7344E-06 |
| F21 | 1.9152E-01 | 2.6230E-01 | 1.9569E-02 | 1.7344E-06 | 7.6909E-06 | 1.9209E-06 | 2.3534E-06 |
| F22 | 4.7162E-02 | 1.7344E-06 | 3.4935E-01 | 6.8359E-03 | 6.3391E-06 | 1.0246E-05 | 5.3070E-05 |
| F23 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F24 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F25 | 1.3183E-04 | 3.7896E-06 | 1.7344E-06 | 1.7344E-06 | 2.5631E-06 | 1.7344E-06 | 1.7344E-06 |
| F26 | 1.7344E-06 | 6.7459E-02 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.6503E-01 |
| F27 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F28 | 2.5631E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F29 | 2.5562E-06 | 1.7344E-06 | 1.7268E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F30 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
Fig. 10 shows the convergence curves of EEFOA and seven well-known algorithms on some functions. Through the convergence curve of F2, although EEFOA converges slowly in the early phase, it eventually converges to a more optimal solution than the other comparison algorithms. From the convergence curves of F5, F8, and F10, although MFO converges slightly faster than EEFOA in the early phase, EEFOA can jump out of the LO more efficiently. From the convergence curves of F23, F25, F27, F29 and F30, EEFOA converges faster than other algorithms and has a lower convergence curve to explore better solutions.
Fig. 10.
Convergence curves of EEFOA and well-known algorithms.
As a result, it can be deduced from the above analytical results that EEFOA demonstrates superior ability and stability to explore optimal solutions for most functions. At the same time, it has a faster convergence rate and a stronger ability to mitigate the LO.
5.2.3. Comparison with improved FOA
In this subsection, EEFOA was further compared with 11 proposed FOA variants; they are BSSFOA [62], SCA_FOA [63], MOFOA[64], CEFOA [101], CIFOA [65], MSFOA [102], SFOA [103], IFOA [104], CAEFOA [105], AMFOA [106], LGMSFOA [107].
Table 6 shows the experimental results of EEFOA and other improved FOAs, which include the AVG, STD, and the analysis of WSRT and FT. The results of AVG show that in 30 benchmark functions, EEFOA achieves the smallest AVG of near-optimal solutions in 26 functions, indicating that EEFOA is the most capable of exploring optimal solutions in the majority of functions. Also, EEFOA obtains the smallest STD on most functions verifying the more substantial stability of the proposed algorithm compared to other improved FOAs. The excellent performance of EEFOA is also clearly evidenced by the results of FT analyses, where EEFOA ranks first among all the compared algorithms with a mean value of 1.367, overwhelmingly more substantial than the second-ranked MOFOA with 1.8. Further, based on the comparison results given by WSRT, EEFOA outperforms the second-ranked MOFOA on 20 functions and has comparable performance on 7 functions. In other words, EEFOA performs better than other improved FOAs in most functions. Besides, according to the p-values of Table A3, the number of p-values greater than 0.05 is minimal, which confirms the competitive advantage of EEFOA.
Table 6.
Results of EEFOA and other FOA variants.
| Fun | Item | EEFOA | BSSFOA | AMFOA | CAEFOA | CEFOA | CIFOA | LGMSFOA | MSFOA | SFOA | SCA_FOA | IFOA | MOFOA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | AVG | 8.5886E + 06 | 2.5433E + 09 | 2.1962E + 09 | 2.2051E + 09 | 2.7788E + 09 | 2.3508E + 09 | 2.2908E + 09 | 2.5549E + 09 | 1.8740E + 09 | 2.1801E + 09 | 1.4988E + 09 | 1.2207E + 09 |
| STD | 3.0561E + 06 | 2.2628E + 08 | 1.1728E + 08 | 1.7591E + 08 | 5.8671E + 07 | 4.4687E + 07 | 7.6998E + 08 | 9.0803E + 08 | 7.9049E + 07 | 4.2286E + 08 | 1.0014E + 08 | 1.1513E + 08 | |
| F2 | AVG | 1.6647E + 05 | 9.4588E + 10 | 9.3905E + 10 | 1.0069E + 11 | 1.0260E + 11 | 9.4478E + 10 | 1.3540E + 11 | 1.1444E + 11 | 9.4661E + 10 | 9.2700E + 10 | 7.7798E + 10 | 7.6176E + 10 |
| STD | 5.5618E + 04 | 2.9453E + 09 | 1.4140E + 09 | 2.2404E + 09 | 3.8128E + 08 | 5.9960E + 08 | 2.0908E + 10 | 1.7067E + 10 | 4.2541E + 09 | 3.9631E + 09 | 2.9532E + 09 | 2.9295E + 09 | |
| F3 | AVG | 6.5404E + 03 | 8.6672E + 04 | 1.9048E + 07 | 3.4724E + 07 | 3.5554E + 07 | 8.2665E + 04 | 2.9050E + 05 | 2.5325E + 05 | 3.5554E + 07 | 8.7226E + 04 | 8.5793E + 04 | 7.9781E + 04 |
| STD | 3.0553E + 02 | 2.0553E + 01 | 1.7948E + 07 | 4.5454E + 06 | 2.2734E-08 | 8.0088E + 02 | 6.6055E + 04 | 7.6773E + 04 | 4.1918E-01 | 1.5390E + 03 | 8.4523E + 02 | 4.5182E + 03 | |
| F4 | AVG | 4.9794E + 02 | 1.8743E + 04 | 2.2625E + 04 | 2.5830E + 04 | 2.5830E + 04 | 2.2081E + 04 | 3.5964E + 04 | 3.1068E + 04 | 2.5557E + 04 | 2.1623E + 04 | 1.1200E + 04 | 9.9425E + 03 |
| STD | 2.7760E + 01 | 2.6237E + 03 | 2.9500E + 03 | 9.3039E-07 | 7.9933E-12 | 1.6808E + 02 | 1.1653E + 04 | 1.0546E + 04 | 1.4936E + 03 | 3.0930E + 03 | 9.7571E + 02 | 8.2160E + 02 | |
| F5 | AVG | 5.2000E + 02 | 5.2147E + 02 | 5.2116E + 02 | 5.2135E + 02 | 5.2154E + 02 | 5.2106E + 02 | 5.2114E + 02 | 5.2109E + 02 | 5.2107E + 02 | 5.2113E + 02 | 5.2114E + 02 | 5.2105E + 02 |
| STD | 1.3512E-05 | 7.7199E-02 | 8.9937E-02 | 6.5747E-02 | 1.5164E-02 | 4.3399E-02 | 1.0033E-01 | 8.2663E-02 | 9.7680E-02 | 1.4095E-01 | 5.5934E-02 | 4.6003E-02 | |
| F6 | AVG | 6.4541E + 02 | 6.5101E + 02 | 6.4860E + 02 | 6.5064E + 02 | 6.5172E + 02 | 6.4773E + 02 | 6.4423E + 02 | 6.4184E + 02 | 6.4615E + 02 | 6.4876E + 02 | 6.4273E + 02 | 6.4096E + 02 |
| STD | 3.6809E + 00 | 1.2154E-01 | 7.7857E-01 | 5.2284E-01 | 2.8864E-01 | 5.0750E-01 | 2.1817E + 00 | 1.6002E + 00 | 1.0670E + 00 | 2.4452E + 00 | 6.7712E-01 | 8.2350E-01 | |
| F7 | AVG | 7.0033E + 02 | 1.7005E + 03 | 1.6655E + 03 | 1.6656E + 03 | 1.7601E + 03 | 1.6850E + 03 | 1.8119E + 03 | 1.7748E + 03 | 1.6434E + 03 | 1.6175E + 03 | 1.4376E + 03 | 1.3859E + 03 |
| STD | 1.1835E-01 | 6.1967E + 01 | 1.3679E + 01 | 3.0395E + 01 | 7.5215E + 00 | 4.7933E + 00 | 2.0332E + 02 | 1.8517E + 02 | 8.9253E + 00 | 9.2092E + 01 | 2.2969E + 01 | 4.9976E + 01 | |
| F8 | AVG | 8.7983E + 02 | 1.2746E + 03 | 1.2816E + 03 | 1.2207E + 03 | 1.3229E + 03 | 1.2175E + 03 | 1.2420E + 03 | 1.2202E + 03 | 1.2718E + 03 | 1.2883E + 03 | 1.2185E + 03 | 1.1706E + 03 |
| STD | 6.5474E + 00 | 4.2430E + 01 | 1.5656E + 01 | 1.1203E + 01 | 5.3671E + 00 | 6.7307E + 00 | 5.1755E + 01 | 5.2519E + 01 | 7.4175E + 00 | 2.1365E + 01 | 2.8646E + 01 | 1.6107E + 01 | |
| F9 | AVG | 1.0851E + 03 | 1.3158E + 03 | 1.3029E + 03 | 1.3616E + 03 | 1.3782E + 03 | 1.2506E + 03 | 1.4626E + 03 | 1.4254E + 03 | 1.3447E + 03 | 1.3180E + 03 | 1.2617E + 03 | 1.2589E + 03 |
| STD | 7.1592E + 00 | 2.1994E + 01 | 1.1166E + 01 | 2.1602E + 01 | 3.8859E + 00 | 5.9524E + 00 | 6.6120E + 01 | 5.5975E + 01 | 3.4206E + 01 | 2.8178E + 01 | 9.0162E + 00 | 9.4492E + 00 | |
| F10 | AVG | 3.0952E + 03 | 1.1183E + 04 | 1.0704E + 04 | 1.0932E + 04 | 1.1531E + 04 | 9.3581E + 03 | 9.2764E + 03 | 9.5051E + 03 | 1.0252E + 04 | 1.0776E + 04 | 1.0038E + 04 | 9.2589E + 03 |
| STD | 1.6815E + 02 | 3.6120E + 02 | 3.7765E + 02 | 2.6668E + 02 | 2.0625E + 02 | 1.8290E + 02 | 4.4643E + 02 | 5.7502E + 02 | 2.5978E + 02 | 5.6494E + 02 | 1.3857E + 02 | 5.0974E + 02 | |
| F11 | AVG | 5.4765E + 03 | 1.2528E + 04 | 1.1601E + 04 | 1.2145E + 04 | 1.3185E + 04 | 1.0305E + 04 | 9.3545E + 03 | 9.7068E + 03 | 1.0709E + 04 | 1.1721E + 04 | 9.4652E + 03 | 9.0709E + 03 |
| STD | 4.0004E + 02 | 8.5973E + 02 | 4.1404E + 02 | 6.2668E + 02 | 5.3899E + 02 | 3.1644E + 02 | 5.3425E + 02 | 4.7172E + 02 | 3.3046E + 02 | 9.4361E + 02 | 2.5855E + 02 | 3.3388E + 02 | |
| F12 | AVG | 1.2017E + 03 | 1.2051E + 03 | 1.2079E + 03 | 1.2082E + 03 | 1.2082E + 03 | 1.2024E + 03 | 1.2033E + 03 | 1.2033E + 03 | 1.2082E + 03 | 1.2050E + 03 | 1.2034E + 03 | 1.2030E + 03 |
| STD | 6.3154E-01 | 3.2654E-01 | 8.8354E-01 | 4.9382E-09 | 2.3126E-13 | 2.2721E-01 | 7.4800E-01 | 4.3988E-01 | 2.9966E-06 | 8.2937E-01 | 3.4020E-01 | 2.7945E-01 | |
| F13 | AVG | 1.3007E + 03 | 1.3100E + 03 | 1.3099E + 03 | 1.3109E + 03 | 1.3109E + 03 | 1.3104E + 03 | 1.3102E + 03 | 1.3100E + 03 | 1.3100E + 03 | 1.3099E + 03 | 1.3082E + 03 | 1.3081E + 03 |
| STD | 1.5679E-01 | 4.3062E-01 | 3.5534E-01 | 2.7779E-01 | 7.8073E-03 | 3.8579E-02 | 1.0746E + 00 | 1.3731E + 00 | 7.1284E-01 | 7.5049E-01 | 2.5494E-01 | 2.9913E-01 | |
| F14 | AVG | 1.4003E + 03 | 1.7763E + 03 | 1.7372E + 03 | 1.7379E + 03 | 1.8045E + 03 | 1.7756E + 03 | 1.7933E + 03 | 1.7878E + 03 | 1.7100E + 03 | 1.7197E + 03 | 1.6666E + 03 | 1.6389E + 03 |
| STD | 1.6654E-01 | 2.8538E + 01 | 1.4282E + 01 | 1.9740E + 01 | 2.5424E + 00 | 1.8728E + 01 | 6.4806E + 01 | 5.8938E + 01 | 7.1977E + 00 | 4.5778E + 01 | 1.2178E + 01 | 1.2809E + 01 | |
| F15 | AVG | 1.6232E + 03 | 7.6913E + 05 | 5.5153E + 05 | 4.1016E + 05 | 9.4214E + 05 | 5.9165E + 05 | 1.7835E + 07 | 1.2185E + 07 | 5.1030E + 05 | 5.3727E + 05 | 2.6625E + 05 | 2.2954E + 05 |
| STD | 1.2893E + 02 | 1.7168E + 05 | 7.2213E + 04 | 1.0329E + 05 | 5.9757E + 04 | 3.1454E + 04 | 1.0923E + 07 | 9.2057E + 06 | 4.4230E + 04 | 1.7967E + 05 | 3.1325E + 04 | 3.2626E + 04 | |
| F16 | AVG | 1.6135E + 03 | 1.6148E + 03 | 1.6145E + 03 | 1.6146E + 03 | 1.6154E + 03 | 1.6139E + 03 | 1.6138E + 03 | 1.6139E + 03 | 1.6141E + 03 | 1.6145E + 03 | 1.6139E + 03 | 1.6134E + 03 |
| STD | 1.2256E-01 | 3.2902E-01 | 2.1356E-01 | 3.6194E-01 | 1.8743E-01 | 5.4944E-02 | 4.3364E-01 | 3.7305E-01 | 2.0798E-01 | 3.3258E-01 | 1.1937E-01 | 1.9132E-01 | |
| F17 | AVG | 9.8597E + 05 | 6.7629E + 08 | 8.0169E + 08 | 9.7960E + 08 | 9.7960E + 08 | 5.2888E + 08 | 2.7242E + 08 | 1.6311E + 08 | 9.7960E + 08 | 6.1732E + 08 | 1.4156E + 08 | 8.2473E + 07 |
| STD | 7.7990E + 05 | 1.8949E + 08 | 1.8203E + 08 | 1.7011E-01 | 2.5720E-07 | 1.3418E + 08 | 1.8567E + 08 | 1.0139E + 08 | 2.0522E + 00 | 5.7229E + 07 | 2.0235E + 07 | 2.8056E + 07 | |
| F18 | AVG | 9.3483E + 03 | 1.1256E + 10 | 1.3083E + 10 | 1.5454E + 10 | 1.5429E + 10 | 1.1588E + 10 | 8.3360E + 09 | 8.1251E + 09 | 1.4949E + 10 | 1.2890E + 10 | 6.2871E + 09 | 5.6435E + 09 |
| STD | 8.3676E + 03 | 1.5667E + 09 | 5.0775E + 08 | 2.2994E-01 | 1.0194E + 08 | 2.2509E + 09 | 3.2354E + 09 | 3.2831E + 09 | 1.0297E + 09 | 6.9665E + 08 | 7.6497E + 08 | 9.3619E + 08 | |
| F19 | AVG | 1.9298E + 03 | 2.5512E + 03 | 2.5648E + 03 | 2.6660E + 03 | 2.8012E + 03 | 2.6001E + 03 | 2.8601E + 03 | 2.7425E + 03 | 2.4873E + 03 | 2.5206E + 03 | 2.2813E + 03 | 2.2366E + 03 |
| STD | 2.5063E + 01 | 5.2450E + 01 | 5.0566E + 01 | 5.9359E + 01 | 4.3729E + 00 | 6.9830E + 00 | 3.5562E + 02 | 3.7807E + 02 | 3.8093E + 01 | 1.1561E + 02 | 1.1408E + 01 | 1.3107E + 01 | |
| F20 | AVG | 1.5024E + 04 | 3.7615E + 07 | 2.1545E + 08 | 1.6941E + 09 | 3.0812E + 09 | 1.1409E + 08 | 4.9474E + 06 | 7.6330E + 06 | 3.4516E + 05 | 1.2911E + 06 | 3.1058E + 05 | 1.5460E + 05 |
| STD | 2.1511E + 03 | 1.9871E + 08 | 2.9452E + 08 | 8.1058E + 08 | 1.0122E + 08 | 1.3363E + 08 | 6.1144E + 06 | 1.2851E + 07 | 2.5673E + 04 | 3.5795E + 06 | 9.6422E + 04 | 7.0896E + 04 | |
| F21 | AVG | 7.7474E + 05 | 1.2863E + 09 | 7.7420E + 08 | 2.0272E + 09 | 2.6490E + 09 | 3.9538E + 08 | 1.0829E + 08 | 7.2381E + 07 | 2.8224E + 08 | 6.5976E + 08 | 6.3891E + 07 | 3.5174E + 07 |
| STD | 3.5737E + 05 | 7.6453E + 08 | 4.1295E + 08 | 2.9651E + 08 | 1.7681E + 08 | 2.6803E + 08 | 1.0352E + 08 | 4.9910E + 07 | 7.4382E + 07 | 4.7870E + 08 | 2.1488E + 07 | 1.0964E + 07 | |
| F22 | AVG | 3.1668E + 03 | 9.4717E + 05 | 1.4389E + 06 | 4.2591E + 06 | 5.7557E + 06 | 1.7777E + 05 | 1.8196E + 04 | 1.5418E + 04 | 8.1396E + 05 | 9.7806E + 05 | 3.0896E + 04 | 2.1206E + 04 |
| STD | 1.5331E + 02 | 1.2787E + 06 | 5.3331E + 05 | 8.7225E + 05 | 1.9152E + 05 | 2.4808E + 05 | 2.5128E + 04 | 2.3492E + 04 | 1.3932E + 06 | 3.9940E + 05 | 1.7884E + 04 | 1.1371E + 04 | |
| F23 | AVG | 2.5000E + 03 | 2.5000E + 03 | 2.5000E + 03 | 2.5000E + 03 | 2.5000E + 03 | 2.5000E + 03 | 4.0121E + 03 | 3.9351E + 03 | 2.5000E + 03 | 2.5000E + 03 | 2.5000E + 03 | 2.5000E + 03 |
| STD | 0.0000E + 00 | 6.8202E-06 | 3.9420E-04 | 3.1114E-07 | 0.0000E + 00 | 0.0000E + 00 | 4.2823E + 02 | 4.4075E + 02 | 6.1752E-06 | 0.0000E + 00 | 2.0856E-05 | 0.0000E + 00 | |
| F24 | AVG | 2.6000E + 03 | 2.6000E + 03 | 2.6000E + 03 | 2.6000E + 03 | 2.6000E + 03 | 2.6000E + 03 | 2.9123E + 03 | 2.9001E + 03 | 2.6000E + 03 | 2.6000E + 03 | 2.6000E + 03 | 2.6000E + 03 |
| STD | 2.3118E-04 | 1.6467E-03 | 2.6006E-03 | 5.5989E-06 | 0.0000E + 00 | 0.0000E + 00 | 3.3273E + 01 | 3.1027E + 01 | 2.6636E-05 | 0.0000E + 00 | 2.1905E-04 | 0.0000E + 00 | |
| F25 | AVG | 2.7000E + 03 | 2.7000E + 03 | 2.7000E + 03 | 2.7000E + 03 | 2.7000E + 03 | 2.7000E + 03 | 2.8857E + 03 | 2.8597E + 03 | 2.7000E + 03 | 2.7000E + 03 | 2.7000E + 03 | 2.7000E + 03 |
| STD | 0.0000E + 00 | 3.5783E-07 | 4.9594E-06 | 3.2902E-09 | 0.0000E + 00 | 0.0000E + 00 | 5.8000E + 01 | 4.4795E + 01 | 8.3252E-08 | 0.0000E + 00 | 2.9187E-07 | 0.0000E + 00 | |
| F26 | AVG | 2.8000E + 03 | 2.8000E + 03 | 2.8000E + 03 | 2.8000E + 03 | 2.8000E + 03 | 2.7928E + 03 | 2.9308E + 03 | 2.9025E + 03 | 2.8000E + 03 | 2.8000E + 03 | 2.8000E + 03 | 2.7916E + 03 |
| STD | 0.0000E + 00 | 1.1174E-09 | 1.6146E-08 | 1.2415E-11 | 0.0000E + 00 | 1.9674E + 01 | 1.3288E + 02 | 1.1687E + 02 | 2.0974E-10 | 0.0000E + 00 | 7.3603E-10 | 2.5794E + 01 | |
| F27 | AVG | 2.9000E + 03 | 2.9000E + 03 | 2.9000E + 03 | 2.9000E + 03 | 2.9000E + 03 | 2.9000E + 03 | 4.4459E + 03 | 4.4087E + 03 | 2.9000E + 03 | 2.9000E + 03 | 2.9000E + 03 | 2.9000E + 03 |
| STD | 0.0000E + 00 | 6.5582E-06 | 6.5912E-05 | 5.0338E-08 | 0.0000E + 00 | 0.0000E + 00 | 2.8364E + 02 | 2.5339E + 02 | 8.6402E-07 | 0.0000E + 00 | 2.9473E-06 | 0.0000E + 00 | |
| F28 | AVG | 3.0000E + 03 | 3.0000E + 03 | 3.0000E + 03 | 3.0000E + 03 | 3.0000E + 03 | 3.0000E + 03 | 9.3929E + 03 | 9.8244E + 03 | 3.0000E + 03 | 3.0000E + 03 | 3.0000E + 03 | 3.0000E + 03 |
| STD | 0.0000E + 00 | 0.0000E + 00 | 1.2567E-04 | 8.8985E-08 | 0.0000E + 00 | 0.0000E + 00 | 9.3438E + 02 | 1.0899E + 03 | 1.8057E-06 | 0.0000E + 00 | 6.8050E-06 | 0.0000E + 00 | |
| F29 | AVG | 3.1000E + 03 | 3.1024E + 03 | 4.6954E + 03 | 3.3237E + 03 | 3.1000E + 03 | 3.1000E + 03 | 6.7656E + 08 | 3.3297E + 07 | 6.1997E + 03 | 3.1000E + 03 | 4.9738E + 03 | 3.1000E + 03 |
| STD | 0.0000E + 00 | 1.3215E + 01 | 4.2486E + 02 | 3.0093E-01 | 0.0000E + 00 | 0.0000E + 00 | 2.8160E + 08 | 1.7352E + 08 | 6.9571E + 00 | 0.0000E + 00 | 1.8308E + 01 | 0.0000E + 00 | |
| F30 | AVG | 3.2000E + 03 | 3.2000E + 03 | 3.3065E + 03 | 3.2153E + 03 | 3.2000E + 03 | 3.2000E + 03 | 7.9249E + 06 | 7.1752E + 06 | 3.4111E + 03 | 3.2000E + 03 | 3.3276E + 03 | 3.2000E + 03 |
| STD | 0.0000E + 00 | 8.2814E-02 | 2.7257E + 01 | 1.9727E-02 | 0.0000E + 00 | 0.0000E + 00 | 6.1797E + 06 | 5.5976E + 06 | 4.2611E-01 | 0.0000E + 00 | 1.1923E + 00 | 0.0000E + 00 | |
| +/-/= | ∼ | 23/0/7 | 30/0/0 | 30/0/0 | 22/1/7 | 22/1/7 | 29/0/1 | 29/0/1 | 29/0/1 | 22/1/7 | 29/0/1 | 20/3/7 | |
| Mean | 1.367 | 7.600 | 7.833 | 8.767 | 8.533 | 4.733 | 8.633 | 8.000 | 7.800 | 5.267 | 5.200 | 1.800 | |
| Rank | 1 | 6 | 8 | 12 | 10 | 3 | 11 | 9 | 7 | 5 | 4 | 2 |
Fig. 11 gives the overall average of the AVG and STD of the solutions for the 30 benchmark functions, and it is clear that the proposed EEFOA has a great improvement in performance over the other FOA variants. Fig. 12 gives some functions' convergence curves of EEFOA and other improved FOAs. EEFOA converges to the optimum at an incredible speed from the convergence curves and has a much lower convergence curve than other improved FOAs. It is also evident that EEFOA can effectively jump out of the LO and converge with much less accuracy.
Fig. 11.
Overall average of AVG and STD on 30 benchmark functions of EEFOA and other FOA variants.
Fig. 12.
Convergence curves of EEFOA and improved FOA.
5.2.4. Comparison with state-of-art algorithms
In this subsection, to verify the progressive nature of EEFOA, it was compared with nine state-of-art algorithms based on 30 benchmark functions of CEC2014. The algorithms involved in the comparison tests are as follows: CESCA [108], CMFO [109], HGWO [110], CGSCA [111], CAGWO [112], MWOA [113], SCADE [114], OBSCA [115], and COSCA [116]. The experimental results are represented in Table 7 , Table A4 and Fig. 14 in the same presentation as in section 5.2.3.
Table 7.
Results of EEFOA and state-of-art algorithms.
| Fun | Item | EEFOA | CESCA | CMFO | HGWO | CGSCA | CAGWO | MWOA | SCADE | OBSCA | COSCA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | AVG | 8.8145E + 06 | 1.3256E + 09 | 3.4457E + 07 | 1.7732E + 08 | 2.7286E + 08 | 4.2133E + 07 | 2.0032E + 09 | 4.3179E + 08 | 4.1158E + 08 | 6.5465E + 08 |
| STD | 2.2183E + 06 | 1.7441E + 08 | 3.5197E + 07 | 5.1378E + 07 | 7.3184E + 07 | 1.7984E + 07 | 7.0739E + 08 | 8.8047E + 07 | 1.0362E + 08 | 4.9664E + 08 | |
| F2 | AVG | 1.7541E + 05 | 7.4896E + 10 | 5.9194E + 08 | 9.2440E + 09 | 1.8373E + 10 | 3.9439E + 08 | 9.4339E + 10 | 2.9229E + 10 | 2.5074E + 10 | 6.1892E + 10 |
| STD | 7.9765E + 04 | 6.1593E + 09 | 2.0601E + 09 | 2.0647E + 09 | 3.3247E + 09 | 3.1663E + 08 | 1.9468E + 10 | 5.4098E + 09 | 4.6068E + 09 | 2.4326E + 10 | |
| F3 | AVG | 6.4477E + 03 | 1.0776E + 05 | 2.0990E + 04 | 6.9663E + 04 | 4.3683E + 04 | 2.9280E + 04 | 6.4650E + 05 | 5.4140E + 04 | 5.3312E + 04 | 5.5733E + 04 |
| STD | 1.8109E + 02 | 1.7251E + 04 | 2.1264E + 04 | 5.0588E + 03 | 5.2267E + 03 | 6.7067E + 03 | 1.2026E + 06 | 7.0759E + 03 | 7.2337E + 03 | 1.4689E + 04 | |
| F4 | AVG | 5.0285E + 02 | 1.2127E + 04 | 6.5758E + 02 | 9.4253E + 02 | 1.7496E + 03 | 5.6919E + 02 | 2.3548E + 04 | 2.4925E + 03 | 2.2478E + 03 | 8.3385E + 03 |
| STD | 3.3248E + 01 | 1.4320E + 03 | 1.9376E + 02 | 6.6126E + 01 | 4.0867E + 02 | 2.6686E + 01 | 8.7884E + 03 | 6.8054E + 02 | 4.6819E + 02 | 3.8559E + 03 | |
| F5 | AVG | 5.2000E + 02 | 5.2105E + 02 | 5.2040E + 02 | 5.2079E + 02 | 5.2093E + 02 | 5.2104E + 02 | 5.2127E + 02 | 5.2095E + 02 | 5.2097E + 02 | 5.2104E + 02 |
| STD | 1.3240E-05 | 4.4205E-02 | 3.4160E-01 | 1.2475E-01 | 5.5623E-02 | 4.9415E-02 | 7.6891E-02 | 5.2431E-02 | 5.1950E-02 | 8.4459E-02 | |
| F6 | AVG | 6.4454E + 02 | 6.4216E + 02 | 6.3554E + 02 | 6.2608E + 02 | 6.3366E + 02 | 6.1044E + 02 | 6.4632E + 02 | 6.3479E + 02 | 6.3194E + 02 | 6.2176E + 02 |
| STD | 3.9127E + 00 | 1.1066E + 00 | 2.6819E + 00 | 1.9790E + 00 | 2.7906E + 00 | 2.1963E + 00 | 2.0446E + 00 | 2.6473E + 00 | 1.4253E + 00 | 3.6519E + 00 | |
| F7 | AVG | 7.0030E + 02 | 1.4123E + 03 | 7.1877E + 02 | 7.4341E + 02 | 8.5421E + 02 | 7.0542E + 02 | 1.4801E + 03 | 9.0532E + 02 | 9.1197E + 02 | 1.2168E + 03 |
| STD | 7.1515E-02 | 4.8944E + 01 | 3.9870E + 01 | 7.0973E + 00 | 3.1636E + 01 | 2.9039E + 00 | 2.1621E + 02 | 2.9383E + 01 | 4.3041E + 01 | 1.4113E + 02 | |
| F8 | AVG | 8.7791E + 02 | 1.2184E + 03 | 9.4996E + 02 | 1.0096E + 03 | 1.0562E + 03 | 9.0056E + 02 | 1.2312E + 03 | 1.0689E + 03 | 1.0621E + 03 | 1.0439E + 03 |
| STD | 7.3042E + 00 | 1.3735E + 01 | 3.8389E + 01 | 9.5762E + 00 | 2.0131E + 01 | 4.6636E + 01 | 4.3191E + 01 | 1.2696E + 01 | 1.8167E + 01 | 9.5867E + 01 | |
| F9 | AVG | 1.0860E + 03 | 1.3023E + 03 | 1.0950E + 03 | 1.1380E + 03 | 1.1842E + 03 | 1.0246E + 03 | 1.3921E + 03 | 1.2051E + 03 | 1.1993E + 03 | 1.1980E + 03 |
| STD | 5.8654E + 00 | 1.4413E + 01 | 3.9320E + 01 | 1.2967E + 01 | 1.8919E + 01 | 5.6528E + 01 | 4.6615E + 01 | 1.9331E + 01 | 1.5451E + 01 | 3.7287E + 01 | |
| F10 | AVG | 3.2025E + 03 | 8.7099E + 03 | 5.4851E + 03 | 5.6287E + 03 | 6.8533E + 03 | 5.2455E + 03 | 9.3285E + 03 | 7.3643E + 03 | 6.1593E + 03 | 3.9548E + 03 |
| STD | 2.7684E + 02 | 3.7437E + 02 | 9.6650E + 02 | 3.3700E + 02 | 4.6224E + 02 | 1.5736E + 03 | 4.3498E + 02 | 3.6013E + 02 | 3.6867E + 02 | 9.2306E + 02 | |
| F11 | AVG | 5.3818E + 03 | 9.2013E + 03 | 6.1665E + 03 | 6.5131E + 03 | 7.9859E + 03 | 7.2624E + 03 | 1.0192E + 04 | 8.1816E + 03 | 7.4191E + 03 | 6.6579E + 03 |
| STD | 4.3629E + 02 | 2.7264E + 02 | 1.1437E + 03 | 5.5554E + 02 | 3.4963E + 02 | 1.3368E + 03 | 4.7021E + 02 | 3.3673E + 02 | 3.3787E + 02 | 6.9072E + 02 | |
| F12 | AVG | 1.2019E + 03 | 1.2035E + 03 | 1.2013E + 03 | 1.2013E + 03 | 1.2025E + 03 | 1.2029E + 03 | 1.2060E + 03 | 1.2026E + 03 | 1.2023E + 03 | 1.2018E + 03 |
| STD | 7.1236E-01 | 4.1988E-01 | 5.6008E-01 | 3.1187E-01 | 2.9088E-01 | 3.0382E-01 | 9.0706E-01 | 3.2259E-01 | 3.5434E-01 | 4.8093E-01 | |
| F13 | AVG | 1.3006E + 03 | 1.3079E + 03 | 1.3005E + 03 | 1.3021E + 03 | 1.3032E + 03 | 1.3004E + 03 | 1.3089E + 03 | 1.3038E + 03 | 1.3036E + 03 | 1.3055E + 03 |
| STD | 1.4514E-01 | 3.8711E-01 | 1.3583E-01 | 2.9321E-01 | 3.2322E-01 | 7.0604E-02 | 1.1857E + 00 | 4.2915E-01 | 4.5911E-01 | 2.8500E + 00 | |
| F14 | AVG | 1.4003E + 03 | 1.6490E + 03 | 1.4023E + 03 | 1.4224E + 03 | 1.4523E + 03 | 1.4004E + 03 | 1.6998E + 03 | 1.4887E + 03 | 1.4666E + 03 | 1.5873E + 03 |
| STD | 4.2757E-02 | 2.1162E + 01 | 6.8058E + 00 | 3.9571E + 00 | 1.0400E + 01 | 1.1111E-01 | 5.8850E + 01 | 1.1375E + 01 | 1.4479E + 01 | 1.1446E + 02 | |
| F15 | AVG | 1.6019E + 03 | 4.3199E + 05 | 2.4766E + 03 | 1.9174E + 03 | 8.0708E + 03 | 1.5187E + 03 | 2.8773E + 06 | 1.7034E + 04 | 1.5098E + 04 | 4.3646E + 05 |
| STD | 9.6717E + 01 | 1.5722E + 05 | 2.2087E + 03 | 2.1262E + 02 | 4.0650E + 03 | 2.6146E + 00 | 4.2081E + 06 | 6.1715E + 03 | 9.2668E + 03 | 1.6085E + 05 | |
| F16 | AVG | 1.6135E + 03 | 1.6136E + 03 | 1.6128E + 03 | 1.6125E + 03 | 1.6128E + 03 | 1.6119E + 03 | 1.6141E + 03 | 1.6127E + 03 | 1.6130E + 03 | 1.6124E + 03 |
| STD | 1.4550E-01 | 1.6595E-01 | 4.0513E-01 | 2.9507E-01 | 2.5491E-01 | 2.7340E-01 | 2.6622E-01 | 1.9261E-01 | 1.9711E-01 | 3.4169E-01 | |
| F17 | AVG | 1.0414E + 06 | 8.4435E + 07 | 2.4197E + 06 | 5.9787E + 06 | 6.8559E + 06 | 1.3555E + 06 | 2.7160E + 08 | 1.3541E + 07 | 9.1521E + 06 | 3.0117E + 07 |
| STD | 8.5750E + 05 | 2.3620E + 07 | 2.7917E + 06 | 1.9134E + 06 | 3.2307E + 06 | 1.1689E + 06 | 1.7031E + 08 | 5.2807E + 06 | 3.0567E + 06 | 3.4731E + 07 | |
| F18 | AVG | 7.3705E + 03 | 4.5299E + 09 | 6.7020E + 07 | 1.2194E + 08 | 1.4983E + 08 | 5.6367E + 05 | 5.8793E + 09 | 1.5712E + 08 | 2.2420E + 08 | 1.1854E + 09 |
| STD | 4.9370E + 03 | 1.0470E + 09 | 3.6705E + 08 | 3.4714E + 07 | 8.0991E + 07 | 9.7637E + 05 | 3.0406E + 09 | 8.3369E + 07 | 1.8795E + 08 | 2.6456E + 09 | |
| F19 | AVG | 1.9260E + 03 | 2.2586E + 03 | 1.9423E + 03 | 1.9933E + 03 | 1.9942E + 03 | 1.9270E + 03 | 2.6341E + 03 | 2.0138E + 03 | 2.0125E + 03 | 2.1522E + 03 |
| STD | 1.6910E + 01 | 6.8304E + 01 | 5.8159E + 01 | 1.0234E + 01 | 2.3123E + 01 | 4.9200E + 00 | 3.3169E + 02 | 1.9533E + 01 | 1.4120E + 01 | 2.5113E + 02 | |
| F20 | AVG | 1.3975E + 04 | 3.8045E + 05 | 2.1726E + 04 | 6.7965E + 04 | 2.0448E + 04 | 2.1288E + 04 | 5.9939E + 06 | 2.7324E + 04 | 2.7686E + 04 | 2.6382E + 04 |
| STD | 2.8163E + 03 | 2.6311E + 05 | 1.7435E + 04 | 2.3946E + 04 | 7.2862E + 03 | 4.6301E + 03 | 5.7634E + 06 | 1.0933E + 04 | 1.0667E + 04 | 1.3938E + 04 | |
| F21 | AVG | 7.4131E + 05 | 3.3111E + 07 | 1.0598E + 06 | 2.6033E + 06 | 1.5955E + 06 | 2.4604E + 05 | 9.4656E + 07 | 2.5900E + 06 | 1.9044E + 06 | 3.8455E + 05 |
| STD | 3.2696E + 05 | 1.5211E + 07 | 1.1618E + 06 | 2.0997E + 06 | 6.7941E + 05 | 1.7347E + 05 | 7.0525E + 07 | 1.3154E + 06 | 9.2952E + 05 | 2.6555E + 05 | |
| F22 | AVG | 3.1779E + 03 | 6.4042E + 03 | 2.9354E + 03 | 3.0265E + 03 | 3.0582E + 03 | 2.6516E + 03 | 2.0228E + 04 | 3.1230E + 03 | 3.1074E + 03 | 2.5152E + 03 |
| STD | 1.4401E + 02 | 2.5000E + 03 | 2.8043E + 02 | 1.6100E + 02 | 1.2857E + 02 | 1.7147E + 02 | 4.2375E + 04 | 1.1861E + 02 | 1.8038E + 02 | 1.2286E + 02 | |
| F23 | AVG | 2.5000E + 03 | 3.1135E + 03 | 2.6390E + 03 | 2.5058E + 03 | 2.5000E + 03 | 2.6255E + 03 | 3.7112E + 03 | 2.5000E + 03 | 2.6888E + 03 | 2.5000E + 03 |
| STD | 0.0000E + 00 | 1.7241E + 02 | 4.2477E + 01 | 3.1521E + 01 | 0.0000E + 00 | 4.1892E + 00 | 4.3934E + 02 | 0.0000E + 00 | 2.0361E + 01 | 0.0000E + 00 | |
| F24 | AVG | 2.6000E + 03 | 2.6574E + 03 | 2.6624E + 03 | 2.6000E + 03 | 2.6000E + 03 | 2.6000E + 03 | 2.8127E + 03 | 2.6000E + 03 | 2.6000E + 03 | 2.6000E + 03 |
| STD | 2.2121E-04 | 2.0988E + 01 | 1.5812E + 01 | 1.8882E-13 | 6.8130E-06 | 1.0747E-04 | 6.1248E + 01 | 1.1998E-06 | 2.5148E-04 | 5.0601E-06 | |
| F25 | AVG | 2.7000E + 03 | 2.7174E + 03 | 2.7297E + 03 | 2.7000E + 03 | 2.7000E + 03 | 2.7000E + 03 | 2.8436E + 03 | 2.7000E + 03 | 2.7000E + 03 | 2.7000E + 03 |
| STD | 0.0000E + 00 | 7.4732E + 00 | 1.0499E + 01 | 0.0000E + 00 | 0.0000E + 00 | 0.0000E + 00 | 5.0188E + 01 | 0.0000E + 00 | 1.4046E-05 | 0.0000E + 00 | |
| F26 | AVG | 2.8000E + 03 | 2.7123E + 03 | 2.7048E + 03 | 2.7531E + 03 | 2.7026E + 03 | 2.7344E + 03 | 2.7862E + 03 | 2.7037E + 03 | 2.7039E + 03 | 2.7668E + 03 |
| STD | 0.0000E + 00 | 1.4969E + 00 | 4.3871E + 00 | 4.8145E + 01 | 4.4486E-01 | 4.6229E + 01 | 1.1465E + 02 | 5.3340E-01 | 4.0490E-01 | 4.7741E + 01 | |
| F27 | AVG | 2.9000E + 03 | 4.0415E + 03 | 3.7932E + 03 | 3.6432E + 03 | 2.9000E + 03 | 3.2693E + 03 | 4.3697E + 03 | 3.2272E + 03 | 3.2468E + 03 | 2.9395E + 03 |
| STD | 0.0000E + 00 | 1.1621E + 02 | 3.9858E + 02 | 1.0707E + 02 | 0.0000E + 00 | 7.0461E + 01 | 2.1433E + 02 | 1.9365E + 02 | 3.6970E + 01 | 8.9826E + 01 | |
| F28 | AVG | 3.0000E + 03 | 5.5265E + 03 | 5.2794E + 03 | 4.2252E + 03 | 3.0000E + 03 | 3.7241E + 03 | 8.1333E + 03 | 4.7008E + 03 | 5.4150E + 03 | 3.0000E + 03 |
| STD | 0.0000E + 00 | 2.1402E + 02 | 5.5302E + 02 | 2.5515E + 02 | 0.0000E + 00 | 6.1043E + 01 | 1.0270E + 03 | 1.1327E + 03 | 3.0703E + 02 | 0.0000E + 00 | |
| F29 | AVG | 3.1000E + 03 | 1.7896E + 07 | 3.4482E + 07 | 3.8008E + 06 | 3.1000E + 03 | 7.3743E + 04 | 2.8485E + 08 | 1.5922E + 07 | 1.9127E + 07 | 1.5269E + 06 |
| STD | 0.0000E + 00 | 2.9444E + 06 | 2.2001E + 07 | 3.6233E + 06 | 2.5358E-06 | 1.0351E + 05 | 1.3746E + 08 | 8.0803E + 06 | 1.1415E + 07 | 6.4489E + 06 | |
| F30 | AVG | 3.2000E + 03 | 1.3559E + 06 | 3.7143E + 05 | 3.2000E + 03 | 1.2023E + 04 | 4.4008E + 04 | 6.2870E + 06 | 4.3745E + 05 | 4.5649E + 05 | 1.0891E + 05 |
| STD | 8.2114E-06 | 2.4462E + 05 | 4.3565E + 05 | 8.5462E-05 | 4.8324E + 04 | 1.8416E + 04 | 3.1880E + 06 | 1.2995E + 05 | 2.1438E + 05 | 2.7419E + 05 | |
| +/-/= | ∼ | 27/2/1 | 19/6/5 | 22/6/2 | 19/5/6 | 18/8/4 | 29/0/1 | 23/4/3 | 25/3/2 | 18/6/6 | |
| Mean | 2.467 | 8.667 | 4.333 | 4.200 | 4.167 | 3.067 | 9.967 | 5.900 | 6.267 | 5.133 | |
| Rank | 1 | 9 | 5 | 4 | 3 | 2 | 10 | 7 | 8 | 6 |
Fig. 14.
Convergence curves of EEFOA and improved algorithms.
From the AVG of Table 7, in 30 benchmark functions, EEFOA obtained the minimum AVG in 20 functions, CAGWO obtained the minimum AVG in 6 functions, HGWO obtained the minimum AVG in 2 functions, and COSCA and CGSCA obtained the minimum AVG in 1 function each. Therefore, EEFOA is more capable of finding the optimal solution than other algorithms in most functions. From the STD, it can be seen that EEFOA takes the optimal value with 0 in F23 and F25-F29. In most of the remaining functions, EEFOA also achieves the smallest STD. Thus, EEFOA has better stability and can find optimal solutions in most functions. Moreover, EEFOA was ranked first, achieving the smallest mean of 2.467 on 30 benchmark functions. From the comparative results of WSRT, EEFOA performs better than the second-ranked CAGWO in 18 functions and ranks equal to it in 4 functions.
The tiny number of p-values greater than 0.05 in Table A4 further proves that EEFOA outperforms other advanced algorithms on 30 benchmark functions of CEC2014. Fig. 13 gives the overall average of AVG and STD on 30 benchmark functions of EEFOA and state-of-art algorithms; it can be found that EEFOA achieves the minimum value compared to other state-of-art algorithms, which indicates that EEFOA has the best performance. From the convergence curves of Fig. 14 , the convergence accuracy of EEFOA is higher than the other compared algorithms. In F5, F10, F11, and F30, it can be found that EEFOA converges the fastest and effectively mitigates the LO problem. Consequently, EEFOA performs more effectively on most functions and has successfully improved convergence speed and solving LO, demonstrating the advanced and competitive nature of the proposed EEFOA in the field of optimization seeking.
Fig. 13.
Overall average of AVG and STD on 30 benchmark functions of EEFOA and state-of-art algorithms.
5.3. Experiments on MIS
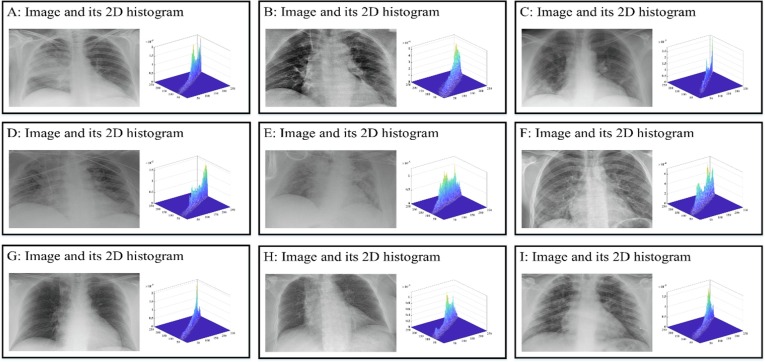
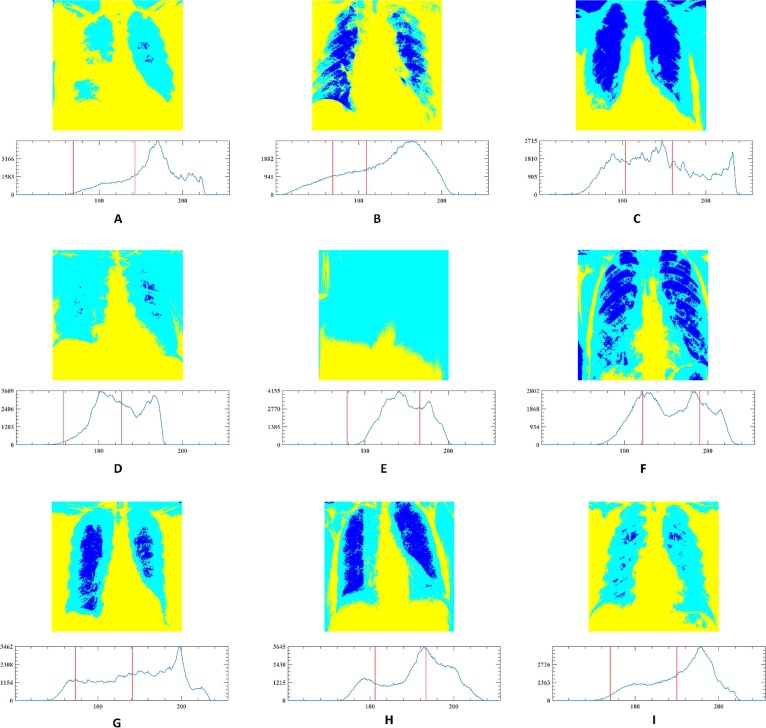
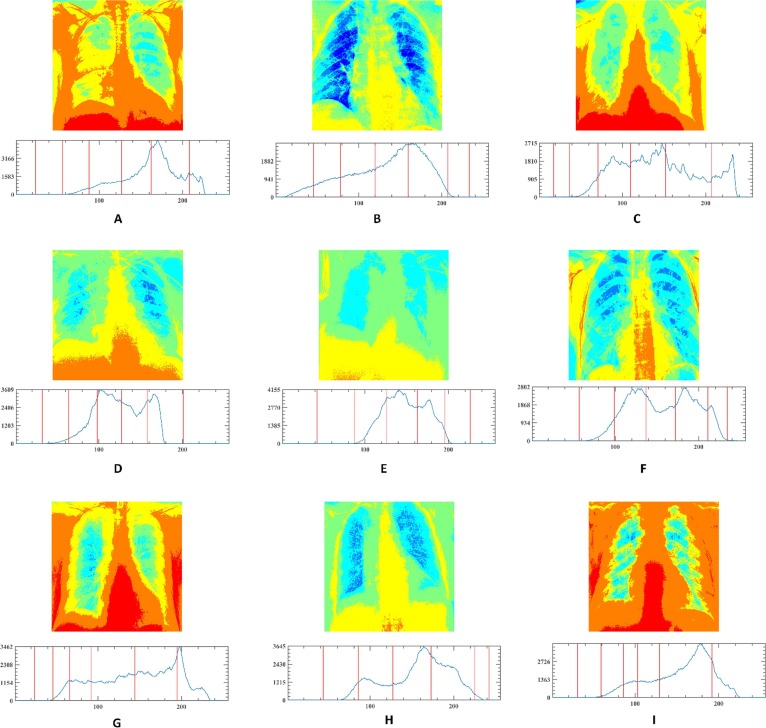
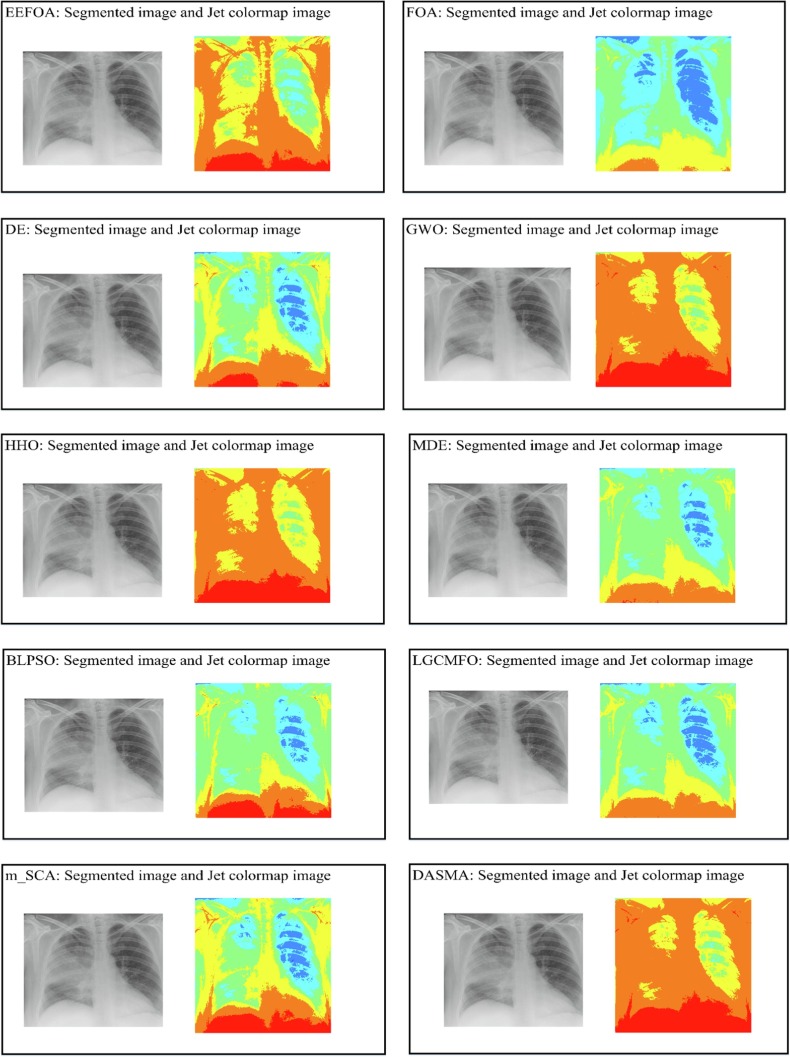
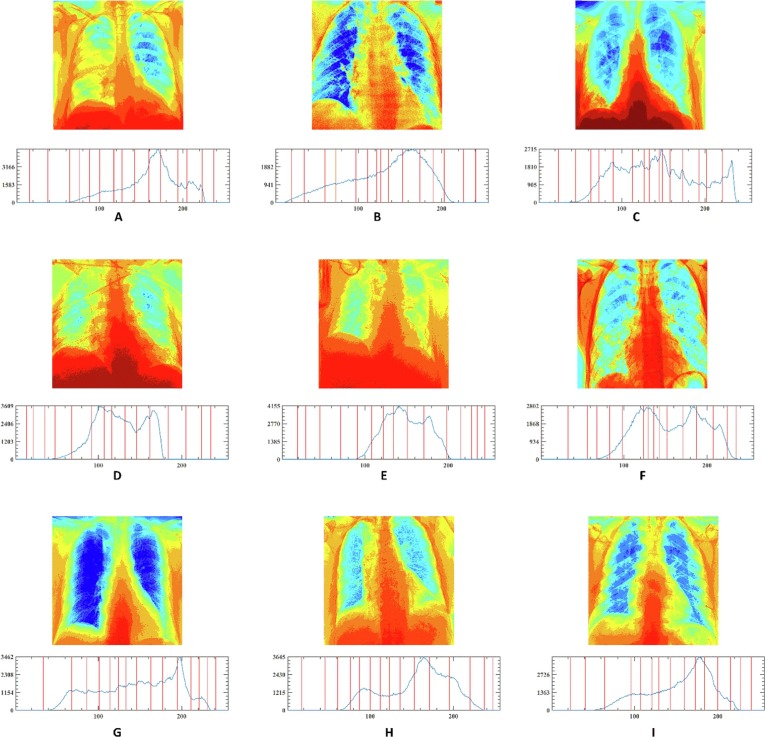
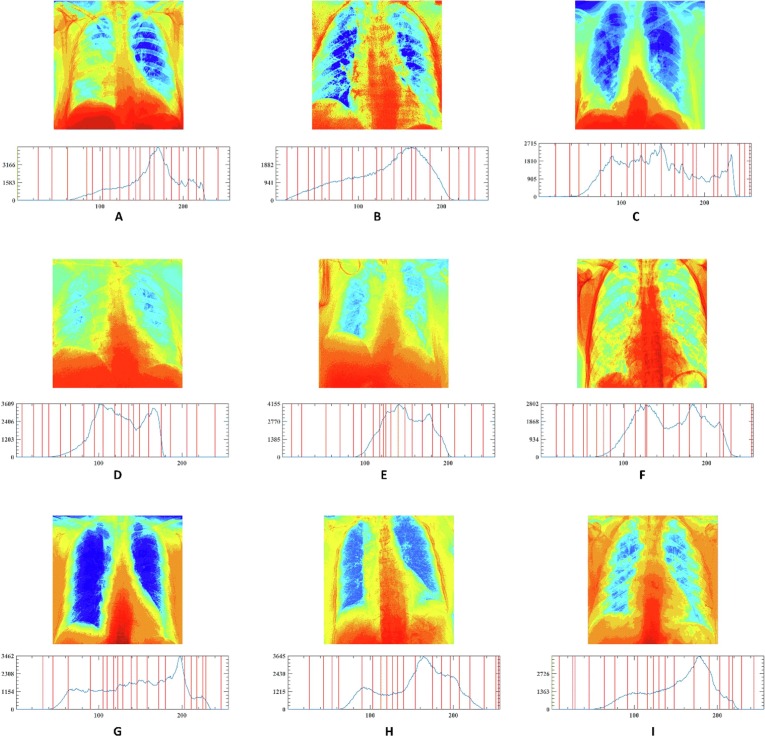
In this section, the outstanding performance of EEFOA in the field of image segmentation is demonstrated experimentally by comparing it with other segmentation methods. The segmentation methods involved in the comparison experiments are FOA, DE, GWO, HHO, MDE [117], BLPSO [118], LGCMFO [119], m_SCA [120], DASMA [121]. Notably, to check the robustness of the proposed method on the experiments for MIS, nine COVID-19 X-ray images were selected randomly from the datasets and segmented at low threshold levels of 2, 4, 6, and high threshold levels 10, 15, 20 separately. On the experiments of MIS, the nine images are marked A, B, C, D, E, F, G, H, I, respectively and displayed in Fig. 15 with their corresponding 2D histograms.
Fig. 15.
Samples of the segmented images and their corresponding 2D histograms.
In addition, Feature Similarity Index (FSIM), Peak Signal Noise Ratio (PSNR), and Structural Similarity Index (SSIM) was utilized to evaluate the segmentation experiment results, and further analysis afterward was given by mean (AVG), variance (STD) and Wilcoxon signed-rank test (WSRT).
5.3.1. Performance evaluation parameters
Three evaluation standards, FSIM, PSNR, and SSIM, for segmentation experiments, provide a reliable assessment of image segmentation quality. In addition, the assessment results were further analyzed by AVG, STD and a WSRT.
FSIM performs quality evaluation by utilizing the feature similarity between the original and segmented images. The principle of FSIM is rooted in two complementary features, phase congruency (PC) and gradient magnitude (GM). The human visual system (HVS) perceives images based on a number of low-level features, whereas PC can portray local structures capably. Also, as the PC is relatively invariant for changes in the image, this facilitates the extraction of stable features in the image but sometimes changes in the image do disrupt the perception, so GM compensation is essential. It has a value of [0,1], with values closer to 1 representing better segmentation quality. It can be given by:
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
| (32) |
where stands for all pixel fields of the original image. is the similarity of PC and GM fusion. represents the phase consistency measure. and are two constants, and indicates gradient descent. stands for local energy. is the amplitude of the Fourier component at position . In the end, denotes a small number.
PSNR evaluates the quality of segmentation by determining the visibility of errors between the original and segmented images. A larger value means better segmentation and it can be expressed as follows:
| (33) |
| (34) |
where denotes the root mean squared error. is the image size. represents the gray value of the pixel in the original image, and is the pixel gray value of the segmented image.
SSIM measures the degree of similarity between two images, the higher the value, the better the segmentation effect. The expression of SSIM can be stated as follows:
| (35) |
where and represent the mean of the original image and the segmented image, respectively. indicates the covariance of the original image and the segmented image. and stand for the standard deviations of the original image and the segmented image. And and are constants for stability.
5.3.2. Experiment analyses at a low threshold level
In this subsection, to verify the effectiveness in segmentation of EEFOA at low threshold levels, EEFOA was compared with other segmentation methods at threshold values of 2, 4 and 6. Table A5, Table A6, Table A7 show the AVG and STD for assessment results of FSIM, PSNR, and SSIM, separately. Table 8, Table 9, Table 10 further analyses assessment results, where ‘+’ denotes that EEFOA outperforms other segmentation methods, ‘-’ denotes that EEFOA underperforms other segmentation methods, ‘=’ denotes that EEFOA equivalent other segmentation methods. Mean stands for the average of overall ranking, and Rank is the ranking level. From Table 8, Table 9, Table 10, it can be seen that EEFOA obtained the smallest Mean and ranked first at each threshold level. The above analysis shows that EEFOA is superior and more stable in the process of finding the optimal threshold at low threshold levels.
Table 8.
The FSIM comparison results at low threshold level.
| T | EEFOA | FOA | DE | GWO | HHO | MDE | BLPSO | LGCMFO | m_SCA | DASMA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | +/-/= | ∼ | 4/2/3 | 3/0/6 | 3/0/6 | 1/1/7 | 5/0/4 | 2/0/7 | 4/0/5 | 2/2/5 | 1/0/8 |
| Mean | 3.667 | 7.000 | 5.778 | 5.444 | 5.889 | 6.778 | 4.778 | 5.556 | 4.889 | 5.222 | |
| Rank | 1 | 10 | 7 | 5 | 8 | 9 | 2 | 6 | 3 | 4 | |
| 4 | +/-/= | ∼ | 7/0/2 | 1/1/7 | 5/1/3 | 3/0/6 | 3/1/5 | 2/0/7 | 4/0/5 | 2/0/7 | 4/0/5 |
| Mean | 3.111 | 8.778 | 3.111 | 7.111 | 5.000 | 4.444 | 5.000 | 6.333 | 5.667 | 6.444 | |
| Rank | 1 | 10 | 1 | 9 | 4 | 3 | 4 | 7 | 6 | 8 | |
| 6 | +/-/= | ∼ | 9/0/0 | 7/0/2 | 9/0/0 | 6/0/3 | 9/0/0 | 8/0/1 | 6/0/3 | 8/0/1 | 9/0/0 |
| Mean | 1.000 | 9.556 | 4.111 | 7.667 | 6.000 | 4.333 | 7.000 | 3.444 | 5.667 | 6.222 | |
| Rank | 1 | 10 | 3 | 9 | 6 | 4 | 8 | 2 | 5 | 7 |
Table 9.
The PSNR comparison results at low threshold level.
| T | EEFOA | FOA | DE | GWO | HHO | MDE | BLPSO | LGCMFO | m_SCA | DASMA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | +/-/= | ∼ | 9/0/0 | 1/2/6 | 2/0/7 | 5/0/4 | 2/2/5 | 3/0/6 | 2/1/6 | 2/0/7 | 2/0/7 |
| Mean | 2.889 | 10.000 | 4.222 | 4.667 | 6.778 | 3.556 | 6.333 | 5.444 | 5.889 | 5.222 | |
| Rank | 1 | 10 | 3 | 4 | 9 | 2 | 8 | 6 | 7 | 5 | |
| 4 | +/-/= | ∼ | 9/0/0 | 1/1/7 | 5/0/4 | 6/0/3 | 1/1/7 | 5/0/4 | 1/0/8 | 4/0/5 | 3/0/6 |
| Mean | 2.222 | 10.000 | 3.556 | 5.222 | 6.667 | 3.000 | 7.444 | 4.333 | 6.778 | 5.778 | |
| Rank | 1 | 10 | 3 | 5 | 7 | 2 | 9 | 4 | 8 | 6 | |
| 6 | +/-/= | ∼ | 9/0/0 | 7/0/2 | 8/0/1 | 8/0/1 | 8/0/1 | 9/0/0 | 2/0/7 | 9/0/0 | 8/0/1 |
| Mean | 1.000 | 10.000 | 4.667 | 6.000 | 7.333 | 3.889 | 7.667 | 2.333 | 7.444 | 4.667 | |
| Rank | 1 | 10 | 4 | 6 | 7 | 3 | 9 | 2 | 8 | 4 |
Table 10.
The SSIM comparison results at low threshold level.
| T | EEFOA | FOA | DE | GWO | HHO | MDE | BLPSO | LGCMFO | m_SCA | DASMA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | +/-/= | ∼ | 5/0/4 | 2/2/5 | 1/1/7 | 1/1/7 | 2/2/5 | 1/3/5 | 2/1/6 | 0/1/8 | 2/0/7 |
| Mean | 4.222 | 9.222 | 4.444 | 6.111 | 5.222 | 5.000 | 4.667 | 5.444 | 4.222 | 6.444 | |
| Rank | 1 | 10 | 3 | 8 | 6 | 5 | 4 | 7 | 1 | 9 | |
| 4 | +/-/= | ∼ | 8/0/1 | 1/2/6 | 5/1/3 | 5/0/4 | 3/1/5 | 3/1/5 | 3/0/6 | 2/0/7 | 2/0/7 |
| Mean | 3.111 | 10.000 | 3.222 | 5.667 | 7.111 | 3.667 | 5.889 | 4.778 | 5.667 | 5.889 | |
| Rank | 1 | 10 | 2 | 5 | 9 | 3 | 7 | 4 | 5 | 7 | |
| 6 | +/-/= | ∼ | 8/0/1 | 5/0/4 | 7/0/2 | 5/0/4 | 4/0/5 | 4/0/5 | 5/0/4 | 4/0/5 | 6/0/3 |
| Mean | 1.444 | 10.000 | 5.111 | 7.000 | 6.556 | 4.222 | 5.667 | 4.222 | 5.000 | 5.778 | |
| Rank | 1 | 10 | 5 | 9 | 8 | 2 | 6 | 2 | 4 | 7 |
Table 11 shows the average time each segmentation method takes to find the optimal threshold values in low levels of 2,4,6. The bolded part of the table reveals that the average time of EEFOA has a 100% probability of reaching the smallest value of all the compared methods, which indicates that EEFOA converges fastest at low threshold levels. To obtain a more intuitive view of the times expressed in Table 11, Fig. 16 gives the average time to find the best thresholds for all segmented images. From Fig. 16, it can be seen that EEFOA is much faster in finding the optimal thresholds at three threshold levels compared to its peers. Table 12 gives all thresholds discovered by all methods in 2, 4, and 6 level threshold segmentation. Fig B1, Fig B2, Fig B3 give the segmented images of the proposed EEFOA for all X-ray images at lower thresholds (2, 4, 6), and also the distribution of the best-selected thresholds on the histogram associated with each test image.
Table 11.
The average time taken by each segmentation method to find the optimal threshold values of low level.
| Image | T | EEFOA | FOA | DE | GWO | HHO | MDE | BLPSO | LGCMFO | m_SCA | DASMA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 2 | 6.1406E + 00 | 1.0069E + 01 | 8.3708E + 00 | 7.7729E + 00 | 1.4741E + 01 | 1.5179E + 01 | 8.6503E + 00 | 3.8887E + 01 | 9.0040E + 00 | 3.4833E + 01 |
| 4 | 6.4285E + 00 | 8.6235E + 00 | 7.4079E + 00 | 7.0210E + 00 | 1.4247E + 01 | 1.4111E + 01 | 6.6497E + 00 | 4.1986E + 01 | 9.0313E + 00 | 3.6384E + 01 | |
| 6 | 9.1612E + 00 | 1.1955E + 01 | 1.0467E + 01 | 1.0555E + 01 | 2.0394E + 01 | 2.0585E + 01 | 9.4814E + 00 | 8.5839E + 01 | 1.2842E + 01 | 5.0038E + 01 | |
| B | 2 | 5.2767E + 00 | 9.2712E + 00 | 7.2453E + 00 | 6.2310E + 00 | 1.2816E + 01 | 1.4149E + 01 | 6.8642E + 00 | 3.6197E + 01 | 8.3789E + 00 | 3.2775E + 01 |
| 4 | 6.1397E + 00 | 8.5922E + 00 | 7.4057E + 00 | 7.0456E + 00 | 1.4299E + 01 | 1.4384E + 01 | 6.6056E + 00 | 4.2124E + 01 | 8.9278E + 00 | 3.6406E + 01 | |
| 6 | 8.9259E + 00 | 1.1975E + 01 | 1.0493E + 01 | 1.0491E + 01 | 2.0074E + 01 | 2.0733E + 01 | 9.3966E + 00 | 8.3532E + 01 | 1.2493E + 01 | 4.9890E + 01 | |
| C | 2 | 5.2007E + 00 | 9.2184E + 00 | 7.1721E + 00 | 6.1737E + 00 | 1.2650E + 01 | 1.3861E + 01 | 6.8229E + 00 | 3.6183E + 01 | 8.0148E + 00 | 3.2541E + 01 |
| 4 | 6.2204E + 00 | 8.6537E + 00 | 7.4703E + 00 | 6.9516E + 00 | 1.4156E + 01 | 1.4115E + 01 | 6.6044E + 00 | 4.2095E + 01 | 9.0518E + 00 | 3.6354E + 01 | |
| 6 | 8.9199E + 00 | 1.1992E + 01 | 1.0461E + 01 | 1.0398E + 01 | 1.9941E + 01 | 2.0625E + 01 | 9.2364E + 00 | 8.3044E + 01 | 1.2190E + 01 | 4.9660E + 01 | |
| D | 2 | 5.1788E + 00 | 9.6334E + 00 | 7.0634E + 00 | 6.1999E + 00 | 1.2557E + 01 | 1.3996E + 01 | 6.8072E + 00 | 3.5709E + 01 | 8.0454E + 00 | 3.2108E + 01 |
| 4 | 6.0588E + 00 | 8.7472E + 00 | 7.4829E + 00 | 7.0555E + 00 | 1.4349E + 01 | 1.4063E + 01 | 6.6381E + 00 | 4.2215E + 01 | 8.8363E + 00 | 3.6378E + 01 | |
| 6 | 8.7367E + 00 | 1.2111E + 01 | 1.0441E + 01 | 1.0495E + 01 | 1.9975E + 01 | 2.0685E + 01 | 9.6387E + 00 | 8.0164E + 01 | 1.2625E + 01 | 4.9649E + 01 | |
| E | 2 | 5.2275E + 00 | 9.6379E + 00 | 7.1409E + 00 | 6.3234E + 00 | 1.2609E + 01 | 1.4143E + 01 | 6.8370E + 00 | 3.5977E + 01 | 8.2197E + 00 | 3.2290E + 01 |
| 4 | 6.0527E + 00 | 8.6912E + 00 | 7.4919E + 00 | 7.0408E + 00 | 1.4124E + 01 | 1.4089E + 01 | 6.6284E + 00 | 4.2090E + 01 | 9.0031E + 00 | 3.6363E + 01 | |
| 6 | 8.9049E + 00 | 1.2100E + 01 | 1.0455E + 01 | 1.0454E + 01 | 2.0137E + 01 | 2.0607E + 01 | 9.8250E + 00 | 8.0985E + 01 | 1.2408E + 01 | 4.9602E + 01 | |
| F | 2 | 5.2322E + 00 | 9.6411E + 00 | 7.1245E + 00 | 6.2874E + 00 | 1.2661E + 01 | 1.4060E + 01 | 6.8537E + 00 | 3.5656E + 01 | 8.1030E + 00 | 3.1921E + 01 |
| 4 | 6.0773E + 00 | 8.6791E + 00 | 7.3933E + 00 | 7.0135E + 00 | 1.4199E + 01 | 1.3876E + 01 | 6.5266E + 00 | 4.2036E + 01 | 8.8892E + 00 | 3.6366E + 01 | |
| 6 | 8.7424E + 00 | 1.2120E + 01 | 1.0546E + 01 | 1.0472E + 01 | 1.9857E + 01 | 2.0746E + 01 | 9.6178E + 00 | 8.2424E + 01 | 1.2432E + 01 | 4.9528E + 01 | |
| G | 2 | 5.2614E + 00 | 9.5537E + 00 | 7.2077E + 00 | 6.3314E + 00 | 1.2585E + 01 | 1.4010E + 01 | 6.7332E + 00 | 3.5309E + 01 | 7.9998E + 00 | 3.1804E + 01 |
| 4 | 6.0536E + 00 | 8.7602E + 00 | 7.4396E + 00 | 7.0578E + 00 | 1.4253E + 01 | 1.4353E + 01 | 6.5954E + 00 | 4.2284E + 01 | 8.9056E + 00 | 3.6565E + 01 | |
| 6 | 8.8895E + 00 | 1.2123E + 01 | 1.0466E + 01 | 1.0406E + 01 | 1.9844E + 01 | 2.0734E + 01 | 9.7704E + 00 | 7.9719E + 01 | 1.2461E + 01 | 4.9661E + 01 | |
| H | 2 | 5.3832E + 00 | 9.5360E + 00 | 7.2532E + 00 | 6.4557E + 00 | 1.2259E + 01 | 1.4071E + 01 | 6.7519E + 00 | 3.6842E + 01 | 8.2167E + 00 | 3.1802E + 01 |
| 4 | 6.1297E + 00 | 8.6698E + 00 | 7.4685E + 00 | 7.0153E + 00 | 1.4333E + 01 | 1.4092E + 01 | 6.5572E + 00 | 4.2190E + 01 | 8.8128E + 00 | 3.6446E + 01 | |
| 6 | 8.9301E + 00 | 1.2088E + 01 | 1.0457E + 01 | 1.0499E + 01 | 2.0159E + 01 | 2.1121E + 01 | 9.5467E + 00 | 9.0040E + 01 | 1.2574E + 01 | 5.0191E + 01 | |
| I | 2 | 5.4241E + 00 | 9.5512E + 00 | 7.2107E + 00 | 6.4471E + 00 | 1.2417E + 01 | 1.3972E + 01 | 6.7667E + 00 | 3.6663E + 01 | 8.2812E + 00 | 3.1738E + 01 |
| 4 | 6.0152E + 00 | 8.5859E + 00 | 7.3435E + 00 | 6.8873E + 00 | 1.4042E + 01 | 1.4125E + 01 | 6.6045E + 00 | 4.1698E + 01 | 8.7704E + 00 | 3.6179E + 01 | |
| 6 | 8.9139E + 00 | 1.2033E + 01 | 1.0451E + 01 | 1.0543E + 01 | 2.0220E + 01 | 2.0969E + 01 | 9.7224E + 00 | 8.8185E + 01 | 1.2668E + 01 | 5.0154E + 01 |
Fig. 16.
Overall average of the time taken to find the best threshold for all segmented images.
Table 12.
Thresholds values at low threshold level.
| Image | T | EEFOA | FOA | DE |
|---|---|---|---|---|
| A | 2 | 69,143 | 57,176 | 69,144 |
| 4 | 35,75,116,171 | 29,77,103,183 | 35,66,85,177 | |
| 6 | 24,56,88,127,162,208 | 27,113,160,188,218,237 | 50,93,134,167,189,217 | |
| B | 2 | 69,110 | 59,128 | 82,150 |
| 4 | 38,76,119,188 | 23,38,113,145 | 40,74,120,190 | |
| 6 | 46,78,120,160,207,233 | 23,45,81,141,183,232 | 39,81,120,160,199,230 | |
| C | 2 | 104,160 | 113,147 | 103,157 |
| 4 | 48,98,156,205 | 45,83,133,213 | 52,102,158,194 | |
| 6 | 18,37,71,110,152,207 | 47,54,81,91,115,143 | 21,44,71,112,152,192 | |
| D | 2 | 58,127 | 56,116 | 58,127 |
| 4 | 43,89,136,197 | 39,98,156,182 | 39,89,123,190 | |
| 6 | 32,64,98,127,158,201 | 35,47,113,125,180,204 | 28,60,96,131,178,217 | |
| E | 2 | 78,166 | 51,143 | 78,167 |
| 4 | 53,107,156,203 | 63,137,162,213 | 65,132,171,209 | |
| 6 | 42,87,126,163,196,226 | 26,96,132,172,186,248 | 45,89,134,162,190,220 | |
| F | 2 | 122,190 | 119,183 | 122,186 |
| 4 | 63,126,188,223 | 57,133,176,224 | 68,137,189,220 | |
| 6 | 57,99,137,172,211,234 | 57,83,95,140,191,198 | 42,86,123,170,206,227 | |
| G | 2 | 73,141 | 88,154 | 68,139 |
| 4 | 60,122,176,216 | 57,105,149,210 | 34,76,117,185 | |
| 6 | 24,46,66,92,144,195 | 109,115,140,157,221,243 | 30,61,90,120,165,206 | |
| H | 2 | 106,167 | 156,198 | 106,167 |
| 4 | 56,121,187,213 | 102,195,214,226 | 60,119,187,223 | |
| 6 | 43,85,127,173,225,242 | 49,61,102,165,203,246 | 49,90,127,161,202,224 | |
| I | 2 | 70,150 | 109,168 | 65,118 |
| 4 | 37,65,85,136 | 86,178,194,222 | 35,71,116,193 | |
| 6 | 31,59,86,103,129,192 | 28,79,144,207,214,235 | 56,88,127,168,191,222 | |
| Image | T | HHO | MDE | BLPSO |
| A | 2 | 47,103 | 69,144 | 68,143 |
| 4 | 97,121,157,205 | 30,62,89,163 | 73,133,176,210 | |
| 6 | 22,38,64,86,143,197 | 44,89,130,178,203,224 | 42,87,132,177,193,210 | |
| B | 2 | 90,144 | 83,150 | 69,138 |
| 4 | 40,67,108,167 | 39,79,121,188 | 63,93,118,186 | |
| 6 | 42,75,116,157,195,229 | 41,80,120,160,199,231 | 28,78,112,154,199,223 | |
| C | 2 | 99,169 | 103,157 | 130,182 |
| 4 | 26,48,104,160 | 52,104,159,210 | 50,113,170,219 | |
| 6 | 18,37,57,104,143,203 | 19,39,75,114,155,202 | 8,62,88,112,162,201 | |
| D | 2 | 58,127 | 58,127 | 61,129 |
| 4 | 54,116,159,201 | 43,85,123,189 | 38,82,151,202 | |
| 6 | 34,52,71,114,171,221 | 23,48,72,112,161,209 | 65,113,127,150,188,231 | |
| E | 2 | 80,162 | 78,167 | 78,167 |
| 4 | 84,136,162,196 | 53,107,154,198 | 54,109,141,199 | |
| 6 | 47,92,137,160,184,206 | 45,91,133,164,195,225 | 34,74,112,141,185,207 | |
| F | 2 | 122,190 | 122,190 | 112,181 |
| 4 | 58,138,189,220 | 64,126,189,218 | 101,142,209,232 | |
| 6 | 42,99,133,176,211,229 | 49,92,124,168,206,228 | 47,81,112,166,202,234 | |
| G | 2 | 123,179 | 75,141 | 123,174 |
| 4 | 68,131,179,214 | 29,59,94,167 | 42,75,121,189 | |
| 6 | 37,82,134,179,212,232 | 22,41,60,100,145,198 | 40,82,121,143,197,219 | |
| H | 2 | 106,165 | 106,167 | 108,170 |
| 4 | 95,153,199,223 | 69,132,188,220 | 84,143,194,230 | |
| 6 | 56,115,156,196,220,238 | 38,83,119,157,200,225 | 36,60,107,171,212,236 | |
| I | 2 | 71,121 | 70,150 | 72,151 |
| 4 | 17,50,81,177 | 34,70,109,174 | 72,128,146,182 | |
| 6 | 16,52,89,109,144,190 | 38,89,126,154,185,220 | 40,79,127,154,175,205 | |
| Image | T | LGCMFO | m_SCA | DASMA |
| A | 2 | 69,144 | 69,144 | 69,144 |
| 4 | 31,59,89,172 | 24,50,88,170 | 34,63,93,174 | |
| 6 | 51,99,138,178,202,225 | 58,95,127,162,185,206 | 22,45,67,89,132,191 | |
| B | 2 | 61,110 | 72,110 | 61,110 |
| 4 | 39,79,121,189 | 27,55,85,176 | 39,78,121,188 | |
| 6 | 39,77,118,161,201,231 | 31,68,100,154,197,233 | 42,81,119,162,201,231 | |
| C | 2 | 103,157 | 80,133 | 103,157 |
| 4 | 50,105,153,194 | 53,108,155,192 | 60,112,155,194 | |
| 6 | 19,42,77,114,158,202 | 19,38,61,89,123,183 | 21,43,79,120,163,209 | |
| D | 2 | 58,127 | 58,127 | 58,127 |
| 4 | 43,83,123,189 | 39,69,101,171 | 24,62,100,177 | |
| 6 | 28,50,72,116,162,207 | 31,52,73,116,144,203 | 39,58,81,104,148,205 | |
| E | 2 | 78,167 | 78,167 | 78,167 |
| 4 | 66,132,171,209 | 47,135,172,208 | 63,132,168,208 | |
| 6 | 46,91,132,163,193,223 | 24,57,101,138,166,204 | 48,91,132,167,194,226 | |
| F | 2 | 122,190 | 122,190 | 122,190 |
| 4 | 64,125,189,219 | 57,118,176,212 | 65,127,189,218 | |
| 6 | 40,84,126,167,206,226 | 39,65,118,171,209,229 | 39,79,123,165,206,228 | |
| G | 2 | 75,141 | 75,136 | 75,141 |
| 4 | 30,60,94,175 | 76,155,202,229 | 29,61,94,166 | |
| 6 | 22,45,70,116,162,207 | 48,98,151,186,224,240 | 20,36,55,95,138,189 | |
| H | 2 | 106,167 | 106,167 | 106,167 |
| 4 | 70,128,188,222 | 75,138,187,219 | 70,129,188,220 | |
| 6 | 39,84,122,161,200,227 | 48,88,121,157,190,219 | 39,78,116,158,199,225 | |
| I | 2 | 66,119 | 67,119 | 66,119 |
| 4 | 38,74,111,181 | 18,58,96,153 | 35,69,103,157 | |
| 6 | 50,96,138,162,187,220 | 22,44,92,135,179,219 | 26,52,76,106,147,198 |
Fig B1.
The segmented results and thresholds obtained by EEFOA of the X-ray images at the threshold value of 2.
Fig B2.
The segmented results and thresholds obtained by EEFOA of the X-ray images at the threshold value of 4.
Fig B3.
The segmented results and thresholds obtained by EEFOA of the X-ray images at the threshold value of 6.
Fig. 17 shows the segmentation results of COVID-19 X-ray image A by all segmentation methods under a threshold value of 6. Detailed analysis and comparison of the segmentation results suggest that EEFOA is more effective than other segmentation methods in overall segmentation and local detail retention. It indicates that the proposed segmentation method will provide higher-quality automatic segmentation of COVID-19 X-ray images to assist physicians in making accurate diagnoses.
Fig. 17.
The segmented results by all segmentation methods of the X-ray image A at threshold value of 6.
EEFOA is more capable and stable in finding the optimal thresholds. At the same time, EEFOA has a faster convergence rate than other segmentation methods, with better overall segmentation effect and local detail retention. Hence, EEFOA has a competitive advantage in the field of image segmentation at low threshold levels.
5.3.3. Experiment analyses at a high threshold level
In this subsection, to further validate the performance of EEFOA for MIS at high threshold levels, EEFOA was compared with other segmentation methods at threshold levels of 10, 15 and 20. Table A8, Table A9, Table A10 show the AVG and STD of evaluation results for MIS of all methods by FIMS, PSNR, and SSIM. Table 13, Table 14, Table 15 show the further analysis of the evaluation results given by the WSRT. In the case of mean and variance, EEFOA is more powerful in finding the optimal threshold and has stronger stability than other methods. According to the results of the WSRT analysis, EEFOA performs superiorly to others.
Table 13.
The FSIM comparison results at a high threshold level.
| T | EEFOA | FOA | DE | GWO | HHO | MDE | BLPSO | LGCMFO | m_SCA | DASMA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | +/-/= | ∼ | 9/0/0 | 6/0/3 | 9/0/0 | 9/0/0 | 7/0/2 | 9/0/0 | 2/0/7 | 8/0/1 | 7/0/2 |
| Mean | 1.222 | 10.000 | 5.000 | 5.889 | 7.444 | 4.222 | 8.667 | 1.889 | 6.889 | 3.778 | |
| Rank | 1 | 10 | 5 | 6 | 8 | 4 | 9 | 2 | 7 | 3 | |
| 15 | +/-/= | ∼ | 9/0/0 | 8/0/1 | 5/0/4 | 9/0/0 | 6/0/3 | 9/0/0 | 2/0/7 | 9/0/0 | 5/0/4 |
| Mean | 1.556 | 10.000 | 5.444 | 4.889 | 7.556 | 4.000 | 8.556 | 1.889 | 7.778 | 3.333 | |
| Rank | 1 | 10 | 6 | 5 | 7 | 4 | 9 | 2 | 8 | 3 | |
| 20 | +/-/= | ∼ | 9/0/0 | 7/0/2 | 5/0/4 | 7/0/2 | 3/0/6 | 9/0/0 | 2/0/7 | 9/0/0 | 2/1/6 |
| Mean | 1.889 | 10.000 | 5.222 | 5.333 | 8.111 | 2.889 | 8.222 | 3.111 | 7.444 | 2.778 | |
| Rank | 1 | 10 | 5 | 6 | 8 | 3 | 9 | 4 | 7 | 2 |
Table 14.
The PSNR comparison results at high threshold level.
| T | EEFOA | FOA | DE | GWO | HHO | MDE | BLPSO | LGCMFO | m_SCA | DASMA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | +/-/= | ∼ | 9/0/0/ | 6/0/3 | 7/0/2 | 8/0/1 | 4/0/5 | 9/0/0 | 0/0/9 | 8/0/1 | 3/0/6 |
| Mean | 1.444 | 10.000 | 5.000 | 6.000 | 7.444 | 3.778 | 8.556 | 1.778 | 7.444 | 3.556 | |
| Rank | 1 | 10 | 5 | 6 | 7 | 4 | 9 | 2 | 7 | 3 | |
| 15 | +/-/= | ∼ | 9/0/0/ | 7/0/2 | 5/0/4 | 8/0/1 | 5/0/4 | 9/0/0/ | 2/0/7 | 9/0/0/ | 5/0/4 |
| Mean | 1.778 | 10.000 | 5.000 | 5.333 | 7.778 | 3.667 | 8.333 | 2.000 | 7.667 | 3.444 | |
| Rank | 1 | 10 | 5 | 6 | 8 | 4 | 9 | 2 | 7 | 3 | |
| 20 | +/-/= | ∼ | 9/0/0/ | 4/0/5 | 6/0/3 | 6/0/3 | 4/0/5 | 9/0/0/ | 2/0/7 | 7/0/2 | 2/0/7 |
| Mean | 2.111 | 10.000 | 4.444 | 6.111 | 7.667 | 3.444 | 8.444 | 2.889 | 7.444 | 2.444 | |
| Rank | 1 | 10 | 5 | 6 | 8 | 4 | 9 | 3 | 7 | 2 |
Table 15.
The SSIM comparison results at high threshold level.
| T | EEFOA | FOA | DE | GWO | HHO | MDE | BLPSO | LGCMFO | m_SCA | DASMA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | +/-/= | ∼ | 9/0/0 | 8/0/1 | 8/0/1 | 8/0/1 | 8/0/1 | 9/0/0 | 7/0/2 | 8/0/1 | 8/0/1 |
| Mean | 1.444 | 9.333 | 5.000 | 5.889 | 6.667 | 5.667 | 8.000 | 2.444 | 5.667 | 4.889 | |
| Rank | 1 | 10 | 4 | 7 | 8 | 5 | 9 | 2 | 5 | 3 | |
| 15 | +/-/= | ∼ | 9/0/0 | 9/0/0 | 8/0/1 | 8/0/1 | 9/0/0 | 9/0/0 | 3/0/6 | 9/0/0 | 9/0/0 |
| Mean | 1.000 | 10.000 | 5.222 | 4.667 | 6.333 | 5.000 | 8.222 | 2.667 | 7.778 | 4.111 | |
| Rank | 1 | 10 | 6 | 4 | 7 | 5 | 9 | 2 | 8 | 3 | |
| 20 | +/-/= | ∼ | 9/0/0 | 9/0/0 | 9/0/0 | 9/0/0 | 8/0/1 | 9/0/0 | 6/0/3 | 9/0/0 | 5/0/4 |
| Mean | 1.000 | 10.000 | 5.333 | 5.778 | 7.111 | 4.111 | 8.667 | 3.000 | 7.000 | 3.000 | |
| Rank | 1 | 10 | 5 | 6 | 8 | 4 | 9 | 2 | 7 | 2 |
Table 16 shows the average time of all segmentation methods performing the MIS on high threshold levels of 10,15, 20. From the average time for each method after 30 independent runs, it can be seen that EEFOA took the shortest time for the vast majority of the operations and deduced that EEFOA converged faster than the other methods.
Table 16.
The average time taken by each segmentation method to find the optimal threshold values of high level.
| Image | T | EEFOA | FOA | DE | GWO | HHO | MDE | BLPSO | LGCMFO | m_SCA | DASMA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 10 | 1.5978E + 01 | 2.4042E + 01 | 2.1733E + 01 | 1.9345E + 01 | 4.0511E + 01 | 3.9446E + 01 | 2.0018E + 01 | 1.0945E + 02 | 2.4218E + 01 | 9.4219E + 01 |
| 15 | 1.9230E + 01 | 2.4881E + 01 | 2.2818E + 01 | 2.2545E + 01 | 4.5102E + 01 | 4.4421E + 01 | 1.9093E + 01 | 1.3206E + 02 | 2.7980E + 01 | 1.1460E + 02 | |
| 20 | 3.1582E + 01 | 3.9323E + 01 | 3.5911E + 01 | 3.5632E + 01 | 7.0354E + 01 | 7.0281E + 01 | 3.0835E + 01 | 2.0408E + 02 | 4.5401E + 01 | 1.7478E + 02 | |
| B | 10 | 1.5249E + 01 | 2.3201E + 01 | 2.1006E + 01 | 1.9154E + 01 | 3.9566E + 01 | 3.8215E + 01 | 1.8384E + 01 | 1.0857E + 02 | 2.2721E + 01 | 9.2292E + 01 |
| 15 | 1.8848E + 01 | 2.4767E + 01 | 2.2736E + 01 | 2.2588E + 01 | 4.5308E + 01 | 4.4297E + 01 | 1.9226E + 01 | 1.3221E + 02 | 2.8024E + 01 | 1.1431E + 02 | |
| 20 | 2.9756E + 01 | 3.8991E + 01 | 3.5132E + 01 | 3.5346E + 01 | 6.9193E + 01 | 6.9423E + 01 | 2.8685E + 01 | 2.0176E + 02 | 4.3261E + 01 | 1.7296E + 02 | |
| C | 10 | 1.5287E + 01 | 2.3138E + 01 | 2.0990E + 01 | 1.8897E + 01 | 3.9618E + 01 | 3.7763E + 01 | 1.8015E + 01 | 1.0780E + 02 | 2.2892E + 01 | 9.2037E + 01 |
| 15 | 1.8911E + 01 | 2.4779E + 01 | 2.2751E + 01 | 2.2687E + 01 | 4.5047E + 01 | 4.4240E + 01 | 1.8966E + 01 | 1.3191E + 02 | 2.7754E + 01 | 1.1429E + 02 | |
| 20 | 2.9756E + 01 | 3.8991E + 01 | 3.5132E + 01 | 3.5346E + 01 | 6.9193E + 01 | 6.9423E + 01 | 2.8685E + 01 | 2.0176E + 02 | 4.3261E + 01 | 1.7296E + 02 | |
| D | 10 | 1.5416E + 01 | 2.3244E + 01 | 2.0962E + 01 | 1.8760E + 01 | 3.9411E + 01 | 3.7610E + 01 | 1.8376E + 01 | 1.0798E + 02 | 2.3029E + 01 | 9.2186E + 01 |
| 15 | 1.8949E + 01 | 2.4769E + 01 | 2.2779E + 01 | 2.2861E + 01 | 4.4955E + 01 | 4.4310E + 01 | 1.9251E + 01 | 1.3170E + 02 | 2.8019E + 01 | 1.1466E + 02 | |
| 20 | 3.0196E + 01 | 3.8799E + 01 | 3.5175E + 01 | 3.5415E + 01 | 6.9489E + 01 | 6.9420E + 01 | 2.8494E + 01 | 2.0162E + 02 | 4.3777E + 01 | 1.7417E + 02 | |
| E | 10 | 1.5251E + 01 | 2.3243E + 01 | 2.0994E + 01 | 1.8741E + 01 | 3.9713E + 01 | 3.7476E + 01 | 1.8659E + 01 | 1.0814E + 02 | 2.2867E + 01 | 9.3185E + 01 |
| 15 | 1.8887E + 01 | 2.4685E + 01 | 2.2759E + 01 | 2.2926E + 01 | 4.5454E + 01 | 4.4377E + 01 | 1.9021E + 01 | 1.3175E + 02 | 2.8298E + 01 | 1.1453E + 02 | |
| 20 | 3.0220E + 01 | 3.8878E + 01 | 3.5302E + 01 | 3.5322E + 01 | 6.9633E + 01 | 6.9374E + 01 | 2.9024E + 01 | 2.0154E + 02 | 4.3735E + 01 | 1.7366E + 02 | |
| F | 10 | 1.4948E + 01 | 2.3312E + 01 | 2.1017E + 01 | 1.8873E + 01 | 3.9619E + 01 | 3.7478E + 01 | 1.8171E + 01 | 1.0839E + 02 | 2.2998E + 01 | 9.3231E + 01 |
| 15 | 1.8764E + 01 | 2.4753E + 01 | 2.2802E + 01 | 2.2974E + 01 | 4.5588E + 01 | 4.4350E + 01 | 1.8638E + 01 | 1.3189E + 02 | 2.7802E + 01 | 1.1461E + 02 | |
| 20 | 3.0388E + 01 | 3.9055E + 01 | 3.5301E + 01 | 3.5357E + 01 | 6.9900E + 01 | 6.9634E + 01 | 2.8197E + 01 | 2.0227E + 02 | 4.3934E + 01 | 1.7363E + 02 | |
| G | 10 | 1.4765E + 01 | 2.3150E + 01 | 2.0916E + 01 | 1.8884E + 01 | 3.9476E + 01 | 3.7529E + 01 | 1.8071E + 01 | 1.0812E + 02 | 2.3314E + 01 | 9.2395E + 01 |
| 15 | 1.8715E + 01 | 2.4668E + 01 | 2.2832E + 01 | 2.3001E + 01 | 4.5227E + 01 | 4.4554E + 01 | 1.8599E + 01 | 1.3180E + 02 | 2.8052E + 01 | 1.1469E + 02 | |
| 20 | 3.0642E + 01 | 3.9104E + 01 | 3.5345E + 01 | 3.4994E + 01 | 6.9119E + 01 | 6.9349E + 01 | 2.7851E + 01 | 2.0232E + 02 | 4.4225E + 01 | 1.7308E + 02 | |
| H | 10 | 1.4771E + 01 | 2.3194E + 01 | 2.0986E + 01 | 1.9089E + 01 | 3.9366E + 01 | 3.7758E + 01 | 1.8198E + 01 | 1.0822E + 02 | 2.3324E + 01 | 9.2303E + 01 |
| 15 | 1.8837E + 01 | 2.4929E + 01 | 2.2767E + 01 | 2.2874E + 01 | 4.5487E + 01 | 4.4601E + 01 | 1.8532E + 01 | 1.3178E + 02 | 2.8410E + 01 | 1.1456E + 02 | |
| 20 | 3.0250E + 01 | 3.8830E + 01 | 3.5342E + 01 | 3.5089E + 01 | 6.9414E + 01 | 6.9432E + 01 | 2.8082E + 01 | 2.0307E + 02 | 4.3530E + 01 | 1.7297E + 02 | |
| I | 10 | 1.4924E + 01 | 2.3059E + 01 | 2.1041E + 01 | 1.9432E + 01 | 3.9756E + 01 | 3.7992E + 01 | 1.8138E + 01 | 1.0810E + 02 | 2.3658E + 01 | 9.2026E + 01 |
| 15 | 1.8696E + 01 | 2.4898E + 01 | 2.2594E + 01 | 2.2585E + 01 | 4.5204E + 01 | 4.4397E + 01 | 1.8878E + 01 | 1.3103E + 02 | 2.7814E + 01 | 1.1363E + 02 | |
| 20 | 2.9968E + 01 | 3.8446E + 01 | 3.4910E + 01 | 3.5088E + 01 | 6.9487E + 01 | 6.9378E + 01 | 2.8259E + 01 | 2.0268E + 02 | 4.3442E + 01 | 1.7332E + 02 |
Fig. 18, Fig. 19, Fig. 20 show the segmented images of the proposed algorithm EEFOA for all images used in the experiments at the number of thresholds (10, 15, 20), and the results also include the distribution of the best-selected thresholds on the histogram associated with each test image. From the segmentation results of Fig. 21 , it can be found that EEFOA retains more detail in local features than other methods. Therefore, based on the above analysis and comparison, it is clear that EEFOA is also a promising segmentation tool for high threshold MIS, a valuable theoretical study for medical images with complex details.
Fig. 18.
The segmented results and thresholds obtained by EEFOA of the X-ray images at the threshold value of 10.
Fig. 19.
The segmented results and thresholds obtained by EEFOA of the X-ray images at the threshold value of 15.
Fig. 20.
The segmented results and thresholds obtained by EEFOA of the X-ray images at the threshold value of 20.
Fig. 21.
The segmented results by all segmentation methods of the X-ray image A at threshold value of 20.
6. Discussions and insights
This section presents a few points of discussion in this paper. In the present study, the proposed EEFOA mitigates the problems of slow convergence and LO and is verified on high-dimensional functions and other comparative experiments. Finally, EEFOA successfully applied to the MIS of COVID-19 X-ray images, providing the most accurate and effective segmentation results at high and low threshold levels. Thus, the proposed EEFOA has core competencies, especially in the area of MIS for COVID-19 x-ray.
The two optimization strategies of ENE and ERM process the elite members of the population similar to the cross recombination and mutation of genes, generating new alternative individuals to update the population. Breaking the original FOA inherent in the general update mode and meanwhile encouraging the algorithm iteration, significantly increasing the algorithm's convergence speed and accuracy.
Unlike other methods [122], [123] that utilized traditional 1D or 2D histograms to represent image information, this study used non-local means (NL-means) 2D histograms consisting of original grayscale images and NL-means images. NL-means image is a product obtained from the original grayscale image with an NL-means filtering technique that sufficiently scans the image's redundant information and retains the maximum image detail while de-noising.
Certainly, we cannot be sure that EEFOA must be superior to the original FOA in any field, which is not rigorous. The performance between EEFOA and FOA is relative, which further confirms the theory of the No Free Lunch (NFL) theorems [66], a certain optimization algorithm is not suitable for all areas of optimization. When dealing with a certain kind of application, the algorithm should be parameterized or otherwise modified to better match the characteristics of the current domain.
Besides, there are also some limitations in this paper. Since each iteration of the algorithm performs both ENE and ERM strategies to optimize FOA, the cost complexity of EEFOA also increases when solving the benchmark functions. To combat this issue, optimization with distributed computing can be considered.
In the future, we can extend the image dataset and increase the thresholds to obtain more reliable results. Further, due to the excellent performance shown by EEFOA in the field of MIS, it could be considered to provide a theoretical basis for building medical diagnostic systems and applying it to segment other classes of medical images. Besides, it also can be applied to additional real-world problems, such as machine learning models [124], fine-grained alignment [125], service ecosystem [126], iris or retinal vessel segmentation [127], [128], computational experiments [129], [130], power distribution network [131], and medical signals [132].
7. Conclusion and future work
This paper proposed EEFOA by fusing ENE and ERM with the original FOA. Specifically, ENE accelerates algorithms' convergence when dealing with complex optimization problems. ERM is effectively able to mitigate local optimum problems. Experimental results comparing EEFOA with the original FOA in dimensions 50, 100, and 200 show that ENE and ERM positively affect FOA, allowing it to be highly competitive despite the high dimensional problems. The CEC2014-based benchmark function experiments demonstrate that when dealing with various types of benchmark function problems, the proposed EEFOA outperforms the original FOA with a probability of 100% in multiple dimensions and an average probability of 77% over other peers. It indicates that EEFOA has an upgraded ability to find the optimal solution compared to other comparative algorithms.
In addition, EEFOA was applied to MIS experiments on COVID-19 X-ray images with other segmentation methods. The proposed method combined the original images with NL-means images to generate the NL-means 2D histogram representing the image information, and Rényi's entropy is employed to select the optimal thresholds. The final segmentation results were analyzed according to three assessment criteria, SSIM, FSIM, and PSNR. The analysis of the evaluation results demonstrates that EEFOA takes the shortest time to find the optimal threshold at both low and high threshold levels and achieves better results in terms of overall segmentation and local detail retention.
In the future, more excellent mechanisms can be applied to improve FOA, and the improved FOAs can be used to assist in the diagnosis of other medical conditions such as chronic obstructive pulmonary disease, skin cancer breast cancer, lupus nephritis. Besides, the proposed method is also considered for other applications, such as feature selection, mega infrastructure projects, engineering optimization, and other applications. Further, more objective functions could be considered as a replacement for Rényi's entropy, such as Kapur’s and Tsallis entropy.
CRediT authorship contribution statement
Shuhui Hao: Software, Visualization, Investigation, Formal analysis, Writing – original draft, Writing – review & editing. Changcheng Huang: Conceptualization, Methodology, Formal analysis, Investigation, Funding acquisition, Supervision, Writing – original draft, Writing – review & editing. Ali Asghar Heidari: Software, Visualization, Investigation, Formal analysis, Resources, Writing – original draft, Writing – review & editing. Zhangze Xu: Software, Visualization, Investigation, Writing – original draft, Writing – review & editing. Huiling Chen: Conceptualization, Methodology, Formal analysis, Investigation, Funding acquisition, Supervision, Project administration, Resources, Software, Writing – original draft, Writing – review & editing. Eatedal Alabdulkreem: Software, Visualization, Investigation, Data curation, Resources, Writing – review & editing. Hela Elmannai: Software, Visualization, Investigation, Data curation, Resources, Writing – review & editing. Xianchuan Wang: Conceptualization, Methodology, Formal analysis, Investigation, Funding acquisition, Supervision, Writing – original draft, Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R161), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia
Declaration of AI and AI-assisted technologies in the writing process
During the preparation of this work the author(s) used chatGPT in order to enhance the English grammar and paraphrase some sentences. After using this tool/service, the author(s) reviewed and edited the content as needed and take(s) full responsibility for the content of the publication.
Footnotes
https://www.aliasgharheidari.com/HHO.html
https://www.aliasgharheidari.com/SMA.html
https://www.aliasgharheidari.com/INFO.html
https://www.aliasgharheidari.com/RUN.html
https://www.aliasgharheidari.com/HGS.html
https://www.aliasgharheidari.com/RIME.html
Appendix A. .
See Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10 .
Table A1.
Details of the CEC2014 function.
| ID | Class | Name | Range | Fi∗ = Fi(x ∗ ) |
|---|---|---|---|---|
| F1 | Unimodal | Rotated High Conditioned Elliptic Function | [−100,100] | 100 |
| F2 | Unimodal | Rotated Bent Cigar Function | [−100,100] | 200 |
| F3 | Unimodal | Rotated Discus Function | [−100,100] | 300 |
| F4 | Multimodal | Shifted and Rotated Rosenbrock’s Function | [−100,100] | 400 |
| F5 | Multimodal | Shifted and Rotated Ackley’s Function | [−100,100] | 500 |
| F6 | Multimodal | Shifted and Rotated Weierstrass Function | [−100,100] | 600 |
| F7 | Multimodal | Shifted and Rotated Griewank’s Function | [−100,100] | 700 |
| F8 | Multimodal | Shifted Rastrigin’s Function | [−100,100] | 800 |
| F9 | Multimodal | Shifted and Rotated Rastrigin’s Function | [−100,100] | 900 |
| F10 | Multimodal | Shifted Schwefel’s Function | [−100,100] | 1000 |
| F11 | Multimodal | Shifted and Rotated Schwefel’s Function | [−100,100] | 1100 |
| F12 | Multimodal | Shifted and Rotated Katsuura Function | [−100,100] | 1200 |
| F13 | Multimodal | Shifted and Rotated HappyCat Function | [−100,100] | 1300 |
| F14 | Multimodal | Shifted and Rotated HGBat Function | [−100,100] | 1400 |
| F15 | Multimodal | Shifted and Rotated Expanded Griewank’s plus Rosenbrock’s Function | [−100,100] | 1500 |
| F16 | Multimodal | Shifted and Rotated Expanded Scaffer’s F6 Function | [−100,100] | 1600 |
| F17 | Hybrid | Hybrid Function 1 | [−100,100] | 1700 |
| F18 | Hybrid | Hybrid Function 2 | [−100,100] | 1800 |
| F19 | Hybrid | Hybrid Function 3 | [−100,100] | 1900 |
| F20 | Hybrid | Hybrid Function 4 | [−100,100] | 2000 |
| F21 | Hybrid | Hybrid Function 5 | [−100,100] | 2100 |
| F22 | Hybrid | Hybrid Function 6 | [−100,100] | 2200 |
| F23 | Composition | Composition Function 1 | [−100,100] | 2300 |
| F24 | Composition | Composition Function 2 | [−100,100] | 2400 |
| F25 | Composition | Composition Function 3 | [−100,100] | 2500 |
| F26 | Composition | Composition Function 4 | [−100,100] | 2600 |
| F27 | Composition | Composition Function 5 | [−100,100] | 2700 |
| F28 | Composition | Composition Function 6 | [−100,100] | 2800 |
| F29 | Composition | Composition Function 7 | [−100,100] | 2900 |
| F30 | Composition | Composition Function 8 | [−100,100] | 3000 |
Table A2.
Results of EEFOA and well-known algorithms.
| Fun | Item | EEFOA | WOA | GWO | MFO | BA | SCA | FA | PSO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | AVG | 8.5836E + 06 | 2.8887E + 07 | 5.8437E + 07 | 9.7958E + 07 | 7.1707E + 05 | 2.2669E + 08 | 2.5051E + 08 | 8.5967E + 06 |
| STD | 2.9166E + 06 | 1.4930E + 07 | 4.6668E + 07 | 9.2608E + 07 | 3.0979E + 05 | 5.6117E + 07 | 3.4384E + 07 | 1.7227E + 06 | |
| F2 | AVG | 1.7535E + 05 | 4.4058E + 06 | 2.7766E + 09 | 1.3355E + 10 | 5.3845E + 05 | 1.7104E + 10 | 1.5995E + 10 | 1.4510E + 08 |
| STD | 9.5152E + 04 | 6.3258E + 06 | 2.1495E + 09 | 9.9068E + 09 | 2.8711E + 05 | 3.1934E + 09 | 1.4392E + 09 | 1.2570E + 07 | |
| F3 | AVG | 6.4619E + 03 | 3.3860E + 04 | 2.9258E + 04 | 1.0373E + 05 | 5.9563E + 02 | 3.6781E + 04 | 6.1822E + 04 | 9.4964E + 02 |
| STD | 2.4861E + 02 | 2.2711E + 04 | 9.3921E + 03 | 6.2659E + 04 | 5.0446E + 02 | 5.5435E + 03 | 8.6951E + 03 | 1.1117E + 02 | |
| F4 | AVG | 4.9659E + 02 | 5.9632E + 02 | 6.5454E + 02 | 1.4170E + 03 | 4.5027E + 02 | 1.4454E + 03 | 1.5430E + 03 | 4.6963E + 02 |
| STD | 3.7248E + 01 | 5.8755E + 01 | 1.0556E + 02 | 9.2901E + 02 | 5.4807E + 01 | 2.2239E + 02 | 1.0927E + 02 | 4.6109E + 01 | |
| F5 | AVG | 5.2000E + 02 | 5.2036E + 02 | 5.2094E + 02 | 5.2031E + 02 | 5.2096E + 02 | 5.2092E + 02 | 5.2095E + 02 | 5.2096E + 02 |
| STD | 2.1319E-05 | 2.1216E-01 | 4.2478E-02 | 1.7986E-01 | 5.1586E-02 | 5.5298E-02 | 5.5033E-02 | 4.5121E-02 | |
| F6 | AVG | 6.4250E + 02 | 6.3515E + 02 | 6.1378E + 02 | 6.2436E + 02 | 6.3420E + 02 | 6.3278E + 02 | 6.3393E + 02 | 6.2206E + 02 |
| STD | 4.0584E + 00 | 4.2478E + 00 | 2.2456E + 00 | 4.3856E + 00 | 3.6742E + 00 | 2.8042E + 00 | 1.1370E + 00 | 3.9536E + 00 | |
| F7 | AVG | 7.0039E + 02 | 7.0099E + 02 | 7.1336E + 02 | 8.1007E + 02 | 7.0063E + 02 | 8.3936E + 02 | 8.3398E + 02 | 7.0228E + 02 |
| STD | 1.2477E-01 | 7.2975E-02 | 1.2103E + 01 | 5.6218E + 01 | 1.9505E-01 | 2.3120E + 01 | 1.8409E + 01 | 1.4442E-01 | |
| F8 | AVG | 8.7711E + 02 | 9.6923E + 02 | 8.8620E + 02 | 9.4006E + 02 | 1.0161E + 03 | 1.0370E + 03 | 1.0241E + 03 | 9.6823E + 02 |
| STD | 8.1603E + 00 | 3.5578E + 01 | 2.1245E + 01 | 4.2183E + 01 | 5.2676E + 01 | 1.9076E + 01 | 9.9214E + 00 | 2.3229E + 01 | |
| F9 | AVG | 1.0856E + 03 | 1.1307E + 03 | 9.9852E + 02 | 1.1144E + 03 | 1.1632E + 03 | 1.1720E + 03 | 1.1579E + 03 | 1.1085E + 03 |
| STD | 6.3662E + 00 | 6.3835E + 01 | 2.7222E + 01 | 3.2747E + 01 | 6.6884E + 01 | 1.5541E + 01 | 1.3012E + 01 | 1.8918E + 01 | |
| F10 | AVG | 3.0941E + 03 | 4.8237E + 03 | 3.2838E + 03 | 4.7021E + 03 | 5.4263E + 03 | 6.9437E + 03 | 7.5735E + 03 | 5.1090E + 03 |
| STD | 2.3798E + 02 | 7.9595E + 02 | 5.4622E + 02 | 8.5911E + 02 | 6.3182E + 02 | 4.4095E + 02 | 2.2455E + 02 | 4.6697E + 02 | |
| F11 | AVG | 5.5460E + 03 | 6.0782E + 03 | 3.8179E + 03 | 5.4047E + 03 | 5.6911E + 03 | 8.0532E + 03 | 7.9292E + 03 | 5.9386E + 03 |
| STD | 3.2820E + 02 | 1.0065E + 03 | 4.7537E + 02 | 7.6627E + 02 | 7.7766E + 02 | 3.3517E + 02 | 3.1222E + 02 | 5.9891E + 02 | |
| F12 | AVG | 1.2019E + 03 | 1.2017E + 03 | 1.2017E + 03 | 1.2005E + 03 | 1.2012E + 03 | 1.2024E + 03 | 1.2025E + 03 | 1.2024E + 03 |
| STD | 7.6651E-01 | 4.5769E-01 | 1.1400E + 00 | 3.0591E-01 | 3.7169E-01 | 2.5411E-01 | 2.4850E-01 | 2.7899E-01 | |
| F13 | AVG | 1.3007E + 03 | 1.3005E + 03 | 1.3004E + 03 | 1.3023E + 03 | 1.3005E + 03 | 1.3030E + 03 | 1.3027E + 03 | 1.3004E + 03 |
| STD | 1.5082E-01 | 1.0751E-01 | 1.2519E-01 | 1.1873E + 00 | 1.2180E-01 | 3.7280E-01 | 3.0928E-01 | 8.4356E-02 | |
| F14 | AVG | 1.4003E + 03 | 1.4003E + 03 | 1.4032E + 03 | 1.4366E + 03 | 1.4003E + 03 | 1.4458E + 03 | 1.4405E + 03 | 1.4003E + 03 |
| STD | 5.3654E-02 | 1.3846E-01 | 4.8931E + 00 | 2.6474E + 01 | 1.1214E-01 | 8.7766E + 00 | 5.2911E + 00 | 8.1421E-02 | |
| F15 | AVG | 1.5988E + 03 | 1.5802E + 03 | 1.6265E + 03 | 7.0823E + 04 | 1.5283E + 03 | 5.5795E + 03 | 1.2860E + 04 | 1.5168E + 03 |
| STD | 9.2522E + 01 | 2.9882E + 01 | 3.9468E + 02 | 1.7288E + 05 | 5.5033E + 00 | 4.3494E + 03 | 6.0838E + 03 | 1.2092E + 00 | |
| F16 | AVG | 1.6135E + 03 | 1.6126E + 03 | 1.6109E + 03 | 1.6127E + 03 | 1.6132E + 03 | 1.6128E + 03 | 1.6129E + 03 | 1.6119E + 03 |
| STD | 7.7929E-02 | 6.3240E-01 | 6.0644E-01 | 6.1279E-01 | 2.9072E-01 | 2.5964E-01 | 1.5005E-01 | 4.8771E-01 | |
| F17 | AVG | 9.6537E + 05 | 4.2375E + 06 | 1.5696E + 06 | 3.1896E + 06 | 9.9959E + 04 | 5.4591E + 06 | 6.5040E + 06 | 2.8910E + 05 |
| STD | 8.4671E + 05 | 2.8515E + 06 | 2.2835E + 06 | 4.0391E + 06 | 5.0974E + 04 | 2.4083E + 06 | 1.9434E + 06 | 1.5602E + 05 | |
| F18 | AVG | 6.9974E + 03 | 5.7808E + 03 | 1.5296E + 07 | 1.6769E + 05 | 8.8301E + 04 | 1.5778E + 08 | 3.0125E + 08 | 1.8289E + 06 |
| STD | 4.0155E + 03 | 5.4942E + 03 | 3.0499E + 07 | 4.0340E + 05 | 4.2853E + 04 | 9.4835E + 07 | 9.7185E + 07 | 4.7513E + 05 | |
| F19 | AVG | 1.9277E + 03 | 1.9396E + 03 | 1.9344E + 03 | 1.9663E + 03 | 1.9217E + 03 | 1.9847E + 03 | 2.0036E + 03 | 1.9176E + 03 |
| STD | 2.0412E + 01 | 2.9719E + 01 | 2.4309E + 01 | 5.4774E + 01 | 2.5110E + 01 | 1.9238E + 01 | 1.2580E + 01 | 2.4437E + 00 | |
| F20 | AVG | 1.5743E + 04 | 2.5397E + 04 | 1.6395E + 04 | 5.7921E + 04 | 2.4252E + 03 | 1.7570E + 04 | 1.8736E + 04 | 2.3290E + 03 |
| STD | 6.4130E + 03 | 1.4328E + 04 | 6.2208E + 03 | 4.2419E + 04 | 1.5534E + 02 | 4.8021E + 03 | 5.9106E + 03 | 6.5172E + 01 | |
| F21 | AVG | 5.8834E + 05 | 8.0119E + 05 | 5.2333E + 05 | 4.4076E + 05 | 4.9098E + 04 | 1.4294E + 06 | 2.0573E + 06 | 1.2327E + 05 |
| STD | 3.8276E + 05 | 5.8505E + 05 | 3.5673E + 05 | 6.0449E + 05 | 3.2731E + 04 | 5.8004E + 05 | 7.3448E + 05 | 9.2983E + 04 | |
| F22 | AVG | 3.1514E + 03 | 3.0243E + 03 | 2.5736E + 03 | 3.0558E + 03 | 3.3330E + 03 | 2.9484E + 03 | 2.9788E + 03 | 2.9080E + 03 |
| STD | 1.8774E + 02 | 2.0171E + 02 | 1.5495E + 02 | 2.9414E + 02 | 3.0486E + 02 | 1.3657E + 02 | 9.6923E + 01 | 1.8342E + 02 | |
| F23 | AVG | 2.5000E + 03 | 2.6309E + 03 | 2.6371E + 03 | 2.6843E + 03 | 2.6152E + 03 | 2.6670E + 03 | 2.7338E + 03 | 2.6161E + 03 |
| STD | 0.0000E + 00 | 7.5116E + 00 | 1.3006E + 01 | 5.7079E + 01 | 2.0115E-03 | 1.3395E + 01 | 1.4434E + 01 | 6.4213E-01 | |
| F24 | AVG | 2.6000E + 03 | 2.6058E + 03 | 2.6000E + 03 | 2.6755E + 03 | 2.6648E + 03 | 2.6001E + 03 | 2.7069E + 03 | 2.6276E + 03 |
| STD | 1.8441E-04 | 3.7395E + 00 | 7.6315E-04 | 2.6840E + 01 | 2.4219E + 01 | 7.4739E-02 | 5.3584E + 00 | 6.2943E + 00 | |
| F25 | AVG | 2.7000E + 03 | 2.7228E + 03 | 2.7107E + 03 | 2.7131E + 03 | 2.7293E + 03 | 2.7284E + 03 | 2.7348E + 03 | 2.7126E + 03 |
| STD | 0.0000E + 00 | 2.3254E + 01 | 3.7824E + 00 | 7.1635E + 00 | 2.1944E + 01 | 8.7819E + 00 | 4.4284E + 00 | 6.6208E + 00 | |
| F26 | AVG | 2.8000E + 03 | 2.7005E + 03 | 2.7636E + 03 | 2.7024E + 03 | 2.7005E + 03 | 2.7023E + 03 | 2.7022E + 03 | 2.7804E + 03 |
| STD | 0.0000E + 00 | 1.3458E-01 | 4.8703E + 01 | 1.3350E + 00 | 1.3939E-01 | 5.4946E-01 | 3.8199E-01 | 4.0685E + 01 | |
| F27 | AVG | 2.9000E + 03 | 3.8346E + 03 | 3.3274E + 03 | 3.6519E + 03 | 3.7788E + 03 | 3.3636E + 03 | 3.8024E + 03 | 3.5207E + 03 |
| STD | 0.0000E + 00 | 3.2212E + 02 | 1.2108E + 02 | 1.9911E + 02 | 4.6154E + 02 | 2.6543E + 02 | 2.8660E + 01 | 2.8849E + 02 | |
| F28 | AVG | 3.0000E + 03 | 4.9869E + 03 | 3.9561E + 03 | 3.9601E + 03 | 5.1437E + 03 | 4.8282E + 03 | 4.2166E + 03 | 6.9262E + 03 |
| STD | 0.0000E + 00 | 7.4006E + 02 | 2.3964E + 02 | 2.4945E + 02 | 6.2340E + 02 | 3.5877E + 02 | 9.7691E + 01 | 9.2918E + 02 | |
| F29 | AVG | 3.1000E + 03 | 5.7129E + 06 | 8.9993E + 05 | 4.1481E + 06 | 3.5645E + 07 | 1.1101E + 07 | 3.3406E + 06 | 5.5124E + 04 |
| STD | 0.0000E + 00 | 5.1165E + 06 | 3.7772E + 06 | 3.8497E + 06 | 4.0310E + 07 | 6.3722E + 06 | 9.3152E + 05 | 1.3841E + 05 | |
| F30 | AVG | 3.2000E + 03 | 9.0090E + 04 | 7.4663E + 04 | 4.2616E + 04 | 4.3856E + 04 | 2.3406E + 05 | 1.8352E + 05 | 1.3148E + 04 |
| STD | 2.9664E-05 | 6.2693E + 04 | 5.5909E + 04 | 4.1349E + 04 | 1.0113E + 05 | 7.9681E + 04 | 4.4064E + 04 | 6.5285E + 03 |
Table A3.
The p-values of EEFOA versus improved FOA variants on WSRT.
| Fun | BSSFOA | AMFOA | CAEFOA | CEFOA | CIFOA | LGMSFOA |
|---|---|---|---|---|---|---|
| F1 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F2 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F3 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F4 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F5 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F6 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.0357E-03 | 8.2206E-02 |
| F7 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F8 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F9 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F10 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F11 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F12 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 4.0715E-05 | 1.9209E-06 |
| F13 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F14 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F15 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F16 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 9.6266E-04 |
| F17 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F18 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F19 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F20 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F21 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F22 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F23 | 5.0000E-01 | 1.7344E-06 | 1.7344E-06 | 1.0000E + 00 | 1.0000E + 00 | 1.7344E-06 |
| F24 | 3.2520E-03 | 1.7344E-06 | 1.7344E-06 | 2.7016E-05 | 2.7016E-05 | 1.7344E-06 |
| F25 | 1.0000E + 00 | 1.7344E-06 | 1.7344E-06 | 1.0000E + 00 | 1.0000E + 00 | 1.7344E-06 |
| F26 | 5.0000E-01 | 1.7322E-06 | 1.4392E-06 | 1.0000E + 00 | 1.2500E-01 | 7.5137E-05 |
| F27 | 5.0000E-01 | 1.7344E-06 | 1.7344E-06 | 1.0000E + 00 | 1.0000E + 00 | 1.7344E-06 |
| F28 | 1.0000E + 00 | 1.7344E-06 | 1.7344E-06 | 1.0000E + 00 | 1.0000E + 00 | 1.7344E-06 |
| F29 | 1.0000E + 00 | 1.7344E-06 | 1.7344E-06 | 1.0000E + 00 | 1.0000E + 00 | 1.7344E-06 |
| F30 | 1.0000E + 00 | 1.7344E-06 | 1.7344E-06 | 1.0000E + 00 | 1.0000E + 00 | 1.7344E-06 |
| Fun | MSFOA | SFOA | SCA_FOA | IFOA | MOFOA |
|---|---|---|---|---|---|
| F1 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F2 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F3 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F4 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F5 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F6 | 6.1564E-04 | 8.4508E-01 | 7.1570E-04 | 3.3789E-03 | 1.9729E-05 |
| F7 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F8 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F9 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F10 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F11 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F12 | 2.8786E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.9209E-06 |
| F13 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F14 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F15 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F16 | 1.0570E-04 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 4.2767E-02 |
| F17 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F18 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F19 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F20 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F21 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F22 | 2.1266E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F23 | 1.7344E-06 | 1.7344E-06 | 1.0000E+00 | 1.7344E-06 | 1.0000E+00 |
| F24 | 1.7344E-06 | 1.7344E-06 | 2.7016E-05 | 2.1266E-06 | 2.7016E-05 |
| F25 | 1.7344E-06 | 1.7344E-06 | 1.0000E+00 | 1.7344E-06 | 1.0000E+00 |
| F26 | 9.7110E-05 | 1.7333E-06 | 1.0000E+00 | 1.7333E-06 | 2.5000E-01 |
| F27 | 1.7344E-06 | 1.7344E-06 | 1.0000E+00 | 1.7344E-06 | 1.0000E+00 |
| F28 | 1.7344E-06 | 1.7344E-06 | 1.0000E+00 | 1.7344E-06 | 1.0000E+00 |
| F29 | 1.7344E-06 | 1.7344E-06 | 1.0000E+00 | 1.7344E-06 | 1.0000E+00 |
| F30 | 1.7344E-06 | 1.7344E-06 | 1.0000E+00 | 1.7344E-06 | 1.0000E+00 |
Table A4.
The p-values of EEFOA versus state-of-art algorithms on WSRT.
| Fun | CESCA | CMFO | HGWO | CGSCA | CAGWO | MWOA | SCADE | OBSCA | COSCA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 1.7344E-06 | 8.4661E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F2 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F3 | 1.7344E-06 | 1.8326E-03 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F4 | 1.7344E-06 | 6.3391E-06 | 1.7344E-06 | 1.7344E-06 | 3.5152E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F5 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F6 | 3.6094E-03 | 3.5152E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 4.7162E-02 | 2.1266E-06 | 1.7344E-06 | 1.7344E-06 |
| F7 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F8 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 4.7162E-02 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F9 | 1.7344E-06 | 4.0483E-01 | 1.7344E-06 | 1.7344E-06 | 2.3704E-05 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F10 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 2.8786E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 2.2248E-04 |
| F11 | 1.7344E-06 | 8.3071E-04 | 3.8822E-06 | 1.7344E-06 | 8.4661E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 4.7292E-06 |
| F12 | 2.3534E-06 | 3.6094E-03 | 4.5336E-04 | 1.3595E-04 | 4.2857E-06 | 1.7344E-06 | 1.0570E-04 | 9.2710E-03 | 4.2843E-01 |
| F13 | 1.7344E-06 | 3.1618E-03 | 1.7344E-06 | 1.7344E-06 | 5.2165E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 7.6909E-06 |
| F14 | 1.7344E-06 | 1.9569E-02 | 1.7344E-06 | 1.7344E-06 | 1.1265E-05 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F15 | 1.7344E-06 | 2.0515E-04 | 1.9209E-06 | 1.7344E-06 | 1.9209E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F16 | 5.3044E-01 | 1.9209E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 2.3534E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F17 | 1.7344E-06 | 1.0444E-02 | 1.7344E-06 | 2.6033E-06 | 4.5281E-01 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 9.3157E-06 |
| F18 | 1.7344E-06 | 6.5833E-01 | 1.7344E-06 | 1.7344E-06 | 3.5152E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 |
| F19 | 1.7344E-06 | 5.0383E-01 | 1.7344E-06 | 2.1266E-06 | 8.9718E-02 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 3.8822E-06 |
| F20 | 1.7344E-06 | 1.0201E-01 | 1.7344E-06 | 3.0650E-04 | 3.1817E-06 | 1.7344E-06 | 1.7344E-06 | 2.8786E-06 | 2.5967E-05 |
| F21 | 1.7344E-06 | 7.1889E-01 | 5.2165E-06 | 7.6909E-06 | 1.3601E-05 | 1.7344E-06 | 1.9209E-06 | 8.4661E-06 | 3.7243E-05 |
| F22 | 1.7344E-06 | 3.5888E-04 | 2.5846E-03 | 6.4242E-03 | 1.7344E-06 | 1.7344E-06 | 3.6004E-01 | 3.8203E-01 | 1.7344E-06 |
| F23 | 1.7344E-06 | 1.7344E-06 | 1.2500E-01 | 1.0000E + 00 | 1.7344E-06 | 1.7344E-06 | 1.0000E + 00 | 1.7344E-06 | 1.0000E + 00 |
| F24 | 1.7344E-06 | 1.7344E-06 | 8.2981E-06 | 1.6114E-04 | 3.3886E-01 | 1.7344E-06 | 1.8726E-05 | 6.3198E-05 | 5.6835E-05 |
| F25 | 1.7344E-06 | 1.7344E-06 | 1.0000E + 00 | 1.0000E + 00 | 1.0000E + 00 | 1.7344E-06 | 1.0000E + 00 | 1.0000E + 00 | 1.0000E + 00 |
| F26 | 1.7344E-06 | 1.7344E-06 | 4.3778E-04 | 1.7344E-06 | 4.0100E-05 | 2.5364E-01 | 1.7344E-06 | 1.7344E-06 | 1.9531E-03 |
| F27 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.0000E + 00 | 1.7344E-06 | 1.7344E-06 | 1.8215E-05 | 1.7344E-06 | 6.2500E-02 |
| F28 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.0000E + 00 | 1.7344E-06 | 1.7344E-06 | 4.0100E-05 | 1.7344E-06 | 1.0000E + 00 |
| F29 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.0000E + 00 | 1.7344E-06 | 1.7300E-06 | 2.5631E-06 | 1.7344E-06 | 5.0000E-01 |
| F30 | 1.7344E-06 | 1.7344E-06 | 1.9379E-03 | 1.0000E + 00 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.7344E-06 | 1.2207E-04 |
Table A5.
The FSIM comparison at low threshold level.
| Image | T | EEFOA | FOA | DE | GWO | HHO | MDE | BLPSO | LGCMFO | m_SCA | DASMA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 2 | AVG | 7.2971E-01 | 7.2421E-01 | 7.3790E-01 | 7.2177E-01 | 7.1763E-01 | 7.3373E-01 | 7.2732E-01 | 7.2421E-01 | 7.2575E-01 | 7.1763E-01 |
| STD | 1.9018E-02 | 2.1391E-02 | 9.4050E-05 | 1.9583E-02 | 2.0538E-02 | 1.2691E-02 | 2.2705E-02 | 2.1391E-02 | 1.9524E-02 | 2.0538E-02 | ||
| 4 | AVG | 7.5479E-01 | 7.2561E-01 | 7.5244E-01 | 7.2804E-01 | 7.3786E-01 | 7.3590E-01 | 7.5119E-01 | 7.3487E-01 | 7.4129E-01 | 7.4172E-01 | |
| STD | 2.0087E-02 | 3.0285E-02 | 2.3926E-02 | 2.4895E-02 | 2.5233E-02 | 3.1252E-02 | 2.1759E-02 | 2.3745E-02 | 2.7725E-02 | 2.5615E-02 | ||
| 6 | AVG | 8.0504E-01 | 7.6564E-01 | 7.9243E-01 | 7.7895E-01 | 7.7447E-01 | 7.8151E-01 | 7.8079E-01 | 7.8158E-01 | 7.7489E-01 | 7.7941E-01 | |
| STD | 2.2493E-02 | 4.1172E-02 | 2.7688E-02 | 2.2247E-02 | 4.5754E-02 | 2.3247E-02 | 2.7204E-02 | 1.6714E-02 | 2.6236E-02 | 2.3523E-02 | ||
| B | 2 | AVG | 6.6278E-01 | 6.2139E-01 | 6.5708E-01 | 6.5077E-01 | 6.6086E-01 | 6.6465E-01 | 6.5141E-01 | 6.5930E-01 | 6.5047E-01 | 6.7085E-01 |
| STD | 1.8015E-02 | 5.2051E-02 | 2.1632E-02 | 1.3754E-02 | 2.8991E-02 | 2.0538E-02 | 2.9210E-02 | 1.8790E-02 | 2.3212E-02 | 2.5272E-02 | ||
| 4 | AVG | 7.9349E-01 | 7.0327E-01 | 7.9231E-01 | 7.7629E-01 | 7.5914E-01 | 7.9297E-01 | 7.6538E-01 | 7.9119E-01 | 7.7645E-01 | 7.8379E-01 | |
| STD | 2.4346E-02 | 6.5059E-02 | 1.4472E-02 | 1.9407E-02 | 6.3604E-02 | 1.1438E-02 | 2.6314E-02 | 2.0676E-02 | 3.9441E-02 | 2.7926E-02 | ||
| 6 | AVG | 8.7929E-01 | 7.6130E-01 | 8.6208E-01 | 8.4926E-01 | 8.4255E-01 | 8.6934E-01 | 8.3684E-01 | 8.7289E-01 | 8.5447E-01 | 8.6626E-01 | |
| STD | 2.5257E-02 | 6.2847E-02 | 1.7391E-02 | 2.3457E-02 | 4.2892E-02 | 1.3296E-02 | 3.0096E-02 | 1.8266E-02 | 3.2450E-02 | 1.9472E-02 | ||
| C | 2 | AVG | 7.2078E-01 | 7.1664E-01 | 7.1867E-01 | 7.2265E-01 | 7.1666E-01 | 7.1858E-01 | 7.2144E-01 | 7.1918E-01 | 7.3052E-01 | 7.2024E-01 |
| STD | 1.5357E-02 | 1.8577E-02 | 3.9555E-03 | 1.4380E-02 | 1.3331E-02 | 4.6325E-03 | 1.8870E-02 | 5.9839E-03 | 1.7023E-02 | 5.9414E-03 | ||
| 4 | AVG | 7.4632E-01 | 6.8396E-01 | 7.3489E-01 | 7.2787E-01 | 7.5296E-01 | 7.5360E-01 | 7.1944E-01 | 7.3591E-01 | 7.2872E-01 | 7.3326E-01 | |
| STD | 3.7767E-02 | 6.4350E-02 | 3.8262E-02 | 3.6406E-02 | 4.5485E-02 | 3.4322E-02 | 3.5449E-02 | 3.6848E-02 | 4.4372E-02 | 3.8244E-02 | ||
| 6 | AVG | 8.2112E-01 | 7.2903E-01 | 7.7652E-01 | 7.8910E-01 | 8.1464E-01 | 8.0192E-01 | 7.6791E-01 | 8.1061E-01 | 7.9314E-01 | 7.9507E-01 | |
| STD | 4.1202E-02 | 6.3164E-02 | 3.6277E-02 | 3.4350E-02 | 5.5552E-02 | 3.2870E-02 | 4.0847E-02 | 3.6487E-02 | 6.0160E-02 | 3.4195E-02 | ||
| D | 2 | AVG | 7.5264E-01 | 7.2748E-01 | 7.5175E-01 | 7.5371E-01 | 7.4039E-01 | 7.5034E-01 | 7.5281E-01 | 7.5099E-01 | 7.5522E-01 | 7.5292E-01 |
| STD | 3.2118E-03 | 2.5436E-02 | 2.6653E-03 | 4.9751E-03 | 2.3744E-02 | 2.5960E-03 | 2.2186E-02 | 1.0353E-03 | 6.5321E-03 | 5.5093E-03 | ||
| 4 | AVG | 7.8148E-01 | 7.7862E-01 | 7.9236E-01 | 7.9096E-01 | 7.7737E-01 | 7.9019E-01 | 7.8781E-01 | 7.8489E-01 | 7.8344E-01 | 7.8416E-01 | |
| STD | 1.3434E-02 | 2.8397E-02 | 8.8352E-03 | 1.5359E-02 | 2.4415E-02 | 9.6752E-03 | 1.7650E-02 | 1.3453E-02 | 1.3080E-02 | 1.3057E-02 | ||
| 6 | AVG | 8.1356E-01 | 7.9521E-01 | 8.0746E-01 | 8.0134E-01 | 7.9617E-01 | 8.0230E-01 | 8.1082E-01 | 8.0355E-01 | 8.0403E-01 | 8.0138E-01 | |
| STD | 1.3856E-02 | 3.2387E-02 | 1.4667E-02 | 1.6637E-02 | 2.5098E-02 | 1.4382E-02 | 2.4329E-02 | 1.4664E-02 | 1.9941E-02 | 1.3363E-02 | ||
| E | 2 | AVG | 7.6054E-01 | 7.5741E-01 | 7.5413E-01 | 7.5741E-01 | 7.5263E-01 | 7.5483E-01 | 7.5189E-01 | 7.5745E-01 | 7.5487E-01 | 7.5697E-01 |
| STD | 7.7368E-03 | 5.3738E-03 | 2.1663E-03 | 5.3738E-03 | 1.6413E-02 | 3.6703E-03 | 5.2665E-03 | 5.5188E-03 | 8.8358E-03 | 4.9022E-03 | ||
| 4 | AVG | 7.1504E-01 | 6.6026E-01 | 7.1735E-01 | 7.0312E-01 | 7.2498E-01 | 7.0549E-01 | 7.0914E-01 | 7.0323E-01 | 7.0838E-01 | 7.0323E-01 | |
| STD | 2.2543E-02 | 3.9444E-02 | 2.7967E-02 | 1.6382E-02 | 2.8396E-02 | 1.7041E-02 | 3.8198E-02 | 1.9397E-02 | 2.3280E-02 | 1.7319E-02 | ||
| 6 | AVG | 8.0520E-01 | 7.1117E-01 | 7.8879E-01 | 7.7914E-01 | 7.9521E-01 | 7.8545E-01 | 7.5936E-01 | 7.9296E-01 | 7.6259E-01 | 7.7873E-01 | |
| STD | 3.4361E-02 | 5.0825E-02 | 3.5363E-02 | 2.4712E-02 | 4.0684E-02 | 2.3353E-02 | 4.3614E-02 | 1.9473E-02 | 3.7053E-02 | 2.7593E-02 | ||
| F | 2 | AVG | 6.1133E-01 | 6.0460E-01 | 6.1205E-01 | 6.0430E-01 | 6.2174E-01 | 6.0460E-01 | 6.1873E-01 | 6.0574E-01 | 6.1070E-01 | 6.0810E-01 |
| STD | 7.8846E-03 | 7.1013E-03 | 8.4494E-03 | 4.2172E-03 | 1.5969E-02 | 7.1013E-03 | 2.3604E-02 | 7.0986E-03 | 8.8311E-03 | 6.0891E-03 | ||
| 4 | AVG | 7.1255E-01 | 6.9614E-01 | 7.1070E-01 | 7.0323E-01 | 7.0883E-01 | 7.1063E-01 | 7.1785E-01 | 6.9489E-01 | 7.0627E-01 | 6.9967E-01 | |
| STD | 2.4029E-02 | 3.0022E-02 | 2.4443E-02 | 1.7216E-02 | 3.1934E-02 | 1.4506E-02 | 2.6872E-02 | 2.2240E-02 | 2.5124E-02 | 3.3032E-02 | ||
| 6 | AVG | 7.7587E-01 | 7.3058E-01 | 7.6127E-01 | 7.4485E-01 | 7.4982E-01 | 7.5345E-01 | 7.5175E-01 | 7.5148E-01 | 7.5389E-01 | 7.4898E-01 | |
| STD | 2.2930E-02 | 3.7004E-02 | 2.3161E-02 | 1.5315E-02 | 2.9919E-02 | 1.7002E-02 | 3.1554E-02 | 1.7506E-02 | 2.6356E-02 | 2.1463E-02 | ||
| G | 2 | AVG | 6.8842E-01 | 6.8121E-01 | 6.9070E-01 | 6.8421E-01 | 6.8180E-01 | 6.8293E-01 | 6.8818E-01 | 6.8349E-01 | 6.8400E-01 | 6.8218E-01 |
| STD | 1.3974E-02 | 2.3841E-02 | 1.5385E-02 | 1.8094E-02 | 1.7913E-02 | 1.4079E-02 | 2.7882E-02 | 1.8601E-02 | 1.5946E-02 | 1.3883E-02 | ||
| 4 | AVG | 7.2407E-01 | 6.9932E-01 | 7.0282E-01 | 6.9551E-01 | 7.2992E-01 | 7.0340E-01 | 7.1325E-01 | 6.9936E-01 | 7.0129E-01 | 7.0025E-01 | |
| STD | 2.5379E-02 | 4.6366E-02 | 1.6423E-02 | 9.7447E-03 | 3.1917E-02 | 1.0392E-02 | 3.2120E-02 | 5.5646E-03 | 1.5866E-02 | 1.3933E-02 | ||
| 6 | AVG | 8.0106E-01 | 7.3282E-01 | 7.8171E-01 | 7.7002E-01 | 7.6656E-01 | 7.8005E-01 | 7.7234E-01 | 7.8869E-01 | 7.7233E-01 | 7.8033E-01 | |
| STD | 2.8989E-02 | 5.4729E-02 | 3.4646E-02 | 1.5636E-02 | 4.8288E-02 | 2.2350E-02 | 4.4058E-02 | 1.7362E-02 | 2.7302E-02 | 1.8367E-02 | ||
| H | 2 | AVG | 6.8457E-01 | 6.5282E-01 | 6.8008E-01 | 6.8051E-01 | 6.8617E-01 | 6.8057E-01 | 6.8684E-01 | 6.8119E-01 | 6.8269E-01 | 6.8234E-01 |
| STD | 8.1115E-03 | 4.1307E-02 | 6.1570E-03 | 2.0339E-03 | 1.6736E-02 | 4.2297E-03 | 2.7850E-02 | 6.1256E-03 | 7.6796E-03 | 9.6186E-03 | ||
| 4 | AVG | 7.4740E-01 | 7.1991E-01 | 7.4026E-01 | 7.2367E-01 | 7.1452E-01 | 7.3067E-01 | 7.3734E-01 | 7.3570E-01 | 7.2450E-01 | 7.2932E-01 | |
| STD | 3.2548E-02 | 5.4175E-02 | 3.2817E-02 | 3.4825E-02 | 4.4976E-02 | 2.3929E-02 | 3.1799E-02 | 2.8358E-02 | 2.8152E-02 | 3.5508E-02 | ||
| 6 | AVG | 8.2146E-01 | 7.4860E-01 | 7.9125E-01 | 7.7678E-01 | 7.7784E-01 | 7.9015E-01 | 7.6946E-01 | 7.8805E-01 | 7.7839E-01 | 7.7294E-01 | |
| STD | 2.9271E-02 | 4.7886E-02 | 2.4923E-02 | 3.0003E-02 | 3.3578E-02 | 2.7221E-02 | 4.0835E-02 | 2.5814E-02 | 3.6118E-02 | 2.6503E-02 | ||
| I | 2 | AVG | 7.0351E-01 | 6.8070E-01 | 6.9835E-01 | 7.0781E-01 | 7.0142E-01 | 6.9755E-01 | 7.0205E-01 | 7.1044E-01 | 7.0217E-01 | 7.0593E-01 |
| STD | 1.3823E-02 | 4.6546E-02 | 8.2499E-03 | 1.1305E-02 | 2.8537E-02 | 2.3917E-03 | 2.4891E-02 | 2.0030E-02 | 2.5581E-02 | 1.6470E-02 | ||
| 4 | AVG | 7.5516E-01 | 7.5885E-01 | 7.5764E-01 | 7.5857E-01 | 7.6300E-01 | 7.5492E-01 | 7.4973E-01 | 7.5539E-01 | 7.5922E-01 | 7.5421E-01 | |
| STD | 1.8705E-02 | 2.1758E-02 | 9.6173E-03 | 1.3567E-02 | 2.7460E-02 | 7.9609E-03 | 1.6479E-02 | 1.4261E-02 | 1.6030E-02 | 1.6194E-02 | ||
| 6 | AVG | 7.9708E-01 | 7.8078E-01 | 7.7952E-01 | 7.7453E-01 | 7.8986E-01 | 7.8080E-01 | 7.7845E-01 | 7.8444E-01 | 7.8255E-01 | 7.8076E-01 | |
| STD | 2.3475E-02 | 2.9526E-02 | 1.8568E-02 | 1.6918E-02 | 2.3851E-02 | 1.6637E-02 | 2.1082E-02 | 1.1004E-02 | 2.0795E-02 | 1.6874E-02 |
Table A6.
The PSNR comparison at low threshold level.
| Image | T | EEFOA | FOA | DE | GWO | HHO | MDE | BLPSO | LGCMFO | m_SCA | DASMA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 2 | AVG | 1.5064E + 01 | 1.1958E + 01 | 1.5550E + 01 | 1.4556E + 01 | 1.3911E + 01 | 1.5459E + 01 | 1.5027E + 01 | 1.4928E + 01 | 1.4897E + 01 | 1.4926E + 01 |
| STD | 1.2295E + 00 | 2.8043E + 00 | 1.1679E-01 | 1.1304E + 00 | 1.9053E + 00 | 3.4182E-01 | 9.2395E-01 | 1.1757E + 00 | 1.2067E + 00 | 8.1599E-01 | ||
| 4 | AVG | 1.8605E + 01 | 1.5309E + 01 | 1.8551E + 01 | 1.7703E + 01 | 1.7263E + 01 | 1.8081E + 01 | 1.8207E + 01 | 1.7878E + 01 | 1.7448E + 01 | 1.8146E + 01 | |
| STD | 1.4651E + 00 | 2.5778E + 00 | 1.7716E + 00 | 1.3549E + 00 | 1.9078E + 00 | 2.0533E + 00 | 1.0813E + 00 | 1.6300E + 00 | 1.7591E + 00 | 1.8441E + 00 | ||
| 6 | AVG | 2.1942E + 01 | 1.8148E + 01 | 2.1574E + 01 | 2.1077E + 01 | 1.9875E + 01 | 2.0895E + 01 | 2.0528E + 01 | 2.1091E + 01 | 2.0062E + 01 | 2.0542E + 01 | |
| STD | 1.2572E + 00 | 3.4058E + 00 | 1.3507E + 00 | 1.2157E + 00 | 2.4244E + 00 | 1.7207E + 00 | 1.3408E + 00 | 1.3285E + 00 | 1.8168E + 00 | 2.0722E + 00 | ||
| B | 2 | AVG | 1.4778E + 01 | 1.2898E + 01 | 1.4613E + 01 | 1.4354E + 01 | 1.4661E + 01 | 1.4770E + 01 | 1.4401E + 01 | 1.4584E + 01 | 1.4249E + 01 | 1.4860E + 01 |
| STD | 5.6379E-01 | 2.0808E + 00 | 7.2596E-01 | 3.4975E-01 | 9.3039E-01 | 5.7566E-01 | 1.0106E + 00 | 4.8562E-01 | 6.4961E-01 | 7.4784E-01 | ||
| 4 | AVG | 1.8501E + 01 | 1.5692E + 01 | 1.8493E + 01 | 1.8148E + 01 | 1.7426E + 01 | 1.8556E + 01 | 1.7779E + 01 | 1.8492E + 01 | 1.8146E + 01 | 1.8350E + 01 | |
| STD | 7.8518E-01 | 2.1348E + 00 | 3.9496E-01 | 5.7023E-01 | 2.1995E + 00 | 3.2921E-01 | 8.3510E-01 | 6.1815E-01 | 1.1236E + 00 | 7.3534E-01 | ||
| 6 | AVG | 2.1324E + 01 | 1.7749E + 01 | 2.0674E + 01 | 2.0361E + 01 | 2.0200E + 01 | 2.0942E + 01 | 1.9995E + 01 | 2.1002E + 01 | 2.0567E + 01 | 2.0849E + 01 | |
| STD | 7.8516E-01 | 2.2876E + 00 | 5.3620E-01 | 8.2466E-01 | 1.5395E + 00 | 4.0217E-01 | 9.7232E-01 | 6.1738E-01 | 1.0446E + 00 | 6.2529E-01 | ||
| C | 2 | AVG | 1.3720E + 01 | 1.1925E + 01 | 1.3442E + 01 | 1.3828E + 01 | 1.3340E + 01 | 1.3644E + 01 | 1.2894E + 01 | 1.3627E + 01 | 1.3179E + 01 | 1.3656E + 01 |
| STD | 5.5944E-01 | 1.5252E + 00 | 8.1360E-01 | 5.8637E-01 | 1.5048E + 00 | 3.7000E-01 | 1.5868E + 00 | 2.6150E-01 | 1.3143E + 00 | 3.7541E-01 | ||
| 4 | AVG | 1.9527E + 01 | 1.5889E + 01 | 1.8773E + 01 | 1.8637E + 01 | 1.9133E + 01 | 1.9547E + 01 | 1.8070E + 01 | 1.8827E + 01 | 1.8509E + 01 | 1.8651E + 01 | |
| STD | 1.3307E + 00 | 2.6390E + 00 | 1.5131E + 00 | 1.6772E + 00 | 1.9288E + 00 | 1.4229E + 00 | 1.8044E + 00 | 1.4384E + 00 | 1.8425E + 00 | 1.5459E + 00 | ||
| 6 | AVG | 2.1984E + 01 | 1.7756E + 01 | 2.0355E + 01 | 2.0832E + 01 | 2.1496E + 01 | 2.1253E + 01 | 1.9769E + 01 | 2.1420E + 01 | 2.0953E + 01 | 2.0996E + 01 | |
| STD | 1.3829E + 00 | 2.5874E + 00 | 1.2444E + 00 | 1.3109E + 00 | 2.3918E + 00 | 1.1525E + 00 | 1.9090E + 00 | 1.4057E + 00 | 2.1340E + 00 | 1.3527E + 00 | ||
| D | 2 | AVG | 1.6369E + 01 | 1.2940E + 01 | 1.6345E + 01 | 1.6417E + 01 | 1.4730E + 01 | 1.6119E + 01 | 1.5726E + 01 | 1.6231E + 01 | 1.6563E + 01 | 1.6277E + 01 |
| STD | 2.3037E-01 | 2.5630E + 00 | 2.4129E-01 | 3.9251E-01 | 2.2843E + 00 | 4.1408E-01 | 1.7628E + 00 | 1.4007E-01 | 5.7364E-01 | 3.3361E-01 | ||
| 4 | AVG | 1.8785E + 01 | 1.6191E + 01 | 1.9265E + 01 | 1.9155E + 01 | 1.7115E + 01 | 1.9365E + 01 | 1.8527E + 01 | 1.9155E + 01 | 1.8413E + 01 | 1.8723E + 01 | |
| STD | 8.9149E-01 | 3.4158E + 00 | 7.0352E-01 | 8.9734E-01 | 2.5774E + 00 | 7.7231E-01 | 2.0743E + 00 | 1.2991E + 00 | 1.3498E + 00 | 1.7158E + 00 | ||
| 6 | AVG | 2.2192E + 01 | 1.8317E + 01 | 2.1442E + 01 | 2.0767E + 01 | 1.9277E + 01 | 2.1441E + 01 | 2.1140E + 01 | 2.1578E + 01 | 2.0615E + 01 | 2.1160E + 01 | |
| STD | 1.1868E + 00 | 3.9487E + 00 | 1.3657E + 00 | 1.5521E + 00 | 2.8737E + 00 | 9.2497E-01 | 1.7601E + 00 | 8.8001E-01 | 1.6127E + 00 | 1.1807E + 00 | ||
| E | 2 | AVG | 1.5128E + 01 | 1.1773E + 01 | 1.3786E + 01 | 1.4625E + 01 | 1.3861E + 01 | 1.3950E + 01 | 1.3640E + 01 | 1.4579E + 01 | 1.4624E + 01 | 1.4516E + 01 |
| STD | 1.2220E + 00 | 3.4035E + 00 | 4.9827E-01 | 1.2341E + 00 | 1.8027E + 00 | 8.5252E-01 | 7.5778E-01 | 1.2973E + 00 | 1.3457E + 00 | 1.1993E + 00 | ||
| 4 | AVG | 1.8175E + 01 | 1.5126E + 01 | 1.8134E + 01 | 1.7794E + 01 | 1.8249E + 01 | 1.7925E + 01 | 1.7479E + 01 | 1.7639E + 01 | 1.8127E + 01 | 1.7696E + 01 | |
| STD | 9.2080E-01 | 2.7259E + 00 | 1.3092E + 00 | 8.2558E-01 | 1.4454E + 00 | 8.9319E-01 | 1.7516E + 00 | 8.0733E-01 | 8.3813E-01 | 7.9343E-01 | ||
| 6 | AVG | 2.1410E + 01 | 1.7363E + 01 | 2.0545E + 01 | 2.0496E + 01 | 2.0605E + 01 | 2.0871E + 01 | 1.9616E + 01 | 2.1085E + 01 | 1.9759E + 01 | 2.0559E + 01 | |
| STD | 1.1429E + 00 | 2.5719E + 00 | 1.4508E + 00 | 8.7549E-01 | 1.7256E + 00 | 7.3509E-01 | 1.6690E + 00 | 6.3854E-01 | 1.3658E + 00 | 1.2466E + 00 | ||
| F | 2 | AVG | 1.3260E + 01 | 1.1754E + 01 | 1.2632E + 01 | 1.2677E + 01 | 1.3426E + 01 | 1.2989E + 01 | 1.3706E + 01 | 1.2805E + 01 | 1.3094E + 01 | 1.1961E + 01 |
| STD | 1.8115E + 00 | 2.6478E + 00 | 1.7165E + 00 | 7.9458E-01 | 2.1660E + 00 | 6.9024E-01 | 2.0352E + 00 | 1.1443E + 00 | 1.4333E + 00 | 1.6323E + 00 | ||
| 4 | AVG | 1.8303E + 01 | 1.4511E + 01 | 1.8005E + 01 | 1.8220E + 01 | 1.6403E + 01 | 1.7916E + 01 | 1.6724E + 01 | 1.7793E + 01 | 1.7163E + 01 | 1.7789E + 01 | |
| STD | 1.2078E + 00 | 2.7962E + 00 | 1.1463E + 00 | 8.5499E-01 | 2.1329E + 00 | 9.8176E-01 | 1.8489E + 00 | 1.0490E + 00 | 1.7230E + 00 | 1.3158E + 00 | ||
| 6 | AVG | 2.1351E + 01 | 1.7071E + 01 | 2.0552E + 01 | 2.0191E + 01 | 1.9087E + 01 | 2.0578E + 01 | 1.9379E + 01 | 2.0622E + 01 | 2.0321E + 01 | 2.0498E + 01 | |
| STD | 9.7884E-01 | 2.9929E + 00 | 1.0054E + 00 | 7.9741E-01 | 2.4511E + 00 | 7.3407E-01 | 1.8972E + 00 | 9.7749E-01 | 1.0917E + 00 | 9.3905E-01 | ||
| G | 2 | AVG | 1.4180E + 01 | 1.1716E + 01 | 1.4156E + 01 | 1.3703E + 01 | 1.3760E + 01 | 1.3865E + 01 | 1.3268E + 01 | 1.3698E + 01 | 1.3681E + 01 | 1.3819E + 01 |
| STD | 6.0650E-01 | 2.2085E + 00 | 6.1030E-01 | 6.3137E-01 | 1.0099E + 00 | 6.1941E-01 | 1.0508E + 00 | 6.3474E-01 | 8.1162E-01 | 5.7638E-01 | ||
| 4 | AVG | 1.8144E + 01 | 1.4338E + 01 | 1.7380E + 01 | 1.7225E + 01 | 1.7569E + 01 | 1.7450E + 01 | 1.6608E + 01 | 1.7549E + 01 | 1.7078E + 01 | 1.7452E + 01 | |
| STD | 1.2739E + 00 | 2.7913E + 00 | 1.0043E + 00 | 8.5014E-01 | 1.4283E + 00 | 7.1341E-01 | 2.0542E + 00 | 3.4796E-01 | 1.1429E + 00 | 8.0090E-01 | ||
| 6 | AVG | 2.1212E + 01 | 1.6785E + 01 | 2.0436E + 01 | 2.0355E + 01 | 1.9099E + 01 | 2.0568E + 01 | 1.9592E + 01 | 2.0970E + 01 | 2.0267E + 01 | 2.0622E + 01 | |
| STD | 1.0398E + 00 | 2.9031E + 00 | 1.3307E + 00 | 6.8994E-01 | 2.2321E + 00 | 9.5494E-01 | 1.9765E + 00 | 6.5082E-01 | 1.1202E + 00 | 5.9609E-01 | ||
| H | 2 | AVG | 1.4227E + 01 | 1.1595E + 01 | 1.4558E + 01 | 1.4513E + 01 | 1.3726E + 01 | 1.4573E + 01 | 1.4183E + 01 | 1.4539E + 01 | 1.4454E + 01 | 1.4142E + 01 |
| STD | 5.6067E-01 | 2.2131E + 00 | 1.9663E-01 | 7.3503E-02 | 1.0626E + 00 | 1.2996E-01 | 1.1424E + 00 | 2.4821E-01 | 3.9369E-01 | 7.0145E-01 | ||
| 4 | AVG | 1.8704E + 01 | 1.5983E + 01 | 1.7817E + 01 | 1.7907E + 01 | 1.6585E + 01 | 1.8395E + 01 | 1.7841E + 01 | 1.8289E + 01 | 1.8076E + 01 | 1.7796E + 01 | |
| STD | 1.5170E + 00 | 2.8494E + 00 | 1.9724E + 00 | 1.2508E + 00 | 2.3085E + 00 | 1.2929E + 00 | 1.5182E + 00 | 1.2821E + 00 | 1.4024E + 00 | 1.3223E + 00 | ||
| 6 | AVG | 2.1632E + 01 | 1.7795E + 01 | 2.1072E + 01 | 2.0372E + 01 | 1.9379E + 01 | 2.0960E + 01 | 1.9779E + 01 | 2.1031E + 01 | 1.9357E + 01 | 2.0339E + 01 | |
| STD | 1.2991E + 00 | 2.6709E + 00 | 1.2177E + 00 | 1.2901E + 00 | 1.7971E + 00 | 1.3973E + 00 | 1.7750E + 00 | 1.2866E + 00 | 1.8838E + 00 | 1.5308E + 00 | ||
| I | 2 | AVG | 1.5454E + 01 | 1.2505E + 01 | 1.5850E + 01 | 1.5493E + 01 | 1.4018E + 01 | 1.5909E + 01 | 1.5570E + 01 | 1.5115E + 01 | 1.5043E + 01 | 1.5251E + 01 |
| STD | 8.3297E-01 | 2.6265E + 00 | 3.9683E-01 | 7.2247E-01 | 1.4535E + 00 | 4.2913E-02 | 6.8090E-01 | 1.1228E + 00 | 1.2681E + 00 | 9.0710E-01 | ||
| 4 | AVG | 1.8074E + 01 | 1.5723E + 01 | 1.8510E + 01 | 1.8100E + 01 | 1.6574E + 01 | 1.8156E + 01 | 1.7562E + 01 | 1.8249E + 01 | 1.7621E + 01 | 1.7987E + 01 | |
| STD | 1.3539E + 00 | 2.1313E + 00 | 8.9714E-01 | 1.0417E + 00 | 2.1551E + 00 | 8.8256E-01 | 1.6630E + 00 | 5.8496E-01 | 1.4736E + 00 | 9.0738E-01 | ||
| 6 | AVG | 2.0889E + 01 | 1.7386E + 01 | 2.0076E + 01 | 2.0443E + 01 | 1.9926E + 01 | 2.0304E + 01 | 2.0193E + 01 | 2.0676E + 01 | 1.9703E + 01 | 2.0654E + 01 | |
| STD | 1.5545E + 00 | 2.5358E + 00 | 1.4056E + 00 | 1.9263E + 00 | 1.8471E + 00 | 1.5762E + 00 | 1.1435E + 00 | 1.0761E + 00 | 1.6359E + 00 | 1.4059E + 00 |
Table A7.
The SSIM comparison at low threshold level.
| Image | T | EEFOA | FOA | DE | GWO | HHO | MDE | BLPSO | LGCMFO | m_SCA | DASMA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 2 | AVG | 7.3092E-01 | 6.4937E-01 | 7.5956E-01 | 7.1391E-01 | 7.0843E-01 | 7.4759E-01 | 7.4190E-01 | 7.1956E-01 | 7.1999E-01 | 7.0394E-01 |
| STD | 5.2275E-02 | 1.3173E-01 | 1.1359E-03 | 5.7121E-02 | 6.6863E-02 | 3.5898E-02 | 3.6365E-02 | 5.7031E-02 | 5.1778E-02 | 5.8127E-02 | ||
| 4 | AVG | 7.6243E-01 | 7.0594E-01 | 7.5776E-01 | 7.3346E-01 | 7.3145E-01 | 7.3795E-01 | 7.6043E-01 | 7.3936E-01 | 7.4597E-01 | 7.4978E-01 | |
| STD | 2.9877E-02 | 5.8441E-02 | 2.9117E-02 | 2.6757E-02 | 4.3285E-02 | 2.9745E-02 | 2.4721E-02 | 2.8471E-02 | 3.4369E-02 | 2.3895E-02 | ||
| 6 | AVG | 7.8366E-01 | 7.5704E-01 | 7.7264E-01 | 7.7021E-01 | 7.6238E-01 | 7.7053E-01 | 7.7620E-01 | 7.7164E-01 | 7.7100E-01 | 7.7204E-01 | |
| STD | 2.0007E-02 | 5.5260E-02 | 1.7339E-02 | 1.7963E-02 | 4.2679E-02 | 1.9514E-02 | 2.4741E-02 | 2.0040E-02 | 2.3667E-02 | 1.8358E-02 | ||
| B | 2 | AVG | 3.8979E-01 | 3.6102E-01 | 3.8020E-01 | 3.7330E-01 | 3.9014E-01 | 3.9227E-01 | 3.8144E-01 | 3.8571E-01 | 3.8060E-01 | 4.0390E-01 |
| STD | 2.7254E-02 | 6.1805E-02 | 2.8335E-02 | 2.4545E-02 | 3.5873E-02 | 3.3627E-02 | 3.7731E-02 | 3.3289E-02 | 3.8729E-02 | 4.4084E-02 | ||
| 4 | AVG | 5.4575E-01 | 4.8147E-01 | 5.3239E-01 | 5.2786E-01 | 5.1563E-01 | 5.3693E-01 | 5.1765E-01 | 5.3594E-01 | 5.2928E-01 | 5.3143E-01 | |
| STD | 3.6238E-02 | 5.9136E-02 | 1.2320E-02 | 1.5714E-02 | 6.2131E-02 | 1.0977E-02 | 2.7427E-02 | 2.8813E-02 | 4.2793E-02 | 3.0318E-02 | ||
| 6 | AVG | 6.5231E-01 | 5.4613E-01 | 6.2457E-01 | 6.2000E-01 | 6.2500E-01 | 6.3760E-01 | 6.0897E-01 | 6.3469E-01 | 6.3248E-01 | 6.3157E-01 | |
| STD | 3.0894E-02 | 5.8980E-02 | 1.3778E-02 | 1.8876E-02 | 4.5728E-02 | 1.9395E-02 | 3.0294E-02 | 2.5464E-02 | 3.4396E-02 | 2.5179E-02 | ||
| C | 2 | AVG | 6.2040E-01 | 5.6717E-01 | 5.8497E-01 | 6.3931E-01 | 6.3007E-01 | 5.8741E-01 | 6.0005E-01 | 5.9253E-01 | 6.7399E-01 | 5.9781E-01 |
| STD | 5.2012E-02 | 1.1284E-01 | 2.0837E-02 | 4.9477E-02 | 4.1445E-02 | 2.6658E-02 | 1.1075E-01 | 3.3369E-02 | 4.2139E-02 | 4.0251E-02 | ||
| 4 | AVG | 6.3759E-01 | 5.6525E-01 | 6.3051E-01 | 6.2645E-01 | 6.5206E-01 | 6.5448E-01 | 6.1397E-01 | 6.3326E-01 | 6.2582E-01 | 6.1758E-01 | |
| STD | 3.5181E-02 | 1.1363E-01 | 5.1126E-02 | 5.1815E-02 | 4.8129E-02 | 4.9123E-02 | 3.7345E-02 | 4.6105E-02 | 5.6565E-02 | 4.9693E-02 | ||
| 6 | AVG | 6.9150E-01 | 6.2163E-01 | 6.5917E-01 | 6.7627E-01 | 6.8713E-01 | 6.7842E-01 | 6.6416E-01 | 6.8739E-01 | 6.7735E-01 | 6.7374E-01 | |
| STD | 3.9747E-02 | 7.3852E-02 | 3.5603E-02 | 3.3105E-02 | 6.2498E-02 | 4.1987E-02 | 3.6324E-02 | 3.2818E-02 | 6.3043E-02 | 2.6806E-02 | ||
| D | 2 | AVG | 7.2057E-01 | 5.9906E-01 | 7.2089E-01 | 7.1832E-01 | 6.5885E-01 | 7.1342E-01 | 7.0785E-01 | 7.1624E-01 | 7.2283E-01 | 7.1738E-01 |
| STD | 8.0721E-03 | 1.3989E-01 | 9.2602E-03 | 7.8577E-03 | 1.0994E-01 | 9.2839E-03 | 3.3466E-02 | 6.5527E-03 | 9.6539E-03 | 7.5162E-03 | ||
| 4 | AVG | 7.5204E-01 | 7.3140E-01 | 7.6984E-01 | 7.6831E-01 | 7.5013E-01 | 7.7081E-01 | 7.6111E-01 | 7.5617E-01 | 7.6078E-01 | 7.5966E-01 | |
| STD | 2.5975E-02 | 1.1180E-01 | 1.8931E-02 | 2.5738E-02 | 5.3240E-02 | 2.1364E-02 | 3.5914E-02 | 2.6540E-02 | 3.0022E-02 | 2.4572E-02 | ||
| 6 | AVG | 7.7240E-01 | 7.5435E-01 | 7.6948E-01 | 7.7016E-01 | 7.6445E-01 | 7.6893E-01 | 7.7649E-01 | 7.6840E-01 | 7.7399E-01 | 7.6870E-01 | |
| STD | 1.3114E-02 | 7.2467E-02 | 1.4741E-02 | 1.8995E-02 | 3.0554E-02 | 1.5420E-02 | 2.5581E-02 | 1.4930E-02 | 2.4002E-02 | 1.3793E-02 | ||
| E | 2 | AVG | 7.3174E-01 | 5.7400E-01 | 7.2646E-01 | 7.2634E-01 | 7.1062E-01 | 7.2655E-01 | 7.1970E-01 | 7.2771E-01 | 7.2816E-01 | 7.2849E-01 |
| STD | 1.1743E-02 | 2.1681E-01 | 1.2968E-03 | 1.5069E-02 | 8.1600E-02 | 5.1384E-03 | 2.1350E-02 | 5.1964E-03 | 2.7603E-02 | 2.9547E-03 | ||
| 4 | AVG | 6.0502E-01 | 5.6439E-01 | 6.0503E-01 | 5.8071E-01 | 6.1615E-01 | 5.9098E-01 | 6.1035E-01 | 5.8767E-01 | 5.9845E-01 | 5.9016E-01 | |
| STD | 2.6731E-02 | 9.7363E-02 | 2.4129E-02 | 1.9773E-02 | 3.3643E-02 | 2.3767E-02 | 3.8454E-02 | 2.5650E-02 | 1.9164E-02 | 2.6093E-02 | ||
| 6 | AVG | 6.8122E-01 | 6.1810E-01 | 6.6566E-01 | 6.5680E-01 | 6.7041E-01 | 6.6644E-01 | 6.5509E-01 | 6.6643E-01 | 6.4675E-01 | 6.5791E-01 | |
| STD | 2.5015E-02 | 6.6146E-02 | 2.4972E-02 | 2.1153E-02 | 3.3626E-02 | 1.8866E-02 | 3.1769E-02 | 1.3359E-02 | 2.4696E-02 | 2.4366E-02 | ||
| F | 2 | AVG | 4.5693E-01 | 4.6087E-01 | 4.4254E-01 | 4.3685E-01 | 5.0311E-01 | 4.5037E-01 | 5.0958E-01 | 4.4497E-01 | 4.5229E-01 | 4.1471E-01 |
| STD | 6.0719E-02 | 1.2857E-01 | 6.7085E-02 | 2.5701E-02 | 1.0228E-01 | 3.3541E-02 | 9.5780E-02 | 4.5278E-02 | 4.7492E-02 | 5.2592E-02 | ||
| 4 | AVG | 6.7381E-01 | 6.0286E-01 | 6.7929E-01 | 6.6881E-01 | 6.3222E-01 | 6.8698E-01 | 6.6290E-01 | 6.6622E-01 | 6.7306E-01 | 6.6241E-01 | |
| STD | 4.3718E-02 | 9.8275E-02 | 3.4137E-02 | 3.5675E-02 | 6.8820E-02 | 2.6260E-02 | 5.9689E-02 | 3.8983E-02 | 4.2718E-02 | 4.7052E-02 | ||
| 6 | AVG | 7.2286E-01 | 6.5422E-01 | 7.1848E-01 | 7.0828E-01 | 6.7862E-01 | 7.1335E-01 | 7.1117E-01 | 7.1440E-01 | 7.1557E-01 | 7.0979E-01 | |
| STD | 2.4459E-02 | 9.1945E-02 | 2.5485E-02 | 1.7177E-02 | 6.5485E-02 | 1.7938E-02 | 3.6559E-02 | 1.4042E-02 | 2.7537E-02 | 1.5297E-02 | ||
| G | 2 | AVG | 5.7683E-01 | 5.4115E-01 | 5.8521E-01 | 5.6194E-01 | 5.7449E-01 | 5.5287E-01 | 5.5907E-01 | 5.5875E-01 | 5.6270E-01 | 5.5072E-01 |
| STD | 5.5888E-02 | 1.0881E-01 | 5.8302E-02 | 6.8731E-02 | 8.5587E-02 | 5.6563E-02 | 7.0027E-02 | 7.2499E-02 | 6.2232E-02 | 5.6143E-02 | ||
| 4 | AVG | 6.3812E-01 | 5.7880E-01 | 6.2322E-01 | 6.2412E-01 | 6.1201E-01 | 6.2535E-01 | 6.2018E-01 | 6.3065E-01 | 6.1711E-01 | 6.2927E-01 | |
| STD | 1.8656E-02 | 8.3929E-02 | 1.4879E-02 | 1.0796E-02 | 4.2634E-02 | 1.0277E-02 | 4.1721E-02 | 4.1748E-03 | 1.5679E-02 | 1.4112E-02 | ||
| 6 | AVG | 6.8440E-01 | 6.3025E-01 | 6.6783E-01 | 6.5326E-01 | 6.6036E-01 | 6.6471E-01 | 6.7465E-01 | 6.6755E-01 | 6.6633E-01 | 6.6788E-01 | |
| STD | 2.0704E-02 | 6.4998E-02 | 3.0086E-02 | 1.8874E-02 | 4.6756E-02 | 1.3604E-02 | 4.2878E-02 | 1.2749E-02 | 2.2713E-02 | 1.8235E-02 | ||
| H | 2 | AVG | 5.4147E-01 | 5.1272E-01 | 5.4796E-01 | 5.4669E-01 | 5.6793E-01 | 5.4736E-01 | 5.6579E-01 | 5.5047E-01 | 5.4636E-01 | 5.3899E-01 |
| STD | 1.1254E-02 | 1.1767E-01 | 4.5133E-03 | 8.3096E-04 | 5.8502E-02 | 3.3012E-03 | 4.7248E-02 | 2.2987E-02 | 7.9778E-03 | 1.5423E-02 | ||
| 4 | AVG | 6.9662E-01 | 6.4342E-01 | 6.9561E-01 | 6.7494E-01 | 6.4725E-01 | 6.8119E-01 | 6.8299E-01 | 6.8916E-01 | 6.7403E-01 | 6.8777E-01 | |
| STD | 3.2600E-02 | 8.0326E-02 | 2.8382E-02 | 3.2842E-02 | 5.8106E-02 | 1.9047E-02 | 2.8825E-02 | 2.5298E-02 | 2.6252E-02 | 3.3089E-02 | ||
| 6 | AVG | 7.4800E-01 | 6.8425E-01 | 7.1727E-01 | 7.1827E-01 | 7.0451E-01 | 7.2245E-01 | 7.1076E-01 | 7.1446E-01 | 7.2214E-01 | 7.0903E-01 | |
| STD | 3.4526E-02 | 5.5913E-02 | 2.3919E-02 | 2.9824E-02 | 5.3287E-02 | 2.3303E-02 | 3.7495E-02 | 2.3611E-02 | 4.4195E-02 | 2.1697E-02 | ||
| I | 2 | AVG | 6.4464E-01 | 5.8619E-01 | 6.7399E-01 | 6.4684E-01 | 6.1665E-01 | 6.6862E-01 | 6.6794E-01 | 6.6243E-01 | 6.4828E-01 | 6.4534E-01 |
| STD | 3.9714E-02 | 1.1252E-01 | 6.4018E-03 | 3.4346E-02 | 6.8030E-02 | 1.3237E-02 | 3.0339E-02 | 3.8707E-02 | 4.0537E-02 | 4.5943E-02 | ||
| 4 | AVG | 7.7025E-01 | 7.2933E-01 | 7.8163E-01 | 7.8185E-01 | 7.6010E-01 | 7.7119E-01 | 7.3660E-01 | 7.7127E-01 | 7.7186E-01 | 7.6003E-01 | |
| STD | 3.1107E-02 | 6.2574E-02 | 2.0547E-02 | 2.3109E-02 | 6.1303E-02 | 2.7010E-02 | 5.0383E-02 | 2.7957E-02 | 4.1720E-02 | 3.5143E-02 | ||
| 6 | AVG | 8.0030E-01 | 7.7585E-01 | 7.9502E-01 | 7.8731E-01 | 7.9794E-01 | 8.0184E-01 | 7.8736E-01 | 8.0188E-01 | 7.9277E-01 | 7.9723E-01 | |
| STD | 2.4631E-02 | 5.0637E-02 | 2.6985E-02 | 1.4936E-02 | 2.7250E-02 | 1.3322E-02 | 2.2412E-02 | 1.0991E-02 | 2.5104E-02 | 1.3740E-02 |
Table A8.
The FSIM comparison at high threshold level.
| Image | T | EEFOA | FOA | DE | GWO | HHO | MDE | BLPSO | LGCMFO | m_SCA | DASMA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 10 | AVG | 8.6413E-01 | 7.9513E-01 | 8.4467E-01 | 8.4008E-01 | 8.3775E-01 | 8.4364E-01 | 8.2097E-01 | 8.6150E-01 | 8.3951E-01 | 8.5671E-01 |
| STD | 2.6363E-02 | 4.2920E-02 | 3.0093E-02 | 3.3378E-02 | 4.0445E-02 | 2.8494E-02 | 4.0946E-02 | 2.9480E-02 | 3.3624E-02 | 2.6866E-02 | ||
| 15 | AVG | 9.1432E-01 | 8.4155E-01 | 8.8617E-01 | 8.8506E-01 | 8.7802E-01 | 8.9574E-01 | 8.6820E-01 | 9.1076E-01 | 8.6973E-01 | 8.9458E-01 | |
| STD | 2.8705E-02 | 3.3236E-02 | 2.9359E-02 | 2.9909E-02 | 4.2280E-02 | 1.8647E-02 | 3.6271E-02 | 2.6919E-02 | 3.5373E-02 | 3.0590E-02 | ||
| 20 | AVG | 9.3092E-01 | 8.7710E-01 | 9.1440E-01 | 9.2346E-01 | 9.0514E-01 | 9.3125E-01 | 8.9423E-01 | 9.2254E-01 | 9.1119E-01 | 9.2126E-01 | |
| STD | 2.0123E-02 | 4.3114E-02 | 2.3904E-02 | 2.1643E-02 | 5.7888E-02 | 1.6303E-02 | 2.2604E-02 | 3.0940E-02 | 2.9622E-02 | 2.4998E-02 | ||
| B | 10 | AVG | 9.4477E-01 | 8.2517E-01 | 9.4178E-01 | 9.3289E-01 | 9.0323E-01 | 9.4197E-01 | 8.9505E-01 | 9.5151E-01 | 9.1951E-01 | 9.3982E-01 |
| STD | 2.4305E-02 | 6.4379E-02 | 1.7158E-02 | 1.3594E-02 | 4.9810E-02 | 1.1851E-02 | 3.6446E-02 | 1.0237E-02 | 2.7700E-02 | 1.7948E-02 | ||
| 15 | AVG | 9.7107E-01 | 8.8820E-01 | 9.6663E-01 | 9.6206E-01 | 9.3535E-01 | 9.6488E-01 | 9.3928E-01 | 9.7472E-01 | 9.5562E-01 | 9.7062E-01 | |
| STD | 1.0955E-02 | 5.0603E-02 | 1.1801E-02 | 1.7336E-02 | 5.1455E-02 | 1.1815E-02 | 2.0144E-02 | 7.5359E-03 | 2.3447E-02 | 1.1158E-02 | ||
| 20 | AVG | 9.7595E-01 | 9.2986E-01 | 9.7152E-01 | 9.7595E-01 | 9.5724E-01 | 9.7796E-01 | 9.5825E-01 | 9.7418E-01 | 9.5744E-01 | 9.8038E-01 | |
| STD | 9.1657E-03 | 3.4505E-02 | 1.4652E-02 | 9.9009E-03 | 2.6061E-02 | 1.0731E-02 | 1.8370E-02 | 1.3626E-02 | 2.8102E-02 | 9.1970E-03 | ||
| C | 10 | AVG | 8.6374E-01 | 7.9620E-01 | 8.3237E-01 | 8.3161E-01 | 8.2713E-01 | 8.3352E-01 | 8.2087E-01 | 8.3673E-01 | 8.1706E-01 | 8.3880E-01 |
| STD | 2.1869E-02 | 3.1040E-02 | 2.2981E-02 | 2.0161E-02 | 2.8764E-02 | 1.8054E-02 | 2.1306E-02 | 2.5744E-02 | 2.6452E-02 | 2.3229E-02 | ||
| 15 | AVG | 9.0366E-01 | 8.2945E-01 | 8.8373E-01 | 8.9084E-01 | 8.8073E-01 | 8.9299E-01 | 8.6646E-01 | 8.9604E-01 | 8.7230E-01 | 8.8220E-01 | |
| STD | 1.5042E-02 | 2.6399E-02 | 2.4898E-02 | 1.9884E-02 | 3.1200E-02 | 1.8734E-02 | 2.3536E-02 | 1.8547E-02 | 2.2982E-02 | 2.9308E-02 | ||
| 20 | AVG | 9.2893E-01 | 8.6506E-01 | 9.1349E-01 | 9.1230E-01 | 9.0157E-01 | 9.2518E-01 | 8.8752E-01 | 9.1910E-01 | 8.9940E-01 | 9.2397E-01 | |
| STD | 1.4032E-02 | 3.0903E-02 | 1.3925E-02 | 2.4294E-02 | 3.1574E-02 | 1.5999E-02 | 2.7742E-02 | 2.1971E-02 | 2.5692E-02 | 1.9511E-02 | ||
| D | 10 | AVG | 8.7797E-01 | 8.0594E-01 | 8.6219E-01 | 8.5759E-01 | 8.6622E-01 | 8.6173E-01 | 8.3422E-01 | 8.7345E-01 | 8.7231E-01 | 8.5188E-01 |
| STD | 3.4734E-02 | 3.6648E-02 | 2.0894E-02 | 2.1160E-02 | 3.6487E-02 | 2.3076E-02 | 2.6703E-02 | 2.6478E-02 | 3.9660E-02 | 3.2568E-02 | ||
| 15 | AVG | 9.3044E-01 | 8.4932E-01 | 8.9973E-01 | 9.1146E-01 | 8.9350E-01 | 9.0786E-01 | 8.7488E-01 | 9.0370E-01 | 9.0350E-01 | 9.1548E-01 | |
| STD | 1.8843E-02 | 3.7149E-02 | 2.0652E-02 | 2.5775E-02 | 4.1211E-02 | 2.1682E-02 | 3.5112E-02 | 3.6051E-02 | 3.4308E-02 | 2.5853E-02 | ||
| 20 | AVG | 9.5391E-01 | 8.9317E-01 | 9.2395E-01 | 9.2984E-01 | 9.2353E-01 | 9.2663E-01 | 9.0238E-01 | 9.3734E-01 | 9.1864E-01 | 9.3588E-01 | |
| STD | 1.6854E-02 | 3.7347E-02 | 2.2328E-02 | 2.4536E-02 | 3.2982E-02 | 1.7446E-02 | 3.1059E-02 | 2.1775E-02 | 3.1911E-02 | 2.6021E-02 | ||
| E | 10 | AVG | 8.7312E-01 | 8.3981E-01 | 8.4997E-01 | 8.4665E-01 | 8.4329E-01 | 8.5179E-01 | 8.4031E-01 | 8.5646E-01 | 8.4734E-01 | 8.5243E-01 |
| STD | 2.5961E-02 | 3.3310E-02 | 1.9350E-02 | 2.4524E-02 | 3.8845E-02 | 2.3321E-02 | 3.1335E-02 | 2.5278E-02 | 3.2525E-02 | 2.3370E-02 | ||
| 15 | AVG | 9.2331E-01 | 8.6199E-01 | 8.9288E-01 | 8.9176E-01 | 8.8950E-01 | 8.9231E-01 | 8.7960E-01 | 9.0155E-01 | 8.8168E-01 | 8.9495E-01 | |
| STD | 1.6669E-02 | 2.9779E-02 | 1.9491E-02 | 2.8780E-02 | 3.3768E-02 | 2.3180E-02 | 2.3882E-02 | 2.6526E-02 | 2.8848E-02 | 3.1456E-02 | ||
| 20 | AVG | 9.4763E-01 | 8.9006E-01 | 9.2378E-01 | 9.0789E-01 | 8.9562E-01 | 9.2608E-01 | 9.0228E-01 | 9.2798E-01 | 9.1052E-01 | 9.1753E-01 | |
| STD | 2.0683E-02 | 3.7289E-02 | 2.1440E-02 | 3.0485E-02 | 4.2464E-02 | 1.7442E-02 | 2.2240E-02 | 3.3121E-02 | 3.4017E-02 | 2.7585E-02 | ||
| F | 10 | AVG | 8.9945E-01 | 8.1143E-01 | 8.7283E-01 | 8.7194E-01 | 8.6413E-01 | 8.7612E-01 | 8.4270E-01 | 8.9161E-01 | 8.7102E-01 | 8.8724E-01 |
| STD | 2.5032E-02 | 5.0113E-02 | 2.3133E-02 | 2.8857E-02 | 5.5114E-02 | 2.2689E-02 | 3.2420E-02 | 3.2475E-02 | 3.3664E-02 | 2.4319E-02 | ||
| 15 | AVG | 9.3435E-01 | 8.3963E-01 | 9.1686E-01 | 9.2414E-01 | 9.0045E-01 | 9.2695E-01 | 9.0675E-01 | 9.3945E-01 | 9.0289E-01 | 9.3155E-01 | |
| STD | 2.1351E-02 | 4.9946E-02 | 2.0670E-02 | 2.4095E-02 | 4.6159E-02 | 1.6158E-02 | 3.1419E-02 | 2.1067E-02 | 3.8373E-02 | 1.9513E-02 | ||
| 20 | AVG | 9.5138E-01 | 8.9093E-01 | 9.5157E-01 | 9.4895E-01 | 9.4075E-01 | 9.5328E-01 | 9.1465E-01 | 9.5721E-01 | 9.2937E-01 | 9.5868E-01 | |
| STD | 1.6680E-02 | 4.9111E-02 | 1.7158E-02 | 1.8936E-02 | 2.9372E-02 | 1.6572E-02 | 2.7187E-02 | 1.6005E-02 | 3.3206E-02 | 2.0645E-02 | ||
| G | 10 | AVG | 8.6037E-01 | 7.8887E-01 | 8.2952E-01 | 8.3522E-01 | 8.1955E-01 | 8.3464E-01 | 8.1195E-01 | 8.5349E-01 | 8.2854E-01 | 8.3550E-01 |
| STD | 2.5197E-02 | 3.8693E-02 | 2.5270E-02 | 2.5995E-02 | 4.3714E-02 | 2.1051E-02 | 3.1684E-02 | 2.5246E-02 | 2.8390E-02 | 2.4271E-02 | ||
| 15 | AVG | 9.0155E-01 | 8.2978E-01 | 8.8603E-01 | 8.9484E-01 | 8.7184E-01 | 8.9973E-01 | 8.6197E-01 | 9.0685E-01 | 8.7104E-01 | 8.9772E-01 | |
| STD | 3.5043E-02 | 4.0594E-02 | 2.1209E-02 | 2.6353E-02 | 4.7429E-02 | 2.1069E-02 | 3.1578E-02 | 2.0596E-02 | 2.6557E-02 | 2.2450E-02 | ||
| 20 | AVG | 9.2936E-01 | 8.5876E-01 | 9.1410E-01 | 9.1432E-01 | 8.8742E-01 | 9.2893E-01 | 8.9105E-01 | 9.2224E-01 | 9.0343E-01 | 9.2823E-01 | |
| STD | 2.1617E-02 | 3.7967E-02 | 1.9314E-02 | 3.0320E-02 | 3.5984E-02 | 1.4831E-02 | 2.9644E-02 | 2.9820E-02 | 2.5266E-02 | 2.2148E-02 | ||
| H | 10 | AVG | 8.9659E-01 | 8.0574E-01 | 8.6608E-01 | 8.7004E-01 | 8.5624E-01 | 8.7408E-01 | 8.6204E-01 | 8.9065E-01 | 8.6077E-01 | 8.8316E-01 |
| STD | 2.4505E-02 | 3.7957E-02 | 2.9409E-02 | 2.2493E-02 | 3.8463E-02 | 2.6291E-02 | 3.5476E-02 | 2.3072E-02 | 3.6456E-02 | 2.5495E-02 | ||
| 15 | AVG | 9.3199E-01 | 8.4932E-01 | 9.1536E-01 | 9.2261E-01 | 8.9918E-01 | 9.1849E-01 | 8.7782E-01 | 9.3853E-01 | 8.9892E-01 | 9.3831E-01 | |
| STD | 2.6834E-02 | 5.3609E-02 | 2.3421E-02 | 2.4749E-02 | 4.5427E-02 | 2.3862E-02 | 4.4017E-02 | 2.5779E-02 | 3.4494E-02 | 1.6824E-02 | ||
| 20 | AVG | 9.5026E-01 | 8.9488E-01 | 9.3965E-01 | 9.3703E-01 | 9.2450E-01 | 9.4395E-01 | 9.2477E-01 | 9.4668E-01 | 9.2403E-01 | 9.5838E-01 | |
| STD | 2.6186E-02 | 3.8523E-02 | 1.6926E-02 | 2.8378E-02 | 3.2608E-02 | 2.0580E-02 | 2.2303E-02 | 2.7583E-02 | 4.1421E-02 | 1.6484E-02 | ||
| I | 10 | AVG | 8.7610E-01 | 8.0188E-01 | 8.5933E-01 | 8.5632E-01 | 8.5264E-01 | 8.6343E-01 | 8.3584E-01 | 8.7652E-01 | 8.4287E-01 | 8.6125E-01 |
| STD | 2.8242E-02 | 5.0200E-02 | 3.1295E-02 | 2.1566E-02 | 4.0970E-02 | 2.3811E-02 | 3.4701E-02 | 2.7541E-02 | 4.3763E-02 | 2.8562E-02 | ||
| 15 | AVG | 9.1999E-01 | 8.4657E-01 | 9.0494E-01 | 9.0695E-01 | 8.8561E-01 | 9.0936E-01 | 8.8550E-01 | 9.1840E-01 | 8.8294E-01 | 9.1267E-01 | |
| STD | 2.7448E-02 | 4.2060E-02 | 2.1016E-02 | 3.0068E-02 | 3.9960E-02 | 2.5915E-02 | 2.3690E-02 | 3.6576E-02 | 4.3605E-02 | 3.3492E-02 | ||
| 20 | AVG | 9.5046E-01 | 8.9282E-01 | 9.3593E-01 | 9.2075E-01 | 9.0584E-01 | 9.3678E-01 | 9.0761E-01 | 9.4720E-01 | 9.2302E-01 | 9.3899E-01 | |
| STD | 1.5948E-02 | 3.4817E-02 | 2.0670E-02 | 3.7206E-02 | 4.2943E-02 | 2.0484E-02 | 2.9921E-02 | 2.1175E-02 | 2.8229E-02 | 2.8001E-02 |
Table A9.
The PSNR comparison at high threshold level.
| Image | T | EEFOA | FOA | DE | GWO | HHO | MDE | BLPSO | LGCMFO | m_SCA | DASMA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 10 | AVG | 2.4785E + 01 | 2.0501E + 01 | 2.4368E + 01 | 2.4158E + 01 | 2.3272E + 01 | 2.4407E + 01 | 2.2845E + 01 | 2.5316E + 01 | 2.3317E + 01 | 2.4916E + 01 |
| STD | 1.3809E + 00 | 2.7177E + 00 | 1.7048E + 00 | 1.7835E + 00 | 2.3096E + 00 | 1.2335E + 00 | 2.4937E + 00 | 1.4173E + 00 | 2.6444E + 00 | 1.5929E + 00 | ||
| 15 | AVG | 2.8165E + 01 | 2.3964E + 01 | 2.6977E + 01 | 2.6756E + 01 | 2.6154E + 01 | 2.7371E + 01 | 2.5767E + 01 | 2.7880E + 01 | 2.5756E + 01 | 2.7187E + 01 | |
| STD | 1.7737E + 00 | 1.9210E + 00 | 1.5475E + 00 | 1.7662E + 00 | 2.3702E + 00 | 9.8712E-01 | 1.9828E + 00 | 2.0836E + 00 | 2.4220E + 00 | 1.6667E + 00 | ||
| 20 | AVG | 2.9312E + 01 | 2.6101E + 01 | 2.8793E + 01 | 2.9043E + 01 | 2.8067E + 01 | 2.9857E + 01 | 2.7533E + 01 | 2.9085E + 01 | 2.8483E + 01 | 2.9142E + 01 | |
| STD | 2.3148E + 00 | 2.9650E + 00 | 1.4081E + 00 | 1.3971E + 00 | 3.6989E + 00 | 1.1548E + 00 | 1.3511E + 00 | 2.4434E + 00 | 1.9356E + 00 | 1.6072E + 00 | ||
| B | 10 | AVG | 2.5161E + 01 | 2.0368E + 01 | 2.4459E + 01 | 2.3740E + 01 | 2.3194E + 01 | 2.4204E + 01 | 2.2742E + 01 | 2.4940E + 01 | 2.3647E + 01 | 2.4083E + 01 |
| STD | 1.1482E + 00 | 2.4546E + 00 | 8.4814E-01 | 7.2136E-01 | 2.1285E + 00 | 6.3154E-01 | 1.5513E + 00 | 6.8792E-01 | 1.1640E + 00 | 1.0580E + 00 | ||
| 15 | AVG | 2.8117E + 01 | 2.3275E + 01 | 2.7124E + 01 | 2.6471E + 01 | 2.5715E + 01 | 2.6812E + 01 | 2.5648E + 01 | 2.7822E + 01 | 2.6519E + 01 | 2.7354E + 01 | |
| STD | 9.4434E-01 | 2.2647E + 00 | 7.7565E-01 | 1.2679E + 00 | 2.7078E + 00 | 9.4989E-01 | 1.0079E + 00 | 8.9760E-01 | 1.4688E + 00 | 1.1263E + 00 | ||
| 20 | AVG | 2.9688E + 01 | 2.5666E + 01 | 2.8746E + 01 | 2.8645E + 01 | 2.7998E + 01 | 2.8985E + 01 | 2.7628E + 01 | 2.9079E + 01 | 2.7632E + 01 | 2.9737E + 01 | |
| STD | 1.0411E + 00 | 1.9534E + 00 | 1.3171E + 00 | 1.2017E + 00 | 2.3082E + 00 | 1.2765E + 00 | 1.3601E + 00 | 1.6224E + 00 | 2.0571E + 00 | 1.1603E + 00 | ||
| C | 10 | AVG | 2.4456E + 01 | 2.0209E + 01 | 2.3335E + 01 | 2.3583E + 01 | 2.2872E + 01 | 2.4255E + 01 | 2.2613E + 01 | 2.4282E + 01 | 2.2242E + 01 | 2.4298E + 01 |
| STD | 1.3161E + 00 | 2.2556E + 00 | 1.3395E + 00 | 1.5001E + 00 | 1.6890E + 00 | 8.4385E-01 | 1.5603E + 00 | 1.2319E + 00 | 1.9720E + 00 | 9.4468E-01 | ||
| 15 | AVG | 2.7314E + 01 | 2.3096E + 01 | 2.6545E + 01 | 2.6780E + 01 | 2.5767E + 01 | 2.7277E + 01 | 2.5745E + 01 | 2.7072E + 01 | 2.5770E + 01 | 2.6430E + 01 | |
| STD | 1.0130E + 00 | 1.9618E + 00 | 1.4543E + 00 | 1.3403E + 00 | 1.8703E + 00 | 1.1959E + 00 | 1.3942E + 00 | 1.5873E + 00 | 1.5833E + 00 | 1.7506E + 00 | ||
| 20 | AVG | 2.8555E + 01 | 2.5382E + 01 | 2.8955E + 01 | 2.8062E + 01 | 2.7726E + 01 | 2.9554E + 01 | 2.6802E + 01 | 2.9004E + 01 | 2.7522E + 01 | 2.9417E + 01 | |
| STD | 1.8132E + 00 | 1.9228E + 00 | 9.0078E-01 | 1.7268E + 00 | 2.2572E + 00 | 1.1860E + 00 | 1.9558E + 00 | 1.4426E + 00 | 1.7386E + 00 | 1.3213E + 00 | ||
| D | 10 | AVG | 2.5656E + 01 | 2.0834E + 01 | 2.4473E + 01 | 2.4273E + 01 | 2.4625E + 01 | 2.4563E + 01 | 2.2853E + 01 | 2.5387E + 01 | 2.4135E + 01 | 2.4516E + 01 |
| STD | 1.6668E + 00 | 2.5680E + 00 | 1.1740E + 00 | 1.0148E + 00 | 2.3851E + 00 | 1.2206E + 00 | 1.9738E + 00 | 1.4842E + 00 | 2.5079E + 00 | 1.4610E + 00 | ||
| 15 | AVG | 2.8881E + 01 | 2.4029E + 01 | 2.6934E + 01 | 2.7175E + 01 | 2.6365E + 01 | 2.7668E + 01 | 2.5208E + 01 | 2.7475E + 01 | 2.6988E + 01 | 2.7862E + 01 | |
| STD | 1.1761E + 00 | 2.3791E + 00 | 1.4727E + 00 | 1.7360E + 00 | 2.9146E + 00 | 1.0705E + 00 | 1.8906E + 00 | 2.1516E + 00 | 2.2927E + 00 | 1.5345E + 00 | ||
| 20 | AVG | 3.1004E + 01 | 2.6531E + 01 | 2.8950E + 01 | 2.9315E + 01 | 2.8577E + 01 | 2.9146E + 01 | 2.7698E + 01 | 2.9636E + 01 | 2.8376E + 01 | 2.9768E + 01 | |
| STD | 1.6495E + 00 | 2.7032E + 00 | 1.2184E + 00 | 1.5110E + 00 | 2.3299E + 00 | 1.1523E + 00 | 2.1244E + 00 | 1.6072E + 00 | 1.9168E + 00 | 1.6572E + 00 | ||
| E | 10 | AVG | 2.5674E + 01 | 2.2596E + 01 | 2.4600E + 01 | 2.4462E + 01 | 2.3451E + 01 | 2.4794E + 01 | 2.3311E + 01 | 2.5199E + 01 | 2.4042E + 01 | 2.5061E + 01 |
| STD | 1.9597E + 00 | 2.3853E + 00 | 1.1607E + 00 | 1.4650E + 00 | 3.0508E + 00 | 1.3761E + 00 | 2.1700E + 00 | 1.3704E + 00 | 1.9084E + 00 | 1.2553E + 00 | ||
| 15 | AVG | 2.8947E + 01 | 2.4707E + 01 | 2.7594E + 01 | 2.7110E + 01 | 2.7078E + 01 | 2.7418E + 01 | 2.5977E + 01 | 2.7888E + 01 | 2.6454E + 01 | 2.7429E + 01 | |
| STD | 1.4011E + 00 | 2.2925E + 00 | 1.2708E + 00 | 1.9116E + 00 | 2.3958E + 00 | 1.2844E + 00 | 2.2799E + 00 | 1.7858E + 00 | 1.8590E + 00 | 2.0404E + 00 | ||
| 20 | AVG | 3.1189E + 01 | 2.6705E + 01 | 2.9703E + 01 | 2.8137E + 01 | 2.7131E + 01 | 2.9522E + 01 | 2.8301E + 01 | 2.9744E + 01 | 2.8480E + 01 | 2.9092E + 01 | |
| STD | 2.2522E + 00 | 3.4192E + 00 | 1.3492E + 00 | 2.0667E + 00 | 4.0248E + 00 | 1.6222E + 00 | 1.5240E + 00 | 2.4974E + 00 | 2.3355E + 00 | 1.8733E + 00 | ||
| F | 10 | AVG | 2.5038E + 01 | 2.1631E + 01 | 2.4011E + 01 | 2.3808E + 01 | 2.3606E + 01 | 2.4025E + 01 | 2.2956E + 01 | 2.4639E + 01 | 2.3839E + 01 | 2.4406E + 01 |
| STD | 1.2770E + 00 | 2.3331E + 00 | 1.0150E + 00 | 1.1354E + 00 | 2.4388E + 00 | 9.1501E-01 | 1.3050E + 00 | 1.3869E + 00 | 1.4795E + 00 | 1.0541E + 00 | ||
| 15 | AVG | 2.7506E + 01 | 2.2879E + 01 | 2.6362E + 01 | 2.6377E + 01 | 2.5947E + 01 | 2.6620E + 01 | 2.6124E + 01 | 2.7561E + 01 | 2.5687E + 01 | 2.6896E + 01 | |
| STD | 1.5083E + 00 | 2.5129E + 00 | 1.0277E + 00 | 1.1865E + 00 | 2.3408E + 00 | 9.7229E-01 | 1.7066E + 00 | 1.3783E + 00 | 1.8213E + 00 | 1.2498E + 00 | ||
| 20 | AVG | 2.9363E + 01 | 2.5790E + 01 | 2.9120E + 01 | 2.8488E + 01 | 2.8600E + 01 | 2.9083E + 01 | 2.7052E + 01 | 2.9327E + 01 | 2.7619E + 01 | 2.9386E + 01 | |
| STD | 1.4230E + 00 | 2.5264E + 00 | 1.0947E + 00 | 1.5198E + 00 | 1.8447E + 00 | 1.1779E + 00 | 1.5376E + 00 | 1.2569E + 00 | 2.1104E + 00 | 1.7057E + 00 | ||
| G | 10 | AVG | 2.4295E + 01 | 2.0963E + 01 | 2.3862E + 01 | 2.3606E + 01 | 2.2029E + 01 | 2.4107E + 01 | 2.2186E + 01 | 2.4868E + 01 | 2.3421E + 01 | 2.4069E + 01 |
| STD | 1.7958E + 00 | 2.4107E + 00 | 1.1828E + 00 | 1.7108E + 00 | 2.5576E + 00 | 7.0802E-01 | 1.6367E + 00 | 1.0205E + 00 | 1.7832E + 00 | 1.2090E + 00 | ||
| 15 | AVG | 2.6852E + 01 | 2.3755E + 01 | 2.6596E + 01 | 2.6876E + 01 | 2.5265E + 01 | 2.7247E + 01 | 2.5606E + 01 | 2.7345E + 01 | 2.5616E + 01 | 2.6935E + 01 | |
| STD | 2.0035E + 00 | 2.2767E + 00 | 1.0362E + 00 | 1.4474E + 00 | 2.5154E + 00 | 1.1232E + 00 | 1.4458E + 00 | 1.2377E + 00 | 1.5809E + 00 | 1.1162E + 00 | ||
| 20 | AVG | 2.8916E + 01 | 2.5510E + 01 | 2.8560E + 01 | 2.8232E + 01 | 2.6686E + 01 | 2.9156E + 01 | 2.7219E + 01 | 2.8712E + 01 | 2.7602E + 01 | 2.8729E + 01 | |
| STD | 1.4525E + 00 | 2.3607E + 00 | 1.1001E + 00 | 1.7404E + 00 | 2.2731E + 00 | 9.2638E-01 | 1.3916E + 00 | 1.8582E + 00 | 1.5447E + 00 | 2.1741E + 00 | ||
| H | 10 | AVG | 2.5077E + 01 | 2.0971E + 01 | 2.3976E + 01 | 2.4049E + 01 | 2.3126E + 01 | 2.4295E + 01 | 2.3611E + 01 | 2.4927E + 01 | 2.3576E + 01 | 2.4623E + 01 |
| STD | 1.3000E + 00 | 2.1089E + 00 | 1.3491E + 00 | 8.1859E-01 | 2.1812E + 00 | 1.0492E + 00 | 1.5330E + 00 | 1.1137E + 00 | 1.8256E + 00 | 1.0485E + 00 | ||
| 15 | AVG | 2.7342E + 01 | 2.3417E + 01 | 2.6862E + 01 | 2.6836E + 01 | 2.6045E + 01 | 2.6634E + 01 | 2.5030E + 01 | 2.7917E + 01 | 2.5620E + 01 | 2.7741E + 01 | |
| STD | 1.7306E + 00 | 3.2220E + 00 | 1.1932E + 00 | 1.2189E + 00 | 2.3287E + 00 | 1.2800E + 00 | 1.9922E + 00 | 1.5215E + 00 | 1.7574E + 00 | 1.0649E + 00 | ||
| 20 | AVG | 2.9506E + 01 | 2.5704E + 01 | 2.8813E + 01 | 2.8153E + 01 | 2.7738E + 01 | 2.8767E + 01 | 2.7727E + 01 | 2.9113E + 01 | 2.7598E + 01 | 2.9697E + 01 | |
| STD | 2.1604E + 00 | 2.1191E + 00 | 1.0309E + 00 | 1.6862E + 00 | 1.9980E + 00 | 1.3230E + 00 | 1.2884E + 00 | 2.1127E + 00 | 2.4505E + 00 | 1.3536E + 00 | ||
| I | 10 | AVG | 2.4654E + 01 | 2.0648E + 01 | 2.4328E + 01 | 2.3754E + 01 | 2.3548E + 01 | 2.4383E + 01 | 2.2948E + 01 | 2.4879E + 01 | 2.3090E + 01 | 2.4321E + 01 |
| STD | 1.6363E + 00 | 2.9334E + 00 | 1.3776E + 00 | 1.2802E + 00 | 2.2401E + 00 | 1.1894E + 00 | 1.7535E + 00 | 1.3024E + 00 | 1.8231E + 00 | 1.2664E + 00 | ||
| 15 | AVG | 2.7484E + 01 | 2.3170E + 01 | 2.6846E + 01 | 2.6808E + 01 | 2.5503E + 01 | 2.6901E + 01 | 2.5761E + 01 | 2.7461E + 01 | 2.5482E + 01 | 2.6894E + 01 | |
| STD | 1.7481E + 00 | 2.5406E + 00 | 1.0697E + 00 | 1.6406E + 00 | 2.3557E + 00 | 1.6441E + 00 | 1.3135E + 00 | 1.9912E + 00 | 2.4289E + 00 | 1.9365E + 00 | ||
| 20 | AVG | 2.9790E + 01 | 2.6224E + 01 | 2.8941E + 01 | 2.7864E + 01 | 2.7084E + 01 | 2.8885E + 01 | 2.7403E + 01 | 2.9820E + 01 | 2.8127E + 01 | 2.8908E + 01 | |
| STD | 1.5117E + 00 | 2.3244E + 00 | 1.5575E + 00 | 2.1994E + 00 | 2.7064E + 00 | 1.5066E + 00 | 1.6138E + 00 | 1.6370E + 00 | 1.9471E + 00 | 2.3196E + 00 |
Table A10.
The SSIM comparison at high threshold level.
| Image | T | EEFOA | FOA | DE | GWO | HHO | MDE | BLPSO | LGCMFO | m_SCA | DASMA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 10 | AVG | 8.3657E-01 | 7.9156E-01 | 8.1406E-01 | 8.0975E-01 | 8.1181E-01 | 8.0931E-01 | 7.9662E-01 | 8.1939E-01 | 8.1519E-01 | 8.1734E-01 |
| STD | 1.7118E-02 | 3.7179E-02 | 1.9985E-02 | 2.0534E-02 | 3.3167E-02 | 2.0576E-02 | 3.0890E-02 | 2.3163E-02 | 2.7305E-02 | 2.0238E-02 | ||
| 15 | AVG | 8.7954E-01 | 8.2391E-01 | 8.5029E-01 | 8.4391E-01 | 8.4642E-01 | 8.5120E-01 | 8.3950E-01 | 8.6688E-01 | 8.3772E-01 | 8.5339E-01 | |
| STD | 2.0090E-02 | 2.3348E-02 | 2.0944E-02 | 2.2001E-02 | 3.3799E-02 | 1.5846E-02 | 2.6355E-02 | 2.4656E-02 | 2.4463E-02 | 2.3836E-02 | ||
| 20 | AVG | 9.0325E-01 | 8.5495E-01 | 8.7703E-01 | 8.8119E-01 | 8.7394E-01 | 8.8562E-01 | 8.6372E-01 | 8.8317E-01 | 8.7433E-01 | 8.7975E-01 | |
| STD | 1.6301E-02 | 3.2390E-02 | 1.7863E-02 | 1.9148E-02 | 4.2316E-02 | 1.3397E-02 | 1.7404E-02 | 2.5785E-02 | 2.1119E-02 | 1.8847E-02 | ||
| B | 10 | AVG | 7.9617E-01 | 6.4403E-01 | 7.6922E-01 | 7.4616E-01 | 7.4212E-01 | 7.6149E-01 | 7.1774E-01 | 7.8554E-01 | 7.4912E-01 | 7.6021E-01 |
| STD | 3.1854E-02 | 7.2533E-02 | 2.9538E-02 | 2.4416E-02 | 6.3306E-02 | 2.2183E-02 | 4.5950E-02 | 2.3197E-02 | 3.4493E-02 | 3.0945E-02 | ||
| 15 | AVG | 8.7340E-01 | 7.3878E-01 | 8.4732E-01 | 8.3197E-01 | 8.1636E-01 | 8.3994E-01 | 8.0265E-01 | 8.6764E-01 | 8.3100E-01 | 8.5638E-01 | |
| STD | 1.7918E-02 | 6.3736E-02 | 2.2800E-02 | 3.0740E-02 | 5.9494E-02 | 2.4222E-02 | 2.8925E-02 | 2.0517E-02 | 3.8879E-02 | 2.8983E-02 | ||
| 20 | AVG | 9.0172E-01 | 8.0479E-01 | 8.7900E-01 | 8.8065E-01 | 8.6227E-01 | 8.8801E-01 | 8.5361E-01 | 8.9156E-01 | 8.5766E-01 | 9.0120E-01 | |
| STD | 1.5753E-02 | 4.8918E-02 | 2.8072E-02 | 2.5889E-02 | 5.0606E-02 | 2.6780E-02 | 3.3591E-02 | 2.9913E-02 | 4.6922E-02 | 2.2321E-02 | ||
| C | 10 | AVG | 8.2046E-01 | 7.7675E-01 | 8.0145E-01 | 8.0535E-01 | 7.9256E-01 | 7.9573E-01 | 7.9578E-01 | 7.9692E-01 | 7.8546E-01 | 7.9987E-01 |
| STD | 2.7136E-02 | 3.6594E-02 | 2.0092E-02 | 1.4704E-02 | 2.9498E-02 | 1.6588E-02 | 1.6304E-02 | 2.3394E-02 | 4.1475E-02 | 2.1228E-02 | ||
| 15 | AVG | 8.6038E-01 | 8.0343E-01 | 8.4220E-01 | 8.4697E-01 | 8.4203E-01 | 8.4651E-01 | 8.3233E-01 | 8.5302E-01 | 8.3742E-01 | 8.3690E-01 | |
| STD | 1.7716E-02 | 2.6702E-02 | 1.8590E-02 | 1.4560E-02 | 2.8362E-02 | 1.4080E-02 | 1.6667E-02 | 1.7876E-02 | 1.9181E-02 | 2.5308E-02 | ||
| 20 | AVG | 8.9170E-01 | 8.3787E-01 | 8.7104E-01 | 8.7514E-01 | 8.6377E-01 | 8.7713E-01 | 8.5006E-01 | 8.7384E-01 | 8.6465E-01 | 8.7950E-01 | |
| STD | 1.8211E-02 | 2.9401E-02 | 1.4426E-02 | 2.0248E-02 | 2.6288E-02 | 1.5214E-02 | 2.6045E-02 | 1.8506E-02 | 1.9361E-02 | 1.8490E-02 | ||
| D | 10 | AVG | 8.0017E-01 | 7.6402E-01 | 8.0022E-01 | 7.9838E-01 | 8.0222E-01 | 7.9960E-01 | 7.7587E-01 | 8.0247E-01 | 8.1391E-01 | 7.8644E-01 |
| STD | 3.4014E-02 | 4.3678E-02 | 2.0354E-02 | 1.9375E-02 | 3.2767E-02 | 2.1504E-02 | 2.3866E-02 | 2.4060E-02 | 3.6545E-02 | 2.6753E-02 | ||
| 15 | AVG | 8.5858E-01 | 7.9620E-01 | 8.3615E-01 | 8.4986E-01 | 8.3872E-01 | 8.3665E-01 | 8.2085E-01 | 8.3393E-01 | 8.4335E-01 | 8.4540E-01 | |
| STD | 2.1648E-02 | 3.3901E-02 | 1.2882E-02 | 2.5582E-02 | 4.1734E-02 | 2.2385E-02 | 3.2193E-02 | 2.7750E-02 | 2.9785E-02 | 2.4653E-02 | ||
| 20 | AVG | 8.9159E-01 | 8.4056E-01 | 8.6170E-01 | 8.6916E-01 | 8.6694E-01 | 8.6003E-01 | 8.4501E-01 | 8.7567E-01 | 8.6349E-01 | 8.7256E-01 | |
| STD | 2.4122E-02 | 3.1363E-02 | 2.1380E-02 | 2.1071E-02 | 3.0035E-02 | 1.8071E-02 | 2.9423E-02 | 2.4047E-02 | 2.4189E-02 | 2.5253E-02 | ||
| E | 10 | AVG | 8.1690E-01 | 8.0012E-01 | 7.9759E-01 | 7.9772E-01 | 7.9488E-01 | 8.0081E-01 | 7.9559E-01 | 8.0205E-01 | 7.9913E-01 | 7.9860E-01 |
| STD | 2.0995E-02 | 3.1280E-02 | 1.6803E-02 | 1.6942E-02 | 3.2835E-02 | 1.6543E-02 | 2.7845E-02 | 2.0490E-02 | 2.7927E-02 | 1.9323E-02 | ||
| 15 | AVG | 8.6595E-01 | 8.2106E-01 | 8.3589E-01 | 8.3441E-01 | 8.3722E-01 | 8.3323E-01 | 8.3307E-01 | 8.4161E-01 | 8.3081E-01 | 8.3347E-01 | |
| STD | 1.4925E-02 | 2.3064E-02 | 1.7369E-02 | 2.4324E-02 | 2.8237E-02 | 2.0599E-02 | 1.9484E-02 | 2.1274E-02 | 2.4244E-02 | 2.5353E-02 | ||
| 20 | AVG | 8.9739E-01 | 8.4910E-01 | 8.6689E-01 | 8.5079E-01 | 8.5228E-01 | 8.6887E-01 | 8.5520E-01 | 8.7151E-01 | 8.5911E-01 | 8.5896E-01 | |
| STD | 2.0257E-02 | 3.5255E-02 | 1.7707E-02 | 2.3414E-02 | 3.1716E-02 | 1.5483E-02 | 1.8040E-02 | 3.3018E-02 | 2.7535E-02 | 2.4238E-02 | ||
| F | 10 | AVG | 7.7761E-01 | 7.1417E-01 | 7.5078E-01 | 7.3611E-01 | 7.5012E-01 | 7.4402E-01 | 7.3202E-01 | 7.5702E-01 | 7.4891E-01 | 7.4968E-01 |
| STD | 2.4195E-02 | 5.0530E-02 | 2.4520E-02 | 2.7289E-02 | 4.3492E-02 | 2.3708E-02 | 2.8503E-02 | 3.4185E-02 | 3.0057E-02 | 2.5034E-02 | ||
| 15 | AVG | 8.4414E-01 | 7.4585E-01 | 8.0528E-01 | 8.0448E-01 | 8.0169E-01 | 8.0907E-01 | 8.0683E-01 | 8.3315E-01 | 7.9651E-01 | 8.1722E-01 | |
| STD | 2.2940E-02 | 4.2532E-02 | 1.9204E-02 | 2.5355E-02 | 4.7041E-02 | 2.2548E-02 | 3.1112E-02 | 2.7572E-02 | 3.5658E-02 | 2.8426E-02 | ||
| 20 | AVG | 8.7411E-01 | 8.0809E-01 | 8.6237E-01 | 8.5048E-01 | 8.5925E-01 | 8.6395E-01 | 8.2841E-01 | 8.6709E-01 | 8.4171E-01 | 8.6786E-01 | |
| STD | 2.3521E-02 | 4.6535E-02 | 2.0501E-02 | 2.9515E-02 | 3.0521E-02 | 2.2072E-02 | 2.6777E-02 | 2.3224E-02 | 3.7605E-02 | 3.1269E-02 | ||
| G | 10 | AVG | 7.9277E-01 | 7.3607E-01 | 7.6702E-01 | 7.8076E-01 | 7.5841E-01 | 7.7124E-01 | 7.6247E-01 | 7.7817E-01 | 7.7201E-01 | 7.7380E-01 |
| STD | 1.8881E-02 | 4.6311E-02 | 2.3061E-02 | 2.2190E-02 | 4.5044E-02 | 2.3335E-02 | 3.0848E-02 | 2.5649E-02 | 3.4532E-02 | 1.8560E-02 | ||
| 15 | AVG | 8.4269E-01 | 7.8411E-01 | 8.2087E-01 | 8.2890E-01 | 8.1541E-01 | 8.2816E-01 | 8.0705E-01 | 8.3680E-01 | 8.1536E-01 | 8.2408E-01 | |
| STD | 2.8218E-02 | 2.9654E-02 | 1.6697E-02 | 2.1097E-02 | 3.7159E-02 | 1.7805E-02 | 2.3596E-02 | 1.8007E-02 | 2.0929E-02 | 1.9970E-02 | ||
| 20 | AVG | 8.7548E-01 | 8.1647E-01 | 8.5188E-01 | 8.5774E-01 | 8.3992E-01 | 8.6228E-01 | 8.3596E-01 | 8.5897E-01 | 8.4908E-01 | 8.6668E-01 | |
| STD | 1.6784E-02 | 2.7559E-02 | 1.6194E-02 | 2.4028E-02 | 3.3424E-02 | 1.5396E-02 | 2.3714E-02 | 2.4546E-02 | 2.0667E-02 | 2.0817E-02 | ||
| H | 10 | AVG | 7.8154E-01 | 7.0590E-01 | 7.4888E-01 | 7.4327E-01 | 7.3936E-01 | 7.4860E-01 | 7.5609E-01 | 7.6310E-01 | 7.4726E-01 | 7.5826E-01 |
| STD | 2.3733E-02 | 4.0019E-02 | 2.5423E-02 | 1.8465E-02 | 3.4489E-02 | 1.8602E-02 | 2.6989E-02 | 2.4185E-02 | 2.5536E-02 | 2.5335E-02 | ||
| 15 | AVG | 8.4123E-01 | 7.6004E-01 | 8.1397E-01 | 8.0740E-01 | 8.0666E-01 | 8.0701E-01 | 7.8475E-01 | 8.3424E-01 | 7.9914E-01 | 8.2841E-01 | |
| STD | 2.5597E-02 | 4.1165E-02 | 2.2651E-02 | 2.3387E-02 | 4.0591E-02 | 2.5336E-02 | 3.6395E-02 | 2.9226E-02 | 3.1787E-02 | 2.0893E-02 | ||
| 20 | AVG | 8.7218E-01 | 8.1022E-01 | 8.5220E-01 | 8.3996E-01 | 8.4285E-01 | 8.5157E-01 | 8.3632E-01 | 8.6340E-01 | 8.3596E-01 | 8.6979E-01 | |
| STD | 3.2687E-02 | 3.2473E-02 | 1.8956E-02 | 2.6091E-02 | 2.8987E-02 | 2.3496E-02 | 2.0471E-02 | 3.2783E-02 | 3.8268E-02 | 2.5955E-02 | ||
| I | 10 | AVG | 7.9912E-01 | 7.3916E-01 | 7.6971E-01 | 7.7519E-01 | 7.7749E-01 | 7.7727E-01 | 7.6285E-01 | 7.8654E-01 | 7.6834E-01 | 7.7188E-01 |
| STD | 2.2632E-02 | 5.3058E-02 | 2.8020E-02 | 2.2056E-02 | 4.3241E-02 | 1.9108E-02 | 2.8320E-02 | 2.6212E-02 | 4.3653E-02 | 2.4391E-02 | ||
| 15 | AVG | 8.5119E-01 | 7.8484E-01 | 8.2323E-01 | 8.2793E-01 | 8.1526E-01 | 8.2325E-01 | 8.1470E-01 | 8.3522E-01 | 8.1007E-01 | 8.3160E-01 | |
| STD | 1.9257E-02 | 4.1651E-02 | 2.1349E-02 | 2.4041E-02 | 3.8524E-02 | 2.7035E-02 | 2.4119E-02 | 2.9871E-02 | 3.5378E-02 | 3.4175E-02 | ||
| 20 | AVG | 8.9084E-01 | 8.3163E-01 | 8.6537E-01 | 8.5088E-01 | 8.4382E-01 | 8.6248E-01 | 8.3841E-01 | 8.7963E-01 | 8.5210E-01 | 8.6911E-01 | |
| STD | 1.9275E-02 | 3.2211E-02 | 1.8207E-02 | 2.9575E-02 | 3.7456E-02 | 2.0744E-02 | 2.3186E-02 | 2.3283E-02 | 2.4855E-02 | 2.3868E-02 |
Appendix B. .
Data availability
Data will be made available on request.
References
- 1.Li Q., Miao Y., Zeng X., Tarimo C.S., Wu C., Wu J. Prevalence and factors for anxiety during the coronavirus disease, (COVID-19) epidemic among the teachers in China. J. Affect. Disord. 2019;277(2020):153–158. doi: 10.1016/j.jad.2020.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hu F., Shi X., Wang H., Nan N., Wang K., Wei S., Li Z., Jiang S., Hu H., Zhao S. Is health contagious?—Based on empirical evidence from China family panel studies' data. Front. Public Health. 2021;9 doi: 10.3389/fpubh.2021.691746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.E.E.-D. Hemdan, M. Shouman, M. Karar, COVIDX-Net: A Framework of Deep Learning Classifiers to Diagnose COVID-19 in X-Ray Images, 2020.
- 4.G. Maguolo, L. Nanni, A Critic Evaluation of Methods for COVID-19 Automatic Detection from X-Ray Images, 2020. [DOI] [PMC free article] [PubMed]
- 5.Ismael A.M., Şengür A. Deep learning approaches for COVID-19 detection based on chest X-ray images. Expert Syst. Appl. 2020;164:114054. doi: 10.1016/j.eswa.2020.114054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Xie B., Li S., Li M., Liu C.H., Huang G., Wang G. Sepico: Semantic-guided pixel contrast for domain adaptive semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2023 doi: 10.1109/TPAMI.2023.3237740. [DOI] [PubMed] [Google Scholar]
- 7.Li B., Lu Y., Pang W., Xu H. Image Colorization using CycleGAN with semantic and spatial rationality. Multimed. Tools Appl. 2023:1–15. [Google Scholar]
- 8.Qin X., Ban Y., Wu P., Yang B., Liu S., Yin L., Liu M., Zheng W. Improved Image Fusion Method Based on Sparse Decomposition. Electronics. 2022;11:2321. [Google Scholar]
- 9.Li Q., Song D., Yuan C., Nie W. An image recognition method for the deformation area of open-pit rock slopes under variable rainfall. Measurement. 2022;188 [Google Scholar]
- 10.Liu H., Liu M., Li D., Zheng W., Yin L., Wang R. Recent Advances in Pulse-Coupled Neural Networks with Applications in Image Processing. Electronics. 2022;11:3264. [Google Scholar]
- 11.Lu S., Yang B., Xiao Y., Liu S., Liu M., Yin L., Zheng W. Iterative reconstruction of low-dose CT based on differential sparse. Biomed. Signal Process. Control. 2023;79 [Google Scholar]
- 12.Lv Z., Chen D., Feng H., Zhu H., Lv H. Digital twins in unmanned aerial vehicles for rapid medical resource delivery in epidemics. IEEE Trans. Intell. Transp. Syst. 2021;23:25106–25114. doi: 10.1109/TITS.2021.3113787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Song X., Wang R., Gao J., Han X., Jin J., Lv C., Yu F. Construction of a biotin-targeting drug delivery system and its near-infrared theranostic fluorescent probe for real-time image-guided therapy of lung cancer. Chin. Chem. Lett. 2022;33:1567–1571. [Google Scholar]
- 14.Tsai C.-Y., Liu T.-Y., Chen W.-C. A Novel Histogram-Based Multi-Threshold Searching Algorithm for Multilevel Colour Thresholding. Int. J. Adv. Rob. Syst. 2012;9:223. [Google Scholar]
- 15.Michetti J., Georgelin-Gurgel M., Mallet J.P., Diemer F., Boulanouar K. Influence of CBCT parameters on the output of an automatic edge-detection-based endodontic segmentation. Dentomaxillofac. Radiol. 2015;44:20140413. doi: 10.1259/dmfr.20140413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dong B., Jin R., Weng G. Active contour model based on local bias field estimation for image segmentation. Signal Process. Image Commun. 2019;78:187–199. [Google Scholar]
- 17.Mignotte M. A label field fusion Bayesian model and its penalized maximum rand estimator for image segmentation. IEEE Trans. Image Process. 2010:1610–1624. doi: 10.1109/TIP.2010.2044965. [DOI] [PubMed] [Google Scholar]
- 18.Narappanawar N., Rao M., Joshi M. Graph theory based segmentation of traced boundary into open and closed sub-sections. Comput. Vis. Image Underst. 2011;115:1552–1558. [Google Scholar]
- 19.Esmaeili L., Mousavirad S.J., Shahidinejad A. An efficient method to minimize cross-entropy for selecting multi-level threshold values using an improved human mental search algorithm. Expert Syst. Appl. 2021;182 [Google Scholar]
- 20.A. Appathurai, G. Manogaran, C. Raja, S. Kadry, S.N. Kumar, C. Ageeskumar, J. T, S. Krishnamoorthy, P. M K, G. Chandra Babu, N. Murugan, P. Panchatcharam, Segmentation by Fractional Order Darwinian Particle Swarm Optimization Based Multilevel Thresholding and Improved Lossless Prediction Based Compression Algorithm for Medical Images, IEEE Access, PP (2019) 89570-89580.
- 21.A. Ŕeny, On measures of entropy and information, Symposium on Mathematics Statistics and Probabilities, (1961) 547-561.
- 22.Lin J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory. 1991;37:145–151. [Google Scholar]
- 23.M.P.d. Albuquerque, I. Esquef, A.d.R. Gesualdi, M.P.d. Albuquerque, Image thresholding using Tsallis entropy, Pattern Recognit. Lett., 25 (2004) 1059-1065.
- 24.Venter G., Jaroslaw S.-S. Particle Swarm Optimization. AIAA J. 2002;41 [Google Scholar]
- 25.Mirjalili S., Dong J.S., Lewis A. Springer; 2019. Nature-inspired optimizers: theories, literature reviews and applications. [Google Scholar]
- 26.B. Basturk, D. Karaboga, An artificial bee colony (ABC) algorithm for numeric function optimization. In Proceedings of the IEEE swarm intelligence symposium, Indianapolis, IN, USA, May, 2006 (2006) 12-14.
- 27.Hansen N., Ostermeier A. Completely derandomized self-adaptation in evolution strategies. Evol. Comput. 2003;11:159–195. doi: 10.1162/106365601750190398. [DOI] [PubMed] [Google Scholar]
- 28.Yang X.-S. A New Metaheuristic Bat-Inspired Algorithm. 2010;284 [Google Scholar]
- 29.Heidari A.A., Mirjalili S., Faris H., Aljarah I., Mafarja M., Chen H. Harris hawks optimization: Algorithm and applications. Futur. Gener. Comput. Syst. 2019;97:849–872. [Google Scholar]
- 30.Chen H., Li C., Mafarja M., Heidari A.A., Chen Y., Cai Z. Slime mould algorithm: a comprehensive review of recent variants and applications. Int. J. Syst. Sci. 2022:1–32. [Google Scholar]
- 31.Li S., Chen H., Wang M., Heidari A.A., Mirjalili S. Slime mould algorithm: A new method for stochastic optimization. Futur. Gener. Comput. Syst. 2020;111:300–323. [Google Scholar]
- 32.Ahmadianfar I., Heidari A.A., Noshadian S., Chen H., Gandomi A.H. INFO: An efficient optimization algorithm based on weighted mean of vectors. Expert Syst. Appl. 2022;195 [Google Scholar]
- 33.Ahmadianfar I., Heidari A.A., Gandomi A.H., Chu X., Chen H. RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Syst. Appl. 2021;181 [Google Scholar]
- 34.Yang Y., Chen H., Heidari A.A., Gandomi A.H. Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts. Expert Syst. Appl. 2021;177 [Google Scholar]
- 35.H. Su, D. Zhao, A. Asghar Heidari, L. Liu, X. Zhang, M. Mafarja, H. Chen, RIME: A physics-based optimization, Neurocomputing, (2023).
- 36.Pan W.-T. A new Fruit Fly Optimization Algorithm: Taking the financial distress model as an example. Knowledge Based Systems - KBS. 2012;26 [Google Scholar]
- 37.Deng W., Zhang X., Zhou Y., Liu Y., Zhou X., Chen H., Zhao H. An enhanced fast non-dominated solution sorting genetic algorithm for multi-objective problems. Inf. Sci. 2022;585:441–453. [Google Scholar]
- 38.Hua Y., Liu Q., Hao K., Jin Y. A Survey of Evolutionary Algorithms for Multi-Objective Optimization Problems With Irregular Pareto Fronts. IEEE/CAA J. Autom. Sin. 2021;8:303–318. [Google Scholar]
- 39.H. ling Chen, B. Yang, S. jing Wang, G. Wang, H. zhong Li, W. bin Liu, Towards an optimal support vector machine classifier using a parallel particle swarm optimization strategy, Applied Mathematics and Computation, 239 (2014) 180-197.
- 40.Zhao F., Di S., Cao J., Tang J. A novel cooperative multi-stage hyper-heuristic for combination optimization problems. Complex System Modeling and Simulation. 2021;1:91–108. [Google Scholar]
- 41.Cai Z., Gu J., Luo J., Zhang Q., Chen H., Pan Z., Li Y., Li C. Evolving an optimal kernel extreme learning machine by using an enhanced grey wolf optimization strategy. Expert Syst. Appl. 2019;138 [Google Scholar]
- 42.Xu Y., Chen H., Heidari A.A., Luo J., Zhang Q., Zhao X., Li C. An Efficient Chaotic Mutative Moth-flame-inspired Optimizer for Global Optimization Tasks. Expert Syst. Appl. 2019;129:135–155. [Google Scholar]
- 43.Yu H., Cheng X., Chen C., Heidari A.A., Liu J., Cai Z., Chen H. Apple leaf disease recognition method with improved residual network. Multimed. Tools Appl. 2022 [Google Scholar]
- 44.Wu S.-H., Zhan Z.-H., Zhang J. SAFE: Scale-adaptive fitness evaluation method for expensive optimization problems. IEEE Trans. Evol. Comput. 2021;25:478–491. [Google Scholar]
- 45.Li J.-Y., Zhan Z.-H., Wang C., Jin H., Zhang J. Boosting data-driven evolutionary algorithm with localized data generation. IEEE Trans. Evol. Comput. 2020;24:923–937. [Google Scholar]
- 46.Xia J., Wang Z., Yang D., Li R., Liang G., Chen H., Heidari A.A., Turabieh H., Mafarja M., Pan Z. Performance optimization of support vector machine with oppositional grasshopper optimization for acute appendicitis diagnosis. Comput. Biol. Med. 2022;105206 doi: 10.1016/j.compbiomed.2021.105206. [DOI] [PubMed] [Google Scholar]
- 47.Xia J., Yang D., Zhou H., Chen Y., Zhang H., Liu T., Heidari A.A., Chen H., Pan Z. Evolving kernel extreme learning machine for medical diagnosis via a disperse foraging sine cosine algorithm. Comput. Biol. Med. 2022;141 doi: 10.1016/j.compbiomed.2021.105137. [DOI] [PubMed] [Google Scholar]
- 48.Ban Y., Wang Y., Liu S., Yang B., Liu M., Yin L., Zheng W. 2D/3D multimode medical image alignment based on spatial histograms. Appl. Sci. 2022;12:8261. [Google Scholar]
- 49.Hu J., Chen H., Heidari A.A., Wang M., Zhang X., Chen Y., Pan Z. Orthogonal learning covariance matrix for defects of grey wolf optimizer: Insights, balance, diversity, and feature selection. Knowl.-Based Syst. 2021;213 [Google Scholar]
- 50.Hu J., Gui W., Heidari A.A., Cai Z., Liang G., Chen H., Pan Z. Dispersed foraging slime mould algorithm: Continuous and binary variants for global optimization and wrapper-based feature selection. Knowl.-Based Syst. 2022;237 [Google Scholar]
- 51.Hussien A.G., Heidari A.A., Ye X., Liang G., Chen H., Pan Z. Boosting whale optimization with evolution strategy and Gaussian random walks: an image segmentation method. Eng. Comput. 2022 [Google Scholar]
- 52.Yu H., Song J., Chen C., Heidari A.A., Liu J., Chen H., Zaguia A., Mafarja M. Image segmentation of Leaf Spot Diseases on Maize using multi-stage Cauchy-enabled grey wolf algorithm. Eng. Appl. Artif. Intel. 2022;109 [Google Scholar]
- 53.Dong R., Chen H., Heidari A.A., Turabieh H., Mafarja M., Wang S. Boosted kernel search: Framework, analysis and case studies on the economic emission dispatch problem. Knowl.-Based Syst. 2021;233 [Google Scholar]
- 54.Chen H., Wang M., Zhao X. A multi-strategy enhanced sine cosine algorithm for global optimization and constrained practical engineering problems. Appl. Math Comput. 2020;369 [Google Scholar]
- 55.Yu H., Qiao S., Heidari A.A., Bi C., Chen H. Individual Disturbance and Attraction Repulsion Strategy Enhanced Seagull Optimization for Engineering Design. Mathematics. 2022;10:276. [Google Scholar]
- 56.Han X., Han Y., Chen Q., Li J., Sang H., Liu Y., Pan Q., Nojima Y. Distributed Flow Shop Scheduling with Sequence-Dependent Setup Times Using an Improved Iterated Greedy Algorithm. Complex System Modeling and Simulation. 2021;1:198–217. [Google Scholar]
- 57.Gao D., Wang G.-G., Pedrycz W. Solving fuzzy job-shop scheduling problem using DE algorithm improved by a selection mechanism. IEEE Trans Fuzzy Syst. 2020;28:3265–3275. [Google Scholar]
- 58.Wang G.-G., Gao D., Pedrycz W. Solving multi-objective fuzzy job-shop scheduling problem by a hybrid adaptive differential evolution algorithm. IEEE Trans. Ind. Inf. 2022 [Google Scholar]
- 59.Ye X., Liu W., Li H., Wang M., Chi C., Liang G., Chen H., Huang H. Modified Whale Optimization Algorithm for Solar Cell and PV Module Parameter Identification. Complexity. 2021;2021:8878686. [Google Scholar]
- 60.Wang R.-Y., Hu P., Hu C.-C., Pan J.-S. A novel Fruit Fly Optimization Algorithm with quasi-affine transformation evolutionary for numerical optimization and application. Int. J. Distrib. Sens. Netw. 2022;18 [Google Scholar]
- 61.Cheng J., Shi T. Structural optimization of transmission line tower based on improved fruit fly optimization algorithm. Comput. Electr. Eng. 2022;103 [Google Scholar]
- 62.Fan Y., Wang P., Mafarja M., Wang M., Zhao X., Chen H. A bioinformatic variant fruit fly optimizer for tackling optimization problems. Knowl.-Based Syst. 2021;213 [Google Scholar]
- 63.Fan Y., Wang P., Heidari A.A., Wang M., Zhao X., Chen H., Li C. Rationalized fruit fly optimization with sine cosine algorithm: a comprehensive analysis. Expert Syst. Appl. 2020;157 [Google Scholar]
- 64.Chen H., Li S., Heidari A.A., Wang P., Li J., Yang Y., Wang M., Huang C. Efficient Multi-population Outpost Fruit Fly-driven Optimizers: Framework and Advances in Support Vector Machines. Expert Syst. Appl. 2019;142 [Google Scholar]
- 65.Ye F., Lou X., Sun L. An improved chaotic fruit fly optimization based on a mutation strategy for simultaneous feature selection and parameter optimization for SVM and its applications. PLoS One. 2017;12 doi: 10.1371/journal.pone.0173516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.D. Wolpert, W. Macready, Macready, W.G.: No Free Lunch Theorems for Optimization. IEEE Transactions on Evolutionary Computation 1(1), 67-82, Evolutionary Computation, IEEE Transactions on, 1 (1997) 67-82.
- 67.J. Liang, B. Qu, P. Suganthan, Problem definitions and evaluation criteria for the CEC 2014 special session and competition on single objective real-parameter numerical optimization, 2013.
- 68.García S., Fernández A., Luengo J., Herrera F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inf. Sci. 2010;180:2044–2064. [Google Scholar]
- 69.Derrac J., García S., Molina D., Herrera F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011;1:3–18. [Google Scholar]
- 70.Huynh-Thu Q., Ghanbari M. Scope of validity of PSNR in image/video quality assessment. Electron. Lett. 2008;44:800–801. [Google Scholar]
- 71.Wang Z., Bovik A., Sheikh H.R., Simoncelli E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2014;13:600–612. doi: 10.1109/tip.2003.819861. [DOI] [PubMed] [Google Scholar]
- 72.Zhang L., Zhang L., Mou X., Zhang D. FSIM: A Feature SIMilarity index for image quality assessment. Image Processing, IEEE Transactions on. 2011;20:2378–2386. doi: 10.1109/TIP.2011.2109730. [DOI] [PubMed] [Google Scholar]
- 73.Liu Y., Yang C., Sun Q. Thresholds Based Image Extraction Schemes in Big Data Environment in Intelligent Traffic Management. IEEE Trans. Intell. Transp. Syst. 2021;22:3952–3960. [Google Scholar]
- 74.Mousavirad S.J., Oliva D., Chakrabortty R., Zabihzadeh D., Hinojosa S. Population-based self-adaptive Generalised Masi Entropy for image segmentation: A novel representation. Knowl.-Based Syst. 2022;108610 [Google Scholar]
- 75.Ning G. Two-dimensional Otsu multi-threshold image segmentation based on hybrid whale optimization algorithm. Multimed. Tools Appl. 2022 [Google Scholar]
- 76.Nama S. A novel improved SMA with quasi reflection operator: Performance analysis, application to the image segmentation problem of Covid-19 chest X-ray images. Appl. Soft Comput. 2022;118 [Google Scholar]
- 77.Vijh S., Saraswat M., Kumar S. Automatic multilevel image thresholding segmentation using hybrid bio-inspired algorithm and artificial neural network for histopathology images. Multimed. Tools Appl. 2022 [Google Scholar]
- 78.Qi A., Zhao D., Yu F., Heidari A.A., Wu Z., Cai Z., Alenezi F., Mansour R.F., Chen H., Chen M. Directional mutation and crossover boosted ant colony optimization with application to COVID-19 X-ray image segmentation. Comput. Biol. Med. 2022;148 doi: 10.1016/j.compbiomed.2022.105810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Aranguren I., Valdivia A., Morales-Castañeda B., Oliva D., Abd Elaziz M., Perez-Cisneros M. Improving the segmentation of magnetic resonance brain images using the LSHADE optimization algorithm. Biomed. Signal Process. Control. 2021;64 [Google Scholar]
- 80.Renugambal A., Selva Bhuvaneswari K. Kapur’s Entropy based Hybridised WCMFO Algorithm for Brain MR Image Segmentation. IETE J. Res. 2021:1–20. [Google Scholar]
- 81.H.S. Naji Alwerfali, M. A. A. Al-qaness, M. Abd Elaziz, A.A. Ewees, D. Oliva, S. Lu, Multi-Level Image Thresholding Based on Modified Spherical Search Optimizer and Fuzzy Entropy, Entropy, 2020. [DOI] [PMC free article] [PubMed]
- 82.Ding G., Dong F., Zou H. Fruit fly optimization algorithm based on a hybrid adaptive-cooperative learning and its application in multilevel image thresholding. Appl. Soft Comput. 2019;84 [Google Scholar]
- 83.Yue X., Zhang H. Improved Hybrid Bat Algorithm with Invasive Weed and Its Application in Image Segmentation. Arab. J. Sci. Eng. 2019;44 [Google Scholar]
- 84.Jun L.U.O., Yongsong Y., Baoyu S.H.I. Multi-threshold Image Segmentation of 2D Otsu Based on Improved Adaptive Differential Evolution Algorithm. J. Electron. Inf. Technol. 2019;41:2017–2024. [Google Scholar]
- 85.Zhou Y., Yang X., Ling Y., Zhang J. Meta-heuristic moth swarm algorithm for multilevel thresholding image segmentation. Multimed. Tools Appl. 2018;77:23699–23727. [Google Scholar]
- 86.Kotte S., Pullakura R.K., Injeti S.K. Optimal multilevel thresholding selection for brain MRI image segmentation based on adaptive wind driven optimization. Measurement. 2018;130:340–361. [Google Scholar]
- 87.Abutaleb A.S. Automatic thresholding of gray-level pictures using two-dimensional entropy. Computer Vision, Graphics, and Image Processing. 1989;47:22–32. [Google Scholar]
- 88.Otsu N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979;9:62–66. [Google Scholar]
- 89.Kapur J.N., Sahoo P.K., Wong A.K.C. A new method for gray-level picture thresholding using the entropy of the histogram. Computer Vision, Graphics, and Image Processing. 1985;29:273–285. [Google Scholar]
- 90.B. Coll, J.-M. Morel, A non-local algorithm for image denoising, 2005.
- 91.Coll B., Morel J.-M. A Review of Image Denoising Algorithms, with a New One. SIAM Journal on Multiscale Modeling and Simulation. 2005;4 [Google Scholar]
- 92.Shen L., Chen H., Yu Z., Kang W., Zhang B., Li H., Yang B., Liu D. Evolving support vector machines using fruit fly optimization for medical data classification. Knowl.-Based Syst. 2016;96:61–75. [Google Scholar]
- 93.Zhang X., Xu Y., Yu C., Heidari A.A., Li S., Chen H., Li C. Gaussian mutational chaotic fruit fly-built optimization and feature selection. Expert Syst. Appl. 2020;141 [Google Scholar]
- 94.Huang H., Feng X.A., Zhou S., Jiang J., Chen H., Li Y., Li C. A new fruit fly optimization algorithm enhanced support vector machine for diagnosis of breast cancer based on high-level features. BMC Bioinf. 2019;20 doi: 10.1186/s12859-019-2771-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Xu S., He Q., Tao S., Chen H., Chai Y., Zheng W. Pig Face Recognition Based on Trapezoid Normalized Pixel Difference Feature and Trimmed Mean Attention Mechanism. IEEE Trans. Instrum. Meas. 2023;72:1–13. [Google Scholar]
- 96.Jin K., Yan Y., Wang S., Yang C., Chen M., Liu X., Terasaki H., Yeo T.-H., Singh N.G., Wang Y. iERM: An Interpretable Deep Learning System to Classify Epiretinal Membrane for Different Optical Coherence Tomography Devices: A Multi-Center Analysis. J. Clin. Med. 2023;12:400. doi: 10.3390/jcm12020400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Lv Z., Yu Z., Xie S., Alamri A. Deep learning-based smart predictive evaluation for interactive multimedia-enabled smart healthcare. ACM Trans. Multimedia Comput. Commun. Appl. (TOMM) 2022;18:1–20. [Google Scholar]
- 98.Zhang X., Huang D., Li H., Zhang Y., Xia Y., Liu J. Self-training maximum classifier discrepancy for EEG emotion recognition. CAAI Trans. Intell. Technol. 2023 [Google Scholar]
- 99.Xie X., Xie B., Xiong D., Hou M., Zuo J., Wei G., Chevallier J. New theoretical ISM-K2 Bayesian network model for evaluating vaccination effectiveness. J. Ambient Intell. Hum. Comput. 2022:1–17. doi: 10.1007/s12652-022-04199-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Lai X., Yang B., Ma B., Liu M., Yin Z., Yin L., Zheng W. An Improved Stereo Matching Algorithm Based on Joint Similarity Measure and Adaptive Weights. Appl. Sci. 2022;13:514. [Google Scholar]
- 101.Han X., Liu Q., Wang H., Wang L. Novel Fruit Fly Optimization Algorithm with Trend Search and Co-evolution. Knowl.-Based Syst. 2017;141 [Google Scholar]
- 102.Zhang Y., Cui G., Wu J., Pan W.-T., He Q. A Novel Multi-scale Cooperative Mutation Fruit Fly Optimization Algorithm. Knowl.-Based Syst. 2016;114 [Google Scholar]
- 103.Hu R., Wen S., Zeng Z., Huang T. A Short-Term Power Load Forecasting Model Based on the Generalized Regression Neural Network with Decreasing Step Fruit Fly Optimization Algorithm. Neurocomputing. 2016;221 [Google Scholar]
- 104.Xie Y., He Y., Cheng A., Zhang J. Study on medical image enhancement based on IFOA improved grayscale image adaptive enhancement. Multimed. Tools Appl. 2016;75 [Google Scholar]
- 105.Li M.-W., Geng J., Han D.-F., Zheng T.-J. Ship motion prediction using dynamic seasonal RvSVR with phase space reconstruction and the chaos adaptive efficient FOA. Neurocomputing. 2015;174 [Google Scholar]
- 106.Wang W., Liu X. Melt Index Prediction by Least Squares Support Vector Machines with an Adaptive Mutation Fruit Fly Optimization Algorithm. Chemom. Intel. Lab. Syst. 2014;141 [Google Scholar]
- 107.Shan D., Cao G., Dong H. LGMS-FOA: An Improved Fruit Fly Optimization Algorithm for Solving Optimization Problems. Math. Probl. Eng. 2013;2013 [Google Scholar]
- 108.A. Lin, Q. Wu, A.A. Heidari, Y. Xu, H. Chen, W. Geng, Y. Li, C. Li, Predicting Intentions of Students for Master Programs Using a Chaos-Induced Sine Cosine-Based Fuzzy K-Nearest Neighbor Classifier, IEEE Access, PP (2019) 1-1.
- 109.Hongwei L., Jianyong L., Liang C., Jingbo B., Yangyang S., Kai L. Chaos-enhanced moth-flame optimization algorithm for global optimization. J. Syst. Eng. Electron. 2019;30:1144–1159. [Google Scholar]
- 110.Zhu A., Xu C., Li Z., Wu J., Liu Z. Hybridizing grey Wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC. Systems Engineering and Electronics, Journal of. 2015;26:317–328. [Google Scholar]
- 111.N. Kumar, I. Hussain, B. Singh, B. Panigrahi, Single Sensor-Based MPPT of Partially Shaded PV System for Battery Charging by Using Cauchy and Gaussian Sine Cosine Optimization, IEEE Transactions on Energy Conversion, PP (2017) 1-1.
- 112.Lu C., Gao L., Yi J. Grey wolf optimizer with cellular topological structure. Expert Syst. Appl. 2018;107:89–114. [Google Scholar]
- 113.Sun Y., Wang X., Chen Y., Liu Z. A modified whale optimization algorithm for large-scale global optimization problems. Expert Syst. Appl. 2018;114:563–577. [Google Scholar]
- 114.Nenavath H., Jatoth R.K. Hybridizing sine cosine algorithm with differential evolution for global optimization and object tracking. Appl. Soft Comput. 2018;62:1019–1043. [Google Scholar]
- 115.Elsayed Abd Elaziz M., Oliva D., Xiong S. An improved opposition-based sine Cosine algorithm for global optimization. Expert Syst. Appl. 2017;90 [Google Scholar]
- 116.Liu G., Jia W., Wang M., Heidari A.A., Chen H., Luo Y., Li C. Predicting Cervical Hyperextension Injury: A Covariance Guided Sine Cosine Support Vector Machine. IEEE Access. 2020;8:46895–46908. [Google Scholar]
- 117.Liu L., Zhao D., Yu F., Heidari A.A., Ru J., Chen H., Mafarja M., Turabieh H., Pan Z. Performance optimization of differential evolution with slime mould algorithm for multilevel breast cancer image segmentation. Comput. Biol. Med. 2021;138 doi: 10.1016/j.compbiomed.2021.104910. [DOI] [PubMed] [Google Scholar]
- 118.Chen X., Tianfield H., Mei C., Du W., Liu G. Biogeography-based learning particle swarm optimization. Soft. Comput. 2017;21:7519–7541. [Google Scholar]
- 119.Xu Y., Chen H., Luo J., Zhang Q., Jiao S., Zhang X. Enhanced Moth-flame optimizer with mutation strategy for global optimization. Inf. Sci. 2019;492:181–203. [Google Scholar]
- 120.Qu C., Zeng Z., Dai J., Yi Z., He W. A modified Sine-Cosine algorithm based on neighborhood search and greedy levy mutation. Comput. Intell. Neurosci. 2018;2018:1–19. doi: 10.1155/2018/4231647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Zhao S., Wang P., Heidari A.A., Chen H., Turabieh H., Mafarja M., Li C. Multilevel threshold image segmentation with diffusion association slime mould algorithm and Renyi's entropy for chronic obstructive pulmonary disease. Comput. Biol. Med. 2021;134 doi: 10.1016/j.compbiomed.2021.104427. [DOI] [PubMed] [Google Scholar]
- 122.Gao H., Kwong S., Yang J., Cao J. Particle swarm optimization based on intermediate disturbance strategy algorithm and its application in multi-threshold image segmentation. Inf. Sci. 2013;250:82–112. [Google Scholar]
- 123.Osuna-Enciso V.N., Cuevas E., Sossa H. A comparison of nature inspired algorithms for multi-threshold image segmentation. Expert Syst. Appl. 2013;40:1213–1219. [Google Scholar]
- 124.C. Zhao, H. Wang, H. Chen, W. Shi, Y. Feng, JAMSNet: A Remote Pulse Extraction Network Based on Joint Attention and Multi-Scale Fusion, IEEE Transactions on Circuits and Systems for Video Technology, (2022) 1-1.
- 125.Wang S., Wang B., Zhang Z., Heidari A.A., Chen H. Class-aware sample reweighting optimal transport for multi-source domain adaptation. Neurocomputing. 2023;523:213–223. [Google Scholar]
- 126.Xue X., Li G., Zhou D., Zhang Y., Zhang L., Zhao Y., Feng Z., Cui L., Zhou Z., Sun X. Research Roadmap of Service Ecosystems: A Crowd Intelligence Perspective, International Journal of Crowd. Science. 2022;6:195–222. [Google Scholar]
- 127.Chen Y., Gan H., Chen H., Zeng Y., Xu L., Heidari A.A., Zhu X., Liu Y. Accurate iris segmentation and recognition using an end-to-end unified framework based on MADNet and DSANet. Neurocomputing. 2023;517:264–278. [Google Scholar]
- 128.Li Y., Zhang Y., Cui W., Lei B., Kuang X., Zhang T. Dual Encoder-Based Dynamic-Channel Graph Convolutional Network With Edge Enhancement for Retinal Vessel Segmentation. IEEE Trans. Med. Imaging. 2022;41:1975–1989. doi: 10.1109/TMI.2022.3151666. [DOI] [PubMed] [Google Scholar]
- 129.Xue X., Yu X.-N., Zhou D.-Y., Wang X., Zhou Z.-B., Wang F.-Y. Computational Experiments: Past. Present and Future. 2022 arXiv preprint arXiv:2202.13690. [Google Scholar]
- 130.Xue X., Yu X., Zhou D., Peng C., Wang X., Liu D., Wang F.-Y. Computational Experiments for Complex Social Systems—Part III: The Docking of Domain Models. IEEE Trans. Comput. Social Syst. 2023 [Google Scholar]
- 131.Cao X., Cao T., Xu Z., Zeng B., Gao F., Guan X. Resilience Constrained Scheduling of Mobile Emergency Resources in Electricity-Hydrogen Distribution Network. IEEE Trans. Sustainable Energy. 2022:1–15. [Google Scholar]
- 132.Dai Y., Wu J., Fan Y., Wang J., Niu J., Gu F., Shen S. MSEva: A musculoskeletal rehabilitation evaluation system based on EMG signals. ACM Trans. Sens. Netw. 2022;19:1–23. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.