Pore formation driven by particle impact in laser powder-blown directed energy deposition

Abstract

Process defects currently limit the use of metal additive manufacturing (AM) components in industries due to shorter fatigue life, potential for catastrophic failure, and lower strength. Conditions under which these defects form, and their mechanisms, are starting to be analyzed to improve reliability and structural integrity of these highly customized parts. We use in situ, high-speed X-ray imaging in conjunction with a high throughput laser, powder-blown directed energy deposition setup to observe powder particle impact behavior within the melt pool. Through fundamental observations of the stochastic, violent powder delivery in powder-blown DED, we uncover a unique pore formation mechanism. We find that a pore can form due to air-cushioning, where vapor from the carrier gas or environment is entrapped between the solid powder particle surface and liquid melt pool surface. A critical time constant is established for the mechanism, and X-ray computed tomography is used to further analyze and categorize the new type of “air-cushioning” pores. It is shown that the air-cushioning mechanism can occur under multiple laser processing conditions, and we show that air-cushioning pores are more likely to be formed when powder particles are larger than 70 $\mathrm{\mu }$m. By quantifying the effect of powder particle impact, we identify new avenues for development of high-quality laser, powder-blown DED products. Furthermore, we deepen knowledge on defect formation in metal additive manufacturing, which is being increasingly utilized in high performance situations such as aerospace, automotive, and biomedical industries.

Significance Statement:

We discover a unique pore formation mechanism caused by air-cushioning during solid particle impact on the liquid melt pool surface in a powder-blown additive manufacturing process. This phenomenon cannot be mitigated by simply modulating energy density used in the process, which is effective in dealing with currently accepted pore formation mechanisms such as keyholing and lack of fusion. We derive a critical time constant as a function of powder particle diameter for the existence of this mechanism, and we analyze physics that dominate during powder particle entrance into the melt pool. By understanding the significance of powder particle size and speed in entrance behavior, we identify critical process parameters that must be considered for development of higher quality parts.

Introduction

Laser directed energy deposition (DED) is an additive manufacturing (AM) process that possesses several attractive characteristics. Its high manufacturing speed is suitable for large-scale, structural components such as in aerospace and marine construction. In the biomedical and automotive industries, the need for light-weighting, customization of material properties, and optimized geometry is met through functionally graded materials. Finally, DED exhibits high process flexibility for surface coating, repairing, and re-manufacturing which improves sustainability of manufacturing processes through re-use (1–3). A powder-blown DED process consists of a powder nozzle and a laser that move as one processing head. The laser creates a melt pool on a substrate, or previously deposited layer, where the blown metal powders impact, melt (fully or partially), and coalesce to deposit new materials; the melt pool solidifies into a clad as it moves where sequentially deposited clads create a 3D part (4). Here, DED will refer to the laser, powder-blown DED process. While this AM technique has shown to be critical in the advancement of multiple industries, current limitations exist which affect its strength and fatigue life such as residual pores (5).

It is well understood that the formation of pores within the melt pool during laser welding (6) can be detrimental to the integrity of the final part. Extending this knowledge to laser AM, pore formation and pore characterization have been studied critically for DED (7–9). The most rigorously studied pore types in AM are keyhole and lack of fusion pores. These pore types have been related to energy density, the measure of energy per volume, that is transferred to the material from the laser (10). A keyhole is an unstable, deep vapor depression formed at high energy densities; chaotic motion of the keyhole can lead to its collapse which forms keyhole pores that are trapped near the bottom of the melt pool by the solidification line (11). Lack of fusion pores arise because of insufficient melting (low energy density) between subsequent layers in the laser AM process, which leads to long, irregular pores (12). Since these two mechanisms lie on opposite sides of the processing window represented by energy density, it is a common practice to define the “good” or optimal processing region in laser AM as the boundary between these two mechanisms. Therefore, a point should exist where pore formation is minimal with respect to energy density given the lack of fusion and keyholing regions (13). This hypothesis has resulted in a multitude of process parameter studies for various materials in DED. However, there are other pore formation mechanisms not captured by energy density such as pores introduced from powder, pores induced by particle movement, and pores induced by gas delivered to the melt pool (14). Pore formation mechanisms that have been proposed for DED are typically based on direct observations of only the top surface of the melt pool through highspeed imaging (15, 9) or analyzed post-process through X-ray computed tomography (CT) (7). These techniques can be used to observe surface defects or residual pores, respectively, but neither can capture direct observation of pore formation that occurs below the melt pool surface within the built part.

This paper describes the discovery of a new pore formation mechanism that is directly connected to powder particle impact on the liquid melt pool, where vapor from the carrier gas or environmental gas is entrapped between the solid powder particle surface and liquid melt pool surface. We uncover this unique pore formation mechanism in DED through high-speed, in situ X-ray imaging, a technique that enables observation of fundamental phenomena in metal AM processes due to high temporal and spatial resolutions (16–19). While pore-pushing in the melt pool (20), pores formed from irregular powder shapes and keyholes (14), and pores formed due to melt pool flow changes (21) have been identified for DED using this technique, we investigate lower energy density regions outside of the keyhole regime with near-spherical powders to mimic industrial processes as well as identify driving forces of the air-cushioning mechanism.

The high-throughput experimental setup (22, 14) consisted of a deposition stage housed in an environmental chamber and utilized a continuous-wave Gaussian beam laser, an in-house designed powder nozzle, and a commercial powder hopper delivery system, Figs. S1–S2. Single clads were deposited with Ti-6Al-4V powders in the middle of an 810 $\mathrm{\mu }$m thick sample in a straight line. Experiments were performed at various laser powers (P) for varying dilution ratios $(\frac{cladheight}{meltpooldepth})$ that avoided the keyhole region to mimic industrial DED settings. X-ray images were captured at 33 kHz (one frame is taken every 33 $\mathrm{\mu }$s) with a pixel size of 1.9 $\mathrm{\mu }$m/pixel. The powder nozzle ejected powder particles into the melt pool at 50${}^{\circ }$ from the horizontal level. The powder particles had a size range of 45–106 $\mathrm{\mu }$m with an approximately Gaussian distribution, Fig. S3. While the melt pool diameter in these experiments is limited by the penetration depth of X-rays and exposure time, the substrates are on average ten times larger than a single powder particle diameter, which minimizes boundary effects and can be used to analyze local powder-melt pool interactions.

Results and discussion

Pore formation through air-cushioning

We show through direct observation that pore formation is driven by powder particle impact in DED. In stark contrast to currently accepted process maps, our result implies that pore formation in DED does not depend solely on the energy density of the process but will also be affected by particle momentum, size, and wettability. Our direct observation confirms the existence of pore sources outside of commonly accepted mechanisms (keyholing pores, lack of fusion pores, and pre-existing pores in the powder). This distinguished mechanism was discovered to occur through the following steps: (i) melt pool surface is deformed by a particle, (ii) vapor layer is trapped between the particle and liquid surface, (iii) surrounding liquid flows back around the vapor layer and melting particle, and (iv) the particle fully melts and the vapor layer is left as a separated pore, Fig. 1. We call this pore type as air-cushioning pores, whose formation has two critical aspects: (i) vapor entrapment for which we measured the deformation of the vapor cavity due to particle impact, and (ii) the time it took for the deformed cavity to collapse. This pore formation mechanism is additionally verified and classified through X-ray computed tomography (XCT). While vapor entrapment has been proposed through simulation (23) and examined through post-process characterization (24, 25), our results reveal the mechanism to entrap vapor as air-cushioning and identifies key factors that affect the likelihood to form a pore. Furthermore, in this work, we fill a gap in the understanding of deformation of the melt pool surface due to powder particle impact.

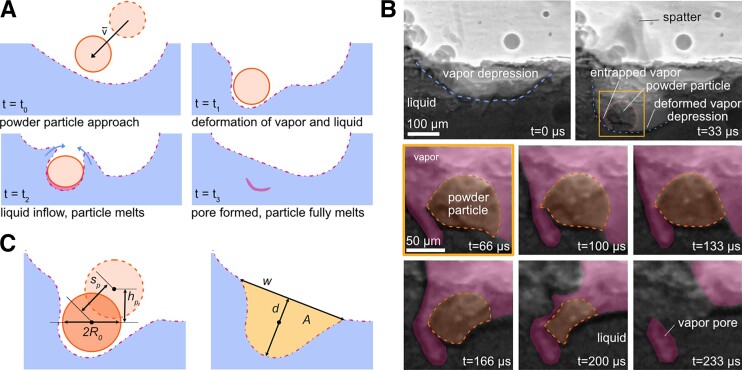
Fig. 1.

Air-cushioning pores due to particle impact on melt pool. A) A schematic of air-cushioning as observed in the X-ray images. There are four steps in air-cushioning: (i) powder particle approach, (ii) deformation of the vapor-liquid surface, (iii) liquid inflow over the partially melted particle, (iv) formation of pore when particle fully melts. B) High-speed X-ray image sequence of powder particle impacting the melt pool, where the vapor depression (blue dotted line) is deformed by an incoming powder particle (orange dotted line). Spatter from the impact is indicated as well as the entrapped vapor (pink area) at the front edge of the particle. The melting sequence of the particle shows how liquid (dark gray) flows back over the particle as it is melting, which causes the entrapped vapor to stay separated from the vapor depression. The entrapped vapor is left as a solidified pore. The original gray scale images are shown in Fig. S4. C) Dimensions associated with deformation of the liquid surface due to particle impact, defined as: powder particle diameter $(2R_0)$, powder particle displacement at angle of entrance $(s_p)$, powder particle displacement in the vertical direction $(h_p)$, width of deformation $(w)$, depth of deformation $(d)$, and area of deformation $(A)$. All dimensions were manually selected/outlined in images and measured by pixel count.

The demonstrated phenomenon of air-cushioning pores in DED can be described by physical models at two stages: (1) solid particle entrance into the liquid and (2) entrapment of vapor during impact on the liquid interface. Air-cushioning occurs during deformation of the melt pool by particle impact. Thus, we will first analyze melt pool deformation and then vapor entrapment to showcase the critical role of particle velocity and diameter at both stages. It is important to note that hydrophobic behavior (contact angle greater than 90${}^{\circ }$) between the solid particle and liquid melt pool is assumed in all presented analyses based on previous observations in particle behavior and simulations (15, 26) as well as the behavior observed in this study.

Before looking at the effect of particle velocity and diameter on deformation of the melt pool, we establish the governing forces that drive powder particle velocity as it impacts the melt pool. The particle velocity (and its displacement) as it enters the melt pool is determined by the hydrodynamic forces, $F_h$, opposing particle entrance into the liquid as well as the surface tension forces, $F_s$, once the particle contacts the liquid (27), Fig. 2. The initial impact of the particle is known as the “slamming” stage, which is driven by the particle’s kinetic energy until hydrodynamic forces oppose the motion (28)

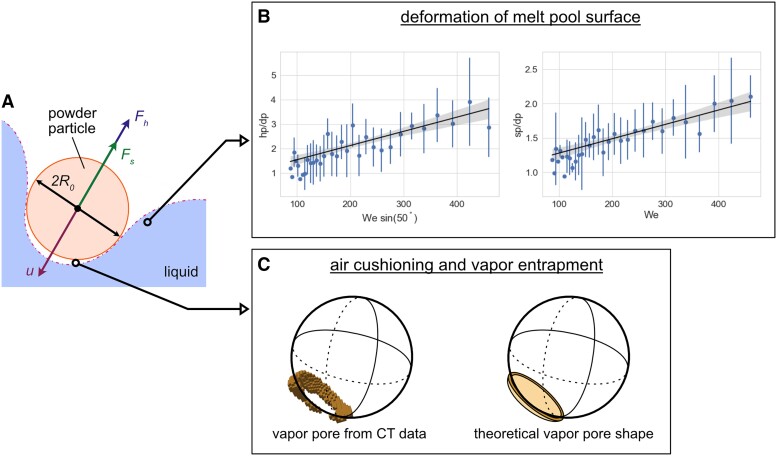
Fig. 2.

Mechanisms in powder particle impact in laser, powder-blown directed energy deposition. A) Schematic of solid powder particle impacting liquid surface, where the particle velocity $(u)$ as it impacts the surface is determined by the hydrodynamic $(F_h)$ and surface tension $(F_s)$ forces. B) The dimensionless depth and particle displacement vs. the Weber $(We)$ number. C) Comparison of air cushioning and vapor entrapment in pore from CT data and theoretical pore shape.

$$F_h=\frac{1}{2}{C}_h\left(\frac{\pi }{4}\right)R_0^2{\rho }_l{U}_0^2$$ (1)

The hydrodynamic forces, $F_h$, in this study, range from 11.5 to 26.3 mN, where the coefficient of resistance $C_h$ is estimated to be 7 based on the calculated Reynolds number for the mean particle diameter of 75 μm. If the particle has not melted during the slamming stage in DED, it will be captured by liquid surface tension forces and continue to move into the liquid (27), where

$$W_{F_s}\sim \sigma R_0{s}_p$$ (2)

Here, σ is the surface tension coefficient, $R_0$ is the particle radius, and $s_p$ is the particle displacement in the liquid. In this study, the work done by surface tension on average was 10.0 nJ and ranged from 3.41 to 32.9 nJ. We take the surface tension coefficient of Ti-6Al-4V to be 1.4 N/m at the solidus, approximately 1930 K (29). It is noted here that the oxide layer on the outside of the powder particle was not considered in our calculation. We can also compare the surface tension force

$$F_s\sim \sigma 2\pi R_0$$ (3)

to $F_h$ to determine their relative importance. $F_s$ ranged from 0.2 to 0.6 mN, which is an order of magnitude smaller than $F_h$. Therefore, particle entrance behavior was dominated by hydrodynamic forces in this study.

The depth reached by the powder particle within the melt pool, $h_p$, is ultimately determined by the balance between hydrodynamic and surface tension forces. Resulting depths of individual particles will determine the volatility of the melt pool surface as many powders are blown at once onto the melt pool surface. While the presented models and analyses have assumed a steady-state surface, a non-steady-state (or more volatile) melt pool surface could affect the penetration behavior of the powder particles. A local “wave” or “trough” from previous particle impacts could also be the initial pool state, where a powder particle will have more shallow penetration into the pool if it enters at a “wave” or deeper penetration into the pool if it enters at a “trough.” In these cases, a “wave” entrance would require more deformation for the powder particle to enter the melt pool and thus larger work by surface tension would occur; the opposite could be said for a “trough” entrance where less deformation of the surface is required. It has been shown in previous studies that the dimensionless penetration depth of the particle, or the ratio of the maximum particle depth in the liquid $h_p$ to the particle diameter $2R_0$ is proportional to the sine component of the Weber number, W, for an oblique impact (27). A non-symmetric impact (such as in this study where powder particles travelled at approximately 50${}^{\circ }$ from horizontal) will cause an imbalance of forces at the leading edge of the particle where one side of the particle will slow down faster, causing the particle to rotate further into the liquid. This relationship is seen in this study as well, Fig. 2B, where both the dimensionless penetration depth and powder particle displacement $(s_p)$ increases linearly as W increases.

Minimizing W in DED, where surface tension forces will dominate during particle entrance into the liquid rather than kinetic energy or drag forces, will minimize oscillation of the melt pool surface. Furthermore, the type of cavity formation behind the entering particle is specifically governed by W and Bond number, B, as demonstrated by (30), where the cavity type becomes larger/more dynamic as W increases. This work had a high Weber number ($W=55$–128) and low Bond number $(B=1.35\times {10}^{-5}$–$7.35\times {10}^{-5})$ in which the formation of surface seal cavities was observed, Fig. S5, and are described using a splash curtain model (30). The powder particle impact causes an expansion of the deformed vapor cavity “walls,” and there is a subsequent collapse around the particle as it melts, Movie S2. Pivotally, the particle velocity will heavily impact the cavity type that is formed and needs to be controlled for in industrial DED, where a splash curtain can possibly lead to additional spatter formation and surface defects. It is important to note, however, that the powder particle velocity must still be large enough to enter the vapor flow above the irradiated laser area, and that laser shielding from powder particles are an additional factor in the development of the melt pool surface (31).

In all, the impact of particle velocity is evidenced through the Weber number, which is the ratio of inertia to surface tension, and hydrodynamic forces that slow down the particle during the “slamming” stage. The Weber number increases with the square of the velocity of the powder particle; thus, as particle velocity increases, inertia of the powder particle will dominate over surface tension forces. Similarly, an increase in powder particle velocity will exponentially increase the hydrodynamic forces $F_h$ that are slowing down the particle, where $F_h\sim U_0^2$. Finally, the vapor trapped beneath a powder particle scales by $r_p\sim U_0^{-1/3}$ where a decrease in velocity will lead to a larger trapped vapor disk. Powder particle velocities measured in this study can be found in Fig. S18.

In addition to deforming the liquid surface, it is evident that vapor can be trapped at the front edge of a particle during its impact. We propose that this occurs through air cushioning, where the free-surface deformation of the liquid traps a pocket of air underneath the center of the sphere (32). This is governed by lubrication theory (with the assumption that the viscosity and density ratios are large between the gas and liquid) where a thin film between the solid particle and liquid surface is squeezed, and the pressure increases in the layer as the gap becomes smaller. Upon contact with the liquid surface, a ring of maximum pressure forms at the solid–liquid boundary of the entering sphere (forming a thin vapor disk) and the vapor is prevented from escaping (33). An ideal trapped vapor pocket would, thus, be a thin disk wrapped around the curvature of the entering sphere. The entrapped vapor pocket with perfect shape predicted by theory is unlikely to be observed in DED due to the following reasons: (i) contact of the powder particle with the molten pool will immediately begin to melt the particle, (ii) the melt pool surface oscillates randomly as other powders hit it, and (iii) surface irregularities on the powder particle could lead to uneven melting and/or pressure distributions within the vapor layer. A theoretical vapor pocket is compared to one from CT data in Fig. 2C, where the real vapor pocket is a thin, annular disk. Further examples of air-cushioning pores from XCT data show incomplete and warped disks that could arise from local oscillations of the melt pool surface, Fig. S6.

Hicks et al. determined the radius of the trapped vapor disk $(r_p)$ scales by

$$r_p=K{\left(\frac{4{\mu }_g}{{\rho }_l{U}_0}\right)}^{1/3}{R}_0^{2/3}$$ (4)

which depends on the initial sphere radius $R_0$, gas dynamic viscosity ${\mu }_g$, liquid density ${\rho }_l$, and particle entrance speed $U_0$, and a scaling factor K (33). This relationship shows that the entrapped vapor volume is proportional to $R_0^{2/3}$ and is inversely proportional to the approach speed, meaning larger impacting particles moving more slowly will trap the most vapor through air-cushioning. A value of $K=14$ was calculated considering an average particle size of 75 μm and an average volume of 9,500 $\mathrm{\mu }{\mathrm{m}}^3$ of an air-cushioning pore, which is on the same order as previous experiments with acryl disks impacting water (32). Our calibrated model based on a spherical particle can be used to predict pore volume for different powder particle diameters based on the powder particle size distribution. In this work, it is predicted that the volume of air-cushioning pores will range between 3,400 and 18,000 $\mathrm{\mu }{\mathrm{m}}^3$ based on a powder particle size distribution between 45 and 106 $\mathrm{\mu }$m. The XCT data confirm that the majority of categorized entrapped vapor pores fall in this range, as shown in Fig. S7. It is noted, however, that this analytical model does not consider surface tension forces, which will be applicable to the microspheres used in DED when considering the formation of the solid–liquid boundary trapping the vapor. Additionally, this model does not consider the rotation of particles which could contribute to the formation of a vapor boundary layer between the solid powder particle and liquid, where an increase in the rotation of the particle will lead to vapor being more readily trapped due to friction of the powder particle’s surface dragging vapor into the melt. The average volume of an air-cushioning pore was 9,500 $\mathrm{\mu }{\mathrm{m}}^3$ in this study, which is on the order of air-cushioning pores in other solid microsphere and droplet experiments (34, 35). However, this value is five times larger than a trapped vapor volume of 1,000 $\mathrm{\mu }{\mathrm{m}}^3$ modeled by the authors of (32). This difference is attributed to the neglect of surface tension effects in (32).

A critical step in air-cushioning pore entrapment by particle impact is the collapse time, $t_c$, which is defined here as the time it takes for the molten pool to fill back in the depression that the particle created, Fig. 1B. During the collapse time, the particle is partially or fully melted depending on the particle diameter and local temperature of the melt pool. The collapse time is dependent on the diameter of the particle due both to melting time and surface area that the liquid must re-fill. For the vapor to be readily trapped beneath the particle after impact, $t_c\ll t_{melt}$, where the particle melt time, $t_{melt}$, was calculated assuming heat conduction as the primary mode of heat transfer (26). Particle melt times were theoretically calculated since the density differences between the liquid and partially liquid particle are indistinguishable in X-ray once the powder particle is covered by liquid during back-flow. Treating the particle as a point heat sink in a hemi-spherically symmetric infinite domain and using classic diffusion equation solutions (36), $t_{melt}$ can be taken as

$$t_{melt}=\frac{1}{4\pi \alpha }{\left(\frac{8}{3}\pi r^3\frac{T_{0,pool}-T_{0,part}}{T_{0,pool}-T_m}\right)}^{2/3}$$ (5)

where α is the thermal diffusivity, $T_{0,pool}$ is the local temperature of the melt pool, $T_{0,part}$ is the starting temperature of the particle, and $T_m$ is the melting temperature of the material. Considering the particle melt time at four different melt pool temperatures and particle diameters from 45 to 106 $\mathrm{\mu }$m, the time to fully melt the particle, $t_{melt}$, ranged from 300 to 3,500 $\mathrm{\mu }$s while the measured collapse time, $t_c$, ranged from $30\pm 10$ to $270\pm 10$$\mathrm{\mu }$s. We show that $t_c$ is an order of magnitude shorter than $t_{melt}$, Fig. 3. This establishes and meets the condition in which liquid can flow back over the particle before it melts, effectively separating the entrapped vapor from the open, inert environment and trapping the air-cushioning pore within the liquid, molten pool. It is noted here that $t_{melt}$ is calculated as a minimum melting time where the powder particle is surrounded by the melt pool, meaning that a powder particle will typically have an even longer melt time when only partially in contact with the melt pool.

Fig. 3.

A) Collapse time, $t_c$, as a function of particle diameter, where the liquid flows back in over the particle and fills the depression the particle made during impact. B) Estimated particle melt time, $t_{melt}$, as a function of particle diameter and melt pool temperature assuming the primary mode of heat transfer between the melt pool and particle is conduction. Note $t_c\ll t_{melt}$ enables the discovered mechanism for forming air-cushioning pores.

Pore formation under different processing conditions

The percentage of pores formed through air-cushioning was estimated through a 3D size and shape analysis of the fully enclosed pores as identified through XCT of a DED specimen for each laser condition (37, 38), Figs. S14 and S16. Considering adequate resolution of size and shape, pores with a volume greater than 1,400 $\mathrm{\mu }{\mathrm{m}}^3$ measured by XCT were separated into three categories based on their shape and orientation: pores from powder (spherical, S), lack of fusion (non-spherical and irregular, NS), and air-cushioning (flat and oriented, VP), Fig. 4. Three characteristic lengths were defined for each pore based on the dimensions of a rotated bounding-box that was fitted to each pore. The three orthogonal lengths of the bounding box were denoted as the length (L), width (W), and thickness (T). Enclosed pores were categorized as spherical or non-spherical based on their sphericity. Non-spherical pores were further investigated to determine which of these pores could be categorized as entrapped vapor based primarily on their flatness [i.e. their (W/T) ratio] and their orientation relative to the powder-flow direction, Fig. S8. Further criteria to ascertain the vapor pores consider the range of possible shapes for air-cushioning pores, as illustrated in Fig. S9.

Fig. 4.

Representative 3D image from X-ray CT showing the three categories of pore types: spherical (S), nonspherical (NS), and entrapped vapor (VP). Solid material consisting of melted and un-melted powder particles is shown in translucent gray. One example of each pore type is shown: spherical pores are shown in green, non-spherical pores are shown in blue, and vapor pores are shown in yellow. The categorization of pore types shows that air-cushioning pores can have a significant impact on the overall porosity of a sample.

A total of 2,260 pores were identified across the considered specimens: 14% (309) were pores from powder, 78% (1771) were lack of fusion pores, and 8% (180) were air-cushioning, Fig. S7. While the majority of pores were due to lack of fusion, the air-cushioning pores occur at the same rate as powder-borne pores, which are a known issue in industrial DED (24). The median pore volume for the powder-borne pores and lack of fusion pores were comparable at approximately 3,500 $\mathrm{\mu }{\mathrm{m}}^3$ while the air-cushioning pores had a much larger median volume of approximately 9,500 $\mathrm{\mu }{\mathrm{m}}^3$, Fig. S7. While there were fewer air-cushioning pores than powder-borne pores or lack of fusion pores, the larger average size and irregular shapes of the air-cushioning pores could be a detriment to the fatigue life of a DED part (5). While pore spherization and release was observed, Movie S1, it was very infrequent and was only observed twice out of approximately two hundred powder particle impact cases. The porosity for each specimen analyzed via XCT was additionally calculated, where the porosity had a decreasing trend from 0.91 to 0.66% as the laser power increased from 350 to 500 W, Fig. S10. This calculated porosity is on the same order as a millimeter-scale DED part, which is typically less than 1.0% (39). This reduction in porosity implies that pores were released through buoyancy forces or less lack of fusion pores were formed as the energy density increased within the laser power range without keyhole pores being formed.

The relative rate of pore release for each pore type can be established through the change in total pore volume, number of pores for each pore type, and processing condition, Fig. S7. There was an increase in the number of pores and total pore volume for both powder-borne pores and lack of fusion pores when the laser power was increased from 350 to 410 W; this is due to more powder being deposited with the increased available energy. When the laser power is increased from 410 to 500 W, however, there is a decrease in both the number of pores and the total pore volume for the powder-borne and lack of fusion pores. Higher energy density leads to more fully melted particles, which prevents lack of fusion between powder particles. Higher energy density also leads to the release of powder-borne pores by (i) fully melting a particle at the top surface of the melt pool where the pore is immediately released into the environment and (ii) buoyancy forces, where powder-borne pores have more time to rise out of the melt pool with a larger melt volume. Note that the average melt pool depth (measured from the substrate top to the deepest point of the pool, Fig. S15) was 161, 236, and 337 $\mathrm{\mu }$m for laser powers 350, 410, and 500 W, respectively, as shown in Fig. S17. For air-cushioning pores, pore release within the melt pool is much less likely to occur because they form closer to the bottom of the melt pool and can become quickly trapped in solidification. Within the studied processing regions, there is no significant change in the number or total volume of air-cushioning pores. This indicates that the rate of release of air-cushioning pores is much slower than that of powder-borne and lack of fusion pores with increasing energy density, which is why powder particle size and velocity need to be considered in DED pore formation.

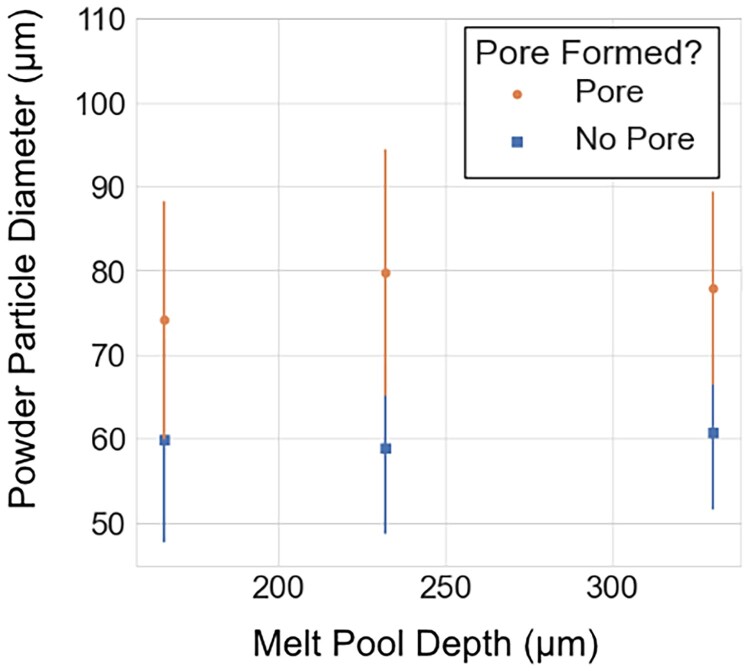
While lack of fusion pore formation is clearly linked to laser energy density, pore formation through particle impact can occur over a range of processing conditions. A total of 230 instances of visible particle impact were identified across the three laser power conditions. Pores were formed in 105 instances or 46% of the impacts. A careful investigation of the effect of powder diameter on the formation of pores, as illustrated in Fig. 5, revealed that air-cushioning pores were more likely to be formed at larger powder particle diameters. On average, air-cushioning pores were more likely to be formed when a particle’s diameter was above 70 $\mathrm{\mu }$m due to its longer melting time and larger surface area to entrap vapor. Pore formation that is driven by particle impact is an important distinction from previously accepted pore formation models that only consider the laser processing parameters (e.g. laser power, scan speed, beam diameter) and the pre-existing pores inside the feedstock powder. Moreover, it is evident that it is important to consider particle size and velocity, i.e. momentum, in addition to the more commonly used parameter “powder flowrate” (41).

Fig. 5.

Air-cushioning pore formation under different processing conditions. Air-cushioning pores were more likely to be formed at larger powder particle diameters. A binomial logistic regression model (40) was used to determine the mean particle diameter in which a pore was formed or not formed. Error bars indicate standard deviation of powder particle diameter. The 95% confidence interval of the logistic regression models are shown in Fig. S11.

Deformation of the melt pool liquid–vapor surface

Visualization of the deformation of the melt pool liquid–vapor line with respect to individual particle impact has not been observed directly or quantified experimentally until this work. The depth of deformation $(d)$ ranged from 50 to 230 $\mathrm{\mu }$m, and the width of deformation $(w)$ ranged from 75 to 310 $\mathrm{\mu }$m, Fig. 6A and B, Fig. S13. Both dimensions were measured when the particle was no longer moving into the fluid along its flight path, where the deformation should be close to its maximum. We found that while the width of deformation $(w)$ was linearly correlated with the powder particle’s diameter $(2R_0)$, the depth of deformation $(d)$ was not well correlated, Fig. 6A and B. Since deformation measurements are performed from a side-view, $(w)$ is the projected side-view of the “diameter” of the dimple-like deformation created in the liquid–vapor surface. It is expected from geometry that the diameter of the deformed liquid–vapor surface will linearly increase as the diameter of the particle becomes larger, as in Fig. 6A. The depth that the powder particle reaches, however, is not solely dependent on powder particle size, as shown in the low correlation in Fig. 6B. As discussed previously, the characteristic velocity and mass of the powder particle will determine its hydrodynamic behavior, which may play larger roles in the depth reached than the particle size itself. For spherical particles, melt pool surface deformation is ultimately governed by the incoming particle’s kinematic momentum compared to the work needed to deform the liquid metal, which is dependent on the density and surface tension properties (surface tension coefficient, liquid temperature, contact angle, advancing contact angle). Therefore, the work of deformation is correlated with the displacement of the liquid surface, which is quantified here by the deformation area, Fig. 6C.

Fig. 6.

Deformation of the liquid surface through particle impact as a function of particle diameter at a laser power of 500 W. Error bars indicate standard deviation of measurements, single data points indicate only one measurement was available. Black, dashed line shows linear regression fit. A) Width of vapor cavity $(w)$ by single particle impact. B) Depth of vapor cavity $(d)$ created by single particle impact. C) Total area of deformation $(A)$ due to single powder particle impact. Definitions of measurements are shown in Fig. 1. The deformation area increased with particle diameter but the aspect ratio remained constant, Fig. S12. Other laser power cases are shown in Fig. S13 with similar trends.

While the melt pool surface deformation increased with particle diameter, the aspect ratio $(\frac{depth}{width})$ of the deformation area is found to remain between 1.4 and 1.5 in all instances of particle impact, Fig. S12. This ratio is thought to be due to the characteristic sizes and velocities of the particles, which determine the behavior of the surrounding liquid during entry of the solid particle into the liquid, as in (30). Nonlinear behavior of the melt pool surface in this work thus consists of stochastic, non-uniform waviness due to many impacting powder particles (42). The significance of impinging powder particles becomes evident when considering melt pool flow pattern (43), which is typically driven by Marangoni convection. We have shown that local deformation of the melt pool surface can be greater than 100 $\mathrm{\mu }$m, Fig. 6; therefore, flow driven by Marangoni convection can be interrupted if the melt pool depth is within this order of magnitude. For example, the particle impact depth reached 125 $\mathrm{\mu }$m with a melt pool depth of 500 $\mathrm{\mu }$m and a particle distribution size of 45–105 $\mathrm{\mu }$m for Ti-6Al-4V, which could influence thermal conditions significantly in the DED process.

Mitigating air-cushioning pores in industrial-scale depositions

While most air-cushioning pores identified in this study were small in volume, the pores could coalesce and become spherical within a much larger molten pool on the scale of millimeters, if not immediately trapped by the solidification front. Additionally, powder particles impacting a deeper melt pool can become submerged, and the vapor cavity behind the particle in the liquid can collapse. It is evident from previous discussions that the particle size distribution common to DED processes will affect the observed pore formation mechanisms. While the presented mechanism was demonstrated with Ti-6Al-4V, it is expected to occur during processing of many DED materials since powder particles are similar in shape, size, and roughness; however, the powder particle entrance behavior could be different if the material has a significant difference in surface tension properties. There are a few ways that the entrapment of air-cushioning pores could be controlled: (i) changes to the solid–liquid surface tension coefficient between the powder and melt pool (e.g. surface coatings on powders), (ii) speed of the particles as they impact the melt pool, and (3) diameter of the powder particles. Controlling both the speed and size of the powder particles will be most effective, where smaller, slower moving particles will both decrease the melt pool surface deformation, more rapidly incorporate powders, and decrease the chance of vapor entrapment. Additionally, current energy density models for DED consider only formulations of energy and/or mass input. While these models have been correlated to pore content, a more holistic energy density model or process parameter model is needed considering the importance of powder flow with respect to powder particle size and speed. In all, the discovery of air-cushioning and its entrapment through powder particle impact is crucial to the development of powder-blown processes, and the driving forces in this mechanism need to be considered in future implementation of DED to advance the quality of produced parts.

Supplementary material

Supplementary material is available at PNAS Nexus online.

Funding

This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science user facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. This research was also funded by the Center for Hierarchical Materials Design (CHiMaD) under Grant No. 70NANB14H012.

Authors’ contributions

Each author’s contribution(s) to the paper using the CRediT model. Conceptualization: J.C., K.E., S.W. Formal Analysis: S.W., N.M., E.G. Methodology: T.S., K.F., S.W., E.G., N.M. Investigation: S.W., T.S., K.F. Visualization: S.W., N.M. Funding acquisition: J.C. Project administration: J.C., K.E. Resources: T.S., K.F. Supervision: T.S., K.F. Writing – original draft: S.W., N.M., E.G. Writing – review & editing: S.W., J.C., K.E., N.M., E.G.

Previous presentation

These results have not been previously presented at a conference.

Data availability

Data are available in the main text or the supplementary materials. For further analysis or recreation, the XCT data for each specimen and the annotated highspeed X-ray image data used for this analysis can be accessed at: http://dx.doi.org/10.17632/t4v46m84tb.1.