The cost of waiting and the death toll in Italy during the first wave of the covid-19 pandemic

Abstract

This paper documents how a prompter implementation of stricter policy measures in Italy would have reduced by about one-fourth of total COVID-19-related deaths during the first wave of the pandemic. The empirical evidence suggests that rigid but timely restrictions would have been a more effective policy tool than implementing progressively stricter measures over an extended period.

1. Introduction

In response to the COVID-19 pandemic, the imposition of a shelter-in-place (SIPO) order has been proven to be effective in fighting the virus reproduction rate in the short run [[1], [2], [3]] despite the cost of hampering the level of economic activity and, eventually, the social environment if such a restriction is put into force for a too prolonged period [4]. When coping with this trade-off, countries have implemented restrictive policy measures that differed remarkably in timing and intensity. Moving from the validated results about the benefits of a SIPO order, we further extend the question about the timely introduction of strict containment measures. The question is relevant as quantifying the costs of delayed adoptions of duly restrictive measures might provide policymakers with relevant information to conduct well-versed interventions.

The economic cost of SIPO has been measured in terms of job losses [5], changes to consumer behaviour [6], households' income and wealth [7], fairness and cooperation [8], uncertainty and expectations [9] or GDP [10], voter turnout (Picchio and Santolini, 2021; Ferraresi and Gucciardi, 2021) and human mobility (Zhang, 2022). Interestingly, heterogeneity in the timing and intensity of stringency measures undertaken can be rationalised based on economic, institutional, and social characteristics [11,12].

This paper contributes to the current debate in several directions. First, it highlights the “cost” of delaying a strict containment measure regarding human lives. Second, we focus on Italy, a paradigmatic experience in the context of the COVID-19 pandemic (see, amongst others, [[4], [11], [13]]). Third, from a strictly methodological point of view, we follow Cerqueti et [1] and apply one of the most recent advances of the well-established Synthetic Control Method, SCM [14,15]: The Ridge Augmented SCM (Ridge ASCM). Cerqueti et al. [1] have shown that the lockdown in Italy effectively saved human lives. This finding is at the basis of our study in that, by exploiting this piece of knowledge, we pose another crucial question. Could Italy have done better?

In other words, an effective SIPO does not imply that the policy was introduced timely and that there was no avoidable loss of human lives. This contribution aims at answering the following question. How many deaths (if any) could have been avoided by a timely introduction of a strict lockdown policy? It is worth noticing also that the contributions to the literature aimed at evaluating the effects of strict containment measures with a counterfactual approach, so far, are either aimed at measuring the adverse effects avoided by the implementation of the policy, such as Cerqueti et al. [1] and Borri et al. [16] or at measuring the adverse effects undergone by a country that did not implement the policy, e.g. Cho (2022) for Sweden. Our point of view straddles the two polar positions. We gauge the adverse effects undergone by a country that implemented a strict policy measure but did not do that promptly. Using the same validated methodology on the same empirical case to answer a different question has the non-negligible benefit of making evidence consistent and complementary. Indeed, we document that Italy hesitated to put into place a strict SIPO order relative to the severity of the first wave of the pandemic in a way consistent with the relevant literature that postulates the timing of adoption as a function of structural rigidities (see amongst others, [12]). Such a delay has implied a “cost” of about 5000 human lives, i.e., more than one-fourth of COVID-19-related deaths in the first wave of the pandemic. In other words, if Italy had introduced timelier lockdown measures, the death toll would have been 25.8% lower than the actual number of COVID-19-related deaths. This finding is consistent with Cho [2], who estimates an excess mortality effect of about 25% for Sweden, one of the few countries not adopting a SIPO. By symmetry, very similar figures have been estimated for Italy by Borri et al. [16], who estimate that about 4800 deaths were avoided during the first 26 days of the lockdown.

The article is structured as follows. Section 2 puts forth the relevance of the Italian case in the COVID-19 context both for its (seeming) early lockdown adoption and its structural rigidities, which make the country an ideal candidate for the analysis. Section 3 briefly describes the methodology adopted and the dataset. Section 4 presents the results. Section 5 discusses the main findings and provides evidence of their robustness. Finally, Section 6 concludes.

2. Background to the pandemic in Italy

In the COVID-19 context, Italy deserves special attention and is worth analysing for several reasons. It is well known that Italy was the first Western country to register COVID-19 cases in January 2020, rapidly becoming the epicentre of the outbreak, with 207,428 confirmed cases and more than 28,000 deaths at the beginning of May 2020, representing around 14% of all confirmed cases and 20% of deaths in Europe (i.e., 6% and 11% at the global level, respectively).

In their event study based on 132 countries, Ferraresi et al. [12] argue that imposing SIPO orders or lockdown policies is particularly costly. Accordingly, political, economic, and institutional factors might have a role in explaining the different timing and intensity of stringency measures undertaken. In particular, the authors show that countries characterised by (i) low political stability; (ii) not being in a pre-electoral year; (iii) a high degree of decentralisation; (iv) a relatively closed economy; (v) low level of digitalisation; and (vi) low level of development have adopted less stringent measures than others. Moreover, a greater abidance to SIPO orders is positively correlated with civic capital, and Italy is well known to be a country with significant differences across provinces (Durante et al., 2020). This geographic unbalance may, on average, offset the final effect of a lockdown policy. Borrowing the intuition from Ferraresi et al. [12], we look at relevant indicators to our purpose, and we observe that: (i) over the 1946–2016 period, 63 governments have succeeded in Italy, as compared to 15 in the UK, 23 in Germany, and 44 in France, with no government that reached the maximum constitutional length of five years. (ii) The date of the first legislative elections after the pandemic outbreak is scheduled for 2023; hence in 2020, the Italian government was reasonably far from elections. (iii) According to the Constitutional Law (Article 140), Italy is a decentralised country with autonomous administrative entities (municipalities, provinces, regions, and metropolitan cities) having their powers. (iv) Italy is an open economy with an openness index (around 30%) similar to the UK and France. (v) Regarding digitalisation, Italy ranks poorly in Europe, with one of the lowest Digital Economic and Society Index scores in 2020 [17]. Finally, (vi) Italy is suffering from a long-lasting decrease in per-capita income: in 2019, Italy stood more than 6% below the European average and 4% below its 2001 level, while France, the UK, and Germany recorded cumulative increases between 14% and 22% over the last two decades.

Overall, it is likely to expect that Italy reacted to the pandemic only gradually and at a relatively slow pace compared to other countries. Putting the Italian case into an international perspective calls for constructing a reliable counterfactual with a proper selection of the donor pool to ensure that the relationship between the predictors and the outcome variable in the control set will be as close as possible to the one of the treated unit. An obvious choice to select the donor pool's elements is to apply a geographical criterion by focusing on European countries since the pandemic spread has not been homogeneous globally and over time. Accordingly, this study compares the Italian experience to 28 European countries, namely all European Union members (except Luxembourg) plus Switzerland, Norway, and the United Kingdom.

To assess the severity of the measures put into place in Italy and the synthetic European aggregate, we have resorted to the overall (headline) Stringency Index (SI; see [18]), which collects daily standardised information on several different common government responses in terms of containment/closure, economic and health system policies for a large number of countries. It ranges from 0 to 100, with each additional policy response increasing the index value.

Remark

The official date of SIPO's introduction is commonly referred to as the lockdown date. This date does not necessarily coincide with the date on which the most stringent measure was introduced, as recorded by the maximum observed value of the SI. Consistent with this article's aim, we will refer to the “lockdown date” as the date on which the SI peaked.

Operatively, we have normalised the time unit of the analysis such that “day 1” refers to the day on which cumulative infection cases per million exceeded one, as in Cho [2]. Moreover, we have defined the lockdown date for the donor pool as the average day on which the SI peaked in each country in a way consistent with the relevant literature ([2,12], amongst others); this occurs on the 26th of March 2020. In contrast, the maximum SI for Italy occurred several days later, on the 12th of April 2020, as the last observation in our sample because all the countries were treated from that day onwards.

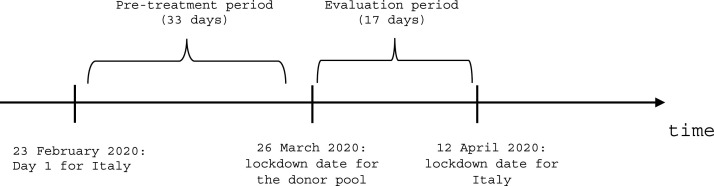
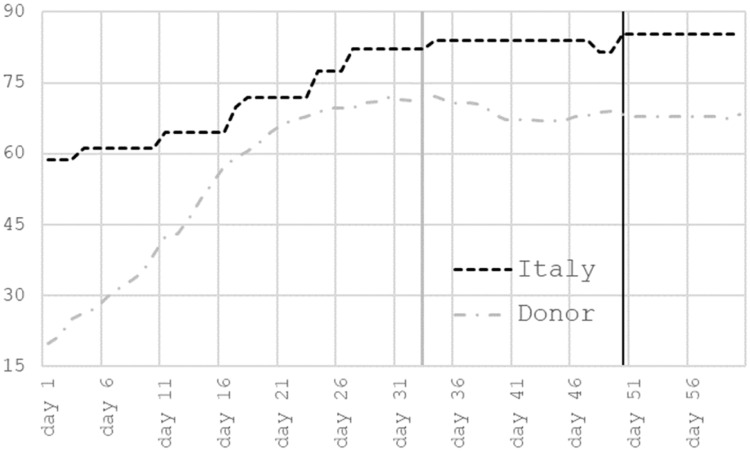
Basic descriptive statistics give explicit support to our priors. As Table 1 shows, our sample covers 50 data points, with a pre-treatment period, when no country was treated, of 33 days (from the 23rd of February, i.e. “day 1”, to the 26th of March, the lockdown date for the donor pool) and an evaluation sample consisting of 17 observations (from the 27th of March to the 12th of April when only the donor pool was treated). Graphical visualisation of the time framework is given in Fig. 1 . Despite a more severe impact of the first wave of the pandemic (also reflected by a much higher initial level of the SI), Italy's SI peak occurred only after 50 days, corresponding to about twice the period computed for the average European aggregate (24 days). Furthermore, the Italian SI increased moderately over time compared to the donor pool's average daily changes (Fig. 2 ) in response to progressively stricter containment measures regarding the intensity and extensivity of closing public transport and stay-at-home requirements.

Table 1.

COVID-19 characteristics and the overall (headline) Stringency Index (SI).

	Italy	Donor pool
Day 1	The 23rd of February 2020	The 3rd of March 2020
Lockdown day	The 12th of April 2020	The 26th of March 2020
Days to lockdown	50	24
Cases (Day 1)	1.259	1.055
Cases (Lockdown date)	2522.683	306.998
Delta cases per day	50.428	6.119
SI (Day 1)	58.65	38.53
SI (Lockdown day)	85.26	72.4
Delta SI per day	0.53	1.41

Note. Day 1 refers to the date the infection per million first exceeds one. The lockdown date refers to the day the overall (headline) Stringency Index (SI) peaked.

Fig. 1.

Time framework of the analysis.

Note. The picture reports the time framework of the analysis.

Fig. 2.

Overall (headline) Stringency Index (SI).

Notes. The horizontal axis indicates the days after the death per million exceeds one. The figure reports the overall (headline) SI for Italy (black line) and the donor pool (grey line). The black (grey) vertical line represents the lockdown date for Italy (the donor pool).

This descriptive evidence is broadly consistent with the result documented by Ferraresi et al. [12]: the performance of Italy in terms of the six key indicators has engendered a slowness of the country in adopting stringent measures, which has been uncovered by aligning the dynamics of the outbreak in terms of the relative number of cases amongst countries.

3. Materials and methods

Our empirical strategy is a variation of the well-known SCM by Abadie et al. [14,15]; see the online Appendix for a concise technical review. At its very essence, the SCM estimator is based on the idea of producing a counterfactual series, the so-called “synthetic”, by minimising the distance between the observed series before treatment and the weighted mean of donor's predictors, including past outcomes (see [19] for an exhaustive overview of the socioeconomic applications of the SCM). Weights sum up to one and are constrained to be nonnegative. It has been noticed that [20] this constraint, on the one hand, allows for sparsity and avoids overfitting; on the other hand, it may prevent reaching a good fit before treatment. In other words, the synthetic series may not be perfectly overlapped with the actual one before treatment, casting doubts about the validity of the post-treatment counterfactual. For this reason, a variation to the standard technique has been proposed by Ben-Michael et al. [20], who substitute the constraint with a penalty factor, the so-called hyperparameter, which penalises the dispersion of the weights following a suggestion by Abadie et al. [15]. This version of the SCM is referred to as (Ridge) ASCM.

In our case, countries underwent asynchronous dynamics of the outbreak, especially in the early stage, making it hard to figure out a credible counterfactual before treatment for Italy, the first country experiencing the European pandemic. The features of ASCM seem tailored to our case, allowing us to reproduce an excellent counterfactual trajectory.

3.1. Data

The outcome variable $Y$ is the mortality rate, which is defined as the cumulative death counts per million population (dth) taken from the Epidemic Intelligence team of the European center for Disease Prevention and Control (ECDC). Due to possible confounding idiosyncratic socioeconomic differences related to healthcare systems and population ageing, daily reported figures for deaths make cross-country comparisons challenging [21]. To consider these factors, we also consider several covariates that are expected to be linked to the outcome variable. We include cumulative cases per million population (num), which are intuitive predictors of mortality rates, as well as variables capturing the “resilience” of the health system like intensive care therapy unit beds per hundred thousand population (icu), under the assumption that the more developed the health system, the less fatal the COVID-19 infection will be. As for the outcome variable, the source for num and icu is the ECDC. We also include socioeconomic characteristics that are likely to be (positively) related to mortality rates, as suggested by Sá [22] and Rocklöv and Sjödin [23], amongst others. Accordingly, the share of the population older than 65 (eld), as well as the average household size (hld) and population density (pdn), are added to the set of covariates. All demographic variables are taken from United Nations [24]. We also control for “mobility trends” across different categories of places by resorting to Google Mobility Reports. Following Chernozhukov et al. [25], we focus on four out of six mobility sub-indices, “Grocery and Pharmacy”, “Transit Stations”, “Retail and Recreation”, and “Workplaces”). “Parks” and “Residential” are dropped because the former does not have clear implications on the spread of COVID-19. The latter shows an extremely high correlation with “Workplaces” and “Retail and Recreation. We distil the information content conveyed by the four mobility indicators into a synthetic index ($mob$) by following a “nonmodel based” aggregation scheme as discussed in Marcellino [26]. In the baseline specification, all time-varying variables are averaged over the first three weeks of the treated sample (i.e. from day 1 to day 21). Figure A1 in the online Appendix compares the weights assigned by the SCM and the ASCM.

4. Results

The synthetic control unit provides a much better-matched profile of Italy along the predictors compared to the simple average of all countries in the donor pool and the weighted average based on the countries identified by the SCM method (see Table 1A in the Online Appendix).

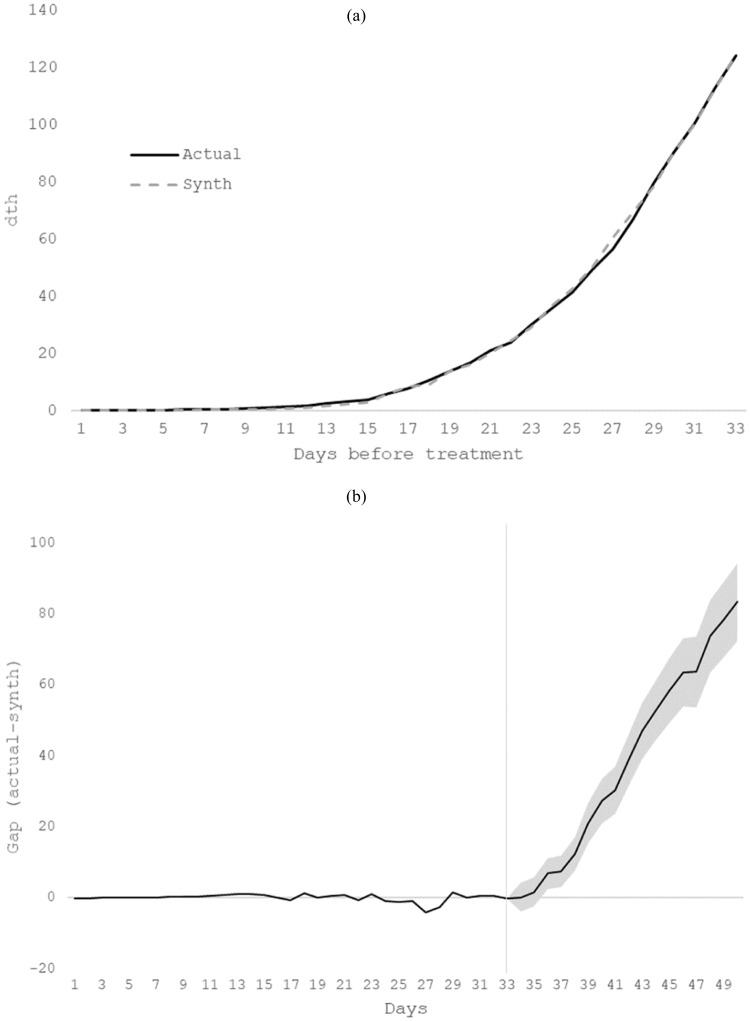
Fig. 3 illustrates the evolution of the mortality rate for actual and synthetic Italy by disentangling pre- and post-treatment periods. While Panel A assesses the quality of fit in the pre-treatment period and refers to the first 33 daily observations (from the 23rd of February 2020, to the 26th of March 2020), Panel B reports the difference between the actual series and its synthetic control (gap) over the pre- and post-treatment period (ranging from the 27th of March 2020, to the 12th of April 2020).

Fig. 3.

Actual and synthetic Italy.

Note. In both panels, the horizontal axis indicates days after the death per million exceeds one. The solid line shows the profile of Italy, while the dashed line refers to the synthetic counterfactual. The vertical line in Panel (B) represents the lockdown date. The shaded area is the confidence interval computed according to the jackknife+ approach of Barber et al. [27].

A close overlap between the two series can be detected over the pre-treatment period; subsequently, after the intervention, a significant positive gap emerges: the Average Treatment Effect on the Treated (ATT) that is the average deviation of the counterfactual series from the actual one over the treatment period turns out to be 39.25 with a p-value of 0.000. More in detail, we find that the cumulative mortality rate in synthetic Italy stands around 240 per million population roughly two weeks after the intervention date, while the corresponding figure for actual Italy is as high as 320. This evidence suggests that with a (positive) gap of more than 80 cases per million, the mortality rate in Italy would have been lower by about 25.8%. Moreover, the deviation from the actual series is statistically significant at the 95% level. Overall, our results suggest that strict but timely measures are likely to be a more effective policy tool than implementing restrictions progressively at a relatively slow pace without any end date. As pointed out by Briscese et al. [4], indeed, people's willingness to comply with restrictive measures in case of extensions beyond their expectations tend to decrease, especially if the endowment of civic capital is relatively scarce because less civic-minded individuals are both less likely to internalise the effect of their mobility on others and to abide by restrictive rules [11].

5. Discussion

We have performed several sensitivity tests to assess the robustness of our findings. The first tool we consider is the leave-one-out test [15], where the model is iterated over to leave out one element of the donor pool at a time to assess whether a given specific country is driving the outcome. The grey area in Figure A2 in the Appendix shows the min-max range of the gaps computed across all leave-one-out synthetic gaps, the mean value across all of them (solid line), and the one for the baseline specification. Regarding ATTs, the average gap across all permutations (54.02, with a p-value of 0.000) is even more significant than the baseline gap, offering additional support to our results.

As a further sensitivity check, we run the “in-time placebo” test, in which the treated unit is always Italy. However, the treatment date is arbitrarily re-assigned during the pre-treatment period. The placebo model sample period ended when the actual treatment occurred (day 33, in our context) to avoid capturing its effects, as devised by Abadie et al. [15].

Operatively, the in-time placebo test is conducted assuming that the treatment occurred one week before the actual treatment date (i.e., on day 26), corresponding to about three-fourths of the baseline pre-treatment period. Apart from the lockdown date, we apply precisely the same baseline setting. As Figure A3 in the Appendix shows, the gap for a placebo treatment on day 26 (dashed line) closely follows the one of the baseline model (continuous line), not only during the first half of the baseline pre-treatment period but also in the second part of the sample. Furthermore, the deviation from the actual series is barely different from zero according to the 95% confidence region (the grey area). Overall, the in-time placebo test assures that the placebo estimate resembles the actual pre-treatment path close enough to rule out the possibility that the above-discussed difference between the synthetic and actual Italy arises for reasons other than the treatment.

At this point, a caveat is in order. Resorting to the ASCM makes it possible to choose the weights to build the counterfactual for the treated unit ([14], p. 494). Nonetheless, such an advantage is weakened by a lack of consensus on how (and what) covariates should be chosen. To mitigate the risk of picking the “best” baseline specification by chance, we run several alternative specifications, and following Brock et al. [28], we have applied model averaging as a critical tool in tackling uncertainty. The online Appendix (Figures A4 and A5) shows full details and results.

6. Concluding remarks

This paper is nested within the recent literature on the trade-off generated by non-pharmaceutical interventions against COVID-19 spread; it specifically evaluates the human “cost” of relatively late adoption of containment measures. In line with extant literature [12], we have found that Italy had no incentives to provide a sufficiently timely and firm answer to the outbreak, as confirmed by the normalisation of the dynamics of the virus spread amongst the European countries. In addition to economic and institutional features making Italy hesitate, some limitations of intangible nature are likely to have played a role. Limiting citizens’ freedom of movement is an unprecedented violation of the Constitutional Law, which generated a lively debate amongst jurists, politicians, and ordinary people. Italy had the first mover's disadvantage, i.e., the Italian policy may have driven the timely reaction of other countries.

Resorting to an extension of the standard SCM, i.e. Ridge ASCM, we have estimated that such a delay has produced a loss of 83.4 human lives per million population. With roughly 60 million as the 2020 Italian population, the delay has produced (83.4·60=) 5004 lives lost, amounting to more than one-fourth of the COVID-19-related deaths during the first wave of the pandemic. This conclusion is robust to alternative specifications as well as to falsification tests. Our finding is very close to Cho [2], who estimates that Sweden could have avoided 25% of deaths from COVID-19-related issues should have introduced a strict containment measure. Likewise, but with a flipped sign, Borri et al. [16] estimate that in Italy, 4800 deaths were avoided over the first 26 days after introducing the lockdown.

Notice that according to our data-driven approach, the designated date of SIPO's initiation, commonly known as the lockdown date, does not align with the date of implementing the strictest measures (indicated by the highest observed value of the SI, as in [2], amongst others). Consequently, all our findings reflect that working assumption. Although disputable, our approach has the merit of ensuring a symmetric treatment to all countries in the sample, thereby minimising the risk of adopting ad-hoc dating procedures. Moreover, any date before the 12th of April misses a proper treatment of specific dimensions of the lockdown policy in Italy (namely, the intensity and extensivity of restrictions for closing public transport and stay-at-home requirements). According to our methodological setup, the empirical evidence suggests that severe but timely restrictive measures will likely be preferred to set up policy responses relatively slowly without any end date. Indeed, negative surprises associated with announcements of lockdown measures to be in effect for a longer time than expected induce a lower willingness to increase compliance [4], especially where civic capital is lacking [11]. In addition, uncertain interventions increase uncertainty in the economy [9], so the count of deaths is only one of the adverse outcomes engendered by the relatively slow adoption of the emergency policy.

Declaration of Competing Interest

None.