N-Heteroacenes as an Organic Gain Medium for Room-Temperature Masers

Abstract

The development of future quantum devices such as the maser, i.e., the microwave analog of the laser, could be well-served by the exploration of chemically tunable organic materials. Current iterations of room-temperature organic solid-state masers are composed of an inert host material that is doped with a spin-active molecule. In this work, we systematically modulated the structure of three nitrogen-substituted tetracene derivatives to augment their photoexcited spin dynamics and then evaluated their potential as novel maser gain media by optical, computational, and electronic paramagnetic resonance (EPR) spectroscopy. To facilitate these investigations, we adopted an organic glass former, 1,3,5-tri(1-naphthyl)benzene to act as a universal host. These chemical modifications impacted the rates of intersystem crossing, triplet spin polarization, triplet decay, and spin–lattice relaxation, leading to significant consequences on the conditions required to surpass the maser threshold.

1. Introduction

Organic solid-state masers are an emerging class of ultralow noise amplifiers for microwave signals.¹⁻³ These devices function by exploiting highly spin-polarized triplet states that are formed by spin-selective intersystem crossing (ISC). Interactions between magnetic dipoles of triplet electrons generate a zero-applied magnetic field splitting (ZFS) of spin sublevels (labeled T_x, T_y, and T_z) characterized by axial |D| and rhombic |E| splitting components. The resonant microwave frequencies correspond to the transition energies between these triplet sublevels and typically correspond to ΔE_Tx-Tz = |D| + |E|, ΔE_Ty–Tz = |D| – |E|, and ΔE_Tx–Ty = 2|E|. The objective of current maser research is the development of materials with a high ISC yield (Φ_T) coupled with a strong electron spin polarization favoring the higher spin sublevels.

For the archetypal organic maser gain material, pentacene-doped p-terphenyl (Pc:PTP), the triplet state populations (P_x:P_y:P_z) are 0.76:0.16:0.08, and hence, the most strongly polarized T_x–T_z transition has been used for masing.^4,5 Innovations in resonator technology have reduced the size of zero-applied field (ZF) maser devices significantly and dulcified the requisite operating conditions,³ however, high signal-to-noise amplification still requires a powerful light source comprising either a Q-switched yellow laser or xenon flash lamp coupled with an invasive Ce:YAG luminescence concentrator.^7,8 Even with these innovations, the demonstration of an organic maser operating as a continuous wave (CW) amplifier has remained elusive. Since masers are fundamentally limited by the electron spin dynamics of their gain media,^4,9 further work is needed to design maser materials that can operate in miniaturized form and with moderate pumping sources.

Previously, semiempirical calculations of pentacene-like aromatic molecules have been used to evaluate their potential as maser gain media. The energy difference (ΔE_ST) between the first excited singlet state (S₁) and the most energetically proximal triplet state (T₂) was used to predict the ISC rates (κ_ISC).¹⁰ Subsequent ab initio investigations revealed that guest–host interactions significantly impact the relative energies of neighboring singlet and triplet states, exemplifying some of the inherent difficulty in computationally predicting maser materials.^11,12 Nevertheless, these studies informed the discovery of 6,13-diazapentacene-doped p-terphenyl (DAP:PTP) as an alternative maser gain media operating with a 620 nm pulsed laser.¹³ The discovery of new maser candidates is also hindered by reliance on doped crystalline materials such as p-terphenyl. Crystalline hosts are highly selective toward their compatible dopants which limits the number of candidates that can be readily explored. Furthermore, the introduction of intricate invasive pump architectures is often not compatible with crystal growth methods such as Bridgman growth.¹⁴ Ideally, a host matrix should accomodate high concentrations of spin-active molecules, while also being compatible with multiple methods of optical pumping and form highly crystalline domains, minimizing inhomogeneous broadening associated with the triplet sublevels.

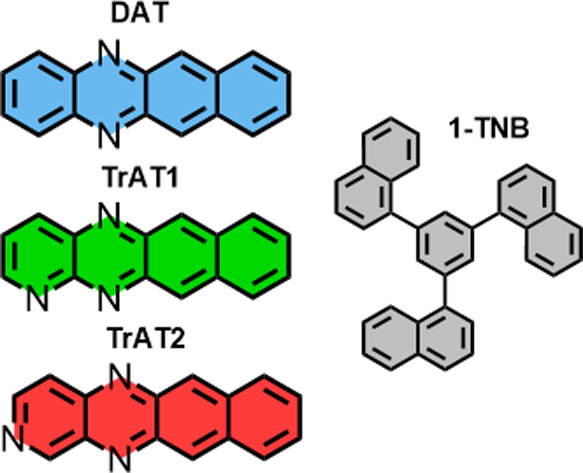
In this work, we employ a universal host material, namely, 1-TNB, which forms an optically transmitting glass following a cycle of rapid heating and cooling.¹⁵⁻¹⁷ To exploit this material as a maser host and explore potential new maser gain materials, we have synthesized a series of nitrogen-substituted tetracene derivatives to modulate their optical activity (Scheme 1). The molecule DAT has previously been used as a source of spin-polarization for dynamic nuclear polarization¹⁸⁻²⁰ and otherwise considered in organic optoelectronic applications.²¹ To modulate the photoexcited spin dynamics of this molecule, further nitrogen substitution was used to generate 1,5,12-triazatetracene (TrAT1) and 2,5,12-triazatetracene (TrAT2). Our analysis demonstrated that the optical band gap was modulated by the degree and position of nitrogen substitution, leading to noticeable differences in triplet formation in both dilute solutions and 1-TNB solid-state hosts. Interestingly, while the ZFS energies were similar between molecules, the triplet state populations varied significantly despite similar molecular architectures. Pulsed Q-boosted maser signals were subsequently recorded for the most favorable candidates.

Scheme 1. Structures of 1,3,5-Tri(1-naphthyl)benzene (1-TNB) Host Molecule and N-Substituted Tetracene Derivatives.

2. Results

2.1. Steady-State Optical Spectroscopy

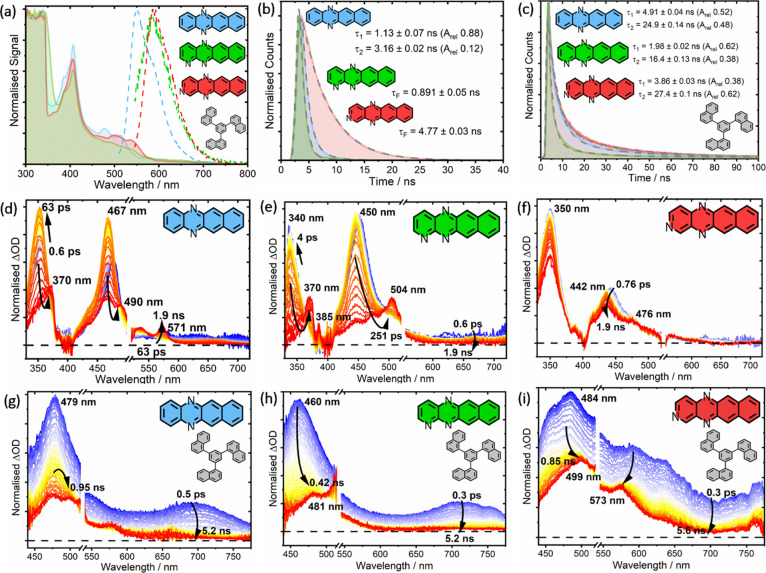
1-TNB melts at 186 °C and can be cooled in air to form a stable pellet of amorphous glass.¹⁵⁻¹⁷ The rapid cooling ensures that candidate molecules remain trapped without aggregation, thereby yielding a sample with diluted spins that are not subject to bimolecular photophysical processes such as singlet fission or triplet–triplet annihilation. To understand how their incorporation into a 1-TNB host affects their photophysical properties, we conducted steady-state UV/Vis and fluorescence spectroscopy on tetrahydrofuran (THF) solutions of DAT, TrAT1, and TrAT2 and doped 1-TNB samples (Figures 1a and S1a). When dissolved in THF, two prominent bands are observed with absorbance bands centered at 405 nm and ca. 510 nm for DAT and 530 nm for TrAT1/TrAT2 (Figure S1a). Excitation with green light results in relatively bright fluorescence that peaks at 540 and 585 nm for DAT and TrAT1/TrAT2, respectively. When doped into a 1-TNB host at 0.1% mol/mol concentration, the main absorption and emission features are red-shifted by approximately 10 nm, peaking at 550 and 600 nm. Interestingly, irradiation at 400 nm yields anti-Kasha’s additional luminescence bands at 450 nm, as previously reported for THF solutions (Figure S1b).²¹ This is particularly evident for TrAT1 where the 450 nm emission dominates the steady-state fluorescence spectrum. However, since 1-TNB is also excited by 405 nm light, this pump wavelength is unlikely to be optimal for downstream maser devices.

Figure 1.

(a) Absorption (solid lines) and luminescence (dashed lines) spectroscopy of DAT, TrAT1, and TrAT2-doped 1-TNB (conc. 0.1% mol/mol). Time-correlated single photon counting (TCSPC) spectroscopy of DAT, TrAT1, and TrAT2 in (b) THF solution or (c) doped in 1-TNB, with representing fits. (d–f) Femtosecond transient absorption spectroscopy (fsTAS) of DAT, TrAT1, and TrAT2 in THF solution, respectively, and fsTAS (g–i) in 1-TNB solid-state host. Samples were excited with 530 nm light except for DAT in THF which was excited at 510 nm. Sample concentrations in THF were set between 1.6 and 2 mM and 0.1% mol/mol in 1-TNB.

2.2. Transient Optical Spectroscopy

To begin probing the excited state dynamics of these materials, we measured their responses by TCSPC spectroscopy to determine their fluorescence lifetimes (τ_F) in THF solution and doped 1-TNB systems (Figure 1b,c). The fluorescence decay curves were fitted using mono- or biexponential lifetimes, showing no significant improvement with additional exponential fitting terms (Figures S2a–c and S3a–c). These data revealed that the emission lifetime of doped 1-TNB systems was significantly slowed compared to THF solutions. TrAT1 exhibited the shortest lifetime in both THF solution and 1-TNB with τ_F = 0.891 ns and a weight-averaged τ_F (τ_F,av) of 7.46 ns, respectively. Similarly, DAT dissolved in THF returned a relatively fast τ_F,av of 1.31 ns, and a longer decay time of 14.5 ns in 1-TNB. The longest decay times of τ_F = 4.77 ns and τ_F,av = 18.5 ns were found for TrAT2 in THF and 1-TNB, respectively. In each case, the dominant decay term for doped 1-TNB samples was similar in magnitude to dominant terms in THF, with the subsequent term ranging between 16.4 and 27.4 ns.

Since the detected transient fluorescence is associated with the absolute rate decay of S₁ (κ_F; κ_F = κ_rad + κ_IC + κ_ISC), we sought to deconvolute contributions of fluorescence (κ_rad), nonradiative internal conversion (κ_IC), and ISC (κ_ISC). Therefore, solutions of THF and doped 1-TNB samples were measured by fsTAS following excitation with green light to monitor the excited state dynamics. In THF solution, two excited state absorption (ESA) bands are initially observed at ∼350 and ∼450 nm for all three materials (Figure 1d–f). These features can be attributed to S₁ → S_n electronic transitions, appearing at similar wavelengths to equivalent processes in tetracene^22,23 and pentacene-derivatives.^24,25 This association is supported by their similar S₁ decay time determined by TCSPC spectroscopy. For TrAT2, the decay of S₁ extends beyond the time window of our experiment (1.9 ns) making kinetic analysis impossible. For all three materials, the ESA bands reduce in intensity after 100 ps followed by the appearance of shoulder peaks which are most clearly observed for DAT at 370, 490, 537, and 571 nm, and for TrAT1 at 370, 385, and 504 nm. Since the growth of these bands is too slow for vibrational cooling, which typically occurs within a few picoseconds,^26,27 and based on their persistent growth up to 1.9 ns, these features are attributed to the lowest triplet state (T₁) following ISC from S₁. The T₁ assignment (over higher T_n states) can be asserted since IC between T_n → T₁ in linear acenes is typically very rapid (<10 ps).^28,29 Furthermore, such processes have been noted for tetracene at similar wavelengths,^22,30 while for DAT an absorption at 580 nm was used to determine the triplet lifetime for DAT:PTP, which is close to the 571 nm band we observed.¹⁸ Since negative bands associated with a ground state bleach or stimulated emission are absent here, it is assumed that the observed spectra are also convoluted with an additional broad ESA which masks their contributions.

For the doped 1-TNB samples, the measured time window was increased to 5.2 ns (5.6 ns for TrAT2:1-TNB) following the more gradual S₁ relaxation indicated by TCSPC spectroscopy, and the detection window was adjusted to 440 and 800 nm due to the change in instrumentation. Again, ESA bands were observed between 460 and 484 nm, coupled with an additional broad ESA covering the entire spectrum (Figure 1h,i). The decay of these features coincides with the emegence of weak bands on similar time scales to T₁ → T_n absorptions in THF solutions, beginning at approximately 1 ns in DAT:1-TNB at 580 nm, and 450 ps in TrAT1:1-TNB at 481 nm. Notably, the absorption band at 580 nm for DAT:1-TNB matches that used by Kouno et al., to determine the triplet lifetime of 120 μs.¹⁸ For TrAT2:1-TNB, S₁ relaxation manifests as a band shift from 484 to 499 nm with the later appearance of an additional weak band at 573 nm. These features persist to the end of the experiment supporting an assignment to the T₁ state, however, an estimation for the onset of absorption is impossible due to the broad nature of these absorptions.

Due to the convoluted spectral components, kinetic analysis required global analysis (GA) following singular value decomposition. In each case, two or three principal components were required to fit the fsTAS data, each of which have lifetimes corresponding to either a mono- or biexponential decay, as with TCSPC spectroscopy (Figure S5). For THF samples, the first and second fitted components generally accounted for S₁ → S_N ESA bands. The third component contains features consistent with the triplet absorption bands. Due to the incomplete excited state decay within the accessible time window of our experiments, the absolute rate values derived from our analysis are likely inaccurate, and for TrAT2 a sensible kinetic analysis was again impossible. However, the magnitude of the rates coupled with the onset time of triplet absorption can be used to infer that TrAT1 (onset 250 ps, est. τ_ISC = 531 ps) undergoes ISC slightly more rapidly than DAT (onset 400 ps, est. τ_ISC = 882 ps), followed distantly by TrAT2. A similar analysis for 1-TNB samples was also conducted, however, due to their weak absorption convoluted with an extremely broad ESA, lower signal-to-noise, and dominance of the laser scatter, the triplet absorptions were not clearly represented in the principal components (Figure S6a–f). Furthermore, due to the incomplete S₁ relaxation captured in these spectra, the corresponding estimated component lifetimes extended beyond the 5.2 ns time window of the experiment. Nevertheless, it is clear from these data that like the rate of fluorescence, the apparent κ_ISC is significantly slowed for DAT:1-TNB, TrAT1:1-TNB, and TrAT2:1-TNB.

With the limited information available following fsTAS of doped 1-TNB samples, we sought to supplement this data by quantifying their fluorescence quantum yield (Φ_F, see SI for details). Since the gain of a maser device is proportional to the number of polarized triplets generated by its spin-active media upon photoexcitation, it is expected that the better candidates would have a lower Φ_F. Indeed, our measurements indicated that the Φ_F for DAT:1-TNB and TrAT1:1-TNB was 37.3 and 38.9%, respectively, while TrAT2:1-TNB exhibited Φ_F = 58.3% (Table 1). The larger Φ_F value for TrAT2:1-TNB is consistent with its extended S₁ lifetime revealed by TCSPC and fsTAS, which is associated with less efficient ISC.

Table 1. Photophysical Parameters Derived from fsTAS and TCSPC.

system	host	ΦF/%	τF/ns	κrada/ns–1	κISCb/ns–1	κIC/ns–1	ΦIC/%	ΦTa/%	τL/μs
pentacene	PTP		∼9					62.534	8918
tetracene	toluene30,32	16	4.2	0.038	0.147	0.053	22	62	0.63
	benzene33	15	5.2	0.029	0.131	0.03	17	68
	anthracene35		18.4
DAT	PTP18								12018
	THF		1.37 ± 0.05
	1-TNB	37.3 ± 1.6	14.5 ± 0.09	0.026	0.043 (κnr)
TrAT1	THF		0.891 ± 0.05
	1-TNB	38.9 ± 1.6	7.46 ± 0.06	0.052	0.082 (κnr)
TrAT2	THF		4.77 ± 0.03
	1-TNB	58.3 ± 1.6	18.5 ± 0.07	0.032	0.022 (κnr)

^a(31) κ_rad = Φ_F/τ_F; τ_F = (κ_rad + κ_nr)⁻¹; κ_nr = κ_ISC + κ_IC.

^b(36) κ_F = κ_rad + κ_IC + κ_ICS; Φ_T = Φ_F(κ_ICS/κ_rad).

For isolated molecules and in the absence of photochemical reactions, κ_F = κ_rad + κ_IC + κ_ISC. Therefore, using the experimentally determined values for Φ_F and τ_F(av) (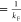), κ_rad can be estimated by κ_rad = 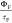.³¹ This further permits the assignment of an upper limit on the overall nonradiative decay rate, κ_nr (= κ_IC + κ_ISC = κ_F – κ_rad; Table 1), as 0.043, 0.082, and 0.022 ns^–1 for DAT:1-TNB, TrAT1:1-TNB, and TrAT2:1-TNB, respectively. Interestingly, these values are similar to those for the values for tetracene in nonpolar aromatic solvents where Φ_F values between 10 and 16% were reported,^30,32,33 indicating less efficient triplet formation in these azatetracene samples.

2.3. Density Functional Theory

To further understand our observed optical properties, we performed density functional theory (DFT) calculations to help characterize the singlet and triplet state energies. Following the formalism described by Bogatko et al., for the computational evaluation of maser candidates,¹⁰ the S₀ state energy was normalized to zero, and subsequent excited states were positioned according to optical band gaps as determined by time-dependent (TD)-DFT calculations (Figure 2, see SI for details). The energy of the ground state triplet (T₁) was estimated using the energy difference between the S₀ state and highest triplet singly occupied molecular orbital energy, defined as ΔE_TS (Table 2). The excited triplet states are thus found by adding ΔE_TS to the optical excitation energies for T₁ → T_n transitions. This approach permits the examination of singlet and triplet state energy gaps (ΔE_ST) and the construction of Jablonski diagrams.

Figure 2.

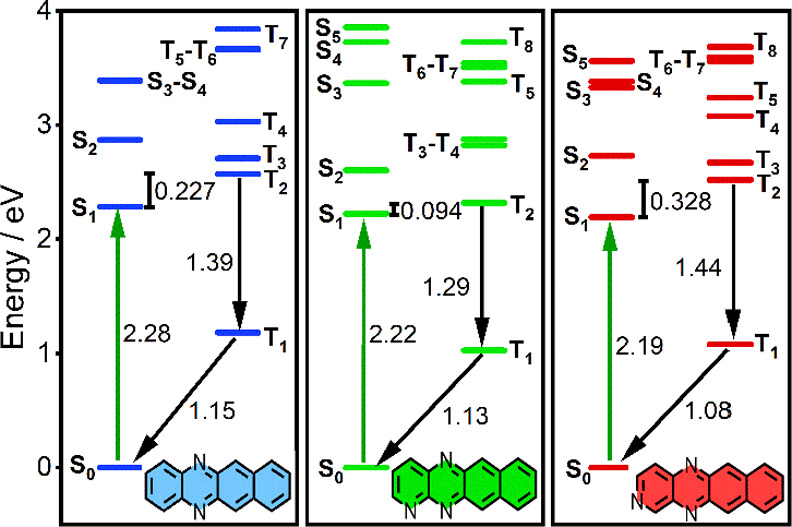
Electronic state Jablonski diagrams for DAT, TrAT1, and TrAT2 estimated using TD-DFT calculations. Calculations were performed at the B3LYP 6-311G++(d,p) level using Gaussian09 software with an IEFPCM solvent model of benzene. Transition energies given in units of eV.

Table 2. Singlet and Triplet Energy Differences Derived by TD-DFT Calculations (in Units of eV).

	S0–S1	Exp.a	ΔEST (S1–T2)	ΔETS (T1–S0)
DAT	2.28	2.45	0.227	1.15
TrAT1	2.22	2.40	0.094	1.13
TrAT2	2.19	2.32	0.328	1.08

^aDetermined from the leading edge λ_max according to UV–Vis spectroscopy.

The calculated optical excitation energies closely reproduced experimental trends observed by UV/Vis spectroscopy with only a ca. 7% difference in the absolute values (see Figure S7), typical for TD-DFT calculations. The band gaps were found to increase from TrAT2 to TrAT1 to DAT, with TrAT1 estimated to exhibit the smallest ΔE_ST (= 0.094 eV) and TrAT2 the largest (= 0.328 eV, Table 2). For small organic materials without high atomic weight species or functional groups that significantly mix singlet and triplet states via spin-orbit coupling,^37,38 κ_ISC is often approximated to exponentially depend on the energy difference between the initial singlet state (S₁) and the final triplet state (T₂), according to the Fermi golden rule.^39,40 To investigate whether this holds true for our nitrogen-substituted tetracene derivatives, quantum calculations were performed to estimate the spin-orbit coupling matrix elements between singlet and triplet states (Tables S5–S7). These data indicate relatively weak coupling values, particularly between S₁ and T_n states, always less than 10 cm^–1_. By comparison, species with enhanced ISC due to species such as transition metals,^41,42 sulfur,^43,44 selenium,^45,46 halogens, or nonbonding functional groups^{37,38,47−49} typically exhibit SOC parameters exceeding 100 cm^–1. Interestingly, analysis of the natural transition orbitals reveals that the T₂ state exhibits a clear nonbonding orbital character, particularly for TrAT1 and TrAT2 (Figure S8). According to El-Sayed rules,^50,51 it might be expected that with a (π,π*)-type S₁ state, TrAT1, and TrAT2 would exhibit enhanced ISC compared to DAT, however, while TrAT1 has been inferred to undergo slightly faster ISC, the slow S₁ relaxation for TrAT2 indicates that this is not the case. Therefore, here it is likely that ISC is still dominated by ΔE_ST. This idea is supported by the larger Φ_F for TrAT2:1-TNB compared to DAT:1-TNB or TrAT2:1-TNB.

2.4. X-Band Time-Resolved Electronic Paramagnetic Resonance Spectroscopy

To further examine whether the triplet states of these materials are suitable as maser gain media, we also performed photoexcited X-band time-resolved electron paramagnetic resonance (trEPR) spectroscopy to determine their triplet sublevel populations and ZFS frequencies.

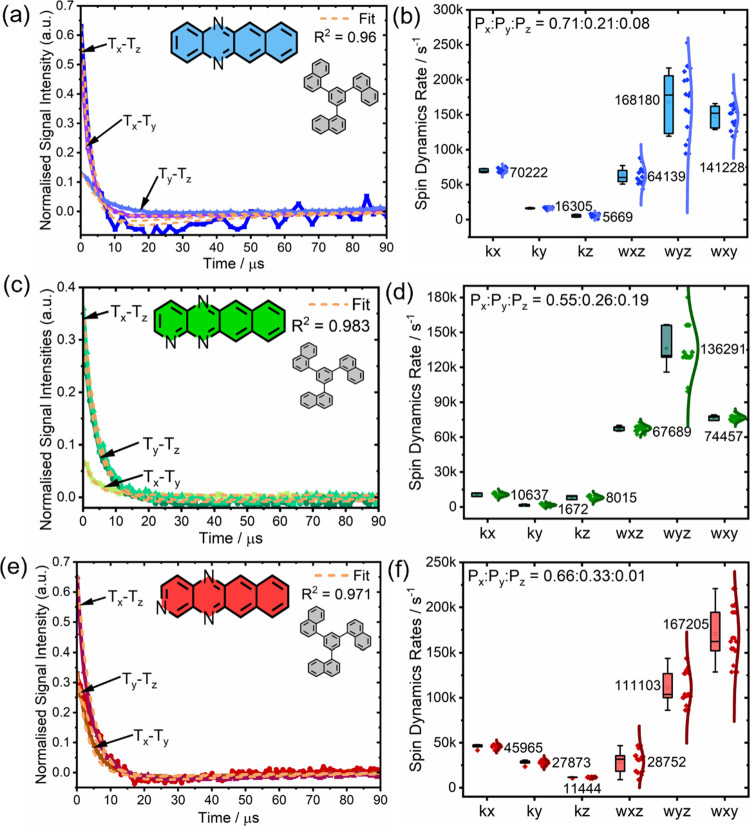
As expected for amorphous glass samples, triplet signals consistent with the presence of powders were recorded for all materials. The transient signals were comprised of emissive (E) low-field and absorptive (A) high-field signals (Figure 3). The emissive phase for each material persists for ∼10 μs followed by a weak absorptive phase lasting up to 90 μs. To determine the triplet sublevel populations and ZFS, the signals were simulated using the Matlab EasySpin (v6.0.0) toolbox (see SI for details).⁵² All our materials were found to have positive T_x–T_z and T_x–T_y population differences (Table 3). It is notable that DAT:PTP exhibits a larger T_z population than DAT:1-TNB (0.18 vs 0.08) but a similar T_x population. Interestingly, the triplet polarization for TrAT1:1-TNB was the weakest, with a T_x:T_z ratio of just 2.9, whilst TrAT2:1-TNB is the only material to present with an apparently enhanced spin polarization compared to Pc:PTP. As expected for such closely related chemical structures, the ZFS energies were also similar with |D| values between 1582 and 1609 MHz, and |E| values between 155 and 193 MHz, similar to tetracene and DAT:PTP.¹⁸ Overall, based on the triplet sublevel populations DAT:1-TNB and TrAT2:1-TNB would appear to be narrowly better maser candidates than TrAT1:1-TNB.

Figure 3.

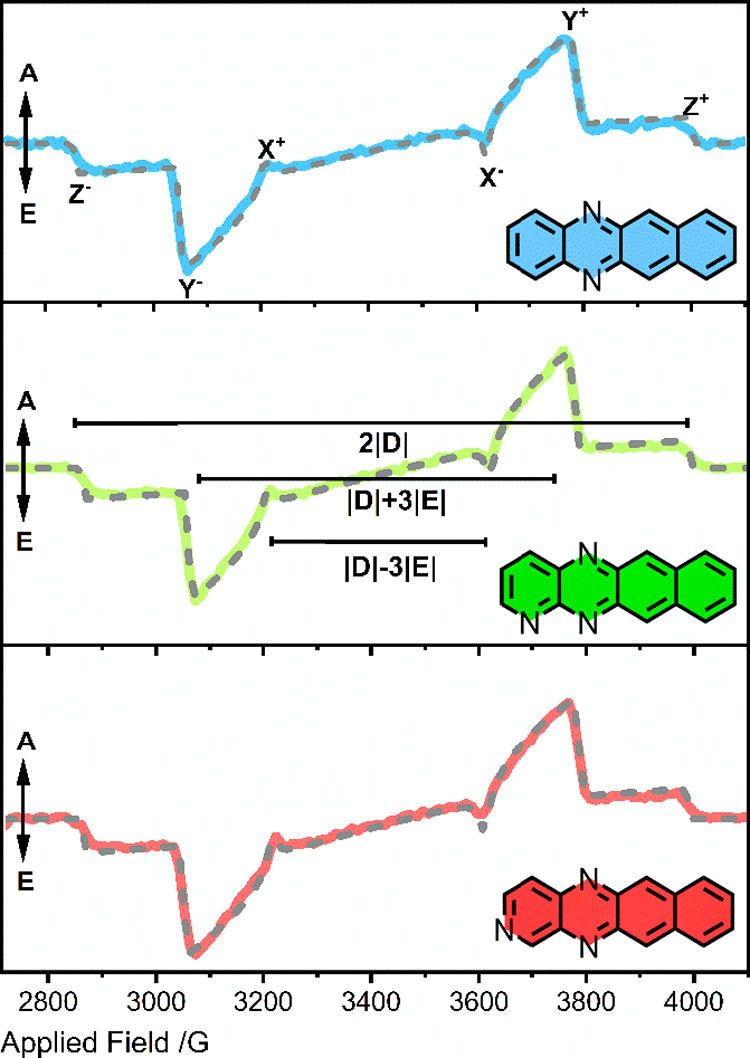
X-band photoexcited trEPR spectra for DAT:1-TNB (blue), TrAT1:1-TNB (green), and TrAT2:1-TNB (red). Traces are taken 400 ns after laser flash, with samples made to a concentration of 0.1% mol/mol and illuminated with 5–8 ns pulses of 532 nm light measured at 7 mJ/pulse. Gray dashed lines represent fittings performed using the EasySpin toolbox (see the SI for details).

Table 3. Triplet Parameters Derived from X-Band trEPR Spectroscopy Experiments.

	host system	2D spectral fitting
		D	E	Tx–Tz (Ty–Tz)	Pz:Py:Px	Px/Pz
		/MHz
pentacene	p-terphenyl	139553	5353	1449 (1341)53	0.08:0.16:0.764	9.5
		131518	5018
	1-TNB17	138517	5017	1435 (1334)17	0.19:0.35:0.4617	2.4
tetracene	p-terphenyl	165354	11254	1765 (1541)54	0.00:0.41:0.5954	N/A
DAT	p-terphenyl18	159818	15318	1751 (1443)18	0.18:0.11:0.7118	3.7
	1-TNBa	1609	156	1765 (1453)	0.08:0.21:0.71	8.9
TrAT1	1-TNBa	1582	193	1775 (1389)	0.19:0.26:0.55	2.9
TrAT2	1-TNBa	1609	155	1764 (1454)	0.01:0.33:0.66	66

^aData from this work.

2.5. Spin Dynamics—ZF trEPR Spectroscopy

With the ZFS and triplet sublevel populations known, we conducted ZF trEPR spectroscopy to individually analyze their T_x–T_z, T_y–T_z, and T_x–T_y transitions. Measurements were collected using inductively coupled (IC) tank resonators fabricated to resonate with each transition frequency band (see the SI for details). To determine the frequency with the most intense signal, measurements were conducted in steps of 5 MHz in proximity to the estimated transition frequencies (Figure S10).

Here, the most intense T_x–T_z signal for DAT:1-TNB was observed at 1765 MHz, closely matching X-band-derived estimations, whereas optimal signals for TrAT1:1-TNB and TrAT2:1-TNB were found at 1755 MHz (Figure 4a–c). The transition linewidths were relatively broad with their full-width half-maximum exceeding 40 MHz, compared to approximately 3 MHz for a typical single crystal sample of Pc:PTP at a concentration of 0.1% mol/mol.⁵⁵ As glass matrices do not exhibit any intrinsic long-range order, inhomogeneous broadening is expected to significantly increase compared to a crystal matrix due to different local magnetic environments. Since the transition linewidth is inversely proportional to the inhomogenous dephasing time (T₂*) which is sensitive to magnetic inhomogeneity, the expected result is relatively broad ZF linewidths. Furthermore, hyperfine coupling to ¹⁴N nuclear spins results in additional broadening and peak asymmetry, as demonstrated by frequency sweep simulations using DFT-derived hyperfine coupling parameters for each molecule (Figure S9). As a result, the microwave power per unit frequency that is emitted by the sample during masing is significantly attenuated in glass matrices.

Figure 4.

(a–c) ZF trEPR spectra of DAT:1-TNB (blue), TrAT1:1-TNB (green), and TrAT2:1-TNB (red); (d–f) transition-specific spin–lattice relaxation (ω_ij) and sublevel-selective triplet decay rates (κ_i) determined by fitting of ZF trEPR signals. Sample concentrations were 0.1% mol/mol and illuminated with 5–8 ns pulses of 510 or 532 nm light at 1 mJ/pulse. Individual signals were obtained at room temperature and averaged 512 times. Spin dynamics fittings are shown as orange dash lines.

To further understand how these ZF trEPR signals might relate to their maser potential, the most intense signals were used to simulate their spin dynamics using the following relationship:

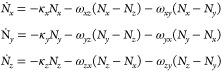1

Here, N_i is the initial population of i-th sublevel as determined following X-band EPR spectroscopy; κ_i is the sublevel specific triplet decay rate to the singlet ground state, S₀; ω_ij is the spin–lattice relaxation rate between the i-th and j-th sublevel. For this analysis, it was assumed that the i-j and j-i transition rates are equal at room temperature, as discussed previously.⁴ Fitted values correspond to R-squared values of >0.96, indicating that the fit represents 96% of the data (Table 4).

Table 4. Room-Temperature ZF trEPR Data and Fitted Spin Dynamics of the Triplet Ground State for Doped 1-TNB Samples^a.

sample	Tx–Tz	Ty–Tz	Tx–Ty	|D|	|E|	κx	κy	κz	ωxz	ωyz	ωxy
Pc:PTP(4,7)	1450	1344	106	1397	53	2.8 ± 0.5	0.6 ± 0.2	0.2 ± 0.1	1.1 ± 0.2	2.2 ± 0.3	0.4 ± 0.2
						2.2	1.4	0.2	1.1	2.8	0.4
DAT:1-TNB	1765	1470	315	1608	158	7.43 ± 0.74	1.4 ± 0.04	0.74 ± 0.30	5.45 ± 2.0	16.9 ± 6.2	16.3 ± 2.9
TrAT1:1-TNB	1755	1375	325	1593	163	1.23 ± 0.23	0.83 ± 0.21	1.11 ± 0.25	7.02 ± 0.24	13.4 ± 0.77	5.39 ± 0.32
TrAT2:1-TNB	1755	1485	295	1608	148	4.17 ± 0.85	2.37 ± 0.61	1.04 ± 0.37	4.69 ± 2.03	8.62 ± 3.42	12.9 ± 4.56

^aUnits for κ_i and ω_i(j) values are given in 10⁴ s^-1.

From these measurements, it was apparent that each compound has quite distinct spin dynamics (Figure 4). For DAT:1-TNB, the largest ω_ij values correspond to the T_y–T_z and T_x–T_y transitions, with T_y and T_z sublevels also exhibiting the smallest κ_i values. In practical terms, this means that relaxation from T_y and T_x states could lead to an accumulation of electrons in the T_z state. This contrasts with TrAT1:1-TNB, where ω_xz and ω_xy are smaller than ω_yz and coupled with a relatively small κ_x value compared to DAT:1-TNB, TrAT2:1-TNB, and even Pc:PTP. The realization of a short κ_x, especially if coupled with a large κ_z parameter, would be an important advancement for the realization of a CW maser. Such a system would benefit from a reduced spontaneous loss of T_x polarization and more efficient recycling of spent T_z electrons. Interestingly, TrAT2:1-TNB essentially presents as a mix of DAT:1-TNB and TrAT1:1-TNB spin dynamics, with a relatively small ω_xz and relatively large κ_i values, where κ_x > κ_y > κ_z. Overall, these azatetracene materials exhibit significantly larger ω_ij and κ_i values compared to Pc:PTP (Table 4), except for the κ_x value for TrAT1:1-TNB. This is consistent with the reduced electron spin polarization time at ZF.

To determine if these values are compatible with their use in a maser device, the spin dynamics can be related to the maser “cooperativity” (see eq 2). For a CW maser, the gain of individual materials can be summarized by the cooperativity factor adapted from ref (9), often denoted as η_maser (or C in ref (56)):

2

Briefly, μ_o is the vacuum permittivity, γ is the reciprocal gyromagnetic ratio for maser transition (≡–g_Jμ_B/ℏ), σ is the transition probability between the maser transition sublevels (assumed to be 0.5 at room temperature), Q_L is the loaded quality factor of the resonator, P_opt is the optical pump power, V_mode is the resonator’s magnetic mode volume, κ_opt is the absorption probability at the pump wavelength, f_opt is the optical pump frequency, θ_ISC^eff is the effective ISC yield, T₂* is the inhomogenous dephasing time, and finally T₁ is the effective spin–lattice relaxation time, which acts as a ratio of the population-weighted spin dynamics.^7,9 Maser oscillation with high signal-to-noise requires η_maser ≫ 1. The cooperativity thus depends on three “bulk” quantities comprised of a set of universal constants (μ_oγ²σ²/2π), resonator-dependent parameters (Q_LP_opt/V_mode), and finally a set of material-dependent parameters (k_optθ_ISC^effT₁T₂^*/f_opt).

While materials with η_maser values close to unity are practically difficult to measure, in principle, the ability to CW mase ultimately depends on T₁^eff—the only parameter with a potentially negative sign (described in ref (9)). The sign of T₁ is determined by its numerator which can be used as a figure of merit concerning the triplet spin dynamics, denoted as κ_rates:⁷

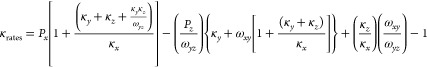3

This term can be straightforwardly determined using the values reported in Table 4, yielding values of −0.06 ± 0.95 for DAT:1-TNB, 0.63 ± 0.51 for TrAT1:1-TNB, and 0.66 ± 0.86 for TrAT2:1-TNB. Therefore, based on this analysis all three azatetracene-doped 1-TNB samples may have the potential to CW mase within experimental error. It is interesting to note the sensitivity of κ_rates to errors in κ_i and ω_ij values. Surprisingly, despite the relatively obtuse nature of the TrAT1:1-TNB triplet decay compared to DAT:1-TNB and TrAT2:1-TNB, κ_rates is close to TrAT2:1-TNB which has a smaller ω_xz value but larger ω_xy value. By comparison, Pc:PTP has an estimated κ_rates value of 0.3, enough to facilitate the operation of a quasi-CW device pumped invasively using a luminescence concentrator.⁷

2.6. Q-Boosted ZF Maser

To finally determine if these materials were suitable as maser gain media, a strontium titanate (STO) resonator suitable for operation between 1700 and 1800 MHz was fabricated (see the SI for details). Compared to alternative materials, STO is known to yield high native quality factors (Q_F, ∼2000 at 1765 MHz) while maintaining a relatively small resonator footprint due to a high relative permittivity resulting in a compressed magnetic mode volume and an enhanced Purcell effect.⁶ By inserting the resonator into a copper cavity with an adjustable height, the resonant frequency could be adjusted to accommodate the transition frequencies for all three azatetracene derivatives.

Initially, native Q_L pulsed maser tests were conducted using pump energies up to 40 mJ/pulse with 520 or 530 nm light, however, no maser signals could be detected. We attribute this to the broad (∼40 MHz) transition linewidths revealed by ZF trEPR spectroscopy. For masers, the consequence is a lower microwave power output per unit frequency, and, therefore, compared to Pc:PTP, the maser signal would be significantly reduced assuming identical operating conditions. The bandwidth of our STO resonator between 1755 and 1765 MHz was measured to be ∼800 kHz from which it can be inferred that much of the microwave output from our materials would not fall within the resonance bandwidth. Thus, if one could dope these materials into a crystal matrix and consequently narrow the emission linewidth, masing could be significantly easier.

Therefore, to effectively determine the cooperativity enhancement that would be required to reach the maser threshold, Q-boosting experiments were performed (see the SI for details). Here, briefly, the output power of the resonator was outcoupled into a feedback loop that amplified the microwave circuit power. This compensated for radiative losses from the resonator cavity and resulted in an artificially increased Q_L.⁵⁷ By adjusting the attenuation of the circuit, the Q_L of the maser cavity could be willingly increased until circuit self-oscillation, which generally occurred when Q_L ≥ 220,000 between 1755 and 1765 MHz. For less intense maser bursts, the Q_L required adjustment closer to the self-oscillation threshold.

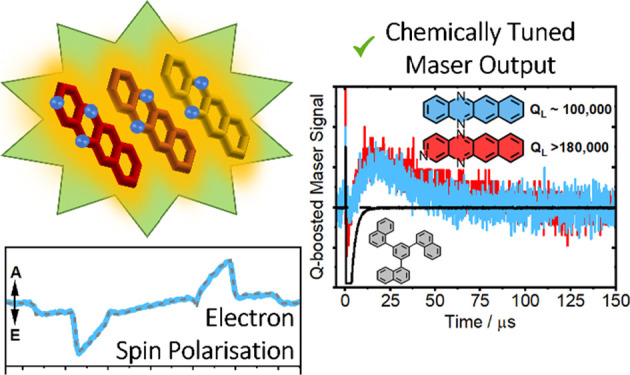
In this configuration, single-shot maser oscillations were observed for DAT:1-TNB and TrAT2:1-TNB samples, but not for TrAT1:1-TNB (Figure 5). DAT:1-TNB required a Q_L of ∼100,000 to reach the threshold, whereas TrAT2:1-TNB required Q_L > 180,000—with the circuit on the verge of self-oscillation. The maser pulse of TrAT2:1-TNB lasted approximately ∼75 μs compared with ∼50 μs for DAT:1-TNB. Since the polarization lifetimes measured at ZF were approximately the same, we attributed the difference in burst duration to the different effective Q_L. Overall, while DAT:1-TNB and TrAT2:1-TNB were found to yield Q-boosted maser signals, an extremely high Q_L was required, making any prospect of masing with native-Q resonators unrealistic in the current 1-TNB host.

Figure 5.

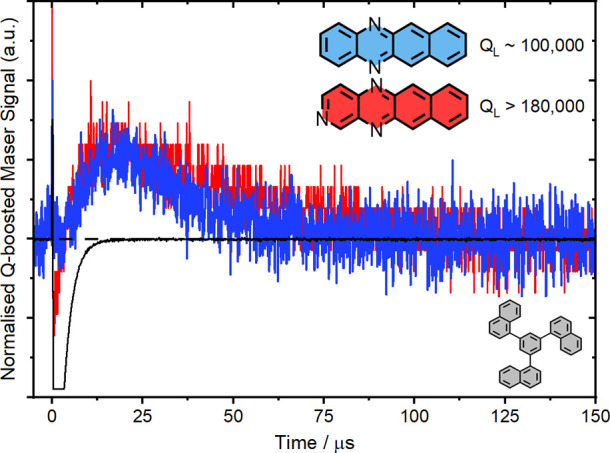
Q-boosted maser signal for DAT:1-TNB (blue) at 1765 MHz and TrAT2:1-TNB (red) at 1755 MHz. Samples were made at a 0.1% concentration. Laser trigger is represented by the black line. Quality factors were measured using a vector network analyzer. To check whether the signals were sample-dependent, the experiments were repeated with a permanent magnet positioned close to the cavity resulting in the disappearance of the signal.

3. Discussion

Despite their discovery over a decade ago, organic maser gain media have remained largely undeveloped, hindering the advancement of low pump threshold and high-gain maser technology. Since the operation of these devices relies on the generation of strong electron spin polarization, we sought to chemically modulate and evaluate the maser potential of three related azatetracene compounds, namely, DAT, TrAT1, and TrAT2, doped into a universal organic glass host, 1-TNB. Indeed, the strongest candidates resulting from this work were DAT:1-TNB and TrAT2:1-TNB, which each demonstrated unique dynamical spin behavior conducive toward masing.

Intelligent chemical approaches to the design of maser host materials have yet to be significantly explored for masers. Hosts such as p-terphenyl offer a structurally well-defined host matrix where dopants become substituted in lattice sites. Compared to an amorphous host, this has the benefit of reducing the inhomogeneous broadening of electron spin transitions.⁵⁸ However, such hosts are extremely selective toward dopants with polarity and size-dependent exclusion mechanisms often leading to the elimination of dopants. As a result, the development of crystalline maser materials remains highly challenging. The host material 1-TNB, although amorphous, permits the evaluation of any soluble organic candidate gain material, including various spin-polarized molecules from the existing literature. Hence, it should serve to make the field more accessible since most maser-related properties can be evaluated using commercial instruments. In practice, if a promising maser material is revealed in 1-TNB, additional resources could thereafter be directed toward finding a crystalline host.

Since the pump frequency (f_opt, eq 2) for maser devices is inversely proportional to their cooperativity, hosts that induce an absorption red-shift without adversely affecting the generation of triplets are expected to dulcify the operating conditions. Stronger red shifts can be achieved through strong guest–host charge-transfer interactions, as has been seen in the context of masers with phenazine:TCNB, however further work is needed to understand the impact of charge-transfer interactions and the mobile nature of triplet states for maser applications.⁵⁷ Compared to Pc:PTP, which is pumped with 590 nm, illumination with 530 nm light represents an expected ∼10% loss of cooperativity. Nevertheless, this also served to place the longest wavelength absorption bands firmly within the range of commercial 532 nm light sources and facilitates the use of powerful OPO laser emission bands for future maser experiments. In principle, the host can be used to realize more efficient and diverse pumping schemes. Alternative crystalline hosts for pentacene, such as benzoic acid,⁵⁹⁻⁶² naphthalene,^63,64 anthracene,^65,66 or tetracene,⁶⁷ are known to modulate the triplet dynamics but have not been demonstrated to exhibit any enhanced maser-related properties compared to p-terphenyl. However, films and single crystals of pentacene-doped picene (1% mol/mol) exhibit delayed modes of optical transfer from the picene host to the pentacene dopant.^68,69 Pentacene-doped trans-1,4-distyrylbenzene (trans-DSB) shows similar guest–host optical transfer activity, but neither has thus far been directly operated in maser devices.⁷⁰ Whether the delayed optical emissions from these materials is matched by extended spin polarization lifetimes is yet to be determined.

Simultaneously to host development, it is essential that new spin-active compounds are found. Here, the fastest relaxation of S₁ states occurred in the order of TrAT1:1-TNB > DAT:1-TNB > TrAT2:1-TNB. Since within structurally similar compounds the relative abruptness of S₁ relaxation is associated with the rate of ISC from S₁ → T_n states,^23,30,32,71 it can be assumed that this order also represents the relative abundance of triplet states following photoexcitation. This is supported by the detection of triplet absorption bands for TrAT1 and DAT, but not TrAT2, and the corresponding reduced Φ_F for TrAT1:1-TNB and DAT:1-TNB. Interestingly, compared to our materials, tetracene appears to exhibit a stronger preference toward triplet formation.^30,32,33 However, 5-azatetracene exhibits 63% Φ_F when measured in dichloromethane,⁷² suggesting that the structures of di- or tri-azatetracenes derivatives are likely still better at forming triplets than this monosubstituted compound. While more efficient ISC has been identified to result from the introduction of N-heteroatoms, this has usually been attributed to an acceleration of singlet fission⁷³⁻⁷⁵ and solvent-induced/intermolecular vibronic or spin-orbit coupling.^51,76−79 Since our dopant-based materials consist of diluted spins, bimolecular processes such as singlet fission or triplet–triplet annihilation can be ruled out. Hence, in our materials, the efficiency of ISC is dominated by variations in ΔE_ST. It is worth mentioning that a precise evaluation of singlet–triplet energies is a particularly challenging subject, especially in the solid state where modeling of guest–host interactions requires a bespoke model.^11,12 Since 1-TNB is a glass-forming host, this approach is not easily feasible. Therefore, while our DFT calculations managed to reproduce the experimental trends, the absolute values are likely inaccurate. An important challenge for the design of maser compounds is a vigorous and accessible methodology for preliminary computational evaluations.

Investigations involving systematic variations within structurally similar compounds remain a cost-effective approach. Here, for example, similar ZFS parameters permitted maser testing with the same high-Q dielectric resonator. This investigation demonstrated that a high triplet yield must be balanced with the degree of spin polarization. Despite the fastest apparent rate of ISC, TrAT1:1-TNB exhibited the smallest T_x:T_z population difference out of the three materials and as a result could not detectably mase. Whilst maser cooperativity is effectively proportional to the Φ_T,⁹ there is limited room for improvement in this parameter compared to Pc:PTP, for example, where Φ_T = 62.5%.⁸⁰ More substantial cooperativity enhancements can be realized by enhancing spin polarization. Organic materials are especially suited for such an approach, with the T_z population approaching virtually nil for some reported systems.⁸¹⁻⁸³ However, since the cooperativity dependence on spin polarization is captured within T₁^eff, a more comprehensive spin dynamics investigation is required at ZF.⁴ An important challenge is the alleviation of the polarization “bottleneck” associated with Pc:PTP that prevents CW masing.⁴ This must also be matched by a relatively narrow microwave emission band, which as this study has demonstrated can be fatal even for pulsed masers. It is notable that despite a relatively poor steady-state spin polarization, dilute spin concentration (≤10^–4%), and hyperfine splitting, negatively charged nitrogen-vacancy (NV^–) diamond can mase due to its narrow transition linewidth (1.7 MHz).^56,84

4. Conclusions

Organic spin systems were the first to be used in room-temperature solid-state maser devices. Uniquely, these systems are tunable by modification of their chemical structure and can thus potentially lead to the synthesis of low pump threshold, high-gain maser devices. Using a universal organic host, our findings systemically demonstrate that careful modification of an azatetracene family of compounds leads to measurable consequences for maser applications. Critically, the cooperativity of candidate materials is a function of spin transition linewidth, triplet yield, triplet sublevel-selective decay rate, spin polarization strength, and lifetime. Therefore, the majority of maser-related properties can be evaluated without the use of bespoke built ZF spectrometers and high-Q resonators. Future development of organic systems should seek to not only synthetically develop materials with enhanced spin dynamics and higher spin concentrations, but also incorporate innovative pump schemes. This highly cross-disciplinary topic is therefore open to fruitful contributions from various chemical and engineering teams interested in the development of novel photonic quantum technologies.

5. Experimental Section/Methods

Sample preparations: 1-TNB (>98%) was purchased from TCI chemicals. Trace colored impurities were removed by column chromatography using an ethyl acetate: hexane (1:100) eluent system.

DAT, TrAT1, and TrAT2 were synthesized according to ref (21). Briefly, 1,2-dihydroxylnaphthalene was ground with a molar equivalent of the corresponding 1,2-diaminopyridine (for DAT) or 1,2-diaminopyrimidine (for TrAT1 & TrAT2) in a pestle and mortar. The mixture was then heated in a round-bottomed flask at 160 °C under argon for 1 h, before being cooled and stirred with acetone to produce a slurry. The suspension was then filtered to yield the crude 5,12-dihydrobenzo- or pyrido-quinoxaline precursors as yellow/green solids. The precursors were co-dissolved with a molar equivalent of chloranil in toluene without further purification and refluxed for 1 h under air before being filtered hot. The filtrate was quickly diluted with excess toluene to prevent the crystallization of co-crystals with 1,2,4,5-tetrachloro-3,6-dihydroxyquinone (TCHQ). TCHQ was removed by extraction with an excess of 1 M NaOH solution until no further precipitation occurred in the extraction funnel. The toluene layer was then dried over Na₂SO₄ and removed under reduced pressure. Further purification was then performed by sublimation at 110 °C in a nitrogen atmosphere at a typical pressure of 10^–3 mbar and flow rate of 30 mL/min.

UV/Vis spectroscopy was performed using a sealed 1 cm quartz cuvette filled with samples diluted to 10^–5 M. Data were measured using a Agilent Cary 5000 UV/Vis/NIR spectrophotometer. Fluorescence emission and excitation spectroscopy were performed using a Horiba Jobin-Yvon Spex Fluorolog-3 fluorimeter, with emission and excitation slit widths set to 2 nm.

For TCSPC and fsTAS experiments, DAT, TrAT1, and TrAT2-doped 1-TNB samples were measured inside rectangular 60 × 4 × 0.4 mm glass tubes (VitroTubes, CMScientific). To load the samples, doped 1-TNB powders were loaded into glass vials made by sealing the end of a glass Pasteur pipette. The capillary tube was pushed into the powder and the whole vial was placed under an inert argon atmosphere inside a larger glass tube. The powder was then carefully melted causing the materials to passively creep into the tube by capillary action. The system was then allowed to cool resulting in the doped 1-TNB samples forming as transparent glasses inside the capillary tubes. Over hours or days, the samples lose their transparency which can be easily restored by remelting the material, taking care not to overheat and force the material to leak out of the tube. When kept in the dark, these samples were found to retain a strong characteristic absorption spectrum over several months. Solution phase measurements were performed in 1 mm quartz cuvettes.

Time-resolved (tr) X-band EPR spectroscopy was performed using a Bruker ELEXSYS-II E500 spectrometer (X-band) at room temperature. Powder samples were decanted into a 4 mm O.D. Wilmad quartz (CFQ) EPR tube and reformed by melting/cooling under an inert argon atmosphere to reduce light scattering. All data were processed using the EasySpin 6.0.0 package for Matlab 2022b (see the SI for details). The least squares fitting was performed using the esfit function and performed with data “as is” using the Nelder/Mead simplex algorithm. The fitting of all three materials was initialized by assuming a Lorentzian lineshape, spin polarization, and ZFS parameters for DAT reported by Kouno et al., 2019¹⁸ and a g-value of 2.0023.

ZF trEPR experiments were performed using a home-built spectrometer. The configuration was similar to that in our previously published paper.⁴ For operation at 1.7 GHz, frequency-dependent components including circulators, bandpass filters, and attenuators were changed to fit the resonate frequency. An OPO (Litron Aurora II Integra) pumped by its own internal Q-switched Nd/YAG laser was used to excite the sample. For DAT:1-TNB, the output wavelength of the OPO was set to 510 nm with a repetition frequency of 10 Hz and a duration of 5.5 ns. For TrAT1:1-TNB and TrAT2:1-TNB, the output was adjusted to 530 nm. After being attenuated by three optical filters, the incident illumination energy on the sample was approximately 1 mJ/pulse. The sample was placed in an IC resonator, with an area and the number of turns adjusted for each transition frequency (e.g., T_x → T_y; T_x → T_z; T_y → T_z). The corresponding signals were captured using I-Q homodyne detection recorded in an oscilloscope (Rigol DS1104 Z-plus) with a total of 512 averages.

The photoluminescence spectra for measurements of the fluorescence quantum yield (Φ_F) were recorded using a home-built system by integrating a charge-coupled device camera (Andor DU420A-BEX2-DD, Oxford Instrument), a spectrograph (Andor KY193, Oxford Instrument), and an integrating sphere (AvaSphere-50-REFL, Avantes). Collimated laser diode modules (CPS532 and CPS405, THORLABS) were used as excitation sources for 532 (50 mW cm^–2) and 405 nm (50 mW cm^–2). The system was calibrated by shining two light sources into the integrating sphere with known spectra. A mercury light calibration source (AvaLight-CAL-MINI, AVANTES) was used for wavelength correction, and a halogen light source (AvaLight-HALCAL-ISP50-MINI, AVANTES) was used for the absolute photon flux calibration. The spectral photon density of the corrected spectrum was then divided by the photon energy followed by a numerical integration to obtain the absolute photon counts for the total emission. The Φ_F was determined by dividing the photoluminescence photon numbers by the absorbed photon numbers.

Data Availability Statement

The data that support the findings of this study are available in the supplementary material or upon reasonable request.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.chemmater.3c00640.

• Further characterization by UV/Vis and fluorescence spectroscopy, transient fluorescence, quantum chemical calculations, and ZF EPR spectroscopy, fitting of fsTAS and EPR data, and details of the Q-boost maser experiments (PDF)

The authors declare no competing financial interest.