Effects of Conformational Constraint on Peptide Solubility Limits

Abstract

Liquid–liquid phase separation of proteins preferentially involves intrinsically disordered proteins or disordered regions. Understanding the solution chemistry of these phase separations is key to learning how to quantify and manipulate systems that involve such processes. Here, we investigate the effect of cyclization on the liquid–liquid phase separation of short polyglycine peptides. We simulated separate aqueous systems of supersaturated cyclic and linear GGGGG and observed spontaneous liquid–liquid phase separation in each of the solutions. The cyclic GGGGG phase separates less robustly than linear GGGGG and has a higher aqueous solubility, even though linear GGGGG has a more favorable single molecule solvation free energy. The versatile and abundant interpeptide contacts formed by the linear GGGGG stabilize the condensed droplet phase, driving the phase separation in this system. In particular, we find that van der Waals close contact interactions are enriched in the droplet phase as opposed to electrostatic interactions. An analysis of the change in backbone conformational entropy that accompanies the phase transition revealed that cyclic peptides lose significantly less entropy in this process as expected. However, we find that the enhanced interaction enthalpy of linear GGGGG in the droplet phase is enough to compensate for a larger decrease in conformational entropy.

Graphical Abstract

INTRODUCTION

Phase separation is the process wherein a homogeneous mixture forms two distinctive phases. In recent years, liquid–liquid phase separations (LLPSs) of biomolecular systems have been shown to play key roles in a variety of cellular processes such as the formation of membraneless organelles, disease-associated protein aggregation, and the structural transitions of disordered protein domains in signaling.^1–5 Membraneless organelles, also called biomolecular condensates, are supra-molecular agglomerations of proteins and nucleic acids that carry out important cellular functions, such as modulating concentration to change the kinetics of chemical reactions by collecting specific molecules from the surrounding solution.^1–3 Notable examples of membraneless organelles are nucleoli,⁶ Cajal bodies,⁷ and stress granules.⁸ Membraneless organelles are known to be enriched in intrinsically disordered proteins (IDPs) or proteins possessing intrinsic disordered regions (IDRs). Disfunction of membraneless organelles is implicated in various disease pathologies. Enlarged nucleoli have been identified as one of the early hallmarks of cancer cells, and increases in the number and size of nucleoli are used as prognostics for tumor development.^9,10 Mutations in stress granule proteins are associated with neurological diseases such as amyotrophic lateral sclerosis (ALS) and frontotemporal dementia.^10,11 LLPS also is reported to occur in disease pathologies as a precursor to the formation of amyloidogenic fibrils, such as in Alzheimer’s, Hungtington’s, or Parkinson’s disease. Many transcription factors and other signaling proteins contain IDRs which are conformationally dynamic and play a role in regulatory signaling processes.^12,13 These regions can utilize phase separations to modulate binding and chemical environment.

During LLPS, disordered domains may transition between various structural states, such as disordered extended and disordered collapsed states.^14–16 Due to the conformational flexibility and the relatively flat free energy landscape associated with disordered ensembles, structural disorder may be remodeled in many ways to enable binding and interaction with other species. Many IDRs of signaling proteins are enriched with glycine residues, and glycine-rich peptides can effectively model the protein backbone of an IDP due to their flexibility and lack of stable secondary structure.^17–21 Previous computational work by our group has shown that systems of sequence GGXGG (X = R, D, G, V, Q, N, F) at high concentration spontaneously undergo LLPS, separating into aqueous and condensed liquid droplet phases. Several of these studies^22,23 investigated the intermolecular interactions at play in the condensed droplets and found that an ensemble of peptide dipole–dipole interactions, as well as less numerous hydrogen bonding (H-bonding), stabilize the protein-rich phase.

We calculated the thermodynamics of phase separation from MD simulations of concentrated GGXGG systems in a recent study²⁴ and observed that, upon transition from the aqueous to the condensed phase, pentapeptides lose ~28 cal mol⁻¹ K⁻¹ of conformational entropy. This decrease in entropy, however, is offset by an accompanying favorable decrease in enthalpy resulting from close-range van der Waals interactions afforded by the dense condensate. Our analysis showed that the electrostatic interaction part of the enthalpy does not change appreciably upon phase transition, demonstrating that both environments provide comparable Coulombic environments. The solvent–peptide H-bonds that stabilize aqueous peptides are replaced in large part by more numerous dipole–dipole peptide–peptide interactions (so-called CO–CO interactions), which the system preferentially utilized rather than structure-forming H-bonds. The results of this work suggest that disordered peptides modulate their conformational free energy through balancing of conformational entropy and interaction enthalpy, and structural disorder may be remodeled via changes in this balance.

A developing concept in the field of protein structure is that structural plasticity provides a reservoir of entropy that may be deployed as free energy by proteins to modulate spontaneity of molecular processes.²⁵ Due to their vast number of accessible conformational states, IDRs represent significant conformational entropy reservoirs which may utilize structural transitions to withdraw or deposit free energy into a process (e.g., binding). Work by various authors has developed and built upon this hypothesis,^26–28 but the field lacks a complete quantitative description of how proteins can tune conformational entropy to modulate function.

In this work, we evaluate the difference in available entropy affected by cyclization of a pentaglycine peptide and the effect that this change in entropy has on the LLPS of cyclic peptides. Cyclic peptides are polypeptides that form a ring structure via linking the ends of the peptide with an amide bond via lactam condensation or another chemically stable covalent bond. Cyclic peptides are of biophysical interest for several reasons. They occur in natural products (e.g., gramicidin S, cyclosporin A, vancomycin), and those naturally occurring cyclic peptides, among others, have clinical use as antibacterials, in the case of gramicidin S and vancomycin, and immunosuppressants in the case of cyclosporin A. Cyclization is of keen interest in the field of synthetic peptide pharmacology because, usually, cyclic peptides can exhibit enhanced biological activity in comparison to their linear counterparts.^29–32 This is due in part because cyclized peptides, unlike linear peptides, do not sacrifice as much conformational entropy upon adopting a bound conformation. Cyclized peptides have other advantages over linear peptides as well, such as resistance to peptidase hydrolysis and higher receptor selectivity.³²

We simulate LLPS in systems of linear and cyclized pentaglycine (cGGGGG) peptides and monitor the difference in thermodynamic properties caused by the more stringent conformational ensemble afforded by cyclization. Specifically considered are the entropic and enthalpic balance of undergoing LLPS in cGGGGG in comparison to linear GGGGG. We anticipate modulation of the available conformational entropy affected by cyclization will alter the LLPS properties of these short peptides. Moreover, the inter- and intramolecular interactions available to the ensemble will be different than those available to linear GGGGG peptides, and we probe the extent to which the molecular interactions change in the cyclized systems. With these simulations we hope to strengthen our understanding of the thermodynamic properties of peptides and how changes in thermodynamics can affect biophysical behavior.

METHODS

We carried out MD simulations of two systems consisting of 625 identical cyclized and linear pentaglycine peptides, respectively. These peptides were randomly situated in a cubic box using Packmol³³ with the restraint that no peptide atom be closer than 6 Å to an atom of another peptide, thus creating a roughly homogeneous aqueous starting (nonequilibrium) state for the peptides. The 625 cGGGGG system was solvated with 91418 TIP3P water molecules using the solvatebox utility in Amber18’s xleap interface.³⁴ The resultant solvated system of cGGGGG amounted to ~300 000 atoms and had a peptide concentration of ~0.3M, a concentration that previous work by our group^22,23 has shown is well above the solubility limit for glycine-rich pentapeptides using modern molecular force fields. The linear system was taken from previous work at the same concentration.^23,24 A 15 Å solvent buffer inside of the periodic boundaries of the cubic box was utilized, as our previous work²⁴ has shown it helps to avoid the initial formation of an infinitely periodic condensed phase. No ions or additional solutes were added to the solution as the cyclic pentaglycines are of neutral charge.

The conjugate gradient method was used to energy minimize the starting configuration of the system. Following this, 10 ns of the beginning of the nonequilibrium phase separation was simulated at a temperature and pressure of 300 K and 1 atm, respectively, under the isothermal–isobaric (NPT) ensemble. Following that, 350 ns of production MD was carried out at the same temperature and pressure. The NAMD package³⁵ was used for all MD simulations, and forces and potentials were calculated using the Amber14SB force field.³⁶ The Amber force field was used here to match the precedent of our group’s 2021 study of linear pentaglycine peptides,²⁴ the results of which are compared to our results for cGGGGG reported here. The Verlet velocity integration method was used with a time step of 2 fs, and covalent bonds of heavy atoms to hydrogen were constrained with the SHAKE algorithm. Nonbonded interactions were calculated for atom pairs at distances less than 12 Å, and a switching function was applied at 10 Å to smoothly truncate the nonbonded potential. The particle mesh Ewald (PME) method³⁷ was employed to efficiently calculate long-range electrostatics. Molecular images of the systems simulated here were created with the VMD visualization suite,³⁸ and data plots were generated with Python’s matplotlib library.

Conformational entropies were obtained using the AC-CENT-MM program developed by Killian et al.,⁴² which implements the mutual information expansion hierarchy (MIE) method.⁴² To perform these calculations, ϕ/ψ backbone dihedral angles for all the peptides were collected from the MD trajectories, and accompanying conformational entropy curves for the peptides in the solvated and condensed states were calculated. Only dihedral contributions were included in the conformational entropy here, as in equilibrium systems, rigid bonds and angles contribute trivially to the conformational entropy change.⁷ The third order approximation was implemented in the MIE calculations, which our previous work³⁹ has shown is more accurate while still being tractable. Entropy curves were extrapolated to an infinite time scale using a fit to a hyperbolic function. Rotational and translational contributions to the total entropy were calculated using PDB2TRENT,⁴⁰ which uses a k-nearest neighbor method.⁴⁰ Peptide interaction enthalpies and hydrogen-bond numbers were collected using Amber 18’s cpptraj suite.^34,41 Here, a peptide’s interaction enthalpy was defined as the sum of the energies from peptide–water and peptide–peptide interactions.

RESULTS

This study is focused on understanding the effect of peptide cyclization on the thermodynamic and physical properties of liquid–liquid phase separation. To monitor the thermodynamic effect of cyclization, both the enthalpic and the entropic components of the free energy are considered for both cyclic and linear peptide systems. Polyglycine sequences are used for both linear (GGGGG) and cyclic (cGGGGG) peptides to ensure that cyclization is the only variable being studied and because glycine is enriched in IDR sequences, making it an attractive, simple model for in silico studies of protein disorder.

Early in the MD simulations of the cyclic peptide system, the solution separated into distinct aqueous and condensed peptide-rich (“peptide droplet”) phases. During the simulation trajectories we classify peptides as being in either the aqueous or the peptide droplet phase based on peptide–peptide distance criteria used previously.²⁴ The criterion is, if an atom of a peptide is within 4 Å of an atom of another droplet peptide, this peptide is in the droplet phase; if not, it is aqueous. Physical attributes of cyclic peptide and linear peptide droplets were analyzed such as interaction types and abundance, water concentration, and peptide density. We calculate conformational (S_conf) and translational-rotational (S_tr) entropies for peptides in both phases. Conformational entropies were calculated utilizing a third order MIE approach,⁴² which takes considerably longer to converge due to including 3-body correlations but is significantly more accurate than the first and second order.³⁹ Peptide total interaction enthalpies (H_int) were calculated for peptides in each phase, taking into account the interaction energies from both other peptides and water molecules.

Previous thermodynamic analysis²⁴ of phase separation in linear pentaglycine systems found that, during phase separation from the aqueous phase to the droplet phase, S_conf is sacrificed but compensated by a decrease in H_int stemming from favorable van der Waals interactions afforded by the droplet phase. Results from this prior study of GGGGG are compared with the results for systems of cGGGGG reported in this study.

Phase Separation.

The system of 625 cGGGGG peptides underwent LLPS early in the MD simulation, forming a large amorphous peptide droplet phase within the first 10 ns of production simulation. Figure 1A shows images of the system at 0, 10, and 350 ns. Peptides existing in the aqueous state are colored blue, and those in the condensed droplet state are colored red. The image demonstrates that a significant amount of phase separation has occurred after only 10 ns of simulation, and in the remaining 340 ns the droplet phase coalesces into a more roughly spherical droplet from the shapeless partition seen early on into the simulation. The LLPS behavior of the cGGGGG system has some similar behavior to the linear GGGGG system simulated in our previous study,²⁴ with one difference being that appreciable phase separation was observed earlier (5 ns) in the simulation with the linear peptide system. Figure 1B shows that the GGGGG system has already formed a more globular droplet phase at 10 ns into the simulation, whereas the cyclic system at this time has partially separated into a largely amorphous peptide phase.

Figure 1.

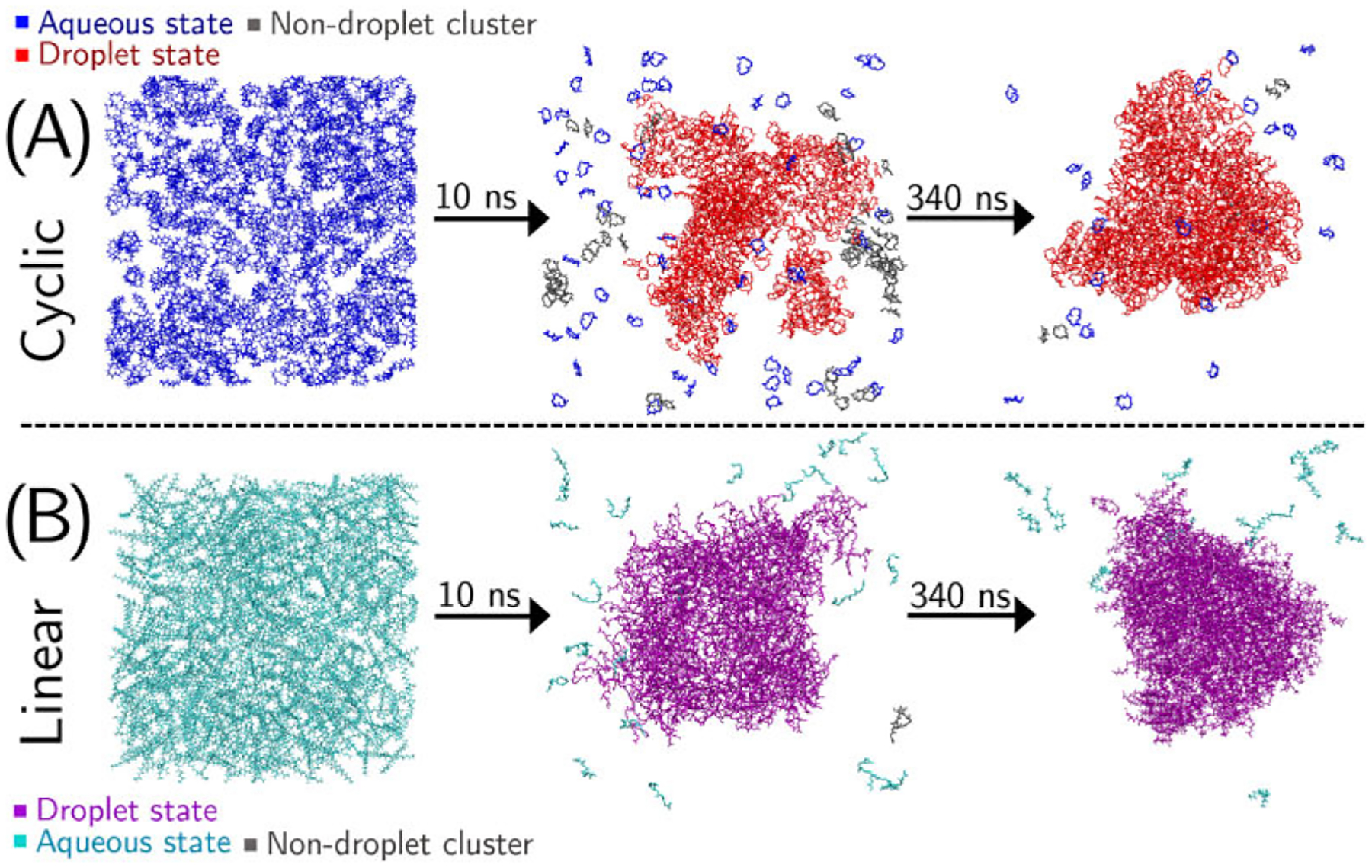
Snapshots from MD simulations showing the peptide droplet (red/purple) and aqueous (blue/cyan) phases in the cGGGGG (A) and GGGGG (B) systems at 0, 10, and 350 ns of the MD simulation. Peptides shown in gray are nondroplet clusters, i.e., peptides with <4 Å interpeptide contacts but not connected to the main droplet. The abundance of this state in the 10 ns cGGGGG system demonstrates the slower phase separation.

The phase separation of the linear GGGGG system appears to reach dynamic equilibration between phases around 20–50 ns sooner than the cGGGGG system. Figure 2 contains plots of the number of aqueous state peptides vs time for each system. Although the data is noisy, it appears that the number of aqueous peptides from both systems bottom out from the initial nonequilibrium decline at about 100 ns, with the cGGGGG system containing about 14 aqueous peptides at this initial minimum in comparison to the 3 aqueous peptides in the linear system. Following this initial decrease in aqueous peptides, the cyclic system reached a point of equilibration with an average value of ~26 peptides in the aqueous state. The linear system appeared to reach equilibrium more quickly after the first minimum, averaging ~14 aqueous peptides postequilibration, significantly less than the cyclic system. This translates to aqueous concentrations of 9 mM for the GGGGG system and 15.5 mM for the cGGGGG system. It is clear that under these conditions cGGGGG is more soluble than GGGGG, which is notable when considering the solvation free energies (ΔG_solv) of both peptides. Using FEP MD calculations in which we solvate and desolvate a peptide in solution, we estimated ΔG_solv to be −27.2 kcal mol⁻¹ and −29.3 kcal mol⁻¹ for cGGGGG and GGGGG, respectively. These values make sense when considering that the linear peptides carry an additional polar amide group as a result of the capped (ACE/NME) termini. The discrepancy between solubility limits and the aqueous ΔG_solv is a reflection of the full chemical potential for the system.

Figure 2.

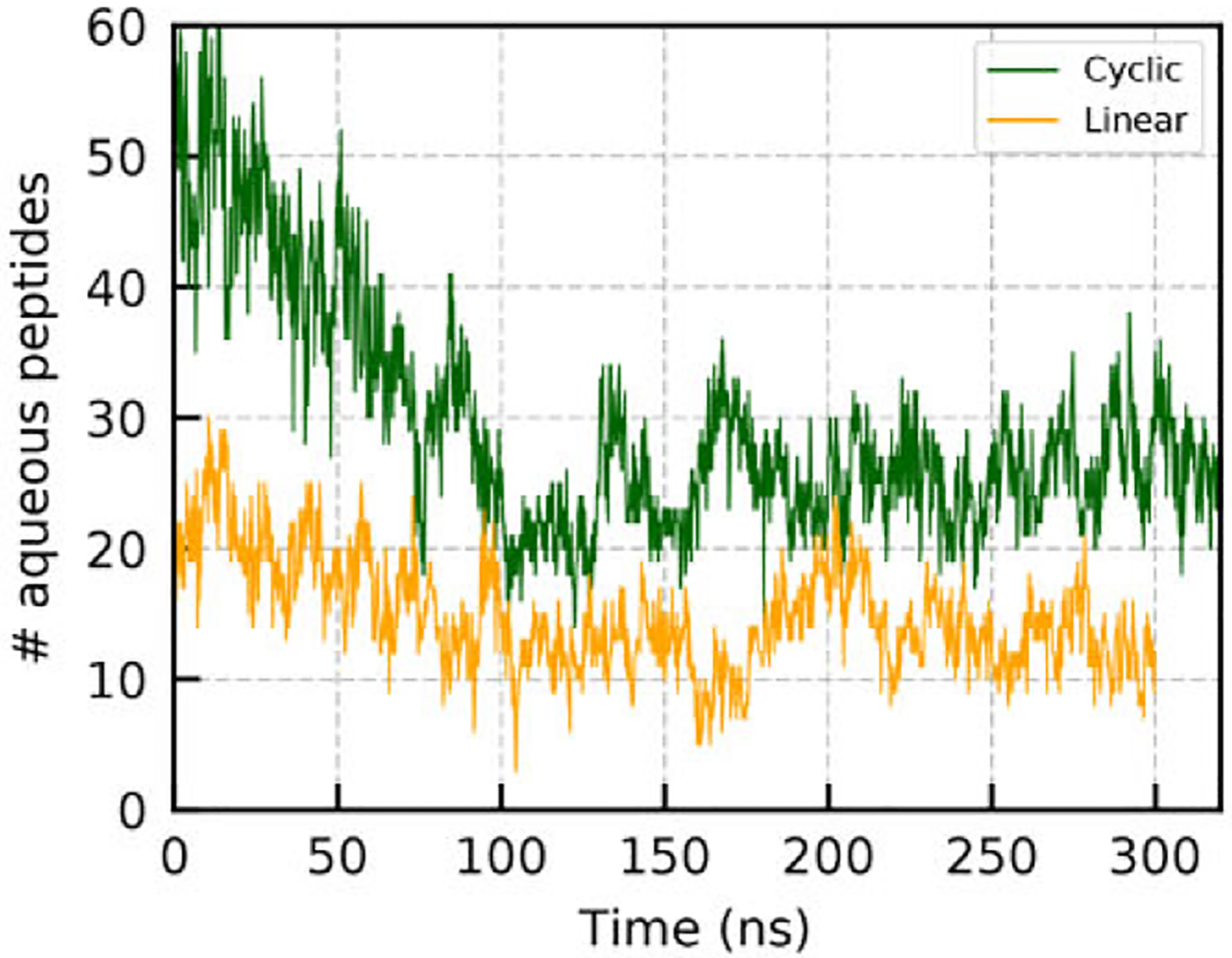
Plot of the number of aqueous peptides vs time for each simulated system.

The proteinaceous liquid droplet phases we observe in these pentaglycine systems are roughly 1000× denser with peptide than the surrounding solution. The interior of the GGGGG droplet has a higher peptide density than that of the cGGGGG droplet, possessing a ρ_peptide of 1.37 g mL⁻¹ compared to 1.23 g mL⁻¹ for cGGGGG. The conformational flexibility of linear pentaglycine allows a measurably tighter packing of peptides into the droplet. Interestingly, both of these densities are on the same order of magnitude as the density of the interior of globular proteins, which are reported to range from 0.5 to 3.0 g mL⁻¹.⁴³ A key difference between these two environments, however, is that a significant amount of water is present in the liquid peptide droplets we observe, due mostly to channels and invaginations, whereas the interior of globular proteins is typically closer to dry with some transient or trapped waters and fewer channels and invaginations. The interior of the cyclic and linear peptide droplets have average water concentrations of 12.1 and 11.7 M for the cyclic and linear systems, respectively. These concentrations are roughly a quarter of the concentration of pure bulk water, which indicates that peptide–water interactions are a nontrivial part of the total interactions in these droplets.

Intermolecular Interactions.

Other computational investigations of LLPS in systems of peptides have mostly utilized coarse-grained peptide models.^15,44–46 These simulations model important spatial and kinetic properties of LLPS events, but they do not allow the atomistic analysis of thermodynamic interactions and energetics that all-atom systems provide. Previous work on linear pentaglycine LLPS by our group^22,23 monitored the types of intermolecular interactions that stabilize the liquid droplet phase. These studies found that numerous peptide dipole–dipole interactions stabilize the phase separation of these peptide solutions. Hydrogen bonds (H-bonds), while crucial for stabilizing structured proteins, were found to not be the only dominant attractive interaction inside the droplets. Backbone dipole–dipole forces such as carbonyl–carbonyl interactions are abundant and provide significant favorable interaction enthalpy.²²

An analysis of the H-bonding present in the cyclic and linear pentaglycine systems reveals that H-bonding is more important in stabilizing the cyclic peptide droplets than in the linear peptide droplets. We calculated populations and H-bond enthalpies for peptide–peptide H-bonds in both systems and found that, in the droplet phase, both the cGGGGG and the GGGGG peptides form roughly 0.9 interpeptide H-bonds per amide. A per amide metric is useful as opposed to per peptide because the linear peptides have an extra amide group due to the termini. The criteria used to classify H-bonds was a maximum heavy atom distance of 3.5 Å and a heavy atom–hydrogen–heavy atom angle of >135°. H-bond enthalpies were obtained by evaluating the nonbonded potential between the H-bonding residues. Where the average enthalpy for linear peptide–peptide H-bonds is −3.6 kcal mol⁻¹, interpeptide H-bonds in the cGGGGG droplet have a strength of −4.1 kcal mol⁻¹). This indicates that, although both the linear and the cyclic peptides form similar numbers of H-bonds in the droplet phase, each H-bond, on average, in the cyclic peptide droplets is more enthalpically favorable. This suggests that interpeptide H-bonding plays a larger role in stabilizing the cGGGGG droplet phase, a result which correlates with specific interactions we observe in the cyclic peptide droplet phase. We also computed the H-bond enthalpy for peptide–water interactions inside the GGGGG and cGGGGG droplet phases and found an average H_H–bond = 4.1 kcal mol⁻¹ for both systems, indicating that cyclization has no effect on the enthalpy of droplet peptide–water H-bonds.

Figure 3 depicts a typical cyclic peptide stacking interaction motif we see in large numbers in the droplet phase. This stacking motif is defined by roughly parallel stacking of the cyclic peptide plane, which enables multiple H-bonds to form between the adjacent peptides. We observe this type of interaction in 72% of interior droplet peptides, and 41% of these peptides engage in stacking chains involving 3 or more peptides. The importance of these stacking interactions in facilitating interpeptide H-bonding is explored further in the last section. The linear peptide chains as opposed to stacking or T-shaped structures do not require high strength H-bonds to maintain their interaction enthalpy and thus can adopt more heterogeneous interaction chains. This phenomenon demonstrates the utility of structural disorder and flexibility in these droplet phases. One might assume the cGGGGG peptides, which form more H-bond interactions, to preferentially separate into the droplet phase, but instead it is the flexible disordered linear peptides that form more stable droplets and fall out of solution more easily than the cyclic peptides. The ability to find favorable enthalpy from a heterogeneous ensemble of intermolecular interactions is a salient feature of the LLPS behavior of disordered peptides.

Figure 3.

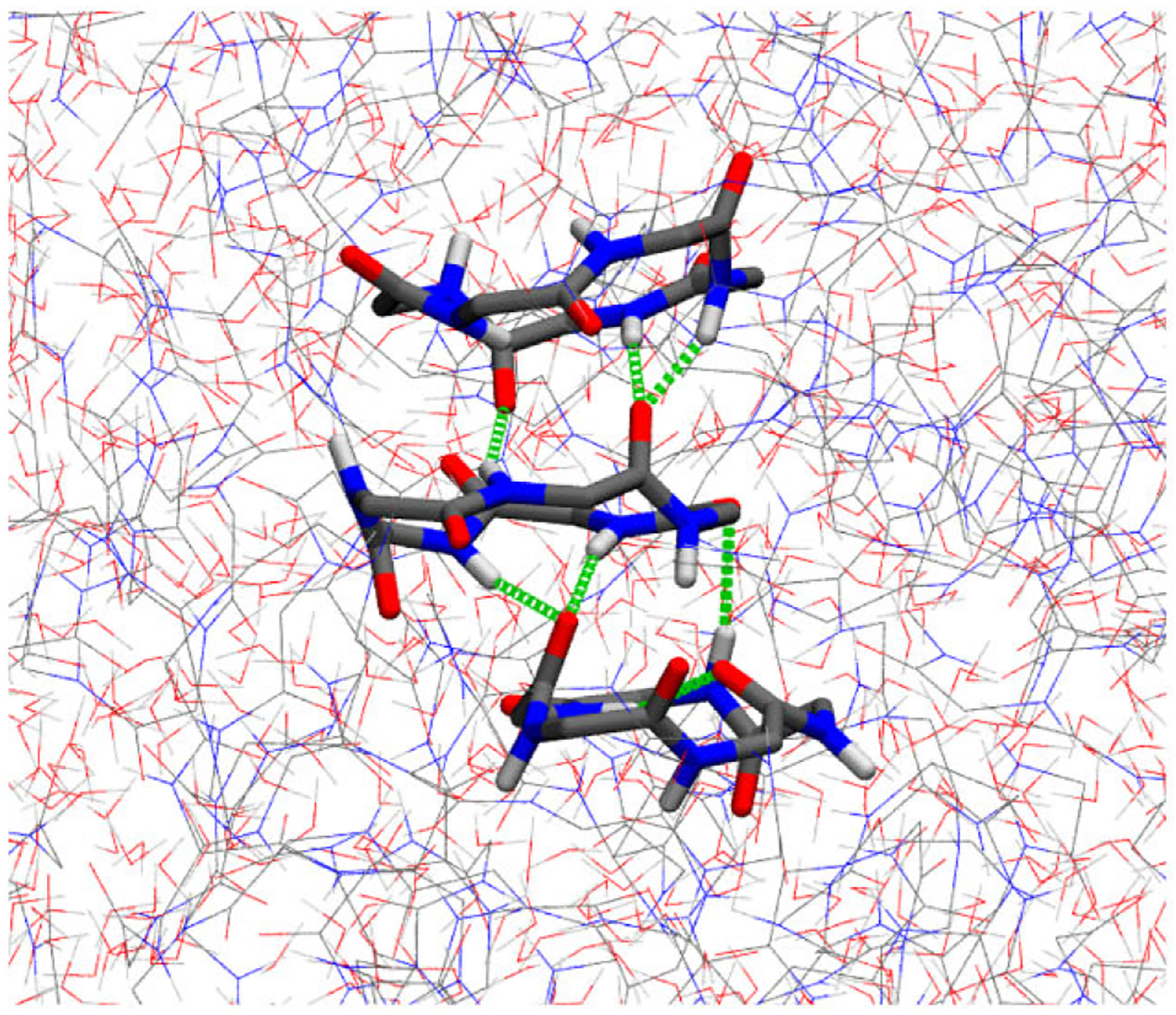
Molecular image of the cyclic peptide stacking H-bond interactions present abundantly in the droplet phase.

Entropy of Cyclic Peptides during LLPS.

Our previous work²⁴ has demonstrated that, upon transition from the aqueous to the droplet phase, linear GGGGG peptides sacrifice a significant amount of conformational and translational/rotational entropy. This is a result of the reduced conformational flexibility as well as the much slower diffusion that occurs in the droplet phase. The entropic properties of cyclic peptides are important in their use as pharmaceuticals. Cyclic peptides can possess higher activity than similar linear peptides,^29,30 and a major cause of this enhanced activity is cyclic peptides not sacrificing conformational entropy upon binding. In this work we calculated both the conformational and translational/rotational entropy change upon transition from the aqueous to the droplet phase for cyclic pentaglycine. We used the third order mutual information expansion (MIE) method⁴² to calculate the dihedral conformational entropy (MIE_conf); work by Drake et al.³⁹ has shown this method is accurate for estimating the conformational entropy of aqueous glycine-rich pentapeptides. MIE estimates the conformational entropy by summation over ρ·ln ρ dihedral density distributions as well as mutual information terms that account for second and third order correlations between adjacent dihedral angles. For a more in depth explanation of the conformational entropy calculations presented here we direct readers to a previous publication.²⁴ To obtain translational/rotational entropy, we used the PDB2TRENT program developed by Fogolari et al.⁴⁰ In k-nearest neighbor calculations, rotational and translational entropy, S_tr, for a peptide is calculated by approximating the multivariate probability density for each of a sample of k = 20 by monitoring how many other structures are found within a given volume around each structure and averaging over all structures.⁴⁰

To get average conformational entropies for peptides simulated here, we first determined which peptides exist in the aqueous or droplet phases for each time step. A bar plot showing average $S_{\text{conf}}^{\text{MIE},\text{fit}}$ values is presented in Figure 4, and these data are also contained in Table 1. The simulations show that the cGGGGG do not lose nearly as much conformational entropy when undergoing LLPS as the GGGGG. Whereas the linear peptides sacrifice 15.87 kcal mol⁻¹ of S_conf upon aqueous → droplet transition, the cyclic peptides only lose 3.01 kcal mol⁻¹. This is a smaller ΔS_conf than we have previously observed in any linear pentapeptide. It is clear that cyclization vastly decreases the amount of S_conf available to the peptide. However, it is worth noting that these peptides still do sacrifice some conformational entropy. We expect that the amount of conformational entropy available to a cyclic peptide will increase with increasing sequence length, and longer cyclic peptides will behave more like linear peptides due to greater flexibility and thus greater S_conf.

Figure 4.

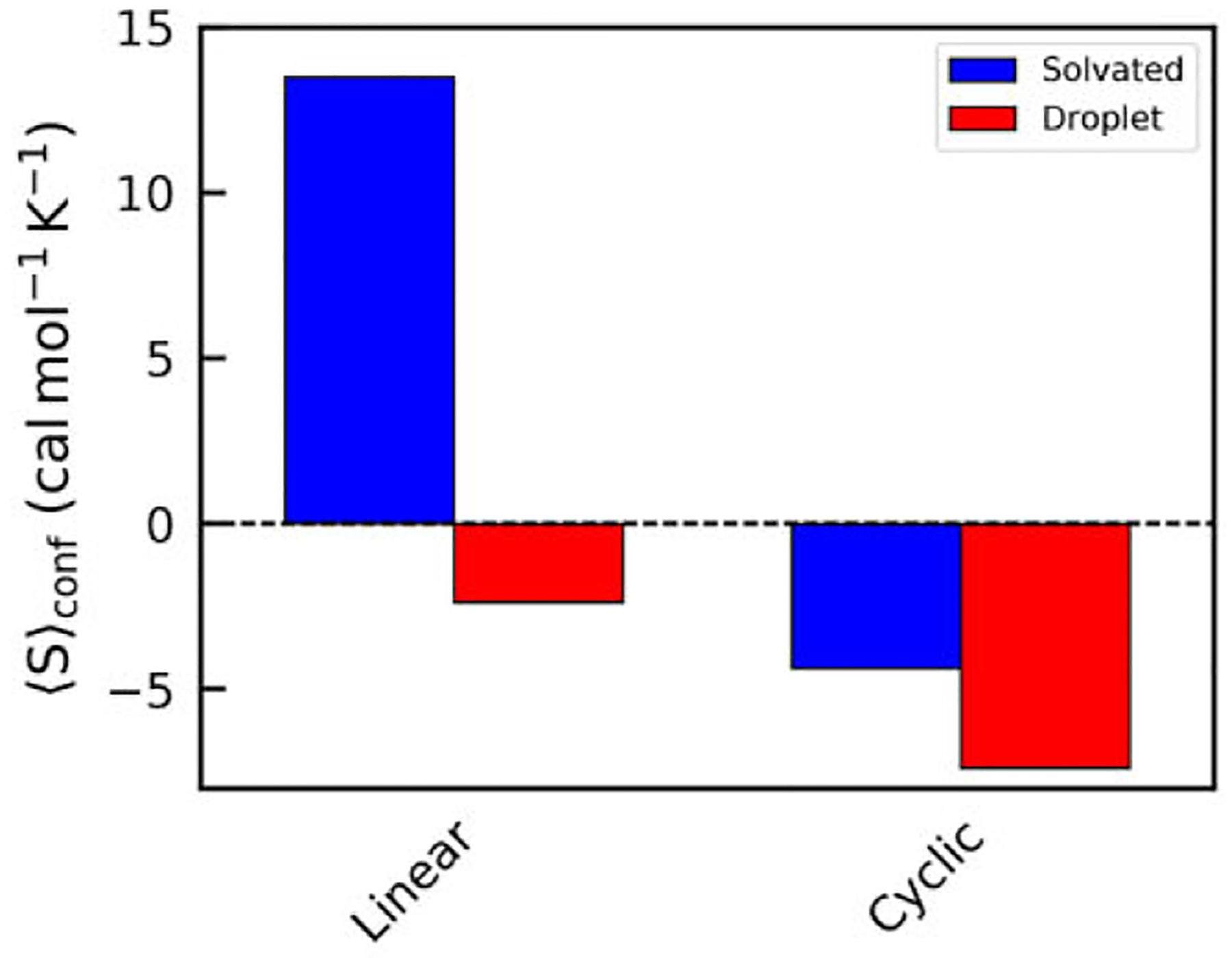
Average conformational entropy values for aqueous (blue) and liquid droplet (red) phase peptides for the linear and cyclic peptide systems.

Table 1.

$\Delta S_{\text{conf}}^{\text{MIE}}$ and ΔS_tr Data for GGGGG Linear/Cyclic Phase Transitions (in cal mol⁻¹ K⁻¹)

	Linear	Cyclic
$\Delta S_{\text{conf}}^{\text{MIE}}(\text{aq}\to \text{drop})$	−15.97 ± 0.81	−3.01 ± 0.5
$\Delta S_{\text{tr}}^{\text{MIE}}(\text{aq}\to \text{drop})$	−33.9 ± 2.9	−28.4 ± 2.1

We also calculated translational/rotational entropy (S_tr) changes upon LLPS for the cyclic peptides, which can be found in Table 1. These results suggest that both the linear and the cyclic peptides lose similar amounts of S_tr upon phase transition, with the cyclic peptides losing slightly more. Interestingly, the changes in S_tr are larger than the ΔS_conf for the linear peptides, but while conformational entropy is sensitive to conformational transitions, S_tr is not significantly modulated in the same way.

It is clear that, while cyclic peptides’ smaller ΔS_conf may play a significant role in binding activity scenarios, it does not account for the fact that the linear pentaglycine preferentially transitions into the droplet phase and has a lower solubility limit in these systems. It would seem that intermolecular interactions and the associated enthalpy play a larger role in stabilizing liquid peptide droplets than entropy changes.

Interaction Enthalpies.

We quantified the nonbonding interactions of the cyclic peptides with their environment to monitor the enthalpy change accompanying phase transition in this system. Interaction enthalpies H_int were gathered by summing the total nonbonded interaction energy of each cyclic peptide with its environment using the Amber14SB force field.³⁶ The total interaction energy data are presented in Figure 5, with the droplet state data shown as the red bars and aqueous state data shown in blue for both the cyclic and the linear pentaglycine systems. This data illustrates that, in both the cyclic and linear peptide systems, peptides in the droplet phase generate higher interaction enthalpies than those in the aqueous phase. This and our previous studies show that, for all peptide sequences studied, transitioning from the aqueous phase to the droplet phase grants peptides, on average, a 120% boost to interaction enthalpy. The total H_int data in Figure 5 shows that the linear peptides have lower, hence more favorable, interaction enthalpies than the cyclic peptides in both the aqueous and the droplet phases. However, when these enthalpies are modified to a per-amide value, due to the linear peptides having an additional amide group, the GGGGG and cGGGGG peptides possess nearly identical H_int per amide. This is a rough approximation of the energetic effect of the capped termini but nonetheless indicates that the amide-proportional interaction enthalpies are fairly equal between the two systems.

Figure 5.

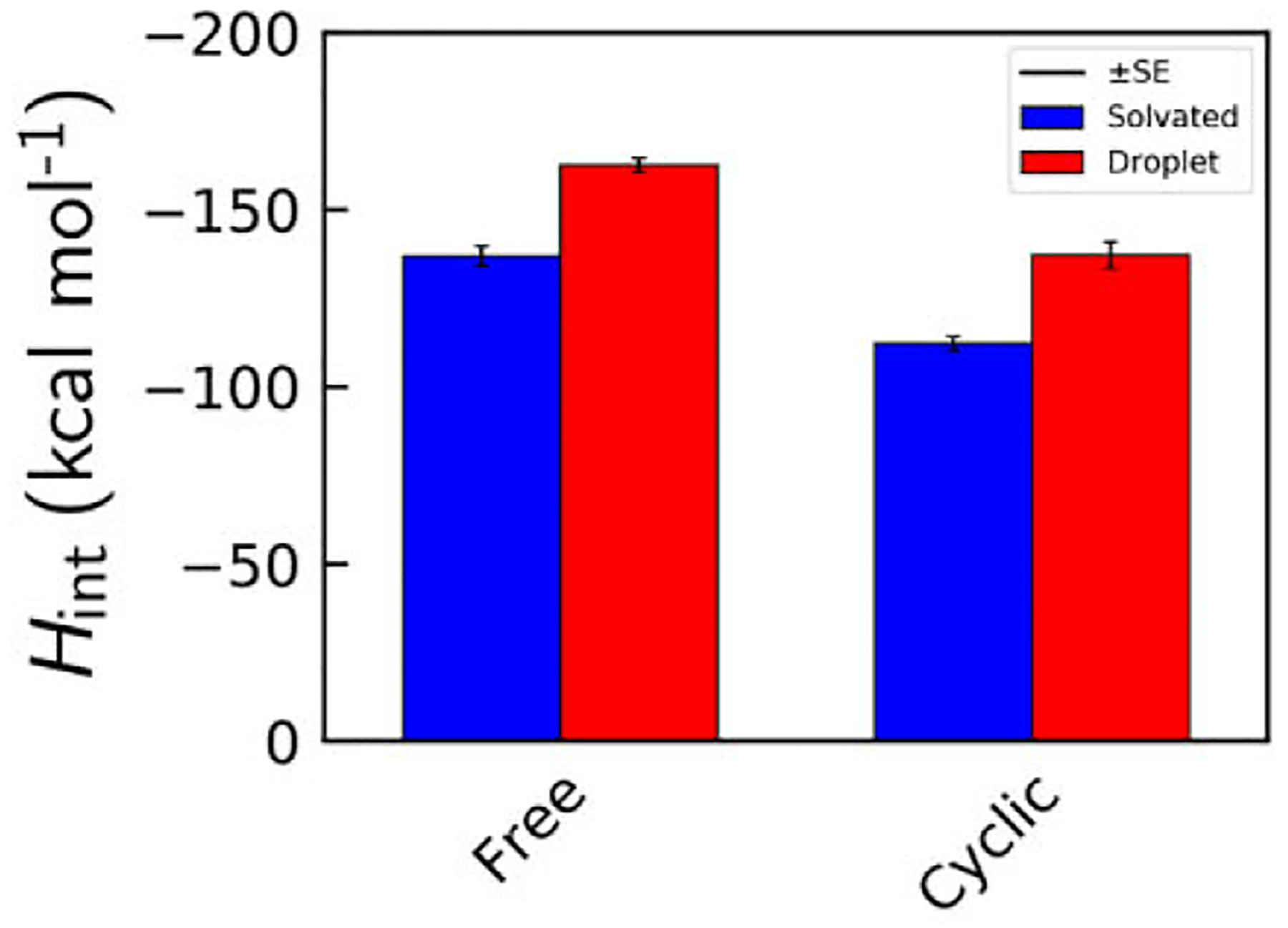
Average interaction enthalpy values for aqueous (blue) and liquid droplet (red) phase peptides. Error bars represent the standard error of the H_int distribution.

Next, we decomposed the total interaction enthalpies into electrostatic and van der Waals components for more detailed information on the types of interactions that predominate during phase transition. This data is seen in Figure 6.

Figure 6.

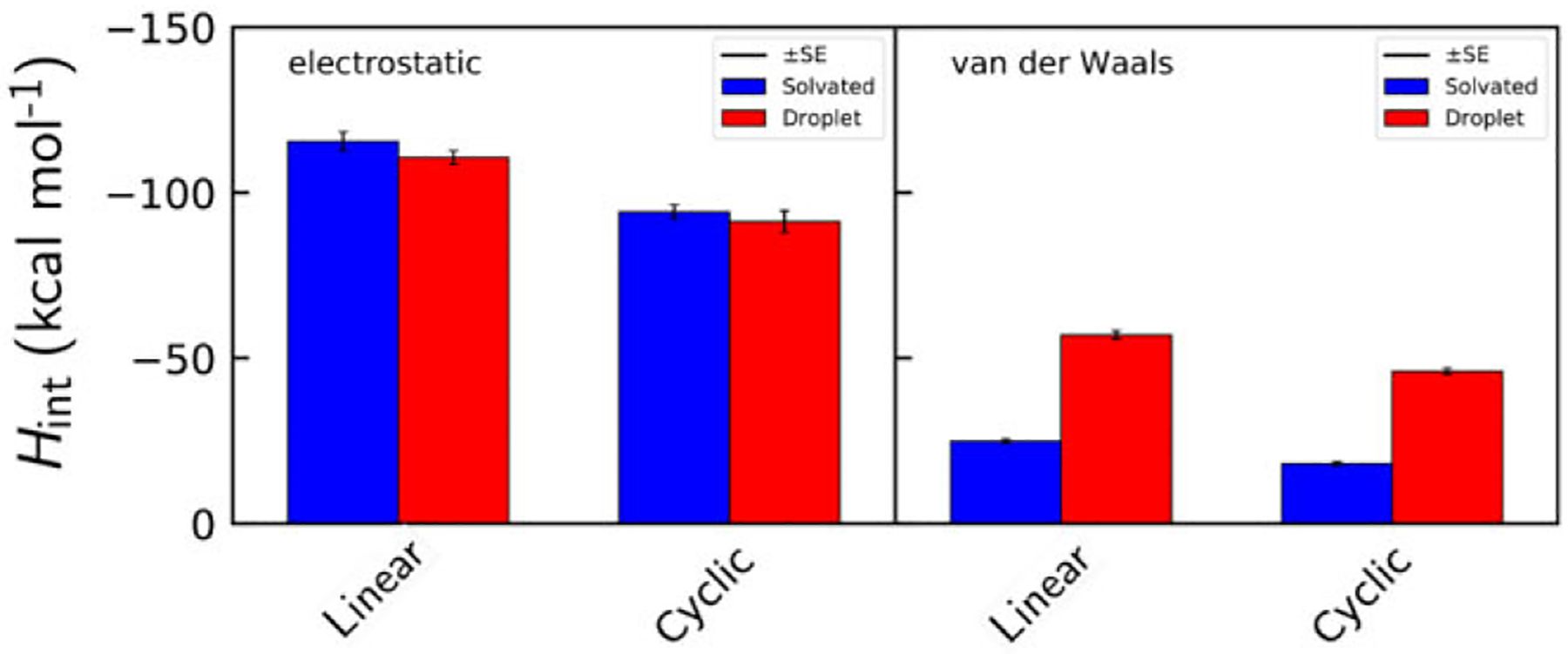
Electrostatic and van der Waals interaction enthalpy values for aqueous (blue) and liquid droplet (red) phase peptides. Error bars represent the standard error of the H_int distribution.

Average H_int from electrostatic interactions are featured on the left, and those from van der Waals (vdw) interactions are on the right. Unsurprisingly, electrostatic enthalpy is markedly higher in magnitude than that from the Lennard-Jones-based van der Waals interactions. Our previous study on linear peptides reported that electrostatic enthalpy does not appreciably change upon phase transition,²⁴ and the cyclic peptide also shows this characteristic. Aqueous GGGGG and cGGGGG form 5.0 and 4.4 more total H-bonds than those in the droplet state, respectively. Favorable H_elec from CO–CO and other dipolar interactions makes up the difference, allowing both states to have roughly equal H_elec. More detailed explorations into such peptide dipole–dipole interactions can be found in previous work by Karandur²⁰ and Sarma²³ et al. The H_int (vdw) is enriched upon transition to the droplet Phase, dropping from −18.1 to −46.0 kcal mol⁻¹. This result demonstrates that the peptide density of the droplet combined with some water molecules filling the space in between peptides creates a potent environment for the formation of favorable vdw packing interactions.

DISCUSSION

Intrinsic disorder is often described in terms of conformational flexibility, a quality that allows IDPs/IDRs to form heterogeneous ensembles of structures that allow many functional states in these molecules. A property of IDRs/IDPs is their propensity to undergo LLPS, transitioning from disordered solvated chains to condensed globular phases that allow for different functionality. Biologically relevant instances of LLPS such as membraneless organelles are facilitated by high concentrations of disordered proteins.^47,48 Here, we simulate LLPS in systems of cyclic pentaglycine that do not possess the conformational flexibility of the intrinsically disordered linear pentaglycine.

In a system of 625 cyclic pentaglycine (cGGGGG) at high concentration (0.3 M), LLPS occurs spontaneously after ~10 ns, eventually reaching an equilibrium of 26 aqueous peptides surrounding a liquid peptide droplet containing 599 peptides (shown in Figure 1). Previous work by our group involved similar simulation using the same protocols of a linear pentaglycine system, and this system possessed an aqueous phase of only 14 peptides.²⁴ It is clear from these results that, in high concentration systems, cGGGGG is more soluble than linear GGGGG and undergoes a transition into the condensed droplet phase less readily.

The liquid droplet formed by LLPS in the cGGGGG system featured many instances of a cyclic peptide stacking interaction motif, as seen in Figure 3, that seemingly enables H-bonding between cyclic peptides. A majority of droplet phase peptides engaged in these interactions, and nearly half were involved in 3+ peptide chains of such stacking motifs. An investigation of H-bonding strength in cyclic versus linear pentaglycine shed some light on the origin of these interactions. Interpeptide H-bonds in the cGGGGG droplet phase have an enthalpy of −4.1 Kcal mol, and the same types of interpeptide H-bonds in GGGGG droplets only have a strength of −3.6 kcal mol. The inflexible cGGGGG rely on these H-bonds much more to supply favorable enthalpy in the droplet phase, which provides a driving force toward the formation of these stacked peptide structures.

Study into the effect of conformational entropy in LLPS has been limited. Several publications have investigated the role of the solvation entropy⁴⁹ or the entropy of mixing^50,51 in driving LLPS, but the changes in conformational, rotational, and translational entropy that occur on the molecular level remain less explored. Our previous work has shown that linear pentaglycine peptides sacrifice ~16 cal mol⁻¹ K⁻¹ of conformational entropy upon aqueous → droplet phase transition, and here we considered how cyclization would potentially mute this free energy exchange. We found that cyclic peptides lose far less conformational entropy when undergoing LLPS, sacrifing roughly 3 cal mol⁻¹ K⁻¹ of entropy. The reduced S_conf of cGGGGG is of interest to drug discovery, as cyclic peptides may possess higher activity than linear peptides.³² The decreased entropy loss upon binding allows cyclic peptides potentially to bind more strongly. Our work shows that although cyclic peptides lose significantly less entropy than linear peptides during LLPS, they do lose some conformational entropy. We also find that both cGGGGG and GGGGG lose roughly the same amount of translational/rotational entropy, ΔS_tr = ~30 cal mol⁻¹ K⁻¹) in both the cyclic and the linear pentaglycine systems (Table 1).

Our previous work has established that interactions drive phase separation. Losses of entropy are offset by favorable decreases in vdw interaction enthalpy upon aqueous to droplet transitions. Figures 5 and 6 demonstrate that this holds true in LLPS of cGGGGG as well, as the peptides experience a ΔH_int of −28 kcal mol⁻¹, coming largely from enriched vdw interactions. As we previously observed, H_int stemming from electrostatic interactions does not change significantly upon phase transition, indicating that both aqueous and peptide-dense environments are able to provide similar levels of Coulombic interactions. We find, however, that the cGGGGG rely more heavily on H-bonds for electrostatic enthalpy.

The interplay between the vdw and electrostatic H_int aligns with results from peptide osmolyte studies.^19,52,53 In that work, discrimination between urea and TMAO cosolvents on the solvation free energy stemmed mainly from the van der Waals interactions, whereas the magnitude of electrostatic energy was larger but did not vary appreciably between structures. Our work here shows that both linear and cyclic peptides can adopt many more vdw contacts in a condensed peptide phase than in aqueous solution. Neither here nor in previous studies do we find H-bonding playing the dominant role in the droplet phase peptides’ electrostatic interactions.

CONCLUSIONS

Simulations of LLPS in systems of cyclic and linear pentaglycine show that cyclization has a pronounced effect on the solubility and, therefore, the LLPS properties of the peptides. Although linear GGGGG possess a more favorable single molecule solvation free energy, cGGGGG are more soluble than linear pentaglycine. This stems from linear peptides’ propensity to form favorable interpeptide interactions, in particular favorable vdw interactions, and thus fall out of solution into the peptide droplet phase. Our results show that cGGGGG peptides, on the other hand, lack the ability to engage in interpeptide interactions to this extent, relying more on semiordered H-bond formation. The linear GGGGG droplets do not rely on high strength H-bonds to maintain interaction enthalpy and, thus, can adopt more varied interaction networks. However, cGGGGG still exhibit the enriched vdw enthalpy upon phase transition that we observe with the linear peptides, albeit to a lesser degree. Our calculations show that cyclic peptides sacrifice far less conformational entropy upon aqueous → droplet phase transition than linear peptides, and this likely plays a role in driving systems of cyclic peptides to phase separation. The balance between entropy loss and enthalpy gain during LLPS remains central to understanding this process. While cyclic peptides lose less conformational entropy, the results presented here highlight the importance of interpeptide interactions and the associated favorable enthalpy in driving LLPS.