Fully Automated Segmentally Boosted VMAT

Abstract

Purpose:

Treatment planning for volumetric modulated arc therapy (VMAT) typically involves the use of multiple arcs to achieve sufficient intensity modulation. Alternatively, we can perform segment boosting to achieve similar intensity modulation while also reducing the number of control points used. Here, we propose the MetaPlanner Boosted VMAT (MPBV) approach, which generates boosted VMAT plans through a fully automated framework.

Methods:

The proposed MPBV approach is an open-source framework that consists of three main stages: meta-optimization of treatment plan hyperparameters, fast beam angle optimization on a coarse dose grid to select desirable segments for boosting, and final plan generation (i.e. constructing the boosted VMAT arc and performing optimization).

Results:

Performance for the MPBV approach is evaluated on 21 prostate cases and 6 head and neck cases using clinically relevant plan quality metrics (i.e. target coverage, dose conformity, dose homogeneity, and OAR sparing). As compared to two baseline methods with multiple arcs, MPBV maintains or improves dosimetric performance for the evaluated metrics while substantially reducing average estimated delivery times (from 2.6 to 2.1 minutes).

Conclusions:

Our proposed MPBV approach provides an automated framework for producing high quality VMAT plans that uses fewer control points and reduces delivery time as compared to traditional approaches with multiple arcs. MPBV applies automated treatment planning to segmentally boosted VMAT to address the beam utilization inefficiencies of traditional VMAT approaches that use multiple full arcs.

1. INTRODUCTION

Radiotherapy plan quality heavily depends on how many degrees of freedom are available in the delivery system¹. Intensity modulated radiation therapy (IMRT) and volumetric modulated arc therapy (VMAT) represent two very popular treatment modalities with substantial differences in the degrees of freedom of plan delivery. On one hand, IMRT offers great flexibility in modulating the intensity of incident beams but might be potentially lacking in angular coverage². On the other hand, VMAT offers great angular coverage but might lack adequate intensity modulation².

A. Problem Formulation and Related Works

Many previous methods have been proposed for both IMRT and VMAT in order to improve plan quality. For IMRT, increasing angular coverage can potentially maintain or improve planning target volume (PTV) dose while better avoiding surrounding organs-at-risk (OARs). Beam angle optimization (BAO), which addresses the problem of selecting incident beam angles, can be applied to IMRT in both coplanar and noncoplanar settings^3–6. Similarly, BAO has also been incorporated into the trajectory selection process of noncoplanar VMAT plans⁷.

In the case of VMAT, plan quality can also be improved by utilizing multiple arcs. Specifically, single arc VMAT plans may have insufficient beam intensity modulation for cases with complex geometries (e.g. head and neck, abdomen, etc.). Planners typically incorporate multiple arcs to improve the intensity modulation of these VMAT plans, but doing so can potentially under-modulate or over-modulate certain directions^2,8. The issue of insufficient intensity modulation was also previously addressed by segmentally boosting a single-arc VMAT plan with small partial arcs⁸. In this method, which we subsequently refer to as boosted VMAT (BVMAT), additional partial VMAT arcs are inserted into a single-arc VMAT plan to improve intensity modulation, which allows boosted VMAT to achieve similar performance to a multiple-arc VMAT plan while substantially reducing delivery time (Figure 1). The original boosted VMAT method, however, has two main limitations: 1) it utilizes a non-standard modulation index function to determine which segments of the arc trajectory to boost and 2) it has previously not been adapted for automated planning.

Figure 1.

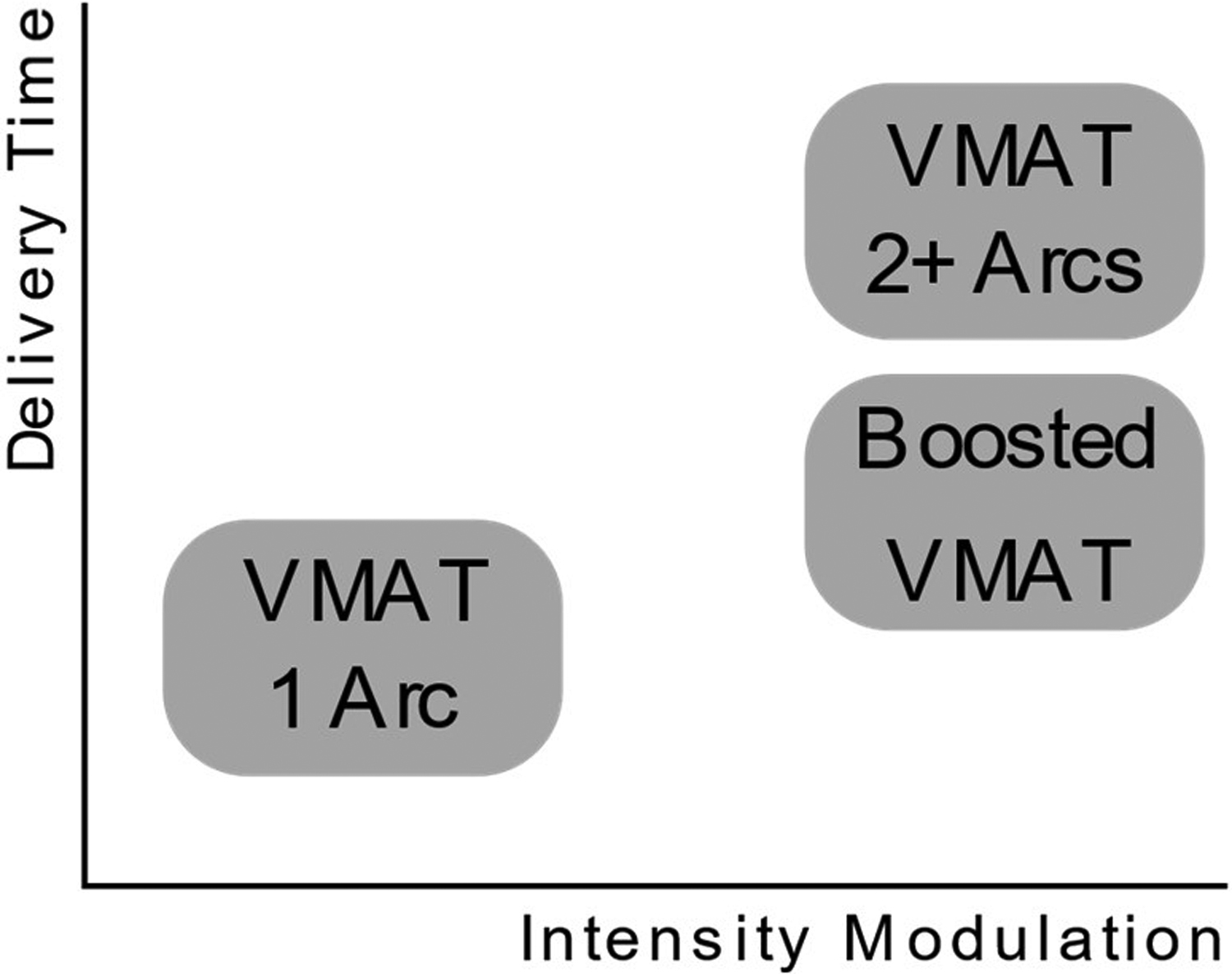
Schematic drawing of the differences in VMAT techniques.

In this current work, we extend on the original boosted VMAT method by incorporating it into an automated treatment planning framework called MetaPlanner (MP)⁹. Our proposed method, MetaPlanner boosted VMAT (MPBV), provides a fully automated framework for creating boosted VMAT plans, and we describe its implementation below.

2. METHODS

The proposed MPBV approach generates segmentally boosted VMAT plans in a fully automated fashion. Figure 2 provides an outline of the workflow for the MPBV approach, which contains three main stages: meta-optimization of plan hyperparameters, beam angle optimization, and final plan generation.

Figure 2.

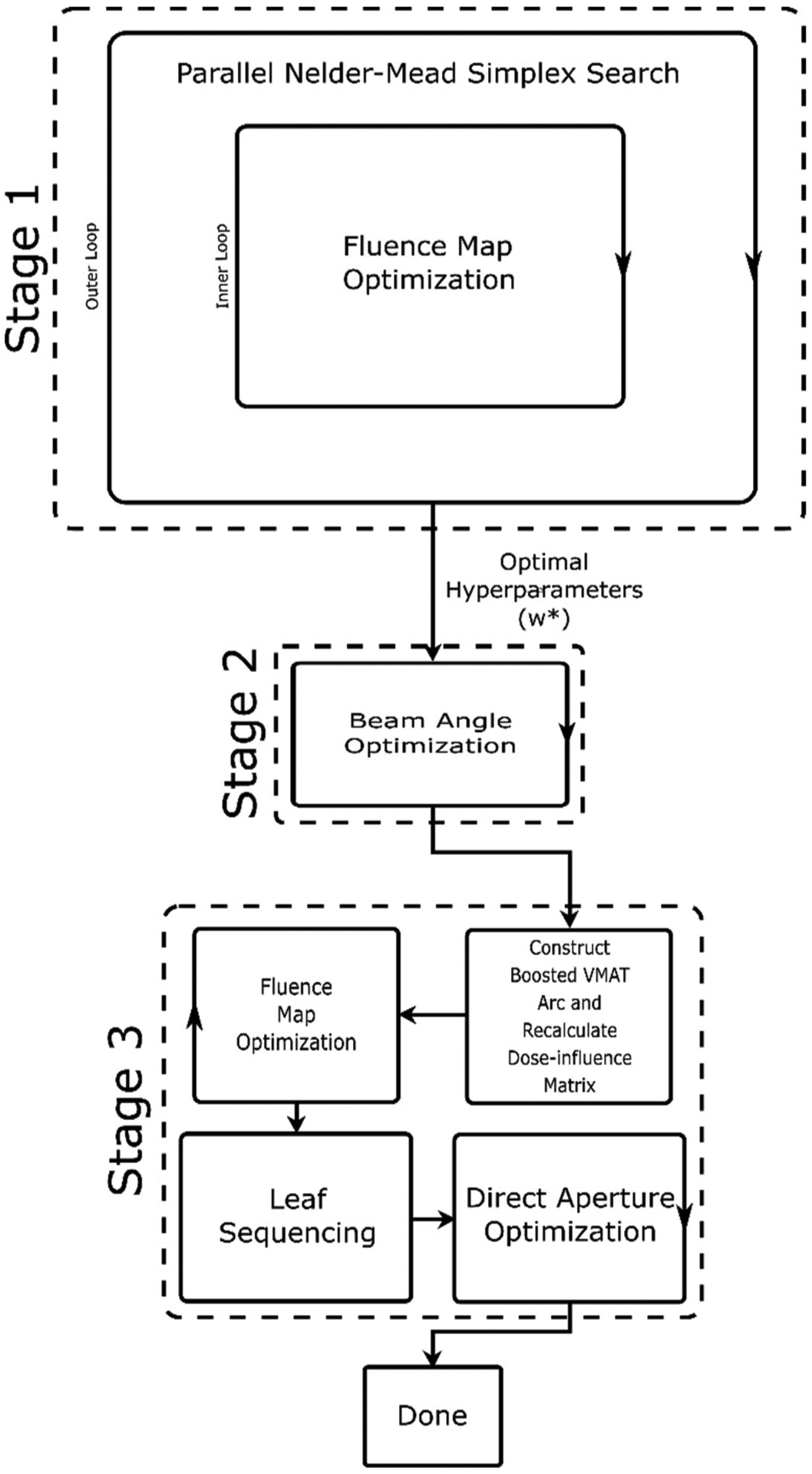
Visualization of the MP approach applied to IMRT and VMAT planning.

A. Meta-optimization (Stage 1)

The first stage of the MPBV approach is meta-optimization, which involves two nested loops of optimization. The inner loop performs fluence map optimization (FMO) using the interior point optimizer (IPOPT)^10,11, and the outer loop performs optimization of plan hyperparameters using the parallel Nelder-Mead simplex search^12,13. Upon completion of the meta-optimization stage, optimal hyperparameters (i.e. objective function weights w*) are passed on to the second stage. Equations 1 and 2 describe the optimization problems in the outer and inner loops, respectively. Here, we only provide a brief summary of the meta-optimization algorithm and refer interested readers to previous work for a more detailed description⁹.

Stage 1 (Outer Loop)
$\underset{w}{\mathit{\text{min}}}$	$f_{\mathit{\text{meta}}}\left(w\right)= \frac{{\sum }_i^m{2}^{-{\tau }_i+1}\cdot F_{{\tau }_i}}{{\sum }_i^m{2}^{-{\tau }_i+1}}$
s.t.	w ≽ 0
	1T w ≤ 1	(1)
Stage 1 (Inner Loop)
$\underset{x}{\mathit{\text{min}}}$	$w_{\mathit{\text{PTV}}}\sum _{s\in \mathit{\text{PTVs}}}\frac{1}{N_s}\sum _{i\in s}{\left(d_i-\widehat{d}\right)}^2+\sum _{s\in \mathit{\text{OARs}}}\frac{w_s}{N_s}\sum _{i\in s}\Theta \left(d_i-\widehat{d}\right){\left(d_i-\widehat{d}\right)}^2$
s.t.	x ≥ 0
	$\stackrel{\rightharpoonup }{\mathit{\text{d}}} = \mathit{D}\stackrel{\rightharpoonup }{\mathit{x}}$	(2)
Meta-scoring Tier List
	$F_{{\tau }_0} = \frac{1}{\left|\mathit{\text{PTVs}}\right|}\sum _{sϵ\left\{\mathit{\text{PTVs}}\right\}}\mathit{\text{min}}\left(1,\mathit{\text{ max}}\left(\frac{H{I}_s - H{I}_{s,(-)}}{H{I}_{s, (+)}- H{I}_{s,(-)}},0\right)\right)$
	$F_{{\tau }_1} = \mathit{\text{min}}\left(1,\mathit{\text{max}}\left(\frac{C{I}_{(+)}-CI}{C{I}_{(+)} -C{I}_{(-)}},0\right)\right)$
	$F_{{\tau }_2} = \frac{1}{\left|\mathit{\text{OARs}}\right|}\sum _{s\in \left\{\mathit{\text{OARs}}\right\}}\mathit{\text{min}}\left(1,\mathit{\text{max}}\left(\frac{{\overline{\text{d}}}_s -{\overline{\text{d}}}_{s,(-)}}{{\overline{d}}_{s,(+)}-{\overline{\text{d}}}_{s,(-)}},0\right)\right)$
	$F_{{\tau }_3} = \frac{1}{\left|\mathit{\text{OARs}}\right|}\sum _{s\in \left\{\mathit{\text{OARs}}\right\}}\mathit{\text{min}}\left(1,\mathit{\text{max}}\left(\frac{{\overline{\text{d}}}_s -{\overline{\text{d}}}_{s,(-)}}{{\overline{d}}_{s,(+)}-{\overline{\text{d}}}_{s,(-)}},0\right)\right)$
		(3)

In Equation 1, w refers to the objective function weights for inverse planning optimization and f_meta refers to the meta-scoring function used to evaluate the clinical acceptability of each treatment plan. In Equation 2, d_i refers to the dose at voxel i, $\widehat{d}$ refers to the structure-specific reference dose, Θ(⋅) refers to the Heaviside function, N_s refers to the number of voxels in structure s, {∙} refers to the set of OARs or PTVs, and D refers to the dose-influence matrix. For FMO, x refers to the pencil beam weights. For DAO, the optimization problem description is provided in the original MatRad papers^10,11.

Here, the adopted auto-planning method MetaPlanner performs a hyperparameter search while guided by a utility function. This utility function, which we subsequently refer to as the meta-scoring function, performs a weighted average of various aspects of the treatment plan dose distribution in order to evaluate its utility. To compute the meta-scoring function, we first construct a tier list (Equation 3) for ranking planner preferences, and the overall meta-scoring function (Equation 1) can be computed as a weighted average of scores for each tier. Similarly, the tier list incorporates many popular dose statistics and indices that are routinely used in clinical decision-making: dose homogeneity^14,15, dose conformity^16,17, dose spillage¹⁸, and mean OAR dose. Desired ranges in the source code (i.e. notations containing {(−),(+)}) are adapted from standard protocol (i.e. RTOG 0126 and NRG HN005). The relevant equations used in meta-scoring are listed together as Equation 3, and we refer interested readers to previous work for an in-depth description⁹.

Table 1 provides definitions for the homogeneity index, conformity index, dose spillage, and mean dose terms that are incorporated into the meta-scoring function. Here, D_(∙) refers to the dose received by (∙)% of the volume, D_p refers to the prescription dose, V_(∙) refers to the volume that receives (∙) dose, TV_(∙) refers to the target volume that receives (∙) dose, d_i refers to the dose at voxel i, and n_s refers to the number of voxels in structure s.

Table 1.

Definitions for dose homogeneity, dose conformity, dose spillage, and mean dose.

	Homogeneity Index	Conformity Index	Dose Spillage	Mean Dose (μ)
Formula	$HI = 100\times \frac{D_5-D_{95}}{D_p}$	$CI = \frac{{\left(T{V}_{95D_p}\right)}^2}{TV\times V_{95D_p}}$	$R50 = \frac{V_{50D_p}}{TV}$ $R90 = \frac{V_{90D_p}}{TV}$	${\overline{d}}_s = \frac{1}{n_s}\sum _{iϵs}^{n_s}{d}_i$

When computing the term $F_{{\tau }_i}$ for each tier τ_i, we normalize each consideration to the range [0,1] and average all the considerations in each tier. For instance, for head and neck cases, we can compute the following $F_{{\tau }_0}$ for Tier 0:

$$F_{{\tau }_0} = \frac{1}{\left|\mathit{\text{PTVs}}\right|}\sum _{sϵ\left\{\mathit{\text{PTVs}}\right\}}\mathit{\text{min}}\left(1,\mathit{\text{ max}}\left(\frac{H{I}_s - H{I}_{s,(-)}}{H{I}_{s, (+)}- H{I}_{s,(-)}},0\right)\right)$$

Other relevant parameters used during meta-optimization are listed in Table 2. For a full description of the meta-scoring function and its terms, please see our original MetaPlanner work, as well as our source code⁹.

Table 2.

Lists the meta-scoring tier list and other relevant parameters used during treatment planning.

	Tier 0 (τ0)	Tier 1 (τ1)	Tier 2 (τ2)	Tier 3 (τ3)		Overlap Priority	Reference Dose ($\widehat{\mathit{d}}$)
Prostate Cases	HI	CI	Sparing (Rectum, Bladder)	Sparing (FH R, FH L, Body)	PTV	1	74
					Rectum	2	0
					Bladder	2	0
					FH R	2	30
					FH L	2	30
					Body	2	30
Head and Neck Cases	HI (PTV 70, PTV 56, PTV 52)	CI (PTV 70)	Sparing (Spinal Cord, Brainstem, Parotid R, Parotid L, Oral Cavity, Larynx,)	Sparing (Body)	PTV 70	1	72
					PTV 56	2	58
					PTV 52	3	54
					Cord	4	30
					Brainstem	4	30
					Parotid R	4	0
					Parotid L	4	0
					Oral Cavity	4	0
					Larynx	4	0
					Body	4	30

B. Beam Angle Optimization (Stage 2)

The second stage of the MPBV approach utilizes BAO to select promising segments of the VMAT arc for boosting. Many viable strategies for BAO have been proposed in literature³. For the current implementation, an iterative BAO method was used to select promising angles^3,19,20. The BAO method used here has been adapted from previous works on selecting noncoplanar VMAT trajectories¹⁹. In this stage, promising beam directions are iteratively added from the set of feasible beams (i.e. beams that do not result in couch-gantry collisions). During each iteration of BAO, we perform FMO for each of the beam angles in the feasible set and add the best performing angle to the growing ensemble. The setup for FMO here follows Equation 2 and utilizes the meta-optimized hyperparameters output by stage 1.

Beam angle optimization typically requires an objective function in order to select desirable beam angles. As there are many conflicting objectives in the overall function, we need to first select optimal hyperparameters before performing BAO. For this reason, our workflow has been to first perform automated planning and then perform iterative BAO, directly utilizing the optimal hyperparameters output by previous stages of the proposed MPBV approach. Alternatively, BAO can be performed without tuning hyperparameters, where we instead utilize various heuristic measures for guessing the objective weights. Bangert et al.³ provides a comparison of tuned vs. guessed hyperparameters for BAO. While it is certainly possible to use these heuristics guesses in our framework, we chose to follow our proposed workflow as we believe it is more principled and reproducible.

C. Final Plan Generation (Stage 3)

The third stage of the MPBV approach involves generating the final boosted VMAT plan. The third stage begins by constructing the boosted VMAT arc, which consists of the original single arc and the additional partial arcs. In the current implementation, the single 360° arc is created by placing control points along a coplanar direction with a 6° gantry angle spacing. For each of the beam angles selected during BAO, a partial VMAT arc (24°) is then added with the center control point of the arc placed at the selected beam angle and surrounding control points placed with a 6° gantry angle spacing. Following the standard pipeline in MatRad, we then recalculate the dose-influence matrix, perform FMO, run leaf sequencing, and perform DAO.

D. Implementation

The proposed approach utilizes a development branch (dev_VMAT) of the open-source MatRad software package^10,11,21. A singular value decomposed pencil beam algorithm was used to compute the dose-influence matrix²². To reduce computation cost, all final plans were generated using a pencil beam size of 5 × 5 mm² and a voxel size of 3.5 × 3.5 × 3.5 mm³. Moreover, the source code for our proposed approach has been made available online (https://github.com/chh105/MetaPlanner).

3. RESULTS

3.1. Experimental Setup and Evaluation

The proposed approach is evaluated on a dataset of 21 prostate cases and a dataset of 6 head and neck cases (Stanford IRB protocol #41335), where both datasets were originally created as part of clinical workflow. We perform comparisons between the proposed approach and two baseline methods. The first baseline method consists of manual plans that utilize two full coplanar arcs. Each arc uses roughly 180 control points (CPs) with a 2° gantry angle spacing (total ~360 CPs). These manual VMAT plans were planned by experienced planners using the Eclipse treatment planning software from Varian Medical Systems. For the second baseline method, fully automated plans were created using the standard form of the MetaPlanner framework in the MatRad treatment planning system. These plans consisted of two full coplanar arcs with a total of 120 CPs (6° gantry angle spacing). Finally, the third method consists of fully automated plans created using the MPBV (MetaPlanner & Boosted VMAT) framework. These plans were also created in MatRad and consisted of a boosted VMAT arc (one full arc and five partial arcs) with a total of 90 CPs.

3.2. Qualitative Comparison

We first perform a qualitative comparison between methods by comparing dose distributions and dose volume histograms (DVHs). The dose distributions of two representative cases, where the top row shows a prostate case and the bottom row shows a head and neck case, are visualized in Figure 3. For the prostate case, the proposed MPBV method substantially improves sparing to the rectum (see white arrows) while maintaining similar target coverage, dose homogeneity, dose conformity, etc. with the baseline methods. For the head and neck case, the proposed method substantially improves dose homogeneity to PTV 52 and dose spillage (see white arrows) while maintaining similar target coverage, conformity, etc. with the baseline methods.

Figure 3.

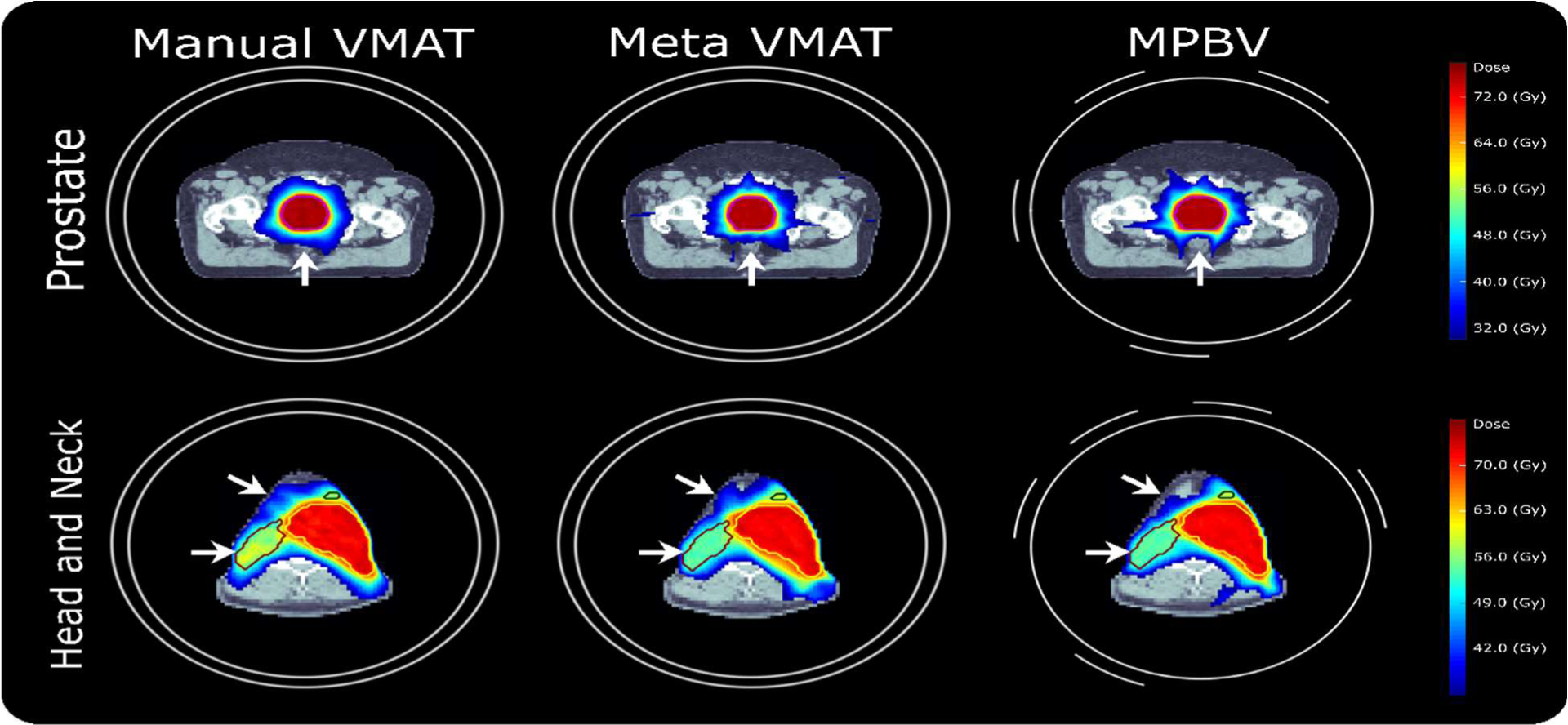
Visual comparison of dose distributions for a representative prostate case and a representative head and neck case.

Figure 4 provides a visualization of the dose-volume histograms for the prostate and head and neck datasets, where mean values are plotted as solid lines and standard deviations are shown as error bands. For prostate cases, we observe that the proposed MPBV approach provides the best performance for bladder and body sparing. Similarly, MP VMAT and MPBV provide improved performance for sparing of the femoral heads, as compared to manual planning. For head and neck cases, the DVHs for most OARs appear visually comparable for the three methods. Manual planning also appears to have a much greater variance in homogeneity for the DVHs of PTV 52 and PTV 56. Both MP VMAT and MPBV provide noticeable reductions in homogeneity variance for those PTVs.

Figure 4.

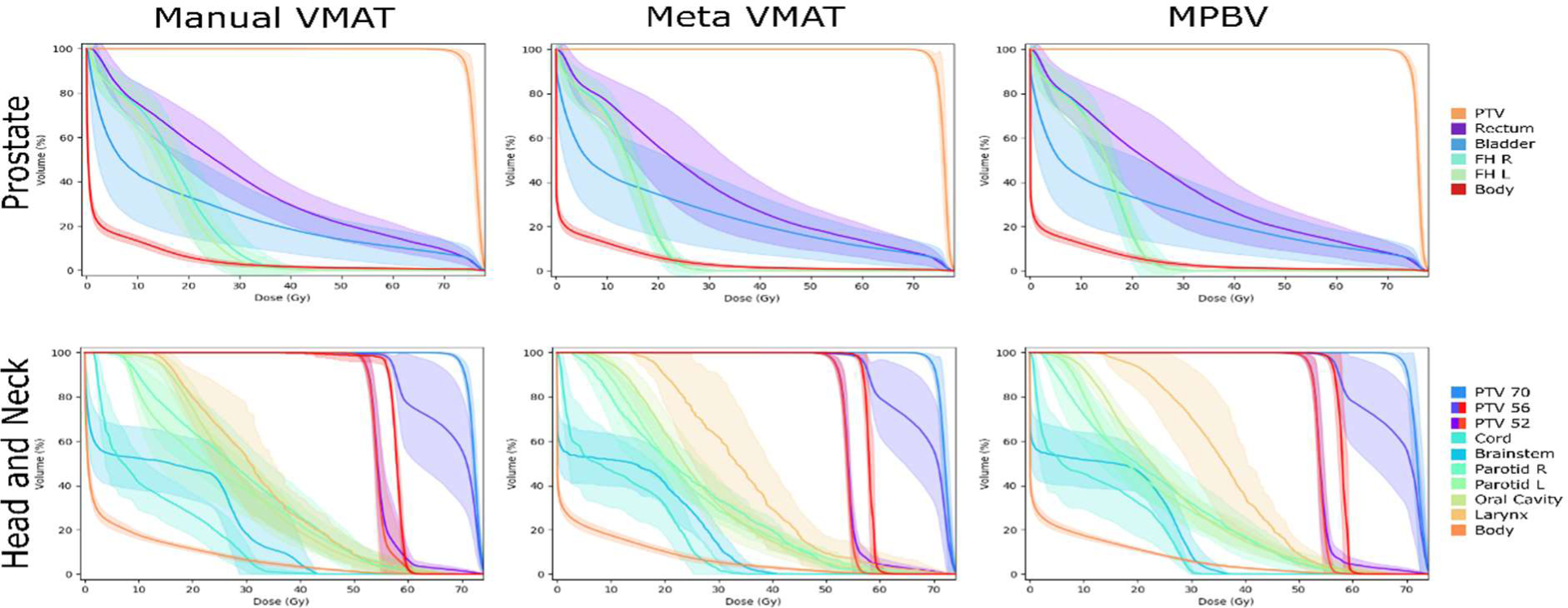
Visual comparison of the dose-volume histograms for both the prostate and head and neck datasets. Here, the means are shown as solid lines and the standard deviations are shown as error bands.

3.3. Quantitative Comparison

Tables 3 (prostate) and 4 (head and neck) provide quantitative comparisons between the MPBV approach and the two baseline methods. Differences in target coverage, dose conformity, dose homogeneity, dose spillage (i.e. R90 and R50), and OAR sparing (mean dose) are quantified using the Wilcoxon signed-rank test (p < 0.05).

Table 3.

Quantitative comparison is performed for prostate cases, where we assess target coverage, dose homogeneity, conformity, spillage, and OAR sparing. Methods are compared using the Wilcoxon signed-rank test (p < 0.05) with the best values bolded for readability.

	PTV			R90	R50	OAR	Mean Dose (μ)	D(2%) (Gy)	D(20%) (Gy)	D(40%) (Gy)
	D 95	HI	CI
Manual VMAT (~360 CPs)	72.0 (0.0)	4.63 (0.98)	0.86 (0.03)	1.29 (0.05)	3.44 (0.20)	Rectum	29.2 (5.4)	73.3 (2.6)	49.7 (10.1)	30.3 (7.3)
						Bladder	18.6 (9.3)	71.0 (6.5)	34.4 (20.4)	14.5 (11.5)
						FH R	15.9 (3.3)	30.5 (5.1)	23.3 (4.6)	19.0 (4.2)
						FH L	14.5 (3.1)	29.7 (5.1)	21.5 (4.5)	16.7 (3.3)
						Body	3.8 (0.8)	34.1 (6.6)	3.1 (1.5)	0.5 (0.2)
MP VMAT (~120 CPs)	72.0 (0.0)	4.14 (0.62)	0.90 (0.01)	1.24 (0.03)	3.26 (0.17)	Rectum	27.8 (8.0)	72.0 (6.7)	44.9 (13.5)	28.1 (9.8)
						Bladder	19.1 (9.9)	71.8 (5.6)	36.1 (19.5)	15.2 (13.1)
						FH R	12.7 (2.0)	23.3 (2.2)	18.3 (1.9)	15.2 (2.0)
						FH L	12.6 (1.6)	23.7 (2.0)	18.6 (1.6)	15.3 (1.5)
						Body	3.5 (0.7)	33.6 (5.5)	2.2 (1.4)	0.1 (0.0)
MP Boosted VMAT (~90 CPs)	72.0 (0.0)	4.17 (0.59)	0.91 (0.01)	1.23 (0.03)	3.27 (0.15)	Rectum	27.5 (8.2)	71.9 (7.0)	44.4 (13.7)	27.7 (10.1)
						Bladder	18.6 (9.6)	71.8 (5.5)	35.5 (19.7)	14.4 (12.8)
						FH R	13.1 (2.3)	23.2 (2.2)	18.5 (2.1)	15.7 (2.5)
						FH L	13.1 (1.6)	23.8 (2.1)	19.0 (1.5)	16.0 (1.4)
						Body	3.4 (0.7)	33.9 (5.6)	2.1 (1.3)	0.1 (0.0)

	PTV		R90	R50	Rectum (μ)	Bladder (μ)	FH R (μ)	FH L (μ)	Body (μ)
	HI	CI
MP Boosted VMAT vs. Manual VMAT (p-value)	0.22883	0.00226	0.00059	0.00312	0.19243	0.79434	0.00130	0.02281	0.00007
MP Boosted VMAT vs. MP VMAT (p-value)	0.31731	0.00082	0.02820	0.34768	0.27358	0.02081	0.09874	0.00414	0.04202
MP VMAT vs. Manual VMAT (p-value)	0.13037	0.00001	0.00001	0.13962	0.52021	0.18084	0.00006	0.00016	0.00009

3.3.1. Prostate Cases

The results for the prostate dataset are summarized in Table 3. We first perform comparisons between the proposed MPBV approach and the baseline manual VMAT method, where performance for dose conformity, dose spillage (i.e. R90 and R50), femoral head sparing, and body sparing is significantly improved by the proposed MPBV approach. MPBV also provides performance for target coverage, dose homogeneity, rectum sparing, and bladder sparing that is comparable to that of the baseline manual VMAT method.

Performance for the proposed MPBV approach was also compared to the baseline MP VMAT method with two full arcs. The proposed MPBV approach provides improved dose conformity, R90 dose spillage, bladder sparing, and body sparing. MPBV and MP VMAT had comparable performance for target coverage, dose homogeneity, R50 dose spillage, rectum sparing, and right femoral head sparing. MPBV was also inferior to MP VMAT in regards to left femoral head sparing.

Among the three methods evaluated here, the proposed MPBV approach provides the best performance for dose conformity, R90 dose spillage, R50 dose spillage (tied with two-arc MP VMAT), bladder sparing (tied with manual VMAT), right femoral head sparing (tied with two-arc MP VMAT), and body sparing. For left femoral head sparing, MPBV provides performance that is superior to manual VMAT but inferior to two-arc MP VMAT. For target coverage, dose homogeneity, and rectum sparing, performance for the three methods was comparable.

3.3.2. Head and Neck Cases

Quantitative results for head and neck cases are summarized in Table 4. We first compare the proposed MPBV approach to baseline manual VMAT planning with two arcs. Performance for target coverage (PTV 52, 56, and 70), dose homogeneity (PTV 52, 56, and 70), dose conformity (PTV 70), and sparing of all OARs except the body and oral cavity is comparable for both methods. For sparing of the body and oral cavity, MPBV provides significantly better performance as compared to manual VMAT. We additionally compare MPBV to the baseline MP VMAT method with two arcs. Both methods achieved comparable performance for all metrics.

Table 4.

Quantitative comparison is performed for head and neck cases, where we assess target coverage, dose homogeneity, conformity, and OAR sparing. Methods are compared using the Wilcoxon signed-rank test (p < 0.05) with the best values bolded for readability.

	PTV 52		PTV 56		PTV 70			OAR	Mean Dose (μ)	D(2%) (Gy)	D(20%) (Gy)	D(40%) (Gy)
	D 95	HI	D 95	HI	D 95	HI	CI
Manual VMAT (~360 CPs)	52.5 (0.5)	7.40 (3.27)	57.6 (0.6)	3.42 (1.15)	70.0 (0.0)	5.22 (0.57)	0.83 (0.02)	Cord	15.7 (6.5)	33.8 (4.6)	29.7 (5.2)	22.1 (11.4)
								Brainstem	12.0 (2.7)	32.3 (4.3)	22.2 (6.9)	12.0 (5.2)
								Parotid R	28.6 (6.1)	55.8 (6.9)	42.3 (6.0)	31.3 (7.0)
								Parotid L	26.2 (5.7)	58.8 (6.4)	40.7 (5.0)	27.0 (8.3)
								Oral Cavity	29.2 (3.2)	55.9 (3.7)	39.0 (4.0)	30.0 (3.9)
								Larynx	32.0 (4.6)	57.2 (5.8)	41.9 (5.8)	32.5 (4.9)
								Body	5.7 (0.7)	45.5 (2.5)	7.4 (2.0)	1.1 (0.3)
MP VMAT (~120 CPs)	52.4 (0.5)	6.03 (1.46)	57.5 (0.6)	2.66 (2.43)	70.0 (0.0)	4.34 (0.72)	0.82 (0.05)	Cord	14.1 (4.6)	35.8 (4.2)	27.9 (4.0)	16.1 (7.2)
								Brainstem	11.1 (4.0)	28.4 (2.5)	20.6 (7.3)	10.0 (7.2)
								Parotid R	22.9 (4.3)	52.4 (4.8)	34.8 (5.2)	21.3 (4.2)
								Parotid L	24.1 (2.4)	56.9 (6.5)	34.5 (4.4)	23.1 (2.9)
								Oral Cavity	27.1 (2.5)	55.7 (3.9)	37.5 (4.1)	24.5 (3.7)
								Larynx	34.3 (5.1)	54.3 (6.7)	41.7 (5.3)	26.7 (4.4)
								Body	5.0 (0.5)	44.3 (2.9)	6.5 (1.9)	0.2 (0.1)
MP Boosted VMAT (~90 CPs)	52.4 (0.5)	5.85 (1.22)	57.5 (0.6)	2.68 (2.37)	70.0 (0.0)	4.37 (0.75)	0.83 (0.04)	Cord	13.7 (3.2)	31.3 (1.4)	27.4 (1.7)	20.4 (8.9)
								Brainstem	11.7 (4.1)	28.9 (1.9)	23.1 (7.3)	14.6 (7.9)
								Parotid R	22.7 (5.4)	54.4 (8.5)	36.7 (8.0)	23.5 (7.9)
								Parotid L	23.1 (2.6)	58.5 (5.4)	35.4 (4.8)	22.5 (4.7)
								Oral Cavity	25.2 (1.7)	52.7 (6.3)	35.6 (4.4)	27.5 (2.6)
								Larynx	36.1 (5.7)	59.3 (4.5)	44.9 (4.3)	37.0 (5.4)
								Body	4.9 (0.4)	44.2 (2.1)	7.5 (2.5)	0.2 (0.1)

	PTV 52		PTV 56		PTV 70		Cord (μ)	Brainstem (μ)	Parotid R (μ)	Parotid L (μ)	Oral Cavity (μ)	Larynx (μ)	Body (μ)
	D 95	HI	D 95	HI	HI	CI
MP Boosted VMAT vs. Manual VMAT (p-value)	0.172	0.345	0.916	0.345	0.074	0.916	0.345	0.600	0.115	0.345	0.027	0.074	0.027
MP Boosted VMAT vs. MP VMAT (p-value)	0.600	0.172	0.916	0.344	0.141	0.753	0.753	0.248	0.916	0.916	0.248	0.115	0.074
MP VMAT vs. Manual VMAT (p-value)	0.172	0.600	0.600	0.345	0.141	0.463	0.172	0.345	0.074	0.463	0.115	0.463	0.027

Comparing between the evaluated methods, MPBV achieves the best performance for sparing of the oral cavity (tied with MP VMAT) and sparing of the body (tied with MP VMAT). Performance for the remaining metrics (i.e. target coverage, dose homogeneity, dose conformity, etc.) was comparable for the three methods.

3.3.3. Estimated Delivery Metrics

Table 5 provides a summary of the number of control points and estimated delivery times for the evaluated methods. The proposed MPBV approach, with an implementation that uses one full arc and five partial arcs, contains 25% less control points than the baseline MP approach with two full arcs and reduces the estimated delivery time by around 20% on average. The number of additional partial arcs is empirically set to five in our implementation, and it can be further reduced if even faster delivery times are desired.

Table 5.

Comparison of VMAT delivery parameters

	Manual VMAT	MP VMAT	MP Boosted VMAT
Control Points	~360	120	90
Estimated Delivery Time		2.6 min	2.1 min

4. DISCUSSION

This study proposed the MPBV approach, which performs fully automated boosted VMAT planning to improve the intensity modulation of VMAT plans. Overall, MPBV produces plans that maintain or improve dosimetric quality, as compared to VMAT with multiple arcs, while substantially reducing estimated delivery time and the number of VMAT control points.

The MPBV approach has three main stages: meta-optimization, beam angle optimization, and final plan generation. The current implementation of the MPBV approach performs meta-optimization using the parallel Nelder-Mead simplex search routine. In the second stage of the MPBV approach, angular segments for VMAT boosting are selected using BAO. The current implementation utilizes five partial arcs, as this results in a number of control points approximately halfway between a one arc VMAT plan and a two arc VMAT plan. The third stage of the MPBV approach involves generating the final boosted VMAT plan and follows the standard workflow used in MatRad.

In this study, we retrospectively compared the proposed MPBV approach to two baseline approaches that utilize multiple VMAT arcs. For the prostate dataset, the proposed MPBV approach provided the best performance for 6 of 10 metrics, the second-best performance for 1 of 10 metrics, and comparable performance for the remaining 3 of 10 metrics. A similar trend arose for the head and neck dataset, where MPBV provided the best performance for 2 of 14 metrics and comparable performance with the baselines for the remaining 12 of 14 metrics.

The proposed MPBV approach requires no active planning and has relatively fast computation times. The first stage, meta-optimization, is performed in around an hour (52.7 ± 13.6 min, maximum of 30 outer-loop iterations), and the second stage is performed in around 15 minutes (14.01 ± 2.2 min). Source code for all components of the proposed method, including the MPBV approach and the MatRad treatment planning software package, are open-source and provided through github. In doing so, we hope to facilitate further development of meaningful tools in radiation therapy. Moving forward, we hope to extend the proposed approach to noncoplanar treatment planning and apply it to the treatment of other body sites (i.e. abdomen, spine, etc.).

The main limitation of this current study concerns the small number of head and neck cases used for evaluation, as our evaluation for those cases may not have sufficient power to determine whether there were significant differences between the proposed and baseline methods. Due to ongoing difficulties associated with data collection during the pandemic, we have been unable to expand the number of head and neck cases used in our evaluation. In future work, however, we expect to substantially increase our cohort size and hopefully address this issue of limited data.

This work investigated a fast, heuristic method that uses BAO to select partial arc segments for VMAT boosting. The BAO method used here has been adapted from previous works on selecting noncoplanar VMAT trajectories¹⁹. One limitation of the this boosting method is that it does not account for the contribution of the initial VMAT arc to the fluence map optimization process, instead assuming that BAO only serves the purpose of selecting regions for improving intensity modulation. Our results do confirm that the boosting methods described in this work improve the efficiency of the overall VMAT trajectories as compared to multiple full arcs.

This work combines heuristic BAO with automated planning. While the entire boosted VMAT trajectory is considered when performing direct aperture optimization for the final plan, the adopted BAO (stage 2) is a heuristic method that does not account for dose contributions of initial VMAT arcs. Our results demonstrate that such a method provides a practical compromise between reducing computation costs and optimally selecting VMAT trajectories. However, a meaningful avenue for future research could be to perform more rigorous experiments comparing the performance of heuristic BAO trajectory selection methods to trajectory selection methods that include the contributions of the initial VMAT arc.

5. CONCLUSION

The present study proposed and evaluated a fully automated framework for boosted VMAT planning, called MPBV. MPBV was evaluated against two baseline methods for both prostate and head and neck cases, demonstrating that high quality VMAT plans can be generated while simultaneously reducing the number of control points used. Moreover, the proposed method has been implemented in the MatRad treatment planning system, and source code for all components have been made available on github.

DATA AVAILABILITY

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.