Multiscale Modeling of Hepatitis B Virus Capsid Assembly and Its Dimorphism

Abstract

Hepatitis B virus (HBV) is an endemic, chronic virus that leads to 800000 deaths per year. Central to the HBV lifecycle, the viral core has a protein capsid assembled from many copies of a single protein. The capsid protein adopts different (quasi-equivalent) conformations to form icosahedral capsids containing 180 or 240 proteins: $T=3$ or $T=4$, respectively, in Caspar–Klug nomenclature. HBV capsid assembly has become an important target for recently developed antivirals; nonetheless, the assembly pathways and mechanisms that control HBV dimorphism remain unclear. We describe computer simulations of the HBV assembly, using a coarse-grained model that has parameters learned from all-atom molecular dynamics simulations of a complete HBV capsid and yet is computationally tractable. Dynamical simulations with the resulting model reproduce experimental observations of HBV assembly pathways and products. By constructing Markov state models and employing transition path theory, we identify pathways leading to $T=3$, $T=4$, and other experimentally observed capsid morphologies. The analysis shows that capsid polymorphism is promoted by the low HBV capsid bending modulus, where the key factors controlling polymorphism are the conformational energy landscape and protein–protein binding affinities.

Graphical Abstract

During the lifecycles of many viruses, hundreds of protein subunits self-assemble into a protein capsid that packages the viral nucleic acid and delivers it to a new host cell. In many cases a particular capsid structure is required for infectivity, and capsid proteins form this structure with high fidelity. Yet, capsid proteins can also exhibit striking polymorphism and adaptability, assembling into structures with different sizes and morphologies in response to changes in solution conditions, the presence of antiviral drugs, or encapsulation of nucleic acids or nanoparticles of varying sizes. Elucidating the factors that control assembly pathways and products could identify important targets for antiviral drugs and would advance our fundamental understanding of the viral lifecycle.

Approximately half of the characterized virus families have icosahedral symmetry. That is, their capsids are comprised of 60 identical asymmetric units. Caspar and Klug (CK) showed how multiples of 60 proteins can form icosahedral capsids, by subtriangulating each asymmetric unit so that individual proteins are forced to adopt slightly different (quasi-equivalent) conformations.^1–3 An icosahedral capsid has 60 $T$ subunits, where the “triangulation number” $T$ specifies the number of different protein conformations and is restricted to certain integer values ($T=h^2+hk+k^2$, where $h$ and $k$ are non-negative integers).²

Hepatitis B virus (HBV) is an important example of self-assembly as a model system, and since chronic HBV infection is a serious public health issue, assembly of its capsid is a target for a recently developed generation of antivirals that may contribute to a cure.⁶ About 300 million people have chronic HBV, which contributes, by cirrhosis, liver failure, and liver cancer, to about 800000 deaths each year.⁷ Within an infected host cell, the HBV capsid protein assembles around the HBV pregenomic RNA and viral polymerase to form a core particle. While capsid structures with $T=4$ symmetry (comprising 120 dimer protein subunits) are appropriate to accommodate the genome, many secreted particles are empty (containing no RNA)⁸ and a small fraction (∼5%) have $T=3$ capsids (with 90 dimers).^9,10 This behavior can be recapitulated in vitro using the assembly domain (residues 1–149 of the capsid protein, Cp149) in the absence of nucleic acids, which leads to a similar mix of $T=4$ and $T=3$ particles (all of which are empty). Moreover, several classes of small-molecule antiviral agents referred to as “core protein allosteric modulators” (CpAMs) have been identified that can bind to HBV capsid proteins and drive inappropriate assembly, leading to failure to package RNA or redirection of the assembly to alternative non-infectious products.^11–18

Recently, Cp149 assembly size distributions have been measured near to or at single-subunit precision using resistive pulse sensing,^19,20 mass spectrometry,²¹ and charge detection mass spectrometry,^22–25 and small intermediates were identified by high-speed AFM.²⁶ These experiments identified a number of long-lived intermediate structures with sizes between 85 and 140 dimers. Notably, some pathways also include “overgrown” intermediates with more than 120 dimers, which eventually dissociate some dimers and rearrange into icosahedral capsids.²⁷ Similarly, small-angle X-ray scattering (SAXS) experiments identified long-lived complexes at sizes between 90 and 120 dimers,²⁸ as well as a three-phase assembly kinetics, with nucleation and elongation phases followed by a slow rearrangement of capsid subunits into icosahedral structures.²⁹

Despite these experimental advances, the mechanisms underlying HBV dimorphism and the factors that separate assembly pathways leading to $T=4$, $T=3$, or asymmetric products remain unclear.

Computational models can reveal details of the assembly process that are not accessible to experiments. However, while atomistic and near-atomistic simulations have revealed the dynamics of complete viruses,^4,30–33 the long time scales (milliseconds to hours) prohibit simulating capsid assembly with atomic resolution, except for specific steps.^34,35 Therefore, coarse-grained models have been used to study the assembly dynamics of icosahedral shells.^36–48 Of particular relevance to our work, elastic interactions between 5-fold defects can funnel the elastic energy landscape of an assembling crystalline shell toward icosahedral structures.^49–52 However, previous works on empty capsids with $T\ge 4$ have focused on material properties (parametrized by the dimensionless ratio of stretching to bending moduli, Föppl von Kármán number) that are orders of magnitude below those of virus capsids. Thus, different mechanisms may be important for HBV assembly.

A significant challenge of coarse-grained (CG) models is linking their predictions to specific experimental systems. It is therefore desirable to inform CG models with atomic-resolution information. For example, multiscale modeling approaches have elucidated the stability and dynamics of viral capsids^30,53–55 and other protein structures (e.g., refs 56–60), and CG models based on protein structures have led to insights about specific virus assembly processes (e.g., refs 61–63).

Here, we employ data from atomic-resolution simulations and solution experiments to constrain and build a multiscale model for HBV capsid assembly. We start from a minimal CG model that captures the geometric features of HBV capsid proteins and their quasi-equivalent conformations. We parametrize this model using data from all-atom molecular (AA) dynamics simulations of a complete HBV capsid, along with atomic-resolution structures of the proteins in different assembly morphologies. We focus on a small number of parameters: binding affinity, subunit length, subunit dihedral angle, binding angles, and associated stretching and bending moduli. These data provide estimates for the relative strengths of the different types of protein–protein interactions that drive HBV assembly, the fluctuations of proteins around their mean interaction geometries, and the corresponding larger-scale elastic properties of the assembled structures.

We then perform dynamic Monte Carlo (MC) simulations to simulate dynamical assembly trajectories and compare these to experimentally observed trajectories. Analyzing these computed trajectories using Markov state model and transition path theory analysis explains the origins of trapped or metastable species observed in experiments.^{22–25,28,29,64} These results provide the confidence to examine the early steps of the reaction, where the diversity of intermediates shows how nucleation can be described as a much more complex series of intermediates than could possibly be isolated in experiments. We identify pathway “hubs”, or intermediates from which pathways diverge toward $T=4$, $T=3$, or asymmetric assembly products. Pathway analysis isolates factors, such as the local symmetry and relative stability of associating subunits, that select which pathway emerges from a hub state. The analysis also shows that the key factors controlling polymorphism are the elastic moduli and the extent of conformation dependence of protein–protein binding affinities. For bending modulus values relevant to virus capsids $\left(~(40-400)k_{\text{B}}T\right)$, the elastic strain alone cannot guide assembly toward large symmetric structures, and the robust assembly of icosahedral capsids with sizes $T\ge 4$ strongly depends on the presence of multiple protein conformations and their conformation-dependent binding affinities. We find that such specificity of interactions plays a key role in the assembly of natural homopolymeric icosahedral capsids by reducing the number of accessible assembly pathways and, thus, guiding assembly toward the target geometry. Finally, the results in the paper are qualitatively applicable to other viruses, and the approach is generalizable.

RESULTS AND DISCUSSION

Overview of Model and Parameters.

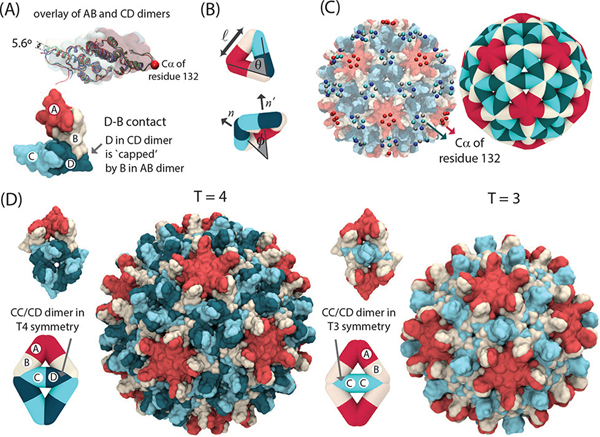
Capsid protein dimers are the basic assembly subunits for HBV.^65,66 Based on the quasi-equivalent conformations of the monomers (denoted as A–D), there are two dimer conformations in the $T=4$ capsid (AB and CD; see Figure 1A), which each make four interdimer interfaces. Dimer–dimer binding is primarily driven by hydrophobic stereospecific contacts at these interfaces. In each such interaction, a monomer of one dimer is capped by a monomer of a second dimer, with the second fitting against a hydrophobic patch on the first. For example, in the D–B contact shown in Figure 1A, the D monomer in the CD dimer is capped by the B monomer in the AB dimer. These interactions are asymmetric the inverse, a B–D contact with B of an AB dimer capped by D of a CD dimer, is structurally different from a D–B contact and, thus, has a different binding affinity.

Figure 1.

Description of the multiscale model. (A) Overlay of AB and CD conformations of the capsid protein from the crystal structure of the $T=4$ HBV capsid (top). Example of a dimer–dimer contact in the $T=4$ HBV capsid, where the D monomer in a CD dimer is “capped” by a B monomer in an AB dimer (bottom). Colors correspond to different monomers in each dimer. (B) Each edge in the elastic sheet coarse-grained model represents an HBV dimer. Model parameters include the equilibrium edge length $l_c^0$ and associated force constant ${\kappa }_l$, which controls the shell stretching modulus, the equilibrium binding angle between two edges ${\theta }_{c,c^{\prime }}^0$ and associated force constant ${\kappa }_{\theta }$, and the equilibrium dihedral angle between the normals of the two adjacent triangles ${\varphi }_c^0$ and force constant ${\kappa }_{\varphi }$, which sets the capsid bending modulus. Here $c$ and $c^{\prime }$ are the conformations of a given edge and the dimer that it interacts with, respectively. (C) Model parameters are optimized by minimizing the difference between the probability distributions of fluctuations of edge lengths, edge–edge angles, and dihedral angles computed from the coarse-grained (CG) model and an all-atom (AA) molecular dynamics simulation of a complete $T=4$ HBV capsid in explicit water.⁴ We coarse-grain the data from the all-atom simulation by selecting the $\text{C}-\alpha$ atom of residue 132 of each monomer and clustering these 240 points to 5-fold and 6-fold vertices based on proximity using the scikit DBSCAN clustering algorithm.⁵ The center of mass of each cluster is then assigned to a vertex of the CG model capsid (see Figure S3 and Movie S1 in the Supporting Information). (D) The configurations of dimers in a $T=4$ capsid (left) and in a $T=3$ capsid (right). A CD/CC dimer in $T=4$ has two interactions with CD dimers and two interactions with AB dimers and is referred to a CD dimer. A CD/CC dimer in a $T=3$ capsid, which has 4 interactions with AB dimers, is referred to as a CC dimer (see Model section and the Supporting Information).

We construct a CG model that enables simulating experimentally relevant time scales as follows. Since HBV dimers assemble with locally triangular lattices,^65,66 the model represents an assembling capsid by an elastic triangular sheet, with edges corresponding to dimers. Dimer diffusion from the bulk and association (dissociation) to (from) capsid structures are represented by the reversible addition/deletion of edges. Thus, the model and dynamics coarse-grain over subunit diffusion and high-frequency fluctuations of interacting dimers. The approach is similar to existing models for a capsid and tubule assembly based on triangular subunits of a single type,^52,67–69 but in our model growth occurs via addition/deletion of edges (dimers), and the model accounts for dimer asymmetry, as well as how the dimer structure and interactions depend on their conformational state (see the Model section, Figure 1, and Figure S6 in the Supporting Information). We see below that these physical features are essential to achieve robust assembly of $T=4$ shells when accounting for the material properties of HBV proteins.

We consider two edge types with different equilibrium lengths and dihedral angles (Figure 1B and Figure S6 in the Supporting Information). The first type represents AB dimers present in $T=4$ and $T=3$ capsids,⁷⁰ while the second, CD/CC, represents both CD and CC dimers in $T=4$ and $T=3$ capsids, respectively. This choice is based on the similarity of the structure and local symmetry environment (i.e., set of conformations of neighboring subunits) of CD and CC dimers in $T=4$ and $T=3$ capsids. For identifying assembly pathways, we will denote such a dimer as CD (CC) if its neighboring subunits are consistent with the $T=4$ ($T=3$) local symmetry (see Figure 1D and Figure S6 in the Supporting Information).

To model dilute, noninteracting capsid structures typical of productive capsid assembly reactions,^71,72 each simulation considers a single assembling capsid. The dynamics, including dimer association, obeys microscopic reversibility. The addition/deletion events occur with probability according to the grand canonical ensemble with a fixed chemical potential, which sets the bulk dimer concentration $C_{\text{tot}}$.^67,69 Technical details are provided in the Model section and Model Details in the Supporting Information.

Optimizing CG Model Parameters against AA Simulations Estimates Protein–Protein Interaction Geometries and Elastic Moduli.

The model potential energy function includes terms that represent subunit–subunit binding interactions and the elastic energy associated with deviations from the ground-state sheet geometry, corresponding to harmonic potentials for stretching of edges, deviations of dimer–dimer binding angles, and intradimer strains associated with deviation of dihedral angles between pairs of triangular faces (see Methods and eq 2). Denoting a dimer conformation for edge $i$ as $c(i)$, the key model parameters are the set of equilibrium edge lengths $\left\{l_c^0\right\}$, dimer–dimer binding angles, and dihedral angles $\left\{{\theta }_{c,c^{\prime }}^0\right\}$ and $\left\{{\varphi }_c^0\right\}$ (Figure 1B). The associated moduli ${\kappa }_1$, ${\kappa }_{\theta }$, and ${\kappa }_{\varphi }$ are independent of edge conformation, with ${\kappa }_1$ and ${\kappa }_{\varphi }$ setting the continuum-limit stretching and bending moduli of the shell (see Model Details in the Supporting Information).

To estimate the model parameter values that correspond to the HBV dimers, we mapped our CG dimers to an AA structure of an HBV capsid (see Methods, Figure 1C and Movie S1). We then used AA simulations of a complete HBV capsid⁴ to optimize the model parameters. We estimated the equilibrium edge lengths, dihedral and binding angles, and associated stretching and bending moduli of the CG model by minimizing the difference between the distributions of edge lengths, dihedral angles, and binding angles obtained from the AA MD and CG MC simulations (see Methods and Figure S8). Optimization against the AA data resulted in high values for the stretching modulus ${\kappa }_1\approx 4200k_{\text{B}}T/{\sigma }^2$ (with the simulation unit length scale $\sigma \approx 8\text{nm}$) and binding angle modulus ${\kappa }_{\theta }\approx 800k_{\text{B}}T$ and a relatively low value for the bending modulus ${\kappa }_{\varphi }\approx 40k_{\text{B}}T$. The 2D Young’s modulus $\epsilon \approx 6000$ can be estimated from $\epsilon ={\kappa }_1+{\kappa }_{\theta }/l_0^2$, where $l_0\approx \sigma$ is the average dimer length.

Mapping the three bending and elastic moduli to the standard Helfrich elastic energy of an elastic sheet^73,74 estimates the Föpple-von Kármán number, $\text{FvK}=\epsilon R_{\text{cap}}^2/{\kappa }_{\varphi }\approx 500$ with $R_{\text{cap}}\approx 2.1\sigma$, the radius of the HBV capsid, which is consistent with results of nanoindentation measurements.⁷⁵ As shown below, using these optimized elastic moduli in our model results in dynamical assembly behaviors that are consistent with experiments on HBV protein assembly, including the distribution of $T=4$ and $T=3$ icosahedral capsids at optimal assembly conditions, as well as large aberrant structures with reduced curvature observed under nonoptimal conditions (including in the presence of CpAMs that strengthen dimer–dimer interactions⁷⁶).

Binding Affinities and Conformational Free Energies.

Experiments identify mean dimer–dimer binding affinity values for $T=4$ capsids in the range $-7.0\le g_{T=4}^{\text{bind}}\le -4.2k_{\text{B}}T$ (with $k_{\text{B}}T\approx 0.6\text{kcal}/\text{mol}$ at $T=300\text{K}$) for different solution conditions and temperatures.⁶⁵ To estimate the binding energies at each quasi-equivalent site, we set the CD binding affinity $g_{\text{C}-\text{D}}^{\text{bind}}$ as a reference value $g_0^{\text{bind}}$ and set the relative values of binding affinities based on their relative buried surface areas (using PDBePISA, Table 1). We define ${\overline{g}}_{m-m^{\prime }}^{\text{bind}}\equiv g_{m-m^{\prime }}^{\text{bind}}/g_0^{\text{bind}}$ with $m$, $m^{\prime }$ as the conformations of the two interacting monomers. Table 1 shows these estimates for ${\overline{g}}_{\text{A}-\text{A}}^{\text{bind}}$, ${\overline{g}}_{\text{B}-\text{C}}^{\text{bind}}$, ${\overline{g}}_{\text{D}-\text{B}}^{\text{bind}}$ and ${\overline{g}}_{\text{C}-\text{D}}^{\text{bind}}$ (the dimer–dimer contacts that are present in the HBV $T=4$ capsid), as well as ${\overline{g}}_{\text{D}-\text{C}}^{\text{bind}}$ (only observed in nonicosahedral structures). We find that simulated assembly behaviors match those observed in experiments with these estimated values, and deviating from the PDBePISA estimates leads to poor agreement. Specifically, the assembly morphology is very sensitive to the value of ${\overline{g}}_{\text{D}-\text{C}}^{\text{bind}}$. The D–C contacts do not occur within icosahedral structures but are a prominent feature of flat hexagonal sheets that occur for nonassembly-competent conditions^77,78 (Figure 4C,D). Our simulations predict the optimal value for this parameter ${\overline{g}}_{\text{D}-\text{C}}^{\text{bind}}=0.2$ (close to the PDBePISA estimate of ≈0.3) to be much less than the affinities of all the contacts in a $T=4$ capsid(Figure 4(C-D)).

Table 1.

Relative Dimer–Dimer Binding Affinities^a

	${\overline{g}}_{\text{A}-\text{A}}^{\text{bind}}$	${\overline{g}}_{\text{B}-\text{C}}^{\text{bind}}$	${\overline{g}}_{\text{C}-\text{D}}^{\text{bind}}$	${\overline{g}}_{\text{D}-\text{B}}^{\text{bind}}$	${\overline{g}}_{\text{D}-\text{C}}^{\text{bind}}$
2G33 $T=4$ Capsid16	1.434	1.247	1	0.854	0.337
6UI7 $T=4$ Capsid70	1.282	1.127	1	0.936	NA
CG model	1.3	1.1	1	0.9	0.2

^aRelative binding affinities between different dimers in our CG model are set based on the interdimer interface analysis of HBV $T=4$ capsid (in PDBePISA^101,102).

Figure 4.

Conformational specificity of interdimer binding affinities is important for assembling $T=4$ capsid morphologies. (A, B) Dependence of selectivity for $T=4$ capsids on binding affinities between dimers with different conformations: (A) $g_{\text{D}-\text{B}}^{\text{bind}}$ and $g_{\text{D}-\text{C}}^{\text{bind}}$; (B) $g_{\text{A}-\text{A}}^{\text{bind}}$ and $g_{\text{D}-\text{C}}^{\text{bind}}$. Selectivity is defined as the ratio of $T=4$ capsids to all closed shells. The asterisk symbols in (A) and (B) indicate the relative binding affinities estimated from PDBePISA, showing that these values result in $T=4$ selectivities close to those observed in experiments. Snapshots of typical morphologies at parameter sets indicated on the plots (I–XII) are shown at the bottom. (C) A diamond from a $T=4$ capsid (left) and a small piece of the hexameric lattice (right) that forms in flat sheets, showing different contacts between quasi-equivalent conformations. The D–C contact is required to form the hexameric sheets and aberrant structures but does not occur in $T=3$ or $T=4$ morphologies. (D) Transmission electron micrographs of the in vitro assembly of HBV dimers in the absence (top) and presence (bottom) of CpAM antiviral molecules. Images adapted from Kondylis et al.⁷⁶ with permission, copyright 2018 ACS Publications.

The model also specifies the equilibrium population distribution of the two dimer conformations AB and CD/CC according to $K_{\text{AB}-\text{CD}}\equiv \frac{[\text{AB}]}{[\text{CD}]}=e^{-\Delta {\text{g}}_{\text{CD}\to \text{AB}}^{\text{conf}}/k_{\text{B}}T}$, where $K_{\text{AB}-\text{CD}}$ is the equilibrium constant for interconversion between the AB and CD conformations and $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$ is the corresponding free energy difference between the two conformations. As noted above, we consider the CD and CC conformations to be equivalent, i.e. $K_{\text{CC}-\text{CD}}\equiv \frac{[\text{CC}]}{[\text{CD}]}=1$, based on the high degree of structural similarity between CD and CC conformations and reduction in the number of model parameters. The parameter $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$ has not been directly estimated, but our results described below suggest that it depends on ionic strength, as previously suggested for the interconversion of HBV capsid protein between conformations that are active or inactive for assembly.^65,79 Experiments suggest that $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$ includes additional entropic contributions, such as different degrees of disorder in the C-terminal region of the assembly domain (Cp149) for the different conformations.⁸⁰

To summarize, we consider two control parameters: $g_0^{\text{bind}}$ (which controls the mean interdimer binding affinity) and the intradimer conformational free energy $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$. To enable direct comparison against experiments, we present our results in terms of the mean value of the dimer–dimer binding affinity (per dimer–dimer contact) in a $T=4$ capsid, which depends on the binding affinities and conformational free energy provided in eq 8 of the Model section. With the binding energy choices from Table 1, the mean dimer–dimer binding affinity in eq 8 can be written as

$$g_{T=4}^{\text{bind}}=\left(4.3g_0^{\text{bind}}+\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}\right)/4$$ (1)

Assembly Products.

The Model Reproduces HBV Polymorphism.

Figure 2A–C shows how the distribution of assembly products depends on the mean dimer–dimer binding energy $g_{T=4}^{\text{bind}}$ and the AB/CD conformational free energy difference $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$. We classify the assembly products into three categories (with representative snapshots shown in Figure 2D): $T=4$ capsids, $T=3$ capsids, and malformed structures, which do not have icosahedral symmetry but are (meta)stable on simulation time scales. Figure 2A shows the selectivity for $T=4$ capsids (defined as ratio of $T=4$ capsids to all closed shells) as a function of $g_{T=4}^{\text{bind}}$ and $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$, while Figure 2B,C shows histograms of assembly product distributions for varying $g_{T=4}^{\text{bind}}$ and $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$, respectively.

Figure 2.

Dependence of assembly product morphologies on binding affinities and the intradimer conformational free energy landscape. (A) Dependence of selectivity for $T=4$ capsids on the mean dimer–dimer binding affinity in a $T=4$ capsid ($g_{T=4}^{\text{bind}}$, eq 1) and the conformational equilibrium between AB and CD dimers, parametrized by $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}=-k_{\text{B}}T\log K_{\text{AB}-\text{CD}}$. The selectivity is defined as the ratio of the number of complete $T=4$ capsids to the number of all closed shells. (B, C) The fraction of assembly product morphologies as a function of (B) the dimer–dimer binding affinity for fixed $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}=3.5k_{\text{B}}T$ and (C) the AB/CD conformational equilibrium for fixed $g_{T=4}^{\text{bind}}=-5.8k_{\text{B}}T$. The four categories of product morphologies are shown in (D). Capsids with $T=4$ and $T=3$ icosahedral symmetry have 120 and 90 dimers, respectively, while most shells with mixed morphology have sizes between 85 and 140 dimers. (D) Snapshots of the three categories of assembly products are shown: $T=4$, $T=3$, and long-lived mixed-morphology capsids that have two distinct parts in $T=4$ and $T=3$ symmetries. Long-lived mixed morphologies (left) fail to close due to incompatible curvatures of the two morphologies, resulting in open boundaries that are sterically blocked from addition of new dimers (Figure S2 in the Supporting Information). Holey capsids (right) frequently form under aggressive assembly conditions, when the two capsid regions with different symmetries bind imperfectly.

The model reproduces the experimental observations that a fraction of $T=3$ capsids assemble, despite the fact that the model is geometrically optimized for the $T=4$ icosahedral symmetry. Further, the malformed products have a broad size distribution with most shells being between ∼85–140 dimers, which is consistent with size distribution measurements by CDMS.²⁴ Malformed structures are typically unclosed, with a mixed morphology that comprises two distinct parts with $T=4$ and $T=3$ morphologies, although we observe strained holey capsids at high binding energies. Examples of mixed-morphology and holey capsids are shown in Figure 2D.

The Intradimer Conformational Equilibrium Strongly Affects the Ratio of $T=4/T=3$ Capsids.

As shown in Figure 2A, the model robustly assembles icosahedral capsids over a broad range of $g_0^{\text{bind}}$ and $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$, but the selectivity for $T=4$ capsids depends strongly on the conformational free energy. For a relatively narrow range $\Delta g_{\text{CD}\to \text{AB}}^{\mathrm{conf}}/k_{\text{B}}T\in \text{[3.5, 5.5]}$, we observe selectivity values that are consistent with experimental observations (on the order of 5–30%). This suggests bounds for the parameter $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$.

Overly Strong Binding Affinities Increase the Fraction of Malformed Structures.

Increasing the base binding affinity ($g_0^{\text{bind}}$) decreases the proportion of assembled shells that have $T=4$ symmetry ($x$ axis of Figure 2A). Interestingly, the yield of $T=3$ capsids is relatively constant over this range, as observed in ref 81; the reduction in $T=4$ morphologies occurs due to an increase in malformed structures, especially the mixed-morphology class. These structures typically have open boundaries, and under moderate assembly conditions (moderate binding affinities or subunit concentrations) they are able to “edit” or reconfigure their assembly geometry to result in icosahedral $T=3$ or $T=4$ capsids (e.g., see Figure 5B).

Figure 5.

Assembly pathways. (A) Examples of assembly trajectories of $T=4$ and $T=3$ capsids, with snapshots of assembly intermediates at $g_{T=4}^{\text{bind}}=-5.8k_{\text{B}}T$, $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}=4.5k_{\text{B}}T$, and $C_{\text{tot}}=20\mu \text{M}$. (B) Examples of assembly trajectories in which overgrown (unclosed) capsids form, followed by “error correction”, or shedding of excess subunits and reconfiguration into complete $T=4$ (blue) and $T=3$ (cyan) capsids. Parameters for the $T=4$ and $T=3$ trajectories are respectively $g_{T=4}^{\text{bind}}=-5.8k_{\text{B}}T$, $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}=4.5k_{\text{B}}T$, $C_{\text{tot}}=15\mu \text{M}$ and $g_{T=4}^{\text{bind}}=-6.0k_{\text{B}}T$, $\Delta g_{\text{CD}\to \text{AB}}^{\mathrm{conf}}=3.5k_{\text{B}}T$, and $C_{\text{tot}}=10\mu \text{M}$. Enlarged views of assembly intermediates of trajectories show the formation of locally incompatible morphologies, which are later corrected. Animations corresponding to these trajectories are provided in Movies S2–S5 in the Supporting Information.

Simulated Assembly Product Size Distributions Are Consistent with Experiments if the Intradimer Conformational Equilibrium Depends on Ionic Strength.

Figure 3A shows the assembly product size distribution measured in CDMS experiments at four different parameter sets, corresponding to two subunit concentrations and two ionic strengths, from ref 24. The fraction of $T=3$ capsids dramatically increases with ionic strength, from ∼5% at $I=210\text{mM}$ (top) to ∼30% at $I=510\text{mM}$ (bottom). In contrast, increasing the subunit concentration from $C_{\text{tot}}=10\mu \text{M}$ (left) to $20\mu \text{M}$ (right) does not significantly change the $T=4/T=3$ ratio but does increase the prevalence of nonicosahedral structures with sizes of between 85 and 140 dimers.

Figure 3.

(A) Comparison of the simulation assembly product size distribution with CDMS experiments (after 10 min). Experimental results are shown for ionic strengths of $I=210\text{mM}$ (top) and $I=510\text{mM}$ (bottom) and dimer concentrations $C_{\text{tot}}=10\mu \text{M}$ (left) and $C_{\text{tot}}=20\mu \text{M}$ (right). The peaks near 3 and 4 MDa correspond to $T=3$ and $T=4$ capsids, respectively. Simulation assembly size distributions are shown for $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}=4.5k_{\text{B}}T$, $g_{T=4}^{\text{bind}}=-5.8k_{\text{B}}T$ (top) and $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}=3.5k_{\text{B}}T$, $g_{T=4}^{\text{bind}}=6.2k_{\text{B}}T$ (bottom) and $C_{\text{tot}}=10\mu \text{M}$ (left) and $C_{\text{tot}}=20\mu \text{M}$ (right). Insets of CDMS spectra in the four panels are respectively from Figure 1A–D of Lutomski et al.²⁴ (B) High-resolution size distribution of assembly products in CDMS experiments²⁵ for $I=200\text{mM}$ and $C_{\text{tot}}=10\mu \text{M}$. Snapshots show the mixed-morphology capsids with 121 and 132 dimers, which are among the most abundant nonicosahedral structures observed in both simulations and experiments. While the 121-dimer shell has 111 of its dimers consistent with $T=4$ symmetry and a small region of 10 dimers with local $T=3$ symmetry, the 132-dimer shell contains an approximately equal mix (∼60 dimers in $T=3$ and ∼62 dimers in $T=4$ environments).

We find that the simulations qualitatively reproduce both of these behaviors (Figure 3A) if the conformational free energy $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$ decreases ($K_{\text{AB}-\text{CD}}$ increases) with increasing ionic strength. In particular, decreasing the free energy difference from $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}=4.5$ (top) to $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}=3.5$ (bottom) changes the $T=4/T=3$ ratio, similar to the effect of increasing the salt concentration in experiments. Here we have also slightly increased the binding affinity, $g_{T=4}^{\text{bind}}=-5.8$ (top) and $g_{T=4}^{\text{bind}}=-6.2$ (bottom), to match the experimental observation that $g_{T=4}^{\text{bind}}$ increases with increasing salt concentration. Increasing the protein concentration (from left to right) results in more mixed-morphology products in simulations and CDMS experimental observations. These results are consistent with previous experimental evidence for a relationship between dimer conformation and ionic strength.^65,79

Figure 3B shows a high-resolution CDMS measurement of the assembly product size distribution for $I=200\text{mM}$ and $C_{\text{tot}}=10\mu \text{M}$. The assembly product size distributions in our higher concentration simulations are qualitatively consistent with the experimental observations, and we observe prevalent nonicosahedral assembly products at consistent sizes: e.g., the 121-dimer and 132-dimer structures shown in the figure.

The Conformational Dependence and Asymmetry of HBV Interdimer Interactions Are Highly Optimized.

The results discussed up to this point have focused on the relative values of dimer–dimer binding affinities estimated from buried surface area (PDBePISA) for each pair of dimer conformations (Table 1). Since we expect these to roughly correspond to the wildtype HBV capsid protein, changes in these affinities would correspond to amino acid substitutions at the dimer–dimer assembly interface or the presence of antiviral agents that bind to the assembly interface.^{11–18,82,83} Note that the dimer–dimer interactions are asymmetric—within a capsid, each dimer is “capped” from one side by another dimer, and thus, for example, the C-D contact (with binding energy $g_{\text{C}-\text{D}}^{\text{bind}}$) where C is capped by D is different from the D–C contact (with binding energy $g_{\text{D}-\text{C}}^{\text{bind}}$) where D is capped by C.

Figure 4A,B shows the assembly products that result when some of the relative binding affinities (${\overline{g}}_{\text{A}-\text{A}}^{\text{bind}}$, ${\overline{g}}_{\text{D}-\text{B}}^{\text{bind}}$, and ${\overline{g}}_{\text{D}-\text{C}}^{\text{bind}}$) deviate from the PDBePISA estimate. Moreover, these results suggest that the binding affinities are highly optimized for the $T=4$ capsid assembly. Selectivities for $T=4$ on the order of those observed experimentally occur only for relative binding affinities that are close to those estimated from buried surface area (denoted by the asterisk symbols in Figure 4A,B).

Deviations in ${\overline{g}}_{\text{A}-\text{A}}^{\text{bind}}$ and ${\overline{g}}_{\text{D}-\text{B}}^{\text{bind}}$ have qualitatively different effects on assembly morphology than ${\overline{g}}_{\text{D}-\text{C}}^{\text{bind}}$. First, optimal values of ${\overline{g}}_{\text{A}-\text{A}}^{\text{bind}}$ and ${\overline{g}}_{\text{D}-\text{B}}^{\text{bind}}$ are ∼1, whereas the optimal value of ${\overline{g}}_{\text{D}-\text{C}}^{\text{bind}}\approx 0.2-0.3$ (i.e., the D–C contact is much weaker than the mean binding affinity). Second, increasing ${\overline{g}}_{\text{A}-\text{A}}^{\text{bind}}$ and ${\overline{g}}_{\text{D}-\text{B}}^{\text{bind}}$ above their optimal values typically results in the mixed-morphology malformed structures described above for overly strong mean binding affinities. In contrast, increasing ${\overline{g}}_{\text{D}-\text{C}}^{\text{bind}}$ above its optimal value, $0.3<{\overline{g}}_{\text{D}-\text{C}}^{\text{bind}}\lesssim 0.7$, leads to assemblies that are closed but lack even partial icosahedral symmetry. In most cases these are asymmetric, but at some parameter sets we observe capsids with $D_{5h}$ symmetry (e.g., image I at ${\overline{g}}_{\text{D}-\text{C}}^{\text{bind}}=0.4$ in Figure 4). Further increasing ${\overline{g}}_{\text{D}-\text{C}}^{\text{bind}}\gtrsim 0.7$ results in large aberrant structures that contain extended hexagonal lattices (V, VI, XI and XII in Figure 4). Interestingly, these structures bear a strong resemblance to those observed in experiments on assembly of HBV dimers in the presence of core protein allosteric modulator (CpAM) molecules (Figure 4E).⁷⁶ CpAMs in general are assembly agonists, increasing dimer–dimer binding affinities; HAPs in particular favor a flattening of quasi-six-folds by binding preferentially to B–C and C–D interdimer interfaces.¹⁴ Increasing the D–C affinity qualitatively mimics this effect.

The strong dependence of assembly morphologies on conformational specificity can be attributed to the relatively low bending modulus estimated from the atomistic simulations (and consistent with experiments), ${\kappa }_{\varphi }\approx 40k_{\text{B}}T$. The difference in elastic energy per subunit between $T=3$ and $T=4$ morphologies is $\Delta {𝓗}_{\text{elastic}}/n_{\text{dimer}}\approx 0.005k_{\text{B}}T$, and even the large aberrant structures (V, VI, XI, and XII in Figure 4) incur only modest elastic energy costs relative to a $T=4$ structure ($\Delta {𝓗}_{\text{elastic}}/n_{\text{dimer}}\approx 0.4k_{\text{B}}T$). Thus, gradients in elastic energy alone are not strong enough to guide assembly trajectories toward the $T=4$ morphology, and conformational dependence is required as well.

For the remainder of this article, all results use the default values for ${\overline{g}}_{\text{A}-\text{A}}^{\text{bind}}$, ${\overline{g}}_{\text{D}-\text{B}}^{\text{bind}}$, and ${\overline{g}}_{\text{D}-\text{C}}^{\text{bind}}$ given in Table 1.

Assembly Pathways.

Error Correction during Assembly and Recovery from Overgrown Structures.

Figure 5A,B and Figure S5A,B show example assembly trajectories that respectively result in $T=3$ or $T=4$ capsids or asymmetric assembly products. Snapshots are shown along each trajectory, along with labels indicating the numbers of dimers in long-lived intermediates. Here we have defined a long-lived intermediate as a state with a population fraction (of the ensemble of all states along dynamical trajectories) that exceeds a threshold value of 1% (Figure S5A). Qualitatively, this corresponds to the fraction of protein in detectable intermediates in SAXS.^28,84

While the assembly products can be classified into different categories as described above, the underlying assembly pathways have a key feature in common. At multiple points along assembly trajectories, subunits can bind with a local geometry that is incompatible with the larger-scale geometry of the existing shell, resulting in regions corresponding to different morphologies (e.g., a combination of $T=4$ and $T=3$ symmetries). This morphology mismatch results in different behaviors depending on the extent of the mismatch and the number of subunits required to dissociate or rearrange to achieve a uniform morphology.

$T=4$ assembly trajectories (Figure 5-II,IV) typically involve several long-lived intermediates, which have geometries such that the next dimer to associate can only form a single bond and is thus relatively unstable. In addition, many of these states have several CD/CC dimers on the boundary, which can act as a “seed” for mixed-morphology excursions in which dimers bind with local $T=3$ symmetry. In this case, successful assembly of a $T=4$ structure requires error correction: i.e., unbinding or reconfiguration of the dimers in local $T=3$ arrangements to recover global $T=4$ symmetry. Thus, trajectories may surmount multiple free energy barriers before assembly proceeds rapidly.

While both $T=3$ and $T=4$ assembly exhibit a long-lived 10-dimer intermediate, we do not observe larger long-lived intermediates in $T=3$ pathways. This trend reflects the fact that the on-pathway $T=3$ intermediates with sizes $n>10$ have either a convex boundary or multiple AB dimers and thus avoid high barriers to additional subunit association or seeds with local $T=4$ symmetry. This suggests that the relatively high value of ${\overline{g}}_{\text{A}-\text{A}}^{\text{bind}}$ plays a key role in the facile completion of $T=3$ capsids.

Overgrown Capsids.

In some cases, regions with mismatched local symmetry remain in the partial capsid structure until the final stages of the assembly, resulting in the formation of “overgrown” structures with more than 120 or 90 dimers for $T=4$ or $T=3$ capsids, respectively. Figure 5B shows an example of a trajectory (blue line, IV) for which a region of local $T=3$ symmetry causes a mismatch between the orientations of boundary dimers as the capsid nears completion, resulting in overgrowth to an unclosed 121-dimer structure. However, eventually the dimers in the region with $T=3$ symmetry disassemble due to their less favorable elastic energy and binding affinities, and then the capsid rapidly forms a complete $T=4$ structure. We observe similar pathways involving correction of overgrown structures that lead to $T=3$ capsids. For example, Figure 5B (cyan line, III) shows a trajectory in which an overgrown mixed-morphology structure with about 97 dimers eventually closes with $T=3$ symmetry. This pathway starts with formation of a 22-dimer structure in $T=4$ symmetry and continues with addition of dimers in $T=3$ symmetry, until reaching a metastable intermediate with 90– 92 dimers that retains the initial $T=4$ region. This long-lived intermediate has ∼9 dimers on the boundary, but further growth is prevented by sterics and elastic strain due to the unfavorable curvature (see Figure S4A). Finally, the structure breaks interactions and undergoes conformational changes in the $T=4$ region, leading to the $T=3$ morphology. Importantly, such error correction only occurs under moderate assembly conditions: i.e., when the net driving force for assembly (determined by binding affinities and dimer concentrations) is such that assembly is nearly reversible (e.g., Figure 2B).

The trajectories and error correction described above are qualitatively consistent with the recent CDMS observations of overgrowth followed by shedding of excess subunits.²⁷ Moreover, slow capsid closure during the final stages of HBV assembly was observed in SAXS experiments by Chevreuil et al.²⁹ Figure S7B shows that $T=4$ trajectories on average spend up to ∼20% of the assembly time in the preclosure states.

Long-Lived Off-Pathway Intermediates in Simulations and Experiments.

At higher concentrations or higher binding affinities, we observe other assembly products (meaning they are (meta)stable on all simulation time scales) with sizes between 85 and 140 dimers. Despite an open boundary that allows further subunit association and dissociation, the sizes of these structures remain relatively constant, due to the mismatch in the curvature of two parts. Simulation trajectories (Figure S3A,B) show that these structures form because of unsuccessful correction when a local mismatch in the geometry forms, resulting in a metastable structure that has two distinct parts with respectively $T=4$ and $T=3$ morphologies. Further details of this mechanism are provided in the Long-lived T = 3-T = 4 mixed morphologies section in the Supporting Information and Figures S3 and S4.

Inferring Mechanisms of Dimorphism and Path Selection.

Following the method introduced in ref85 we built Markov state models (MSMs) from the simulated assembly trajectories and then used transition path theory⁸⁶ to enable further insight into factors that control morphology selection during assembly and when pathways resulting in $T=4$ or $T=3$ morphologies diverge from each other. To this end, we decomposed the set of simulated capsid structures into a state space defined by two order parameters: (1) the number of dimers $n_{\text{dimer}}$ in a partial capsid structure and (2) an order parameter that distinguishes the assembly morphology. We chose different quantities for the second order parameter depending on the morphology of interest: namely, the number of CD dimers $n_{\text{CD}}$ or the number of CC dimers $n_{\text{CC}}$ for pathways leading to $T=4$ or $T=3$. From the set of simulation trajectories at a given parameter set, we estimated the transition probability matrix $\mathbf{T}(\tau )$, which has elements $T_{ij}$ that give the probability of a transition between a pair of states $i$,$j$ in a lag time $\tau$ (see Methods).

To evaluate the accuracy of the constructed MSMs, we compare the MSM prediction for the fraction of assembled structures with sizes corresponding to $T=4$ and $T=3$ capsids as a function of time to the unbiased MC dynamics (Figure S1A,B). This comparison provides a stringent test of the MSM, as it requires an accurate estimate of all statistically relevant elements of the transition matrix. The results closely agree and show that $T=3$ capsids form much earlier in the reaction than $T=4$ capsids, in agreement with experimental observations.⁸¹ The constructed MSM also predicts that, on longer time scales, $T=3$ sized structures convert to $T=4$ capsids, as seen in experiments.²⁴ We also validated the state decomposition by the Chapman–Kolmogorov test (see Markov State Models (MSMs) in the Supporting Information and Figure S2).

With the constructed MSMs, we use transition path theory to identify dominant pathways, key structural intermediates, and points at which pathways are committed to certain morphology products as follows.

Committor Probabilities Identify Pathway Selection Hub States.

The committor probability, $q_i^B$, is the conditional probability that a trajectory that is in state $i$ will visit a set of outcome states (denoted as $B$) before returning to the initial unassembled state^85,86 (see Markov State Models (MSMs) in the Supporting Information). Figure 6 shows the committor probabilities for the complete $T=4$ capsid $q_i^{T=4}$ at two different dimer concentrations, $C_{\text{tot}}=10\mu \text{M}$ (left) and $C_{\text{tot}}=20\mu \text{M}$ (right). The most notable difference between the two concentrations involves the committor probabilities of the states close to $T=4$ capsid ($n_{\text{dimer}}>100$, $n_{\text{CD}}>25$). While the majority of states end up in $T=4$ capsids ($q_i^{T=4}\approx 1$) at the lower concentration, a fraction of these states have $q_i^{T=4}\approx 0$ at higher dimer concentration: i.e., they remain trapped in other morphologies for the finite simulation time.

Figure 6.

$T=4$ pathway “hubs”. (A) The structure of the “$T=4$ dodecamer”. (B) Committor probabilities for $T=4$ capsids $q_i^{T=4}$ computed from a Markov state model (MSM) analysis, shown as a function of the number of CD dimers $n_{CD}$ and the total number of dimers $n_{\text{dimer}}$ for $C_{\text{tot}}=10\mu \text{M}$ at $g_{T=4}^{\text{bind}}=-5.8k_{\text{B}}T$ and $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}=4.5k_{\text{B}}T$. The committor probability $q_i^{T=4}$ corresponds to the probability that a trajectory initiated at a given structure will form a complete $T=4$ shell before disassembling. Circles indicate the $T=4$ pathway “hubs”$\left(q_i^{T=4}\approx 0.5\right)$, from which a trajectory is equally likely to form a $T=4$ capsid or other product morphology. Other snapshots are labeled as ($n_{\text{dimer}}$, $n_{\text{CD}}$). The (17, 4) intermediate in (B) is the smallest structure that has a complete $T=4$ dodecamer. (C) $T=4$ committor probabilities for $C_{\text{tot}}=20\mu \text{M}$ at parameters similar to those in (B). At $C_{\text{tot}}=10\mu \text{M}$ (B), the smallest hub states lack a complete $T=4$ dodecamer, while at the higher concentration (C) the smallest hub state has a mixed morphology that includes a $T=4$ dodecamer. The region indicated by an oval at large sizes in (C) shows that at high concentrations there is a high propensity to form long-lived mixed-morphology structures with sizes between 85 and 140 dimers.

We identify the intermediates at which assembly pathways are most likely to diverge from formation of a $T=4$ capsid, resulting in an alternative assembly product, by identifying hub states as those for which the $T=4$ committor probability $q_i^{T=4}\approx 1/2$. The five of these states with the highest forward flux (discussed next), as well as the smallest hub state, are shown with circles on the plots in Figure 6B,C. At the lower concentration, pathways diverging at the hub states typically result in $T=3$ capsids, whereas at the higher concentration assembly pathways are significantly more likely to diverge from $T=4$ to mixed-morphology states.

A comparison of the committor probabilities and assembly products at the different concentrations reveals that formation of a “$T=4$ dodecamer” (snapshot in Figure 6A) is the key event that determines whether pathways are more likely to proceed to $T=4$ or $T=3$ products. The $T=4$ dodecamer is the smallest relatively stable partial capsid intermediate that occurs in $T=4$ capsids but not $T=3$ capsids. The hub states at $C_{\text{tot}}=10\mu \text{M}$ (Figure 6B) that lead to $T=3$ capsids occur before formation of a structure with a complete $T=4$ dodecamer, whereas hub states at $C_{\text{tot}}=20\mu \text{M}$ (e.g., the 28-dimer structure shown in Figure 6C) occur after formation of a complete $T=4$ dodecamer and consequently diverge to mixed-morphology malformed states. We find that, with increasing concentration, pathways typically do not commit to the $T=4$ morphology until larger sizes and the size of the smallest hub state increases. Thus, increasing concentration results in a higher probability of forming mixed-morphology structures across a range of large sizes (85–140 dimers). The increasing proportion of long-lived intermediates in this size range with increasing concentration is consistent with CDMS measurements.²⁴

The predicted significance of the $T=4$ dodecamer to the formation of $T=4$ capsids qualitatively agrees with AFM experiments of of HBV dimer assembly on mica plates, which frequently observed this intermediate.²⁶

Forward Flux Reveals Most Probable Assembly Pathways.

While the committor probabilities in Figure 6B,C identify the “hub” states for $T=4$ assembly, the forward flux $f_{ij}^{+}$ shows the relative probability of different reaction channels and hence the relative importance of different classes of assembly pathways. Figure 7A,B shows the forward flux toward $T=4$ and $T=3$ morphologies, respectively. The first order parameter is the number of capsid dimers. The second order parameter in each plot is chosen to show deviations from the target stucture pathway: i.e., the $y$ axis is the number of CC dimers in a given state for $T=4$ pathways (Figure 7A) and number of CD dimers for $T=3$ pathways (Figure 7B).

Figure 7.

MSM analysis of intermediate stabilities and assembly pathway probabilities. Total forward flux to (A) $T=4$ and (B) $T=3$ capsids as the function of the number of dimers $n_{\text{dimer}}$ and the number of $\text{CC}\left(n_{\text{CC}}\right)$ or $\text{CD}\left(n_{\text{CD}}\right)$ dimers for $T=4$ or $T=3$ pathways, respectively. States with CC dimers $\left(n_{\text{CC}}>0\right)$ are off-pathway for $T=4$ assembly, and states with CD dimers $\left(n_{\text{CD}}>0\right)$ are off-pathway for $T=3$ assembly. For the $T=4$ pathway all the states with high forward flux are on-pathway states, while on $T=3$ pathways many of the states with high forward flux are off-pathway, and there are off-pathway states with up to 5 CD dimers in structures with high forward flux to a $T=3$ capsid. The 18-dimer (18*,4CD) state on the $T=3$ pathway is actually an on-pathway $T=4$ intermediate, but it can also generate pathways that form mixed-morphologies that undergo annealing to form $T=3$ capsids. Simulation parameters are $g_{T=4}^{\text{bind}}=-5.8k_{\text{B}}T$, $\Delta g_{\text{CD}\to \text{AB}}^{\mathrm{conf}}=4.5k_{\text{B}}T$, and $C_{\text{tot}}=20\mu \text{M}$. Examples of assembly intermediates in the initial and final stages of the assembly are shown. Middle states are not shown for clarity.

States with the largest flux between the initial and final configurations identify the most probable assembly pathways for each morphology. Interestingly, these states coincide with the long-lived intermediates discussed above (Figure 5). The states with high forward flux toward $T=4$ capsids (Figure 7A) can be understood by visualizing individual trajectories (Movie S2). Typically, growth from one of these states begins with multiple off-pathway excursions, in which dimers bind with configurations incompatible with the final morphology, followed by stalling of growth, dissociation, and a return to the long-lived intermediate state, before eventual on-pathway growth.

While the states with highest forward flux on $T=4$ pathways are all on-pathway states (with no CC dimers), the $T=3$ pathway exhibits several off-pathway states with high forward flux, and we do not observe any trajectories that transition from a $T=3$ pathway to a complete $T=4$ capsid.

CONCLUSIONS

We have investigated the assembly pathways of HBV capsid proteins using a coarse-grained model, informed by atomic-resolution data from molecular dynamics simulations and structure-based estimates of binding affinities for different protein conformations. The simulations reproduce key assembly products observed in experiments, including polymorphic assembly into $T=3$ and $T=4$ icosahedral structures and nonicosahedral complexes. Notably, our simulations predict the structural characteristics of the off-pathway intermediates, which could not be inferred from the CDMS experiments.^22–25 At the optimized values of the elastic moduli and binding energies, the off-pathway products have a mixed morphology comprising a combination of local $T=4$ and $T=3$ symmetry environments. The curvature of such structures is not geometrically compatible with self-closure, leading to shells with defects or holes, as well as overgrown structures in which the assembling structure spirals around itself until assembly is stalled due to excluded volume and elastic strain. These observations elucidate the experimental finding that metastable asymmetric intermediates can convert into icosahedral capsids over several days,²⁴ as well as slow capsid closure during the final stages of HBV assembly observed using SAXS experiments.²⁹ The simulations also predict key factors in the assembly of large aberrant structures with lower curvature observed in HBV experiments with CpAM modulators and demonstrate that the combination of specific molecular-scale interactions and flexibility, in particular the relatively small bending modulus in comparison to other virus capsids, enable HBV to undergo high-fidelity assembly into the infectious capsid structure while retaining the capability to form other polymorphs.

The simulations suggest that, due to this flexibility, a coupling between the protein conformational state and its protein–protein interactions is critical for determining assembly pathways and products. These results suggest additional interpretations of existing experimental data. For example, existing models have not been able to explain the experimental observations that higher proportions of $T=3$ capsids assemble at higher ionic strengths and in ammonium acetate buffer compared to NaCl.^29,84

The observation from our simulations that $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$ has a strong effect on morphology selectivity suggests that the ionic strength shifts the conformational equilibrium toward CD dimer conformations. That is, increasing the salt concentration decreases $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$ and thereby increases the driving force for 5-fold dimer coordination during the assembly process, thus favoring pathways that lead to the $T=3$ morphology. These results are also consistent with recent suggestions that coupling between conformational interconversion and interaction strengths provides an important means of regulatory control over the timing and robustness of assembly.^80,87–89 Moreover, Biela et al.⁹⁰ recently demonstrated that assembly of larger capsids from MS2 capsids ($T=4$ and $D_5$) could be achieved by engineering insertions into the capsid protein that likely shift the capsid protein conformational equilibrium (analogous to changing our parameter $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$).

The need for conformational specificity when accounting for HBV material properties sheds light on previous results for a model of icosahedral capsid assembly with only one subunit species, which found that much higher values of the bending modulus, corresponding to much smaller values of the Föppl von Kármán number number ($\text{FvK}<0.25$, compared to $\text{FvK}\approx \text{500}$ for HBV), were required to observe assembly into $T=4$ structures.^51,91 Here we find that $T=4$ capsids assemble with high yields at $\text{FvK}\approx \text{500}$, provided that the dimer subunits can adopt quasi-equivalent conformations with different binding affinities.

Trajectory analysis shows that, while the products of HBV assembly can be qualitatively classified into $T=4$ capsids, $T=3$ capsids, and long-lived malformed structures, the assembly pathways all have key features in common. We identified hub states or intermediates at which assembly pathways frequently diverge from $T=4$ pathways, as well as structural features of such hub states that determine the classes of products they will form. A key feature is whether a hub state intermediate contains a dodecamer of dimers in the quasi-6-fold arrangement found in $T=4$ capsids (the $T=4$ dodecamer in Figure 6A).

Trajectories that form such an intermediate will go on to form either $T=4$ capsids or malformed structures, whereas trajectories that diverge from the $T=4$ pathway before forming a complete $T=4$ dodecamer form either $T=3$ capsids or malformed structures. This prediction is consistent with recent AFM observations of HBV capsid protein assembly.²⁶ Knowledge of hub states could suggest previously unexplored antiviral drug targets.

Outlook.

The simulation results and buried surface area estimates suggest that, although the different quasi-equivalent conformations of HBV capsid proteins have high structural similarity, their differences play a key role in guiding assembly pathways. This conclusion is further supported by the fact that the antiviral assembly effectors (CpAMs) bind preferentially to interfaces between certain conformational pairs (e.g., within the quasi-6-fold interfaces). It would thus be of great interest to extend recent atomic-resolution simulations of CpAM-HBV capsid protein interactions^92,93 to investigate the molecular-scale factors that couple the protein conformational state to its interactions. This information could facilitate designing more effective assembly effectors.

The importance of conformational heterogeneity in the HBV assembly highlights the inherent tradeoff between minimizing the complexity of a self-assembly reaction and maximizing the selectivity for target structures. Recent experiments and simulations of synthetic subunits designed to assemble into capsids and tubules demonstrated that multiple species with species-specific subunit–subunit interactions can significantly increase specificity for a target geometry, by blocking assembly pathways that would lead to other geometries with similar thermodynamic stabilities.^94–96 However, the additional information content associated with encoding for multiple species or conformations incurs extra costs, such as material and design costs in the synthetic realm, or additional selective pressure on protein sequences in natural systems. Understanding how this tradeoff has shaped evolution in other natural systems would provide important information for developing treatments for pathogenic diseases that work by redirecting assembly pathways and could guide a more efficient design of synthetic self-assembly systems.

METHODS

Coarse-Grained (CG) Model.

In our CG model, an assemblage is represented as a triangulated elastic sheet. Each edge in the elastic network corresponds to a dimer, the basic assembly unit for HBV.^65,66 It is straightforward to generalize the model to other common basic assembly subunits, such as monomers, trimers, and pentamers/hexamers, by changing the graph structure of the elastic sheet (e.g., refs 52, 67, and 69). Each HBV dimer is modeled as an edge with two asymmetric half-edges. Half-edges have orientations (e.g., CD conformation edges comprise CD and DC half-edges in the model), and the edge–edge bindings are type- and order-dependent (e.g., $g_{\text{C}-\text{D}}^{\text{bind}}\ne g_{\text{D}-\text{C}}^{\text{bind}}$). This is an important feature for modeling viruses that assemble from protein dimers (e.g., HBV, MS2, BMV) because the dimer–dimer interfaces in these viral capsids are asymmetric—one dimer is “capped” at one end by the other dimer. The model HBV $T=4$ capsid has 120 edges corresponding to the 120 dimers in a complete $T=4$ HBV capsid.

The energy for a model capsid configuration is given by

$${𝓗}_{\text{capsid}}={𝓗}_{\text{elastic}}+{𝓗}_{\text{steric}}+{𝓗}_{\text{bind}}+{𝓗}_{\text{conf}}$$ (2)

The elastic energy accounts for the harmonic potentials for edge length fluctuations $l$, dihedral angles $\varphi$ between the planes of each pair of adjacent triangles, and binding angles $\theta$ between each pair of edges meeting at a vertex, with moduli ${\kappa }_l$, ${\kappa }_{\theta }$, and ${\kappa }_{\varphi }$ respectively:

$${𝓗}_{\text{elastic}}={𝓗}_{\text{stretch}}+{𝓗}_{\text{bend}}+{𝓗}_{\text{angle}}$$ (3)

$${𝓗}_{\text{stretch}}=\frac{{\kappa }_l}{2}\sum _i^{\text{all edges}}{\left(l_i-l_{c(i)}^0\right)}^2$$ (4)

$${𝓗}_{\text{bend}}={\kappa }_{\varphi }\sum _i^{\text{bound edges}}1-\cos \left[{\varphi }_i-{\varphi }_{c(i)}^0\right]$$ (5)

$${𝓗}_{\text{angle}}={\kappa }_{\theta }\sum _{\langle ij\rangle }^{\text{bound edge pairs}}1-\cos \left[{\theta }_{ij}-{\theta }_{c(i),c(j)}^0\right]$$ (6)

with $c(i)$ being the dimer conformation for edge index $i$ and $c(i)$, $c^{\prime }(j)$ the conformations of two bound edges, with $i$, $j$ the edge indices.

The term ${𝓗}_{\text{steric}}$ represents the excluded volume interaction of dimers and is represented by hard-sphere excluders with positions relative to the edge axis that are based on the dimer structure (see Figure S4). Excluders move as a rigid body with the edge position and orientation. Configurations in which excluders overlap have infinite energy and thus are forbidden.

The binding energy ${𝓗}_{\text{bind}}$ is the sum of binding energies between pairs of bound edges ($i$, $j$), with a binding affinity that depends on the edge conformations, $g_{c(i),c^{\prime }(j)}$. The half-edge data structure used in our implementation has an orientation and thus efficiently represents the conformation- and order-dependent binding energies in HBV capsids.

The term ${𝓗}_{\text{conf}}$ represents the intradimer conformational free energy landscape: i.e., the relative equilibrium populations of different conformational states for the capsid protein dimers (see Overview of Model and Parameters). Since CD and CC monomers are set as the zero free energy reference conformational states, the total conformational energy of an assembly is given by the number of AB dimers $n_{\text{AB}}$ in the structure, ${𝓗}_{\text{conf}}=n_{\text{AB}}\Delta g_{\text{CD}\to \text{AB}}^{\mathrm{conf}}$. Although there is evidence that the conformations of HBV dimers in solution differ from those in the capsid^{80,87–89,97}, NMR and crystallography experiments show that the free dimer has the same fundamental structure as in the capsid.^80,98 Therefore, while it is straightforward to allow for additional dimer conformations, we have not done so here to minimize the number of parameters.

Monte Carlo (MC) Simulations.

The initial configuration for each simulation is three edges (dimers) bound in a triangular geometry, with the initial conformation of each triangle being chosen randomly. The MC algorithm includes 7 moves, which include association or dissociation of either single dimers or pairs of dimers, binding or unbinding of the dimers in the shell, conformational switches of individual dimers, and thermal relaxation of the shell by vertex displacement moves (Figure S7).

Estimating CG Model Parameters from an AA Simulation of a Complete HBV Capsid.

We estimate the parameters for ${𝓗}_{\text{elastic}}$, ${\kappa }_l$, ${\kappa }_{\theta }$, ${\kappa }_{\varphi }$, $\left\{l_c^0\right\}$, $\left\{{\theta }_{c,c^{\prime }}^0\right\}$, and $\left\{{\varphi }_c^0\right\}$, by comparison against AA molecular dynamics simulations of a complete $T=4$ HBV capsid.⁴ We coarse-grain the data from the AA simulations in two steps. First, we select the $\text{C}-\alpha$ atom of residue 132 of each capsid protein monomer. The rationale for using residue 132 as an anchor residue is 2-fold. One, it provides a convenient point of reference due to its position near opposite ends of the dimers principle axis. Two, it is a well-studied residue; amino acid substitutions at this site have shown measurable effects on capsid assembly and capsid stability.⁹⁹ These 240 points are clustered based on proximity using the scikit DBSCAN algorithm,⁵ which identifies the 5-fold and quasi-6-fold axes. The center of mass of each cluster is then assigned to a vertex in the CG capsid. Calculating the set of CG edge lengths, dihedral angles, and binding angles for each residue based on 50,000 conformers from the $1\mu \text{s}\text{AA}$ simulation provides the data for estimating the equilibrium distribution of these parameters in the CG model (see Figure 1C and Movie S1).

We perform MC simulations on complete $T=4$ capsids to estimate the corresponding distribution of edge lengths and angles in the CG model. In particular, we use the complete $T=4$ capsid mapped from a frame in the AA simulation as the initial condition and only perform vertex displacement moves to relax the structure. In each simulation, we initially perform 50000 MC sweeps to equilibrate the system and then an additional 50000 sweeps to estimate the edge length and angle distributions. We optimize parameter values by minimizing the Kullback–Leibler divergence of the CG and AA distributions for each quantity, using the Tree-structured Parzen Estimator (TPE) algorithm in the Hyperopt package.¹⁰⁰

As shown in Figure S8,the distribution of edge lengths is bimodal, and thus the edge-length distribution can only be fit by a CG model with at least two edge types (corresponding to two different conformations, AB and CD). Thus, in addition to the elastic moduli, we fit equilibrium edge lengths for both conformations $l_{\text{AB}}^0$, $l_{\text{CD}}^0$, dihedral angles ${\varphi }_{\text{AB}}^0$, ${\varphi }_{\text{CD}}^0$, and binding angles $\left\{{\theta }_{c,c^{\prime }}^0\right\}$ with $\left(c,c^{\prime }\right)\in \{(\text{BA},\text{AB}),(\text{AB},\text{CD}),(\text{CD},\text{BA}),(\text{DC},\text{DC})\}$.

In addition to the binding angle conformation pairs listed above for $T=4$ and $T=3$ capsids, structures of HBV dimers in drug-mediated assembled structures (and similarly hexagonal sheets of HBV dimers) include a binding angle pair CD–CD, for which we set ${\theta }_{\text{CD},\text{CD}}^0=\pi /3$ since the sheet is composed of equilateral triangles.

Estimating Binding Energy Parameter Values.

Atomic-resolution structures of different HBV capsids and assemblies^16,70 show that there are significant structural differences between the binding interfaces for different dimer conformations. Therefore, in our model the dimer–dimer binding affinities depend on the dimer conformations. Since the dimers are not head–tail symmetric, the binding affinities also depend on the relative orientations of the monomers within each dimer. Thus, there are 16 possible binding arrangements for two dimer types AB and CD. However, only 7 of these binding arrangements can be found in available structures of HBV capsids: (BA–AB, AB–CD, and CD–BA in both $T=4$ and $T=3$ capsids, DC–DC in $T=4$ capsids, AB–CC and CC–BA in $T=3$ capsids, and CD(CC)–CD(CC) in drug-mediated assembled structures (and similarly hexagonal sheets of HBV dimers).^16,70,77,78

To estimate the relative difference in binding affinity between different dimer–dimer conformation pairs, we use the buried surface area computed from atomic-resolution structures using PDBePISA, a tool for examining macromolecular interfaces.^101,102Table 1 shows relative binding energies calculated from the two different $T=4$ HBV capsid crystal structures 2G33¹⁶ and 6UI7,⁷⁰ where we have set the reference binding energy parameter $g_0^{\text{bind}}={\overline{g}}_{\text{C}-\text{D}}^{\text{bind}}$. In $T=3$ capsids, AB–CC and CC–BA have buried surface areas similar to those of AB–CD and CD–BA in $T=4$ capsids⁷⁰ (Table S2), and thus we consider them to be the same in the model. The CD–CD interaction is not present in $T=4$ or $T=3$ capsids, but calculation of the CD–CD binding affinity for CD conformations in the $T=4$ structure¹⁶ gives ${\overline{g}}_{\text{D}-\text{C}}^{\text{bind}}\approx 0.3$. We have optimized this parameter in Figure 2A,B and set ${\overline{g}}_{\text{D}-\text{C}}^{\text{bind}}=0.2$. Similarly, estimates for all other binding affinities result in small values of $(0.01-0.1)g_0^{\text{bind}}$; thus, to limit the number of model parameters we set all other interactions to $0.05g_0^{\text{bind}}$.

Mapping the Free Model Parameters to Experimental Values.

The structure and dynamics-based procedures described thus far to set model parameters leave two free parameters, $g_0^{\text{bind}}$, which controls the mean interdimer binding affinity, and $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$, the intradimer conformational interconversion free energy. These parameters together set the mean free energy of a dimer in a capsid ground-state configuration (meaning subunits are at their equilibrium position so that ${𝓗}_{\text{elastic}}=0$), according to

$$K_{\text{bind}}=v_{\text{b}}{C}_0{e}^{-\beta g_{T=4}^{\text{bind}}}$$ (7)

with

$$g_{T=4}^{\text{bind}}=\left({𝓗}_{\text{bind}}^{\text{T}=4}+{𝓗}_{\text{conf}}^{\text{T}=4}\right)/240$$ (8)

where ${𝓗}_{\text{bind}}^{\text{T}=4}=60g_{\text{A}-\text{A}}^{\text{bind}}+60g_{\text{B}-\text{C}}^{\text{bind}}+60g_{\text{D}-\text{B}}^{\text{bind}}+60g_{\text{C}-\text{D}}^{\text{bind}}$ and ${𝓗}_{\text{conf}}^{\text{T}=4}=60\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}},v_{\text{b}}$ is the binding volume parameter (see the Supporting Information), and $c_0=1\text{M}$ is the standard state volume. $C_0=1\text{M}$ is also used for calculating the chemical potential $\mu =\ln \left(C_{\text{tot}}/C_0\right)$.

The mean dimer–dimer binding free energy corresponding to $K_{\text{bind}}$ has been estimated from experimental measurement of the equilibrium capsid assembly yields as a function of total subunit concentration under different experimental conditions (e.g., ref 65). However, the assembly equilibrium depends on both $g_0^{\text{bind}}$ and $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$, and it is likely that both of these parameters depend on solution conditions.^{65,79,80,87,103} Thus, it is not straightforward to estimate both of these parameters from the experimental data. Instead, we consider $g_0^{\text{bind}}$ and $\Delta g_{\text{CD}\to \text{AB}}^{\text{conf}}$ but note that their ranges and relative values are constrained by experimental data according to eq 7.