Sequence Patterning, Morphology, and Dispersity in Single-Chain Nanoparticles: Insights from Simulation and Machine Learning

Abstract

Single-chain nanoparticles (SCNPs) are intriguing materials inspired by proteins that consist of a single precursor polymer chain that has collapsed into a stable structure. In many prospective applications, such as catalysis, the utility of a single-chain nanoparticle will intricately depend on the formation of a mostly specific structure or morphology. However, it is not generally well understood how to reliably control the morphology of single-chain nanoparticles. To address this knowledge gap, we simulate the formation of 7680 distinct single-chain nanoparticles from precursor chains that span a wide range of, in principle, tunable patterning characteristics of cross-linking moieties. Using a combination of molecular simulation and machine learning analyses, we show how the overall fraction of functionalization and blockiness of cross-linking moieties biases the formation of certain local and global morphological characteristics. Importantly, we illustrate and quantify the dispersity of morphologies that arise due to the stochastic nature of collapse from a well-defined sequence as well as from the ensemble of sequences that correspond to a given specification of precursor parameters. Moreover, we also examine the efficacy of precise sequence control in achieving morphological outcomes in different regimes of precursor parameters. Overall, this work critically assesses how precursor chains might be feasibly tailored to achieve given SCNP morphologies and provides a platform to pursue future sequence-based design.

1. Introduction

Single-chain nanoparticles (SCNPs) are an intriguing class of materials obtained by collapsing or folding a polymer chain into a stable nanostructure. The formation and stability of a SCNP is driven by intrachain interactions, which are characteristically noncovalent (e.g., hydrophobic, electrostatic, polar), covalent, or dynamic covalent.^1,2 Inspired by proteins, SCNPs have prospective applications in catalysis, nanomedicine, and biosensing.²⁻⁸ Ultimately, the functionality and utility of a SCNP depends on its morphology, which may determine factors such as hydrophobic character near catalytic active sites.⁹ Consequently, fundamental study regarding the structures formed by single polymer chains has implications for the technological advancement of SCNPs^10,11 and understanding of single-chain polymer physics.¹²⁻¹⁴

Significant progress has been made in both developing facile chemical pathways for synthesis of possible precursors (i.e., the initial, unfolded polymer chains) and the characterization of resultant morphologies for SCNPs. Typically, precursors are obtained by first synthesizing a polymer with specific functional groups and then performing postpolymerization reactions at dilute conditions to promote structure formation.² Experimental scattering techniques (e.g., small-angle X-ray and neutron scattering, dynamic light scattering, etc.) have shown that the conformational behavior of SCNPs ranges between a self-avoiding random walk (ν ≈ 0.56) and globular (ν ≈ 1/3) behavior, depending on the nature of the linking chemistry.^3,12,15−20 Reaction conditions may also be varied or advanced synthetic techniques employed to achieve more precise monomer and functional-group placement and bias formation of target structures in SCNPs.²¹⁻²⁵ Substantial structural dispersity, though, can exist among SCNPs that formed from identical precursors in even polymers with relatively small numbers of chemical moieties.²⁶ Knowledge relating a precursor to structure formation (and its reliability) in resulting SCNPs will be crucial in achieving target functional properties of these materials.

Molecular dynamics (MD) simulation provides a useful tool to examine the formation of SCNPs under well-controlled conditions and with exquisite structural resolution. Prior MD studies have supported experimental observations while also generating insight regarding both the detailed nanoscopic structure of SCNPs and the mechanisms by which they might form.^{11,15,16,20,27−30} For example, good solvent conditions limit contact between distal portions of the polymer chain, thereby promoting intrachain linkages over shorter backbone contour distances and resulting in pearl-necklace-like structures.^16,20,28,29 MD simulations have also highlighted new strategies, such as the use of ring-polymer architectures for the precursor or manipulation of solvent quality²⁹ to bias formation of more compact, globular structures,¹¹ which have been experimentally challenging to achieve. Nevertheless, most simulations probe either random or regular sequence patterning of cross-linking moieties on SCNP structure formation.²⁹ Moreover, although structural dispersity is often noted in simulations of SCNP formation, it is rarely characterized, and its implications in technological applications is largely unexplored. Thus, a comprehensive view of the impact of sequence patterning of cross-linking moieties, a thorough assessment of structural dispersity in SCNP, and examination of their interplay is needed.

Exploring and characterizing the structure–function landscape of polymeric materials is generally nontrivial given the multitude of behaviors enabled by a large chemical and architectural space.³¹⁻³⁵ To contend with this challenge, machine learning (ML) techniques have been increasingly utilized to probe and understand structure–function relationships in soft materials.³⁶⁻⁴⁴ In the context of single polymer chains,⁴⁵⁻⁴⁷ supervised ML models have been proven effective at relating polymer chain characteristics to average conformational behavior, thereby expediting targeted sequence- and composition-based design tasks. Meanwhile, unsupervised ML algorithms have usefully discriminated among morphological structures formed in many-chain soft materials assembly by noncovalent and supramolecular interactions.^48,49 Collective variables obtained from unsupervised ML can also form the basis for predicting and designing morphology.⁵⁰ Overall, these works illustrate the promise of ML to help understand the distribution of morphologies that are accessible by a given precursor and to reveal potential strategies to control that distribution.

In this study, we use molecular simulation in tandem with machine learning analyses to assess how the patterning of cross-linking moieties on precursor chains impacts the morphology and properties of SCNPs. To comprehensively probe the sequence–structure space, we simulate the formation of 7680 SCNPs from precursors chains that are predominantly distinguished by the fraction and distribution of reactive cross-linking groups along the backbone. These simulations are analyzed to characterize resulting SCNPs via structural analysis and unsupervised manifold learning. These analyses reveal not only the landscape of possible SCNP morphologies but also the dispersity of structures arising from given precursor specifications, which has not been previously well-characterized. We further examine the variability in morphological outcomes for different sequences with the same patterning descriptors to assess the efficacy of tuning SCNP properties with more precise control over the precursor sequence. In aggregate, this work provides a critical assessment of how precursors might be feasibly tailored to achieve given SCNP morphologies and a platform to pursue SCNP design with specific consideration of structural fidelity.

2. Methods

2.1. Systems

2.1.1. Model of Precursor Chains and Single-Chain Nanoparticles

We adopt a coarse-grained, phenomenological model to study the formation of SCNPs from precursor polymer chains. Within the model, precursor chains are comprised of backbone beads as well as pendant beads that can function as cross-linking moieties (Figure 1a); these pendant beads are colloquially referenced as “linkers”. SCNPs are thus obtained from precursor chains by allowing linkers to react and form bonds. A modified Kremer–Grest model⁵¹ describes the interactions among beads in both precursor chains and SCNPs. The standard elements include (i) excluded-volume interactions characteristic of good-solvent conditions (captured by a Weeks–Chandler–Andersen pair potential) and (ii) covalent-bond interactions (captured by the typical finite extensible nonlinear elastic potential function with standard parameters); good-solvent conditions are often experimentally used to avoid intermolecular linkages between different precursor molecules.² The modified components include (i) the introduction of chain semiflexibility, which is common,^52,53 and (ii) the reactivity of linker beads, which has been handled similarly in prior studies of SCNPs.^11,16,20,28 All beads (backbone and linker) are of the same characteristic size σ, the repulsive interaction from the Weeks–Chandler–Andersen pair potential is set by ε = k_bT, and all bonds are treated equivalently, irrespective of whether they are between backbone–backbone, backbone–linker, or linker–linker beads. Interaction parameters are kept uniform in this study to emphasize the role of patterning of cross-linking moieties, although manipulation of monomer chemistry and sequence effects to bias structure formation⁴⁵ may be of future interest.

Figure 1.

Overview of model and precursor chain parameters. (a) Simulation snapshot of a precursor chain. Annotations highlight the presence of backbone beads (pink) and linker beads (teal). Single-chain nanoparticles are formed by allowing the linker beads to react based on specific geometric criteria. (b) Schematic depiction of the precursor parameter blockiness, b. (c) Visualization of the precursor chain parameter space. Ten distinct precursor chains are generated for each (b, f) pair indicated by the markers. The underlying shaded region visualizes the accessible space subject to the bound on b imposed by f. (d) Visualization of the precursor chain parameter space in the normalized blockiness β–f plane. For a given f, points are uniformly distributed with respect to β. In panels c and d, the markers are colored according to f to illustrate the mapping from b to β.

Chain semiflexibility is introduced via 1–3 bending interactions of the form

1

for which θ_ijk is the angle formed by two consecutive bonds between polymer backbone beads (i with j and j with k) and K controls the local bending rigidity, which we set to K = 5k_bT. Future phenomenological models may benefit from additional bending and torsional interactions that include the linker beads, but these are not included in the present work.

Reactions between linkers to form SCNPs are handled in the following manner. First, reactions between two linkers results in the formation of a covalent bond; this bond is modeled equivalently as with any other covalent bond in the model. Second, reactions between two linkers can and will proceed only if certain geometric criteria are satisfied. In particular, the distance between two linkers must be within a “capture” radius of 1.3σ, and the angle formed by bond vectors adjoining the linker and their respective backbone bead must be 180 ± 30°. Third, reactions may not proceed between linkers on adjacent backbone beads. Fourth, reactions are irreversible (i.e., covalent bonds are preserved for the duration of the subsequent simulation). Fifth, a linker may only participate in one reaction (i.e., its valency is one and saturates upon formation of a covalent bond with another linker). With respect to prior literature on modeling SCNPs, the utilization of a capture radius is common and follows work from Moreno and collaborators,^16,29 whereas the addition of an angle-based criterion is not ubiquitous but has been employed in atomistic simulations.²⁷ Here, this constraint and the null reactivity among topologically adjacent linkers is motivated by considering steric and electronic factors of conventional cross-linking chemical moieties.² Without this addition, we find that linkers on adjacent backbone beads can undergo facile reaction, which seems generally unphysical given the disposition of cross-linking agents.

2.1.2. Precursor Chain Parameters

Many facets of precursor chains (chain length, chemistry, patterning, architecture, etc.) might be feasibly manipulated to control SCNP morphology. Here, only particular parameters of precursor chains are varied while others are common to all precursor chains. Specifically, all precursors consist of N_bb = 400 backbone beads arranged in a purely linear topology; each backbone bead may be considered as a monomer or constitutional unit. We choose this number of constitutional units inspired by Lo Verso et al.²⁹ who noted apparent differences in structures formed by precursors with random sequence patterning versus those formed from regular sequences at this length. In principle, the number of backbone units is another physical parameter that can be tuned and experimentally realized by controlling the extent of polymerization. The primary variable parameters herein are (i) the extent of functionalization or linker fraction f = N_l/N_bb and (ii) a descriptor b, which relates to the “blockiness” of linker beads as distributed along the polymer chain (Figure 1b). The parameter b is given by

2

where k and k + 1 are indices of backbone beads along the polymer chain (∈[0, N_bb – 1]) and 1_i,j is an indicator function, such that

3

In this fashion, a precursor sequence with backbone beads perfectly alternating between having and not having a linker would yield b = N_bb^–1, while a sequence with all backbone beads possessing linkers followed by all backbone beads without linkers would yield b = 1. This blockiness parameter bears some similarity to but is not equivalent to the correlation parameter used to describe the statistics of random copolymers.^54,55

An overview of precursor chain parameter combinations examined in this study is shown in Figure 1c. Notably, eq 2 implicitly depends on the linker fraction f, such that the minimum accessible b varies with f (i.e., min b(f) ≈ |2(f – 0.5)|). Consequently, precursor chains are studied for f ∈ {0.1, 0.15, 0.2, 0.3, 0.4, 0.6, 0.8}, and values of b at each composition are chosen such that β ∈ {0.2, 0.4, 0.6, 0.8} where

4

is a normalized blockiness parameter that can be sampled uniformly irrespective of composition (Figure 1d). We emphasized study at lower f with the expectation that heterogeneity in SCNP morphologies would diminish at higher f.

Based on prior work,^40,46 we hypothesized that these parameters would enable study of a vast set of precursor chains that would result in distinct SCNPs. Although a precise connection of f and β to experimental synthetic conditions may be nontrivial, we expect that such parameters would meaningfully relate to aspects of monomer concentration and reactivity ratios.^56,57 In the long term, advances in sequence-level polymerization may enable more precise definitions.^21−25,58

2.1.3. Precursor Chain Sequence Generation

Ten unique sequences are generated for each combination of (f_i, β_j) to assess dispersity of SCNP morphologies as a function of precursor parameters. Thus, in total, 320 unique precursor chains are considered. To generate a given precursor chain sequence at a specified (f_i, β_j), a fixed number of linkers (set by f_i) are first randomly distributed across the polymer backbone, and the resulting initial normalized blockiness β_j⁽⁰⁾ is computed. Supposing that β_j ≠ β_j, a random pair of backbone beads (one with a linker and one without) is selected, and the linker position is swapped if it would yield |β_j⁽¹⁾ – β_j| < |β_j – β_j|. This process is repeated until the trial |β_j^(k) – β_j| < 0.001. All sequences generated by this process can be found in the Supporting Information.

2.1.4. Simulation

All MD simulations are performed using a modified version of the 3 Mar 2020 distribution of the LAMMPS simulation package.⁵⁹ Simulations are performed in reduced units with characteristic quantities of m, σ, and ε for mass, distance, and energy, respectively; the reduced time unit is τ = (mσ²/ε)^1/2. Simulations correspond to a single polymer chain in implicit solvent. There are no periodic boundary conditions to prevent self-interaction. The simulations therefore correspond to SCNPs forming at infinite dilution. Additional details regarding general simulation protocols, precursor preparation, precursor equilibration, SCNP formation, and SCNP simulation are provided in the Supporting Information.

2.2. Analysis

2.2.1. SCNP Structural Descriptors

Topological descriptors of the SCNP are assessed via its representation as a molecular graph^60,61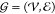. Here, the beads of the SCNP comprise the set of vertices , and bonds among beads comprise the set of undirected edges or bonds between beads, ; coordinates of beads are not used for this analysis. Using this framework, we compute two topological descriptors: the number of free backbone beads n_f and the number of topological domains n_d; both of these descriptors have been previously examined in simulation studies to assess SCNP structure.^28,62 For their computation, we adopt the labeling algorithm of Moreno et al. reported in ref (62). In brief, for any pair of bonded linkers v_m, v_n, the backbone vertices along the directed contour path comprise a set 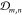; if there are n_b linker–linker bonds, then there will be such sets. Then, a domain 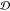is defined as the union of sets, for which every set has nonempty intersection with at least one other set in 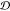. Backbone beads that are not found in any path set (i.e., the complement of the set of all backbone beads with the union of all domains) constitute a set of free segments 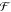, such that 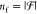is the cardinality (number of members) of the free-segment set.

SCNP structures are also characterized by shape descriptors derived from their gyration tensor:

5

where r_i is a column vector of the position of the ith backbone bead, r_cm is the center-of-mass position of the SCNP, and T denotes the transpose. Subsequent diagonalization of eq 5 yields S = diag(λ₁², λ₂², λ₃²), where the diagonal elements are the principal moments of the gyration tensor such that λ₁² ≤ λ₂² ≤ λ₃². From these, conventional shape descriptors⁶³ are computed, including the radius of gyration

6

which indicates the overall size of the SCNP; the acylindricity

7

which measures departure from cylindrical symmetry with respect to the eigenvectors of λ₂ and λ₁; the asphericity

8

which measures the overall symmetry of the distribution of beads with respect to three coordinate axes; and the relative shape anisotropy

9

which assesses departure from spherical symmetric morphologies (κ² = 0). Notably, both b and κ² will yield zero for spherically symmetric configurations, while b will yield zero for any Platonic solid. Ensemble averages of the shape parameters are computed using the final 10⁷ time steps of the production trajectory.

2.2.2. Unsupervised Machine Learning

SCNP morphologies are also identified, distinguished, and compared with the aid of unsupervised ML. The essence of the approach is to discriminate between SCNP morphologies in a data-driven fashion on the basis of collective differences in the local environments of the composite backbone beads; this is largely inspired by methods and analyses by Reinhart, Statt, and co-workers in the context of colloidal crystals, ice crystals, binary mesophases, and model polymer aggregation.^48,50,64 Here, we consider the local density of backbone beads n(r_c) = N/σ³ to be descriptive of the local environment of a bead, such that a given configuration of a SCNP can be numerically represented by a histogram of such local densities. In this study, local densities are measured only for backbone beads using a spherical cutoff of r_c = 6σ, and histograms possess 40 evenly spaced bins over the range [6.63 × 10^–3, 0.239]σ^–3, which spans observed values across all configurations.

The histograms can be constructed for any given configuration of a SCNP to provide a 40-dimensional feature vector x_i. To obtain a representative ensemble, 20 distinct configurations for each SCNP (dumped at a frequency of 2.5 × 10⁶ time steps) are featurized. This results in 320 sequences × 24 independently formed SCNPs per sequence × 20 configurations per SCNP = 153,600 total feature vectors; the 20 configurations taken for each SCNP accounts for structural fluctuations, which may be of interest in certain applications. Subsequently, the uniform manifold approximation and projection (UMAP) algorithm is used to learn a low-dimensional numerical embedding of the SCNP morphologies and the manifold over which they are distributed. To facilitate visualization and interpretation, we simply target a two-dimensional embedding. Hyperparameters related to UMAP include the size of the local neighborhood (set to 200), the overall density of the embedding (minimum distance between points set to 1), and the distance metric for points in the feature space (Euclidean). In effect, this approach generates a mapping 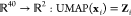where Z_i is a coordinate vector in the learned low-dimensional representation of the set of local densities around monomers. As such, Z_i provides information on the nanostructural characteristics of SCNPs. We note that additional descriptions of the local environment, including that used by Reinhardt,⁶⁴ as well as those equivalent to atom-centered symmetry functions,⁶⁵ were also examined for the embedding described above (see Supporting Information, Figure S2). However, all approaches yielded qualitatively similar organization of morphologies, and local density was thus employed for its ease of interpretability, despite it being the least descriptive of the local environment.

2.2.3. Metrics of Dispersity and Sequence Variability

To quantify morphological dispersity in SCNPs and assess the importance of precise sequence control, we introduce a series of so-called dispersity and sequence variability metrics. Dispersity metrics primarily address variability in outcomes of SCNPs for a given precursor chain, while sequence variability metrics address the range of possible outcomes for a given specification of f and β, which is associated with a set of realizable precursor chains. In the following, a given SCNP is characterized by a tuple (c(f, β), s_c) where c denotes a precursor chain from the set 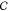of all possible precursor chains with characteristics f and β, and s_c is an element of the set 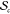of all possible SCNP structures that can form from precursor c. In addition, the notation x∼Y indicates that the variable x was sampled from the set Y. In the present study, relevant sets practically correspond to (i) the 24 independent trajectories that yield unique SCNPs from a given precursor chain or (ii) the ten distinct precursor chains generated for each combination of f and β; these sets are respectively used in the calculation of expectation values indicated by 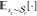and .

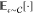Dispersity in the size of the SCNPs arising from a given precursor chain is given by

10

where ⟨R_g⟩_sc is the ensemble-average R_g for a given SCNP; this is the variance in ⟨R_g⟩_sc sampled over 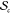. Dispersity in ⟨Z⟩ (related to the density of local environments) for SCNPs arising from a given precursor chain is given by

11

where “x|c” denotes conditioning the variable x on c. This quantity is the entropy of the distribution of ⟨Z⟩ and measures the differences in the nanostructures of the SCNP that are formed from a given precursor c.

Because not all manifestations of c(f, β) are expected to yield the same distribution of SCNPs, we define four sequence variability metrics. Sequence variability on the outcome of R_g at a particular f and β is defined as

12

which probes the variance of the mean SCNP sizes formed from c across all c in 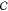. Sequence variability on the dispersity of chain sizes is similarly defined as

13

This probes the variance of the dispersities of SCNP sizes (eq 10) formed from c across all c in . Because the position on the manifold ⟨Z⟩ is two-dimensional, sequence variability of Z is instead defined as

14

This is the entropy of the distribution formed by the expectation values of ⟨Z⟩_sc over 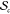for all c in . Lastly, we define the sequence variability in the dispersity of positions on the manifold:

15

This is related to the variance in the dispersity of nanostructures (eq 11) formed from c across all c in .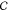

3. Results and Discussion

3.1. Characterization of Morphologies

3.1.1. Unsupervised Learning Facilitates Understanding of SCNP Morphologies

To effectively process and identify morphological archetypes of all simulated SCNPs, we utilized unsupervised machine learning to construct a low-dimensional manifold of SCNP morphologies (section 2.2) wherein the structure of every SCNP can be represented via a two-dimensional coordinate vector Z = (Z₁, Z₂). Importantly, the morphologies of SCNPs are expected to share similar features when closely positioned on the manifold (e.g., when |Z_i – Z_j| is small).

Figure 2a shows that the manifold of SCNP morphologies, as determined by the unsupervised machine learning, is primarily organized by the average local density of backbone beads n̅. Moving from left-to-right (increasing Z₁), SCNPs transition from compact (high n̅, green colors) to expanded (low n̅, blue colors) structures. Figure 2b reveals a secondary level of organization, more so along Z₂, wherein structures are differentiated by the distribution of local environments, which is quantified by the standard deviation of local densities around backbone beads, σ(n). Moving from the bottom toward the top of the manifold within a band of constant n̅, morphologies transition from having relatively homogeneous local environments toward having increasingly heterogeneous nanostructures. Thus, the unsupervised learning approach distinguishes between, for example, different manifestations of similarly compact SCNP morphologies (i.e., dense core and less confined shell versus more homogeneous structure).

Figure 2.

Visualization and analysis of single-chain nanoparticle (SCNP) morphologies. (a) A two-dimensional manifold organization of morphologies for SCNPs based on the Uniform Manifold Approximation and Projection (UMAP) unsupervised learning algorithm. For visual clarity, only a fraction of the overall data is shown (see also Figure S3). Each marker corresponds to a single configuration of a SCNP and is colored by the average local density around backbone beads, n̅, revealing bands of constant n̅ distributed across the manifold. Five additional markers (warm colors) that correspond to selected coordinates that span the manifold for each band are also shown; these coordinates are used for analysis in panel (b). Particular examples are noted within the figure axes for n̅ = 80. (b) The standard deviation of local densities around backbone beads, σ(n), as a function of fractional distance λ across each band. The distance across each band is estimated by selection of two distal reference points z₀(n̅) and z₁(n̅), such that intermediate positions can be selected as z_λ = (1 – λ)z₀(n̅) + λz₁(n̅). Each marker corresponds to the average of σ(n) for a collection of structures found within 0.3 units of the corresponding marker in panel a; the line colors reflect the band for each n̅. Error bars report the standard deviation of σ(n) across the aforementioned collection of structures. (c) Simulation snapshots of 103 representative configurations across the latent space manifold. Each rendering is positioned above its coordinate position in the manifold. In the renderings, only backbone beads are shown and are colored by the local density of other backbone beads within a 6σ radius.

Figure 2c illustrates how representative SCNP structures are distributed across the low-dimensional manifold, revealing several archetypal morphologies that arise in congruence with the specific local environments. Specifically, structures on the left side of the manifold (Z₁ < 5) are globular, typified by relatively large n̅. Structures on the top-right side of the manifold (Z₁ ≈ 5, Z₂ > 5) resemble pearl-necklace and tadpole-like morphologies, typified by larger σ(n). Structures on the bottom-right side (Z₁ > 10, Z₂ ≈ 0) are populated with diffuse globular, worm-like, and rod-like morphologies, with lesser σ(n). Therefore, it becomes possible to make a distinction between stringy versus clumpy pearl-necklace-like structures based on the heterogeneity of local environments. Collectively, these results indicate that (i) the precursor chains over the β–f parameter space yield a rich array of SCNP morphologies and (ii) the manifold coordinates Z, which broadly correlate to the average and heterogeneity of nanostructural environments within a SCNP, provide a reasonable organization of those structures.

Observed archetypes also resemble those of prior studies, albeit with some distinctions. While Moreno and co-workers observe many of the same archetypes, they noted an abundance of pearl-necklace-like structures^16,20,28 which are represented to a much lesser degree across our morphologies. We suggest that this difference arises due to our use of angular constraints for linker-bond formation, which inhibits linkers forming bonds over short contour distances of the polymer backbone. In another study, Tulsi and Simmons found SCNPs that also adopt pearl-necklace, worm-like, and dense globular structures.³⁰ They further identified “gnarled” structures, which are similar to the more diffuse globules observed in this study. Interestingly, their SCNPs arise from a model with different physical characteristics and distinct mechanism for assembly; this suggests that the present and prior theoretical studies may be homing in on a general set of readily realizable SCNP morphologies. In addition, many of our structures resemble tadpole morphologies which are similar to morphologies observed in experiments.⁶⁶⁻⁶⁸

3.1.2. Sequence Characteristics of Precursors Bias Structure Formation

To assess how linker patterning impacts SCNP structure, we examine how precursor parameters f and β dictate position on the manifold of SCNP morphologies (Figure 3a,b). While f and β both impact morphology, they have different effects. Roughly, trends with f and Z track with n̅. This suggests that structures formed from high-f precursors (left) predominantly display more compact, globular morphologies typified by high n̅, while structures formed from low-f precursors (right) result in more diffuse, low-n̅ morphologies. The impact of β is less striking but evident at low f (i.e., f ≲ 0.3). In particular, β impacts how cross-links are distributed over the SCNP topology: at fixed and low f, high-β precursors yield SCNPs with few centralized “hubs” of cross-links, while the low-β precursors result in SCNPs with cross-links that are more evenly distributed over the chain. As a result, increasing β biases morphologies from worm- or rod-like (bottom right) to more pearl-necklace- and tadpole-like structures (top right); the nature of this effect is further resolved in Figure S4.

Figure 3.

Relationship between sequence characteristics of precursors and structural features of resulting single-chain nanoparticles. Variation of (a) linker fraction f and (b) normalized blockiness β as a function of manifold coordinates Z₁ and Z₂. In both panels a and b, grid points within the manifold are colored by the median value of single-chain nanoparticles within a small radius of the grid point. Heat maps showing the average over single-chain nanoparticles generated from precursors at specified β and f for (c) the number of free backbone beads n_f, (d) the number of topological domains n_d, (e) the radius of gyration R_g, and (f) the standard deviation of the distribution of local densities around monomer beads. The values used to color (f) are normalized by the mean value observed at a given f to highlight trends with respect to β.

We characterized 7680 unique SCNPs across the β–f space by the number of free backbone beads n_f, the number of domains n_d, and the radius of gyration R_g to quantitatively examine how particular morphologies arise as a result of β and f. Figure 3c–f show the averages of these structural descriptors over the ensemble of SCNPs generated from precursors with specific blockiness and linker-fraction combinations; precise numerical values are reported in the Supporting Information. All four descriptors possess identifiable trends that resonate with the qualitative observations from Figures 2c and 3a,b. Figure 3c shows that decreasing f and increasing β typically increases the extent of polymer chain that is not present in any cross-linked domain. Meanwhile, Figure 3d indicates that decreasing β and f tends to result in SCNPs with more domains that possess fewer beads. Together, these results suggest that β and f can be manipulated to tune aspects of SCNP topology, although not arbitrarily. Beyond a certain f, it appears these structural descriptors are not strongly affected by β. This is evident by the flat color saturation at f ≥ 0.6, indicating that all SCNPs are essentially one large topological domain in this precursor regime. The nature of these topological structures has clear implications on the size of the SCNP, as seen in Figure 3e. To first order, SCNP size, as given by R_g, is controlled by the number of free segments, which is strongly biased by f; only at low f does β appear to have subtle impact on R_g; we observe near-identical trends for shape descriptors derived from the gyration tensor (Figure S5). Rather, β mostly controls the extent of heterogeneity of SCNP nanostructures (Figure 3f). In particular, decreasing β biases from morphologies that feature more heterogeneous local environments around beads toward those with more homogeneous ones, even while R_g is largely unaffected. Collectively, these results illustrate how sequence patterning of precursors can be manipulated to bias the morphological characteristics of SCNPs.

3.2. Characterization of Structural Dispersity

3.2.1. Morphological Dispersity Depends on Sequence Patterning

We next investigate the impact of precursor patterning on the consistency of forming SCNP morphologies. Figure 4 illustrates that a single precursor sequence can give rise to a set of SCNPs with diverse morphological characteristics. This is first demonstrated in Figure 4a, which compares P(⟨R_g⟩) for ten SCNPs originating from precursor chains with f = 0.1 and β = 0.2 and ten originating from precursor chains with f = 0.1 and β = 0.8. Selected sequences (e.g., 5, 6, and 9 for f = 0.1 and β = 0.8) are noted to have particularly broad distributions, which result from averaging over the 24 replicate simulations. Across both precursor conditions, many distributions are non-Gaussian, bordering on bimodal or heavy-tailed, which would indicate that the different trajectories produce disparate morphologies rather than exhibit a single, dominant archetypal morphology. Figure 4b,c shows that there can also be substantial nanostructural diversity in the ensemble SCNPs formed by a given precursor sequence; this would be evidenced by a diffuse P(⟨Z⟩) for a given sequence. Such diffuse distributions are particularly identifiable for sequence 0, 1, and 3 in Figure 4b, which derive from low-blocky precursors. However, sequence patterning can significantly impact the tightness of P(⟨Z⟩), as sequence 2 for β = 0.2 is much more strongly peaked than that of sequence 0. Diffuse P(⟨Z⟩) for β = 0.8 (Figure 4c) are not quite as evident, and the P(⟨Z⟩) are generally similar in shape, hinting at the possible role of precursor parameters like β on dispersity.

Figure 4.

Morphological dispersity of single-chain nanoparticles originating from given precursor sequences. (a) Comparison of distribution of radius of gyration P(⟨R_g⟩) for distinct single-chain nanoparticles. The distributions are obtained from 24 independent replicate simulations of the same precursor chain sequence. The data are for SCNPs formed from ten precursor sequences each from f = 0.1 and β = 0.2 (yellow, left) and f = 0.1 and β = 0.8 (green, right). The width of violins correspond to the density obtained from Gaussian kernel density estimation; the edges of box plots in the violin depict the interquartile range, while white dots indicate the median value. Comparison of the distribution of manifold-coordinate vectors P(⟨Z⟩) for single-chain nanoparticles formed from selected precursor chain sequences with parameters of (b) f = 0.1 and β = 0.2 and (c) f = 0.1 and β = 0.8. In panels b and c, the color reflects Gaussian kernel density estimation over the ⟨Z⟩ for each of the 24 distinct SCNPs formed by each precursor sequence. The color scheme reflecting precursor parameters and sequence labels is the same across panels.

3.2.2. Precursor Parameters Have Disparate Effects on Different Measures of Dispersity

Figure 5 elucidates the role of f and β on both dispersity in P(⟨R_g⟩) and dispersity in P(⟨Z⟩). Intriguingly, we find that these measures of dispersity are generally anticorrelated. This is evident by examining trends with increasing f, which tends to decrease dispersity in P(⟨R_g⟩) and increase dispersity in P(⟨Z⟩). This can be understood by considering the high-f regime, for which well-connected globular morphologies would have similar overall size and limited capacity to change (low dispersity in P(⟨R_g⟩)) but can nonetheless have disparate populations of local environments (low dispersity in P(⟨Z⟩)), such as observed in Figure 2. At low f but high β, dispersity in P(⟨R_g⟩) is high yet dispersity in P(⟨Z⟩) is diminished. Combined with the observation that SCNPs formed from precursors with these characteristics resemble pearl-necklace-like morphologies, diminished dispersity in P(⟨Z⟩) suggests that the formation of dense (pearl) and diffuse (lace) nanostructures is relatively consistent. Furthermore, heightened dispersity in P(⟨R_g⟩) suggests that how these nanostructures are arranged or connected (i.e., the precise topology) could result in relatively large changes P(⟨R_g⟩). In addition, we observe an apparent maximum in P(⟨Z⟩) dispersity at intermediate f (0.25, 0.3) and intermediate β (0.4, 0.6), suggesting relatively greater diversity in the set of nanostructures between SCNPs formed from these precursors. Moving away from this maximum toward higher f decreases the entropy of the distributions but to a lesser degree than moving away from the maximum toward lower f. This reflects the consistent, high-density core formed by structures at high f but high variability in local densities around the outside of the structure that depends on the precise folded shape of the SCNP even when broadly characterized as a compact globule.

Figure 5.

Effect of precursor parameters on morphological dispersity. Heat maps at a given linker fraction f and normalized blockiness β for the average (a) dispersity in ⟨R_g⟩ given by 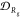in eq 10 and (b) dispersity in manifold coordinates given by 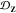in eq 11. For both panels, average effects are estimated by considering the ten unique precursor chains generated at a given f and β.

3.2.3. Specific Sequences Enable More Precise Control over Morphology

Differences in the distributions of ⟨R_g⟩ and ⟨Z⟩ across sequences with the same β and f exhibit differences (Figure 4) suggesting that sequences might be precisely crafted to fine-tune characteristics of formed morphologies. To examine this, we calculate four “sequence variability” metrics that report how distinct aspects of SCNP morphologies are across different sequences for the same f and β. In particular, we specifically examine the sequence variability in the mean of P(⟨R_g⟩), the dispersity in P(⟨R_g⟩), the mean of P(⟨Z⟩), and the dispersity in P(⟨Z⟩). We anticipate that understanding sequence variability may be useful to ascertain whether tailoring sequences would offer prospective advantages over an ensemble of sequences defined by a given f and β.

Figure 6a,b shows that sequence variability is highest for the mean value and dispersity of P(⟨R_g⟩) at low f and high β values. By contrast, sequence variability in the mean and dispersity of P(⟨R_g⟩) is diminished at high f, suggesting that precise sequence control would be less valuable; this observation is consistent with prior results (Figure 3 and Figure 5) that indicated negligible impact of β on structure formation at high f. Furthermore, Figure 6c indicates that sequence variability in the mean of P(⟨Z⟩) follows a similar trend, peaking at small f and intermediate values of β and decreasing at large f. There are no discernible trends in sequence variability for the dispersity of P(⟨Z⟩) (Figure 6d). Together, these results suggest that precisely tailoring sequences to manipulate the distribution of formed SCNPs, whether it be aspects of the SCNP size or its average local environment, is likely to be most effective for low f and intermediate to high β.

Figure 6.

Analysis of sequence effects on morphological control. Heat maps show sequence variability as a function of linker fraction f and normalized blockiness β calculated as (a) variance in the means of P(⟨R_g⟩), (b) variance in dispersities of P(⟨R_g⟩), (c) entropy of the means of P(⟨Z⟩), and (d) variance in the dispersity of P(⟨Z⟩). Quantities are computed from 10 independently generated sequences for each specified f and β.

4. Conclusions

In this work, we examined how sequence patterning of intramolecular cross-linking moieties (linkers) in polymer chains impacts the formation of single-chain nanoparticles (SCNPs). To do so, we simulated the formation of 7680 unique SCNPs from precursor chains, which altogether comprehensively spanned a parameter space defined by the number of linkers in the chain, f, and the blockiness of the chain, β. The morphologies of the SCNPs were subsequently characterized using unsupervised machine learning and several structural descriptors to elucidate the general roles of β and f on morphological outcomes of SCNPs. Finally, we assessed how β and f impact dispersity in the sizes of SCNPs (P(⟨R_g⟩)) and their characteristic nanostructural environments (P(⟨Z⟩)), and we explored how precise sequence control might be useful to further tune SCNP properties.

Overall, we found several major trends with respect to SCNP topology, morphology, and precursor parameters. Using manifold learning, we showed that SCNP morphologies could be distinguished principally by the mean-density of beads and secondarily by the heterogeneity of local nanostructural environments. For example, we identified two distinct globular morphologies (one with a dense core–flexible shell structure and one with more homogeneous density throughout). Specific archetypal morphologies were also found to be strongly associated with certain regimes of precursor parameters. Low-f precursors tend to adopt topologically diffuse structures with several domains and large chain segments between domains; in this regime, increasing β biases structure formation toward fewer and larger domains but a higher proportion of the polymer chain that is not within any topological domain. By contrast, precursors with high f consistently give rise to SCNPs with globular structures that show weak sensitivity to β. In addition, while low-β precursors tend to result in SCNPs with rod-like morphologies (i.e., several domains of similar nanostructures), high-β precursors result in tadpole-like morphologies (i.e., fewer domains with disparate nanostructures). By examining the set of structures formed from every precursor, we found that low-f precursors yield SCNPs with substantial diversity in size but overall consistent local environments, while high-f precursors generate SCNPs with the opposite trend. Furthermore, comparing the distributions of SCNPs generated from specific sequences that all correspond to the same β and f highlighted the potential to leverage precise sequence patterning for morphological control, manifest in either specific average values or distribution characteristics. Investigation of new “sequence variability” metrics revealed that precursor chains with low f and large β illustrate the widest range of possible morphology and dispersity outcomes. Therefore, we hypothesize that this regime could benefit most from precise sequence control to tailor the morphological properties of SCNPs.

Ultimately, the methods and analyses herein may spawn several directions of future research. First, while the present and many prior studies emphasized the final SCNP morphologies, future work may aim to quantify the physical implications of SCNP structure and understand their relationship to other SCNP properties (e.g., response to shear flow, mechanical unfolding, etc.). Furthermore, there is significant opportunity to establish how precursor patterning dictates the mechanism(s) or pathway(s) of SCNP formation. Examination of formation pathways may facilitate additional understanding as to how SCNP morphology might be more tightly controlled. Finally, our results point to the possibility of tuning the dispersity of SCNP morphologies in numerous ways. While prior work has leveraged assembly protocols to bias structure formation (e.g., toward globular morphologies²⁹), here we show that dispersity outcomes (either SCNP size or nanostructural environments) might be manipulated either by setting particular precursor parameters or by tailoring sequences. Furthermore, with many demonstrations of using statistical ensembles of chains in functional materials,⁶⁹⁻⁷⁴ it will be interesting to consider how distributions of chains can be designed to achieve target properties. Approaches to navigate such design tasks, particularly in the context of experimentally verifiable systems will be needed.

Data Availability Statement

Derived data associated with single-chain nanoparticles, their characteristics, and accompanying Python scripts are available for download at https://github.com/webbtheosim/scnp_public. The configurations of all single-chain nanoparticles used for analysis in this manuscript is published in ref (75).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acspolymersau.3c00007.

• A complete data set including SCNP properties and list of SCNP precursor sequences (ZIP)

• Information regarding simulation protocols, additional strategies explored for unsupervised learning, correlation between topological descriptors, and correlation between topological and morphological descriptors. (PDF)

Author Contributions

CRediT: Roshan A. Patel conceptualization (equal), data curation (lead), formal analysis (lead), investigation (lead), methodology (lead), software (lead), supervision (supporting), validation (lead), visualization (lead), writing-original draft (lead), writing-review & editing (supporting); Sophia Colmenares conceptualization (supporting), data curation (supporting), formal analysis (supporting), investigation (supporting), methodology (supporting), software (supporting), writing-original draft (supporting), writing-review & editing (supporting); Michael A. Webb conceptualization (lead), data curation (supporting), formal analysis (supporting), funding acquisition (lead), investigation (supporting), methodology (equal), project administration (lead), resources (lead), software (supporting), supervision (lead), validation (equal), visualization (equal), writing-original draft (supporting), writing-review & editing (lead).

The authors declare no competing financial interest.

Special Issue

Published as part of the ACS Polymers Auvirtual special issue “2023 Rising Stars”.