Evolution of Emergent Monopoles into Magnetic Skyrmion Strings

Abstract

Topological defects are fundamental concepts in physics, but little is known about the transition between distinct types across different dimensionalities. In topological magnetism, as in field theory, the transition between 1D strings and 0D monopoles is a key process whose observation has remained elusive. Here, we introduce a novel mechanism that allows for the controlled stabilization of emergent monopoles and show that magnetic skyrmion strings can be folded into monopoles. Conversely, they act as seeds out of which the entire string structure can unfold, containing its complete information. In chiral magnets, this process can be observed by resonant elastic X-ray scattering when the objects are in proximity to a polarized ferromagnet, whereby a pure monopole lattice is emerging on the surface. Our experimental proof of the reversible evolution from monopole to string sheds new light on topological defects and establishes the emergent monopole lattice as a new 3D topological phase.

Topological defects play crucial roles in a large variety of systems, such as the cosmology of the early universe,^1,2 liquid crystals,³ superconductors,^4,5 crystallography,⁶ magnetism,⁷ and many more. Their formation mechanism is attributed to spontaneous symmetry breaking, where the defects can be classified based on the dimensionality, i.e., 2D domain walls, 1D strings, and 0D monopoles.^1,2,8 Their existence can be traced back to a more fundamental origin, where distinct types of topological defects can evolve across dimensions.⁹⁻¹¹ In field theory, magnetic monopoles are topological defects with the lowest dimensionality.^1,2 Following their formation, monopoles extend into higher dimensions, i.e., from 0D point defects to 1D strings or 2D/3D bifurcation networks,^12,13 and further develop increasingly subtle structures that fill space-time.^10,11,14 In other words, monopoles initially carry the information about strings and subsequently unfold out of them, i.e., their topological properties are preserved independent of the length scale. While the evolution from monopoles to strings is an integral part of the framework of topological defects, its experimental observation remains challenging.⁹

Emergent phenomena in condensed matter systems are known to be ideal test beds for exploring topological defects,^1,8,15 and in particular topological magnetic systems have shown great promise.^1,8,15−17 For example, in chiral magnets, the order parameter is identified as a magnetization vector field m(r), and the spontaneous SO(3) symmetry breaking is caused by competing exchange interaction terms leading to local topological defects, such as 1D skyrmion strings^{13,16,18−21} and Bloch points.^17,22−25 Bloch points were proven to be in fact emergent monopoles that mediate a number of phase transitions and dynamics.^17,22

In principle, as a consequence of broken symmetry,²⁶ skyrmion strings are 1D topological defects that can be traced back to a lower dimension, i.e., 0D emergent monopoles.¹⁷ In other words, in the early stages of the process of skyrmion formation, only monopoles are nucleated as local topological defects. These monopoles carry the information about the strings, unfolding the entire string structure through a phase transition.²⁶ This picture demonstrates the elegant generality of field theory and provides significant insights into the topological origin of magnetic skyrmions. However, the observation of the evolution process from emergent monopoles to skyrmion strings remains elusive, since pure emergent monopoles, reminiscent of magnetic monopoles in the early universe, are not equilibrium structures in a common chiral magnet.^17,22,26 In this Letter, we experimentally demonstrate the stabilization of a 2D monopole lattice that floats on top of a chiral magnet Cu₂OSeO₃. Such a controlled monopole state offers great opportunities for the observation and manipulation of the folding process from monopoles to strings (and vice versa).

Cu₂OSeO₃ is a typical chiral magnet that hosts a number of solitonic states with topological properties.^27,28 The dominating energetics includes the isotropic exchange interaction with exchange stiffness A, the Dzyaloshinskii–Moriya interaction (DMI) that is parametrized by D, and the Zeeman energy due to the external magnetic field B. The nonlinearity introduced by the DMI induces local instabilities through which topological defects are nucleated.^26,27 One of the well-known topologically ordered phases is the skyrmion phase, whose 3D extension resembles topological strings.^{13,16,18−21} Occasionally, the strings have finite length and terminate at a Bloch point singularity.²⁹⁻³¹ These so-called chiral bobbers²⁹ are exemplified in Figure 1a–c.

Figure 1.

Folding a skyrmion string into a monopole. (a–c) Bobber structure stabilized in the near-interface region of the Cu₂OSeO₃/pFM heterostructure, obtained through micromagnetic simulations. The terminating end resembles an emergent monopole configuration. (d–f) Upon decreasing the temperature, the stray field from the pFM becomes stronger, favoring a reduced penetration length of the bobber. (g–i) Eventually, this results in a pure monopole that floats on top of the chiral magnet. (j) Illustration of the heterostructure used in this work. (k) On a larger scale, emergent monopoles form a quasi-2D lattice. (l and m) Calculated 3D REXS intensity distribution in reciprocal space visualized in different perspectives.

In fact, a chiral bobber can be regarded as an intermediate topological defect that is a hybrid between a 1D string and a monopole.⁹⁻¹¹ Therefore, it is reasonable to assume that a similar mechanism to the cosmological model exists through which the string’s length, quantified by the penetration depth L_p (as shown in Figure 1a), can be manipulated. This way, the string can be either extended or folded back toward the surface, as shown in Figure 1d–f. In the extreme limit, the string would be completely folded into a monopole that then floats on the very top surface, as shown in Figure 1g–i. In other words, the mechanism illustrated in Figure 1a, d, and g, together with the reversed process, describes the evolution between monopoles and strings.

First, we identify and test a mechanism for controlling the string length via numerical calculations. As illustrated in Figure 1j, we consider a typical thin film system with perpendicular anisotropy (20 nm) on top of a Cu₂OSeO₃ substrate, separated by a Ta layer to suppress the direct interfacial exchange interaction (see section S1). It is important to note that at the field at which the skyrmion string lattice is formed in the bulk crystal, the ferromagnetic thin film has to be completely polarized. Our micromagnetic simulations (section S2) suggest that the stray field from the polarized ferromagnet (pFM) favors the breakdown of the skyrmion strings, thus forming bobbers with finite L_p (Figure 1a). The monopole configuration is therefore found at the terminating end of the string (Figure 1b and c).

When the saturation magnetization of the pFM layer is increased, the enhanced stray field leads to shorter strings. In practice, the pFM layer magnetization can be controlled by varying the temperature. As shown in Figure 1d–f, a slightly stronger magnetization (achieved by lowering the temperature) effectively reduces the penetration depth of the bobber. Eventually, such topological defect shrinks into a “levitated” singularity at the surface of Cu₂OSeO₃, as shown in Figure 1g–i. In other words, the 1D topological string is folded into a 0D emergent monopole. From the simulations, the depth of the singular point is L_p = 3 nm. Importantly, such a process is reversible, i.e., by increasing the temperature, the monopole point continuously develops into the string structure.

On a larger length scale, the monopoles (Figure 1g–i) crystallize into a hexagonally ordered state, the emergent monopoles lattice (EML) state. We used resonant elastic X-ray scattering (REXS)³² to search for signatures of the formation of the EML state. The REXS experiments were carried out at the RASOR diffractometer on beamline I10 at the Diamond Light Source. For the purpose of this work, we define the circular dichroism signal (the CD-REXS signal) as the difference in diffraction intensity for the same skyrmion peak at the same geometrical condition, which was obtained using left- and right-circularly polarized soft X-rays. Using CD-REXS, the helicity angle χ of a 2D skyrmion can be unambiguously determined.³³⁻³⁶ Further details can be found in sections S3, S4, and S6.

As shown in Figure 1k, the ideal EML state can be regarded as a perfectly ordered 2D lattice. The unit cell and the lattice constant a = 69 nm are shown in Figure 1k, associated with a magnetic reciprocal lattice unit (m.r.l.u.) of 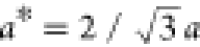in units of nm^–1.^34,37Figure 1l and m show the calculated REXS pattern in different perspectives. When projected onto the q_x–q_y plane, a sixfold-symmetric pattern with second-order peaks (Figure 1l) is expected due to the anharmonic soliton nature of the EML.¹⁶ More interestingly (Figure 1m), the first-order peaks are further extended into extremely long magnetic crystalline truncation rods along q_z. The magnetic truncation rods theory³¹ was recently developed to recover the depth information on near-surface magnetic structures, i.e., to determine L_p and the configuration of the magnetic motif. For a quasi-2D EML sheet, the magnetic rods have almost infinite length due to the lack of confinement in the third dimension.

Experimental Results

Using a combination of bulk and thin film growth techniques, we synthesized a heterostructure using a Ta/CoFeB/MgO multilayered thin film as the pFM. In order to investigate the modification of the near-surface magnetic structure due to the introduction of the pFM, we studied the identical Cu₂OSeO₃ crystal before and after pFM growth. First, the main results are summarized in Figure 2, showing the phase diagrams probed by both AC susceptibility and REXS. We employed a 40 mT field-cooling field-sweep-up protocol to map the magnetic phases shown in Figure 2b–d. The complementary results that are measured under other protocols can be found in Figure S3. Note that AC susceptibility is a bulk-sensitive technique that averages the response of the entire Cu₂OSeO₃ crystal,³⁸ i.e., the pFM layer only contributes an indiscernible signal. On the other hand, REXS with its resonance energy tuned to the Cu L edge uniquely probes the magnetic structure of Cu₂OSeO₃ below the pFM heterostructure.^32,34 Therefore, by comparing the differences of the phase diagrams mapped by both experiments, it is straightforward to identify the exotic phases in the interface region.

Figure 2.

Magnetic phase diagrams and the characteristic magnetic phases. For the phase diagrams, the field was applied along [001]. The magnetic phases were defined based on their 3D RSM patterns, which are shown as the lower row. The black dots are the measured data points. (a) Standard phase diagram measured by AC susceptibility before the pFM layer was grown. It remains the same after the growth of the pFM. (b–d) Phase diagrams mapped following the field-cool-field-sweep-up protocol with a 40 mT cooling field. (b) Phase diagram mapped by AC susceptibility, which is identical for the pFM-coated and pristine Cu₂OSeO₃ bulk sample. (c) Phase diagram for the pristine Cu₂OSeO₃ bulk crystal mapped by REXS. (d) REXS phase diagram after the pFM was grown on top of the identical Cu₂OSeO₃ bulk crystal. (e–h) Characteristic 3D RSM patterns for the basic magnetic orders found in chiral magnets. The q_z = 0 plane is highlighted in pink. Additional phases that emerge due to the introduction of the pFM layer are as follows: (i) bobber lattice for which the skyrmion lattice peaks extend into finite rods, (j) folded bobber lattice with further elongation of the bobber lattice rods and two extra conical peaks, (k) coexistence of the folded bobber lattice and helical order, (l and m) low-temperature bobber lattice with elongated rods and reduced a*, and (n) the expected low-temperature skyrmion phase.

Figure 2a shows the standard phase diagram probed by AC susceptibility for both pristine and overgrown Cu₂OSeO₃, confirming that the pFM does not change the bulk properties. Figure 2b and c show the phase diagrams of the pristine bulk sample determined by AC susceptibility and REXS, respectively. After the growth of the pFM layer, the REXS phase diagram (Figure 2d) undergoes drastic changes (cf. Figure 2c). Meanwhile, the AC susceptibility phase diagram remains identical to that of Figure 2b for the heterostructure sample. This directly suggests a magnetic modification of the surface structure due to the introduction of the pFM. The distinct magnetic orders can be unambiguously classified via their 3D REXS patterns, as shown in Figure 2e–n, as well as their 3D visualizations (SI Movies S1–7).

First, four basic magnetic phases from the pristine bulk sample can be identified through 3D reciprocal space mapping, namely, the helical (Figure 2e), conical (Figure 2f), skyrmion string lattice (Figure 2g), and tilted conical phases (Figure 2h).²⁸ Second, the additional stray field effectively modifies the energy hierarchy of the interface such that the skyrmion-based phase is extended into the entire experimentally accessible phase space (Figure 2d). In the high temperature region near T_C, the bobber lattice phase emerges above the bulk-dominated skyrmion string lattice pocket at 40–70 mT, which is characterized by the six extended rods along q_z (Figure 2i). In the low temperature domain (Figure 2j), the skyrmion lattice rods have significantly increased in length compared to Figure 2i. Further, these rods can coexist (and mix) with helical and conical peaks. At higher fields, instead of the expected low temperature skyrmion phase with its signature pattern (Figure 2n), we observed the pattern associated with the bobber lattice (Figure 2l and m). Here, the bobber lattice has a reduced a* value, ranging from 0.0167 to 0.0102 nm^–1, i.e., an increased real space lattice constant.

To better understand the string-folding process, we focused on the folded bobber lattice region (pink area in Figure 2d; state illustrated in Figure 2j) in the temperature range from 30 to 58 K, and in particular the temperature evolution of the 3D reciprocal space mapping (RSM) pattern. Figures 3a and b show the RSM pattern for the standard skyrmion string lattice phase at 58 K and 34 mT in pristine Cu₂OSeO₃, represented in top and side views, respectively. Such a reciprocal space structure is in excellent agreement with the 3D skyrmion string lattice structure in real space in which the strings extend into the bulk.³¹ From the top view, only first-order and double-scattering peaks are visible, which is due to the harmonic spin modulations in the xy-plane, i.e., the triple-q structure.^16,37 In the side view, the six peaks show a slight vertical extension, which is attributed to the natural peak broadening due to the finite penetration length of the resonant soft X-rays. After the growth of the pFM, the sample shows the emergence of a bobber lattice at higher fields (40 mT at 58 K). As shown in Figure 3c and d, despite the fact that the sixfold-symmetric peaks exhibit the same configuration in the top view, they turn into sharp rods with a finite length. This key feature reflects the fact that the strings are broken up near the surface and that L_p is shallower than the probing depth. By analyzing the rod profiles in detail, an L_p value of 28 ± 1 nm and the exact shape of the bobber motif can be quantitatively obtained. In short, the longer the rods, the shallower the bobbers are buried beneath the surface. Figure 3h shows the extracted L_p from the 3D RSM as a function of temperature at 40 mT. Upon cooling, the stray field from the pFM becomes stronger, thus encouraging shorter strings. An extreme case is reached when L_p approaches the pure emergent monopole limit, leading to almost infinitely long rods along q_z.

Figure 3.

3D reciprocal space mapping. The 3D RSM measurements were carried out at three selected temperature and field points, which are marked by a triangle, a square, and a star, respectively, in Figure 2. The RSMs are visualized as top and side views for (a and b) the skyrmion string lattice for pristine Cu₂OSeO₃, (c and d) the bobber lattice from the heterostructure, and (e and f) the emergent monopole lattice from the heterostructure. (g) Detailed view of the (0, 0, q_z)-rod from (f), obtained after blocking the other contributions. (h) Extracted penetration depth of the skyrmion strings as a function of temperature, obtained after a quantitative magnetic rod analysis.

Such a quasi-2D scenario is realized by further cooling the system down below a threshold value of ∼45 K, and at 40 K (at 40 mT) the 3D RSM suddenly develops three additional features (Figure 3e and f). First, second-order peaks can be clearly identified, which is consistent with the monopole lattice having pronounced anharmonic components of the 2D modulations. Second, the magnetic truncation rods become extremely long, i.e., the rod intensity does not drop even beyond the instrumental limit in q_z. A quantitative rod analysis reveals that L_p = 3.0 ± 0.9 nm (see Figure 3h). This in excellent agreement with the calculated REXS pattern in the 3D RSM representation using the EML model (Figures 1l and m). Third, we observe two extra conical peaks along the (0, 0, q_z)-rod (Figure 3g), measuring (0, 0, ± 0.0167) nm^–1, that do not appear for the string lattice or the (folded) bobber lattice above 45 K. This can be understood by assuming that the skyrmions beneath the top surface are absent, leaving the conical order to fill the space that is probed by the X-rays. Therefore, these three remarkable features strongly indicate that below 45 K the strings are completely folded into emergent monopoles.

In order to provide additional evidence for the observed state (Figure 3e and f) being a lattice of emergent monopoles, we carried out circular dichroism (CD)-REXS measurements. CD-REXS was recently developed in order to retrieve the internal twisting degree of freedom of the skyrmion motif, i.e., the helicity angle χ.³⁴ By carrying out photon-energy-dependent CD-REXS measurements, the detailed helicity angle evolution profile, χ(z), can be reconstructed.^35,39 The CD-REXS data for a fixed incidence photon energy is represented in Figure 4a, from which a vector that separates the positive and negative dichroism REXS signals can be obtained. The direction of this vector directly corresponds to χ_m, i.e., the weighted average over all χ(z) values for the skyrmion layers within the probing depth. For a 3D skyrmion-based structure, such as strings or bobbers, due to the broken translational symmetry at the surface, χ(z) always develops pronounced profiles.^30,35,39 Uniform helicity angles at the near-surface region are usually not observed. Therefore, by varying the photon energy, a spectrum-like χ_m curve can be observed; see, for example, Figure 4c. As the χ_m spectrum contains the full information about the helicity angle over all layers, by knowing the X-ray probing length as a function of energy, the χ(z) profile can be reconstructed using an iterative fitting algorithm (section S6). In other words, if the motif reaches the 2D limit by forming an emergent monopole, the z-dependence of the helicity angle collapses, leading to single-valued χ_m for all photon energies.

Figure 4.

CD-REXS investigation of the emergent monopole lattice phase. To further prove that the state shown in Figures 3e and f is indeed the EML phase, a comparative CD-REXS study was carried out on (a–d) the low-temperature bobber lattice phase and (e–g) the EML state. (a) CD-REXS pattern measured at the Cu L₃ peak maximum, resulting in a probing depth of 94 nm, and (b) that at a slightly shifted photon energy yielding a larger probing depth of 264 nm. (c) Energy dependence of χ_m. The measured data are shown as dots (with error bars). (d) χ(z) profile obtained using an iterative reconstruction algorithm. The red/blue curve in (c) shows the calculated χ_m spectrum obtained from the red/blue χ(z) profile shown in (d). The blue curves represent the results determined using the standard skyrmion string model. (e–g) Corresponding measurements carried out in the EML state. The red line in (g) stems from EML model calculations with a single-valued χ of 47°. (h) Real-space model of the EML state refined using the complementary REXS results.

First, we show the CD-REXS data measured in the low temperature bobber lattice phase for comparison. Figure 4a and b show the CD-REXS patterns at two selected photon energies, between which a clear χ_m difference of 10° is found. Further systematic energy scans are shown in Figure 4c, allowing for the extraction of the detailed χ(z) evolution (red profile in Figure 4d). Notably, this profile is consistent with the measured data shown in Figure 4c (red curve). As a reference, we show the χ(z) profile for a standard skyrmion string lattice^35,39 as the blue curves in Figure 4c and d. It is thus clear that the low temperature bobbers develop well-defined 3D structures with finite L_p. Importantly, CD-REXS is sensitive to the fine details of the χ(z) configuration, as evidenced by the large difference between the blue and red curves in Figure 4c.

Figures 4e and f show the CD-REXS patterns for the EML state using the same protocol as for Figure 4a–d. Strikingly, despite measuring at two distinct photon energies, χ_m remains practically the same. Further energy scans reveal a flat χ_m curve with a value of ∼47° for all photon energies. This immediately leads to the conclusion that the measured lattice has a single-valued χ for all layers along z. We can thus argue that the only possible magnetic structure with a single-valued χ(z) profile is that of the EML state, as for all other known states a nonuniform configuration would develop due to the surface twist effect. The reconstructed real-space texture of the EML is shown in Figure 4h, which can also be well produced by our simulations, as shown by the twisted motif in Figure 1h. It is worth noting that the EML is not a pure 2D atomic layer, requiring a small but finite thickness of ∼3 nm in order to accommodate the Bloch point. The EML model is able to seamlessly explain all experimental findings, i.e., (1) the pronounced second-order peaks in the q_x–q_y plane below 45 K, (2) the extremely long truncation rods that in turn reveal L_p ≈ 3 nm, and (3) the breakdown of the 3D skyrmion model, as evidenced by a single-valued helicity angle of χ = 47°.

We have presented clear evidence that the theoretically proposed string-folding process between a 0D monopole and a 1D string (Figure 1a–g) has been experimentally observed (Figure 3h). This observation has deeper implications for the understanding of the fundamental origin of topological defects. It reveals that the information about the rich structures of a system is initially encoded in zero-dimensional singular points and subsequently unfold through phase transitions. In our work, the folding and unfolding process is reversible via tuning the temperature; this means that the string can be folded back to a monopole, while a singular point can in turn unfold into a string via a continuous transformation. The EML may also serve as a novel topological phase that hosts unconventional emergent physics, as well as providing a robust means for encoding information.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.3c01117.

• 3D visualization of the skymion string lattice magnetic order (MP4)

• 3D visualization of the tilted conical magnetic order (MP4)

• 3D visualization of the bobber lattice magnetic order (MP4)

• 3D visualization of the folded bobber lattice magnetic order (MP4)

• 3D visualization of the folded bobber lattice + helical magnetic order (MP4)

• 3D visualization of the low temperature bobber lattice magnetic order (MP4)

• 3D visualization of the low temperature bobber lattice + tilted conical magnetic order (MP4)

• Additional experimental details on sample growth and characterization, micromagnetic simulations, REXS calculations, and phase diagrams, including additional measurement and simulation results (PDF)

Author Contributions

H.J., K.R., R.F., G.L., T.H., and S.Z. performed the REXS experiments. H.J., W.T., and S.Z. developed the magnetic rod analysis package and the CD-REXS iterative algorithm. Y.S. and J.W. prepared the bulk crystals, and G.Y. and Y.G. grew the thin film heterostructures. W.T. and Y.L. carried out micromagnetic simulations. S.Z. conceived the project and supervised the analysis. S.Z., T.H., and G.L. prepared the first draft of the manuscript. All authors discussed the results and reviewed the manuscript.

This work was supported by the National Key R&D Program of China under contract numbers 2022YFA1403602 and 2020YFA0309400, the Science and Technology Commission of the Shanghai Municipality (21JC1405100), the National Natural Science Foundation of China (Grants 12074257 and 12241406), and the Double First-Class Initiative Fund of ShanghaiTech University. T.H. acknowledges support from the Engineering and Physical Science Research Council (UK) under Grant EP/N032128/1. K.R. acknowledges the support from the Shanghai Sailing Program (Grant 20YF1430600) and the National Natural Science Foundation of China (Grant 12004249). G.Y. acknowledges the Beijing Natural Science Foundation (Grant Z190009), the Science Center of the National Science Foundation of China (Grant 52088101), and the National Natural Science Foundation of China (Grants 12274437). The work at Nanjing University was supported by the National Key Projects for Research and Development of China with Grant 2021YFA1400400 and the National Natural Science Foundation of China with Grants 12225407 and 12074174.

The authors declare no competing financial interest.