Abstract

Strong coupling between molecules and quantized fields has emerged as an effective methodology to engineer molecular properties. New hybrid states are formed when molecules interact with quantized fields. Since the properties of these states can be modulated by fine-tuning the field features, an exciting and new side of chemistry can be explored. In particular, significant modifications of the molecular properties can be achieved in plasmonic nanocavities, where the field quantization volume is reduced to subnanometric volumes, thus leading to intriguing applications such as single-molecule imaging and high-resolution spectroscopy. In this work, we focus on phenomena where the simultaneous effects of multiple plasmonic modes are critical. We propose a theoretical methodology to account for many plasmonic modes simultaneously while retaining computational feasibility. Our approach is conceptually simple and allows us to accurately account for the multimode effects and rationalize the nature of the interaction between multiple plasmonic excitations and molecules.
Keywords: plasmonics, strong coupling, coupled cluster theory
Strong light–matter coupling between molecules and electromagnetic fields leads to the formation of new hybrid states, known as polaritons, where the quantum nature of the electromagnetic field entangles with purely molecular states.1−8 The resulting polaritons can display different key features compared to the original states, potentially leading to new chemical/photochemical reactivity,1,9−15 energy transfer processes,16−21 or relaxation channels,15,22−24 among others. While photonic cavities are an obvious choice, other fields, like the ones produced by electronic excitations in plasmonic nanostructure, can also be used to achieve the strong coupling regime. Despite their highly lossy nature, plasmonic nanocavities can confine the electromagnetic fields even down to subnanometric volumes.25 The resulting interaction could be instrumental for a wide range of applications, such as sensing,26−29 high-resolution spectroscopy,30−32 single-molecule imaging,32−34 and photocatalysis.35−39
Recent works point out that the simultaneous contribution of multiple plasmonic modes, going beyond the simplest dipolar resonances, might be critical for a number of phenomena,40−43 e.g., the chiro-optical response of light–matter systems.44−51 In such cases, theoretical models that capture multiple plasmon modes simultaneously are of the utmost importance.
Several ab initio quantum electrodynamics (QED) methods for strongly coupled systems have been proposed, e.g., quantum electrodynamics density functional theory (QEDFT),3,52,53 QED coupled cluster (QED-CC),54−58 and quantum electrodynamics full configuration interaction (QED-FCI).55,59 Despite its computational affordability, QEDFT inherits the intrinsic problems of exchange and correlation functionals,60,61 whereas QED-CC, albeit more accurate, is computationally demanding. The latter method has recently been extended to model quantized plasmonic modes obtained through a polarizable continuum model (PCM)62 description of the nanoparticle response (Q-PCM-NP).63 In its current implementation, however, QED-CC cannot take into account more than one plasmon mode at a time. Generalization of the original theory to the multimode case will quickly become computationally unfeasible.
In this paper, we couple the existing plasmon QED-CC method to a scheme that captures the main effects of multiple plasmons into a single effective mode. This allows us to retain the same computational cost of a single-mode QED-CC calculation while accounting for the multimode effects.
We first present a formal definition of the effective mode, followed by a numerical example on a test case system. Specifically, the effective mode approach is tested on a system composed of three nanoparticles (NPs) surrounding either a hydrogen or a para-nitroaniline (PNA) molecule. For hydrogen, we benchmark the effective mode approach against multimode QED-FCI. At the end, our final considerations and perspectives on the proposed method are given.
In our framework, the nanoparticle (NP) is described using the Drude–Lorentz dielectric function model,64 that is
| 1 |
where ΩP is the bulk plasma frequency; ω0 is the natural frequency of the bound oscillator; and γ is the damping rate. Together, these quantities define the nanoparticle material. The technique to quantize the NP linear response through a PCM-based theory has already been reported in a previous work.63 In summary, the nanoparticle surface is described as a discretized collection of tesserae, labeled by j, each of which can host a variable surface charge representing the NP response to a given external perturbation.65−67 The key quantity obtained from the PCM-based quantization scheme is qpj which can be identified as the transition charge sitting on the jth tessera of the NP for a given excited state p. The collection of all the charges for a given p-mode represents one possible normal mode of the NP (a plasmon), with frequency ωp. The detailed theory formulation can be found in the original work63 where the above-mentioned quantities are explicitly derived.
On this basis, the Hamiltonian used to describe the interaction between the nanoparticle and the molecule equals
| 2 |
where He is the
standard electronic Hamiltonian;68 ωp is the frequency of the pth nanoparticle mode; and the operators 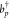 and bp create and annihilate plasmonic excitations of frequency ωp, respectively. The interaction between the
molecule and the plasmon is mediated through the bilinear term
and bp create and annihilate plasmonic excitations of frequency ωp, respectively. The interaction between the
molecule and the plasmon is mediated through the bilinear term
| 3 |
In eq 3, Vj is the molecular electrostatic potential operator evaluated at the jth tessera of the NP, while qpj is the quantized charge of mode p that lies on the jth tessera. From eq 3, the plasmon–molecule coupling for a transition going from the molecular state S0 to Sn and exciting the plasmon mode p reads
| 4 |
where 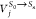 is the potential coming from the S0 → Sn transition density at the jth tessera of
the NP surface. The coupling terms in eq 4 are the key quantities for simpler approaches to the
strong-coupling regime, such as the Jaynes–Cummings (JC) model.69 This is also the starting point of the effective
mode derivation presented in this work. Using the full Hamiltonian
in eq 2 is indeed computationally
expensive because of the elevated number of plasmon modes that need
to be considered. For this reason, it is customary to only include
one mode in the Hamiltonian. While the single-mode approximation has
been used with great success in the past, there are instances where
a multimode approach is necessary. One example, for instance, is when
multiple plasmonic excitations are almost resonant with the same molecular
excitation or, as already discussed previously, when circular dichroism
phenomena are studied. To reduce the computational cost while retaining
a reasonable accuracy, it would be desirable to define a single effective
boson that accounts, on average, for the effect of many modes. In
our framework the effective mode will be obtained starting from a
multimode JC Hamiltonian.
is the potential coming from the S0 → Sn transition density at the jth tessera of
the NP surface. The coupling terms in eq 4 are the key quantities for simpler approaches to the
strong-coupling regime, such as the Jaynes–Cummings (JC) model.69 This is also the starting point of the effective
mode derivation presented in this work. Using the full Hamiltonian
in eq 2 is indeed computationally
expensive because of the elevated number of plasmon modes that need
to be considered. For this reason, it is customary to only include
one mode in the Hamiltonian. While the single-mode approximation has
been used with great success in the past, there are instances where
a multimode approach is necessary. One example, for instance, is when
multiple plasmonic excitations are almost resonant with the same molecular
excitation or, as already discussed previously, when circular dichroism
phenomena are studied. To reduce the computational cost while retaining
a reasonable accuracy, it would be desirable to define a single effective
boson that accounts, on average, for the effect of many modes. In
our framework the effective mode will be obtained starting from a
multimode JC Hamiltonian.
The generalization of the single-mode JC Hamiltonian to a multimode plasmonic system is
| 5 |
where ωn is the frequency of the S0 → Sn excitation and σ†, σ is the molecular raising and lowering operators.
| 6 |
In our case, ωn and gpn are the excitation energies and the plasmon-mediated transition coupling elements computed using coupled cluster singles and doubles (CCSD) (more details can be found in the SI). Diagonalization of the Hamiltonian in eq 5 yields the mixed plasmonic–molecular wave functions with corresponding energies. We will simply use the term “polaritonic” to generally refer to those hybrid states from now on even though a mixed plasmon–electronic excitation state is properly called plexciton.63 In the single mode case, the two eigenstates, typically called lower and upper polaritons (LP, UP), are given by
| 7 |
with  and
and 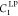 being the coefficients of the molecular
excited state with no plasmons and the molecular ground state with
one plasmonic excitation, respectively. These coefficients also appear
in the UP wave function because of the orthogonality constraints.
being the coefficients of the molecular
excited state with no plasmons and the molecular ground state with
one plasmonic excitation, respectively. These coefficients also appear
in the UP wave function because of the orthogonality constraints.
On the other hand, the eigenfunctions of the Hamiltonian in eq 5 for the multimode case read
 |
8 |
where the coefficients defining the two polaritonic wave functions do not have to satisfy the strict relation in eq 7. Moreover, they can be rewritten as
 |
9 |
where index p labels the plasmon modes and the normalization factors NLP and NUP are defined as
| 10 |
The effective lower and upper polariton bosons are given by
 |
11 |
and they have been introduced to describe the plasmon part of the lower and upper polaritons. The normalization term NLP/UP is needed to ensure that the bosons still respect the commutation relations:
| 12 |
We point out that, unlike the single-mode case in eq 7, the effective lower and upper polariton boson operators are different from each other. Moreover, the two bosons have a nonzero overlap such that
| 13 |
The effective mode approximation comes into
play when we seek a single effective mode  that replaces both
that replaces both 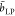 and
and 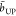 such that the energies obtained using the
effective upper and lower polaritonic states
such that the energies obtained using the
effective upper and lower polaritonic states
 |
14 |
are as close as possible to the ones obtained using the multimode JC model. We notice that in eq 14 the Cp coefficients are now common to both the lower and upper polariton wave functions. Specifically, they are optimized by minimizing the functional
 |
15 |
where 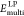 and
and  are the LP and UP energies obtained by
diagonalizing the Hamiltonian in eq 5. The optimal coefficients defining the effective mode
are the actual output of that functional minimization and are system
specific; that is, the effective mode composition will vary if the
molecule and/or the plasmonic system change. Besides this, we note
that the two solutions shown in eq 14 resemble the structure of the exact single-mode case
in eq 7. Nonetheless,
the plasmonic part of the wave function captures the effect of multiple
modes at the same time. The procedure described here can easily be
generalized to the case of an optical cavity.
are the LP and UP energies obtained by
diagonalizing the Hamiltonian in eq 5. The optimal coefficients defining the effective mode
are the actual output of that functional minimization and are system
specific; that is, the effective mode composition will vary if the
molecule and/or the plasmonic system change. Besides this, we note
that the two solutions shown in eq 14 resemble the structure of the exact single-mode case
in eq 7. Nonetheless,
the plasmonic part of the wave function captures the effect of multiple
modes at the same time. The procedure described here can easily be
generalized to the case of an optical cavity.
Once the effective mode has been defined, the Hamiltonian in eq 2 can be rewritten as
| 16 |
where 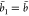 is the effective mode defined in the previous
section and the other bosonic operators fulfill
is the effective mode defined in the previous
section and the other bosonic operators fulfill
| 17 |
The two bosonic bases are related by a unitary transformation U
| 18 |
Truncating the plasmon modes in eq 16 to only include the effective
mode  , the Hamiltonian reads
, the Hamiltonian reads
| 19 |
where the following quantities have been introduced
| 20 |
The quantized charge  , of the effective plasmon mode
, of the effective plasmon mode  , allows for a direct visualization of the
effective mode properties (see Figure 2c).
, allows for a direct visualization of the
effective mode properties (see Figure 2c).
Figure 2.
First (a) and second (b) quasi-degenerate plasmon modes of the setup shown in Figure 1. The energy splitting between these two modes is ≈16 meV, and they both significantly couple to the S0 → S1 transition of H2. Their contribution to the effective mode is shown at the top of the panel. (c) Visualization of the optimized effective mode. Only the two most important modes are reported in panels (a) and (b), but the first 12 modes coupling to the molecular transition contribute to the effective mode optimization.
Starting from the Hamiltonian in eq 19, we can use any single-mode QED method to study the effects of multiple plasmonic modes on molecular properties. In this work, we focus on the QED-CC approach. The QED-CC approach is the natural extension of standard coupled cluster theory to the strong coupling regime. The wave function is parametrized as
| 21 |
where |HF⟩ is the reference Slater determinant (usually obtained through a Hartree–Fock like procedure), while |0⟩ denotes the plasmonic vacuum. The cluster operator T is defined as
 |
22 |
with each term corresponding to an electron, electron–plasmon, or plasmon excitation. In eq 22, the electronic second quantization formalism has been adopted such that68
| 23 |
where 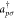 and aqσ create and annihilate an electron with spin σ in orbitals p and q, respectively. Following the commonly
used notation, we denote the unoccupied HF orbitals with the letters a, b, c..., while for
the occupied orbitals we use i, j, k.68 Inclusion of the
full set of excitations in eq 22 leads to the same results as QED-FCI. In this work we truncate T to include up to one plasmon excitation as well as single
and double electronic excitations in line with what has been presented
in ref (54). The parameters
and aqσ create and annihilate an electron with spin σ in orbitals p and q, respectively. Following the commonly
used notation, we denote the unoccupied HF orbitals with the letters a, b, c..., while for
the occupied orbitals we use i, j, k.68 Inclusion of the
full set of excitations in eq 22 leads to the same results as QED-FCI. In this work we truncate T to include up to one plasmon excitation as well as single
and double electronic excitations in line with what has been presented
in ref (54). The parameters 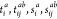 , and Γ are called amplitudes. They
are determined solving the projection equations
, and Γ are called amplitudes. They
are determined solving the projection equations
| 24 |
where μ is an electronic excitation, while n is a plasmonic excitation. We adopted the notation
| 25 |
The 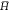 operator is the molecule-plasmon Hamiltonian
in eq 19 transformed
with a coherent state. This accounts for the polarization of the plasmonic
system induced by the molecular charge density in the HF state.
operator is the molecule-plasmon Hamiltonian
in eq 19 transformed
with a coherent state. This accounts for the polarization of the plasmonic
system induced by the molecular charge density in the HF state.
| 26 |
The setup we employed to test the effective mode approach consists of three identical ellipsoidal NPs, each one featuring a long-axis length of 6.0 nm and a short-axis length of 2.0 nm. In between the nanoellipses we placed first an H2 and later a PNA molecule that are approximately 0.6 nm away from the three structures, as shown in Figure 1. This setup was chosen because it has degenerate (or almost degenerate) plasmon modes with significant coupling to the molecule. Moreover, the plasmon frequencies can easily be modulated, for instance by changing the aspect ratio of the ellipsoidal NPs (see Figure S2 in the SI as an example). Additional details about the computational methodologies can be found in the last section of the SI.34,70,71
Figure 1.
Setup employed to test the effective mode scheme. The plasmonic system consists of 3 ellipsoidal NPs surrounding an H2 molecule in the yz plane. The beads composing the NPs represent the centroids of each tessera upon surface discretization and host a given quantized charge qpj. The lowest (in energy) plasmon mode is shown. Red beads refer to positive charges, whereas blue ones refer to negative charges. Each NP is ≈0.6 nm far from H2.
The NP setup shown in Figure 2 has two almost degenerate low excitations (Figure 2 a and b) at 12.661 and 12.677 eV, whose coupling parameters with the first H2 transition are 8.6 and 15.2 meV, respectively. Both excitations will significantly contribute to the effective mode. Specifically, their coefficients in the expansion of the effective mode (see eq 18) are reported in the top part of Figure 2.
In Figure 3 we show how the inclusion of multiple plasmon modes affects the H2 Rabi splitting. Results are shown for the multimode JC Hamiltonian, QED-FCI, and the effective mode approach for QED-CC. We notice that, as expected, the single-mode approximation underestimates the Rabi splitting by almost a factor of two. All the multimode methods therefore show a large improvement once the second mode has been added. Inclusion of additional modes still enlarges the splitting, although we note that the change is quite small when compared to the improvement observed adding the second plasmon in the picture. Despite using a single bosonic operator, the effective mode QED-CC allows us to almost exactly capture the multimode effect with a predicted Rabi splitting of 40.49 meV compared to 41.09 meV (QED-FCI value). We notice that the QED-FCI and JC results are not exactly equal and that the error increases when more modes are considered. This difference is due to the relaxation of the electronic ground and excited states induced by the presence of the nanoparticle. This effect is not captured unless an ab initio approach is used. If the electronic wave function is not optimized in the QED-FCI calculations, thus not accounting for the mutual polarization with the NP (the no corr. QED-FCI in Figure 3), the difference between QED-FCI and JC is dramatically reduced. Nonetheless, the differences between the ab initio method and the two-level approximation are small when compared to the improvement from 1 to 2 modes.
Figure 3.
Computed Rabi splitting for the setup shown in Figure 1 as a function of the number of plasmonic modes included in the Hamiltonian. The calculations have been perfomed with the following methods: multimode Jaynes–Cummings, QED-FCI, and QED-FCI without relaxation of the electronic wave function (no corr. QED-FCI). We highlight that the latter curve is basically overlapped with the blue one. The effective mode QED-CC (dashed red line) recovers most of the multiphoton contribution. We note that the effective mode optimization has been computed using the first 12 plasmon modes of the nanoparticle setup with nonzero coupling with the molecular transition, starting from the low-energy modes. In order to contribute significantly to the splitting, the modes need to both couple with the electronic transition and be close in energy to the molecular excitation. Only some of the relevant modes are bright (such as those shown in Figure 2a,b); that is, they have a nonzero transition dipole moment. Others are dark, even though their coupling with the molecule is sizable.
We also investigated other excited-state properties, like the molecular contribution to the transition dipole moment in the GS → LP/UP transition. As shown in Figure 4a,b, the ratio between the molecular y and z components (the H2 molecule lies in the yz plane) of the polaritonic transition dipole approaches the exact QED-FCI limit when the effective mode is used. On the other hand, the agreement is significantly worse using either mode 1 or mode 2 separately. This shows that the effective mode not only improves the Rabi splitting description compared to the single-mode approximation but also provides a better description of the most important excited state properties, e.g., transition dipoles/densities.
Figure 4.
Ratio of the y and z components of the LP (a)/UP (b) transition dipole for the setup of Figure 1 in 4 different cases: QED-CC using mode 1 (dashed green line) or mode 2 only (dashed red line), effective mode QED-CC (dashed blue line), and QED-FCI (solid black curve). The QED-FCI data are reported as a function of the number of plasmonic modes included in the Hamiltonian, up to 12, which corresponds to the maximum number of modes employed in the effective mode optimization.
The qualitative picture does not change if a more
complicated molecule
like paranitroaniline (PNA) is placed between the three nanoellipsoidal
structures (see Figure S6 of the SI). Comparing
the multimode JC results with the effective mode approach for PNA,
we notice that, similarly to the H2 case, the effective
mode QED-CC recovers most of the multimode contribution. Specifically,
the Rabi splitting predicted by QED-CC is almost the same as using
5 field modes in the JC approach (78.3 meV). In Figure 5, we compare the GS → LP transition
densities of PNA when either the effective mode or a single-mode approach
is used. Notably, an enhancement of the LP charge transfer character
can be observed moving from the single-mode QED-CC with the lowest
plasmon mode (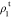 of Figure 2a) to the effective mode QED-CC,
of Figure 2a) to the effective mode QED-CC, 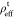 . The difference between the two transition
densities,
. The difference between the two transition
densities, 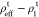 , indeed shows an increased negative density
contribution on the NO2 group (acceptor) and an increased
positive density contribution on the NH2 group (donor).
The opposite trend is observed in the case of mode 2 (Figure 2b), meaning that in the mode
2 case more charge is transferred compared to the effective mode case.
These findings can easily be rationalized using the theory described
above. Indeed, since mode 2 favors the charge separation more than
mode 1, the effective plasmon, that is, a linear combinations of mode
1 and mode 2, predicts an intermediate transfer between the two. Since
an increasing number of modes are coupled with the main molecular
transition, nanoplasmonic systems with multiple almost degenerate
excitations represent a promising option to increase the field effects
without reducing the field quantization volume.
, indeed shows an increased negative density
contribution on the NO2 group (acceptor) and an increased
positive density contribution on the NH2 group (donor).
The opposite trend is observed in the case of mode 2 (Figure 2b), meaning that in the mode
2 case more charge is transferred compared to the effective mode case.
These findings can easily be rationalized using the theory described
above. Indeed, since mode 2 favors the charge separation more than
mode 1, the effective plasmon, that is, a linear combinations of mode
1 and mode 2, predicts an intermediate transfer between the two. Since
an increasing number of modes are coupled with the main molecular
transition, nanoplasmonic systems with multiple almost degenerate
excitations represent a promising option to increase the field effects
without reducing the field quantization volume.
Figure 5.
PNA transition density plots for the GS → LP transition (see setup of Figure S6 in the SI), computed using QED-CC with modes 1 and 2 or the effective mode. Positive density contributions are reported in yellow, whereas negative ones are reported in green. The difference between the transition density obtained with the effective mode and either mode 1 or mode 2 is also shown, thus allowing an easier visualization of the major changes in the PNA transition density upon changing the plasmonic part of the QED-CC Hamiltonian.
To conclude, building on the previously developed Q-PCM-NP/QED-CC model,63 we propose here a framework to account for multimode environments using a single effective mode. Our approach captures the main features arising from the simultaneous coupling to multiple plasmons while retaining the same computational cost of single-mode methods.54,63 Physical quantities, such as Rabi splittings and transition dipoles, are correctly reproduced, as verified by benchmarking against exact multimode QED-FCI for the hydrogen molecule surrounded by 3 ellipsoidal nanoparticles. The same theoretical approach is applied to a larger organic molecule, para-nitroaniline (PNA), where QED-FCI or multimode calculations are out of reach. Our results demonstrate that the inclusion of multiple modes is critical to correctly evaluate the plasmon–matter interaction in the case of quasi-degenerate plasmonic modes. In these cases, indeed, the single-mode approximation naturally breaks down. We notice that the effective mode scheme can be applied to any kind of wave function approximation and is not specific for plasmonic systems. We also point out that the effective mode is optimized to correctly reproduce the upper and lower polaritons only. Therefore, no improvement in the description of the ground state should be expected with this methodology. A generalization of the method should, however, be able to model the effect of multiple plasmonic modes on the molecular ground state. This topic will be the subject of a future publication. As a number of ab initio QED methods have started to appear recently,3,52−57,59,72 the here-developed effective mode approach will be of great use in all those cases where multimode effects need to be taken into account, while retaining a computationally feasible methodology.44−48
Acknowledgments
R.R.R, T.S.H., and H.K. acknowledge funding from the Research Council of Norway through FRINATEK Project No. 275506. This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation Programme (grant agreement No.101020016). M.R. acknowledges MIUR “Dipartimenti di Eccellenza” under the project Nanochemistry for energy and Health (NExuS) for funding the Ph.D. grant.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.3c00735.
Author Contributions
¶ These authors equally contributed to the work.
The authors declare no competing financial interest.
Supplementary Material
References
- Fregoni J.; Garcia-Vidal F. J.; Feist J. Theoretical Challenges in Polaritonic Chemistry. ACS Photonics 2022, 9, 1096–1107. 10.1021/acsphotonics.1c01749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloch J.; Cavalleri A.; Galitski V.; Hafezi M.; Rubio A. Strongly correlated electron–photon systems. Nature 2022, 606, 41–48. 10.1038/s41586-022-04726-w. [DOI] [PubMed] [Google Scholar]
- Flick J.; Ruggenthaler M.; Appel H.; Rubio A. Atoms and molecules in cavities, from weak to strong coupling in quantum-electrodynamics (QED) chemistry. P. Natl. Acad. Sci. 2017, 114, 3026–3034. 10.1073/pnas.1615509114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galego J.; Garcia-Vidal F. J.; Feist J. Cavity-induced modifications of molecular structure in the strong-coupling regime. Phys. Rev. X 2015, 5, 041022. 10.1103/PhysRevX.5.041022. [DOI] [Google Scholar]
- Scholes G. D. Polaritons and excitons: Hamiltonian design for enhanced coherence. P. R. Soc. A 2020, 476, 20200278. 10.1098/rspa.2020.0278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramezani M.; Halpin A.; Fernandez-Dominguez A. I.; Feist J.; Rodriguez S. R.-K.; Garcia-Vidal F. J.; Gomez Rivas J. Plasmon-exciton-polariton lasing. Optica 2017, 4, 31–37. 10.1364/OPTICA.4.000031. [DOI] [Google Scholar]
- Sáez-Blázquez R.; Cuartero-González Á.; Feist J.; García-Vidal F. J.; Fernández-Domínguez A. I. Plexcitonic quantum light emission from nanoparticle-on-mirror cavities. Nano Lett. 2022, 22, 2365–2373. 10.1021/acs.nanolett.1c04872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sánchez-Barquilla M.; Fernández-Domínguez A. I.; Feist J.; García-Vidal F. J. A theoretical perspective on molecular polaritonics. ACS photonics 2022, 9, 1830–1841. 10.1021/acsphotonics.2c00048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feist J.; Galego J.; Garcia-Vidal F. J. Polaritonic Chemistry with Organic Molecules. ACS Photonics 2018, 5, 205–216. 10.1021/acsphotonics.7b00680. [DOI] [Google Scholar]
- Fregoni J.; Granucci G.; Coccia E.; Persico M.; Corni S. Manipulating azobenzene photoisomerization through strong light–molecule coupling. Nat. comm. 2018, 9, 1–9. 10.1038/s41467-018-06971-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison J. A.; Schwartz T.; Genet C.; Devaux E.; Ebbesen T. W. Modifying chemical landscapes by coupling to vacuum fields. Angew. Chem., Int. Ed. 2012, 51, 1592–1596. 10.1002/anie.201107033. [DOI] [PubMed] [Google Scholar]
- Lather J.; Bhatt P.; Thomas A.; Ebbesen T. W.; George J. Cavity catalysis by cooperative vibrational strong coupling of reactant and solvent molecules. Angew. Chem. 2019, 131, 10745–10748. 10.1002/ange.201905407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fregoni J.; Granucci G.; Persico M.; Corni S. Strong coupling with light enhances the photoisomerization quantum yield of azobenzene. Chem. 2020, 6, 250–265. 10.1016/j.chempr.2019.11.001. [DOI] [Google Scholar]
- Kowalewski M.; Bennett K.; Mukamel S. Cavity femtochemistry: Manipulating nonadiabatic dynamics at avoided crossings. J. Phys. Chem. Lett. 2016, 7, 2050–2054. 10.1021/acs.jpclett.6b00864. [DOI] [PubMed] [Google Scholar]
- Antoniou P.; Suchanek F.; Varner J. F.; Foley IV J. J. Role of cavity losses on nonadiabatic couplings and dynamics in polaritonic chemistry. J. Phys. Chem. Lett. 2020, 11, 9063–9069. 10.1021/acs.jpclett.0c02406. [DOI] [PubMed] [Google Scholar]
- Coles D. M.; Somaschi N.; Michetti P.; Clark C.; Lagoudakis P. G.; Savvidis P. G.; Lidzey D. G. Polariton-mediated energy transfer between organic dyes in a strongly coupled optical microcavity. Nat. Mater. 2014, 13, 712–719. 10.1038/nmat3950. [DOI] [PubMed] [Google Scholar]
- Du M.; Martínez-Martínez L. A.; Ribeiro R. F.; Hu Z.; Menon V. M.; Yuen-Zhou J. Theory for polariton-assisted remote energy transfer. Chem. Sci. 2018, 9, 6659–6669. 10.1039/C8SC00171E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgiou K.; Michetti P.; Gai L.; Cavazzini M.; Shen Z.; Lidzey D. G. Control over energy transfer between fluorescent BODIPY dyes in a strongly coupled microcavity. ACS Photonics 2018, 5, 258–266. 10.1021/acsphotonics.7b01002. [DOI] [Google Scholar]
- Zhong X.; Chervy T.; Zhang L.; Thomas A.; George J.; Genet C.; Hutchison J. A.; Ebbesen T. W. Energy transfer between spatially separated entangled molecules. Angew. Chem., Int. Ed. 2017, 56, 9034–9038. 10.1002/anie.201703539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sáez-Blázquez R.; Feist J.; Fernández-Domínguez A.; García-Vidal F. Organic polaritons enable local vibrations to drive long-range energy transfer. Phys. Rev. B 2018, 97, 241407. 10.1103/PhysRevB.97.241407. [DOI] [Google Scholar]
- Sáez-Blázquez R.; Feist J.; Romero E.; Fernández-Domínguez A. I.; García-Vidal F. J. Cavity-modified exciton dynamics in photosynthetic units. J. Phys. Chem. Lett. 2019, 10, 4252–4258. 10.1021/acs.jpclett.9b01495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Munkhbat B.; Wersäll M.; Baranov D. G.; Antosiewicz T. J.; Shegai T. Suppression of photo-oxidation of organic chromophores by strong coupling to plasmonic nanoantennas. Science adv 2018, 4, eaas9552 10.1126/sciadv.aas9552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felicetti S.; Fregoni J.; Schnappinger T.; Reiter S.; de Vivie-Riedle R.; Feist J. Photoprotecting uracil by coupling with lossy nanocavities. J. Phys. Chem. Lett. 2020, 11, 8810–8818. 10.1021/acs.jpclett.0c02236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu B.; Mukamel S. Manipulating nonadiabatic conical intersection dynamics by optical cavities. Chem. Sci. 2020, 11, 1290–1298. 10.1039/C9SC04992D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chikkaraddy R.; De Nijs B.; Benz F.; Barrow S. J.; Scherman O. A.; Rosta E.; Demetriadou A.; Fox P.; Hess O.; Baumberg J. J. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 2016, 535, 127–130. 10.1038/nature17974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petryayeva E.; Krull U. J. Localized surface plasmon resonance: Nanostructures, bioassays and biosensing—A review. Anal. Chim. Acta 2011, 706, 8–24. 10.1016/j.aca.2011.08.020. [DOI] [PubMed] [Google Scholar]
- Cathcart N.; Chen J. I. L. Sensing Biomarkers with Plasmonics. Anal. Chem. 2020, 92, 7373–7381. 10.1021/acs.analchem.0c00711. [DOI] [PubMed] [Google Scholar]
- Etchegoin P. G.; Le Ru E. C. A perspective on single molecule SERS: current status and future challenges. Phys. Chem. Chem. Phys. 2008, 10, 6079–6089. 10.1039/b809196j. [DOI] [PubMed] [Google Scholar]
- Vo-Dinh T. SERS chemical sensors and biosensors: new tools for environmental and biological analysis. Sensor Actuat B-Chem. 1995, 29, 183–189. 10.1016/0925-4005(95)01681-3. [DOI] [Google Scholar]
- Maccaferri N.; Barbillon G.; Koya A. N.; Lu G.; Acuna G. P.; Garoli D. Recent advances in plasmonic nanocavities for single-molecule spectroscopy. Nanoscale Adv. 2021, 3, 633–642. 10.1039/D0NA00715C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haran G. Single-molecule Raman spectroscopy: a probe of surface dynamics and plasmonic fields. Acc. Chem. Res. 2010, 43, 1135–1143. 10.1021/ar100031v. [DOI] [PubMed] [Google Scholar]
- Zhang R.; Zhang Y.; Dong Z.; Jiang S.; Zhang C.; Chen L.; Zhang L.; Liao Y.; Aizpurua J.; Luo Y. E.; et al. Chemical mapping of a single molecule by plasmon-enhanced Raman scattering. Nature 2013, 498, 82–86. 10.1038/nature12151. [DOI] [PubMed] [Google Scholar]
- Yang B.; Chen G.; Ghafoor A.; Zhang Y.; Zhang Y.; Zhang Y.; Luo Y.; Yang J.; Sandoghdar V.; Aizpurua J.; et al. Sub-nanometre resolution in single-molecule photoluminescence imaging. Nat. Photonics 2020, 14, 693–699. 10.1038/s41566-020-0677-y. [DOI] [Google Scholar]
- Romanelli M.; Dall’Osto G.; Corni S. Role of metal-nanostructure features on tip-enhanced photoluminescence of single molecules. J. Chem. Phys. 2021, 155, 214304. 10.1063/5.0066758. [DOI] [PubMed] [Google Scholar]
- Cortés E.; Besteiro L. V.; Alabastri A.; Baldi A.; Tagliabue G.; Demetriadou A.; Narang P. Challenges in plasmonic catalysis. ACS Nano 2020, 14, 16202–16219. 10.1021/acsnano.0c08773. [DOI] [PubMed] [Google Scholar]
- Zhang X.; Chen Y. L.; Liu R.-S.; Tsai D. P. Plasmonic photocatalysis. Rep. Prog. Phys. 2013, 76, 046401. 10.1088/0034-4885/76/4/046401. [DOI] [PubMed] [Google Scholar]
- Kale M. J.; Avanesian T.; Christopher P. Direct photocatalysis by plasmonic nanostructures. ACS Catal. 2014, 4, 116–128. 10.1021/cs400993w. [DOI] [Google Scholar]
- Zhou L.; Swearer D. F.; Zhang C.; Robatjazi H.; Zhao H.; Henderson L.; Dong L.; Christopher P.; Carter E. A.; Nordlander P.; et al. Quantifying hot carrier and thermal contributions in plasmonic photocatalysis. Science 2018, 362, 69–72. 10.1126/science.aat6967. [DOI] [PubMed] [Google Scholar]
- Lou Z.; Wang Z.; Huang B.; Dai Y. Synthesis and activity of plasmonic photocatalysts. ChemCatChem. 2014, 6, 2456–2476. 10.1002/cctc.201402261. [DOI] [Google Scholar]
- Delga A.; Feist J.; Bravo-Abad J.; Garcia-Vidal F. Theory of strong coupling between quantum emitters and localized surface plasmons. J. Opt. 2014, 16, 114018. 10.1088/2040-8978/16/11/114018. [DOI] [Google Scholar]
- Feist J.; Fernández-Domínguez A. I.; García-Vidal F. J. Macroscopic QED for quantum nanophotonics: emitter-centered modes as a minimal basis for multiemitter problems. Nanophotonics 2020, 10, 477–489. 10.1515/nanoph-2020-0451. [DOI] [Google Scholar]
- Medina I.; García-Vidal F. J.; Fernández-Domínguez A. I.; Feist J. Few-mode field quantization of arbitrary electromagnetic spectral densities. Phys. Rev. Lett. 2021, 126, 093601. 10.1103/PhysRevLett.126.093601. [DOI] [PubMed] [Google Scholar]
- Sánchez-Barquilla M.; García-Vidal F. J.; Fernández-Domínguez A. I.; Feist J. Few-mode field quantization for multiple emitters. Nanophotonics 2022, 11, 4363–4374. 10.1515/nanoph-2021-0795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carone A.; Mariani P.; Désert A.; Romanelli M.; Marcheselli J.; Garavelli M.; Corni S.; Rivalta I.; Parola S. Insight on Chirality Encoding from Small Thiolated Molecule to Plasmonic Au@Ag and Au@Au Nanoparticles. ACS Nano 2022, 16, 1089–1101. 10.1021/acsnano.1c08824. [DOI] [PubMed] [Google Scholar]
- Mun J.; Rho J. Importance of higher-order multipole transitions on chiral nearfield interactions. Nanophotonics 2019, 8, 941–948. 10.1515/nanoph-2019-0046. [DOI] [Google Scholar]
- Mun J.; Rho J. Surface-enhanced circular dichroism by multipolar radiative coupling. Opt. Lett. 2018, 43, 2856–2859. 10.1364/OL.43.002856. [DOI] [PubMed] [Google Scholar]
- Wu T.; Zhang W.; Wang R.; Zhang X. A giant chiroptical effect caused by the electric quadrupole. Nanoscale 2017, 9, 5110–5118. 10.1039/C6NR09419H. [DOI] [PubMed] [Google Scholar]
- Govorov A. O.; Fan Z. Theory of Chiral Plasmonic Nanostructures Comprising Metal Nanocrystals and Chiral Molecular Media. ChemPhysChem 2012, 13, 2551–2560. 10.1002/cphc.201100958. [DOI] [PubMed] [Google Scholar]
- Stevenson P. R.; Du M.; Cherqui C.; Bourgeois M. R.; Rodriguez K.; Neff J. R.; Abreu E.; Meiler I. M.; Tamma V. A.; Apkarian V. A.; et al. Active Plasmonics and Active Chiral Plasmonics through Orientation-Dependent Multipolar Interactions. ACS Nano 2020, 14, 11518–11532. 10.1021/acsnano.0c03971. [DOI] [PubMed] [Google Scholar]
- Lininger A.; Palermo G.; Guglielmelli A.; Nicoletta G.; Goel M.; Hinczewski M.; Strangi G.; et al. Chirality in light–matter interaction. Adv. Mater. 2022, 2107325. 10.1002/adma.202107325. [DOI] [PubMed] [Google Scholar]
- Khaliq H. S.; Kim I.; Zahid A.; Kim J.; Lee T.; Badloe T.; Kim Y.; Zubair M.; Riaz K.; Mehmood M. Q.; et al. Giant chiro-optical responses in multipolar-resonances-based single-layer dielectric metasurfaces. Photonics Res. 2021, 9, 1667–1674. 10.1364/PRJ.424477. [DOI] [Google Scholar]
- Ruggenthaler M.; Flick J.; Pellegrini C.; Appel H.; Tokatly I. V.; Rubio A. Quantum-electrodynamical density-functional theory: Bridging quantum optics and electronic-structure theory. Phys. Rev. A 2014, 90, 012508. 10.1103/PhysRevA.90.012508. [DOI] [Google Scholar]
- Tokatly I. V. Time-Dependent Density Functional Theory for Many-Electron Systems Interacting with Cavity Photons. Phys. Rev. Lett. 2013, 110, 233001. 10.1103/PhysRevLett.110.233001. [DOI] [PubMed] [Google Scholar]
- Haugland T. S.; Ronca E.; Kjønstad E. F.; Rubio A.; Koch H. Coupled Cluster Theory for Molecular Polaritons: Changing Ground and Excited States. Phys. Rev. X 2020, 10, 041043. 10.1103/PhysRevX.10.041043. [DOI] [Google Scholar]
- Haugland T. S.; Schäfer C.; Ronca E.; Rubio A.; Koch H. Intermolecular interactions in optical cavities: An ab initio QED study. J. Chem. Phys. 2021, 154, 094113. 10.1063/5.0039256. [DOI] [PubMed] [Google Scholar]
- DePrince A. E. III Cavity-modulated ionization potentials and electron affinities from quantum electrodynamics coupled-cluster theory. J. Chem. Phys. 2021, 154, 094112. 10.1063/5.0038748. [DOI] [PubMed] [Google Scholar]
- Pavosevic F.; Flick J. Polaritonic unitary coupled cluster for quantum computations. J. Phys. Chem. Lett. 2021, 12, 9100–9107. 10.1021/acs.jpclett.1c02659. [DOI] [PubMed] [Google Scholar]
- Riso R. R.; Haugland T. S.; Ronca E.; Koch H. On the characteristic features of ionization in QED environments. J. Chem. Phys. 2022, 156, 234103. 10.1063/5.0091119. [DOI] [PubMed] [Google Scholar]
- Riso R. R.; Haugland T. S.; Ronca E.; Koch H. Molecular orbital theory in cavity QED environments. Nat. comm. 2022, 13, 1–8. 10.1038/s41467-022-29003-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flick J.; Schäfer C.; Ruggenthaler M.; Appel H.; Rubio A. Ab Initio Optimized Effective Potentials for Real Molecules in Optical Cavities: Photon Contributions to the Molecular Ground State. ACS Photonics 2018, 5, 992–1005. 10.1021/acsphotonics.7b01279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pellegrini C.; Flick J.; Tokatly I. V.; Appel H.; Rubio A. Optimized Effective Potential for Quantum Electrodynamical Time-Dependent Density Functional Theory. Phys. Rev. Lett. 2015, 115, 093001. 10.1103/PhysRevLett.115.093001. [DOI] [PubMed] [Google Scholar]
- Mennucci B. Polarizable continuum model. Wires. Comput. Mol. Sci. 2012, 2, 386–404. 10.1002/wcms.1086. [DOI] [Google Scholar]
- Fregoni J.; Haugland T. S.; Pipolo S.; Giovannini T.; Koch H.; Corni S. Strong Coupling between Localized Surface Plasmons and Molecules by Coupled Cluster Theory. Nano Lett. 2021, 21, 6664–6670. 10.1021/acs.nanolett.1c02162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson J. D.Classical electrodynamics; John Wiley & Sons: New York, 1999. [Google Scholar]
- Cances E.; Mennucci B.; Tomasi J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. 10.1063/1.474659. [DOI] [Google Scholar]
- Corni S.; Pipolo S.; Cammi R. Equation of Motion for the Solvent Polarization Apparent Charges in the Polarizable Continuum Model: Application to Real-Time TDDFT. J. Phys. Chem. A 2015, 119, 5405–5416. 10.1021/jp5106828. [DOI] [PubMed] [Google Scholar]
- Mennucci B.; Corni S. Multiscale modelling of photoinduced processes in composite systems. Nat. Rev. Chem. 2019, 3, 315–330. 10.1038/s41570-019-0092-4. [DOI] [Google Scholar]
- Helgaker T.; Jorgensen P.; Olsen J.. Molecular electronic-structure theory; John Wiley & Sons, 2014. [Google Scholar]
- Jaynes E.; Cummings F. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. 10.1109/PROC.1963.1664. [DOI] [Google Scholar]
- Folkestad S. D.; Kjønstad E. F.; Myhre R. H.; Andersen J. H.; Balbi A.; Coriani S.; Giovannini T.; Goletto L.; Haugland T. S.; Hutcheson A.; et al. e T 1.0: An open source electronic structure program with emphasis on coupled cluster and multilevel methods. J. Chem. Phys. 2020, 152, 184103. 10.1063/5.0004713. [DOI] [PubMed] [Google Scholar]
- Geuzaine C.; Remacle J.-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Meth. Eng. 2009, 79, 1309–1331. 10.1002/nme.2579. [DOI] [Google Scholar]
- Mandal A.; Montillo Vega S.; Huo P. Polarized Fock states and the dynamical Casimir effect in molecular cavity quantum electrodynamics. J. Phys. Chem. Lett. 2020, 11, 9215–9223. 10.1021/acs.jpclett.0c02399. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.







