RETROFIT: Reference-free deconvolution of cell-type mixtures in spatial transcriptomics

Abstract

Spatial transcriptomics (ST) profiles gene expression in intact tissues. However, ST data measured at each spatial location may represent gene expression of multiple cell types, making it difficult to identify cell-type-specific transcriptional variation across spatial contexts. Existing cell-type deconvolutions of ST data often require single-cell transcriptomic references, which can be limited by availability, completeness and platform effect of such references. We present RETROFIT, a reference-free Bayesian method that produces sparse and interpretable solutions to deconvolve cell types underlying each location independent of single-cell transcriptomic references. Results from synthetic and real ST datasets acquired by Slide-seq and Visium platforms demonstrate that RETROFIT outperforms existing reference-based and reference-free methods in estimating cell-type composition and reconstructing gene expression. Applying RETROFIT to human intestinal development ST data reveals spatiotemporal patterns of cellular composition and transcriptional specificity. RETROFIT is available at https://bioconductor.org/packages/release/bioc/html/retrofit.html.

Introduction

Tissue formation and function rely on the spatial organization of diverse cell types and states, along with coordinated activities of numerous genes pertinent to each cellular context. Recent advances in ST have enabled genome-wide measurements of gene expression throughout intact tissue sections ¹, offering a powerful approach to elucidating tissue architecture ². The widespread adoption of ST technologies has provided new insights into spatial biology of many complex mammalian tissues, such as brains ³ and intestines ⁴.

ST measures gene expression at each spatial location, henceforth referred to as a “spot”, on a two-dimensional slide of tissue sample. In some ST platforms, spots can cover an area equivalent to multiple mammalian cells. For example, the Visium platform generates ST slides with spots covering an area of 55μm diameter and encompassing 6–10 cells when applied to human intestinal samples ⁵. Even for ST technologies at resolutions comparable to the sizes of individual cells, such as Slide-seq ⁶ (10μm diameter), predetermined locations of high-resolution spots in a slide may overlap with multiple cells of different types. Therefore, it is likely that gene expression in multiple cell types frequently contributes to the ST measurement at a single spot. However, cell-type-specific transcriptional profiles and their contributions to the ST measurement at each spot are not observed as part of the existing ST readout. To improve our understanding of cell-type-specific spatial localization and transcriptional signature underlying tissue organization and function, it is crucial to decompose the cell-type mixture at each spot into individual cell types.

Various cell-type deconvolution methods have recently been developed to infer cell-type composition for ST data ^7,8. However, the majority of these methods require a reference of cell-type-annotated gene expression, often acquired by single-cell technologies such as single-cell RNA-sequencing (scRNA-seq). Typically, these methods place cell-type deconvolution in a supervised learning framework, where each ST spot is represented as an unknown combination of individual cell types present in the ST sample, and the proportion of each cell type for each spot is estimated by approximating the observed ST data based on the external transcriptional profiles of these cell types from a single-cell reference.

Because of their supervised nature, reference-based deconvolution methods rely heavily on the availability of single-cell transcriptomic data and the quality of cell-type-annotated gene expression references. While ongoing efforts to profile single-cell transcriptomes in diverse mammalian tissues ^9,10 may help alleviate such limitations, compiling a high-quality reference of cell-type-annotated gene expression for certain ST studies remains difficult due to sample limitations and experimental challenges to capture all the relevant cell types through single-cell transcriptomics ^11,12. Even with a high-quality transcriptomic reference in place, supervised deconvolutions are further complicated by platform effect ¹³— a phenomenon that systematic technical variation across single-cell and ST technologies can overshadow relevant biological signals ¹⁴. Hence, a reference-free, unsupervised deconvolution approach that does not require the input of single-cell gene expression provides a valuable alternative when a suitable reference is unavailable. However, reference-free methods are currently under-developed, with only one approach, STdeconvolve ¹⁵, published at the time of our investigation.

Here, we introduce reference-free spatial transcriptomic factorization (RETROFIT), an unsupervised method to decompose cell-type mixtures in ST data without using single-cell gene expression. Built on a Bayesian hierarchical model, RETROFIT decomposes the ST data matrix into two matrices, one reflecting gene expression of cellular components and the other capturing proportions of these components present in each spot. RETROFIT is designed to produce a sparse and intepretable solution, aiding identification of the most relevant cellular components present in the ST sample. Our results demonstrate that RETROFIT outperforms existing reference-based methods in estimating cell-type composition and reconstructing gene expression in synthetic ST data with varying spot size and sample heterogeneity, irrespective of the quality of single-cell transcriptomic references. When applied to a mouse cerebellum Slide-seq dataset ⁶, RETROFIT localizes known cell types in the mouse brain without using any single-cell information. When applied to a Visium dataset from a human intestinal development study ⁵, RETROFIT reveals spatiotemporal patterns of cellular composition and transcriptional specificity in adult and fetal intestinal samples, yielding insights into human intestinal development and function. Across all the synthetic and real-world ST datasets examined in this study, RETROFIT consistently outperforms STdeconvolve, the only reference-free approach published at the time of our analysis.

Results

RETROFIT deconvolves ST data independent of single-cell gene expression references

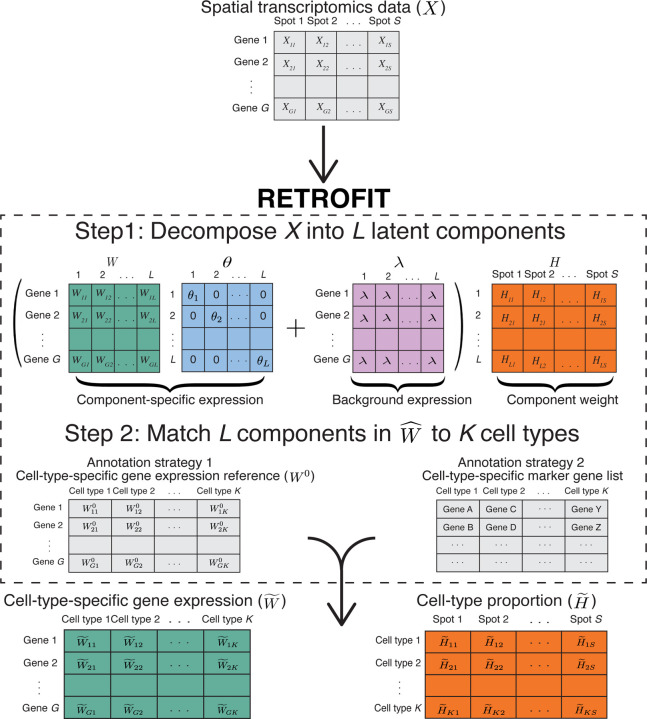
RETROFIT is a reference-free approach for cell-type deconvolution of ST data (Fig. 1). In brief, RETROFIT takes a ST count matrix $\mathbf{X}$, which consists of $G$ genes at $S$ spots, as its sole input, and then conducts an unsupervised projection of $\mathbf{X}$ onto a low-dimensional space spanned by $L$ non-negative latent components, independent of any external reference. Typically, the value of $L$ is set larger than the actual number of cell types $\left(K\right)$ present in the ST sample. This allows RETROFIT to produce a sparse solution ¹⁶ that capture all the relevant cellular components present in each spot. The expression of each gene at each spot for each component is further decomposed into the expression specific to the gene and the background expression shared by all genes. The $L$ latent components, which are mined from ST data alone, often contain information that distinguishes cell types of distinct transcriptomic profiles, forming the basis for cell-type deconvolution.

Figure 1:

Overview of RETROFIT. Step 1: RETROFIT takes a ST data matrix as the only input and decomposes this matrix into latent components in an unsupervised manner (Algorithm 1). Step 2: RETROFIT matches these latent components to known cell types using either a cell-type-specific gene expression reference (Algorithm 2) or a list of cell-type-specific marker genes (Algorithm 3) for the cell types present in the ST sample, and outputs a cell-type-specific gene expression matrix and a cell-type proportion matrix.

RETROFIT is formulated as a Bayesian hierarchical model with a Poisson likelihood for the observed ST data and Gamma priors for the unknown parameters (Methods). RETROFIT deconvolves the ST data matrix into two matrices: one reflecting component-specific gene expression and the other reflecting the proportion of each component. To facilitate the analysis of large-scale ST data, RETROFIT is implemented with a structured stochastic variational inference (SSVI) algorithm ¹⁷ that scales well with thousands of genes and spots (Algorithm 1; Supplementary Table 1). The software is available as a Bioconductor R package at https://bioconductor.org/packages/release/bioc/html/retrofit.html.

Like any unsupervised learning, RETROFIT produces unlabeled results. To assign known cell types to the latent components inferred by RETROFIT, we develop two simple post hoc cell-type annotation strategies. The first strategy requires a cell-type-annotated gene expression reference $\left({\mathbf{W}}^0\right)$ for all $K$ cell types present in the ST data, which is a standard assumption made by most ST deconvolution methods to date ^7,8. The cell-type-annotated expression reference can be derived from external single-cell transcriptomics data that match the tissue type of ST data. With this reference, we can calculate correlations between the component-specific expression profiles estimated by RETROFIT and the observed cell-type-specific expression profiles in the reference. We then treat the cell type with the largest correlation for a component as the most probable annotation (Algorithm 2). The second strategy does not require any gene expression references, but requires a curated list of cell-type-specific marker genes for all $K$ cell types present in the ST data. This approach complements the first strategy when a proper cell-type-specific expression reference is unavailable. With the marker gene list in place, we calculate a marker expression score for each component in each cell type. This score is defined as the sum of normalized component-specific expression levels of marker genes in this cell type. We then annotate each component by the cell type with the largest marker expression score (Algorithm 3). Once the latent components are matched to cell types by either strategy, RETROFIT outputs a cell-type-specific expression matrix for all genes $\left(\tilde{\mathbf{W}}\right)$ and a cell-type proportion matrix for all spots $\left(\tilde{\mathbf{H}}\right)$ as the final results.

RETROFIT adapts better to spot size and cell-type heterogeneity than existing methods

We compared RETROFIT with existing methods on simulated data (Fig. 2). To imitate ST data from different platforms and samples, we used a real-world scRNA-seq dataset ⁶ to simulate ST data with different levels of sequencing depth, spot size and cell-type heterogeneity (Algorithm 4). We varied the levels of spot size and cell-type heterogeneity by changing the number of cells per spot $\left(N\right)$ and the maximum number of cell types per spot $\left(M\right)$ respectively. We also assessed how the quality of single-cell transcriptomic reference affected reference-based methods by altering the levels of cell-type match between ST data and single-cell references.

Figure 2:

Evaluating RETROFIT on synthetic ST data with different spot size, cell-type complexity and reference quality. Column 1: small spots ($N=10$ cells per spot) with low cell-type complexity (up to $M=3$ cell types per spot from $K=10$ cell types in the slide). Column 2: large spots $\left(N=20\right)$ with high cell-type complexity ($M=5$ and $K=10$). Columns 3–4: $N=10$,$M=3$ and $K=5$. Reference-based methods were provided with the following single-cell transcriptomic references. Columns 1–2: exact reference of all 10 ground truth cell types. Column 3: all 5 ground truth plus 5 irrelevant cell types. Column 4: only 3 out of 5 ground truth plus 5 irrelevant cell types. a Distribution of RMSE and b ranked correlation between true $\left(\mathbf{H}\right)$ and estimated cell-type proportions $\left(\tilde{\mathbf{H}}\right)$ across all cell types at each spot. c Distribution of NRMSE and d ranked correlation between observed $\left(\mathbf{X}\right)$ and reconstructed expression $\left(\widetilde{\mathbf{\text{X}}}\right)$ across all genes at each spot. The one-sided KS P-values are shown in a and c (black: P < 0.05; yellow: P > 0.05). A small P-value indicates that RETROFIT estimates have stochastically lower RMSEs compared to another method. The AUC of ranked correlations is shown for each method with matching color in b and d. e Ranked correlation between the single-cell observation $\left({\mathbf{W}}^0\right)$ and RETROFIT estimation $\left({\mathbf{W}}^0\right)$ of cell-type-specific expression across all genes for each cell type.

On each simulated ST dataset, we compared RETROFIT with 4 reference-based methods: NMFreg ⁶, Stereoscope ¹⁸, SPOTlight ¹⁹ and RCTD ¹³, and a reference-free method: STdeconvolve ¹⁵. We evaluated each method in two aspects: (1) explanatory power measured by the root-mean-square error (RMSE; Fig. 2a) and correlation (Fig. 2b) between the true and estimated cell-type proportions at each spot; (2) predictive power measured by the normalized RMSE (NRMSE; Fig. 2c) and correlation (Fig. 2d) between the observed and reconstructed gene expression profiles at each spot, where the reconstructed expression profiles were sums of the single-cell expression profiles in individual cell types weighted by the estimated cell-type proportions. Details of simulation and evaluation are provided in Methods.

We started with an ideal use case for reference-based methods, where reference-based methods were provided with an exact reference of the same single-cell expression profiles for all 10 cell types that were used to simulate ST data. In contrast, reference-free methods would benefit little from the availability of such an exact reference, because they decompose the ST data free of any external references. The first two columns of Fig. 2 show the simulation results for this case in two scenarios: (1) one with smaller spot size and lower cell-type heterogeneity: $N=10$ cells and up to $M=3$ cell types per spot; (2) the other with larger spot size and higher cell-type heterogeneity: $N=20$ cells and up to $M=5$ cell types per spot. In both scenarios, we simulated ST data for $G=500$ genes and $S=1000$ spots with $K=10$ cell types.

Although the simulations were designed to favor reference-based methods, RETROFIT performed competitively compared to reference-base methods and significantly outperformed the only other reference-free method (STdeconvolve) in the scenario with smaller spot size and lower cell-type heterogeneity ($N=10$ and $M=3$). Specifically, RETROFIT achieved similar accuracy in estimating cell-type proportions as the best reference-based method (Stereoscope, KS test $P=0.31$) and outperformed remaining methods by producing significantly smaller RMSEs (Fig. 2a; KS test P ≤ 7.1 × 10⁻⁷). RETROFIT also consistently showed higher concordance between the estimate and ground truth than existing methods (Fig. 2b; AUC = 0.964 versus 0.764 – 0.958). Furthermore, RETROFIT achieved similar reconstruction accuracy as several reference-based methods (Fig. 2c) and showed consistently higher concordance between the reconstructed and observed expression than existing methods (Fig. 2d; AUC = 0.962 versus 0.802 – 0.946). In contrast, STdeconvolve performed worse than most of the reference-based methods in both cell-type proportion estimation (Fig.s 2a–b) and gene expression reconstruction (Fig.s 2c–d), and it was outperformed by RETROFIT in all measures.

With increased spot size and cell-type heterogeneity ($N=20$ and $M=5$), the accuracy and concordance of existing methods decreased in cell-type proportion estimation (Fig.s 2a–b), and there was a similar trend in the concordance of gene expression reconstruction for multiple existing methods (Fig. 2d). For example, while RCTD, especially its ‘doublet’ mode (RCTD-D) that assumes up to two cell types per spot, performed reasonably well in the previous scenario ($N=10$ and $M=3$), its performance deteriorated with increased spot size and cell-type heterogeneity ($N=20$ and $M=5$). In contrast, RETROFIT was robust to these changes and significantly outperformed all methods in both accuracy (KS test P ≤ 8.4 × 10⁻¹⁹; Fig. 2a) and concordance (AUC = 0.970 versus 0.628 – 0.939; Fig. 2b) for cell-type proportion estimation. When reconstructing gene expression, RETROFIT also generated significantly smaller NRMSEs than existing methods (KS test P ≤ 8.2 × 10⁻⁵; Fig. 2c) except for Stereoscope (KS test P = 0.03), and consistently showed higher concordance with the observed expression than all methods (AUC = 0.979 versus 0.741 – 0.973; Fig. 2d).

Altogether, even without exploiting the exact single-cell expression reference, RETROFIT performs competitively with the best-performing reference-based deconvolution, and it adapts better to spot size and cell-type heterogeneity than existing methods.

RETROFIT surpasses reference-based deconvolutions when key cell types are missing

We next considered a more realistic use case with imperfect single-cell transcriptomic references that included irrelevant or excluded relevant cell types, and we evaluated the impact of such imperfection on reference-based and reference-free deconvolutions of ST data. Here we simulated ST data of $G=500$ genes for $S=1000$ spots with $N=10$ cells from up to $M=3$ out of $K=5$ cell types per spot, using the same data and scheme as before (Methods). We then created two imperfect single-cell expression references: (1) 5 extra cell types and the complete set of 5 ground truth cell types used to generate ST data; (2) 5 extra cell types and only 3 out of 5 ground truth cell types. We evaluated all methods on the same ST data using the 5 ground truth cell types.

For all reference-based methods, we observed a heavy reliance on the completeness of relevant cell types in the single-cell reference. While reference-based methods showed robustness to irrelevant cell types when the reference contained 5 cell types in addition to the 5 ground truth cell types (Fig. 2, column 3), their performance significantly decreased when 2 out of 5 ground truth cell types were missing in the reference (Fig. 2, column 4), highlighting the negative impact of incomplete single-cell references on reference-based deconvolutions.

In contrast, RETROFIT consistently demonstrated optimal performance regardless of reference quality. When the single-cell reference consisted of all 5 ground truth and 5 extra cell types, RETROFIT significantly outperformed Stereoscope, the best performing reference-based method in this scenario, in both cell-type proportion estimation (KS test P = 2.3 × 10⁻¹⁰; AUC = 0.985 versus 0.967; Fig.s 2a–b) and gene expression reconstruction (KS test P = 4.9 × 10⁻²; AUC = 0.990 versus 0.983; Fig.s 2c–d). When 2 out of 5 ground truth cell types were missing in the single-cell reference, RETROFIT showed substantial gains in accuracy over all reference-based methods for both cell-type proportion estimation (KS test P ≤ 3.7 × 10⁻¹³⁰; Fig. 2a) and gene expression reconstruction (KS test P ≤ 1.4 × 10⁻⁵³; Fig. 2c). In nearly all spots (≥ 97.4%), the estimated cell-type proportions (AUC= 0.985) and reconstructed gene expression profiles (AUC=0.990) from RETROFIT were strongly correlated with the ground truth (Pearson R ≥ 0.9), whereas only less than 45.3% and 40.2% of spots achieved the same level of concordance for estimated proportions (AUC = 0.316 – 0.571; Fig. 2b) and reconstructed expression profiles (AUC = 0.421 – 0.546; Fig. 2d) from reference-based methods, respectively.

Like RETROFIT, STdeconvolve also showed robustness against cell-type incompleteness of single-cell reference (Fig. 2, column 4), as both methods deconvolve ST data independent of single-cell transcriptomic references. However, compared with RETROFIT, STdeconvolve underperformed in cell-type proportion estimation, as reflected in the significantly larger RMSE (KS test P = 4.8 × 10⁻¹⁰²; Fig. 2a) and smaller AUC (0.985 versus 0.693; Fig. 2b). STdeconvolve also underperformed in gene expression reconstruction, as reflected in the significantly larger NRMSE (KS test P = 4.9 × 10⁻³⁹; Fig. 2c) and smaller AUC (0.990 versus 0.722; Fig. 2d).

Lastly, we evaluated the concordance between cell-type-specific gene expression profiles estimated by RETROFIT and observed single-cell expression profiles for each cell type (Fig. 2e). Across all simulations, RETROFIT estimates were highly correlated with the single-cell data for all cell types (Pearson R > 0.75 when N = 10, M = 3 and K = 10; R > 0.84 when N = 20, M = 5 and K = 10; R > 0.89 when N = 10, M = 3 and K = 5), confirming that the reference-free estimation in RETROFIT effectively captures cell-type-specific transcriptional characteristics.

Altogether, these simulations demonstrate the major limitation of reference-based deconvolutions, as well as the evident advantage of RETROFIT over reference-based methods, especially when key cell types relevant to the ST data are absent in the single-cell transcriptomic reference.

RETROFIT outperforms existing methods to deconvolve mouse cerebellum Slide-seq data

We evaluated RETROFIT on a mouse cerebellum Slide-seq dataset ⁶ of 17919 genes at 27261 spots, which has been widely used to benchmark ST deconvolution methods. We compared RETROFIT with Stereoscope and RCTD, two top-performing reference-based methods in our simulations (Fig. 2), as well as the reference-free method STdeconvolve. RCTD and Stereoscope were further provided with a scRNA-seq reference for 10 cell types from the same study ⁶. RETROFIT and STdeconvolve did not use this single-cell reference to deconvolve the ST data into latent components; they only used this scRNA-seq dataset to match latent components to known cell types post hoc. Details of applying each method to the Slide-seq study are available in Methods.

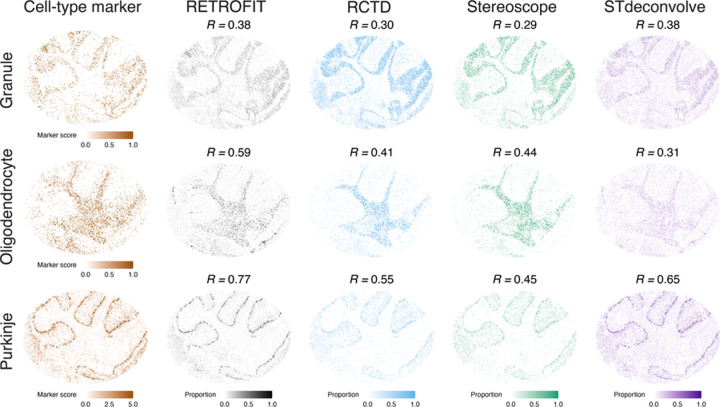
To benchmark the deconvolution methods on the Slide-seq dataset, we focused on 3 cell types in the mouse cerebellum for which known cell-type marker genes were available: granule, oligodendrocyte and Purkinje (Methods; Supplementary Table 2). We found that the estimated cell-type proportions from each method (Fig. 3, columns 2–5; Supplementary Tables 3–5) agreed with the spatial expression patterns of known marker genes in each cell type (Fig. 3, column 1), showing qualitatively similar results across methods.

Figure 3:

Benchmarking RETROFIT on mouse cerebellum Slide-seq data. Column 1 (leftmost) shows spatial patterns of ST expression scores (Methods) for curated cell-type marker genes in granule cells, oligodendrocytes and Purkinje cells. Columns 2–5 show cell-type proportions at each spot estimated by each of the 4 ST deconvolution methods. Pearson correlations (R) between cell-type marker ST expression scores and estimated cell-type proportions are shown for all methods and cell types.

To further quantify the performance difference among methods, we calculated the correlation between estimated cell-type proportions and cell-type marker ST expression scores across all spots for each cell type (Methods). A higher correlation indicates better performance, as spots with a large proportion of a cell type are expected to have high expression levels of marker genes specific to that cell type. Based on this evaluation metric, RETROFIT was the best-performing method across all 3 cell types (Fig. 3). For granule cells, RETROFIT and STdeconvolve (both R = 0.38) showed marginally better performance than RCTD (R = 0.30) and Stereoscope (R = 0.29). For Purkinje cells, RETROFIT (R = 0.77) and STdeconvolve (R = 0.65) showed more obvious gains over RCTD (R = 0.55) and Stereoscope (R = 0.45). For oligodendrocytes, STdeconvolve (R = 0.31) performed worse than Stereoscope (R = 0.44) and RCTD (R = 0.41), whereas RETROFIT remained the best method by a wide margin (R = 0.59). Together these results demonstrate that RETROFIT outperforms existing deconvolution methods on the mouse cerebellum Slide-seq dataset, consistent with our simulation assessments.

RETROFIT extracts relevant cellular compartments from human intestine Visium data

We applied RETROFIT to a Visium spatial gene expression study of human intestinal development ⁵. This study provided ST data of 33538 genes and 9330 spots on intestinal tissues from adults and from fetuses at 12 and 19 post-conceptual weeks (PCW). For each of the three developmental stages, we selected the ST slide with the clearest anatomical markings (Fig. 4a) and input the ST expression count matrices to RETROFIT after quality control (Methods). Specifically, we used a matrix of 722 genes and 1080 spots for 12 PCW, a matrix of 681 genes and 1242 spots for 19 PCW, and a matrix of 1051 genes and 2649 spots for adult. The study also provided scRNA-seq data on fetal samples, revealing 101 intestinal cell types categorized as 8 cellular compartments with distinct transcriptional signatures: endothelial, epithelial, fibroblast, immune, muscle, myofibroblast (MyoFB)/mesothelial (MESO), neural and pericyte. To reduce computation and avoid ambiguity caused by a large number of highly correlated cell types, we estimated the proportions of these 8 distinct compartments at each tissue-covered spot of fetal and adult intestinal samples using RETROFIT. The most abundant compartment identified at each spot is shown in Fig. 4b.

Figure 4:

Cellular compartments identified by RETROFIT in human fetal and adult intestine Visium data. a H&E images of human fetal (12 and 19 PCW) and adult intestinal tissues. b Localization of all 8 cellular compartments in each ST slide, marked by the compartment with the largest proportion estimate at each spot. c-d ST expression scores of compartment marker genes (row 1) and RETROFIT estimates of compartment proportion (row 2) across spots for c epithelial and d muscle compartments in 3 ST slides. Pearson correlation (R) between compartment marker ST expression scores and compartment proportion estimates across all spots is shown for every combination of cellular compartments and developmental stages in c and d.

To estimate compartment proportions at each spot, we matched the L = 16 latent components extracted by RETROFIT to the K = 8 cellular compartments. Since the human intestine study ⁵ only provided scRNA-seq data for 12 and 19 PCW but not the adult stage, we annotated RETROFIT-extracted components using a curated list of 37 intestinal compartment marker genes ⁵ for all three stages (Algorithm 3; Supplementary Tables 6–8). All of our primary analyses for the human intestine ST data were conducted using this marker-based approach. To evaluate this strategy, we also annotated the RETROFIT results for 12 and 19 PCW stages using compartment-specific gene expression derived from the corresponding scRNA-seq data (Algorithm 2; Supplementary Tables 9–10). We then compared the compartment proportions from the two annotation strategies for the same ST slide. For both fetal stages, the proportion estimates produced by the two strategies were concordant across spots in 4 compartments: muscle (12 PCW: R = 0.93; 19 PCW: R = 0.92), endothelial (12 PCW: R = 0.85; 19 PCW: R = 0.92), fibroblast (12 PCW: R = 0.60; 19 PCW: R = 0.88) and epithelial (12 PCW: R = 0.49; 19 PCW: R = 0.86). In addition, the two strategies produced highly comparable proportions across spots in the immune compartment at 12 PCW (R = 0.86) and the neural compartment at 19 PCW (R = 0.94).

To assess the accuracy of the two annotation strategies, we examined the correlation between compartment proportions estimated by each strategy and compartment marker ST expression scores across all spots for each compartment and slide (Table 1; Fig.s 4c–d). We found that for the four compartments where two annotation strategies produced consistent results in 12 and 19 PCW samples, their proportion estimates from both strategies were positively correlated with the corresponding marker ST expression scores across spots (R > 0.54). Moreover, in compartments where the results of two annotations differed, the proportion estimates based on the marker annotation aligned better with the compartment marker ST expression scores than those based on the scRNA-seq annotation. For example, MyoFB/MESO marker ST expression scores were positively correlated with the marker-based proportion estimates of MyoFB/MESO across spots for both stages (12 PCW: R = 0.34; 19 PCW: R = 0.61), whereas they were negatively correlated with the proportion estimates based on the scRNA-seq annotation (12 PCW: R = −0.09; 19 PCW: R = −0.20). Together, these results validate the marker-based annotation strategy in the RETROFIT analysis of human intestine ST data.

Table 1:

Comparison of RETROFIT and STdeconvolve on human fetal intestine Visium data. Pearson correlations between ST expression scores of known marker genes and estimated proportions across spots are reported for all methods and cellular compartments. RETROFIT-extracted components were mapped to known cellular compartments using either a curated list of 37 intestinal compartment marker genes (Algorithm 3) or the companion scRNA-seq data in fetal intestinal samples (Algorithm 2). STdeconvolve was run with L = 6, which was the optimal number of components determined by STdeconvolve, and L = 16, which was the same number of components used by RETROFIT. “NA” indicates no match between a cellular compartment and any STdeconvolve-extracted components.

Compartment	12 PCW ST slide				19 PCW ST slide
	RETROFIT (L = 16)		STdeconvolve		RETROFIT (L = 16)		STdeconvolve
	Marker	scRNA-seq	L = 6	L = 16	Marker	scRNA-seq	L = 6	L = 16
Endothelial	0.68	0.57	NA	NA	0.54	0.56	NA	NA
Epithelial	0.55	0.73	0.73	0.73	0.64	0.62	0.36	0.50
Fibroblast	0.68	0.66	0.35	0.48	0.77	0.87	0.68	0.77
Immune	0.10	0.11	NA	NA	−0.15	−0.16	NA	NA
Muscle	0.87	0.83	0.81	0.77	0.71	0.83	0.68	0.69
MyoFB/MESO	0.34	−0.09	−0.05	−0.10	0.61	−0.20	−0.09	NA
Neural	0.69	0.22	NA	NA	0.72	0.81	NA	NA
Pericyte	0.11	0.08	NA	0.02	0.34	−0.08	−0.26	−0.17

We compared the deconvolution performance of RETROFIT and STdeconvolve on the ST data from two fetal samples, since the component annotation step of STdeconvolve requires single-cell transcriptomic profiles from tissues matching the ST data ¹⁵. Although both samples were characterized by 8 cellular compartments ⁵, STdeconvolve determined the optimal number of latent components as L = 6 and failed to produce components that could represent the endothelial and neural compartments (Supplementary Fig.s 1–2; Supplementary Tables 11–12), resulting in the absence of estimated proportions for these two compartments in all spots (Table 1). Increasing the number of latent components in STdeconvolve to L = 16 did not identify endothelial and neural compartments (Table 1; Supplementary Fig.s 3–4; Supplementary Tables 13–14). In contrast, RETROFIT effectively captured these two components and produced proportion estimates consistent with ST profiles of their known marker genes (endothelial: R = 0.68 at 12 PCW and R = 0.54 at 19 PCW; neural: R = 0.69 at 12 PCW and R = 0.72 at 19 PCW). While STdeconvolve performed comparably to RETROFIT for other compartments (Table 1), the absence of STdeconvolve-extracted components for endothelial and neural compartments demonstrates the superior performance of RETROFIT in this Visium dataset.

For all three stages of intestinal development, the cellular compartment proportions estimated by RETROFIT correlated well with the anatomical locations and ST profiles of compartment-specific marker genes (Fig.s 4b–d; Supplementary Fig.s 5–10). In all three stages, spots with a high proportion of epithelial cells localized near the lumen and expressed high levels of epithelial marker genes (12 PCW: R = 0.55; 19 PCW: R = 0.64; adult: R = 0.71; Fig.s 4b–c), while spots with a high proportion of muscle cells often corresponded to the smooth muscle layers and expressed high levels of muscle marker genes (12 PCW: R = 0.87; 19 PCW: R = 0.71; adult: R = 0.71; Fig.s 4b and d). In the 19 PCW slide, spots with a high proportion of neural cells localized in the myenteric plexuses and expressed high levels of neural marker genes (R = 0.72; Fig. 4b; Supplementary Fig. 9). In the adult slide, spots with a high proportion of immune cells localized around submucosal lymphoid follicles and expressed high levels of immune marker genes (R = 0.40; Fig. 4b; Supplementary Fig. 7). Additionally, spots with a high proportion of fibroblasts in the adult tissue were adjacent to vasculature structures and expressed high levels of fibroblast marker genes (R = 0.31; Fig. 4b; Supplementary Fig. 6). Overall, these findings recapitulate the anatomical features and transcriptomic signatures of human intestine, confirming the effectiveness of RETROFIT as a reference-free approach to ST deconvolution.

RETROFIT identifies spatiotemporal patterns of cellular composition in intestinal development

The cellular compositions inferred by RETROFIT on the ST samples of 3 developmental stages shed light on the temporal dynamics in human intestine development (Fig.s 5a–b). The 12 PCW slide had more than twice as high an average proportion of fibroblasts as the other two stages (12 PCW: 24.4% across 1080 spots, 19 PCW: 11.0% across 1242 spots, adult: 11.4% across 2649 spots), aligning with abundant presence of stromal 1–4 (S1–S4) fibroblasts ⁵ in the formation of submucosal structure (S1), crypt-villus axis (S2), enteric vasculature (S3) and lymphoid tissue (S4) during early intestinal development. The 19 PCW slide had the highest average proportions of epithelial (26.3%) and immune (15.6%) cells, indicating the maturation of fetal intestinal epithelium and lymphoid tissue to form the structural basis for essential functions of nutrient absorption and host immunity ^5,20. The adult slide had the highest average proportions of endothelial (19.8%) and muscle (15.8%) cells, reflecting the fully developed enteric vessels and smooth muscle layers in the mature intestine ⁵.

Figure 5:

Cellular compositions and spatiotemporal patterns identified by RETROFIT in human intestinal development. a Distribution of 8 cellular compartments across all spots in each ST slide. b Compartment composition of each spot in each ST slide. c Distribution of spots with 3 levels of cellular diversity in each slide. Group 1: spots with a dominant compartment. Group 2: spots with at least two moderately representative compartments. Group 3: spots with highly heterogeneous composition. d In each heatmap, each off-diagonal entry shows the fraction of Group 2 spots for each compartment pair, and each diagonal entry shows the fraction of Group 1 spots for each compartment. The off-diagonal entry colored in grey indicates that the number of Group 2 spots is 0 for the corresponding compartment pairs. e Spatial distribution of spots with a dominant compartment (Group 1) in each ST slide. f-h Spatial distribution of spots with at least two moderately representative compartments (Group 2), with the anchor compartment as f endothelial, g epithelial or h muscle compartment. The color of each spot in f-h represents the other cellular compartment that co-localizes with the anchor compartment and has the largest proportion estimate. Counts and percentages of Group 2 spots for 6 pairs of co-localized compartments are shown in f-h.

The vast majority of spots in all 3 ST slides encompassed cells from multiple intestinal compartments (Fig. 5b). To help elucidate the dynamics of cell-type complexity across intestinal development, we categorized spots into 3 groups based on their cellular diversity estimated by RETROFIT (Fig. 5c). Group 1 comprised spots dominated by a single compartment, where at least 50% of cells in each spot belonged to one compartment (Fig.s 5d diagonals and 5e). These spots mark regions in a tissue slide dominated by a single cellular compartment. Group 2 comprised spots with at least two moderately representative compartments, each contributing between 25–50% to the spot’s compartment composition (Fig.s 5d off-diagonals and 5f–h). These spots indicate boundaries between two compartments in the slide. Group 3 comprised spots with highly heterogeneous composition, with at most one compartment contributing 25–50% and no other compartment proportion exceeding 25%. These spots represent regions with highly complex compositions of cell types.

Compositions of the 3 spot groups varied across development (Fig.s 5c–d). Group 1 spots were the most prevalent in all three stages (12 PCW: 46.1%; 19 PCW: 38.5%; adult: 45.3%), and they exhibited layering and clustering patterns that matched known cellular anatomy of the human intestine ⁵, particularly evident in the adult sample (Fig. 5e). Group 2 spots were less common in the adult sample than fetal samples (12 PCW: 31.6%; 19 PCW: 37.2%; adult: 21.1%), but they exhibited a higher degree of pairwise cellular diversity in the adult sample. Out of 28 possible pairwise co-localization patterns among 8 cellular compartments, 27 were present in Group 2 spots for the adult sample, compared to 20 and 24 for 12 and 19 PCW samples respectively (Fig. 5d). The adult sample also had the largest fraction of Group 3 spots (12 PCW: 22.3%; 19 PCW: 24.3%; adult: 33.6%), highlighting the intricate composition of cell-types in the adult intestine. Taken together, the dynamics of spot-level cellular diversity inferred by RETROFIT effectively captures the increasing complexity of cellular compositions as the human intestine develops.

We then examined the co-localization patterns of 8 cellular compartments in Group 2 spots across the 3 developmental stages. We identified some commonalities in cellular co-localization across intestinal development (Fig. 5d). For example, muscle cells consistently exhibited the highest prevalence of co-localization with neural cells in Group 2 spots across all stages (12 PCW: 51/69 spots, 73.9%; 19 PCW: 40/56 spots, 71.4%; adult: 26/68 spots, 38.2%; Supplementary Fig. 11), recapitulating the intestinal anatomy that myenteric plexuses are surrounded by muscles ⁵. Similarly, epithelial cells consistently displayed the highest prevalence of co-localization with immune cells across Group 2 spots throughout development (12 PCW: 12/62 spots, 19.4%; 19 PCW: 112/166 spots, 67.5%; adult: 18/53 spots, 34.0%; Supplementary Fig. 11), highlighting the crucial role of epithelial cells in mediating homeostasis of immune cells in the intestine ²¹.

Notably, distinct cellular co-localization patterns emerged in Group 2 spots between fetal and adult samples (Fig. 5d). In both fetal stages, fibroblasts were the most common in Group 2 spots co-localized with endothelial cells (Fig. 5f), supporting the coordination of S3 fibroblasts and endothelial cells during fetal intestinal angiogenesis ⁵. In the adult sample, however, epithelial cells prevailed in Group 2 spots co-localized with endothelial cells (Fig. 5f). The endothelial-epithelial co-localization in the adult sample, which was obtained from a patient undergoing intestinal surgery ⁵, aligns with a recent mouse study showing that lymphatic endothelial cells reside in proximity to crypt epithelial cells and support renewal and repair of intestinal epithelium after injury ²². Contrasting the predominant co-localization of endothelial and epithelial compartments in the adult sample, MyoFB/MESO compartment prominently co-localized with epithelial cells in both fetal samples (Fig. 5g). This finding reflects the signaling circuit between epithelial stem cells and myofibroblasts during fetal intestinal development ⁵. Moreover, cellular co-localization of muscle cells also exhibited temporal variation across stages. For Group 2 spots co-localized with muscle cells, neural cells were predominant in the fetal stages, while fibroblasts were the most common in the adult stage (Fig. 5h). This difference can be attributed to the role of S1 fibroblasts in forming submucosa structures that join mucosa to smooth muscle layers of the mature intestine ⁵.

Overall, the reference-free inference of cellular composition and co-localization enabled by RETROFIT provides insights into the dynamic interplay of cellular processes that shapes intestinal development and function, demonstrating the potential for RETROFIT to yield new hypotheses of tissue biology from ST data alone.

RETROFIT captures cell-type transcriptional specificity without using single-cell references

RETROFIT estimates cell-type-specific gene expression and cell-type composition simultaneously (Fig. 1). In simulations we demonstrated the high concordance between cell-type-specific transcriptional profiles estimated by RETROFIT and those measured by single-cell technologies (Fig. 2e). Here we examined compartment-specific transcriptional profiles estimated by RETROFIT on the human intestine ST data (Supplementary Tables 15–20).

First, we compared the estimated compartment-specific expression with the observed single-cell expression for 37 curated marker genes ⁵ in 8 cellular compartments (Fig. 6a; Methods), using the companion scRNA-seq data of 12 and 19 PCW stages from the same human intestine study ⁵. To quantify how well RETROFIT estimates corresponded to single-cell observations, we computed Pearson correlation between estimated expression levels and scRNA-seq measurements across 8 cellular compartments for each marker gene in each fetal stage. Of 37 compartment marker genes, 25 (67.6%) showed high concordance (R > 0.95) in at least one stage, and 12 (32.4%) showed high concordance in both stages. Many of these 12 genes, such as ACTG2 (muscle), PECAM1 (endothelial), PHOX2B (neural) and PTPRC (immune), exhibited strong cellular specificity as expected.

Figure 6:

Transcriptional signatures and biological pathways identified by RETROFIT in human intestinal development. a Normalized expression of 37 marker genes for 8 cellular compartments in two fetal stages, obtained from RETROFIT estimates and scRNA-seq data. Each marker gene (y-axis) has a matching color with the compartment it characterizes (x-axis). b Normalized expression of 34 putative compartment-specific genes estimated by RETROFIT for 12 PCW and adult stages. Gene colors represent the compartment-specific transcriptional specificity identified in 12 PCW (orange) or adult (green) or both stages (purple). Grey colors indicate that genes were not identified as compartment-specific in a given stage. Asterisks (*) indicate that the identified genes are also markers in a. c Normalized expression of 7 compartment-specific non-marker genes obtained from RETROFIT estimates and scRNA-seq data for 12 PCW stage. The 7 genes were identified by RETROFIT in b but were not labeled as markers in a. d Top-ranked biological pathways enriched in muscle-specific genes identified by RETROFIT in b for 12 PCW and adult stages (FDR < 0.05), with the multiplicity adjusted enrichment P-value (FDR) in log base 10 shown after each pathway.

Next, we sought to identify compartment-specific genes based on RETROFIT expression estimates alone, without using any single-cell transcriptomic information. To ensure reliable results, we only considered developmental stages (12 PCW and adult) with biological replicates available (Supplementary Tables 18–20), and selected genes with consistent patterns of high expression (count > 40) measured by ST and strong compartment specificity (entropy < 1.5 and Gini index > 0.85) estimated by RETROFIT across all replicates in a given stage (Methods). Despite the stringent criteria, we identified 34 genes that showed strong compartment specificity in at least one developmental stage, 7 of which were compartment-specific in both stages (Fig. 6b).

We identified 14 and 27 compartment-specific genes in 12 PCW and adult stages, respectively (Fig. 6b). Among them, 7 (50.0%) and 6 (22.2%) were curated as compartment markers (Fig. 6a) in the original human intestine study ⁵. To validate the compartment specificity of identified genes that were not curated as markers ⁵, we compared the compartment-specific expression estimates with the companion scRNA-seq measurements at 12 PCW for these genes (Fig. 6c). Across 7 genes and 8 compartments, we observed a strong correlation between expression estimates and single-cell measurements (R = 0.96, P = 3.1 × 10⁻³¹). The inferred compartment specificity of the identified genes also agreed with their biological functions. For example, COL1A1, identified as fibroblast-specific by RETROFIT, encodes a fibril-forming collagen found in most connective tissues ²³. DES, identified as muscle-specific by RETROFIT, encodes an intermediate filament with critical roles in muscular structure and function ²⁴. Our findings are further supported by a recent mouse scRNA-seq study ²⁵ that determined COL1A1 as a fibroblast-specific expression signature and DES, CNN1 and ACTA2 as mural-specific signatures. Together, these results demonstrate the potential of RETROFIT to identify genes with cell-type-specific expression from ST data alone, without relying on prior knowledge or external single-cell data.

Lastly, we examined the temporal patterns of compartment-specific genes identified by RETROFIT across developmental stages (Fig. 6b). The majority of identified genes (27 out of 34) showed compartment specificity in only one stage. For example, 3 known neural marker genes (ELAVL4, GAP43, PHOX2B) were identified as neural-specific only in 12 PCW but not in the adult stage. These 3 genes are involved in the process of unspecialized cells acquiring specialized neuronal features (Supplementary Table 21) and human embryonic ventral midbrain development (Supplementary Table 22), corroborating their neural specificity in fetal stage only. As another example, 7 genes (including FABP1 and FABP2, 2 known epithelial markers) were identified as epithelial-specific only in adult but not in 12 PCW stage. Among these 7 genes, FABP1, FABP2 and MUC13 are involved in the digestive system process (Supplementary Table 21), and they showed significant transcriptional specificity for epithelial cells in multiple single-cell transcriptomic studies of human intestinal tissues (Supplementary Table 22). Since nutrient absorption manifests late in intestinal development (typically after villus formation ²⁰), the adult-specific genes likely capture transcriptional signatures of absorptive function in the mature intestinal epithelium.

From RETROFIT estimates, we obtained 10 muscle-specific genes in 12 PCW and 15 in adult stages, with 7 genes exhibiting muscle specificity in both stages (Fig.s 6b and d). The muscle-specific genes identified by RETROFIT in human intestine ST data showed stronger enrichments of single-cell transcriptional signatures in smooth muscle cells from human intestinal tissues compared to smooth muscle cells from other tissues such as lung, stomach and heart (Supplementary Table 22). Specifically, 8 out of 10 muscle-specific genes in 12 PCW (FDR = 1.0 × 10⁻¹⁶) and 10 out of 15 in adult stages (FDR = 1.0 × 10⁻²⁰) showed significant transcriptional specificity for the smooth muscle cells from intestinal tissues in a single-cell gene expression study of 15 human organs ⁹. In contrast, 4 out of 10 muscle-specific genes in 12 PCW (FDR = 3.2 × 10⁻⁶) and 3 out of 15 in adult stages (FDR = 1.6 × 10⁻³) showed significant transcriptional specificity for the smooth muscle cells from heart tissues in the same 15-organ single-cell study ⁹. These results highlight the spatial context specificity of these muscle-specific genes identified by RETROFIT in the intestine compared to other muscle-rich organs.

The muscle-specific genes identified by RETROFIT in both developmental stages share relevant functional themes. Specifically, these genes were significantly enriched in biological pathways (Fig. 6d; Supplementary Table 21) related to muscle contraction (12 PCW: FDR = 3.8 × 10⁻⁵; adult: FDR = 3.6 × 10⁻⁷) and muscle structure development (12 PCW: FDR = 3.2 × 10⁻²; adult: FDR = 3.6 × 10⁻⁷). Among the 7 muscle-specific genes shared by both stages, TAGLN is involved in structure development, ACTG2, CNN1 and KCNMB1 are involved in contraction, and DES and MYH11 are involved in both contraction and structure development. The muscle-specific genes from fetal and adult stages also show functional differences. For example, the mesenchyme migration pathway was significantly enriched only in 12 PCW (FDR = 5.9 × 10⁻⁶) but not in adult stage, driven by 2 muscle-specific genes that were present in 12 PCW only (ACTA2, ACTC1). This fetal-specific enrichment is consistent with the experimental evidence that serosal mesothelial cells undergo epithelial-to-mesenchymal transition, migrate throughout the gut, and differentiate into vascular smooth muscle cells ²⁶.

Discussion

We present RETROFIT, an unsupervised Bayesian framework for reference-free cell-type deconvolution of ST data. Through extensive simulations and analyses of the mouse cerebellum Slide-seq and human intestine Visum data, we demonstrate significant performance gains of RETROFIT over existing methods. We provide the open-source software of RETROFIT as an R package in Bioconductor.

The most distinctive feature of RETROFIT is the reference-free design, while the vast majority of existing ST deconvolution methods require a single-cell gene expression reference as input ^7,8. In comparison to STdeconvolve ¹⁵, which is the only published reference-free method to date, RETROFIT consistently outperforms in both synthetic and real ST data. Our work, together with STdeconvolve, demonstrates the effectiveness of reference-free deconvolutions for ST data, offering a powerful alternative to reference-based deconvolutions when an appropriate cell-type-annotated transcriptomic reference is unavailable.

As a reference-free method, RETROFIT separates cell-type annotation from ST data decomposition. By removing the dependence on a single-cell transcriptomic reference in the decomposition step, RETROFIT is more robust against the availability and quality of single-cell gene expression data, as demonstrated in this study. Moreover, the separation of annotation and decomposition offers flexibility to update the ST deconvolution results when improved references of cell-type-specific transcriptomic data or marker genes become available. In such cases, reference-free methods require only an update on the annotation without the need to rerun the decomposition, whereas reference-based methods require a rerun of the entire deconvolution process.

Besides cell-type composition, RETROFIT also estimates cell-type-specific gene expression for each ST spot. Our analyses have demonstrated the statistical accuracy of these estimates in simulations and their biological relevance in human intestinal development ⁵. The ST-derived expression estimates reveal cell-type-specific transcriptional profiles in native cellular contexts of intact tissues, thus helping researchers identify effects of tissue space and cellular environment on gene expression ¹³ and generate new hypotheses of tissue biology ².

The ST-derived estimates of cell-type-specific transcriptional profiles can also be integrated with a wide range of disease-centric datasets more broadly. One simple analysis is to correlate the ST-derived transcriptional profiles with a curated list of known disease-causing genes ⁵. This can help link disease manifestation to likely tissue regions and cell types via distinct transcriptional signatures of disease genes. Another downstream analysis is to combine the ST-derived transcriptional profiles with genome-wide association studies. This can help prioritize likely disease-causing genes among numerous candidates in light of spatial and cellular transcriptional specificity ²⁷. Altogether, these future applications enabled by RETROFIT can help track disease-relevant genes to highly specific contexts, yielding novel insights into human diseases.

Reference-free deconvolutions require specifying the total number of latent components $\left(L\right)$ as an input, which can be challenging to estimate from the ST data alone. STdeconvolve determines the optimal value for $L$ by minimizing model perplexity and the number of ‘rare’ deconvolved cell types simultaneously. Despite being data-driven, this approach consistently underestimated the number of known cell types for both simulated and real-world ST datasets in our study. For the current version of RETROFIT, we recommend specifying a large $L$ that is much greater than the known number of cell types in the ST sample. This simple strategy has proven effective in our empirical assessments. Alternatively, one could attempt to incorporate more principled approaches to estimating $L$ into the Bayesian hierarchical model underlying RETROFIT. For example, automatic selection of $L$ may be enabled by Gamma process prior ¹⁶ that induces sparsisty on $\mathit{\theta }$ or automatic relevance determination ²⁸ that ties the priors of $\mathbf{W}$ and $\mathbf{H}$ through a common shrinkage parameter.

Like most ST deconvolution approaches to date ^7,8, RETROFIT omits the spatial coordinates of spots in a slide and models the ST measurements across spots exchangeably. Despite this modeling simplification, RETROFIT was able to reveal known spatial dependencies of cell-type composition and transcriptional specificity in the analysis of mouse cerebellum and human intestine ST data. Specifically, RETROFIT results adhere to the fundamental principle of tissue organization— cells in close spatial proximity within a tissue are more likely of the same type than cells that are spatially distant. Techniques such as Gaussian process ²⁹ and hidden Markov random field ³⁰ have been recently explored to enhance ST data analyses through sophisticated modeling of spatial correlations among ST spots. However, these techniques often incur additional computation and may not scale well to large ST datasets. As such, we view introducing spatial awareness to RETROFIT while maintaining its computational efficiency as a promising future enhancement.

Overall, RETROFIT is an interpretable and scalable framework to deconvolve ST data, with the distinct advantage that it can simultaneously reveal cell-type composition and cell-type-specific gene expression for each ST spot independent of any single-cell transcriptomic references. As more ST data are generated and cell-type deconvolution becomes a routine analysis, we expect that RETROFIT will facilitate the high-throughput translation of genome-wide ST readouts to new insights in tissue biology.

Methods

Bayesian hierarchical model

Let $\mathbf{X}=\left[X_{gs}\right]$ be the $G\times S$ count matrix of expression levels for $G$ genes at $S$ spots obtained from a ST experiment. Since only a finite number of cell types constitute the ST sample, we represent $\mathbf{X}$ as a low-rank matrix spanned by $L$ non-negative components that capture transcriptional signatures of distinct cell types in the ST sample. Specifically, we model the observed expression level of gene $g$ at spot $s$, $X_{gs}$, as the sum of unobserved expression counts in $L$ latent components:

$$X_{gs}=\sum _{\ell =1}^L{Z}_{g\ell s}.$$ (1)

We further attribute each latent component $Z_{g\ell s}$ to two independent sources in an additive manner:

$$Z_{g\ell s}=Z_{g\ell s}^0+Z_{g\ell s}^1,$$ (2)

where $Z_{g\ell s}^0$ denotes the background expression level shared by all genes in component $\ell$ at spot $s$ and $Z_{g\ell s}^1$ denotes the expression level specific to gene $g$ in component $\ell$ at spot $s$. We model the unobserved gene expression counts $Z_{g\ell s}^0$ and $Z_{g\ell s}^1$ as two independent Poisson random variables ^13,31:

$$Z_{g\ell s}^0~𝓟\left(\lambda H_{\ell s}\right),\hspace{1em}{Z}_{g\ell s}^1~𝓟\left(W_{g\ell }{\theta }_{\ell }{H}_{\ell s}\right).$$ (3)

Here $W_{g\ell }>0$ denotes the average expression level of gene $g$ in component $\ell$, ${\theta }_{\ell }>0$ represents the contribution from component $\ell$, $H_{\ell s}>0$ denotes the weight of component $\ell$ at spot $s$, and $\lambda \ge 0$ denotes an ‘offset’ constant capturing the background expression level shared by all genes across all components and spots ^32,33. When a sparsity-inducing prior is placed on $\mathit{\theta }=\left[{\theta }_{\ell }\right]$, only a small subset of elements in θ are expected to be substantially greater than 0, leading to a preference for a sparse model with relatively few components ¹⁶. Taken together, we obtain the following generative model of ST data:

$$X_{gs}~𝓟\left(\sum _{\ell =1}^L\left(W_{g\ell }{\theta }_{\ell }+\lambda \right)H_{\ell s}\right).$$ (4)

The mean of Poisson model (4) implies two non-negative matrix factorization (NMF) models. When $\lambda =0$, the mean of Poisson model (4) implies the Gamma Process NMF ¹⁶: $\text{E}\left(X_{gs}\right)={\sum }_{\ell =1}^L{W}_{g\ell }{\theta }_{\ell }{H}_{\ell s}$. When $\lambda =0$ and ${\theta }_{\ell }=1$ for $\ell =1,\dots ,L$, the mean of Poisson model (4) implies the standard NMF ³⁴: $\text{E}\left(X_{gs}\right)={\sum }_{\ell =1}^L{W}_{g\ell }{H}_{\ell s}$.

We take a Bayesian approach to learn the unknown parameters $\left\{W_{g\ell },{\theta }_{\ell },H_{\ell s}\right\}$ in the Poisson generative model (4) from the observed ST data $\mathbf{X}$. Specifically, we place independent Gamma priors ¹⁶ on them:

$$W_{g\ell }~𝓖\left({\alpha }_0^W,{\beta }_0^W\right),\hspace{1em}{\theta }_{\ell }~𝓖\left({\alpha }_0^{\theta },{\beta }_0^{\theta }\right),\hspace{1em}{H}_{\ell s}~𝓖\left({\alpha }_0^H,{\beta }_0^H\right).$$ (5)

We choose the Gamma priors (5) mainly for computational convenience, because combining the Poisson generative model (4) with the Gamma priors (5) leads to conditional conjugacy, which will simplify the development of SSVI algorithm described in the next section.

In this study, we fix $\left\{L,\lambda ,{\alpha }_0^W,{\beta }_0^W,{\alpha }_0^{\theta },{\beta }_0^{\theta },{\alpha }_0^H,{\beta }_0^H\right\}$ as known constants to further simplify large-scale computation. For each dataset analyzed here, we set $L$ as twice the number of known cell types in the tissue sample to ensure that all the cell types present in the ST slide can be potentially captured by the $L$ latent components. This choice of $L$ is informed by Gamma Process NMF ¹⁶, a related method that recommends using a relative large $L$. For all datasets, we set $\lambda =0.01$ in the Poisson model (4) and we set the hyper-parameters in Gamma priors (5) as ${\alpha }_0^W=0.05$, ${\beta }_0^W=0.0001$, ${\alpha }_0^{\theta }=1.25$, ${\beta }_0^{\theta }=10$, ${\alpha }_0^H=0.2$, ${\beta }_0^H=0.2$. In particular, the Gamma prior on the component contribution ${\theta }_{\ell }~𝓖\left({\alpha }_0^{\theta }=1.25,{\beta }_0^{\theta }=10\right)$ has mean 0.125 and variance 0.0125, and thus this prior favors small values of ${\theta }_{\ell }$ and induces a sparse solution in practice. In use cases where specific information about $\left\{L,\lambda ,{\alpha }_0^W,{\beta }_0^W,{\alpha }_0^{\theta },{\beta }_0^{\theta },{\alpha }_0^H,{\beta }_0^H\right\}$ is available, it can be further used to guide their specifications.

Structured stochastic variational inference

To compute the posteriors of $\left\{W_{g\ell },{\theta }_{\ell },H_{\ell s}\right\}$ we implement a SSVI algorithm ¹⁷ that scales well with thousands of genes and spots (Supplementary Table 1). To formulate the SSVI algorithm, we use the following notation: $\mathbf{Z}=\left\{{\mathbf{Z}}_{gs}^0,{\mathbf{Z}}_{gs}^1\right\}$ for $g=1,\dots G$ and $s=1,\dots ,S$, L-length vector ${\mathbf{Z}}_{gs}^0=\left[Z_{g\ell s}^0\right]$, L-length vector ${\mathbf{Z}}_{gs}^1=\left[Z_{g\ell s}^1\right]$, $G\times S$ matrix $\mathbf{W}=\left[W_{gs}\right]$, L-length vector $\mathit{\theta }=\left[{\theta }_{\ell }\right]$ and $L\times S$ matrix $\mathbf{H}=\left[H_{\ell s}\right]$. SSVI seeks a variational distribution $q\left(\mathbf{Z},\mathbf{W},\mathit{\theta },\mathbf{H}\right)$ of the following form to minimize its Kullback–Leibler (KL) divergence to the actual posterior distribution $p\left(\mathbf{Z},\mathbf{W},\mathit{\theta },\mathbf{H}|\mathbf{X}\right)$:

$$q\left(\mathbf{Z},\mathbf{W},\mathit{\theta },\mathbf{H}\right)=\prod _{g,\ell }q\left(W_{g\ell }\right)\prod _{\ell }q\left({\theta }_{\ell }\right)\prod _{\ell ,s}q\left(H_{\ell s}\right)\prod _{g,s}q\left({\mathbf{Z}}_{gs}^0,{\mathbf{Z}}_{gs}^1|\mathbf{W},\mathit{\theta },\mathbf{H}\right),$$ (6)

where $\left\{q\left(W_{g\ell }\right),q\left({\theta }_{\ell }\right),q\left(H_{\ell s}\right)\right\}$ are required by SSVI to be in the same exponential family as the priors of $\left\{W_{g\ell },{\theta }_{\ell },H_{\ell s}\right\}$ while $\left\{q\left({\mathbf{Z}}_{gs}^0,{\mathbf{Z}}_{gs}^1|\mathbf{W},\mathit{\theta },\mathbf{H}\right)\right\}$ can have any distributional form. By restoring dependence between model parameters $\left\{\mathbf{W},\mathit{\theta },\mathbf{H}\right\}$ and latent variables $\mathbf{Z}$ through $\left\{q\left({\mathbf{Z}}_{gs}^0,{\mathbf{Z}}_{gs}^1|\mathbf{W},\mathit{\theta },\mathbf{H}\right)\right\}$, the variational distribution specified by Eq. (6) improves upon the standard mean-field variational distribution that (incorrectly) enforces independence between $\left\{\mathbf{W},\mathit{\theta },\mathbf{H}\right\}$ and $\mathbf{Z}$. Consequently, SSVI often outperforms mean-field variational inference on a wide range of Bayesian hierarchical models ¹⁷.

Since our Bayesian model is defined by the Poisson likelihood (4) and Gamma priors (5), $\left\{q\left(W_{g\ell }\right),q\left({\theta }_{\ell }\right),q\left(H_{\ell s}\right)\right\}$ in Eq. (6) are automatically Gamma distributions, which satisfy the distributional requirement in SSVI:

$$q\left(W_{g\ell }\right)=𝓖\left(W_{g\ell };{\alpha }_{g\ell }^W,{\beta }_{g\ell }^W\right),\hspace{1em}q\left({\theta }_{\ell }\right)=𝓖\left({\theta }_{\ell };{\alpha }_{\ell }^{\theta },{\beta }_{\ell }^{\theta }\right),\hspace{1em}q\left(H_{\ell s}\right)=𝓖\left(H_{\ell s};{\alpha }_{\ell s}^H,{\beta }_{\ell s}^H\right).$$ (7)

We specify $q\left({\mathbf{Z}}_{gs}^0,{\mathbf{Z}}_{gs}^1|\mathbf{W},\mathit{\theta },\mathbf{H}\right)$ as the exact conditional posterior distributions of $\left\{{\mathbf{Z}}_{gs}^0,{\mathbf{Z}}_{gs}^1\right\}$ given $\left\{\mathbf{W},\mathit{\theta },\mathbf{H}\right\}$:

$$q\left({\mathbf{Z}}_{gs}^0,{\mathbf{Z}}_{gs}^1|\mathbf{W},\mathit{\theta },\mathbf{H}\right)=p\left({\mathbf{Z}}_{gs}^0,{\mathbf{Z}}_{gs}^1|\mathbf{X},\mathbf{W},\mathit{\theta },\mathbf{H}\right).$$ (8)

This specification is chosen for two reasons. First, Eq. (8) provides the best possible approximation by achieving zero KL divergence to the actual conditional posterior ¹⁷. Second, because $\left\{Z_{g\ell s}^0,Z_{g\ell s}^1\right\}$ are independent Poisson random variables (3) that constitute the ST expression profile $X_{gs}={\sum }_{\ell }\left(Z_{g\ell s}^0,Z_{g\ell s}^1\right)$, the right-hand side of Eq. (8) has a closed form of a multinomial distribution:

$$\mathrm{Pr}\left({\mathbf{Z}}_{gs}^0={\mathbf{\text{z}}}_{gs}^0,{\mathbf{Z}}_{gs}^1={\mathbf{\text{z}}}_{gs}^1|\mathbf{X}=\mathbf{x},\mathbf{W},\mathit{\theta },\mathbf{H}\right)=\left(\begin{array}{c}{x}_{gs}\\ z_{g1s}^0,\cdots ,z_{gLs}^0,z_{g1s}^1,\cdots ,z_{gLs}^1\end{array}\right)\prod _{\ell =1}^L{\left({\pi }_{g\ell s}^0\right)}^{z_{g\ell s}^0}\prod _{\ell =1}^L{\left({\pi }_{g\ell s}^1\right)}^{z_{g\ell s}^1},$$ (9)

where $x_{gs}={\sum }_{\ell }\left(z_{g\ell s}^0+z_{g\ell s}^1\right)$ is the observed ST expression count for gene $g$ at spot $s$ and

$${\pi }_{g\ell s}^0=\frac{\lambda H_{\ell s}}{{\sum }_{\ell }\left(W_{g\ell }{\theta }_{\ell }+\lambda \right)H_{\ell s}},\hspace{1em}{\pi }_{g\ell s}^1=\frac{W_{g\ell }{\theta }_{\ell }{H}_{\ell s}}{{\sum }_{\ell }\left(W_{g\ell }{\theta }_{\ell }+\lambda \right)H_{\ell s}},$$ (10)

for each component $\ell$. With the variational distribution defined by Eq.s (6)–(10), we optimize the corresponding variational parameters $\left\{{\alpha }_{g\ell }^W,{\beta }_{g\ell }^W,{\alpha }_{\ell }^{\theta },{\beta }_{\ell }^{\theta },{\alpha }_{\ell s}^H,{\beta }_{\ell s}^H,{\pi }_{g\ell s}^0,{\pi }_{g\ell s}^1\right\}$ through an iterative and stochastic procedure ¹⁷ defined in Algorithm 1. The derivation of Algorithm 1 is provided in Supplementary Note 1.

In this study, we initialize $\left\{{\alpha }_{g\ell }^W,{\beta }_{g\ell }^W,{\alpha }_{\ell }^{\theta },{\beta }_{\ell }^{\theta },{\alpha }_{\ell s}^H,{\beta }_{\ell s}^H\right\}$ in Algorithm 1 as

$${\alpha }_{g\ell }^W\left(0\right)~𝓤\left(0,0.5\right)+{\alpha }_0^W,\hspace{1em}{\alpha }_{\ell }^{\theta }\left(0\right)~𝓤\left(0,1\right)+{\alpha }_0^{\theta },\hspace{1em}{\alpha }_{\ell s}^H\left(0\right)~𝓤\left(0,0.1\right)+{\alpha }_0^H,$$

$${\beta }_{g\ell }^W\left(0\right)~𝓤\left(0,0.005\right)+{\beta }_0^W,\hspace{1em}{\beta }_{\ell }^{\theta }\left(0\right)~𝓤\left(0,1\right)+{\beta }_0^{\theta },\hspace{1em}{\beta }_{\ell s}^H\left(0\right)~𝓤\left(0,0.5\right)+{\beta }_0^H,$$

where $\left\{{\alpha }_0^W,{\beta }_0^W,{\alpha }_0^{\theta },{\beta }_0^{\theta },{\alpha }_0^H,{\beta }_0^H\right\}$ are hyper-parameters specified in the previous section and $𝓤\left(a,b\right)$ denotes a continuous uniform distribution on the interval $\left[a,b\right]$. In use cases where specific initialization schemes are available, they can be easily used in our R package to run Algorithm 1.

Cell-type annotation strategies

After running Algorithm 1 on the ST data matrix, the expression profile of each gene at each spot is deconvolved into $L$ latent components represented by columns of the $G\times L$ matrix $\widehat{\mathbf{W}}$. To map the $L$ latent components to $K$ known cell types present in the ST data, we develop two simple strategies (Fig. 1). The first approach is suitable when a reference of cell-type-specific gene expression is available, such as cell-type-annotated scRNA-seq data from the same tissue type. This approach computes correlations between the deconvolved component-specific expression profiles $\left(\widehat{\mathbf{W}}\right)$ and the cell-type-specific expression profiles $\left({\mathbf{W}}^0\right)$, and then matches each component to the cell type with the largest correlation for this component. This approach is implemented as Algorithm 2. The second approach is suitable when marker genes are known for relevant cell types in the ST sample. This approach calculates a marker expression score for each component in each cell type $\left(\mathbf{\text{M}}\right)$, defined as the sum of normalized component-specific expression of known marker genes in this cell type, and then annotates each component by the cell type with the largest score. This approach is implemented as Algorithm 3.

After matching the latent components to known cell types, we obtain a cell-type-specific expression matrix for all genes $\left(\tilde{\mathbf{W}}\right)$ and a cell-type proportion matrix for all spots $\left(\tilde{\mathbf{H}}\right)$ as follows. Let $𝓛=\left\{{\ell }_1,{\ell }_2,\dots ,{\ell }_K\right\}\subseteq \left\{1,2,\dots ,L\right\}$ denote the set of latent components that are matched to $K$ cell types, where ${\ell }_k$ indicates that the ${\ell }_k$-th column of the $G\times L$ matrix $\widehat{\mathbf{W}}$ is matched to cell type $k$. We extract these columns in $\widehat{\mathbf{W}}$ to form a $G\times K$ matrix $\tilde{\mathbf{W}}=\left[{\widehat{W}}_{g{\ell }_k}\right]$, where $g=1,2,\dots ,G$ and $k=1,2,\dots ,K$. This matrix $\tilde{\mathbf{W}}$ represents the cell-type-specific expression estimates of $G$ genes in $K$ cell types. Similarly, we extract the rows in $\widehat{\mathbf{H}}$ corresponding to the cell-type-matched columns of $\widehat{\mathbf{W}}$ and then normalize them to estimate the proportions of $K$ cell types at $S$ spots. We denote this $K\times S$ matrix $\tilde{\mathbf{H}}=\left[{\tilde{H}}_{ks}\right]$, where ${\tilde{H}}_{ks}={\widehat{H}}_{{\ell }_{k}s}/{\sum }_{\ell \in 𝓛}{\widehat{H}}_{\ell s}\in \left[0,1\right]$, $k=1,\dots ,K$ and $s=1,2,\dots ,S$.

Existing methods for comparison

We compared RETROFIT with 5 recently published cell-type deconvolution methods for ST data: STdeconvolve ¹⁵ (https://bioconductor.org/packages/release/bioc/html/STdeconvolve.html, version 1.2.0), RCTD ¹³ (https://github.com/dmcable/spacexr, version 1.2.0), SPOTlight ¹⁹ (https://github.com/MarcElosua/SPOTlight, version 0.1.0), Stereoscope ¹⁸ (https://github.com/almaan/stereoscope, version 03) and NMFreg ⁶ (https://github.com/broadchenf/Slideseq, version 1.0). The software package versions were up-to-date at the time of analysis. For RCTD, we used both the full (allowing an unconstrained number of cell types per spot) and doublet (allowing up to two cell types per spot) modes. For SPOTlight, we set the minimum expected contribution from a cell type in a spot as 0.01. For Stereoscope, we set the number of epochs for fitting both single-cell and ST data as 10000 and the learning rate as 0.1. For the remaining specifications, we used the default setting of each software package in the present study.

$$\underset{¯}{\overline{\begin{array}{l}\underset{¯}{\mathbf{\text{Algorithm 1}} \text{SSVI for reference-free decomposition of ST data matrix}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Input the }G\times S\hspace{0.17em}\hspace{0.17em}\text{ST data matrix}\hspace{0.17em}\mathbf{\text{X}}=\left[X_{gs}\right]\hspace{0.17em}\text{and pre-specified constants}\hspace{0.17em}\left\{L,\lambda ,{\alpha }_0^W,{\beta }_0^W,{\alpha }_0^{\theta },{\beta }_0^{\theta },{\alpha }_0^H,{\beta }_0^H\right\}.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Initialize}\hspace{0.17em}\hspace{0.17em}\left\{{\alpha }_{g\ell }^W,{\beta }_{g\ell }^W,{\alpha }_{\ell }^{\theta },{\beta }_{\ell }^{\theta },{\alpha }_{\ell s}^H,{\beta }_{\ell s}^H\right\}\hspace{0.17em}\text{as}\hspace{0.17em}\hspace{0.17em}\left\{{\alpha }_{g\ell }^W\left(0\right),{\beta }_{g\ell }^W\left(0\right),{\alpha }_{\ell }^{\theta }\left(0\right),{\beta }_{\ell }^{\theta }\left(0\right),{\alpha }_{\ell s}^H\left(0\right),{\beta }_{\ell s}^H\left(0\right)\right\}.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{for}} \text{iteration }i\text{ = 1,2,}\dots \text{, }I \mathbf{\text{do}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(1) Sample}\hspace{0.17em}\hspace{0.17em}\mathbf{W}\left(i\right)=\left[W_{g\ell }\left(i\right)\right],\text{θ}\left(i\right)=\left[{\theta }_{\ell }\left(i\right)\right],\mathbf{H}\left(i\right)=\left[H_{\ell s}\left(i\right)\right]\hspace{0.17em}\text{from the Gamma distributions defined in Eq. (7):}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{W}_{g\ell }\left(i\right)\sim 𝓖\left({\alpha }_{g\ell }^W\left(i-1\right),{\beta }_{g\ell }^W\left(i-1\right)\right),{\theta }_{\ell }\left(i\right)\sim 𝓖\left({\alpha }_{\ell }^{\theta }\left(i-1\right),{\beta }_{\ell }^{\theta }\left(i-1\right)\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{H}_{\ell s}\left(i\right)\sim 𝓖\left({\alpha }_{\ell s}^H\left(i-1\right),{\beta }_{\ell s}^H\left(i-1\right)\right).\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(2) Update the multinomial distribution defined in Eq.s (9)-(10):}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\pi }_{g\ell s}^0\left(i\right)=\frac{\lambda H_{\ell s}\left(i\right)}{{\Sigma }_{\ell }\left[W_{g\ell }\left(i\right){\theta }_{\ell }\left(i\right)+\lambda \right]H_{\ell s}\left(i\right)},\hspace{0.17em}\hspace{0.17em}{\pi }_{g\ell s}^1\left(i\right)=\frac{W_{g\ell }\left(i\right){\theta }_{\ell }\left(i\right)H_{\ell s}\left(i\right)}{{\Sigma }_{\ell }\left[W_{g\ell }\left(i\right){\theta }_{\ell }\left(i\right)+\lambda \right]H_{\ell s}\left(i\right)}.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(3) Update the Gamma parameters in Eq. (7) using a stochastic gradient with step size }\rho \left(i\right)=i^{-0.5}:\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\alpha }_{g\ell }^W\left(i\right)=\left[1-\rho \left(i\right)\right]\cdot {\alpha }_{g\ell }^W\left(i-1\right)+\rho \left(i\right)\cdot \left[\hspace{0.17em}{\alpha }_0^W+\sum _s{X}_{gs}{\pi }_{g\ell s}^1\left(i\right)\right],\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\beta }_{g\ell }^W\left(i\right)=\left[1-\rho \left(i\right)\right]\cdot {\beta }_{g\ell }^W\left(i-1\right)+\rho \left(i\right)\cdot \left[\hspace{0.17em}{\beta }_0^W+\sum _s{\theta }_{\ell }\left(i\right)H_{\ell s}\left(i\right)\right],\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\alpha }_{\ell }^{\theta }\left(i\right)=\left[1-\rho \left(i\right)\right]\cdot {\alpha }_{\ell }^{\theta }\left(i-1\right)+\rho \left(i\right)\cdot \left[\hspace{0.17em}{\alpha }_0^{\theta }+\sum _{g,s}{X}_{gs}{\pi }_{g\ell s}^1\left(i\right)\right],\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\beta }_{\ell }^{\theta }\left(i\right)=\left[1-\rho \left(i\right)\right]\cdot {\beta }_{\ell }^{\theta }\left(i-1\right)+\rho \left(i\right)\cdot \left[\hspace{0.17em}{\beta }_0^{\theta }+\sum _{g,s}{W}_{g\ell }\left(i\right)H_{\ell s}\left(i\right)\right],\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\alpha }_{\ell s}^H\left(i\right)=\left[1-\rho \left(i\right)\right]\cdot {\alpha }_{\ell s}^H\left(i-1\right)+\rho \left(i\right)\cdot \left\{{\alpha }_0^H+\sum _g{X}_{gs}\left[{\pi }_{g\ell s}^1\left(i\right)+{\pi }_{g\ell s}^0\left(i\right)\right]\right\},\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\beta }_{\ell s}^H\left(i\right)=\left[1-\rho \left(i\right)\right]\cdot {\beta }_{\ell s}^H\left(i-1\right)+\rho \left(i\right)\cdot \left\{{\beta }_0^H+\sum _g\left[W_{g\ell }\left(i\right){\theta }_{\ell }\left(i\right)+\lambda \right]\right\}.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{end for}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{return}} \text{estimates of }G\times L\hspace{0.17em}\text{matrix}\hspace{0.17em}\hspace{0.17em}\widehat{\mathbf{W}}=\left[{\widehat{\mathbf{W}}}_{g\ell }\right],\hspace{0.17em}L\text{-length vector}\hspace{0.17em}\hspace{0.17em}\widehat{\mathit{\theta }}=\left[{\widehat{\theta }}_{\ell }\right]\hspace{0.17em}\text{and}\hspace{0.17em}L\times S\hspace{0.17em}\text{matrix}\hspace{0.17em}\hspace{0.17em}\widehat{\mathbf{\text{H}}}=\left[{\widehat{H}}_{\ell s}\right]\hspace{0.17em}\hspace{0.17em}\text{where}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{W}}_{g\ell }=\frac{{\alpha }_{g\ell }^W\left(I\right)}{{\beta }_{g\ell }^W\left(I\right)},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{\theta }}_{\ell }=\hspace{0.17em}\frac{{\alpha }_{\ell }^{\theta }\left(I\right)}{{\beta }_{\ell }^{\theta }\left(I\right)},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{H}}_{\ell s}=\frac{{\alpha }_{\ell s}^H\left(I\right)}{{\beta }_{\ell s}^H\left(I\right)}.\end{array}}}$$

Among the 5 existing methods, only STdeconvolve is reference-free, while the other 4 methods require the input of a single-cell gene expression reference for ST deconvolution. For each ST dataset analyzed in this study, we ran the 4 reference-based methods with the same single-cell expression reference, as described in the following sections. We also used the single-cell expression reference to annotate STdeconvolve results by cell types, as described in the STdeconvolve publication ¹⁵. When multiple latent components (topics) extracted by STdeconvolve were matched with the same cell type, we merged these components into one component so that STdeconovle produced one proportion estimate for each cell type, consistent with the other methods. For each ST dataset, each method outputs an estimated proportion for each cell type at each spot, which can be compared with the cell-type proportion estimates $\left(\tilde{\mathbf{H}}\right)$ produced by RETROFIT.

$$\overline{\underset{¯}{\begin{array}{l}\underset{¯}{\mathbf{\text{Algorithm 2}} \text{Cell-type mapping based on cell-type-specific gene expression}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Input the }G\times L\text{ matrix }\widehat{\mathbf{W}}\hspace{0.17em}\hspace{0.17em}\text{and} L\times S\hspace{0.17em}\hspace{0.17em}\text{matrix }\widehat{\mathbf{\text{H}}}\hspace{0.17em}\hspace{0.17em}\text{produced by Algorithm 1 and a}\hspace{0.17em}\hspace{0.17em}G\times K\hspace{0.17em}\hspace{0.17em}\text{reference matrix}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbf{W}}^0=\left[W_{ij}^0\right]\hspace{0.17em}\hspace{0.17em}\text{of cell-type-specific expression with}\hspace{0.17em}\hspace{0.17em}{W}_{ij}^0\hspace{0.17em}\hspace{0.17em}\text{indicating the expression level of gene }i\text{ in cell type}\hspace{0.17em}\hspace{0.17em}j.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Normalize each row of}\hspace{0.17em}\hspace{0.17em}{\mathbf{W}}^0\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\widehat{\mathbf{W}}\hspace{0.17em}\hspace{0.17em}\text{by their row sums:}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbf{W}}^{0*}=\left[W_{ij}^{0*}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{W}_{ij}^{0*}=\frac{W_{ij}^0}{{\sum }_{k=1}^K{W}_{ik}^0};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{\mathbf{W}}}^{*}=\left[{\widehat{W}}_{ïj}^{*}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{W}}_{ïj}^{*}=\frac{{\widehat{W}}_{ij}}{{\sum }_{\ell =1}^L{\widehat{W}}_{i\ell }}.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Compute the}\hspace{0.17em}\hspace{0.17em}K\times L\hspace{0.17em}\hspace{0.17em}\text{correlation matrix} \mathbf{\text{R}}=\left[R_{ij}\right]\hspace{0.17em}\hspace{0.17em}\text{where the (}i\text{, }j\text{)-th entry of} \mathbf{\text{R}} \text{is the Pearson correlation}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{between the} i\text{th column (cell type) of}\hspace{0.17em}\hspace{0.17em}{\widehat{\mathbf{W}}}^{*}\hspace{0.17em}\hspace{0.17em}\text{and the }j\text{th column (latent component) of}\hspace{0.17em}\hspace{0.17em}{\widehat{\mathbf{W}}}^{*}.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{repeat}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(1) Find the entry of} \mathbf{\text{R}} \text{with the largest value:}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(r,c\right)=\underset{\left(i,j\right)}{\arg \max }{R}_{ij}.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(2) Assign cell type }r\text{ to latent component }c\text{.}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(3) Delete the }r\text{th row and the }c\text{th column from} \mathbf{\text{R}}.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{until}} \text{each cell type }k\text{ is matched with a unique latent component (column)}\hspace{0.17em}\hspace{0.17em}{\ell }_k\hspace{0.17em}\hspace{0.17em}\text{of}\hspace{0.17em}\hspace{0.17em}\widehat{\mathbf{W}},\hspace{0.17em}\hspace{0.17em}k=1,2,\dots ,K.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{return}}\hspace{0.17em}\hspace{0.17em}G\times K\hspace{0.17em}\hspace{0.17em}\text{cell-type-specific gene expression matrix}\hspace{0.17em}\hspace{0.17em}\widetilde{\mathbf{\text{W}}}=\left[{\widehat{W}}_{g\ell k}\right]\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}K\times S\hspace{0.17em}\hspace{0.17em}\text{cell-type proportion matrix}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\tilde{\mathbf{H}}=\left[{\tilde{H}}_{ks}\right]\hspace{0.17em}\hspace{0.17em}\text{with}\hspace{0.17em}\hspace{0.17em}{\tilde{H}}_{ks}={\widehat{H}}_{{\ell }_{k}s}/{\Sigma }_{\ell \in L}{\widehat{H}}_{\ell s}\in \left[0,1\right],\hspace{0.17em}\hspace{0.17em}g=1,2,\dots ,G,\hspace{0.17em}\hspace{0.17em}k=1,2,\dots ,K\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}s=1,2,\dots ,S.\end{array}}}$$

$$\overline{\underset{¯}{\begin{array}{l}\underset{¯}{\mathbf{\text{Algorithm 3}}\text{ Cell-type mapping based on cell-type-specific marker gene list}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Input the}\hspace{0.17em}\hspace{0.17em}G\times L\hspace{0.17em}\hspace{0.17em}\text{matrix}\hspace{0.17em}\hspace{0.17em}\widehat{\mathbf{W}}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}L\times S\hspace{0.17em}\hspace{0.17em}\text{matrix}\hspace{0.17em}\hspace{0.17em}\widehat{\mathbf{\text{H}}}\hspace{0.17em}\hspace{0.17em}\text{produced by Algorithm 1 and known marker gene lists}\hspace{0.17em}\hspace{0.17em}{\left\{M_k\right\}}_{k=1}^K\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for }K\text{ cell types with }{M}_k\hspace{0.17em}\hspace{0.17em}\text{indicating the list of marker genes for cell type }k.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Normalize each row of}\hspace{0.17em}\hspace{0.17em}\widehat{\mathbf{W}}\hspace{0.17em}\hspace{0.17em}\text{by its row sum:}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{\mathbf{W}}}^{*}=\left[{\widehat{W}}_{ij}^{*}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{W}}_{ij}^{*}=\frac{{\widehat{W}}_{ïj}}{{\sum }_{\ell =1}^L{\widehat{W}}_{i\ell }}.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Compute the}\hspace{0.17em}\hspace{0.17em}K\times L\hspace{0.17em}\hspace{0.17em}\text{cell-type marker score matrix}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{M}}=\left[M_{ij}\right]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{where the }(i, j)\text{-th entry of} \mathbf{\text{M}}\text{ is given by}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{M}_{ij}=\frac{1}{\left|{𝓜}_i\right|}\sum _{g\in {𝓜}_i}{\widehat{W}}_{gj}^{*},\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{where}\hspace{0.17em}\hspace{0.17em}\left|{𝓜}_i\right|\hspace{0.17em}\hspace{0.17em}\text{is the total number of marker genes for cell type }i.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{repeat}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(1) Find the entry of} \mathbf{\text{M}}\text{ with the largest value:}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(r,c\right)=\underset{\left(i,j\right)}{\arg \max }{M}_{ij}.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(2) Assign cell type }r\text{ to latent component }c.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(\text{3) Delete the }r\text{th row and the cth column from} \mathbf{\text{M}}.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{until}}\text{ each cell type }k\text{ is matched with a unique latent component (column)}\hspace{0.17em}\hspace{0.17em}{\ell }_k\hspace{0.17em}\hspace{0.17em}\text{of}\hspace{0.17em}\hspace{0.17em}\widehat{\mathbf{W}},\hspace{0.17em}\hspace{0.17em}k=1,2,\dots ,K.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{return}}\hspace{0.17em}\hspace{0.17em}G\times K\hspace{0.17em}\hspace{0.17em}\text{cell-type-specific gene expression}\hspace{0.17em}\hspace{0.17em}\text{matrix}\hspace{0.17em}\hspace{0.17em}\tilde{\mathbf{W}}=\left[{\widehat{W}}_{g{\ell }_k}\right]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}K\times S\hspace{0.17em}\hspace{0.17em}\text{cell-type proportion matrix}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\tilde{\mathbf{H}}=\left[{\tilde{H}}_{ks}\right]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{with}\hspace{0.17em}\hspace{0.17em}{\tilde{H}}_{ks}={\widehat{H}}_{{\ell }_{k}s}/{\Sigma }_{\ell \in 𝓛}{\widehat{H}}_{\ell s}\in \left[0,1\right],\hspace{0.17em}\hspace{0.17em}g=1,2,\dots ,G,\hspace{0.17em}\hspace{0.17em}k=1,2,\dots ,K\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}s=1,2,\dots ,S.\end{array}}}$$

Simulation studies

Multiple factors in ST data may affect the performance of cell-type deconvolution. First, spot size differs across ST technologies and affects the complexity of the cell-type mixture at each spot. Second, cell-type heterogeneity in a ST slide also varies. A ST slide from a highly heterogeneous tissue (e.g., mammalian brains and intestines) tends to produce spots with multiple cell types. Methods that limit the number of cell types at a spot ¹³ are likely inadequate for deconvolving ST data with high cell-type heterogeneity. Third, sequencing depths on the same slide may vary across spots, requiring methods to be adaptive and robust. Lastly, while RETROFIT does not require a single-cell gene expression reference for deconvolution, many existing methods do and thus their performance relies on the reference quality. We conducted simulations to investigate the impact of these factors on the performance of RETROFIT and several existing ST deconvolution methods.

To imitate ST experiments from various platforms and tissue samples, we simulate ST data with different spot sizes and cell-type heterogeneity levels. Specifically, we characterize spot size by the number of cells per spot $\left(N\right)$ and cell-type heterogeneity by the maximum number of cell types per spot $\left(M\right)$. For each combination of $N$ and $M$, we simulate the ST data matrix of $G$ genes and $S$ spots as follows. For each spot $s$, we randomly select an integer $K_s$ between 1 and $M$, and then randomly select $K_s$ cell types from the $K$ cell types present in the ST sample, denoted as ${𝓚}_s$. We simulate the proportions of the $K_s$ selected cell types using a flat Dirichlet distribution, ${\mathit{\pi }}_s={\left[{\pi }_{is}\right]}_{i\in {𝓚}_s}~{𝓓}_{K_s}\left(1,\dots ,1\right)$, and obtain the cell counts for the $K_s$ selected cell types at spot $s$ as ${\mathbf{\text{n}}}_s=N{\mathit{\pi }}_s={\left[N{\pi }_{is}\right]}_{i\in {𝓚}_s}$, rounding to the nearest integer. We randomly select ${\mathbf{\text{n}}}_s$ unique cells from a single-cell gene expression reference of the $K_s$ selected cell types and aggregate their single-cell expression profiles of $G$ genes to produce the expression profile for spot $s$. For example, if a spot contains $N=10$ cells from cell types a, b and c with proportions 0.1, 0.7 and 0.2, respectively, we randomly select 1, 7 and 2 unique cells from the corresponding single-cell expression reference of cell types a, b and c, and then add their gene expression profiles up as the aggregated expression profile for this spot. To incorporate sequencing depth variation across spots, we simulate a spot-specific effect ${ϵ}_s$ for each spot $s$ from a Gamma distribution, ${ϵ}_s~𝓖\left(3,1\right)$, and multiply the aggregated expression level for each gene at spot $s$ by ${ϵ}_s$ to obtain the final ST expression level. The step-by-step protocol to generate synthetic ST data is given by Algorithm 4.

$$\overline{\underset{¯}{\begin{array}{l}\underset{¯}{\mathbf{\text{Algorithm 4}}\text{ Synthetic ST data generation}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Input the total numbers of genes (}G\text{), spots (}S\text{) and cell types (}K\text{) on a ST slide, the number of cells per spot}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(}N\text{), the maximum number of cell types per spot (}M\text{) and single-cell expression references}\hspace{0.17em}\hspace{0.17em}{\left\{{\mathbf{\text{Y}}}_k\right\}}_{k=1}^K\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}K\hspace{0.17em}\hspace{0.17em}\text{cell}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{types with}\hspace{0.17em}\hspace{0.17em}{\mathbf{\text{Y}}}_k=\left[Y_{ij}^k\right]\text{ and }{Y}_{ij}^k\hspace{0.17em}\hspace{0.17em}\text{indicating the single-cell expression level of gene }i\text{ in cell }j\text{ from cell type }k.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{for}}\text{ each spot }s\text{ = 1,2,}\dots \text{,}S \mathbf{\text{do}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(1) Randomly select an integer}\hspace{0.17em}\hspace{0.17em}{K}_s\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{between 1 and }M\text{ as the number of cell types at spot }s\text{.}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(2) Randomly select}\hspace{0.17em}\hspace{0.17em}{K}_s\hspace{0.17em}\hspace{0.17em}\text{different cell types from}\hspace{0.17em}\hspace{0.17em}\left\{\text{1,2,}\dots \text{,}K\right\},\text{denoted as}\hspace{0.17em}\hspace{0.17em}{K}_s.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(3) Generate the proportions for the}\hspace{0.17em}\hspace{0.17em}{K}_s\hspace{0.17em}\hspace{0.17em}\text{selected cell types at spot }s\text{ from a flat Dirichlet distribution and}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{set the proportions of remaining}\hspace{0.17em}\hspace{0.17em}K-K_s\hspace{0.17em}\hspace{0.17em}\text{cell types as 0}:{\left[{\pi }_{is}\right]}_{i\in {𝓚}_s}\sim {𝓓}_{K_s}\left(1,\dots 1\right)\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}{\pi }_{is}=0\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\hspace{0.17em}i\notin {𝓚}_s.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(4) Generate the number of cells from cell type }k\text{ at spot }s\text{ as}\hspace{0.17em}\hspace{0.17em}{n}_{ks}=\text{Round}\left(N{\pi }_{ks}\right),\hspace{0.17em}\hspace{0.17em}k=1,\dots ,K.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(5) Randomly select}\hspace{0.17em}\hspace{0.17em}{n}_{ks}\hspace{0.17em}\hspace{0.17em}\text{different cells for cell type }k\text{ from the single-cell expression reference}\hspace{0.17em}\hspace{0.17em}{\mathbf{\text{Y}}}_k,\text{denoted}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{as}\hspace{0.17em}\hspace{0.17em}{𝓛}_{ks},\hspace{0.17em}\text{and compute the aggregated expression level of gene }g\text{ for cell type }k\text{ at spot }s\text{ as}\hspace{0.17em}\hspace{0.17em}{\tilde{Y}}_{gks}={\sum }_{c\in L_{ks}}{Y}_{gc}.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(6) Generate the spot-level effect from a Gamma distribution:}\hspace{0.17em}\hspace{0.17em}{ϵ}_s\sim 𝓖\left(3,1\right).\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{(7) Generate the ST expression level of gene }g\text{ at spot }s\text{ as}\hspace{0.17em}\hspace{0.17em}{X}_{gs}={ϵ}_s{\sum }_{k=1}^K{\tilde{Y}}_{gks}.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{end for}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{return}}\hspace{0.17em}\hspace{0.17em}G\times S\hspace{0.17em}\hspace{0.17em}\text{ST data matrix}\hspace{0.17em}\hspace{0.17em}\mathbf{X}=\left[X_{gs}\right].\end{array}}}$$

To simulate ST data for this study, we applied Algorithm 4 to a mouse cerebellum scRNA-seq dataset ⁶ of 2505 genes and 26139 cells for 10 annotated cell types; see the next section for more details on this dataset. We selected 30 cells from each of the 10 cell types in this scRNA-seq dataset, based on the highest sum of single-cell expression levels across the 2505 genes. Next, we identified the 500 genes with the most variability across the 300 selected cells and used them to simulate three ST datasets with $G=500$ genes and $S=1000$ spots: (1) $N=10$ cells from up to $M=3$ of the $K=10$ cell types per spot (column 1 of Fig. 2); (2) $N=20$ cells from up to $M=5$ of the $K=10$ cell types per spot (column 2 of Fig. 2); (3) $N=10$ cells from up to $M=3$ of the $K=5$ ground-truth cell types per spot (columns 3–4 of Fig. 2) with the 5 ground-truth cell types being Bergmann glia, choroid plexus, endothelial, oligodendrocyte and Purkinje.

We used STdeconvolve and RETROFIT for reference-free deconvolution of simulated ST data. On each ST dataset, we ran STdeconvolve with the default setting. STdeconvolve determined the optimal $L=9$ for the first ST dataset $\left(K=10\right)$, $L=8$ for the second ST dataset $\left(K=10\right)$ and $L=7$ for the third ST dataset $\left(K=5\right)$. When running RETROFIT, we set $L=20$ for the first two ST datasets $\left(K=10\right)$ and $L=10$ for the third ST dataset $\left(K=5\right)$. On each ST dataset, we ran RETROFIT for $I=4000$ iterations. To map results of STdeconvolve and RETROFIT to ground-truth cell types, we created a cell-type-specific transcriptomic reference ${\mathbf{W}}^0=\left[W_{gk}^0\right]$ for the $𝓖$ genes and $K$ ground-truth cell types in each ST dataset, using the same scRNA-seq data ⁶ that produced the ST data. Specifically, we set $W_{gk}^0$ as the average scRNA-seq expression level of gene $g$ across the 30 cells from cell type $k$ that were used to simulate the ST data. We used this reference to annotate STdeconvolve results as previously described ¹⁵. We applied Algorithm 2 to the same reference to annotate RETROFIT results.

To perform reference-based deconvolution in simulations, we applied RCTD, SPOTlight, Stereoscope and NMFreg to each of the three simulated ST datasets. For the first two ST datasets, we used the exact scRNA-seq data ⁶ of the 10 ground-truth cell types that were used to simulate the ST data as the single-cell gene expression reference (columns 1–2 of Fig. 2). For the third ST dataset, we created two ‘imperfect’ references for the reference-based methods based on the same scRNA-seq dataset. Specifically, one reference contained 5 ground-truth and 5 irrelevant cell types (column 3 of Fig. 2), while the other reference contained only 3 of the 5 ground-truth cell types (absent: choroid plexus and oligodendrocyte) and 5 irrelevant cell types (column 4 of Fig. 2). When a ground-truth cell type was absent from the single-cell gene expression reference, all the reference-based methods were unable to estimate its proportion at each spot, and we set the estimate as zero.

We evaluated the performance of RETROFIT and 5 existing methods on the synthetic ST data as follows. Given a ST dataset, each method produced a proportion estimate of each cell type $k$ for each spot $s$: ${\tilde{\mathbf{H}}}_s=\left[{\tilde{H}}_{ks}\right]$. These estimates were used to reconstruct the ST expression profile for spot $s$ as ${\widetilde{\mathbf{\text{X}}}}_s={\mathbf{W}}^0{\tilde{\mathbf{H}}}_s$ with ${\mathbf{W}}^0$ being the cell-type-specific expression reference of $G$ genes for $K$ cell types as described above. We compared ${\tilde{\mathbf{H}}}_s$ with the true cell-type proportions at the same spot, ${\mathbf{H}}_s=\left[H_{ks}\right]$, by computing (1) their RMSE (Fig. 2a), defined as $\sqrt{K^{-1}{\sum }_{k=1}^K{\left(H_{ks}-{\tilde{H}}_{ks}\right)}^2}$ and (2) their Pearson correlation (Fig. 2b). Similarly, we compared ${\widetilde{\mathbf{\text{X}}}}_s$ with the true ST expression profile at the same spot, ${\mathbf{X}}_s=\left[X_{gs}\right]$, by computing (1) their normalized RMSE (Fig. 2c), defined as ${\text{SD}}^{-1}\left({\mathbf{X}}_s\right)\sqrt{G^{-1}{\sum }_{g=1}^G{\left(X_{gs}-{\tilde{X}}_{gs}\right)}^2}$ with $\text{SD}\left({\mathbf{X}}_s\right)$ being the standard deviation of ST expression levels across $G$ genes at spot $s$, and (2) their correlation (Fig. 2d). For both estimated cell-type proportions $\left(\tilde{\mathbf{H}}\right)$ and reconstructed gene expression levels $\left(\widetilde{\mathbf{\text{X}}}\right)$, lower RMSEs and higher correlations indicate better cell-type deconvolution results that are closer to and more concordant with the ground truth, respectively. To evaluate the cell-type specificity of RETROFIT-extracted components, we computed the correlation between the estimated $\left({\tilde{\mathbf{W}}}_k\right)$ and observed $\left({\mathbf{W}}_k^0\right)$ cell-type-specific expression levels across $G$ genes for each cell type $k$ (Fig. 2e), with a higher value indicating a better performance.

Mouse cerebellum data analysis

The mouse cerebellum study ⁶ provided Slide-seq data of 17919 genes at 27261 spots (https://singlecell.broadinstitute.org/single_cell/study/SCP354/slide-seq-study). This study also provided scRNA-seq data of 2505 genes from 26139 cells that were annotated as 10 cell types in the mouse cerebellum (astrocyte, Bergmann glia, choroid plexus, endothelial, granule, microglia, mural, oligodendrocyte, Purkinje and interneuron). We ran RCTD and Stereoscope on the Slide-seq and scRNA-seq data provided in this study. We ran STdeconvolve on the Slide-seq data only, created a cell-type-specific gene expression reference $\left({\mathbf{W}}^0\right)$ from the companion scRNA-seq data as described in our simulation studies, and then used this reference to match the extracted components with the most probable cell types in the mouse cerebellum. STdeconvolve determined the optimal number of latent components as $L=7$. The remaining details of using RCTD, Stereoscope and STdeconvolve were identical to those described in the previous section.

We used RETROFIT to analyze the mouse cerebellum Slide-seq data as follows. To ensure deconvolution accuracy and computation efficiency, we combined three complementary strategies to down-select genes before running RETROFIT. First, we selected 61 overdispersed genes with significantly higher-than-expected ST expression variances across spots ¹⁵ using the default setup of the STdeconvolve package. Second, we identified 54 cell-type-specific genes by computing entropy and Gini index on the companion scRNA-seq data (Supplementary Note 2). Third, we obtained 61 marker genes ³⁵ curated for 3 mouse brain cell types (granule: 15; oligodendrocyte: 4; Purkinje: 42) from NeuroExpresso (www.neuroexpresso.org; Supplementary Table 2). We took the union of these 3 gene lists and used the resulting 153 unique genes to construct the input ST data matrix $\left(\mathbf{X}\right)$ for RETROFIT. We then ran RETROFIT on the 153 × 27261 ST data matrix $\mathbf{X}$ with $I=5000$ iterations and $L=20$ latent components. To map the RETROFIT-extracted components to the 10 mouse brain cell types, we applied Algorithm 2 to the cell-type-specific gene expression reference $\left({\mathbf{W}}^0\right)$ from the companion scRNA-seq data as described in the previous section.

We evaluated the performance of 4 deconvolution methods on 3 mouse brain cell types (granule, oligodendrocyte, Purkinje) using curated marker genes available in NeuroExpresso ³⁵. Given a cell type $k$, we define the cell-type marker ST expression score at spot $s$ in a slide as

$$T_{ks}=\sum _{g\in {𝓜}_k}{X}_{gs},$$ (11)

where ${𝓜}_k$ denotes the list of marker genes for cell type $k$ and $X_{gs}$ denotes the ST expression level of gene $g$ at spot $s$. For each combination of the 4 methods and the 3 cell types, we computed the Pearson correlation between the observed cell-type marker ST expression scores $\left(\mathbf{\text{T}}\right)$ and the estimated cell-type proportions $\left(\tilde{\mathbf{H}}\right)$ across all spots. A higher correlation indicates a better performance.

Human intestine data analysis

The human intestine study ⁵ made available Visium ST data from 3 tissue slides, including a 12 PCW slide with 1080 spots, a 19 PCW slide with 1242 spots and an adult slide with 2649 spots, providing expression measurements for 33538 genes in each slide (https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE158328). The study provided H&E images of the ST slides (https://doi.org/10.17632/gncg57p5x9.2). This study also provided scRNA-seq data of 76592 cells from 77 intestinal samples spanning 8 to 22 PCW (https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE158702) that were grouped into 8 distinct cellular compartments (endothelial, epithelial, fibroblast, immune, muscle, MyoFB/MESO, neural, pericyte).

We used RETROFIT to analyze the human intestine Visium ST data as follows. Similar to our analysis of the mouse cerebellum Slide-seq data, we down-selected genes prior to running RETROFIT. Specifically, for each of the 3 ST slides, we only included (1) significantly overdispersed genes across spots ¹⁵ and (2) 37 known marker genes of the 8 cellular compartments (Fig. 6a) in the input ST data matrix $\left(\mathbf{X}\right)$ for RETROFIT, resulting in 722 genes for 12 PCW, 681 genes for 19 PCW and 1051 genes for adult. On each ST data matrix, we then ran RETROFIT with $I=4000$ iterations and $L=16$ latent components. To match RETROFIT-extracted components with the 8 intestinal compartments, we utilized Algorithm 3 together with the 37 known marker genes (Fig. 6a) curated in the human intestine study ⁵. For the 12 and 19 PCW slides, we also applied Algorithm 2 to annotate their RETROFIT results, using the compartment-specific gene expression reference $\left({\mathbf{W}}^0\right)$ generated from the companion scRNA-seq data of 12 and 19 PCW samples respectively. Specifically, for each fetal stage we selected 25 cells from each of the 8 compartments that resulted in the highest sum of single-cell expression levels across all genes, and then we set $W_{gk}^0$ as the average scRNA-seq expression level of gene $g$ across the 25 cells selected from compartment $k$. Unless otherwise specified, estimates of compartment proportion $\left(\tilde{\mathbf{H}}\right)$ and compartment-specific expression $\left(\tilde{\mathbf{W}}\right)$ for all 3 ST slides were generated with Algorithm 3.

For comparison, we also used STdeconvolve to perform reference-free deconvolution of the same human intestine ST data. Since the cell-type annotation step in STdeconvolve requires a cell-type-specific gene expression reference, we only ran STdeconvolve on the ST data of 12 and 19 PCW tissues that had companion scRNA-seq data available. For each ST slide we ran STdeconvolve with two different numbers of latent components (topics): $L=6$, which was determined by STdeconvolve, and $L=16$, which was used in RETROFIT. The remaining details of running STdeconvolve were the same as those described in previous sections.

To evaluate the accuracy of RETROFIT in estimating cellular compartment proportions $\left(\tilde{\mathbf{H}}\right)$, we computed the correlation between the ST expression scores of compartment-specific marker genes defined in Eq. (11) and the estimated compartment proportions across all spots for each of the 8 cellular compartments and 3 ST slides (Table 1; Fig.s 4c–d; Supplementary Fig.s 5–10).

To evaluate the accuracy of RETROFIT in estimating compartment-specific expression levels $\left(\tilde{\mathbf{W}}\right)$, we compared the compartment-specific expression levels estimated from 12 and 19 PCW ST slides with the compartment-specific expression levels based on the companion scRNA-seq data from 12 and 19 PCW intestinal samples $\left({\mathbf{W}}^0\right)$. To account for different scales of ST and scRNA-seq data, we first normalized rows of the two expression matrices ($\tilde{\mathbf{W}}$ and ${\mathbf{W}}^0$) by their sums as we did in Algorithm 2:

$${\tilde{W}}_{gk}^{\ast }=\frac{{\tilde{W}}_{gk}}{{\sum }_{j=1}^K{\tilde{W}}_{gj}},\hspace{1em}{W}_{gk}^{0\ast }=\frac{W_{gk}^0}{{\sum }_{j=1}^K{W}_{gj}^0},$$

and then compared the normalized expression matrices ${\tilde{\mathbf{W}}}^{\ast }=\left[{\tilde{W}}_{gk}^{\ast }\right]$ and ${\mathbf{W}}^{0\ast }=\left[W_{gk}^{0\ast }\right]$ in each of the 8 cellular compartments and 2 fetal stages (Fig.s 6a and c).

Based on the normalized cell-type-specific expression levels $\left({\tilde{\mathbf{W}}}^{\ast }\right)$ estimated by RETROFIT, we further developed a simple method to identify genes with high cell-type specificity. Given the normalized cell-type-specific expression estimates of gene $g$ for $K$ cell types $\left\{{\tilde{W}}_{g1}^{\ast },\dots ,{\tilde{W}}_{gK}^{\ast }\right\}$, we calculated two dispersion measures:

$$\text{entropy}\hspace{0.33em}{E}_g=-\sum _{k=1}^K{\tilde{W}}_{gk}^{\ast }{\log }_2\left({\tilde{W}}_{gk}^{\ast }\right),$$

$$\text{Gini}\hspace{0.33em}\text{index}\hspace{0.33em}{G}_g=\frac{{\sum }_{i=1}^K{\sum }_{j=1}^K\left|{\tilde{W}}_{gi}^{\ast }-{\tilde{W}}_{gj}^{\ast }\right|}{2\left(K-1\right){\sum }_{k=1}^K{\tilde{W}}_{gk}^{\ast }}.$$

Lower entropy and higher Gini index indicate an excess of normalized expression for one cell type, thus suggesting the cell-type specificity. In the human intestine data analysis, we identified a cell-type-specific gene $g$ from the ST data if this gene had (1) entropy $E_g<1.5$, (2) Gini index $G_g>0.85$, (3) maximum ST expression level ${\max }_s{X}_{gs}>40$ and (4) consistent cell-type specificity across all ST replicate samples (e.g., the same tissue type from the same developmental stage). We performed this analysis only on adult and 12 PCW stages (Fig. 6b), because they were the only stages with ST replicate samples available in the human intestine study ⁵ (Supplementary Tables 18–20), in addition to the ST samples used in our primary analysis (Fig. 4a).

To assess biological themes of cell-type-specific genes identified by RETROFIT (Fig. 6d; Supplementary Tables 21–22), we performed the gene set enrichment analysis using Metascape ³⁶ (https://metascape.org, version 3.5). Metascape calculates the enrichment P-values based on the cumulative hypergeometric distribution and then adjusts the P-values for multiple testing based on the Benjamini-Hochberg procedure.