Summary
Real-time pricing demand response programs (RTP-DRPs) are practical measures that ensure the end user’s profitability from using electricity by adjusting the supply and demand equilibrium without activating costly solutions. This study explores the potential of RTP-DRPs by developing and applying a region-wise modeling approach based on maximizing the end user’s social welfare in the wholesale electricity market in Japan. The regions of the wholesale market are classified based on their response into regions with excess supply, regions with high demand burden, and regular suppliers of inter-regional connections. The results revealed that the RTP-DRPs could potentially reduce the peak demand of the residential sector in Chubu, Chugoku, Kansai, Kyushu, Tokyo, and Tohoku by 1.91%–7.81%. Meanwhile, in Hokkaido, Hokuriku, and Shikoku, by 16.13%–22.9%. The avoided greenhouse emission (GHG) in Tokyo is estimated to be 82.6 and 192.2 tons in summer and winter, respectively.
Subject areas: Electrical system, Energy management, Energy policy
Graphical abstract

Highlights
-
•
Estimating elasticity matrix of demand considering regional wholesale prices
-
•
Integrated region-wise and price-based demand response modeling approach
-
•
Investigating the regional potential of avoided GHG emissions
Electrical system; Energy management; Energy policy
Introduction
Background
In Japan, electricity sector liberalization is one of the measures toward climate change and maximizing social welfare. This introduced several forms of electricity markets where the price varies based on the offered supply and demand biddings per time intervals. The dominant electricity price over other electricity markets is the wholesale market clearing price (MCP), which is the unique product of a double-blind auction among independent power producers, retailers, and demand aggregators. The wholesale biddings and market clearing mechanisms (MCM) are operated based on the microeconomic balance of the offered supply and demand patterns organized by the Japan Electric Power eXchange (JEPX) market. The JEPX arranges the offered supply bidding curve based on the price-quantity bids of the energy in ascending order, while the demand aggregators’ price-quantity bids curve is arranged in descending order.1 Sequentially, the MCM finds the cross-section between the two curves to be the MCP for the particular hour, as demonstrated in Figure 1.
Figure 1.
Conceptualization of the microeconomic MCM
On the other hand, the interconnected national grid is fragmented into nine regional grids, which are Chubu, Chugoku, Hokkaido, Hokuriku, Kansai, Kyushu, Shikoku, Tokyo, and Tohoku, as depicted in Figure 2. Each regional grid has an independent electric power utility, whereas it operates its own regional supply and demand resources.2 This produces nine regional MCPs as well as a nationwide MCP. Although the nationwide MCP applies to all energy transactions nationwide, the regional MCPs override it when the regional interconnections are employed to balance other regional supply and demand patterns. This can be justified due to the absence of a real-time frequency balancing market. Sequentially, the use of regional interconnections is a costly solution that produces numerous regional supply and demand equilibriums that fragment the MCM, which causes spatiotemporal price volatility.3
Figure 2.
National topology of the electricity grid
Alternatively, demand response (DR) can tackle the regional microeconomic supply-demand imbalance without the need for inter-regional connections in a cost-effective manner. The DR is the management measures to control the electricity demand during peaks, enhance energy efficiency, and reduce greenhouse gas emissions (GHG). Responding to the shortage of supply, electricity end users can be motivated to adjust their consumption, which can be reflected in the overall regional supply and demand equilibrium.4 The demand response programs (DRP) are implemented in Japan by electric utilities, demand aggregators, retailers, and governmental agencies.5 Currently, residential customers are billed with regulated prices (i.e., flat-rate tariffs) for their electricity consumption. Meanwhile, the government plans to install digital smart meters for countrywide households and apply the deregulated electricity prices to the residential sector are scheduled to be implemented by 2024.5 The viability of DRPs was validated by Tokyo Electric Power Company in the Tokyo power grid region for a few days in January 2018. The outcomes reported that DR has supported in critical management of supply-demand imbalance by preserving a capacity equivalent to a medium-sized thermal power plant, which demonstrates the potential capability of DRPs.6
The potential of demand response programs in Japan
The Japanese electricity sector has multiple initiatives to promote and investigate the viability of DRPs. The smart community program, launched in 2012, aims to encourage smart grid technologies adoption with the implementation of DRPs.7 Furthermore, the Japan Smart Community Alliance, established in 2010, promotes energy-saving technology by optimizing energy consumption through DRPs and energy management systems.8 On the wholesale electricity market scale, since 2017, demand aggregators have normally been bidding for negawatts contracts based on their customized DRPs.5
On the other hand, several contributions have developed various DRP modeling approaches oriented to the Japanese electricity market to evaluate the effectiveness of different DRPs and their policy implications.9 Rohman and Kobayashi have investigated the potential of DRP for peak reduction, considering outage scenarios in Japanese rural residential customers. To determine actual demand, the study applied load measurements on 18 households in Tsuru and 8 houses in Izu for a week in winter, spring, and summer. The results indicated that this scheme has the potential to decrease peak demand by 5.2%–10.2%.10 Mizutani et al. have explored the impact of DR on household behavior using the influence of a reference price effect, considering peak and off-peak periods. The findings revealed that households tend to decrease their consumption when the current price is higher than the previous, and vice versa. Furthermore, based on various DRPs, residential customers can reduce their consumption by an average of 4.7%–14% based on the implemented DRP. In addition,11 Li et al. have assessed the economic viability and technological benefits of demand-side management in residential buildings, focusing on analyzing critical peak pricing (CPP) impact on electricity conservation and distribution patterns among different types of end users in the Kitakyushu Smart Community Project.12 Malehmirchegini and Farzaneh have developed a mathematical modeling technique to maximize the welfare of residential end users in Japan’s wholesale market, considering a price-based DR mechanism. The model was applied to JEPX wholesale market, which found the potential reduction in peak demand for flexible customers in Tokyo using time-of-use (TOU) and real-time pricing (RTP) schemes are 7.3% and 10.7%, respectively. Furthermore, the RTP for curtailable loads can reduce the daily peak demand by 7.7% with a daily electricity consumption reduction of 1.6%.13 Lu et al. have developed a dynamic price DRP targeting the residential sector in Japan. The study collected consumption patterns of smart community and household surveys, whereas the obtained results have revealed that the air conditioner number, household income, family members number, and floor area are the major parameters affecting the DRP program. The developed DRP has the potential to reduce the residential demand by 7.8%–16.2% in the winter and 11.3%–13% in the summer.
However, based on the earlier contributions that have applied the DRPs in JEPX, it is observed that although the conducted studies have reported a high potential of DRPs to decrease the peak demand in the residential sector, it lacks correlating the amount of energy saved and peak demand reduction of end users considering the regions of the wholesale market. Therefore, this study aims to add a region-wise perspective to the earlier contributions. The region-wise evaluation in this study is considered by estimating the hourly price elasticity matrix of demand (PEMD) for each region precisely. Then, sequentially, the estimated regional PEMD will be substituted in the applied price-based RTP-DRP to realize the potential responses of each region in terms of energy saving, residential sector peak demand reduction, and GHG reduction.
Literature survey on demand response modeling approach in the wholesale electricity market
The DRPs in this study can be quantified into two main categories: price- or incentive-based programs. The price-based programs incentivize the end users to adjust their electricity usage by sending price signals, which include TOU, CPP, and RTP.14 The incentive-based programs are based on sending quantity signals to the end users to adjust their electricity usage of pre-identified load types based on time variation in return for incentives paid by the service provider. The former notifies the price signal to the end users to avoid consuming electricity at peak prices, while the latter incentives the end users to shift the consumptions out of peak time.15,16 This can further classify the methodological modeling approaches of DR applications into end-user scope and electricity market scope. Particularly, in the wholesale electricity market, the market participants of demand aggregation submit demand quantity-price bids in the form of negawatt contracts, which the market operator further employs to adjust the microeconomic equilibrium of the supply and demand quantities.17 In this context,18 Jing et al. have proposed the conceptual architecture of a blockchain-based negawatt trading platform to discuss two trading scenarios, involving negawatt trading between a demand response aggregator and buildings. The study highlighted the potential of building energy management units while maintaining occupant comfort requirements by considering double auction and game theory to calculate market clearing prices. Furthermore,19 Tushar et al. have comprehensively reviewed the prospects and challenges of negawatt trading considering the recent technological advancements. However, the earlier contributions either limit their investigation on the microeconomic equilibrium to formulate the biddings considering various market participants or explore the potential of a specific market form such as wholesale and real-time prices.
On the other hand, DRPs can participate in the real-time balancing market, in which the price of power is decided depending on the instantaneous balance between demand and supply patterns. In this context, several contributions have investigated the end user’s behavior toward considering real-time market prices.20 Furthermore, customer behavior toward the real-time retailer’s pricing scheme can be explored versus TOU,21 CPP,22 and RTP.23,24 Zhu et al. have applied the alternating direction method of multipliers algorithm with Gaussian back substitution to develop an RTP method in guiding customers' consumption behavior and cutting peaks, as well as the rationality and validity of the proposed algorithm.25 Hafeez et al. have proposed an optimization approach to manage the energy consumption in residential buildings using day-ahead demand response. The approach aimed to reduce consumer electricity bills by 23.90% and the peak-to-average ratio by 47.05% compared to the benchmark strategies. In the study by Hu et al.,26 a RTP-DRP was utilized to schedule energy consumption and balance the rising demand for energy with the available power supply. The primary objectives were to effectively manage the demand for energy in relation to power supply, leading to increased social welfare and decreased energy bills. Furthermore,27 Tostado-v et al. have proposed a day-ahead scheduling model for prosumers in energy communities, which takes into account energy transactions with different entities. The model addressed uncertainties using a stochastic-robust approach, considering both predictable and volatile parameters. The case study results have shown that storage assets play a vital role in reducing electricity bills by 86%, while the impact of uncertainties leads to an increase in monetary cost. The RTP-DRPs were further explored by Jordehi et al.,28 considering the operation of microgrids with dispatchable generators and wind turbines under uncertain demands and renewable power. The study modeled a two-stage stochastic optimization problem to minimize the expected operation cost considering the day-ahead and real-time decision variables.
The development of computational modeling methodologies necessitates examining the influence of customer participation in various DRPs on load management in a wholesale energy market. Several modeling approaches have been proposed in the literature to facilitate the implementation of demand response strategies in end-user applications. These include stochastic modeling,27,29 which can be used to predict energy consumption patterns based on historical data, and optimization modeling,30,31 which can be used to identify the most cost-effective demand response strategies for a given set of conditions. In the study by Hassan et al.,32 a dynamic electricity pricing system based on linear regression was developed to optimize the profit of customers (changeable and unchangeable) in an integrated DR sustainable microgrid using the particle swarm optimization (PSO) approach. In the study by Yu et al.,33 a dynamic economic model of DRPs was developed as a mix of incentive-based and price-based programs based on the benefit function concept of customers and flexible demand elasticity considering the quadratic benefit function. Table 1 presents an overview of demand response models developed in earlier contributions considering different scopes.
Table 1.
Summary of demand response models developed in the previous studies
| Reference | Category | Type | Domain | Scope |
|---|---|---|---|---|
| Moghimi et al.34 | Price based | RTP | Wholesale and retail electricity markets | Profit and social welfare of the distribution company |
| Parvania et al.35 | Price based | Load curtailment (LC) Load shifting (LS) Onsite generation (OG) Energy storage (ES) |
Wholesale energy markets | Aggregator benefit |
| Malehmirchegini et al.12 | Price based | RTP CPP TOU |
Wholesale electricity market | End-user welfare |
| Xu et al.20 | Hybrid DR mechanism (PB – IBDRPs) | Real-time pricing Real-time incentive |
Retailer market | User welfare Retailers’ profits |
| Wei et al.36 | Price based | RTP | Retailer market | Retailer’s profit |
| Cortés-Arcos et al.37 | Price based | RTP | Wholesale market | End user’s cost of electricity and dissatisfaction |
| Hafeez et al.38 | Price based | CPP RTP |
Wholesale market | Utility of end user and power company |
| Hafeez et al.39 | Price based | TOU RTP day-ahead pricing scheme (DAPS) |
Wholesale market | End-user comfort |
| Fan et al.40 | Price based | TOU | Retailer market | Social welfare of the distribution company |
| Javadi et al.41 | Price based | TOU RTP |
Wholesale market | End user’s discomfort |
| Vahid-Ghavidel et al.42 | Price based Incentive based |
TOU IBDRP |
Wholesale market | Aggregator profit |
| This study | Price based | RTP | Regionally fragmented wholesale market | End-user welfare using region-wise price elasticity matrix of demand |
Research gap and paper contributions
Based on the literature survey, several contributions have reported the significance of DRP in reducing the residential sector demand, which reflects the customer’s profitability from regulating their electricity demand. However, these contributions are either related to the negawatt microeconomic bidding mechanism or lack of correlation between the amount of energy saved and peak demand reduction of end users considering the regions of the wholesale market. On the other hand, although the earlier contributions have developed a sophisticated modeling approach to demonstrate the potential of DRPs considering multi-layer wholesale and real-time market forms, it lacks a fundamental exploration of determining the potential of fragmented regional wholesale markets. This can be explored through the region-wise evaluation, which estimates the PEMD of each regional market considering the microeconomic price-driving parameters of each region. Therefore, this study aims to investigate the potential of DRPs in the fragmented wholesale electricity market concerning the achieved peak reduction, energy saving, and GHG emission avoidance for each region. To achieve this, the study applies a single price-based RTP-DRP optimization model on various fragmented markets in different regions, considering the regional wholesale prices and using dedicatedly estimated PEMD for each market’s region.
Furthermore, in Japan, due to the absence of a real-time balancing market, the use of regional interconnections fragments the national supply and demand equilibrium, which causes region-wise MCMs and, consequently, regional MCPs. The study aims to explore DR programs’ potential to adjust the microeconomic balance by estimating the capability of each region to adjust the supply and demand equilibrium. The microeconomic equilibrium is considered in this study using the wholesale MCP for all the regions, along with estimating the region-wise PEMD. The outcome is expected to demonstrate the capability of each region to reduce its peak or maximize energy savings. To this aim, the study proposes integrating the customer profitability of the residential sector with the utility scale using a single price-based RTP-DRP optimization model for all the regions, while considering the microeconomic equilibrium of the regional wholesale prices through estimating the PEMD for each region dedicatedly. Therefore, this study investigates the region-wise potential of energy savings, peak shaving, and avoided GHG emissions from implementing a DRP on a region-wise scale considering the regions of the wholesale electricity market. Thus, the contribution of this study is 3-fold.
-
•
Formulating the PEMD for a regionally fragmented wholesale electricity market by estimating the self- and cross-price elasticity matrix of demand, considering spatial-temporal wholesale electricity prices and demand profiles.
-
•
Development of integrated region-wise and price-based demand response modeling approach based on applying customer welfare maximization in regionally fragmented wholesale electricity markets.
-
•
Investigating the region-wise potential benefits of peak reduction, energy savings, and avoided emissions from implementing the DRP in Japan’s wholesale electricity market.
The rest of the paper is organized as follows: first, data acquisition and model development are described, where regional hourly price elasticity of demand is estimated, customer welfare maximization DRP is modeled, and avoided emissions are calculated. In the following, the main results and findings are discussed.
The developed methodological approach is divided into three parts: 1) data acquisition, 2) modeling of price elasticity of demand, and 3) designing the price-based demand response program. The data are collected nationwide, covering all the regions of the wholesale market of Japan. The data include electricity demand, wholesale prices, temperatures, regional emission factors, and penetration of variable renewable energy (VRE). The price elasticity of demand is modeled in two milestones. Firstly, estimating the hourly self-elasticity for each region, and then, formulating the self- and cross-price elasticity matrix of demand. Eventually, the RTP-DRP to maximize the customer’s welfare is formulated, and avoided emissions are calculated. The overall research methodology in this paper is presented in Figure 3.
Figure 3.
Overall methodological approach
Results
Price elasticity of demand estimation
The estimated price elasticity of demand (PED) values and the risk aversion coefficients for all the regions depicted in Figure 4 can be elaborated based on three major parameters: hourly regional prices, supply and demand equilibrium, and penetration of the VRE. In addition, Figures 5 and 6 show the average regional prices and regional electricity patterns, respectively. Although the PED of all the regions, including the national dimension, varies hourly between −0.005 and −0.09, the PED of Hokkaido, Hokuriku, and Shikoku varies between −0.09 and −0.21. Meanwhile, the estimated risk aversion coefficients that evaluate end users’ willingness to engage in RTP-DRP vary in all the ranges and nationally in a similar range of 0.001–0.003. This means that the PED variation is not caused by the end-user side, but rather by the price-driving parameters of inter-regional connections, penetration of VRE, and the supply and demand equilibrium. For Hokkaido, the low electricity demand, the highest regional price, and the topology of the national grid that connects Hokkaido from the side of Tohoku only, drive the elasticity to the high ranges. For Hokuriku and Shikoku, although the supply patterns are higher than their demand patterns, their price is interdependent to Kansai reported by Rassi and Kanamura1, driving the PED to high levels. This is demonstrated by the negative patterns of the inter-regional connections between Hokuriku and Shikoku, which meets a positive pattern in Kansai, as depicted in Figure 6. This implies that Kansai imports electricity from these regions, whereby the demand is ranked the highest after Tokyo. Furthermore, the quantity produced of VRE in Hokkaido, Hokuriku, and Shikoku is the least among all the regions, whereas the estimated elasticities drop to the least between hours 11:00 and 14:00 when the penetration of the VRE is at the peak.
Figure 4.
Estimated hourly region-wise and national PED and risk aversion coefficient
Figure 5.
Region-wise hourly day-ahead market prices on an average basis (2016–2022)
Figure 6.
Region-wise and National Electricity Patterns from 2016 to 2022
(The hourly electricity demand and supply for all the regions participating in JEPX is collected from all the regional utilities43,44,45,46,47,48,49,50,51).
Regional implementation of the demand response program
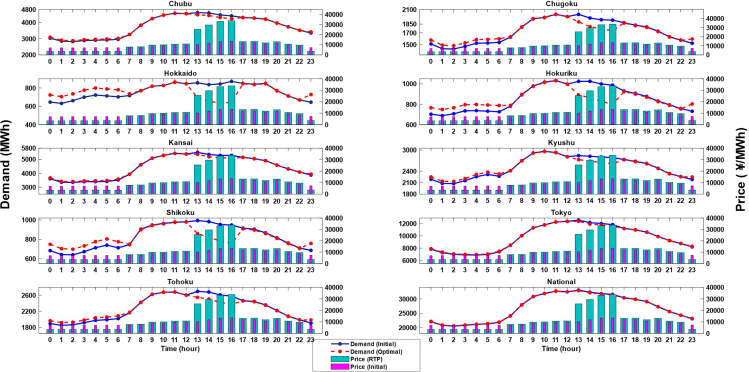
The resulting hourly demand loads after the RTP implementation on the shiftable residential loads are plotted for August 11th, 2021, and December 1st, 2021, in Figures 7 and 8, respectively. It can be observed that the price drops during valleys up to half of the initial price and increases during off-peaks and peaks to up to half and triple folds, respectively. This incentivizes the residential end users to shift their flexible loads to the valley period.
Figure 7.
Implementation of the RTP with the shiftable loads (11th August 2021)
Figure 8.
Implementation of the RTP with the shiftable loads (1st December 2021)
The results of the RTP-DRP implementation on the residential sector’s shiftable loads for the selected days in summer and winter for all the regions of Japan are shown in Table 2. For the selected summer and winter days, the implemented RTP-DRP can shave the peak of national demand of the residential sector by 0.54% during both seasons. Meanwhile, it can reduce the national energy consumption in the selected summer and winter days by 0.03% and 0.02%, respectively. On the other hand, implementing the developed RTP-DRP in different regions individually has the potential for reducing the peak demand of the residential sector ranging from 1.91% to 7.81% in winter and summer. Meanwhile, the peak reduction for the residential sector of Hokkaido, Hokuriku, and Shikoku varies between 16.13% and 22.9%. The obtained daily energy saving varies regionally between 0.16% and 1.02%.
Table 2.
Optimization results of the RTP-DRP
| Season | Region | Initial Electricity Consumption (MWh/day) | Optimized Electricity Consumption (MWh/day) | Electricity Saving (%) | Peak Reduction (%) | Load Factor Enhancement | Avoided GHG emission (kgCO2/kWh) |
|---|---|---|---|---|---|---|---|
| Summer | Chubu | 90,588 | 90,361 | 0.25 | 3.43 | 0.5 | 86,767 |
| Chugoku | 41,524 | 41,374 | 0.36 | 7.81 | −0.23 | 77,973 | |
| Hokkaido | 18,372 | 18,210 | 0.88 | 22.93 | 0.03 | 89,051 | |
| Hokuriku | 20,605 | 20,412 | 0.94 | 16.13 | −0.66 | 89,825 | |
| Kansai | 107,126 | 106,874 | 0.24 | 3.16 | 0.88 | 67,208 | |
| Kyushu | 60,212 | 60,090 | 0.20 | 4.83 | −0.05 | 44,720 | |
| Shikoku | 19,859 | 19,656 | 1.02 | 16.96 | 0.44 | 106,477 | |
| Tokyo | 233,920 | 233,534 | 0.16 | 1.91 | 1.13 | 174,332 | |
| Tohoku | 54,662 | 54,466 | 0.36 | 6.73 | 0.16 | 89,732 | |
| National | 646,870 | 646,624 | 0.04 | 0.54 | 0.34 | 107,998 | |
| Winter | Chubu | 105,834 | 105,662 | 0.16 | 3.45 | 0.01 | 65,460 |
| Chugoku | 48,406 | 48,286 | 0.25 | 7.86 | 0.13 | 62,525 | |
| Hokkaido | 23,940 | 23,836 | 0.43 | 22.99 | 0.09 | 56,982 | |
| Hokuriku | 24,068 | 23,926 | 0.59 | 16.19 | 0.07 | 65,802 | |
| Kansai | 110,663 | 110,479 | 0.17 | 3.17 | −0.01 | 49,037 | |
| Kyushu | 68,671 | 68,563 | 0.16 | 4.86 | 0.13 | 39,310 | |
| Shikoku | 21,643 | 21,518 | 0.58 | 17.07 | 0.28 | 65,640 | |
| Tokyo | 209,458 | 209,292 | 0.08 | 1.92 | −0.002 | 74,951 | |
| Tohoku | 64,889 | 64,743 | 0.23 | 6.77 | 0.33 | 67,056 | |
| National | 710,448 | 710,319 | 0.02 | 0.54 | −0.002 | 56,719 |
The findings indicate that the load factor has been enhanced in all the regions, emphasizing a lower performance for Chugoku, Hokuriku, Kyushu, and Kansai during summer. This can be attributed to the daily load profile of these regions, which peaks between 10:00 and 12:00, as depicted in Figure 9.
Figure 9.
Hourly load profiles for each region on an average basis (2016–2022)
Figure 10 shows the peak-to-valley ratio that measures the demand peak to the valley in summer and winter for all the regions. All the regions have shown remarkable peak-to-valley improvements, yet Hokkaido, during the winter, has shown lower performance in the peak-to-valley metric. This can be justified by the nature of the RTP-DRP, which is formulated to reduce the national peak demand by shifting it to the valley period. However, due to the unique climate nature of Hokkaido, where the temperature during the winter decreases to −8, shifting the peak demand to the valley has shown an extra burden to the existing loading of heating appliances. In other words, the fact that more demand reduction occurs during the designated peak periods, resulting in a lower minimum demand than the initial demand, leads to a higher peak-to-valley ratio compared to the initial ratio. On the other hand, Tokyo has shown substantial improvement in the peak-to-valley ratio during winter, demonstrating the efficiency of the developed RTP-DRP since Tokyo dominates around 32% of the national demand.
Figure 10.
Region-wise peak-to-valley ratio improvement
(A) Summer.
(B) Winter.
Estimating the regional avoided GHG emission
The avoided emissions of each region are calculated based on the regional energy saved from the implementation of the RTP-DRP. Figure 11 shows the region-wise avoided emissions in summer and winter. During summer, Tokyo has avoided emissions of 82.6 and 192.2 (TonCO2e) in summer and winter, respectively, which is the highest compared to the rest of the regions. This is justified due to the highest demand in Tokyo, which is the highest demand reduction consequently. In the winter, even though Chubu and Kansai have the highest demand reduction, Tokyo is still considered the region with the highest avoided emissions resulting from the demand amount and the emissions factors.
Figure 11.
Region-wise GHG emission reduction
(A) Summer.
(B) Winter.
Region-wise evaluation of price-based demand response program
Figure 12 shows the major output indices of the implemented RTP-DRP along with the topological connections of the national electricity grid. This can be classified based on the supply and demand equilibrium, VRE penetration, and regional prices into three categories; regions with excess supply, regions with high demand burden, and regular suppliers of inter-regional connections. Kyushu is a region with excess supply that is the richest VRE region with 15.52% penetration to the local demand of 9.79 GWh in the period of 2016–2022, whereby this implies that Kyushu, on average, produces 1.52 GWh per hour. In addition, the price in Kyushu is the least among the other regions. Given this, its response to the energy savings and peak reduction of the RTP-DRP is the least. On the other hand, Tokyo and Kansai are regions with a high demand burden and low supply resources, whereby their response to the developed RTP-DRP is high. This implies that their local utilities can avoid importing around 0.82 GWh and 0.66 GWh during the peaks from the inter-regional connections, respectively. Chugoku, Hokuriku, and Shikoku are regular suppliers of inter-regional connections for Kansai, which have a moderate response to energy savings and peak reduction of the RTP-DRP. It can be further elaborated that Chugoku, Hokuriku, and Shikoku utilities can take advantage of the end-user response to maximize their profits by trading in Kansai, where the price is higher during the supply shortage periods. However, although Tohoku can be classified as a region with excess supply, it has a high response to RTP-DRP. This is due to the high demand burden of its neighboring regions, whereas during the peaks, its response to the RTP-DRP is very high, considering the local demand and the price interdependency between Tohoku and Tokyo. Similarly, Hokkaido is a region with high demand burden (i.e., resulting in low supply capacity), the highest average price, low VRE penetration, and positive inter-regional connection patterns influencing the estimated PED to be the highest. Consequently, it has high energy saving and peak reduction response, considering the small amount of demand.
Figure 12.
Region-wise performance map of the RTP-DRP Figure Time schedules of the price elasticity matrix of demand
Discussion
The demand response programs can potentially adjust the supply and demand imbalance cost-effectively. In this work, a mathematical modeling technique focused on maximizing the customer’s welfare was implemented, taking into account an RTP scheme in Japan’s wholesale market. The region-wise impact of the wholesale electricity market was explored by formulating the price elasticity matrix of demand for each region dedicatedly, while applying a single mathematical modeling technique of the customer’s welfare to all the regions similarly. The region-wise price elasticity matrix of demand was formulated by estimating the hourly self and cross-price elasticities, considering the flexibility of consumers. Furthermore, the region-wise self-elasticity was calculated using two stages of econometrics, which estimate the regional wholesale price based on the VRE penetration and then evaluate the self-PED. The developed model was then applied to investigate the region-wise potential benefits (peak reduction, energy savings, and avoided emissions) of implementing the RTP-DRP in Japan’s wholesale electricity market.
The obtained results indicate a wide variation range of the hourly estimated region-wise PED of −0.005 to −0.21. Meanwhile, the estimated risk aversion coefficients that evaluate end users’ willingness to engage in RTP-DRP vary in all the ranges in a similar range of 0.001–0.003. This implies that the PED variation is not caused by the end-user side, but rather by the price-driving parameters of supply and demand microeconomic equilibrium. In addition, given the application of similar RTP-DRP to all the regions, the potential for daily peak reduction of the residential sector considering flexible customers and shiftable load varies between 1.91% and 22.9%. The energy saved from the developed RTP-DRP for all regions varies between 0.16% and 1.02%. On the other hand, the potential avoided GHG emissions resulting from the proposed program in the Tokyo region are remarkable, with values of 82.6 and 192.2 (TonCO2e) in the summer and winter, respectively.
The crucial observation from implementing the proposed RTP-DRP in all the regions is that each region has a specific characteristic in terms of the supply-demand equilibrium, wholesale prices, VRE penetration, and load profiles. This has been reflected in the regional responses toward the implemented RTP-DRP, which have been classified into three categories; regions with excess supply, regions with high demand burden, and regular suppliers to the inter-regional connections. The estimated PEMD has shown high elasticity indices for Hokkaido, Hokuriku, and Shikoku, which have been justified by the increased wholesale price considering their VRE penetration and the dependency on the inter-regional connections.
The future work of this study can evaluate the effective interaction approaches between service providers and end users in the demand-responsive market that uses incentives. This can be formulated to target each region, specifically considering the supply-demand equilibrium, wholesale prices, VRE penetration, and load profiles. Furthermore, the impact of the gross regional product, population, demographics, and gross inland energy consumption on price elasticity can be considered for further analysis using distinct PEM. On the other hand, the region-wise evaluation can further be investigated considering the interaction of DRPs, and supply resources aggregation through regional bidding strategies using virtual power plants.
Limitations of the study
This modeling bears potential limitations in using similar relationships among service providers and end users in the demand-responsive market of various regions. However, emphasizing the potential of adjusting the supply and demand imbalance cost-effectively in the different areas proposed in this study leads to a new formulation to target each region, with specific consideration for the regional supply-demand equilibrium, wholesale prices, VRE penetration, and load profiles.
STAR★Methods
Key resources table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Software and algorithms | ||
| Linear panel regression using Fixed Effect (FE) and Two Stage Least Squares (2SLS) using RStudio software | This paper | https://posit.co/download/rstudio-desktop/https://cran.r-project.org/ |
| Optimization utilizing the MINOS solver of GAMS (General Algebraic Modeling System) software | This paper | https://www.gams.com/ |
Resource availability
Lead contact
Further information and requests for resources and materials should be directed to and will be fulfilled by the lead contact, Dr. Hooman Farzaneh (farzaneh.hooman.961@m.kyushu-u.ac.jp (H. Farzaneh)).
Materials availability
No materials were used in this study.
Method details
Formulating the nationwide price elasticity matrix of demand
The price elasticity of demand is a crucial parameter for formulating DRP, which measures the degree of demand quantity response to the price change. The direct impact of changing the pricing on the demand quantity at the same hour is named self-elasticity, while the reflection resulting from the price change of this hour to the other hours is named cross-elasticity. This study estimates the national self-elasticity coefficient indicating the direct impact of price changes by one ¥/kWh on the quantity of demand. Sequentially, the price elasticity matrix of demand is formulated based on the obtained self-elasticity and calculating the cross elasticity. The study applies linear panel regression using Fixed Effect (FE) and Two Stage Least Squares (2SLS) to model the effect of regional cross-section dimension against the time.54 The price is estimated in the first stage of the 2SLS based on the VRE penetration to the demand, while the PED is estimated in the second stage.55 The first stage is expressed in Equation 1:
| (Equation 1) |
Where is the dependent variable of regional wholesale price in a vector of . , d, and denote the regional cross-section panels (i.e., the nationwide wholesale regions depicted in Figure 6), timing dummy variables, and hourly intervals, respectively. is the panel’s vertical time intervals from 2016 to 2022, which forms 52,560 observations for one panel of . For all the regions, the total observations number = 525,600 records of data. are the VRE electricity capacities assigned as independent variables. are the timing dummy variables. are the first stage estimates coefficients. is the error value of the first stage, which captures the unobserved effect of the regional cross-sections . is the idiosyncratic error, which captures the variation across and . The first-stage consistency is validated orthogonally versus the second-stage equation’s idiosyncratic error based on strict exogeneity conditions. The estimated price, , based on VRE contribution, is then substituted into the second stage equation of estimating the self-PED as expressed in Equation 2.
| (Equation 2) |
Where is the dependent variable of regional demand quantity in a vector of . are the temperature and lagged demand values assigned as the second-stage independent variable. are the timing dummy variables indicating weekend, hour of the day, and seasonality, respectively. denotes the second stage estimates coefficients. is the second stage error value, which captures the unobserved effect of the regional cross-sections . is the idiosyncratic error, which captures the variation across and . Sequentially, the hourly self-elasticity in percent is calculated for each region using the estimated PED coefficient, , as expressed using Equation 3.56:
| (Equation 3) |
Where is the self PED for region at hour . is the average hourly wholesale price for each region. is the average regional demanded quantity per hour.
Figure demonstrates the formulated matrix based on self and cross-elasticity dimensions to formulate the demand elasticity matrix for the flexible end-users. In Figure, the vertical and horizontal axis represent the hourly time intervals, while the diagonal axis presents the self-elasticity values. The values upper and lower regions of the diagonal axis are the cross-elasticity values, which indicate how much one variable is affected by changes in other variables. Furthermore, it is assumed only 5% of self-elasticity in each column is assigned to peak hours, and the share of the shifted demand in off-peak and valley periods accounts for 95%.
Modeling of demand response program
The DRPs are classified into incentive-based and Price-based programs. The price-based program seeks to flatten the load by varying consumer electricity costs at specific periods. This study applies a price-based RTP-DRP that relies on dynamic pricing to encourage end-users to respond promptly by reducing their power consumption at specific periods of the day.4 The prime aspect of designing nation-scale RTP-DRP is ensuring equal benefits for the utility sector as a service provider and customers as end-users. Therefore, it is crucial to determine the end-users willingness based on their behavior patterns toward the RTP-DRP; meanwhile, maximizing the service provider profits. This can be done by identifying the price-responsive customers for the RTP-DRP to estimate the cost savings on electricity and energy quantity reduced during high-demand periods. This study explores the customer’s welfare function as a combination of the customer’s expected utility function and the cost of electricity. The customer’s economic consumption model is formulated by subtracting the cost of electricity from their utility function to determine changes in their demand based on their participation in the RTP-DRP. The maximization of customer’s welfare in regional wholesale electricity may be formulated as follows12,33:
| (Equation 4) |
Where is the customer’s welfare resulting from the adjusted demand, , after implementing the proposed DRP. This is divided into the expected utility and cost incurred by consuming electricity. is the expected utility function, and is the suggested new price in the RTP scheme implemented by the proposed DRP. is the calibration coefficient that aligns the utility function unit from "Utils" to the monetary unit.57 denotes daily time intervals in hours, and denotes the regional indices.
The welfare’s function is maximized considering the constraints of the customer’s demand changes as expressed in Equation 5:
| (Equation 5) |
Where is the initial demand before participation in the RTP-DRP. and are self and cross PED coefficients, respectively. and are employed to calculate the change in electricity use in relation to the change in electricity price before and after RTP-DRP, as denoted by and , respectively.
The utility function, , models the satisfaction of the end-user from utilizing electricity, which is influenced by consumption patterns at various times of the day. This is formulated in an exponential form as expressed in Equation 6.58,59
| (Equation 6) |
Where is the risk aversion parameter that evaluates the end-user’s willingness to engage in the proposed RTP-DRP. The risk attitude of the end-user is intimately connected to the exponential curvature of the utility function, as explained in.60 and are the mean and variance of electricity consumption.61 The RTP scheme constraints is conditioned as expressed in Equation 7:
| (Equation 7) |
Where is the optimal RTP. and are the minimum and maximum RTP boundaries, respectively. The price-changing mechanism for the RTP scheme in this study is formulated based on the peak hours as expressed in condition (8), off-peak hours as expressed in Equation 9, and valley as expressed in Equation 10:
| (Equation 8) |
| (Equation 9) |
| (Equation 10) |
Where and are the wholesale price and RTP, respectively.
The model was performed, utilizing the MINOS solver of GAMS (General Algebraic Modeling System) software, which uses the Lagrangian project algorithm by solving subproblems, involving linear versions of the nonlinear constraints, as well as the original linear constraints and bounds to satisfy the optimality criterion of the developed model in this research.62
GHG emissions reduction
The electricity market in Japan is a significant source of GHG emissions, whereby the power sector accounts for about a third of total national GHG emissions.63 In this study, the potential of avoided emissions stems from the demand reduced by the implemented RTP-DRP. The mathematical formulation of the avoided GHG emissions considering the dedicated regional emission factor is expressed in Equation 11.
| (Equation 11) |
Where is the avoided CO2 emission for region . is the CO2 emission factor. is the total daily demand reduced after implementing the proposed DRP in each region.
Acknowledgments
The authors wish to thank the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan for providing the doctoral program scholarship to Ladan Malehmirchegini and Mohamed Saad Suliman.
Author contributions
L.M.: Conceptualization, Methodology, Data collection, Software, Investigation, Writing-Reviewing and Editing. M.S.S.: Conceptualization, Methodology, Data collection, Software, Investigation, Writing-Reviewing and Editing. H.F.: Conceptualization, Methodology, Writing-Reviewing and Editing, Supervision.
Declaration of interests
The authors declare no competing interests.
Published: May 30, 2023
Data and code availability
The hourly electricity prices from the period of 2016–2022 are collected for all regions in half-hourly intervals.5 The hourly electricity demand for all the regions participating in JEPX is collected from all the regional utilities.43,44,45,46,47,48,49,50,51 The collected demand capacity is lumped in regional demand. The share of the residential sector from the regional demand is assumed to be 27%.52 In addition, the amount of VRE (i.e., the sum of solar PV and wind power) are collected regionally for the same period. To align the half-hourly time intervals of prices with the demand and VRE quantities, the price intervals were converted using the weighted average and the market contracted volume. On the other hand, the CO2 emissions factors (i.e., for thermal electricity generation including coal, crude oil, liquefied natural gas, and biomass) per kWh for all the regions are collected from the electricity utilities∗, as shown in Table below. The hourly temperatures of the major cities in the regions (i.e., Hiroshima, Matsuyama, Sapporo, Nagano, Fukuoka, Nîgata, Osaka, Yamagata, and Tokyo) were acquired for the same period from.53
| Region | Emissions Factora (Kg-CO2/kWh) | Region | Emissions Factor (Kg-CO2/kWh) |
|---|---|---|---|
| Chubu | 0.382 | Kyushu | 0.365 |
| Chugoku | 0.521 | Shikoku | 0.525 |
| Hokkaido | 0.549 | Tokyo | 0.452 |
| Hokuriku | 0.465 | Tohoku | 0.457 |
| Kansai | 0.266 | National | 0.439 |
Annual average emission factor for the fossil-based powerplants, including was-to-electricity and biomass power.
References
- 1.Rassi S., Kanamura T. Electricity price spike formation and LNG prices effect under gross bidding scheme in JEPX. Energy Pol. 2023;177:113552. doi: 10.1016/j.enpol.2023.113552. [DOI] [Google Scholar]
- 2.JEPIC . Japan Electr. Power Inf. Center, Inc; 2020. The Electric Power Industry in Japan 2020.https://www.jepic.or.jp/en/data/epijpdf.html [Google Scholar]
- 3.Suliman M.S., Farzaneh H. Econometric analysis of pricing and energy policy regulations in Japan electric power exchange spot market. Cleaner Engineering and Technology. 2022;9:100523. doi: 10.1016/j.clet.2022.100523. [DOI] [Google Scholar]
- 4.Farzaneh H., Malehmirchegini L., Bejan A., Afolabi T., Mulumba A., Daka P.P. Artificial intelligence evolution in smart buildings for energy efficiency. Appl. Sci. 2021;11:763–826. doi: 10.3390/app11020763. [DOI] [Google Scholar]
- 5.Japan Electric Power Information Center . 2022. The Electric Power Industry in Japan 2022. Executive Summary.https://www.jepic.or.jp/en/data/pdf/epijJepic2022.pdf [Google Scholar]
- 6.Yorita Y. 1–17. 2018. https://eneken.ieej.or.jp/data/8003.pdf (Recent Developments in Virtual Power Plants and Demand Response). [Google Scholar]
- 7.Electricity Review Japan. The Federation of Electric Power Companies of Japan; 2016. pp. 1–15.https://www.fepc.or.jp/english/library/electricity_eview_japan/__icsFiles/afieldfile/2016/08/24/2016ERJ_full.pdf The Ten Electric Power Companies by Main Service Area. [Google Scholar]
- 8.Japan Smart Community Alliance (JSCA) 2015. Smart community-Japan’s Experience.https://www.smart-japan.org/english/vcms_lf/Resources/JSCApamphlet_eng_web.pdf [Google Scholar]
- 9.Rohman A., Kobayashi H. Estimation on possibility and capacity of residential peak electricity demand reduction by demand response scenario in rural areas of Japan. Energy Proc. 2014;61:887–890. [Google Scholar]
- 10.Mizutani F., Tanaka T., Nakamura E. The effect of demand response on electricity consumption under the existence of the reference price effect: evidence from a dynamic pricing experiment in Japan. Electr. J. 2018;31:16–22. [Google Scholar]
- 11.Li Y., Gao W., Ruan Y., Ushifusa Y. Demand response of customers in Kitakyushu smart community project to critical peak pricing of electricity. Energy Build. 2018;168:251–260. doi: 10.1016/j.enbuild.2018.03.029. [DOI] [Google Scholar]
- 12.Malehmirchegini L., Farzaneh H. Demand response modeling in a day-ahead wholesale electricity market in Japan, considering the impact of customer risk aversion and dynamic price elasticity of demand. Energy Rep. 2022;8:11910–11926. doi: 10.1016/j.egyr.2022.09.027. [DOI] [Google Scholar]
- 13.Lu Y., Gao W., Kuroki S., Ge J. Household characteristics and electricity end-use under dynamic pricing in the collective housing complex of a Japanese smart community. J. Asian Architect. Build Eng. 2022;21:2564–2579. doi: 10.1080/13467581.2021.1987244. [DOI] [Google Scholar]
- 14.Ida T., Murakami K., Tanaka M. Electricity demand response in Japan: experimental evidence from a residential photovoltaic power-generation system. Economics of Energy & Environmental Policy. 2016;5:73–88. https://www.jstor.org/stable/26189399 [Google Scholar]
- 15.Malehmirchegini L., Farzaneh H. Incentive-based demand response modeling in a day-ahead wholesale electricity market in Japan, considering the impact of customer satisfaction on social welfare and profitability. Sustainable Energy, Grids and Networks. 2023;34:101044. doi: 10.1016/j.segan.2023.101044. [DOI] [Google Scholar]
- 16.Dranka G.G., Ferreira P. Review and assessment of the different categories of demand response potentials. Energy. 2019;179:280–294. doi: 10.1016/j.energy.2019.05.009. [DOI] [Google Scholar]
- 17.Azim M.I., Tushar W., Saha T.K., Yuen C., Smith D. Peer-to-peer kilowatt and negawatt trading: a review of challenges and recent advances in distribution networks. Renew. Sustain. Energy Rev. 2022;169:112908. doi: 10.1016/j.rser.2022.112908. [DOI] [Google Scholar]
- 18.Jing Z., Pipattanasomporn M., Rahman S. Blockchain-based negawatt trading platform: conceptual architecture and case studies. IEEE PES GTD Gd Int Conf Expo Asia, GTD Asia. 2019:68–73. doi: 10.1109/GTDAsia.2019.8715890. [DOI] [Google Scholar]
- 19.Tushar W., Saha T.K., Yuen C., Smith D., Ashworth P., Poor H.V., Basnet S. Challenges and prospects for negawatt trading in light of recent technological developments. Nat. Energy. 2020;5:834–841. [Google Scholar]
- 20.Xu B., Wang J., Guo M., Lu J., Li G., Han L. A hybrid demand response mechanism based on real-time incentive and real-time pricing. Energy. 2021;231:120940. doi: 10.1016/j.energy.2021.120940. [DOI] [Google Scholar]
- 21.Kamyab F., Bahrami S. Efficient operation of energy hubs in time-of-use and dynamic pricing electricity markets. Energy. 2016;106:343–355. doi: 10.1016/j.energy.2016.03.074. [DOI] [Google Scholar]
- 22.Chen W., Qiu J., Chai Q. Customized critical peak rebate pricing mechanism for virtual power plants. IEEE Trans. Sustain. Energy. 2021;12:2169–2183. doi: 10.1109/TSTE.2021.3084211. [DOI] [Google Scholar]
- 23.Yang J., Zhang G., Ma K. Matching supply with demand: a power control and real time pricing approach. Int. J. Electr. Power Energy Syst. 2014;61:111–117. doi: 10.1016/j.ijepes.2014.03.014. [DOI] [Google Scholar]
- 24.Zhu H., Gao Y., Hou Y. Real-time pricing for demand response in smart grid based on alternating direction method of multipliers. Math. Probl Eng. 2018;2018:1–10. doi: 10.1155/2018/8760575. [DOI] [Google Scholar]
- 25.Hafeez G., Alimgeer K.S., Wadud Z., Khan I., Usman M., Qazi A.B., Khan F.A. An innovative optimization strategy for efficient energy management with day-ahead demand response signal and energy consumption forecasting in smart grid using artificial neural network. IEEE Access. 2020;8:84415–84433. doi: 10.1109/ACCESS.2020.2989316. [DOI] [Google Scholar]
- 26.Hu M., Xiao J.W., Cui S.C., Wang Y.W. Electrical Power and Energy Systems Distributed real-time demand response for energy management scheduling in smart grid. Electr Power Energy Syst. 2018;99:233–245. doi: 10.1016/j.ijepes.2018.01.016. [DOI] [Google Scholar]
- 27.Tostado-v M., Rezaee A., Icaza D., Amir S., Jurado F. Vol. 147. 2023. (International Journal of Electrical Power and Energy Systems . Optimal Participation of Prosumers in Energy Communities through a Novel Stochastic-Robust Day-Ahead Scheduling Model). [DOI] [Google Scholar]
- 28.Jordehi A.R., Tabar V.S., Mansouri S.A., Sheidaei F., Ahmarinejad A., Pirouzi S. Two-stage stochastic programming for scheduling microgrids with high wind penetration including fast demand response providers and fast-start generators. Sustain Energy, Grids Networks. 2022;31:100694. doi: 10.1016/j.segan.2022.100694. [DOI] [Google Scholar]
- 29.Mansourshoar P., Yazdankhah A.S., Vatanpour M., Mohammadi-Ivatloo B. Impact of implementing a price-based demand response program on the system reliability in security-constrained unit commitment problem coupled with wind farms in the presence of contingencies. Energy. 2022;255:124333. doi: 10.1016/j.energy.2022.124333. [DOI] [Google Scholar]
- 30.Derakhshan G., Shayanfar H.A., Kazemi A. The optimization of demand response programs in smart grids. Energy Pol. 2016;94:295–306. doi: 10.1016/j.enpol.2016.04.009. [DOI] [Google Scholar]
- 31.Honarmand H.A., Rashid S.M. A sustainable framework for long-term planning of the smart energy hub in the presence of renewable energy sources, energy storage systems and demand response program. J. Energy Storage. 2022;52:105009. doi: 10.1016/j.est.2022.105009. [DOI] [Google Scholar]
- 32.Hassan M.A.S., Assad U., Farooq U., Kabir A., Khan M.Z., Bukhari S.S.H., Jaffri Z.U.A., Oláh J., Popp J. Dynamic price-based demand response through linear regression for microgrids with renewable energy resources. Energies. 2022;15:1385–1417. doi: 10.3390/en15041385. [DOI] [Google Scholar]
- 33.Yu D., Xu X., Dong M., Nojavan S., Jermsittiparsert K., Abdollahi A., Aalami H.A., Pashaei-Didani H. Modeling and prioritizing dynamic demand response programs in the electricity markets. Sustain. Cities Soc. 2020;53:101921. doi: 10.1016/j.scs.2019.101921. [DOI] [Google Scholar]
- 34.Moghimi F.H., Barforoushi T. A short-term decision-making model for a price-maker distribution company in wholesale and retail electricity markets considering demand response and real-time pricing. Int. J. Electr. Power Energy Syst. 2020;117:105701. doi: 10.1016/j.ijepes.2019.105701. [DOI] [Google Scholar]
- 35.Parvania M., Fotuhi-Firuzabad M., Shahidehpour M. Optimal demand response aggregation in wholesale electricity markets. IEEE Trans. Smart Grid. 2013;4:1957–1965. doi: 10.1109/TSG.2013.2257894. [DOI] [Google Scholar]
- 36.Wei W., Liu F., Mei S. Energy pricing and dispatch for smart grid retailers under demand response and market price uncertainty. IEEE Trans. Smart Grid. 2015;6:1364–1374. doi: 10.1109/TSG.2014.2376522. [DOI] [Google Scholar]
- 37.Cortés-Arcos T., Bernal-Agustín J.L., Dufo-López R., Lujano-Rojas J.M., Contreras J. Multi-objective demand response to real-time prices (RTP) using a task scheduling methodology. Energy. 2017;138:19–31. doi: 10.1016/j.energy.2017.07.056. [DOI] [Google Scholar]
- 38.Hafeez G., Islam N., Ali A., Ahmad S., Alimgeer M.S. A modular framework for optimal load scheduling under price-based demand response scheme in smart grid. Processes. 2019;7:499. doi: 10.3390/pr7080499. [DOI] [Google Scholar]
- 39.Hafeez G., Wadud Z., Khan I.U., Khan I., Shafiq Z., Usman M., Khan M.U.A. Efficient energy management of IoT-enabled smart homes under price-based demand response program in smart grid. Sensors. 2020;20:3155. doi: 10.3390/s20113155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Fan S., Ai Q., Piao L. Bargaining-based cooperative energy trading for distribution company and demand response. Appl. Energy. 2018;226:469–482. doi: 10.1016/j.apenergy.2018.05.095. [DOI] [Google Scholar]
- 41.Javadi M.S., Nezhad A.E., Nardelli P.H., Gough M., Lotfi M., Santos S., Catalão J.P. Self-scheduling model for home energy management systems considering the end-users discomfort index within price-based demand response programs. Sustain. Cities Soc. 2021;68:102792. doi: 10.1016/j.scs.2021.102792. [DOI] [Google Scholar]
- 42.Vahid-Ghavidel M., Javadi M.S., Santos S.F., Gough M., Mohammadi-Ivatloo B., Shafie-Khah M., Catalao J.P.S. Novel hybrid stochastic-robust optimal trading strategy for a demand response aggregator in the wholesale electricity market. IEEE Trans. Ind. Appl. 2021;57:5488–5498. doi: 10.1109/TIA.2021.3098500. [DOI] [Google Scholar]
- 43.Chubu electric power grid, demand data. https://powergrid.chuden.co.jp/denkiyoho/
- 44.Chugoku electric power transmission and distribution company, demand data. https://www.energia.co.jp/nw/service/retailer/data/area/index.html
- 45.Hokkaido electric power network, demand data. https://www.hepco.co.jp/network/renewable_energy/fixedprice_purchase/supply_demand_results.html
- 46.Hokuriku electric power transmission and distribution company, demand data. http://www.rikuden.co.jp/nw_jyukyudata/area_jisseki.html
- 47.Kansai transmission and distribution, demand data. https://www.kansai-td.co.jp/denkiyoho/area-performance.html
- 48.Kyushu electric power transmission and distribution, demand data. https://www.kyuden.co.jp/td_service_wheeling_rule-document_disclosure.html
- 49.Shikoku electric power transmission and distribution company, demand data. https://www.yonden.co.jp/nw/index.html#s02
- 50.TEPCO power grid, demand data. https://www.tepco.co.jp/forecast/html/area_data-j.html
- 51.Tohoku electric power network, demand data. https://setsuden.nw.tohoku-epco.co.jp/download.html
- 52.Japan electric power exchange (JEPX), 2022. Trading information. http://www.jepx.org/english/market/index.html
- 53.Japan Meteorological Agency . 2022. Various Data and Materials.https://www.jma.go.jp/jma/menu/menureport.html [Google Scholar]
- 54.Wooldridge J.M. Wooldridge, Jeffrey M. Econometric Analysis of Cross Section and Panel Data. MIT Press; 2010. Basic linear unobserved effects panel data models; pp. 281–344. [DOI] [Google Scholar]
- 55.Suliman M.S., Farzaneh H. Synthesizing the market clearing mechanism based on the national power grid using hybrid of deep learning and econometric models: evidence from the Japan Electric Power Exchange (JEPX) market. J. Clean. Prod. 2023;411:137353. doi: 10.1016/j.jclepro.2023.137353. [DOI] [Google Scholar]
- 56.Holmes A., Illowsky B. In: Introductory Business Statistics. Holmes A., Illowsky, editors. 2017. Interpretation of regression coefficients: elasticity and logarithmic transformation.http://keep.hcmiu.edu.vn:8080/handle/123456789/3582 [Google Scholar]
- 57.Niromandfam A., Yazdankhah A.S., Kazemzadeh R. Modeling demand response based on utility function considering wind profit maximization in the day-ahead market. J. Clean. Prod. 2020;251:119317. doi: 10.1016/j.jclepro.2019.119317. [DOI] [Google Scholar]
- 58.Johnstone D., Lindley D. Mean–variance and expected utility: the borch paradox. Stat. Sci. 2013;28:223–237. doi: 10.1214/12-STS408. [DOI] [Google Scholar]
- 59.Buccola S., French B. Estimating exponential utility functions. Teor. Veroyatnostei i ee Primen. 1978;23:445. doi: 10.22004/ag.econ.142853. [DOI] [Google Scholar]
- 60.Niromandfam A., Choboghloo S.P. 1–33. 2020. (Modeling Electricity Demand , Welfare Function and Elasticity of Electricity Demand Based on the Customers ’ Risk Aversion Behavior). [Google Scholar]
- 61.Buccola S.T. Selection under exponential portfolio and quadratic utility. West. J. Agric. Econ. 2013;7:43–51. [Google Scholar]
- 62.Murtagh B.A., Saunders M.A. Department of Operations Research, Stanford University; 1983. MINOS 5.0 User`s Guide, Report SOL 83-20. (Revised as MINOS 5.1 User`s Guide, Report SOL 83-20R, 1987.) [Google Scholar]
- 63.Energy Policy Review. 2021. https://iea.blob.core.windows.net/assets/3470b395-cfdd-44a9-9184-0537cf069c3d/Japan2021_EnergyPolicyReview.pdf [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The hourly electricity prices from the period of 2016–2022 are collected for all regions in half-hourly intervals.5 The hourly electricity demand for all the regions participating in JEPX is collected from all the regional utilities.43,44,45,46,47,48,49,50,51 The collected demand capacity is lumped in regional demand. The share of the residential sector from the regional demand is assumed to be 27%.52 In addition, the amount of VRE (i.e., the sum of solar PV and wind power) are collected regionally for the same period. To align the half-hourly time intervals of prices with the demand and VRE quantities, the price intervals were converted using the weighted average and the market contracted volume. On the other hand, the CO2 emissions factors (i.e., for thermal electricity generation including coal, crude oil, liquefied natural gas, and biomass) per kWh for all the regions are collected from the electricity utilities∗, as shown in Table below. The hourly temperatures of the major cities in the regions (i.e., Hiroshima, Matsuyama, Sapporo, Nagano, Fukuoka, Nîgata, Osaka, Yamagata, and Tokyo) were acquired for the same period from.53
| Region | Emissions Factora (Kg-CO2/kWh) | Region | Emissions Factor (Kg-CO2/kWh) |
|---|---|---|---|
| Chubu | 0.382 | Kyushu | 0.365 |
| Chugoku | 0.521 | Shikoku | 0.525 |
| Hokkaido | 0.549 | Tokyo | 0.452 |
| Hokuriku | 0.465 | Tohoku | 0.457 |
| Kansai | 0.266 | National | 0.439 |
Annual average emission factor for the fossil-based powerplants, including was-to-electricity and biomass power.