Optimized cell type signatures revealed from single-cell data by combining principal feature analysis, mutual information, and machine learning

Aylin Caliskan; Deniz Caliskan; Lauritz Rasbach; Weimeng Yu; Thomas Dandekar; Tim Breitenbach

doi:10.1016/j.csbj.2023.06.002

. 2023 Jun 5;21:3293–3314. doi: 10.1016/j.csbj.2023.06.002

Optimized cell type signatures revealed from single-cell data by combining principal feature analysis, mutual information, and machine learning

Aylin Caliskan ¹, Deniz Caliskan ^1,¹, Lauritz Rasbach ^1,¹, Weimeng Yu ¹, Thomas Dandekar ^1,^⁎, Tim Breitenbach ^1,^⁎

PMCID: PMC10276237 PMID: 37333862

Abstract

Machine learning techniques are excellent to analyze expression data from single cells. These techniques impact all fields ranging from cell annotation and clustering to signature identification. The presented framework evaluates gene selection sets how far they optimally separate defined phenotypes or cell groups. This innovation overcomes the present limitation to objectively and correctly identify a small gene set of high information content regarding separating phenotypes for which corresponding code scripts are provided. The small but meaningful subset of the original genes (or feature space) facilitates human interpretability of the differences of the phenotypes including those found by machine learning results and may even turn correlations between genes and phenotypes into a causal explanation. For the feature selection task, the principal feature analysis is utilized which reduces redundant information while selecting genes that carry the information for separating the phenotypes. In this context, the presented framework shows explainability of unsupervised learning as it reveals cell-type specific signatures. Apart from a Seurat preprocessing tool and the PFA script, the pipeline uses mutual information to balance accuracy and size of the gene set if desired. A validation part to evaluate the gene selection for their information content regarding the separation of the phenotypes is provided as well, binary and multiclass classification of 3 or 4 groups are studied. Results from different single-cell data are presented. In each, only about ten out of more than 30000 genes are identified as carrying the relevant information. The code is provided in a GitHub repository at https://github.com/AC-PHD/Seurat_PFA_pipeline.

Keywords: Single cell analysis, Machine learning, Explainability of machine learning, Principal, Feature analysis, Model reduction, Feature selection

Graphical Abstract

1. Introduction

Single-cell technology provides methods to measure gene expression levels in single cells [1], [2]. Each measurement provides a snapshot of the genetic dynamic within a cell. Assuming that the genetic dynamics of regulation are identical within the cells, a research question is to find the differences in the expression profile of a genotype responsible for phenotypic variants. One example is stem cells that differentiate into different cell types to create specific tissues [3]. To analyze the differences between cell types on a genetic level, we need to identify the genes whose expressions are different in both cell types and appear characteristic of the difference of the cell types. Our innovation: As mathematical concept we introduce new principal feature analysis [4] to identify those genes which carry the highest information suitable to separate the groups we want to distinguish. It does not matter how many groups we want to distinguish nor by which method (or combination of methods) the different groups were established first. As long as our mathematical approach has not yet been applied to the data, we can use it to improve the analysis in identifying the genes with the highest information content regarding separation of the groups.

Gene selection methods: After explaining the core concept of our gene selection method, we examine existing methods to better explain differences between gene groups and then how the results obtained by these gene selection methods can be improved applying our method of principle feature analysis to objectively determine how well each individual gene contributes to separate between clusters. Some genes are regulated by other genes, like genes in a pathway, and can thus be seen as a function of those regulating key genes that act as the pacemaker genes of that function.

Mathematically the pacemaker genes are called “argument genes”: As an example, if several other genes regulate a gene, we mathematically write $gen 1 = f (ge n 2, gen 3, \dots)$ where the regulating genes $gen 2, gen 3, \dots$ are called arguments of the function $f$ that models the expression of the gene $gen 1$ . Such function genes are redundant since if we need $gen 1$ as an argument for another gene, we can directly construct the functional relation from $gen 2, gen 3, \dots$ .

Keeping these redundant genes would add no further information but would rather make the genetic model unnecessary big. Bigger model sizes can cause issues in drawing conclusions from the identified genes since too many genes impede an overview of the relations to be investiaged or combinatorial issues leading to calculation time problems.

Evaluation of gene selection by a principle feature analysis tool: We illustrate our mathematical concept of principle feature analysis by implementing it into a handy software tool that provides a small set of genes. These genes might explain differences between cell clusters to foster subsequent analyses, e.g., drug target identification, by clearly directing the view to the relevant genes that carry the information for the difference.

To identify a small but meaningful set of genes, which make the difference between two or more classes of cells, we can reduce the redundancy by removing genes that are – mathematically speaking – functions of others. Removing these genes facilitates a small set of genes covering a wide span of relevant information regarding which cells belong to a specific phenotype and class.

We span the space of information, which describes the differences between phenotypes, with a basis of stochastically independent genes (features).

The selected genes mathematically act like a basis known from linear algebra to span vector spaces. Since the expression of each gene in the returned set of best-describing genes is formed by genes independent of each other, each gene carries its own individual and specific aspect of the difference between the phenotypes.

To solve the task of removing genes that are functions of others, thus carrying redundant information, and to select only those genes from the remaining genes necessary for identifying the respective cell type, we use the principal feature analysis (PFA) [4]. This method generates a graph where each node represents a gene. Two nodes are connected by an undirected edge if the corresponding genes take their expression values not independent of each other. This is tested with a chi-square test of independence. The key observation is that functions are linkers between disjunct subgraphs in which the genes are independent of the genes of the other subgraphs. Genes of each subgraph act as arguments of the dependent gene (function), determining its expression through a deterministic function, such as the molecular dynamics of regulation. It is shown that removing these linkers leaves the arguments. The corresponding “argument genes” or “pacemaker genes” take their values independent of each other and carry the information to describe the total system of regulation of the genes.

Application examples: Once redundancy is removed from the gene data set, another prerequisite of our method is the existence of groups in which the single cells are clustered and labeled accordingly. Between these groups or only between a portion of the groups, e.g., at least between two groups, we would like to obtain a small set of genes that describes all the relevant differences in their expression profile. Such labels can be obtained in several ways. One way is to measure a phenotypic characteristic of cells, like a surface protein. Another way is to apply clustering techniques to define marker genes [5], [6], [7] that single cells have in common, defining cell types.

In some cases, once these groups/clusters are defined, we would like to get alternative gene sets to marker genes since, e.g., marker genes may not be an appropriate drug target. Furthermore, since the expression of marker genes might also depend on each other to some degree, our approach complements these techniques in so far that we focus on providing a minimal and redundancy-free set of genes being able to distinguish between the clusters.

Another related task might be the annotation of cells [8], where cells are associated with reference expression patterns or known marker genes. Furthermore, there are methods using machine learning techniques to perform cell annotation and enhance clustering of single cells [9], [10], [11], [12].

However, our approach does not intend to annotate or to cluster cells but to contribute to finding genes that make a significant difference in the expression profile between defined phenotypes/groups of cells. Thus, the algorithm requires some characteristics with which we can distinguish cells into clusters. Consequently, our approach is rather to investigate unknown cases in terms of expression profile and to direct the focus to relevant differences that could help define cell types and subsequent reference expression or marker genes more effectively. Moreover, we would like to contribute to the interpretability of found genes and their annotations, in particular if gene identification has been done with the help of a deep neural network [9], [10], [12].

The aim of our algorithm is to extend or enhance the capabilities of existing tools in these scenarios.

Overview on analysis flow and techniques: For gene selection there are a number of different techniques, including gene expression algorithms, improved clustering, and single-cell sequencing analysis methods. This allows readers to readily discern how our concept of evaluation of the gene selection made using PFA differs from existing gene selection methods and see how our method extends these existing ones by offering a novel approach to identifying a concise set of genes that best represents the signature for a certain group of cells in this analysis step.

To start our analysis, single-cell data obtained via the Single Cell Portal were processed using the Seurat workflow [13], [14], [15], [16] and DoubletFinder [17]. The R package Seurat, which got its name due to its depiction of single cells resembling a pointillist painting such as those painted by Georges Seurat [13], integrates in situ RNA patterns and single-cell data, allowing the mapping of cellular localization [13]. Additionally, Seurat objects, such as those shared by Emont et al. (2022) [18] contain various information about the cells, including tissue type and cell type. Utilizing this information, we prepared the datasets employed in our subsequent software pipeline.

Next, we implemented several helpful existing methods for gene selection in our software package. One approach to obtaining differences between cell types is to screen for differentially expressed genes (DEGs). Several RNA-sequencing analysis tools, including edgeR [19], DESeq2 [20] and Seurat [13], [14], [15], [16], are commonly used to identify DEGs between different groups of samples. The Seurat package [13], [14], [15], [16] offers various test methods for finding differential gene expression, including the Wilcoxon rank sum test [21], which is also known as the Mann-Whitney U test [22]. An application example of DEG is the design of synthetic locus control regions (sLCR) [23] to mark cells that show a certain phenotype by expressing a fluorescent reporter upon a characteristic transcription factor (TF) profile. In Schmitt et al. (2021) [23], these phenotypes are different glioblastoma subtypes. After the identification of the DEGs, corresponding TFs and binding sites are identified that regulate the expression of the characteristic signature genes. Subsequently, methods are required to select a limited number of short DNA strands for the sLCR that cover most of the binding sites of the characteristic TFs (to ensure specificity) since the length of the sLCR is limited. While in Schmitt et al. (2021) [23], the selection is mainly done manually, in Breitenbach et al. (2022) [24] a mathematical framework based on integer optimization is developed to automate the selection process. Our presented selection method might be an alternative to provide a small number of genes that clearly characterizes the expression differences between phenotypes. Since this selection has a high distinction power and is small, the number of corresponding TFs might already be limited as well. Based on the small number of genes and limited variety, the sLCR could be designed by the approved methods more efficient.

In addition to the DEG methods, there are other methods that try to find genes with a high discrimination power between cell types based on their expression level while minimizing the predictive power the genes have among each other, which reduces redundancy, in order to minimize the size of the required gene set [25], [26]. Cai et al. (2009) [25] use a greedy solver for the minimize redundancy (between the selected genes) maximize relevance (with the label/cell types) algorithm (mRMR) [27]. In Guyon et al. (2002) [25], [26], a selection algorithm based on support vector machines is provided that cancels genes/features out according to their ability to separate the labels. Since we use a different technique for gene selection and our method thus relies on other assumptions than the mentioned techniques, our method may offer supplementary insights, generate alternative gene datasets, identify potential drug targets, or facilitate deeper analysis to better comprehend the differences between the corresponding clusters.

For the task of gene (or in general feature) selection, respectively, there are other methods available (details in Li et al. (2017) [28] and Breitenbach et al. (2022) [4]). An example is the similarity-based method described by Li and colleagues [28], which does not provide a redundant-free set of features. Furthermore, a method purely based on mutual information also provides features that might be redundant. We remark that redundancy does not always have to cause a (significantly) bigger set of genes depending on the data set. On the other hand, the minimize redundancy / maximize relevance method may suffer from a longer calculation time than the PFA, as elaborated in Breitenbach et al. (2022) [4] when solved by integer programming. The sparse learning methods (described in detail in Li et al. (2017) [28]) use a specific model to select genes. Such an assumption is not necessary for the PFA as it selects genes based on statistical independence, independent of a concrete model choice.

There are further feature reduction methods in addition to the PFA. The principal component analysis (PCA) provides the principal components of the cloud consisting of the data points (expression pattern of each single cell), which are linear combinations of the original genes. Another method is the autoencoder which is a neural network that compresses the original input features into a layer with fewer neurons (new compressed feature) such that the values of the neurons of the output layer still equal those of the input layer. By this procedure, the encoder finds a compression of the input feature set that can still recover the information. However, both methods provide transformations of the original dataset, making it challenging to interpret the new (compound) features – in particular, the non-linear autoencoder case – since the transformation of the original genes to the compound genes is not explicitly given. Rather, the transformation is only implicitly given by the weights in the neurons which is not immediately easy to interpret, as discussed in Breitenbach et al. (2022) [4]. Consequently, it is challenging to tell which genes are essential in the concrete use case.

Overall, the advantage of the PFA for the gene selection part is that it is relatively fast and reduces redundancy between the genes, selecting them from the original dataset, not transforming them into new compound genes, and opening the door to understandable models by providing only a small number of genes; this is in line with Occam’s razor. This principle intends to construct explanations with the smallest possible set of elements.

We have to keep in mind that all these mentioned methods, including our presented method, provide genes whose expression highly correlates with the difference between the cell types. A correlation does not necessarily imply causality: a causal relationship is a specific type of correlation. As such, the expression (or lack thereof) of the identified genes may not necessarily be the cause of differing cell types; it may simply correlate with the cell type. Experimentally altering these genes might not significantly influence the cell type. For this reason, employing multiple selection methods based on distinct mathematical concepts can generate different small and meaningful gene sets. This plurality of sets provides different views of the same problem and thus generates more chances to find the genes that not only correlate but also cause the difference between the cell types by, e.g., using a correlating gene to arrive at genes that also cause the differences which might be in the set of another method. In addition, all methods rely on different assumptions on the data according to the used mathematical methods which might sometimes be more or sometimes be less fulfilled depending on the properties of the data set and thus might not work. This is a further reason why a broad toolbox of different gene selection methods is beneficial. Thus, we rather intend to extend the current toolbox by a new evaluation of the separation power between clusters achieved and we don’t have the intention to replace any of these well-working tools for gene selection.

Besides the contribution to the portfolio of methods for explaining differentiating cell clusters measured by characteristic markers [1], our pipeline, like others mentioned above for feature selection, can also be used to analyze the differences in the single-cell data groups clustered by methods like t-SNE [29] or UMAP [30], [31]. These methods are representatives of unsupervised learning and project high-dimensional expression data into a plane. The main goal of these methods is to cluster data points together in the plane that are also close in the high-dimensional space while keeping the distance to the other points that are not close in the high-dimensional space. These methods provide an excellent way to visualize single-cell data and to find single cells with a similar expression pattern while separating them from single cells with a fundamentally different expression pattern. These clusters might serve as a data-driven definition of cell types/phenotypes. However, once we visualize these relations via clusters in the plane, we do not get an explanation of what exactly made these methods cluster as they have done. Once the clusters are defined, e.g., by an unsupervised learning technique like UMAP and the single cells of each cluster are correspondingly labeled, our pipeline can be used to identify the genes whose expression patterns describe the difference between cell clusters.

Consequently, a further contribution of our pipeline is in the area of explainable artificial intelligence (AI) since we may construct understandable reasoning for the difference from the identified genes. This is specifically within the scope of our framework since the pipeline is optimized for providing a small gene set in the original feature (gene) space that is meaningful for explaining the difference. The reasoning for the explainability is that based on the expression level of the identified genes, we show the existence of a function/model that predicts to which cluster a single cell belongs. Thus, these genes contain relevant information and thus an explanation for the clustering that the unsupervised learning constructed could be reasoned with these genes. Since the set is meaningful, it contains all relevant information, and since it is small, it makes it easier for humans to keep the overview and to construct an explanation. In general, the approach is generic and can be applied to any unsupervised cluster technique to make the differences between the identified clusters explainable to humans.

In summary, our method directs the view to essential genes in a dataset that make the differences in the measured scenario for clearly separable phenotypes. The selection method (PFA) is novel and thus brings a new perspective into the gene selection portfolio, extending existing methods. The clear view of the relevant information makes the contrast of the phenotypes significantly visible and thus better understandable for humans. Since we provide the code of our entire pipeline via a GitHub repository, starting from the preprocessing and ranging to the ML-validation part, the application is immediate, and the pipeline can be easily extended in the future.

The rest of this work is organized as follows: We explain our pipeline in detail in the Methods section and provide the results from the analysis of publicly available single-cell data derived from human white adipose tissue [18] and human thoracic aorta [32] in the Results section. In the Discussion, we explain variants of our pipeline and future research in which the pipeline can be used. Possible applications include analyzing the differences between cells that are resistant to therapy and those that react to a specific treatment or potential therapy approach. Further applications investigate the effect of therapy on resistant cells and the differences between resistant cells before and after therapy. The Conclusion summarizes the advances and future perspectives of our work.

2. Methods

In this section, we describe the components of our software pipeline that is available via a GitHub repository under https://github.com/AC-PHD/Seurat_PFA_pipeline. Fig. 1 shows an overview of how the different scripts are used sequentially and what their purpose is for the analysis pipeline.

Fig. 1 — Workflow including data preparation, randomization, PFA gene selection and validation. The workflow figure was created using BioRender.

Using two different publicly available Single Cell datasets (see Supplementary Table 1 “datasets”), we tested our software pipeline. We chose the “single-cell atlas of human and mouse white adipose tissue” (WAT), published by Emont et al. in 2022 [18] and available via the Single Cell Portal (https://singlecell.broadinstitute.org/single_cell), as a Seurat object (in RDS-file format) [13], [14], [15], [16] to train and test the software.

To verify the promising results obtained from this dataset, we used a second data-set, the Single Cell data generated during the study “Deep learning enables genetic analysis of the human thoracic aorta” by Pirruccello (2022) [32], which is available in the h5ad-format via the Single Cell Portal.

The first requirement is a Seurat [13], [14], [15], [16] framework for preprocessing the single-cell dataset. The preprocessing works as follows.

2.1. Data preprocessing in R

The first Single Cell Portal dataset was available as an RDS-file. After loading the Seurat object containing all cells of the WAT into an R session, we filtered it according to cell type and tissue type using the information in the Seurat object’s metadata, as the authors of the Seurat object identified several cell types, including endothelial and mesothelial cells, adipose stem and progenitor cells (ASPCs), and adipocytes [18]. Furthermore, since all of the cell types contained cells isolated from adipose tissue and only some contained cells isolated from the non-adipocyte stromal-vascular fraction (SVF) of the adipose tissue [18], we filtered our cell types of interest also by tissue type.

Each cell type of interest (adipocytes, ASPCs, endothelial and mesothelial cells as well as “Fibroblast I” and “Macrophage” of the second dataset) was subsequently filtered for quality as recommended in the literature, e.g., by Luecken and Theis (2019) [33]. By removing cells with a low count depth, a high number of mitochondrial counts, and a small number of detected genes, we removed cells with broken membranes and dying cells [33]. Subsequently, we removed doublets, i.e. two cells sequenced together as one cell, using the R package DoubletFinder following the recommended workflow [17].

Using these results, the Seurat object was filtered. Only the remaining cells were used for the subsequent workflow. As the Seurat object is filtered using tags generated during the respective analyses, it is technically possible to use other doublet finding tools such as the Jupyter Notebook and Python-based tools Scrublet (Single-Cell Remover of Doublets) [34] or DoubletDetection [35], although this might possibly disrupt the workflow. Considering that the data preparation workflow is conducted in R, using an R-based tool such as DoubletFinder [17] or DoubletDecon [36] would be more convenient for doublet detection.

Finally, the resulting “cleaned and filtered” Seurat objects were transformed into count tables, the required input for the ML workflow. The counts of the Seurat object were saved as data.frame, creating a column containing the row names. As the last preparation step, we removed all rows containing ribosomal and mitochondrial genes and added a label row to the data.frame. This label is required to mathematically distinguish between the different cell types during the PFA and machine learning process.

Since we compared two cell types as a class and thus did not require detailed sample information, we used either 0 or 1 as the label, removing the Seurat sample names. After preparing one cell type as a table labeled with 0 and another as a table labeled with 1, we merged both tables by gene name.

2.2. Data preprocessing in Python

Subsequently, the input datasets for the ML pipeline were prepared using our Python script “Randomizer”. With the input data table as input, this script selects 1000 random cells of each cell type (e.g., ASPCs and adipocytes, also referred to as each group) from the pool of all single cells that are given after preprocessing, creating a “results” file (“results_1” to “results_n”, with n being the last run of the randomizing script). The number of cells can be adjusted by changing the variable “cell_count” in the Randomizer script (1000 is set as the default). The remaining cells of the two groups that were not selected from the pool for the results file are saved as “rest” (“rest_1” to “rest_n”). This process is repeated until there are less than 1000 cells of one of the two groups left (n times, depending on the size of the dataset), using no single cell twice. Thus, a table containing 4200 cells of one cell type (the first group, labeled as “0”) and 3900 cells of the other cell type (the second group, labeled as "1") after cleaning and filtering would result in a pool set containing 8100 single cells. However, with a Randomizer setting of 1000 cells, it can only yield three results-files, which equals three data sets containing 1000 cells of each of the two cell types for subsequent analysis. This would be sufficient for three PFA analyses.

This step can be rather time-consuming, depending on the size of the input data table and the machine used. For reference: on a PC with 83 AMD Ryzen 9 3900X, 12-Core Processor, 64 GB RAM, 64-Bit-Operating System, and an x64–84 based processor, using a VM Linux environment (Ubuntu 20.04.2 LTS (OS-Type: 64-bit) using Virtual Box 6.1) and on a Macbook Air, 2022, M2, 8 GB RAM, this calculation took about a day for the datasets generated using the single-cell atlas of human and mouse white adipose tissue [18]. Smaller data sets, such as the one generated using “Fibroblast I” and “Macrophage” of the human thoracic aorta data [32], require less time (six to eight hours).

2.3. Principal feature analysis (PFA)

Next, the preprocessed data is analyzed using the PFA [4] to identify the genes required to distinguish between the cell types (labels). This is a new concept we present here: We objectively determine which selection of genes separates given clusters of cells best from each other (or more general: which selection of features separates given clusters best from each other). In the paper [4] the mathematical properties of our PFA and the mathematical application areas ranging from advantages for classical modeling to regression analysis and analysis of differential equations and machine learning are given.

More specific, we use Algorithm 2 of Breitenbach et al. (2022) [4] where the maximum number of nodes per subgraph (called cluster_size in the implementation) controls the size of the dependence graphs that are dissected to reduce redundancy. Too big and too small values compared to the number of total genes can cause long calculation times. In order to discretize the continuous expression levels of genes, we use Algorithm 4 of Breitenbach et al. (2022) [4] where the parameter for the minimum number of data points in a bin (called min_n_datapoints_a_bin in the implementation) controls how many data points (measurements of a gene expression; equivalent to the number of measured single cells) form a discrete event meaning “the expression level of this gene in this single cell is between the number of the measurement with the lowest and the highest gene expression of measurements forming this bin”. Once the expression levels of each gene are discretized into events, we can formulate the contingency table for the chi-square test of independence where we compare two genes to see if their expression is independent of each other. We note that the label is handled with the same discretization algorithm to define the events like “this measurement belongs to a single cell labeled with 0”. The higher the min_n_datapoints_a_bin is, the coarser the discretization of the continuous gene expression is, which could delete information as well. However, if it is too small, then too few data points could be in some events which could result in some expected frequencies in the entries of the contingency table (meaning that gene A has expression level x and gene B has expression level y) being below 5 data points; this means that this combination of “gene A has expression level x and gene B has expression level y” is expected in only 5 single cells, violating the requirements for a reliable test of independence. The concrete choices of the parameters are given with the data sets in the Results section.

With the same discretization, we can calculate the mutual information between the expression of a gene and the label of the single cells. The mutual information provides a measure of how much we know about the label if we know the expression level of a gene (and vice versa).

Let the discretized gene expression of gene $i$ be modeled by the random variable $X_{i}$ where $Z_{i}$ is the space of bins in which the expression of the gene $i$ is discretized with $z_{k} \in Z_{i}$ , $k \in \{1, \dots, m_{i}\}$ , $m_{i} \in N$ . Analogously for the label that is modeled as the random variable $Y$ with $z_{l} \in Z_{Y}$ , $l \in \{1, \dots, m_{Y}\}$ , $m_{Y} \in N$ . In our example with a label of 0 or 1, $m_{Y} = 2$ . Now, let $P (X_{i} = z_{k})$ be the probability that among all single cells gene $i$ is expressed at a level assigned to the bin $z_{k}$ (number of data points in that bin divided by the number of all single cells) and let $P (Y = z_{l})$ be the probability that a single cell is labeled with $z_{l}$ (number of single cells with label $z_{l}$ divided by all single cells). Furthermore, let $P (X_{i} = z_{k} \land Y = z_{l})$ be the probability that a measurement of gene $i$ being expressed at a level assigned with $z_{k}$ and the corresponding single cell is label with $z_{l}$ (all gene measurements where $X_{i} = z_{k}$ and the single cell is labeled $Y = z_{l}$ divided by the number of all single cells). Then, we can define the mutual information $I$ between the discretized expression level $X_{i}$ and $Y$ as follows

I (X_{i}, Y) = \sum_{k = 1}^{m_{i}} \sum_{l = 1}^{m_{Y}} P (X_{i} = z_{k} \land Y = z_{l}) \log \frac{P (X_{i} = z_{k} \land Y = z_{l})}{P (X_{i} = z_{k}) P (Y = z_{l})} .

An illustration of why the mutual information measures the relatedness of two random variables is the following:

P (X_{i} = z_{k}) = P (X_{i} = z_{k} | Y = z_{l}) ≔ \frac{P (X_{i} = z_{k} \land Y = z_{l})}{P (X_{j} = z_{l})}

where the first equality sign holds if the expression of a gene is independent of the kind of single cell and the second one due to definition. The total equation defines stochastic independence of two random variables. The conditional probability $P (X_{i} = z_{k} |Y = z_{l})$ is defined by the right hand-side of the equality sign “ $≔$ ”. If the quotient $\frac{P (X_{i} = z_{k} \land Y = z_{l})}{P (X_{i} = z_{k}) P (Y = z_{l})}$ is close to 1, it means that the equality is fulfilled and $\log \frac{P (X_{i} = z_{k} \land Y = z_{l})}{P (X_{i} = z_{k}) P (Y = z_{l})} \approx 0$ . If the equation holds for any $k \in \{1, \dots, m_{i}\}$ and $l \in \{1, \dots, m_{Y}\}$ , it means that the two random variables are stochastically independent of each other and the knowledge of a value of one random variable (expression level of a gene) does not allow reliable conclusions about the value of the other random variable, which is the label of the cell, meaning which cell type we have. In this case the mutual information takes the minimum 0. In all other cases, the mutual information is> 0 and weights the correlation of the outcomes of the two random variables.

After describing our mathematical toolbox, we explain further how we analyzed the data sets. We take three different sets of single cells from the randomizer script, each containing two cell types and 1000 single cells of each type. We perform the PFA analysis on the first set, called “PFA set”. The other two sets are left for validations, explained later.

The genes returned by the PFA are highly correlated with the differences between the cell types. These genes are ranked by the mutual information they share with the label, as explained in Breitenbach et al. (2022) [4]. The more mutual information an expression of a gene and a label have in common, the more information about the label can be derived from the measurement of the corresponding gene expression. In our pipeline, the mutual information between each gene and label is exported as a file named “gene_mutual_information.csv”, containing the genes deemed important by the PFA. These genes can be used during the validation step. However, it is also possible to use another gene set for validation of which one assumes to contain relevant information to separate the phenotypes.

According to the ranking, we might neglect genes that only have a low amount of mutual information, e.g., because their expression level only contributes minorly to which cell type a cell belongs or these genes are only important in a very small portion of single cells to decide the cell fate. However, as explained in Breitenbach et al. (2022) [4], this procedure is only an approximation since it is also possible that many genes, which all have a small amount of mutual information, can, when seen in combination, be important to determine the cell type, which a suitable model would “learn” from the data. To summarize, the ranking with the mutual information is an approximation that worked well in our experiments. In case, the pairwise mutual information does not work, our validation framework, which we explain later, works for any set of genes that one thinks captures the information about the difference of the different phenotypes, e.g. if we have a hypothesis from domain knowledge or intuition for the set of important genes, we can test if it provides sufficient information to differentiate the cells into their clusters.

We note that we optimized the PFA script to use more than one kernel by parallelizing the dissections of the dependency subgraphs. This considerably reduced the calculation time up to 25% in our experiments depending on the structure of the interaction of the features and thus of the PFA’s dependence graph. The implementations of both versions are such that the output of the serial and parallel version is identical. The parallel PFA script is available by a GitHub repository via https://github.com/LauritzR/Parallel-Principal-Feature-Analysis.

The serial version of the PFA can be found via https://github.com/LauritzR/Principal-Feature-Analysis. In the supplementary material, we provide documentation where we describe the high-level differences between the serial and parallel PFA version.

2.4. Validation

To check how much information is lost due to neglecting genes with little mutual information and thus balance explorative power with a small set of genes, we use the following workflow. This workflow can be used to validate any promising set of genes from any source that is assumed to provide sufficient information for distinguishing between the different phenotypes.

The main idea of the validation is the following. If the expression levels of our selected genes contain sufficient information, it should be possible to fit a function that can classify to which cell type/cluster/label a single cell belongs with a high accuracy based only on the expression level of the selected genes. This function contains the rules or explanation, i.e., what in the expression levels determines the cluster designation. All of our analysis is performed on the “PFA set” generated by the Randomizer script, as described above, which is the result_1 set from the randomizer. For the validation step, we now include the two other sets generated by the Randomizer script on which we only fit a function (e.g., a ML model) to show that our gene selection is not sensitive to our “PFA set” sampled from the pool; rather, it contains generic information about the relationship of gene expression of the selected genes and the assignment to a cell type/label.

We would like to stress that the model we fit is not the main result of our analysis, but rather the set of selected genes. We simply use the supervised ML framework because it provides a well-developed toolbox to fit a function that maps input (expression level of genes) to output (labels). Consequently, if we know a well-working function exists which can do the mapping based on our selected genes on each set generated by the randomizer, we conclude that our (small) selection of genes is meaningful with regard to describing the difference between the labels (i.e., cell types or clusters).

The reverse is of course not true, meaning if the validation fails that our selection does not contain enough information since maybe the model training fails (e.g., disadvantageous convergence parameters) or the model type does not match the real dynamics that drive the relevant gene expression (e.g., linear vs. non-linear models).

We remark that we would like to verify the gene selection with respect to non-sensitivity for the data set and not necessarily a concrete model. That is why it is justified to retrain a new model on each set based on the same genes. One possible extension might be to train the model only on “PFA set” and perform only inference on the other two sets, not training again from the scratch.

This validation procedure, having a set for analysis and several sets for validation, can also be applied for other gene selection methods, e.g. for those mentioned in the Introduction.

More specifically, we train an ML model (MLPClassfier from Python's sklearn) on a training dataset and predict the cell type on a test set for each set from the randomizer, as described above, based on different gene selections to validate our selection’s information content. We use an 80/20 ratio split of a dataset for training and testing/predicting: i.e., 80% of the dataset for each set from the randomizer are used for training and the remaining 20% are subsequently analyzed as test to see whether the model can correctly distinguish the different cell types (see discussion for justification).

We start on all available non-constant genes as the input space for the ML model. Non-constant genes mean that there is at least one single cell where the expression level differs from the others. The procedure on all non-constant genes serves as a control to check the accuracy given all available information since genes are also included that might have been sorted out by our analysis but contain relevant information. Consequently, we assume that in this case the accuracy should be the best possible which we should also achieve by our gene selection assuming that we pick genes relevant for describing the difference of the investigated labels and we only remove non-relevant genes.

Next, we train another model of the same type (MLPClassifier) on the genes we analyzed with the PFA and exceed a certain threshold for mutual information. This analysis is only done on the set “PFA set”. Now, we can see how the accuracy varies depending on the threshold for the mutual information compared to the model trained on all genes. If the threshold was set correctly, an analysis using a significantly lower number of genes than all of the genes contained in the Seurat object results in a prediction with comparable accuracy to the prediction made using all genes. Since Seurat objects can contain several thousand genes, an analysis requiring only a fraction of this number will result in a shorter calculation time, and thus, in faster results for the researcher. On the other two sets, the selected genes are kept (no adjustment of the mutual information threshold) and the training and testing is performed. If the selection of the genes provides a model with sufficient accuracy and is not sensitive to the PFA set, a function should exist as well on the other data sets based on the same gene set with a comparable accuracy to the one of the previous function/model fit on the PFA set.

To evaluate how much better the PFA selection is compared to randomly selected genes, we train another model of the same type (MLPClassifier) based on randomly selected non-constant genes where the number of selected genes corresponds to the number of PFA-selected genes that passed the mutual information threshold.

To take the randomness of the training process into account, we repeat each procedure twenty times and take the mean accuracy of the corresponding models. In the case of random gene selection, for each sweep, new genes (number equals the PFA gene; drawing with put back) are selected from the pool of non-constant genes. We use only the standard settings for the MLPClassifier as they worked fine in our cases. We will see in the Results section that with the standard setting we could achieve sufficient accuracy proving the existence of a function being able to map gene expression of our gene selection to labels. However, the process would also be valid for performing a hyperparameter tuning for each model or choosing the best model type in each case since we only need the existence of a function to prove the information content of our selection.

The complete workflow is summarized in Fig. 1, which was created using BioRender (https://biorender.com/, accessed on 01 April 2023).

As explained in Breitenbach et al. (2022) [4], we cannot conclude that the gene selection is bad if the accuracy is bad, since it is possible that the corresponding ML model is not appropriate to capture the functional relations. However, we argue that if we have one model that has an accuracy sufficient for the use case, we can conclude that our gene selection captures the relevant information.

2.5. Multiple cell types validation

As a final step, we demonstrate that our method is also capable of discerning between more than two different cell types. Therefore, we generated a validation dataset containing three cell types and a validation data set containing four cell types, using 1000 cells of each cell type. For the dataset containing three cell types, we used ASPCs, adipocytes and mesothelium (“0”, “1″, and “2”, respectively), for the dataset containing four cell types, we used ASPCs and adipocytes as well as endothelium and mesothelium (labeled as “0″, “1”, “2”, and “3”, respectively).

These datasets were subsequently analyzed with our method in order to demonstrate that our algorithm can also discern three or four different cell types.

2.6. Biological validation

Since our analysis results in genes that are – according to our algorithm – important for recognizing the differences between two cell types, we treat the resulting genes as differentially expressed genes (DEGs) or marker genes. If these genes have predictive value, they should help analyze the differences between the cell types, e.g., result in pathways or biological processes. Thus, we employed clusterProfiler [37], [38] (version 4.4.2), in combination with the R-packages enrichplot [39] (version 1.16.1) and ggplot2 [40] (version 3.3.6) to visualize biological processes related to the genes resulting from our analysis (subsequently also referred to as “PFA genes”). The information on the GO biological processes, which is necessary for the enrichment analysis, was obtained via the Molecular Signatures Database (MSigDB) [41], [42], [43], [44], [45] (version 7.5.1). The results were visualized as bar plots and CNET plots.

Additionally, we analyzed the respective cells of the Seurat object using the standard Seurat workflow [13], [14], [15], [16] to find marker genes: genes which are differentially expressed between the two cell types. To validate our PFA genes, we used three of the different testing options available via the Seurat FindMarkers() function: DESeq2, Wilcoxon Rank Sum test, and Student’s t-test.

3. Results

First, we provide the results of our software pipeline exemplified with several datasets (see Supplementary Table 1 datasets). Each data set consists of several thousand single cells of each type.

The Seurat parameters in the pipeline were set to use only cells with more than 800 molecules per cell (nCount_RNA), more than 500 genes (nFeature_RNA), and less than 5% mitochondrial DNA (named mt.percent or percent_mito, depending on the dataset). Additionally, we removed all ribosomal and mitochondrial genes as described above.

After preprocessing, each data set with all single cells (with label either 0 or 1) is called the pool set for the corresponding cell types.

For the subsequent analyses, the pool set (e.g., the set containing ASPCs and adipocytes) is randomly split into further subsets using the Randomizer script, as described in the Methods section, resulting in subsets containing 1000 single cells of each type, 2000 cells in total per file (“result_1″ to “result_n”).

The training set from each subset consists of 80% of all single cells of each type, resulting in training data consisting of 800 cells of each cell type. The test set contains the remaining 20% of single cells.

The set “Set PFA” was randomly selected from the pool set (“results_1″) and used for the PFA analysis to select the genes. The sets “Set 1″ and “Set 2″ are additionally randomly sampled from the pool set (“results_2″ and “results_3″, respectively), and no single cell is used in more than one subset.

These sets are used to show that the PFA gene selection (done only on the “PFA set”) is not sensitive to a particular set but has general predictive power regarding the cell types. Consequently, the gene selection from “Set PFA” is used to train and test models on “Set 1″ and “Set 2″. Furthermore, taking the gene selection from one set and applying it to sets from the pool shows that the gene set not only contains sufficient information, but also that the chosen sets with 1000 single cells of each type were large enough to present the statistical properties of the pool set.

The PFA parameters were set to “calculate_mutual_information=True”, “cluster_size= 300″, “min_n_datapoints_a_bin= 100″, and to a mutual information that was sufficient to achieve at least 98% accuracy with as few genes as possible (mutual information>0.5 for ASPCs and adipocytes (13 PFA genes) as well as endothelium and mesothelium (10 PFA genes); or 0.6 for adipocytes and mesothelium, resulting in 12 PFA genes), for analyzing different cell types from the single-cell atlas of human and mouse white adipose tissue [18]. If not further noted, we used the default values of the methods.

The calculation time for the PFA and validation procedure was approximately 2–5 h, depending on the data set.

3.1. Analyzing adipocytes and ASPCs as an example

The first pool data for demonstrating our pipeline was generated using the single-cell data on human white adipose tissue (WAT) made available by Emont et al. (2022) [18] via the Single Cell Portal. We used ASPCs and adipocytes derived from human WAT, labeled with the tissue type “adipose” according to the metadata of the Seurat object, and combined the data as described in the method section to a table containing both cell types, labeled as cell type “0” and cell type “1”, respectively. According to the visualization of the study (“A single cell atlas of human and mouse white adipose tissue”) in the Single Cell Portal, both cell types are clearly distinguishable in a UMAP plot (Fig. 2).

Fig. 2 — Screenshot of the cluster visualization of adipocytes (red) and ASPCs (blue) available at the Single Cell Portal via this link, accessed on December 13th, 2022.

PFA of a subset (“results_1″, containing 1000 cells of each cell type) required only 13 genes (“PFA genes”) for a prediction accuracy of almost 100% (Table 1). The accuracy of the models based on all non-constant genes (also referred to as “all genes”) was 100% for all three of the analyzed subsets (“results_1″, “results_2″, and “results_3″, generated by using the Randomizer script on the table containing adipocytes and ASPCs) during training. The subsequent tests on the remaining 20% of subsets had an accuracy between 99.5% and 100%. The (almost) zero difference between training and testing accuracy shows that there is no overfitting of the ML model. In addition, the high accuracy on both sets of the splitting indicates that the gene selection contains information for deterministic rules by which to classify the cells independent of the sampling/splitting.

Table 1.

Prediction results based on PFA gene selection, all genes, and random genes for ASPCs and adipocytes, using the ideal PFA threshold of 0.5, which results in 13 PFA genes.

	Set PFA			Set 1			Set 2
	PFA genes	All genes	Random genes	PFA genes	All genes	Random genes	PFA genes	All genes	Random genes
Train	0.99246875	1.0	0.6476875	0.996125	1.0	0.68415625	0.9934375	1.0	0.65375
Test	0.997625	0.9975	0.621375	0.990125	1.0	0.650875	0.9975	0.997	0.648375

Open in a new tab

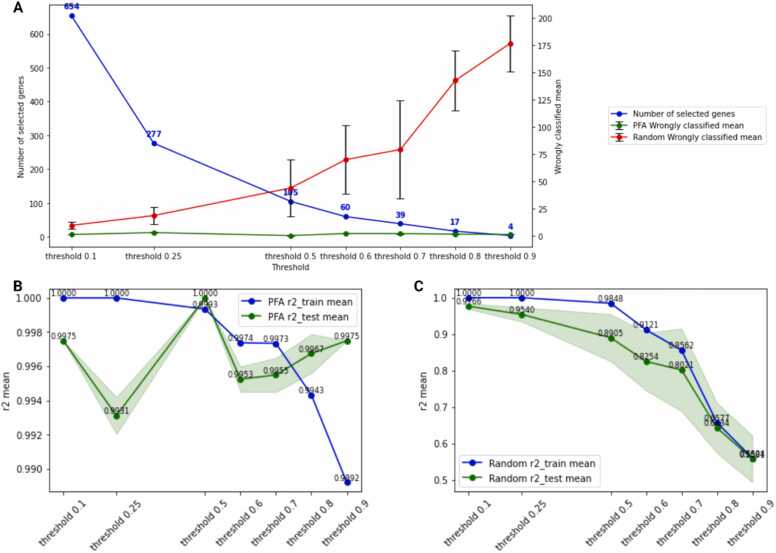
To find a small set of PFA genes, we tested several thresholds of mutual information for each analysis (Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7 and Supplementary Table 2 PFA results). For the analysis of ASPCs and adipocytes, we evaluated the thresholds 0.1, 0.25, 0.5, and 0.6 (Fig. 3). While the prediction accuracy using PFA genes is rather constant, the number of wrongly classified cells using an equal number of random genes rises with more stringent thresholds. While a threshold of 0.1, which equals 439 randomly selected genes for the analysis of ASPCs and adipocytes, results in a wrongly classified mean of 26.15, a threshold of 0.25 (105 random genes) results in a wrongly classified mean of 73.15. Using the PFA genes instead results in much lower wrongly classified means. For instance, with only 5 PFA genes, which equals a threshold of 0.6, the wrongly classified mean is 7.1, which is still considerably smaller than the wrongly classified mean of analyzing 439 randomly selected genes (26.15 wrongly classified cells) and significantly smaller than the wrongly classified mean of analyzing 5 randomly selected genes, which is 168.1 (see Supplementary Data “1 ASPCs & adipocytes PFA” for the analysis of the first subset (“results_1”) and Fig. 3A and Supplementary Table 2 PFA results).

Fig. 5 — Accuracy of the prediction results of the PFA gene selection for analyzing endothelium and mesothelium. (A) Relation of the number of selected genes (blue line) and the mean of wrongly classified single cells (green line using the genes predicted by PFA, red line using an equal number of randomly selected genes). (B) Differences between training (blue line) and test (green line, the green “shadow” indicates the standard deviation generated by repeating training and testing on different data splits) when using different accuracy thresholds. Here a threshold of 0.5, which results in 10 PFA genes, yielded the best result for analyzing endothelium and mesothelium. (C) Differences between training (blue line) and test (green line, the green “shadow” indicates the standard deviation) when using the same number of random genes instead of the respective PFA genes. The random genes result in a considerably lower accuracy (for a threshold of 0.5: 58.52% in test using 10 random genes compared to an accuracy of 100% in test using the 10 PFA genes).

Fig. 6 — Accuracy of the prediction results of the PFA gene selection for analyzing two cells of the same cell type (hAd1 and hAd2, different subtypes of human adipocytes). (A) Relation of the number of selected genes (blue line) and the mean of wrongly classified single cells (green line using the genes predicted by PFA, red line using an equal number of randomly selected genes). (B) Differences between training (blue line) and test (green line, the green “shadow” indicates the standard deviation generated by repeating training and testing on different data splits) when using different accuracy thresholds. Here, a threshold of 0.07, which results in 249 PFA genes, yielded an accuracy of 86.27% in test. (C) Differences between training (blue line) and test (green line, the green “shadow” indicates the standard deviation) when using the same number of random genes instead of the respective PFA genes. The random genes result in a lower accuracy (for a threshold of 0.07: 73.28% in test using 249 random genes compared to an accuracy of 86.27% in test using the 249 PFA genes).

Fig. 7 — Accuracy of the prediction results of the PFA gene selection for analyzing “Fibroblast I” and “Macrophage” of the dataset by Pirruccello et al. (2022) [32]. (A) Relation of the number of selected genes (blue line) and the mean of wrongly classified single cells (green line using the genes predicted by PFA, red line using an equal number of randomly selected genes). (B) Differences between training (blue line) and test (green line, the green “shadow” indicates the standard deviation generated by repeating training and testing on several splits of the data) when using different accuracy thresholds. Here a threshold of 0.5, which results in 105 PFA genes, yielded the best result for analyzing fibroblast and macrophage. However, even a threshold of 0.9, which uses only four genes, still results in an accuracy of about 99%. (C) Differences between training (blue line) and test (green line, the green “shadow” indicates the standard deviation) when using the same number of random genes instead of the respective PFA genes. The random genes result in a considerably lower accuracy (for a threshold of 0.5: 89.05% in test using 105 random genes compared to an accuracy of 100% in test using the 105 PFA genes, and even greater differences for a threshold of 0.9: an accuracy of 55.81% in test using 4 random genes, compared to an accuracy of 99.75 in test using 4 PFA genes).

In the plots (Fig. 3) we see that the prediction accuracy of random genes on training and test sets (repeated 20 times, mean of all sweeps is plotted) significantly drops at a threshold value of 0.25 (145 genes). However, when using the PFA genes, the accuracy starts to drop between threshold values of 0.5 (13 genes) and 0.6 (5 genes). Above the threshold of 0.5, the prediction accuracy drops below the minimum criterium of 98%, which means that a gene whose expression level has a significant impact on cell type cluster assignment is missing. Consequently, our gene set should contain that gene carrying important information for the difference. On the other hand, such genes might be interesting for experiments since a knockout or knockdown of their expression might prevent expressing the phenotypic characteristics of cells, which could be a resistance against a therapy or the transition to a different cell state. Thus, in this example, the four genes (ranked 1st to 4th according to PFA) found using the “threshold below the drop” might be vital for the differences between adipocytes and ASPCs, while the other PFA genes (the genes ranked 5th to 13th according to PFA) might be of interest for predicting changes or differences between the cell types. Summarizing, taking the genes directly before the accuracy on the test set drops, is a practical way to determine a reasonable size for the gene set.

Using only the 13 genes selected by the PFA algorithm (also referred to as “PFA genes”), with the ideal threshold of 0.5 (see Table 1, indicated by the green line in Fig. 3B and C with the standard deviation being shown as green shadow (generated by repeating training and testing on different data splits), and Supplementary Data), resulted in an accuracy of at least 99.25% and up to 99.61% during training and a prediction accuracy of up to 100% in testing (with a minimum accuracy of 99.7%).

When training with all non-constant genes, the accuracy was 100% on the training and 99.75% on the test dataset, while using 13 randomly selected genes instead of the PFA genes caused the accuracy to drop to 64.77% on the training and 62.14% on the test dataset (Table 1). Using this gene selection for two different sets generated from the same pool produced comparable results (Table 1, Set 1 and Set 2). Decreasing the threshold for mutual information and thus including more than 13 genes increases the accuracy up to 100% as expected when including genes that might explain corner cases and thus might be ranked lower.

To prove the efficiency of our PFA, we repeated the same training and testing using 13 random genes. The significantly lower accuracy indicates that the 13 PFA genes have more predictive power than 13 randomly selected genes.

3.2. Validation: accuracy of PFA for analyzing other cell types

Additionally, we verified the algorithm using several cell type comparisons derived from the human WAT data set by Emont et al. (2022) [18].

The prediction accuracy of our MLP classifier of the sklearn framework on the training and test set based on different gene selections is summarized in Table 2; the detailed analyses of the respective datasets (adipocytes and mesothelial cells, endothelial and mesothelial cells, hAd1 and hAd2 of the dataset by Emont et al. (2022) [18] as well as “Fibroblast I” and “Macrophage” of the dataset by Pirruccello et al. (2022) [32]) are available in the Supplementary Data.

Table 2.

Prediction accuracy summarized for each experiment.

	Number of required genes	Set PFA			Set 1			Set 2
	Number of required genes	Accuracy using PFA genes	Accuracy using random genes	Accuracy using all genes	Accuracy using PFA genes	Accuracy using random genes	Accuracy using all genes	Accuracy using PFA genes	Accuracy using random genes	Accuracy using all genes
ASPCs and adipocytes (31328 genes in the input table, threshold = 0.5)
Train	13	0.99246875	0.6476875	1.0	0.996125	0.68415625	1.0	0.9934375	0.65375	1.0
Test	13	0.997625	0.621375	0.9975	0.990125	0.650875	1.0	0.9975	0.648375	0.997
adipocytes and mesothelium (31328 genes in the input table, threshold = 0.6)
Train	12	0.9945625	0.652214285714286	1.0	0.9961875	0.6823125	1.0	0.995375	0.6889375	1.0
Test	12	1.0	0.632	1.0	1.0	0.6425	1.0	0.995	0.66825	1.0
endothelium and mesothelium (31328 genes in the input table, threshold = 0.5)
Train	10	0.996875	0.60221875	1.0	0.99571875	0.62240625	1.0	0.99628125	0.61821875	1.0
Test	10	1.0	0.58525	1.0	0.9975	0.6125	1.0	1.0	0.599375	1.0
two samples of the same cell type (adipocytes hAd1 and hAd2) (31328 genes in the input table, threshold = 0.07)
Train	249	1.0	0.9995625	1.0	1.0	0.99971875	1.0	1.0	0.9994375	1.0
Test	249	0.86275	0.73275	0.893875	0.8415	0.7035	0.877375	0.845375	0.68425	0.862125
fibroblast and macrophage (33486 genes in the input table, threshold = 0.9)
Train	4	0.98921875	0.5604375	1.0	0.99065625	0.57578125	1.0	0.995375	0.59328125	1.0
Test	4	0.9975	0.558125	0.993875	0.9925	0.57175	0.997375	0.9925	0.587375	0.999875

Open in a new tab

For the analysis of adipocytes and mesothelium, a threshold of 0.6, equaling12 PFA genes, was ideal (Fig. 4 and Supplementary Data).

Comparing endothelium and mesothelium, which were also derived from the single cell atlas of human and mouse white adipose tissue by Emont et al. (2022) [18], yields similar results (Fig. 5): 10 PFA genes (a threshold of 0.5), were sufficient for a prediction accuracy of 100% during test.

3.3. Validation: using PFA to analyze the same cell type

For further validation, we compared subtypes of the same cell type (adipocytes hAd1 and hAd2, also part of Emont et al.’s data [18]). For the same cell type analysis, a mutual information value of> 0.05 was used, which resulted in 249 PFA genes but yielded an accuracy of less than 87% (86.27%) in test using the PFA genes (Fig. 6).

This result was to be expected because in the UMAP plot these two clusters do not separate well since they might have a similar expression pattern (see Supplementary Fig. S3 in the Supplementary Analyses). Notice also that the prediction accuracy on all non-constant genes was not significantly better, which could be interpreted that the gene expression data might not contain the relevant information to differentiate between the cell subtypes.

Considering the obvious overlaps of the two subclusters hAd1 and hAd2 (see Supplementary Data, Fig. S3), which becomes even more evident when viewing the interactive online visualization at Single Cell Portal, it is clear that the two subclusters share some similarities, possibly resulting in an overlapping expression pattern. This overlap could indicate that the label or the clustering (in different cell types/phenotypes) based on a genetic level is ambiguous. Therefore, a low prediction accuracy was to be expected since maybe due to a high noise or the recorded gene expression does not allow a clear deterministic relation between the two cell types.

3.4. Validation: using PFA to analyze a second dataset

To rule out the possibility that the observed high accuracy was specific to the data of this study [18] and to further validate our method, we generated another pool dataset with single-cell data published by another research group (“Deep learning enables genetic analysis of the human thoracic aorta” [32]) who provided their results in the h5ad-format. After converting the file into a Seurat object, we performed the same filtering steps as described above, creating Seurat objects for the cell types “Fibroblast I” and “Macrophage”. Since both subsets contained cells from the ascending aorta and the descending aorta, we split the subsets according to their ontology label before performing the filtering and the DoubletFinder workflow. Due to the relatively small number of macrophages, we created the pool data table using both ontologies, labeling all macrophages (derived from the ascending aorta and the descending aorta) as “0” and all cells of the “Fibroblast I” subset (derived from ascending and descending aorta) as “1″. Fig. 4 in the Supplementary Data shows the visualization of the two subsets (subset by cell type like our pool dataset).

Using single cell data derived from another data set yields similar results, indicating the utility of the PFA prediction for multiple types of data sets (Fig. 7 and Supplementary Data). For the analysis of “Fibroblast I” and “Macrophage”, a threshold of 0.5 (105 PFA genes) resulted in a test accuracy of 100%, whereas 105 random genes resulted in a test accuracy of less than 90% (89.05%). Even with a threshold of 0.9 (4 PFA genes), both test and training accuracy were greater than 98% (99.75% for test and 98.92% for train) when using the PFA genes, while the test and train accuracies obtained using 4 random genes were around 55%.

3.5. PFA validation summary

Table 2 summarizes the PFA results for the different analyses. As in Table 1, the prediction results based on the PFA gene selection in Table 2 are provided under “PFA genes”. The prediction accuracy based on all non-constant genes (meaning there is at least one single cell where the expression level differs from the others) is provided under “All genes”. This accuracy is provided as a control to estimate the highest possible accuracy on a dataset. The “Random genes” are the results based on randomly selected genes among all non-constant genes. The number coincides with the number of the PFA genes and delimits the PFA results from guessing genes.

When analyzing the same cell type (the adipocytes hAd1 and hAd2 of the human WAT data by Emont et al. (2022) [18]), a much greater number of genes (249 genes) was required for analysis. This resulted in a maximum accuracy of 100% in train and 86.27% in test, indicating the similarity between both adipocyte subtypes.

The pool data generated using the aorta cells of the second study [32], contained 33486 genes. However, our prediction method achieved up to 99.75% accuracy using only four genes.

In Table 1, Table 2, the prediction results based on the PFA gene selection are provided. The accuracy scores in the tables are the mean of twenty training sweeps since, besides the random selection of genes, the training procedure of the MLP classifier also includes random steps, where in each sweep a standard model is trained until convergence.

The mutual information files containing the names of the genes used during the respective predictions are available for all experiments in the supplementary information as correspondingly named CSV files, e.g., “gene_mutual_information_ASPCs_adipocytes.csv”.

All pool datasets derived from the single-cell data on human white adipose tissue published via the Single Cell Portal by [18] contained 31328 genes and the pool data generated using the aorta cells of the second study [32] contained 33486 genes. However, our predictions only required a fraction of these genes to achieve a prediction accuracy of at least 98.92% when analyzing two different cell types (Table 2). The prediction analyzing ASPCs and adipocytes required 13 genes, the prediction analyzing adipocytes and mesothelium required 12 genes, and the prediction analyzing endothelium and mesothelium required 10 genes.

When analyzing the same cell type (the adipocytes hAd1 and hAd2), a much greater number of genes (249 genes) was required for analysis. This resulted in a maximum accuracy of 100% in train and 86.27% in test, indicating the similarity between both adipocyte subtypes.

The pool data generated using the aorta cells of the second study [32] contained 33486 genes. However, our prediction method achieved up to 99.75% accuracy using only four genes.

3.6. Multiple cell types validation

Performing the same analysis steps using a dataset containing three or four different cell types, resulted in a comparable accuracy. For three cell types (1000 cells each of ASPCs, adipocytes, and mesothelium), a threshold of 0.38 resulted in 43 PFA genes and an accuracy of 99.06% for the training data and 99.63% for test data. This has a comparable accuracy as using all genes for the calculation (100% accuracy for train, 98.93% for test). Using 43 random genes instead of the selected PFA genes, resulted in an accuracy of 73.73% for train and 55.22% for test.

Analyzing four cell types at the same time (1000 cells each of ASPCs, adipocytes, endothelium, and mesothelium) resulted in a threshold of 0.35 and 51 PFA genes for an accuracy of 99.64% for train and 98.94% for test. This has a comparable accuracy as using all genes for the calculation (100% accuracy for train, 99.23% for test). Using 51 random genes instead of the 51 PFA genes caused the accuracy to drop to 69.11% for train and 51.35% for test. The detailed PFA results are available in the supplementary data.

3.7. Biological validation

We used several approaches to further validate our method and the resulting genes, which are also referred to as PFA genes. To validate the PFA genes, which were obtained by analyzing a subset containing 1000 cells of each cell type, we performed a PFA of the complete dataset containing all cells instead of only 1000 cells of each of the two cell types. Additionally, we analyzed the complete dataset using the Seurat test options DESeq2, Wilcoxon Rank Sum test, and Student’s t-test.

3.7.1. Validating the PFA genes

The original PFA dataset was created using the R-packages Seurat [13], [14], [15], [16] and DoubletFinder [17], following the respective preparation steps previously described [14], [17]. For the validation, we applied the same steps, but instead of keeping only the counts and replacing the cell names with the labels 0 and 1 for the respective groups, we merged the Seurat objects after removing the doublets. Thus, instead of a table containing the counts of the two analyzed groups (adipocytes and ASPCs in this example) and 0 and 1 instead of the individual cell names, we received a Seurat object containing all the information of the two cell types. This Seurat object, containing the same cells as the complete PFA table, was subsequently analyzed. The dimensional reduction plots generated using the Seurat Package show that this validation Seurat project only contains cells from the adipose tissue (Fig. 8A), has no batch effects and thus shows no differences between the cell types that are based on technical, non-biological factors (e.g., different sample handling procedures) (Fig. 8B), and contains only adipocytes and ASPCs (Fig. 8C).

The differences between adipocytes and ASPCs can be seen in Fig. 8C. While the adipocytes cluster closer to the top of the plot, the ASPCs cluster closer to the bottom of the plot, indicating differences between the expression of the two cell types. If the PFA genes allow a valid prediction of the respective cell types, their expression should be specific for one cell type. This is demonstrated in Fig. 8C by the clear separation of adipocytes and ASPCs. Subsequently, we visualized the gene expression of the 13 most significant PFA genes using the FeaturePlot() function with the respective gene name set as feature (Fig. 9 and Fig. 10).

The gene expression of the top-ranked PFA genes appears to be cell type specific for the nine highest ranked PFA genes (Fig. 9 and Fig. 10), and even MALAT1 (Fig. 10D), which is expressed by adipocytes and ASPCs, appears to be higher expressed in adipocytes. The last three PFA genes (HOOK2, ADIPOQ, and AL356479.1) also appear to be specific for adipocytes (Fig. 10).

When the complete data set is analyzed (containing all single cells of both cell types), all cells are taken into account, a total of 24589 cells. Using the same threshold of 0.5 as for the original PFA analysis, this results in four significant genes: CD36, ACACB, AQP7, and ADIPOQ, which appear to be specific for adipocytes (Fig. 11) and are among the 13 PFA genes (CD36 was ranked third, ACACB was ranked second, AQP7 was ranked fourth, and ADIPOQ was ranked 12th).

Fig. 11 — Results of the Seurat package FeaturePlot() visualization of the four most significant PFA genes (applying a threshold of 0.5) found using the complete data for PFA containing all cells of each group/cell type (adipocytes and ASPCs). (A) According to the complete PFA, CD36 was ranked first, the visualization shows that its expression appears to be specific for adipocytes. (B) According to the complete PFA, ACACB was ranked second, the visualization shows that its expression appears to be specific for adipocytes. (C) According to the complete PFA, AQP7 was ranked third, the visualization shows that its expression appears to be specific for adipocytes. (D) According to the complete PFA, ADIPOQ was the last of the significant genes (ranked fourth, last gene before the cut off), the visualization shows that its expression appears to be specific for adipocytes.

Since the PFA genes should be related to significant differences between the two cell types, we validated the PFA results using GO enrichment, treating the PFA genes as differentially expressed genes. Performing a GO Enrichment analysis using the PFA genes resulted in several biological processes related to metabolism and lipid storage (Fig. 12).

Fig. 12 — GO Enrichment analysis of the five PFA genes obtained by performing a standard PFA (1000 cells of each group) with a threshold of 0.6. (A) Pathways related to the five PFA genes that were selected by PFA to discern between adipocytes and ASPCs. (B) CNET Plot visualizing the linkages between the top five GO biological processes and the genes related to them.

3.7.2. Downstream analysis of the PFA genes – GO enrichment

Since the PFA genes should be related to significant differences between the two cell types, we validated the PFA results using GO enrichment, treating the PFA genes as differentially expressed genes. This analysis resulted in several biological processes related to metabolism and lipid storage (Fig. 12), indicating that the two cell types have different functions.

In their single cell atlas, Emont et al. (2022) chose the term ASPCs (“adipose stem and progenitor cells”) to refer to cells serving as stem cells or precursors or progenitors for adipocytes, which are also known under a variety of other names, including Lin(-) cells, ASCs (for adipose stem cells or adipose stromal cells), and pre-adipocytes [18]. ASPCs are a heterogeneous cell population and can be described as “adipocytes-to-be” [46]. A subpopulation of these cells which is referred to as adipose stem cells (ASCs) is assumed to represent mesenchymal stem cells that are multipotent, barely express genes specific for adipocytes, only commit to adipogenesis after exposure to the correct factors [46], and can be used in regenerative medicine [47].

Mature adipocytes are also a heterogenous cell population [18], [46] and are involved in systemic physiology and the regulation of the adipose depot [18]. In the post-prandial period, adipose tissue is involved in controlling circulating fatty acids [47]. Upon insulin stimulation, the uptake of fatty acids from circulating lipoproteins and glucose and the storage of triglycerides in the adipose tissue are increased, and lipolysis in adipocytes is inhibited [47]. In the long term, both differentiation of preadipocytes, another ASPC subpopulation [46], and lipogenesis in adipose tissue are promoted [47]. While the visceral adipose tissue (VAT) has been associated with obesity-related cardiometabolic diseases and inflammation, the subcutaneous adipose tissue (SAT) might even have a protective function [47]. Additionally, the adipose tissue metabolism might be connected to the expression of several sirtuins, indicating their potential therapeutic use for treating obesity [47]. For instance, reduced expression of the sirtuin SIRT6, which has been associated with genomic stability and aging as well as lipid metabolism and glucose homeostasis, might be involved in adipose tissue expansion [47].

To see whether the next threshold (0.6), which still resulted in a high accuracy but required only five genes, is still sufficient for subsequent analyses, we performed GO enrichment for the five PFA genes of the 0.6-threshold (Fig. 12). The CNET plot in Fig. 12B visualizes the top five biological processes of this analysis and the genes associated with them.

The GO enrichment analysis was repeated using the genes required to discern between adipocytes and ASPCs when using all cells (the complete data set, containing all single cells) and a threshold of 0.6 for PFA (Fig. 13). The CNET plot in Fig. 13B visualizes the top five biological processes of this analysis and the genes associated with them.

Fig. 13 — GO Enrichment analysis of the three PFA genes obtained via the complete PFA with a threshold of 0.6. (A) Pathways related to the three PFA genes that were selected by PFA to discern between adipocytes and ASPCs. (B) CNET Plot visualizing the linkages between the top five GO biological processes and the genes related to them.

Both enrichment analyses of the PFA genes result in pathways related to lipid storage, metabolism and energy homeostasis, which is unsurprising and highly relevant considering the known role of adipocytes in energy metabolism [48]. Please see Fig. 12 visualizing the top five pathways and the genes associated with these pathways when analyzing the genes that resulted from the PFA using 1000 cells of each cell type, and Fig. 13 visualizing the top five pathways and the genes associated with these pathways for the analysis using all cells of the pool data set (all cells of the adipocytes and ASCPs instead of only 1000 each). Via the lipogenic pathway, e.g., adipocytes in the WAT store excess energy in the form of triglycerides and release glycerol and fatty acids via the lipolytic pathway [49], [50]. Additionally, adipose tissue-derived factors can modulate the systemic metabolism [49], [50] and adipose tissue is known to regulate energy homeostasis [51]. This indicates that both the PFA genes and the genes resulting from analyzing the complete dataset are associated with adipocyte specific processes, which in turn indicates the importance of the PFA genes for discerning adipocytes and ASPCs. The results of the enrichment analyses of the other datasets as well as the PFA genes are available in the supplementary data (Pathways and mutual information, respectively).

3.7.3. Comparing the PFA results to standard methods

As a last validation step, we compared our PFA genes to marker genes found using the Seurat [13], [14], [15], [16] function FindMarkers(). Therefore, we analyzed the Seurat data set described above using the standard parameters of the FindMarkers() function and choosing three analysis options: “wilcox”, the default option, which identifies differentially expressed genes using a Wilcoxon Rank Sum test; “DESeq2″, which implements the functionalities of the DESeq2 package [20]; and “t”, which uses the Student’s t-test.

The respective results, which are available in the Supplementary Data (Supplementary Table 3 and the respective *.txt-files), were filtered according to their adjusted p-values, keeping only genes with p_val_adj< 0.05. This resulted in 2399 genes according to the Wilcoxon Rank Sum test (Fig. 14, green), 7827 according to the DESeq2 implementation (Fig. 14, yellow), and 2702 genes according to the Student’s t-test (Fig. 14, red). Except for MALAT1, which was not among the DEGs of the DESeq2 analysis, all of the 13 PFA genes were found by all three test methods.

Fig. 14 — Comparison of the PFA genes and the genes found using the FindMarkers() function of the Seurat package when analyzing adipocytes and ASPCs Comparing the top 13 PFA genes resulting from a threshold of 0.5 (blue) and all significant up- and downregulated genes according to the Seurat FindMarkers() test option “DESeq2″ (yellow, see Supplementary Data), all significant up- and downregulated genes according to the Seurat FindMarkers() test option “wilcox” (green, see Supplementary Data), and all significant up- and downregulated genes according to the Seurat FindMarkers() test option “t” (red, see Supplementary Data), respectively.

This demonstrates that all of the PFA genes are relevant marker genes for distinguishing between the two cell types. That seven of these genes are not among the most relevant genes of the standard Seurat analysis methods indicates that our algorithm is able to recognize possibly relevant genes that might have been overlooked using the other methods. Table 3 summarizes the respective ranks of the 13 PFA genes using the different methods.

Table 3.

The 13 PFA genes comparing adipocytes and ASPCs (threshold = 0.5) compared to their rank according to Seurat analysis using DESeq2, Wilcoxon Rank Sum test, and Student’s t-test, respectively.

Gene	PFA rank	DESeq2	Wilcoxon	Student's t test
GPAM	1	8 upregulated	2 upregulated	2 upregulated
ACACB	2	6 upregulated	4 upregulated	4 upregulated
CD36	3	5 upregulated	6 upregulated	6 upregulated
AQP7	4	38 upregulated	16 upregulated	16 upregulated
LIPE-AS1	5	14 upregulated	7 upregulated	7 upregulated
ITGA7	6	69 upregulated	24 upregulated	24 upregulated
NEGR1	7	5 downregulated	1 downregulated	1 downregulated
GYG2	8	40 upregulated	15 upregulated	15 upregulated
DIRC3	9	13 upregulated	9 upregulated	9 upregulated
MALAT1	10	-	189 upregulated	189 upregulated
HOOK2	11	68 upregulated	29 upregulated	29 upregulated
ADIPOQ	12	43 upregulated	25 upregulated	25 upregulated
AL356479.1	13	45 upregulated	18 upregulated	18 upregulated

Open in a new tab

The ranking depends on the analysis method. The different ranking of several of the genes using different analysis methods (Table 3) indicates that some genes resulting from PFA analysis might not have been among the genes of interest resulting from one of the other methods. Other genes, such as ACACB, were among the top genes for all analysis methods. This shows that the PFA removes redundancy without removing relevant information.

In summary, our method is able to find a set of genes that appear characteristic for the differences between the cell types. With a threshold of 0.5 of mutual information between a gene expression and the label, about half of these genes are also among the top DEGs found by other methods. However, the other genes are also cell type specific even though they are not among the top-rated genes when using the other methods. This opens two possible uses: (i) As a threshold of 0.6 still yields sufficient accuracy, not all of the genes are required to correctly identify the cell type, which means that reducing the number of genes might improve the time required for sorting the cell types. (ii) The genes that are not strictly necessary for recognizing the cell type efficiently are still cell type specific but not among the top genes other methods find. Therefore, these genes might reveal interesting insights that might not have been obvious using other methods. One example is ITGA7.

4. Discussion

In this work, we use principal feature analysis (PFA) to identify those genes which carry the highest information suitable to separate the groups we want to distinguish. The PFA is a powerful new approach brought in this paper to the analysis of gene selection or biological features in general. It does not matter how many groups we want to distinguish nor by which method the different groups were established first. This can be done by any gene method of choice or any combination of several methods. However, as long as our mathematical approach has not yet been applied to these data, we can use it advantageously to improve the analysis in identifying the genes with the highest information content regarding separation of the two groups.

To illustrate the power of our approach we implemented, provided and explained PFA in a software pipeline starting with gene selection using Seurat and using PFA to judge and improve the quality of the separation of the gene clusters established by our gene selection method (starting with Seurat). PFA hence delivers optimally separating small gene sets and hence PFA and our implemented pipeline is advantageously used to analyze single-cell data. Our pipeline identifies genes carrying information to determine to which cluster/cell type a single cell belongs based on the expression data of the genes. It allows to objectively determine cell-type specific signatures for any type of omics data by these criteria.

We trained and tested the application with a subset of single-cell data downloaded from the Single Cell Portal using a study that identified different cell types in human white adipose tissue [18]. To verify the application, we used different subsets of the study [18] as well as single-cell data generated during another study of human thoracic aorta [32].

Validation is necessary for our method. However, as we do not have a clustering method but rather a method to evaluate the genes best separating clusters established by any method of choice. K-fold validation cannot be directly applied but the procedure has to be modified as follows: K-fold cross validation would mean to do the PFA selection process on each of the K sets and do the mutual information approximation on each of the K sets. Subsequently, we could compare intersections of the results and come to an overall gene set.

Though this is a valid selection procedure, however, each run might not deliver a unique set of genes that each fulfils the requirement of carrying the necessary information: As an example, take two disjunct pathways with each 5 genes that are linearly downstream connected in each pathway. The expression of the 5 genes in one pathway is correlated assuming that only the top gene gets regulated by the environment. Then any combination of two genes where the first one is from the first pathway and the second one is from the second pathway is a valid result of the PFA selection process. Depending on small variations of the (pool sampled K-fold) data set, different combination can come out. However, each combination fulfils our requirement of carrying the full information needed to describe the expression state of the total gene network. With a K-fold selection process it can be that we get each time a different combination.

The validation of our pipeline is as follows: We take a part of our data (samples), decide for a selection of genes, and if they pass the validation, meaning carrying the information to separate cells also on other not seen data, then we can proceed to go into a reasoning process where the causality is in the focus and an explanation why these genes are important for the difference from a biological perspective.

Our pipeline can of course be used in a K-fold cross validation by dividing the total data set into K data sets and do our pipeline within each auf the K data sets. However, in terms of correlation and the example mentioned above, there is no evidence why a broad intersection of genes from each K-fold set indicates causality or why the intersection has potential for a good explanation.

From our pipeline, we used a small but meaningful set of genes on which a model could be built to classify the single cells. We used cell types that showed a clear clustering in a UMAP plot and thus demonstrate for the first time that our pipeline can be used to explain UMAP plots in an explainable AI scenario applied in life science.

Apart from explaining UMAP or t-SNE plots or the differences between cell types that are defined, e.g., via markers, there are further applications such as the following.

If we have, e.g., tumor cells in culture that are known to be resistant to a specific treatment, we can split the culture and measure the gene expression of single cells before (one split) and during/after (the other split) the treatment. The genes resulting from our pipeline might be the genes that are triggered by the treatment and might be responsible for the resistance. Blocking these genes with another drug during therapy and thus avoiding the transition to the different gene expression program might result in a successful compound therapy.

Another approach could be to analyze resistant and non-resistant tumor cells with our pipeline. The differences in the expression profiles could also hint at which genes/genetic expression program is important for the resistance. The resulting potential therapeutic targets might be adjusted with a drug before or during treatment.

Similarly, healthy and tumor cells can be analyzed to see differences in the expression profile.

The unique contribution of our pipeline is that it does not focus on approximating the whole dataset by capturing some amount of variance, like the principal component analysis, but directs the view to the genes in the dataset relevant for describing the differences. Furthermore, since we reduce redundancy, we provide a minimal span of genes that is important for this difference. Since the set might be much smaller than a gene set provided by a differential expression study, it fosters experimental investigation by narrowing down possible drug targets, for instance.

In case the important pathways in total are of interest, there are two ways to approach this. If one knows the associated pathways of the genes selected by our, e.g., by experience/domain knowledge or a database, then pathways are identified. If there is no hint for pathways, we can use the adjacency matrix of the independence graph assembled during the PFA to check with which genes a PFA-selected gene is associated. Since genes within the same pathway take their expression value not independent of each other, the adjacency matrix connects genes that take their expression values not independently of each other and thus provides valuable information for identifying pathways starting from the genes returned by our pipeline checking to which genes a PFA-gene is connected in the dependence graph. Please see Breitenbach et al. (2022) [4], particularly Section 2, for details about the chi-square test of independence and the resulting dependence graph with corresponding adjacency matrix. By this procedure for identifying pathways, we can reinduce redundancy purposefully.

The PFA is not limited to discrete labels representing the output function as the cell types. Apart from a binary label, multi classes can also be investigated where our pipeline provides a minimal set of genes to cluster a single cell into one of the multi classes. The PFA can also be used for vector-valued output functions with continuous ranges to describe, e.g., RNA counts as a function of morphological information, as presented in Haghighi et al. (2022) [52].

A further application of a multi-dimensional output function with continuous values is the integrative model (Fig. 6F in Neftel et al. (2019) [53]) where the 2-dimensional coordinates of the cells in the plot can be used as the values for the output function of the PFA method to obtain genes from where the transitions to the different cell states might be modeled.

The label row in the input data file only needs to be filled accordingly or the several first rows in the file in case of an output vector, adjusting the number_output_functions in the PFA scripts to the dimension of the label vector. No code needs to be adjusted. Thus, the PFA may support the cut-off of relevant data in such big data scenarios, which may improve model accuracy, explainability of the models, and scalability of the data.

The rationale is that our approach is generic, not limited to purely genetic data, and thus a strong method to identify the key features of complex datasets and reduce the complexity of large-scale datasets while identifying the key gene clusters/features and signatures. The recent publication by Haghighi et al. (2022) [52] provides a case in point.

The limitations of our pipeline are essentially the same as those of the method used for gene selection. We applied the novel mathematical method of PFA to biological data, focusing on single cell sequencing data focusing on identification of gene sets representing each cluster.

Resulting mathematical limitations are discussed in detail in Breitenbach et al. (2022) [4]. Briefly, the main point is that if the dataset is missing independent information, e.g., the expression of some genes or DNA segments, respectively, is not measured and included in the dataset, then important information can be lost by removing genes from the dataset that carry important information for classifying the single cells. Mathematically spoken, if not all relevant arguments of a function are in the data set, the function that is removed could have had some information to restore the information of the missing argument in some cases. However, with our pipeline setting, this effect has never been relevant, if it happened at all, since the accuracy of our validation step was very high, indicating that sufficient relevant genes have been selected. Since in the current implementation a chi-square test for independence is used, we need to ensure that the mathematical assumptions for the chi-square test are fulfilled, like that in each entry of the contingency table at least 5 data points are expected. As an alternative to the chi-square test, we can use any other statistical test which fits more to a small number of single cells and which does not rely on the assumptions of the chi-square test. However, if the number of single cells (or in general measurements) is low, we never know how sensitive results are when we would do the analysis on another small data set. In the case of a small data set, we rather recommend working on the measurement process to make a bigger data set possible. Such an improvement is always beneficial independent of the methods used.

Even if there is a lack of labels between which a difference in the expression profile is to be identified, the PFA could be used. For this purpose, the first stage of the PFA could be utilized to reduce the dimensionality of the space that represents the single-cell measurements where the expression of each gene is a dimension. The first stage of the PFA cancels out genes that are a function of others, leaving the relevant genes that drive the dynamic in the single-cell dataset. As described in Breitenbach et al. (2022) [24], performing this reduction as a preprocessing step might mitigate the curse of dimensionality [31], facilitating the clustering with, e.g., t-SNE or UMAP. Thus, in future research, it will be valuable to investigate how this first part of our pipeline might contribute to clustering single cells and thus identifying or defining cell types in sophisticated scenarios where genes with redundant information cause a curse of dimensionality.

More specific, the procedure could look as follows in the case of unknown cell types. Before the UMAP or t-SNE clustering, we could use the part of the PFA that reduces redundant genes and return only these genes that are relevant as arguments for the measured dynamics within the single-cell dataset. Next, for the determined clusters in the plane returned by the UMAP/t-SNE algorithms, a density-based clustering could be performed like DBSCAN to automatically label according to the UMAP/t-SNE clustering. Alternatively, marking the clusters manually by defining coordinates (guided by the UMAP/t-SNE clusters) within which data points should get the same label is also possible. In a final step, identifying differences in the expression levels between clusters might provide markers to define and separate these cell types from each other on a phenotypic level in the considered scenario. Additionally, we can use the identified differences on a genetic as well as on an expression level to analyze and explain if cell type definitions are reasonable, including context information in which the single-cells are cultured and measured.

Next, we discuss our findings from our investigated data sets, using the top thirteen PFA genes found by analyzing adipocytes and ASPCs. First ranked (according to PFA) was glycerol-3-phosphate acyltransferase (GPAM), which is mainly expressed in adipose tissue by adipocytes, according to its entry in the Human Protein Atlas [54], [55]. Acetyl-CoA carboxylase beta (ACACB), which was ranked second by PFA, is also associated with adipose tissue and is, according to its entry in the Human Protein Atlas, most abundant in adipocytes [54], [55]. CD36, which is also associated with adipose tissue and adipocytes [54], [55], is known to play a role in the absorption of long-chain fatty acids [56]. The fourth PFA gene, aquaporin 7 (AQP7), is also involved in energy metabolism and expressed in adipose tissue [57]. The LIPE antisense RNA 1 (LIPE-AS1), which has recently been reported as spanning the genes Ceacam1 to Lipe and potentially playing a role in adipogenesis [58], is primarily expressed in adipose tissue but also in adrenal and testis tissue [54], [55]. The integrin subunit alpha 7 (ITGA7), which is primarily expressed in adipose but also in heart tissue [54], is, according to the Human Protein Atlas, expressed in several tissues and cell type enriched in adipocytes in subcutaneous, visceral and breast tissue [55]. The seventh PFA gene, neuronal growth regulator 1 (NEGR1), is the only PFA gene that was associated with ASPCs in our analysis, and while it is also expressed in adipose tissue, it is primarily expressed in the brain [54] and has only recently been associated with a possible role in human obesity [59] and interaction with CD36 [60]. The glucose-metabolism-related glycogenin 2 (GYG2) [61], is highly expressed in adipose tissue [54], and according to the Human Protein Atlas, cell type enriched in adipocytes in several tissues [55]. Like GYG2, the ninth PFA gene, disrupted in renal carcinoma 3 (DIRC3), has been associated with renal cancer [61], [62]. It is expressed in a variety of tissues, including adipose tissue [54]. The tenth PFA gene metastasis associated lung adenocarcinoma transcript 1 (MALAT1) is primarily expressed in bone marrow although it is also expressed in a variety of other tissues, including adipose tissue [54]. According to our analysis, it is slightly higher expressed in adipocytes compared to ASPCs (Fig. 9I). Although it is included in the PFA genes resulting from using a threshold of 0.5, it might not carry substantial information for the classification, since a threshold of 0.6, which results in only five PFA genes, is sufficient for a correctness of 99% (see Supplementary Data) where MALAT1 is not contained. However, the result might also indicate a need for further research since the ML algorithm also predicted LIPE-AS1, whose role in adipogenesis only recently emerged [58] and NEGR1, whose participation in regulating the cellular fat content was only reported last year [60]. HOOK2, which was ranked 11th, has been found to be differentially methylated in individuals with obesity and type 2 diabetes and might play a role in type 2 diabetes [63]. ADIPOQ, which was identified as an adipose gene in 1996 [64], might be a candidate gene for renal disease and diabetes [65]. AL356479.1 has – as MALAT1 – been associated with breast cancer [66] and appears to have significant effect on breast cancer survival [67]. This could be due to the majority of the tissue donors in Emont et al.’s study being female [18] and might indicate existing or future health problems for some of the study participants, or might indicate a so far unknown function of AL356479.1 in adipocytes. All of these genes coincide with the most relevant genes of the PFA analysis, indicating that PFA is a reliable method for finding potentially relevant DEGs or cell type markers and can be used to find DEGs that might have been overlooked by using the standard analysis methods.

5. Conclusion

In this work, we have applied a principal feature analysis (PFA) to analyze single cell data sets to identify genes separating cell types/phenotypes/classes (cell type-specific signatures). A software pipeline was developed consisting of a preprocessing Seurat framework and an analysis part consisting of the PFA and mutual information. The gene selection was tested with a machine learning framework to balance accuracy and the number of relevant genes in a meaningful small set of selected genes. A further contribution of our pipeline is in the area of explainable artificial intelligence (AI) since the pipeline provides foundations for understandable reasoning for the phenotypic difference from the identified genes. Future research will apply the pipeline to discover even molecular disease pathways, for instance those responsible for tumor cells becoming resistant to therapies. In the example, this would be new pharmacological inhibitors that prevent cells from switching to a tumor resistance program and reducing side-effects in general by better targeting the relevant genes and their gene products.

Author’s contribution

AC performed the data analysis and the Seurat analyses validating the PFA results. AC, DC, TB implemented the code for the analysis pipeline. DC created the Randomizer script. LR, TB worked out the parallel version of the PFA and LR implemented and optimized the corresponding version. WY was involved in the data analysis. TB drafted the manuscript and AC, TB, TD were involved in writing and revising the manuscript. TB drafted and worked out the concept of the pipeline. AC prepared the data sets for the pipeline and created the preparation workflow. TB and LR implemented the subsequent steps. TB and TD co-supervised the study.

Declaration of Competing Interest

The authors declare that they have no competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

We thank Sara Giddins for proofreading of the manuscript. Furtermore, we thank DFG for funding (project number 492620490/SFB1583-INF) and the Julius-Maximilians-University of Würzburg for support by its open access publication program.

Footnotes

^{Appendix A}

Supplementary data associated with this article can be found in the online version at doi:10.1016/j.csbj.2023.06.002.

Contributor Information

Thomas Dandekar, Email: dandekar@biozentrum.uni-wuerzburg.de.

Tim Breitenbach, Email: tim.breitenbach@mathematik.uni-wuerzburg.de.

Appendix A. Supplementary material

Supplementary material

mmc1.zip^{(502.7KB, zip)}

Supplementary material

mmc2.pdf^{(17.3KB, pdf)}

Supplementary material

mmc3.zip^{(5.6MB, zip)}

Supplementary material

mmc4.xlsx^{(9.4KB, xlsx)}

References

1.Solé-Boldo L., et al. Single-cell transcriptomes of the human skin reveal age-related loss of fibroblast priming. Commun Biol. 2020;3(1):188. doi: 10.1038/s42003-020-0922-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Hwang B., Lee J.H., Bang D. Single-cell RNA sequencing technologies and bioinformaticspipelines. Exp Mol Med. 2018;50(8):1–14. doi: 10.1038/s12276-018-0071-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
3.What are stem cells? Nature Reports Stem Cells, 2007.
4.Breitenbach T., et al. A principal feature analysis. J Comput Sci. 2022;58 [Google Scholar]
5.Pont F., Tosolini M., Fournié J.J. Single-cell signature explorer for comprehensive visualization of single cell signatures across scRNA-seq datasets. Nucleic Acids Res. 2019;47(21) doi: 10.1093/nar/gkz601. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Levitin H.M., et al. De novo gene signature identification from single-cell RNA-seq with hierarchical Poisson factorization. Mol Syst Biol. 2019;15(2) doi: 10.15252/msb.20188557. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Cortal A., et al. Gene signature extraction and cell identity recognition at the single-cell level with Cell-ID. Nat Biotechnol. 2021;39(9):1095–1102. doi: 10.1038/s41587-021-00896-6. [DOI] [PubMed] [Google Scholar]
8.Pasquini G., et al. Automated methods for cell type annotation on scRNA-seq data. Comput Struct Biotechnol J. 2021;19:961–969. doi: 10.1016/j.csbj.2021.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Lopez R., et al. Deep generative modeling for single-cell transcriptomics. Nat Methods. 2018;15(12):1053–1058. doi: 10.1038/s41592-018-0229-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Hu J., et al. Iterative transfer learning with neural network for clustering and cell type classification in single-cell RNA-seq analysis. Nat Mach Intell. 2020;2(10):607–618. doi: 10.1038/s42256-020-00233-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Wang B., et al. Visualization and analysis of single-cell RNA-seq data by kernel-based similarity learning. Nat Methods. 2017;14(4):414–416. doi: 10.1038/nmeth.4207. [DOI] [PubMed] [Google Scholar]
12.Brbić M., et al. MARS: discovering novel cell types across heterogeneous single-cell experiments. Nat Methods. 2020;17(12):1200–1206. doi: 10.1038/s41592-020-00979-3. [DOI] [PubMed] [Google Scholar]
13.Satija R., et al. Spatial reconstruction of single-cell gene expression data. Nat Biotechnol. 2015;33(5):495–502. doi: 10.1038/nbt.3192. [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Butler A., et al. Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat Biotechnol. 2018;36(5):411–420. doi: 10.1038/nbt.4096. [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Stuart T., et al. Comprehensive integration of single-cell data. Cell. 2019;177(7):1888–1902. doi: 10.1016/j.cell.2019.05.031. e21. [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Hao Y., et al. Integrated analysis of multimodal single-cell data. Cell. 2021;184(13):3573–3587. doi: 10.1016/j.cell.2021.04.048. e29. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.McGinnis C.S., Murrow L.M., Gartner Z.J. DoubletFinder: doublet detection in single-cell RNA sequencing data using artificial nearest neighbors. Cell Syst. 2019;8(4):329–337. doi: 10.1016/j.cels.2019.03.003. e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Emont M.P., et al. A single-cell atlas of human and mouse white adipose tissue. Nature. 2022;603(7903):926–933. doi: 10.1038/s41586-022-04518-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Robinson M.D., McCarthy D.J., Smyth G.K. edgeR: a Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics. 2010;26(1):139–140. doi: 10.1093/bioinformatics/btp616. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Love M.I., Huber W., Anders S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014;15(12):550. doi: 10.1186/s13059-014-0550-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Hafemeister C., Satija R. Normalization and variance stabilization of single-cell RNA-seq data using regularized negative binomial regression. Genome Biol. 2019;20(1):296. doi: 10.1186/s13059-019-1874-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
22.McKnight P.E., Najab J. Mann-Whitney U Test. Corsini Encycl Psychol. 2010:1-1. [Google Scholar]
23.Schmitt M.J., et al. Phenotypic mapping of pathologic cross-talk between glioblastoma and innate immune cells by synthetic genetic tracing. Cancer Discov. 2021;11(3):754–777. doi: 10.1158/2159-8290.CD-20-0219. [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Breitenbach T., Schmitt M.J., Dandekar T. Optimization of synthetic molecular reporters for a mesenchymal glioblastoma transcriptional program by integer programing. Bioinformatics. 2022;38(17):4162–4171. doi: 10.1093/bioinformatics/btac488. [DOI] [PubMed] [Google Scholar]
25.Cai R., et al. An efficient gene selection algorithm based on mutual information. Neurocomputing. 2009;72(4):991–999. [Google Scholar]
26.Guyon I., et al. Gene selection for cancer classification using support vector machines. Mach Learn. 2002;46(1):389–422. [Google Scholar]
27.Peng H., Long F., Ding C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans Pattern Anal Mach Intell. 2005;27(8):1226–1238. doi: 10.1109/TPAMI.2005.159. [DOI] [PubMed] [Google Scholar]
28.Li J., et al. Feature selection: a data perspective. ACM Comput Surv. 2017;50:6. [Google Scholar]
29.Kobak D., Berens P. The art of using t-SNE for single-cell transcriptomics. Nat Commun. 2019;10(1):5416. doi: 10.1038/s41467-019-13056-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Dorrity M.W., et al. Dimensionality reduction by UMAP to visualize physical and genetic interactions. Nat Commun. 2020;11(1):1537. doi: 10.1038/s41467-020-15351-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Rather A.A., Chachoo M.A. Manifold learning based robust clustering of gene expression data for cancer subtyping. Inform Med Unlocked. 2022;30 [Google Scholar]
32.Pirruccello J.P., et al. Deep learning enables genetic analysis of the human thoracic aorta. Nat Genet. 2022;54(1):40–51. doi: 10.1038/s41588-021-00962-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Luecken M.D., Theis F.J. Current best practices in single-cell RNA-seq analysis: a tutorial. Mol Syst Biol. 2019;15(6) doi: 10.15252/msb.20188746. [DOI] [PMC free article] [PubMed] [Google Scholar]
34.Wolock S.L., Lopez R., Klein A.M. Scrublet: computational identification of cell doublets in single-cell transcriptomic data. Cell Syst. 2019;8(4):281–291. doi: 10.1016/j.cels.2018.11.005. e9. [DOI] [PMC free article] [PubMed] [Google Scholar]
35.Gayoso A., Shor J. Zenodo; 2022. JonathanShor/DoubletDetection: doubletdetection v4.2 (v4.2) [Google Scholar]
36.DePasquale E.A.K., et al. DoubletDecon: deconvoluting doublets from single-cell RNA-sequencing data. Cell Rep. 2019;29(6):1718–1727. doi: 10.1016/j.celrep.2019.09.082. e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
37.Wu T., et al. clusterProfiler 4.0: a universal enrichment tool for interpreting omics data. Innovation. 2021;2(3) doi: 10.1016/j.xinn.2021.100141. [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Yu G., et al. clusterProfiler: an R Package for Comparing Biological Themes Among Gene Clusters. OMICS: A J Integr Biol. 2012;16(5):284–287. doi: 10.1089/omi.2011.0118. [DOI] [PMC free article] [PubMed] [Google Scholar]
39.Yu, G., enrichplot: Visualization of Functional Enrichment Result. 2022, R package: 〈https://www.bioconductor.org/packages/release/bioc/html/enrichplot.html〉 and 〈https://yulab-smu.top/biomedical-knowledge-mining-book/〉.
40.Wickham H. Springer-Verlag New York; 2016. ggplot2: Elegant Graphics for Data Analysis. [Google Scholar]
41.Subramanian A., et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci. 2005;102(43):15545–15550. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
42.Liberzon A., et al. The molecular signatures database hallmark gene set collection. Cell Syst. 2015;1(6):417–425. doi: 10.1016/j.cels.2015.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
43.Ashburner M., et al. Gene Ontology: tool for the unification of biology. Nat Genet. 2000;25(1):25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
44.The Gene Ontology Consortium The gene ontology resource: enriching a gold mine. Nucleic Acids Res. 2021;49(D1):D325–D334. doi: 10.1093/nar/gkaa1113. [DOI] [PMC free article] [PubMed] [Google Scholar]
45.Mi H., et al. PANTHER version 14: more genomes, a new PANTHER GO-slim and improvements in enrichment analysis tools. Nucleic Acids Res. 2019;47(D1):D419–D426. doi: 10.1093/nar/gky1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
46.Ferrero R., Rainer P., Deplancke B. Toward a consensus view of mammalian adipocyte stem and progenitor cell heterogeneity. Trends Cell Biol. 2020;30(12):937–950. doi: 10.1016/j.tcb.2020.09.007. [DOI] [PubMed] [Google Scholar]
47.Porro S., et al. Dysmetabolic adipose tissue in obesity: morphological and functional characteristics of adipose stem cells and mature adipocytes in healthy and unhealthy obese subjects. J Endocrinol Investig. 2021;44(5):921–941. doi: 10.1007/s40618-020-01446-8. [DOI] [PubMed] [Google Scholar]
48.Morigny P., et al. Lipid and glucose metabolism in white adipocytes: pathways, dysfunction and therapeutics. Nat Rev Endocrinol. 2021;17(5):276–295. doi: 10.1038/s41574-021-00471-8. [DOI] [PubMed] [Google Scholar]
49.Rosen E.D., Spiegelman B.M. Adipocytes as regulators of energy balance and glucose homeostasis. Nature. 2006;444(7121):847–853. doi: 10.1038/nature05483. [DOI] [PMC free article] [PubMed] [Google Scholar]
50.Luo L., Liu M. Adipose tissue in control of metabolism. J Endocrinol. 2016;231(3):R77–R99. doi: 10.1530/JOE-16-0211. [DOI] [PMC free article] [PubMed] [Google Scholar]
51.Parra-Peralbo E., Talamillo A., Barrio R. Origin and development of the adipose tissue, a key organ in physiology and disease. Front Cell Dev Biol. 2021:9. doi: 10.3389/fcell.2021.786129. [DOI] [PMC free article] [PubMed] [Google Scholar]
52.Haghighi M., et al. High-dimensional gene expression and morphology profiles of cells across 28,000 genetic and chemical perturbations. Nat Methods. 2022;19(12):1550–1557. doi: 10.1038/s41592-022-01667-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
53.Neftel C., et al. An integrative model of cellular states, plasticity, and genetics for glioblastoma. Cell. 2019;178(4):835–849. doi: 10.1016/j.cell.2019.06.024. e21. [DOI] [PMC free article] [PubMed] [Google Scholar]
54.Fagerberg L., et al. Analysis of the human tissue-specific expression by genome-wide integration of transcriptomics and antibody-based proteomics *. Mol Cell Proteom. 2014;13(2):397–406. doi: 10.1074/mcp.M113.035600. [DOI] [PMC free article] [PubMed] [Google Scholar]
55.Uhlén M., et al. Tissue-based map of the human proteome. Science. 2015;347(6220):1260419. doi: 10.1126/science.1260419. [DOI] [PubMed] [Google Scholar]
56.Masuda D., et al. Chylomicron remnants are increased in the postprandial state in CD36 deficiency. J Lipid Res. 2009;50(5):999–1011. doi: 10.1194/jlr.P700032-JLR200. [DOI] [PMC free article] [PubMed] [Google Scholar]
57.Iena F.M., Lebeck J. Implications of aquaglyceroporin 7 in energy metabolism. Int J Mol Sci. 2018:19. doi: 10.3390/ijms19010154. [DOI] [PMC free article] [PubMed] [Google Scholar]
58.Thunen A., et al. Role of lncRNA LIPE-AS1 in adipogenesis. Adipocyte. 2022;11(1):11–27. doi: 10.1080/21623945.2021.2013415. [DOI] [PMC free article] [PubMed] [Google Scholar]
59.Kim H., et al. The new obesity-associated protein, neuronal growth regulator 1 (NEGR1), is implicated in Niemann-Pick disease Type C (NPC2)-mediated cholesterol trafficking. Biochem Biophys Res Commun. 2017;482(4):1367–1374. doi: 10.1016/j.bbrc.2016.12.043. [DOI] [PubMed] [Google Scholar]
60.Yoo A., et al. Neuronal growth regulator 1 promotes adipocyte lipid trafficking via interaction with CD36. J Lipid Res. 2022;63(6) doi: 10.1016/j.jlr.2022.100221. [DOI] [PMC free article] [PubMed] [Google Scholar]
61.Wang S., et al. Identification of a glucose metabolism-related signature for prediction of clinical prognosis in clear cell renal cell carcinoma. J Cancer. 2020;11(17):4996–5006. doi: 10.7150/jca.45296. [DOI] [PMC free article] [PubMed] [Google Scholar]
62.Bodmer D., et al. Disruption of a novel gene, DIRC3, and expression of DIRC3-HSPBAP1 fusion transcripts in a case of familial renal cell cancer and t(2;3)(q35;q21) Genes Chromosomes Cancer. 2003;38(2):107–116. doi: 10.1002/gcc.10243. [DOI] [PubMed] [Google Scholar]
63.Rodríguez-Rodero S., et al. Altered intragenic DNA methylation of HOOK2 gene in adipose tissue from individuals with obesity and type 2 diabetes. PLoS One. 2017;12(12) doi: 10.1371/journal.pone.0189153. [DOI] [PMC free article] [PubMed] [Google Scholar]
64.Hu E., Liang P., Spiegelman B.M. AdipoQ is a novel adipose-specific gene dysregulated in obesity. J Biol Chem. 1996;271(18):10697–10703. doi: 10.1074/jbc.271.18.10697. [DOI] [PubMed] [Google Scholar]
65.Simeone C.A., et al. A dominant negative ADIPOQ mutation in a diabetic family with renal disease, hypoadiponectinemia, and hyperceramidemia. npj Genomic Med. 2022;7(1):43. doi: 10.1038/s41525-022-00314-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
66.Wang D., et al. Comprehensive biological function analysis of lncRNAs in hepatocellular carcinoma. Genes Dis. 2021;8(2):157–167. doi: 10.1016/j.gendis.2019.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
67.Wang J.J., et al. Comprehensive analysis of the lncRNA‑associated competing endogenous RNA network in breast cancer. Oncol Rep. 2019;42(6):2572–2582. doi: 10.3892/or.2019.7374. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary material

mmc1.zip^{(502.7KB, zip)}

Supplementary material

mmc2.pdf^{(17.3KB, pdf)}

Supplementary material

mmc3.zip^{(5.6MB, zip)}

Supplementary material

mmc4.xlsx^{(9.4KB, xlsx)}

[bib1] 1.Solé-Boldo L., et al. Single-cell transcriptomes of the human skin reveal age-related loss of fibroblast priming. Commun Biol. 2020;3(1):188. doi: 10.1038/s42003-020-0922-4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib2] 2.Hwang B., Lee J.H., Bang D. Single-cell RNA sequencing technologies and bioinformaticspipelines. Exp Mol Med. 2018;50(8):1–14. doi: 10.1038/s12276-018-0071-8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib3] 3.What are stem cells? Nature Reports Stem Cells, 2007.

[bib4] 4.Breitenbach T., et al. A principal feature analysis. J Comput Sci. 2022;58 [Google Scholar]

[bib5] 5.Pont F., Tosolini M., Fournié J.J. Single-cell signature explorer for comprehensive visualization of single cell signatures across scRNA-seq datasets. Nucleic Acids Res. 2019;47(21) doi: 10.1093/nar/gkz601. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib6] 6.Levitin H.M., et al. De novo gene signature identification from single-cell RNA-seq with hierarchical Poisson factorization. Mol Syst Biol. 2019;15(2) doi: 10.15252/msb.20188557. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib7] 7.Cortal A., et al. Gene signature extraction and cell identity recognition at the single-cell level with Cell-ID. Nat Biotechnol. 2021;39(9):1095–1102. doi: 10.1038/s41587-021-00896-6. [DOI] [PubMed] [Google Scholar]

[bib8] 8.Pasquini G., et al. Automated methods for cell type annotation on scRNA-seq data. Comput Struct Biotechnol J. 2021;19:961–969. doi: 10.1016/j.csbj.2021.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib9] 9.Lopez R., et al. Deep generative modeling for single-cell transcriptomics. Nat Methods. 2018;15(12):1053–1058. doi: 10.1038/s41592-018-0229-2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib10] 10.Hu J., et al. Iterative transfer learning with neural network for clustering and cell type classification in single-cell RNA-seq analysis. Nat Mach Intell. 2020;2(10):607–618. doi: 10.1038/s42256-020-00233-7. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib11] 11.Wang B., et al. Visualization and analysis of single-cell RNA-seq data by kernel-based similarity learning. Nat Methods. 2017;14(4):414–416. doi: 10.1038/nmeth.4207. [DOI] [PubMed] [Google Scholar]

[bib12] 12.Brbić M., et al. MARS: discovering novel cell types across heterogeneous single-cell experiments. Nat Methods. 2020;17(12):1200–1206. doi: 10.1038/s41592-020-00979-3. [DOI] [PubMed] [Google Scholar]

[bib13] 13.Satija R., et al. Spatial reconstruction of single-cell gene expression data. Nat Biotechnol. 2015;33(5):495–502. doi: 10.1038/nbt.3192. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib14] 14.Butler A., et al. Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat Biotechnol. 2018;36(5):411–420. doi: 10.1038/nbt.4096. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib15] 15.Stuart T., et al. Comprehensive integration of single-cell data. Cell. 2019;177(7):1888–1902. doi: 10.1016/j.cell.2019.05.031. e21. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib16] 16.Hao Y., et al. Integrated analysis of multimodal single-cell data. Cell. 2021;184(13):3573–3587. doi: 10.1016/j.cell.2021.04.048. e29. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib17] 17.McGinnis C.S., Murrow L.M., Gartner Z.J. DoubletFinder: doublet detection in single-cell RNA sequencing data using artificial nearest neighbors. Cell Syst. 2019;8(4):329–337. doi: 10.1016/j.cels.2019.03.003. e4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib18] 18.Emont M.P., et al. A single-cell atlas of human and mouse white adipose tissue. Nature. 2022;603(7903):926–933. doi: 10.1038/s41586-022-04518-2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib19] 19.Robinson M.D., McCarthy D.J., Smyth G.K. edgeR: a Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics. 2010;26(1):139–140. doi: 10.1093/bioinformatics/btp616. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib20] 20.Love M.I., Huber W., Anders S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014;15(12):550. doi: 10.1186/s13059-014-0550-8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib21] 21.Hafemeister C., Satija R. Normalization and variance stabilization of single-cell RNA-seq data using regularized negative binomial regression. Genome Biol. 2019;20(1):296. doi: 10.1186/s13059-019-1874-1. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib22] 22.McKnight P.E., Najab J. Mann-Whitney U Test. Corsini Encycl Psychol. 2010:1-1. [Google Scholar]

[bib23] 23.Schmitt M.J., et al. Phenotypic mapping of pathologic cross-talk between glioblastoma and innate immune cells by synthetic genetic tracing. Cancer Discov. 2021;11(3):754–777. doi: 10.1158/2159-8290.CD-20-0219. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib24] 24.Breitenbach T., Schmitt M.J., Dandekar T. Optimization of synthetic molecular reporters for a mesenchymal glioblastoma transcriptional program by integer programing. Bioinformatics. 2022;38(17):4162–4171. doi: 10.1093/bioinformatics/btac488. [DOI] [PubMed] [Google Scholar]

[bib25] 25.Cai R., et al. An efficient gene selection algorithm based on mutual information. Neurocomputing. 2009;72(4):991–999. [Google Scholar]

[bib26] 26.Guyon I., et al. Gene selection for cancer classification using support vector machines. Mach Learn. 2002;46(1):389–422. [Google Scholar]

[bib27] 27.Peng H., Long F., Ding C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans Pattern Anal Mach Intell. 2005;27(8):1226–1238. doi: 10.1109/TPAMI.2005.159. [DOI] [PubMed] [Google Scholar]

[bib28] 28.Li J., et al. Feature selection: a data perspective. ACM Comput Surv. 2017;50:6. [Google Scholar]

[bib29] 29.Kobak D., Berens P. The art of using t-SNE for single-cell transcriptomics. Nat Commun. 2019;10(1):5416. doi: 10.1038/s41467-019-13056-x. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib30] 30.Dorrity M.W., et al. Dimensionality reduction by UMAP to visualize physical and genetic interactions. Nat Commun. 2020;11(1):1537. doi: 10.1038/s41467-020-15351-4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib31] 31.Rather A.A., Chachoo M.A. Manifold learning based robust clustering of gene expression data for cancer subtyping. Inform Med Unlocked. 2022;30 [Google Scholar]

[bib32] 32.Pirruccello J.P., et al. Deep learning enables genetic analysis of the human thoracic aorta. Nat Genet. 2022;54(1):40–51. doi: 10.1038/s41588-021-00962-4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib33] 33.Luecken M.D., Theis F.J. Current best practices in single-cell RNA-seq analysis: a tutorial. Mol Syst Biol. 2019;15(6) doi: 10.15252/msb.20188746. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib34] 34.Wolock S.L., Lopez R., Klein A.M. Scrublet: computational identification of cell doublets in single-cell transcriptomic data. Cell Syst. 2019;8(4):281–291. doi: 10.1016/j.cels.2018.11.005. e9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib35] 35.Gayoso A., Shor J. Zenodo; 2022. JonathanShor/DoubletDetection: doubletdetection v4.2 (v4.2) [Google Scholar]

[bib36] 36.DePasquale E.A.K., et al. DoubletDecon: deconvoluting doublets from single-cell RNA-sequencing data. Cell Rep. 2019;29(6):1718–1727. doi: 10.1016/j.celrep.2019.09.082. e8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib37] 37.Wu T., et al. clusterProfiler 4.0: a universal enrichment tool for interpreting omics data. Innovation. 2021;2(3) doi: 10.1016/j.xinn.2021.100141. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib38] 38.Yu G., et al. clusterProfiler: an R Package for Comparing Biological Themes Among Gene Clusters. OMICS: A J Integr Biol. 2012;16(5):284–287. doi: 10.1089/omi.2011.0118. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib39] 39.Yu, G., enrichplot: Visualization of Functional Enrichment Result. 2022, R package: 〈https://www.bioconductor.org/packages/release/bioc/html/enrichplot.html〉 and 〈https://yulab-smu.top/biomedical-knowledge-mining-book/〉.

[bib40] 40.Wickham H. Springer-Verlag New York; 2016. ggplot2: Elegant Graphics for Data Analysis. [Google Scholar]

[bib41] 41.Subramanian A., et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci. 2005;102(43):15545–15550. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib42] 42.Liberzon A., et al. The molecular signatures database hallmark gene set collection. Cell Syst. 2015;1(6):417–425. doi: 10.1016/j.cels.2015.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib43] 43.Ashburner M., et al. Gene Ontology: tool for the unification of biology. Nat Genet. 2000;25(1):25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib44] 44.The Gene Ontology Consortium The gene ontology resource: enriching a gold mine. Nucleic Acids Res. 2021;49(D1):D325–D334. doi: 10.1093/nar/gkaa1113. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib45] 45.Mi H., et al. PANTHER version 14: more genomes, a new PANTHER GO-slim and improvements in enrichment analysis tools. Nucleic Acids Res. 2019;47(D1):D419–D426. doi: 10.1093/nar/gky1038. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib46] 46.Ferrero R., Rainer P., Deplancke B. Toward a consensus view of mammalian adipocyte stem and progenitor cell heterogeneity. Trends Cell Biol. 2020;30(12):937–950. doi: 10.1016/j.tcb.2020.09.007. [DOI] [PubMed] [Google Scholar]

[bib47] 47.Porro S., et al. Dysmetabolic adipose tissue in obesity: morphological and functional characteristics of adipose stem cells and mature adipocytes in healthy and unhealthy obese subjects. J Endocrinol Investig. 2021;44(5):921–941. doi: 10.1007/s40618-020-01446-8. [DOI] [PubMed] [Google Scholar]

[bib48] 48.Morigny P., et al. Lipid and glucose metabolism in white adipocytes: pathways, dysfunction and therapeutics. Nat Rev Endocrinol. 2021;17(5):276–295. doi: 10.1038/s41574-021-00471-8. [DOI] [PubMed] [Google Scholar]

[bib49] 49.Rosen E.D., Spiegelman B.M. Adipocytes as regulators of energy balance and glucose homeostasis. Nature. 2006;444(7121):847–853. doi: 10.1038/nature05483. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib50] 50.Luo L., Liu M. Adipose tissue in control of metabolism. J Endocrinol. 2016;231(3):R77–R99. doi: 10.1530/JOE-16-0211. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib51] 51.Parra-Peralbo E., Talamillo A., Barrio R. Origin and development of the adipose tissue, a key organ in physiology and disease. Front Cell Dev Biol. 2021:9. doi: 10.3389/fcell.2021.786129. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib52] 52.Haghighi M., et al. High-dimensional gene expression and morphology profiles of cells across 28,000 genetic and chemical perturbations. Nat Methods. 2022;19(12):1550–1557. doi: 10.1038/s41592-022-01667-0. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib53] 53.Neftel C., et al. An integrative model of cellular states, plasticity, and genetics for glioblastoma. Cell. 2019;178(4):835–849. doi: 10.1016/j.cell.2019.06.024. e21. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib54] 54.Fagerberg L., et al. Analysis of the human tissue-specific expression by genome-wide integration of transcriptomics and antibody-based proteomics *. Mol Cell Proteom. 2014;13(2):397–406. doi: 10.1074/mcp.M113.035600. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib55] 55.Uhlén M., et al. Tissue-based map of the human proteome. Science. 2015;347(6220):1260419. doi: 10.1126/science.1260419. [DOI] [PubMed] [Google Scholar]

[bib56] 56.Masuda D., et al. Chylomicron remnants are increased in the postprandial state in CD36 deficiency. J Lipid Res. 2009;50(5):999–1011. doi: 10.1194/jlr.P700032-JLR200. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib57] 57.Iena F.M., Lebeck J. Implications of aquaglyceroporin 7 in energy metabolism. Int J Mol Sci. 2018:19. doi: 10.3390/ijms19010154. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib58] 58.Thunen A., et al. Role of lncRNA LIPE-AS1 in adipogenesis. Adipocyte. 2022;11(1):11–27. doi: 10.1080/21623945.2021.2013415. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib59] 59.Kim H., et al. The new obesity-associated protein, neuronal growth regulator 1 (NEGR1), is implicated in Niemann-Pick disease Type C (NPC2)-mediated cholesterol trafficking. Biochem Biophys Res Commun. 2017;482(4):1367–1374. doi: 10.1016/j.bbrc.2016.12.043. [DOI] [PubMed] [Google Scholar]

[bib60] 60.Yoo A., et al. Neuronal growth regulator 1 promotes adipocyte lipid trafficking via interaction with CD36. J Lipid Res. 2022;63(6) doi: 10.1016/j.jlr.2022.100221. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib61] 61.Wang S., et al. Identification of a glucose metabolism-related signature for prediction of clinical prognosis in clear cell renal cell carcinoma. J Cancer. 2020;11(17):4996–5006. doi: 10.7150/jca.45296. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib62] 62.Bodmer D., et al. Disruption of a novel gene, DIRC3, and expression of DIRC3-HSPBAP1 fusion transcripts in a case of familial renal cell cancer and t(2;3)(q35;q21) Genes Chromosomes Cancer. 2003;38(2):107–116. doi: 10.1002/gcc.10243. [DOI] [PubMed] [Google Scholar]

[bib63] 63.Rodríguez-Rodero S., et al. Altered intragenic DNA methylation of HOOK2 gene in adipose tissue from individuals with obesity and type 2 diabetes. PLoS One. 2017;12(12) doi: 10.1371/journal.pone.0189153. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib64] 64.Hu E., Liang P., Spiegelman B.M. AdipoQ is a novel adipose-specific gene dysregulated in obesity. J Biol Chem. 1996;271(18):10697–10703. doi: 10.1074/jbc.271.18.10697. [DOI] [PubMed] [Google Scholar]

[bib65] 65.Simeone C.A., et al. A dominant negative ADIPOQ mutation in a diabetic family with renal disease, hypoadiponectinemia, and hyperceramidemia. npj Genomic Med. 2022;7(1):43. doi: 10.1038/s41525-022-00314-z. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib66] 66.Wang D., et al. Comprehensive biological function analysis of lncRNAs in hepatocellular carcinoma. Genes Dis. 2021;8(2):157–167. doi: 10.1016/j.gendis.2019.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib67] 67.Wang J.J., et al. Comprehensive analysis of the lncRNA‑associated competing endogenous RNA network in breast cancer. Oncol Rep. 2019;42(6):2572–2582. doi: 10.3892/or.2019.7374. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Optimized cell type signatures revealed from single-cell data by combining principal feature analysis, mutual information, and machine learning

Aylin Caliskan

Deniz Caliskan

Lauritz Rasbach

Weimeng Yu

Thomas Dandekar

Tim Breitenbach

Abstract

Graphical Abstract

1. Introduction

2. Methods

Fig. 1.

2.1. Data preprocessing in R

2.2. Data preprocessing in Python

2.3. Principal feature analysis (PFA)

2.4. Validation

2.5. Multiple cell types validation

2.6. Biological validation

3. Results

3.1. Analyzing adipocytes and ASPCs as an example

Fig. 2.

Table 1.

Fig. 3.

Fig. 4.

Fig. 5.

Fig. 6.

Fig. 7.

3.2. Validation: accuracy of PFA for analyzing other cell types

Table 2.

3.3. Validation: using PFA to analyze the same cell type

3.4. Validation: using PFA to analyze a second dataset

3.5. PFA validation summary

3.6. Multiple cell types validation

3.7. Biological validation

3.7.1. Validating the PFA genes

Fig. 8.

Fig. 9.

Fig. 10.

Fig. 11.

Fig. 12.

3.7.2. Downstream analysis of the PFA genes – GO enrichment

Fig. 13.

3.7.3. Comparing the PFA results to standard methods

Fig. 14.

Table 3.

4. Discussion

5. Conclusion

Author’s contribution

Declaration of Competing Interest

Acknowledgement

Footnotes

Contributor Information

Appendix A. Supplementary material

References

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases