Multi-wavelength analytical ultracentrifugation of biopolymer mixtures and interactions

Abstract

Multi-wavelength analytical ultracentrifugation (MW-AUC) is a recent development made possible by new analytical ultracentrifuge optical systems. MW-AUC extends the basic hydrodynamic information content of AUC and provides access to a wide range of new applications for biopolymer characterization, and is poised to become an essential analytical tool to study macromolecular interactions. It adds an orthogonal spectral dimension to the traditional hydrodynamic characterization by exploiting unique chromophores in analyte mixtures that may or may not interact. Here we illustrate the utility of MW-AUC for experimental investigations where the benefit of the added spectral dimension provides critical information that is not accessible, and impossible to resolve with traditional AUC methods. We demonstrate the improvements in resolution and information content obtained by this technique compared to traditional single- or dual-wavelength approaches, and discuss experimental design considerations and limitations of the method. We further address the advantages and disadvantages of the two MW optical systems available today, and the differences in data analysis strategies between the two systems.

1. Introduction

Interactions between biopolymers are essential for most biological processes, such as metabolic and developmental control and cell regulation [1], and therefore are of great research interest. Common approaches to study macromolecular interactions include affinity chromatography, gel shift assays, co-immunoprecipitation, x-ray crystallography, mass spectrometry, thermophoresis, isothermal titration calorimetry, and surface plasmon resonance. While these methods have achieved many breakthroughs, they also have their limitations. For example, X-ray crystallography and transmission electron microscopy offer atomic resolution, but are not intended for studying molecules in the solution state where the analyte concentration can be adjusted over a wide range for measurement of dynamic properties, such as mass action and reversible association. Hence, they do not lend themselves to the measurement of binding isotherms and equilibrium constants. Similarly, surface plasmon resonance requires one of the molecules to be covalently attached to a solid support, preventing free diffusion. Methods such as isothermal titration calorimetry often require prohibitive amounts of sample, and most other solution methods lack the necessary resolution to distinguish multiple association states when more than two interaction partners are involved. Nuclear magnetic resonance spectroscopy is another powerful high-resolution technique to study molecules in the solution state, but is limited by the size of molecules or complexes studied. In our work we discuss applications of a recently developed alternative called multi-wavelength analytical ultracentrifugation (MW-AUC). This method can be used to study biopolymer interactions in a physiological environment, where ionic strength, pH, redox potential can be easily controlled. Drugs and other small molecules can be titrated to study their interactions in a reversible environment, and multiple distinct molecules can participate in hetero-interactions. Taking advantage of unique chromophores and their extinction profiles, MW-AUC can extract additional information from the orthogonal spectral dimension. Previously, a variation of this theme proposed a multi-signal analysis by Brautigam et al. [2], which included Rayleigh interference measurements in the AUC to gain orthogonal information.

In 2008 the Cölfen lab introduced the first fiber-based UV–visible multi-wavelength detector for the analytical ultracentrifuge [3], adding an optical characterization dimension to the traditional hydrodynamic separation. This accomplishment added an important method to the toolkit of analytical ultracentrifugation (AUC), further enhancing the potential for discovery through the already capable and time-honored AUC method. This optical system was further improved in 2015 [4], and our laboratory contributed the data analysis framework implemented in UltraScan [5] for data generated by this detector [6]. In 2018 this method was further enhanced by the addition of mirror optics [7] (here referred to as “Cölfen optics”). This design has been successfully employed in multi-wavelength experiments of biopolymers with chromophores in the visible range [8], protein-DNA mixtures [6], and protein-RNA interactions [9]. The Cölfen optics design has been made available under an open source license [10]; it is intended to be retrofit into a preparative ultracentrifuge sold by Beckman-Coulter. In addition to the multi-wavelength analysis program implemented in UltraScan for the Cölfen optics, analysis of the same data was also integrated into Sedanal [11], developed by Walter Stafford. This program employs the time-derivative method, which fits differences of scans simulated by finite element solutions of the Lamm equation to experimental scan differences. This approach has the benefit of largely eliminating contributions from time-invariant noise, at the expense of amplifying stochastic noise by a factor of $\sqrt{2}$ from the pairwise subtraction of experimental data scans. In contrast to Sedanal, UltraScan avoids the amplification of stochastic noise by directly fitting time- and radially-invariant noise, and by fitting experimental data directly to linear combinations of finite element solutions [12]. In 2016, Beckman-Coulter released a new generation of analytical ultracentrifuges, the Optima AUC^™ series. It was equipped with Rayleigh interference optics and multi-wavelength capable UV/visible absorption optics (here referred to as “Beckman optics”), and is currently the only commercially available analytical ultracentrifuge. MW-AUC experiments with biopolymers performed with the Beckman optics are starting to emerge and include studies on heme proteins [13–15], triphenylmethane dyes binding to peptide trimers derived from amyloid-β peptides [16], and protein-DNA interactions [17]. Here, we describe the pros and cons of both optical systems, provide guidance for experimental designs of MW-AUC experiments, consider the limitations of the MW-AUC approach, and illustrate the significant advantages of MW-AUC over traditional single wavelength AUC experiments. We further describe the distinctions in the data analysis algorithms required to correctly evaluate data from the two optical systems, and document the use and implementation of UltraScan analysis modules required to process MW-AUC experiments.

1.1. Principles of MW-AUC

Analytical ultracentrifugation is a technique used to measure the partial concentrations, sedimentation coefficients, and the diffusion coefficients of analytes present in colloidal molecular mixtures. From this information, details about the analyte’s size and degree of globularity can be obtained [18]. Detection of the molecules is traditionally performed by scanning the sedimenting sample using single-wavelength absorbance spectroscopy as a function of radius and time. In a MW-AUC experiment, the sedimenting sample is scanned at multiple wavelengths. If the solution contains different analytes, each characterized by a different absorbance spectrum, MW-AUC detection provides a second, orthogonal characterization method by resolving analytes not just by differences in their hydrodynamic properties, but also by the differences in their absorbance spectra. If the intrinsic molar extinction profiles for each pure analyte are known, and they are sufficiently dissimilar, the spectrum of the mixture can be decomposed into the partial absorbance contributions from each analyte, and the molar quantity of each constituent can be determined [9]. Molecules that form complexes will sediment faster than their unbound forms due to the increase in mass of the complex. The stoichiometry and molar ratio of each analyte in the complex can be deduced by integrating the decomposed spectra. This second dimension adds important information to the hydrodynamic properties, extending the value and impact of traditional AUC.

1.2. Differences between the two MW-AUC optical systems

While both UV/visible optical systems mentioned above share mirror-based optics and support the acquisition of experimental data at multiple wavelengths, important differences in the two systems affect how data are collected, stored, and analyzed. These differences also determine the types of experiments that can be performed with the instruments. Both optics use a stepping motor to scan the radial domain rapidly. The Cölfen optics employ a data collection system where white light passes through the sample, and then is passed through a slit assembly, coupled to an optical fiber, and then to a diffraction grating. The diffracted light is then imaged on a linear CCD spectrophotometer, producing a wavelength intensity scan with approximately 0.5 nm resolution for each radial position imaged with the device. In the Beckman optics, white light passes over a diffraction grating before passing monochromatic light with 1 nm resolution through the sample. The resulting monochromatic intensity is imaged for each wavelength sequentially on a photomultiplier tube at each radial position in the AUC cell, producing multiple single-wavelength velocity experimental data sets.

1.3. Advantages and limitations for each MW-AUC optical system

These fundamentally different optical systems have pros and cons to be considered in the design, application, and analysis of experiments. An important difference between these optical designs is the order in which data are collected. With the Cölfen optics, experimental data from different wavelengths are collected simultaneously, which offers a distinct scanning speed advantage. The Beckman optics employ a photomultiplier tube which scans monochromatic light at a single wavelength, requiring each wavelength to be acquired sequentially. The use of a photomultiplier tube offers distinct dynamic range advantages, especially in the lower UV range, where fiber-based CCD systems suffer from reduced light intensity and therefore lack sufficient sensitivity. This presents a problem for the case of biopolymers (nucleic acids, proteins, lipids, carbohydrates), where detection often relies on the measurement of chromophores that absorb between 210 nm–240 nm (see Fig. SI 1). This lack of sensitivity is further exacerbated when buffer components that absorb below 260 nm are used, because it decreases the dynamic range available for the detection of the intended analytes. Higher sensitivity can be achieved with the photomultiplier design by scaling the photomultiplier voltage, and therefore, for measurements below 240 nm the Beckman optics are preferred. On the other hand, serial wavelength detection imposes significant throughput limitations, especially when more than 20 wavelengths, or more than two samples need to be measured in a single run. Since the Cölfen optics permit the simultaneous acquisition of a broad range of closely spaced wavelengths for multiple cells, these optics are eminently well suited for measuring systems where chromophores need to be examined over a large wavelength range, especially in the visible range where the Cölfen optics have sufficient dynamic range. When using UltraScan to acquire multi-wavelength data from the Beckman optics [19], data acquisition is restricted to a maximum of 100 wavelengths per cell, but they do not have to be spaced in regular intervals. However, 100 wavelengths are often too many, especially for rapidly sedimenting analytes, since significant delays are encountered during the initial calibration of the photomultiplier gain setting, which needs to be performed for each wavelength and channel. This delay prevents data collection at the beginning of the experiment, causing potential loss of detection for large molecules and aggregates. Consequently, the scan frequency for each wavelength is significantly decreased, despite rapid radial scanning. For experiments with more than 15–20 wavelengths, it is often not advisable to scan more than a single cell, while in the Cölfen optics, all rotor positions can be filled, and scans early in the experiment are not missed. With the Beckman optics, it may be necessary to sacrifice sedimentation resolution by scanning rapidly sedimenting analytes at slower than optimal rotor speed to gain more time for scanning. Nevertheless, the signal-to-noise level in the Beckman optics is exceptional, typically resulting in residual mean square deviations of less than 2.0 × 10⁻³ absorbance units, with a radial resolution of 0.001 cm. Hence, comparable statistics can be achieved with the Optima AUC even with fewer scans in a sedimentation velocity experiment.

2. Methods

2.1. Design of MW-AUC experiments

We describe here how the features of each optical system are best exploited for multi-wavelength analytical ultracentrifugation experiments involving biopolymers, in particular with a focus on macromolecular interactions. We focus on the experimental design and describe how the spectral features of each analyte can be used to optimize the information obtained. We also discuss the algorithms used to analyze multi-wavelength data obtained from the Optima AUC since they differ from the earlier described procedure that is suitable only for the Cölfen optics [6].

Multi-wavelength AUC (MW-AUC) is a valuable method for investigating solution-based mixtures of interacting or non-interacting analytes, where each analyte contributes a unique chromophore. In addition to traditional single-wavelength methods, MW-AUC also characterizes the hydrodynamically separated molecules based on their spectral contributions, identifying free and complexed species they may form, as well as the stoichiometries of their complexes. This technique relies on the ability to spectrally separate the absorbing species present in a mixture. In order to successfully separate the spectral contributions from different analytes, several requirements need to be met. First, the mixing event should not induce a change of the analyte’s absorbance properties. For example, in the case of complex formation, the absorbance spectra of the interacting analytes should not red- or blue-shift, or change molar absorptivity. Second, the absorbance spectra of the pure analytes should be known, preferably in molar dimensions, such that molar stoichiometries can be derived from the analysis. Third, the absorbance spectra of the analytes need to be sufficiently orthogonal in order to be linearly separable. This requirement can be checked by calculating the angle θ between the molar extinction vectors u and v of two analytes to be spectrally separated, given by Equ 1:

$$\theta ={\mathit{\text{Cos}}}^{-1}\left(\frac{u\cdot v}{\parallel u\parallel \cdot \parallel v\parallel }\right)\mathit{\text{ where }}u=\left[\begin{array}{c}{ϵ}_{u1}\\ {ϵ}_{u2}\\ \cdots \\ {ϵ}_{ui}\end{array}\right]\mathit{\text{ and }}v=\left[\begin{array}{c}{ϵ}_{v1}\\ {ϵ}_{v2}\\ \cdots \\ {ϵ}_{vi}\end{array}\right]$$ Equ 1

and ∈_ui is the molar extinction coefficient of analyte u at wavelength i and ∈_vi the molar extinction coefficient of analyte v at the same wavelength. It is necessary that u and v contain the same wavelengths.

Theoretically, if the angle θ is larger than zero, the spectra can be separated. An angle of 90° indicates perfect orthogonality (for example, two spectra with baseline separation between their absorbance peaks), but angles much smaller than 90° can be separated. The degree of success depends on the total signal available and the quality of the data. In general, the larger the angle θ, the better the chance the analytes can be spectrally separated. For analytes where the absorbance spectra show significant overlap (small θ), it is often helpful to expand the measured wavelength range. For example, when comparing the absorbance spectra of a protein and DNA molecule, using just the typical 260 nm/280 nm absorbance pairs, θ is 27.8°, however, when considering the absorbance range between 230 and 300 nm with 2 nm increments (36 wavelengths), the angle increases to 42.7°, offering significantly improved resolution (also see Fig. SI 1). The final requirement is that molar extinction profiles are within the same order of magnitude, ensuring that the observed signal is comparable between the different species. This can be a challenge when the molar extinction of a protein at 280 nm is much less than the molar extinction of an interacting nucleic acid at 260 nm. In such cases, mixtures quickly reach the dynamic range of the detector without providing sufficient signal from the protein. A solution is to shift or expand the measured wavelength range.

For example, nucleic acids have a particularly strong extinction in the 250–260 nm region. This absorbance band partially overlaps with the 280 nm absorbance band of aromatic amino acids. Hence, measuring wavelength range between 240 and 300 nm is well suited to characterizing protein-nucleic acid interactions when proteins contain a large mole fraction of tryptophan and tyrosine, and the nucleic acids are short [9]. Systems with longer fragments of nucleic acids in a mixture with proteins containing a small mole fraction of tryptophan and tyrosine provide limited absorbance signal for multi-wavelength experiments conducted in this wavelength range, because the relatively small molar absorbance from aromatic amino acids is overwhelmed by the absorbance from the nucleic acid, and equimolar protein concentrations will be difficult to detect. In such cases, sufficient signal from the protein can be achieved by including wavelengths in the region between 215 and 240 nm, were the peptide bond absorbance provides significantly higher absorbance (see Fig. SI 1). This equalizes the absorptivity between protein and nucleic acid and at the same time increases the orthogonality between the absorption profiles of protein and nucleic acid.

In all cases it is important to use a buffer system that does not absorb significantly in the measured wavelength range. Suitable buffer systems include phosphate- or low concentration optically pure TRIS-based buffers, and those that do not contain absorbing additives such as nucleotides, chelators, or reductants.

For the Beckman optics, it is beneficial to minimize the number of wavelengths scanned because each wavelength has to be measured sequentially. That reduces the number of scans available for each individual wavelength compared to the Cölfen optics, which scans all wavelengths simultaneously in each radial scan. One approach to maximizing the orthogonality of the measured spectra, while minimizing the number of measured wavelengths, is to interpolate spectral regions in the absorbance spectrum that exhibit linear change and to measure only wavelengths required for a faithful interpolation of the spectrum. For example, in regions where the change in the spectrum is linear over multiple wavelengths, only the endpoints of the linear region need to be measured [14]. This will reduce the number of measured wavelengths and the time required to complete the scan cycle, thereby increasing the total number of scans collected for each wavelength. Another trick for the Beckman optics is to choose a rotor speed that is optimally synchronized with the flash lamp timing, which decreases the elapsed time between successive scans. The timing delays between scans, as a function of rotor speed, are calculated in the UltraScan data acquisition module for the Optima AUC [19] (see Fig. SI 3), optimal rotor speeds include 14,600–14,900, 31,500–32,900, 45,800–50,900, and 59,600–60,000 RPM. In these ranges, scan times are 8 s/channel or less. Unfortunately it is not possible in the Optima to scan only one channel of a cell. Therefore, for multi-wavelength AUC experiments acquired with the Optima AUC, it is advisable to run a single cell containing two samples, one in each channel sector, because a reference channel is not required when using UltraScan. Importantly, experiments should always be measured in intensity mode to reduce stochastic noise contributions to the data [12].

2.2. Identification of basis spectra

For hetero-associating systems, AUC can separate free and complexed species based on differences in their hydrodynamic properties. In addition to the hydrodynamic separation, optical deconvolution can identify the molar contribution of each interacting partner in a molecular complex, and provide the stoichiometry of binding [6,9]. Reliable interpretation of the stoichiometry requires that accurate molar extinction coefficients are known for each analyte in the mixture contributing to the absorbance of the sample over the entire spectral range examined in a MW-AUC experiment. To obtain these molar extinction coefficient profiles, high-quality absorbance scans of each analyte are required. Depending on the spectral properties of the analyte, the dynamic range of the detector (0.1–0.9 OD) can be readily exceeded at some of the selected wavelengths when only a single analyte concentration is measured. For example, the molar extinction coefficient of a protein at 215 nm can easily exceed the extinction coefficient at 280 nm by 1–2 orders of magnitude when aromatic side chains are sparse or absent in the protein sequence (e.g., histones, collagen). To address this challenge, multiple dilutions need to be measured in the spectrophotometer. This approach ensures that overlapping wavelength ranges for one or more dilutions fall within the dynamic range of the detector, yielding a reliable intrinsic extinction profile over the entire wavelength range. To obtain the intrinsic extinction spectrum of an analyte over the entire wavelength range, the extinction profile fitter in UltraScan [5] is used to globally fit multiple dilution spectra from the analyte to sums of Gaussian terms using the Levenberg-Marquardt non-linear least squares fitting algorithm [20,21] (see Fig. SI 4). The fitted model is normalized with a known molar extinction coefficient (typically at 280 nm for proteins), which can be retrieved directly from the UltraScan LIMS database and derived from the associated protein sequence based on the molar absorptivity of the amino acid composition at 280 nm. The global molar extinction profile is used downstream to decompose experimental MW-AUC data into molar concentrations of spectral constituents (discussed below).

If the buffer used to dissolve the analytes absorbs in the measured wavelength range, then all absorbance measurements of the analytes of interest should be performed in a spectrophotometer blanked against the buffer. Also, since all MW-AUC experiments should be performed in intensity mode, the absorbing buffer must be considered as a separate spectral species in the downstream MW decomposition. In order to obtain its absorbance spectrum, the buffer’s absorbance profile must be measured by blanking the spectrophotometer with distilled water. We recommend to use spectrophotometers with a 1 cm pathlength, fitted with quartz cuvettes. For all studies reported here we used a benchtop GENESYS^™ 10S UV–Vis spectrophotometer from ThermoFisher.

For reversibly interacting systems, the thermodynamic binding isotherms are most reliably determined by measuring MW-AUC experiments of multiple titration points with different ratios of the interacting partners mixed together [9]. The spectral decomposition module in UltraScan is used to obtain the mixing ratio from each titration point. The absorbance spectrum of the titration mixture and the intrinsic molar extinction spectra for each distinct analyte in the mixture (the basis spectra) are loaded into the program. The program will determine the overlapping wavelengths available from each spectrum, and use this range to calculate the molar composition, providing residuals to the fit. The program also reports on the angle θ (see Equ 1) between each pair of basis spectra (see Fig. SI 5). By monitoring θ, the program can also be used to optimize the wavelength selection to aid in the experimental design. If a hypochromic or hyperchromic shift occurs in the absorbance profile due to mixing, the fitting residuals will appear to be non-random, providing feedback on the suitability of including selected wavelength ranges in the decomposition.

2.3. Analysis of MW-AUC experiments

Due to the design differences between the two multi-wavelength optical systems, experimental data differ in their structure and need to be analyzed with different strategies. The Cölfen optics collect all wavelengths simultaneously and provide a complete spectrum for the entire wavelength range, which is determined by the diffraction grating used in the optics [4]. As a result, each radial observation in the scan simultaneously produces a complete wavelength scan, and all wavelengths for that radial point are collected at the same time. This produces a 3D scan image (absorbance as a function of wavelength and radius, see Fig. 1, left panel). This image can immediately be decomposed to obtain isolated optical signals for each separated analyte in the mixture [6] for each radial point in each scan. In the Beckman optics, multiple wavelengths are collected sequentially, which causes radial scans at each wavelength to be collected at a different time. The time difference observed between the first and last wavelength collected for a multi-wavelength scan depends on the rotor speed and the total number of wavelengths collected, and is estimated by UltraScan. The difference in time between individual scans at different wavelengths is not obviously apparent from visual inspection of the 3D data (see Fig. 1, right panel), but must be addressed before spectral decomposition can be performed.

Fig. 1.

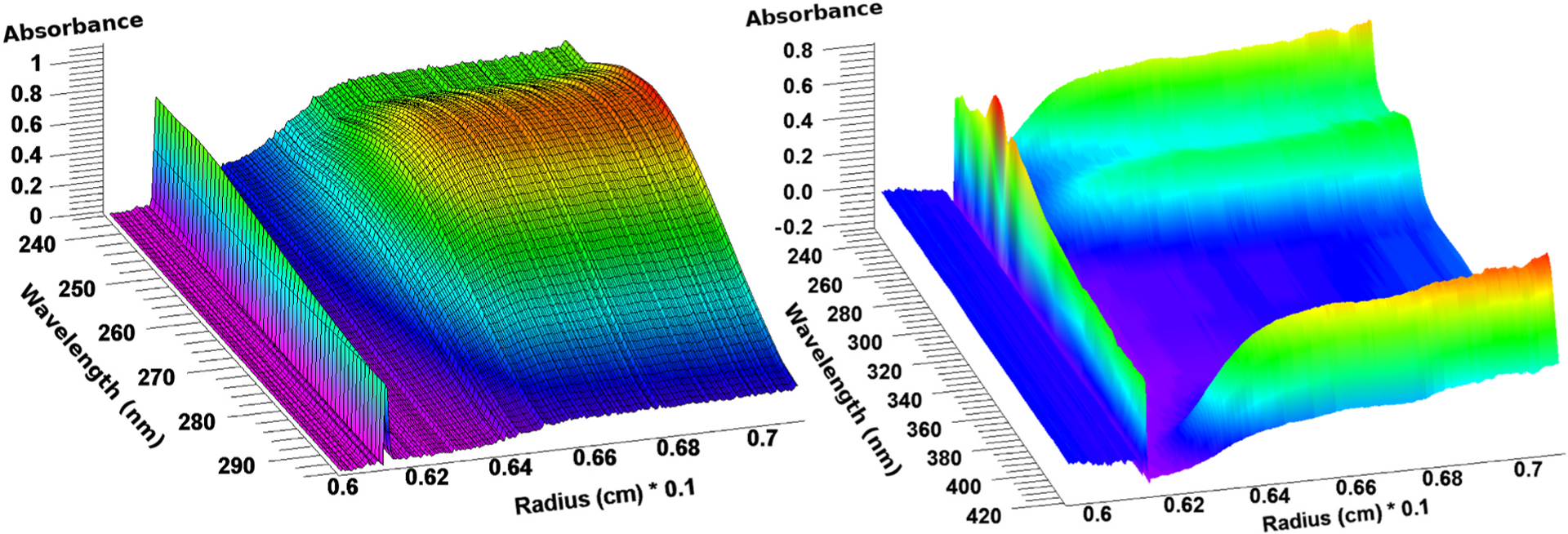
Multi-wavelength AUC data from a protein-RNA mixture acquired in the Cölfen optics (left) and a heme protein acquired from the Beckman optics (right). Only the Cölfen optics produce time-synchronous data, the displayed data from the Beckman optics contain wavelength data that are collected at different times, an issue that must be addressed before analysis. In both cases the meniscus is visible at the left, the sedimentation direction is to the right. The 410 nm heme peak is clearly visible in the right image.

For both optics, the analysis procedure before spectral decomposition is identical. The analysis starts by removing all systematic noise from each triple (a triple is a complete experimental dataset from a unique cell, channel, and wavelength) and fitting the boundary conditions (meniscus and bottom of the cell). At this point, sedimentation velocity data from each triple are processed separately. The analysis proceeds through several refinement steps. In the first refinement step, a two-dimensional spectrum analysis (2DSA) [22] is performed with simultaneous time-invariant noise subtraction. In the Optima AUC, intensity data obtained from a photomultiplier tube contains significant time-invariant noise contributions, which must be removed first. This intensity variation is less of an issue with the linear CCD array used in the Cölfen optics, but the same step is still recommended to remove time invariant noise resulting from other sources, such as imperfections in the optical path or scratches in the cell windows. In the next step, a second refinement is performed with the 2DSA, adding time- and radially invariant noise correction, and fitting of the boundary conditions (meniscus and bottom of cell). Computing times for a 2DSA analysis varies based on grid resolution, data size, number of wavelengths to be analyzed, analysis sub-type, and compute resources available. A typical multi-wavelength scan has only 40–60 scans, since all acquired scans are distributed over all wavelengths. This significantly reduces the compute time to 10–30 s/triple on a modern multi-core architecture, such as a 128-core AMD Epyc server. Since UltraScan is highly parallelized, and implemented on NSF-XSEDE/Access high-performance computing infrastructure, all triples can often be analyzed in parallel, where each 2DSA analysis utilizes 16 cores. Hence, the more wavelengths are acquired, the fewer scans are collected per wavelength, and since all triples can be analyzed at the same time, the faster the individual analysis of a triple proceeds, the overall compute time is typically reduced for all wavelengths to less than 30 s for the entire calculation. Evaluation of boundary conditions (meniscus, bottom radius) requires typically one order of magnitude more time, but only a single triple from each dataset needs to be analyzed, since all wavelengths from the same channel have identical boundary conditions. Typically a wavelength with optimal signal-to-noise (absorbance between 0.5 and 0.7 OD, and RMSD values less than 0.002) is chosen to determine the meniscus and bottom position. 2DSA-IT calculations are on the same order of magnitude, and need to be performed for each triple. Deconvolution is a very fast process, typically finishing within 10–20 s. On account of the mirror optics, both optical systems are essentially free of chromatic aberration [7]. However, in the Optima AUC, chromatic aberration in some instruments is large enough to require correction. This is handled in the UltraScan software by uploading a chromatic aberration profile into the LIMS database, which is applied to all data acquired from the Optima AUC during the data import stage. This process is further discussed by Stoutjesdyk et al. [23]. After chromatic aberration correction, the boundary condition fitting step only needs to be performed on a single wavelength from each channel, and the fitted positions are applied to the edit profiles of all other wavelengths in that dataset, since they are all from the same channel and therefore have the same boundary conditions. For best results in the boundary condition fit, it is recommended to select a wavelength which contains sufficient signal and low stochastic noise contributions. In the final refinement, an iterative 2DSA is performed with simultaneous time- and radially invariant noise correction for each triple [22]. The simultaneous processing of hundreds of triples for multiple channels and wavelengths is best performed on a supercomputer, where all triples can be analyzed in parallel and in batch mode [24]. Sedimentation and frictional ratio parameter ranges for the 2DSA fits should be carefully adjusted to capture all hydrodynamic species in the sample. Fits for all triples should be inspected to ensure the fits result in random residuals for the entire AUC experiment by overlaying raw data and fitted models using the Finite Element Model Viewer in UltraScan. Root mean square deviations (RMSD) values for good fits range between 0.0015 and 0.003 absorbance units on the Optima AUC, and 0.0025–0.006 on the Coelfen optics, depending on wavelength and total absorbance at that wavelength. RMSD values are listed in the UltraScan “Finite Element Model Viewer” and the analysis report for each 2DSA-IT fit. Residuals are displayed in the same module, as well as a red-green residual bitmap to aid in the assessment of fit quality. At this point, all systematic noise contributions should be removed from the data, and the final 2DSA refinement can be expected to be an accurate representation of the underlying data. The analytes contained in the 2DSA models will faithfully reproduce the hydrodynamic profiles from the experimental data, and the random residuals in the fitted data should only represent the stochastic noise contributions and have Gaussian distributions.

2.4. Generation of a synchronous time grid for optima AUC data

Before multi-wavelength data are decomposed into spectral basis vectors, one additional step is required with data from the Beckman optics. All wavelength data from the same channel must be transposed onto a synchronous time grid to handle the time discrepancies incurred during sequential wavelength acquisition. This is accomplished by loading the iterative 2DSA models from each triple belonging to a single channel into the Optima multi-wavelength fit simulator (started from the “Multiwavelength” menu in UltraScan’s main menu). Using the fitted, iterative 2DSA models, this module simulates the entire MW-AUC experiment, such that all triples from different wavelengths are now on a common and synchronous time grid. The synchronous time grid ensures that each scan from every wavelength has the same time stamp and can be used to obtain a reliable wavelength scan for each radial position. During the simulation of the synchronous time grid, the user can set all specifics of this simulation (rotor speed, meniscus position, run duration, number of scans) to match the settings of the original experiment (further described in SI-6). Partial concentrations of all analytes will be faithfully reproduced from the 2DSA models. Next, the simulations are uploaded to the LIMS database and edited to produce an equivalent MW-AUC experiment to the original experimental dataset. There is no requirement to add stochastic or other systematic noise to the data since all noise components have already been identified and subtracted from the data in earlier refinement steps. At this point, the data from the Cölfen optics and the Beckman optics are equivalent and can be further processed by the spectral decomposition module.

2.5. Spectral decomposition of MW-AUC data

Spectral decomposition of MW-AUC data resolves species with unique chromophores in a mixture based on their individual absorbance properties. Data processed as described above result in a set of three-dimensional surfaces for each scan’s time point in the experiment, representing the absorbance as a function of wavelength and radius. Hence, for each surface, each radial position of this surface gives rise to a wavelength scan. This wavelength scan can be decomposed into its basis absorbance spectra as described earlier and shown in SI 5. The decomposition is accomplished by using the non-negatively constrained least squares algorithm (NNLS) developed by Lawson and Hansen [25]. It assures that only positive contributions, or zero, are generated during the decomposition. For each basis vector, a two-dimensional (2D) space-time sedimentation velocity dataset will be generated during this process. Together, all basis vectors solve the linear equation subject to the constraint x_i > 0 (see Equ 2):

$$A_j=x_1{v}_1+x_2{v}_2+\dots +x_n{v}_n$$ Equ 2

where A_j is the absorbance wavelength scan at data point j, composed of spectral vectors v_i with amplitudes x_i. After processing all data in a MWAUC dataset, the decomposition results in n traditional 2D sedimentation velocity experiments, each representing a separate, unique spectral species in the mixture. If the spectral vectors contain molar extinction coefficients, the resulting 2D datasets inherit units of molar concentration. If only relative concentrations are needed, a normalized absorbance scale can be used as well. The decomposition is carried out by the UltraScan “MWL Species Fit” module from the “Multiwavelength” menu in the UltraScan main menu. This process is further detailed in SI-7. The resulting traditional 2D datasets (molar concentration as a function of radius and time) for each spectral component can be uploaded to the UltraScan LIMS system, edited, and analyzed by standard UltraScan procedures (2DSA [22], PCSA [26], GA [27,28], van Holde – Weischet [29] or other methods available in UltraScan). There is no further need to fit the boundary conditions, remove systematic noise contributions, or perform a Monte Carlo noise analysis. Comparing spectrally separated hydrodynamic analyses will reveal both free and complexed species, where species with identical hydrodynamic parameters represent complexes. Importantly, integrating each spectral species found in a complex, the molar stoichiometry of the species in that complex is revealed, as long as the spectral basis vectors are expressed in terms of molar extinction coefficients [9].

2.6. Preparations and experimental design of oilseed protein extracts

Oilseed material was extracted by homogenizing with an aqueous solution. The liquid phase was separated from the fibers using a centrifuge decanter. The extract was defatted using a disc-stack separator and the resulting protein dispersion underwent pH modification and centrigfugal clarification to remove insoluble aggregates. The remaining soluble protein was recovered by concentrating via ultrafiltration and diluted with phosphate buffered saline to approximately 1.0 OD at 280 nm for analytical ultracentrifugation. The sample was placed into a 2-channel 1.2 cm epon charcoal centerpiece fitted with quartz windows (Beckman Coulter, Indianapolis) and measured in an50Ti rotor at position 4, opposite a counterbalance, and spun for 13 h at 50,000 rpm, and at 20 °C. 34 wavelengths were collected for each sample between 250 and 349 nm, with 3 nm increments.

2.7. Preparations and experimental design of fluorescent proteins

Hexahistidine-tagged fluorescent proteins (mPapaya1, Teal, and Ultramarine) were expressed in E. coli and purified by Ni-Sepharose chromatography according to methods described earlier [31–33]. All proteins were buffer exchanged to standard phosphate buffered saline (PBS) for analytical ultracentrifugation measurements. The absorbance of the three protein samples was adjusted to 0.5 OD at each protein’s peak absorbance wavelength in the visible region (see Fig. SI 2). Samples were then mixed at the following ratios: TFP:UFP (5:1, 1:1, 1:3); UFP: TFP:mPapaya 1:3:3; UFP:TFP:mPapaya 1:1:1. Up to two samples were measured simultaneously in each run by scanning one cell. The samples were placed into the two channels of a 2-channel 1.2 cm epon charcoal centerpiece fitted with quartz windows (Beckman Coulter, Indianapolis) and measured in an50Ti rotor at position 4, opposite a counterbalance, and spun for 12 h at 46,000 rpm at 20 °C. Ninety-one wavelengths were collected for each sample between 420 and 600 nm, with 2 nm increments.

Fluorescent proteins and oilseed samples were measured at the Canadian Center for Hydrodynamics at the University of Lethbridge with an Optima AUC instrument. Data analysis was performed at the Chinook cluster at the University of Lethbridge.

3. Results

The hydrodynamic separation of free and associated analytes alone often does not provide sufficient resolution to permit a clear and unambiguous interpretation of AUC experiments for two important reasons: First, different analytes may have similar hydrodynamic properties, such as size, degree of globularity, and density, and therefore would not be distinguishable by hydrodynamic separation alone. Secondly, the ability to uniquely identify each analyte decreases with an increasing number of analytes because the observed signal is proportional to the relative amount of each analyte. If too many analytes are present, it is impossible to distinguish them based on hydrodynamic information alone. In MW-AUC experiments, the additional spectral information provides a second dimension to identify analytes by their unique chromophores. We distinguish two basic experiments: a) cases where spectral properties are not available in pure form for each unique chemical species present in a mixture, and b) cases where the pure spectra for each unique chemical species are known, and molar extinction coefficients are available for each measured wavelength. In the case of (a), it is still possible to extract and review the spectral properties after hydrodynamically separating all species. Even though molar extinction coefficients may not be available, the spectral pattern may still provide useful insights. For cases described by (b), a mathematical deconvolution of spectral contributors will then identify the chemical nature of each hydrodynamic species, determine the relative amount of each species, and for complexes, the stoichiometry of assembly. Representative examples for both cases are presented below. In a MW-AUC experiment, multiple datasets from traditional single-wavelength experiments are collected at multiple wavelengths and combined for a global analysis, which can extract a second approach to characterize the identity of the analytes, based on their unique spectral contributions to the overall signal. Since different types of biopolymers have unique spectral properties, it is therefore possible to resolve them not only based on their hydrodynamic properties, but also based on their absorbance spectra.

3.1. Hydrodynamic separation of spectral components

In cases where absorbance spectra from individual analytes with unique spectral characteristics are not available in pure form for all components in a mixture, an optical deconvolution of individual analytes will not be possible. Instead, a different strategy can prove valuable. A plot of the sedimentation coefficient distribution as a function of wavelength displays the spectral profiles of the hydrodynamically separated species, and may allow identification of some or all species in the mixture by reviewing the shape of their absorbance spectrum. This approach can be very effective and useful, provided multiple components in the mixture can be hydrodynamically separated. A representative example of this approach was demonstrated for mixtures of CdTe quantum dots by Karabudak et al. [30], where 24 unique hydrodynamic species were identified, and unique spectral properties of at least seven components could be derived over the examined wavelength range. In this method, s-values with non-zero amplitude obtained at different wavelengths are integrated at each wavelength to generate a spectral absorbance pattern for each unique hydrodynamic species.

The hydrodynamic separation of biopolymers typically has a lower size resolution than the highly dense metal quantum dots. However, if hydrodynamic separation is achieved, this method is still effective for classifying individual components. UltraScan offers a three-dimensional (3D) viewer, which projects the integrated sedimentation profile as a function of wavelength, or an integrated 2D plot of the absorbance profile at a particular sedimentation coefficient.

Example 1. –. Identification of components in an oil seed protein extract.

Fig. 2 shows analytical ultracentrifugation experiments performed with a heterogeneous oil seed plant protein extract after removing the lipid phase. In this example, the plant extract contains water-soluble polyphenols, small molecules with a 315 nm absorbance peak, as well as proteins of unknown size. When single wavelength experiments from two different wavelengths are compared (280 and 340 nm), the hydrodynamic results are strikingly different, producing apparently contradictory results (Fig. 2, panel A). The absorbances of the 0.5–2.5S, and the 12.5S species differ greatly, despite having been measured from the same sample. The reason for this discrepancy is the presence of different chemicals which possess dissimilar chromophores, and therefore different molar extinction coefficients at the same wavelengths. As can be seen from panel A, the information derived even from a dual wavelength experiment is insufficient to provide an unambiguous explanation of the observed results. However, in addition to providing a hydrodynamic separation of the species present in this sample, a MWAUC experiment successfully answers the following questions: 1. What are the identities of the species sedimenting at 0.5–12.5S? 2. Does the sample contain polyphenols, proteins, or both? 3. Are there interactions between polyphenols and the protein components? 4. Are the protein components degraded or intact? First, the majority of the polyphenols, identified by their 315 nm absorbance peak, sedimented, as expected, with a very low sedimentation coefficient (~0.5–1.0S) and did not appear to be bound to any larger molecules. However, a small amount of protein degradation products was visible between 1.0 and 2.5S, with a spectral signature of a protein molecule, potentially also bound to a small amount of polyphenol. A peak around 12.5S displayed a spectral signature of a typical protein with an absorbance maximum around 280 nm. The protein sedimenting at 12.5S has a narrow size distribution, suggesting that this protein is intact, and the absence of 315 nm absorbance indicates that no polyphenols are bound. A smaller amount of protein signal was found at < 2S, suggesting the presence of a second protein or a small fraction of a potentially degraded protein. Its absorbance spectrum suggests that a small amount of polyphenols could be binding to the degraded protein samples.

Fig. 2. Sedimentation velocity experiment of oil seed protein extracts.

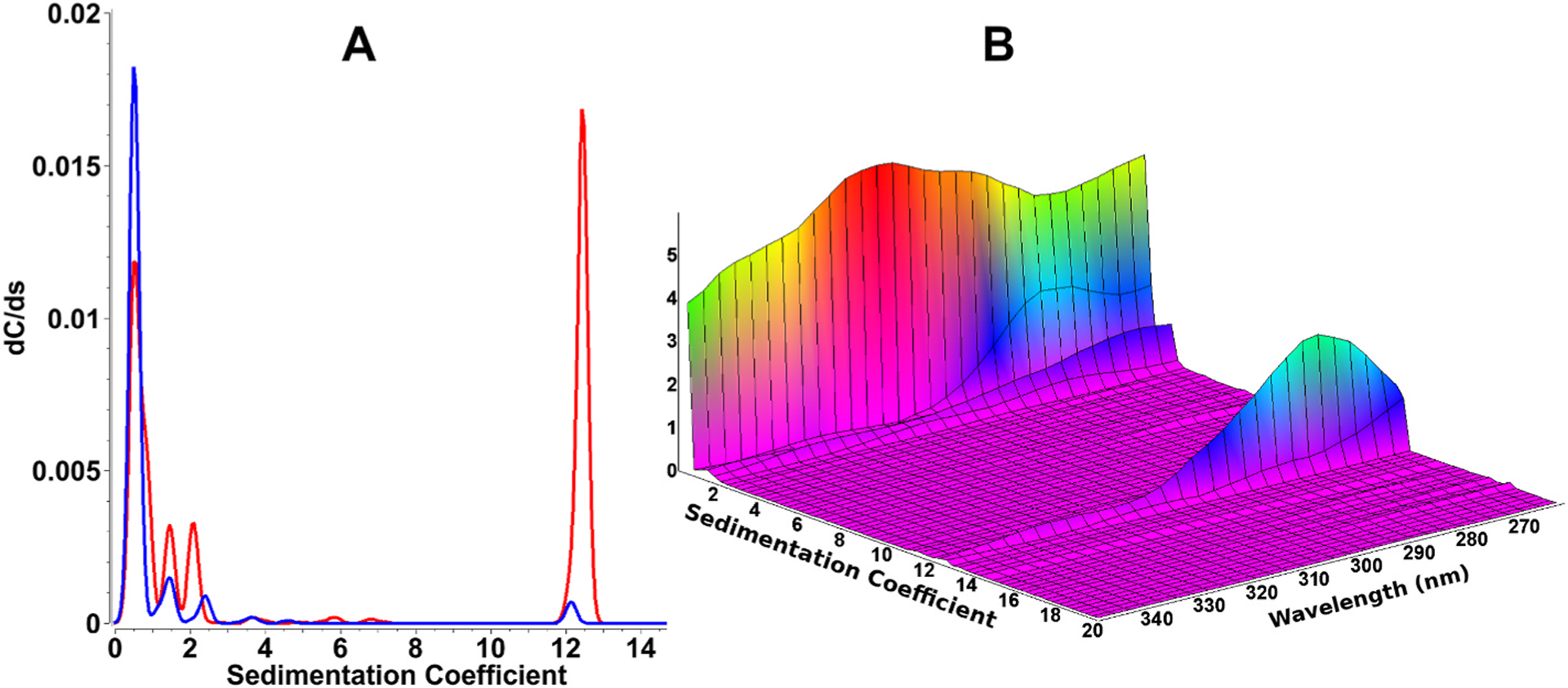
Panel A: Traditional single-wavelength analytical ultracentrifugation analysis (using 2DSA-IT analysis) at 340 nm (blue trace) and 280 nm (red trace). The two wavelengths clearly result in completely different concentrations for the hydrodynamic species present in the same sample, making an unambiguous interpretation impossible when considering a single, or only a few wavelengths.

Panel B: MW-AUC analysis of the same experiment shown in panel A, covering 260–350 nm. A 3-dimensional representation of absorbance as a function of sedimentation coefficient as well as wavelength is much more informative (composite generated from 2DSA-IT models). For example, the 0.8 S species is easily identified as a polyphenol because of its 315 nm absorbance maximum, while the 12.5 S species displays the typical absorbance profile of a protein, with an absorbance maximum at ~280 nm. Smaller species sedimenting at 1.5–2.2S appear to be degraded proteins, with some associated polyphenols. All data shown were collected with the Beckman optical system.

3.2. Spectral separation of hydrodynamic components

If pure spectra are available for individual species in a mixture, along with their molar extinction coefficients, spectral decomposition can be applied to determine absolute molar amounts of each species, whether free in solution or interacting with another molecule. In this case, also the stoichiometry of an interaction is available. A large class of experimental applications lend themselves to this approach.

Example 2. –. use of fluorescent tags:

To study biopolymers without distinct chromophores (lipids, carbohydrates) or protein-protein interactions between proteins with very similar absorbance profiles in the ultraviolet, fluorescent tags or fluorescent protein fusions can be used to impart a unique chromophore to each interaction partner molecule. Excitation spectra from commercially available fluorescent dyes for tagging biopolymers and fluorescent proteins span a wide range of the visible spectrum, and they can be used to add a unique chromophore to any molecule of interest. By mixing multiple, differentially tagged molecules, it is possible to study the assembly of complex, multi-protein systems, and follow the order of assembly as well as the stoichiometry of assembly. To validate the performance of this approach, we mixed ultramarine [31], mTeal [32], and mPapaya [33] fluorescent proteins at different ratios and measured their sedimentation between 400 and 600 nm, the region containing the most significant difference in their absorbance spectra (see SI 2). After spectrally deconvoluting the MW-AUC experimental data, all three species can be baseline-resolved and accurately quantified (see Fig. 3, panels 1–4). In contrast, a single wavelength analysis of an equal molar mixture of the same three molecules measured at a single wavelength of 486 nm was impossible to distinguish (see Fig. 3, panel 5). When analyzed by MW-AUC, varying ratios of absorbance recovered from the peak integrations shown in Fig. 3 accurately reflect the pipetted ratios, confirming the ability of the method to resolve complex mixtures accurately. This result is even more remarkable considering that mTeal and mPapaya have identical hydrodynamic properties and therefore are not distinguishable when measured using traditional single-wavelength AUC. Unlike the monomeric mTeal and mPapaya, Ultramarine sediments as a constitutive dimer with a higher sedimentation coefficient, allowing it to be hydrodynamically separated.

Fig. 3. MW-AUC analysisresolves mixtures of fluorescent proteins.

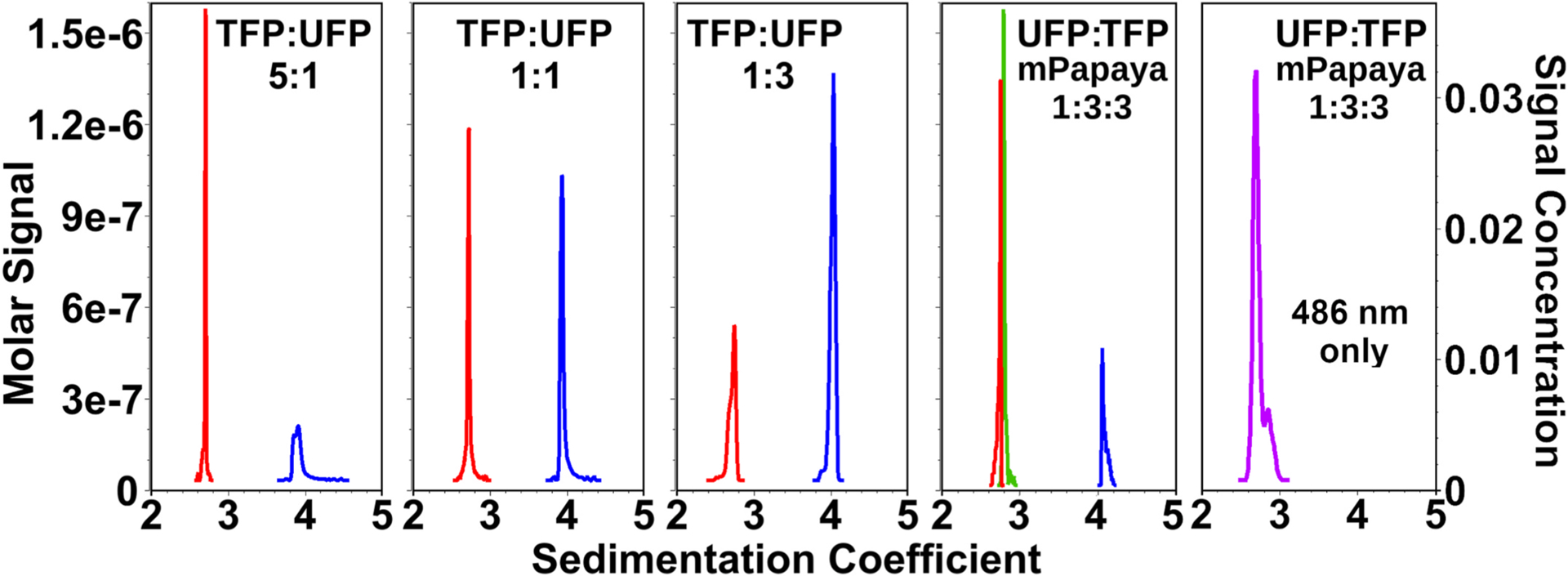
MW-AUC analysis of mixtures of two or three fluorescent proteins mixed at different ratios: Ultramarine fluorescent protein (UFP, blue), mTeal fluorescent protein (TFP, red), and mPapaya (green). Relative ratios of mixed proteins can be resolved within pipetting error. Panels 1–5 from left to right: 1: TFP:UFP 5:1, 2: TFP:UFP 1:1, 3: TFP:UFP 1:3, 4: UFP:TFP:mPapaya 1:3:3.5: UFP:TFP:mPapaya 1:3:3 (purple), measured at 486 nm only (see SI 2 for spectral overlap at 486 nm). All proteins have identical monomeric mass, but UFP exists as a constitutive dimer, which results in a higher sedimentation coefficient. Note that loading concentrations of mPapaya and TFP are correctly resolved despite having identical sedimentation coefficients, but only when analyzed by MW-AUC. A single wavelength analysis of a 1:1:1 mixture of all three proteins only produces an indistinguishable single peak at 486 nm, where TFP and mPapaya have maximum overlap, because UFP barely absorbs at this wavelength, and TFP and mPapaya have the same sedimentation coefficient.

All analyses shown here were generated from differential g(s) profiles derived from van Holde-Weischet analysis of the spectrally decomposed datasets, except the results in Panel 5, which are based on a traditional AUC experiment at 486 nm.

4. Discussion

The MW-AUC method extends the capabilities of an important biophysical characterization tool by adding a spectral characterization dimension to the hydrodynamic separation traditionally achieved by AUC. As is documented in examples representing two classes of MWAUC experiments, distinct advantages are realized in the resolution and information content when studying heterogeneous systems where multiple analytes with unique chromophores are present in mixtures. MW-AUC adds a new tool to study and validate biopolymer interactions under physiological solution conditions, and to measure equilibrium constants for hetero-interactions by sedimentation velocity experiments [34]. As demonstrated in example 2 (see Fig. 3) highly precise molar quantities can be measured for each component in a complex mixture, which is required for accurate determination of assembly stoichiometry and thermodynamic interaction coefficients. Even if pure basis spectra of each analyte in a mixture are not available, this method can still prove useful in understanding the composition of an unknown sample, as is demonstrated in example 1 (see Fig. 2). Taken together, these new capabilities provide important new avenues for the solution-based investigation of complex, interacting systems by providing higher resolution details about composition, binding strength, and stoichiometry of interaction than can be achieved with traditional single wavelength or Rayleigh interference AUC approaches, or even with other solution-based methods. Our results point to the potential of significantly improved solution characterization possibilities, and open the door to novel investigation of complex systems, promising revolutionary insights. New instrumentation available in the form of the Cölfen and Beckman optical systems, as well as software advances in the UltraScan software contribute to the advances reported here, and provide convenient access to this technology. The open source UltraScan software used for the analysis of MW-AUC experiments can be freely retrieved from Github in source code or binary format for Windows, Macintosh and Linux computers [35].

Abbreviations:

MW-AUC

Multi-wavelength Analytical Ultracentrifugation

TFP

teal fluorescent protein

UFP

ultramarin fluorescent protein

AUC

Analytical Ultracentrifugation