Abstract
Background
Alcoholism is a catastrophic condition that causes brain damage as well as neurological, social, and behavioral difficulties.
Limitations
This illness is often assessed using the Cut down, Annoyed, Guilty, and Eye-opener examination technique, which assesses the intensity of an alcohol problem. This technique is protracted, arduous, error-prone, and errant.
Method
As a result, the intention of this paper is to design a cutting-edge system for automatically identifying alcoholism utilizing electroencephalography (EEG) signals, that can alleviate these problems and aid practitioners and investigators. First, we investigate the feasibility of using the Fast Walsh–Hadamard transform of EEG signals to explore the unpredictable essence and variability of EEG indicators in the suggested framework. Second, thirty-six linear and nonlinear features for deciphering the dynamic pattern of healthy and alcoholic EEG signals are discovered. Subsequently, we suggested a strategy for selecting powerful features. Finally, nineteen machine learning algorithms and five neural network classifiers are used to assess the overall performance of selected attributes.
Results
The extensive experiments show that the suggested method provides the best classification efficiency, with 97.5% accuracy, 96.7% sensitivity, and 98.3% specificity for the features chosen using the correlation-based FS approach with Recurrent Neural Networks. With recently introduced matrix determinant features, a classification accuracy of 93.3% is also attained. Moreover, we developed a novel index that uses clinically meaningful features to differentiate between healthy and alcoholic categories with a unique integer. This index can assist health care workers, commercial companies, and design engineers in developing a real-time system with 100% classification results for the computerized framework.
Keywords: Alcoholism, Electroencephalography (EEG), Classification, Features, Automatic identification
Introduction
In accordance with the World Health Organization (WHO), alcohol addiction is responsible for close to 3,300,000 fatalities annually, or 5.9% about the global death toll [1]. Nearly 2,000,000,000 individuals are inebriated, with 81,700,000 suffering from acute alcoholism along visible signs [2]. Excessive alcohol use can have various social, sentimental, and physiological consequences for the person. Cirrhosis of the liver, heart disease, mental illnesses, malignancies, and traffic accident deaths and injuries are all linked to excessive alcohol consumption [3, 4].
Alcoholism can be prevented from having irreversible repercussions, such as disability and death if it is detected early [3, 5]. Traditional approaches for measuring the effects of alcohol on individuals include blood testing, interviews, and physiology examination. Regrettably, each of these methods has constraints. For example, a series of questions study findings can give rise to inaccurate information about medical and mental health circumstances when some patients avoid revealing accurate information because of feeling ashamed or afraid of stigmatization, and blood tests are the invasive method [4]. Electroencephalography (EEG) is a medically successful method for examining brain rhythms with advantages of low cost, scalability, non-invasive nature, and superior resolution. EEG signals are electrical representation of how the brain works, and they indicate numerous pathophysiologic behaviors such as alcoholism.
Numerous automated techniques are available in the literature for detecting alcoholic EEG patterns [6, 7]. These techniques are broadly divided into four types: time-domain, frequency-domain, time–frequency, and deep learning. Each of the aforementioned types has its benefits and demerits. For instance, the time-domain features are most superficial because they identify different amplitude variations. Yet, time-domain features are not stable because they are prone to noise and also restrict to discuss spectral changes in signals. Thus, frequency-domain features are employed in the literature and help provide spectral information of EEG signals. Some well-known time- and frequency-domain methods are listed as, hidden Markov models (HMMs) [8], largest Lyapunov exponent (LLE), approximate entropy (ApEn), sample entropy (SamEn), higher-order spectra (HOS) [9, 10], granger causality [11] and synchronization likelihood [12]. Despite the significant advantages of spectral information, frequency-domain methods failed to deliver time-domain information.
Thus, time–frequency domain approaches are assets for highly nonlinear and non-stationary EEG signals [13, 14]. Several important time–frequency methods are listed as, “ wavelet packet transform (WPT)” [10], “continues wavelet transform (CWT) [15], tuned-Q wavelet transform (TQWT) [16], dual-tree complex wavelet transform (DT-CWT)” [17], “three-band orthogonal wavelet filter bank (TBOWFB)” [18], “flexible analytical wavelet transform (FAWT)” [19], “empirical mode decomposition (EMD)” [20], “Fourier-Bessel series expansion based empirical wavelet transform (FBSE-EWT)” [21], “empirical wavelet transform (EWT)” [22] and “Fourier intrinsic band functions (FIBFs)” [23]. Time–frequency methods showed several difficulties such as, too many intrinsic-mode function (IMF) generation, IMF mixing, wrong decomposition level, multi-channel and multi-frequency analysis.
In recent times deep learning-based approaches are getting popularity for alcoholism EEG classification. In studies [24-31] transfer learning, a multilayer perceptron neural network, and convolutional neural network-based methods are developed for alcoholism EEG identification. These techniques deliver reasonable classification outcomes yet are complex, not specific, extensive weight initialization training, and require heavy computations with more resources.
Some downsides or restrictions are noted in the literature, as mentioned earlier. To begin with, the majority of the studies used time–frequency approaches, which might result in incorrect frequency orientation, mode mixing, end effects, noise influence, closely spaced frequencies, and difficulties in picking a mother wave. To store decomposed coefficients, these approaches necessitate complex computations and storage capacity. Second, EEG data is acquired from several channel signals, resulting in a large number of attributes; nevertheless, very few researches have concentrated on attribute selection, notably in the classification of alcoholism EEG. Third, tracking the diversity of chosen attributes among the healthy and alcoholic classes to achieve an effective examination is exceedingly challenging; thus, an index or single feature is required regardless of previous methodologies.
In order to overcome the issues raised above, this work intends to develop a new layout that can intelligently distinguish healthy and alcoholic classes with greater ease and accuracy. The suggested design is made up of various components, including (i) identifying abrupt changes of EEG signals in the frequency domain, (ii) combining several linear and non-linear features for decision making, (iii) formulating a scheme for choosing the best attribute set, (iv) determine a feasible categorization solution for the acquired attribute data, (v) develop novel alcoholism indicative index and single feature.
For the first time in the alcoholism EEG field, the Fast Walsh Hadamard Transform (FWHT) approach is implemented to recognize abrupt changes in EEG signals in the frequency domain. Because the FWHT requires addition and subtraction operations, it is a quick method for complex EEG signal analysis. Second, a combination of linear and non-linear attributes is introduced to get a deeper understanding of alcoholic EEG signals, including novel matrix determinants and successive decomposition index-based features. A correlation-based robust feature selection strategy is developed to select suitable features. Another unique aspect of this research is formulating a new index to help physicians and patients. The proposed index can also act as a single feature, resulting in 100% classification accuracy for normal vs. alcoholic EEG signals.
The following are the article’s contributory factors: A new computerized system for detecting alcoholic EEG signals has been designed and tested. EEG time-series signals are converted to frequency-domain using the FWHT, which aids in capturing abrupt changes in EEG signal amplitudes. We introduce matrix determinants and successive decomposition index-based features in the detection of alcoholism. A powerful feature selection method is proposed to identify the best features for the development of a computerized system. In addition to the automated framework, a new index is being developed to aid health workers and corporate goals.
The rest of the paper is structured as follows: section “Materials and methods” is about the materials and methods. The findings are presented in section “Results”. Section “Discussion” discusses the experimental results, and section “Conclusion” summarizes this work.
Materials and methods
We used the freely accessible dataset available in [32, 33]. The data contain EEG signals of 122 normal and 122 alcoholic subjects recorded by employing 64 EEG electrodes according to the 10–20 system [34] at a sampling rate of 256 Hz. Each subject performed 120 trials for various stimuli that consist of 90 images of different selected items. The duration and resolution of the EEG signals are 32 s and 12 bits, respectively. Finally, the signals were divided into four eight-second segments after removing the artifacts caused by blinking and unwanted body movements, and each segment have 2048 samples. The detailed information about the dataset can be found in [32, 33]. Figure 1 an illustration of healthy and alcoholic subjects signals respectively.
Fig. 1.
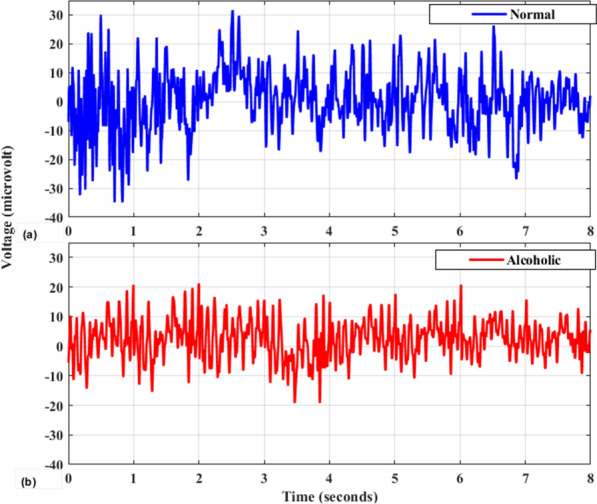
Visualization of a healthy vs b alcoholic EEG signals
The proposed computerized framework consists of several modules as shown in Fig. 2. The details of all modules are given subsequently.
Fig. 2.
Schematic representation of automated alcoholism identification
Fast Walsh Hadamard transform
In this research, a frequency domain-based approach Walsh–Hadamard Transform (FWHT) for classifying normal and alcoholic EEG data is developed. The FWHT is an effective tool for determining the Walsh–Hadamard Transform, which essentially involves converting time-domain signals into frequency-domain signals. The signal is decomposed by FWHT into a sequence of orthogonal, rectangular waveforms known as Walsh functions, which have values of + 1 or 1. Each Walsh function is given a unique sequence number. The basic arithmetic functions are used to carry out the FWHT algorithm. The FWHT has the ability to recognize an abrupt distortion in the signal with high clarity. The signal samples having a length of are decomposed into coefficients by FWHT. The coefficient of the signal’s Discrete Walsh–Hadamard Transform (DWHT) is returned by FWHT. The FWHT of the data samples of y(p) with is formulated as [35],
| 1 |
where P represents the number of samples and is the walsh matrix which is mathematically given as,
| 2 |
For illustration, and are mathematically expressed as,
| 3 |
| 4 |
For any p value, the Walsh function can also be describe as,
| 5 |
Because the FWHT method is analogous to the fast Fourier Transform (FFT) algorithm, the complicatedness of the FWHT method is . The butterfly operations are used exclusively in the FWHT algorithm. As a result, FWHT can be implemented utilizing simple addition and subtraction calculations employing butterflies. The key benefit of this transform is that it uses less memory storage space for decomposed coefficients and leads to faster signal reconstruction. Typical visual representation of Hadamard coefficient for normal and alcoholic EEG signals are shown in Fig. 3.
Fig. 3.
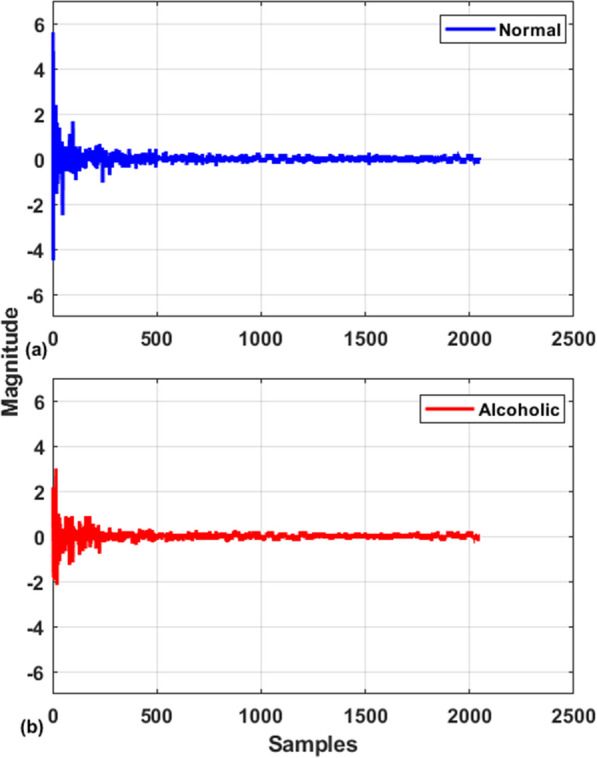
Visual representation of Hadamard coefficient for a normal and b alcoholic EEG signals
Feature extraction
EEG signals are highly dependent on the physiological traits of a particular subject, making it almost impossible to find important attributes for a general computerized system [36, 37]. In order to gain a better knowledge of various physiological EEG signals, several features were extracted from diverse domains in this work. These attributes include linear, non-linear, and complexity-based characteristics. The simplicity of time-domain and statistical features is due to the fact that they just assess amplitude fluctuations of signals rather than any transformation. Another benefit of statistical features is that they provide comprehensive information or a trend for data analysis. Physiological signals are the result of a structured biological system’s various physiological complicated interactions. Such shifting behaviors can provide important hidden knowledge about the dynamics of a system. To quantify uncertainties, complexity, and tiny variations in EEG signals, numerous energy and entropy-based nonlinear features were retrieved in this study. The specifics of the retrieved features are presented as follows:
Minima (F1): For , the minima represents the minimum value in the data samples as described in Sadiq et al. [36]. The minimum value is calculated using the formula:
| 6 |
Maxima (F2): For , the maxima represents the maximum value in the data samples as described in Sadiq et al. [36]. The maximum value is calculated using the formula:
| 7 |
Autoregressive Model (F3): The autoregressive (AR) technique is used to measure the power spectrum by employing a linear practice called a model. The AR model is formulated mathematically as
| 8 |
as presented in Sadiq et al. [38]. Here, y(p) represents the prediction model, b(j) are the AR complex variables, P is the AR model parameter, u(p) is the noise function, and p is the sampling time. The AR model order in this investigation was determined as 4 through experimentation.
Median (F4): The median is a statistical measure that represents the middle number in a list of values arranged in ascending or descending order. In this study, with 2048 DWHT coefficients for each signal, the median formula for even numbers is utilized. It is given as:
| 9 |
as described in Sadiq et al. [36].
Variance (F5): Variance is a statistical evaluation of the dispersion among samples in a dataset. It expresses how far each sample in the set deviates from the mean and other samples. The variance is calculated using the formula:
| 10 |
where is the ith sample observation, is the mean of all sample observations, and P is the total number of samples, as described in Sadiq et al. [36].
Standard Deviation (F6): The standard deviation is a statistic that measures the variability or spread in a set of numbers. A lower value indicates that the numbers are closer to the mean, while a larger value indicates a wider spread. The standard deviation is calculated using the formula:
| 11 |
where represents the time series EEG, as described in Sadiq et al. [36].
Arithmetic Mean (F7): Arithmetic mean is the sum of a series of values divided by the total of those values. Its formula is presented in Sadiq et al. [36],
| 12 |
Renyi Entropy (F8): Renyi Entropy calculates the spectral complexities of a time series using Renyi’s principle, which is given by [39],
| 13 |
where is a non-negative number. In the present study and is fixed as 2 empirically.
Log Energy Entropy (F9): The amplitude of the EEG signal varies over time. The most straightforward approach to acquiring all of the details from such a signal is to square it, leading to larger energy values, which help to improve discrimination among normal and alcoholic EEG classes. To achieve this goal, Log energy entropy (LEE) feature is used, which is calculated as follows [40]:
| 14 |
Shannon Wavelet Entropy (F10): We integrated Shannon entropy and wavelet decomposition to perform Shannon wavelet entropy (ShWE) for every signal DWHT coefficients. The key benefit of ShWE is its brevity, as it does not demand any parameters during the entire process and can readily distinguish between normal and alcoholic EEG classes without imposing excessive computing costs. The ShWE can be represented mathematically as follows [40]:
| 15 |
Tsallis Entropy (F11): Tsallis entropy is a variant of extensive entropy that can be used to investigate the intricacy of non-additive networks. Extensive entropy cannot describe the aberrant experimental findings of complex systems. The computation of Tsallis entropy is given as follows [40]:
| 16 |
where, in the present study, and is fixed as 2 empirically.
Log root sum of sequential variations (F12): In [41], the Log root sum of sequential variations (LRSSV) is presented as a method for measuring the successive fluctuations among signal samples. The LRSSV is computed by applying the following formula [41]:
| 17 |
Mean Teager Energy (F13): The mean Teager–Kaiser energy (MTKE) is a nonlinear feature that may detect even little changes in non-stationary signals. Relevant data might be extracted from minor variations in the amplitude and frequency of an EEG signal utilizing MTKE. The mathematical formula for MTKE is as follows [40]:
| 18 |
Mean Energy (F14): The mean energy of an EEG signal provides important information, as a high mean energy value aids in obtaining good judgment abilities between normal and alcoholic EEG signals. The numerical expression for mean energy is written as follows [40]:
| 19 |
Mean Curve Length (F15): In study [41], mean curve length is presented to obtain an approximation for the Katz fractal dimension. It is frequently used to detect activity in EEG readings. MCL is defined as follows [41]:
| 20 |
where y[p] is DWHT coefficients for the EEG signal, Q is the window length, and k is the end coefficient in the epoch.
First Difference (F16): First difference tells the relationship among DWHT coefficients for the EEG signal and is presented as [41]:
| 21 |
Normalized First Difference (F17): The normalized first difference, also known as the normalized length density, detects similarity among DWHT coefficients for the EEG signal and is presented as [41]:
| 22 |
Second Difference (F18): The second difference aids in determining whether or not a pattern exists in DWHT coefficients for the EEG signal and is presented as [41]:
| 23 |
Normalized Second Difference (F19): The normalized second difference reveals the type of the trend in DWHT coefficients for the EEG signal and is presented as [41]:
| 24 |
Kurtosis (F20): Kurtosis is a higher-order statistical metric that measures the “peakedness” of density near the mean value. It is written as follows [36]:
| 25 |
where denotes the mean value.
Skewness (F21): Skewness is a measurement of the asymmetrical of a DWHT coefficients for EEG signal probability distribution around its mean. The skewness is formulated as [36],
| 26 |
where denoting mean value.
Hjorth Activity (F22): The signal strength and unpredictability of a time function are both represented by the activity variable. This may represent the frequency domain spectrogram area. It is mathematically presented as [41],
| 27 |
Hjorth Mobility (F23): The average frequency or percentage of variance of the frequency distribution is measured by the Hjorth mobility variable. It is written as [41],
| 28 |
Hjorth Complexity (F24): The frequency change is represented by the Hjorth complexity factor. This parameter evaluates the resemblance of the signal to a pure sine wave, with the number convergent to 1 if the signal seems to be more identical. It is presented as follows [41],
| 29 |
Fluctuation Index (F25): The fluctuation index (FI) measures time series irregularities. The harmonic components produced by the spectra of EEG signals have a strong connection with the rhythms in EEG signals. Because the DWHT adaptively delivers the coefficients in the spectral domain for an EEG signal, the FI of coefficients can help achieve good differentiation between normal and alcoholic groups. Consequently, in this study, the FI of coefficients is employed as a predictive marker to differentiate between normal and alcoholic EEG data, and it is expressed as follows [42],
| 30 |
where P indicates to lengths of DHWT coefficients.
Successive Decomposition Index (F26): The successive decomposition index (SDI) technique depends on the discrete wavelet transform (DWT). In the first step of DWT, the DHWT coefficients with length p of an EEG signal are passed through a low-pass filter (LPF) and a high-pass filter (HPF). In the next step, the LPF output is passed through LPF and HPF, and this process is repeated for fixed decomposition levels. At last, each decomposition level’s coefficients are used to extract attributes. Opposite to DWT, the SDI does not require a predefined number of decomposition levels and considers the coefficient from the last level for classifier input. The formula for SDI feature is given as [43]
| 31 |
where is scaler quantity, and represent the average of absolute value and average difference of DWHT coefficients for EEG signal. The relationship among and are calculated by and .
The resulting SDI is a biomarker with a single number for an EEG signal of length P. The advantage of SDI is that it can capture the fluctuations of the DWHT coefficient for an EEG signal and combine them into a unique possible result. Furthermore, there is no restriction to define decomposition levels. Consequently, SDI is a linear and non-complex feature, making it an excellent candidate for developing a computerized alcoholism EEG detection system [44].
Matrix Determinant Feature (F27–F36): We exploited matrix determinant quantity as a particular feature in the suggested study to discriminate normal or alcoholic EEG tasks. For each EEG signal, the matrix was made up of the DWHT coefficient, and the determinant quantity calculated fluctuations in peak amplitude [45]. The Gauss elimination method was used to convert the square matrix into a diagonal matrix, and the determinant was then determined using the product of diagonal elements. Because the DWHT coefficient for each EEG signal was non-linear and non-stationary, we did not obtain a periodical duplication of zeros in the signal, and consequently the procured matrix was invertible with a non-zero determinant value. In this study matrix determinant features 10, 13, 16, 20, 23, 26, 30, 33, 36 and 40 are determined which are notated as features F27, F28, F29, F30, F31, F32, F33, F34, F35 and F36 accordingly. As an illustration, the algorithm for calculating the matrix determinant for order 11 is demonstrated as following [45, 46]
Input = DHWT coefficients of EEG signals
Initialization a = 1
Rows = 11 and columns = 11
For j = 1 to rows
For k = 1 to columns
A(j,k) = Input(a)
a = a+1
End
End
D =
Feature selection
To choose the best features acquired from the DWHT coefficients, the Best-First strategy is being utilized to look over the gatherings of features by means of hill climbing, which is improved by a backtracking module [47]. Next, the correlation-based feature measures are utilized to decide the worth of a congregation of features by unequivocally evaluating the proactive capability of each feature and its level of unwavering quality. This feature selection strategy gathers features firmly associated with the class but has feeble interconnections. The mathematical formulation of correlation feature selection (CFS) approach is given as [47],
| 32 |
where C compares two features F and G, tag represents the normal or alcoholic class, and “symmetric uncertainty” is executed for the experimentation.
Classification
To classify the selected features by CFS, nineteen machine learning and five neural network classifiers are implemented. The reason for considering extensive amount of classifiers is to choose the best classifier for our study. The details of these classifiers is given as follows [48–54],
BayesNet: A BayesNet is a predictive model for modelling knowledge in an uncertainty, with every node representing a random number and each edge representing the conditional distribution for the uncertain variables.
Naive Bayes: Naive Bayes (NB) is a simple and widely employed predictive model that uses Bayes’ theorem with strict (naive) independence assumptions. The existence (or absence) of a specific class feature is assumed to be unrelated to the availability (or lack) of any other feature by the NB classifier. The NB classifier can be trained relatively efficiently in a supervised learning context based on the particular type of probability model. In reality, the maximum likelihood technique estimates parameters for NB classification models. In this classifier, the resultant class has the highest post-probability.
Logistic: Logistic regression (LR) assumes that the input variables are numeric and have a Gaussian distribution. The LR can still produce good results if your data is not Gaussian. The algorithm learns a coefficient for each input value, which is then linearly concatenated into a regression function and transformed using a logistic function. LR is a quick and easy strategy that can be pretty successful on specific difficulties. In this study Ridge estimators are employed in LR to tweak the parameters estimates and to reduce the errors made by future estimations.
Simple Logistic: Simple logistic works in a similar fashion as LR, however, it employed LogitBoost to improve the parameters estimates and to fit a model.
Sequential Minimal Optimization: The sequential minimal optimization (SMO) algorithm’s main characteristic is that it iteratively picks only subsets of size two to maximize chunking and then optimizes the target function with the features provided. Since it does not need a quadratic optimizer, this technique can perform analytically superior than other support vector learnings. SMO has excelled at scaling across all datasets. This method is straightforward, trustworthy, and simple to implement. In summary, the SMO method executes substantially faster than any other SVM algorithm.
K-Nearest Neighbor: The K-nearest neighbor (KNN) is a supervised learning model that is simple to develop. In KNN algorithms, the distance among each input sample and the K nearest training samples is calculated. Two important parameters affecting the validity of the KNN algorithm are the distance computation method and the number of K. For categorization purposes, Euclidean distance with K = 3 is empirically consider.
K Star: K is an instantiation classifier, meaning implies that the category of a testing set is determined by the category of training instances that are most similar to it, as defined by a similarity measure. It is distinguished from other instance-based classifiers by its use of an entropy-based distance function.
Locally Weighted Learning: A weight function is used in locally weighted learning (LWL) to represent the training data and the current estimate. This function gives more weight to data points near together and less weight to data points that are further apart. It is considered that the indications are better at the spots closest to the desired ones.
Adaboost: The adaboost strategy, which stands for adaptive boosting, is used as an ensemble approach. These classifiers scores are reassigned to each sample, with greater scores assigned to incorrectly classified sampl+es. This concept is termed adaptive boosting and is used to minimize bias and variation. It is based on the notion of successive learning. Each succeeding learner, except the first, is developed from previously produced learners. In other words, weak learners are transformed into strong learners. The adaboost method works on the same idea as boosting with modification.
Bagging: Bagging, also known as “bootstrap aggregating,” is a two-step process for creating highly reliable, resilient, and accurate models. Bagging is a robust ensemble learning approach used to resample the training dataset. The first stage entails bootstrapping the primary data samples comprising the multiple training data pairs. Numerous models are constructed from these training datasets. Continuous training methods for datasets and numerous models create predictions. The core concept of the bagging method is simple. Rather than creating estimates using a single model that is adequate for the actual data, numerous models are developed to define the correlation.
LogitBoost: Another boosting technique is the logitboost algorithm. This approach is developed to address the issue of overfitting induced by excessive noise, which the adaboost algorithm suffers. To tackle this challenge, logitboost linearly lowers training error. As a result, it delivers more flexibility and reduces the exponential loss. In summary, logitboost increases the weight of the data and outperforms the adaboost algorithm in terms of overfitting.
Decision Table: Decision Table develops a decision table classifier that uses best-first search and cross-validation to examine the subset of attributes. A choice uses the nearest-neighbor strategy, as opposed to the table’s global vote, to choose the class with each case that has not been covered by an item in a decision table, based on the same set of criteria.
JRip: JRip leverages sequential covering tools to develop organized rule sets and incorporates a propositional rule learner called “Repeated Incremental Pruning to Produce Error Reduction (RIPPER).” This algorithm is divided into four stages: making rule, prune, optimize, and selection. We employed minimum description length to avoid overfitting issues
Decision Stump: A decision stump is a classification model made up of a single-level decision tree. Specifically, it is a decision tree with just a root node connected directly with its leaves. A decision stump predicts an outcome depending on the amount of a single input feature.
Hoeffding Tree: A Hoeffding tree is an incremental decision tree technique that can train from large data sets if the distribution producing instances does not vary over time. Hoeffding trees take advantage of the notion that modest sample group can frequently be sufficient to select an appropriate splitting attribute. The Hoeffding bound, which quantifies the number of data points utilized to calculate various statistics within a specified precision, lends mathematical credence to this viewpoint.
J48: The J48 classifier is a straightforward C4.5 decision tree for classification. It performs classification using decision trees or rules derived from them. Once the tree has been constructed, it is applied to instances in the database, yielding identification tasks. The J48 has a list of advantages, notably missing value accounting, decision tree pruning, continuous feature values ranges, rule derivation, and so on.
Logistic Model Tree: The logistic model tree (LMT) technique incorporates decision tree and logistic regression (LR) techniques. The information gain method is implemented to subdivide the tree, and the logitboost procedure is used to fit the LR in the tree nodes. To discover over-fitting concerns, the classification and regression tree (CART) is used.
Random Forest: The random forest is a classification technique that classifies data by using a large number of decision trees. It utilises bagging and attribute randomness while building each particular tree in order to produce a statistically independent forest of trees for whom the aggregate estimate has been more precise compared to any single tree.
Random Tree: At each node, the random tree evaluates a set of K randomly selected features to divide on. The term “random” refers to the fact that each tree in the collection has an equally probable of becoming sampled, resulting in a uniform distribution of trees. Random trees may be constructed quickly, and merging huge sets of random trees produces realistic models in most cases. It doesn’t prune anything.
Artificial Neural Networks with single layer: Artificial Neural Networks (ANN) are computing architectures made up of a collection of complicated, intimately correlated processing units called neurons that conceivably replicate the structure and function of the biological nervous system. ANN learning is accomplished by the development of specific training procedures based on learning laws that are intended to mimic the learning processes of biological systems. For linear issues, a typical ANN has two layers: input and output, however for non-linear issues, an another layer called a hidden layer is used. Depending on the task, the amount of concealed layers is determined experimentally. With more hidden layers, the training method is time-consuming–consuming. To obtain the appropriate parameters, we use a backpropagation algorithm with a scaled conjugate gradient method. In this case one layer with ten neurons are utilized [55-58].
Artificial Neural Networks with multiple layer: In this ANN model three layers (MANN) each with ten neurons is implemented for the normal and alcoholic EEG signals identification.
Feed-forward neural networks: Neurons are grouped in numerous layers in feed-forward neural networks (FFNN), and information is transferred from source to destination. Once an error appears, neurons are sent back to the preceding layer, and the parameters are reset to lower the likelihood of an error. We employ the tan-sigmoid transfer function, a single hidden layer with ten analyzed neurons, and the Levenberg–Marquardt algorithm for quick learning in this investigation [59].
Cascade-Forward Neural Networks: Neurons in cascade-forward neural networks (CFNN) are interconnected to neurons in preceding and succeeding layers. A three-layer CFNN, for illustration, exhibits direct connections among first three layers, meaning that neurons in the input and output layers are related both indirectly and directly. These additional interconnections aid in achieving a faster learning rate for the appropriate association. In CFNN, we employed same parameters as used in FFNN [59].
Recurrent Neural Networks (RNN): Neurons in RNN may circulate in a loop due to one or more feedback pathways. The RNN’s properties enable the system to process data temporarily and identify trends. Elman recurrent neural networks, the most prevalent family of RNN, are used in this research. The Levenberg–Marquardt approach and a single hidden layer with experimentally selected ten neurons are used to quickly train the model [60].
Results
Experimental setup
This study’s investigations were conducted employing personal computer with an Intel(R) Core i5 CPU and 8 GB RAM, employing MATLAB 2020a and WEKA v.3.9.5. The FWHT was implemented in the first step to obtain normal and alcoholic EEG signal coefficients. Next, thirty-six linear and nonlinear features were extracted. Except for F3 and F27–F36, all other features provide a single feature vector. The AR order (F3) is four, resulting in four feature vectors. Our newly introduced feature SDI (F27) yields a single feature vector. The matrix determinant features (F27–F36) result in different feature vectors for distinct determinant orders. For example, when we selected matrix determinant order ten (F27), the total EEG trial length was divided into twenty segments. Thus, we obtained twenty feature vectors for this case. Likewise, for matrix determinant order thirteen (F28), a single EEG trial results in thirteen segments, representing thirteen feature vectors. In total, we obtained a feature matrix of 24085 dimension, where 120 trials are for normal and 120 trials are for alcoholic. To reduce the feature matrix dimension, a correlation-based feature selection method was implemented, which results in twelve feature vectors only. We employed seventeen distinct machine learning classifiers and five different neural network classifiers for classification tasks. Performance evaluation parameters such as accuracy, sensitivity, specificity, precision, recall, F-measure, Matthew’s correlation coefficient, kappa statistics, and area under the receiver operating curve are measured in a tenfold cross-validation scheme.
Statistical analysis
The statistical analysis compares the categorization capabilities of healthy vs alcoholic EEG characteristics. Table 1 displays the mean and standard deviation (std) results for each feature vector. Table 1 exhibits that the mean values for almost all the feature sets in the healthy category are higher than in the alcoholism category, implying that the FHWT coefficients measured values of health EEG signals are larger compared to the alcoholic class, as seen in Fig. 3. Furthermore, the standard deviations for the majority of the feature sets in the healthy category are higher than the alcoholic group, indicating that alcoholism signals seem to be more comparable to one another than other category.
Table 1.
Mean, standard deviation and probability values for feature vectors of normal (C1) and alcoholic (C2) EEG signals
| Feature vector | Mean C1 | Std C1 | Mean C2 | Std C2 | p-value |
|---|---|---|---|---|---|
| Fv1 | − 3.7478 | 1.7119 | − 1.7051 | 0.92203 | 3.54E−24 |
| Fv2 | 3.5915 | 1.652 | 2.036 | 1.1493 | 4.70E−17 |
| Fv3 | 0.035276 | 0.19694 | 0.029947 | 0.17472 | 0.90379 |
| Fv4 | − 0.041406 | 0.13285 | − 0.068376 | 0.11319 | 0.066454 |
| Fv5 | 0.035757 | 0.14851 | 0.061092 | 0.10944 | 0.13345 |
| Fv6 | 0.026683 | 0.11042 | 0.0057301 | 0.1124 | 0.086783 |
| Fv7 | 0.00015939 | 0.0024409 | − 0.00015135 | 0.0022975 | 0.37408 |
| Fv8 | 0.058123 | 0.016426 | 0.019885 | 0.0089974 | 4.19E−39 |
| Fv9 | 0.23874 | 0.033711 | 0.13723 | 0.032591 | 4.19E−39 |
| Fv10 | − 7.47E−05 | 0.0074369 | 8.90E−05 | 0.0057533 | 0.48444 |
| Fv11 | 4.2108 | 1.2401 | 4.9836 | 1.4575 | 3.96E−05 |
| Fv12 | − 12695 | 1137.8 | − 14092 | 1312.1 | 6.83E−15 |
| Fv13 | 6.2738 | 1.0753 | 7.1219 | 1.1835 | 3.30E−08 |
| Fv14 | 0.92139 | 0.077459 | 0.94678 | 0.068014 | 3.96E−05 |
| Fv15 | 1.1675 | 0.080738 | 0.9231 | 0.12327 | 1.10E−34 |
| Fv16 | 0.043291 | 0.017025 | 0.014955 | 0.0074783 | 1.39E−34 |
| Fv17 | 0.058149 | 0.016435 | 0.019908 | 0.0089856 | 3.99E−39 |
| Fv18 | 0.14985 | 0.031577 | 0.10002 | 0.025934 | 5.18E−25 |
| Fv19 | 0.14993 | 0.031593 | 0.10007 | 0.025947 | 5.18E−25 |
| Fv20 | 0.63052 | 0.1161 | 0.73978 | 0.14266 | 3.24E−09 |
| Fv21 | 0.14604 | 0.029378 | 0.097755 | 0.026258 | 8.39E−25 |
| Fv22 | 0.61426 | 0.10524 | 0.72422 | 0.1509 | 1.77E−09 |
| Fv23 | 160.82 | 158.46 | 108.91 | 139.22 | 4.13E−05 |
| Fv24 | − 0.21747 | 6.9411 | 1.1331 | 5.4352 | 0.015874 |
| Fv25 | 0.058123 | 0.016426 | 0.019885 | 0.0089974 | 4.19E−39 |
| Fv26 | 1.4458 | 0.14586 | 1.4433 | 0.14282 | 0.75191 |
| Fv27 | 1.2246 | 0.088167 | 1.2304 | 0.1044 | 0.83067 |
| Fv28 | 0.14985 | 0.031577 | 0.10002 | 0.025934 | 5.18E−25 |
| Fv29 | − 0.0061863 | 0.17985 | − 0.36913 | 0.22813 | 1.94E−26 |
| Fv30 | − 2.4777 | 1.9797 | − 7.6497 | 2.703 | 5.73E−33 |
| Fv31 | − 8.1599 | 3.3398 | − 12.805 | 2.5057 | 5.50E−23 |
| Fv32 | − 12.148 | 2.7094 | − 16.244 | 2.2009 | 5.38E−25 |
| Fv33 | − 12.174 | 2.8847 | − 16.209 | 2.451 | 1.44E−21 |
| Fv34 | − 14.095 | 2.246 | − 18.023 | 2.627 | 7.70E−24 |
| Fv35 | − 17.112 | 2.5127 | − 20.088 | 2.9929 | 4.22E−13 |
| Fv36 | − 17.522 | 2.5942 | − 20.448 | 2.9331 | 2.30E−13 |
| Fv37 | − 18.661 | 2.4586 | − 21.719 | 3.1003 | 5.33E−14 |
| Fv38 | − 18.185 | 2.6493 | − 21.273 | 3.0834 | 2.06E−13 |
| Fv39 | − 19.444 | 2.9186 | − 22.058 | 4.0565 | 1.75E−06 |
| Fv40 | − 23.013 | 5.3179 | − 24.576 | 5.7275 | 0.036609 |
| Fv41 | − 22.919 | 4.738 | − 24.342 | 5.3491 | 0.06062 |
| Fv42 | − 23.258 | 4.9047 | − 24.761 | 5.6252 | 0.049787 |
| Fv43 | − 23.142 | 3.3548 | − 24.861 | 4.2673 | 0.0036995 |
| Fv44 | − 22.276 | 2.7708 | − 24.282 | 3.5097 | 4.33E−05 |
| Fv45 | − 22.11 | 2.6971 | − 24.457 | 3.213 | 5.47E−08 |
| Fv46 | − 22.127 | 2.6831 | − 24.531 | 3.4081 | 4.34E−08 |
| Fv47 | − 22.274 | 3.1471 | − 24.559 | 3.9719 | 1.85E−05 |
| Fv48 | − 22.182 | 3.3402 | − 24.568 | 4.0664 | 1.60E−05 |
| Fv49 | − 22.686 | 3.3144 | − 25.268 | 4.1291 | 1.35E−06 |
| Fv50 | − 4.0519 | 2.7382 | − 10.719 | 3.0861 | 1.55E−33 |
| Fv51 | − 12.957 | 3.8711 | − 18.501 | 2.9788 | 1.90E−23 |
| Fv52 | − 16.144 | 3.0342 | − 21.441 | 3.2217 | 2.56E−24 |
| Fv53 | − 20.825 | 3.222 | − 24.765 | 3.5228 | 2.64E−15 |
| Fv54 | − 22.45 | 3.2222 | − 26.415 | 3.9156 | 2.01E−14 |
| Fv55 | − 23.365 | 3.3523 | − 26.882 | 4.5632 | 6.21E−09 |
| Fv56 | − 28.471 | 6.9701 | − 29.991 | 7.6696 | 0.18551 |
| Fv57 | − 29.699 | 5.2715 | − 31.729 | 6.3249 | 0.020915 |
| Fv58 | − 27.732 | 3.5546 | − 30.325 | 4.6442 | 1.80E−05 |
| Fv59 | − 27.04 | 3.2397 | − 30.128 | 4.2737 | 2.97E−08 |
| Fv60 | − 27.753 | 3.6696 | − 30.755 | 4.8113 | 4.10E−06 |
| Fv61 | − 26.739 | 4.9887 | − 29.29 | 6.6591 | 0.0064096 |
| Fv62 | − 11.78 | 4.985 | − 18.591 | 3.8952 | 1.43E−25 |
| Fv63 | − 20.615 | 4.0745 | −26.263 | 3.8894 | 3.15E−21 |
| Fv64 | − 27.067 | 4.0608 | − 32.231 | 4.3037 | 1.87E−17 |
| Fv65 | − 32.309 | 3.8302 | − 38.096 | 3.7436 | 8.85E−22 |
| Fv66 | − 45.72 | 4.5742 | − 50.476 | 4.3889 | 1.74E−13 |
| Fv67 | − 37.335 | 4.2057 | − 41.602 | 4.9021 | 1.29E−10 |
| Fv68 | − 35.553 | 3.8449 | − 40.087 | 4.4451 | 1.74E−14 |
| Fv69 | − 40.397 | 4.1345 | − 45.852 | 4.1337 | 2.75E−18 |
| Fv70 | − 11.455 | 4.4853 | − 20.434 | 4.2408 | 8.03E−30 |
| Fv71 | − 28.624 | 4.2088 | − 35.849 | 5.0736 | 9.93E−23 |
| Fv72 | − 40.61 | 5.0568 | − 46.662 | 6.0188 | 6.50E−14 |
| Fv73 | − 42.361 | 5.6241 | − 47.011 | 6.5228 | 7.02E−08 |
| Fv74 | − 39.519 | 5.3645 | − 44.655 | 6.6635 | 4.34E−09 |
| Fv75 | − 14.451 | 4.9447 | − 24.74 | 4.9917 | 6.92E−30 |
| Fv76 | − 35.844 | 4.9037 | − 42.824 | 6.4363 | 3.26E−16 |
| Fv77 | − 46.63 | 7.4271 | − 51.271 | 9.0097 | 5.46E−05 |
| Fv78 | − 19.486 | 5.2222 | − 30.443 | 5.5773 | 7.07E−30 |
| Fv79 | − 47.065 | 7.424 | − 53.729 | 9.0372 | 8.28E−09 |
| Fv80 | − 49.028 | 6.5155 | − 55.256 | 8.8471 | 5.03E−08 |
| Fv81 | − 26.154 | 6.0719 | − 38.17 | 6.4825 | 3.63E−28 |
| Fv82 | − 56.522 | 8.4374 | − 63.285 | 10.77 | 9.24E−07 |
| Fv83 | − 32.575 | 6.6007 | − 44.912 | 7.5683 | 7.62E−26 |
| Fv84 | − 41.589 | 7.0482 | − 54.176 | 8.4344 | 9.65E−24 |
| Fv85 | − 50.88 | 8.135 | − 64.1 | 9.794 | 5.37E−21 |
Relating to the observations made thus far, it is reasonable to conclude that alcoholic EEG signals resemble more with fewer fluctuations when compared to normal EEG signals. The Kruskal Wallis (KW) test is used for probability values (p-value) since it is a non-parametric test that does not require specific feature distributions. Table 1 further shows that the p-value for the majority of the features is less than 0.001, implying that the suggested features are statistically significant. We also discovered that our newly proposed features (F26–F36) in the alcoholic EEG field provide very low p values, showing the relevance of those features in differentiating between normal and alcoholic EEG signals.
In addition, we also displayed the extracted features to analyze them further statistically. We used t-distributed stochastic neighbour embedding (t-SNE), a statistical method for displaying high-dimensional features by assigning a two-dimensional map to each feature [61]. T-SNE is a nonlinear technique. Thus, it is an excellent choice for our extracted linear and nonlinear features. Figure 4 display the distribution of the two-dimensional feature. The extracted features indicate significant differences among normal and alcoholic classes.
Fig. 4.
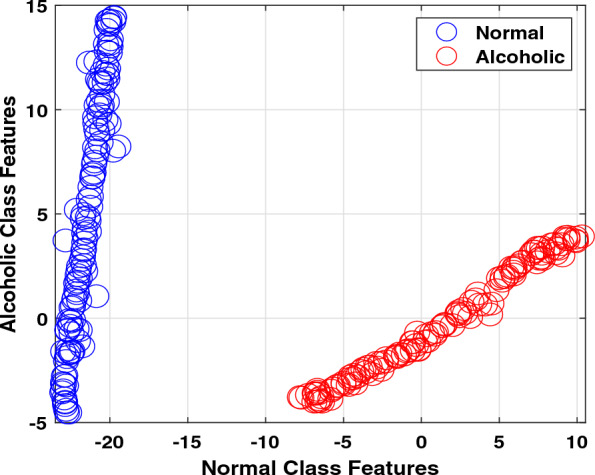
Two-dimensional samples distribution of features
Analysis with all features and classifiers
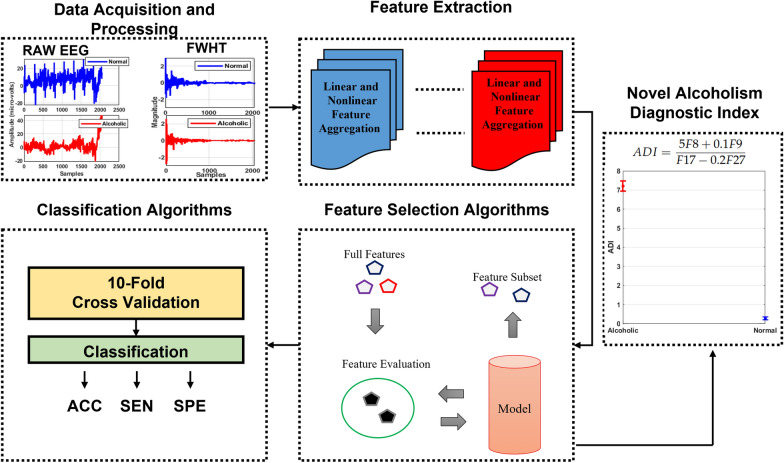
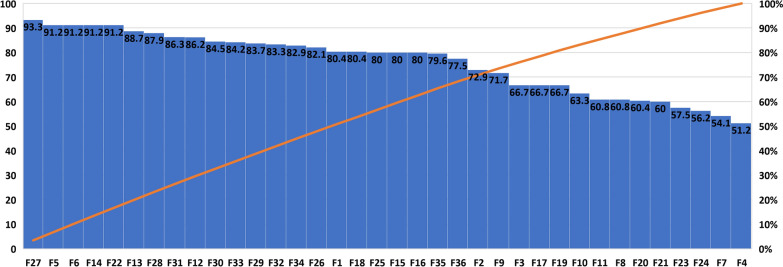
First, we decided on normal vs. alcoholic EEG signals identification by employing all features and classifiers. It is noted in Fig. 5 that SMO obtains the highest classification accuracy of 93.3%. The RF ranked second with 92.9% of classification accuracy, followed by J48 and adaboost. On the other hand, the lowest outcome of 81.2% is delivered by the logistic. Although all the classification results obtained by different classifiers provide more than 80% classification accuracy outcome, their practical applicability is difficult due to the computational complexity produced by 85 feature vectors.
Fig. 5.
Results (%) obtained with all features by employing several classifiers and performance measures
Analysis with all features vs. selected features
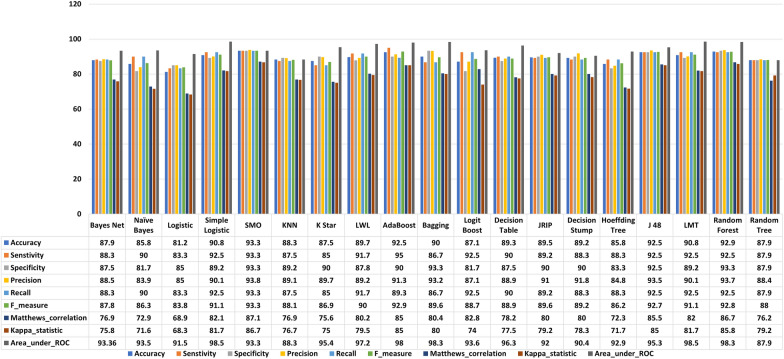
Figure 4 displays that the same class features overlap indicating these are redundant, and there is a need to implement a feature selection method to reduce redundancy. We implemented a CFS-FS method and obtained twelve feature vectors out of a total of eighty-five. There is an 86% reduction in the feature matrix. The selected feature vectors are Fv1, Fv8, Fv9, Fv15, Fv17, Fv22, Fv29, Fv30, Fv34, Fv50, Fv75, and Fv79. It is observed that F29 represents the SDI whereas, Fv30, Fv34, Fv50, Fv75, and Fv79 denoted the matrix determinant features. It infers that 50% selected feature matrix is made up with SDI and matrix determinant indicating that these features play a significant role in identifying normal and alcoholism EEG signals. Figure 6 shows the comparison among all features and chosen features accuracies. It is demonstrated in Fig. 6 that the FS strategy significantly increases the classification accuracy for most of the cases. It is noted that logistic regression ranked at number one in classification accuracy improvement with an 11.7% of accuracy rise. Hoeffding tree and Naive Bayesclassifiers ranked at second and third with 8.4% and 7.5% of classification accuracy improvements. The classification accuracy for simple logistic, SMO, adaboost, bagging, decision stump, J48 and LMT remains the same, concluding that all other feature vectors were redundant for these classifiers. The same accuracy can be achieved with relatively fewer feature vectors. It is summarized that the proposed FS strategy provides up to 13% classification accuracy improvement with the Hoeffding tree classifier compared to all other classifiers.
Fig. 6.
Classification accuracy (%) obtained with all and selected features
Analysis with neural network classifiers
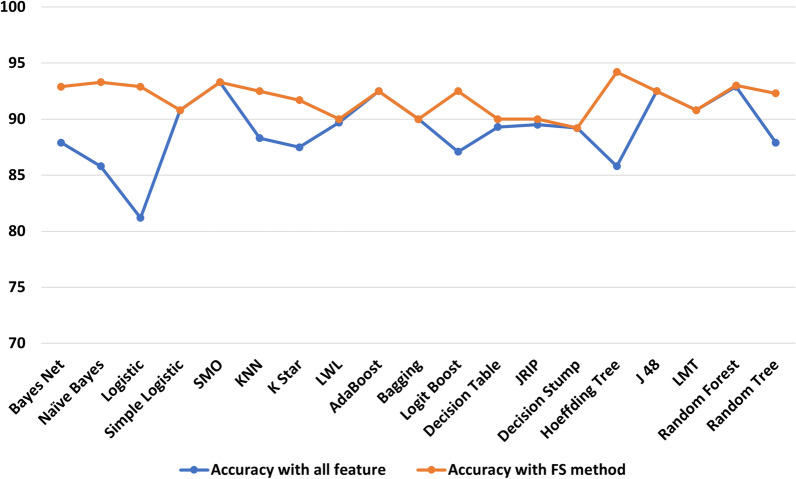
We used selected features for subsequent investigation, considering feature selection improves classification accuracy substantially. Results from different neural network (NN) models were used to see if NN improve classification accuracy compared to machine learning classifiers. Figure 7 shows the results of the performance evaluation with NN. The RNN achieves the highest classification accuracy of 97.5%, whilst the FFNN achieves the lowest classification accuracy of 96.3%. All other NN models have a classification accuracy of 96.7%. Compared to machine learning classifiers, the RNN improves classification accuracy by up to 16.3%. Another noteworthy aspect of Fig. 7 is that all of the NN classification modes exhibited minimal variations across various performance measures. Standard deviation values of 1.92, 1.57, 1.6, 2.4, and 1.2 are produced using ANN, MANN, FFNN, CFNN, and RNN. This implies that the results of NN classification are reasonably consistent and reliable.
Fig. 7.
Results (%) obtained with neural network classifiers
Analysis with single feature
The RNN classification model is used to determine the importance of each feature in detecting normal and alcoholic EEG signals. The classification accuracy results with single feature are shown in Fig. 8. It is worth noting that the very first time the matrix determinant order ten feature (F27) has been used in the alcoholism domain, it attained a prediction performance of 93.3%. Also, it is worth noting that the F28, F31, F30, F33, F29, F32, and F34 matrix determinant orders all obtained more than 80% prediction performance [37]. Furthermore, the SDI feature, which is being offered for its first time in the alcoholic domain, yielded 82.1% classification performance. We suggest that the individual classification accuracy provided by matrix determinants and SDI features is far above the baseline accuracy needed to handle an automated system [37]. It is concluded that proposed matrix determinant order ten feature deliver up to 42.1% of classification accuracy improvement in comparison with all other individual features.
Fig. 8.
Results (%) obtained with single feature
Analysis with proposed index
Another significant aspect of this work is establishing a new alcoholic screening index. It is harder to pinpoint the variety of desired traits among healthy and alcoholic patients to build a suitable prognosis. Although classifiers are utilized for assessment, physicians prefer to pay attention towards a unique score showing different categories’ presence [42, 62]. With this specific goal, a unique alcoholic index is constructed using features specified by the CFS technique following a series of investigations to identify alcoholic EEG signals. The mathematical formulation of proposed index is given as,
| 33 |
The alcoholic diagnostic index (ADI) findings (mean ± std) for normal and alcoholic categories are shown in Table 2. The readings of the ADI for the distinct types are totally distinguishable from one another, as shown in Table 2.
Table 2.
The mean ± std and p-value for the ADI
| Index | Alcoholic | Normal | p-value |
|---|---|---|---|
| ADI | 7.055E−41 |
The ADI ranges for the two classes are also shown in Fig. 9, and it give a clear distinction among them. As a result, the proposed index may clearly distinguish between healthy and alcoholic individual with the aid of a unique number, assisting healthcare experts.
Fig. 9.
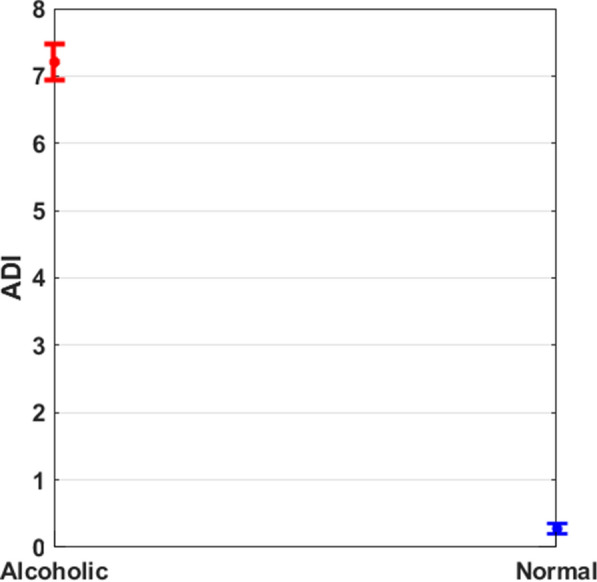
Results with proposed index
Employing ADI as a single feature
We utilized the proposed ADI as a single feature in a computerized framework. It is worth mentioning here the proposed ADI delivers 100% classification accuracy, sensitivity, and specificity measures indicate normal and alcoholic EEG signal identification’s perfect capability. The kappa and AUC measures were also 1 showing the correct title by the classifier. All these measures were obtained by employing the RNN classification model. Thus, we conclude that computerized framework and ADI are perfect choices for correctly identifying normal or alcoholic EEG signals.
Discussion
In this research, the FWHT technique examines EEG signals’ intricacy and disordered behaviour in normal and alcoholic categories. As seen in Fig. 3, the healthy group’s visual depiction of FWHT of an EEG signal has a larger amplitude than the alcoholic group’s. This signifies that the FWHT approach might be used as an alcoholism graphical potential treatment for clinicians and aid neuroscientists in examining the impact of alcohol on the brain. Table 1 shows that the alcoholic EEG signal features have lesser average scores than the normal group, demonstrating that the morphologies in the alcoholic EEG signal are significantly more obvious. We utilized several linear and nonlinear features [63, 64] with multiple machine learning classifiers to determine the optimal amalgamation to the built computerized framework. The neural network classification models were also evaluated to identify whether machine learning classifiers perform best or neural network classifiers. The classification ability of a single feature with the best classifier was also tested. It is noted that SMO and RNN are the best choices in machine learning and neural network classification models. In addition, the matrix determinant feature provides maximum classification accuracy when used as a single feature. Table 3 shows that nearly all of the available techniques are developed using time–frequency with irregular features, that has various drawbacks like incompatible frequency sequence, mode mixing, tightly packed spectrum, and computationally intensive procedures. The storage demand for these techniques is also high due to various signal components. On the contrary, the proposed FWHT is a relatively simple technique as it involves only arithmetic operations thus, require significantly less storage capacity. By looking in Table 3, it is noted that the proposed FS strategy and RNN classification model significantly increase the classification accuracy in comparison with all features tested with machine learning classifiers. By employing the CFS FS approach with the RNN classifier, the average classification accuracy of 97.5%, the sensitivity of 96.7% and specificity of 98.3% is achieved with a tenfold cross-validation strategy. This can be inferred that the proposed CFS FS strategy is not only helping to raise classification accuracy but also significantly reduces the feature matrix dimension. It is also worth mentioning here that neural network classification models help to achieve higher and stable performance evaluation measures in comparison with machine learning models.
Table 3.
Comparison of the proposed computerized work with available work
| References | Method, feature | FS | CV | Classifier | Acc | Sen | Spe |
|---|---|---|---|---|---|---|---|
| [8] | HMMs + Coupled HMMs, 2002 | Not used | Tenfold | NN | 82.98 | – | – |
| [9] | Nonlinear + HOS Features, 2012 | p-value | Threefold | SVM | 91.7 | 90 | 93.33 |
| [10] | WPT + HOS Features, 2013 | p-value | Tenfold | KNN | 95.8 | 95.8 | 95.8 |
| [15] | CWT + Statistical Features, 2014 | Not used | Tenfold | SVM | 94.29 | – | – |
| [16] | TQWT + Nonlinear Features, 2017 | PCA | Tenfold | LS-SVM | 97.02 | 96.53 | 97.5 |
| [11] | Granger Causality, 2017 | Not used | Fivefold | SVM | 90 | 95.3 | 82.4 |
| [17] | DTCWT + Nonlinear Features, 2018 | p-value | Tenfold | SVM | 97.91 | – | – |
| [18] | TBOWFB + Nonlinear Features, 2018 | p-value | Tenfold | LS-SVM | 97.08 | 97.08 | 97.08 |
| [12] | Synchronization Likelihood, 2018 | ROC | Tenfold | SVM | 98 | 99.9 | 95 |
| [20] | EMD + Power Band + Fractal Dimension, 2019 | ICA | Tenfold | KNN | 98.91 | 99.02 | 99.24 |
| [21] | FBSE-EWT + Nonlinear Features, 2020 | Not used | Leave one out | LS-SVM | 98.8 | 98.3 | 99.1 |
| [22] | EWT + Statistical Features, 2020 | p-value | Leave one out | LS-SVM | 98.75 | 98.35 | 99.16 |
| [30] | NN, 2020 | Not used | Tenfold | LSTM | 93 | 95 | 92 |
| This work | FHWT + All Features, 2022 | No | Tenfold | SMO | 93.3 | 93.3 | 93.3 |
| This work | FHWT + Selected Features, 2022 | CFS | Tenfold | Hoeffding Tree | 94.2 | 97.5 | 90.8 |
| This work | FHWT + Selected Features, 2022 | CFS | Tenfold | RNN | 97.5 | 96.7 | 98.3 |
| This work | FHWT + Matrix Determinant, 2022 | No | Tenfold | RNN | 93.3 | 93.3 | 93.3 |
| This work | FHWT + ADI, 2022 | No | Tenfold | RNN | 100 | 100 | 100 |
Another critical aspect of this research is to introduce a matrix determinant and alcoholic diagnostic index (ADI) as a single feature to develop the computerized framework. Using matrix determinants and ADI, a classification accuracy of 93.3% and 100% is obtained with RNN in 10-fold cross-validation. It is concluded that the proposed framework is the most straightforward choice for the correct identification of alcoholic EEG signals.
The time complexity of our proposed experiments is presented in Table 4. This time is collected for all trials and the best classifier in each case. It is noted in Table 4 that SMO needed 0.007 s for training while 0 s is required to test with all features. While CFS help to reduce the training and test time as obtained with Hoeffding Tree. RNN needed 0.57 s, 0.29 s, and 0.05 s of training time by employing CFS selection, matrix determinant, and ADI features. Also, the test time is 0, 0.0005 s and 0.0007 s. We conclude that the ADI is also computationally efficient in identifying normal and alcoholic EEG signals.
Table 4.
Computational time of proposed experiments
| Classifier | Features | Training time | Test time |
|---|---|---|---|
| SMO | All | 0.007 | 0 |
| Hoeffding Tree | CFS selected | 0.005 | 0.006 |
| RNN | CFS selected | 0.5748 | 0 |
| RNN | Matrix determinant | 0.29 | 0.0005 |
| RNN | ADI | 0.05 | 0.0007 |
In this work, we proposed an innovative index, the ADI, as a specific diagnostic marker for alcoholic diseases. The suggested indicator can be used as a measure during alcoholism monitoring and as a benchmark for a specialist to determine how much brain damage an alcoholism individual has experienced. Notwithstanding, our proposed index does not require a certain time–frequency decomposition method prior to actually extracting the features, and the features are derived straightaway from the FWHT coefficients of EEG signals, resulting in simple and quick computation.
The strengths of this research included (i) the FWHT is used in a fairly straightforward way to distinguish between the nonlinear features of healthy and alcoholic Brain activity; (ii) a variety of features and classifiers have been investigated; (iii) design a robust feature selection strategy; (iv) introduction of matrix determinant and successive decomposition index for computerized alcoholic framework; (v) offering innovative diagnostic indexes and new biomarkers that can be used as treatment aids by medical experts.
Conclusion
Alcoholism is now one of the world’s most widespread problems. It can increase the risk of heart illness, loneliness, self-harm, or homicide if left untreated. Despite the fact that experienced doctors can identify alcoholism through medical imaging and counseling, automated procedures are required to circumvent potential mistakes. In this study, a new automated paradigm for detecting alcoholic subjects is built using the Fast Walsh–Hadamard transform of EEG signals. Essentially, the essential linear and nonlinear features of EEG signals are retrieved from the FWHT coefficients, then chosen and given to classification techniques. With the suggested alcoholic screening index as a specific attribute in the tenfold cross-validation technique, the suggested scheme obtained a prediction accuracy of 100%. Furthermore, the suggested unique index can be used by medical professionals to diagnose alcoholic subjects using a single number signal. The suggested framework features extremely quick processing, making it an excellent candidate for practical uses. The proposed scheme could be used to examine various cognitive deteriorating conditions in the future.
Acknowledgements
This work was supported by King Saud University, Riyadh, Saudi Arabia, through Researchers Supporting Project Number RSP2023R184.
Declarations
Conflict of interest
Authors declared there is no conflict of interest.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.World Health Organization . Global status report on alcohol and health 2018. Geneva: World Health Organization; 2018. [Google Scholar]
- 2.Prince J. Substance use disorder and suicide attempt among people who report compromised health. Subst Use Misuse. 2018;53(1):9–15. doi: 10.1080/10826084.2017.1323925. [DOI] [PubMed] [Google Scholar]
- 3.Arunkumar N, Kumar KR, Venkataraman V. Entropy features for focal EEG and non focal EEG. J Comput Sci. 2018;27:440–444. [Google Scholar]
- 4.Siuly S, Li Y, Zhang Y. EEG signal analysis and classification. In: Health information science. Springer; 2016. ISBN: 978-3-319-47653-7.
- 5.Khan DM, Yahya N, Kamel N, Faye I. Effective connectivity in default mode network for alcoholism diagnosis. IEEE Trans Neural Syst Rehabil Eng. 2021;29:796–808. doi: 10.1109/TNSRE.2021.3075737. [DOI] [PubMed] [Google Scholar]
- 6.Zhu G, Li Y, Wen PP, Wang S. Analysis of alcoholic EEG signals based on horizontal visibility graph entropy. Brain Inform. 2014;1(1–4):19–25. doi: 10.1007/s40708-014-0003-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhu G, Li Y, Wen P. Evaluating functional connectivity in alcoholics based on maximal weight matching. J Adv Comput Intell Intell Inform. 2011;15(9):1221–1227. [Google Scholar]
- 8.Zhong S, Ghosh J. HMMS and coupled HMMS for multi-channel EEG classification. In: Proceedings of the 2002 international joint conference on neural networks. IJCNN’02 (Cat. No. 02CH37290), vol 2. IEEE; 2002. p. 1154–9.
- 9.Acharya UR, Sree SV, Chattopadhyay S, Suri JS. Automated diagnosis of normal and alcoholic EEG signals. Int J Neural Syst. 2012;22(03):1250011. doi: 10.1142/S0129065712500116. [DOI] [PubMed] [Google Scholar]
- 10.Faust O, Yu W, Kadri NA. Computer-based identification of normal and alcoholic EEG signals using wavelet packets and energy measures. J Mech Med Biol. 2013;13(03):1350033. [Google Scholar]
- 11.Bae Y, Yoo BW, Lee JC, Kim HC. Automated network analysis to measure brain effective connectivity estimated from EEG data of patients with alcoholism. Physiol Meas. 2017;38(5):759. doi: 10.1088/1361-6579/aa6b4c. [DOI] [PubMed] [Google Scholar]
- 12.Mumtaz W, Kamel N, Ali SSA, Malik AS, et al. An EEG-based functional connectivity measure for automatic detection of alcohol use disorder. Artif Intell Med. 2018;84:79–89. doi: 10.1016/j.artmed.2017.11.002. [DOI] [PubMed] [Google Scholar]
- 13.Akbari H, Sadiq MT, Siuly S, Li Y, Wen P. Identification of normal and depression EEG signals in variational mode decomposition domain. Health Inf Sci Syst. 2022;10(1):1–14. doi: 10.1007/s13755-022-00187-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sadiq MT, Yu X, Yuan Z, Aziz MZ, Rehman N, Ding W, Xiao G. Motor imagery BCI classification based on multivariate variational mode decomposition. IEEE Trans Emerg Top Comput Intell. 2022;6(5):1177–1189. [Google Scholar]
- 15.Upadhyay R, Padhy P, Kankar P. Alcoholism diagnosis from EEG signals using continuous wavelet transform. In: 2014 annual IEEE India conference (INDICON). IEEE; 2014, p. 1–5.
- 16.Patidar S, Pachori RB, Upadhyay A, Acharya UR. An integrated alcoholic index using tunable-Q wavelet transform based features extracted from EEG signals for diagnosis of alcoholism. Appl Soft Comput. 2017;50:71–78. [Google Scholar]
- 17.Sharma M, Sharma P, Pachori RB, Acharya UR. Dual-tree complex wavelet transform-based features for automated alcoholism identification. Int J Fuzzy Syst. 2018;20(4):1297–1308. [Google Scholar]
- 18.Sharma M, Deb D, Acharya UR. A novel three-band orthogonal wavelet filter bank method for an automated identification of alcoholic EEG signals. Appl Intell. 2018;48(5):1368–1378. [Google Scholar]
- 19.Anuragi A, Sisodia DS. Alcohol use disorder detection using EEG signal features and flexible analytical wavelet transform. Biomed Signal Process Control. 2019;52:384–393. [Google Scholar]
- 20.Thilagaraj M, Rajasekaran MP. An empirical mode decomposition (EMD)-based scheme for alcoholism identification. Pattern Recognit Lett. 2019;125:133–139. [Google Scholar]
- 21.Anuragi A, Sisodia DS, Pachori RB. Automated alcoholism detection using Fourier–Bessel series expansion based empirical wavelet transform. IEEE Sens J. 2020;20(9):4914–4924. [Google Scholar]
- 22.Anuragi A, Sisodia DS. Empirical wavelet transform based automated alcoholism detecting using EEG signal features. Biomed Signal Process Control. 2020;57:101777. [Google Scholar]
- 23.Mehla VK, Singhal A, Singh P. A novel approach for automated alcoholism detection using Fourier decomposition method. J Neurosci Methods. 2020;346:108945. doi: 10.1016/j.jneumeth.2020.108945. [DOI] [PubMed] [Google Scholar]
- 24.Zhang H, Silva FH, Ohata EF, Medeiros AG, Rebouças Filho PP. Bi-dimensional approach based on transfer learning for alcoholism pre-disposition classification via EEG signals. Front Hum Neurosci. 2020;14:365. [DOI] [PMC free article] [PubMed]
- 25.Mukhtar H, Qaisar SM, Zaguia A. Deep convolutional neural network regularization for alcoholism detection using EEG signals. Sensors. 2021;21(16):5456. doi: 10.3390/s21165456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Buriro AB, Ahmed B, Baloch G, Ahmed J, Shoorangiz R, Weddell SJ, Jones RD. Classification of alcoholic EEG signals using wavelet scattering transform-based features. Comput Biol Med. 2021;139:104969. doi: 10.1016/j.compbiomed.2021.104969. [DOI] [PubMed] [Google Scholar]
- 27.Dong S, Yuan Z, Yu X, Zhang J, Sadiq MT, Zhang F. On-line gait adjustment for humanoid robot robust walking based on divergence component of motion. IEEE Access. 2019;7:159507–159518. [Google Scholar]
- 28.Dong S, Yuan Z, Yu X, Sadiq MT, Zhang J, Zhang F, Wang C. Flexible model predictive control based on multivariable online adjustment mechanism for robust gait generation. Int J Adv Robot Syst. 2020;17(1):1729881419887291. [Google Scholar]
- 29.Sadiq MT, Akbari H, Rehman AU, Nishtar Z, Masood B, Ghazvini M, Too J, Hamedi N, Kaabar MKA. Exploiting feature selection and neural network techniques for identification of focal and nonfocal EEG signals in TQWT domain. J Healthc Eng. 2021;2021:24. doi: 10.1155/2021/6283900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Farsi L, Siuly S, Kabir E, Wang H. Classification of alcoholic EEG signals using a deep learning method. IEEE Sens J. 2020;21(3):3552–3560. [Google Scholar]
- 31.Sadiq MT, Aziz MZ, Almogren A, Yousaf A, Siuly S, Rehman AU. Exploiting pretrained CNN models for the development of an EEG-based robust BCI framework. Comput Biol Med. 2022;143:105242. doi: 10.1016/j.compbiomed.2022.105242. [DOI] [PubMed] [Google Scholar]
- 32.Snodgrass JG, Vanderwart M. A standardized set of 260 pictures: norms for name agreement, image agreement, familiarity, and visual complexity. J Exp Psychol Hum Learn Mem. 1980;6(2):174. doi: 10.1037//0278-7393.6.2.174. [DOI] [PubMed] [Google Scholar]
- 33.Sadiq MT, Akbari H, Siuly S, Li Y, Wen P. Fractional Fourier transform aided computerized framework for alcoholism identification in EEG. In: International conference on health information science. Springer; 2022. p. 100–12.
- 34.Sadiq MT, Siuly S, Rehman AU, Wang H. Auto-correlation based feature extraction approach for EEG alcoholism identification. In: International conference on health information science. Springer; 2021. p. 47–58.
- 35.Subathra M, Mohammed MA, Maashi MS, Garcia-Zapirain B, Sairamya N, George ST, et al. Detection of focal and non-focal electroencephalogram signals using fast Walsh–Hadamard transform and artificial neural network. Sensors. 2020;20:4952. doi: 10.3390/s20174952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sadiq MT, Yu X, Yuan Z, Fan Z, Rehman AU, Li G, Xiao G. Motor imagery EEG signals classification based on mode amplitude and frequency components using empirical wavelet transform. IEEE Access. 2019;7:127678–127692. [Google Scholar]
- 37.Yu X, Aziz MZ, Sadiq MT, Fan Z, Xiao G. A new framework for automatic detection of motor and mental imagery EEG signals for robust BCI systems. IEEE Trans Instrum Meas. 2021;70:1–12. [Google Scholar]
- 38.Sadiq MT, Siuly S, Rehman AU. Evaluation of power spectral and machine learning techniques for the development of subject-specific BCI. In: Artificial intelligence-based brain–computer interface. Elsevier; 2022. p. 99–120.
- 39.Akbari H, Sadiq MT, Rehman AU. Classification of normal and depressed EEG signals based on centered correntropy of rhythms in empirical wavelet transform domain. Health Inf Sci Syst. 2021;9(1):1–15. doi: 10.1007/s13755-021-00139-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sadiq MT, Yu X, Yuan Z, Zeming F, Rehman AU, Ullah I, Li G, Xiao G. Motor imagery EEG signals decoding by multivariate empirical wavelet transform-based framework for robust brain–computer interfaces. IEEE Access. 2019;7:171431–171451. [Google Scholar]
- 41.Şen B, Peker M, Çavuşoğlu A, Çelebi FV. A comparative study on classification of sleep stage based on EEG signals using feature selection and classification algorithms. J Med Syst. 2014;38(3):1–21. doi: 10.1007/s10916-014-0018-0. [DOI] [PubMed] [Google Scholar]
- 42.Akbari H, Sadiq MT, Siuly S, Li Y, Wen P. An automatic scheme with diagnostic index for identification of normal and depression EEG signals. In: International conference on health information science. Springer; 2021. p. 59–70.
- 43.Raghu S, Sriraam N, Rao SV, Hegde AS, Kubben PL. Automated detection of epileptic seizures using successive decomposition index and support vector machine classifier in long-term EEG. Neural Comput Appl. 2019;32:8965–8984. [Google Scholar]
- 44.Sadiq MT, Yu X, Yuan Z, Aziz MZ. Identification of motor and mental imagery EEG in two and multiclass subject-dependent tasks using successive decomposition index. Sensors. 2020;20(18):5283. doi: 10.3390/s20185283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sadiq MT, Yu X, Yuan Z, Aziz MZ, Siuly S, Ding W. A matrix determinant feature extraction approach for decoding motor and mental imagery EEG in subject specific tasks. IEEE Trans Cogn Dev Syst. 2020 doi: 10.1109/TCDS.2020.3040438. [DOI] [Google Scholar]
- 46.Raghu S, Sriraam N, Hegde AS, Kubben PL. A novel approach for classification of epileptic seizures using matrix determinant. Expert Syst Appl. 2019;127:323–341. [Google Scholar]
- 47.Sadiq MT, Yu X, Yuan Z, Aziz MZ, Siuly S, Ding W. Toward the development of versatile brain–computer interfaces. IEEE Trans Artif Intell. 2021;2(4):314–328. [Google Scholar]
- 48.Witten IH, Frank E, Hall MA, Pal CJ, DATA M. Practical machine learning tools and techniques. Data Min. 2005;2:4. [Google Scholar]
- 49.Akhter MP, Jiangbin Z, Naqvi IR, Abdelmajeed M, Mehmood A, Sadiq MT. Document-level text classification using single-layer multisize filters convolutional neural network. IEEE Access. 2020;8:42689–42707. [Google Scholar]
- 50.Akhter MP, Jiangbin Z, Naqvi IR, Abdelmajeed M, Sadiq MT. Automatic detection of offensive language for Urdu and Roman Urdu. IEEE Access. 2020;8:91213–91226. [Google Scholar]
- 51.Zhang J, Yuan Z, Dong S, Sadiq MT, Zhang F, Li J. Structural design and kinematics simulation of hydraulic biped robot. Appl Sci. 2020;10(18):6377. [Google Scholar]
- 52.Fan Z, Jamil M, Sadiq MT, Huang X, Yu X, et al. Exploiting multiple optimizers with transfer learning techniques for the identification of COVID-19 patients. J Healthc Eng. 2020 doi: 10.1155/2020/8889412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Tufail AB, Ullah I, Rehman AU, Khan RA, Khan MA, Ma Y-K, Khokhar NH, Sadiq MT, Khan R, Shafiq M, et al. On disharmony in batch normalization and dropout methods for early categorization of Alzheimer’s disease. Sustainability. 2022;14(22):14695. [Google Scholar]
- 54.Sarki R, Ahmed K, Wang H, Zhang Y, Wang K. Convolutional neural network for multi-class classification of diabetic eye disease. EAI Endorsed Trans Scalable Inf Syst. 2022;9(4):e5. [Google Scholar]
- 55.Alvi AM, Siuly S, Wang H. A long short-term memory based framework for early detection of mild cognitive impairment from EEG signals. IEEE Trans Emerg Top Comput Intell. 2023;7(2):375–388. doi: 10.1109/TETCI.2022.3186180. [DOI] [Google Scholar]
- 56.Hu H, Li J, Wang H, Daggard G, Shi M. A maximally diversified multiple decision tree algorithm for microarray data classification. Intell Syst Bioinform 2006;2006
- 57.Sarki R, Ahmed K, Wang H, Zhang Y. Automated detection of mild and multi-class diabetic eye diseases using deep learning. Health Inf Sci Syst. 2020;8(1):32. doi: 10.1007/s13755-020-00125-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Supriya S, Siuly S, Wang H, Zhang Y. Automated epilepsy detection techniques from electroencephalogram signals: a review study. Health Inf Sci Syst. 2020;8:1–15. doi: 10.1007/s13755-020-00129-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Sadiq MT, Yu X, Yuan Z, Aziz MZ. Motor imagery BCI classification based on novel two-dimensional modelling in empirical wavelet transform. Electron Lett. 2020;56(25):1367–1369. [Google Scholar]
- 60.Sadiq MT, Yu X, Yuan Z. Exploiting dimensionality reduction and neural network techniques for the development of expert brain–computer interfaces. Expert Syst Appl. 2021;164:114031. [Google Scholar]
- 61.Yu X, Aziz MZ, Sadiq MT, Jia K, Fan Z, Xiao G. Computerized multidomain EEG classification system: a new paradigm. IEEE J Biomed Health Inform. 2022 doi: 10.1109/JBHI.2022.3151570. [DOI] [PubMed] [Google Scholar]
- 62.Sadiq MT, Akbari H, Siuly S, Li Y, Wen P. Alcoholic EEG signals recognition based on phase space dynamic and geometrical features. Chaos Solitons Fractals. 2022;158:112036. [Google Scholar]
- 63.Akbari H, Ghofrani S, Zakalvand P, Sadiq MT. Schizophrenia recognition based on the phase space dynamic of EEG signals and graphical features. Biomed Signal Process Control. 2021;69:102917. [Google Scholar]
- 64.Akbari H, Sadiq MT, Jafari N, Too J, Mikaeilvand N, Cicone A, Serra-Capizzano S. Recognizing seizure using Poincaré plot of EEG signals and graphical features in DWT domain. Bratisl Lek Listy. 2023;124(1):12–24. doi: 10.4149/BLL_2023_002. [DOI] [PubMed] [Google Scholar]