Deep Learning Assisted Detection of Glaucoma Progression in Spectral-Domain Optical Coherence Tomography

Abstract

Purpose:

To develop and validate a deep learning (DL) model for detection of glaucoma progression using spectral-domain optical coherence tomography (SDOCT) measurements of retinal nerve fiber layer (RNFL) thickness.

Design:

Retrospective cohort study.

Participants:

A total of 14,034 SDOCT scans from 816 eyes from 462 individuals.

Methods:

A DL convolutional neural network was trained to assess SDOCT RNFL thickness measurements of two visits (a baseline and a follow-up) along with time between visits to predict the probability of glaucoma progression. The ground truth was defined by consensus from subjective grading by glaucoma specialists. Diagnostic performance was summarized by the area under the receiver operator characteristic curve (AUC), sensitivity, and specificity, and was compared to conventional trend-based analyses of change. Interval likelihood ratios were calculated to determine the impact of DL model results in changing the post-test probability of progression.

Main outcome measures:

AUC, sensitivity, and specificity of the DL model.

Results:

The DL model had an AUC of 0.938 (95% confidence interval [CI]: 0.921, 0.955), with sensitivity of 87.3% (95% CI: 83.6%, 91.6%) and specificity of 86.4% (95% CI: 79.9%, 89.6%). When matched for the same specificity, the DL model significantly outperformed trend-based analyses. Likelihood ratios for the deep learning model were associated with large changes in probability of progression in the vast majority of SDOCT tests.

Conclusions:

A DL model was able to assess the probability of glaucomatous structural progression from SDOCT RNFL thickness measurements. The model agreed well with expert judgements and outperformed conventional trend-based analyses of change, while also providing indication of the likely locations of change.

INTRODUCTION

Glaucoma is a progressive optic neuropathy, characterized by loss of retinal ganglion cells, and typical patterns of optic nerve damage and visual function loss.¹ Due to its irreversible nature, the main goal of glaucoma management is to prevent further damage caused by the disease. Accurate and prompt assessment of progression is therefore essential to determine whether escalation of therapy is necessary.

Traditionally, glaucoma progression has been identified by the deterioration of visual function sensitivity, measured by standard automated perimetry (SAP). With the advent of technologies such as spectral-domain optical coherence tomography (SD-OCT), it became possible to acquire objective and reproducible structural measurements, such as retinal nerve fiber layer (RNFL) thickness, that can be used to monitor glaucomatous changes over time.^2–4 Progressive RNFL thinning has been shown to be associated with future development of visual field loss^{5, 6} and, particularly in early glaucoma stages, the chance of detecting progression may be higher with SD-OCT than SAP.^{7, 8}

There is, however, no consensus on how to determine whether an eye is presenting progression based on SD-OCT results. Aside from subjective clinical judgement, the two objective strategies most used in clinical practice and in research studies are trend- and event-based analyses. In trend-based analysis, a rate of change is calculated by estimating a linear trend of measurements over time, usually by ordinary least-squares linear regression. Although the rate of change is a useful parameter in clinical decision making, trend-based assessment relies on summary parameters, such as global peripapillary RNFL thickness, which may be insensitive to small, localized changes. Event-based analysis compares the amount of change from a baseline test to the expected limits of test-retest variability.⁹ Although event-based algorithms may be more sensitive to small, localized progression, they do not take into account the time during which the changes have occurred. In addition, currently available event-based algorithms rely on short-term test-retest variability which may lead to spurious results when monitoring patients over the long-term.^{10, 11}

Artificial intelligence algorithms, such as deep learning (DL) models, are (with sufficient and appropriate training data) capable of identifying complex patterns in data and make classifications or predictions with performance comparable, sometimes even superior, to the evaluation of experts. Particularly for glaucoma, several studies have proposed the use of DL to detect signs of glaucomatous optic neuropathy on cross-sectional SD-OCT scans or optic disc volumes.^12–21 However, there has been a lack of studies on using DL models for improving the assessment of longitudinal data and detection of progression with SD-OCT. In the present work, we report on the development of a DL model to detect structural glaucoma progression on SD-OCT tests and compare its performance to that of conventional analyses.

METHODS

This study used data from the Duke Glaucoma Registry, a database of electronic medical and research records developed by the Vision, Imaging, and Performance Laboratory at Duke University.²² The Duke University Health System Institutional Review Board approved this study, and a waiver of informed consent was granted due to the retrospective nature of this work. All methods adhered to the tenets of the Declaration of Helsinki for research involving human subjects and the study was conducted in accordance with regulations of the Health Insurance Portability and Accountability Act.

The database contained longitudinal information on comprehensive ophthalmologic examinations during follow-up, diagnoses, medical history, visual acuity, slit-lamp biomicroscopy, intraocular pressure measurements, results of gonioscopy and dilated slit-lamp funduscopic examinations. In addition, the registry contained fundus photographs, standard automated perimetry (SAP; Humphrey Field Analyzer II, Carl Zeiss Meditec, Inc., Dublin, CA) and Spectralis SD-OCT (Software version 6.8, Heidelberg Engineering, GmbH, Dossenheim, Germany) images and data. Individuals were included in the study if they were adults 18 years and older and if they had at least one year of follow-up and three visits with SD-OCT scans. Individuals were excluded from the study if they did not meet the criteria above and if they had other ocular or systemic diseases that could affect the optic nerve or the visual field.

Diagnosis of glaucoma was defined based on the presence of glaucomatous repeatable visual field loss on SAP (pattern standard deviation <5% or glaucoma hemifield test results outside normal limits) and signs of glaucomatous optic neuropathy as based on records of slit-lamp fundus examination. Glaucoma suspects were those with a history of elevated intraocular pressure, suspicious appearance of the optic disc on slit-lamp fundus examination, or other risk factors for the disease. Healthy participants were required to have a normal optic disc appearance on slit-lamp fundus examination in both eyes as well as no history of elevated intra-ocular pressure and normal SAP results.

RNFL thickness measurements were obtained from peripapillary circle scans, acquired using the Spectralis SD-OCT. The device uses a dual-beam SD-OCT and a confocal laser-scanning ophthalmoscope that employs a super luminescent diode light with a center wavelength of 870 nm and an infrared scan to provide simultaneous images of ocular microstructures. The SD-OCT software acquires a total of 1536 A-scans from a 3.45mm-diameter circle scan (for scans from the Glaucoma Mode Premium Edition) or a 12-degree (for single circle scans) centered on the optic disc and automatically calculates the point-by-point RNFL thickness profile as well as global and sectoral RNFL thickness averages. Tests were acquired using the latest available software version at the time of the scan and exported using the latest available version at the time of the analysis. Corneal curvature measurements were entered into the instrument software to ensure accurate scaling of all measurements, and the device’s eye-tracking capability was used during image acquisition to adjust for eye movements and to ensure that the same location of the retina was scanned over time. All scans were manually reviewed and excluded in the presence of artifacts or segmentation errors. In addition, scans with a quality score lower than 15 were excluded from this analysis, according to manufacturer recommendations.

Glaucoma progression grading

The presence of glaucoma progression was defined by the assessment of two fellowship-trained glaucoma specialists (EBM and LSS). For the grading process, the entire series of SD-OCT tests performed for each eye was summarized in an overview report and presented to each grader individually. The overview report is illustrated in Figure 1 and contained the B-scan images with the segmentation lines included, the RNFL thickness profiles (768 equally spaced RNFL thickness measurements on a 3.45-mm circle centered on the optic disc), and global and sectoral averages.

Figure 1.

Example of an overview report presented to the glaucoma specialists for the grading process. Each overview report contained the B-scan image (left column) with segmentation lines, the retinal nerve fiber layer (RNFL) thickness profile (middle column), and global and sectoral averages (right column). For follow-up tests, the RNFL thickness profile included a comparison with the baseline test, where regions of thinning were shaded in red and regions of thickening were shaded in green.

Initially, each grader evaluated the entire series of SD-OCTs in the overview report to determine whether the eye had glaucoma progression at any point of the follow-up or whether it had remained stable throughout the follow-up. If no progression was identified, the label “stable” was assigned to all follow-up tests. If the graders considered that progression had occurred, they were asked to define at which visit progression was first detected. The follow-up tests that were performed in that visit as well as those performed after that visit received a label “progression”, while the tests performed before that visit received a label “stable”. To ensure that the changes were not due to variability alone, the graders were encouraged to analyze the entire series of SD-OCT tests and to only label progression if the observed RNFL thinning was present in the subsequent visits. This was performed to improve the quality of the labels (i.e, the reference standard), aiding the DL model to differentiate true progression from test-retest variability. If progression was identified solely at the very last visit, due to the impossibility of confirmation, such visit was excluded from the analyses. Of note, since the last visit of each series was excluded from the development and evaluation of the DL algorithm, some eyes had a follow up shorter than one year included in the analyses. Finally, if the graders did not agree in their classification, a third fellowship-trained glaucoma specialist (AAJ) provided adjudication by agreeing with one of the two primary graders while blinded for the grader’s identities.

Development of the deep learning model

A DL model (details discussed below) was developed to predict whether a SD-OCT test presented glaucoma progression or remained stable compared to a baseline SD-OCT. The input to the DL model was the RNFL thickness profile (768 measurements at equally spaced points around the optic nerve) from two SD-OCT tests (the baseline and one follow-up test). The time between the two visits was also included as an input to modulate the probability prediction. The DL model was trained to output the probability of glaucoma progression, where the ground truth for “stable” versus “progression” was defined according to the assessment of glaucoma specialists. For each eye, each follow-up test was paired to the baseline test and used as input to the DL network.

To maximize the use of our sample, we used a 5-fold cross-validation method to train and evaluate the DL model. Initially the whole sample was split into five different partitions, randomized at the patient level. Next, one partition was reserved as a separate test sample. Then, the remaining partitions were used to train a model (three partitions combined as a training sample and one as validation sample). The trained model was used to get the predictions on the partition reserved as test sample. This process was repeated with a new partition as test sample, and a new model was trained, until all partitions were used once as test sample. This approach allows predictions to be obtained in the whole sample, producing more precise estimates of performance.

We designed a custom convolutional neural network (CNN) for the DL model architecture, illustrated in Figure 2. The input to the CNN contained two channels of 1D vectors of size 768 that contained the RNFL thickness profiles of the baseline and follow-up tests. The CNN consisted of three convolutional blocks. The first convolutional block had four branches with convolutional layers of different kernel sizes (7×1, 15×1, 31×1, 63×1), in order to capture both localized and general features. The idea to include convolutional layers at various scales came from natural language processing, which has a similar input (1D vectors where there is a correlation between closer positions, but also an influence of the whole context of the input). The time between visits was input in a separate branch of the model and the resulting vector was added to the CNN features (outputs of the third convolutional block). The last layer of the DL model was a single fully connected layer with a “softmax” activation and output of size two: the probability of “stable” and the probability of “progression”. Training was performed to minimize the cross entropy loss function with stochastic gradient descent (with mini batches of size 1024) optimized by the Adam algorithm.²³ The initial learning rate was 10⁻⁴, gradually decreasing to a minimum of 10⁻⁵. The DL model was trained for 1000 epochs with early stopping based on the lowest loss on the validation set.

Figure 2.

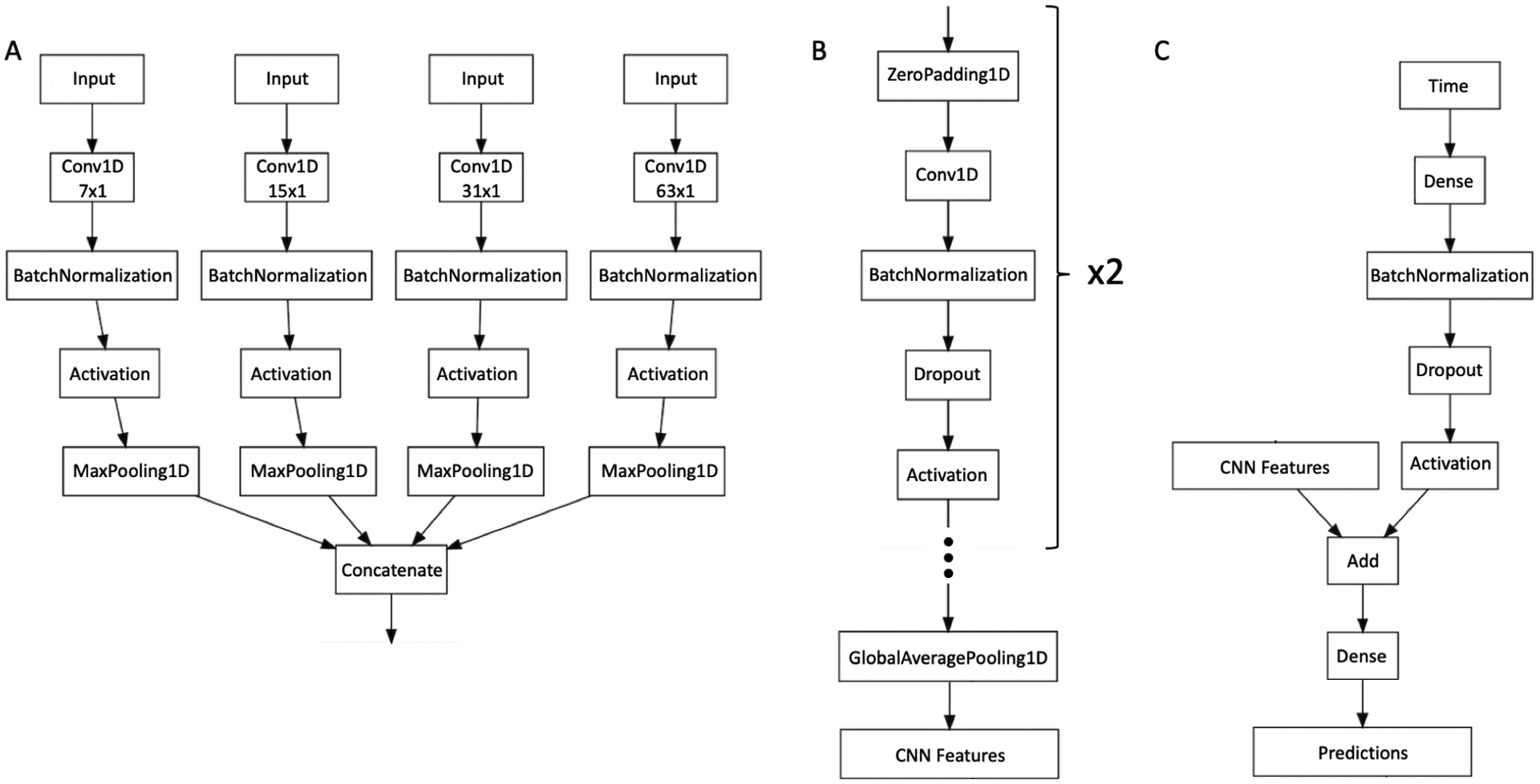
Architecture of the convolutional neural network (CNN) used in the current work. The first block of layers is represented in (A) and has convolutional layers (Conv1D) of different kernel sizes (7×1, 15×1, 31×1, 63×1) to handle features of both local and global relevance. The next two blocks of layers are represented in (B). After these two blocks, there is a global average pooling layer (GlobalAveragePooling1D) that outputs the features from the CNN. As described in (C), time is introduced as a single number in a separate input. A block of layers uses it as input and outputs a vector with the same dimensions of the CNN features, which are added together. A fully connected layer (Dense) uses the resulting vector to predict the probability of “stable” versus “progressing”.

We also developed a visualization tool that illustrates, through a heatmap, the relative importance of each location of the RNFL thickness profile for the probability of progression given by the DL model. To generate the heatmap, we modified the original input to assess the impact of different regions of interest in the RNFL thickness profile. The RNFL thickness values of the follow-up test were replaced by the RNFL thickness values of the baseline test in all points outside those of the region of interest. For this report, we selected a size of 30° for the regions of interest. For example, to assess the impact of the sector from 0–30°, we used the original baseline and follow-up RNFL thickness values for this sector but replaced all the thickness values for all the other points outside that sector by their baseline values. Therefore, the only change possible would be in the sector under evaluation. We then repeated this process for all sectors along the 360°, to assess which region had the greatest impact on the algorithm’s predictions. The DL predictions of each location were then plotted as a heatmap along with the RNFL thickness profile. It is worth noting that the size of the region of interest can be adjusted to represent the probability of progression in more localized (smaller size) or more diffuse (larger size) areas.

Performance of the deep learning model

The diagnostic accuracy of the DL model was evaluated by the ability of the DL probability of progression to discriminate between tests that presented progression versus those that were stable, as determined by the evaluation of glaucoma specialists. A receiver operating characteristic (ROC) curve and the area under the ROC curve (AUC) were used to summarize diagnostic performance. In brief, a ROC curve demonstrates the tradeoff between the true positive rate (sensitivity) and the false positive rate (1-specificity) for different thresholds of a continuous variable to discriminate between two groups. The AUC summarizes the diagnostic ability of the parameter, with 1.0 representing perfect discrimination and 0.5 representing chance discrimination. Sensitivity and specificity were reported for the optimal cut-off point, i.e. the threshold that resulted in highest accuracy, selected with the Youden method.²⁴ We also investigated the performance of the DL model as a function of disease status, patient demographics, time of follow up and disease severity by RNFL thickness and SAP mean deviation (MD). Continuous variables were categorized using mean ± 1 SD if normally distributed and using quartiles if they did not have a normal distribution. SAP MD was categorized using cut-offs described in Hodapp-Parrish-Anderson severity classification (−6 and −12 dB).²⁵

We compared the performance of the DL model with trend-based analysis of glaucoma progression. Trend-based analysis was performed by calculating rates of RNFL thickness change over time from the baseline visit up to the date of the follow-up visit under consideration. Progression was considered if a rate of change of global RNFL thickness over time was statistically significant (P < 0.05) relative to and more negative than −1 μm/year.²⁶ To increase sensitivity and to detect localized RNFL thinning, a second criteria was also used, in which progression was considered if either global RNFL thickness or any of the sectoral averages presented a rate of change statistically significant (P < 0.05) relative to and more negative than −1 μm/year. We selected cut-off points for the DL predictions to match the specificity of each criterion and then compared the sensitivities of the different methods.

Likelihood Ratios

In order to better gauge the impact of the DL model in changing the probability of progression when used under different clinical scenarios, we also report likelihood ratios (LRs) for different DL model results. LRs have been proposed as the best way to incorporate results from a diagnostic test into clinical practice, according to principles of evidence-based medicine.²⁷ The LR is calculated by dividing the probability of a given test result in those that are truly positive for the outcome, i.e., presence of glaucoma progression by expert subjective assessment, by the probability of that same test result in those that are negative for the outcome, i.e., stability according to expert evaluation.^{27, 28} LRs indicate how much a particular test result will change the probability of a certain outcome from a pre-test probability to a post-test probability. For example, it is desirable that a high probability of progression given by the DL model would induce a large change in the pre-test probability of progression to a new, high, post-test probability of progression (see discussion). Similarly, it is also desirable that a result of the DL model indicating low probability of progression would significantly decrease the pre-test probability to a new, low, post-test probability of progression. LRs greater than 10 or lower than 0.1 are generally associated with large effects on post-test probability, whereas LRs from 5 to 10 or from 0.1 to 0.2 with moderate effects, LRs from 2 to 5 or from 0.2 to 0.5 with small effects, and LRs closer to one with insignificant effects.²⁸ We have previously described in detail the value of LRs in assessing diagnostic accuracy of imaging tests in glaucoma in other scenarios.^29–31

Statistical analyses

Normality was checked by inspection of distributions and by using the Shapiro-Wilk test. Variables that were individual-specific were compared across groups using Student’s t-test when distribution was normal and Wilcoxon rank-sum test for non-normally distributed variables. Pearson’s chi-squared was used for categorical variables. Characteristics that were eye-specific were compared using generalized estimating equations (GEE) to account for the presence of both eyes of the same individual in the analysis. Due to the inclusion of both eyes of the same individual and the presence of multiple tests for each eye, a bootstrap procedure with resampling performed at the individual level was used to calculate 95% confidence intervals (CI). This procedure has been widely used to account for correlated measurements.³²

Development of the DL model was performed in Keras, an open-source neural-network library written in Python, and statistical analyses were performed in Stata (version 15, StataCorp LP, College Station, TX). The alpha level (type I error) was set at 0.05.

RESULTS

The study included 14,034 SD-OCT tests (816 baseline and 13,218 follow-up tests) from 816 eyes of 462 individuals, where 446 (54.7%) eyes had glaucoma, 129 (15.8%) were suspects of having glaucoma and 241 (29.5%) were healthy eyes. The mean ± standard deviation (SD) age at baseline was 64.5 ± 12.6 years and 270 individuals (58.4%) were female. An average of 16.2 ± 11.4 SD-OCT tests were available for analyses, from 6.0 ± 4.1 visits. Average follow-up time was 3.5 ± 1.8 years, ranging from 0.3 to 7.0 years. The intergrader agreement for progression was of 86%. Based on the labels assigned by the glaucoma specialists after adjudication, progression was detected in 1655 tests from 124 eyes of 106 individuals, whereas 11563 tests from 790 eyes of 460 individuals were considered stable. The average rate of global RNFL loss was −0.28 μm/year (95% CI: −0.50, −0.08 μm/year) for the stable group and −1.45 μm/year (95% CI: −1.72, −1.20 μm/year) for progressors (P<0.001; GEE). Table 1 shows the demographic and clinical characteristics of the eyes and individuals included in the study.

Table 1.

Demographic and clinical information of tests, eyes and individuals categorized as stable or progressing according to the expert grading of optical coherence tomography scans.

	Stable	Progression	P value
Tests (%)	11,563 (87.5)	1,655 (12.5)
Eyes (%)	692 (84.8)	124 (15.2)
Individuals (%)	356 (77.1)	106 (22.9)
Age, mean ± SD, years	64.6 ± 13.0	64.5 ± 11.1	0.969a
Race: (%)			0.199b
Black or African American	87.0 (22.3)	23.0 (31.9)
White or Caucasian	271.0 (69.5)	43.0 (59.7)
Other	32.0 (8.2)	6.0 (8.3)
Ethnicity: (%)			0.661b
Hispanic or Latino	39.0 (10.0)	6.0 (8.3)
Female (%)	227.0 (58.2)	43.0 (59.7)	0.810b
SAP MD at baseline, mean (95% CI), dB	−2.34 (−2.76, −1.92)	−1.58 (−2.39, −0.76)	0.073c
RNFL thickness at baseline, mean (95% CI), μm	84.0 (82.5, 85.4)	84.2 (81.7, 86.7)	0.845c
Follow-up time, mean (95% CI), years	3.4 (3.2, 3.5)	4.0 (3.8, 4.3)	0.000c
Number of tests, mean (95% CI)	15.8 (14.8, 16.8)	17.1 (15.4, 18.7)	0.106c
Number of follow-up visits, mean (95% CI)	5.8 (5.5, 6.2)	6.3 (5.8, 6.9)	0.069c
DL probability of progression, median (IQR), %	1.4 (0.3, 5.1)	47.4 (18.5, 89.0)	<0.001c

Abbreviations: SD = standard deviation; SAP = standard automated perimetry; MD = mean deviation; RNFL = retinal nerve fiber layer; CI = confidence interval; DL = deep learning; IQR = interquartile range.

^a= Student’s t-test;

^b= Pearson’s chi-squared;

^c= generalized estimating equations

The median [interquartile range; IQR] DL probability of progression was 1.4% [0.3%, 5.1%] for tests that were deemed stable by expert grading, and 47.4% [18.5%, 89.0%] for tests that were deemed to have progressed (P < 0.001, GEE). Figure 3 illustrates the distribution of the DL probability of progression in progressing versus stable eyes. The DL model had an AUC of 0.938 (95% CI: 0.921, 0.955) to discriminate between tests that were stable versus those that showed progression according to expert grading and an area under the precision-recall curve of 0.737 (95% CI: 0.715, 0.756). Table 2 shows the performance of the algorithm as a function of demographic and clinical characteristics. The performance to detect glaucoma progression was generally similar among categories, with largely overlapping confidence intervals.

Figure 3.

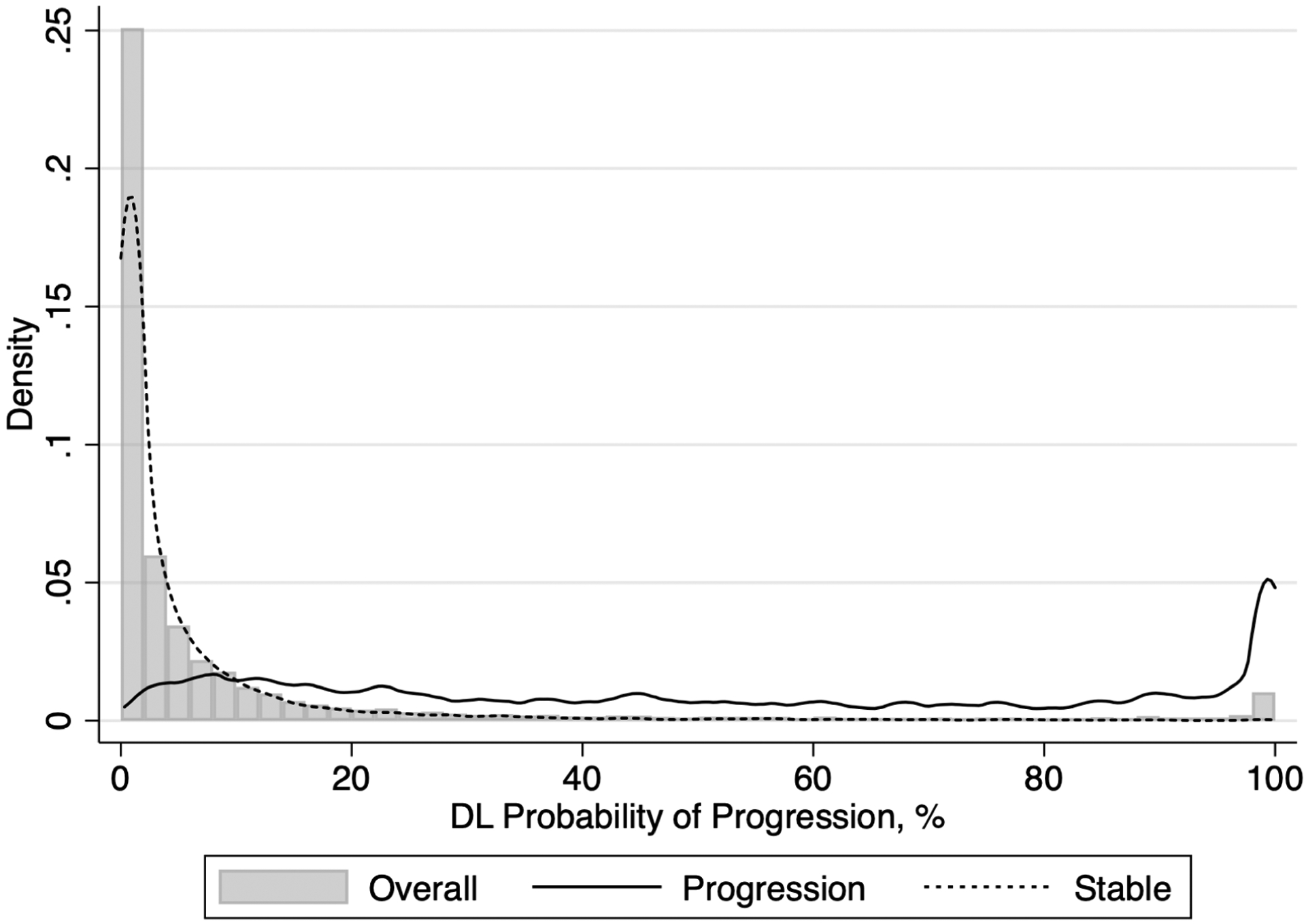
Distribution of deep learning (DL) probability of progression for tests that presented progression and tests that were stable according to the subjective grading by glaucoma specialists.

Table 2.

Model performance as a function of different demographics and clinical characteristics at baseline.

Variable	AUC (95% confidence interval)
Disease status
Suspect	0.914 (0.862, 0.953)
Glaucoma	0.953 (0.933, 0.969)
Age, yearsa
Younger than 51.9	0.982 (0.950, 0.996)
Between 51.9 and 64.5	0.898 (0.847, 0.933)
Between 64.5 and 77.1	0.943 (0.918, 0.962)
Older than 77.1	0.955 (0.902, 0.99)
Sex
Male	0.929 (0.901, 0.955)
Female	0.942 (0.909, 0.961)
Race
Black	0.895 (0.842, 0.939)
White	0.945 (0.926, 0.961)
Others	0.978 (0.940, 0.999)
Time from baseline, yearsb
Less than 1.2	0.970 (0.942, 0.986)
Between 1.2 and 2.3	0.911 (0.880, 0.938)
Between 2.3 and 3.5	0.910 (0.878, 0.943)
More than 3.5	0.912 (0.869, 0.940)
RNFL thickness at baseline, μmb
Less than 74	0.974 (0.953, 0.989)
Between 74 and 86	0.940 (0.904, 0.965)
Between 86 and 97	0.927 (0.892, 0.958)
More than 97	0.888 (0.842, 0.947)
SAP MD at baseline, dB
Higher than −6	0.933 (0.911, 0.949)
Between −6 and −12	0.940 (0.628, 1.000)
Lower than −12	0.994 (0.985, 0.999)

^aCategories defined using mean − 1 SD, mean, mean + 1 SD as cut-offs.

^bCategories defined using p25, p50, p75 as cut-offs.

The sensitivity was 87.3% (95% CI: 83.6%, 91.6%) and specificity was 86.4% (95% CI: 79.9%, 89.6%) for the optimal cut-off point. Trend-based analysis using global RNFL thickness showed a sensitivity of only 46.1% (95% CI: 36.7%, 55.0%) and specificity of 92.6% (95% CI: 90.7%, 94.3%). When matched at the same specificity of 92.6%, the DL model had a sensitivity of 75.8% (95% CI: 66.7%, 83.1%), with an absolute difference of 29.7% (95% CI: 18.7%, 39.4%) versus trend-based analysis. For the trend-based analysis considering global and sectoral RNFL thickness, the sensitivity was 83.7% (95% CI: 78.4%, 88.7%) but specificity decreased to 68.6% (95% CI: 65.5%, 71.7%). At this level of specificity, the sensitivity of DL model was 96.2% (95% CI: 94.3%, 97.8%), with a significant absolute difference of 12.5% (95% CI: 7.6%, 17.8%). Figure 4 illustrates the ROC curve and the precision-recall curve of the DL probability of progression, as well as for each trend-based analysis.

Figure 4.

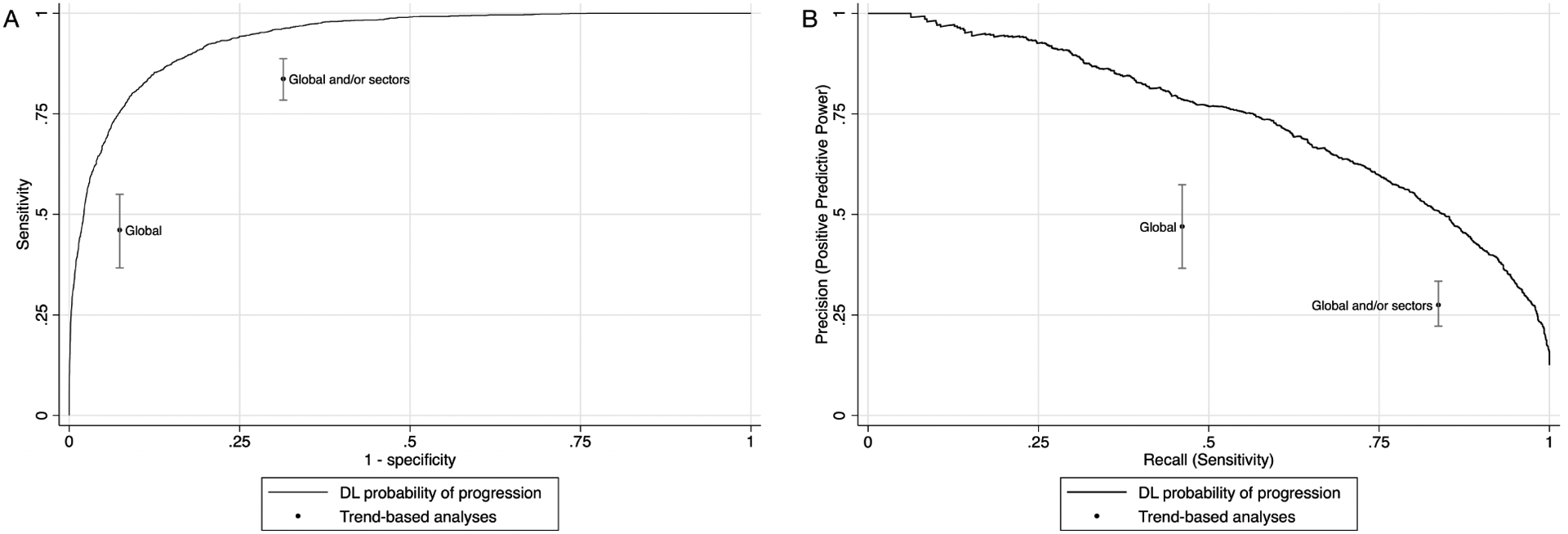
(A) Receiver operating characteristic curve and (B) precision-recall curve illustrating the performance of the deep learning (DL) model to discriminate between tests that presented glaucoma progression and those that remained stable, according to the subjective grading by glaucoma specialists. The performances of trend-based analyses of change are plotted for comparison.

Table 3 shows LRs for different intervals of DL probability of progression. DL results with probability lower than 5% were associated with large effects to decrease the post-test probability of having glaucoma progression, whereas DL results with probability larger than 50% would result in large changes in increasing the post-test probability of having glaucoma progression. Importantly, LRs for the DL model were associated with large changes in probability of progression in approximately 74% of the SD-OCT tests, indicating that in the vast majority of SD-OCT tests the DL model would provide useful information to clarify the presence of progression.

Table 3.

Likelihood ratios for different intervals of deep learning probability of progression.

DL probability of progression (%)	Number of tests graded as progression (%)	Number of tests graded as stable (%)	Total of tests (%)	Interval Likelihood Ratio
< 5	94 (5.7)	8625 (74.6)	8719 (66.0)	0.08
5 to < 10	132 (8.0)	1328 (11.5)	1460 (11.0)	0.69
10 to < 50	629 (38.0)	1375 (11.9)	2004 (15.2)	3.20
50 to < 90	408 (24.7)	207 (1.8)	615 (4.7)	13.77
90 to < 95	69 (4.2)	9 (0.1)	78 (0.6)	53.56
95 to < 100	315 (19.0)	19 (0.2)	334 (2.5)	115.83

Abbreviation: DL = deep learning.

Figure 5 illustrates the series of SD-OCT tests performed for the same eye of Figure 1. Progression was first identified by subjective expert grading on the second follow-up visit. For the first visit, that was considered stable by expert grading, the DL model also predicted a low probability of progression, and the heatmap did not highlight any particular location of the RNFL thickness profile. As the disease progressed, the DL model predicted increasingly higher probabilities of progression, with the heatmaps initially highlighting localized regions with increasing intensity. As larger changes were seen on subsequent tests, the DL heatmap showed large areas of high probability of progression across most of the RNFL thickness profile.

Figure 5.

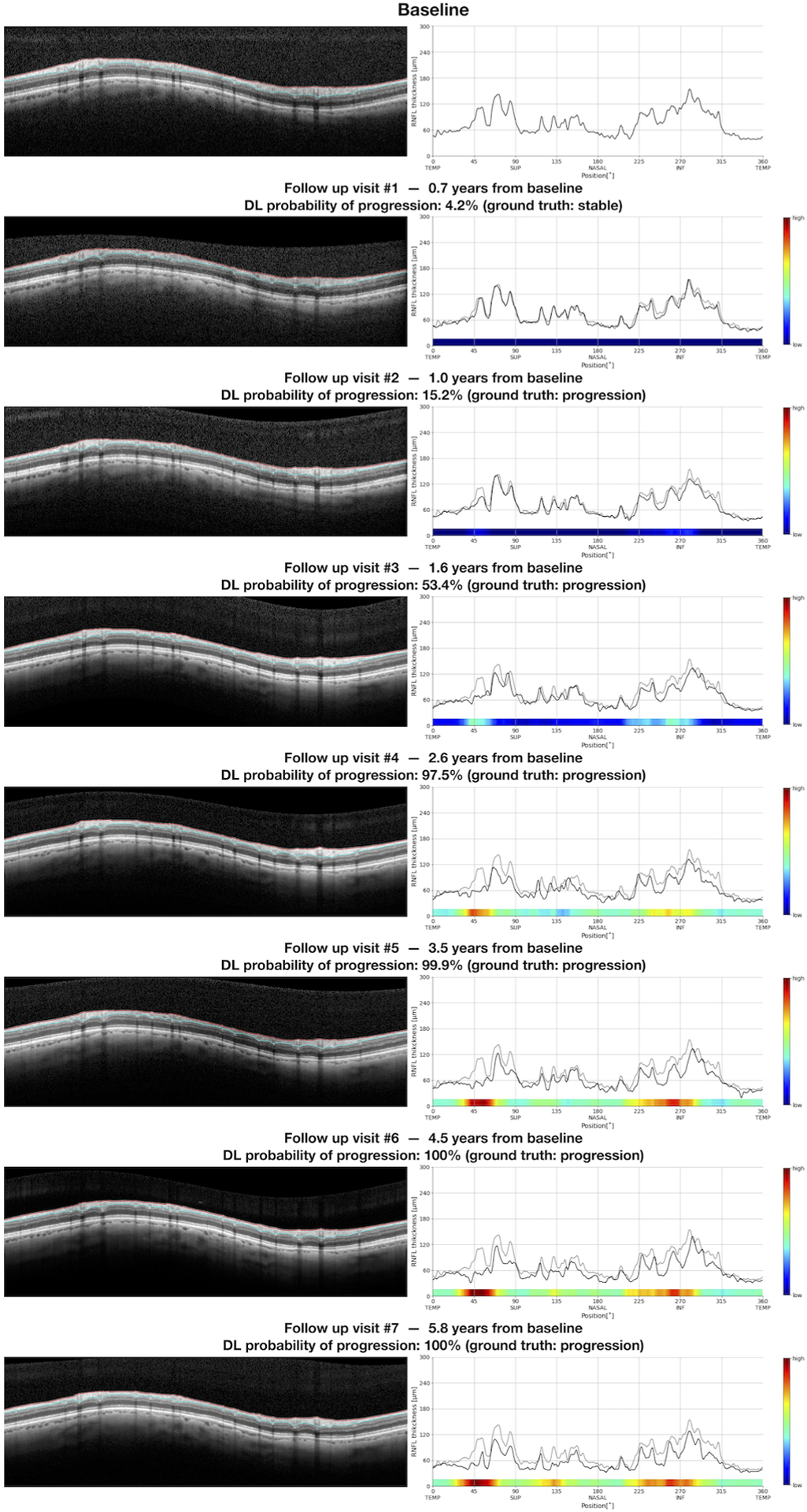
Overview report of the same series of tests from Figure 1, with inclusion of deep learning (DL) probability of progression and the heatmaps illustrating the areas of the retinal nerve fiber layer thickness profile that were most relevant for the DL assessment of progression. In this example, the heatmap highlights localized areas in the temporal superior and inferior regions. With progressive RNFL thinning, the heatmaps highlight larger areas with higher probability of glaucoma progression.

DISCUSSION

In the present study, we developed a DL model to assess the presence of glaucoma progression on RNFL thickness measurements obtained by SD-OCT. The performance of the proposed DL model agreed well with expert assessment and proved to be a significant improvement over conventional trend-based analyses of progression. The model was also able to pinpoint the location of regions of likely progression using heatmaps. To the best of our knowledge, this is the first study to show an application of DL to assess progression with SD-OCT.

The DL model developed in our study was able to accurately discriminate between progressing and stable glaucoma cases, achieving an AUC of 0.938, with sensitivity of 87.3% and specificity of 86.4%. In addition, the DL model showed a significant improvement when compared to trend-based analyses, the most commonly used method to objectively assess progression with the Spectralis SD-OCT. One likely reason for the improvement in performance is that while trend-based analysis relies on summary metrics, like global RNFL thickness and sectoral averages, the DL model takes as input all the RNFL thickness measurements. Using global or sectors averages can potentially miss small, localized regions of RNFL thinning. In contrast, DL models may be better suited to handle complex data that present with large number of measurements, such as the full RNFL thickness measurement profile. The models can learn to identify locations that may be particularly important for detecting progression, while also retaining higher levels of specificity.

Although sensitivity and specificity are useful for an overall evaluation of model performance, they have limited direct applicability in clinical practice. When faced with a particular test result on an individual case, a clinician is interested in knowing how such result will increase or decrease the chance of a particular outcome. LRs can be used to provide such estimates, by showing how much the probability of progression would change from a pre-test to a post-test probability, after obtaining a particular test result. To illustrate, consider the case represented in Figures 1 and 5. We can assume that a reasonable estimate for a pre-test probability of glaucoma progression (i.e., before the test is acquired) is the overall prevalence of progression on a similar population. For this example, the pre-test probability can be estimated at 25%, which corresponds to the approximate percentage of eyes that had progression by SD-OCT on a large previous cohort study.²² We can then assess the impact that different results of the DL model would have in modifying such pre-test probability. In the first follow-up visit, the DL model prediction was 4.2%, which was associated with a LR of 0.08. With this test result, the post-test probability of progression would decrease to 2.5%. For the second visit, the DL model prediction was 15.2% (LR = 3.2), resulting in a post-test probability of 51.6%. In the third visit (DL model prediction = 53.4%; LR = 13.8), the post-test probability would increase to 82.1%, and from visits four to seven (DL model prediction > 95%; LR = 118.8) the post-test probability of progression would increase to essentially 100%. Therefore, it can be seen how the DL test results would greatly modify the probability of progression in this individual case. Although clinicians are not routinely trained to objectively quantify pre-test probabilities and use LRs, clinical decision making routinely involves subjective assessments of probability, even if they may sometimes appear unconscious. LRs, as illustrated here, could be easily provided as part of software printouts or displays. Even easier, post-test probabilities could be automatically calculated for plausible pre-test probabilities and a given test result, helping clinicians to better gauge the impact of the test findings in a particular case.

A concern regarding deep learning algorithms is the relative uncertainty related to the features that are used in their predictions. It is certainly a lot more reassuring for a clinician to know that a high probability of progression is shown associated with the depiction of the area where the progression is likely to occurred. Visualization tools, such as heatmaps, are attempts to open the “black box” of deep learning models, helping to better understand their predictions. In the present work, we developed an innovative visualization tool that highlighted the areas of the RNFL thickness profile that had the greatest impact on the algorithm’s predictions. Although current commercially available reports may also highlight areas of potential change in the RNFL thickness profile, the analyses provided by these reports are often inadequate or insufficient. In fact, some reports simply present the absolute amount of change according to a color-coding scheme, giving no indication of their statistical significance. Even when formal statistical analyses are performed, they are mostly limited to comparisons to short-term estimates of test-retest variability, which may be inadequate to assess progression.¹⁰ As such, current reports fail to account for important features that can be easily captured by a DL model, such as time elapsed between tests and the overall context in which the changes happened, such as baseline RNFL thickness. In addition, the use of a convolutional network in our DL model allowed it to capture the spatial relationship between different areas of the RNFL thickness profile and their impact on the estimates of probability of progression.

Our work relied on gradings of glaucoma specialists as the reference standard for progression. This was necessary given the lack of a perfect reference standard for progression in glaucoma. We required a consensus of 2 expert graders with adjudication by a third one, and the entire series of follow-up tests was available when grading an individual eye. This likely helped improve the accuracy and reliability of final grading and distinguish variability from true change. However, it is possible that some misclassifications might still have occurred. As an example, some tests that were labelled as stable within a series in which progression happened later in the follow-up may have already had changes that were not detected by the expert gradings. It is also possible that some changes due to aging may have been graded as progression. However, the ultimate goal of our work was to demonstrate the feasibility of a deep learning model that could replicate gradings of glaucoma specialists. When applied in practice, such model could potentially bring non-specialists to a level close to specialists when assessing SD-OCTs for progression. Of note, the performance of our model was compared only to trend-based analysis of progression. It is known that SD-OCT measurements suffer from floor effects which may limit their ability to detect progression in advanced disease. Previous studies have shown, however, that subjective assessment of scans can often identify regions of interest with remaining neural tissue that can be assessed for detecting further change, even in cases of advanced disease.^33–35 This may further explain the superior performance obtained by our model as compared to conventional trend analyses. Of note, we used a cut-off of −1 μm/year to take into account age-related changes in conventional trend-based analyses, based on a previous publication on follow-up of normal eyes.²⁶ This ensured a high specificity of trend analyses. However, no set criteria could be used for detection of age-related changes when subjective evaluation of the images was performed by the expert graders. This may introduce difficulties in the comparison between the methods.

This work has limitations. Developing a reference standard for glaucoma progression is challenging and many would advocate for the inclusion of visual field information to determine whether an eye was progressing or was stable. While it is true that in clinical practice both structural and functional assessment are used in complementary ways, only a minority of eyes present with unequivocal progression that is detected by both methods. When using the proposed algorithm in clinical practice, clinicians should be aware that it represents an analysis of structure alone and that assessment of functional changes would still be necessary by means of perimetry. Important to note, the proposed method is more akin to event-based analysis of progression. As such, it does not allow for an assessment of the rate of progression neither for prediction of the rate of future deterioration.

The size of the sample was relatively small when compared to some very large datasets that are often used to develop DL models. Our sample size was limited by the time-consuming step of expert labeling. To optimize the use of our sample, we employed cross validation to train the DL model and test the predictions on independent test samples, while still making use of the full data. Our results showed high accuracy, but it is possible that larger samples and the use of more complex networks may achieve even better performance. Our model made use of raw RNFL thickness measurements extracted from the SD-OCT software, which rely on accurate segmentation of the RNFL boundaries. We and others have shown previously the potential of segmentation-free assessment of SD-OCT B-scans for cross-sectional glaucoma assessment.^{12, 36, 37} It is possible that more complex neural networks may be devised to make use of the full raw B-scan image for assessment of change. Development of such complex networks will likely require larger samples, though. Importantly, although the dataset used in the study contained a diverse population with a sizable proportion of Black/African-American individuals, our proposed model should be validated on external datasets from independent populations to further assess its generalizability.

In conclusion, we developed and validated a DL model to assess the probability of glaucoma progression from SD-OCT measurements of the RNFL thickness. The model agreed well with expert judgements of progression and outperformed conventional trend-based analyses. Probabilities of progression provided by the model along with the visualization heatmaps may help clinicians in identifying structural glaucoma progression with SD-OCT.

PRÉCIS.

A deep learning model was developed to assess the probability of glaucoma progression from OCT retinal nerve fiber layer thickness measurements. The model agreed well with expert judgements of progression and outperformed conventional trend-based analyses.