Abstract
Two sensory neurons usually display trial-by-trial spike-count correlations given the repeated representations of a stimulus. The effects of such response correlations on population-level sensory coding have been the focal contention in computational neuroscience over the past few years. In the meantime, multivariate pattern analysis (MVPA) has become the leading analysis approach in functional magnetic resonance imaging (fMRI), but the effects of response correlations among voxel populations remain underexplored. Here, instead of conventional MVPA analysis, we calculate linear Fisher information of population responses in human visual cortex (five males, one female) and hypothetically remove response correlations between voxels. We found that voxelwise response correlations generally enhance stimulus information, a result standing in stark contrast to the detrimental effects of response correlations reported in empirical neurophysiological studies. By voxel-encoding modeling, we further show that these two seemingly opposite effects actually can coexist within the primate visual system. Furthermore, we use principal component analysis to decompose stimulus information in population responses onto different principal dimensions in a high-dimensional representational space. Interestingly, response correlations simultaneously reduce and enhance information on higher- and lower-variance principal dimensions, respectively. The relative strength of the two antagonistic effects within the same computational framework produces the apparent discrepancy in the effects of response correlations in neuronal and voxel populations. Our results suggest that multivariate fMRI data contain rich statistical structures that are directly related to sensory information representation, and the general computational framework to analyze neuronal and voxel population responses can be applied in many types of neural measurements.
SIGNIFICANCE STATEMENT Despite the vast research interest in the effect of spike-count noise correlations on population codes in neurophysiology, it remains unclear how the response correlations between voxels influence MVPA in human imaging. We used an information-theoretic approach and showed that unlike the detrimental effects of response correlations reported in neurophysiology, voxelwise response correlations generally improve sensory coding. We conducted a series of in-depth analyses and demonstrated that neuronal and voxel response correlations can coexist within the visual system and share some common computational mechanisms. These results shed new light on how the population codes of sensory information can be evaluated via different neural measurements.
Keywords: functional magnetic resonance imaging, multivariate pattern analysis, population codes, spike-count noise correlation, visual cortex
Introduction
It is well established that even simple sensory stimuli can activate a large group of neurons, a phenomenon called population codes in computational neuroscience (Averbeck et al., 2006; Kohn et al., 2016). The most distinctive feature of population codes, compared with single-unit recording data, is the trial-by-trial response correlations (RCs) between units. How correlated variability affects the fidelity of population codes has been a focal contention in neuroscience in recent years. On the one hand, theoretical studies have shown that the effects of neuronal RCs depend on many factors, such as the form of the RC, tuning heterogeneity, or its relevance to behavior (Zohary et al., 1994; Sompolinsky et al., 2001; Averbeck et al., 2006; Shamir and Sompolinsky, 2006; Haefner et al., 2013; Kohn et al., 2016). On the other hand, empirical physiological studies have consistently shown that improved behavioral performance is accompanied by a reduction of RC in a number of cognitive processes, such as locomotion (Vinck et al., 2015), task engagement (Downer et al., 2015), wakefulness (Reimer et al., 2014), and perceptual training (Gu et al., 2011), suggesting the detrimental role of RC in sensory coding.
In contrast to invasive neurophysiology, functional magnetic resonance imaging (fMRI) is a noninvasive technique and naturally measures the responses of many units in the brain, although the basic unit is voxel rather than neuron. Here, we use “population codes” as a unified term for both neurophysiology (i.e., a population of neurons) and fMRI (i.e., a population of voxels). In fMRI research, multivariate pattern analysis (MVPA) has become a mainstream approach to interpret sensory coding (Haxby et al., 2014). In the fMRI literature, correlations between the trial-by-trial responses (i.e., beta weights) of two voxels (Fig. 1D) are referred to as Beta-series correlation (Rissman et al., 2004; Di et al., 2021). Similarly, trial-by-trial spike-count correlations between neurons are called noise correlation in neurophysiology (Cohen and Kohn, 2011). We hereafter unify both Beta-series correlation in fMRI and noise correlation in neurophysiology as response correlation.
Figure 1.
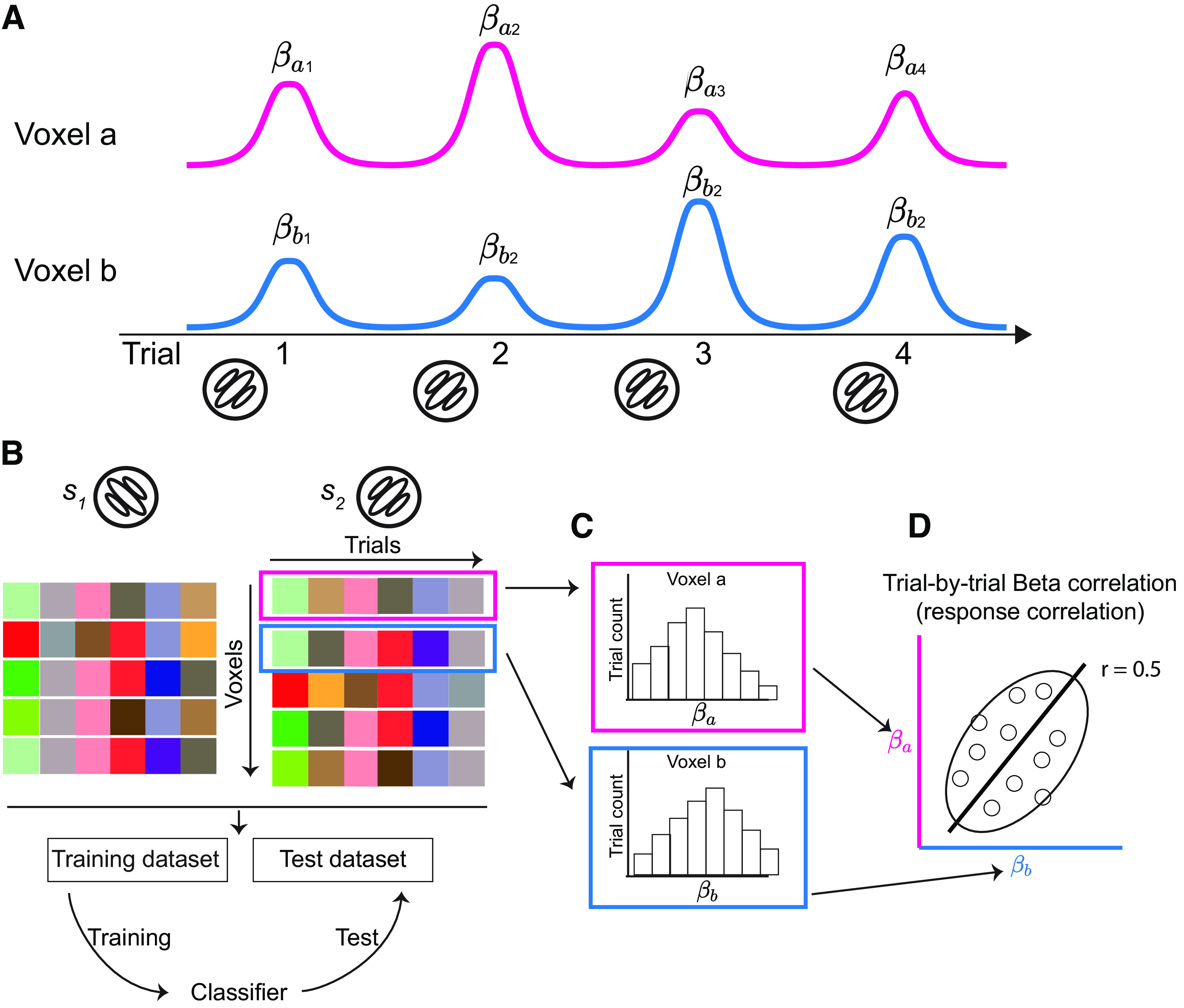
Trial-by-trial response correlation in multivariate fMRI data. A, Estimations of single-trial voxel responses. Magenta and blue lines represent the time series of voxels a and b across four trials of the same grating stimulus. For MVPA, the stimulus in each trial is modeled as a single predictor in general linear modeling to estimate single-trial voxel activity (i.e., beta weight). and indicate the response of voxels a and b, respectively, in the ith trial. B, In the problem of binary classification, multivariate voxel responses for each stimulus can be summarized as a voxel-by-trial matrix. Each item in this matrix is the activity of the ith (row) voxel in the jth trial (column). Combining the two data matrices for the two stimuli, a classifier can be trained on a training dataset and then evaluated on a test dataset. C, Responses of a single voxel across trials (i.e., a row in a data matrix in B) is a random variable following some distribution. D, Beta-series correlation shown by the scatter plot of the responses of voxels a and b (i.e., two rows in a data matrix in B). The solid line is the correlation line, the open circles represent the activity of individual trials. The ellipse illustrates the shape of the 2 d response distribution, and the direction of the ellipse depicts a positive response correlation (e.g., r = 0.5 in this example) between the two voxels. We particularly emphasize that between-voxel beta-series correlation is neither resting-state functional connectivity nor task-based functional connectivity calculated by correlating the residual time series after regressing out stimulus-evoked responses from general linear modeling.
In fMRI, the quality of stimulus encoding is usually operationally defined as multivariate decoding accuracy; that is, a higher decoding accuracy indicates higher fidelity of stimulus encoding (Haynes and Rees, 2005; Kamitani and Tong, 2005). This multivariate decoding approach has been widely used to study the neural mechanisms of various cognitive processes, such as attention (Ling et al., 2015) and learning (Jehee et al., 2011). Compared with the rich theoretical and empirical evidence for the effects of RCs in neurophysiology, little is known about how voxelwise RCs affect MVPA decoding accuracy in fMRI. Unveiling the effects of RCs can provide insight into the mechanisms of many cognitive processes. For example, if decoding accuracy is elevated by a particular cognitive process (e.g., attention), it is unclear whether it warps response correlations (Fig. 2C) or simply reduces the response variability of individual voxels (Fig. 2D).
Figure 2.
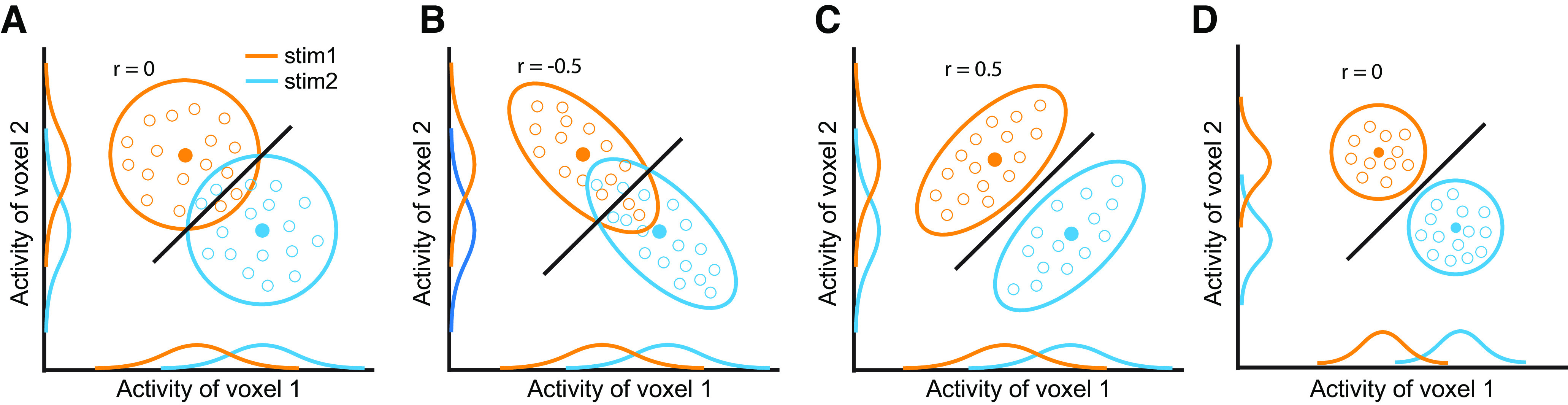
A two-voxel scenario showing the effects of RCs on decoding. The blue and orange circles or ellipses represent 2 d response distributions toward two stimuli. The solid dots represent the mean of the distributions, and the open dots represent individual trials consisting of the distributions. The solid lines are classifiers. The 1 d distributions are the projection of the 2 d distributions on the x-axis and y-axis. In this example, compared with the case of no RCs (e.g., r = 0 in A), negative RCs impair (e.g., r = −0.5 in B) and positive RCs improve (e.g., r = 0.5 in C) decoding accuracy. Note that the example correlation values correspond to the 2 d distributions, not the classifier lines. The amount of stimulus information is directly linked to decoding accuracy. As such, stimulus information in C, D is higher than in A, B. Importantly, the marginal distributions in A–C are identical, but the decoding accuracies are markedly different across the three cases. In D the variance of the two distributions shrinks and consequently induces higher decoding accuracy. C and D demonstrate that identical decoding accuracy can correspond to two distinct underlying representational geometries.
Here, we combine information-theoretic and conventional decoding approaches to analyze the fidelity of stimulus encoding in multivariate fMRI data. Specifically, we directly calculate the linear Fisher information of stimuli encoded by trial-by-trial multivariate voxel responses. Surprisingly, in contrast to the detrimental effects documented in neurophysiological literature, stimulus information follows a U-shaped function of RC strength and ultimately is higher than the scenario without RC. We built voxel-encoding models to show that these two apparently opposite effects can coexist in the visual system. Further computational analyses reveal that the apparent difference in the effects of RCs in neuronal and voxel populations share some common mechanisms; RCs reduce and simultaneously enhance information in high- and medium- or low-variance eigendimensions, respectively. This unified mechanism of RC not only helps to resolve the long-standing debate about the effects of RCs on sensory coding but also extends the conventional understanding of the computational nature of MVPA. Moreover, the methods used here to analyze population responses are general and can be applied to a wide range of scenarios for deciphering multivariate neural data.
Materials and Methods
fMRI experiment
Stimuli and task
We analyzed the fMRI data collected by Sengupta et al. (2017). The datasets are publicly available on the OpenNeuro website (https://openneuro.org/datasets/ds000113/versions/1.3.0). Six subjects (five males) participated in the study. Briefly, two flickering sine-wave gratings (0.8°–7.6° eccentricity, 160° angular width on each visual hemifield with a 20° gap on the vertical meridian) were presented on both sides of the fixation point. The orientations of the two gratings varied independently across trials. The orientations were drawn from 0°, 45°, 90°, and 135° with equal probabilities. A stream of letters was presented at the center of gaze throughout each scanning run. Subjects were instructed to maintain their fixation and perform a reading task. To ensure subjects' task engagement, they were tested on a question related to the reading text at the end of each run.
On each trial, an orientation stimulus lasted 3 s and was followed by a 5 s blank. Each scanning run consisted of 30 trials. The 30 trials also included 10 randomized blank trials. The first trial could not be a blank trial, and there were no two consecutive blank trials. Blank trials could appear on either side, whereas the grating on the other side was intact. Each subject completed 10 scanning runs. Because of the setting of blank trials setting, each stimulus was presented for 60–70 trials in each subject.
MRI data acquisition and processing
A T2*-weighed echo-planar imaging (TR/TE = 2000/22 ms) sequence was used to acquire fMRI data. In the original experiment, the subjects were scanned at four different resolutions. Here, we only analyzed the 2 mm isotropic data because they gave the best decoding accuracy (Sengupta et al., 2017). One hundred twenty-one functional volumes were acquired in each run (FOV = 200 mm, matrix size 100 × 100, 37 slices, GRAPPA acceleration factor 3). The echo-planar images covered the occipital and parietal lobes. Each subject was also scanned for a high-resolution T1-weighted image (0.67 mm isotropic). Additionally, we conducted standard retinotopic scans to define low-level visual areas.
The pial and white surfaces were reconstructed based on the high-resolution T1-weighted images using the standard FreeSurfer software pipeline. All functional volumes underwent slice-timing correction, motion correction, and registration to T1 images. Retinotopic data were analyzed using the 3dRetinophase tool in Analysis of Functional NeuroImages (AFNI) software to generate polar angle and eccentricity maps on cortical surfaces.
Bilateral V1–V3 were defined on spherical cortical surfaces based on polar angle and eccentricity maps. The vertices in each region of interest (ROI) on cortical surfaces were then transformed back to EPI space using the AFNI 3dSurf2Vol function to locate corresponding voxels.
We used the AFNI 3dDeconvolve function to build general linear models (GLMs). Particularly, the -stim_times_IM option of the function was used to model each presentation of stimuli (i.e., trial) as an independent predictor. We implemented two GLMs separately for two hemispheres because of independent stimuli presentations for each hemisphere, and each GLM only included the stimuli presented contralaterally. In each GLM, demeaned head motion parameters and constant, linear, and quadratic polynomial terms were also included as nuisance predictors. In each subject, we concatenated the time series of 10 scanning runs and fitted a single GLM to the combined data.
Calculation of linear Fisher information in population responses
In computational neuroscience, Fisher information is a standard metric that assesses the amount of information carried by observed neuronal responses r with respect to stimulus variable s. Two signatures of r should be noted. First, the neuronal response r is high dimensional (i.e., a vector) because it represents the responses of many neurons or voxels. Second, because of trial-by-trial variability, the r across trials follows a multivariate response distribution in the high-dimensional space. If the response distribution belongs to the exponential family with linear sufficient statistics (i.e., information can be optimally decoded via a linear decoder), Fisher information can be further simplified as linear Fisher information (Beck et al., 2011). Hereafter, we call it “information” for short.
Suppose that in an experiment we attempt to discriminate two stimuli, s1 and s2, based on the measured responses of N voxels in T trials for each stimulus. This is a typical binary classification scenario in fMRI (Haynes and Rees, 2005; Kamitani and Tong, 2005). Here, Fisher information can be understood as the extent to which the two stimuli can be discriminated based on population responses.
In the ideal case that we have an infinite number of trials T, the information delivered by population responses can be written as follows:
| (1) |
where and are defined as follows:
| (2) |
| (3) |
where and are vectors, representing the mean responses across trials of the neuronal population for stimuli and , respectively, and is the absolute stimulus difference (i.e., ). is an N × 1, indicating the standard deviation of responses of N units. C is the response correlation matrix. and are the covariance matrices of the population responses toward stimuli and , respectively. Note that Equation 1 has no assumption about Gaussian response variability.
Equation 1 has several important implications. First, stimulus information depends on (1) the Euclidean distance between the two high-dimensional response distributions [i.e., ], (2) the covariance (i.e., the variance of individual voxel response and voxelwise response correlations) of the population (i.e., and ), and (3) the interaction between (1) and (2). We illustrate this issue in Figure 2. Equation 1 also highlights the complexity of quantifying information as any effort that merely considers one factor might fail to yield meaningful results because all factors (i.e., mean responses, variance, and response correlations) and their interactions matter.
Any real experiment, however, must have a finite number of trials T. The estimations of the statistical properties (e.g., and ) of population responses therefore might be imprecise. Imperfect estimations of these statistics can lead to potential biases in the estimation of information. This is especially common in the field of fMRI because the number of trials sampled in an experiment is usually smaller than the number of voxels. Kanitscheider et al. (2015) have shown that the bias induced by imperfect estimations of response properties indeed exists but fortunately can be corrected analytically. The bias-corrected linear Fisher information () can be written as follows:
| (4) |
where it has been also proved that the bias manifests differently in populations with and without response correlations (Kanitscheider et al., 2015). In the latter case, voxel responses are independent, and this is equivalent to shuffling the responses of each voxel separately across many trials, a popular strategy used in the literature to investigate the effect of neuronal response correlations. In this case, linear Fisher information () can be corrected by the following:
| (5) |
where and are the mean responses of the ith voxel across trials, and is the averaged variance (i.e., ), where and are the variance of the responses of ith voxel across trials. We used Equation 4 to calculate stimulus information in the empirical data (Fig. 3B, puce bars) and Equation 5 to calculate stimulus information when RCs are removed (Fig. 3B, gray bars). Note that although linear Fisher information per se (Eq. 1) has no assumption of Gaussian variability, the analytical solution for bias correction assumes Gaussian variability (Eqs. 4, 5). But it has also been shown that this bias correction solution is also robust to non-Gaussian cases (Kanitscheider et al., 2015). Also, the bias-correction method is only valid when T > (N + 2)/2. In our experiment, each stimulus was presented for 60–70 trials. We thus chose N = 50 in all neuron- and voxel-encoding modeling below and also when analyzing empirical fMRI data.
Figure 3.
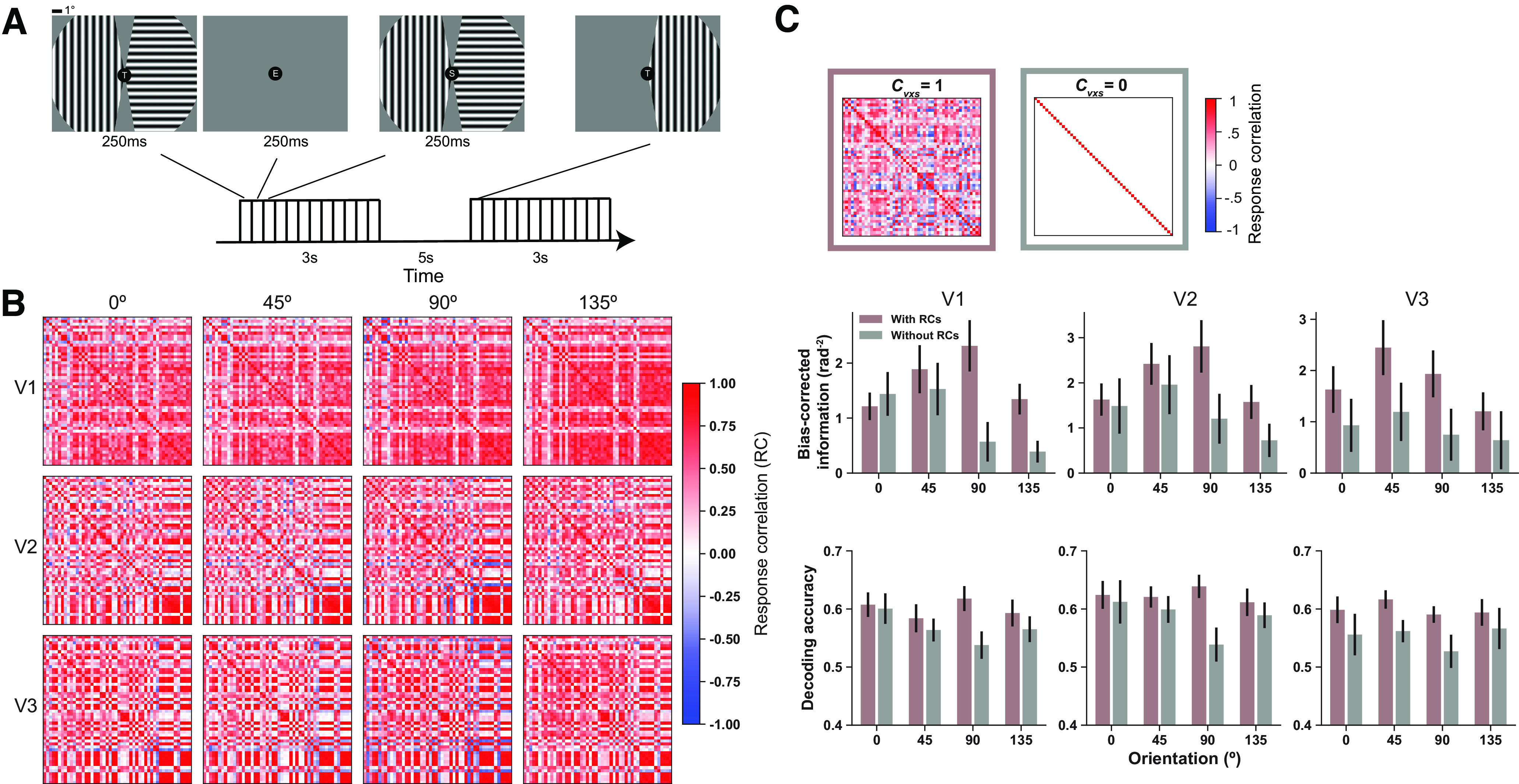
Voxelwise response correlations enhance stimulus information. A, Schematic illustration of example trials in the orientation experiment. Two gratings are presented in each visual field. Their orientations are independently selected from four orientations (0°, 45°, 90°, 135°). In some baseline trials, only one grating is presented. Subjects are asked to attend to and understand the letter stream presented at the fixation point. B, example correlation matrices of V1–V3 in one hemisphere of one subject. These results show that the correlations between the same pool of voxels but across different stimuli are similar. In other words, the noise correlations between voxels are mostly stimulus invariant. C, Left, Matrix is the identity matrix. Right, Matrix is an example response correlation matrix estimated from data. Hypothetical removal of response correlations between voxels (gray bars) reduces the amount of information (middle row) and decoding accuracy (bottom row) compared with the case that all response correlations are preserved (puce bars). Error bars indicate SEM across 12 independent samples (6 subjects × 2 hemispheres). Note that the information here is bias corrected using Equations 4 and 5 (see Materials and Methods).
For each orientation, we defined the information of each orientation as the averaged information of pairwise discriminating that orientation and the other three orientations. For example, the information of 0° is defined as follows:
| (6) |
Multivariate Gaussian variability of trial-by-trial voxel responses
Linear Fisher information has no assumption about Gaussian variability of trial-by-trial responses. The analytical solution of bias correction given a limited number of units and samples, however, rests on the assumption that the trial-by-trial population responses follow a multivariate Gaussian distribution. Although Gaussian variability of voxel responses has been either implicitly assumed or explicitly formulated in several previous studies (van Bergen et al., 2015; van Bergen and Jehee, 2018), it remains a presumption rather than a grounded finding.
We tested whether trial-by-trial population responses follow multivariate Gaussian distribution in our data. For each stimulus, the data can be represented as an N (voxels) × T (trials) matrix (Fig. 1B). Here, voxels and trials can be viewed as features and samples, respectively. We performed the Henze–Zirkler multivariate normality test (implemented by the multivariate_normality function from the pingouin Python package) on the data matrix. The Henze–Zirkler test has good power against alternatives to normality and is feasible for any dimension and sample size (Henze and Zirkler, 1990). We performed the Henze–Zirkler multivariate normality test for the voxels in each ROI, hemisphere, and subject. We found no significant violation (all p values > 0.05) of multivariate Gaussian variability in a total of 144 tests (6 subjects × 2 hemispheres × 3 ROIs × 4 stimuli), revealing multivariate Gaussian distributions as an appropriate approximation of trial-by-trial voxel responses.
The titration approach to derive information as a function of response correlation strength
We parametrically manipulated the strength of RCs between voxels. We multiplied the off-diagonal items in the covariance matrices and with a coefficient, , but kept the diagonal items intact. For the item () at the ith row and the jth column in or , we have the following:
| (7) |
where is the Kronecker δ ( = 1 if i = j and = 0 otherwise). We then used the resultant matrices and instead of or to calculate information using Equations 1–3. By this method can we titrate the strength of RC and investigate how it has an impact on information. Note that the two scenarios (i.e., with and without RC) in Figure 1 correspond to the condition that = 1 and 0, respectively. Here, we use Equation 3 instead of Equations 4 and 5 to calculate bias-corrected linear Fisher information because (1) it is unclear the exact format of the bias when is within [0, 1], and (2) we are interested in the overall changing trend of information as a function of RC strength rather than the absolute magnitude of information.
Neuron- and voxel-encoding modeling
Neuron-encoding model
We simulated 50 orientation-selective neurons whose preferred orientations equally span within (0, ]. The von Mises tuning curve of the kth neuron is the following:
| (8) |
where , , control the baseline, amplitude, and tuning width, and we set them as , , (Ecker et al., 2011); is the preferred orientation of that neuron. We assume that neuronal spikes follow Poisson statistics (i.e., variance equal to mean firing rate).
Two types of RC structures were investigated here. The first one is tuning-compatible RC (TCRC), indicating that the RC between a pair of neurons is proportional to the similarity of their tuning functions as follows:
| (9) |
where is the tuning-compatible RC between the ith and the jth neurons, and and are tuning functions of the two neurons (i.e., mean responses toward each of all orientations in 0 ∼ ), and is the Kronecker δ ( = 1 if i = j and = 0 otherwise). is the vector of all possible orientations within (0, ]. We denote as the tuning-compatible RC matrix. The theoretical derivation and empirical measurement of tuning-compatible RC is introduced later.
We also investigated a control type of RCs called tuning-irrelevant response correlation (TIRC). We shuffled the pairwise RCs in such that the rows and columns were rearranged in a random order, but the diagonal items were kept unchanged. We denote the resultant matrix as By this shuffling method, the overall distribution of the items in and are identical, but the pairwise RCs in no longer resemble the tuning similarity between two neurons.
We also applied the titration approach (response correlation coefficient ) to manipulate the strength of RCs in both cases and calculated the linear Fisher information of discriminating orientations 0 and in the neuronal population. For the case of tuning-compatible RC, the information is deterministic because is fixed; for the case of tuning-irrelevant RC, we created and calculated information 100 times.
Voxel-encoding model
The voxel-encoding model is built based on the neuron-encoding model. Given the 50 orientation-selective neurons, we further simulated 50 voxels using the voxel-encoding model as follows:
| (10) |
where is the tuning curve of the ith voxel, and is the connection weight between the kth neuron and the ith voxel. The weighting matrix W maps neuronal tuning curves to voxel tuning curves. Note that Equation 10 also suggests that voxel tuning curves look irregular (e.g., multimodal tuning curves) compared with the unimodal bell-shaped tuning curve of neurons (Zhang et al., 2019). However, orientation decoding per se does not require formal tuning curves as long as the voxels show differential responses to two orientations. Instead of Poisson noise, we assumed additive noise on voxel activity the response variance () of each voxel is drawn from a gamma distribution (i.e., , where a = 1.5 and b = 4 are the scale and the shape parameters corresponding to the gamma distribution with mean = 6, and variance = 24.
Similar to the neuron-encoding model, we also assumed tuning-compatible response correlations between voxels as follows:
| (11) |
where and are the tuning functions of the ith and jth voxels. The voxel correlation coefficient is used to control the magnitude of correlation between voxels. As a control, we also assumed tuning-irrelevant response correlations () by shuffling rows and columns of as described above.
We manipulated and calculated the information under the regimes of tuning-compatible RCs and tuning-irrelevant RCs (Fig. 5D). Because the voxel tuning curves and response variance depend on the weighting matrix W (Eq. 10) and the gamma distribution, respectively. We run the simulation 100 times, and in each simulation, a new weighting matrix W is created by the following:
| (12) |
where is the number of hypothetical neurons (i.e., 50 in our case) in the voxel-encoding model. We set the scaling factor to ensure the voxel activity was mostly below 5%, which is consistent with the percentage bold signal change in real fMRI data.
Figure 5.
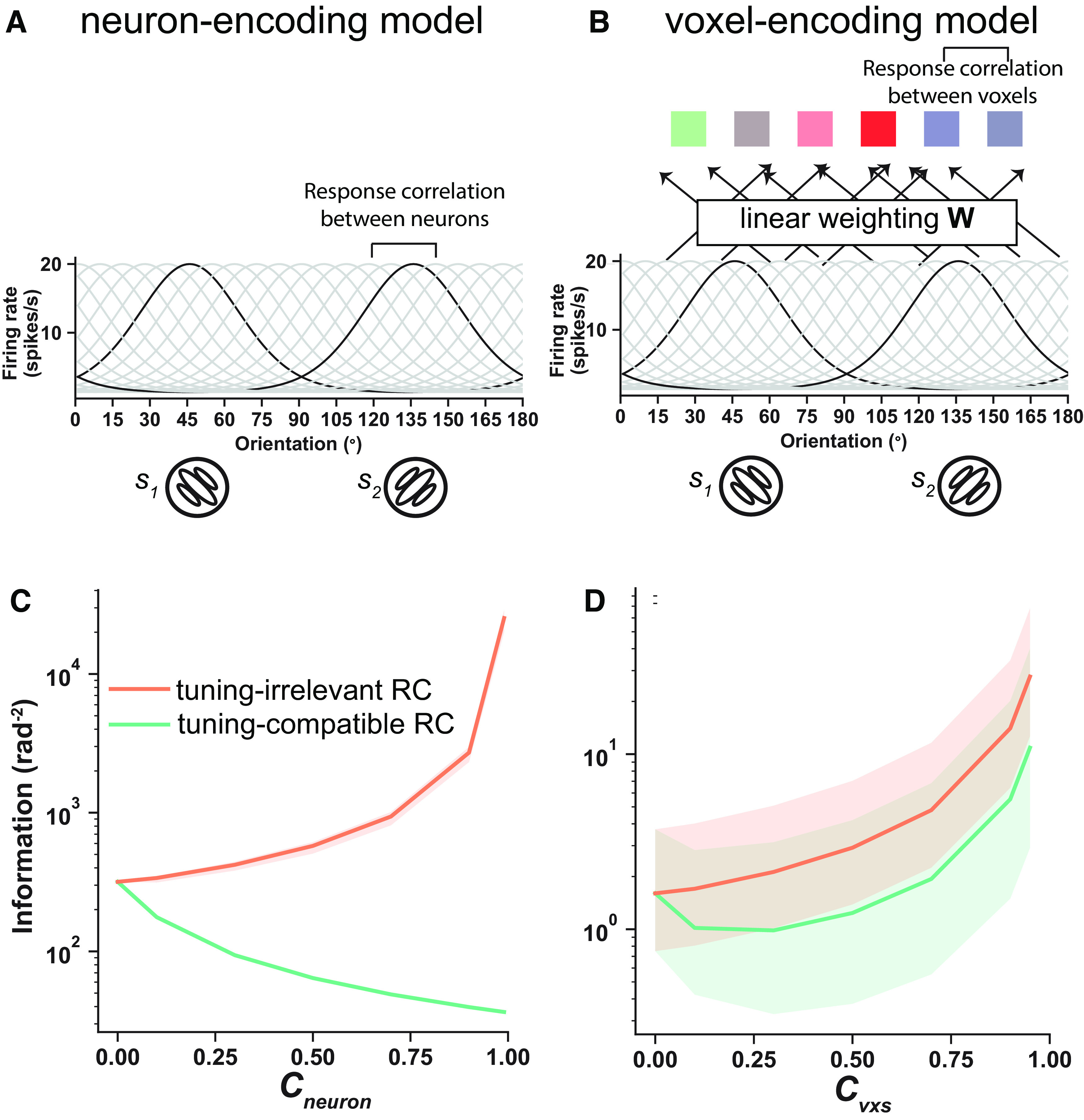
A–D, Neuron- (A) and voxel-encoding (B) models reproduce the effects of RCs reported in the previous neurophysiological literature (C) and our fMRI data (D). and are the RC coefficients controlling the RC strength in the neuron- and the voxel-encoding model, respectively. The shaded areas of the pink curve in C and those of the two curves in D represent the 95% confidence interval for 100 simulations. Note that the green curve in C (i.e., the neuron-encoding model with tuning-compatible RCs) has no variability because neuronal tuning curves and variance are fixed in this condition (see above, Neuron-encoding model).
Eigen-decomposition of information
Equation 1 can be further reformulated as follows:
| (13) |
where and are the ith unit eigenvector and its corresponding eigenvalue; , the signal vector, is defined in Equation 2. The can be viewed as the projected signals on the ith eigendimension; , the eigenvector, indicates the variance on the ith eigendimension. Thus can be considered as the signal-to-noise ratio, or information, on the ith eigendimension. Because eigendimensions are linearly uncorrelated, the total information should be the sum of information across all eigendimensions.
Theoretical derivation of tuning-compatible response correlations in voxel populations
To derivate the theoretical feasibility of tuning-compatible RCs in voxel populations, we simulated the RC matrix using the voxel-encoding model 1000 times. In each simulation, we randomly generated the weighting matrix W (using Eq. 12) and only considered the variability propagated from the neuronal to the voxel level. Tuning curves of voxels can be computed based on W (Eq. 10), and the tuning similarity between the ith and the jth voxels can be computed by Note that here we did not assume any RCs at the neuron level as that in the neuron-encoding model above. For a given stimulus s, because of Poisson variance, the covariance matrix () of neuronal responses in Equation 1 should be . We can analytically derive the covariance () of voxel responses as follows:
| (14) |
And the RC matrix can be calculated based on the covariance Given and we calculated the correlation between the off-diagonal items below the diagonal. For an example correlation scatter plot, see Figure 6A. For the distribution of the r value of 1000 simulations, see Figure 6B.
Figure 6.
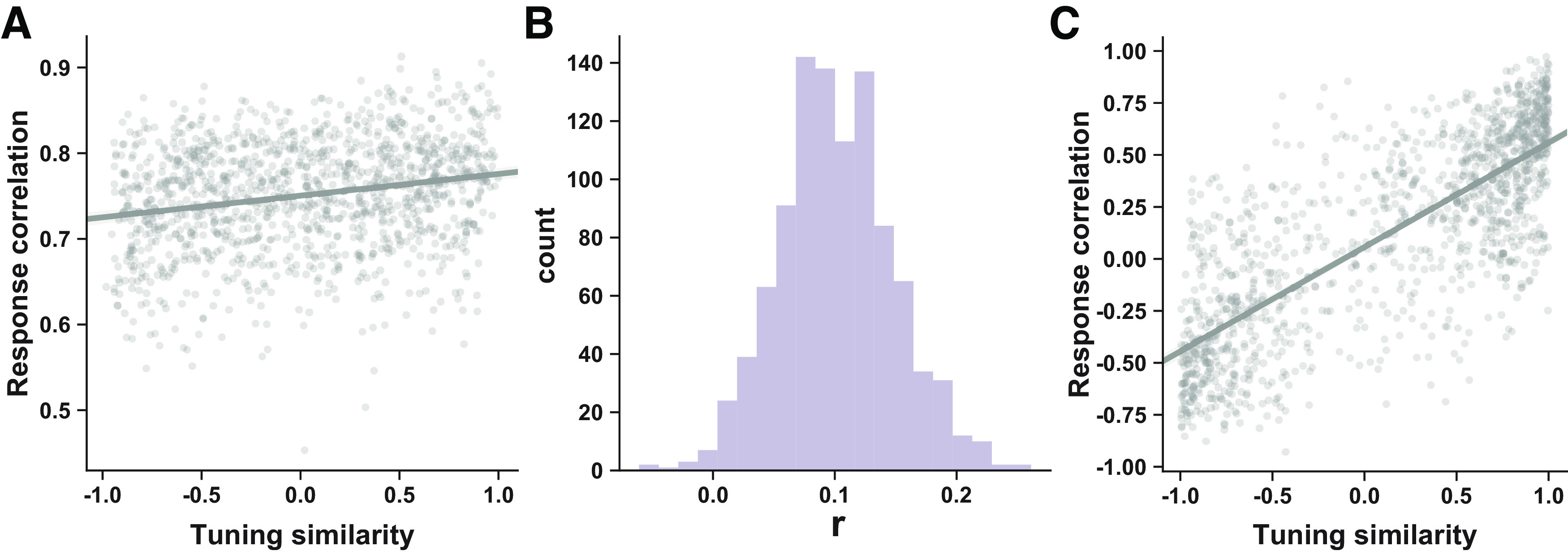
theoretical derivation and empirical measures of tuning-compatible RCs. A, An example scatter plot of RCs (y-axis) and tuning similarity (x-axis) in one simulation of the voxel-encoding model. B, The distribution of the correlation value across 1000 simulations. In each simulation, we randomly generate a new weighting matrix W. C, Example scatter plot of RCs (y-axis) and tuning similarity (x-axis) in a total of 144 cases (6 subjects × 2 hemispheres × 3 ROIs × 4 stimuli).
The link between linear Fisher information and the discrimination thresholds of the optimal linear decoder
Fisher information can be converted to orientation discrimination threshold () as follows:
| (15) |
where I is Fisher information, ACC is the accuracy to which the threshold corresponds, and is the inverse cumulative normal function. Given 75% accuracy, 1 rad−2 information corresponds to the discrimination threshold of 1.349 radians (i.e., ∼77°).
Results
Voxelwise response correlations enhance stimulus information in human early visual cortex
We analyzed the trial-by-trial voxel activity in early visual cortex when six human participants viewed gratings with four orientations (i.e., 0°, 45°, 90°, and 135°; see above, Materials and Methods; Fig. 3A). As in classical decoding experiments (Kamitani and Tong, 2005), each orientation was presented for several trials, allowing us to estimate the single-trial activity of individual voxels. Instead of the conventional decoding approach, we calculated linear Fisher information—how well two stimuli can be discriminated based on population responses—in early visual areas (i.e., V1–V3) of all subjects. The calculation of linear Fisher information requires estimates of the response mean and variance of individual voxels as well as the response correlation matrices between voxels (Eqs. 1–3). As we show later, this information-theoretic approach is advantageous because it allows one to symmetrically manipulate RC strength in the data and examine its consequences.
To demonstrate the effects of trial-by-trial RCs, we compared stimulus information in each brain region under two regimes. In one regime, linear Fisher information was computed directly from empirically measured voxel responses with all voxelwise RCs fully preserved. In the other regime, linear Fisher information was calculated with all voxelwise RCs being hypothetically removed. To do so, we manually set the RC matrices to identity matrices (Eqs. 1–3). Notably, this procedure forces the RCs between voxels to be zero (i.e., removes all RCs) without changing the marginal response distributions (i.e., mean and variance) of individual voxels. Intuitively, this is equivalent to warping the two response distributions in Figure 2, B and C (i.e., RCs are nonzero), to Figure 2A (i.e., RCs are zero). This method has been used to illustrate the effects of RCs in previous studies (Kanitscheider et al., 2015; Montijn et al., 2019). Note that the estimated statistical properties (e.g., mean, covariance) given a limited number of units and trials may introduce bias in the estimation of information. Therefore, we computed bias-corrected linear Fisher information under these two regimes (Kanitscheider et al., 2015).
We found that the information with RCs being preserved is significantly higher than that with RCs being hypothetically removed, suggesting that voxelwise RCs in general enhance stimulus information. Our finding here stands in contrast to the findings in neurophysiology, where the majority of animal studies demonstrated the detrimental effects of neuronal RCs. This discrepancy is explained later.
Information as a U-shaped function of correlation strength in voxel populations
The above analyses demonstrate the potential beneficial effects of voxelwise RCs by contrasting two regimes; voxelwise RCs are completely preserved or removed. The result shows that voxelwise RCs seem to enhance stimulus information. However, according to our previous theoretical work (Di et al., 2021), the relationships between RCs and stimulus strength may not be monotonic. To gain a full picture of the possible effects of RCs, we further used a titration approach; we computed stimulus information while progressively manipulating RC strength. Specifically, all off-diagonal elements of empirically measured RC matrices were multiplied by an RC coefficient (i.e., ). The RC matrices are identity matrices when the coefficient is set to zero, and they remain unchanged when when the coefficient is set to one (Fig. 4A). In other words, the two regimes in Figure 3 can be viewed as the two special cases (i.e., ) of the titration analyses here.
Figure 4.
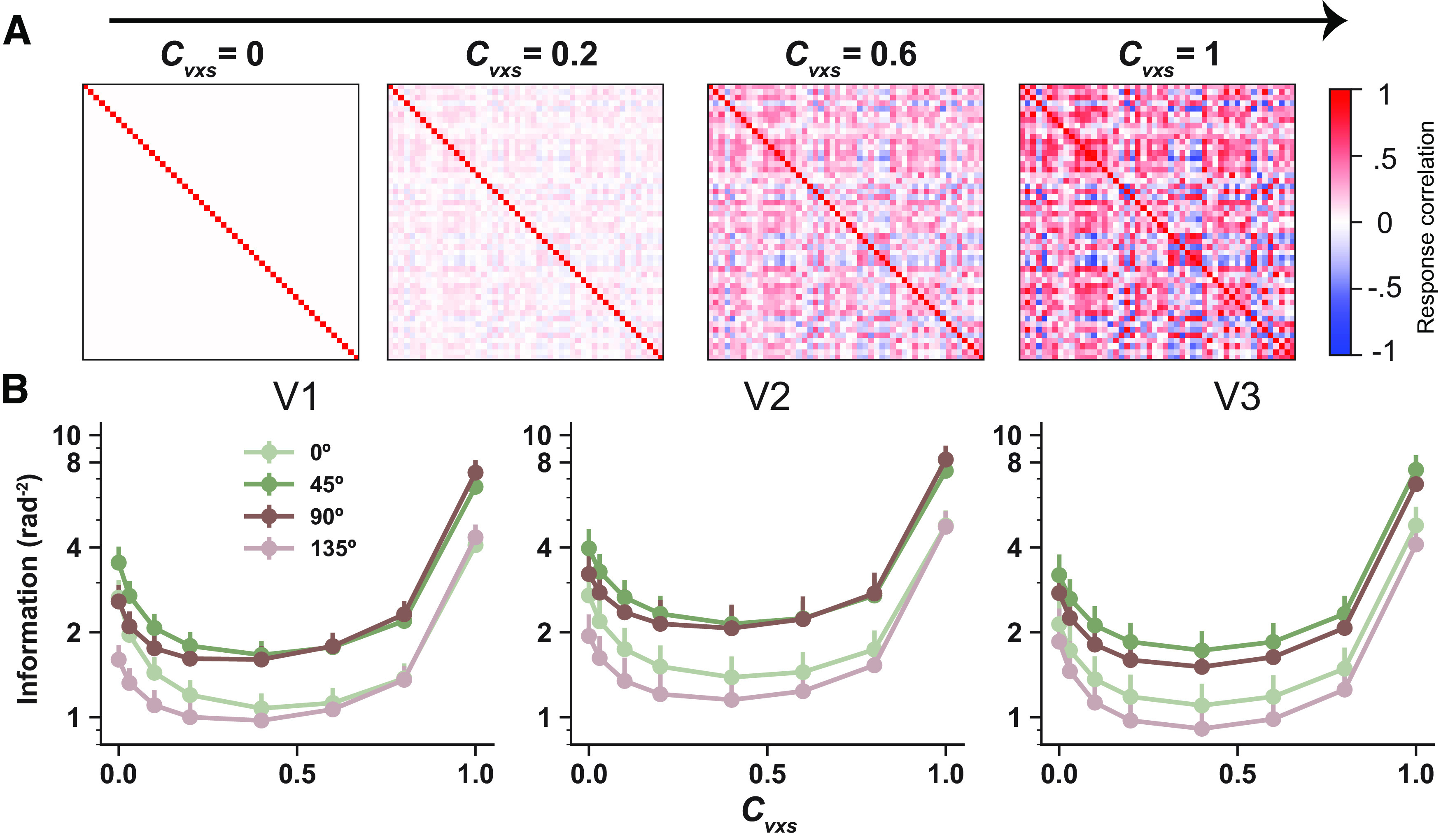
Stimulus information as U-shaped functions of voxelwise RC strength. is the RC coefficient controlling RC strength. A, The off-diagonal items in RC matrices emerge as increases. B, Information depicted as U-shaped functions of Note that the two conditions in Figure 3 correspond to the first and the last data points of the curves shown here. But Figure 1 shows bias-corrected linear Fisher information, and here information is calculated using Equation 1 without bias correction because we are interested in the changing trend rather than the absolute amount of information. Error bars (B) indicate SEM across 12 independent samples (6 subjects × 2 hemispheres).
Interestingly, we found that although RCs improve information when all RCs are preserved, and the effects of RCs are nonmonotonic; stimulus information first declines then rises with increasing RC strength, manifesting as a U-shaped function. The ebb and flow can reach half and double magnitude of that without RCs. This result held for all four orientations and in all three ROIs. Note that some previous studies examined the effects of RCs by shuffling population responses across trials to remove RCs and then comparing decoding accuracy between unshuffled and shuffled data (Cohen and Maunsell, 2009). That approach is similar to the analyses in Figure 3. However, the shuffling approach has two major shortcomings, namely, it has been proven to be less efficient when the number of trials and units are relatively small (Kanitscheider et al., 2015), and it cannot easily reveal the full changing trend of information when RC strength is progressively manipulated (e.g., the U-shaped function observed here).
Voxel-encoding models explain the discrepancy between the effects of response correlations in neuronal and voxel populations
Why does stimulus information exhibit a U-shaped function as RC strength increases? More importantly, why do the effects of RCs manifest differently in neurophysiological and fMRI data? One notable difference between neuronal and voxel activity is that voxel activity is thought to reflect the aggregation of the activity of many neurons. We then show that this neuron-to-voxel activity summation naturally produces the observed U-shaped function.
We first sought to replicate the classical detrimental effects of neuronal RCs using a neuron-encoding model and applied the same data analyses to fMRI data. One well-established finding in neurophysiology is that the response correlation between two neurons is proportional to their tuning similarity, called tuning-compatible RC (Kohn et al., 2016). In the neuron-encoding model, we simulated 50 orientation-selective neurons with Poisson response statistics and assumed the tuning-compatible RCs between the neurons (Fig. 5A; Eq. 7). We also simulated a control type of RCs, called tuning-irrelevant response correlations. For tuning-irrelevant RC, the elements in RC matrices are identical to those in tuning-compatible RC matrices but are rearranged across columns and rows so that the RC between a pair of voxels bears no resemblance to their tuning similarity (van Bergen and Jehee, 2018). We found that tuning-compatible RCs always degrade information (Fig. 5C, green line), whereas tuning-irrelevant RCs always enhance information (Fig. 5C, orange line) in the neuron-encoding model. These results are consistent with a wide range of empirical or theoretical studies in neurophysiology (Zohary et al., 1994; Cohen and Kohn, 2011; Downer et al., 2015; Vinck et al., 2015).
Next, we turn to modeling the effects of voxelwise RCs on sensory information in fMRI data. Before doing so, we first investigated the structure of voxelwise RCs. It remains unclear whether tuning-compatible RCs also exist in fMRI data. To our best knowledge, only one study found evidence for the existence of tuning-compatible RCs in fMRI (van Bergen and Jehee, 2018). We thus quantified the relationship between tuning similarity and response correlations in our empirical data (see above, Materials and Methods). We found that there is a significantly positive relationship between tuning similarity and response correlations in all 144 tests (all correlation p values < 0.05, 6 subjects × 2 hemispheres × 3 ROIs × 4 stimuli; see above, Materials and Methods), supporting the existence of tuning-compatible RCs in realistic fMRI data. Furthermore, previous fMRI studies have suggested that spatial distance may be an another important factor mediating RCs between voxels (Haak et al., 2013; Ryu and Lee, 2018). Therefore, we run a regression analysis with tuning similarity and 3D spatial distance of two voxels as the predictors of their response correlations. The significant positive relationship between tuning similarity and response correlation was still observed in 138 of 144 tests, further supporting their functional links.
With tuning-compatible RCs being established in fMRI, we next established a voxel-encoding model that incorporates an additional layer of voxel activity on top of the neuron-encoding model and assumes voxel activity as linear combinations of underlying neuronal activity (see above, Materials and Methods; Fig. 5B). This encoding-model approach has been widely used in fMRI studies on a variety of topics, including attention (Sprague and Serences, 2013), memory (Ester et al., 2015), and learning (Chen et al., 2015). Note that in this voxel-encoding model the parameters (e.g., amplitude, baseline firing rate, tuning width) at the neuron-encoding stage are identical to those in the neuron-encoding model above. Similarly, we assumed that the voxelwise RCs were (1) either proportional to their tuning similarity (i.e., tuning-compatible RCs) or as a control and (2) unrelated to their tunings (i.e., tuning-irrelevant RCs). Interestingly, the model with tuning-compatible RCs can well reproduce the U-shaped information function (Fig. 5D, green line). Like neurons, the tuning-irrelevant RCs between voxels always improve stimulus information (Fig. 5D, orange line). This quantitative voxel-encoding modeling suggests that the detrimental effects of RCs at the neuronal level and the potential beneficial effects of RCs at the voxel level can coexist and that we obtain opposite results simply because brain activity is acquired at different spatial scales (i.e., neurons at the microscopic level and voxels at the mesoscopic level).
These results are also consistent with our previous theoretical work that voxel tuning heterogeneity contributes to the U-shaped function of the effects of voxelwise RCs (Zhang et al., 2020). In contrast to the relatively homogeneous tuning curves in the neuron-encoding model (i.e., similar peak, baseline of tuning functions) of individual neurons, voxel tuning curves computed by the aggregations of neuronal activity are remarkably heterogeneous (i.e., different baseline, response range). And such tuning heterogeneity attenuates the detrimental effects of RC. We show this more formally later.
Using the voxel-encoding model, we also investigated the nature of tuning-compatible RCs. Although we found tuning-compatible RCs in our empirical voxel responses, it remains theoretically elusive why they should exist at all. We hypothesized that the mapping from neuronal to voxel activity naturally produces tuning-compatible RCs between voxels. We first showed analytically that the weighting matrix W bridges the (co)variability from neurons to voxels (Eq. 13; van Bergen et al., 2015). Then, using the above voxel-encoding model and a weighting matrix W, we calculated the tuning similarity and response correlation between each pair of voxels in the voxel-encoding model and examined their relationships (Fig. 6A, example scatter plot). We repeated this calculation 1000 times and found a significant positive relationship between tuning similarity and response correlations between voxels (bootstrap test, p < 0.013; Fig. 6B). In other words, we theoretically proved that there should exist tuning-compatible RCs between voxels as long as voxel activity is considered as an aggregation of underlying neuronal activity.
Opposite effects of response correlations on stimulus information in neuronal and voxel populations revealed by eigen information decomposition analysis
The above results only show that neuron- and voxel-encoding models, which assume voxel activity as aggregations of underlying neuronal activity, can well reproduce the effects of RCs observed in empirical data. However, what are the exact computational mechanisms underlying this discrepancy? Why does the transformation from the neuronal to the voxel level alter the effect of RCs? To address this question, we first introduce the method of information decomposition and then describe how it can serve as a unified mathematical framework for understanding information coding in multivariate data.
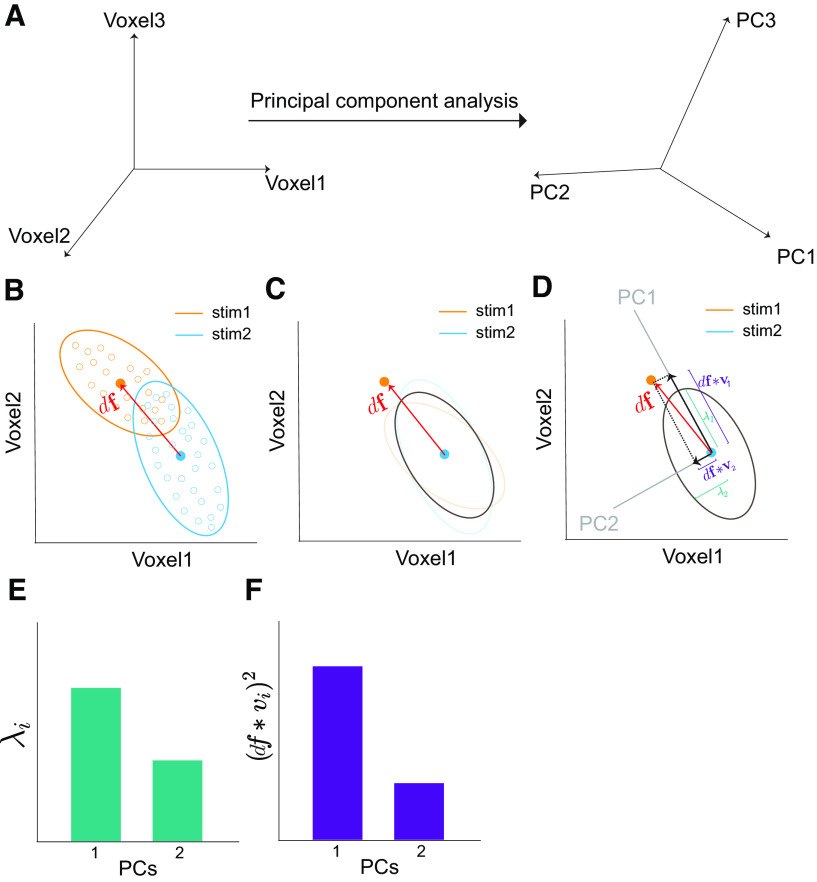
The key formulation of information decomposition (as shown below; Eqs. 1, 13) is to convert the computation of linear Fisher information () in the original neuron/voxel space () to the eigenspace as follows:
where is the signal vector normalized to the absolute difference between the two stimuli (Eq. 13; Fig. 7C, the red vector). is the averaged covariance matrix of the voxel responses toward two stimuli (Eq. 3); and are the ith eigenvector and its corresponding eigenvalue (i.e., variance) of , respectively. This approach avoids the tedious matrix inversion () and represents the information of the whole population as the summation of the information along each eigendimension.
Figure 7.
Schematics of eigen decomposition of information. A, The information contained by trial-by-trial high-dimensional population responses can be calculated in the eigenspace (obtained by principal component analysis) instead of the original voxel space (Eq. 13). Thanks to the linear independence of the eigenspace, the information of the whole population can be simply reformulated as the summation of information along each eigendimension (Eq. 13). B, Two 2 d response distributions of two voxels toward two stimuli. The yellow and blue ellipses also show the direction of covariances ( and ). The red vector () can be viewed as the Euclidean distance between the two distributions (Eq. 2 with the assumption of = 1). C, The gray ellipse depicts the averaged covariance (averaged and ; Eq. 3). D, The averaged covariance can be decomposed into two principal components (PC1 and PC2). E, The variance along each PC is illustrated. Intervoxel RCs result in a larger variance in PC1 () than PC2 (). F, The squared projected signals on each PC are illustrated. Note that the sum of squared projected signals [i.e., the sum of bars in F, )] is a constant, which amounts to the norm of the signal vector
The intuition of this formulation can be illustrated in the two-voxel scenario in Figure 7. In Figure 7A, the two voxels/neurons have substantial RCs, and the majority of the variance lies in the first eigendimension [i.e., principal component (PC)]. Here, indicates the amount of variance associated with the ith PC, and indicates the squared projection of the signal vector () onto this PC. The information on this PC is equal to the ratio between the squared projected signals and the variance . Obviously, the larger the projected signals , the smaller variance , and the more information will be on a PC. Furthermore, the total information in a population is the sum of information across all eigendimensions . This formulation allows us to disentangle the contributions of the projected signals and the variance on each eigendimension. This method of information decomposition has been previously proposed and shown to be sensitive when a relatively small number of units and trials are analyzed (Huang et al., 2019; Montijn et al., 2019).
We first performed the information decomposition analysis to examine the effects of tuning-compatible RCs in the neuron-encoding model. Specifically, we calculated the eigenvalue (; Fig. 8A), the squared projected signal (; Fig. 8B), their ratio (i.e., the information on that PC, ; Fig. 8C) on each PC, the cumulated information across the first few PCs (Fig. 8D), and the total information (Fig. 8E) as a function of RC strength. We found that the variance of population responses is concentrated in the first few PCs as RC strength increases (Fig. 8A). This is not surprising because increasing RCs inevitably produce a low-dimensional manifold along which population activity fluctuates. Interestingly, increasing tuning-compatible RCs also heightens the projected signals on the first few PCs. More projected signals on high-variance PCs result in less signals on low-variance PCs. Because both the projected signal as the numerator and the variance as the denominator decrease significantly, it is difficult to intuitively predict the changing direction of their ratio . By plotting , we found that tuning-compatible RCs significantly reduce information in the majority of PCs (Fig. 8C). Although there are some nonmonotonic effects (e.g., information increased and then decreased on the first PC; medium strength RCs enhance information on a few low-variance PCs), the overall effect of information reduction is much more dominant, resulting in less total information in neuronal populations (Fig. 8D). In other words, the detrimental effects of tuning-compatible RCs in neurons (Fig. 8E) are primarily driven by information reduction on high-variance PCs.
Figure 8.
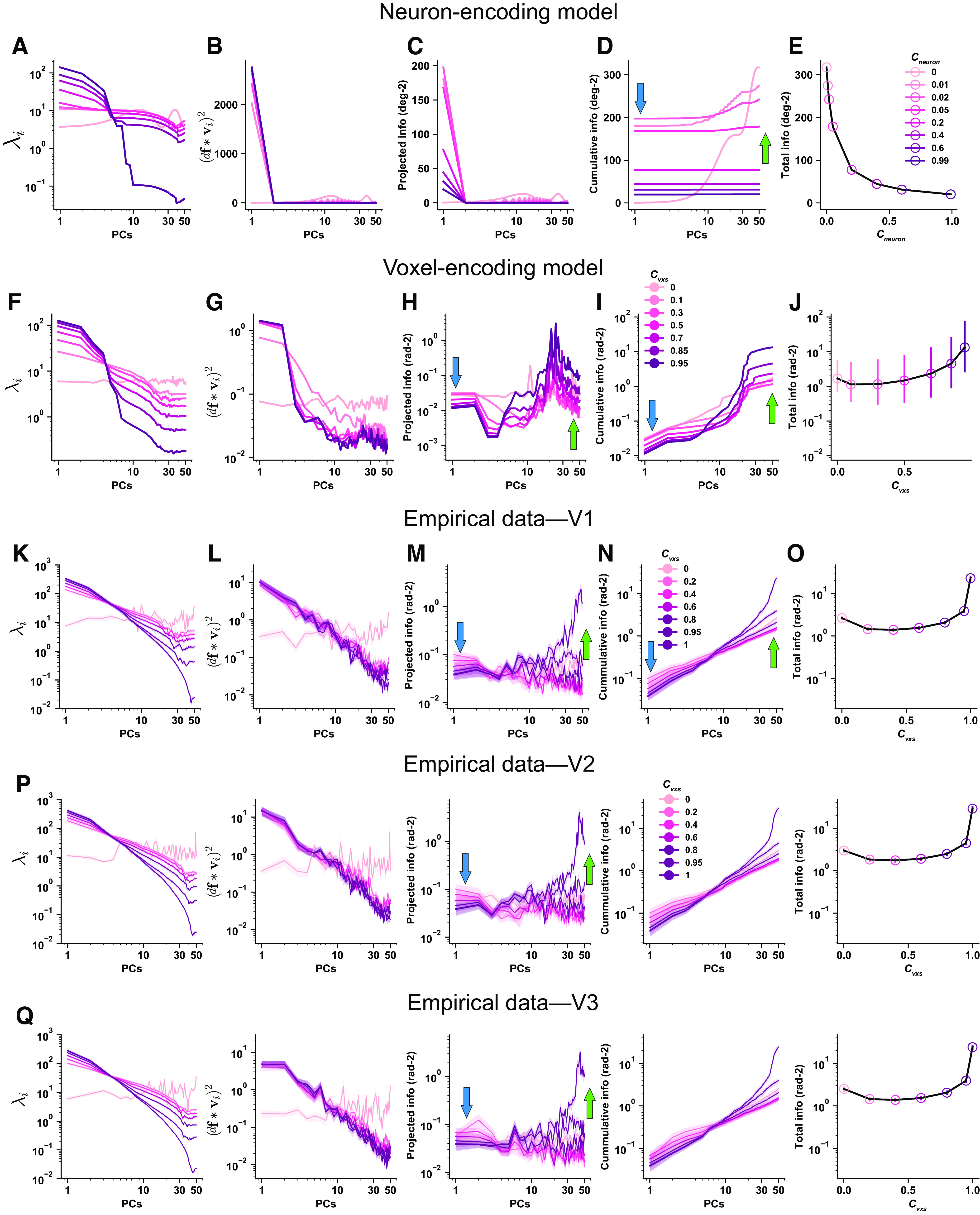
A–Q, Eigen-decomposition information analyses for the effects of tuning compatible response correlations in the neuron-encoding model (A–E), the voxel encoding model (F–J), empirical data of V1 (K–O), V2 (P), and V3 (Q). Columns 1–4, The x-axes are PCs ranked by their variance from high to low. The eigenvalue (i.e., variance ) on each PC (A). The variance of population responses is heightened on the first few PCs and reduced on the last few PCs when RC strength increases. Squared projected signals on each PC (B). As RC strength increases, the projected signals also increase on the first few PCs. More projected signals on the first few PCs will inevitably lead to fewer projected signals on other PCs. Information () on each PC (C). Cumulative information of the first few PCs (D, i.e., the sum of the first few data points in C). Information quickly saturates given the presence of tuning-compatible RC. Without RC, information slowly increases but eventually reaches a higher level. The blue and green arrows highlight the antagonistic information change on high- and low-variance PCs, respectively. Information as a decreasing function of RC strength (E). Note that the data points in E correspond to the last data points (i.e., PC = 50) of the curves in D. The results of the same analyses for tuning-compatible RCs in the voxel encoding model (F–J). Error bars in J indicate the 95% confidence intervals of 100 independent simulations. The key difference here is that the information enhancements on low-variance PCs are much more pronounced in voxels compared with neurons, producing a U-shaped function (J). These effects are further validated in the empirical fMRI responses in human V1. K–O, For each line, we calculated 72 independent samples (6 subjects × 2 hemispheres × 6 pairwise comparisons). There are six pairwise comparisons because of the four stimulus orientations. The solid lines and the shaded areas represent the mean and the SEM of the samples. O, The error bars are very small. The results of V2 and V3 (P, Q). The conventions of the arrows are kept in subsequent figures.
We then applied the same analyses to examine the effects of tuning-compatible RCs in the voxel-encoding model. Similar to neurons, tuning-compatible RCs between voxels induce higher variance (Fig. 8F) and higher projected signals (Fig. 8G) on the first few PCs. Thus, it is nontrivial to predict the changing trend of their ratio Again, we found that tuning-compatible RCs also reduce and enhance information on high- (Fig. 8H, blue arrow) and low-variance PCs (Fig. 8H, green arrow), respectively. In contrast to the scenario of neurons, these two antagonistic effects together produce a U-shaped function (Fig. 8I,J). In addition, the information enhancements on low-variance PCs dominate, eventually resulting in an overall larger amount of information (Fig. 8I,J).
We further performed the same analyses on the empirical fMRI data in V1. We found similar results as predicted by the voxel-encoding model. Increasing RCs inevitably produces a few high-variance PCs (Fig. 8K) and stronger projected signals on these PCs (Fig. 8L). Although RCs reduce the information on those high-variance PCs (Fig. 8M,N, blue arrows), they also disproportionately enhance information on low-variance PCs (Fig. 8M,N, green arrows), producing a U-shaped function of total information (Fig. 8O). These results are consistent with the above voxel-encoding model. Analyses in V2 (Fig. 8P) and V3 (Fig. 8Q) show highly similar results to those in V1. As a control, we also performed the information decomposition analysis on the neuron- and voxel-encoding models assuming tuning-irrelevant RCs. The results showed that tuning-irrelevant RCs significantly attenuate the information reduction effect on high-variance PCs, and the overall enhanced information comes mainly from the information enhancements on low-variance PCs (Fig. 9).
Figure 9.
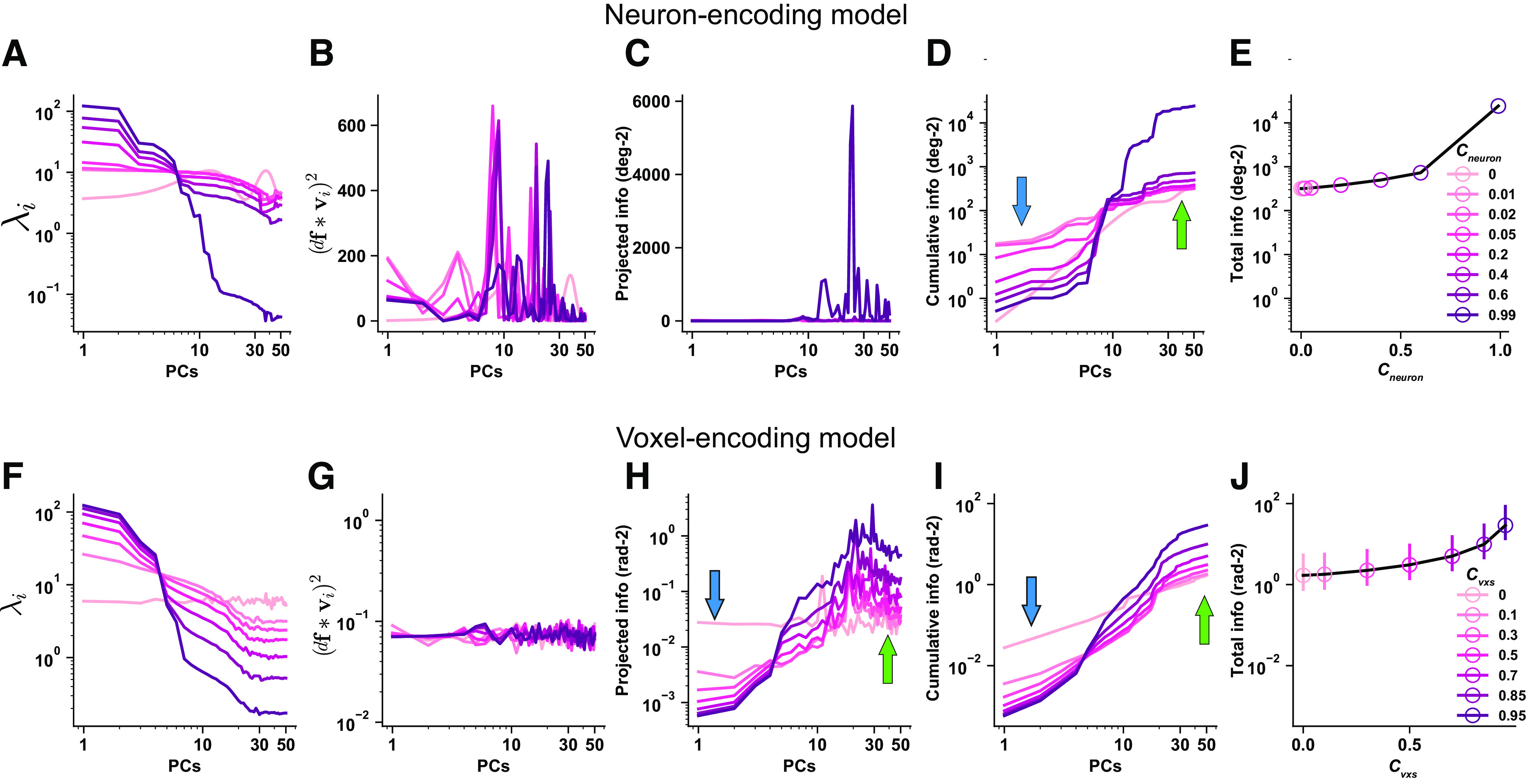
A–J, Eigen-decomposition information analyses for the effects of tuning irrelevant response correlations in the neuron-encoding model (A–E) and the voxel encoding model (F–J). Figure conventions are similar to those in Figure 8. Tuning irrelevant response correlations significantly improves population codes by primarily enhancing information on low-variance PCs.
In summary, despite the seemingly drastically opposite effects of tuning-compatible RCs in neuronal and voxel populations, we found a unified mechanism underlying the two scenarios. In both types of data, increasing tuning-compatible RCs has two antagonistic consequences—information enhancement on high variance PCs and information enhancement on low-variance PCs. The relative balance of these two effects determines the exact shape of the information function as RC strength increases because a continuum of possible effects (i.e., monotonic increasing/decreasing, U-shaped function) can occur. For neurons, the effect of information reduction dominates, and thus tuning-compatible RCs monotonically reduce information. For voxels, the effect of information enhancement is more pronounced, resulting in the U-shaped function of information. These effects are further validated in the empirical fMRI data.
These results complicate the interpretations of improved MVPA accuracy. We know that linear Fisher information is monotonically related to MVPA accuracy and sensory information is a U-shape function of RC here. Thus, enhanced sensory information (i.e., improved MVPA accuracy) thus can arise from many possibilities. For example, both increasing and decreasing RCs can lead to enhanced information as long as the baseline condition lies at the ridge part of the U-shaped function. It remains largely unclear how cognitive factors modulate population response properties in fMRI. More broadly, the brain can attain a better coding scheme by modulating tuning, noise, and response correlations, or combinations of all of these factors, a much more flexible mechanism than previously thought. This implication also invites deeper consideration of previous empirical studies using MVPA accuracy to characterize brain functions.
U-shaped information function in larger voxel pools
It has been shown that detrimental response correlations may masquerade as beneficial given noisy measurements and a limited number of neurons in an empirical study (Fig. 10A; Kohn et al., 2016). We further systematically modeled the effects of correlation strength and pool sizes. As shown in Figure 10C, the U-shaped function held when the number of voxels increased up to 2000, which is much larger than the number of voxels in a typical MVPA analysis. These results are also consistent with our past theoretical work (Zhang et al., 2020). We cannot completely exclude the possibility that sensory information will eventually saturate at a lower asymptote level when pool size goes infinite (i.e., the signature of information-limiting correlation). But our results should hold for the majority of MVPA fMRI studies.
Figure 10.
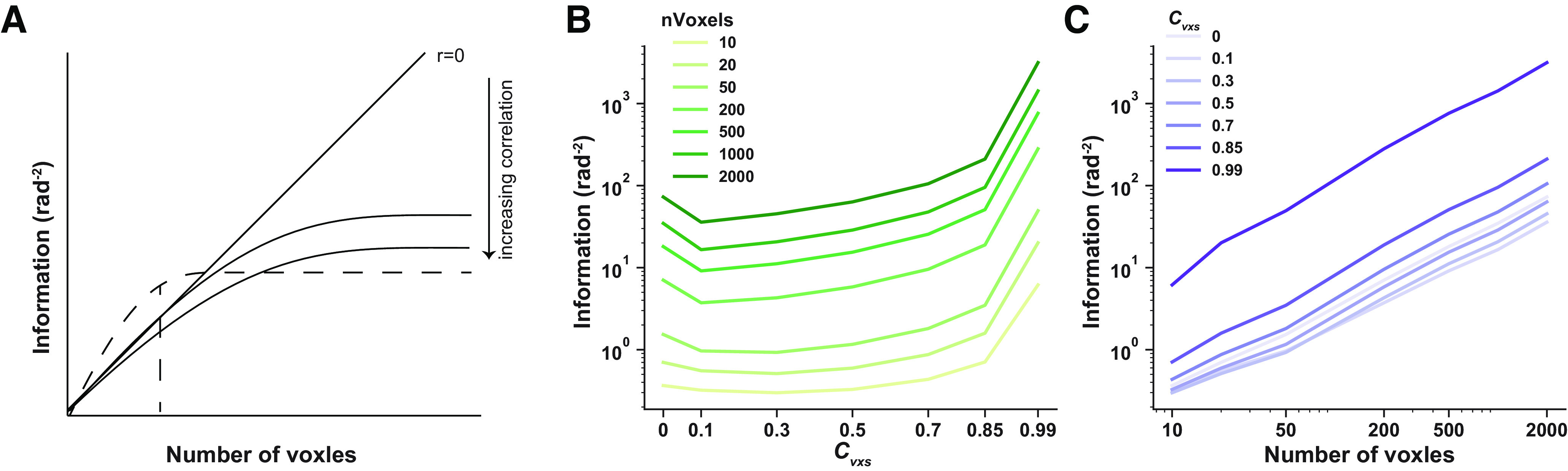
The effect of pool size on stimulus information. Theoretically detrimental neural correlations may manifest as beneficial because of noisy measurements in limited pool size. A, The solid lines are the stimulus information as a function of pool sizes (i.e., the number of voxels). Increasing correlations dampen the stimulus information, and stimulus information will eventually saturate given the presence of correlation. The dashed line indicates stimulus information calculated in empirical data. Correlations may masquerade as beneficial (i.e., the dashed line is higher than the diagonal line for small pool size). B, C, We further calculated stimulus information as a function of correlation strength (B) and pool sizes (i.e., number of voxels, C). Results showed that the U-shaped function is ubiquitous for increasing pool sizes, and information does not saturate up to 2000 voxels, which is far more than the number of voxels used in MVPA analyses in a typical empirical study.
Discussion
In this study, we investigate the effects of RCs in fMRI by calculating the bias-corrected linear Fisher information between the data where RCs are intact or hypothetically removed. We find higher stimulus information in the former case, supporting the beneficial role of RCs in fMRI data. We then systematically manipulate RC strength and find that stimulus information follows a U-shaped function of RC strength. These results stand in stark contrast to the monotonically detrimental effects of RCs documented in neurophysiology. Interestingly, this discrepancy between neurophysiology and fMRI can be well explained by a voxel-encoding model that bridges neuronal and voxel activity. Most importantly, information decomposition analyses further suggest that RCs reduce information on higher-variance PCs and, in the meantime, may enhance information on lower-variance PCs in most scenarios. The two antagonistic effects together may result in increasing, decreasing, or U-shaped information functions, producing a wide range of theoretical and empirical findings. This information decomposition approach also highlights the complexity of quantifying information and can serve as a unified mathematical framework that helps resolve debates in computational neuroscience.
The effects of response correlations in neurophysiology
The effects of RCs on stimulus information have been a matter of debate over the decades (Kohn et al., 2016). One major contribution of our work is to use a unified framework—information decomposition—to quantify stimulus information in fMRI data. This method in theory can be used on different modalities (e.g., neuronal spikes, fMRI, EEG sensors). It has been shown that only a specific type of correlation—differential correlation—limits information but its presence might be hard to detect because of the limited number of trials and neurons recorded in empirical data (Moreno-Bote et al., 2014). The information decomposition analysis has been previously proposed as a feasible solution to circumvent this limitation and help detect differential correlations using a much smaller number of units and trials (Montijn et al., 2019). Instead of the reduced information on high-variance PCs, we find a significant contribution of enhanced information on low-variance PCs, which is usually ignored in the previous literature. This phenomenon indicates that careful quantification of covariance structure in fMRI data and formal calculation of information are needed in future empirical studies.
The comparisons between MVPA and information-theoretic approaches
Fisher information is tightly linked to MVPA decoding accuracy because the inverse of Fisher information is defined as the lower bound of (co)variance of an unbiased maximum likelihood decoder (Abbott and Dayan, 1999).
Both Fisher information and MVPA have their respective advantages and disadvantages. Decoding employs a discriminative modeling approach requiring no assumption of the generative distributions of fMRI data. But decoding only provides a single accuracy value without showing sufficient details of representational geometry (Naselaris and Kay, 2015). In particular, decoding falls short in disentangling the effects of signal, noise, and response correlations on population codes (e.g., differentiate the cases in Fig. 2C,D). In contrast, linear Fisher information is based on the generative mechanism of data because by definition it is related to maximum likelihood decoding and thus guaranteed to be statistically optimal. However, using a limited number of units and trials may yield a biased estimation of linear Fisher information. The analytical solution to correct the bias is based on the assumption of Gaussian variability.
The interpretation of linear Fisher information
Fisher information can be converted to the discrimination threshold of an optimal linear decoder. We emphasize that this information-behavior comparison in typical unit-recording studies is inappropriate in fMRI because of the intrinsic low signal-to-noise ratio of fMRI data. Unlike neurophysiology, decoding accuracy in fMRI rarely reaches human behavioral performance on the same stimuli. For example, to discriminate two high-contrast gratings with orthogonal orientations, decoding accuracy on fMRI data can only achieve ∼70−80% accuracy, but human behavior can easily reach nearly 100% (Haynes and Rees, 2005; Kamitani and Tong, 2005). Here, we obtained ∼1 rad−2 information (Fig. 3), and this corresponds to the ∼77° orientation discrimination threshold given the 75% accuracy. This is consistent with classical fMRI decoding results (Haynes and Rees, 2005; Kamitani and Tong, 2005) but far worse than the human behavioral threshold of orientation discrimination (∼1–2°). Like MVPA, we can only compare the relative change of linear Fisher information across different cognitive states (e.g., attention vs unattention).
The low signal-to-noise ratio of fMRI data is also a potential limitation of this study. Here, large orientation differences (i.e., 45° and 90°) are used in the fMRI experiment and for the calculation of linear Fisher information. This is indeed consistent with the majority of decoding studies in fMRI. However, Fisher information by definition only measures the local curvature of log-probability distributions, and neurophysiological studies typically use a pair of stimuli with small differences (e.g., <10°). Theoretically, the calculation of the covariance matrix via Equation 3 may be imprecise when a pair of stimuli with large disparities are used. We argue that this should not be a problem for fMRI because (1) the signal-to-noise ratio is intrinsically low in fMRI signals, and (2) Figure 3B shows that the empirically measured covariance matrices for different stimuli with large disparities are highly similar (i.e., stimulus-invariant covariance matrices). Equation 3 is therefore appropriate here. The calculation of linear Fisher information in the neuron-encoding model may be imprecise (Fig. 5C), but this does not affect the conclusion as here we only focus on the qualitatively detrimental effects of tuning-compatible noise correlations (Fig. 5C, decreasing line) in neuronal populations, a phenomenon that is consistent with the case of stimuli with slight differences.
Voxel trial-by-trial variability may reflect underlying neuronal variability as well as many other sources of noise. There exist at least three types of noise that can cause the variability of voxel activity. The first is the measurement noise related to fMRI data acquisition, such as thermal noise, electronic noise, and so on. These types of noise are unlikely related to voxel tuning and thus unlikely produce tuning-compatible RCs. How to best control and minimize the influences of head motion or measurement noise during data acquisition and processing remains an active field of research in fMRI (Kay et al., 2013). The second type of noise is related to some global brain functions (e.g., arousal), and this type of noise is unlikely related to voxel tuning either. The third type of variability comes from the underlying neuronal variability in a voxel and should produce tuning-compatible RCs as we show analytically and empirically above. The existence of tuning-compatible RCs also suggests that voxel variability contains a substantial fraction of underlying neuronal variability in addition to measurement noise and global brain functions. The third type of variability is of most interest to neuroscientists because it usually reflects important aspects of stimuli (Cohen and Kohn, 2011; Kohn et al., 2016). Unfortunately, current fMRI technology does not allow us to distinguish between different sources of noise, and it remains a challenge for future fMRI studies to analyze the effects of noise on empirical data.
Implications for future fMRI studies
What are the implications for future fMRI practice? We would like to emphasize three possible areas where our framework is useful.
First, we manipulated the strength of RC and then calculated the resultant linear Fisher information of stimuli. Our results suggest that one should use the decoding method that takes into consideration the correlation structure in data if RCs in general improve decoding. For example, some recent efforts on Bayesian decoding require explicit modeling of the correlation structure. Thus, measuring and quantifying voxel correlations is an essential step toward more robust brain decoding (van Bergen and Jehee, 2018).
Second, although many factors (e.g., acquisition noise) may result in voxel RCs, and these RCs may help decoding, we still want to carefully control these factors during fMRI data acquisition and processing. This is because (1) they may lower the signal-to-noise ratio of individual voxels and (2) more importantly lead to inaccurate neuroscientific interpretations of fMRI data (Kay et al., 2019).
Third, cognitive states of the brain may have substantial impacts on RC structures. Despite the profound evidence of top-down modulations on RCs in neurophysiology (Ruff and Cohen, 2014), it remains unclear whether altered RC structures underpin cognitive processes in humans. For example, attention and perceptual training have been shown to enhance decoding accuracy in human visual cortex (Jehee et al., 2011; Chen et al., 2016). But it remains unclear whether the enhanced decoding accuracy arises because of altered RCs. The effects of RCs on stimulus information suggest that modulating RCs is an effective way to alter stimulus information in multivariate fMRI data. In particular, in this article we isolate the effects of RCs by keeping other aspects of voxel responses intact. In realistic experiments, cognitive processes (e.g., attention) can alter signals, noises, RCs, or combinations of these factors. It is the interactions among these factors that produce the outcome stimulus information. Future studies are needed to further dissect the computational mechanisms of altered decoding accuracy in human fMRI.
Footnotes
This work was supported by National Natural Science Foundation of China Grant 32100901, Shanghai Pujiang Program Grant 21PJ1407800), Natural Science Foundation of Shanghai Grant 21ZR1434700, Research Project of Shanghai Science and Technology Commission and Fundamental Research Funds for the Central Universities Grant 20dz2260300 (to R.-Y.Z.). We thank the team of the StudyForrest project (http://www.studyforrest.org/) that acquired and shared the fMRI data. We thank Kendrick Kay and Peter Bandetinni for comments on the manuscript.
The authors declare no competing financial interests.
References
- Abbott LF, Dayan P (1999) The effect of correlated variability on the accuracy of a population code. Neural Comput 11:91–101. 10.1162/089976699300016827 [DOI] [PubMed] [Google Scholar]
- Averbeck BB, Latham PE, Pouget A (2006) Neural correlations, population coding and computation. Nat Rev Neurosci 7:358–366. 10.1038/nrn1888 [DOI] [PubMed] [Google Scholar]
- Beck J, Bejjanki VR, Pouget A (2011) Insights from a simple expression for linear Fisher information in a recurrently connected population of spiking neurons. Neural Comput 23:1484–1502. 10.1162/NECO_a_00125 [DOI] [PubMed] [Google Scholar]
- Chen N, Bi T, Zhou T, Li S, Liu Z, Fang F (2015) Sharpened cortical tuning and enhanced cortico-cortical communication contribute to the long-term neural mechanisms of visual motion perceptual learning. Neuroimage 115:17–29. 10.1016/j.neuroimage.2015.04.041 [DOI] [PubMed] [Google Scholar]
- Chen N, Cai P, Zhou T, Thompson B, Fang F (2016) Perceptual learning modifies the functional specializations of visual cortical areas. Proc Natl Acad Sci U S A 113:5724–5729. 10.1073/pnas.1524160113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, Maunsell JH (2009) Attention improves performance primarily by reducing interneuronal correlations. Nat Neurosci 12:1594–1600. 10.1038/nn.2439 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, Kohn A (2011) Measuring and interpreting neuronal correlations. Nat Neurosci 14:811–819. 10.1038/nn.2842 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di X, Zhang Z, Biswal BB (2021) Understanding psychophysiological interaction and its relations to beta series correlation. Brain Imaging Behav 15:958–973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Downer JD, Niwa M, Sutter ML (2015) Task engagement selectively modulates neural correlations in primary auditory cortex. J Neurosci 35:7565–7574. 10.1523/JNEUROSCI.4094-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ecker AS, Berens P, Tolias AS, Bethge M (2011) The effect of noise correlations in populations of diversely tuned neurons. J Neurosci 31:14272–14283. 10.1523/JNEUROSCI.2539-11.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ester EF, Sprague TC, Serences JT (2015) Parietal and frontal cortex encode stimulus-specific mnemonic representations during visual working memory. Neuron 87:893–905. 10.1016/j.neuron.2015.07.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu Y, Liu S, Fetsch CR, Yang Y, Fok S, Sunkara A, DeAngelis GC, Angelaki DE (2011) Perceptual learning reduces interneuronal correlations in macaque visual cortex. Neuron 71:750–761. 10.1016/j.neuron.2011.06.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haak KV, Winawer J, Harvey BM, Renken R, Dumoulin SO, Wandell BA, Cornelissen FW (2013) Connective field modeling. Neuroimage 66:376–384. 10.1016/j.neuroimage.2012.10.037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haefner RM, Gerwinn S, Macke JH, Bethge M (2013) Inferring decoding strategies from choice probabilities in the presence of correlated variability. Nat Neurosci 16:235–242. 10.1038/nn.3309 [DOI] [PubMed] [Google Scholar]
- Haxby JV, Connolly AC, Guntupalli JS (2014) Decoding neural representational spaces using multivariate pattern analysis. Annu Rev Neurosci 37:435–456. 10.1146/annurev-neuro-062012-170325 [DOI] [PubMed] [Google Scholar]
- Haynes JD, Rees G (2005) Predicting the orientation of invisible stimuli from activity in human primary visual cortex. Nat Neurosci 8:686–691. 10.1038/nn1445 [DOI] [PubMed] [Google Scholar]
- Henze N, Zirkler B (1990) A class of invariant consistent tests for multivariate normality. Commun Stat Theory Methods 19:3595–3617. 10.1080/03610929008830400 [DOI] [Google Scholar]
- Huang C, Ruff DA, Pyle R, Rosenbaum R, Cohen MR, Doiron B (2019) Circuit models of low-dimensional shared variability in cortical networks. Neuron 101:337–348.e4. 10.1016/j.neuron.2018.11.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jehee JF, Brady DK, Tong F (2011) Attention improves encoding of task-relevant features in the human visual cortex. J Neurosci 31:8210–8219. 10.1523/JNEUROSCI.6153-09.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamitani Y, Tong F (2005) Decoding the visual and subjective contents of the human brain. Nat Neurosci 8:679–685. 10.1038/nn1444 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanitscheider I, Coen-Cagli R, Kohn A, Pouget A (2015) Measuring Fisher information accurately in correlated neural populations. Plos Comput Biol 11:e1004218. 10.1371/journal.pcbi.1004218 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay K, Jamison KW, Vizioli L, Zhang R, Margalit E, Ugurbil K (2019) A critical assessment of data quality and venous effects in sub-millimeter fMRI. Neuroimage 189:847–869. 10.1016/j.neuroimage.2019.02.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay KN, Rokem A, Winawer J, Dougherty RF, Wandell BA (2013) GLMdenoise: a fast, automated technique for denoising task-based fMRI data. Front Neurosci 7:247. 10.3389/fnins.2013.00247 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohn A, Coen-Cagli R, Kanitscheider I, Pouget A (2016) Correlations and neuronal population information. Annu Rev Neurosci 39:237–256. 10.1146/annurev-neuro-070815-013851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ling S, Pratte MS, Tong F (2015) Attention alters orientation processing in the human lateral geniculate nucleus. Nat Neurosci 18:496–498. 10.1038/nn.3967 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montijn JS, Liu RG, Aschner A, Kohn A, Latham PE, Pouget A (2019) Strong information-limiting correlations in early visual areas. bioRxiv 842724. 10.1101/842724. [DOI] [Google Scholar]
- Moreno-Bote R, Beck J, Kanitscheider I, Pitkow X, Latham P, Pouget A (2014) Information-limiting correlations. Nat Neurosci 17:1410–1417. 10.1038/nn.3807 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naselaris T, Kay KN (2015) Resolving ambiguities of MVPA using explicit models of representation. Trends Cogn Sci 19:551–554. 10.1016/j.tics.2015.07.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reimer J, Froudarakis E, Cadwell CR, Yatsenko D, Denfield GH, Tolias AS (2014) Pupil fluctuations track fast switching of cortical states during quiet wakefulness. Neuron 84:355–362. 10.1016/j.neuron.2014.09.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rissman J, Gazzaley A, D'Esposito M (2004) Measuring functional connectivity during distinct stages of a cognitive task. Neuroimage 23:752–763. 10.1016/j.neuroimage.2004.06.035 [DOI] [PubMed] [Google Scholar]
- Ruff DA, Cohen MR (2014) Attention can either increase or decrease spike count correlations in visual cortex. Nat Neurosci 17:1591–1597. 10.1038/nn.3835 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryu J, Lee SH (2018) Stimulus-tuned structure of correlated fMRI activity in human visual cortex. Cereb Cortex 28:693–712. 10.1093/cercor/bhw411 [DOI] [PubMed] [Google Scholar]
- Sengupta A, Yakupov R, Speck O, Pollmann S, Hanke M (2017) The effect of acquisition resolution on orientation decoding from V1 BOLD fMRI at 7T. Neuroimage 148:64–76. 10.1016/j.neuroimage.2016.12.040 [DOI] [PubMed] [Google Scholar]
- Shamir M, Sompolinsky H (2006) Implications of neuronal diversity on population coding. Neural Comput 18:1951–1986. 10.1162/neco.2006.18.8.1951 [DOI] [PubMed] [Google Scholar]
- Sompolinsky H, Yoon H, Kang K, Shamir M (2001) Population coding in neuronal systems with correlated noise. Phys Rev E Stat Nonlin Soft Matter Phys 64:051904. 10.1103/PhysRevE.64.051904 [DOI] [PubMed] [Google Scholar]
- Sprague TC, Serences JT (2013) Attention modulates spatial priority maps in the human occipital, parietal and frontal cortices. Nat Neurosci 16:1879–1887. 10.1038/nn.3574 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Bergen RS, Jehee JFM (2018) Modeling correlated noise is necessary to decode uncertainty. Neuroimage 180:78–87. 10.1016/j.neuroimage.2017.08.015 [DOI] [PubMed] [Google Scholar]
- van Bergen RS, Ma WJ, Pratte MS, Jehee JF (2015) Sensory uncertainty decoded from visual cortex predicts behavior. Nat Neurosci 18:1728–1730. 10.1038/nn.4150 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinck M, Batista-Brito R, Knoblich U, Cardin JA (2015) Arousal and locomotion make distinct contributions to cortical activity patterns and visual encoding. Neuron 86:740–754. 10.1016/j.neuron.2015.03.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang R-Y, Wei X-X, Kay KN (2019) Trial-by-trial voxelwise noise correlations improve population coding of orientation in human V1. Paper presented at the Conference on Cognitive Computational Neuroscience, Berlin, September. [Google Scholar]
- Zhang RY, Wei XX, Kay K (2020) Understanding multivariate brain activity: evaluating the effect of voxelwise noise correlations on population codes in functional magnetic resonance imaging. Plos Comput Biol 16:e1008153. 10.1371/journal.pcbi.1008153 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zohary E, Shadlen MN, Newsome WT (1994) Correlated neuronal discharge rate and its implications for psychophysical performance. Nature 370:140–143. 10.1038/370140a0 [DOI] [PubMed] [Google Scholar]