Abstract
Significance Statement
Changes in albuminuria and GFR slope are individually used as surrogate end points in clinical trials of CKD progression, and studies have demonstrated that each is associated with treatment effects on clinical end points. In this study, the authors sought to develop a conceptual framework that combines both surrogate end points to better predict treatment effects on clinical end points in Phase 2 trials. The results demonstrate that information from the combined treatment effects on albuminuria and GFR slope improves the prediction of treatment effects on the clinical end point for Phase 2 trials with sample sizes between 100 and 200 patients and duration of follow-up ranging from 1 to 2 years. These findings may help inform design of clinical trials for interventions aimed at slowing CKD progression.
Background
Changes in log urinary albumin-to-creatinine ratio (UACR) and GFR slope are individually used as surrogate end points in clinical trials of CKD progression. Whether combining these surrogate end points might strengthen inferences about clinical benefit is unknown.
Methods
Using Bayesian meta-regressions across 41 randomized trials of CKD progression, we characterized the combined relationship between the treatment effects on the clinical end point (sustained doubling of serum creatinine, GFR <15 ml/min per 1.73 m2, or kidney failure) and treatment effects on UACR change and chronic GFR slope after 3 months. We applied the results to the design of Phase 2 trials on the basis of UACR change and chronic GFR slope in combination.
Results
Treatment effects on the clinical end point were strongly associated with the combination of treatment effects on UACR change and chronic slope. The posterior median meta-regression coefficients for treatment effects were −0.41 (95% Bayesian Credible Interval, −0.64 to −0.17) per 1 ml/min per 1.73 m2 per year for the treatment effect on GFR slope and −0.06 (95% Bayesian Credible Interval, −0.90 to 0.77) for the treatment effect on UACR change. The predicted probability of clinical benefit when considering both surrogates was determined primarily by estimated treatment effects on UACR when sample size was small (approximately 60 patients per treatment arm) and follow-up brief (approximately 1 year), with the importance of GFR slope increasing for larger sample sizes and longer follow-up.
Conclusions
In Phase 2 trials of CKD with sample sizes of 100–200 patients per arm and follow-up between 1 and 2 years, combining information from treatment effects on UACR change and GFR slope improved the prediction of treatment effects on clinical end points.
Keywords: surrogate end point, albuminuria, glomerular filtration rate, kidney failure, clinical trial, biomarkers, chronic kidney disease
Introduction
Developing new therapies for patients with CKD is challenging since established clinical end points, doubling of serum creatinine or kidney failure with replacement therapy, can take a long time to manifest in many patients. Accordingly, large clinical trials recruiting patients with advanced stage or rapidly progressive CKD are required to accrue sufficient end points to properly establish drug efficacy. Valid surrogate end points can help to facilitate clinical trial conduct and can also be used to assess the efficacy of new therapies in earlier stages of CKD.
Changes in urinary albumin-to-creatinine ratio (UACR) and GFR slope are commonly used as end points in Phase 2 clinical trials of CKD progression. Previous trial-level analyses have supported the validity of these end points by demonstrating that treatment effects on UACR or GFR slope are associated with treatment effects on the established clinical end point.1–3 Treatment effects on GFR slope are more predictive of treatment effects on the clinical end point than treatment effects on UACR. This greater predictive accuracy for GFR slope must be weighed against the potential complexities of using GFR slope, particularly the common requirement for longer follow-up time for many trial settings, and the frequently encountered initial effect of the intervention on GFR (i.e., the acute effect) which may differ from the intervention's longer term effect.
The contrasting strengths and limitations of change in UACR and GFR-based surrogate end points raise the possibility to develop a strategy that allows for incorporation of both surrogate end points to strengthen inferences concerning clinical benefit. We here describe a two-part approach for the design and analysis of phase II clinical trials on the basis of the combined use of change in UACR and GFR slope. We first develop a multivariate meta-regression model that relates treatment effects on early change in UACR, GFR slope, and the clinical end point to each other. Subsequently, we apply this multivariate meta-regression to the design and analysis of Phase 2 clinical trials of 1–2-year duration to assess the implications for using the surrogates jointly in decision making to advance to a Phase 3 trial. These results can be used as impetus for the design and evaluation of future Phase 2 clinical trials.
Methods
Systematic Review and Datasets
As previously described, randomized controlled trials (RCTs) of CKD progression were identified using a systematic search, and individual patient data from the identified clinical trials were obtained and analyzed at Tufts Medical Center or at the local study sites or shared servers using the same code with the results integrated into the joint analyses across all studies.1 As we have performed previously for RCTs that evaluated more than one intervention (e.g., factorial or 3-arm RCTs), we included a separate randomized treatment comparisons for each independent treatment versus control comparison reported (referred to as studies throughout). We pooled RCTs with fewer than 100 participants that evaluated the same disease and intervention. A priori, we excluded three studies with interventions in which change in albuminuria was not believed to have biologic plausibility as a surrogate end point (nurse coordinated management4,5 and allopurinol6) and studies with UACR data only after 6-month randomization.7–9 These exclusions resulted in a dataset with 41 studies. The Tufts Medical Center Institutional Review Board approved this study.
Surrogate and Clinical End Points
The methods used to measure albuminuria varied among studies, with most studies measuring UACR or urine protein excretion rate. Because guidelines recommend the use of UACR, we converted all urine protein excretion rate measurements to UACR as described earlier.1 GFR was estimated using the Chronic Kidney Disease Epidemiology Collaboration 2009 serum creatinine equation.10 Creatinine was standardized to isotope dilution mass spectroscopy traceable reference methods using direct comparison or was reduced by 5% as described previously.11 The clinical end point was defined as a composite of a sustained doubling of serum creatinine, GFR <15 ml/min per 1.73 m2, or kidney failure with replacement therapy.
Statistical Analyses
Our primary analytic objective was to implement a methodology for combining information from treatment effects on UACR and GFR slope to predict treatment effects on clinical end points by modeling the associations between treatment effects on UACR, chronic GFR slope, and clinical end points. We used a Bayesian approach to enable us to simplify computations and to provide probabilities of benefit on the clinical end point.
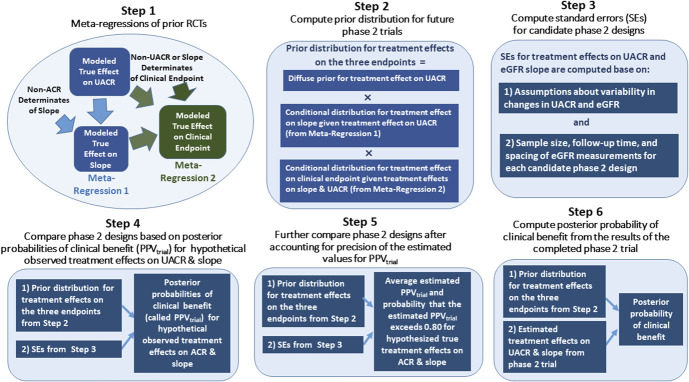
We performed six steps starting with analyses of the relationship between the three end points—UACR, GFR slope, and the clinical end point—in previously conducted RCTs and ending with the design and interpretation of results of a newly conducted hypothetical Phase 2 clinical trial. This Methods section provides a conceptual overview of each of the six steps. A complete analytic presentation of the six steps is provided in the statistical supplement. A schematic overview is presented in Figure 1.
Figure 1.
Study design. PPVtrial, trial-level positive predictive value; RCT, randomized controlled trial; UACR, urinary albumin-to-creatinine ratio. Figure 1 can be viewed in color online at www.jasn.org.
Step 1: Conduct meta-regressions of previous trials. We performed two trial-level meta-regressions on the basis of a two-stage analysis to characterize the relationships among the treatment effects on the three end points.
In the first stage of Step 1, treatment effects on UACR were estimated by applying separate analyses of covariance models for each study to relate the change in the log-transformed UACR from baseline to 6 months to the randomized treatment assignment while controlling for the baseline log UACR. The treatment effects on UACR were expressed as ratios of the 6-month geometric mean UACR levels between the active treatment and control groups with adjustment for baseline log UACR. The treatment effects on GFR slope were estimated using a shared parameter mixed-effects model described previously.2,12 Because interventions designed to slow progression of CKD often produce acute GFR changes that differ from their long-term effects, our mixed model estimated treatment effects on both the chronic GFR slope, defined as the mean rate of change in GFR starting 3 months after randomization, and the total GFR slope, defined as a time-weighted average of the mean GFR slopes during the first three months and over the chronic phase. For this article, we focused on the chronic slope, with treatment effects expressed as differences in the mean GFR slopes between the treatment versus control groups, in units of ml/min per 1.73 m2 per yr. The treatment effects on the clinical end point were estimated by performing separate Cox proportional hazards regression to estimate log hazard ratios (HRs) for the treatment in each RCT. In addition to the estimated treatment effects, the first stage of Step 1 provided the associated SEMs and robust sandwich estimates of the correlations between the estimated effects for each of the three end points.
In the second stage of Step 1, presented in the top left portion of Figure 1, we fit a pair of Bayesian mixed-effects meta-regressions to the results of the first stage with study as the unit of analysis to relate (1) the treatment effects on GFR slope to the treatment effects on UACR and (2) the treatment effects on the clinical end point jointly to the treatment effects on UACR and on GFR slope. These meta-regressions used similar methods to those described in previous publications, and details are described in the statistical supplement.1,2 Taken together, the two meta-regressions describe the relationships between the “true” treatment effects on the clinical end point, GFR slope, and UACR across the previously conducted RCTs. The meta-regression analyses account for varying SDs of the random errors in the estimated effects on the three end points in each RCT and for the correlations of these random errors with each other. As a result, larger trials generally had more influence on the results of our analyses than smaller trials.
Step 2: Construct the prior distribution for the treatment effects in new Phase 2 trials. Step 2 uses the results of Step 1 to construct the joint prior distribution which can be used to estimate the treatment effects on the three end points in new Phase 2 trials. The joint prior distribution is a product of three terms (Step 2 in Figure 1). The first term defines a diffuse, noninformative prior for the treatment effect on UACR which assures that inferences made in the new trial are not influenced by the sizes or directions of the treatment effects on UACR in previous trials. The second term is the conditional distribution for the treatment effect on GFR slope given the treatment effect on UACR. The third term is the conditional distribution of the treatment effect on the clinical end point given the treatment effects on both GFR slope and UACR. The conditional distributions in the second and third terms are provided directly by the two meta-regressions on the basis of previously conducted RCTs from Step 1. Because of this, the application of the conditional distributions to new trials requires the assumption that the relationships among the treatment effects on the surrogate and clinical end points that were observed in the previous RCTs apply also for the relationship between the treatment effects on the surrogate and clinical end points in the new Phase 2 trial. However, no assumptions are required regarding the relationship of treatment effect on UACR in the new trial compared with the previous trials.
Step 3: Estimate SEMs for treatment effects on UACR and GFR slope for candidate designs for the new Phase 2 trial. This step corresponds closely to conventional power calculations that are routinely used for the design of Phase 2 trials that use either UACR or GFR slope as their primary end point. The SEs depend on assumptions about the variability of changes in log UACR and in GFR over time as well as on the characteristics of the Phase 2 trial design. The key design characteristics that influence the SEs are the sample size, the duration of follow-up, and the frequency and spacing of GFR measurements during the follow-up period of the Phase 2 trial. Reflecting previous CKD trials,1,2,13 we computed the SEMs corresponding to five potential Phase 2 designs of different sizes and durations as well as one Phase 3 design assuming that the residual root mean square error for the 6-month log UACR after controlling for baseline log UACR is 0.725, a SD for the “true” chronic GFR slopes of 4 ml/min per 1.73 m2, and a residual SD for the individual GFR measurements of 5.16 ml/min per 1.73 m2. The five designs are as follows: Design A, 60 patients per treatment group with quarterly GFR measurements for 1.25 years; Design B, 120 patients per treatment group with quarterly GFR measurements for 1.25 years; Design C, 120 patients per treatment group with monthly GFR measurements for 1.25 years; Design D, 120 patients per treatment group with quarterly GFR measurements for 2 years; and Design E, 240 patients per treatment group with quarterly GFR measurements for 2 years. In each design, we assume that 2 GFR measurements are obtained at baseline.
Step 4: Compare Phase 2 designs on the basis of posterior probabilities of clinical benefit (denoted trial-level positive predictive value [PPVtrial]) for hypothetical observed treatment effects on UACR and GFR slope. In conventional power calculations, the SEs from Step 3 are used to provide the minimum detectable treatment effects of the candidate designs on UACR and GFR slope themselves. This provides the smallest hypothesized treatment effects which are required to provide the desired power (usually 80% or 90%) to demonstrate that the true effects on the UACR or GFR slope end points differ by any amount from the null hypothesis of 0, including very small differences which are too small to provide confidence in clinical benefit. When we are considering UACR and GFR slope as surrogate end points to determine whether to proceed to a Phase 3 trial, it is also of interest to assess whether the treatment effects on UACR and GFR slope are not only nonzero but also sufficiently large to provide confidence that the treatment will ultimately provide a clinical benefit.
Step 4 applies the SEMs from Step 3 in conjunction with the prior distribution from Step 2 to compute the Bayesian posterior probability of a benefit on the clinical end point across a range of hypothetical values for the observed treatment effects on UACR and GFR slope in the Phase 2 trial. We consider three thresholds for clinical benefit: A HR <1 for the clinical end point, in which case any benefit is considered important, no matter how small, and HRs <0.9 and <0.8, in which case we only consider treatments that reduce the hazard by at least 10% or 20%, respectively, to be clinically useful.
The posterior probability of benefit on the true clinical end point is analogous to the positive predictive value in diagnostic testing. In this analogy, a true treatment benefit in the newly conducted trial substitutes for the presence of true disease in the patient, the observed treatment effects on the surrogate end points substitute for the diagnostic test results, and the prior distribution which relates the treatment effects on the clinical and surrogate end points from Step 2 substitutes for the disease prevalence. Accordingly, we refer to the posterior probability of benefit on the clinical end point as the PPVtrial, denoted by PPVtrial, to stress the reference to an entire trial rather than an individual patient. Figure 2 compares PPVtrial between the five designs described in Step 3.
Figure 2.
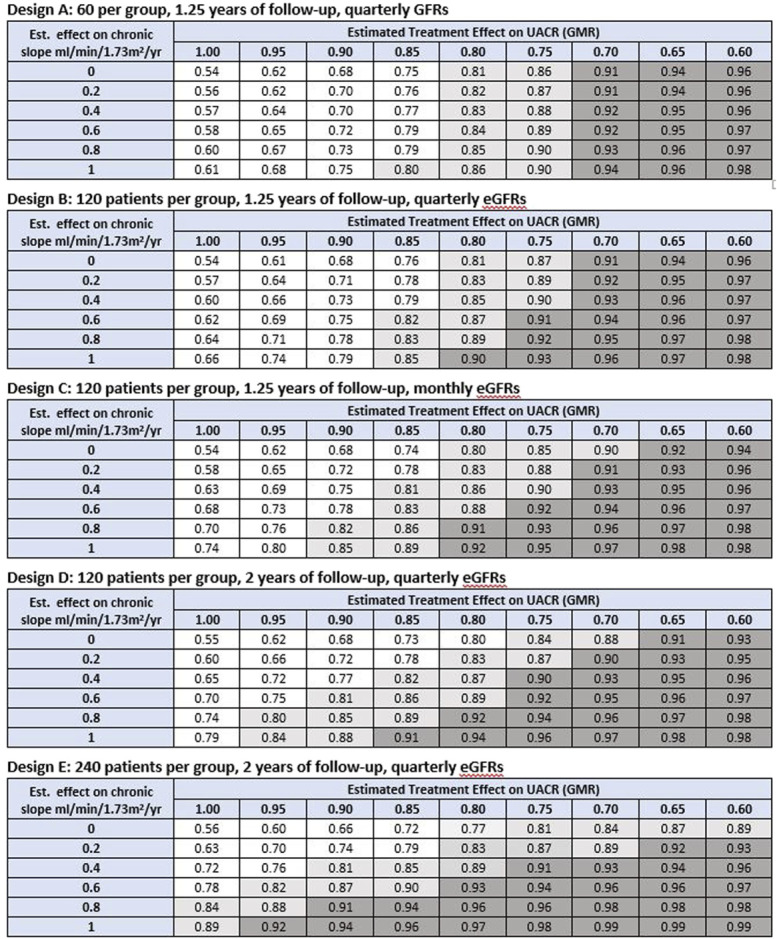
PPVtrial on the basis observed treatment effects on UACR and slope to infer clinical benefit defined as HR<1. Shown are the PPVtrial for inferring clinical benefit defined as a HR for the clinical end point which is <1 based on combinations of observed treatment effects on slope and ACR in the Phase 2 trial. The unshaded region designates values for PPVtrial <0.80. The light shaded region indicates values of PPVtrial between 0.80 and 0.90. The dark shaded region indicates PPVtrial ≥0.90. If PPVtrial is estimated based on the treatment effect on UACR alone, under design 1, the average positive predictive values are 0.54, 0.61, 0.67, 0.73, 0.79, 0.86, 0.90, 0.94, and 0.96 for true GMRs ranging from 1.00 to 0.60, respectively. Under designs 2–4, the corresponding values are 0.53, 0.61, 0.69, 0.77, 0.84, 0.88, 0.92, 0.95, and 0.97, respectively. Under design 5, the corresponding values for PPVtrial are 0.53, 0.62, 0.7, 0.78, 0.85, 0.90, 0.94, 0.96, and 0.98. GMR, geometric mean ratio; HR, hazard ratio; PPVtrial, trial-level positive predictive value; UACR, urine albumin-to-creatinine ratio. Figure 2 can be viewed in color online at www.jasn.org.
Step 5: Compare Phase 2 designs for the sampling distribution of the estimated values for PPVtrial. From the standpoint of study design, a limitation of Step 4 is that the values of PPVtrial are computed for estimated treatment effects on UACR and GFR slope which themselves can contain substantial random sampling error, particularly for smaller Phase 2 trials. Step 5 addresses this limitation by providing two quantities which are derived from the sampling distribution of the estimated values for PPVtrial but which are computed at hypothesized true values for the true treatment effects on UACR and GFR slope.
First, given a specific combination of hypothesized true treatment effects on UACR and GFR slope, we provide the average estimated value of PPVtrial after accounting for the random variation in the estimated treatment effects around the hypothesized true effects. We perform this calculation across the range of combinations of hypothesized true treatment effects on UACR and GFR slope. A good Phase 2 design from the surrogate end point perspective will have sufficient sample size, duration, and frequency of GFR measurements to demonstrate both a low average estimated PPVtrial under the null hypothesis of no effect on both UACR and GFR slope and a high average estimated PPVtrial under plausible research hypotheses for treatment benefit on the two surrogates. Figure 3 compares the average estimated PPVtrial across the five designs.
Figure 3.
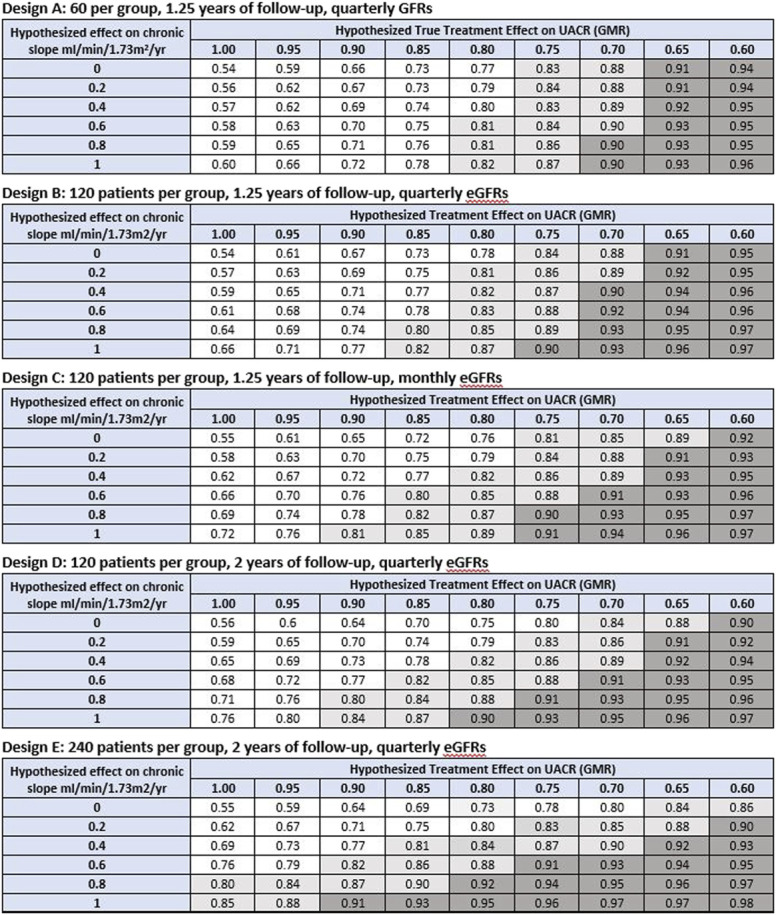
Average estimated PPVtrial to infer clinical benefit defined as HR <1. Shown are the average estimated values of PPVtrial for inferring clinical benefit defined as a HR for the clinical end point which is <1 based on combinations of hypothesized true treatment effects on slope and UACR. The estimated values for PPVtrial are averaged over the sampling distributions for the estimated treatment effects on slope and ACR given the true hypothesized treatment effects on these end points. The unshaded region designates average estimated PPVtrial <0.80. The light shaded region indicates average estimated PPVtrial between 0.80 and 0.90. The dark shaded region indicates average estimated PPVtrial ≥0.90. If the average estimated PPVtrial is computed based on the treatment effect on UACR alone, under design 1, the average estimated PPVtrial values are 0.55, 0.61, 0.68, 0.76, 0.83, 0.89, 0.92, 0.96, and 0.97 for observed GMRs ranging from 1.00 to 0.60, respectively. Under designs 2–4, the corresponding values are 0.53, 0.62, 0.70, 0.78, 0.85, 0.90, 0.94, 0.96, and 0.98, respectively. Under Design 5, the corresponding average estimated PPVtrial values are 0.54, 0.62, 0.70, 0.79, 0.86, 0.91, 0.95, 0.97, and 0.98. GMR, geometric mean ratio; HR, hazard ratio; PPVtrial, trial-level positive predictive value; UACR, urine albumin-to-creatinine ratio. Figure 3 can be viewed in color online at www.jasn.org.
Second, given a specific combination of hypothesized true effects on UACR and GFR slope, we compute the probability that the estimated PPVtrial exceeds a target level, such as 0.85, which is deemed sufficient to proceed to a Phase 3 trial. We can view the probability that the estimated PPVtrial exceeds the target threshold as an analog of Type 1 error for the surrogate end point setting under the null hypothesis of no effects on either surrogate and as an analog of statistical power for the surrogate end point setting when favorable treatment effects are hypothesized for the two surrogates. Figure 4 illustrates the probabilities that the estimated PPVtrial exceeds 0.85 for the five designs.
Figure 4.
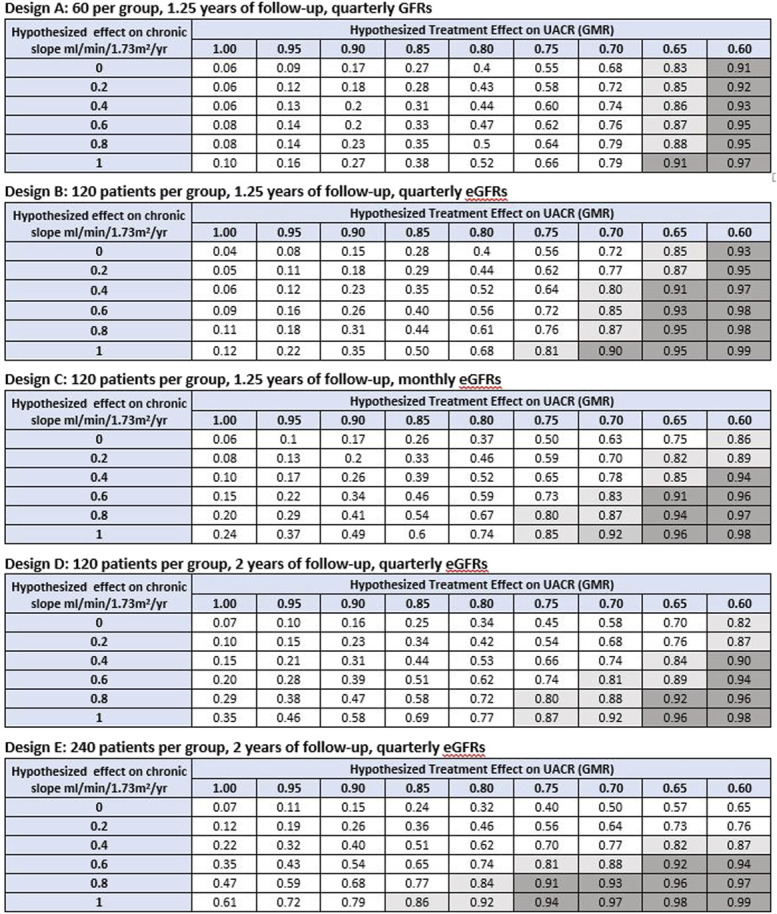
Probability of demonstrating clinical benefit given hypothesized treatment effects on UACR and GFR slope. Clinical benefit defined by a PPVtrial ≥0.85 for inferring a HR <1 for the clinical end point. Shown are the probabilities under alternative Phase 2 designs for obtaining an estimated trial-level positive predictive value (PPVtrial) >0.85 for demonstrating clinical benefit defined as a HR for the clinical end point which is <1 based on combinations of hypothesized true treatment effects on slope and UACR. A total of five Phase 2 designs are considered, with sample size ranging from 60 to 240 patients per group, follow-up time ranging from 1.25 to 2 years, and GFR measurements obtained quarterly or monthly. The probability of demonstrating clinical benefit can be viewed as Type 1 error when the hypothesized treatment effects on both slope and UACR are null (given by the cell in the upper left corner of each table) and as an analog of statistical power relevant to surrogate end points for non-null hypotheses on one or both surrogate end points. The unshaded region designates probabilities of <0.80 for demonstrating a PPVtrial >0.85. The light shaded region indicates probabilities between 0.80 and 0.90 for demonstrating a PPVtrial >0.85. The dark shaded region indicates probabilities ≥0.90 for demonstrating a PPVtrial >0.85. For comparison, under conventional power calculations for testing the null hypotheses that treatment effects on UACR or GFR slope are identical to 0, the minimum detectable treatment effects for UACR are 35.4% under Design A, 26.3% under Designs B-D, and 19.4% under Design E. The minimum detectable treatment effects for GFR slope are 4.73, 3.31, 2.57, 2.23, and 1.57 ml/min per 1.73 m2 per yr, respectively. As noted in the methods section, the minimum detectable effects under conventional power calculations provide information about the smallest effects necessary to demonstrate that effects on UACR or slope differ from 0 but do not indicate whether these nonzero effects are large enough to provide evidence of clinical benefit. GMR, geometric mean ratio; HR, hazard ratio; PPVtrial, trial-level positive predictive value; UACR, urine albumin-to-creatinine ratio. Figure 4 can be viewed in color online at www.jasn.org.
Step 6: Use Bayesian computations to estimate the posterior probability of clinical benefit given the observed treatment effects on the two surrogate end points in the Phase 2 trial. Whereas Steps 4 and 5 are implemented during the design phase of the Phase 2 trial, before enrollment of patients, Step 6 is implemented after the completion of the Phase 2 trial to interpret the actual results from the trial. Step 6 uses the same Bayesian calculations as Steps 4 and 5, but in this case, the posterior probability of clinical benefit is computed from the treatment effects which are actually observed at the completion of the Phase 2 trial.
Results
Study Characteristics
The 41 RCTs included in this study enrolled 29,979 participants that had at least one UACR measurement within 6 months after randomization. Aggregate characteristics of included studies stratified by disease are summarized in Supplemental Table 1. The median baseline UACR was 272 mg/g (2.5th to 97.5th Percentile [P]: 30–1134 mg/g), and the mean baseline GFR was 58.2 ml/min per 1.73 m2 (SD: 25.0). There were ten studies of participants with diabetes (6 of which had participants with CKD), nine studies of participants in whom the cause of kidney disease was glomerular, six in whom it was hypertension or polycystic kidney disease, and 16 where the cause could not be specified.
Meta-Regression Relating Treatment Effects on Albuminuria and GFR Slope to Treatment Effects on the Established Kidney End Point
Across the 41 RCTs, compared with the control treatment arm, under the Bayesian joint model, the active treatment resulted in a 24% decrease in hazard of the clinical end point % (average HR 0.76, 95% Bayesian Credible Interval [BCI] 0.67–0.85). Compared with the control treatment arm, the active treatment reduced the mean rate of the chronic GFR decline by 0.63, 95% BCI (0.38, 0.89) ml/min per 1.73 m2 per yr, and reduced the geometric mean UACR by 22%, 95% BCI (17%, 26%).
Table 1 presents the means and SDs of the treatment effects on each of the three end points and the parameters for the two meta-regressions that define the joint model relating the treatment effects on the clinical end point, GFR slope, and change in UACR. In the meta-regression establishing the relationship between combined treatment effects on GFR slope and UACR with the clinical end point, the posterior median intercept was −0.03 (95% BCI −0.21 to 0.14), indicating that the model predicts a neutral treatment effect for the clinical end point when the treatment effects on the two surrogates are equal to 0 (Table 1). The median meta-regression coefficients were −0.41 (95% BCI −0.64 to −0.17) per 1 ml/min per 1.73 m2 per yr for the treatment effect on the chronic slope and −0.06 (95% BCI −0.90 to 0.77) for the treatment effect on log UACR, indicating that the chronic GFR slope contributed to a larger extent than log UACR to the prediction of the treatment effect on the clinical end point (Table 1). The median R2 was 0.93 for joint meta-regression of treatment effects on the clinical end point versus treatment effects on the chronic slope and log UACR. The joint model also established the relationship between “true” treatment effects on UACR and GFR slope, which showed a median intercept of −0.04 (95% BCI −0.56 to 0.44) and a coefficient of −2.74 (95% BCI −4.71 to −0.96) ml/min/1.73 m2 per yr. The relationship between treatment effects on the clinical end point and GFR slope for various treatment effects on UACR is presented in Supplemental Figure 1.
Table 1.
Treatment effects and meta-regression parameters
| Meta-Regression Parameters | Mean | SD | 2.5th Percentile | 25th Percentile | 50th Percentile | 75th Percentile | 97.5th Percentile |
|---|---|---|---|---|---|---|---|
| Means and SDs of treatment effects on the three end points | |||||||
| Mean treatment effect on clinical end point (log HR) | −0.28 | 0.06 | −0.40 | −0.31 | −0.27 | −0.24 | −0.16 |
| SD for treatment effects on clinical end point (log HR) | 0.28 | 0.07 | 0.16 | 0.23 | 0.27 | 0.32 | 0.42 |
| Mean treatment effect on chronic slope (ml/min per 1.73 m2 per yr) | 0.63 | 0.13 | 0.38 | 0.54 | 0.63 | 0.72 | 0.89 |
| SD for treatment effects on chronic slope (ml/min per 1.73 m2 per yr) | 0.65 | 0.13 | 0.43 | 0.56 | 0.64 | 0.73 | 0.93 |
| Mean treatment effect on log UACR | −0.25 | 0.03 | −0.30 | −0.26 | −0.25 | −0.23 | −0.19 |
| SD for treatment effects on log UACR | 0.15 | 0.03 | 0.10 | 0.13 | 0.15 | 0.17 | 0.21 |
| Meta-regression relating treatment effects on CE jointly to treatment effects on chronic slope and UACR | |||||||
| Intercept | −0.03 | 0.09 | −0.21 | −0.09 | −0.03 | 0.03 | 0.14 |
| Coefficient of treatment effect on chronic slope | −0.41 | 0.12 | −0.64 | −0.49 | −0.41 | −0.34 | −0.17 |
| Coefficient of treatment effect on log UACR | −0.06 | 0.42 | −0.90 | −0.33 | −0.06 | 0.21 | 0.77 |
| RMSE | 0.08 | 0.04 | 0.02 | 0.04 | 0.07 | 0.11 | 0.18 |
| R2 | 0.88 | 0.13 | 0.54 | 0.83 | 0.93 | 0.98 | 1.00 |
| Meta-regression relating treatment effects on chronic slope to treatment effects on UACR | |||||||
| Intercept | −0.04 | 0.25 | −0.56 | −0.20 | −0.04 | 0.12 | 0.44 |
| Coefficient of treatment effects on log UACR | −2.76 | 0.95 | −4.71 | −3.36 | −2.74 | −2.13 | −0.96 |
| R2 | 0.42 | 0.18 | 0.06 | 0.29 | 0.43 | 0.56 | 0.75 |
Shown are the mean and SDs as well as the 2.5th, 25th, 50th, 75th, and 97.5th percentiles of the posterior distributions of the treatment effects and the meta-regression parameters that define the joint model. The top panel summarizes the posterior distributions of the means and SDs of the treatment effects on the three end points. The middle panel summarizes the meta-regression coefficients for the joint meta-regression relating the treatment effects on the clinical end point to the treatment effects on both the chronic slope and UACR. The bottom panel summarizes the meta-regression coefficients relating the treatment effects on the chronic slope to the treatment effects on log UACR. HR, hazard ratio; UACR, urine albumin-to-creatinine ratio; RMSE, root mean square error; R2, squared multiple correlation.
PPVtrial on the Basis of Observed Treatment Effects on UACR and Slope
We subsequently examine the implications of the joint model that incorporated treatment effects on UACR and GFR slope to inform the design of Phase 2 clinical trials. The five panels of Figure 2 display PPVtrial for the five designs given hypothetical combinations of treatment effects on UACR and GFR slope which are observed after the Phase 2 trial is completed. As expected, for each of the five designs, PPVtrial increases, indicating a higher likelihood of a favorable effect on the clinical end point, with larger treatment effects on GFR slope and change in UACR. The values of PPVtrial are driven almost entirely by UACR when the sample size is small and the follow-up is short, but the importance of GFR slope increases when the sample size and follow-up times increase. For comparison, the figure legend provides the values of PPVtrial if the model is applied to UACR only, ignoring GFR slope. In an example, Phase 3 design with 600 patients per treatment group and a 2-year follow-up, the PPVtrial is determined almost exclusively by GFR slope (Supplemental Figure 4).
As expected, larger observed effects on the two surrogates are required to provide high values for PPVtrial when clinical benefit was defined as HR <0.8 or <0.9 (Supplemental Figures 2 and 3).
Average Estimated PPVtrial on the Basis of Hypothesized True Treatment Effects on UACR and GFR Slope
Figure 3 presents the projected average estimated PPVtrial for the five Phase 2 designs for the same combinations of treatment effects on UACR and GFR slope that were presented in Figure 2, but in this case, the effects represent hypothesized true treatment effects rather than estimated effects. Similar to what was found with the use of observed treatment effects, the average estimated PPVtrial is driven almost entirely by UACR when the sample size is small and the follow-up is short, with the importance of GFR slope increasing when the sample size and follow-up times increase. In most cases, the average estimated PPVtrial on the basis of a particular combination of hypothesized true treatment effects in Figure 3 is slightly smaller than the PPVtrial at these corresponding observed treatment effects on slope and UACR in Figure 2. This reduction reflects the added uncertainty resulting from the variability of the estimated treatment effects around the true treatment effects in the Phase 2 trial. Supplemental Figures 5 and 6 show the average estimated PPVtrial for hypothesized true treatment effects on UACR and GFR slope when clinical benefit is defined as a HR of 0.9 or 0.8, respectively.
Probability of Inferring Clinical Benefit on the Basis of Hypothesized True Treatment Effects on UACR and Slope
Figure 4 presents the probabilities that the estimated value for PPVtrial exceeds 0.85 for the same set of treatment effects on UACR and slope presented in Figures 2 and 3. These probabilities can be interpreted as an analog of statistical power for demonstrating clinical benefit on the basis of surrogate end points. Comparison of Figures 2 and 4 shows that the sizes of the hypothesized true treatment effects required to assure an 80% probability of reaching a target PPVtrial of 0.85 are considerably larger than the sizes of observed treatment effects required to reach the same value for PPVtrial. This reflects the sampling error in the estimated treatment effects; the true treatment effects must be more favorable than the estimated effects to assure a high probability that the estimated effects fall into a range that provides high confidence of a benefit on the clinical end point.
These calculations can also be used to compute the minimum sample size necessary to achieve a desired statistical power for demonstrating that PPVtrial exceeds a target threshold, which is calibrated, so that the threshold is exceeded by PPVtrial with probability 0.05 under the joint null hypothesis of no effect on either surrogate end point. For example, if a moderate treatment effect of 22.5% is hypothesized for the treatment effect on UACR, the minimum sample size per group required for 80% power to achieve the designated PPVtrial threshold in a 2-year trial with quarterly GFR assessments is 102 patients per group if the hypothesized treatment effect on the chronic GFR slope is 0.8 ml/min per 1.73 m2 per yr and 470 patients per group if the hypothesized treatment effect on the chronic GFR slope is 0.6 ml/min per 1.73 m2 per yr.
Discussion
We have previously demonstrated that the treatment effects on change in albuminuria and GFR slope, both commonly used and accepted end points in Phase 2 trials of CKD progression, are associated with the treatment effects on clinical end points. In this study, we extend these findings and develop a strategy to define the probability of benefit on the clinical end point by incorporating information from both surrogates. We demonstrated that combining information from both treatment effects on albuminuria and GFR slope does improve the prediction of treatment effects on the clinical end point for Phase 2 trials of moderate sample sizes or duration of follow-up ranging between 1 and 2 years, whereas in smaller Phase 2 trials of short duration, the prediction of clinical benefit was almost exclusively due to the treatment effects on albuminuria. The contribution of GFR slope increases when the sample sizes or duration of follow-up increases. These results may help inform design of clinical trials for interventions aimed at slowing CKD progression.
GFR slope has been proposed to be a better surrogate end point than albuminuria because it is more directly related to kidney failure and occurs in all patients with CKD regardless of cause of kidney disease. Indeed, a patient must experience a decline in GFR to develop kidney failure. Observational studies and clinical trials have demonstrated substantially stronger associations between changes in GFR and a clinical end point and between treatment effects on GFR slope and treatment effects on the clinical end point, than similar comparisons with albuminuria.2,14 However, compared with albuminuria, estimating the effect of a treatment on GFR slope requires larger studies of longer duration. Furthermore, acute effects, which are frequently observed, complicate the utility of GFR slope. These challenges may limit the use of GFR slope in Phase 2 studies. Conversely, albuminuria is only applicable for interventions whose mechanism of action goes through albuminuria and the strength of the relationship between early treatment effects on albuminuria and clinical end points is weaker than GFR slope. Thus, for interventions that work through albuminuria and for study populations with some minimal level of albuminuria, the complementary strengths and limitations of both surrogates provide an opportunity to combine both to improve the prediction of treatment effects on clinical end points. This notion is supported by observational studies demonstrating that the combination of albuminuria change and GFR slope improves prediction of clinical end points compared with each risk marker alone.15
The effect of an intervention on total GFR slope from baseline to a time point late in this study reflects the combination of the immediate or acute effect and the effect during the subsequent chronic phase. Acute effects are often believed to be reversible after treatment cessation and not related to the mechanism of action of the drug on CKD progression. In the present analyses, we elected to model the treatment effect on chronic GFR slope because the treatment effect on the chronic slope reflects the loss of functioning nephrons and may be subject to less confounding by potential reversible acute effects on GFR. In addition, for studies of <24-month duration, acute effects would limit the ability to use the total slope. Future studies can help to inform as to whether total GFR slope, that incorporates acute and chronic effects, provides any additional information beyond albuminuria change on prediction of clinical benefit. It is possible that drugs that have an acute effect on GFR but do not have beneficial effects on albuminuria are less likely to lead to clinical benefit than drugs with an acute effect and benefit on albuminuria.
The results of our study have implications for future Phase 2 and Phase 3 clinical trials of new interventions to slow CKD progression. First, typical Phase 2 dose-finding studies for interventions intended to slow progression of CKD generally last 6 months and recruit 100 to 200 patients per treatment arm.16,17 We demonstrated that change in albuminuria is a preferred end point for studies of this duration and size and could be used for dose selection and decision making to proceed to a confirmatory trial for interventions that work through albuminuria and populations with increased albuminuria. For some drug development programs evaluating interventions with mechanisms of action not previously studied or in those where there is uncertainty concerning the extent to which the drug's mechanisms of action for slowing CKD progression is reflected in an early change in albuminuria, incorporating information from GFR slope will improve the prediction of clinical benefit and inform decision making to proceed to a confirmatory Phase 3 trial. As preliminary evidence that our proposed method can be used, these results have been included in the design and analysis of at least two Phase 2 clinical trials with drug classes not included in our analysis (e.g., NCT04419467). The primary end point in these trials was albuminuria assessed after 6 months. However, participants were followed for 12 months to assess the effects on GFR slope. The strategy described in this article is used to combine effects on albuminuria and GFR slope to estimate the probability of clinical benefit and to help inform a go/no-go decision to proceed to a Phase 3 trial. The results of these studies will provide more insight into the applicability of our approach to novel interventions and populations and will likely support implementation in future Phase 2 clinical trials.16
The results of this study may also have implications for trials evaluating interventions to slow progression in rare kidney diseases. In rare kidney diseases, albuminuria has been accepted as a surrogate end point to grant accelerated approval by drug regulation agencies followed by full approval if the intervention slows GFR decline during prolonged treatment and is safe and well-tolerated.18–21 At the time when albuminuria data have been collected and dossiers are prepared for accelerated regulatory approval, GFR data are often available but insufficient to determine drug efficacy because of the short follow-up duration. The joint model we developed allows investigators to combine albuminuria and GFR slope data to strengthen inferences about potential beneficial drug effects on clinical end points taking advantage of both surrogate end points. The joined information from both surrogates can thus inform trialists and drug regulatory officers to improve their benefit-risk assessment.
We presented three metrics which may be used in the design phase of a Phase 2 trial when the objective is to incorporate information from both albuminuria and GFR slope to assess the likelihood of clinical benefit. The first metric, denoted PPVtrial, provides the posterior probability of benefit on the clinical end point corresponding to combinations of hypothetical values for the observed treatment effects on UACR and GFR slope. The second metric, average estimated PPVtrial, provides similar information to PPVtrial but is the average of the sampling distribution of the PPVtrial over the estimated treatment effects on UACR and GFR slope. The third metric provides the probability of obtaining a sufficiently large estimated PPVtrial for inferring a benefit on the clinical end point to warrant proceeding to a Phase 3 trial. All three metrics can be used by investigators to compare and select between alternative Phase 2 designs. We emphasize that the calculation of the probability of obtaining a sufficiently large PPVtrial to proceed to a Phase 3 trial differs fundamentally from conventional power calculations. A conventional power calculation with albuminuria (or GFR slope) as the end point provides information as to how large a study should be to infer a nonzero benefit on albuminuria (or GFR slope) itself. The bar is considerably higher when we seek to demonstrate a high probability of clinical benefit on the basis of the surrogate end points, as we must demonstrate not just that the effects of the treatment on the surrogates are nonzero but also that they are sufficiently large to infer clinical benefit.
Strengths of this study include a large and diverse collection of RCTs identified through a systematic literature search and a rigorous evaluation using individual patient data. Because we analyzed patient-level data, we were able to characterize agreement between treatment effects on albuminuria, GFR slope, and clinical end points after adjusting for spurious correlations in sampling error that resulted from inclusion of the same GFR measurements in the GFR slope and clinical end points. In addition, we applied a uniform analysis of GFR slope across all RCTs by using a robust method for analysis of GFR slope that accounted for informative censoring and multiple potential sources of variability in GFR measurements over time. The developed Bayesian meta-regression model with diffuse prior distributions for albuminuria allowed us to rigorously account for multiple sources of uncertainty and to translate treatment effects on the surrogate end points to probabilities of benefit on the clinical end point.
There are also several limitations. First, we used studies mostly with 3 years of follow-up to estimate treatment effect on GFR slope but then apply these estimates to treatment effects for shorter studies expected in Phase 2 clinical trials which may have led to an overestimation of the precision of treatment estimates on GFR slope. However, in previous work, we demonstrated that chronic slope estimated over 24 months provided similar results as that estimated over the study duration.22 Second, our joint model represents the treatment effect on GFR slope solely through the effect of the treatment on the chronic slope, and the performance of the chronic slope as a surrogate may be reduced in trials with large acute effects. Subsequent work should extend the joint model considered in this article to relate the treatment effect on the clinical end point jointly to the treatment effects on UACR as well as both the acute and chronic slopes. Third, we assume that the relationships among the treatment effects on the surrogate and clinical end points that were observed in the previous RCTs apply also for the relationship between the treatment effects on the surrogate and clinical end points in the new Phase 2 trial. This assumption requires that past relationships among the end points are applicable to future drugs with novel mechanisms of interaction which may not always be true. Fourth, monthly GFR assessments increase the precision of the treatment effect estimate on GFR slope, and we showed that in settings where the drug slows GFR decline, it increases PPVtrial compared with quarterly GFR assessments. However, this advantage needs to be balanced with operational and practical aspects as monthly GFR assessment is cumbersome for trial participants and may decrease interest in participation. Fifth, while our analyses account for the estimated SEMs of the estimated treatment effects on the surrogate and clinical end points within each trial, we do not account for uncertainty in the estimates of the SEMs themselves. Our approach is consistent with most published meta-analyses. Finally, we use a linear model to combine GFR slope and albuminuria. Additional work is needed to relax the assumptions in the trial-level analysis.
In conclusion, we developed a trial-level meta-regression model relating a clinical end point to two surrogate end points to guide the design of a Phase 2 clinical trials in the setting of CKD. The model demonstrated that with sample sizes between 100 and 200 patients per group or follow-up times ranging between 1 and 2 years combining the information from treatment effects on UACR change and GFR slope improved the prediction of treatment effects on clinical end points.
Supplementary Material
Acknowledgements
We thank all investigators, study teams, and participants of the studies included in the meta-analysis. A variety of sources have supported the RCTs included in the CKD-EPI CT. These funding sources include government agencies such as national institutes of health and medical research councils as well as foundations and industry sponsors listed in Appendix 1 in the supplement. The HALT-PKD Study A and B were conducted by the HALT-PKD Study Investigators and supported by the National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK). The data from this study reported here were supplied by the NIDDK Central Repository. The manuscript does not necessarily reflect the opinions or views of the HALT-PKD Study, the NIDDK Central Repository, or the NIDDK. This work received support from the Utah Study Design and Biostatistics Center, with funding in part from the National Center for Advancing Translational Sciences of the National Institutes of Health under Award No. UL1TR002538.
CKD-EPI investigators/collaborators are listed with their affiliations here:
AASK: Tom Greene;
ABCD: Robert W. Schrier, Rebecca Hanratty;
AIPRI (Maschio): Giuseppe Maschio, Francesco Locatelli;
ALTITUDE: Hans-Henrik Parving;
Bari (Schena): Manno Carlo;
Bologna (Zucchelli): Pietro Zucchelli (deceased), Mauro Saddelli;
Boston (Brenner): Barry M. Brenner;
Copenhagen (Kamper): Anne-Lise Kamper, Svend Strandgaard;
CSG (Lewis 1992, 1993): Edmund Lewis;
EMPA-REG OUTCOME: Christoph Wanner; Maximilian von Eynatten;
Groningen (van Essen): Paul E. de Jong, GG van Essen, Dick de Zeeuw;
Guangzhou (Hou): Fan Fan Hou;
HALT-PKD: Arlene Chapman, Vicente Torres, Alan Yu, Godela Brosnahan;
HKVIN: Kai-Ming Chow, Cheuk-Chun Szeto, Chi-Bon Leung;
IDNT: Lawrence G. Hunsicker, Jamie Dwyer, Marc Pohl, Itamar Raz;
Lecco (Pozzi): Lucia Del Vecchio, Simeone Andrulli, Claudio Pozzi, Donatella Casartelli;
Leuven (Maes): Thomas Malfait, An Vanacker;
Madrid (Praga): Fernando Caravaca-Fontán, Hernando Trujillo, Teresa Cavero, Eduardo Gutierrez;
MDRD Study: Gerald Beck, John Kusek, Garabed Eknoyan;
Milan (Ponticelli): Claudio Ponticelli, Giuseppe Montagnino, Patrizia Passerini, Gabriella Moroni;
ORIENT: Fumiaki Kobayashi, Hirofumi Makino, Sadayoshi Ito, Juliana CN Chan;
Hong Kong Lupus Nephritis (Chan): Colin Tang;
REIN: Flavio Gaspari, Maria Domenica Lesti, Giulia Gherardi, Sara Gamba;
RENAAL: Dick De Zeeuw, William Keane;
ROAD: Fan Fan Hou;
Rochester (Donadio): James Donadio;
STOP-IgAN: Thomas Rauen, Claudia Seikrit, Stefanie Wied, Jürgen Floege;
SUN-MACRO: Jamie Dwyer, Edmund Lewis;
Victoria (Ihle): Gavin J. Becker, Benno U. Ihle, Priscilla S. Kincaid-Smith.
Footnotes
CKD-EPI CT members include: Robert W. Schrier, Rebecca Hanratty, Giuseppe Maschio, Manno Carlo, Mauro Saddelli, Barry M. Brenner, Edmund Lewis, Maximilian von Eynatten, Paul E. de Jong, GG van Essen, Fan Fan Hou, Arlene Chapman, Vicente Torres, Alan Yu, Godela Brosnahan, Kai-Ming Chow, Cheuk-Chun Szeto, Chi-Bon Leung, Lawrence G. Hunsicker, Jamie Dwyer, Marc Pohl, Itamar Raz, Lucia Del Vecchio, Simeone Andrulli, Claudio Pozzi, Donatella Casartelli, Thomas Malfait, An Vanacker, Fernando Caravaca-Fontán, Hernando Trujillo, Teresa Cavero, Eduardo Gutierrez, Gerald Beck, John Kusek, Garabed Eknoyan, Claudio Ponticelli, Giuseppe Montagnino, Patrizia Passerini, Gabriella Moroni, Fumiaki Kobayashi, Hirofumi Makino, Sadayoshi Ito, Juliana CN Chan, Colin Tang, Flavio Gaspari, Maria Domenica Lesti, Giulia Gherardi, Sara Gamba, William Keane, James Donadio, Thomas Rauen, Claudia Seikrit, Stefanie Wied, Jamie Dwyer, and Gavin J. Becker.
Contributor Information
Collaborators: Robert W. Schrier, Rebecca Hanratty, Giuseppe Maschio, Manno Carlo, Mauro Saddelli, Barry M. Brenner, Edmund Lewis, Maximilian von Eynatten, Paul E. de Jong, GG van Essen, Fan Fan Hou, Arlene Chapman, Vicente Torres, Alan Yu, Godela Brosnahan, Kai-Ming Chow, Cheuk-Chun Szeto, Chi-Bon Leung, Lawrence G. Hunsicker, Jamie Dwyer, Marc Pohl, Itamar Raz, Lucia Del Vecchio, Simeone Andrulli, Claudio Pozzi, Donatella Casartelli, Thomas Malfait, An Vanacker, Fernando Caravaca-Fontán, Hernando Trujillo, Teresa Cavero, Eduardo Gutierrez, Gerald Beck, John Kusek, Garabed Eknoyan, Claudio Ponticelli, Giuseppe Montagnino, Patrizia Passerini, Gabriella Moroni, Fumiaki Kobayashi, Hirofumi Makino, Sadayoshi Ito, Juliana CN Chan, Colin Tang, Flavio Gaspari, Maria Domenica Lesti, Giulia Gherardi, Sara Gamba, William Keane, James Donadio, Thomas Rauen, Claudia Seikrit, Stefanie Wied, Jamie Dwyer, and Gavin J. Becker
Disclosures
G.B. Appel reports Consultancy: Achillion, Alexion, Apellis, Arrowhead, Aurinia, Bristol Myers Squibb, Chemocentryx, Chinook, EMD Serono, Genentech, Genzyme-Sanofi, Glaxo-Smith-Kline, E. Lilly, Merck, Mallinkrodt, Novartis, Omeros, Pfizer, Reata, Travere therapeutics, and Vertex therapeutics; Research Funding: achillion-alexion, Apellis, Chemocentryx, Equillium, Genentech-Roche, Goldfinch, Mallinkrodt, Novartis, Reata, and Sanofi-Genzyme; Honoraria: Aurinia and Glaxo Smith Kline; Patents or Royalties: UpToDate; Advisory or Leadership Role: UpToDate—Editorial Board, Med Advisory board for Alexion, Alexion-Achillion, Apellis, Arrowhead, Aurinia, BM Squib, Chinook, Genentech, Glaxo-Smith-Kline, Lilly, Reata, Roche, and Sanofi; and Speakers Bureau: Aurinia—lectures on Lupus Nephritis and GSK—lectures on Lupus Nephritis. T.M. Chan reports Consultancy: GSK and Novartis; Research Funding: Astellas Pharma Inc, Baxter; and Honoraria: Visterra. F. Fervenza reports Consultancy: Alexion Pharmaceuticals, ByoCrystal, Galapagos, GSK, Novartis, Otsuka, and Takeda; Research Funding: Chemocentryx, Genentech, Hoffman La Roche, Janssen Pharmaceutical, Morphosys, and Retrophin; Honoraria: UpToDate; and Advisory or Leadership Role: Kidney International, Nephrology, UpToDate; Nephrology Dialysis and Transplantation, Journal of the American Society of Nephrology. J. Floege received lecture and consultancy honoraria from Alnylam, Amgen, Astellas, AstraZeneca, Bayer, Boehringer, Calliditas, Novartis, Omeros, and Travere and is a member of data safety monitoring board for Novo Nordisk and Visterra. J. Floege reports Consultancy: Amgen, AstraZeneca, Bayer, Boehringer, Calliditas, Chinook, Novo Nordisk, Novartis, Omeros, Travere, Vifor, and Visterra; Honoraria: Amgen, AstraZeneca, Bayer, Boehringer, Calliditas, Chinook, Novo Nordisk, Novartis, Omeros, Travere, Vifor, and Visterra; Advisory or Leadership Role: Calliditas, Omeros, and Travere; and Speakers Bureau: Amgen, AstraZeneca, Novartis, and Vifor. T. Greene reports grant support from Durect Corporation, Janssen Pharmaceuticals, Pfizer statistical consulting AstraZeneca, Boehringer-Ingleheim, and CSL. T. Greene reports Consultancy: AstraZeneca, Invokana, Janssen Pharmaceuticals, Novartis, and Pfizer Inc; and Research Funding: AstraZeneca, Boehringer-Ingleheim, CSL, and Vertex. B. Haaland reports Consultancy: AstraZeneca, Guidepoint Global, National Kidney Foundation, Prometic Life Sciences, and Value Analytics Labs; and Ownership Interest: ABR, AGNC, AQN, ARLP, BCS, BHP, DOW, DVN, ENB, EPD, ET, GOOD, GSK, Haaland Consulting, IBM, IEP, KMI, LLC, MMP, MPLX, MPW, NLY, OCSL, OHI, PBR, PFE, PFLT, RIO, SBRA, SQM, T, TD, UTG, VALE, VICI, VOD, VZ, WBA, WPC, and ZIM. H.J.L. Heerspink is consultant for AbbVie, AstraZeneca, Bayer, Boehringer Ingelheim, Chinook, CSL Behring, Dimerix, Eli-Lilly, Gilead, GoldFinch, Janssen, Merck, Novo Nordisk, and Travere Pharmaceuticals. H.J.L. Heerspink also reports Research Funding: AstraZeneca, Novo Nordisk, and Janssen research support (grant funding directed to employer); Honoraria: Lecture fees from AstraZeneca; and Speakers Bureau: AstraZeneca. E. Imai received research funding and honorarium for lecture from AstraZeneca, Boehringer Ingelheim, Daiich Sankyo, Kyowa Kirin, Novo, and Tanabe Mitsubishi. E. Imai also reports Honoraria: Eli-Lilly and Ono. L.A. Inker reports Consultancy: Diamtrix; Research Funding: funding to institute for research and contracts with the Chinnocks, National Institutes of Health, National Kidney Foundation, and Omeros and Reata Pharmaceuticals; consulting agreements with Tricida Inc.; Advisory or Leadership Role: Alport Foundation—Medical Advisory Council, NKF—Scientific Advisory Board; and Other Interests or Relationships: American Society of Nephrology member and National Kidney Foundation member. J.B. Lewis is consultant for BIOVIE, CSL, NIH Nations Study, REPRIEVE, TEUCER, treasurer and board member of the CSG, and Chair of FDA Cardiorenal Advisory Committee. J.B. Lewis also reports Consultancy: Veno Stent; Ownership Interest: circle medical management a dialysis company; and Honoraria: CSL bering, BIOVIE. P.K.T. Li received speaker honorarium from AstraZeneca, Baxter, and FibroGen. P.K.T. Li also reports Speaker Honoraria for Kyowa—Kirin; Advisory or Leadership Role: KI and PDI; and Other Interests or Relationships: President of International Association of Chinese Nephrologists. F. Locatelli is/was a member of an advisory board of Akebia, Amgen, Astellas, AstraZeneca, Baxter, GSK, Otsuka, Roche, Travere Pharmaceuticals, and Vifor Pharma and was a speaker at meetings supported by unrestricted grants from Amgen, Astellas, Roche, and Vifor Pharma. F. Locatelli reports Consultancy: Amgen, Asyellas, Baxter, GSK, Travere, and Vifor; Advisory or Leadership Role: Accelsior, Amgen, Astellas, AstraZeneca, GSK, Norgine, Otsuca Roche, Travere, and Vifor Pharma; Speakers Bureau: Amgen and Astellas; and Other Interests or Relationships: DOPPS, ERA, KDIGO, and SIN. B.D. Maes reports Consultancy: AstraZeneca, GSK, Novartis, Travere, Vera Therapeutics and Advisory or Leadership Role: GSK and Novartis. R.D. Perrone received research support from Kadmon, Otsuka, Reata, Sanofi Genzyme, and the US Department of Defense (TAME PKD); has been a member of steering committees for Otsuka, Sanofi Genzyme, and TAME PKD with fees paid to employing institutions; and has provided consultancy for Navitor, Otsuka, Palladiobio, and Reata. R.D. Perrone also reports Consultancy: Caraway, Janssen, and Sanofi-Genzyme; Research Funding: Palladiobio and Reata; Honoraria: Otsuka, Reata, and Sanofi-Genzyme; Advisory or Leadership Role: PalladioBio; and Other Interests or Relationships: UpToDate; PKD Foundation, Critical Path Institute. M. Praga is consultant for Alexion, Apellis, Aurinia, GlaxoSmithKline, Novartis, Otsuka, Roche-Genetech, Silence, and Travere. M. Praga also reports Consultancy: AstraZeneca, Silence, and Vifor; and Honoraria: Alexion, GSK, Novartis, Otsuka, Travere, Vand ifor. F.P. Schena reports grants from Puglia Region and from the Italian Ministry of University. F.P. Schena reports Research Funding: Puglia Region in Italy, Ministry of University in Rome Italy, and Ministry of Health in Rome Italy. C. Wanner received speaker honoraria from AstraZeneca, Bayer, Boehringer Ingelheim, Ely-Lilly, and FMC and was a member of an advisory board of Bayer, Boehringer Ingelheim, Gilead, GSK, MSD, and Sanofi Genzyme. C. Wanner also reports Consultancy: Akebia, Bayer, Boehringer-Ingelheim, Gilead, GSK, MSD, Sanofi, Triceda, and Vifor; Research Funding: Sanofi grant to institution and Idorsia grant to institution; Honoraria: Amgen, Astellas, Chiesi, Sanofi, and Takeda; Advisory or Leadership Role: President European Renal Association (ERA); and Other Interests or Relationships: European Renal Association (ERA). D. Xie reports Other Interests or Relationships: ISN member. All remaining authors have nothing to disclose.
Funding
The study was funded by the National Kidney Foundation.
Author Contributions
Conceptualization: Tom Greene, Hiddo Heerspink, Lesley Inker,
Data curation: Gerald Appel, Tak Mao Chan, Raymond Estacio, Fernando Fervenza, Jürgen Floege, Tom Greene, Hiddo Heerspink, Enyu Imai, Lesley Inker, Tazeen Jafar, Julia Lewis, Philip Li, Francesco Locatelli, Bart Maes, Annalisa Perna, Ronald Perrone, Manuel Praga, Francesco P. Schena, Christoph Wanner, Di Xie
Formal analysis: Willem Collier, Tom Greene, Benjamin Haaland, Jiyu Luo, Hocine Tighiouart
Funding acquisition: Tom Greene, Hiddo Heerspink, Lesley Inker
Writing – original draft: Tom Greene, Hiddo Heerspink, Lesley Inker, Francesco P. Schena
Writing – review & editing: Gerald Appel, Tak Mao Chan, Willem Collier, Raymond Estacio, Fernando Fervenza, Jürgen Floege, Tom Greene, Benjamin Haaland, Hiddo Heerspink, Enyu Imai, Lesley Inker, Tazeen Jafar, Julia Lewis, Philip Li, Francesco Locatelli, Jiyu Luo, Bart Maes, Annalisa Perna, Ronald Perrone, Manuel Praga, Hocine Tighiouart, Christoph Wanner, Di Xie
Data Sharing Statement
Data were shared with the CKD-EPI CT group under strict data use agreements which prohibit the group from sharing data with parties external to the agreement. Some datasets, however, were accessed via public data sharing platforms and could be requested by other interested researchers: NIDDK: HALT-PKD A and B (NCT00283686).
Supplemental Material
This article contains the following supplemental material online at http://links.lww.com/JSN/E37.
Part 1A. Rationale for Bayesian approach.
Part 1B. Details on analyses of GFR slope within each trial.
Part 2. Six steps to applying a trial-level meta-regression of previous trials to the design and analysis of a new randomized trial.
Supplemental Table 1. Clinical characteristics of the population stratified by disease etiology.
Supplemental Figure 1. Credible and prediction intervals for true treatment effect on established renal end point given true treatment effects on GFR slope and UACR.
Supplemental Figure 2. Trial-level positive predictive value (PPVtrial) on the basis of observed treatment effects on UACR and slope to infer clinical benefit defined as HR<0.9.
Supplemental Figure 3. Trial-level positive predictive value (PPVtrial) on the basis observed treatment effects on UACR and slope to infer clinical benefit defined as HR<0.8.
Supplemental Figure 4. Trial-level positive predictive value (PPVtrial) on the basis observed treatment effects on UACR and slope to infer clinical benefit defined as HR<1 for an example Phase 3 trial.
Supplemental Figure 5. Average estimated PPVtrial on the basis hypothesized treatment effects on UACR and GFR slope to infer clinical benefit defined as HR<0.9.
Supplemental Figure 6. Average estimated PPVtrial on the basis hypothesized treatment effects on UACR and GFR slope to infer clinical benefit defined as HR<0.8.
Appendix 1. Study funding sources.
References
- 1.Heerspink HJL, Greene T, Tighiouart H, Gansevoort RT, Coresh J, Simon AL. Change in albuminuria as a surrogate endpoint for progression of kidney disease: a meta-analysis of treatment effects in randomised clinical trials. Lancet Diabetes Endocrinol. 2019;7(2):128–139. doi: 10.1016/S2213-8587(18)30314-0 [DOI] [PubMed] [Google Scholar]
- 2.Inker LA, Heerspink HJL, Tighiouart H, Levey AS, Coresh J, Gansevoort RT. GFR slope as a surrogate end point for kidney disease progression in clinical trials: a meta-analysis of treatment effects of randomized controlled trials. J Am Soc Nephrol. 2019;30(9):1735–1745. doi: 10.1681/ASN.2019010007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Levey AS, Gansevoort RT, Coresh J, Inker LA, Heerspink HL, Grams ME. Change in albuminuria and GFR as end points for clinical trials in early stages of CKD: a scientific workshop sponsored by the national kidney foundation in collaboration with the US Food and drug administration and European medicines agency. Am J Kidney Dis. 2020;75(1):84–104. doi: 10.1053/j.ajkd.2019.06.009 [DOI] [PubMed] [Google Scholar]
- 4.Van Zuilen AD, Wetzels JF, Bots ML, Van Blankestijn PJ. MASTERPLAN: study of the role of nurse practitioners in a multifactorial intervention to reduce cardiovascular risk in chronic kidney disease patients. J Nephrol. 2008;21(3):261–267. [PubMed] [Google Scholar]
- 5.Barrett BJ, Garg AX, Goeree R, Levin A, Molzahn A, Rigatto C. A nurse-coordinated model of care versus usual care for stage 3/4 chronic kidney disease in the community: a randomized controlled trial. Clin J Am Soc Nephrol. 2011;6(6):1241–1247. doi: 10.2215/CJN.07160810 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Goicoechea M, Garcia de Vinuesa S, Verdalles U, Verde E, Macias N, Santos A. Allopurinol and progression of CKD and cardiovascular events: long-term follow-up of a randomized clinical trial. Am J Kidney Dis. 2015;65(4):543–549. doi: 10.1053/j.ajkd.2014.11.016 [DOI] [PubMed] [Google Scholar]
- 7.Patel A. Effects of a fixed combination of perindopril and indapamide on macrovascular and microvascular outcomes in patients with type 2 diabetes mellitus (the ADVANCE trial): a randomised controlled trial. Lancet. 2007;370(9590):829–840. doi: 10.1016/S0140-6736(07)61303-8 [DOI] [PubMed] [Google Scholar]
- 8.Patel A, MacMahon S, Chalmers J, Neal B, Billot L, Woodward M. Intensive blood glucose control and vascular outcomes in patients with type 2 diabetes. New Engl J Med. 2008;358(24):2560–2572. doi: 10.1056/NEJMoa0802987 [DOI] [PubMed] [Google Scholar]
- 9.Baigent C, Landray MJ, Reith C, Emberson J, Wheeler DC, Tomson C. The effects of lowering LDL cholesterol with simvastatin plus ezetimibe in patients with chronic kidney disease (Study of Heart and Renal Protection): a randomised placebo-controlled trial. Lancet. 2011;377(9784):2181–2192. doi: 10.1016/S0140-6736(11)60739-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Levey AS, Stevens LA, Schmid CH, et al. A new equation to estimate glomerular filtration rate. Ann Intern Med. 2009;150(9):604–612. doi: 10.7326/0003-4819-150-9-200905050-00006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Skali H, Uno H, Levey AS, Inker LA, Pfeffer MA, Solomon SD. Prognostic assessment of estimated glomerular filtration rate by the new chronic kidney disease Epidemiology Collaboration equation in comparison with the modification of diet in renal disease study equation. Am Heart J. 2011;162(3):548–554. doi: 10.1016/j.ahj.2011.06.006 [DOI] [PubMed] [Google Scholar]
- 12.Vonesh E, Tighiouart H, Ying J, Heerspink HL, Lewis J, Staplin N. Mixed-effects models for slope-based endpoints in clinical trials of chronic kidney disease. Stat Med. 2019;38(22):4218–4239. doi: 10.1002/sim.8282 [DOI] [PubMed] [Google Scholar]
- 13.Greene T, Teng CC, Inker LA, Redd A, Ying J, Woodward M. Utility and validity of estimated GFR-based surrogate time-to-event end points in CKD: a simulation study. Am J Kidney Dis. 2014;64(6):867–879. doi: 10.1053/j.ajkd.2014.08.019 [DOI] [PubMed] [Google Scholar]
- 14.Oshima M, Jun M, Ohkuma T, Toyama T, Wada T, Cooper ME. The relationship between eGFR slope and subsequent risk of vascular outcomes and all-cause mortality in type 2 diabetes: the ADVANCE-ON study. Diabetologia. 2019;62(11):1988–1997. doi: 10.1007/s00125-019-4948-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Neuen BL, Weldegiorgis M, Herrington WG, Ohkuma T, Smith M, Woodward M. Changes in GFR and albuminuria in routine clinical practice and the risk of kidney disease progression. Am J Kidney Dis. 2021;78(3):350–360.e1. doi: 10.1053/j.ajkd.2021.02.335 [DOI] [PubMed] [Google Scholar]
- 16.Heerspink HJL, Stack AG, Terkeltaub R, et al. Rationale, design, demographics, and baseline characteristics of the randomised, controlled, phase 2b SAPPHIRE study of verinurad plus allopurinol in patients with chronic kidney disease and hyperuricaemia. Nephrol Dial Transplant. 2022;37(8):1461–1471. doi: 10.1093/ndt/gfab237 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Heerspink HJL, Law G, Psachoulia K, Connolly K, Whatling C, Ericsson H. Design of FLAIR: a phase 2b study of the 5-lipoxygenase activating protein inhibitor AZD5718 in patients with proteinuric CKD. Kidney Int Rep. 2021;6(11):2803–2810. doi: 10.1016/j.ekir.2021.08.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Komers R, Diva U, Inrig JK, Loewen A, Trachtman H, Rote WE. Study design of the phase 3 sparsentan versus irbesartan (DUPLEX) study in patients with focal segmental glomerulosclerosis. Kidney Int Rep. 2020;5(4):494–502. doi: 10.1016/j.ekir.2019.12.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Barratt J, Rovin B, Diva U, Mercer A, Komers R. Implementing the kidney health initiative surrogate efficacy endpoint in patients with IgA nephropathy (the PROTECT trial). Kidney Int Rep. 2019;4(11):1633–1637. doi: 10.1016/j.ekir.2019.08.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fellström BCBJ, Cook H, Coppo R, et al. NEFIGAN Trial Investigators: targeted-release budesonide versus placebo in patients with IgA nephropathy (NEFIGAN): a double-blind, randomised, placebo-controlled phase 2b trial. Lancet. 2017;389(10084):2117–2127. doi: 10.1016/S0140-6736(17)30550-0 [DOI] [PubMed] [Google Scholar]
- 21.US Food and Drug Administration; Center for Drug Evaluation and Research. FDA Approves First Drug to Decrease Urine Protein in IgA Nephropathy, a Rare Kidney Disease. 2021. Available at: https://www.fda.gov/drugs/fda-approves-first-drug-decrease-urine-protein-iga-nephropathy-rare-kidney-disease. Accessed April 1, 2023. [Google Scholar]
- 22.Inker LA, Heerspink HJL, Tighiouart H, Chaudhari J, Miao S, Diva U. Association of treatment effects on early change in urine protein and treatment effects on GFR slope in IgA nephropathy: an individual participant meta-analysis. Am J Kidney Dis. 2021;78(3):340–349.e1. doi: 10.1053/j.ajkd.2021.03.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data were shared with the CKD-EPI CT group under strict data use agreements which prohibit the group from sharing data with parties external to the agreement. Some datasets, however, were accessed via public data sharing platforms and could be requested by other interested researchers: NIDDK: HALT-PKD A and B (NCT00283686).