Detection of N-H···N hydrogen bonding in RNA via scalar couplings in the absence of observable imino proton resonances

Abstract

Hydrogen bond networks stabilize RNA secondary and tertiary structure and are thus essentially important for protein recognition. During structure refinements using either NMR or X-ray techniques, hydrogen bonds were usually inferred indirectly from the proximity of donor and acceptor functional groups. Recently, quantitative heteronuclear J(N,N)-HNN COSY NMR experiments were introduced that allowed the direct identification of donor and acceptor nitrogen atoms involved in hydrogen bonds. However, protons involved in base pairing interactions in nucleic acids are often not observable due to exchange processes. The application of a modified quantitative J(N,N)-HNN COSY pulse scheme permits observation of ^2hJ(N,N) couplings via non-exchangeable protons. This approach allowed the unambiguous identification of the A27·U23 reverse Hoogsteen base pair involved in a U-A·U base triple in the HIV-2 transactivation response element–argininamide complex. Despite a wealth of NOE information, direct evidence for this interaction was lacking due to the rapid exchange of the U23 imino proton. The ability to directly observe hydrogen bonds, even in D₂O and in the presence of rapid exchange, should facilitate structural studies of RNA.

INTRODUCTION

The existence of scalar couplings due to hydrogen bonds between imino proton donors and acceptor nitrogens in Watson–Crick base pairs of RNA (1) and DNA (2) was recently demonstrated. Hydrogen bonds have a partially covalent character that gives rise to scalar spin–spin couplings of the type ^2hJ(N,N) and ^1hJ(H,N) that are an important additional NMR parameter for the structure determination of biomacromolecules in solution (1–4). Quantum mechanical calculations predict a correlation of the distance between the coupled nuclei and the size of the scalar coupling (5–7).

In early stages of a structural study, these experiments allow the rapid identification of basic secondary structural elements such as A-form Watson–Crick duplexes in RNA. In addition, non-canonical base pairs play important roles in defining the structure and function of nucleic acids, in particular for RNA. ^2hJ(N,N) couplings with non-Watson–Crick imino hydrogen bonded G-A base pair and reverse Hoogsteen A-U base pairs have been observed in RNA (8), and a novel experiment that correlates the N6 amino and N7 nitrogens of adenosines forming an A-A base pair in DNA has recently been introduced (4). All of these experiments rely on direct observation of the proton resonances involved in the hydrogen-bonding interaction. Unfortunately, some hydrogen bonding interactions are difficult to observe due to rapid imino proton exchange. For example, imino resonances from terminal base pairs are rarely observable under typical conditions for NMR studies.

Here we have applied a modified quantitative J(N,N)-HNN COSY pulse scheme (3) to ¹⁵N-labeled RNA that allowed the observation of ^2hJ(N,N) couplings in the absence of detectable imino protons. Instead of measuring the coupling by detection of the imino protons, the ^2hJ(N,N) couplings are observed via ²J(H,N) correlations with non-exchangeable base protons. The experiment provides a sensitive measure of base pairing interactions, even in D₂O solution. This approach has led to the confirmation of the existence of the U38-A27·U23 base triple in the HIV-2 transactivation response element (TAR)–argininamide complex. Furthermore, experiments can be carried out at higher temperatures because they do not rely on the observation of potentially exchange-broadened proton resonances. Thus, the quantitative ²J_HN HNN–COSY is a sensitive alternative for the investigation of hydrogen bonding interaction in larger RNAs where structural studies at lower temperatures are hampered by unfavorable relaxation properties.

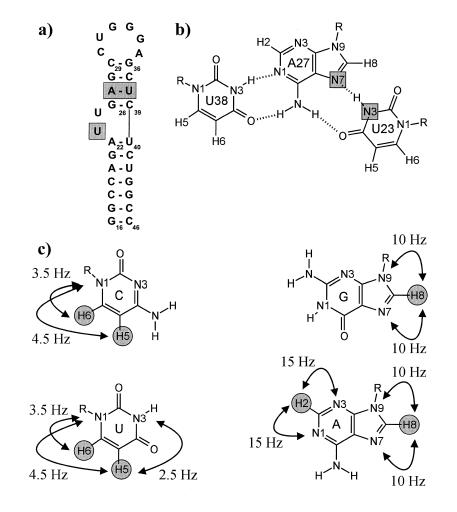
Tat is one of the regulatory proteins encoded by the Human immunodeficiency virus type-1 (HIV-1), containing an arginine-rich motif responsible for binding to its target, the TAR RNA hairpin loop (9,10). Formation of the Tat–TAR interaction is critical for viral replication, resulting in an increase in the expression of viral mRNA. The nucleotides on TAR important for Tat binding are clustered around a 3-nt bulge, shown in Figure 1a. Peptides from the basic region of Tat retain the specificity of RNA binding, and remarkably, the amide derivative of arginine also binds specifically to TAR, although with greatly reduced affinity (11,12). Upon binding of Tat, Tat peptides or argininamide, the TAR RNA undergoes a major conformational change in the bulge region. In the bound form, the essential nucleotides, U38, A27 and U23, are proposed to form a base triple, shown in Figure 1b, which results in an opening of the major groove for peptide recognition.

Figure 1.

(a) Sequence and secondary structure of HIV-2 TAR. The sequence is identical to HIV-1 TAR except for the deletion of the C24 bulge nucleotide. The nucleotides forming the base triple are shaded in gray. (b) Schematic representation of the HIV-2 TAR base triple formed upon binding argininamide. ^2hJ(N,N) scalar coupled nitrogens forming the reverse Hoogsteen part of the base triple are shown shaded. (c) Observable long range H,N correlations with approximate coupling constant values in cytidine, guanosine, adenosine and uridine, shown as arrows, with the observed non-exchangeable base protons shaded as gray circles.

The existence of the U38-A27·U23 base triple in the bound form of the HIV TAR RNA has been the subject of debate in the literature. The U38-A27·U23 base triple was first suggested on the basis of internucleotide NOEs between U23 and G26 by Puglisi et al. in a low resolution ¹H-NMR study of the HIV-1 TAR RNA argininamide complex (13). However, the imino proton of U23 that would have provided strong support for the proposed hydrogen bonding, was not observed. Further indirect evidence supporting the formation of a base triple came from argininamide binding studies on an isomorphic C38-G27·C23+ base triple mutant that adopts the same conformation as wild-type TAR (14,15). Complementary biochemical and mutagenesis experiments supported the importance of the Hoogsteen interaction in the base triple for argininamide binding (16–18). In contrast, based on heteronuclear NMR studies of the HIV-1 TAR RNA in the presence of the Tat ADP-1 polypeptide, Varani and co-workers concluded that the formation of the base triple was inconsistent with their experimental data (19) and that the proposed hydrogen bonding between U23 and A27 was misidentified (20). However, no specific counterproposal for the critical role of U23 and A27 functional groups in arginine or Tat binding was made. Detailed NMR investigations of the two base bulge HIV-2 TAR RNA argininamide complex were consistent with the original model of Puglisi et al. with the U23 positioned in the major groove and within hydrogen bonding distance to A27 (21), however, the U23 imino proton was never directly observed. In addition, the conformation of a 24 residue Tat peptide bound to a shortened form of HIV-1 TAR determined by NMR supports the model of base triple formation (22).

In the present study, we have adapted the quantitative ²J_HN HNN–COSY for correlation of non-exchangeable base protons with base nitrogens, and exploited this experiment to directly observe ^2hJ(N,N) couplings in the absence of observable imino proton resonances. The observable multiple bond ¹H,¹⁵N correlations used in the present study are summarized in Figure 1c. The experiment can be used to observe base pairing in D₂O, or to observe hydrogen bonding interactions in the presence of rapid imino proton exchange at higher temperatures. The present study complements previous assignments and chemical shift analysis based on multiple bond ¹H,¹⁵N correlations (23,24).

MATERIALS AND METHODS

Sample preparation

A sample of 1.5 mM uniformly ¹⁵N-labeled HIV-2 TAR RNA in the presence of 6 mM argininamide was prepared as described previously (21). The sample buffer contained 10 mM phosphate buffer, pH 6.4, 50 mM sodium chloride and 0.1 mM EDTA in 90% H₂O, 10% D₂O. For experiments in D₂O, the sample was flash frozen in liquid nitrogen prior to lyophyllization for 12 h, followed by three lyophyllizations from 100% D₂O.

NMR spectroscopy

All spectra were recorded on a three-channel Bruker AMX600 spectrometer equipped with an actively shielded z-gradient triple-resonance probe, at a temperature of 298 K. For the quantitative J-correlation ²J_HN HNN–COSY spectrum, 64 complex points were recorded with an acquisition time of 10.5 ms for ¹⁵N (ω₁), and 2048 complex points with an acquisition time of 166.0 ms for ¹H (ω₂). A repetition delay between transients of 1.2 s was used, with 384 scans per complex increment (total measuring time 18.7 h). For the ⁿJ_HN HMQC spectrum, 128 complex points were recorded with an acquisition time of 21.0 ms for ¹⁵N (ω₁), and 1024 complex points with an acquisition time of 166.0 ms for ¹H (ω₂). A repetition delay between transients of 1.8 s was used, with 32 scans per complex increment (total measuring time 4.5 h). For the jump–return HMQC experiment in 90% H₂O, 10% D₂O, 64 complex points were recorded with an acquisition time of 45.4 ms for ¹⁵N (ω₁), and 1024 complex points with an acquisition time of 74.0 ms for ¹H (ω₂). A repetition delay between transients of 1.8 s was used, with 16 scans per complex increment (total measuring time 1.1 h). Spectra were processed using the NMRPipe program package (25). A solvent suppression filter was used in the ω₂ dimension to eliminate distortions from residual water prior to apodization with a 72° shifted squared sinebell window function. Data sets were zero-filled twice before Fourier transformation and only the aromatic ¹H region of the spectra was retained. The ω₁ data were zero-filled and apodized with a 72° shifted squared sinebell window function prior to Fourier transformation. The absorptive part of the final 2D matrices were 4096 × 2048 points for the ²J_HN HNN–COSY, and 4096 × 256 points for the ⁿJ_HN HMQC spectrum, respectively. Peak positions and intensities were determined using polynomial interpolation with PIPP and CAPP (26). All proton chemical shifts are referenced to the internal standard TSP and nitrogen shifts are referenced indirectly according to the chemical shift ratio (27).

Quantification of ²J(N,N) coupling constants

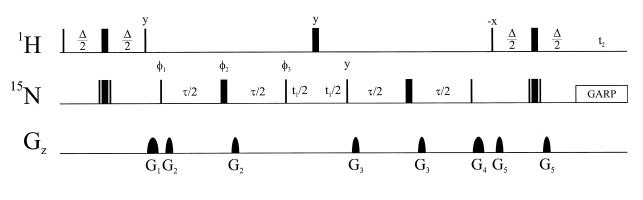
The pulse sequence for the determination of homonuclear ²J(N,N) coupling constants in the absence of detectable imino proton magnetization is very similar to the quantitative J-correlation ²J_HN HNN–COSY scheme previously published for the determination of hydrogen bond ^2hJ(N,N) coupling constants of imidazole nitrogens for histidine residues in apomyoglobin (3), and is shown in Figure 2. The essential difference between the new experiment and the well established quantitative J(N,N)-HNN–COSY pulse schemes is the fact that magnetization both originates and is detected on non-exchangeable aromatic protons, allowing the determination of scalar coupling across hydrogen bonds in the absence of detectable imino proton resonances. Consequently, measurements can be carried out in D₂O, overcoming solvent suppression problems and saturation transfer phenomena. A direct comparison with respect to the sensitivity of the established HNN–COSY and the applied ²J_HN HNN–COSY pulse scheme is difficult due to the contributions of several different factors. The line-widths of aromatic protons are significantly smaller compared to those of exchangeable imino protons, although potential gains in sensitivity are compensated by longer INEPT delays in the case of the ²J_HN HNN–COSY pulse scheme. The ²J_HN HNN–COSY pulse scheme also benefits from longer transverse relaxation times of the non-protonated purine ¹⁵N7/9 or adenosine ¹⁵N1/3 with respect to the protonated ¹⁵N1 guanosine or ¹⁵N3 uridine nitrogens during the period τ. Further gain in sensitivity for the ²J_HN HNN–COSY pulse scheme can potentially be achieved by ²H broadband decoupling during τ and t₁ eliminating ¹⁵N broadening effects that arise from scalar relaxation of the second kind (28). In addition, the different solvent viscosities of D₂O and H₂O will influence the overall tumbling rates.

Figure 2.

Pulse sequence for the quantitative J-correlation ²J_HN HNN–COSY experiment. Carrier positions in the present work were 189.1 p.p.m. for ¹⁵N, and 4.75 p.p.m. for ¹H^N, respectively. All ¹H pulses were given on resonance for the water signal. High power proton pulses were applied with a field strength of 26.2 kHz. ¹⁵N decoupling during acquisition employed a 1.26 kHz GARP field (40), while high power ¹⁵N pulses were applied with a field strength of 7.0 kHz. The inversion of nitrogen magnetization during the first and the final INEPT transfer step is achieved using composite 90_x180_y90_x 180° (N) pulses. The phase cycling is φ₁ = x, –x, φ₂ = x, φ₃ = 2(y), 2(–y), receiver = x, –x. Quadrature detection was obtained in the t₂ dimension by altering φ₁, φ₂ and φ₃ according to States–TPPI (41). The delays for the INEPT and N,N transfers were Δ = 28 ms and τ = 45 ms, respectively (see text). Sine-shaped gradient durations and amplitudes were: G₁ 0.32 ms (5 G/cm); G₂ 0.64 ms (3.5 G/cm); G₃ 0.64 ms (–8.5 G/cm); G₄ 0.32 ms (7.5 G/cm); G₅ 1.28 ms (15 G/cm). For experiments carried out in 90% H₂O, 10% D₂O the last non-selective 180° (H) pulse in the reverse INEPT transfer was replaced by the binomial WATERGATE sequence in order to achieve adequate water suppression (42).

The two-bond ²J_HN couplings within the purine bases depicted in Figure 1c allow reasonably efficient magnetization transfer during the INEPT delays. The duration of delay Δ (28 ms ª 1/2J, J = ²J_H8N7 + ²J_H8N9 ª 20 Hz) was empirically optimized to offset transverse proton relaxation, giving the most efficient transfer for the H8/N9 or H8/N7 correlations. This value is suboptimal for the investigation of N1 and N3 hydrogen bond acceptor sites in adenosine residues because both corresponding two-bond couplings ²J_H2N1/3 are significantly larger (²J_H2N1/3 ª 15 Hz). Optimal sensitivity for the investigation of N1 and N3 hydrogen bond acceptor sites in adenosine can be achieved by tuning Δ to 18 ms (18 ms ª 1/2J, J = ²J_H2N3 + ²J_H2N1 ª 30 Hz). All possible long range correlations, including long range H5/H6,N1/3 correlations within the pyrimidines that are shown in Figure 1c, can be observed using a longer INEPT delay duration Δ ≥ 36 ms (29) as a compromise.

After the excitation of the non-exchangeable aromatic protons, an INEPT transfer creates transverse ¹⁵N magnetization. This ¹⁵N source magnetization defocuses with respect to its long-range ¹⁵N coupling partner during a tunable period τ = 45 ms. The fraction of magnetization giving rise to the reference peak intensity is proportional to cos(πJ_NsNdτ)Π_kcos(πJ_NsNkτ), k ≠ s, d, where the index s characterizes the source ¹⁵N nuclei while the index d characterizes the scalar coupled destination ¹⁵N nuclei. Similarly, the transfer function of magnetization giving rise to the cross peak intensity is proportional to sin(πJ_NsNdτ)Π_kcos(πJ_NsNkτ). After chemical shift evolution of the ¹⁵N magnetization during t₁, the same fractions are refocused following the reverse pathway. Thus, the ratio of the transfer amplitudes of the reference and the cross peak intensity equals –tan²(πJ_NsNdτ). Because the line shapes of the cross and the reference signal are the same in ω₂ (¹H8,2) and the line shape in the ω₁ (¹⁵N) dimension is limited by digitization and the apodization function, values of ²J(N,N) can be derived from the intensity ratio, I^cross/I^ref = –tan²(πJ_NsNdτ) (30). The reported uncorrected coupling constant values may be systematically underestimated by up to 10% due to incomplete ¹⁵N inversion and differential relaxation of ¹⁵N in-phase and antiphase magnetization due to finite ¹⁵N T₁ relaxation times during the defocusing periods τ (1,31). Estimated coupling constant errors based on the signal-to-noise ratio of the individual experiments and according to standard error propagation analysis are in the range of 0.2–0.4 Hz.

RESULTS AND DISCUSSION

The non-canonical part of the base triple

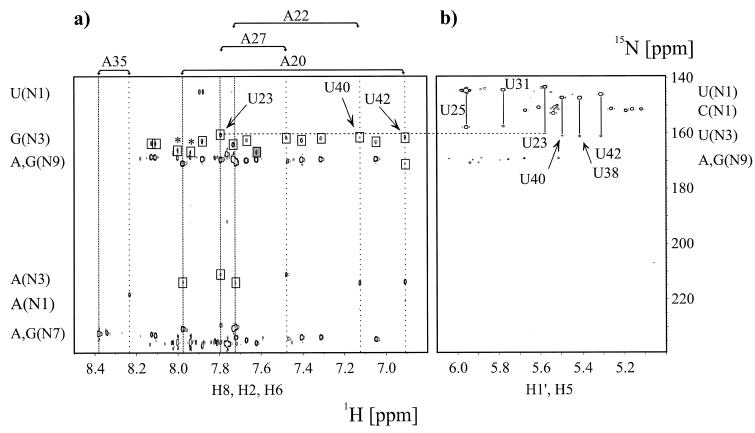
The Watson–Crick base pairing between A27 and U38 was directly observable due to the strong NOE between the U38 imino proton and the A27 H2 proton (13). However, the U23 imino proton involved in the putative Hoogsteen base triple between U23 and A27 was not observed. If the U23 imino proton and the A27 N7 (Fig. 1b) were involved in a hydrogen bond, then there should be an observable N7-N3 coupling, irrespective of the presence of the U23 imino proton. Several quantitative J-correlation ²J_HN HNN–COSY experiments were carried out on ¹⁵N-labeled TAR–argininamide complex in 90% H₂O, 10% D₂O as well as in 99.9% D₂O. The expected intraresidue two-bond correlations to the N7 and N9 nitrogens detected on the non-exchangeable H8 resonance of A27 are shown in Figure 3a. In addition, there is a correlation to the A27 H8 proton assigned to intraresidue magnetization transfer from the source N9 to the N3 nitrogen via ²J(N9,N3). Most importantly, there is a correlation to the A27 H8 proton from the source N7 nitrogen of A27 to the N3 of U23 across a hydrogen bond due to ^2hJ(N7,N3). The ω₁ (¹⁵N) resonance frequency of the N3 nitrogen of U23 that was not observed in one-bond ¹H,¹⁵N correlations due to the exchange of the U23 imino proton, was independently verified through long range ³J(H5,N3) intraresidue couplings in a HMQC experiment optimized for ²J(H,N) and ³J(H,N) correlations, shown in Figure 3b. The ^2hJ(N7,N3) coupling constant for the U23(H3)-A27(N7) hydrogen bond in the HIV-2 U38-A27·U23 base triple was measured to be 5.3 Hz in 99.9% D₂O, and 5.1 Hz in 90% H₂O, 10% D₂O, respectively. These values are identical within the estimated error range of ±0.2–0.4 Hz on the individual J values. Two independent experiments with different defocusing periods τ = 45 and 37 ms were recorded in 99.9% D₂O giving rise to individual values of 5.5 and 5.1 Hz, respectively, while two independent experiments with identical defocusing periods τ = 45 ms were recorded in 90% H₂O, 10% D₂O, both yielding ^2hJ(N7,N3) = 5.1 Hz. The reported ^2hJ(N7,N3) coupling constant is similar to ^2hJ(N,N) values reported for Watson–Crick G-C and A-U base pairs, and to the observed ^2hJ(N7,N3) coupling constant values of 5.5 Hz for reverse Hoogsteen A·U base pairs in the E-loop of 5S ribosomal RNA (5SDE) and a shortened RNA fragment 5SE complexed with its cognate ribosomal protein L25 (8).

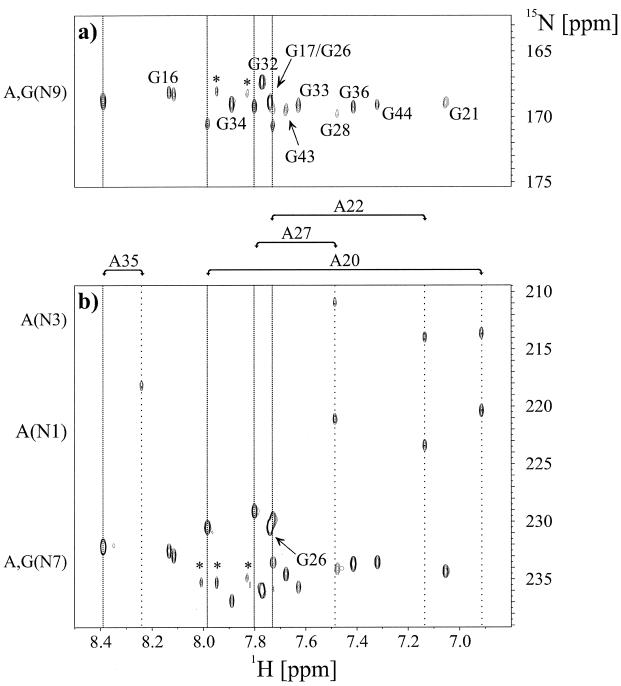
Figure 3.

Direct observation of scalar cross hydrogen bond ^2hJ(N,N) and intraresidue ²J(N,N) coupling constants in the HIV-2 TAR–argininamide complex at 298 K in D₂O. (a) Quantitative J-correlation ²J_HN HNN–COSY spectrum recorded with the pulse scheme shown in Figure 2. Assignments for all adenosine residues in HIV-2 TAR are given on top of the spectrum. The corresponding H2 and H8 proton resonance frequencies are highlighted by vertical wide and narrow dotted lines, respectively. Cross peaks that are due to ²J(N,N) couplings have opposite signs and are shown in boxes. The unusual N3 chemical shift of G33 is shaded in dark gray. A dashed horizontal line connects the N3 resonance frequency of U23 as obtained from (a) ²J_HN HNN–COSY and (b) ⁿJ_HN HMQC experiments. Arrows point to the A20-U42 Watson–Crick base pair correlation, the A22-U40 correlation and to the A27-U23 correlation at the H8 proton resonance frequency of A27. Chemical shift regions for the nitrogen and proton resonances giving rise to the observable correlations are given next to the corresponding axis. Peaks marked with an asterisk are due to minor impurities from sample degradation. (b) Identification of cross-hydrogen bond couplings using intraresidual ⁿJ_HN HMQC correlations. The applied delay duration 2Δ = 42 ms allowed a straightforward identification of H5,N1 and H5,N3 connectivities for uridine residues due to small intraresidue couplings (³J_H5N1 ª 4.5 Hz, ³J_H5N3 ª 2.5 Hz). Assignments for all uridine residues in HIV-2 TAR are given. The corresponding H5,N1 and H5,N3 cross peaks are connected by vertical solid lines. Chemical shift regions for the nitrogen and proton resonances giving rise to the observable correlations are given next to the corresponding axis.

¹⁵N chemical shifts and one-bond deuterium isotope shifts related to the base triple

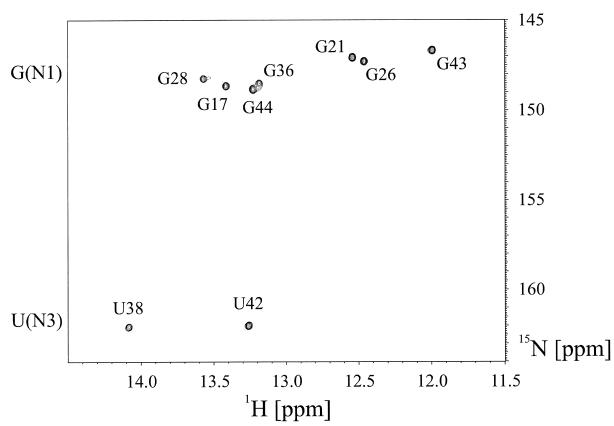
The complete assignment of the intraresidue ³J(H5,N3) and ³J(H5,N1) correlations for the uridine residues in HIV-2 TAR was obtained from a high resolution HMQC experiment recorded in 99.9% D₂O, optimized for ²J(H,N) and ³J(H,N) correlations, shown in Figure 3b. The chemical shifts of the N3 resonances of residues U25 and U31 cluster around 157.64 ± 0.18 p.p.m., while the N3s of residues U40, U38 and U42 resonate around 161.04 ± 0.05 p.p.m. The latter three residues are involved in Watson–Crick base pairs, while residues U25 and U31, located in the bulge and the loop region, respectively, are not base paired. The ¹⁵N chemical shift of the N3 nitrogen for U23, involved in the reverse Hoogsteen A27·U23 base pair, adopts an intermediate value of 160.09 p.p.m. in 99.9% D₂O. This value is closer to the values obtained for Watson–Crick base paired uridine residues, which is also consistent with a hydrogen-bonding interaction. The chemical shift data should be interpreted cautiously because other factors, such as base stacking, also influence the nitrogen chemical shifts (32). As expected, a significant one-bond deuterium isotope effect is observed for the nitrogen chemical shifts of the uridine N3 nitrogens (33). Comparison of ¹⁵N chemical shifts obtained from the high resolution HMQC experiment recorded in 99.9% D₂O, optimized for ²J(H,N) and ³J(H,N) correlations, and from a jump–return HMQC experiment recorded in 90% H₂O, 10% D₂O shown in Figure 4, optimized for ¹J(H,N) correlations in the imino spectral region, yielded one-bond deuterium isotope effects ¹ΔN(D) of 1.00 and 0.94 p.p.m. for the Watson–Crick base paired imino N3 nitrogens of U38 and U42, respectively. In contrast, the U40 imino proton resonance is not observable at 298 K due to exchange broadening as can be verified by inspection of Figure 4. This particular resonance sharpens and becomes observable at 278 K (21). A one-bond deuterium isotope effect ¹ΔN(D) of 0.74 p.p.m. was observed for the N3 nitrogen of U23 forming the reverse Hoogsteen base pair. This value was derived from chemical shift comparisons obtained from the HMQC experiment recorded in 99.9% D₂O and the quantitative J-correlation ²J_HN HNN–COSY experiments carried out in 90% H₂O, 10% D₂O.

Figure 4.

Assignments of the imino region of the HIV-2 TAR–argininamide complex from a jump–return HMQC experiment recorded in 90% H₂O, 10% D₂O at 298 K. No evidence for the U23 imino resonance forming the reverse Hoogsteen part of the base triple is observed. In addition, the terminal 5′G·C3′ G16 imino resonance as well as the U40 imino resonance from the base pair that terminates the upper stem are missing due to unfavorable exchange properties with the solvent.

The chemical shift of non-protonated purine N7 and N1,3 adenosine nitrogens can be monitored using two-bond correlations, as a measure of internal hydrogen bonding (23,24,34). Complete residue specific assignments of the N7, N1 and N3 nitrogens in the bound form of HIV-2 TAR were obtained from the ⁿJ_HN HMQC experiment, shown in Figure 5a and b. Upfield shifts of the nitrogen resonance frequencies are expected for hydrogen bond acceptor sites (34). The large chemical shift change of the N7 resonance of G26 induced by ligand binding was interpreted to be due to hydrogen bonding interaction with the charged arginine guanidinium group (19,23). However, the less pronounced chemical shift changes and the similarity of N7 chemical shifts observed for A22 and A27 in the bound form of HIV-2 TAR were used to argue against the proposed hydrogen bonding in the base triple upon ligand binding (23). While chemical shifts can be sensitive probes of hydrogen bonding, the A27(N7) shift apparently does not report on the existence of the hydrogen bond clearly revealed by the ^2hJ(N7,N3) coupling. It should be noted that some confusion with respect to the correct assignments of N1 and N3 nitrogen chemical shifts of adenosines exists in the literature (23,24,29). The present study unambiguously assigns the N1 of A20, A22 and A27 in HIV-2 TAR (δ¹⁵N1 ~ 222 p.p.m.) to resonate downfield with respect to the N3 chemical shifts (δ¹⁵N3 ~ 213 p.p.m.) as shown in Figure 5b consistent with the shifts originally reported (34,35). Chemical shift assignments for non-protonated nitrogens in the bound form of HIV-2 TAR for purine bases are summarized in Table 1.

Figure 5.

Assignment of the purine non-exchangable nitrogens in the HIV-2 TAR–argininamide complex at 298 K in D₂O. (a) Region of the ²J_HN HMQC experiments showing H8,N9 cross peaks for adenosines and guanosines. Residue specific assignments for all guanosine residues in HIV-2 TAR are given. The H8 proton resonance frequencies of the adenosine residues are highlighted by vertical narrow dotted lines. (b) Region of the ²J_HN HMQC experiments showing H8,N7 cross peaks for adenosine and guanosine residues as well as H2,N1/N3 crosspeaks for adenosine residues. Assignments for all adenosine residues in HIV-2 TAR are given on top of the spectrum (b). The corresponding H2 and H8 proton resonance frequencies are highlighted by vertical wide and narrow dotted lines, respectively. The N7 resonance of G26 interacting with the charged arginine guanidinium group is assigned. Chemical shift regions for the nitrogen resonances giving rise to the observable correlations are given. Peaks marked with an asterisk are due to minor impurities from sample degradation.

Table 1. Aromatic proton and nitrogen chemical shifts (p.p.m.) for TAR RNA bound to argininamide at 25°C in D₂O.

Residue	δ(1H2)	δ(1H5)	δ(1H8)	δ(15N1)	δ(15N3)	δ(15N7)	δ(15N9)
Uridine residues
U23		5.58		144.31	160.09
U25		5.96		144.54	157.77
U31		5.78		143.28	157.51
U38		5.41		147.25	161.07
U40		5.49		147.17	160.98
U42		5.31		146.00	161.06
Cytidine residuesa
C18		5.26		151.17
C29		5.12		151.37
C37		5.19		151.88
C39		5.61		150.64
C41		5.67		151.75
C45		5.16		151.32
Adenosine residues
A20	6.92		7.98	220.40	213.61	230.53	170.56
A22	7.14		7.73	223.40	213.94	229.78	170.66
A27	7.49		7.80	221.12	210.93	229.12	169.21
A35	8.24		8.39	b	218.21	232.20	168.84
Guanosine residues
G16c			8.12		163.31	233.07	168.28
G16c			8.13		163.23	232.60	168.15
G17			7.73		d	233.57	169.67
G21			7.06		162.85	234.33	168.98
G26			7.74		d	230.50	168.91
G28			7.48		d	234.10	169.70
G32			7.77		d	235.99	167.34
G33			7.63		166.50	235.69	169.14
G34			7.89		162.46	236.89	169.02
G36			7.41		162.12	233.69	169.20
G43			7.68		162.08	234.59	169.45
G44			7.32		161.39	233.54	169.08

All proton chemical shifts are referenced to the internal standard TSP and nitrogen shifts are referenced indirectly according to the chemical shift ratio (27).^aCytidine residues 19, 30 and 46 are not assigned due to resonance overlap of the corresponding H5 protons.^bOnly one correlation at the H2 resonance frequency of A35 between the typical N1 and N3 chemical shift regions was observed as seen in Figure 5.^cTwo sets of correlations of similar intensity were observed for the terminal guanosine residue G16, which is likely to be due to 3′-end heterogeneity.^dNot assigned due to resonance overlap.

Watson–Crick A-U base pairs

The INEPT delay (Δ = 28 ms) in the ²J_HN HNN–COSY experiments is suboptimal for the observation of N1 and N3 hydrogen bond acceptor sites in adenosine residues. However, the Watson–Crick base paired N1 nitrogens of A27, A22 and A20 exhibit correlations between the ω₂ (¹H2) protons and the ω₁ (¹⁵N3) nitrogens of U38, U40 and U42, respectively. These correlations were either very weak, or not detected in case of the ²J_HN HNN–COSY experiments carried out in 90% H₂O, 10% D₂O. The observed ^2hJ(N1,N3) coupling constants were 6.0 (A22-U40) and 6.5 (A20-U42) in 99.9% D₂O. Remarkably, the ^2hJ(N1,N3) coupling defining the A22-U40 Watson–Crick base pair can be readily determined using the ²J_HN HNN–COSY experiment, as shown in Figure 3a. The corresponding U40 imino proton is severely exchange-broadened at 298 K and thus not observable in a conventional jump–return HMQC experiment recorded in 90% H₂O, 10% D₂O (Fig. 4), although the U40 imino proton can be observed upon lowering the temperature to 278 K. This typical approach to obtaining NMR data for exchangeable proton resonances at low temperature suffers from the major drawback of significantly broadened lines due to increased solvent viscosity at lower temperatures. The ²J_HN HNN–COSY experiment permits useful cross hydrogen bond correlations to be obtained for Watson–Crick A-U base pairs, independent of imino proton exchange regimes at higher temperatures. The ^2hJ(N1,N3) cross hydrogen bond correlation A27-U38 defining the Watson–Crick part of the base triple could not be analyzed quantitatively using ²J_HN HNN–COSY experiments due to resonance overlap. A single quantitative HNN–COSY experiment carried out in 90% H₂O, 10% D₂O, relying on observable imino proton resonances, yielded ^2hJ(N1,N3) coupling constant values of 6.4 (A27-U38) and 6.2 Hz (A20-U42) (data not shown) (1). Watson–Crick G-C base pairs are not observable using the ²J_HN HNN–COSY experiment. Neither the N3 nitrogens of cytidine residues nor the N1 nitrogens of guanosine residues are accessible via long range ⁿJ(H,N) coupling constants involving non-exchangeable protons, as can be seen in Figure 1c.

Intraresidue two-bond correlations

A number of initially unexpected strong correlations can be observed for guanosines in HIV-2 TAR in the ²J_HN HNN–COSY experiments as shown in Figure 3a. The correlations to guanosine H8 protons at 163 p.p.m. were assigned to intraresidue two-bond transfers from the N9 to the N3. Due to the different electron-donating substituents associated with the guanine ring, the ¹⁵N3 resonance frequencies differ by ~50 p.p.m. with respect to the adenine ring. As expected, the intraresidue ²J(N9,N3) coupling constants for the guanosine residues in HIV-2 TAR are rather uniform with an average value of 3.5 ± 0.2 Hz (n = 8). This is in good agreement with the value of ²J(N9,N3) = 3.7 Hz reported by Buchner et al. for ¹⁵N labeled 3′GMP (35). The complete assignments of the H8,N9 correlations for guanosine residues in the bound form of HIV-2 TAR are shown in Figure 5a. The ¹⁵N chemical shifts for the N3 resonances in guanosine residues are quite uniform, with the exception of G33, which is located in the loop region. The N3 chemical shift of 166.50 p.p.m. differs considerably from the mean value of 162.99 ± 1.55 p.p.m. (n = 8, see Table 1). In addition, the measured associated intraresidue ²J(N9,N3) coupling constant of 3.8 Hz is at the upper limit of the range of observed values. One possible explanation for these small deviations is an intraresidue hydrogen bond formed between the 2′-OH group and the N3 nitrogen. The detailed NOE-based structural studies on the HIV-2 TAR–argininamide complex positioned the O2′ and the N3 nuclei on average within 3.2 Å with 16 out of 20 lowest energy structures fulfilling hydrogen bond criteria, d_O2′ _N3 < 3.9 Å (21). The sugar pucker for G33 is C2′-endo as estimated from ³J(H1′,H2′) couplings and intraresidue NOEs between the aromatic H8 and the H1′, H2′, H3′ and H4′ sugar protons, and the glycosydic torsion angle is anti. No intraresidue ²J(N9,N3) correlation could be observed for the preceding loop residue G32 which most likely can be attributed to degenerate N9 and N3 chemical shifts. Residue G34 shows no noticeable ¹⁵N chemical shift or ²J(N9,N3) coupling constant differences with respect to the other guanosine residues located in regular A-form Watson–Crick duplex regions. The A-form C3′-endo sugar pucker separates the 2′-OH group and the N3 nitrogen by at least 4.1 Å. Additional intraresidue ²J(N9,N3) correlations could be assigned for adenosine residues. As a consequence of the chosen delay duration during the ¹H,¹⁵N INEPT transfer step, these cross peaks are more intense at the H8 proton resonance frequency. However, the corresponding ²J(N9,N3) correlation is also visible at the H2 proton frequency of A20. The measured intraresidue ²J(N9,N3) coupling constant values are 2.9 and 2.8 Hz for A20 and A27, respectively, which is comparable to the reported a value of ²J(N9,N3) = 2.2 Hz for ¹⁵N labeled 3′AMP (35).

Conclusions

The quantitative ²J_HN HNN–COSY experiment may prove to be a general approach for the observation of hydrogen bonding interaction in oligonucleotides where imino protons are often exchange-broadened. Experiments can be carried out in a reasonably sensitive manner under favorable conditions such as D₂O solution and higher temperature because magnetization both originates and is detected on non-exchangeable aromatic protons. The unambiguous identification of hydrogen-bonding interactions allows the introduction of additional distance restraints between donor and acceptor functional groups. This is especially important for structure determination of RNA because of the sparse proton environment with a significant number of protons potentially involved in exchange processes. The application of the ²J_HN HNN–COSY experiment provided chemical shift assignments of N3 resonances in guanosine residues. These potential hydrogen bond acceptor sites are not accessible at all using commonly used multidimensional NMR experiments. ¹⁵N chemical shifts have been used as a guide to identify hydrogen-bonding interaction. The present study revealed an almost complete assignment for non-protonated nitrogen nuclei in purine bases for the bound form of HIV-2 TAR.

The unambiguous verification using NMR spectroscopy of the U38-A27·U23 base triple in the HIV-2 TAR argininamide complex is an important result with implications for similar binding motifs that have been recently observed in other RNA structures. The Tetrahymena group I intron ribozyme active site consists of an identical U-A·U base triple accomplishing substrate docking and catalysis (36). An arginine binding site in the Rev peptide–aptamer complex involves a U-A·U base triple (37). The same base triple forms an arginine recognition site in the bovine immunodeficiency virus (BIV) Tat–TAR complex (38). Furthermore, small molecules mimicking the arginine guanidinium group bind the HIV TAR bulge in a similar manner (39).