Predicting Protein–Ligand Docking Structure with Graph Neural Network

Abstract

Modern day drug discovery is extremely expensive and time consuming. Although computational approaches help accelerate and decrease the cost of drug discovery, existing computational software packages for docking-based drug discovery suffer from both low accuracy and high latency. A few recent machine learning-based approaches have been proposed for virtual screening by improving the ability to evaluate protein–ligand binding affinity, but such methods rely heavily on conventional docking software to sample docking poses, which results in excessive execution latencies. Here, we propose and evaluate a novel graph neural network (GNN)-based framework, MedusaGraph, which includes both pose-prediction (sampling) and pose-selection (scoring) models. Unlike the previous machine learning-centric studies, MedusaGraph generates the docking poses directly and achieves from 10 to 100 times speedup compared to state-of-the-art approaches, while having a slightly better docking accuracy.

Graphical Abstract

INTRODUCTION

The broad area of computational drug discovery has seen significant advancements during the past decade, achieving impressive results for identifying drugs targeting different diseases.^1–5 The traditional drug discovery process typically takes multiple years and costs billions of dollars.^6–9 To accelerate the drug discovery process, various computational docking approaches^10–15 have been proposed, in the past, for virtual drug screening. Most existing computational docking methods are based on physical force fields and customized potential functions. Unfortunately, docking software usually suffers from both low accuracy and long latency.

In general, existing computational docking protocols include two main steps—sampling and scoring. The first step involves sampling as many ligands poses as possible in a reasonable (or user-specified) number of steps. Since searching the whole conformational space is impractical, mainly due to a large number of flexible rotamers of the ligand and protein side chains, many docking software adopt heuristic strategies to reduce the searching space. For example, MedusaDock,^10,11,16,17 MCDOCK,¹² and ProDock¹⁸ employ Monte Carlo (MC)¹⁹ algorithms. In comparison, AutoDock^13,20–22 and GOLD¹⁴ adopt genetic algorithms (GA),²³ which start first with an initial pose and then progressively identify more precise poses. In contrast, FlexX¹⁵ employs a fragment-based method,²⁴ which starts the search with fragments with low binding affinities. Unfortunately, all the aforementioned approaches cannot investigate all possible docking structures in a single run due to the immense searching space. The initial searching status and the searching direction are highly dependent on the random seed. As a result, to identify at least one good pose by those searching algorithms, the users have to invoke the software many times (sometimes up to thousands of times), thus spending several hours to several days to obtain the final docking pose of one protein–ligand complex.^25–27 Ideally, if given an infinite execution time budget, the users can exhaustively search all possible docking poses (which is unrealistic) and definitely visit the best docking pose. However, this will generate an extensive number of not-acceptable poses, which have to be discarded after scoring. Motivated by this observation, if we could somehow refine/convert some “bad” poses into “better” poses, we can avoid the time wasted in the sampling process.

In the scoring step, the free energy of the protein–ligand complex is calculated to evaluate the binding affinity. The accuracy of the scoring function dictates the accuracy of the docking. There are two major types of scoring functions: physics-based,^22,28–33 knowledge-based,^34–38 or hybrid.^39–42 Physics-based scoring functions compute the interactions among atoms based on force fields. For example, MedusaDock^10,11,16,43 employs MedusaScore¹⁷ as the scoring function, which takes into consideration covalent bonding, van der Waals (VDW⁴⁴) interaction, hydrogen bonding, and solvation effects. On the other hand, knowledge-based scoring functions calculate the energy based on known knowledge extracted from experimentally solved protein–ligand 3D structures. The primary limitation of the knowledge-based scoring functions is the difficulty of evaluating the binding affinity of unknown protein–ligand complexes. As a result, although knowledge-based scoring functions improved the docking accuracy for known protein–ligand complexes, they suffer from limited accuracy for complexes that have not been solved before.

Recently, various machine learning-based scoring functions have been proposed. For example, Wang and Zhang⁴⁵ employ a random-forest scoring function to evaluate the goodness of a protein–ligand docking pose. AGL-Score⁴⁶ learns the protein–ligand binding affinity based on the algebraic graph theory. Sánchez-Cruz et al.⁴⁷ extract the learning features based on the protein–ligand atoms-pair interconnection and predict the binding affinity with random forest (RF) and gradient boosting trees (GBT). AtomNet⁴⁸ maps the atoms near a binding site into a 20 Å grid and uses a 3D-CNN model to predict the binding probability for each protein–ligand complex. Similarly, Ragoza et al.⁴⁹ also build a 3D-CNN model to predict the protein–ligand binding affinity. Kdeep⁵⁰ employs a 3D-CNN model to predict the binding affinity of a protein–ligand complex based on its 3D structure. TopologyNet⁵¹ employs a hierarchical structure of a convolutional neural network to estimate the protein–ligand binding affinity upon mutation. Graph neural network (GNN)-based approaches have also been proposed to target the protein–ligand scoring problem. For instance, Lim et al.⁵² employ two GNN models with attention mechanisms to calculate docking energies. The first model takes the structure of the protein–ligand complex as the input graph, whereas the second one takes, as input, the protein and ligand structures separately. The binding affinity is inferred by the subtraction between the two models. In comparison, Morrone et al.⁵³ investigate the ranking of a docking pose from the docking software as a feature to predict the score of that pose. Torng et al.⁵⁴ compute the total energy of both the protein and ligand with different GNNs. TorchMD-NET⁵⁵ is an equivariant transformer that predicts properties of the molecules. The output features of the two networks are then concatenated together to predict the docking energy.

Although these machine learning-based approaches improve the scoring, they rely heavily on the pose sampling strategies adopted in conventional docking software. More specifically, to obtain the final docking pose of a protein–ligand complex, all previous machine learning-based approaches evaluate all the ligand poses sampled by conventional docking software and then select the near-native ones^a. As a result, it may still take hundreds of runs of conventional docking software to obtain a good ligand pose. Additionally, some machine learning-based approaches are not able to distinguish the poses with RMSDs between 2 and 4 Å (with respect to the crystal structure) since they omitted such poses in the training and testing sets.

Motivated by these observations, in this work, we propose and evaluate a new GNN-based approach, MedusaGraph. Compared to existing neural network based methods,^{48,49,52,54,56} MedusaGraph can (i) predict the docking poses directly without an additional sampling process in the computational docking software, (ii) accurately identify not only near-native poses and far-native poses but also the poses around the borderline (e.g., the pose with RMSD between 2 and 4 Å), and (iii) have a higher chance to identify the good poses for a protein–ligand complex compared to the computational docking software and existing machine learning-based docking approaches.

METHODS

Our proposed approach includes two GNNs. The first network predicts the best docking pose for a protein–ligand pair from an initial docking pose, and the second one evaluates the output pose from the first network and predicts if the pose is near native. Our extensive evaluations reveal that we can efficiently predict “good docking poses” without sampling thousands of possible docking poses. The Methods section is divided into two parts where each part corresponds to a GNN. In each part, we first explain how to prepare the data for the model training/testing and then introduce the details of the model. After that, we give an example to illustrate how we use MedusaGraph to obtain the docking pose for a protein–ligand complex.

Pose Prediction.

Data Preparation.

For the pose-prediction GNN model, we compiled a data set based on the PDBbind 2017 refined set⁵⁷ using the strategy outlined in Wang and Dokholyan.¹¹ The protein–ligand complexes with less than two rotatable bonds as well as the proteins that have more than one ligand have been removed. We have also removed the proteins with missing residue or duplicated residues. The final data set contains 3738 protein–ligand complexes. To train the GNN model, we have randomly selected 80% of the proteins as training data, and the remaining 20% have been reserved as testing data. To make sure the training set and the testing set do not share similar proteins, we use CD-HIT^58,59 to cluster the proteins with CD-HIT’s default setting (sequence identity cutoff as 0.9) before we do the random splitting. In our method, we use MedusaDock to generate an initial docking pose for each protein–ligand complex. More specifically, we run MedusaDock with a given random seed to perform one iteration of the sampling process to generate several candidate docking poses as the initial docking pose. Note that the binding site information is already given in the PDBbind data set. The initial pose is then translated into a graph representation, where each vertex represents an atom in the complex, and the edges in the graph indicate the connection between the nodes (e.g., the covalent bond or the interactions between nearby atoms). The input feature of the pose-prediction model is a N by 21 tensor, where N indicates the number of atoms in the complex. The feature for each vertex has a length of 21. The first 18 elements represent a categorical feature that indicates the type of the atom. The last three elements include the 3D coordinate of the atoms ($x,y,z$)in the initial pose. To construct the graph from the protein–ligand complex, we add an edge between the atoms if there is a covalent bond between these two atoms. We also add an edge between a protein atom and a ligand atom if their distance is less than 6 Å since the nearby atoms will have a higher chance to interact with each other. We select this 6 Å threshold inspired by some previous work.^16,49,52,60 The edge features in the graph include the distance between the vertices and the type of connection (protein–ligand, protein–protein, or ligand–ligand). We list the node features and the edge features in Table 1.

Table 1.

Summary of Node Features and Edge Features^a

	Index	Features
Node Features	1–18	Atom type (N, C, O, S, Br, Cl, P, F, I)
	19–21	3D coordinates in $x,y,z$
Edge Features	1	Ligand–ligand distance
	2	Protein–ligand distance
	3	Protein–protein distance

^aFor the atom type feature, we consider the same type of atoms in the protein and ligand as different atom types. We use one-hot encoding for atom types where only the corresponding index has the value of one, while other indices contain zero values.

Graph Neural Network Model.

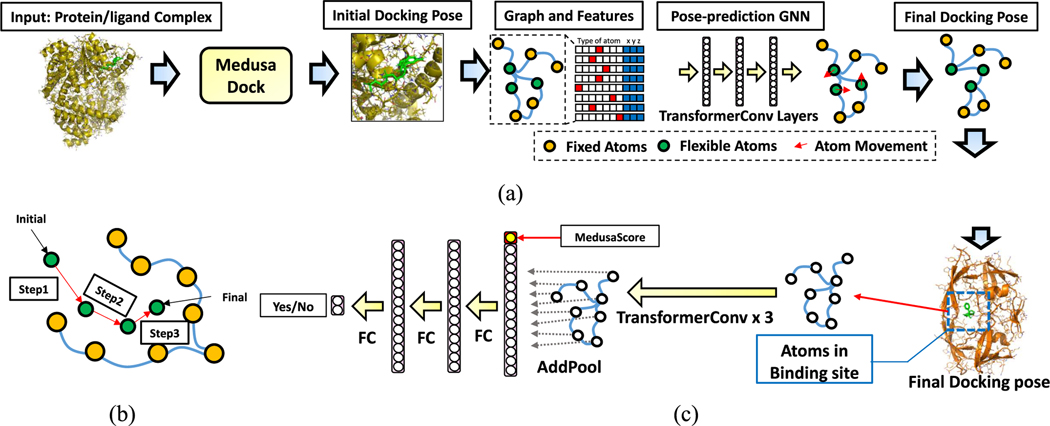
As shown in Figure 1a, our first GNN, called the Pose Prediction GNN, takes the initial pose of a protein–ligand pair as the input. During docking, the positions of the ligand atoms will move, while the protein atoms are more likely to be immobile. On the basis of this observation, we divide the nodes in the graph into two parts–fixed nodes and flexible nodes. The pose-prediction graph neural network is a vertex regression model which calculates the movement for the flexible nodes and outputs the moving vector $(x,y,z)$, which indicates the movement along each axis. We use the TransformerConv layer⁶¹ to implement this network. The transformer convolution layer employs the attention mechanism which captures the importance between each pair of atoms. Also, it includes the edge features (e.g., edge type, distance) as inputs feature. As a result, the TransformerConv can more precisely compute the interactions between the atoms in a protein–ligand complex. The TransformerConv layer calculates the output feature of each node using the following equation

$$x_i^{\prime }=W_1{x}_i+\sum _{j\in N(i)}{\alpha }_{ij}\left(W_2{x}_j+W_3{e}_{ij}\right)$$

where $x_i$ is the input feature vector of the node $i$, $x_i^{\prime }$ the output feature vector for node $i$, and $N(i)$ the set of the neighboring nodes for node $i$. The attention matrix ${\alpha }_{ij}$ is calculated using

$${\alpha }_{ij}=\text{softmax}\left(\frac{{\left(W_4{x}_i\right)}^{\text{T}}\left(W_5{x}_j+W_3{e}_{ij}\right)}{\sqrt{d}}\right)$$

where $x_i$ indicates the input feature of node $i$, $e_{ij}$ the edge feature of edge $\langle i,j\rangle$, and $d$ the hidden size of the node feature; all Ws are “learnable” weight matrices. The attention matrix ${\alpha }_{ij}$ helps the network distinguish between the importance of different neighbors for each and every atom. The output feature vector of the first three TransformerConv layers has 256 hidden neurons, while the last TransformerConv layer has an output size of three (which indicates the movement in $x$, $y$, $z$ axes). We then add up the coordinates of the flexible nodes in the initial pose with the moving vector of those nodes to obtain the coordinate of the flexible nodes in the final docking pose. Unlike equivariant networks,⁵⁵ we have fixed the location of the protein atoms, and the coordinates of the ligand atoms are related to the protein atoms. As a result, rotating the entire protein–ligand complex does not affect the final complex structure prediction. Similar to some human body pose prediction work,^62,63 we use L1-loss⁶⁴ as the loss function as below

$$L=\sum \left|x_c^i-x_1^i-x^i\right|+\left|y_c^i-y_1^i-y^i\right|+\left|z_c^i-z_1^i-z^i\right|$$

where $\left(x_1^i,y_1^i,z_1^i\right)$ is the initial coordinate of the $i\text{th}$ atom, $(x_c^i,y_c^i,z_c^i)$ the coordinate of the $i\text{th}$ atom in the X-ray crystal structure, and $\left(x^i,y^i,z^i\right)$ the moving vector predicted by MedusaGraph for the $i\text{th}$ atom. During the training, only the flexible nodes contribute to the loss function, since we only want to predict the movement of the flexible nodes.

Figure 1.

(a) Flow of the pose-prediction GNN model. We first run MedusaDock on a protein–ligand complex to achieve a candidate docking pose. Then, the pose-prediction model calculates the movement of each flexible atom in the complex. Flexible atoms include all the ligand atoms and the receptor atoms that are near the receptor surface. Finally, we obtain the final docking pose based on the movement prediction. The pose-prediction GNN model contains several TransformerConv layers. (b) Multistep pose-prediction. An atom moves from the initial location to the final location step-by-step. (c) Flow of the pose-selection GNN model. The final poses generated by the pose-prediction model travel through three TransformerConv layers and three fully connected layers. The final output is the Yes/No neuron indicating the docking probability.

Multistep Pose Prediction.

In our exploration, we observe that our pose-prediction GNN model cannot accurately estimate the movement of some atoms (from an initial location to a ground-truth location). This is because our estimation is highly based on the interactions between the atoms. Ideally, for each atom, the model will calculate the force from other atoms and calculate which direction this atom will move and how long it will move. However, for some atoms which are far away from the ground-truth pose, we need additional iterations to simulate the movement from the initial location to the final location. As a result, we propose a multistep pose-prediction mechanism to calculate the final location of each atom step-by-step (as shown in Figure 1b). More specifically, we divide the path from the initial location to the final location into several steps, and we train multiple models to predict the atom movement in each step. The output of the $i\text{th}$ model will be the input of the $(i+1)\text{th}$ model. The output of the last model (for all atoms) will be considered as the final predicted pose. It is important to note that we also change the connection between the protein atoms and the ligand atoms after each iteration of the atom movement prediction. This is because the location of the atoms are changed, and some nearby atoms could become far away from each othe,r while some other atoms could come closer.

Pose Selection.

Data Preparation.

We also compile a pose-selection data set from the PDBbind pose prediction data set,²⁵ which is generated as described in the previous section. After we obtain the initial docking pose (the graph structure) for each complex, we apply our pose-prediction GNN to the initial docking poses and obtain the final docking poses for each complex. We divide all the final poses into two groups: (i) good poses and (ii) bad poses. Good poses have RMSD values that are less than or equal to 2.5 Å with respect to the crystallographic structure, and bad poses have RMSD values that are greater than 2.5 Å. We choose the split threshold as 2.5 Å based on the choice of the previous works. Usually, this threshold is selected between 2 and 4 Å.^25,49,52 This data set will be used to train and evaluate our pose-selection GNN model. The pose-selection GNN model is expected to identify if a pose is a good one or not. The training/testing sets split remains the same as the data set for pose prediction. The poses for the same protein will be included in either the training set or the testing set.

Graph Neural Network Model.

After the final docking pose is generated, our second GNN, referred to as the Pose-Selection GNN, will predict if such a pose is a good pose or not. This network is basically a graph binary classification model. The input feature format is the same as the first network, which means we translate a pose into the graph representation. As shown in Figure 1c, our model includes three TransformerConv layers to calculate the features of each and every node based on its neighbors. After that, the features of the flexible nodes are added together with an add-pooling layer. The MedusaDock energy (MedusaScore) of that pose is concatenated into the feature vector after the pooling layer. This MedusaScore can be obtained when we generate the initial docking pose with MedusaDock. Finally, there are three fully connected layers at the end of the network to predict the probability of each pose, i.e., if it is a good pose or not. The output of the network is a two-neuron tensor, which indicates (in a probabilistic fashion) whether the pose is a good one or a bad one.

Example Docking Process with MedusaGraph.

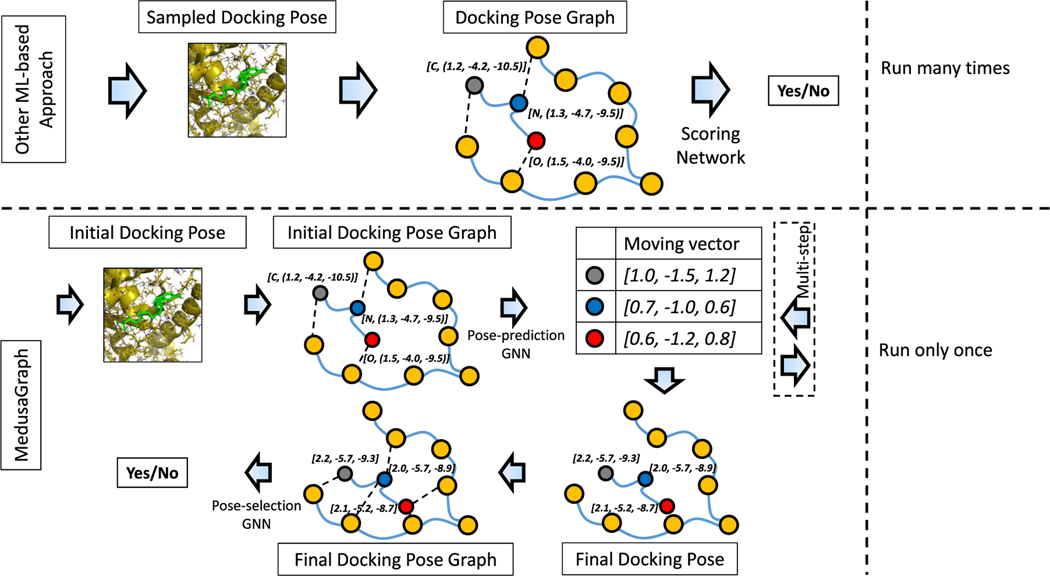
To better explain the flow of our proposed framework, in this section, we go over an example use of MedusaGraph to obtain a docking pose for the protein–ligand complex depicted in Figure 2 and compare it against the prior ML-based docking approach. In the prior ML-based approaches, a user first generates the sampled docking poses for a protein–ligand complex using a conventional docking software. After that, the sampled poses are converted into the docking pose graphs. These graphs are then input to the scoring networks to predict the docking probability of each corresponding docking pose. On the basis of the prediction results, the user can select the good poses from among the sampled poses. Note that this process is typically repeated many times since a single running of the conventional docking software might not be able to find any good pose.

Figure 2.

Example of generating the docking pose with MedusaGraph and other ML-based approach.

On the other hand, in our proposed MedusaGraph, after MedusaDock generates the initial pose for the protein–ligand complex, the first step is to convert the initial pose into the graph structure (complex graph). In this example, three ligand atoms (blue, red, and gray nodes) are considered flexible nodes, whereas the remaining atoms (orange nodes) are fixed nodes, which represent the protein atoms.^b We add edges between the atom pairs with covalent bonds. We also add an edge between a protein atom and a ligand atom if they are close, since nearby atoms have a higher chance of affecting each other. Each node contains the type of the atom and the 3D coordinate as a “node feature”, and each edge contains the type of the connection and the distance as “edge feature”. This graph structure annotated with the mentioned features is then fed into the pose-prediction GNN model to predict the movement of each atom. The output of the model is a 3 by 3 tensor, indicating the $(x,y,z)$ of the moving vector for three flexible nodes. We can compute the final position of each flexible atom by adding the initial coordinate and the moving vector together. For example, for the nitrogen atom (blue node) with an initial 3D coordinate of (1.2, −4.2, −10.5), the GNN model predicts its moving vector as (1.0, −1.5, 1.2), and the final position is calculated as (2.2, −5.7, −9.3). To apply our multistep prediction, we reconstruct the complex graph with the calculated coordinate as the initial coordinate and iteratively feeds it into the pose-prediction model. After we obtain the final docking pose, we construct a final docking pose graph (similar to the docking pose graph in other ML-based approaches) and send the graph representing the final docking pose to the pose-selection GNN model. This GNN model in turn predicts the probability that this final docking pose is a good pose. We want to emphasize that, compared with other ML-based approaches, MedusaGraph does not have to be invoked multiple times to ensure at least one good pose is sampled. This is because, even if an initial pose generated by MedusaDock is a bad pose, the pose-prediction GNN model will very likely convert it into a good pose.

RESULTS

Comparison of MedusaGraph against Existing Pose-Prediction Schemes.

We first evaluate the quality of the poses generated by our pose-prediction GNN model trained on the PDBbind pose-prediction data set. In this context, we measure the “goodness” of the pose by RMSD with respect to the X-ray crystal pose (ground-truth pose). Additionally, since our model can predict the final docking pose directly, we expect our approach to be much faster than other existing approaches. We compare our approach against two state-of-the-art docking frameworks (MedusaDock^10,17 and Autodock Vina²¹). To find the best docking pose for each protein–ligand complex, MedusaDock and Autodock Vina need to sample different candidate poses and calculate the energy score of each candidate. We run MedusaDock and Autodock Vina with different random seeds until we cannot find a pose with a lower energy score. We also compare MedusaGraph against two convolutional neural network (CNN)-based approaches (AtomNet⁴⁸ and MedusaNet²⁵) and a graph neural network (GNN)-based approach (Graph-DTI⁵²). Since these neural network models can only do scoring, we utilize conventional docking approaches (MedusaDock and Autodock Vina) to generate the poses for them. For the CNN-based approaches (AtomNet and MedusaNet), we generate poses with MedusaDock. Specifically, we run MedusaDock with different random seeds and stop when the CNNs determine they have found eight good poses. Finally, for Graph-DTI, we run AutoDock Vina²¹ with a random seed of 0 and set the exhaustiveness parameter to 50 to ensure that AutoDock searches the conformational space thoroughly.

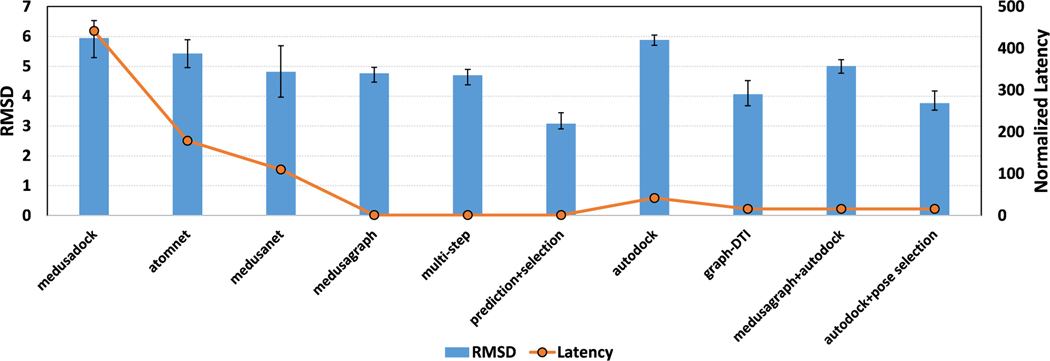
We report, in Figure 3, the average RMSD of output poses for each of the approaches tested. We also report the normalized latency of each method. Note that the execution time of the neural network is usually negligible compared to conventional docking software (MedusaDock and AutoDock). As a result, we consider the latency of one run of MedusaDock as 1 unit and normalize the latencies of all other approaches. One can observe the following from these results: (i) MedusaGraph achieves significant speedups compared to the other approaches. (ii) MedusaGraph’s output poses have similar average RMSD values to other approaches (less than 0.7 Å). Further, if we apply our pose-selection model to the output poses, the average RMSD of the output poses drops to 2.9, which is much better than those obtained by using the other methods. This indicates that it is easy to distinguish the near-native pose from the poses generated by the pose-prediction GNN model. (iii) MedusaGraph can also be applied to other docking software (e.g., Autodock) to improve their generated poses.

Figure 3.

Average RMSD of the output poses for each approach. For the normalized latency, we set the execution time of one running of MedusaDock as 1 and normalized all other approaches. We randomly split the data set into a training set and a testing set 10 times to perform the cross-validation, and the error bar indicates the min/max RMSD value of each cross.

Statistical Analysis of Predicted Poses.

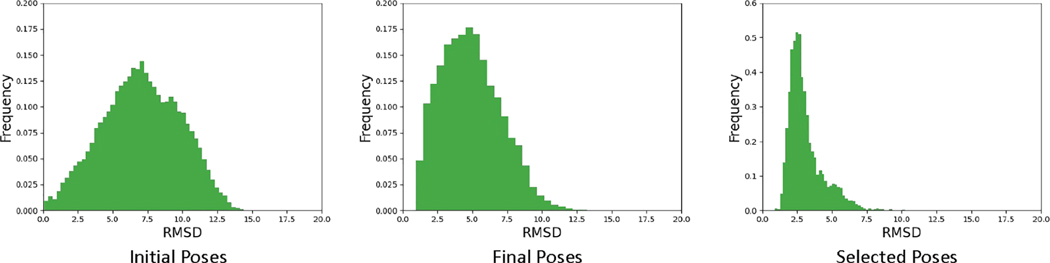
We observe that the average RMSD of the poses generated from the pose-prediction GNN model is around 5 Å. This is far away from the crystal structure. However, this result is still good enough considering that these values are the average RMSD of all the poses. On the other hand, one can also be interested in the “percentage of good poses” among all generated poses. In other words, have our pose-prediction models improved the percentage of good poses compared to the original MedusaDock output poses? To answer this question, we have also evaluated the distribution of the poses we generated. We plot the histograms for the RMSDs of all selected poses in Figure 4. It can be observed that the RMSD distributions of the poses generated by the pose-prediction model have significant shifts to the left compared to the original poses, indicating that our pose-prediction model can improve the poses generated by MedusaDock. After we have applied the pose-selection models to the output poses, most poses have a small RMSD as shown in the right panel.

Figure 4.

Histograms of RMSDs of all poses for initial docking poses generated by MedusaDock: the final docking poses generated by the three-step pose-prediction model and the poses selected by the pose-selection model.

We have also calculated the percentage of the poses with an RMSD value less than 2.5 Å (which we consider a “good pose”) among all the poses generated by each approach. Here, 5.9% of the original poses generated by MedusaDock have their RMSD less than 2.5 Å. After we have applied our pose-prediction model, 14.4% of the poses are less than 2.5 Å. Additionally, 37.6% of poses are near native if we use the pose-selection model. These results clearly show that our pose-prediction model can help the protein–ligand complexes find more near-native poses. Further, our pose-selection model can help to choose good poses among all candidate poses.

Study of Ligands with Different Properties.

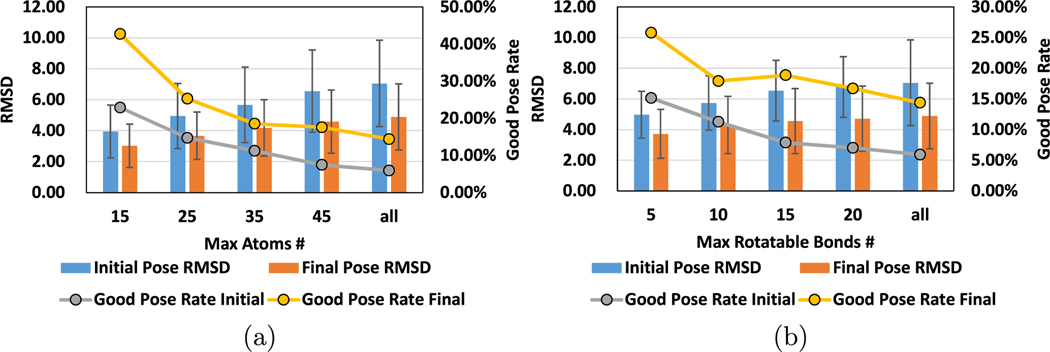
As also discussed in prior studies,^16,25,60 some protein–ligand complexes are easier to find good poses than others. This is mainly because the flexibility of each complex can be different from the others. In general, if a ligand has more atoms, or the ligand has more rotatable bonds, the resulting complex makes it more difficult to find good poses. In this part of the evaluation, we first classify all the complexes we evaluated in our approaches based on the number of atoms and the number of rotatable bonds. We then show the accuracy results of our approach with each class of the complexes in Figure 5. It can be seen from this plot that the complexes with ligands that have fewer atoms and rotatable bonds result in low RMSD poses. However, it should be emphasized that, for all classes of complexes tested, our approach can improve the final docking poses in terms of the RMSD value.

Figure 5.

We show the average RMSD of the initial poses and final docking poses for the complexes with different properties. We also calculate the good pose (with RMSD less than 2.5 Å) rates in initial docking poses and final docking poses. (a) Results of the complexes with a different number of atoms. (b) Results of the complexes with a different number of rotatable bonds.

Evaluation of Pose-Selection Models.

Our pose-selection GNN model can select the good poses from among all generated poses to potentially improve the final pose. In this part of our evaluation, we performed two computational experiments to test the robustness of the pose-selection GNN model. We first train the pose-selection model (and three state-of-the-art machine learning-based models) on the original poses generated by MedusaDock. Second, we train the pose-selection model on the poses generated by our pose-prediction GNN model. We show the accuracy and AUC in Table 2. Here, Accuracy is defined as the fraction of the total poses an evaluated approach correctly predicts. On the other hand, AUC is the area under the ROC curve, which is widely used to determine how well a binary classification model can distinguish between two groups of data. It is defined as the true-positive rate against the false-positive rate. Hence, an AUC of 1 indicates a perfect model, while an AUC of 0 means an entirely wrong model. A model with an AUC of 0.5 is considered to be close to a random selection. We can observe from these results that our pose-selection GNN model performs better on the poses generated by the pose-prediction model than the poses generated by MedusaDock, meaning that it is easier to select good poses from the poses generated by our pose-prediction GNN model than selecting from the initial set of poses.

Table 2.

Evaluation of MedusaGraph against Other Approaches in Terms of Classification Accuracy and AUC^a

	Accuracy			AUC
Evaluation metric	avg	min	max	avg	min	max
Medusadock	N/A	N/A	N/A	0.474	0.462	0.489
Atomnet	0.741	0.628	0.872	0.863	0.849	0.885
Medusanet	0.855	0.705	0.93	0.893	0.868	0.915
Autodock Vina	N/A	N/A	N/A	0.615	0.592	0.636
Graph-DTI	0.895	0.836	0.953	0.906	0.876	0.933
Pose selection	0.914	0.855	0.954	0.892	0.866	0.923
Pose prediction+selection	0.958	0.940	0.981	0.960	0.943	0.985

^aWe evaluate these approaches on the PDBbind test set. Note that the accuracies for MedusaDock and Autodock Vina are marked as N/A because the scoring function of MedusaDock and the affinity score of Autodock cannot be used to distinguish between a good pose and bad pose. It can only be used to compare the goodness of two poses.

Evaluation on External Data set: CASF.

To evaluate the effectiveness of MedusaGraph on external data sets, we train our graph neural network model with the aforementioned PDBbind data set and test it with the CASF data set.^65–67 CASF contains 285 proteins with their corresponding ligands, and it also provides the optimal docking structure for each protein–ligand pair. When training the GNN model with PDBbind data set, we remove the proteins that are also included in the CASF data set to avoid data bias. From Table 3, we can observe that the proposed poses predicted by MeusaGraph are better than other approaches, indicating that MeusaGraph can work on different docking power benchmarks that are widely used in the drug discovery community.

Table 3.

Average RMSD of All Poses Generated by Each Approach on CASF

	MedusaDock	Autodock	Pose prediction	Pose prediction+selection
RMSD	5.491	5.617	4.331	2.812

DISCUSSION

We would like to emphasize that MedusaGraph differs from other neural network-based methods^52,54,56 in three aspects. First, existing ML-based approaches can only predict, for each candidate docking pose generated by docking software, if it is a good pose or not, whereas MedusaGraph takes a candidate docking pose as the input and produce the good docking pose directly. Second, while other ML-based approaches require conventional docking software to sample a large amount of the possible docking poses, MedusaGraph only requires one running of the conventional docking software, as we can convert a candidate docking pose (initial pose) to a good docking pose. Since the sampling process in the docking software is the latency bottleneck, MedusaGraph can significantly save the execution time compared with other neural networks. Third, MedusaGraph explicitly leverages the “atom distances” as “edge features” by employing the transformer convolution layers. This implementation can improve the accuracy of the network since distance plays an important role in the atom-wise interaction.²⁵

DATA AND SOFTWARE AVAILABILITY

All the protein–ligand data are available though the website of PDBbind at http://www.pdbbind.org.cn. MedusaDock, MedusaNet, and implementation of AtomNet are available via https://github.com/j9650/MedusaNet. The script of data preprocessing and the implementation of MedusaGraph can be found at https://github.com/j9650/MedusaGraph.