Abstract
Colorectal cancer is the third most common type of cancer diagnosed annually, and the second leading cause of death due to cancer. Early diagnosis of this ailment is vital for preventing the tumours to spread and plan treatment to possibly eradicate the disease. However, population-wide screening is stunted by the requirement of medical professionals to analyse histological slides manually. Thus, an automated computer-aided detection (CAD) framework based on deep learning is proposed in this research that uses histological slide images for predictions. Ensemble learning is a popular strategy for fusing the salient properties of several models to make the final predictions. However, such frameworks are computationally costly since it requires the training of multiple base learners. Instead, in this study, we adopt a snapshot ensemble method, wherein, instead of the traditional method of fusing decision scores from the snapshots of a Convolutional Neural Network (CNN) model, we extract deep features from the penultimate layer of the CNN model. Since the deep features are extracted from the same CNN model but for different learning environments, there may be redundancy in the feature set. To alleviate this, the features are fed into Particle Swarm Optimization, a popular meta-heuristic, for dimensionality reduction of the feature space and better classification. Upon evaluation on a publicly available colorectal cancer histology dataset using a five-fold cross-validation scheme, the proposed method obtains a highest accuracy of 97.60% and F1-Score of 97.61%, outperforming existing state-of-the-art methods on the same dataset. Further, qualitative investigation of class activation maps provide visual explainability to medical practitioners, as well as justifies the use of the CAD framework in screening of colorectal histology. Our source codes are publicly accessible at: https://github.com/soumitri2001/SnapEnsemFS.
Subject terms: Cancer, Health care, Engineering, Mathematics and computing
Introduction
Colorectal cancer (CRC)1 is caused by the growth of polyps on the inner lining of the colon (or rectum) which is primarily due to mutation in certain genes that trigger an uncontrollable cell division, causing malignant cells to rapidly grow throughout the layers of the rectum as well as into the blood or lymph vessels. Being one of the leading causes of death in both developing and developed nations with a mortality rate of nearly , the lifetime risk of developing CRC is about among men and among women2. However, early detection and diagnosis of this disease can increase the survival rate by almost 3, which stresses the requirement of a robust framework for the same. The conventional medical practices to detect CRC include stool-based tests and structural analysis of spectral imaging of colon and rectum linings4. However, stool-based tests only provide results for a limited time and therefore, needs to be done more often, while visual screening is prone to subjective variability as it is highly dependent on the observational capabilities of the pathologists5. Thus, an automation-assisted Computer-Aided Diagnosis (CAD) framework for histological analysis becomes a pressing need for robust detection of CRC while it is still in its early stages to prevent the spread of the disease to other vital organs.
Machine learning-based methods have largely been used in the past for the detection of CRC like the methods proposed by6–8. However, traditional machine learning methods require handcrafted features to be extracted from the image data. Such methods fail for complex pattern recognition tasks and it is also difficult to design a set of features that can accurately represent varied kinds of data.
On the contrary, deep learning methods9–11 alleviate the problem of traditional machine learning methods by performing end-to-end classification. Deep learning-based methods, especially Convolutional Neural Networks (CNNs) have become popular for medical image diagnosis tasks because of their ability to learn relevant features automatically from the input data. However, CNNs require a large amount of training data for achieving desirable performance which is often expensive to obtain, especially in the biomedical domain. Transfer learning is one of the solutions to this problem, where a model trained on a large dataset such as ImageNet12 is reused on the current problem containing a small dataset. In this study, we use the MobileNet-V213 CNN model pre-trained on the ImageNet12 dataset that contains 14M images belonging to 1000 classes.
Ensemble learning10,11,14 is a fusion strategy that amalgamates the salient properties of multiple models and is popularly used in literature. However, ensembling two or more deep learning models can be a very computationally costly operation since each model needs to be trained separately for the fusion. This limits its use in many practical applications where there is a resource constraint. To this end, in this paper, we explore a different approach, where we perform an ensemble of snapshots of the same CNN model. That is, the CNN model is trained only once, and during its training, model snapshots are saved at different checkpoints. We extract features from the model snapshots (from the CNN model’s penultimate fully connected layer) and fuse them. However, since the features are extracted from the same CNN model (MobileNet-V2 in this case) at different training epochs, there must be some degree of redundancy in the overall feature vector. This is because though we take different snapshots, however, all the CNN models (here snapshots) will try to learn some common features from the data fed to the model. Hence, to eliminate the redundancy and to retain the important features only, we use a swarm-intelligence based meta-heuristic, called Particle Swarm Optimization (PSO) algorithm15, which in turn, selects the optimal subset of features from the feature space. This also reduces the storage requirements of the framework and makes the overall model computationally more efficient. We evaluate the performance of the proposed framework on the CRC detection problem using the publicly available dataset prepared by16, where our model is seen to outperform many state-of-the-art methods. Furthermore, we employ gradient-weighted class-activation mapping (Grad-CAMs), a weakly supervised segmentation algorithm17 that produces a heat map corresponding to the activations of the last convolutional layer, followed by its superimposition on the original histological image (please refer to section “Analysis of the proposed model” for a lucid explanation). This highlights the class-discriminative regions of interest found by our proposed model, which can of great help to medical practitioners in their decision-making process, making our framework a very useful CAD tool that can be easily leveraged in real-world prognosis.
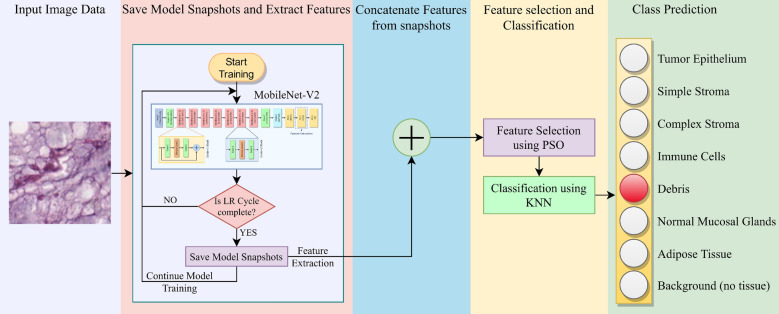
The overall workflow of the proposed method is shown in Fig. 1. Specifically, our key contributions may be summarized as follows:
An ensemble learning-based deep FS framework is proposed for efficient and improved classification of CRC histological images.
Snapshot ensemble technique18 is adopted which allows using an ensemble of neural networks at the cost of training a single CNN model only.
PSO15 algorithm is used to perform FS on the fused feature set to choose the most relevant features from the feature space, thereby enhancing the performance of the framework as well as reducing storage requirements.
The proposed model is evaluated on a publicly available CRC histology dataset16 using a 5-fold cross-validation scheme and compared with several state-of-the-art methods, justifying its reliability and robustness for the CRC detection.
Last but not the least, the present work also investigates into Grad-CAMs obtained by the proposed model, which provide visual explainability and justification of the CAD pipeline that can aid medical practitioners in localising the region(s) of interest for medical prognosis.
The rest of the paper is organized as follows: Section “Related work” provides a comprehensive literature survey pertaining to the development of state-of-the-art in the domain of CRC detection; section “Proposed method” presents a detailed description of the proposed framework for the classification of histological images for CRC detection; section “Results and discussion” evaluate the proposed method on a publicly available dataset and provides a comparative study to establish the superiority of the method with respect to existing methods in the literature; and finally, section “Conclusion” concludes the findings from this research.
Figure 1.
Overall framework for the detection of colorectal cancer from histology images. The Learning Rate (LR) cycle refers to the cycle intervals according to the cosine annealing learning rate scheduler used in this study. The model training continues until the maximum number of epochs is reached, while the features are extracted from the penultimate fully connected layer of the CNN model (refer to section “Transfer learning-based snapshot model training” for further explanation).
Related Work
The development of a robust framework for the diagnosis of CRC is essential owing to its high mortality rate and widespread prevalence. One of its facets includes texture analysis of histological images16,19–22, which typically consist of an image pre-processing step followed by feature extraction, after which classification is performed using traditional machine learning algorithms. The handcrafted features may be extracted using texture filters such as Haralick23, Gabor24 and Local Binary Pattern (LBP)25, to name a few. Extracted LBP features from digitized colorectal tissue microarrays and trained a support vector machine (SVM) to classify between epithelium and stroma based on texture19. Studied multispectral imagery analysis of CRC histology biopsy samples and achieved an accuracy of by training an SVM classifier with LBP features20. Proposed a texture analysis framework for CRC detection by extracting features from multispectral optical microscopy images based on Laplacian-of-Gaussian (LoG) filter, discrete wavelets (DW) and grey level co-occurrence matrix (GLCM) based features21. Feature selection (FS)26–29 methods have also been leveraged in literature to select the most relevant features from the original feature set, extracted by some means, for improving upon the textural classification task. Performed spatial analysis of colon biopsy samples using Circular LBP features followed by a novel clustering-based FS method; the selected features were then used for training an SVM for classification, obtaining an accuracy of 30. The authors of31 performed FS using the Genetic algorithm on the fractal, curvelet coefficients and Haralick textural features from H &E stained histological images and reported an accuracy of 31. The authors of32 proposed a clustering-based modified Harmony Search Algorithm33 for FS on a CRC gene expression dataset, achieving an accuracy of . However, these approaches may not be suitable enough for practical use as they were focused on the binary classification of tissue types, whereas histological images generally comprise multiple categories. The first study on multi-class texture separation of colorectal tissues was proposed by16, which presented a new dataset of 5000 histological images of human CRC including 8 tissue categories (described in Table 1)—the dataset we have used in this research. The authors performed classification by training several classifiers using multiple textural features, obtaining the highest accuracy of on the multi-class classification task.
Table 1.
Classes of images in the CRC histology dataset16 used in this research.
| Class | Category |
|---|---|
| 0 | Tumour epithelium |
| 1 | Simple stroma |
| 2 | Complex stroma |
| 3 | Immune cells |
| 4 | Debris |
| 5 | Normal mucosal glands |
| 6 | Adipose tissue |
| 7 | Background (no tissue) |
Each class contains 625 images.
Deep learning methods, on the other hand, do not require handcrafted features to be extracted from the input images; rather, they exhibit self-learning behaviour in which the model learns the relevant informative features from the inputs by itself. This is particularly useful if the input data have very complex underlying patterns which are often difficult to capture using handcrafted feature engineering, as in the case of CRC tissue texture investigation. As such, CNN based models are preferred for image analysis as they can efficiently extract translationally invariant features from image data using blocks of convolution filters. The authors of34 proposed a bi-linear CNN-based model to extract and fuse features from stain decomposed histological images and obtained a multi-class classification accuracy of and sensitivity of 34. The authors of35 investigated the importance of stain normalization pertaining to tissue classification using a CNN model but achieved a classification accuracy of only . Raczkowski et al.36 introduced a Bayesian deep learning framework for end-to-end classification of multi-class CRC histological images and achieved the highest accuracy of following a 10-fold cross-validation scheme36, while37 proposed an explainable classifier mechanism for ease of human interpretability whose performance was enhanced using a fine-tuned CNN model which obtained an accuracy of on the multi-class classification problem. Researchers have also leveraged the concept of transfer learning38—the process of fine-tuning a deep learning model pre-trained on a large dataset to suit the given task at hand—to cope with the limited amount of data available in biomedical image analysis tasks. The authors in39 explored several deep CNN models pre-trained on the ImageNet dataset12 for feature extraction from the histological images. That was followed by multi-class classification using a pool of traditional classifiers like the random forest, Multi-layer Perceptron, K-nearest neighbours (KNN) and Bayesian classifier. Out of the 108 possible combinations of feature extractors and classifiers, they achieved the highest classification accuracy of and an F1-score of , using a pre-trained DenseNet-169 model as the feature extractor and an SVM as the classifier. In40, the authors proposed a semi-supervised algorithm wherein they constructed a hypergraph constructed with the features extracted from the CRC tissue images using a pre-trained VGG-19 network. The features were passed through a feed-forward neural network for multi-class tissue classification. They achieved an accuracy of along with an average true positive rate of . Note that all of the aforementioned studies have used the multi-class CRC tissue dataset by16 for training and evaluation.
Ensemble learning14 is a strategy that takes into account information obtained from multiple models and combines them at inference time to compute the final predictions. This strategy poses the advantage of capturing potentially diverse information from the base learners as well as improving the generalization capability by reducing the overfitting of the model, especially when the data are scarce. As such, an ensemble of models has been found to perform better than a single neural network model10,11 and hence, has been of significant interest among the research community41,42. The most common ensemble strategies in the literature apply some fusion schemes on the decision scores obtained by the individual models to produce the final predictions. Dif et al.43 proposed a dynamic ensemble learning approach in which the most optimal models were selected from a pool of transfer learning-based CNN models using PSO algorithm15, which were then combined using voting and averaging ensemble techniques. The authors in44 proposed a two-phase ensemble deep neural network (DNN) framework for end-to-end CRC histology classification and achieved an accuracy of , while the work done in45 proposed two ensemble approaches on the decision scores obtained by four pre-trained deep CNN models of varying architectures, and obtained a mean classification accuracy of on the CRC histology dataset16.
Although the mentioned ensemble learning approaches have been effective, a major drawback it faces is that training multiple DNN models incurs a large computational cost, which may be infeasible on several occasions such as in a resource-constrained environment. A seminal work that sought to tackle this limitation was proposed by18, which introduced the concept of snapshot ensemble–training multiple snapshots of the same DNN during a single run. The authors followed the cyclic learning rate scheduling proposed by46 that allowed the DNN model to converge to and escape from multiple local minima in fewer training epochs, ensuring diversity among the snapshot models being trained. Hence, ensemble learning can be leveraged without incurring any additional computational costs of training multiple models; all of the base learners can be generated at the expense of training a single neural network only. Snapshot ensemble techniques have been used by researchers in various sub-domains of biomedical image classification47–50.
PSO15 is a popular swarm-intelligence based meta-heuristic algorithm that has been leveraged on a wide range of problems pertaining to the optimization paradigm, including continuous optimization51, task scheduling52, data clustering53, image thresholding54 and segmentation55. Binary variants of PSO56,57 have also been introduced and used for FS tasks58. The main difference between the binary and continuous variants lies in the use of a transfer function57, which maps the continuous search space of PSO to a binary one based on a threshold condition. The primary merits of this meta-heuristic lie in its simple concept, less number of parameters and computational efficiency over other meta-heuristics. These facts have been the key reasons for its successful application over various domains as mentioned.
All of the aforementioned snapshot ensemble methods generate decision scores from the snapshot models and fuse them for the final prediction. In this research, we adopt a different approach, where deep features are extracted from the model snapshots and fused, after which the obtained feature vector is passed through a meta-heuristic, called PSO, for dimensionality reduction. Based on these optimally selected feature subsets, the final classification is performed using the KNN classifier. Since the deep features are extracted from the same CNN model at different learning environments through the training process and fused, there may be redundant features in the feature space that can be eliminated for efficient storage of data. For this, the selection of the optimal feature subset is an important step in the proposed framework. The obtained results on a publicly available CRC dataset by16 support the viability of the proposed method.
Proposed method
In this section, we aptly describe the steps of the proposed framework for CRC histological image analysis. Specifically, the sequential stages of the proposed method are:
Transfer learning-based snapshot model training: a pre-trained MobileNet-V2 model is fit on the CRC histological data for fine-tuning the model.
Feature extraction and fusion from model snapshots: while training the MobileNet-V2 model at certain epochs, the features are extracted from the penultimate fully connected layer of the model. These features are then concatenated to yield the ensembled feature vectors.
FS using PSO algorithm: upon the concatenated features, PSO algorithm is used for dimensionality reduction of the feature set and removal of the redundant features for the classification.
Transfer learning-based snapshot model training
The motivation behind the transfer learning approach is to fine-tune a DNN pre-trained on a large dataset, like ImageNet12, for classification on the dataset of the current problem which consists of a limited amount of data. We use the MobileNet-V213 CNN model pre-trained on the ImageNet12 dataset as the backbone of our framework. Proposed by13, MobileNet-V2 is a lightweight state-of-the-art CNN model developed as an improvement upon its predecessor59. With the introduction of inverted residual blocks instead of the conventional residual blocks60,61, and depth-wise separable convolutions, which are the combination of the depth-wise and point-wise convolution, the number of parameters and thereby, the computational cost of MobileNet-V2 is greatly reduced when compared to the other DCNN architectures59,60,62.
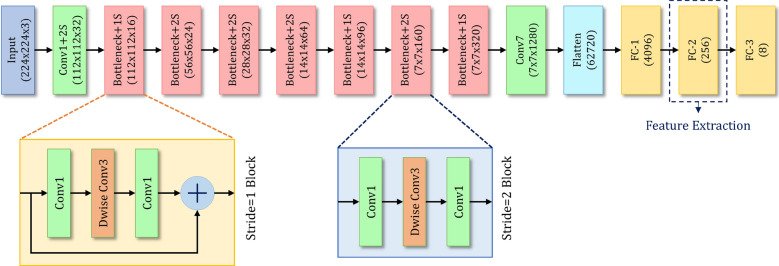
To capture the information in an effective way from the histological images using the pre-trained MobileNet-V2 model, two fully connected (FC) layers have been added after flattening the final Rectified Liner Unit— layer of the base CNN. The flattened layer consists of 62720 units and directly mapping them to the final classification layer may lose important information. For this, we introduce two intermediate FC layers to capture the important information before mapping the same to the classification layer. The first customized FC layer (FC–1) comprises 4096 neurons and the second layer (FC–2) comprises 256 neurons, following which is the final classification layer. Both the layers are associated with LeakyReLU63 activation function. Both of these FC layers are trained from scratch and the features are extracted from the FC–2 layer. The final classification layer is an FC layer having 8 units (i.e. number of classes of the given dataset) associated with the softmax activation function which maps the input to the respective class probabilities. The architecture of the customized MobileNet-V2 CNN model used in this study is shown in Fig. 2.
Figure 2.
Architecture of the customized MobileNet-V2 CNN model used in this research.
The primary need for ensemble learning is the availability of multiple trained deep learning models. However, training a deep CNN model is a time exhaustive process and also requires high computational resources, often making it infeasible to train several models for ensemble learning. To alleviate it, we leverage the snapshot ensemble technique18 by training multiple snapshots of the same deep learning network during a single training run of the model.
A fundamental requisition for effective model ensembling is that the individual models should be diverse enough to capture information that is complementary to each other. If this is ensured, it implies that the ensemble framework has taken into account the various facets of the training data and hence, can be able to classify the tissue images with greater accuracy. Further, the diverse nature of the individual models reduces the overfitting of the framework on the training samples. However, as the ensemble proposed in this study comprises snapshots of the same deep learning model over a single training run, the individual models may tend to be similar and lack in the said diversity. To address this potential limitation, an aggressive learning rate schedule is taken46 during the training run that causes large changes to the model weights, which in turn enhances diversity among the model snapshots, making the individual models suitable for a robust ensemble framework.
We have used the cosine annealing learning rate scheduler proposed in46. The intuition followed here is to accelerate the lowering of the learning rate which forces the model to converge to a local minimum during a cycle of decay. The periodic nature of the cosine function ensures that the learning rate is re-initialized to its initial value at the beginning of each cycle, implying a drastic increase in the learning rate from its previous epoch, which considerably perturbs the weights of the model and thereby allows the model to escape from the minimum it had converged to earlier. The weights of the converged models obtained at the end of each cycle are essentially the “snapshot” base learners constituting the ensemble framework, which are saved and used in subsequent stages.
| 1 |
The learning rate at current epoch (t) is given by Eq. (1), where is the initial learning rate at the start of training, E is the total number of training epochs and C is the number of cycles into which the training loop is divided uniformly. In this study, we have trained our model for epochs with cycles, the initial learning rate being set as . Figure 3 shows the variation of learning rate under the aforementioned cyclic learning rate scheduler over training epochs.
Figure 3.
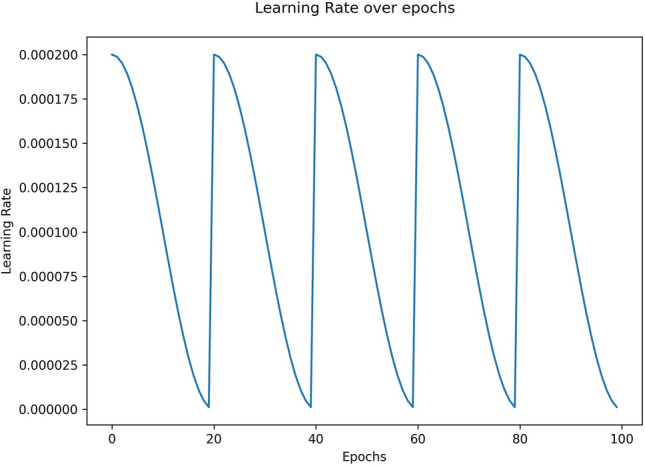
Cyclic variation of learning rate under cosine annealing learning rate schedule over training epochs.
Feature extraction and fusion from model snapshots
After having the generated snapshots from the MobileNet-V2 model, we use them to extract features from both the training and test sets. The features are extracted from the FC–2 layer (described in section “Transfer learning-based snapshot model training”), thereby getting a 256 dimension feature vector for each image from every snapshot model. We stack up the corresponding feature vectors obtained from each snapshot model, thus obtaining a dimension fused feature vector for every individual image. We have also taken particular care to ensure that the train-test split is maintained throughout and there is no data leakage.
Feature selection using PSO
FS is the process of selecting a subset from a set of features such that the most discriminatory features are chosen, thereby enhancing performance and reducing redundancy among the features. Out of a set of N features, an exhaustive search for the most optimal subset would incur number of computations, which being exponential is a combinatorially hard problem. This has led to researchers resorting to population-based meta-heuristic search algorithms27, which are probabilistic in nature and search over the search space for a near-optimal solution in polynomial time. Due to their stochastic behaviour, require a feasible number of iterations and population size so as to perform an effective search over the domain with a higher probability of finding the global/near optimal solution. In this work, we have adopted the PSO15, a popular swarm-based meta-heuristic algorithm to perform FS on the fused feature set (as described in section “Feature extraction and fusion from model snapshots”) so as to eliminate the implicit redundancy that may have crept in due to the use of same CNN backbone over the respective snapshot models.
In a typical PSO setup, the population comprises particles having velocities and positions as their attributes. For current iteration (t), if the velocity and position of the particle in the dimension are and respectively, then Eq. (2) is used to update the velocities in the iteration.
| 2 |
Here, is the best solution that the particle has obtained so far, indicates the best solution the swarm has achieved so far. The parameter governs the exploration ability of the population and is updated using Eq. (3), while and are random numbers in the range [0, 1]. The expressions and quantify local intelligence and collaboration of particles, respectively. For this study, the values of the constant parameters have been set experimentally as: .
| 3 |
Here, T is the maximum number of iterations.
Being originally suited for continuous function optimization, PSO is not directly suitable for a discrete (binary) valued problem such as FS57. Thus, we first map the real-valued search space of PSO to [0, 1] using the S-shaped sigmoid transfer function as shown in Eq. (4). After this, a threshold-like operation is employed to yield the desired discrete output, using Eq. (5). By convention, a feature index is set to be “1” if it is selected, “0” otherwise.
| 4 |
| 5 |
where, rand is a random number uniformly distributed between 0 and 1.
Population-based search procedures rely on the use of a fitness function that quantifies the suitability of a particular agent configuration (feature subset in this case). Here, we have formulated our fitness function by aptly combined the classification accuracy (which needs to be maximized) and feature subset cardinality (which needs to be minimized), so as to combine the contrasting objectives in a single fitness function, shown in Eq. (6). Higher the value of the fitness, better is the quality of the feature subset chosen.
| 6 |
where, is the classification accuracy of the feature subset obtained using the embedded KNN classifier64, quantifies the feature reduction given by Eq. 7, and [0, 1] represents the relative weightage between the classification accuracy and the feature reduction. Following9, we have taken , while the value of ‘k’ for the KNN classifier has been experimentally set to 6.
| 7 |
where, |d| is the number of features selected, and |D| is the original feature dimension. In our work, (as specified in section “Feature extraction and fusion from model snapshots”).
Finally, the local best (pbest) and global best (gbest) solutions are updated as given by Eqs. (8) and (9) respectively.
| 8 |
| 9 |
where, is the fitness function defined in Eq. (6). Figure 4 shows the flowchart of the PSO algorithm used in this research.
Figure 4.
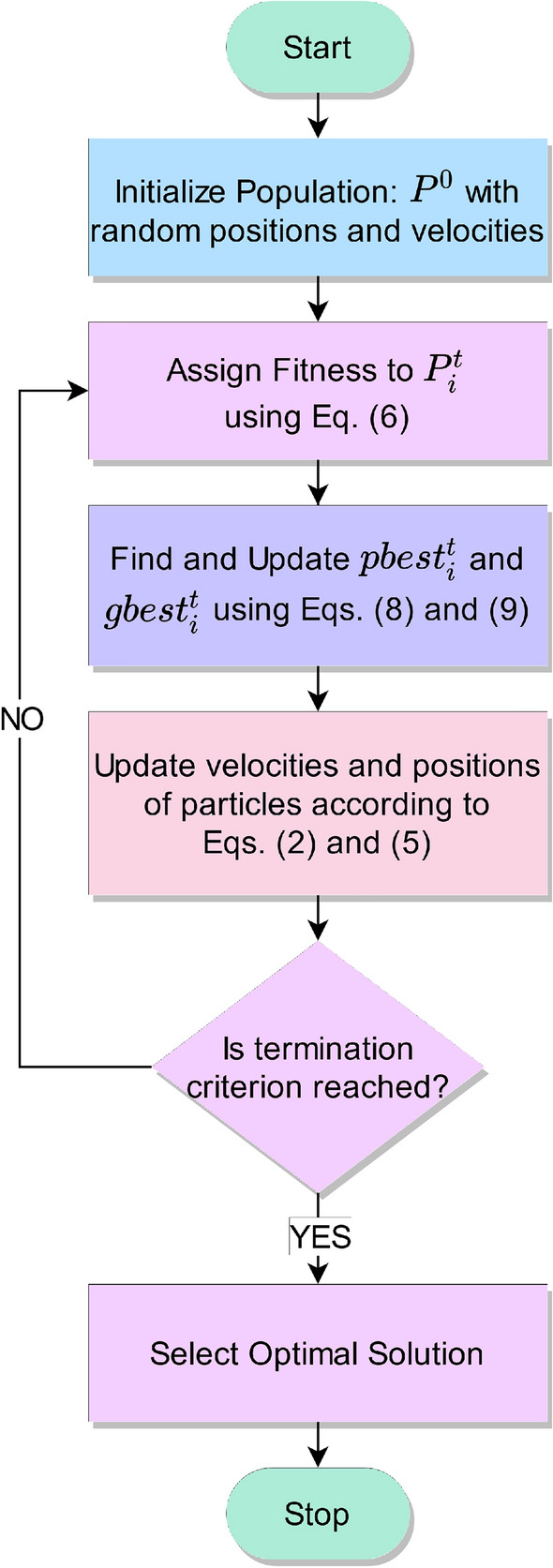
Flowchart of the PSO algorithm.
Statement
All experiments and methods were carried out in accordance with relevant guidelines and regulations.
Results and discussion
In this section, we provide details of the dataset used for evaluating our proposed method, as well as show and compare the results obtained with existing state-of-the-art approaches in literature to justify the superiority and reliability of the proposed method.
Dataset description
In this study, we have used the CRC histology dataset by16, a collection of textures in histological images of human CRC containing 5000 images of px each ( ). Each image belongs to exactly one of eight tissue categories as given in Table 1. The dataset is class-balanced with each class comprising 625 images. Following a 5-fold cross-validation scheme for our experiments, we split each tissue category into 500/125 images for train/test respectively.
Evaluation metrics
Four commonly used metrics, namely Accuracy, Precision, Recall and F1-Score, have been employed for evaluation of the proposed method on the publicly available CRC histology dataset16.
For a multi-class system (N-class), if we have a confusion matrix M, with the rows depicting the predicted class and columns depicting the true class, these evaluations metrics can be formulated as in Eqs. (10)–(13).
| 10 |
| 11 |
| 12 |
| 13 |
Implementation
The proposed framework has been implemented in PyTorch73 on a 8GB Nvidia GeForce 2080 GPU. The base snapshot CNN was trained for 100 epochs with 5 cycles comprising 20 epochs each (as discussed in section “Transfer learning-based snapshot model training”) with an initial learning rate of using the Stochastic Gradient Descent74 optimizer. All histological images were resized to using bilinear interpolation before being fed into the CNN.
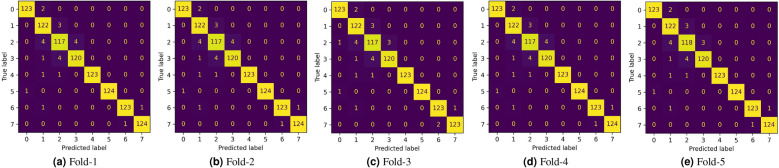
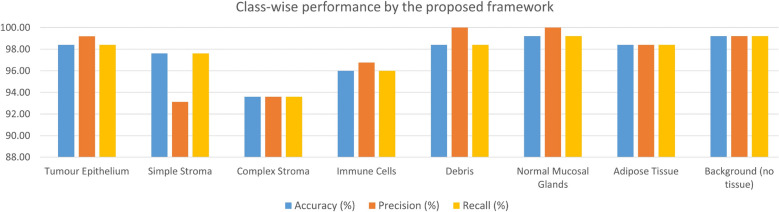
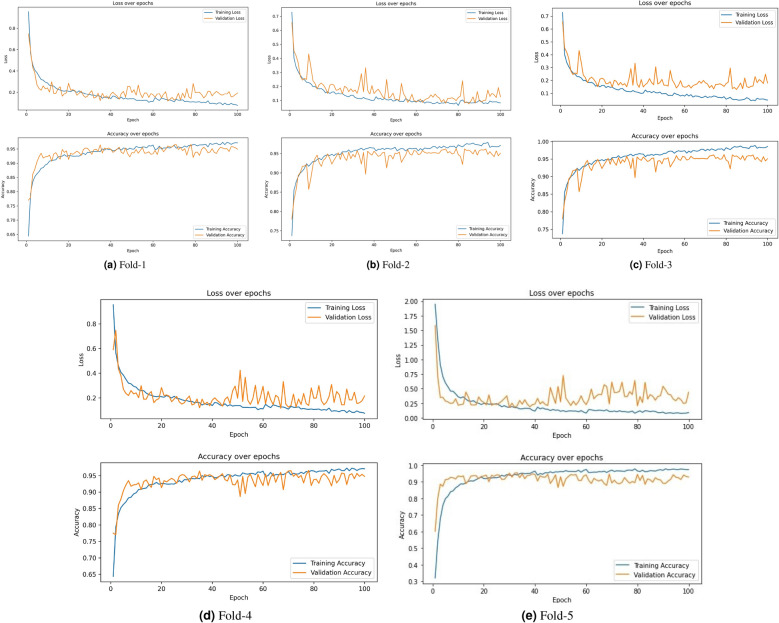
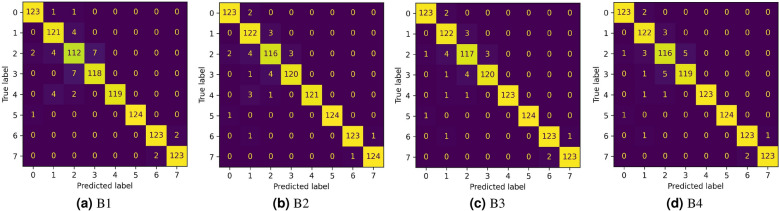
In this study, we have employed a 5-fold cross-validation scheme for evaluating the proposed pipeline on the CRC histology dataset16. The results obtained by the proposed method on each fold of the cross-validation along with the average and standard deviation values over the five folds are tabulated in Table 2. Further, the performance of the proposed method on each class of the dataset (described in Table 1) is shown in
Figure 5 which comprises the confusion matrices obtained on each fold of cross-validation, and
Figure 6 which gives a graphical representation of the class-wise metric scores averaged over the five folds of cross-validation.
For the transfer learning phase, different state-of-the-art pre-trained CNN models are customized and fine-tuned on the given dataset, the results of which are tabulated in Table 3. We can see that MobileNet-V213 shows the best performance among all the CNN models, while AlexNet65 achieves comparable performance to the former. Owing to its superior performance, we justify the usage of MobileNet-V2 as the base CNN model to be used for deep snapshot ensembling.
Table 2.
Results obtained by the proposed method on the 5-folds of cross validation on the CRC histology dataset.
| Fold | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) |
|---|---|---|---|---|
| 1 | 97.60 | 97.64 | 97.60 | 97.61 |
| 2 | 97.60 | 97.64 | 97.60 | 97.61 |
| 3 | 97.50 | 97.54 | 97.50 | 97.51 |
| 4 | 97.60 | 97.64 | 97.60 | 97.61 |
| 5 | 97.70 | 97.74 | 97.70 | 97.71 |
| Avg.± Std. Dev. | 97.60 ± 0.07 | 97.64 ± 0.07 | 97.60 ± 0.07 | 97.61 ± 0.07 |
Figure 5.
Confusion matrices obtained by the proposed method on the 5-folds of cross validation on the CRC histology dataset.
Figure 6.
Class-wise results obtained by the proposed method on the CRC histology dataset. The average performance over the 5 folds of cross-validation are reported.
Table 3.
Results obtained from the transfer learning phase by training various CNN models on the said dataset for 100 epochs; the average values over 5-folds of cross validation are reported.
Table 4 tabulates the validation accuracies obtained by individual snapshot models during deep snapshot training on each fold of the 5-fold cross-validation scheme. The learning curves obtained during the CNN model training process over 100 epochs for each fold are shown in Fig. 7. Most of the learning curves show a gradual decrease in the losses (and a similar rate of increase in accuracy), ensuring that the models have converged effectively and are not overfitted, except that in Fold-3, the somewhat divergent behaviour of the training and validation loss curves do depict a comparatively weaker learning behaviour.
Table 4.
Accuracy (%) obtained by each snapshot model during training the base CNN on each fold of 5-fold cross validation.
| Snapshot Model | Fold 1 (%) | Fold 2 (%) | Fold 3 (%) | Fold 4 (%) | Fold 5 (%) |
|---|---|---|---|---|---|
| Snapshot 1 | 94.80 | 94.60 | 94.50 | 95.00 | 95.00 |
| Snapshot 2 | 96.40 | 96.00 | 95.30 | 94.90 | 95.30 |
| Snapshot 3 | 95.60 | 95.80 | 95.60 | 96.00 | 96.00 |
| Snapshot 4 | 96.60 | 95.90 | 95.90 | 96.60 | 96.50 |
| Snapshot 5 | 95.80 | 96.00 | 96.00 | 96.00 | 96.60 |
Figure 7.
Learning curves obtained by the base CNN model of the proposed method on the 5-folds of cross validation on the CRC histology dataset.
PSO algorithm57 has been adopted in this study to select the most optimal features from the fused feature set obtained from the respective snapshot models. To justify its use quantitatively, it has been compared with the following state-of-the-art metaheuristic optimization algorithms in literature:
Grey Wolf Optimizer (GWO)68
Sine Cosine Algorithm (SCA)69
Gravitational Search Algorithm (GSA)70
Cuckoo Search Algorithm (CSA)71
Whale Optimization Algorithm (WOA)72
For every fold, each of the algorithms is run separately for 10 times on the fused feature set with and the average values of the evaluation metrics are considered. For each run, the maximum number of iterations for the FS algorithm is set to 50. This is done to ensure robustness in the performance of the algorithms, as they are stochastic in nature. The results of the aforementioned comparative study are tabulated in Table 5. It can be observed that PSO shows the best performance in terms of all the evaluation parameters and is also found to show very competitive performance in terms of the number of selected features. GSA ranks second in terms of the metric values, whereas CSA is found to select the minimal number of features. The results justify the effectiveness of using PSO for FS in the proposed study.
Table 5.
Comparison of results obtained on performing FS on the ensembled feature set; the average values over 5-folds of cross validation are reported.
Comparison with state-of-the-art methods
Table 6 compares the results obtained by the proposed framework against existing state-of-the-art methods for CRC tissue classification. It can be observed that the proposed method outperforms all of the existing works in literature by a significant margin in terms of all the four evaluation metrics used in this study. Further, several of the methods in the literature have mentioned accuracy as their sole evaluation metric, which does not provide information about false positives (or true negatives) and thereby is not a sufficient parameter to evaluate a multi-class classification framework. On the other hand, our results justify that the proposed study is a highly effective and superior approach in CRC detection from the histological analysis.
Table 6.
Comparison of the proposed framework with state-of-the-art methods on CRC histology dataset16 used in this study.
| Method | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) |
|---|---|---|---|---|
| Kather et al.16 | 87.40 | – | – | – |
| Ciompi et al.35 | 79.66 | – | – | – |
| Wang et al.34 | 92.60 | – | 92.80 | – |
| Rkaczkowski et al.36 | 92.44 | – | – | – |
| Dif et al.43 | 94.52 | – | – | – |
| Sabol et al.37 | 92.74 | 92.50 | 92.76 | 92.64 |
| Ohata et al.39 | 92.08 | – | – | 92.12 |
| Paladini et al.45 | 96.16 | – | – | – |
| Bakht et al.40 | 95.46 | – | – | 94.00 |
| Ghosh et al.44 | 92.83 | 92.83 | 93.11 | 92.97 |
| Marik et al.75 | 95.22 | 95.34 | 95.22 | 95.26 |
| Proposed method | 97.60 | 97.64 | 97.60 | 97.61 |
Most of the existing methods on the CRC dataset16 use a single deep learning model for the classification of the histological slide images. Among the compared methods shown in Table 6, only45 explored the ensemble learning approach by leveraging a simple probability averaging ensemble of decision scores, and their performance ranks closest to that obtained by the proposed method (96.16% accuracy). However, this work used multiple CNN classifiers to form the ensemble making them computationally expensive. In contrast, our proposed method requires the training of one CNN model for the ensemble, and still outperforms45 by a fair margin.
Ablation study
To investigate the use of snapshot feature fusion over cyclic learning rate scheduling episodes, we compare its performance against baseline setups obtained on conducting an ablation study on the framework. For each of the baselines, a 5-fold cross-validation scheme is adopted during experimentation.
B1: Features are extracted using the base CNN model without any fusion, the rest of the experimental setup remains unaltered. For this setup, the dimension of extracted feature vector has been set to 512.
B2: Features are extracted using the top-2 performing snapshot models and fused, keeping the rest of the experimental setup unchanged (i.e. output feature dimension is 512).
B3: Features are extracted using the top-3 performing snapshot models and fused, without any changes in the rest of the experimental setup.
B4: Features are extracted using the top-4 performing snapshot models and fused without altering the rest of the experimental setup.
Table 7 tabulates the results of the aforementioned comparative study. It can be observed that the proposed approach outperforms all of the chosen baseline setups in terms of all the evaluation metrics. Baselines B2 and B4 show very similar performance in terms of accuracy and F1-Score, with a marginal difference in precision values. The setup B3 performs best among the chosen baselines, although it falls short as compared to the proposed method. Further, the fact that B1 shows the weakest performance, highlights the superiority of ensemble learning over a single network. The confusion matrices depicting class-wise performances for each baseline setup are shown in Fig. 8.
Table 7.
Results of the Ablation study obtained from each setup as described in section “Ablation study”; the average values over 5-folds of cross-validation are reported.
| Baseline | Feature Dimension | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) |
|---|---|---|---|---|---|
| B1 | 512 | 96.30 | 96.35 | 96.30 | 96.32 |
| B2 | 512 | 97.30 | 97.36 | 97.30 | 97.31 |
| B3 | 768 | 97.50 | 97.54 | 97.50 | 97.51 |
| B4 | 1024 | 97.30 | 97.33 | 97.30 | 97.31 |
| Proposed method | 1280 | 97.60 | 97.64 | 97.60 | 97.61 |
Figure 8.
Confusion matrices obtained from each baseline setup as described in section “Ablation study”.
Analysis of the proposed model
In this section, we thoroughly analyse the performance of the proposed model both quantitatively and qualitatively so as to prove its robustness and justify the significance of the results obtained.
Statistical test
To statistically analyze the significance of the proposed method, the McNemar’s statistical test76 is performed between the PSO algorithm used in the proposed method and other popular metaheuristics used in the comparisons. McNemar’s test is a non-parametric test77,78, which assumes the null hypothesis that two models are statistically similar. To reject this null hypothesis, the p-value obtained must be lower than . The results of McNemar’s test are shown in Table 8. It can be noted that for every scenario, , and thus the null hypothesis is rejected, justifying that the proposed model is statistically dissimilar to other methods.
Table 8.
Results (in terms of p-values) attained by applying McNemar’s statistical test between PSO algorithm used in the proposed model versus other popular metaheuristic algorithms (GWO, Grey Wolf Optimizer; SCA, Sine-Cosine Algorithm; GSA, Gravitational Search Algorithm; CSA, Cuckoo Search Algorithm; WOA, Whale Optimization Algorithm).
| McNemar’s test | p-value |
|---|---|
| PSO vs. GWO | 3.53E−02 |
| PSO vs. SCA | 2.81E−02 |
| PSO vs. GSA | 2.95E−02 |
| PSO vs. CSA | 1.17E−02 |
| PSO vs. WOA | 3.48E−02 |
t-SNE visualization
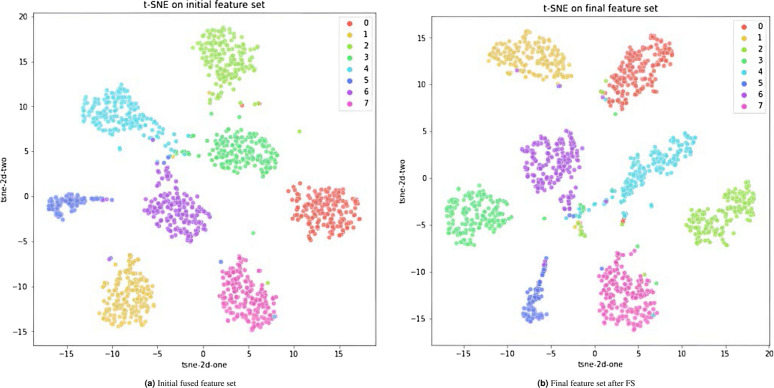
The Distributed Stochastic Neighbourhood Embedding (or simply SNE) is a dimensionality reduction algorithm79 that converts high-dimensional dataset into a matrix of pairwise similarities, which can be subsequently visualized in 2D (or 3D) using suitable tools. In this paper, we have employed SNE to the snapshot fused feature set and that obtained after FS, and visualized the low-dimensional resultant in a 2D scatter-plot, as shown in Fig. 9. We can observe in both figures that the features are mostly well-clustered in their own classes, as well as separated apart from other classes. Furthermore, the class-wise separation in the final feature subset is more prominent compared to the initial feature set, thus highlighting the usefulness of FS and justifying its role in boosting performance. Thus, we can conclude that the snapshot fusion technique enables the formation of a highly discriminative embedding space, which justifies the high performance of our model.
Figure 9.
SNE visualization of (a) the snapshot fused features obtained from base model training and (b) the final feature subset obtained by the full framework.
Grad-CAM analysis
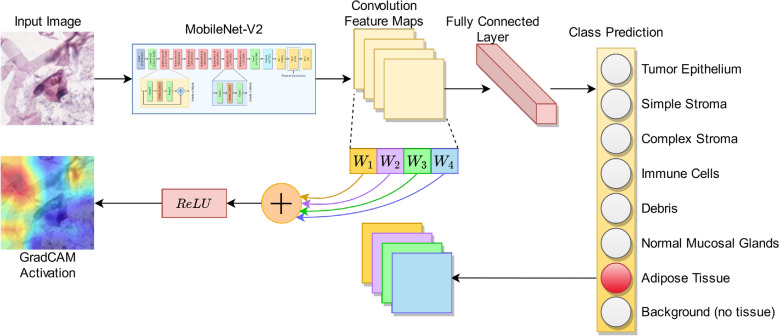
Gradient-weighted Class Activation Mapping (Grad-CAM) is a class-discriminative localization process introduced by17 that produces a visual representation of the regions of a given image identified by the CNN model to be most distinguishing and thereby, highly pertinent to its class prediction. The process followed is that the input image is first passed through the CNN model for label prediction, after which the weighted average of the activation maps is taken from the last convolutional layer of the network to form the activation heat map, which is then superimposed on the original image to highlight the distinct regions of particular interest shown by the model for the classification task. An explanatory diagram for this process is illustrated in Fig. 10.
Figure 10.
Explanation of the Grad-CAM activation process.
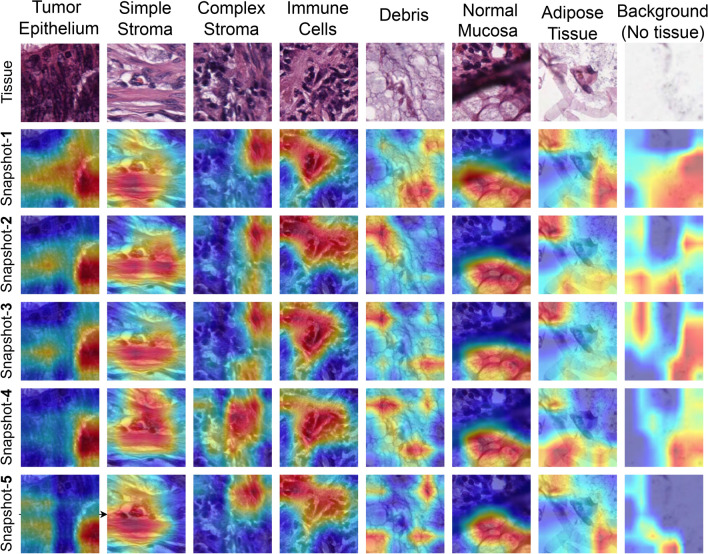
We have used Grad-CAM analysis on each of the snapshot models obtained during the training to investigate the regions focused on by each snapshot model on a given CRC histological image, which would give insights into the information captured by the individual snapshots. Figure 11 shows the Grad-CAM visualisations using each of the snapshot models on correctly classified sample tissue images from the testing samples of the CRC histology dataset16 used in this study. It is observed that different snapshots have generally been shown to have activated diverse regions of the original image of most classes, implying that complementary information has been extracted by the different snapshots leading to the success of the fusion framework. Further, for some of the classes (i.e. Tumour Epithelium and Simple Stroma), all of the snapshot models seem to have captured almost the same regions of the original image, showing little diversity. This implies that a considerable percentage of the information is redundant after fusing the features, which in turn justifies the inclusion of FS in the proposed framework.
Figure 11.
Grad-CAM activations obtained on some samples taken from the CRC dataset16 at different snapshots are shown. As can be seen, there is both redundancy as well as diversity among regions activated by the network, which qualitatively explains the benefit of snapshot ensembling and as well as need for FS.
Additional testing
To further validate the applicability and robustness of the proposed method, we additionally test it on the publicly available LC25000 dataset80, which consists of histopathology images of the human lung and colon for detection of cell carcinoma and adenocarcinoma. The lung dataset has 3 class while the colon dataset has 2 classes, with each class comprising 5000 images. Since our work focuses on colorectal histological analysis, we evaluate our method on the 2-class colon dataset only, the classes, the classes being “normal” and “adenocarcinoma”.
Keeping all elements of the experimental protocol identical (i.e., the same hyperparameters, five-fold cross-validation with 8000 and 2000 train and test images, respectively etc.), we test our proposed framework on the colon dataset80. The result (accuracy in %) obtained along with a comparison to state-of-the-art methods found in literature has been shown in Table 9. As evident from the empirical values, our model achieves a high accuracy of , surpassing all prior state-of-the-arts81–84 on the said dataset by a significant margin, thus proving its applicability across CRC datasets.
Table 9.
Comparison of accuracy scores attained by the proposed model against prior state-of-the-art methods on the colon dataset taken from the LC25000 dataset80.
| Method | Description | Accuracy (%) |
|---|---|---|
| Liang et al.81 | Multi-scale feature fusion with shearlet transform | 96.00 |
| Mangal et al.82 | Shallow CNN | 96.00 |
| Qasim et al.83 | Lightweight and fast CNN | 99.60 |
| Yildirim et al.84 | A CNN variant | 99.75 |
| Proposed | FS-aided snapshot ensemble | 99.99 ± 0.002 |
For the sake of convenience, we have included a one-liner description of each of the comparative methods.
Furthermore, we have applied SNE79 on the features obtained by the proposed model on the colon dataset to visualize the embedding space in a 2D plot, depicted in Fig. 12. As expected, based on the near-perfect results obtained, the two classes are highly segregated apart without any overlap of samples. This qualitatively conforms to the empirical results reported in Table 9 and further justifies the robustness of our approach on generalizing to other dataset.
Figure 12.
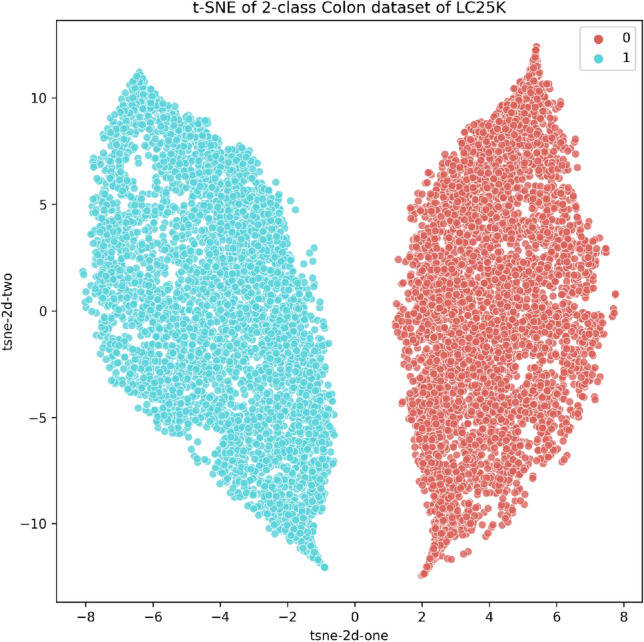
SNE visualization of features obtained by the proposed framework on the LC25000 Colon dataset80.
Conclusion
CRC accounts for more than 800 K deaths annually and is the third most common type of cancer diagnosed. The detection of CRC requires expert pathologists to classify each cell from histological slides of the colon. Such a tedious and expensive process hinders the population-wide screening and thus often the disease is diagnosed at a much later stage. Hence, Computer-Aided Detection frameworks are being developed for the automated and early diagnosis of the disease. In this research, we use a deep learning-based approach to detect CRC from histological slide images. Specifically, we apply an ensemble model for the disease prediction, where instead of fusing different base learners, we use one single CNN model and take model snapshots at different epochs and form an ensemble. This is computationally much cheaper than fusing two or more base learners since the training process is undergone only once. However, in literature, snapshot ensemble has been performed in other domains by fusing the decision scores obtained at the different checkpoints. In this research, we adopt a different approach, wherein we extract deep features from the penultimate FC layers of the MobileNet-V2 CNN model to form the ensemble. The extracted features from the different model snapshots are fused and binary PSO is employed to reduce the dimensionality of the feature space, eliminating the redundant features and for the final classification. We have obtained a feature reduction of (592 features selected out of 1280), which implies that redundant information has been eliminated sufficiently from the fused feature space. The proposed framework applied on a publicly available CRC dataset16 outperforms state-of-the-art methods on the same, justifying the reliability of the model. Grad-CAM analysis on the different model snapshots provides for visual explainability of the pipeline and also shows that complementary information is supplied by the CNN model at those snapshots which are efficiently fused by the proposed learning process.
In this work, we have used the cosine annealing learning rate scheduler. In future, we may try other methods for the same. Also, for the FS stage, we may try improving the PSO algorithm by, for example, by adding local search methods or initializing with a guided population, etc. The developed framework is domain-independent, and thus may be applied to other image classification problems as well. In future, we may also try to perform segmentation on the histology images before classification, since an RoI localization may help the medical experts to identify abnormalities in the cells more easily. As seen from the class-wise results obtained by the proposed framework in Fig. 6, relatively poor performance is obtained in some classes like the “Complex Stroma”. From the confusion matrices, it can be seen that some instances from this class are classified into “Simple Stroma” or “Immune Cells”. We may try to analyse and alleviate this problem in the future.
Acknowledgements
The authors would like to thank the Centre for Microprocessor Applications for Training, Education and Research (CMATER) research laboratory of the Computer Science and Engineering Department, Jadavpur University, Kolkata, India for providing the infrastructural support.
Author contributions
Conceptualization, P.K.S. and S.C.; methodology, R.S.; software, S.C.; validation, M.F.I., P.K.S. and R.S.; formal analysis, S.C.; investigation, P.K.S.; resources, S.K.; data curation, S.C.; writing—original draft preparation, S.C. and P.K.S.; writing—review and editing, M.F.I.; visualization, P.K.S.; supervision, P.K.S. and S.K.; project administration, P.K.S. and R.S.; funding acquisition, S.K. and M.F.I.; All authors have read and agreed to the published version of the manuscript.
Funding
This research work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government (MSIT) (NRF-2023R1A2C1005950).
Data availability
No datasets are generated during the current study. The datasets analyzed during this work are made publicly available in this published article.
Code availability
Our source codes are publicly accessible at: https://github.com/soumitri2001/SnapEnsemFS.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Muhammad Fazal Ijaz, Email: fazal.ijaz@unimelb.edu.au.
SeongKi Kim, Email: skkim9226@smu.ac.kr.
References
- 1.Society AC. What is Colorectal Cancer? American Cancer Society; 2020. [Google Scholar]
- 2.Society AC. Survival Rates for Colorectal Cancer. American Cancer Society; 2021. [Google Scholar]
- 3.Society AC. Can Colorectal Polyps and Cancer be Found Early? American Cancer Society; 2020. [Google Scholar]
- 4.Society AC. Colorectal Cancer Screening Tests. American Cancer Society; 2020. [Google Scholar]
- 5.Hamilton PW, Van Diest PJ, Williams R, Gallagher AG. Do we see what we think we see? the complexities of morphological assessment. J. Pathol. 2009;218:285–291. doi: 10.1002/path.2527. [DOI] [PubMed] [Google Scholar]
- 6.Dimitriou N, Arandjelović O, Harrison DJ, Caie PD. A principled machine learning framework improves accuracy of stage ii colorectal cancer prognosis. NPJ Digital Med. 2018;1:1–9. doi: 10.1038/s41746-018-0057-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Xu Y, Ju L, Tong J, Zhou C-M, Yang J-J. Machine learning algorithms for predicting the recurrence of stage iv colorectal cancer after tumor resection. Sci. Rep. 2020;10:1–9. doi: 10.1038/s41598-020-59115-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Takamatsu M, et al. Prediction of early colorectal cancer metastasis by machine learning using digital slide images. Comput. Methods Progr. Biomed. 2019;178:155–161. doi: 10.1016/j.cmpb.2019.06.022. [DOI] [PubMed] [Google Scholar]
- 9.Chattopadhyay S, Kundu R, Singh PK, Mirjalili S, Sarkar R. Pneumonia detection from lung x-ray images using local search aided sine cosine algorithm based deep feature selection method. Int. J. Intell. Syst. 2021;2021:1–38. [Google Scholar]
- 10.Manna A, Kundu R, Kaplun D, Sinitca A, Sarkar R. A fuzzy rank-based ensemble of cnn models for classification of cervical cytology. Sci. Rep. 2021;11:14538. doi: 10.1038/s41598-021-93783-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kundu R, et al. Fuzzy rank-based fusion of cnn models using gompertz function for screening covid-19 ct-scans. Sci. Rep. 2021;11:1–12. doi: 10.1038/s41598-021-93658-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Deng, J. et al. Imagenet: A large-scale hierarchical image database. In 2009 IEEE Conference on Computer Vision and Pattern Recognition 248–255 (2009).
- 13.Sandler, M., Howard, A., Zhu, M., Zhmoginov, A. & Chen, L.-C. Mobilenetv2: Inverted residuals and linear bottlenecks. In 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition 4510–4520 (2018).
- 14.Sagi O, Rokach L. Ensemble learning: A survey. Wiley Interdiscipl. Rev. Data Min. Knowl. Discov. 2018;8:e1249. [Google Scholar]
- 15.Kennedy, J. & Eberhart, R. Particle swarm optimization. In Proceedings of ICNN’95—International Conference on Neural Networks, vol. 4 1942–1948 (1995).
- 16.Kather JN, Weis C-A, Bianconi F, et al. Multi-class texture analysis in colorectal cancer histology. Sci. Rep. 2016;6:27988. doi: 10.1038/srep27988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Selvaraju, R. R. et al. Grad-cam: Visual explanations from deep networks via gradient-based localization. In 2017 IEEE International Conference on Computer Vision (ICCV) 618–626 (2017).
- 18.Huang, G. et al. Snapshot ensembles: Train 1, get m for free (2017). arxiv:1704.00109.
- 19.Linder N, et al. Identification of tumor epithelium and stroma in tissue microarrays using texture analysis. Diagn. Pathol. 2012;7:1–11. doi: 10.1186/1746-1596-7-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Peyret, R., Bouridane, A., Al-Maadeed, S. A., Kunhoth, S. & Khelifi, F. Texture analysis for colorectal tumour biopsies using multispectral imagery. In 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) 7218–7221 (2015). [DOI] [PubMed]
- 21.Chaddad A, et al. Multi texture analysis of colorectal cancer continuum using multispectral imagery. PLoS ONE. 2016;11:e0149893. doi: 10.1371/journal.pone.0149893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Komura D, Ishikawa S. Machine learning methods for histopathological image analysis. Comput. Struct. Biotechnol. J. 2018;16:34–42. doi: 10.1016/j.csbj.2018.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Haralick RM, Shanmugam K, Dinstein I. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973;SMC–3:610–621. doi: 10.1109/TSMC.1973.4309314. [DOI] [Google Scholar]
- 24.Kamarainen J-K, Kyrki V, Kalviainen H. Invariance properties of gabor filter-based features-overview and applications. IEEE Trans. Image Process. 2006;15:1088–1099. doi: 10.1109/TIP.2005.864174. [DOI] [PubMed] [Google Scholar]
- 25.Nanni L, Lumini A, Brahnam S. Local binary patterns variants as texture descriptors for medical image analysis. Artif. Intell. Med. 2010;49:117–125. doi: 10.1016/j.artmed.2010.02.006. [DOI] [PubMed] [Google Scholar]
- 26.Remeseiro B, Bolon-Canedo V. A review of feature selection methods in medical applications. Comput. Biol. Med. 2019;112:103375. doi: 10.1016/j.compbiomed.2019.103375. [DOI] [PubMed] [Google Scholar]
- 27.Rostami M, Berahmand K, Nasiri E, Forouzande S. Review of swarm intelligence-based feature selection methods. Eng. Appl. Artif. Intell. 2021;100:104210. doi: 10.1016/j.engappai.2021.104210. [DOI] [Google Scholar]
- 28.Dey A, et al. Mrfgro: A hybrid meta-heuristic feature selection method for screening covid-19 using deep features. Sci. Rep. 2021;11:24065. doi: 10.1038/s41598-021-02731-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Basak H, et al. A union of deep learning and swarm-based optimization for 3d human action recognition. Sci. Rep. 2022;12:5494. doi: 10.1038/s41598-022-09293-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Masood, K. & Rajpoot, N. Texture based classification of hyperspectral colon biopsy samples using clbp. In 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro (2009).
- 31.Taino, D. F. et al. A model based on genetic algorithm for colorectal cancer diagnosis. In Iberoamerican Congress on Pattern Recognition 504–513 (Springer, 2019).
- 32.Bae JH, Kim M, Lim J, Geem ZW. Feature selection for colon cancer detection using k-means clustering and modified harmony search algorithm. Mathematics. 2021;9:570. doi: 10.3390/math9050570. [DOI] [Google Scholar]
- 33.Geem ZW, Kim JH, Loganathan GV. A new heuristic optimization algorithm: Harmony search. Simulation. 2001;76:60–68. doi: 10.1177/003754970107600201. [DOI] [Google Scholar]
- 34.Wang, C., Shi, J., Zhang, Q. & Ying, S. Histopathological image classification with bilinear convolutional neural networks. In 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) 4050–4053 (2017). [DOI] [PubMed]
- 35.Ciompi, F. et al. The importance of stain normalization in colorectal tissue classification with convolutional networks. In 2017 IEEE 14th International Symposium on Biomedical Imaging 160–163 (2017).
- 36.Raczkowski L, Mozejko M, Zambonelli J, Szczurek E. Ara: Accurate, reliable and active histopathological image classification framework with Bayesian deep learning. Sci. Rep. 2019;9:1–12. doi: 10.1038/s41598-019-50587-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sabol P, Sinčák P, Hartono P, Kočan P, et al. Explainable classifier for improving the accountability in decision-making for colorectal cancer diagnosis from histopathological images. J. Biomed. Inf. 2020;109:103523. doi: 10.1016/j.jbi.2020.103523. [DOI] [PubMed] [Google Scholar]
- 38.Pan SJ, Yang Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010;22:1345–1359. doi: 10.1109/TKDE.2009.191. [DOI] [Google Scholar]
- 39.Ohata EF, et al. A novel transfer learning approach for the classification of histological images of colorectal cancer. J. Supercomput. 2021;2022:893. [Google Scholar]
- 40.Bakht, A. B., Javed, S., AlMarzouqi, H., Khandoker, A. & Werghi, N. Colorectal cancer tissue classification using semi-supervised hypergraph convolutional network. In 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI) 1306–1309 (IEEE, 2021).
- 41.Kundu R, Singh PK, Mirjalili S, Sarkar R. Covid-19 detection from lung ct-scans using a fuzzy integral-based cnn ensemble. Comput. Biol. Med. 2021;138:104895. doi: 10.1016/j.compbiomed.2021.104895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kundu R, Das R, Geem ZW, Han G-T, Sarkar R. Pneumonia detection in chest x-ray images using an ensemble of deep learning models. PLoS ONE. 2021;16:e0256630. doi: 10.1371/journal.pone.0256630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dif N, Elberrichi Z. A new deep learning model selection method for colorectal cancer classification. Int. J. Swarm Intell. Res. (IJSIR) 2020;11:72–88. doi: 10.4018/IJSIR.2020070105. [DOI] [Google Scholar]
- 44.Ghosh S, et al. Colorectal histology tumor detection using ensemble deep neural network. Eng. Appl. Artif. Intell. 2021;100:104202. doi: 10.1016/j.engappai.2021.104202. [DOI] [Google Scholar]
- 45.Paladini E, et al. Two ensemble-cnn approaches for colorectal cancer tissue type classification. J. Imaging. 2021;7:89. doi: 10.3390/jimaging7030051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Loshchilov, I. & Hutter, F. Sgdr: Stochastic gradient descent with warm restarts (2016). arxiv:1608.03983.
- 47.Annavarapu CSR. Deep learning-based improved snapshot ensemble technique for covid-19 chest x-ray classification. Appl. Intell. 2021;51:3104–3120. doi: 10.1007/s10489-021-02199-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Tang S, et al. Edl-covid: Ensemble deep learning for covid-19 cases detection from chest x-ray images. IEEE Trans. Ind. Inf. 2021;17:6539–6549. doi: 10.1109/TII.2021.3057683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Tanveer M, et al. Classification of alzheimer’s disease using ensemble of deep neural networks trained through transfer learning. IEEE J. Biomed. Health Inf. 2021;2021:598. doi: 10.1109/JBHI.2021.3083274. [DOI] [PubMed] [Google Scholar]
- 50.Banerjee A, Sarkar A, Roy S, Singh PK, Sarkar R. Covid-19 chest x-ray detection through blending ensemble of cnn snapshots. Biomed. Signal Process. Control. 2022;78:104000. doi: 10.1016/j.bspc.2022.104000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Wang F, Zhang H, Zhou A. A particle swarm optimization algorithm for mixed-variable optimization problems. Swarm Evol. Comput. 2021;60:100808. doi: 10.1016/j.swevo.2020.100808. [DOI] [Google Scholar]
- 52.Zhang L, Chen Y, Sun R, Jing S, Yang B. A task scheduling algorithm based on pso for grid computing. Int. J. Comput. Intell. Res. 2008;4:37–43. [Google Scholar]
- 53.Rana S, Jasola S, Kumar R. A review on particle swarm optimization algorithms and their applications to data clustering. Artif. Intell. Rev. 2011;35:211–222. doi: 10.1007/s10462-010-9191-9. [DOI] [Google Scholar]
- 54.Farshi TR, Ardabili AK. A hybrid firefly and particle swarm optimization algorithm applied to multilevel image thresholding. Multimedia Syst. 2021;27:125–142. doi: 10.1007/s00530-020-00716-y. [DOI] [Google Scholar]
- 55.Farshi TR, Drake JH, Özcan E. A multimodal particle swarm optimization-based approach for image segmentation. Expert Syst. Appl. 2020;149:113233. doi: 10.1016/j.eswa.2020.113233. [DOI] [Google Scholar]
- 56.Khanesar, M. A., Teshnehlab, M. & Shoorehdeli, M. A. A novel binary particle swarm optimization. In 2007 Mediterranean Conference on Control and Automation 1–6 (2007).
- 57.Mirjalili S, Lewis A. S-shaped versus v-shaped transfer functions for binary particle swarm optimization. Swarm Evol. Comput. 2013;9:1–14. doi: 10.1016/j.swevo.2012.09.002. [DOI] [Google Scholar]
- 58.Ghosh M, et al. Binary genetic swarm optimization: A combination of GA and PSO for feature selection. J. Intell. Syst. 2020;29:1598–1610. [Google Scholar]
- 59.Howard, A. G. et al. Mobilenets: Efficient convolutional neural networks for mobile vision applications (2017). arxiv:1704.04861.
- 60.He, K., Zhang, X., Ren, S. & Sun, J. Deep residual learning for image recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 770–778 (2016).
- 61.Zagoruyko, S. & Komodakis, N. Wide residual networks (2016). arxiv:1605.07146.
- 62.Zhang, X., Zhou, X., Lin, M. & Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition 6848–6856 (2018).
- 63.Xu, B., Wang, N., Chen, T. & Li, M. Empirical evaluation of rectified activations in convolutional network (2015). arxiv:1505.00853.
- 64.Altman NS. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992;46:175–185. [Google Scholar]
- 65.Krizhevsky, A., Sutskever, I. & Hinton, G. E. Imagenet classification with deep convolutional neural networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems 1097–1105 (2012).
- 66.Simonyan, K. & Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 3rd International Conference on Learning Representations (2015). arxiv:1409.1556.
- 67.Huang, G., Liu, Z., Van Der Maaten, L. & Weinberger, K. Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2017).
- 68.Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Adv. Eng. Softw. 2014;69:46–61. doi: 10.1016/j.advengsoft.2013.12.007. [DOI] [Google Scholar]
- 69.Mirjalili S. Sca: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016;96:120–133. doi: 10.1016/j.knosys.2015.12.022. [DOI] [Google Scholar]
- 70.Rashedi E, Nezamabadi-Pour H, Saryazdi S. Gsa: A gravitational search algorithm. Inf. Sci. 2009;179:2232–2248. doi: 10.1016/j.ins.2009.03.004. [DOI] [Google Scholar]
- 71.Yang, X.-S. & Deb, S. Cuckoo search via lévy flights. In 2009 World Congress on Nature Biologically Inspired Computing (NaBIC) 210–214 (IEEE, 2009).
- 72.Mirjalili S, Lewis A. The whale optimization algorithm. Adv. Eng. Softw. 2016;95:51–67. doi: 10.1016/j.advengsoft.2016.01.008. [DOI] [Google Scholar]
- 73.Paszke A, et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural. Inf. Process. Syst. 2019;32:8026–8037. [Google Scholar]
- 74.Sutskever, I., Martens, J., Dahl, G. & Hinton, G. On the importance of initialization and momentum in deep learning. In International Conference on Machine Learning 1139–1147 (PMLR, 2013).
- 75.Marik, A., Chattopadhyay, S. & Singh, P. K. Supervision meets self-supervision: A deep multitask network for colorectal cancer histopathological analysis. In Machine Learning and Computational Intelligence Techniques for Data Engineering: Proceedings of the 4th International Conference MISP 2022, Volume 2 475–485 (Springer, 2023).
- 76.Dietterich TG. Approximate statistical tests for comparing supervised classification learning algorithms. Neural Comput. 1998;10:1895–1923. doi: 10.1162/089976698300017197. [DOI] [PubMed] [Google Scholar]
- 77.Singh PK, Sarkar R, Nasipuri M. Statistical validation of multiple classifiers over multiple datasets in the field of pattern recognition. Int. J. Appl. Pattern Recogn. 2015;2:1–23. doi: 10.1504/IJAPR.2015.068929. [DOI] [Google Scholar]
- 78.Singh PK, Sarkar R, Nasipuri M. Significance of non-parametric statistical tests for comparison of classifiers over multiple datasets. Int. J. Comput. Sci. Math. 2016;7:410–442. doi: 10.1504/IJCSM.2016.080073. [DOI] [Google Scholar]
- 79.Van der Maaten L, Hinton G. Visualizing data using t-sne. J. Mach. Learn. Res. 2008;9:89. [Google Scholar]
- 80.Borkowski, A. A. et al. Lung and colon cancer histopathological image dataset (lc25000). arXiv:1912.12142 (2019).
- 81.Liang M, Ren Z, Yang J, Feng W, Li B. Identification of colon cancer using multi-scale feature fusion convolutional neural network based on shearlet transform. IEEE Access. 2020;8:208969–208977. doi: 10.1109/ACCESS.2020.3038764. [DOI] [Google Scholar]
- 82.Mangal, S., Chaurasia, A. & Khajanchi, A. Convolution neural networks for diagnosing colon and lung cancer histopathological images. arXiv:2009.03878 (2020).
- 83.Qasim, Y., Al-Sameai, H., Ali, O. & Hassan, A. Convolutional neural networks for automatic detection of colon adenocarcinoma based on histopathological images. In Innovative Systems for Intelligent Health Informatics: Data Science, Health Informatics, Intelligent Systems, Smart Computing 19–28 (Springer, 2021).
- 84.Yildirim M, Cinar A. Classification with respect to colon adenocarcinoma and colon benign tissue of colon histopathological images with a new cnn model: Ma\_colonnet. Int. J. Imaging Syst. Technol. 2022;32:155–162. doi: 10.1002/ima.22623. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No datasets are generated during the current study. The datasets analyzed during this work are made publicly available in this published article.
Our source codes are publicly accessible at: https://github.com/soumitri2001/SnapEnsemFS.