Dependence of cortical neuronal strength-duration properties on TMS pulse shape

Abstract

Objective:

The aim of present study was to explore the effects of different combinations of transcranial magnetic stimulation (TMS) pulse width and pulse shape on cortical strength-duration time constant (SDTC) and rheobase measurements.

Methods:

Resting motor thresholds (RMT) at pulse widths (PW) of 30, 45, 60, 90 and 120 μs and M-ratios of 0.2, 0.1 and 0.025 were determined using figure-of-eight coil with initial posterior-to-anterior induced current. The M-ratio indicates the relative phases of the induced current with lower values signifying a more unidirectional stimulus. Strength-duration time constant (SDTC) and rheobase were estimated for each M-ratio and various PW combinations. Simulations of biophysically realistic cortical neuron models assessed underlying neuronal populations and physiological mechanisms mediating pulse shape effects on strength-duration properties.

Results:

The M-ratio exerted significant effect on SDTC (F_(2,44)=4.386, P=0.021), which was longer for M-ratio of 0.2 (243.4±61.2 μs) compared to 0.025 (186.7±52.5 μs, P=0.034). Rheobase was significantly smaller when assessed with M-ratio 0.2 compared to 0.025 (P=0.026). SDTC and rheobase values were most consistent with pulse width sets of 30/45/60/90/120 μs, 30/60/90/120 μs, and 30/60/120 μs. Simulation studies indicated that isolated pyramidal neurons in layers 2/3, 5, and large basket-cells in layer 4 exhibited SDTCs comparable to experimental results. Further, simulation studies indicated that reducing transient Na⁺ channel conductance increased SDTC with larger increases for higher M-ratios.

Conclusions:

Cortical strength-duration curve properties vary with pulse shape, and the modulating effect of the hyperpolarising pulse phase on cortical axonal transient Na⁺ conductances could account for these changes, although a shift in the recruited neuronal populations may contribute as well.

Significance:

The dependence of the cortical strength-duration curve properties on the TMS pulse shape and pulse width selection underscores the need for consistent measurement methods across studies and the potential to extract information about pathophysiological processes.

Introduction

Transcranial magnetic simulation (TMS) is a non-invasive and painless neurophysiological technique utilised for assessment of cortical excitability in human brains as well as for the treatment of neurological and psychiatric diseases (Chen et al., 2008, Rossini et al., 1999, Rossini et al., 2015, Vucic and Kiernan, 2017, Vucic et al., 2018, Vucic et al., 2013). Single and paired pulse TMS paradigms assess the function of different inhibitory and facilitatory motor cortical interneuronal circuits, as well as corticospinal tracts (Rossini et al., 2015, Vucic et al., 2013, Ziemann et al., 2015). The physiological effects of TMS are measured by a number of parameters including motor evoked potential (MEP) amplitude, resting motor threshold, short interval intracortical inhibition and facilitation, intracortical facilitation, cortical silent period duration and long interval intracortical inhibition (Kujirai et al., 1993, Van den Bos et al., 2018, Vucic S. et al., 2006, Ziemann et al., 1996).

Strength-duration properties of axons describe the relationship between the stimulus strength (amplitude) and duration, resulting in unique biomarkers of peripheral neuronal excitability (Kiernan et al., 2020, Krishnan et al., 2009). Specifically, the strength-duration time constant (SDTC) and rheobase quantify the relationship between the stimulus strength and duration (Kiernan et al., 2020, Krishnan et al., 2009, Mogyoros et al., 1998, Mogyoros et al., 1996, Park et al., 2017, Weiss, 1901). The SDTC characterizes the increase of threshold for brief pulses, while the rheobase is the threshold for an infinitely long pulse (Kiernan et al., 2020, Kiernan et al., 2001). The SDTC and rheobase reflect properties of the nodal membrane, being related to dynamics and resistance of Na⁺ conductance as well as passive membrane properties, including capacitance (Bostock et al., 1998, Bostock and Rothwell, 1997, Burke et al., 2001, Kiernan and Bostock, 2000, Kiernan et al., 2020, Kiernan et al., 2000, Krishnan et al., 2009, Mogyoros et al., 1998). The rheobase is also affected by factors unrelated to neuronal properties, such as the distance from the TMS coil and other individual variables but can be informative of cortical activation if exogenous factors are controlled for. Abnormalities of SDTC and rheobase have been widely reported in human diseases, resulting in a greater understanding of disease pathophysiology and development of novel biomarkers (Kiernan et al., 2020, Krishnan et al., 2009, Park et al., 2017).

Controllable pulse parameter TMS (cTMS) devices, with their ability to deliver near-rectangular electric field pulses of different durations, have enabled an estimation of SDTC and rheobase from human motor cortical neurons (D’Ostilio et al., 2016, Peterchev et al., 2013). Initial studies utilising a custom-built cTMS device induced a monophasic TMS pulse oriented in a posterior-anterior direction, and successfully estimated the SDTC and rheobase by measuring resting motor thresholds (RMT) and input-output (IO) curves (Peterchev et al., 2014, Peterchev et al., 2013). Cortical SDTC estimates generated by RMT methodology reflect properties of cortical neuronal populations, including excitatory interneurons that transsynaptically excite pyramidal cells to threshold producing a motor evoked potential ≥ MEP 50 μV (Rossini et al., 2015, Rothwell et al., 1999). Inhibitory interneurons, which are activated at lower intensities (Aberra et al., 2020, Hanajima et al., 2002, Kallioniemi et al., 2014, Kujirai et al., 1993, Tokimura et al., 2000, Van den Bos et al., 2018), may also be recruited. Consequently, estimated cortical strength-duration properties may not simply reflect threshold intensity, where the most excitable excitatory interneurons are recruited, but rather the intensity where net transsynaptic excitation of pyramidal neurons is sufficient to drive a motoneuronal population and produce an arbitrary threshold of 50 μV MEP amplitude. At a physiological level, cortical and peripheral axonal SDTC estimates are likely mediated by similar ion channel conductances. Cortical SDTC measurements are further complicated by the poly-synaptic pathways involved in transmission of cortical impulses to produce an MEP response and by the heterogeneous population of corticomotor neurons activated trans-synaptically by TMS to generate motor thresholds required for SDTC estimation. Further, corticomotoneuronal orientation is variable relative to the posteroanterior direction of TMS stimulation, with implications for neuronal activation (D’Ostilio et al., 2016, Di Lazzaro and Rothwell, 2014).

Prior cTMS findings implied that selective activation of neuronal elements, with distinct strength-duration properties, could be achieved by manipulating the pulse width and coil orientation (D’Ostilio et al., 2016). Additionally, the TMS pulse direction and M-ratio were reported to influence a variety of TMS parameters including motor thresholds, MEP amplitudes and IO curve gradient (Sommer et al., 2018). In cTMS devices generating monophasic magnetic pulses, the M-ratio parameter controls the amplitude of the second phase relative to first phase of the induced electric field pulse. Thus, lower M-ratios reflect more unidirectional electric field pulses, while higher M-ratios yield more bidirectional electric field pulses. Monophasic TMS pulses with M-ratio of 0.2 were associated with lower RMTs, smaller IO curve gradients and lower MEP amplitudes when the TMS coil was oriented in a posterior-anterior compared to anterior-posterior direction (Sommer et al., 2018).

The effects of different pulse width combinations and M-ratios on estimating SDTC and rheobase has not been previously investigated. Previous cTMS studies utilised a combination of three pulse widths and a single pulse shape, typically with the M-ratio set to 0.2 (D’Ostilio et al., 2016, Halawa et al., 2021, Peterchev et al., 2014, Peterchev et al., 2013). Manipulating TMS pulse shape may reveal novel physiological insights into the strength-duration properties of distinct cortical neuronal populations, previously observed for anterior-posterior stimulation (D’Ostilio et al., 2016, Sommer et al., 2018), with pathophysiological implications for neurological disease states. Additionally, modelling studies undertaken to assess the effects of TMS pulse shape on SDTC and rheobase across different neuronal populations, could potentially yield further physiological insights. Consequently, the present study used experiments and simulations to investigate whether changes in the TMS pulse characteristics (M-ratio) could activate cortical neuronal populations with distinct SDTC and rheobase properties, with the aim of providing further insights into motor cortical physiology.

Methods

Subjects

Cortical and peripheral stimulation was performed on healthy subjects who were recruited consecutively and were free of neurological and psychiatric illnesses. None of the subjects were prescribed psychotropic medications at the time of the cTMS testing. Hand dominance was determined using the Edinburgh Handiness Inventory (Oldfield, 1971). The study was approved by the local hospital ethics committee (Sydney Local Area Health Service and Human Research Ethics Committees) and subject enrolment was performed in accordance with principles of the Declaration of Helsinki. Written informed consent was obtained from every subject prior to participation in the experiment.

Peripheral nerve assessment

Prior to assessing cortical function, the integrity of the peripheral nerve system was assessed. The median nerve was stimulated at the wrist and peak-to-peak compound muscle action potential (CMAP) recorded over the abductor pollicis brevis (APB) muscle in the thenar eminence of the palm. Recording electrode placement was in a belly tendon montage with ground electrode placed over the dorsum of the same hand. The peak-peak CMAP amplitude of the APB muscle (in mV) was recorded along with the median nerve distal motor onset latency (ms) and minimum F wave latency. Subsequently, axonal excitability studies were undertaken according to previously described methodology to record SDTC (μs) and rheobase (mA) (Kiernan et al., 2020). Briefly, the electrical pulses were monophasic rectangular in shape with pulse width (PW) of 200, 400, 800 and 1000 μs duration. The SDTC and rheobase are measures of the relationship between the intensity of a threshold stimulus to the pulse width. Expressing the threshold charge (y-axis) as a function of pulse-duration (x-axis) establishes a linear correlation in the hyperbolic model of the strength–duration curve (Mogyoros et al., 1996). The point at which the curve intersects the x-axis is referred to as SDTC, while the gradient of the linear curve is the rheobase (Kiernan et al., 2020).

Cortical stimulation

A commercial cTMS device (ElevateTMS, Rogue Research, Canada) was used to deliver single pulse TMS in a posterior-anterior direction of induced electric field over the dominant motor cortex via a dedicated figure-of-eight coil (70 mm diameter, Rogue Research, Canada). The electric field induced by the cTMS device was varied by pulse width and M-ratio. Pulse width is defined as the duration of the first phase of the electric field pulse [Figure 1] (D’Ostilio et al., 2016, Peterchev et al., 2013), and pulse widths of 30, 45, 60, 90 and 120 μs were used. Three different M-ratios were also utilised (0.2, 0.1, and 0.025) and combined with the PWs (Figure 1). Smaller M-ratio values indicate a more unidirectional electric field pulse with a main posterior-anterior-directed phase, followed by a longer lasting, lower amplitude phase in the opposite direction. Both phases have equal area under the curve resulting in zero net electric charge delivered to the tissue. The maximum stimulator output (MSO) of the Elevate cTMS device corresponds to a peak coil voltage of 2750 V. The device limited the maximum pulse amplitude at each pulse width as follows: 30 μs—100% MSO; 45 μs—95% MSO; 60 μs—74%; 90 μs—55% MSO; and 120 μs—50% MSO.

Figure 1:

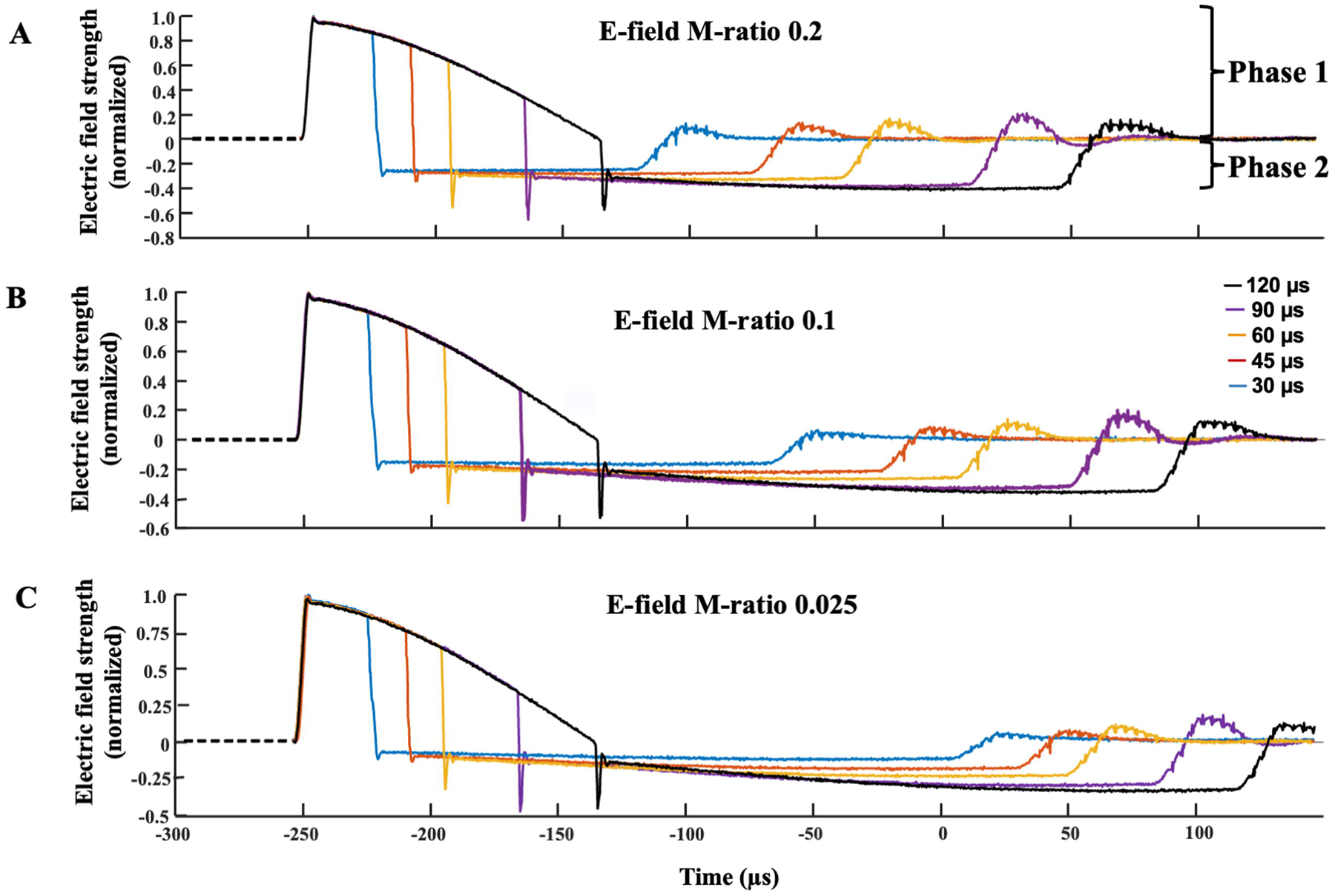
The cTMS electric field pulse recorded and normalised to unity for pulse widths of 30, 45, 60, 90 and 120 μs across the three M-ratios. The M-ratio parameter controls the ratio between the amplitude of the anterior-posterior-directed Phase 2 and posterior-anterior-directed Phase 1 of the electric field pulse. Since posterior-anterior stimulation in primary motor cortex has a lower threshold than the reverse current direction, Phase 1 and Phase 2 can be interpreted as depolarising and hyperpolarising, respectively, for the main target neuronal population. Lower M-ratio values reflect smaller amplitude and longer duration of Phase 2 of the electric field pulse. M-ratios of 0.2, 0.1 and 0.025 were used in the current experiment to determine the effects of different predominantly unidirectional pulses on cortical strength-duration measures.

Procedure:

Subjects were seated in a comfortable chair, with the 70mm figure-of-eight coil applied tangentially to the contralateral scalp. The TMS coil was positioned laterally at 45° to the sagittal midline and perpendicular to the central sulcus (Day et al., 1987, Di Lazzaro et al., 2002b, Di Lazzaro et al., 1998, Werhahn et al., 1994) to induce a posterior-anterior initial current in the motor cortex. Motor evoked potential (MEP) responses were recorded from the dominant abductor pollicis brevis (APB) muscle via 3M Red Dot (3M, MN, USA) solid gel electrodes. The active electrode was placed over the motor point of the APB muscle and the reference electrode on the interphalangeal joint of the thumb. The ground electrode was positioned over the dorsum of the hand. The motor hot spot, defined as the spot on the contralateral scalp where the largest MEP response amplitude was induced by lowest TMS intensity, was determined by moving the coil in ~ 0.5 cm steps around the motor hand area (M1). The optimal position was marked with a skin marking pencil and coil position was referenced to the markings during the experiment.

The RMT, defined as the lowest TMS intensity required to evoke MEP responses greater than 50 μV in at least 5 out of 10 consecutive trials (Rossini-Rothwell method), was determined for each PW (30, 45, 60, 90, 120 μs) and M-ratio value (0.025, 0.1, 0.2). The M-ratios were randomized while the PWs were delivered in a same pseudo-random sequence for each M-ratio (60, 120, 45, 90, 30 μs) to counterbalance any time dependence of the RMT estimation, keep consistent the strength-duration curve sampling and hence the SDTC and rheobase estimation. Visual feedback was provided to ensure that subjects were at rest and facilitated MEP responses which could alter RMT measurement were excluded. Consequently, SDTC and rheobase were estimated for each M-ratio and different combination and number of PWs s, including 5 PWs (1 combination), 4 PWs (4 combinations) and 3 PWs (4 combinations) (Table 1). The rationale was to determine whether different PW combinations would impact the strength-duration measure.

Table 1:

Relative root-mean-square difference of strength-duration time constant (SDTC) and rheobase for strength-duration curves comprising various three and four pulse width (PW) combinations and M-ratios compared to the values calculated when using all 5 PWs. All data are expressed as a percentage of relative difference from the estimates when all 5 PW are included. The cortical strength-duration estimates generated by 5 PW combinations served as a denominator.

SDTC (μs)	M-ratio 0.2	M-ratio 0.1	M-ratio 0.025
4 pw (30/45/60/120)	21.0	28.8	21.0
4 pw (30/45/60/90)	32.1	26.5	68.2
4 pw (30/60/90/120)	13.0	12.2	8.6
4 pw (45/60/90/120)	363.6	43.0	40.5
3 pw (30/60/120)	17.5	29.2	21.8
3 pw (30/60/90)	34.2	29.0	27.7
3 pw (45/60/120)	372.1	73.7	74.0
3 pw (45/60/90)	330.2	29.9	29.8
Rheobase (%MSO)	M-ratio 0.2	M-ratio 0.1	M-ratio 0.025
4 pw (30/45/60/120)	15.3	19.1	15.3
4 pw (30/45/60/90)	51.3	34.7	40.6
4 pw (30/60/90/120)	10.9	9.2	6.0
4 pw (45/60/90/120)	42.1	22.1	20.6
3 pw (30/60/120)	14.1	16.6	15.5
3 pw (30/60/90)	56.3	38.6	40.5
3 pw (45/60/120)	46.0	30.3	30.4
3 pw (45/60/90)	42.3	41.6	38.1

MEP responses were amplified with a gain of 1000, bandpass filtered 2–2000 Hz, digitized at 5 kHz, and recorded using Signal 7 software (Cambridge Electronic Design, Cambridge, United Kingdom). CMAP responses were amplified with a gain of 1000 and bandpass filtered (3 Hz – 5 kHz) using a D440 Isolated amplifier (Digitimer, UK), and sampled at 10 kHz using a 16-bit data acquisition card (National Instruments USB-6341). Data acquisition and stimulus delivery were controlled by QTRACS software (Version 2017, Digitimer, United Kingdom).

Cortical strength–duration time constant:

Estimations of cortical SDTC and rheobase were performed according to methodology previously reported using motor thresholds (D’Ostilio et al., 2016, Peterchev et al., 2013). An MEP is generated when the depolarisation strength (or factor) reaches threshold (rheobase). As such, the relationship between RMT and PW was modelled by the following equation which represents the strength–duration curve:

$${\text{RMT}}^{\prime }(\text{PW})=\frac{\text{ rheobase }}{r(\text{ SDTC,PW })},$$ (1)

where RMT′(PW)is the modelled RMT and r(SDTC,PW) is the depolarisation factor, defined as the peak of the normalized recorded cTMS electric field pulse waveform for a specific PW passed through a low-pass filter with time constant SDTC (Peterchev et al., 2013). For rectangular stimulus pulses, the low-pass filtering would yield the conventional exponential form of the strength-duration curve (Mogyoros et al., 1996). Since the hyperbolic form of the strength-duration curve, which is used for the peripheral axonal SDTC estimation, is not meaningful for non-rectangular pulses such as the cTMS waveforms, this approach was adopted. To estimate the cortical SDTC and rheobase, the empirical RMT (PW) values were fitted to the parametric model RMT′ (PW) by minimizing

$$\sum _{\text{PW}}{\left(\frac{{\text{RMT}}^{\prime }(\text{PW})}{\text{RMT}(\text{PW})}-1\right)}^2.$$ (2)

The SDTC and rheobase estimation was implemented in MATLAB (version R2020b, The Mathworks, Inc., Natick, MA, USA). The electric field pulse waveform was recorded for each pulse width and M-ratio using a digital oscilloscope (DSO2C15, Hantek, Poland) and the waveforms were digitised and stored offline for SDTC and rheobase calculations.

Cortical neuron threshold simulations:

Simulations were run to determine the threshold for activation of biophysically realistic models of human cortical neurons with the experimental cTMS waveforms used in this study, depicted in Figure 1, in accordance with previously reported methods (Aberra et al., 2018, Aberra et al., 2020). Briefly, we simulated in NEURON software pyramidal neurons from cortical layers (L) 2/3, and 5, as well as large basket cells from layer 4. Cells from layers 1 and 6 were not simulated because their high TMS thresholds relative to the L2–4 cell types make them unlikely to be directly activated by TMS (Aberra et al., 2020). For each cell type, we simulated five variants with similar electrical properties (thresholds of activation) and stochastically varied morphologies, (Aberra et al., 2018, Aberra et al., 2020). Ion channel function varies across neuronal morphologies, being identified by M-ratios, and thereby influencing SDTC. The simulation time step was set to 1 μs. The amplitude threshold was determined using a binary search algorithm (Aberra et al., 2020). Since we did not explore the effect of neuron placement within the cortex, the electric field was approximated as uniform in the vicinity of the neuron. Eight directions of the electric field relative to each neuron were simulated: down the somatodendritic axis, up the somatodendritic axis, and perpendicular to the somatodendritic axis with 6 different rotations in steps of 60°. For each cell type, M-ratio, and PW, we took the median threshold across all cell variants and rotations. The median thresholds were then used to estimate the SDTC and rheobase in the same way as for the experimental motor threshold data. Since the threshold units between the simulation data and the experimental data are not directly comparable, the threshold for the 60 μs PW was used to normalize the thresholds across all PWs.

To further explore the relative contributions of morphology and membrane dynamics to observed changes of SDTC across M-ratios, we also simulated simplified straight axon models. The straight axon models had a synapse-like terminal on one side, with soma, dendrites, and axonal branches removed. For each layer (L2/3, L4, L5), we generated seven straight 1-mm long axons with diameters sampling the range of the terminal branch diameters in the axonal arbors: 0.3–1.2 μm, 0.3–0.95 μm, 0.4–1.4 μm for the L2/3, L4, and L5 neurons, respectively. We simulated the thresholds for a uniform electric field directed parallel to the axon for all PWs and M-ratios and estimated the SDTC and rheobase with the same method described above. The proximal side of the axon was disabled from activation by increasing its diameter to 1000 μm, leading to exclusive activation of the distal axon terminal.

Lastly, we simulated activation thresholds for a published peripheral nerve axon model, the McIntyre-Richardson-Grill (MRG) model (McIntyre et al., 2002), again with the uniform electric field directed parallel to the axon. Briefly, the MRG model is a geometrically and electrically accurate model of mammalian motor nerve fibers, incorporating a double cable structure, with representation of nodes of Ranvier, paranodal, and internodal sections of the axon as well as a finite impedance myelin sheath. The model established that both active (persistent Na⁺) channel activation and passive membrane properties contributed to the depolarising potential, while the hyperpolarizing afterpotential was generated through activation of slow K⁺ currents. Thresholds for each PW and M-ratio were determined for nine fiber diameters ranging from 5.7 to 16.0 μm.

Data Availability

The data will be made available on request.

Statistical analysis

Two factor repeated measures analysis of variance (ANOVA) was used to evaluate the effect of the pulse width and M-ratio on motor thresholds. Greenhouse-Geisser correction was applied to correct for violations of sphericity when required. One-way repeated measures ANOVA, using post-hoc t-test with Bonferroni correction, was subsequently used to assess differences between SDTC and rheobase across different M-ratios for specific combinations of PWs. In addition, one-way ANOVA, using post-hoc pairwise t-test with Bonferroni correction was used to assess differences between simulated SDTC across different M-ratios. Root means square percentage error (RMSPE) was used to assess the accuracy of estimating SDTC and rheobase when using 3 and 4 PWs combinations compared to values obtained by using 5 PW combinations, which was treated as the reference. Pearson correlation coefficient was utilised to assess for correlations between cortical and axonal excitability parameters. Statistical analysis was performed using SPSS statistics software (Version 28). Data is expressed as mean ± standard deviation. P value < 0.05 was regarded as significant.

Results

A total of 18 subjects participated in the study (7 males; mean age of 51.1±12.2 years, range 29–79 years). Most subjects were right-handed (94%) while one was left-handed. None of the participants stopped the cTMS testing prematurely. In three participants with low RMTs, estimation of SDTC and rheobase was not possible with the M-ratio set to 0.025 due to low-output limit of the cTMS device. Additionally, the time to discharge the cTMS device capacitor generating the second electric field pulse phase was longer when the M-ratio was set to 0.025, leading to longer time interval between successive stimuli compared to stimuli with an M-ratio of 0.1 and 0.2. The interstimulus time interval across the M-ratios was not measured.

Peripheral nerve studies

Prior to undertaking cTMS studies, peripheral nerve function was assessed with transcutaneous electrical stimulation. The peak-to-peak CMAP amplitude was 13.5±5.5 mV and distal motor onset-latency 3.9±0.4 ms, being within normal limits (Vucic S et al., 2006). The axonal SDTC was 440.6±66.7 μs and rheobase 2.25±1.07 mA. As expected, there was a significant correlation between axonal SDTC and rheobase (R = −0.487, P = 0.048).

Cortical strength-duration properties

Cortical strength-duration curves recorded in the 18 participants for M-ratios of 0.025, 0.1, and 0.2 using 5 PWs are depicted in Figure 2. Two-factor repeated measures ANOVA disclosed a significant effect of PW (F_(1,4 = 1005.8, P < 0.001) and M-ratio * PW interaction (F_(1,4) = 3.557, P < 0.01) on RMT. There was no significant effect of M-ratio in isolation on RMT (F_(1,2) = 0.81, P = 0.454).

Figure 2:

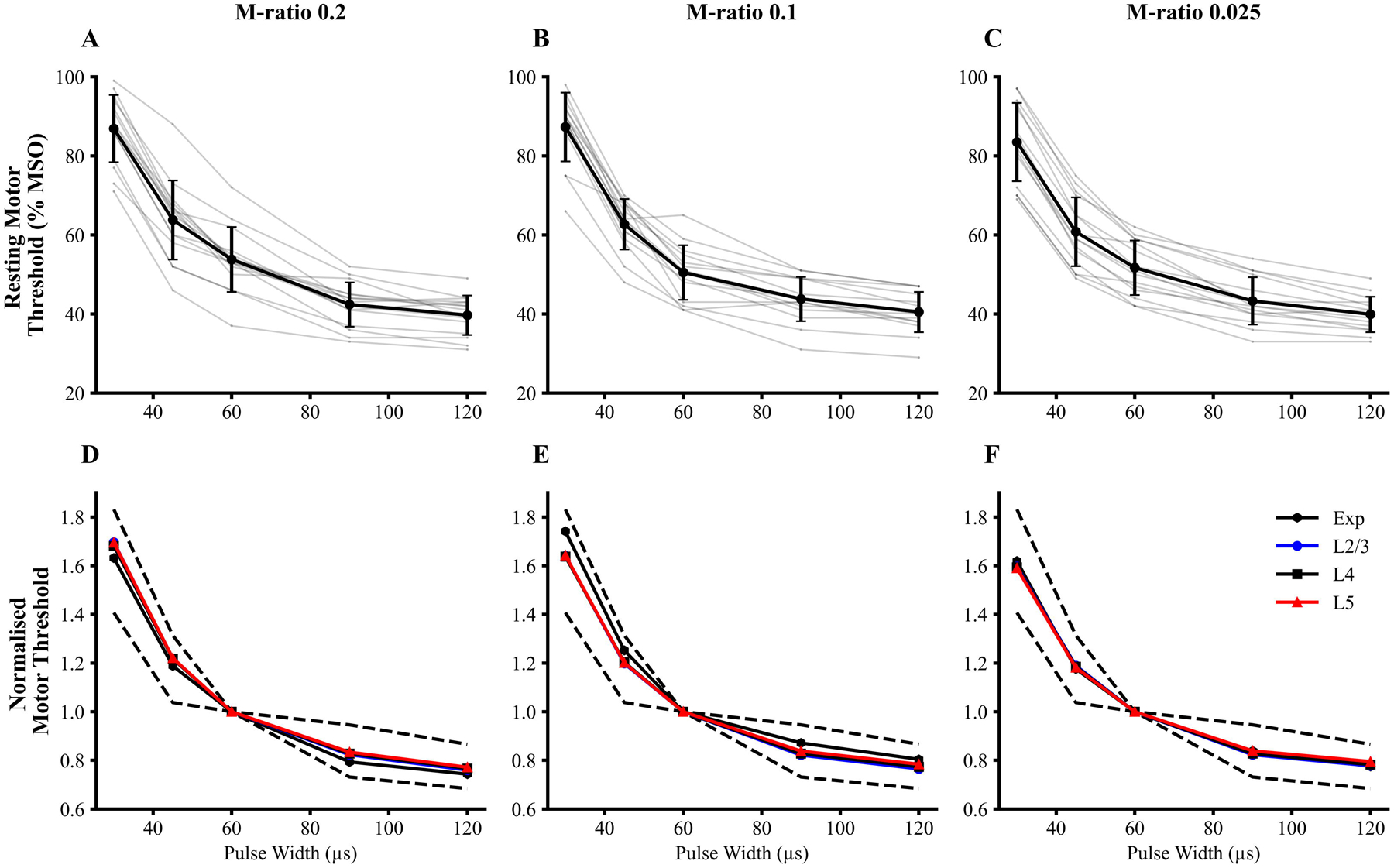
(A-C) Strength-duration curves for each M-ratio. Mean (black) and individual (light grey) experimental strength-duration curve are depicted for the three M-ratio pulse shapes. The stimulus strength is reflected by the resting motor threshold (RMT) (% maximum stimulator output, MSO). (D-F) Simulated strength-duration curves for pyramidal neurons from layers 2/3 (L2/3) and layer 5 (L5) and inhibitory neurons from layer 4 (L4) were normalised to the respective threshold at pulse width 60 μs. The 95% confidence interval of the experimental data is depicted by black dashed lines. The medians of individual simulated cell strength-duration curves are presented. The experimental and simulated curves showed similar dependencies on PW and M-ratio.

The pulse M-ratio exerted significant effects on SDTC (F_(2,44)=4.386, P=0.021). For M-ratio set to 0.2, SDTC was estimated to be 243.4±61.2 μs and was significantly longer when compared to SDTC estimated with M-ratio set to 0.025 (186.7±52.5 μs, P=0.034), but comparable to SDTC with M-ratio 0.1 (201.6±58.1 μs, P=0.087, Figure 3A). Additionally, the M-ratio significantly impacted the rheobase (F=3.42_(2,44), P=0.041). Specifically, the estimated rheobase with M-ratio set to 0.2 was 8.4±2.0 %MSO and was significantly lower than the estimated rheobase with M-ratio of 0.025 (11.0±2.6%MSO, P= 0.026). The rheobase values estimated with M-ratios of 0.2 and 0.1 (9.8±2.9 %MSO, P= 0.185, Figure 3B) were comparable.

Figure 3:

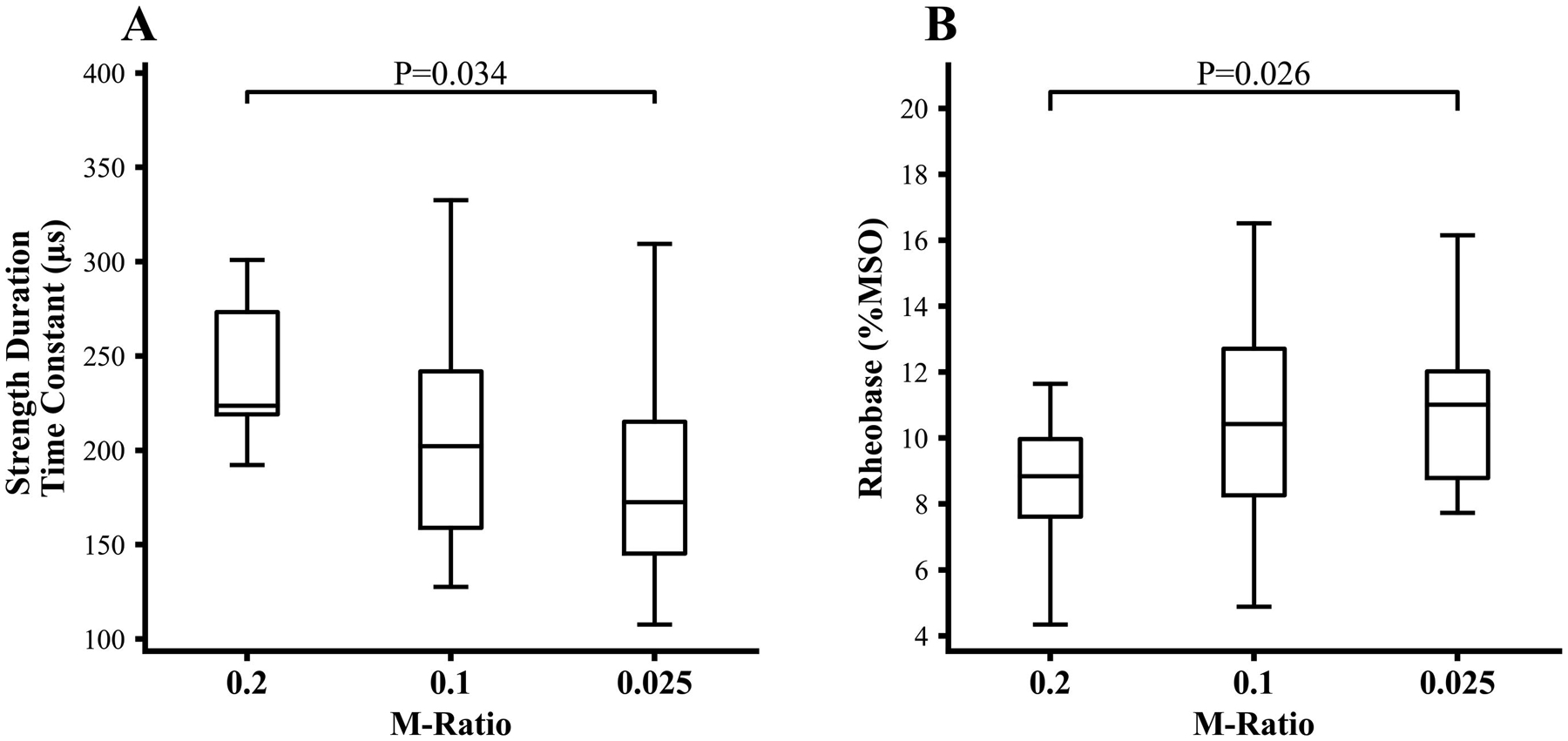
(A) The cortical strength-duration time constant (SDTC), estimated by using 5 pulse widths, was significantly longer when recorded with M-ratio of 0.2 compared to M-ratio 0.025, but not significantly different from that recorded with M-ratio of 0.1. (B) The rheobase (expressed as % of maximum stimulator output, MSO) was significantly smaller with the M-ratio set to 0.2 compared to M-ratio of 0.025, but not significantly different from that recorded with M-ratio of 0.1.

There was a significant correlation across subjects for the SDTC and rheobase recorded with M-ratios set to 0.2 (R = −0.60, P =0.004), 0.1 (R= −0.80, P < 0.001) and 0.025 (R=0.83, P < 0.001). The SDTC estimated with M-ratio set to 0.2 correlated with SDTC values recorded with M-ratio set to 0.1 (R= 0.48, P =0.024) but not 0.025 (P=0.475). Similarly, the rheobase estimated with M-ratio set to 0.2 correlated with rheobase recorded with M-ratio set to 0.1 (R=0.66, P=0.003) but not 0.025 (P=0.39). There was no significant correlation between peripheral and cortical SDTC measurements at any of the M-ratios.

Estimation of SDTC and rheobase with reduced number of pulse widths:

The cortical strength-duration properties were subsequently estimated using the same measured RMT but different combinations of three or four PWs.

When assessing 3 PW conditions, the root means square percentage error for SDTC and rheobase was lowest for the 30/60/120 μs PW combination (Table 1), which was the set of PWs used in the original measurement (D’Ostilio et al., 2016). Conversely, the worst root means square percentage error were observed for conditions missing the 30 μs PW data, which would be expected since the curvature of the strength-duration relationship is larger at low PWs. The combination of 30, 60, and 120 μs PW with M-ratio set to 0.2 resulted in SDTC (258.67±61.68 μs) and rheobase (8.05±2.56 %MSO) estimates that were similar to previously reported values (251±55 μs; 6.29±1.05 %MSO) (D’Ostilio et al., 2016).

With combinations of 4 PWs, the RMSPEs were lowest for the 30/60/90/120 μs PW combination, which also outperformed the best estimate with 3 PWs. Including the extra sample at 90 μs, which fills the widest gap in the 30/60/120 μs PW data, resulted in even sampling of the PW range, thereby improving the estimation performance. Again, the worst RMSPE was observed for PW combinations missing 30 μs PW data. Consequently, preserving the range of PWs, especially at low PW levels and providing sufficient sampling density, leads to better strength-duration estimates. This is not an unexpected finding since this PW sampling strategy provides the most information about the curvature of the strength-duration relationship.

Computational neuron model results:

The simulated strength-duration curves closely matched the experimental data for all three M-ratio values across the three simulated neuronal layers (Figure 2D–F). Additionally, simulated SDTC for each neuronal layer agreed with the cortical SDTC measured in subjects (termed experimental SDTC) for all three M-ratios (Figures 4A). As observed in experimental data, the simulated SDTC was significantly higher with M-ratio 0.2 compared to M-ratio of 0.025 in layer 2/3 (F_(2,12) = 14.111, P<0.001), layer 5 (F_(2,12) = 8.064, P=0.006) and in the layer 4 large basket cells (F_(2,12) = 3.524, P=0.063). Additionally, simulated rheobase was similar to experimental findings, being lowest at M-ratio 0.2 and greatest with M-ratio of 0.025 across all three layers (Figure 4B).

Figure 4:

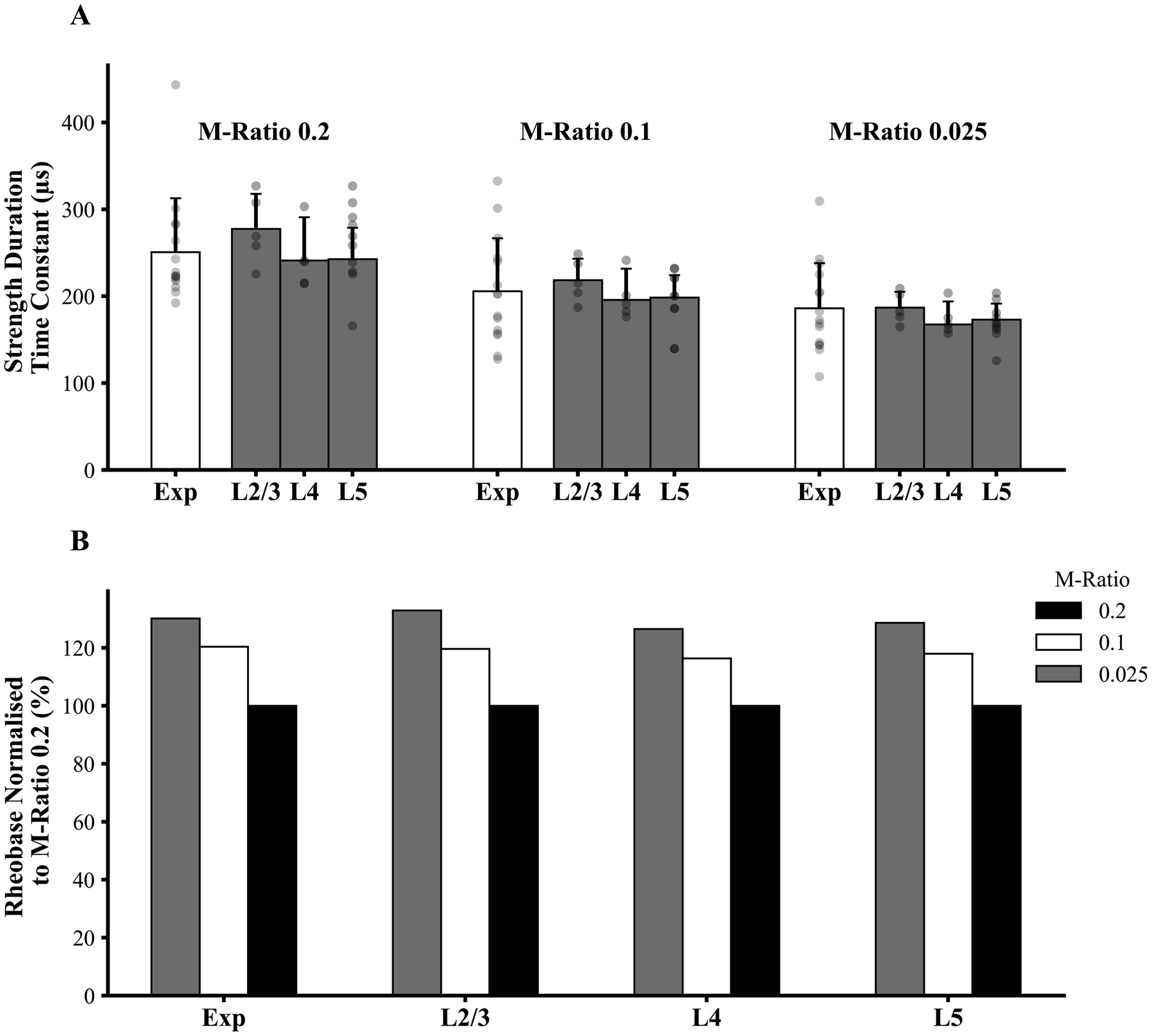
(A) Simulation studies disclosed that experimental strength-duration time constant (SDTC) was comparable to simulated values from layer (L) 2/3, 4, and 5. Grey dots represent individual experimental and individual simulated cell data. The rectangular bars represent mean values while the error bars represent standard deviations. (B) Rheobase values simulated with M-ratios set to 0.025 and 0.1 were normalised to simulated rheobase generated by M-ratio of 0.2 across the three cortical layers and compared to normalised experimental values. The simulated rheobase values were similar to experimental findings, with values lowest at M-ratio of 0.2 and highest for M-ratio of 0.025.

To further assess effects of M-ratio on strength-duration properties, RMTs for M-ratios of 0.2 and 0.1 were normalised by RMT values generated with M-ratio 0.025 at each pulse width, and these values were compared to simulated normalised thresholds. The normalised experimental thresholds elicited by M-ratio of 0.2 followed trends similar to those for the simulated thresholds at M-ratio 0.2 for neurons in layers 2/3, 4 and 5 (Figure 5A). Similarly, experimental thresholds elicited by M-ratio of 0.1 were comparable to simulated thresholds for neurons in layers 2/3, 4 and 5 at M-ratio of 0.1 (Figure 5B). The mean RMTs were greater for TMS pulse shapes exhibiting a larger hyperpolarizing phase (M-ratio of 0.2) at shorter pulse widths (30, 45 and 60 μs), as signified by the mean normalised threshold being > 100% and the lower limit of the 95% confidence interval not crossing the 100% point (Figure 5A). However, for large PWs (90 and 120 μs) the normalized RMTs for M-ratio of 0.2 were lower than 100% indicating reduced thresholds relative to M-ratio of 0.025. This phenomenon did not occur for the simulated data and the discrepancy with the simulated thresholds was also evident for PW of 30 μs. In the Discussion section we hypothesize that this effect stems from the recruitment of an additional neuronal population.

Figure 5:

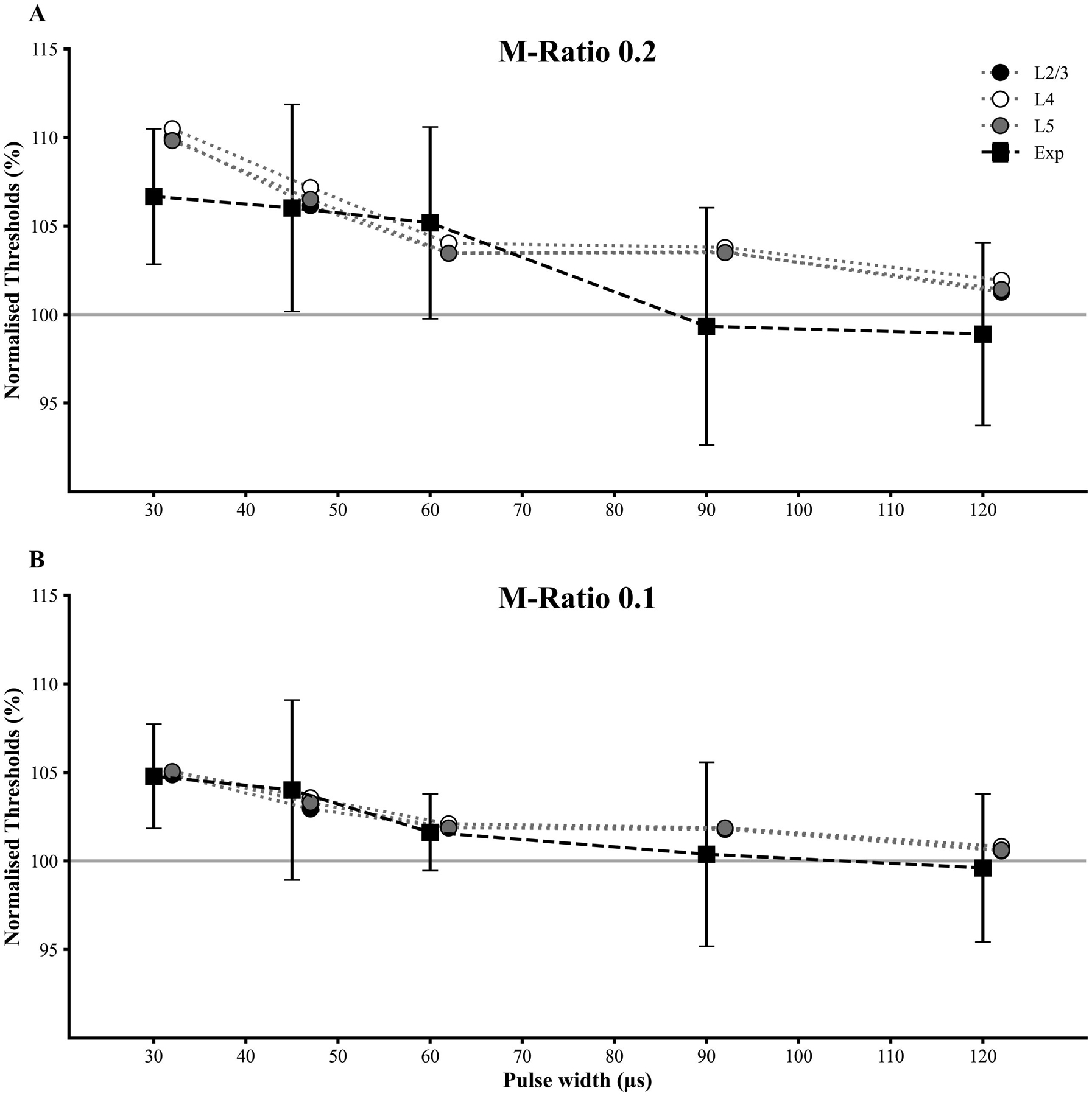
Resting motor threshold (RMT) for TMS pulses with M-ratio of (A) 0.2 and (B) 0.1 were normalised against RMT values for M-ratio of 0.025 across the 5 pulse widths (PW). The simulated thresholds for layer 2/3, 4 and 5 neurons for M-ratios of 0.2 and 0.1 were also normalised against the values for M-ratio of 0.025. The experimental data are expressed as mean ± standard deviation (error bars). The normalised curves matched well between the experimental and simulated data, with the notable exception of PWs of 30, 90 and 120 μs for M-ratio of 0.2 where the experimental thresholds were lower than the simulated ones (see discussion in main text).

To test whether trends in SDTC depend on axonal geometry, we reduced the realistic cortical neuron models to simplified, straight myelinated axons with the same electrical parameters as the axons of the original model neurons. For these straight axons, the SDTCs increased with higher M-ratios (Figure 6), similar to experimental observations. The same trend in SDTCs with M-ratio was observed in the MRG peripheral nerve model across fiber diameters (Figure 7). Subsequently, we varied individually the peak conductances of the main voltage-gated Na⁺ and K⁺ channels of the cortical straight axon models. The transient Na⁺ conductance (g_NaT) had a significant effect on SDTCs for all three cell-types; reducing this conductance increased SDTCs with larger increases evident with higher M-ratios, and increasing g_NaT reduced SDTCs (Figure 8). These results suggest the effect of M-ratio on SDTC is governed by local membrane dynamics, rather than axon morphology.

Figure 6:

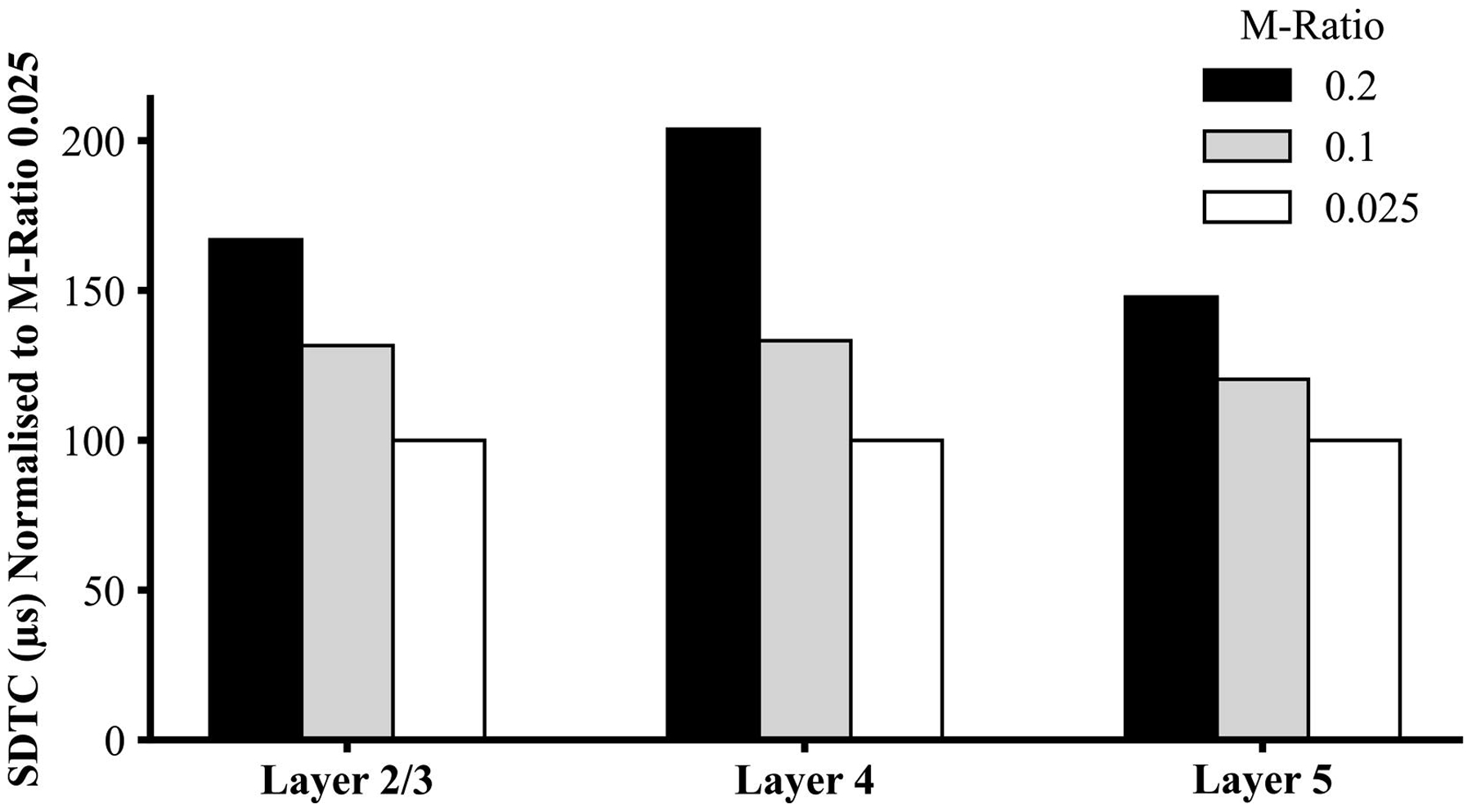
Simulation studies of single straight axons median strength-duration time constant (SDTC) at M-ratio 0.2 and 0.1 were normalised against simulated SDTC with M-ratio 0.025. SDTC was increased with higher M-ratios across the three cell layers, similar to experimental observations.

Figure 7:

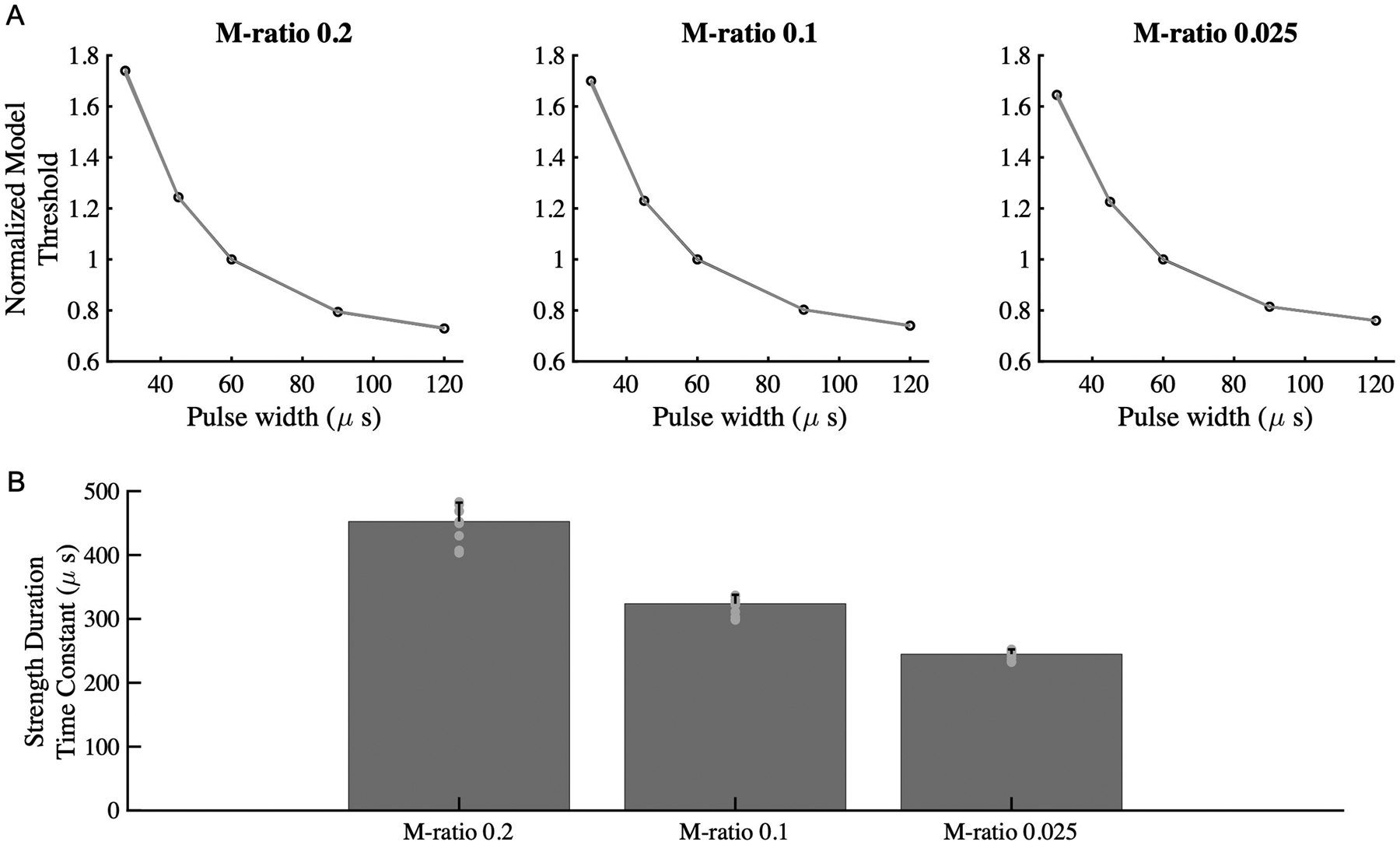
(A) Simulation of activation thresholds for the McIntyre-Richardson-Grill (MRG) peripheral nerve axon model across the M-ratios, normalized for thresholds at PW 60us. (B) The strength-duration time constant exhibited a similar trend as for cortical neurons, being highest with M-ratio of 0.2, followed by M-ratio of 0.1 and 0.025.

Figure 8:

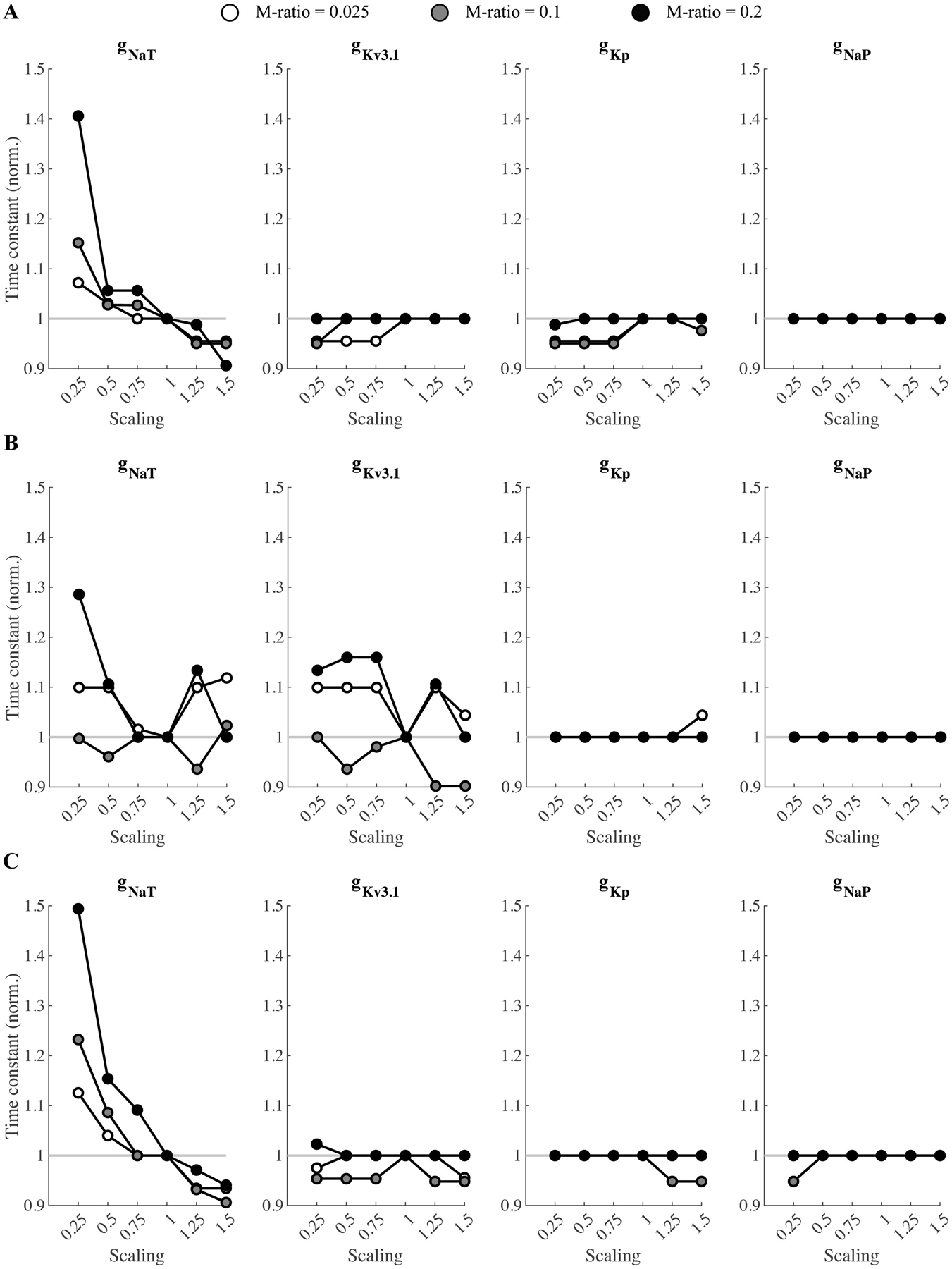
Effect of varying ion channel conductance on SDTC in straight axon models (see Figure 6) of A) L2/3, (B) L4, and (C) L5 neurons. Peak conductances of transient Na⁺ (g_NaT), delayed-rectifier ${\text{K}}^{+}\left({\mathit{\text{g}}}_{{\mathit{\text{K}}}_{v}3.1}\right)$, persistent K⁺ (g_Kp), and persistent Na⁺ (g_NaT) channels were varied individually by scaling the initial value by a factor of 0.25–1.5. The curves are normalized to the respective values for scaling of 1.

Discussion

Utilising a commercially available cTMS device, strength-duration properties of human motor cortical neurons were investigated by determining motor thresholds across different TMS pulse shape and width combinations. The present study demonstrated that the TMS pulse shape, as reflected by M-ratio, influenced cortical SDTC and rheobase measures. TMS pulses with higher M-ratios, reflected a higher amplitude of the second phase of the electric field pulse, resulted in longer SDTC and smaller rheobase values. Different PW combinations at which RMT was measured, also influenced SDTC and rheobase estimates, with 5 PW combinations providing more reliable measures as reflected by root mean square percentage errors. Computational modelling suggested that neuronal populations within cortical layers 2/3, 4 and/or 5 contributed to the experimental strength-duration curves and SDTC, on account of similar SDTCs and previously demonstrated low thresholds relative to other cell types (Aberra et al., 2020). At a single cell level, voltage-gated sodium channel dynamics appeared to mediate the effects of TMS pulse shape on cortical strength-duration properties via axonal transient Na⁺ conductance. While the physiological mechanisms underlying cortical strength-duration properties remain to be fully elucidated, the role of cortical neurons and ion channels will be discussed.

Measures of motor cortical strength–duration properties and physiological implications

Prior to undertaking a discussion on the physiological mechanisms underlying cortical SDTC and rheobase, it is important to first confirm the validity of the current approach. Using the same method, D’Ostilio and colleagues reported mean cortical SDTC values of 251±55 μs and rheobase of 6.29±1.05%MSO using three PW samples (30/60/120 μs) and an M-ratio of 0.2 (D’Ostilio et al., 2016). In the same study, a recruitment curve regression method using input-output curve data was also used to model the cortical strength-duration properties and yielded similar results. The findings in the present study are comparable to the previously reported values by D’Ostilio and colleagues utilising an identical stimulation paradigm (D’Ostilio et al., 2016), thereby supporting the veracity of the methodology used in the current study.

The present study extended the previous findings, establishing an importance of pulse shape (as reflected by M-ratio) and number of PWs in modelling of SDTC and rheobase. Lower M-ratios were associated with significantly shorter estimated cortical SDTC and larger rheobase values. The current findings are consistent with the collective data from Barker and colleagues [152±26 μs] (Barker et al., 1991), Peterchev and colleagues [200±33 μs] (Peterchev et al., 2013), and D’Ostilio and colleagues [251±55 μs] (D’Ostilio et al., 2016), that used monophasic pulses with progressively larger amplitude of the second electric field phase.

The physiological mechanisms underlying cortical SDTC and rheobase remain to be elucidated. Orientation of the TMS coil in a posterior-anterior direction preferentially activates interneuronal circuits located in layers 2–4 of the primary motor cortex (M1), as well as pyramidal cells within layers 2/3 and 5 (Aberra et al., 2020, Di Lazzaro et al., 2003, Di Lazzaro et al., 2002a, Di Lazzaro et al., 2012, Hamada et al., 2013, Higashihara et al., 2020). Consequently, the SDTC and rheobase reported in the present study may correspond to activation of cortical interneurons and pyramidal cells located in layers 2/3, 4 and 5 of the motor cortex, a notion supported by simulation studies. Since most (75%) of the simulated electric field orientations were perpendicular to the somato-dendritic axis, the threshold data represents neurons in the gyral crown region where the electric field orientation is mostly tangential to the pial surface and its magnitude is strongest making neural activation most likely (Aberra et al., 2020). It should be stressed that cortical SDTC may not simply reflect the properties of the most excitable excitatory interneurons, but rather the properties of subliminally activated interneuronal populations where summation of transsynaptic excitation of pyramidal neurons is sufficient to drive a motoneuronal population to the arbitrary threshold of 50 μV MEP amplitude. Future modeling studies could simulate a distribution of neuron models across the hand knob to assess dependence of SDTC on neuronal location (Aberra et al., 2020), thereby potentially providing evidence for specific site of activation.

Based on peripheral axon studies, SDTC and rheobase are influenced by transient [I_NaT] and persistent Na⁺ currents [I_NaP] (Bostock and Rothwell, 1997, Burke et al., 2001, Kiernan et al., 2020, Krishnan et al., 2009, Mogyoros et al., 1998, Mogyoros et al., 1996). Physiological and anatomical factors, such as resting membrane potential, structural axonal and myelin integrity, as well as type of nerves assessed, influence SDTC and rheobase (Kiernan et al., 2020). The straight axon model suggested that only I_NaT significantly modulated the M-ratio effects on SDTC, with lower conductances leading to more pronounced differences in SDTCs between M-ratios. It should be acknowledged that the kinetics and spatial distribution of I_NaT and I_NaP in cortical axons within each layer is not well characterized. Consequently, a contribution from I_NaP should not been ruled out from current models. The I_NaP currents appear to be important in setting the threshold for action potential generation (Gorman et al., 2021, Müller et al., 2018, Schattling et al., 2016). In the present study, cortical SDTC values estimated for different M-ratios were comparable to previously reported peripheral SDTC values estimated by magnetic stimulation of the ulnar nerve [Barker et al., 150±55 μs versus SDTC_M0.025 186.7±52.5 μs; D’Ostilio and colleagues 197 ± 47 μs versus SDTC_M0.2 243.4±61.2 μs] (Barker et al., 1991, D’Ostilio et al., 2016). This observation suggests that similar sodium channel isoforms and kinetics mediate both cortical and peripheral axonal strength-duration properties.

Previous modelling studies predicted that sites of maximal depolarization and action potential initiation by TMS were at the level of intracortical axonal terminations in the superficial gyral crown and lip regions. Layer 5 pyramidal cells exhibited the lowest thresholds, followed by layer 4 inhibitory basket cells and layer 2/3 pyramidal neurons, although the distributions of thresholds in these layers overlapped (Aberra et al., 2020). Consequently, cortical SDTC and rheobase may be determined by the density and distribution of voltage gated Na⁺ channels located within the intracortical axon terminal branches of interneuronal and pyramidal cells located in layers 2–5 of M1, although this needs further validation.

The present study highlights the importance of TMS pulse shape for estimating SDTC and rheobase. Motor thresholds were affected by a significant M-ratio*PW interaction, leading to TMS pulses with lower M-ratios (smaller amplitude of the second phase) being associated with significantly shorter cortical SDTC and larger rheobase values, in keeping with previous studies (Barker et al., 1991, D’Ostilio et al., 2016, Peterchev et al., 2013). Based on our simulations, a larger hyperpolarising phase likely exerts a stronger modulating effect on Na⁺ channels, as observed in previous studies (Koponen et al., 2018, Maccabee et al., 1998). Increasing the M-ratio from 0.2 to 0.8 for posterior-anterior stimulation produced a trend for increasing RMT with a significant effect of pre-activation (Sommer et al., 2018). For TMS pulse shapes with higher M-ratios, the larger hyperpolarising phase of the electric field pulse may potentially block action potential generation and increase motor thresholds, particularly at lower PW durations, thereby influencing SDTC and rheobase. This notion is supported by present findings where normalised thresholds were higher in both experimental and simulated data at lower pulse widths with higher M-ratios (Figure 5). Simulation of straight cortical and peripheral axons reproduced the experimental finding of increasing SDTC with higher M-ratios, suggesting the effect of M-ratio on SDTC is dependent on ion channel mechanisms shared between central and peripheral nerves and independent of axon morphology. It seems likely that neuronal voltage-gated Na⁺ channels kinetics explains the influence of pulse shape on SDTC, as previously suggested (Koponen et al., 2018).

Nonetheless, some aspects of the observed differences in the strength-duration curves across different M-ratios may be explained by recruitment of distinct neuronal populations, not captured in our simulations of single neurons. Notably, the experimental RMTs for large PWs (90 and 120 μs) at M-ratio of 0.2 were lower compared to the corresponding thresholds for smaller M-ratios (Figure 5). Moreover, the normalised experimental thresholds at these PWs as well as at 30 μs appear lower than the simulation results. A potential explanation may relate to recruitment of neurons sensitive to anterior-to-posterior electric field. Specifically, previous studies have shown that anterior-to-posterior sensitive neurons are activated by biphasic TMS pulses (Di Lazzaro et al., 2001). Additionally, previous studies have demonstrated shifts in neuronal population recruitment for anterior-to-posterior, but not posterior-to-anterior, directed pulses with the same pulse shapes utilised in the present study (D’Ostilio et al., 2016, Sommer et al., 2018). Given that TMS pulses with long PWs and higher M-ratios (0.2) are more biphasic than pulses with lower M-ratios (0.025), it is conceivable that the unexpected reduction of thresholds for M-ratio of 0.2 reflects additional recruitment of anterior-to-posterior sensitive neurons that contribute to the evoked corticospinal volley. This competing effect partially counteracts the increase of threshold with larger M-ratio driven by the Na⁺ channel response, leading to the observed lack of a statistically significant effect on RMT of M-ratio by itself.

In the present study, cortical SDTC estimates were significantly shorter compared to peripheral axonal SDTC estimates obtained with transcutaneous electrical stimulation (Kiernan et al., 2020). It should be noted that cortical SDTC estimates generated by conventional electrical stimuli [432.2±70.5 μs] (Burke et al., 2000), were comparable to peripheral axonal SDTC estimates from the present study 440.6±66.7 μs. As discussed above, the cortical SDTC estimates in the present study were comparable to those generated by peripheral magnetic stimulation (150±55 μs), which were close to the cortical time constants in the same subjects (152±26 μs) (Barker et al., 1991). A likely explanation for differences between cortical and peripheral strength-duration parameters may relate to stimulation methodologies (Patrick Reilly, 2010, Recoskie et al., 2009). Specifically, the shape of the cTMS pulse is not perfectly rectangular, compared to electrical pulses, with a reverse phase which may influence action potential generation and thereby estimated SDTC values (Koponen et al., 2018). Additionally, the limited and different range of pulse durations used with cTMS protocols (120 μs longest) can also impact cortical strength-duration properties, since the neural membrane is nonlinear and rheobase is estimated by regression from the available short pulses, potentially resulting in uncertainty of estimation. Another potential source of differences is the local distribution of the electric field near the activated membrane (Kuhn et al., 2009). The time constants for estimating cortical and peripheral strength-duration parameters utilize different models, namely the first-order low-pass filter (magnetic) and the hyperbolic strength–duration curve model (electrical), potentially yielding different estimates.

The study methods have some limitations. Generally, a cTMS device or another device with an adjustable pulse width and M-ratio is required to implement these measurements clinically. TMS pulse shapes with very low M-ratio, such as 0.025, and large pulse widths, such as 120 μs, require the stimulator to generate extremely low negative voltages for the second phase of the electric field pulse, and the cTMS device has limits on the lowest voltage it can produce stably. Consequently, for three participants with low RMTs, the minimum machine output limit of the device was reached for M-ratio set to 0.025, and therefore it was not possible to measure the strength-duration curve for that M-ratio. Additionally, the interstimulus interval across different M-ratios was not determined, and different interstimulus intervals could affect the RMT measurement (Möller et al., 2009). Such effects would apply for all M-ratio’s with more prominent effects expected at M-ratio 0.025 due to slow capacitor charging. Despite this possibility, higher SDTC and lower rheobase values with higher M-ratios recorded in the present study corresponded with the results of the stimulation studies, support the robustness of the experimental data. Further, although pulse widths were pseudo-randomized, the delivery of multiple TMS stimuli to measure the strength-duration curve could have influenced the RMT values depending on the PW sequence. Since the same PW order was used in all M-ratio conditions, this is unlikely to affect the comparisons across M-ratios, although the possibility that multiple TMS stimuli could have influenced membrane properties (namely transient and persistent Na⁺ channel conductances) is not discounted. To minimize the influence of potential PW order effects, the measurements of the RMT for the different PW conditions can be interleaved in future studies (Peterchev et al., 2013). Finally, since the strength-duration curve characteristics are determined primarily by the passive neuron membrane properties, and the effect of ion channel dynamics is a secondary effect, other paradigms, such as measuring the RMTs for different spacings between the first and second phase of the electric field (Koponen et al., 2018), could provide additional and/or more direct information about the ion channel dynamics.

Clinical implications

Despite advances in ion channel pathophysiology in neurodegenerative diseases such as amyotrophic lateral sclerosis (ALS), a greater understanding of precise neuronal dysfunction in cortical circuits is required. Prolongation of peripheral axonal SDTC has been consistently identified in a variety of neurological disorders, such as ALS, and associated with disease pathogenesis (Geevasinga et al., 2015, Kanai et al., 2003, Kiernan et al., 2020, Kuo et al., 2005, Mogyoros et al., 1998, Park et al., 2017, Shibuya et al., 2013, Stys, 2004, 2005, 2007, Vucic S. and Kiernan M.C., 2006, Vucic S and Kiernan M. C., 2006, Vucic and Kiernan, 2007, 2010). In ALS, abnormalities of Na⁺ conductances appears to underlie SDTC prolongation at a peripheral nerve level and are associated with clinical features such as fasciculations, muscle cramps as well as neurodegeneration (Kanai et al., 2006, Kuo et al., 2005, Kuwabara et al., 2008, Menon et al., 2013, Tamura et al., 2006, Urbani and Belluzzi, 2000, Vucic and Kiernan, 2010, Wilbourn, 2000). Modulation of Na⁺conductances with blocking agents, such as flecainide and mexiletine, was associated with symptom improvement (Park et al., 2015, Weiss et al., 2021, Weiss et al., 2016).

Although identifying the precise cortical neurons activated by TMS in general, and cTMS in particular, remains a matter of ongoing research (Siebner et al., 2022), our approach has relevance for understanding disease pathogenesis. The present study suggests a role for cTMS in dissecting out the contribution of interneuronal (basket cell) and pyramidal cell circuits (Layers 2/3 and 5) dysfunction in development of cortical hyperexcitability in neurodegenerative disorders. Specifically, SDTC and rheobase appear to be biomarkers of fast sodium channel function as well as passive membrane properties of corticomotor neurons, and measuring these in ALS patients could provide insights into mechanisms underlying development of cortical hyperexcitability and neurodegeneration. Additionally, altering the TMS pulse shape may result in recruitment of selective neuronal populations which could shed further insights into disease pathogenesis. The specific targeted neuronal population could be varied with further developments to the methods such as detection of responses lower than 50 uV and changes of the induced current orientation. If confirmed, novel pathogenic biomarkers could be developed, that could be utilised in future therapeutic trials, with cTMS measures serving as a biomarker of disease progression and drug effectiveness in clinical trials.

Finally, this study supports several practical methodological recommendations. First, if suppressing the threshold-altering effect of the trailing phase of the TMS pulse is advantageous, then an M-ratio of 0.1 appears to be a good choice since decreasing the M-ratio further results in comparable SDTC and rheobase but runs into technological limitations. Choosing a low M-ratio ≤ 0.1 also appears to result in more unidirectional, and hence selective, neural stimulation effects. Second, for sampling the strength-duration curves with a limited number of pulse widths, we recommend the sets of 30/45/60/90/120 μs, 30/60/90/120 μs, and 30/60/120 μs for 5, 4, and 3 PW combinations, respectively, since they produce the most consistent SDTC and rheobase values. The present study also provides normative data from healthy subjects that can be compared to measurements in patients.

Highlights.

1. The TMS pulse shape and selection of pulse widths influences the properties of the cortical strength-duration curve.

2. Larger hyperpolarizing TMS pulse trailing phase increases motor thresholds resulting in longer cortical strength-duration time constant and smaller rheobase.

3. Modulation of transient sodium channels by the trailing hyperpolarising phase is likely to mediate the effects of TMS pulse shape on cortical strength-duration curve properties.