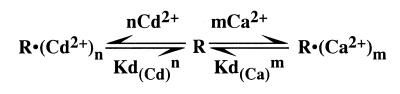A further investigation and reappraisal of the thio effect in the cleavage reaction catalyzed by a hammerhead ribozyme

Abstract

We synthesized three types of 11mer substrate, namely the natural substrate S11O and the thiosubstituted substrates S11SpS and S11RpS, in which the respective pro-Sp and pro-Rp oxygen atoms were replaced by sulfur, and subjected them to detailed kinetic analysis in the cleavage reaction catalyzed by a hammerhead ribozyme. In agreement with previous findings, in the presence of Mg²⁺ or Ca²⁺ ions the rate of ribozyme-catalyzed cleavage of S11SpS was as high as that of S11O, whereas the corresponding rate for S11RpS was nearly four orders of magnitude lower than that for either S11O or S11SpS. However, the rate of the ribozyme-catalyzed reaction with each of the three substrates was enhanced by Cd²⁺ ions. Such results have generally been taken as evidence that supports the direct interaction of the sulfur atom at the Rp position of the cleavage site with the added Cd²⁺ ion. However, our present analysis demonstrates that (i) the added Cd²⁺ ion binds at the P9 site; (ii) the bound Cd²⁺ ion at the P9 site replaces two Mg²⁺ or two Ca²⁺ ions, an observation that suggests a different mode of interaction with the added Cd²⁺ ion; and, most importantly and in contrast to the conclusion reached by other investigators, (iii) the Cd²⁺ ion does not interact with the sulfur atom at the Rp position of the scissile phosphate either in the ground state or in the transition state.

INTRODUCTION

Hammerhead ribozymes are metalloenzymes that require divalent metal ions for the cleavage of RNA phosphodiester linkages (1–17), although high concentrations of monovalent metal ions (1 to 4 M monovalent cations, such as Li⁺, Na⁺ and NH₄⁺) can also perform the functions of the divalent metal ions that are normally included in reaction mixtures (18). Although the exact roles of metal ions have been discussed for more than a decade, they remain controversial. One of the proposed major roles of metal ions is neutralization of the negative charge of a non-bridging phosphoryl oxygen (pro-Rp oxygen) at the cleavage site (electrophilic catalysis) (19–22). This proposal is based on the fact that when the pro-Rp oxygen is replaced by a sulfur atom (RpS substrate; Fig. 1), the cleavage rate in the presence of Mg²⁺ ions is dramatically reduced (the so-called thio effect) (19–23). Moreover, the reduced rate of cleavage of the RpS substrate is raised to the rate with the normal substrate in the presence of Mn²⁺ ions. This phenomenon is called ‘manganese rescue’ and has been explained using the HSAB (hard soft and acid base) rule (24,25). According to this rule, a ‘hard acid’, such as a Mg²⁺ ion, prefers to bind to a ‘hard base’ oxygen atom rather than to a ‘soft base’ sulfur atom. In contrast, a ‘soft acid’, such as a Cd²⁺ ion, prefers to bind to a ‘soft base’ sulfur atom. A Mn²⁺ ion is softer than a Mg²⁺ ion and, thus, the former can bind to a soft sulfur atom (as well as to a hard oxygen atom). This binding is believed to be the origin of manganese rescue. Analysis of the thio effect and of manganese rescue has contributed significantly to the elucidation of the mechanism of action of ribozymes in general (26–31). However, we have suggested that observations of the thio effect and manganese rescue by themselves do not guarantee that the direct coordination of a metal ion with the pro-Rp oxygen at the cleavage site occurs in hammerhead ribozyme-catalyzed reactions (15,32,33). Moreover, we have attempted to explain the thio effect and manganese rescue by mechanisms that do not involve the direct coordination of a metal ion at the pro-Rp oxygen.

Figure 1.

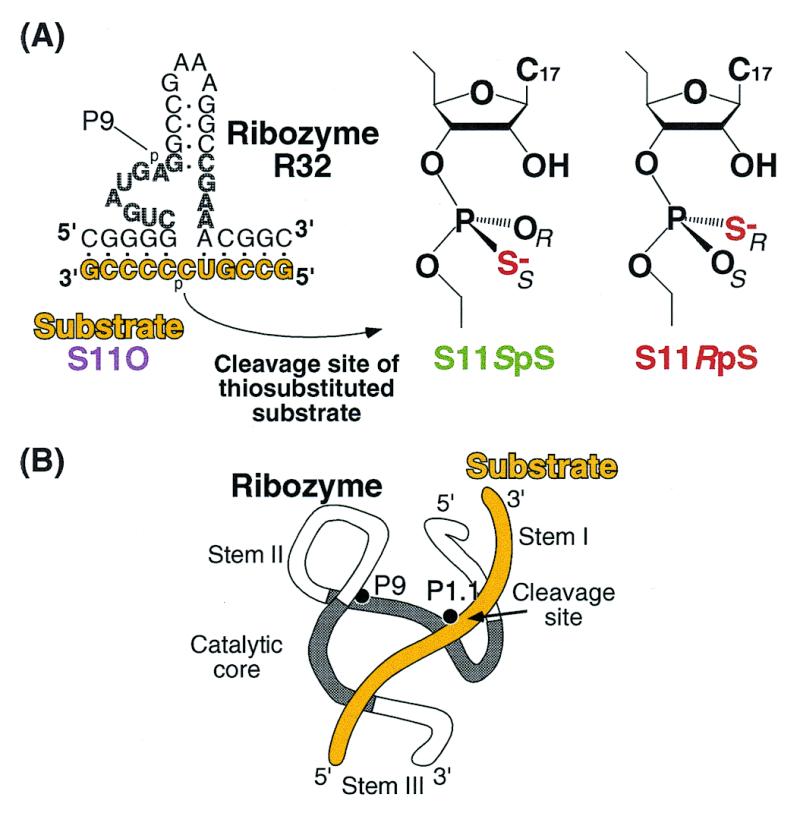
(A) Structures of the ribozyme (R32) and the three substrates. S11O has a natural phosphate group at cleavage site; in S11SpS, the pro-Sp non-bridging oxygen is replaced by sulfur at the cleavage site; in S11RpS, the pro-Rp non-bridging oxygen is replaced by sulfur. (B) Schematic illustration of the three-dimensional structure of a ribozyme–substrate complex showing two important metal-binding sites (P9 and the cleavage site, P1.1). In (A) and (B), the substrate is drawn in yellow and catalytic core is shaded.

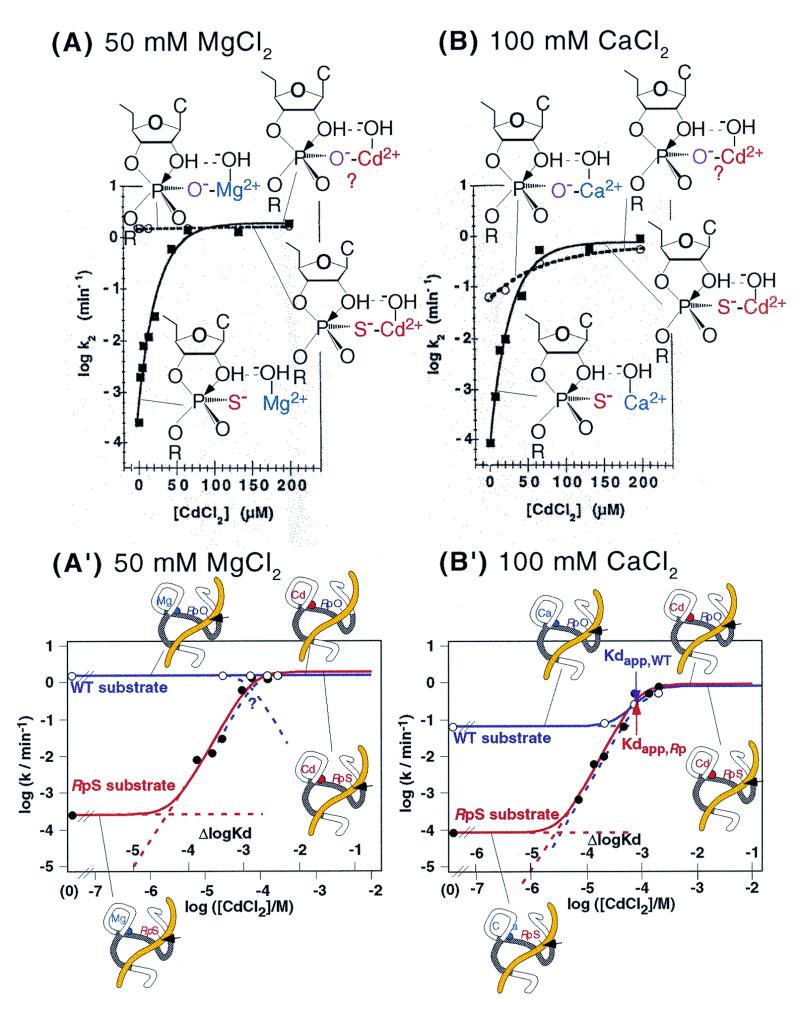
The thio effect and manganese rescue have been examined in great detail in ribozyme-catalyzed reactions (hereafter the term ribozyme denotes exclusively a hammerhead ribozyme unless otherwise noted). Results showing the thio effect and ‘cadmium rescue’ are reproduced in Figure 2A and B (23). Clearly, in the absence of soft Cd²⁺ ions, the cleavage rate for the RpS substrate was ∼10⁴-fold lower than that for the natural, unmodified substrate (WT substrate). The addition of soft Cd²⁺ ions to a hard Mg²⁺ ion-catalyzed reaction (Fig. 2A) or a hard Ca²⁺ ion-catalyzed reaction (Fig. 2B) restored the efficient cleavage of RpS and, at high concentrations of Cd²⁺ ions, the cleavage rate reached that observed with the WT substrate. These observations would appear to prove the direct coordination of a metal ion with the pro-Rp oxygen, as shown schematically in Figure 2A and B. However, performing essentially very similar experiments to those whose results are reported in Figure 2, we reached completely different conclusions. We replotted the published data in the same way as we plotted our own data (see below and Fig. 5). Our graphs are shown in Figure 2A′ and B′, which are based on the data shown in Figure 2A and B, respectively.

Figure 2.

The Cd²⁺ rescue experiment, with cleavage of natural and RpS substrates, that was described by Scott and Uhlenbeck with 50 mM MgCl₂ (A) or 100 mM CaCl₂ (B) as background (modified from 23). Rate constants for the WT substrate are shown by open circles and rate constants for the RpS substrate are shown by closed squares. Proposed interactions are shown schematically. (A′) and (B′) show the data in (A) and (B) replotted on a log-log scale. The rate constants for the WT substrate are shown by open circles and violet lines, and the rate constants for the RpS substrate are shown by closed circles and red lines. Kd_apps are shown by arrows in (B′) (WT substrate, violet arrow; RpS substrate, red arrow). Replacement of the P9 metal ion is shown schematically.

Figure 5.

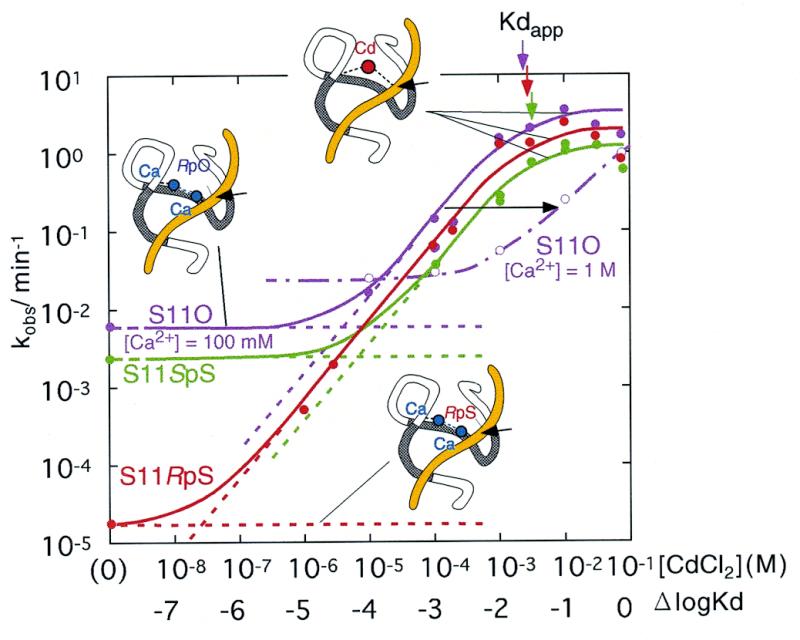
Titrations with Cd²⁺ ions of R32 ribozyme-catalyzed reactions for each substrate (S11O, violet; S11SpS, green; and S11RpS, red) with 100 mM Ca²⁺ ions as background [50 mM MES-Na, pH 6, 37°C]. The dotted lines indicate the activities for the Ca²⁺-bound state (the less active state) and the fraction of Cd²⁺-bound state (the activated state), and the unbroken lines that connect experimentally obtained rate constants (represented by circles) indicate the total activities (summation of the activities originating from the less active Ca²⁺-bound species and the more active Cd²⁺-bound species). The arrows indicate the Kd_apps for each ribozyme–substrate complex (colors correspond to each respective substrate). The open circles and broken lines indicate rate constants with 1 M Ca²⁺ ions as background. Two Ca²⁺ ions are replaced by a single Cd²⁺ ion. In the ribozyme–substrate complex, potential metal binding sites are indicated by dotted lines.

Figure 2B′ raises several questions that must be answered. It is true that Cd²⁺ ions at higher concentrations replace the background Ca²⁺ ions and that, finally, RpS is cleaved at a fixed rate when the apparent dissociation constant of the Cd²⁺ ions is exceeded (indicated by Kd_app with a red arrow in Figure 2B′) because the Ca²⁺ ion(s) has been replaced by a catalytic Cd²⁺ ion(s) above the Kd_app for Cd²⁺ ions. It should be noted, however, that Cd²⁺ ions at higher concentrations similarly replaced the background Ca²⁺ ions in the reaction with the WT substrate and, finally, the natural substrate was cleaved at a fixed rate identical to the rate for RpS above the Kd_app for Cd²⁺ ions (indicated by Kd_app with a violet arrow). Clearly, Cd²⁺ ions enhanced the cleavage rate not only of the thiosubstituted substrate but also of the unmodified substrate, indicating that Cd²⁺ ions replaced bound Ca²⁺ ions even in the case of the unmodified substrate. Moreover, we must also ask why the affinity for Cd²⁺ ions is the same for both the RpS and WT substrates (Kd_app with red arrow is the same as Kd_app with violet arrow). We would expect RpS to have a higher affinity for Cd²⁺ ions because the soft Cd²⁺ ion is known to interact with a sulfur atom with significantly higher affinity (two orders of magnitude higher) than with a hard oxygen atom (34–36).

Most studies of crystal structures of hammerheads have identified a metal-binding site between the pro-Rp oxygen of the phosphate of A₉ (P9 oxygen) and the N7 atom of G_10.1 (37–39). Even though this metal-binding site (P9 site) within the crystal structure is located ∼20 Å from the scissile phosphodiester bond (Fig. 1), this metal-binding site is thought to play a crucial role in achieving maximal cleavage activity for the following reasons. The substitution of the pro-Rp phosphoryl P9 oxygen by a sulfur atom (in the P9-RpS ribozyme) results in a decrease in Mg²⁺-dependent catalytic activity (40). Furthermore, replacement of G_10.1 by a pyrimidine also results in a substantial decrease in the ribozyme’s activity (41,42). Moreover, from their kinetic studies of ribozymes with a phosphorothioate modification at the P9 phosphate, Uhlenbeck’s group and Herschlag’s group reported that an Rp phosphorothioate linkage reduced the cleavage rate by a factor of 10³ (43). However, the rate returned to the control value after the addition of a low concentration of Cd²⁺ ions, which are thiophilic (43). A noteworthy aspect of such studies (43) is that, as reproduced in Figure 3, the affinity of Cd²⁺ ions was indeed higher for the P9-RpS ribozyme than for the wild-type ribozyme (WT ribozyme) [Kd_app (25 µM; red arrow) for the P9-RpS ribozyme is smaller than Kd_app (220 µM; violet arrow) for the WT ribozyme]. Thus, it appears that (i) in contrast to the observations shown in Figure 2B′, a metal ion coordinates directly with the P9 oxygen; and (ii) the P9 oxygen is one of the metal-binding sites that is required for efficient catalysis.

Figure 3.

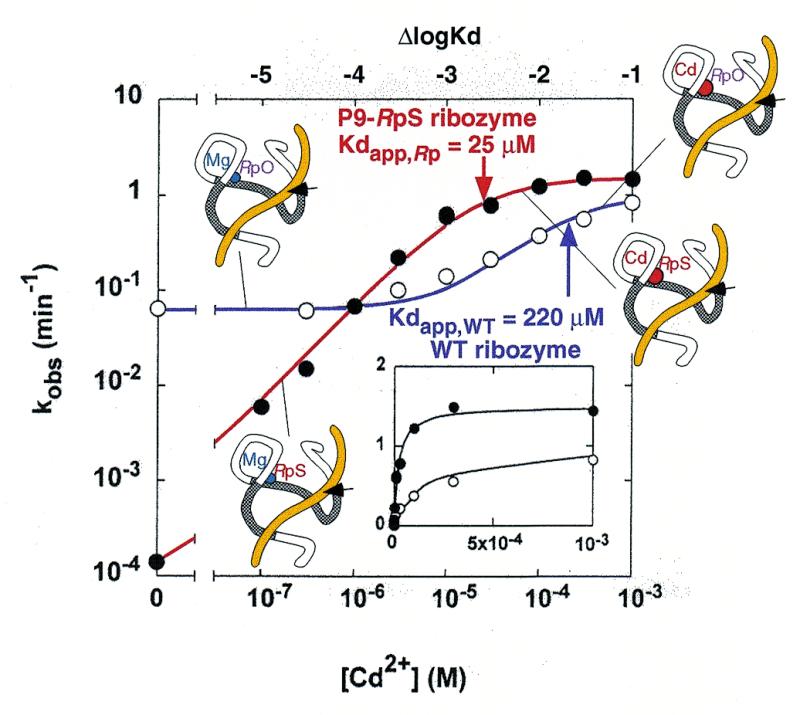
The Cd²⁺ rescue experiment that was described by Peracchi et al., with thiosubstitution at the P9-pro-Rp oxygen of the ribozyme (modified from 43). Rate constants for the WT ribozyme are shown by open circles and a violet line, and rate constants for the P9-RpS ribozyme are shown by closed circles and a red line. Replacement of the P9 metal ion is shown schematically. The Kd_apps are shown by arrows (WT ribozyme, violet arrow; P9-RpS ribozyme, red arrow).

The above analysis and our own data indicate that a Cd²⁺ ion binds first to the pro-Rp phosphoryl P9 oxygen (not with the pro-Rp phosphoryl oxygen at the cleavage site). When we were preparing the present report, in which we hoped to demonstrate that the thio effect and cadmium rescue, observed with the RpS substrate (Fig. 1), are not correlated with the binding of a metal ion to the pro-Rp phosphoryl oxygen at the cleavage site, the report of a nearly identical analysis by Wang et al. appeared in the literature (17). Although we noted that our experimental data were very similar to those of Wang et al., our analysis indicated, in contrast to their conclusions, that all their data and ours can be explained without invoking the direct coordination of a metal ion with the pro-Rp oxygen at the cleavage site. We present here our analysis that provides evidence against the direct coordination of a Cd²⁺ ion with the pro-Rp oxygen at the cleavage site either in the ground state or in the transition state.

MATERIALS AND METHODS

Preparation of ribozyme and substrates

The ribozyme R32, the unmodified substrate S11O and the substrates S11S with thiosubstitutions at the cleavage site (a mixture of RpS and SpS phosphorothioate isomers, S11SpS and S11RpS), as shown in Figure 1, were synthesized with a DNA/RNA synthesizer (model 394; PE Applied Biosystems, Foster City, CA) or purchased from Genset (Paris, France). The R32 ribozyme was purified by polyacrylamide (20%) gel electrophoresis. The two isomers of the thiosubstituted substrate, S11SpS and S11RpS, were separated by reverse-phase HPLC, and all three substrates, namely S11O, S11SpS and S11RpS, were labeled at the 5′-end with T4 kinase and [γ-³²P]ATP.

Analysis of reaction kinetics

Metal salts, namely MgCl₂, MnCl₂, CdCl₂ and CaCl₂, were purchased from Sigma-Aldrich (St Louis, MO) and were of the highest grade available. Metal ion-buffer mixtures were prepared by mixing respective stock solutions, as follows, with either 250 mM Tris–HCl (pH 6.0) or 250 mM MES (pH 6.0): 250 mM MgCl₂, 250 mM MnCl₂, 100 nM–250 mM CdCl₂, 200 mM or 2 M CaCl₂. Even though dissolving Cd²⁺ ions can significantly increase the concentration of H⁺ ions, depending on the interactions with specific buffers, Cd²⁺ ions had only a negligible effect on the pH in MES-buffered reaction mixtures. When Tris–HCl buffer was used, the pH was adjusted to 6.0 before reactions. Mixtures of trace amounts of labeled substrate and R32 ribozyme (final concentration, 600 nM) were added to 4 vol of metal ion–buffer mixture to start the reactions after prior incubation at the reaction temperature, 37°C. Aliquots of reaction mixtures were removed at specified times and mixed with ice-cold stop solution (9 M urea, 100 mM EDTA, pH 5.8, 0.02% xylene cyanol and 0.02% bromophenol blue). The substrate and the cleaved products were separated on a 20% polyacrylamide gel, and relative levels were calculated from their radioactivities, measured with an imaging analyzer STORM 830 system (Molecular Dynamics, Sunnyvale, CA). Cleavage rates were determined by fitting the time-course of changes in levels of cleavage products to an exponential curve.

Effects of counter anions

There was a possibility that the Cd²⁺ ions might be strictly coordinated with Cl^– ions and, moreover, at >10 mM, that the concentration of free Cd²⁺ ions might not be proportional to the concentration of added CdCl₂. A Cd²⁺ ion coordinated with a Cl^– ion, Cd²⁺(OH₂)Cl^–, has a reduced total positive charge and the complex must have a chelated water molecule with a high pKa, which leads to a reduction in the concentration of the hydroxide form, Cd²⁺(OH^–)Cl^–, which might be an important species in the ribozyme reaction. Because the cleavage rate with 1 M CaCl₂ (Fig. 5, broken violet curve) was shifted to the right compared with the rate with 100 mM Ca²⁺ (Fig. 5, solid violet curve) and cleavage was not saturated above 10 mM CdCl₂, saturation in the presence of 100 mM CaCl₂ was not due to the coordination of a Cl^– ion to Cd²⁺ ion. Furthermore, we also examined the effects of NO^3–, which might be a better chelator of the Cd²⁺ ion than Cl^–, but NO^3– ions had no effect on cleavage reactions (data not shown).

RESULTS

Thio effects and cooperative rescues

For kinetic measurements, we used the well characterized 32mer ribozyme R32 and the three 11mer substrates S11O, S11SpS and S11RpS, whose sequences are shown in Figure 1A (10,12,15,33,44–47). S11O is a substrate with natural phosphodiester linkages. In S11SpS and S11RpS, the pro-Sp oxygen and the pro-Rp oxygen, respectively, at the cleavage site are replaced by sulfur (33). The Kd value for the R32–S11O complex was ∼20 nM in the presence of 25 mM Mg²⁺ at pH 7.0. In the present study, we used 600 nM ribozyme under single turn-over conditions. Reduction of the concentration of R32 to 200 nM did not change the rate of cleavage of the natural substrate S11O and it also did not affect the slow cleavage of S11RpS, confirming that, under the conditions of our kinetic measurements, all substrate molecules, regardless of thiosubstitution, had formed Michaelis–Menten complexes with excess R32 prior to the subsequent chemical cleavage reaction. Furthermore, we confirmed that, in the presence of 25 mM Mg²⁺ at pH 7.0, our ribozyme–substrate complex remains in its active conformation (46).

Figure 4 shows rates of ribozyme-mediated cleavage for the three types of substrate in the presence of a total of 25 mM metal ions (either one or two types of metal ion). In Figure 4A, a significant thio effect can be recognized for S11RpS and smaller thio effects can be recognized for S11SpS. It is also apparent that Mn²⁺ ions supported the highest cleavage activity, not only with the thio-substrates but also with unmodified S11O. With S11O, the ribozyme-catalyzed cleavage in the presence of Cd²⁺ ions was much slower than the expected rate, based on the pKa of a Cd²⁺-bound water molecule: the rank order of the activities (Mn²⁺ >> Mg²⁺ > Cd²⁺) was not related to the magnitude of pKa [pKa_Cd = 9.6; pKa_Mn = 10.6; pKa_Mg = 11.4; (48)] and it was also not the same rank order as the rank order of the metal-catalyzed cleavage (without ribozymes) of dinucleotides [Cd²⁺ > Mn²⁺ > Mg²⁺; (49–51)]. It should be mentioned that, in the metal-catalyzed cleavage of dinucleotides, thiophilic Cd²⁺ ions enhance the cleavage of both Sp and Rp thio-substrates specifically, as compared with the cleavage of the normal phosphodiester bond (50). In general, the rate of cleavage of ribozyme-catalyzed reactions depends on the pKa of the metal ion used (19). The low cleavage rate in the presence of Cd²⁺ ions might indicate that the ribozyme–substrate complex adopts a slightly different conformation in the presence of Cd²⁺ ions than it does in the presence of other metal ions, such as Mg²⁺ and Mn²⁺ ions. Nevertheless, Cd²⁺ ions appeared to rescue the ribozyme-mediated cleavage of S11RpS, as if a Cd²⁺ ion might have coordinated with the Rp sulfur atom.

Figure 4.

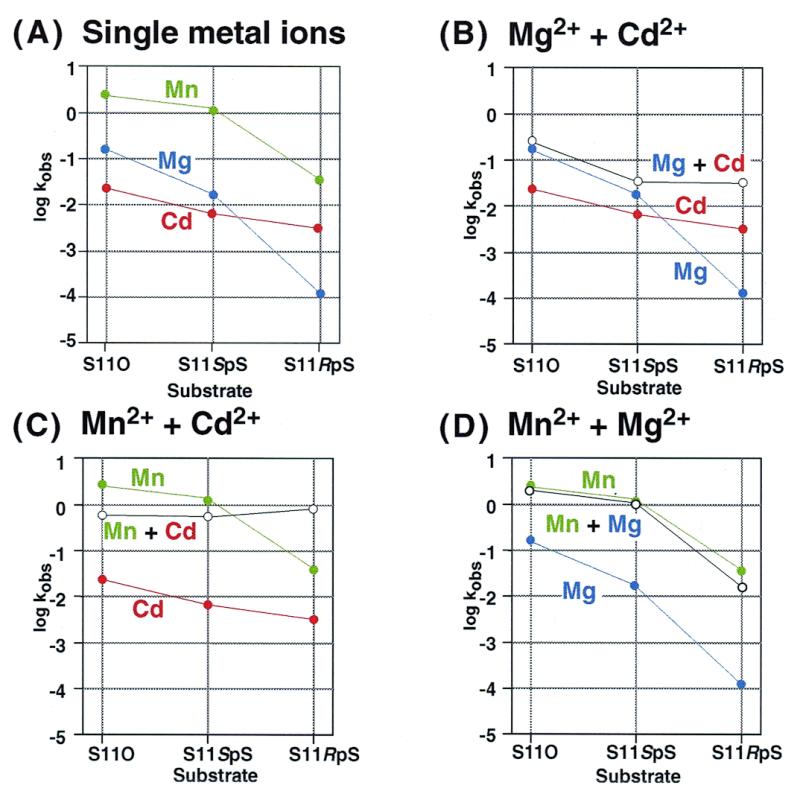
Rate constants for the cleavage of S11O, S11SpS and S11RpS by the R32 ribozyme ([metal chloride] = 25 mM; 50 mM Tris–HCl, pH 6, 37°C). Metal salts were as follows: CdCl₂, red; MgCl₂, blue; and MnCl₂, green. The rate constants for reactions in the presence of single metal ions are shown in (A) and the effects of mixing two metal ions on the rate constants as shown for: MgCl₂ + CdCl₂, MnCl₂ + CdCl₂ and MnCl₂ + MgCl₂ in (B), (C) and (D), respectively. The open circles show the results of mixing two metal ions (1:1; total concentration, 25 mM).

Figure 4B–D shows the reciprocal rescues effected by Mg²⁺, Mn²⁺ and Cd²⁺ ions, when the total concentration of metal ions was kept at 25 mM. In the mixture of Mg²⁺ and Cd²⁺ ions (Fig. 4B), the low activity with S11RpS and Mg²⁺ ions was rescued by Cd²⁺ ions. In the mixture of Mn²⁺ and Cd²⁺ ions (Fig. 4C), the low activity with S11RpS and Mn²⁺ ions was also rescued by Cd²⁺ ions. However, for the cleavage of S11O, Cd²⁺ ions actually inhibited the Mn²⁺-mediated cleavage reaction (Fig. 4C). With the combination of Mn²⁺ and Mg²⁺ ions (Fig. 4D), no mutual rescue occurred.

All the data presented in Figure 4 appear to support the direct coordination of a Cd²⁺ ion with the Rp sulfur atom, since Cd²⁺ ions seemed to specifically rescue the ribozyme-mediated cleavage of S11RpS. In order to test this possibility, we performed even more detailed analysis, described below.

A Cd²⁺ ion binds with identical affinity to S11O and to the two thio-substrates S11RpS and S11SpS, an indication that each of the ribozyme–substrate complexes with a bound Cd²⁺ ion has an identical structure

As can be seen from Figure 4B, since the addition of Cd²⁺ ions to the Mg²⁺-catalyzed reaction did not change the cleavage rate of S11O (see also Fig. 2A and A′), we investigated the effects of Cd²⁺ ions in reactions on a background of Ca²⁺ ions (17,23). The results shown in Figure 5 correspond to those in Figure 2B′ (replotted from the data in 23) and they also correspond to more recently published data, namely the data in figure 3 of Wang et al. (17), even though the reaction conditions, such as pH, incubation temperature and the concentration of background metal ions, were not the same in every set of experiments. Despite the fact that the sequence of the ribozyme used by each group of researchers was also completely different, all groups produced a practically identical result, namely the same dependence of ribozyme activity on the concentration of Cd²⁺ ions in the presence of Ca²⁺ as background metal ions.

As Figure 5 demonstrates, for the cleavage of each of the three types of substrate, each curve of the logarithm of activity versus the logarithm of the concentrations of Cd²⁺ ions can be divided into three regions. At low concentrations of Cd²⁺ ions (in the absence of Cd²⁺ ions), the ribozyme–substrate complex remains in a less active state with background Ca²⁺ ions. However, at saturating concentrations of Cd²⁺ ions, the ribozyme–substrate complex remains in an activated state with the incorporation of added Cd²⁺ ion(s). Specifically, in the case of S11O at background concentrations of Ca²⁺ ions of 100 mM (violet curve), the ribozyme–substrate complex remains in a less active state when the concentration of Cd²⁺ ions is below 1 µM. Upon further addition of Cd²⁺ ions, a Cd²⁺ ion(s) replaces pre-existing Ca²⁺ ion(s) within the ribozyme–substrate complex and, in proportion to the extent of such replacement, the activity of the ribozyme increases linearly until the relevant Ca²⁺ ion(s) has been completely replaced by the Cd²⁺ ion(s). After the completion of the replacement of Ca²⁺ by Cd²⁺ ion(s), above the Kd_app of ∼3 mM, the ribozyme–substrate complex enters the activated state with the bound Cd²⁺ ion(s). A nearly identical phenomenon was observed in the case of S11SpS (Fig. 5, green curve).

Analysis of the three titration curves (for S11O, S11SpS and S11RpS) indicates that the value of Kd_app is the same in each case (see the vertical arrows at the top of Fig. 5) despite the difference in the atom at the cleavage site (oxygen or sulfur at the Sp or Rp position) that is believed to interact with the added Cd²⁺ ion (23). If the added Cd²⁺ ion had indeed interacted with the sulfur atom at the Rp position, the Kd_app for S11RpS should have been smaller than that for either S11O or S11SpS. No such result has been obtained in any experiments (17,23; this study). Moreover, the rate of cleavage of the activated ribozyme–substrate complex with the Cd²⁺ ion(s) was almost the same for all three substrates (S11O, S11SpS and S11RpS), indicating that the activated complex has a nearly constant structure, irrespective of the nature of the scissile phosphate, even though the less cleavable S11RpS in its less active state (in the absence of Cd²⁺ ions; far left in red curve of Fig. 5) appears to yield a completely different structure from that obtained with either S11O or S11SpS (in the absence of Cd²⁺ ions; far left in violet or green curve).

The basis of rescue is the replacement of two Ca²⁺ ions by one Cd²⁺ ion

Another feature of Figure 5 that should be emphasized is the fact that the lines that connect the less active state, without Cd²⁺ ions, with the activated state, at saturating concentrations of Cd²⁺ ions, have a slope of unity. This feature clearly demonstrates that a single Cd²⁺ ion is responsible for the conversion from the less active state to the activated state. To analyze the replacement of metal ions in more detail, we changed the concentration of the background metal ion from 100 mM (solid curves) to 1 M (the broken violet curve in Figure 5 shows the rate constants for the cleavage of S11O on a background of 1 M CaCl₂). Since the concentration of the background Ca²⁺ ions was increased 10-fold, if one Cd²⁺ ion were to compete for binding with one Ca²⁺ ion, the broken violet curve should be shifted by one unit (10-fold) toward higher concentrations of Cd²⁺ ions compared with the results obtained with 100 mM Ca²⁺ ions (solid violet curve). As is apparent from a comparison of the two violet curves, the broken violet curve was shifted by almost two units (100-fold). Essentially the same trend was observed with S11RpS when we changed the concentration of the background Ca²⁺ ions from 100 mM to 1 M (data not shown). These findings demonstrate unambiguously that one Cd²⁺ ion replaced two Ca²⁺ ions and this replacement converted a less active form to an activated form (see Appendix for more detailed quantitative analysis).

The data reported by Wang et al. (see table 2 of 17) also support our conclusion since, in reactions on both a Mg²⁺ and a Ca²⁺ background, a 10-fold increase in the concentration of the background metal ion shifted the affinity of Cd²⁺ ions by almost two logarithmic units (100-fold). Therefore, one Cd²⁺ ion clearly replaced either two Mg²⁺ ions (in reactions on a Mg²⁺ background) or two Ca²⁺ ions (in reactions on a Ca²⁺ background), not only in the case of the unmodified natural substrate but also in the case of the phosphorothioate-containing substrates.

Desulfurization

During the course of our kinetic analysis, the results of which are shown in Figure 5, we were concerned about the potential for desulfurization because (i) all three substrates had the same Kd_app and (ii) the rate of cleavage of the activated ribozyme–substrate complex with saturating Cd²⁺ ions was almost identical for the three substrates, indicating that each activated complex had a nearly identical structure. If the Cd²⁺-catalyzed desulfurization reaction was more rapid than the ribozyme reaction, then each activated complex would indeed be expected to have the identical structure. Metal-catalyzed, non-enzymatic desulfurization reactions were investigated extensively by Lönnberg’s group (49–51) but desulfurization of ribozyme–substrate complexes remains to be fully characterized. It was possible that the rate of desulfurization might have been much higher within the ribozyme–substrate complex than the corresponding metal-catalyzed, non-enzymatic process because the ribozyme complex might create a metal-binding cavity near the phosphorothioate linkage that might significantly enhance the desulfurization process. Therefore, we investigated desulfurization in the presence and in the absence of the ribozyme under various reaction conditions.

Figure 6A shows the products of metal-catalyzed, non-enzymatic desulfurization reactions. We treated the three substrates (S11O, S11SpS and S11RpS) with the ribozyme for 3 days in the presence of Mg²⁺ ions (under the reaction conditions described in the legend to Fig. 4A; blue line) to ensure the partial cleavage of the least active substrate, S11RpS. We then added Cd²⁺ ions to each mixture to a final concentration of 12.5 mM and continued the incubation for an additional 1 h. The initial 3 day incubation with the ribozyme in the presence of Mg²⁺ ions almost completely hydrolyzed S11O (lane 4) and S11SpS (lane 3). We observed that the speed of migration of reaction products decreased in the following order: 2′ or 3′ acyclic (thio)phosphate (c) > cyclic phosphate (b) > cyclic thiophosphate (a). In agreement with the findings of Ora et al. (50), who reported that the cyclic thiophosphate (a) undergoes a Cd²⁺-catalyzed ring-opening reaction more than two orders of magnitude faster than the corresponding cyclic phosphate (b) to yield either a 2′ or a 3′ acyclic product (c), we found that the initial cyclic phosphate (b; lane 4) that had been produced during the 3 day treatment with the ribozyme in the presence of Mg²⁺ ions did not undergo ring-opening during the subsequent treatment with Cd²⁺ ions (lane 5). In contrast, in the case of S11SpS, the initial product, produced during the 3 day treatment with the ribozyme in the presence of Mg²⁺ ions, was a cyclic thiophosphate (a; lane 3) which, during subsequent treatment with Cd²⁺ ions, yielded the cyclic phosphate (b) and the ring-opened 2′ or 3′ acyclic phosphate (c) at a ratio of about 1:2 (lane 2). Ora et al. (50) reported that, in the case of the Sp thioate, the rate constant for the Cd²⁺-catalyzed, non-enzymatic ring-opening of cyclic thiophosphate [(a)→(c)] was twice that for the desulfurization that yielded cyclic phosphate [(a)→(b)]. Our results (compare lanes 3 and 2) can be rationalized by reference to these rate constants.

Figure 6.

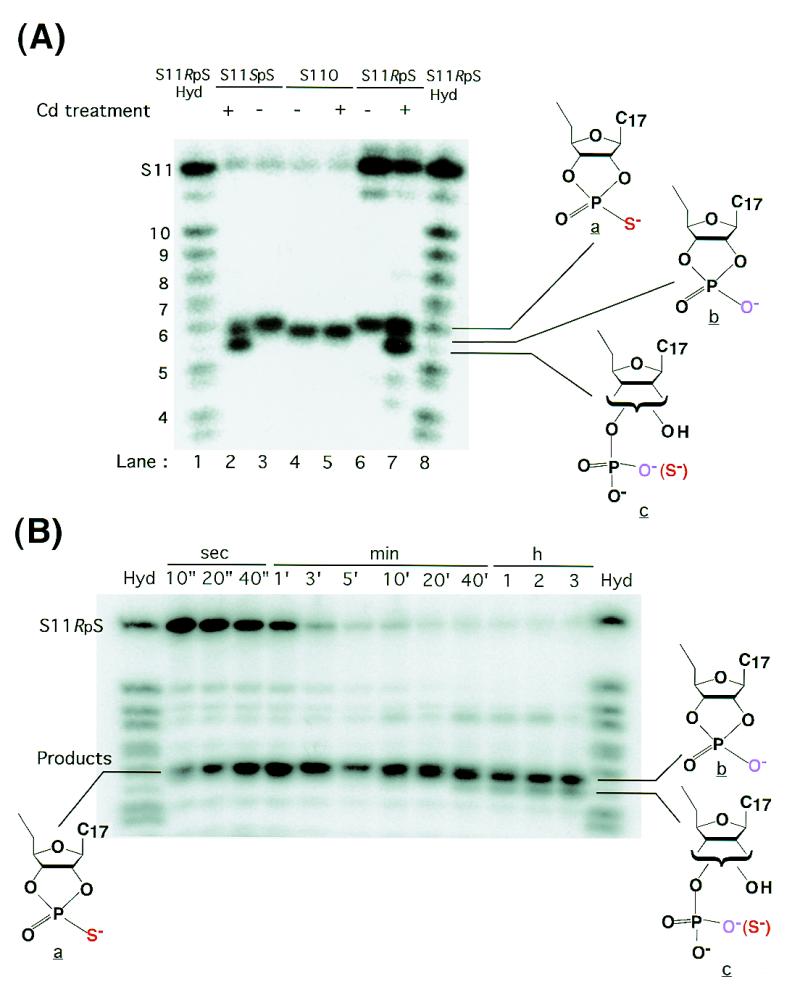
Detection of desulfurization. (A) The products of ribozyme-catalyzed cleavage of each substrate [S11O (lanes 4 and 5), S11SpS (lanes 2 and 3) and S11RpS (lanes 6 and 7)] in the presence of 25 mM Mg²⁺ ions as background [50 mM MES-Na, pH 6, 37°C, 3 days]. The cleavage of S11O and S11SpS was complete (lanes 4 and 3) and the extent of cleavage of S11RpS was ∼2.5% (lane 6). Hyd indicates an alkaline-hydrolysis ladder of S11RpS (lanes 1 and 8). The alkaline-hydrolysis ladder of S11SpS was almost the same as that of S11RpS (data not shown). The alkaline-hydrolysis ladder of S11O had a band that corresponded to b instead of a (data not shown). Cd treatment refers to incubation with 12.5 mM Cd²⁺ ions for 1 h after the ribozyme-catalyzed cleavage reaction. (B) Time-course of R32-mediated cleavage of S11RpS in 100 mM Ca²⁺ ions and 50 mM Cd²⁺ ions. Hyd refers to the alkaline-hydrolysis ladder of S11RpS.

In the case of S11RpS, the initial product of the 3 day incubation with Mg²⁺ ions was also a cyclic thiophosphate (a; lane 6) that, upon subsequent treatment with Cd²⁺ ions, might have yielded cyclic phosphate (b) and acyclic phosphate (c). However, in this case, since the intact S11RpS kept producing cyclic thiophosphate (a) in Mg²⁺- and Cd²⁺-catalyzed reactions (Fig. 4B; black line), it was not possible to calculate the ratio of (b) to (c). Nevertheless, Figure 6A clearly demonstrates that the extent of desulfurization was not negligible when the duration of incubation with higher concentrations of Cd²⁺ ions was long.

We then examined desulfurization within the ribozyme–substrate complex at various concentrations of Cd²⁺ ions (data not shown). Under the conditions used for most of our kinetic measurements, the results of which are shown in Figure 5, desulfurization did indeed occur at higher concentrations of Cd²⁺ ions (with long incubation time). The highest concentration of metal ions used in Figure 5 was 50 mM Cd²⁺ ions. Figure 6B shows the time course of the ribozyme-mediated cleavage of S11RpS in the presence of 50 mM Cd²⁺ ions, with 100 mM Ca²⁺ ions as background. As can be seen from the figure, the ribozyme-catalyzed hydrolysis of S11RpS was almost complete within a few minutes and all the initial products were cyclic thiophosphates (a) that subsequently underwent desulfurization to yield cyclic phosphate (b), as well as the acyclic phosphate (c). Note that rapidly migrating bands become discernible after a 10 min incubation.

Recognition of cyclic thiophosphate (a) as the initial product demonstrates clearly that no desulfurization occurred prior to the ribozyme-mediated cleavage of S11RpS. In this specific case (Fig. 6B), the conclusion is based on data obtained in incubations of no longer than 3 min (3′) when the extent of desulfurization was negligible. In the generation of Figure 5, we were very careful to confirm that desulfurization did not affect the measured rate constants. Herschlag’s group also concluded that desulfurization was not a problem in their kinetic measurements (17).

DISCUSSION

The essence of the present studies is presented in Figure 5. For cleavage of the natural substrate S11O, as well as of the two thio-substrates S11SpS and S11RpS, there exist two states. Less active complexes contain Ca²⁺ ions and activated complexes contain not only Ca²⁺ ions but also one essential Cd²⁺ ion. The observed cleavage activity is the sum of the cleavage activities that originate from each type of complex, as shown by the dotted lines in Figure 5. For both the natural and thio-substrates, only one Cd²⁺ ion is required to generate the activated complex or to rescue cleavage of the least active substrate S11RpS. In this process, two hard metal ions such as Ca²⁺ and Mg²⁺ ions are removed from the less active complex and replaced by one essential Cd²⁺ ion, as shown schematically in Figure 5. This conclusion is based on the observation that, in order to replace Ca²⁺ ions presented at 10× higher concentration (one logarithmic unit), the concentration of Cd²⁺ ions had to be increased 100-fold (two logarithmic units), as shown for S11O by the violet curves in Figure 5.

It is also important to note that (i) all three, potentially different, activated ribozyme–substrate complexes, in which the substrate is S11O, S11SpS or S11RpS, are associated with identical cleavage activity; and (ii) the affinity of the single essential Cd²⁺ ion for each activated complex (the respective values of Kd_app are indicated by violet, green and red arrows) is identical in all three complexes. These data suggest the existence of a common activated structure with one essential Cd²⁺ ion.

Structure of the activated complex

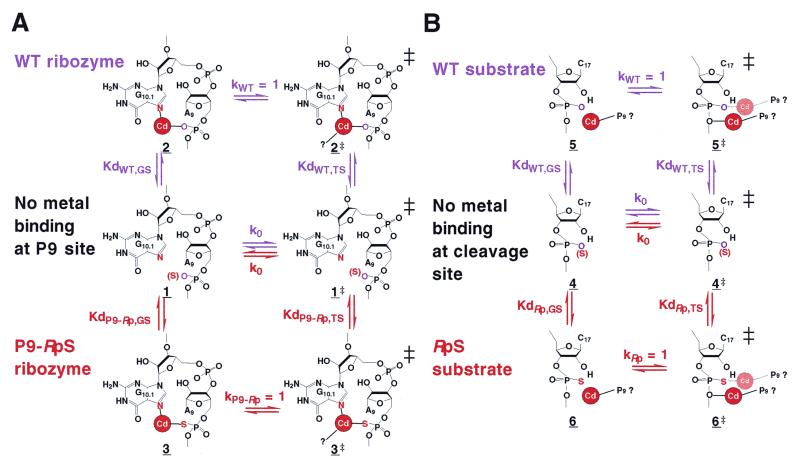
What is the common activated structure of the complexes with a single essential Cd²⁺ ion? In an earlier report, Uhlenbeck and Herschlag and their colleagues demonstrated that a thiosubstituted ribozyme, in which the pro-Rp oxygen at P9 position had been replaced by sulfur (P9-RpS ribozyme), had higher affinity for the essential Cd²⁺ ion [with its lower Kd_app (red line in Fig. 3)] (43), as reproduced here in Figure 3. We propose that, in the activated structure, the essential Cd²⁺ ion binds directly to the pro-Rp oxygen at the P9 position rather than to the pro-Rp oxygen at the cleavage site: this situation holds even in the case of the activated structures of complexes with RpS substrates that have been rescued by Cd²⁺ ions. Thus, the essential Cd²⁺ ion binds directly to the pro-Rp oxygen at the P9 position rather than binding to the Rp sulfur at the cleavage site.

For a discussion of the binding affinity of Cd²⁺ ions, Figure 7A shows schematically the thermodynamic cycles of Cd²⁺ ion-binding status both for the WT ribozyme (violet lettering; top) and the P9-RpS ribozyme (red lettering; bottom). The activated structures are labeled 2 and 3 for the wild-type (WT) and P9-RpS ribozymes, respectively. In Figure 7, each Kd represents an equilibrium constant and should be distinguished from the Kd_app values that are shown in Figures 2, 3 and 5. As discussed earlier, the values of Kd_app change, depending on the concentration of the background metal ions. For example, the value of Kd_app for S11O in a background of 100 mM Ca²⁺ ions (solid violet curve in Fig. 5) increases by almost two orders of magnitude when the concentration of background Ca²⁺ ions is raised to 1 M (broken violet line). When we consider Kd_app, structure 1 actually contains the background metal ion (either a Ca²⁺ ion or a Mg²⁺ ion) that is replaced by the added, essential Cd²⁺ ion in the process 1→2 and, thus, the concentration of Cd²⁺ ions that is required for the replacement of the metal ion depends directly on the concentration of the background metal ions. It is apparent, therefore, that the lower the concentration of background metal ions, the lower the concentration of Cd²⁺ ions that are required to replace the pre-existing background metal ions.

Figure 7.

(A) Thermodynamic cycles for the rescue by Cd²⁺ ions of cleavage by the WT and P9-RpS ribozymes. The violet lettering refers to the WT ribozyme and the red lettering to the P9-RpS ribozyme. The bound Cd²⁺ ion is shown by a Cd in a red circle. Additional interactions in the transition state are shown by ‘Cd—?’. ‘No metal binding’ means that the P9 site is empty but other metal-binding sites are occupied by background metal ions. (B) Thermodynamic cycles for the rescue by Cd²⁺ ions of cleavage of WT and RpS substrates. The violet lettering refers to the WT substrate and the red lettering to the RpS substrate. The bound Cd²⁺ ion proposed in this report is shown by Cd in a red circle, which might bind to the 5′ or 2′ oxygen in the transition state (10,15,62). The Cd²⁺ ion that binds to the Rp position of the scissile phosphate in the scheme proposed by other groups (17,19–23,62) is shown by Cd in a faint red circle. ‘No metal binding’ means that the cleavage site is empty but other metal-binding sites are occupied by background metal ions. Direct coordination of a metal ion to the 5′-oxygen was supported by our previous experiment using 5′-thiosubstituted substrate (12). There exist other interpretations based on experiments by the use of a similar 5′-thio-modified substrate (63,64). However, in the latter case, the slope of the pH-rate profile was 0.24 or 0.36, respectively, in the presence of Mn²⁺ or Mg²⁺ ions, indicating that the chemical step was hidden by other step(s) at higher pH regions [an indication that the chemical step was not the (sole) rate-limiting step]. Then, since the corresponding slope for the natural substrate was unity (since the chemical step was the sole rate-limiting step), it is not valid to make a comparison of the activities between the unmodified and the 5′-thio-modified substrate at higher pH regions (15). Our 5′-thiosubstituted substrate showed a slope of unity in the pH-rate profile (unpublished data) and our own data support the interaction between the metal ion and the 5′-oxygen (10,12,15,65).

Since the Kds in Figure 7 represent real equilibrium constants, structure 1 does not include metal ions at the P9 site; the metal-binding site is empty. Since this site is at a distance from the cleavage site and since it is empty, the rate of background cleavage (represented by the rate constant k₀) should be identical for both WT ribozyme-catalyzed and P9-RpS ribozyme-catalyzed reactions (Fig. 7A). Nevertheless, although the Kds are different from Kd_app, the relative Kds can be estimated from Kd_app. According to the reported data (43), in order to reach the activated structures 2 and 3 from 1, with the WT ribozyme and the P9-RpS ribozyme, respectively, the respective values of Kd_app are Kd_app,WT,GS = 220 µM and Kd_app,P9-Rp,GS = 25 µM for the thiophilic Cd²⁺ ions, in the presence of 10 mM background Mg²⁺ ions, which favors the P9-RpS ribozyme (Fig. 3; GS, ground state). Since the activated structures 2 and 3 are still ground-state structures, they must undergo conformational changes to reach the respective transition states, 2‡ and 3‡.

In the case of the WT ribozyme (violet lettering; top in Fig. 7A), in order to reach the transition state 2‡, the WT ribozyme–substrate complex 1 can capture the essential Cd²⁺ ion first in its ground-state conformation (1→2) and then 2 can undergo conformational changes to reach 2‡ (1→2→2‡). Alternatively, 1 can undergo conformational changes first to establish the transition state-like structure (1→1‡) and then 1‡ can capture the essential Cd²⁺ ion (1→1‡→2‡). It is thermodynamically determined that the two processes, 1→2→2‡ and 1→1‡→2‡, should have the identical overall energy requirement. Therefore, according to transition state (TS) theory, the following equation should hold:

(1/Kd_WT,GS) · k_WT (for 1→2→2‡) =

k₀ · (1/Kd_WT,TS) (for 1→1‡→2‡) [1]

Since the activated complex is 2, which is hydrolyzed with a rate constant of ~1 min^–1 (see Figs 3 and 5), k_WT is ~1 min^–1 in the presence of Cd²⁺ ions. Since the uncatalyzed reaction in the absence of metal ions is at least four orders of magnitude slower than the Cd²⁺-catalyzed reaction, k₀ must be <10^–4 min^–1. This means, from equation [1], that the affinity for the complex of the essential Cd²⁺ ion in the transition state is at least four orders of magnitude stronger than that in the ground state. In other words, since the rate constant k₀ is at least four orders of magnitude smaller than the rate constant k_WT, the equilibrium constant Kd_WT,TS is at least four orders of magnitude smaller than the equilibrium constant Kd_WT,GS. In conclusion, the essential Cd²⁺ ion binds to the transition state-like structure (1‡) at least four orders of magnitude more tightly than to the ground-state structure (1), an observation that suggests the involvement of additional interactions with the Cd²⁺ ion (indicated by ‘—?’ in Fig. 7) in the transition state.

Similarly, for the P9-RpS ribozyme-catalyzed reaction, there are two pathways to the transition state, namely 1→3→3‡ and 1→1‡→3‡. Therefore, the following equation should hold:

(1/Kd_P9-Rp,GS) · k_P9-Rp (for 1→3→3‡) = k₀ · (1/Kd_P9-Rp,TS) (for 1→1‡→3‡) [2]

At a sufficiently high concentration of Cd²⁺ ions, the activated P9-RpS ribozyme complex 3 was as reactive as the activated WT ribozyme complex 2 and, thus, k_P9-Rp = k_WT = ~1 min^–1 (43; Fig. 3). For both types of ribozyme, the rate constant of the uncatalyzed reaction k₀ should have the identical value because, in this process, the empty P9 position should not be involved in catalysis. Then, as discussed above, since k₀ is at least four orders of magnitude smaller than the k_P9-Rp, the dissociation constant Kd_P9-Rp,TS in the transition state is at least four orders of magnitude smaller than the corresponding Kd_P9-Rp,GS in the ground state. Again, the essential Cd²⁺ ion binds to the transition state-like structure 1‡ at least four orders of magnitude more tightly than to the ground-state structure 1, suggesting the involvement of additional interactions with the Cd²⁺ ion (indicated by ‘—?’) in the transition state.

It should be noted, however, that the respective values of Kd_app, from which relative Kd values might be estimated, are Kd_app,WT,GS = 220 µM and Kd_app,P9-Rp,GS = 25 µM for the thiophilic Cd²⁺ ion (in the presence of 10 mM Mg²⁺ ions), which favors the P9-RpS ribozyme (Fig. 3). This situation demands, from the thermodynamic cycle, that Kd_WT,TS should also be larger (for example, ∼10-fold larger) than Kd_Rp,TS, which favors the P9-RpS ribozyme in the transition state. Therefore, importantly, the ratio in the transition state, namely Kd_WT,TS/Kd_P9-Rp,TS, should be the same as the ratio in the ground state, namely, Kd_WT,GS/Kd_P9-Rp,GS.

In other words, from a comparison of the two sets of thermodynamic cycles (in violet and in red) for the WT and P9-RpS ribozymes, the following equation should hold:

(1/Kd_WT,GS) · k_WT · Kd_WT,TS (for 1→2→2‡→1‡) =

(1/Kd_P9-Rp,GS) · k_P9-Rp · Kd_P9-Rp,TS (for 1→3→3‡→1‡) [3]

Then, since k_WT = k_P9-Rp = ~1 min^–1, equation [3] can be simplified as follows:

Kd_WT,GS/Kd_P9-Rp,GS = Kd_WT,TS/Kd_P9-Rp,TS [4]

Before closing this section of the Discussion, we will briefly examine reactions on a background of Mg²⁺ ions. In the case of Mg²⁺-catalyzed reactions in the absence of added Cd²⁺ ions, the activity of the P9-RpS ribozyme was three orders of magnitude lower than that of the WT ribozyme, namely k_WT >> k_P9-Rp. Then, instead of equation [4] for the activated structures, the following equation holds for reactions catalyzed in the presence of Mg²⁺ ions only (in this case, the metal ions in Fig. 7A would be Mg²⁺ ions rather than the Cd²⁺ ions shown):

Kd_WT,GS/Kd_P9-Rp,GS >> Kd_WT,TS/Kd_P9-Rp,TS [5]

This equation can be explained by disruption of the interaction between the P9-Rp oxygen and a Mg²⁺ ion(s) caused by the presence of a sulfur atom, especially in the transition state (Kd_P9-Rp,TS is much larger than Kd_WT,TS). It should be emphasized that the P9 metal-binding site is occupied by Mg²⁺ ion(s) in the ground state because the value of Kd_app changes depending on the concentration of the background Mg²⁺ ions. Nevertheless, apparently, this interaction between the P9-Rp oxygen and a metal ion is more important in the transition state than in the ground state.

In conclusion, all three, potentially different, activated ribozyme–substrate complexes, in which the substrate is S11O, S11SpS or S11RpS, are associated with identical cleavage activity and an identical Kd_app (Fig. 5) because the activated structure, with one essential Cd²⁺ ion, has essentially the same structure (2 or 3 in Fig. 7A) in every case. Moreover, in every case, Kd for the Cd²⁺ ion is significantly smaller in the transition state than in the ground state, indicating the existence of additional favorable interactions in the transition state. Moreover with both types of ribozyme considered, the Cd²⁺ ion binds to the transition state-like structure 1‡ at least four orders of magnitude more tightly than to the ground state structure 1 and, thus, there are likely to be additional, common interactions (indicated by Cd²⁺—? in 2‡ and 3‡ in Fig. 7A) with the Cd²⁺ ion in the transition state. However, it is important to note that the additional favorable interactions in the transition state (—?) must be the same for both the WT and the P9-RpS ribozyme since the extent of the favorable interaction in the transition state remains the same in both cases, as indicated by equation [4] (replacement of the P9-Rp oxygen by sulfur enhanced the affinity of the Cd²⁺ ion equally in the ground state and in the transition state and, thus, Kd_WT,GS/Kd_WT,TS = Kd_P9-Rp,GS/Kd_P9-Rp,TS).

Effects on thermodynamics of thiosubstitution at the scissile phosphate: the nature of the potential additional interactions in the transition state

In Figure 7A, the thermodynamic cycle for the P9-RpS ribozyme (red lettering) is compared with that for the WT ribozyme (violet lettering). Let us now perform a similar analysis for the cleavage of S11RpS (red lettering in Fig. 7B) in comparison with the cleavage of the unmodified substrate (violet lettering). The significant difference between the P9-RpS ribozyme-catalyzed reaction (red lettering in Fig. 7A) and the R32-catalyzed cleavage of S11RpS (red lettering in Fig. 7B) is that, in the absence of added Cd²⁺ ions, the background metal ion binds to the P9 site in the former case, in the ground state, whereas the metal ion does not interact with the Rp position at the scissile phosphate in the latter case since values of Kd_app,WT,GS and Kd_app,Rp,GS are identical (Fig. 5). Although Kd_app is different from Kd, the relative Kd can be estimated from Kd_app, and the identical values of Kd_app,WT,GS and Kd_app,Rp,GS indicate strongly that Kd_WT,GS and Kd_Rp,GS are likely to be identical. Therefore, in the thermodynamic cycle, the added Cd²⁺ ion first binds to the P9 site without interacting with the Rp position at the scissile phosphate (4→5 or 4→6). Moreover, here again, since the rate of non-metal ion-catalyzed cleavage of the phosphodiester bond is very similar for both the unmodified and the thiosubstituted linkage (51), the value for k₀, which represents the rate constant of the non-metal ion-catalyzed cleavage, must also be very similar for the two sets of thermodynamic considerations. From a comparison of these two sets of thermodynamic cycles (compare Fig. 7A and equation [3]),

(1/Kd_WT,GS) · k_WT · Kd_WT,TS (for 4→5→5‡→4‡) = (1/Kd_Rp,GS) · k_Rp · Kd_Rp,TS (for 4→6→6‡→4‡) [6]

In this case also, the two rate constants were very similar: k_WT = k_Rp = ~1 min^–1 (see Fig. 5 for the cleavage of both substrates in the respective activated complexes). Thus, equation [6] can be condensed to the simpler equation [7], which is equivalent to equation [4].

Kd_WT,GS/Kd_Rp,GS = Kd_WT,TS/Kd_Rp,TS [7]

As mentioned above, since the value for Kd_WT,GS is likely to equal the value of Kd_Rp,GS (as estimated from the identical values of Kd_app,WT,GS and Kd_app,Rp,GS), equation [7] can be simplified to yield equation [8]:

Kd_WT,TS = Kd_Rp,TS [8]

This equation indicates that, since the affinity of the Cd²⁺ ion is the same in the transition state for both the WT and the RpS substrates, there are no additional interactions in the transition state with the sulfur atom at the scissile phosphate, as compared with the interactions with the unmodified phosphate.

If the added Cd²⁺ ion had interacted with the Rp position at the scissile phosphate, as illustrated by the faint red Cd in Figure 7B, the thiophilic Cd²⁺ ion should have had interacted more strongly in 6‡ than in 5‡, which would have resulted in Kd_Rp,TS being smaller than Kd_WT,TS. Since (i) this did not happen, and (ii) there should exist additional interactions in the transition state as compared with interactions in the activated complex (as illustrated by Cd—? in Fig. 7A), and also since (iii) the P9-bound Cd²⁺ ion was able to stimulate the otherwise very poor cleavage of the RpS substrate, it seems very likely that the added Cd²⁺ ion interacts with the cleavage site and not with the Rp oxygen or sulfur of the scissile phosphate. Instead, the additional interaction might have occurred at the 5′-leaving oxygen, as illustrated by the red Cd in 5‡ and in 6‡ in Figure 7B or, alternatively, the interaction could have also occurred at the 2′-attacking oxygen (9–16,32,33,45–47,52). In both such cases, the strength of the additional interaction must be the same for both the WT and RpS substrates since the site of interaction is the oxygen, but not the sulfur, and, thus, the identical values of Kd_WT,TS and Kd_Rp,TS can be rationalized.

In conclusion, analysis of the thermodynamic cycles shown in Figure 7B clearly demonstrates that the added Cd²⁺ ion does not interact with the Rp position at the scissile phosphate in the ground state or in the transition state. The added Cd²⁺ ion makes stronger interactions in the transition state because it can interact with other atoms, such as the 2′-attacking oxygen, the 5′-leaving oxygen or, possibly, with other atoms but not with the Rp position at the scissile phosphate.

Concluding remarks

We analyzed reactions with three types of substrate, S11O, S11SpS and S11RpS. Although the rate of the ribozyme-mediated cleavage of S11RpS was three to four orders of magnitude lower than that of S11O in the presence of Ca²⁺ or Mg²⁺ ions, all three substrates were cleaved at the same rate when reactions were stimulated by the addition of Cd²⁺ ions. Moreover, the Kd_app for the Cd²⁺ ion in the presence of background metal ions was also identical for the three substrates, as shown previously by Herschlag’s group (17). These findings (Fig. 5) suggest the formation of identical Cd²⁺-containing activated complexes and transition-state structures (Fig. 7). Upon addition of Cd²⁺ ions, the essential Cd²⁺ ion binds first to the P9 site with weaker affinity and then, when the transition state is achieved, the affinity of the Cd²⁺ ion increases because it starts to interact with additional sites (17). Herschlag’s group demonstrated unambiguously that the essential Cd²⁺ ion binds to the pro-Rp sulfur at P9 (17). However, no additional interaction between the Cd²⁺ ion and the Rp position at the scissile phosphate occurs, as demonstrated here by the fact that the affinity of the Cd²⁺ ion was the same in the transition state with both S11O and S11RpS (equation [8]). All the published data can be explained by this interpretation without the assumption that the Cd²⁺ ion interacts with the Rp position at the scissile phosphate. To our knowledge, there exist no unambiguous data that support a direct interaction between the sulfur atom at the Rp position of the cleavage site and the added Cd²⁺ ion, either in the ground state or in the transition state.

The essential Cd²⁺ ion at the P9 site replaced two pre-existing Ca²⁺ or Mg²⁺ ions. This result suggests that the nature of the binding of the Cd²⁺ ion does not have to be identical to that of the two pre-existing Ca²⁺ or Mg²⁺ ions. The two pre-existing Ca²⁺ or Mg²⁺ ions that are replaced might be either catalytic metal ions or structural metal ions (15,16,52,53). It should also be noted that the larger Cd²⁺ ion appears, coincidentally, to fit better than the pre-existing Ca²⁺ or Mg²⁺ ions into the active ribozyme conformation: as can be seen in Figure 5, low millimolar concentrations of the Cd²⁺ ions were able to replace Ca²⁺ ions at 100 mM (see Appendix for more detailed analysis). Therefore, care must be taken in the analysis of the Cd²⁺ rescue of ribozyme-catalyzed reactions, as is the case also for Hg²⁺-binding interactions. As pointed out by Herschlag’s group (17), the extremely strong interaction between a Hg²⁺ ion and a sulfur atom might also have resulted in binding of a Hg²⁺ ion to the phosphorothioate at the cleavage site in the ground state (54), even in the absence of such a metal ion interaction in the ground state of the WT ribozyme–substrate complex. It should be emphasized that the observed rescue of the thio effect by a single Cd²⁺ ion, as a result of replacement of two pre-existing Ca²⁺ or Mg²⁺ ions, provides no information about the validity or invalidity of the proposed double-metal-ion mechanism of catalysis (9–17,52).

Our analysis provides evidence against a direct interaction between the sulfur atom at the Rp position of the cleavage site and added Cd²⁺ ions, not only in the ground state but also in the transition state. However, we still cannot explain explicitly why the rate of the ribozyme-mediated cleavage of S11RpS was four orders of magnitude lower than that of S11O in the presence of Mg²⁺ ions. Although substitution of oxygen by sulfur is considered, in general, to be a very conservative modification, several cases are known in which such a substitution abolished catalytic function (55,56), directed cleavage to the next unmodified phosphodiester bond (31,55–57) or displaced essential catalytic metal ions from the active site as a consequence of the size of the bulky sulfur atom (58). The incomplete rescue of the P9-RpS ribozyme-catalyzed cleavage of the RpS substrate by added Cd²⁺ ions might also have originated from the combination of geometric constraints at two phosphorothioate linkages (17) and/or a difference in the mode of binding of the Cd²⁺ ion, as mentioned above. Moreover, the effect of sulfur substitution at the Rp position of the cleavage site does not have to be the same as that at the Sp position (33,59–61): the observed thio effects for the RpS substrate might be reconciled by effects of asymmetry at the Rp position. However, at the very least, the proposal that the sulfur atom at the Rp position interacts directly with a Cd²⁺ ion in rescue experiments is not supported by the available data.

APPENDIX

Thermodynamic considerations

In the case of the P9-RpS ribozyme, if we define the rate without a metal ion at the P9 site as k₀ (as shown in Fig. 7A; red lettering), the Kd value in the transition state for the Cd²⁺ ion [Kd_P9-Rp,TS(Cd)] can be calculated as follows (equation [9] is equivalent to equation [2]):

Kd_P9-Rp,TS(Cd) = Kd_P9-Rp,GS(Cd) · (k₀/k_P9-Rp(Cd)) [9]

In the absence of thiosubstitution, since the rate without a metal ion at the P9 site is also represented by k₀, as shown in Figure 7A (the values of k₀ in violet and red lettering are the same), the Kd for the normal phosphodiester linkage at the P9 site in the transition state for Cd²⁺ ions (violet lettering) can be calculated as follows (equation [10] is equivalent to equation [1]):

Kd_WT,TS(Cd) = Kd_WT,GS(Cd) · (k₀/k_WT(Cd)) [10]

Equivalent equations can also be written for Mg²⁺ ions with equations [11] and [12] corresponding to equations [9] and [10], respectively:

Kd_P9-Rp,TS(Mg) = Kd_P9-Rp,GS(Mg) · (k₀/k_P9-Rp(Mg)) [11]

Kd_WT,TS(Mg) = Kd_WT,GS(Mg) · (k₀/k_WT(Mg)) [12]

In order to calculate the experimentally obtainable values of Kd_app, shown in equation [14], the ratio of equilibrium constants, for example, equation [10] divided by equation [12] for the WT ribozyme or equation [9] divided by equation [11] for the P9-RpS ribozyme, can be used, as represented in equation [13]:

Kd_TS(Cd)/Kd_TS(Mg) = [Kd_GS(Cd)/Kd_GS(Mg)] · (k_(Mg)/k_(Cd)) [13]

Because Kd_app = [Kd_(Cd)/Kd_(Mg)] · [Mg²⁺], when [Mg²⁺] is greater than Kd_(Mg) (this relationship can be derived from equation [27]), the experimentally obtainable Kd_app can be calculated as:

Kd_app,TS = Kd_app,GS · (k_(Mg)/k_(Cd)) [14]

This equation holds even when m ≠ 1 in equation [27]. From equation [14], we can calculate the Kd_app for replacement of Mg²⁺ by Cd²⁺ in the transition state. Using equation [14], we can write the relative magnitudes of Kd_app in the transition state for the WT ribozyme and the P9-RpS ribozyme as:

Kd_app,P9-Rp,TS/Kd_app,WT,TS = [Kd_app,P9-Rp,GS/Kd_app,WT,GS] ·

[(k_P9-Rp(Mg)/k_P9-Rp(Cd))/(k_WT(Mg)/k_WT(Cd))] [15]

With this equation, we can discuss only relative values (e.g., relative affinities and relative rate constants) for Cd²⁺ and Mg²⁺. The limits to the use of Kd_app (equation [15]) are pointed out below. If we use the reported values (43), the rate constants with saturating Cd²⁺ ions for each ribozyme, k_P9-Rp(Cd) and k_WT(Cd), are the same, and the ratio of the rate constants with saturating Mg²⁺ ions for each ribozyme can be written as k_P9-Rp(Mg)/k_WT(Mg) = 10^–4. Then, when the Cd²⁺ ion(s) replaces Mg²⁺ ion(s),

Kd_app,P9-Rp,TS/Kd_app,WT,TS = (Kd_app,P9-Rp,GS/Kd_app,WT,GS) · 10^–4 [16]

From this equation, it appears and we can conclude that the Cd²⁺ ion has 10⁴-fold stronger affinity in the transition state for the P9-RpS ribozyme (reflected by the smaller Kd_app,P9-Rp,TS). Alternatively, however, the value of Kd_app,P9-Rp,TS might have decreased as a result of the decreased affinity of the background Mg²⁺ ions in the transition state relative to that in the ground state. Other possibilities also exist. Therefore, we cannot tell whether the change in affinity upon thiosubstitution is due to modulation of binding of the Mg²⁺ ion(s) or of Cd²⁺ ion(s).

For a more quantitative discussion of the effects of thiosubstitution, it is convenient to consider real Kd values, as used in Figure 7. If we can obtain the affinities for binding of the Cd²⁺ ion(s) and the Mg²⁺ ion(s) as shown in equations [9]–[12], independently, then

Kd_P9-Rp,TS/Kd_WT,TS = (Kd_P9-Rp,GS/Kd_WT,GS) · (k_WT/k_P9-Rp) [17]

Here the rate constants with saturating Cd²⁺ ions for each ribozyme, k_P9-Rp(Cd) and k_WT(Cd), are the same (43), so for binding of the Cd²⁺ ion(s) to the empty P9 site,

Kd_P9-Rp,TS/Kd_WT,TS = Kd_P9-Rp,GS/Kd_WT,GS [18]

This equation means that the effect of thiosubstitution on the binding of the Cd²⁺ ion to the empty P9 site is the same in the transition state and in the ground state and, therefore, the additional interaction, if it exists, does not depend on the thiosubstitution at the P9 site.

The number of metal ions

When ‘m’ Ca²⁺ ions are replaced by ‘n’ Cd²⁺ ions, the dependence of k_obs on the concentrations of Ca²⁺ and Cd²⁺ can be described by the following scheme, in which ‘R’ represents the ribozyme–substrate complex.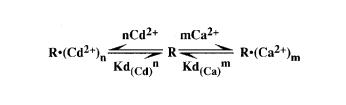

According to this scheme, the dissociation constants Kd_(Ca) and Kd_(Cd) for Ca²⁺ and Cd²⁺ ions can be expressed by:

Kd_(Ca)^m = [R][Ca²⁺]^m/[R·(Ca²⁺)_m] Kd_(Cd)ⁿ = [R][Cd²⁺]ⁿ/[R·(Cd²⁺)_n]

[R·(Ca²⁺)_m] = [R][Ca²⁺]^m/Kd_(Ca)^m [R·(Cd²⁺)_n] = [R][Cd²⁺]ⁿ/Kd_(Cd)ⁿ,

where Kd_(Ca)^m and Kd_(Cd)ⁿ represent Kd_(Ca) and Kd_(Cd) raised to the ‘mth’ and ‘nth’ power, respectively. Then, the total concentration of the ribozyme–substrate complex, [R]_T, is the sum of the concentrations of free, Ca²⁺-bound and Cd²⁺-bound complexes:

[R]_T = [R] + [R·(Ca²⁺)_m] + [R·(Cd²⁺)_n] = [R](1 + [Ca²⁺]^m/Kd_(Ca)^m + [Cd²⁺]ⁿ/Kd_(Cd)ⁿ) [19]

Then, the relative levels of free, Ca²⁺-bound and Cd²⁺-bound complexes can be calculated from equations [20]–[22].

[R]/[R]_T = (1 + [Ca²⁺]^m/Kd_(Ca)^m + [Cd²⁺]ⁿ/Kd_(Cd)ⁿ)^–1 [20]

[R·(Ca²⁺)_m]/[R]_T = ([R]/[R]_T) · ([Ca²⁺]^m/Kd_(Ca)^m) = (1 + Kd_(Ca)^m/[Ca²⁺]^m)^–1 · [1 + [Cd²⁺]ⁿ/{Kd_(Cd)ⁿ(1 + [Ca²⁺]^m/Kd_(Ca)^m)}]^–1 [21]

[R·(Cd²⁺)_n]/[R]_T = ([R]/[R]_T) · ([Cd²⁺]ⁿ/Kd_(Cd)ⁿ) = [1 + {Kd_(Cd)ⁿ(1 + [Ca²⁺]^m/Kd_(Ca)^m)}/[Cd²⁺]ⁿ]^–1 [22]

The observed rate constant for ribozyme-mediated reactions can be expressed by the sum of the rate constants for Ca²⁺-catalyzed and Cd²⁺-catalyzed reactions, while the extent of the non-metal ion-catalyzed reaction can be considered to be negligible:

k_obs = k_(Ca) · [R·(Ca²⁺)_m]/[R]_T + k_(Cd) · [R·(Cd²⁺)_n]/[R]_T =

k_(Ca) · (Kd_(Ca)^m/[Ca²⁺]^m + 1)^–1 · (1 + [Cd²⁺]ⁿ/Kd_appⁿ)^–1 +

k_(Cd) · (1 + Kd_appⁿ/[Cd²⁺]ⁿ)^–1 [23]

where Kd_appⁿ = Kd_(Cd)ⁿ(1 + [Ca²⁺]^m/Kd_(Ca)^m) [24]

The rate of cleavage from the activated state (Cd²⁺-catalyzed reactions) can be expressed as the second term of equation [23], k_(Cd)·(1 + Kd_appⁿ/[Cd²⁺]ⁿ)^–1, and the number of Cd²⁺ ions ‘n’ is obviously 1, in view of the slope of the dependence of the ribozyme-catalyzed cleavage reaction on the concentration of Cd²⁺ ions on a logarithmic scale (Fig. 5). Then, equation [24] becomes:

Kd_app = Kd_(Cd){1 + [Ca²⁺]^m/Kd_(Ca)^m} [25]

or, in a logarithmic representation,

logKd_app = log(Kd_(Cd)/Kd_(Ca)^m) + log(Kd_(Ca)^m + [Ca²⁺]^m) [26]

If the background concentration of Ca²⁺ ions is larger than Kd_(Ca), namely if [Ca²⁺] >> Kd_(Ca), then:

logKd_app = log(Kd_(Cd)/Kd_(Ca)^m) + m·log[Ca²⁺] [27]

From the dependence of Kd_app on the increasing concentration of background metal ions [Ca²⁺], we can derive the number of replaced metal ions from a graphical representation of equation [27]. Analysis of Figure 5 in this paper and of the related equilibrium constants given in table 2 of Wang et al. (17) indicates that the value of ‘m’ is ∼2, not only for reactions with a Ca²⁺ background but also for reactions with a Mg²⁺ background. Therefore, one Cd²⁺ ion replaces two Ca²⁺ or two Mg²⁺ ions.

If the background concentration of Ca²⁺ ions is lower than Kd_(Ca), namely if [Ca²⁺] << Kd_(Ca), equation [26] becomes:

Kd_app = Kd_(Cd) [28]

and Kd_app becomes constant and does not depend on the concentration of background Ca²⁺ ions. This observation means that, if the metal-binding site is unoccupied by the background metal ions ([Ca²⁺] << Kd_(Ca)), equation [28] clearly demonstrates that the Kd_app for Cd²⁺ ions should not vary when the concentration of background metal ions is changed. However, this was not what we observed. As shown by the difference between the solid violet line and the broken violet line in Figure 5, the Kd_app for the Cd²⁺ ion changed, a clear demonstration of the existence of pre-bound Ca²⁺ ions at the Cd²⁺-binding site.

Last of all, some comments are appropriate with respect to the relative affinities of Ca²⁺ and Cd²⁺ ions. The apparent difference in affinities, ΔlogKd, can be calculated from a rearrangement of equation [27] and, when m = 1, equation [27] becomes:

ΔlogKd = logKd_(Cd) – logKd_(Ca) = logKd_app – log[Ca²⁺] [29]

In this paper (Figs 2, 3 and 5), values of ΔlogKd are tentatively represented by equation [29] (m = 1).

If m ≠ 1, the apparent difference in the logarithm of Kd, derived from equation [27], is:

ΔlogKd = logKd_app – log[Ca²⁺] = logKd_(Cd) – logKd_(Ca) +

(m – 1)·log([Ca²⁺]/Kd_(Ca)) [30]

The last term in equation [30], (m – 1)·log([Ca²⁺]/Kd_(Ca)), is always positive regardless of the value of m, as long as background Ca²⁺ ions occupy the metal-binding site, namely when Kd_(Ca) < [Ca²⁺]. Then, the negative value of ΔlogKd in our results and in previous results (17,23,43) demands that the sum of first two terms, logKd_(Cd) – logKd_(Ca), should be negative: this requirement demands, in turn, that logKd_(Cd) should always be smaller than logKd_(Ca), namely Kd_(Cd) should always be smaller than Kd_(Ca). Therefore, the stronger binding affinity of Cd²⁺ than of Ca²⁺ is required to explain the negative value of ΔlogKd. In Figure 5, the value of ΔlogKd is about –1.5 for the three different substrates when the concentration of Ca²⁺ ions was set at 100 mM. Thus, Cd²⁺ ions at 3 mM were required to replace Ca²⁺ ions at 100 mM, providing evidence for the stronger binding affinity of Cd²⁺ than of Ca²⁺ ions.

Scheme 1.