Extending EpiEstim to estimate the transmission advantage of pathogen variants in real-time: SARS-CoV-2 as a case-study

Abstract

The evolution of SARS-CoV-2 has demonstrated that emerging variants can set back the global COVID-19 response. The ability to rapidly assess the threat of new variants is critical for timely optimisation of control strategies.

We present a novel method to estimate the effective transmission advantage of a new variant compared to a reference variant combining information across multiple locations and over time. Through an extensive simulation study designed to mimic real-time epidemic contexts, we show that our method performs well across a range of scenarios and provide guidance on its optimal use and interpretation of results. We also provide an open-source software implementation of our method. The computational speed of our tool enables users to rapidly explore spatial and temporal variations in the estimated transmission advantage.

We estimate that the SARS-CoV-2 Alpha variant is 1.46 (95% Credible Interval 1.44–1.47) and 1.29, (95% CrI 1.29–1.30) times more transmissible than the wild type, using data from England and France respectively. We further estimate that Delta is 1.77 (95% CrI: 1.69–1.85) times more transmissible than Alpha (England data).

Our approach can be used as an important first step towards quantifying the threat of emerging or co-circulating variants of infectious pathogens in real-time.

1. Introduction

The SARS-CoV-2 pandemic has highlighted the potentially dramatic influence that emerging novel pathogen variants can have on transmission dynamics and on the control measures needed to mitigate the epidemic burden. The emergence of the Alpha variant of SARS-CoV-2 in September 2020, and of the Delta variant in December 2020 drastically altered the trajectory of the COVID-19 epidemic in several countries leading to renewed imposition of public health measures such as lockdowns (Anon, 2020, Anon, 2021f). The continued high level of transmission of SARS-CoV-2 globally makes the emergence of new variants very likely. As of April 2023, the World Health Organization has classified five variants of SARS-CoV-2 as “variants of concern” or VOCs (i.e. Alpha, Beta, Gamma, Delta, and Omicron), because of their increased transmissibility, severity, and/or immune escape properties compared to the circulating SARS-CoV-2 variants (Anon, 2021a). Rapidly quantifying characteristics of such emerging variants is critical to anticipate their potential impact and adjust interventions accordingly. Estimates of the transmission advantage of a new variant over previously circulating variants can help re-evaluate key metrics which depend on the reproduction number, e.g. the herd-immunity threshold, and adjust short-term projections of the epidemic trajectory. They can also help to disentangle the impact on transmission levels of the newly introduced variant from other factors, such as concurrent changes in control measures (Sonabend et al., 2021). Shortly after the emergence of the Alpha variant in England in September 2020 (Rambaut et al., 2020), a number of studies aimed to estimate its transmission potential, compared to the previously circulating non-VOC lineages (Volz et al., 2021, Davies et al., 2021, Leung et al., 2021, Yang and Shaman, 2021, Zhao et al., 2021a, Zhao et al., 2021b, Chand et al., 2021, Graham et al., 2021, Piantham et al., 2021). More recently, several papers have evaluated the transmissibility of the Delta variant compared to Alpha (Anon, 2021h, Ferguson, 2021, Sonabend et al., 2021, Alizon et al., 2021, Campbell et al., 2021, Keeling, 2021), and of one or more VOCs (Yang et al., 2022, Yang and Shaman, 2021, Coutinho et al., 2021, Campbell et al., 2021, Faria et al., 2021, van Dorp et al., 2021, van Dorp et al., 2022, Anon, 2021g). All of these studies have developed new approaches to estimate the transmission advantages of the Alpha and the Delta variants, often synthesising evidence from multiple data sources including genomic data. The time and expertise required to design and implement such approaches, with methods tailored to the specificity of each dataset and context, often limit their widescale and real-time use.

In this study, we present a new Bayesian inference method, MV-EpiEstim (for Multi-Variant EpiEstim), to estimate in real-time the transmission advantage of a new variant of a pathogen compared to a reference variant, using simple data consisting of the time series of incidence of cases of each variant in one or more locations. The aims of this work are to: 1) develop a method and tool for such analyses; 2) assess how well it can estimate the transmission advantage across a range of simulated and real-life epidemic scenarios.

In the rest of the manuscript, we refer to different “variants” but the method can be equally applied to different strains. We present the method for one reference and one new variant, but the method naturally extends to more than one new variant. Our work builds on a previously published methodology (Cori et al., 2013, Thompson et al., 2019) to estimate the instantaneous reproduction number $R_t$ (defined as the average number of secondary cases that an individual infected at time $t$ would generate if conditions remained the same as at time $t$).

We assume that locally, the transmissibility of all variants follows the same temporal pattern, i.e. the reproduction number of the new variant is the same as that of the reference variant, albeit with a multiplicative factor. We refer to this multiplicative factor as the “effective transmission advantage” of the new variant, compared to the reference variant. We further assume that the effective transmission advantage remains constant over a user-defined time-window and across all locations under consideration. Note that both the time-window and the set of locations over which the effective transmission advantage is assumed to be constant can be varied by the user.

We provide an open source implementation of our method in the R package EpiEstim (Cori, 2021). The approach, which we validate on an extensive simulation study, is computationally efficient as it takes advantage of an analytical formulation of marginal posterior densities of both the instantaneous reproduction number for the reference variant, and the transmission advantage of the new variant.

We illustrate the use of our tool by retrospectively estimating the effective transmission advantage of SARS-CoV-2 VOCs (Alpha, Beta/Gamma, and Delta) over the previously circulating variants using data from England and France. In addition, we perform a literature review to summarise other existing approaches and tools available for estimating the transmission advantage of new variants from incidence data. We show that the estimates from our method are consistent with those from other studies, and that our fast ready-to-use tool allows timely estimation and easy exploration of changes in the transmission advantage over time and space. Our inference framework and open source software should allow rapid quantification and monitoring of the effective transmission advantage of future new variants in real-time.

2. Methods

We extend the methodology from Cori et al. (2013) and Thompson et al. (2019) to develop an inference framework for jointly estimating the transmissibility (instantaneous reproduction number $R_t$) of a reference variant and the effective transmission advantage of novel variants, compared to the reference. For simplicity, we present the method for two variants only (a reference and a new variant). The method is applicable to, and has been implemented for, estimating the transmission advantages of multiple variants over a single reference.

Assumptions. Our method relies on daily incidence data of the reference and the variant. Where data from more than one location are used, we assume that the epidemics in each location are independent and closed except for cases of each variant on the first day who are assumed to be imported. The effective reproduction number is defined as the ratio of newly infected cases to the total infectiousness (due to past cases) in a location. For more details, see Cori et al., 2013, Thompson et al., 2019.

Notation. We use the following notations:

• •Indexes $t$ for time, $l$ for location and $v$ for variant, with $v$ $=$ 0 denoting the reference variant and $v$ $=$ 1 the new variant,
• •$n_l$ the number of locations considered
• •$T$ the number of days of observation
• •$I_t^{l,v}$ denotes the number of incident cases of variant $v$ at time $t$ in location $l$,
• •$R_t^{l,v}$ denotes the instantaneous reproduction number for variant $v$ at time $t$ in location $l$. For simplicity we use $R_t^l$ to denote the instantaneous reproduction number for the reference variant in location $l$ i.e. $R_t^l=R_t^{l,0}$.
• •$w^v$ is the probability mass function of the discrete serial interval for variant $v$, assumed the same across all locations, but potentially different between variants ($w_s^v$ is the probability that the serial interval lasts s days, $s=1,\dots ,S{I}_{max}$; and we assume $w_0^v=0$).
• •${\Lambda }_t^{l,v}={\sum }_{s=1}^t{I}_{t-s}^{l,v}{w}_s^v$ is the overall infectiousness for variant $v$ at time $t$ and in location $l$ due to past incident cases of that variant in that location.
• •For simplicity we introduce the generic notation ${\mathbf{X}}_t^{L,V}={\left\{X_t^{l,v}\right\}}_{l=1,\dots ,n_l;v=0,1}$ for the variable $X$ at time $t$ across all locations and both variants.

We assume that $R_t^{l,1}=ϵR_t^l$, i.e. the reproduction number of the new variant is proportional to that for the reference variant; the proportional factor $ϵ$ is the effective transmission advantage (if $ϵ>1$, or disadvantage if $ϵ<1$) of the new variant compared to the reference variant, assumed constant over a time-window and across a set of locations defined by the user.

We explored values of $ϵ>1$ in all simulation scenarios as values of $ϵ<1$ correspond to swapping the reference and new variant.

We assume the number of secondary infections generated by each case is Poisson distributed. Under these assumptions, the likelihood of the time series of incident cases of the reference and the new variants can be written as

$${\mathcal{L}}_t=P\left({\mathbf{I}}_t^{L,V}|{\mathbf{I}}_0^{L,V},\dots ,{\mathbf{I}}_{t-1}^{L,V},{\mathbf{w}}^V,{\mathbf{R}}_t^{L,V},ϵ\right)=\prod _{l=1}^{n_l}\prod _{v=0}^1\frac{{\left(R_t^{l,v}\right)}^{I_t^{l,v}}{e}^{-R_t^{l,v}{\Lambda }_t^{l,v}}}{I_t^{l,v}!}\propto \prod _{l=1}^{n_l}\left({\left(R_t^l\right)}^{\sum _{v=0}^1{I}_t^{l,v}}{ϵ}^{I_t^{l,1}}{e}^{-R_t^l\left({\Lambda }_t^{l,0}+ϵ{\Lambda }_t^{l,1}\right)}\right)\propto {ϵ}^{\sum _{l=1}^{n_l}{I}_t^{l,1}}{e}^{-\sum _{l=1}^{n_l}{R}_t^l\left({\Lambda }_t^{l,0}+ϵ{\Lambda }_t^{l,1}\right)}\prod _{l=1}^{n_l}{\left(R_t^l\right)}^{\sum _{v=0}^1{I}_t^{l,v}}$$

We assume Gamma priors for each $R_t^l$, with same shape $a$ and scale $b$ across times and locations, and for $ϵ$, with shape $c$ and scale $d$. The joint posterior distribution of parameters given the observations is (assuming the serial interval distributions for both variants ${\mathbf{w}}^V$ are known):

$$P\left(ϵ,{\mathbf{R}}_1^L\dots ,{\mathbf{R}}_T^L|{\mathbf{I}}_0^{L,V},\dots ,{\mathbf{I}}_T^{L,V},{\mathbf{w}}^V\right)\propto \prod _{t=1}^T\left({\mathcal{L}}_t\prod _{l=1}^{n_l}{\left(R_t^l\right)}^{a-1}{e}^{-\frac{R_t^l}{b}}\right){ϵ}^{c-1}{e}^{-\frac{ϵ}{d}}\propto \left(\prod _{t=1}^T\prod _{l=1}^{n_l}{\left(R_t^l\right)}^{a-1+\sum _{v=0}^1{I}_t^{l,v}}\right){ϵ}^{c-1+\sum _{t=1}^T\sum _{l=1}^{n_l}{I}_t^{l,1}}\times e^{-\frac{ϵ}{d}-\sum _{t=1}^T\sum _{l=1}^{n_l}{R}_t^l\left(\frac{1}{b}+{\Lambda }_t^{l,0}+ϵ{\Lambda }_t^{l,1}\right)}$$

The marginal posterior distribution for $ϵ$ given the data (i.e. the incidence for all variants, at all locations and for all time steps) and given the reproduction number for the reference variant in all locations and at all time steps is given by:

$$P\left(ϵ|{\mathbf{I}}_0^{L,V},\dots ,{\mathbf{I}}_T^{L,V},{\mathbf{R}}_1^L\dots ,{\mathbf{R}}_T^L,{\mathbf{w}}^V\right)\propto {ϵ}^{c-1+\sum _{t=1}^T\sum _{l=1}^{n_l}{I}_t^{l,1}}{e}^{-ϵ\left(\frac{1}{d}+\sum _{t=1}^T\sum _{l=1}^{n_l}{R}_t^l{\Lambda }_t^{l,1}\right)}$$

Therefore, the marginal posterior distribution of $ϵ$ given the data and other parameters is a Gamma distribution with shape $c+{\sum }_{t=1}^T{\sum }_{l=1}^{n_l}{I}_t^{l,1}$ and scale $\frac{1}{\frac{1}{d}+{\sum }_{t=1}^T{\sum }_{l=1}^{n_l}{R}_t^l{\Lambda }_t^{l,1}}$.

Similarly, the marginal posterior distribution for $R_t^l$ at time step $t$ and in location $l$ given the data, $ϵ$, and the reproduction number at other locations and time steps, is given by:

$$P\left(R_t^l\right|{\mathbf{I}}_0^{L,V},\dots ,{\mathbf{I}}_T^{L,V},ϵ,{\mathbf{R}}_1^L\dots ,{\mathbf{R}}_{t-1}^L,{\mathbf{R}}_{t+1}^L,\dots ,{\mathbf{R}}_T^L,{\mathbf{R}}_t^1\dots ,{\mathbf{R}}_t^{l-1},{\mathbf{R}}_t^{l+1}\dots ,{\mathbf{R}}_t^{n_l},{\mathbf{w}}^V)\propto {\left(R_t^l\right)}^{a-1+\sum _{v=0}^1{I}_t^{l,v}}{e}^{-R_t^l\left(\frac{1}{b}+{\Lambda }_t^{l,0}+ϵ{\Lambda }_t^{l,1}\right)}$$

Therefore, the marginal posterior distribution of $R_t^l$ given the data and other parameters is a Gamma distribution with shape $a+{\sum }_{v=0}^1{I}_t^{l,v}$ and scale $\frac{1}{\frac{1}{b}+{\Lambda }_t^{l,0}+ϵ{\Lambda }_t^{l,1}}$.

Precision in$ϵ$estimates. An analytical formulation of the marginal posterior distribution of $ϵ$ allows us to quantify the expected precision in $ϵ$ estimates. Since the coefficient of variation (CV) of a gamma distributed random variable is $1/\sqrt{shape}$, the CV of the marginal posterior distribution of $ϵ$ is

$$CV\left(ϵ|{\mathbf{I}}_0^{L,V},\dots ,{\mathbf{I}}_T^{L,V},{\mathbf{R}}_1^L\dots ,{\mathbf{R}}_T^L,{\mathbf{w}}^V\right)=\frac{1}{\sqrt{a+\sum _{v=0}^1{I}_t^{l,v}}}\le \frac{1}{\sqrt{\sum _{v=0}^1{I}_t^{l,v}}}$$

That is, the CV of $ϵ$ scales inversely with the square root of the total incidence across all locations in the time-window used for estimation.

Monte Carlo Markov Chain (MCMC) inference. The analytical formulation of the marginal posterior distributions for $R_t^l$ and $ϵ$ allow us to use a multi-stage Gibbs sampler for the MCMC inference.

To initialise $R_t^l$, we use EpiEstim to estimate a single reproduction number for the reference variant over the entire time period of observations, and using incidence aggregated across all locations. The posterior mean is then used as the initial value for $R_t^l$. We independently use the same approach to estimate a single reproduction number for the new variant; $ϵ$ is then initialised to the median of the ratio of the reproduction numbers for the new variant and the reference.

We first sample from the marginal distribution of $R_t^l$, conditional on $ϵ$, and then we sample from the marginal distribution of $ϵ$, conditional on the newly sampled value of $R_t^l$. We repeat this procedure for a fixed number of iterations or until convergence is achieved. Convergence is assessed using Gelman–Rubin convergence diagnostic (Gelman and Rubin, 1992) using 1.1 as a cut-off value.

Implementation. The inference method is implemented in a new function “estimate_advantage” of the development version of the R package EpiEstim available at https://github.com/mrc-ide/EpiEstim.

Choosing a time-period for estimation of$ϵ$. Users can set the time period over which estimation will be carried out. We recommend that the estimation is started after at least one generation of cases has been observed. The default starting point in the software is set to the first day of non-zero incidence across all locations plus the 95th percentile of the serial interval distribution.

Classification of a variant. We used the posterior distribution of the effective transmission advantage to classify a new variant (in relation to the reference variant) as:

• •‘More transmissible’ if the 2.5th quantile of the posterior distribution was greater than 1;
• •‘Less transmissible’ if the 97.5th quantile of the posterior distribution was less than 1; and,
• •‘Unclear’ if the 95% CrI contained 1.

We note that here we used the 2.5 and 97.5 posterior percentiles for variant classification, which provides an easy metric to summarise across simulations. However our EpiEstim implementation of the approach provides the entire posterior distribution of the transmission advantage, and therefore the user could use different thresholds for classification, balancing the desired sensitivity and specificity. The user could also quantify the posterior probability that a novel variant is more transmissible.

Method validation. We assessed the validity of our method using a large simulation study, where we considered several scenarios with different values for the transmissibility of each variant, allowing for superspreading, under-reporting or time-varying transmission advantages, as well as differences in natural history between variants (Suppl Secs. 5 and 5.1). We measured method performance on the simulations using several metrics (detailed in Suppl Sec. 5.1)). First, we measured the bias as the difference between the mean posterior estimate of the effective transmission advantage and its true value. Second, we measured uncertainty in the posterior distribution and considered the coverage probability, which measures whether uncertainty in estimates is adequate. Finally, we considered the ability of the model to adequately classify the variant as “more transmissible”, “less transmissible” than the reference or “unclear”.

Literature review. On 21st February 2023, we searched for all studies published from 2020 onward which estimated the transmission advantage of SARS-CoV-2 variants. The following search terms were entered into Web of Science: AB=((Transmission OR Transmissibility) & (Variant OR VOC) & (estimat*) & (SARS-CoV-2 OR COVID)). In total, 336 studies were identified in the search and uploaded to Covidence for screening. 244 studies were excluded after title and abstract screening, and an additional 31 studies were excluded during full text screening. For completeness, 5 additional papers that were found prior to the search were also included. Of these 66 (61 + 5) studies, 53 explicitly provided one of more estimates of the transmission advantage of one variant over another. For these, we extracted the value and type of transmission advantage estimated, as well as the method used and its availability (or not) as packaged software. See section 6 of the Supplementary Material and the Supplementary Database for further details.

3. Results

3.1. Transmission advantage of SARS-CoV-2 variants

We used MV-EpiEstim to retrospectively estimate the transmission advantage of SARS-CoV-2 variants using data from England and France. The Alpha variant originated in late summer to early Autumn 2020 in England (before vaccination was initiated), where it became dominant in early 2021 (Fig. 1A). The Delta variant, first detected in India, emerged in England around March 2021 and accounted for most SARS-CoV-2 cases in all regions by late Spring 2021 (Fig. S1). England never experienced substantial transmission of the Beta and Gamma variants, first detected in South Africa and Brazil respectively (Anon, 2021a).

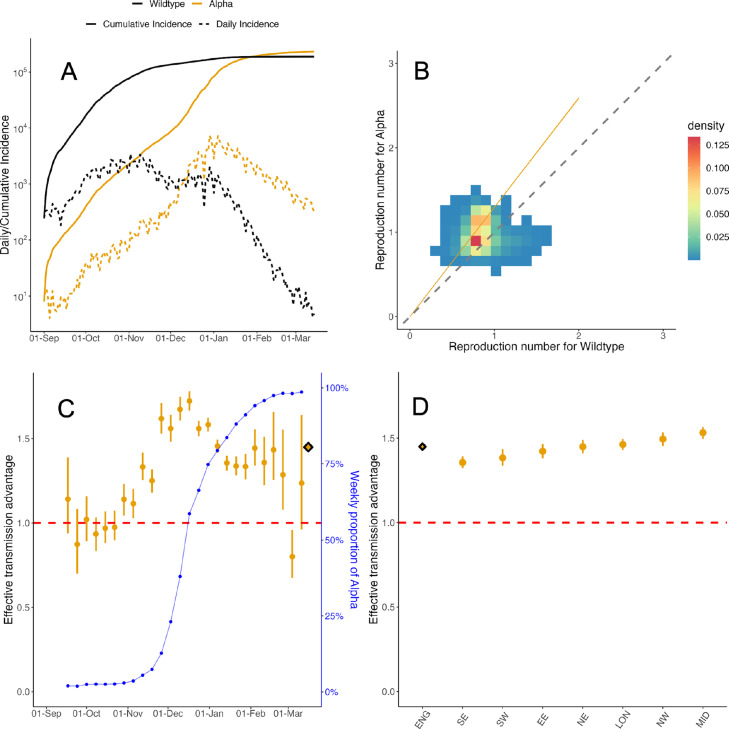
Fig. 1.

Effective transmission advantage of Alpha over wildtype in England (A) The daily reported incidence of cases of the wildtype (black) and Alpha (yellow) in England from September 2020 to March 2021. (B) The effective reproduction number $R_t$ estimated independently for the wildtype (x-axis) and Alpha (y-axis) on sliding weekly windows. The colour of the cells indicates the density of the draws from the respective posterior distributions of $R_t$. The dashed diagonal line indicates the $x=y$ threshold. Coloured cells lying above the diagonal line suggest that Alpha is more transmissible. The yellow line denotes the median effective transmission advantage estimated using MV-EpiEstim, assuming no temporal or spatial heterogeneity. 95% CrI were so narrow that they could not be distinguished from the line. (C) Effective transmission advantage estimated using MV-EpiEstim using data in the week ending on the date specified on the $x$-axis (yellow) and the entire time series (diamond). The dark blue circles and the vertical bars denote respectively the mean and 95% binomial confidence interval of the proportion of incidence of Alpha (right y-axis) in the week of estimation. Because of the high incidence of both wildtype and Alpha in the study period, the 95% CI are small and hence difficult to distinguish. (D) Effective transmission advantage estimated using MV-EpiEstim for all NHS England regions together (diamond) and separately (solid circles), using data from 1^st September 2020 to 14th March 2021. The NHS England regions are - East of England (EE), London (LON), Midlands (MID), North-East (NE), North-West (NW), South-East (SE), South-West (SW). In panels (C) and (D), the solid yellow circles denote the median estimate, the vertical lines indicate the 95% CrI, and the red dashed line denotes the $ϵ=1$ threshold. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

In France, the Alpha variant emerged in early 2021, rapidly dominating cases in metropolitan France and the French West Indies (Anon, 2021b, Anon, 2021c). The Beta and Gamma variants were also circulating from January 2021 in most regions, and accounted for the majority of cases in French Guyana and la Réunion from Spring 2021 (Anon, 2021d) (Fig. S2). The Delta variant emerged in France in early June 2021 after the period covered in this study.

We considered daily variant-specific incidence data from 7 National Health Service (NHS) regions in England between 1^st September 2020 and 14th March 2021 (Fig. S1), and from 18 ADM2 regions in France between 18th February and 30th May 2021 (Figs. S2 and S6).

For simplicity, we refer to all lineages of SARS-CoV-2 other than the VOCs that were circulating at the time as ‘wildtype’. $R_t$ estimates obtained independently for the wildtype and for Alpha indicated that Alpha was more transmissible (Fig. 1B). However, the magnitude of the transmission advantage (naively estimated as the ratio between the two $R_t$s, see Suppl Sec. 3 for details) varied over time and across regions. Pooling these non-parametric estimates over time and regions yielded a highly uncertain and non-significant transmission advantage of 1.41 (95% Credible Interval (CrI) 0.86-2.01) for Alpha compared to the wildtype across all times and regions in England.

MV-EpiEstim allows further exploring how the effective transmission advantage, which we denote as $ϵ$, varies over time and space, by estimating $ϵ$ over various temporal and spatial units, within which it is assumed constant.

We first assumed that $ϵ$ was constant across all regions but potentially varied over time. Using weekly data aggregated across regions, $ϵ$ estimates from MV-EpiEstim showed a strong temporal variation with the central estimate initially increasing from 1.01 (95% CrI 0.89-1.15) in October to 1.72 (95% CrI 1.67-1.78) in December, and then declining again to 1.24 (95% CrI 0.95-1.62) in March 2021. We found a similar trend over time when $ϵ$ was estimated independently for each region (Fig. S5). We also used MV-EpiEstim to estimate $ϵ$ separately for each NHS region assuming that it remains constant over time. This highlighted minor regional differences with $ϵ$ estimated across the whole time period ranging from 1.36 (95% CrI 1.33-1.39) in the South-East to 1.54 (95% CrI 1.50-1.58) in the Midlands (Fig. 1D, Suppl Tab. S1).

The consistent temporal variability in $ϵ$ estimates when using data from all or individual regions suggests an underlying change in transmission dynamics. Across the entire time period and all regions we found strong evidence that Alpha was more transmissible than the wildtype, with an overall central estimate of $ϵ$ at 1.45 (95% CrI 1.43-1.46) when ignoring differences in time and space (see also Suppl Tab. S1). However these results mask substantial temporal heterogeneity and small levels of spatial heterogeneity (Fig. S3).

We estimated a similar, albeit slightly lower, overall effective transmission advantage for Alpha using data from the 18 ADM2 regions in France (central $ϵ$ estimate assuming no temporal or spatial heterogeneity at 1.29 (95% CrI 1.29-1.31), see Fig. S6). As for Alpha in England, these estimates masked changes in the transmission advantage over time, declining from 1.46 (95% CrI 1.44-1.48) in March to 0.90 (95% CrI 0.86-0.95) in May 2021 (Fig. S7), and to a lesser extent between regions (from 1.21 (95% CrI 1.20-1.23) in Île-de-France to 1.41 (95% CrI 1.37-1.46) in Bourgogne-Franche-Comté, excluding regions where Beta/Gamma were dominant, Fig. S6 and Suppl Tab. S2).

Following the same approach, and using data from France, we demonstrated that the Beta and Gamma variants (combined) are also more transmissible than the wildtype, with $ϵ$ estimated to be 1.25 (95% CrI 1.25-1.27). However behind this overall central estimate we identified a decline in $ϵ$ over time, and heterogeneities between regions Fig. S8 and Suppl Tab. S3 . Finally, using data from England, we estimated that Delta is 1.77 (95% CrI 1.69-1.85) times more transmissible than Alpha (Fig. S10 and Suppl Tab. S4). The spatial and temporal trends in $ϵ$ estimates for Delta, while present, were less marked (Fig. S11).

4. Method validation

The method performed well across most scenarios considered, with a small bias (defined as the difference between the mean posterior estimate and the true $ϵ$ value, Fig. 2). The coverage probability, which measures whether uncertainty in estimates is adequate (Suppl Sec. 5.1), was also good across most scenarios (Fig. S12 to Fig. S31).

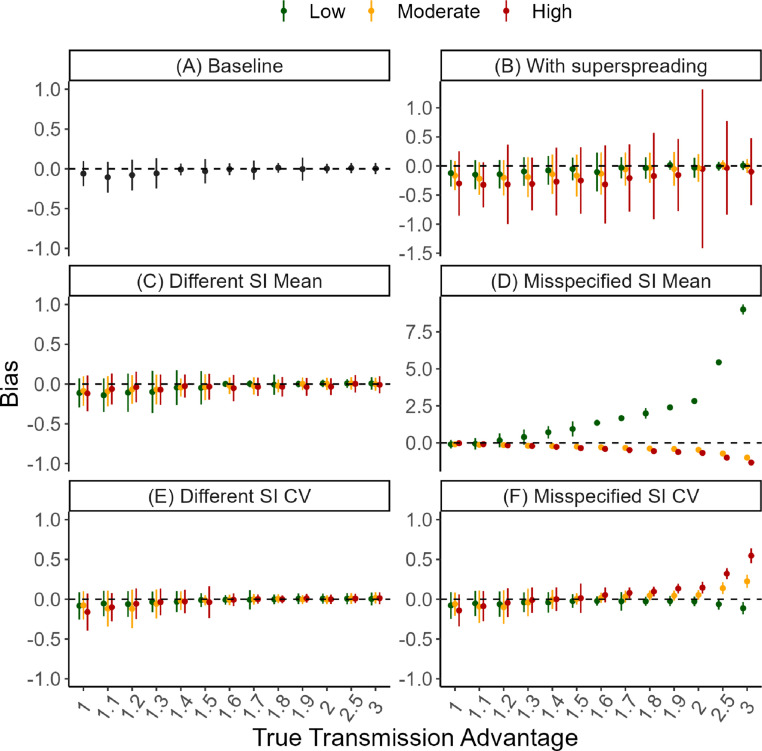
Fig. 2.

Method performance on simulated data. We assessed the performance of MV-EpiEstim on a range of scenarios. In each panel, the $x$-axis shows the true value of the effective transmission advantage (on categorical scale). The $y$-axis shows the bias i.e., the difference between the posterior mean estimate of the transmission advantage and the true value. The solid dots represent the mean bias (across 100 simulations) and the vertical bars show the standard deviation (SD) of the bias. Each panel corresponds to a different simulation scenario. In all scenarios, the $R_t$ for the reference variant was 1.1 and the $R_t$ for the new variant was $ϵ$ times the reference $R_t$ (see Suppl Sec. 5 for details). (A) In the baseline scenario, we assumed no superspreading and the same natural history for both variants. (B) As (A), but with low (overdispersion parameter $\kappa$ = 1), moderate ($\kappa$$=$ 0.5) and high ($\kappa$$=$ 0.1) levels of superspreading. (C) As (A), but the mean serial interval of the new variant is 0.5 (low), 1.5 (moderate) or 2 (high) times that of the reference and is correctly specified during estimation. (D) As (C), but the mean serial interval of both variants are assumed to be the same during estimation. (E) As (A), but the coefficient of variation (CV, ratio of standard deviation to mean) of the serial interval distribution of the new variant is 0.5 (low), 1.5 (moderate) or 2 (high) times that of the reference and is correctly specified during estimation. (F) As (E), but the CV of the serial interval distribution of the reference and new variants are assumed to be the same during estimation. Note that the $y$-axis range is different for panel D. Results using $R_t=1.6$ for the reference and using fewer days of data are presented in Suppl Secs. 5.3 to 5.9. Results using time-varying reference $R_t$ in one or two locations are shown in Suppl Secs. 5.10 and 5.11.

MV-EpiEstim was able to accurately estimate the transmission advantage when variants were known to differ in their natural history (characterised by the serial interval distribution, i.e., the delay between onset of symptoms in a case and their infector, Fig. 2c and e, Suppl Secs. 5.4 and 5.6). We also explored a scenario typical of real-time outbreak analysis where the natural history of the new variant is different, but in the absence of information, is assumed to be the same as that of the reference (Suppl Secs. 5.5 and 5.7). Misspecifying the mean serial interval led to substantial bias (median bias ranged from −1.8 to 16.7) and poor coverage, especially when the transmission advantage was moderate (more than 1.5) and the mean serial interval of the new variant was much shorter (0.5 times) than that of the reference (Suppl Secs. 5.5 and 5.7). Misspecifying the coefficient of variation of the serial interval had little impact on the quality of the estimates (range of median bias: −0.4 to 1.0), unless the transmission advantage was very high (more than 2, Fig. 2f).

Even in the presence of substantial superspreading (i.e., equivalent to that of SARS-CoV-1, Fig. 2b) or poor case-reporting (i.e., up to 80% cases not reported, Fig. S26), neither of which is explicitly accounted for by MV-EpiEstim, the transmission advantage remained unbiased (range of median bias with overdispersion parameter 0.1 (−0.3, 0.1); range of median bias with probability of reporting 0.2 (−0.5, 0.0)). However, coverage tended to be low in the presence of high superspreading or high underreporting, indicating that the credible intervals were too narrow in these scenarios (Suppl Secs. 5.8 and 5.9).

In all scenarios, using more days of data reduced both the bias and the uncertainty (defined as the posterior standard deviation) in the estimated effective transmission advantage (Fig. S14 and Suppl Secs. 5.3 to 5.7).

We used the uncertainty in the estimates of $ϵ$ (i.e., the width of the 95% CrI) to determine if the effective transmission advantage was significant and classify the variant as more or less transmissible than the reference (see Methods). Crucially, in many scenarios including some where the bias was substantial, MV-EpiEstim was able to correctly characterise a variant as being more transmissible than the reference. For instance, when the mean serial interval of the new variant was shorter but misspecified, the variant was correctly classified as more transmissible since $ϵ$ was over-estimated (Fig. S18, scenario type low). Conversely, when the mean serial interval of the new variant was longer but was misspecified, classification performance was generally poor and correct classification was only feasible with sufficient days of data and a large transmission advantage (Fig. S18, scenario type high).

We also tested the performance of our method in a scenario in which the transmission advantage is changing over time (Fig. S30). We show that, when applied to short time windows, our method is able to detect the changes in transmission advantage, but it can give misleading estimates if applied to a longer time window where the transmission advantage varies (Fig. S31).

More results demonstrating the performance of the method when using fewer days of data, two locations, time-varying $R_t$ and accounting for underreporting are shown in Suppl Sec. 5.

4.1. Literature review results

105 estimates for the transmission advantage of SARS-CoV-2 variants were found across 53 studies. Of the literature which provided estimates for the transmission advantage in the reproduction number R, the estimated advantage for Alpha was in the range of 1.35-1.75, with associated uncertainty estimates (95% CrIs/CIs) ranging from 1.02-2.30. Similarly, the range of the central estimates of the transmission advantage for the Delta variant in the literature was 1.5-2.4.

Out of the 53 studies, only 5 provided packaged code, with a single package requiring only incidence data for the estimation. All literature review results, including extracted estimates of the transmission advantages and hyperlinks to the available code and R packages can be found in the Supplementary Database.

5. Discussion

In this study we present a novel method, MV-EpiEstim, to estimate the transmission advantage of a new variant of a pathogen over a reference variant. MV-EpiEstim builds on the EpiEstim method (Cori et al., 2013, Thompson et al., 2019). As such, MV-EpiEstim offers the same functionalities as EpiEstim. Because it is based on analytical formulations of the marginal posterior densities, the run time of a typical analysis using MV-EpiEstim is less than a few minutes on a standard laptop. MV-EpiEstim is implemented as a new function in the R package EpiEstim (Anon, 2021e).

To illustrate the use of MV-EpiEstim, we retrospectively estimated the effective transmission advantage of Alpha, Delta and Beta/Gamma combined over the wildtype variants in England and France. Our analyses showed substantial changes in the effective transmission advantage of Alpha over time, particularly in England, where our analysis covers the full period from early emergence to dominance. The consistency of these temporal trends across regions provides stronger evidence of underlying changes in transmission trends. Volz et al. found a broadly similar temporal trend in the transmission advantage in the UK (Volz et al., 2021), which Kraemer et al. suggested may be in part explained by spatial patterns of spread (Kraemer et al., 2021).

Our analysis also identified temporal changes in the transmission advantage of Beta and Gamma over the wildtype, and Delta over Alpha. Such temporal changes may be due to a combination of factors. First, the detection of a VOC can trigger interventions (such as increased testing and contact tracing) targeted at sub-populations in which the VOC is circulating (e.g. travellers). This can lead to a lower rate of spread of the VOC early on, before its spread is generalised, and therefore an apparent increase in the transmission advantage over time. Changes in population immunity over time, such as increasing immunity to Alpha and waning immunity to previous variants can also contribute to the observed temporal trends in its transmission advantage. Future work could explore extending our approach to incorporate explanatory variables such as the proportion of population susceptible to specific variants over time and across different locations.

The fast run-time and reliance solely on variant-specific incidence time-series and serial interval distributions make it easy to explore several hypotheses about spatio-temporal trends. We recommend that future users of MV-EpiEstim run multiple sensitivity analyses exploring the spatio-temporal heterogeneities in effective transmission advantage. Consistent signals of a significant transmission advantage independently estimated across these analyses can help raise early warnings about emergence of VOCs.

Our method works well across a range of simulated scenarios, designed to mimic a variety of real-time epidemic contexts, including in the presence of superspreading and when the natural history of the new variant is imperfectly characterised. As expected, the performance deteriorated with larger errors and lower coverage probability in scenarios with high superspreading or under-reporting, and with large misspecification of natural history. Of the packaged tools identified in our literature review, one did explicitly account for overdispersion, but did not demonstrate method performance on simulated data (Hinch et al., 2022). Moreover, other than a couple of studies, which did not provide a packaged tool (Blanquart et al., 2022, Ito et al., 2022), all other approaches to estimate the transmission advantage suffer from a similar identifiability issue between a change in generation time versus a change in transmission (see Supplementary Database for details).

In the absence of precise information on natural history, MV-EpiEstim’s fast run time offers the possibility of exploring various assumptions and in turn estimate a range of plausible transmission advantages. Our method is robust to moderate levels of under-reporting and temporal changes in reporting if these affect both the reference and the variant equally.

Importantly, we show that our method can accurately characterise a variant as being ‘more’ or ‘less’ transmissible than a reference variant across many scenarios, including some where the performance at estimating the transmission advantage was only modest. This simple but robust characterisation could be as important as estimating the exact value of the transmission advantage, especially in informing public health response during the early phase of a new variant emerging. For example, in scenarios where the emerging variant has a shorter serial interval, as was the case for Omicron for example (Backer et al., 2022), our method will generally be able to detect an increase in transmission, albeit with an overestimated transmission advantage. Where the new variant has a longer serial interval though, our approach will have poor ability to detect the increased transmissibility. However, again, these caveats are common to many approaches.

Classification performance depends on multiple factors including the characteristics of the reference and new variants and the amount of data available for estimation. Across all scenarios, the probability of correctly classifying a more transmissible variant (i.e., true positive rate) increases with increasing baseline transmissibility, higher transmission advantage, and as more data are used for estimation. Conversely, in scenarios with high levels of superspreading or large misspecification of the natural history of the variant, the sensitivity of the classification is reduced (Figs. S17 and S23) but improves when either more data are used (Figs. S18 and S24) or with increasing transmission advantage. It is worth noting that in all scenarios, including scenarios where method sensitivity is low, the probability of misclassifying a variant as “more transmissible” when it is not (i.e., false positive rate) remains low (Suppl Tab. S6) i.e., the method specificity is high. Critically, we note that in such cases, the variant is classified as “unclear”, with very low probability of incorrectly classifying it as less transmissible. Further, both the true and false positive rate of classification also depend on the threshold (quantile of the posterior distribution of $ϵ$) used for classifying a variant as more transmissible, which can easily be modified by the user depending on the relative costs of false negatives and false positives.

We emphasise that our method estimates the effective transmission advantage, which will often reflect a combination of several factors such as a true increase in underlying transmissibility and the ability of a new variant to escape immunity. Disentangling these effects is particularly challenging in the context of changing population immunity e.g., due to vaccination roll-out, and may require additional data (see Supplementary Database for details). However, regardless of its drivers, early identification of a transmission advantage is a critical first step to a timely response.

We note that in the extreme case where estimates are made independently at all time steps and locations, our method reduces to what we have called the “non-parametric” approach as it provides a non-parametric estimate of the transmission advantage at each time and location as the ratio between the reproduction numbers for each variant. While such an approach can help in initial exploration, the assumption of independence across time and space can lead to highly uncertain estimates. MV-EpiEstim allows combining information across time and/or locations, assuming that the effective transmission advantage is constant across these. This allows reducing the uncertainty in the estimates. Temporal or spatial heterogeneity in the transmission advantage (e.g. reflecting heterogeneity in population immunity) can also be characterised by applying the method separately by location or time period, which is easy to do in our software.

Our estimated transmission advantage of the SARS-CoV-2 Alpha variant (over the wildtype) is consistent with those from other analyses identified in our literature review, with estimates in the range of 1.02 to 2.30 (See Supplementary Database). Similarly, our estimates of the transmission advantage of the Delta variant over the Alpha variant are broadly consistent with the literature, with central estimates of the advantage in the range of 1.5 to 2.4. In addition, our results highlight temporal changes in the transmission advantage which were overlooked by some of these studies. The agreement of our findings with those from other studies employing a diversity of modelling approaches including renewal equations, semi-mechanistic models, and phylodynamic models suggests that MV-EpiEstim can be a useful tool for early characterisation of new variants. Importantly, where specific bio-markers are sufficient to distinguish variants (e.g. S-gene), MV-EpiEstim does not need any whole-genome sequencing data. Therefore, it could be used in near real-time, relying only on routinely collected incidence data and not necessarily suffering from potential delays in the sequencing pipeline.

Given the continued transmission of SARS-CoV-2 and low vaccination coverage globally (Mathieu et al., 2021), new variants are likely to continue emerging. Our tool can be used to monitor their transmissibility and rapidly identify variants of concern. Our estimates of the transmission advantage of Delta have been used to inform UK national policy in real-time.

Applications of our work are not limited to SARS-CoV-2; our generic method could easily be used to monitor other pathogens with multiple co-circulating strains such as influenza or streptococcus pneumoniae.

CRediT authorship contribution statement

Sangeeta Bhatia: Conceptualization, Software, Validation, Formal analysis, Writing – original draft, Writing – review & editing. Jack Wardle: Conceptualization, Software, Validation, Formal analysis, Writing – review & editing. Rebecca K. Nash: Conceptualization, Software, Validation, Formal analysis, Writing – review & editing. Pierre Nouvellet: Conceptualization, Methodology, Software, Formal analysis, Writing – review & editing, Supervision. Anne Cori: Conceptualization, Methodology, Software, Formal analysis, Writing – original draft, Writing – review & editing, Supervision.

Declaration of Competing Interest

AC has received payment from Pfizer for teaching of mathematical modelling of infectious diseases.

Appendix A. Supplementary data

The following is the Supplementary material related to this article.

MMC S1

.

MMC S2

.

Data availability

All data and code used in this analysis are available at https://github.com/mrc-ide/epiestims. MV- EpiEstim is available in the development version of EpiEstim at https://github.com/mrc-ide/EpiEstim.