Machine Learning & Molecular Radiation Tumor Biomarkers

Abstract

Developing radiation tumor biomarkers that can guide personalized radiotherapy clinical decision making is a critical goal in the effort towards precision cancer medicine. High-throughput molecular assays paired with modern computational techniques have the potential to identify individual tumor-specific signatures and create tools that can help understand heterogenous patient outcomes in response to radiotherapy, allowing clinicians to fully benefit from the technological advances in molecular profiling and computational biology including machine learning. However, the increasingly complex nature of the data generated from high-throughput and “omics” assays require careful selection of analytical strategies. Furthermore, the power of modern machine learning techniques to detect subtle data patterns comes with special considerations to ensure that the results are generalizable. Herein, we review the computational framework of tumor biomarker development and describe commonly used machine learning approaches and how they are applied for radiation biomarker development using molecular data, as well as challenges and emerging research trends.

INTRODUCTION

Radiation therapy is a core component of the treatment of cancer patients, with over 50% of patients receiving radiation therapy at some point during their treatment course, and approximately 60% of these patients are treated with curative intent¹. Personalization of radiation therapy is a critical goal for radiation oncologists who aim to increase the chance of controlling disease while limiting the harmful side-effects and toxicities of treatment. Current strategies center around several frameworks – utilizing clinical characteristics to stratify patients, image guided radiation therapy that allows for higher doses to the tumor with improved sparing of normal tissue², and biomarkers to guide treatment^3–5. The first two are widely clinically adopted, but development of radiation tumor biomarkers has proven more difficult. Prognostic tests can help guide decisions about treatment intensification in high-risk patients or de-intensification in low-risk patients, but they provide limited insight into the most appropriate type of intervention. The ideal radiation tumor biomarker for the radiation oncologist would be treatment predictive, that is it would provide insight into whether a patient’s specific cancer is radiosensitive or radioresistant, or on the benefit of radiation. Such predictive biomarkers could then guide the decision on whether to treat with radiation and help determine the appropriate dose and fractionation schedule. Predictive biomarker discovery can be more difficult than identifying prognostic biomarkers, but advances in high-throughput molecular profiling technologies have provided an opportunity to create clinically useful radiation-based predictive biomarkers, and many biomarkers of radiation sensitivity and resistance have been developed using various machine learning techniques⁶ to harness the power of these assays. However, there are no tumor biomarkers specifically designed for radiation therapy that are clinically used today. One of the challenges with modern high-throughput assays is the complex nature of the data produced and the special analytical considerations required. In this review we set out to provide a broad overview of the computational machine learning methodologies used in of the development of high-throughput radiation biomarkers as well as review challenges and future possibilities.

High-throughput techniques and the “curse of dimensionality”

Modern high-throughput assays, or “omics” technologies, have revolutionized the study of biological systems. The assays provide an opportunity to comprehensively characterize the tumor DNA alterations (genomics), gene expression profiles (transcriptomics), protein abundance and modifications (proteomics), epigenetic modifications (epigenomics), metabolic profiles (metabolomics), etc. Herein, we will focus on the special analytical considerations needed for these molecular data. The common theme for all “omics” assays is that for every tumor sample (observation) there are hundreds to thousands to millions of variables measured (features, or dimensions, e.g. genes, proteins, etc.). The number of observations is usually lower than the number of features due to sample availability and cost. Given that 1) most features are typically not informative for the specific question asked, thus contributing only “noise”, and 2) there is a level of background random variability for each feature, there are usually features that can distinguish between groups by pure chance. Thus, adding hundreds or thousands of variables of which most are contributing noise does not necessarily make it easier to find the true biological signal in the data, a phenomenon that is sometimes called the “curse of dimensionality”. The key analytical challenge in biomarker development is to find the true signal in the noise.

This challenge is compounded by the power of modern machine learning techniques, which can be extremely efficient at finding subtle patterns in the data. Given the high-dimensional nature of “omics” data, it is easy for these methods to fit models on the noise in a specific dataset and the more flexible a model is, the easier it may be to pick up the noise in the data. By picking up noise instead of signal, the model weights are more sensitive to changes in the input data, and the model will have a high variance. Conversely, less flexible models usually have a bias towards the constraints of that model, making it more robust against noise, but also less flexible to the true signal. Ideally, a good model is flexible enough to find a close fit to the true signal (low bias) and have low variance. There is usually a trade-off between these properties, referred to as the bias-variance trade-off. In summary, these properties of high-dimensional data and the flexibility of models available in modern machine learning, requires a specific strategy and a set of steps for model development and validation where a model is trained, tuned, tested, and finally validated in independent data to ensure that the model has indeed found a true signal in the noise.

Sample handling and data pre-processing

Before the machine learning procedures can start, the data needs to be pre-processed for further analysis. The full details of these techniques are outside the scope of this review. Briefly, pre-processing typically includes normalization, batch-effect correction, and feature selection. Normalization is intended to reduce the technical variability between samples and can be done for a set of samples together (cohort) or on a single-sample basis. Single-sample techniques have the advantage of easier implementation in personalized medicine workflows as it can be performed continuously on each new sample that is processed and independently of other cohorts. Batch-effects refer to systematic technical variability in the data due to groups of samples having similar patterns due to experimental or technical factors, in contrast to biological differences. This can be due to different assay platforms being used, samples being processed at different centers or at different timepoints, differences in sample handling, storage, processing, etc. It is important to reduce these potential sources of variability, and to identify and account for batch-effects when present. Feature selection is intended to reduce the number of non-informative, or noise, features. It can be done based on unbiased data-driven methods (such as removing lowly expressed genes and selecting the most variable genes), by prior biological knowledge (e.g. selecting genes in specific biological pathways) or at later analytical stages by how the features contribute to model performance. The overall goal of the pre-processing is to yield a dataset with as little noise and as much true signal as possible.

STRATEGIES FOR MACHINE LEARNING ANALYSIS

Definition Overview

The terms artificial intelligence (AI) and machine learning (ML) are used colloquially and often interchangeably, but they do hold separate meanings. AI refers to any technique utilized on a computer that seems to replicate a form of intelligence. ML represents a subset of AI where computers can learn directly from labeled (i.e. patient outcomes or radiosensitivity status of a sample is known) or unlabeled data. The goal of all ML methods is to take data as input and create a more structured and simplified output. There are two primary methodologies to perform this task – unsupervised learning and supervised learning. The primary difference between these two methods is that supervised models train on labeled data for a specific outcome – a continuous variable (regression) such as the survival fraction of cells after receiving 2 Gy of radiation (SF2) or a discrete variable (classification) such as whether a tumor is known to be radiation sensitive or resistant – while unsupervised models are used to identify the intrinsic structure in a dataset without utilizing any labels (e.g. clustering).

Data Spending

Since the number of observations usually is limited, how the limited data gets used is one of the most important aspects of ML to ensure generalizability to future samples. Data spending refers to the task of splitting up data at steps throughout the workflow so that the model reproducibly finds signal instead of noise. The data used to build a model is called training data, while we refer to the data that the final and locked model is run on to validate the performance as independent validation data. The training data can be further split for model tuning, which we refer to as a hold-out test set. A true validation data set is meant to be entirely separate from the model training workflow and only used as a final independent confirmation of model performance. Various strategies have been utilized to train radiation signatures, such as Eschrich et al. utilizing the NCI-60 cell lines⁷, Zhao et al. utilizing orthotopic glioblastoma patient-derived xenografts⁸, and Sjöström et al. utilizing breast cancer patient samples⁹. All three studies had independent clinical validation datasets that were used to confirm the clinical validity and generalizability of the models. A critical requirement for radiation biomarkers is a validation dataset which is independent from training^7,8,10–15, such that no validation data is used to adjust the model. If the validation data is used for training, or informing the training (i.e. information leakage), the model may pick up noise that is present in both the training and validation data, instead of true signal, and will not generalize to future datasets. Validation data may come from a different source than the training data. In that case, differences in platforms or experimental protocols may need to be accounted for via normalization and/or batch correction strategies described above. However, this would not generally be considered a major component of information leakage, since the validation data is not being directly trained on the outcome of interest.

Hyperparameter Fitting and Model Selection

As discussed above, ML models can be so flexible and effective in finding patterns that they find noise that does not represent true biological signal and is only specific to that data set, which is referred to as overfitting¹⁶. Thus, a model that is over-fit to a particular training dataset usually performs poorly on validation. A bias term making the model less flexible can be added so that the model’s fit is reduced on training data, increasing the generalizability and ideally with improved performance on validation (regularization, described in detail later) (Figure 1A). The bias term represents a hyperparameter, which is a feature that can only be optimized through evaluation of a model’s performance, unlike a traditional parameter in a linear regression model which has a best-fit solution. Both the selection of an appropriate model with the optimal level of flexibility and multiple hyperparameters need to be tested to identify the optimal model and settings. However, selecting the best model and settings in the training data commonly leads to over-fitting, while selection based on the validation data would be information leakage. Thus, one strategy is to further split the training data into a model building set and a hold-out test set from which optimal model and bias hyperparameters are selected (Figure 1B), so that all of this occurs only within the training data, keeping the validation data separate.

Figure 1 – Machine Learning Toolkit.

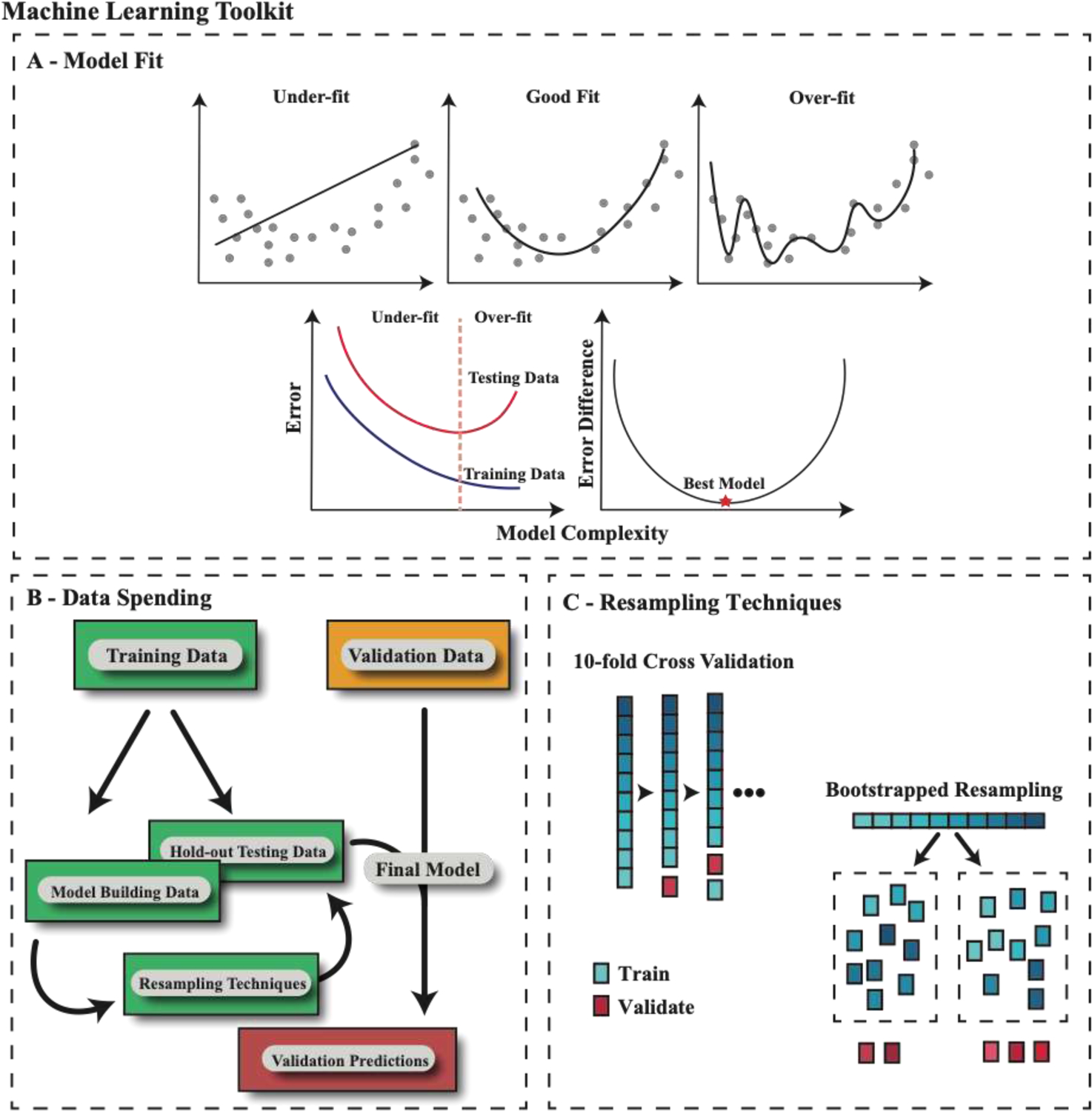
A – A model that tries to overlearn features in the training data is at risk of over-fitting that data and performing poorly on the testing (or validation) set. A bias term can be added to the model training procedure so that it performs worse on training but better on testing (or validation), finding a minimum point in the error difference. B – Depiction of an appropriate data spending schema where all modeling is performed on the training data and an independent validation dataset is utilized only to confirm the prediction of the model. The training data is further split into model building and a hold-out testing set, where resampling is performed only on the model building data. C – Depiction of the two most common resampling techniques, 10-fold cross validation (CV) and bootstrapped resampling. Note, CV will train on all but one partition of the data at a time, cycling through all combinations, while bootstrapped resampling will create N resampled groups with repeat samples so that every bootstrapped group matches the size of the original dataset.

Resampling Methods

Selecting a hold-out test dataset within the training data can result in very different results depending on how the data are split. Resampling by repeatedly generating the hold-out test set multiple times is one way to minimize this variability. The two most common resampling techniques are k-fold cross validation (CV) and bootstrapped resampling (Figure 1C). CV involves randomly splitting the data into k groups, with a model trained on k-1 groups and validated on that final hold out group (repeated k times). Leave-one-out CV is a special case where k equals the number of observations. Bootstrapping is where observations are randomly sampled from the data (allowing for repeats). The model is then trained on that sampled group and tested on the remaining observations. This can be performed n times and averaged out. To use this technique for hyperparameter optimization, one approach is performing resampling within the training data. Once the best hyperparameters are selected, the model can be locked and validated on that hold out test set. This is called double-loop resampling, with Sjöström et al.⁹ using this approach to develop a breast cancer radiation sensitivity signature. The training data they collected was split 50/50 into a model building and hold-out test set, where both gene selection and model hyperparameter optimization were performed using cross validation within the model building set. The model was first validated against their own hold-out test set and then on independent, publicly available datasets, demonstrating the clinical utility of the signature as prognostic for ipsilateral breast tumor recurrence and predictive of radiotherapy benefit in estrogen receptor positive patients. In summary, strict data spending schema and proper training using resampling minimizes information leakage, while maximizing the performance and generalizability of machine learning models.

MACHINE LEARNING APPROACHES

Unsupervised Learning

Unsupervised learning searches for intrinsic structure in a dataset while blinded to any labels. Clustering describes an unsupervised learning approach to grouping based on similarity. The two most common clustering algorithms used in biomarker development are k-means clustering and hierarchical clustering¹⁷. K-means clustering algorithm partitions data into k clusters with an algorithm that first randomly selects k observations (centroids), then calculates the distance from all other observations to the centroids (e.g. Euclidian distance), designates observations to a cluster based on the minimum distance to a centroid, and finally recalculates new centroids based on the mean values of all the observations in a cluster. This process is repeated until observations stop changing clusters, producing groups that minimize within-cluster variances. Hierarchical clustering tries to define clusters through either a bottom-up approach, where each observation starts in its own cluster, and are iteratively paired as the hierarchy ascends, or a top-down approach, where all observations start in one cluster and splits are made recursively as the hierarchy descends. Hierarchical approaches are advantageous as they produce readily interpretable structure among clusters. However, they are limited by the increased computational complexity with larger datasets. Conversely, k-means clustering is more computationally efficient but often produces more homogenous clusters with less readily interpretable structure¹⁸. Both methods have been used in radiation biomarker development, with Piening et al. using hierarchical clustering of differentially expressed genes (cell lines compared before and after radiation exposure) to identify prognostic breast cancer patient clusters¹⁹ and Weichselbaum et al. utilizing k-means clustering of interferon-related DNA damage resistance genes in breast cancer patients to identify patient clusters, creating clusters that had utility in predicting recurrence after radiation therapy²⁰.

Dimensionality reduction aims to reduce the number of features in a dataset (e.g. genes) into a lower dimensional space. Each feature in a dataset can be thought of as an additional dimension. There are three primary reasons for reducing the dimensions in a feature set – 1) too many features can be uninterpretable, 2) many features may represent experimental noise unrelated to the structure of the data, and 3) many features may be redundant, such as two genes that are correlated in all samples. While low dimensional datasets can be understood more intuitively, such as plotting each sample’s expression of three genes in a 3-D scatter plot, it’s difficult to visualize data in higher dimensions. Thus, dimensionality reduction is a key strategy for visualizing data in a lower dimensional space that can be more interpretable.

Principal Component Analysis (PCA) is the most common and easily interpretable form of dimensionality reduction²¹. PCA takes the original features of a dataset and creates new principal components (PC) that are linear combinations of those original features. For example, if a dataset had 10 genes, PCA would instead produce 10 PCs that are linear combinations of each gene. Importantly, these new PCs are explicitly de-correlated (i.e., no variable is redundant) and the PCs are ordered based on how much variability in the data each explains (e.g., PC1 will explain the most variance). By plotting PCs in a 2D or 3D space, this reduced representation of the data can readily be visualized to help understand the structure of the samples. Importantly, because PCA relies on linear combinations, any non-linear effects (gene A increases exponentially with respect to gene B) will not be accurately captured. PCA is often used for radiation signature development, with Kim et al. utilizing PCA for dimensionality reduction to plot the expression of their radiation signature, showing that radiosensitive and radioresistant cell lines were well separated in a 3D space²². Starmans et al. were able to use PCA to identify a batch effect between cell lines in their hypoxic radiosensitivity signature, warranting downstream analysis that accounted for this confounding variable²³.

A methodology that tries to improve upon some of the limitations with PCA is the t-distributed stochastic neighbor embedding (t-SNE) method²⁴, in which distances between points are scaled onto a t-distributed curve and those scaled distances are then used to map samples to a lower dimensional space, preserving some of the higher dimensional clustering structure that can be lost with PCA. Uniform Manifold Approximation and Projection (UMAP)²⁵ is a more recent and very similar algorithm that has allows for increased computational efficiency. These techniques are still dimensionality reduction techniques and do not explicitly map samples to a specified cluster, however, samples can be color coded in a 2D t-SNE or UMAP projection based on the groupings from a k-means or hierarchical clustering, a technique that is commonly used to identify cell types from single cell RNA (scRNA) expression data²⁶. Gao et al. utilized scRNA data from a breast cancer cell line treated with and without radiation and identified clusters on a t-SNE plot that identified heterogeneity of response to radiation²⁷.

Supervised Learning

In contrast to unsupervised techniques which are aimed at finding unknown structures within the data, supervised learning methods utilize models that are trained using known labeling of the data, such as radiosensitive vs. radioresistant tumors. Supervised learning can be structured based on the goal of the learning task – either developing inferential models or predictive models. An inferential model is used to identify the significance of a specific association, where the priority is producing a highly interpretable model. Conversely, the goal of a predictive model is to optimize prediction performance, often sacrificing interpretability. The most common inferential models are those utilized in clinical studies, such as a univariate or multivariate Cox regression or logistic regression. Another example commonly used in biomarker discovery is differential gene expression analysis of RNA-seq²⁸, where a generalized linear model provides a log-fold change and significance test for the comparison between two experimental groups across every gene. Differential expression analysis is commonly used for radiosensitivity biomarker identification, such as in comparisons of gene expression levels in irradiated and non-irradiated cell lines to identify induced and repressed genes¹⁹, performing cell line survival experiments and utilizing integral survival²⁹ or SF2³⁰ to define radioresistant and sensitive cell lines, and evaluating varying hypoxic conditions in cell lines^23,31 and patients³² to identify hypoxia related genes relevant for radiation response. While inference and prediction can be two separate goals, the reality is that there is a spectrum – ideally inferential models are predictive and vice versa. Below, we review several commonly used supervised learning predictive models for radiation biomarkers, again focusing on studies with independent clinical validation. Many other ML algorithms exist beyond these (support vector machines, Bayesian networks, etc.), but will not be covered below.

Generalized Linear Models

Simple univariate and multivariate generalized linear models (GLMs; including linear, logistic, Poisson, negative binomial, Cox regressions, etc.) all represent supervised ML methods, as they utilize labeled training data to build models that predict a specific outcome. The benefit of GLMs is that they are highly interpretable and have a single best-fit solution, allowing a model to be built that utilizes all data without necessarily needing resampling-based hyperparameter optimization. Nevertheless, there are many other decisions that need to be made – picking a generalized linear model distribution, transforming non-linear variables, or adding interaction terms. A major advantage of GLMs is their interpretability. The importance of each variable is directly proportional to its weight in the model.

A common strategy in radiation biomarker development is to use GLMs for feature selection, such as evaluating the correlation between gene expression and SF2^12,22,33. Yard et al. performed the largest such analysis to date, where they radiated 533 cell lines from the Cancer Cell Line Encyclopedia (CCLE) and evaluated the correlation coefficients between gene expression and cell viability (in addition to evaluating DNA variant and copy number changes)³⁴. Eschrich et al. used an approach whereby many multivariate linear models were trained to identify the genes for their radiation sensitivity index (RSI)⁷, representing one model for each expressed gene. Included in each model was the value of the expressed gene, p53 and RAS mutation status, and tissue of origin which were trained on cell lines to predict SF2. The 500 gene-models with the lowest error in this procedure was used to identify 10 genes based on gene hub identity, which was then used to train a multivariate linear model that predicts radiosensitivity.

Regularized Models

As introduced above, regularization is a procedure where a bias term is added to a GLM to prevent over-fitting and reduce the model’s reliance on less important variables. Regularization is used in both Ridge and the least absolute shrinkage and selection operator (LASSO) regression methods³⁵. In a linear model, each feature is multiplied by a weight, which are then added to a y-axis intercept to produce a prediction. With regularization, a bias (penalization) term is added to this linear model (weight squared for Ridge and the absolute value of the weight for LASSO) to make the model less flexible and thus less prone to overfitting. These penalization values are then scaled by the regularization hyperparameter λ (ranging from 0 to 1) and added to the linear model. The benefit of LASSO is that it can penalize the weights of features to zero, removing less important variables from the model, representing a type of within-model feature selection. Elastic Net regression³⁶ is a hybrid approach that adds a second hyperparameter scaling the amount of each type of regularization bias (Ridge or LASSO).

Zhao et al. utilized the strategy of regularization in the development of the Post-Operative Radiation Therapy Outcomes Score (PORTOS)¹³. PORTOS performed feature selection through utilization of previously defined gene sets that were then filtered based on the genes that had interaction effects with radiation in Cox models for predicting metastasis in post-operative prostate cancer patients. This filtered down gene list was then used to build two separate ridge penalized Cox models (radiation and no radiation), trained to predict metastasis, with the final PORTOS score representing the difference between the radiation and no radiation model predictions.

Decision Based Models

A limitation of the GLM framework is that these models do not incorporate non-linear effects or interaction terms, and while such features can be directly added to the model, that requires creation of a new variable (feature engineering - such as squaring the expression of one gene or multiplying the expression of two genes together). Decision-based models are desirable as they can account for these effects and thus no added feature engineering steps are required. The most used decision-based models in radiation biomarker development are tree-based models and top scoring pair (TSP) classifiers.

Central to the idea of tree-based methods is recursive partitioning³⁷, where the best possible split of the data is identified. For example, if trying to find how to best separate radiation sensitive and resistant cells based on the expression of 5 genes, a recursive partitioning strategy would evaluate each gene and find the split that has the best classification performance. The same would hold for a regression problem where the split creates groups of samples where the mean of those new groups produces the lowest error. The tree-based model can then repeat these splits, creating multiple “branches”, until you have a tree that has separated samples at a level sufficient to produce good predictions. Unfortunately, while individual tree models are advantageous for their highly interpretable structure, overfitting is a perennial problem.

Tree-based methods can have considerable improvement in predictive performance with a method called ensemble learning, where the combined predictions of many tree models are aggregated into a “forest”. This can be done by producing N trees through the bootstrapped resampling technique, and getting the prediction based on the call with the highest number of votes (classification) or the average for continuous predictions (regression). Unfortunately, another issue can arise, where there may be such a strong signal from one gene that almost every tree has the same first split, resulting in correlated trees. The random forest algorithm³⁸ solves this problem by allowing for random sampling of the features that get used in each tree, thus decorrelating the trees.

Another strategy that has been very successful is to use an ensemble of “weak” models. With respect to tree-based methods, such a strategy will create trees with fewer splits, creating a weak model that explains just part of the data. That model is used to get a first round of predictions and a resulting error for those predictions. Rather than creating a completely independent tree for the next step, like was done with the previously described models, the next tree is created to reduce that error as much as possible through a gradient descent algorithm (a gradient boosted tree). A popular iteration of this is extreme gradient boosting (XGBoost)³⁹. A non-tree, decision-based algorithm that also functions by aggregating “weak” models is the k-Top Scoring Pairs (TSP) classifier. TSP methods are based on pairwise comparisons of feature values⁴⁰, with a commonly used iteration being k-TSP that creates ensembles of top scoring, non-overlapping feature pairs to create model decision rules (e.g. expression of gene A is higher than gene B), a method that has shown similar efficacy to many other machine learning based methods in evaluating gene expression profiles⁴¹. The k-TSP method is similar to the ensemble methods used in gradient boosting decision trees where each new tree works to reduce the error. The difference is that each rule involves a comparison of two features that were not present in any prior model. An advantage of TSP methods is that they are based on relative values of features within one observation, and not absolute values, making them better suited to generalize across different assay platforms. A trade-off of the more complex forest-based approaches is the reduction in interpretability of the model.

A range of decision-based methods have been used in the development of radiation biomarkers. Speers et al. utilized a random forest model trained on breast cancer cell lines to predict SF2¹². Lewis et al. utilized the XGBoost algorithm to integrate multiple data types into a model to predict radiation response, which combined genomic, transcriptomic, kinetic, and thermodynamic parameters into a flux balance analysis (FBA) model⁴². Luxton et al. also used XGBoost, trained on telomere length from blood samples, before and after receiving 4 Gy, and used that to predict telomere length post radiation⁴³. Weichselbaum et al. utilized a k-TSP model trained on cell lines to predict radioresistant and radiosensitive clusters²⁰, while Sjöström et al. utilized k-TSP trained on breast cancer samples to predict in breast tumor recurrence after lumpectomy with/without radiation therapy⁹.

Beyond Classical ML Techniques: Deep Learning

Deep learning (DL) represents a subset of ML methodologies that rely on multi-layered neural networks. Neural networks have existed for many decades, but recent advances in GPU-based processing have made these computationally expensive models feasible. The advantage of DL compared to other ML methods is its ability to model non-linear and interaction effects, perform higher order feature engineering, and produce excellent performance, especially on image analysis tasks. An example of this higher order feature engineering is in convolutional neural networks trained on large image databases, where an inner layer of the neural network may represent a square or circle feature. Prior to deep learning techniques, feature engineering had to be performed to include such features in a model, such as the use of radiomics in medical imaging prediction⁴⁴, where higher-order features are extracted from images with mathematical formulae and then used in machine learning models. This type of feature engineering is similar to an unsupervised learning approach, as these intermediate radiomic features are created with no knowledge of the outcome of interest. DL allows for bypassing this step through creation of higher order features within the network that are optimized to the outcome of interest.

Deep learning is most advantageous in settings with very large training datasets, and thus has not been as popular for radiation signature development. Transfer learning is a strategy in deep learning that allows smaller datasets to build a model utilizing features from a previously trained model, which has been beneficial in radiology based deep learning models⁴⁵, where models trained on large databases of non-radiologic images can be utilized to improve model prediction on radiologic images, and could be one way of overcoming limited sample sizes for radiation signatures. Neural networks can also be utilized in unsupervised learning tasks, as was used in the radiosensitivity signature developed by Chen et al., which utilized a neural network autoencoder for feature selection⁴⁶. Finally, digital pathology-based DL represents an emerging technique for biomarker development⁴⁷, that may be applicable for radiation biomarker development.

SUMMARY, CURRENT CHALLENGES, AND EMERGING TRENDS

The machine learning methodologies described herein provide a broad range of strategies for developing radiation tumor biomarkers, but there are some consistently used approaches across the literature. Most studies start with feature selection to determine what features to use in the biomarker, which can be done by utilizing previously curated lists of known biology, e.g. genes involved in pathways that are known to be involved in radiation response^20,48, differential expression analysis^29,30,32, correlative analysis^8,22,34,49, or through feature selection as part of a modeling approach^7,9,42,46,50. Next, a method is used to stratify patients, either through an unsupervised clustering approach^19,22, a supervised model-based approach^{7–9,12,13,33}, or with a combination of both²⁰. Finally, independent clinical validation is the most critical step in the development of radiation biomarkers. Good validation datasets should include clinical samples with clearly defined outcomes, be independent (i.e. not used, and preferably from a different dataset altogether to asses generalizability) from the training set, and ideally should include patients that did and didn’t receive radiation or patients that had different doses. This last feature is critical as it distinguishes a treatment-predictive biomarker, such as identifying a benefit of radiation in those classified as radiosensitive and no benefit in those classified as radioresistant, from prognostic biomarkers. In Table 1 we provide examples of tumor biomarkers that were developed with an explicit goal of modeling radiation sensitivity or benefit (in contrast to many of the currently on the market genomic biomarkers), focusing on those that have independent clinical validation. We also identify markers that have been statistically assessed as predictive biomarkers, defined via an interaction term between radiation treatment/dose and the biomarker, and adjustment for treatment selection bias.

Table 1 –

Examples of Radiation Biomarkers with Independent Validation.

Signature	Feature selection	ML method	Training	Validation	Validation outcome	Prognostic	Predictive (pint reported)	Treatment selection bias corrected (if pint)
Weichselbaum 2008 - IRDS20	Correlation	Clustering, k-TSP	Breast Cancer Patients	Breast Cancer	LRC	X
Piening 200919	Differential Expression	Hierarchical Clustering	Cell Lines	Breast Cancer Patient Survival	OS	X
Eschrich 2012 - RSI10	Linear Regression	Linear Regression	Cell Lines	Breast Cancer Recurrence Free Survival	RFS	X	X	None
Speers 2015 - RSS12	Correlation	Random Forest	Cell Lines	Breast Cancer Patient LRR and Survival	LRR and OS	X
Zhao 2016 - PORTOS13	Interaction Terms	Ridge Regression	Post-operative Prostate Cancer Patients	Post-operative Prostate Cancer Patients	DM	X	X	Matching
Sjöström2018 - SSP9	Random Forest	k-TSP	Breast Cancer Patients	Breast Cancer	IBTR	X	X	None
Cui 2018 - RSS and IMS51	Cox Regression	Ridge and LASSO Regression	Breast Cancer Patients	Breast Cancer	DSS	X	X	Matching
Sjöström2019 - ARTIC50	Cox Regression	Ridge Regression	Breast Cancer Patients	Breast Cancer	LRR	X	X	RCT
Zhao 2019 - RT-GS and ChemoRT-GS8	Correlation	Average	Glioblastoma PDXs	Glioblastoma	OS	X	X	MVA
Chen 202046	Neural Network Autoencoder	LASSO Regression	Breast Cancer Patients	Breast Cancer	OS	X
Speers 202052	Correlation	Elastic Net Regression	Breast Cancer Patients	Breast Cancer	Early vs Late Recurrence	X
Scott 2021 - GARD15	See RSI	Scaled RSI	Cell Lines	Pan-Cancer	Time to first recurrence and OS	X	X	None

Abbreviations: ML – Machine Learning, IRDS – Interferon-related DNA damage resistance signature, RSI – Radiosensitivity index, RSS – Radiation Sensitivity signature, PORTOS – Post-operative radiation therapy outcome score, SSP – Single sample predictor, IMS – Immune signature, ARTIC – Adjuvant Radiotherapy Intensification Classifier, RT-GS – Radiotherapy Gene Signature, GARD – Genome-based model for adjusting radiotherapy dose, MVA – Multivariate analysis, TSP – Top scoring pairs, LASSO - Least absolute shrinkage and selection operator, PDX – Patient-derived xenograft, LRC – Locoregional control, OS – Overall survival, RFS – Recurrence free survival, LRR – Locoregional recurrence, DM – Distant metastasis, IBTR – Ipsilateral breast tumor recurrence, DSS – Disease specific survival, p_int – interaction p-value between receipt of radiotherapy and the signature, RCT – Randomized Control Trial.

While many radiation tumor biomarkers have been developed, none are currently used in the clinic. Surprisingly, there is little overlap in many of the genes used in these signatures⁶, despite many being trained on the same data and/or outcomes. A major challenge is the availability of high-quality datasets. A common strategy has been to train models on cell lines^7,12,19, but these models inherently lack features from the tumor microenvironment, host immune system, and vasculature. Patient-derived xenografts may provide an opportunity to better replicate the host environment, a strategy used by Zhao et al. in development of their glioblastoma radiation and chemo-radiation gene signatures⁸, but xenograft development and radiation experimentation is more resource intensive than cell line based experimentation. Collaboration with veterinary colleagues using companion species with de novo tumors treated with radiation is another potential model system, though these genomes are not identical to humans. Clinical datasets are preferred, but typically have other limitations, such as the lack of robust annotation of radiation-related clinical endpoints such as locoregional recurrence, or a limited number of patients. Non-randomized data should account for clinicopathologic variables potentially leading to treatment selection bias (e.g. with matching, propensity adjustment, multi-variate analysis, etc.). Large, randomized trials represent the ideal training and validation datasets, but availability of molecular data is a challenge. Improvements in data sharing and availability, and integration of biomarker development into clinical trials are critical in advancing the development of radiation tumor biomarkers that will be able to provide clinical utility in radiation oncology decision making.