Cascading Affine and B-spline Registration Method for Large Deformation Registration of Lung X-rays

Abstract

Accurate registration of lung X-rays is an important task in medical image analysis. However, the conventional methods usually cost a lot in running time, and the existing deep learning methods are hard to deal with the large deformation caused by respiratory and cardiac motion. In this paper, we attempt to use deep learning methods to deal with large deformation and enable it to achieve the accuracy of conventional methods. We proposed the cascading affine and B-spline network (CABN), which consists of convolutional cross-stitch affine block (CCAB) and B-splines U-net-like block (BUB) for large lung motion. CCAB makes use of the convolutional cross-stitch model to learn global features among images. And BUB adopts the idea of cubic B-splines which is suitable for large deformation. We separately demonstrated CCAB, BUB, and CABN on two chest X-ray datasets. The experimental results indicate that our methods are highly competitive both in accuracy and runtime when compared to both other deep learning methods and iterative conventional approaches. Moreover, CCAB also can be used for the preprocessing of non-rigid registration methods, replacing affine in conventional methods.

Introduction

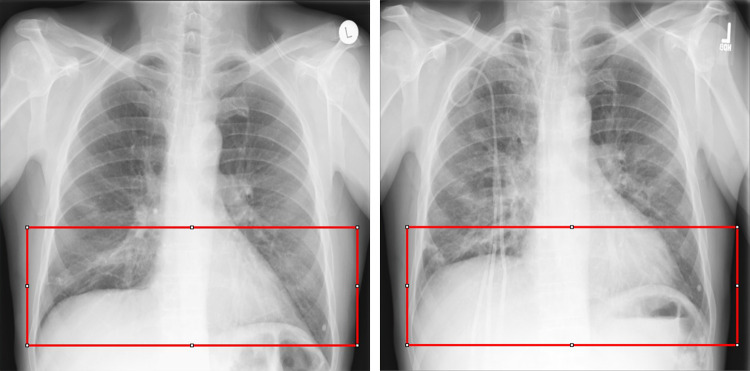
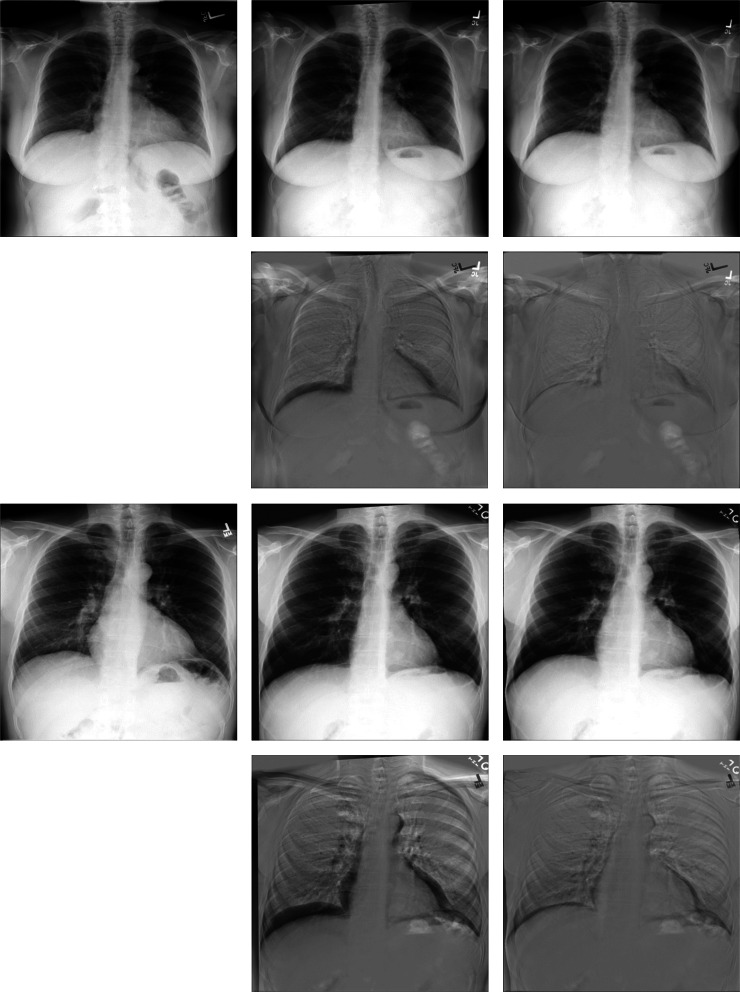
Image registration is the process of aligning two different images with a transformation model. It is one of the most basic tasks in the field of medical image processing which has important applications in a variety of medical image analysis, including diagnostic tasks, radiotherapy, segmentation, and image-guided surgery [1, 2]. In clinical diagnosis, doctors have different needs for variant diseases, and it leads to the increasing diversity of images after registration. As for lung X-ray images, they can clearly record the general lesions of the lung, e.g., lung inflammation, mass, and tuberculosis. Reading lung X-ray images requires high-level knowledge of doctors, and years of experience, and needs more time for analysis. The registration of lung images can be used as preprocessing to help subsequent segmentation tasks, thus helping doctors diagnose patients’ conditions better and faster in clinical practice. Nevertheless, there are various factors that affect radiography, including the difference in the position of the instruments, the deviation of the patient’s position to varying degrees, and the influence of the patient’s internal organ movement such as breathing motion and heart beating. The chest X-rays obtained from the same patient in different periods have large and complex non-rigid deformation [3], as shown in Fig. 1. It will affect the judgment of doctors, resulting in misdiagnosis and missed diagnosis. Therefore, the registration of chest X-rays is a significant task. Applying lung registration to follow-up inspection and motion estimation in treatment planning will go a long way to improving the treatment of patients and speedups in clinical workflows [4, 5].

Fig. 1.

Large deformation in chest X-rays taken by the same patient at different periods

Since the breakthrough of AlexNet [6] in the ImageNet challenge of 2012, deep learning has been applied in many computer vision tasks including image registration. Recently, many researchers proposed unsupervised deep learning–based image registration methods [7–10]. These approaches have demonstrated accuracy and running time in a variety of registration tasks. However, when it comes to chest image registration with large deformation, they may not be suitable for two reasons [11]. First, the gradient of the similarity metric at the finest resolution is rough in general, as many possible transformations of the moving image could yield similar measurements of similarity. Second, the optimization problem is hard to solve without the initialized transformation at the finest resolution because of the large degrees of freedom in the transformation parameters. Therefore, conventional iterative optimization algorithms based on machine learning are still a common method in chest X-ray registration because of their good effect on dealing with large deformation. These conventional algorithms [12–15] are optimized iteratively according to the extracted features. But these approaches also have a common problem, which is their high cost of running time.

To solve these problems, De Vos et al. [16] divided the whole registration task into direct affine and deformable image registrations, which are optimized separately. They also proposed a deep learning image registration (DLIR) network by stacking multiple convolutional neural networks (CNN). Hu et al. [17]. introduced a network architecture that consists of GlobalNet and LocalNet, effectively learning global and local interventional deformation. RCN [18] also utilizes an end-to-end recursive cascaded network to divide large deformations into small ones and optimize them step by step. The idea of recursive networks has also been applied to chest X-ray image registration. Recursive refine network (RRN) [19] applies a recursive network on chest CT registration. For the large deformation of the lung, they have performed several multi-scale refinements to achieve coarse-to-fine registration. Hering et al. [3] also employed a Gaussian pyramid–based multilevel framework that can solve the lung CT registration optimization in a coarse-to-fine fashion.

When it comes to selecting the spatial transform model, Murphy et al. [4] have proved that free form deformation (FFD) and demons perform better in chest registration than other algorithms. However, the demons algorithm is not suitable for large deformation. FFD model was originally used in the computer graphics community. After combing with cubic B-splines [20], it has been widely used in the field of medical image registration [21–23]. Therefore, we decided to adopt the idea of FFD in our network to deal with large deformation.

In this paper, we propose a network that employs the convolutional cross-stitch affine block (CCAB) for rigid registration and the B-splines U-net-like block (BUB) for nonlinear registration. In our method, we propose the convolutional cross-stitch module (CCM) in our network to combine the information of fixed and moving images. Meanwhile, in the BUB, we use the cubic B-spline method, which is more suitable for large deformation than dense deformation fields.

Methods

Overview

Let F and M present the fixed images and moving images respectively. Medical image registration aims to find a spatial transformation ϕ that aligns a fixed image I_F and a moving image I_M, which is also called the deformation field. In our deep learning method, we use CNN to train it as the function:

$$g_{\theta }\left(I_F,,,I_M\right)=\varphi ,$$ 1

where θ are the parameters of g. Our method warps moving images I_M to warped image I_M(ϕ) and evaluates the loss function L between I_F and I_M(ϕ) to update θ. So, the optimization problem can be written as:

$$\theta =\underset{\theta }{argmin}\left\{L,\left(I_F,,,I_M,,,\varphi \right)\right\},$$ 2

where

$$L\left(I_F,,,I_M,,,\varphi \right)=L_{\mathit{sim}}\left(I_F,,,I_{M\left(\varphi \right)}\right)+\lambda L_{\text{smooth}}\left(\varphi \right),$$ 3

function L_sim(∙, ∙) is the image similarity measure, and L_smooth(∙) is an optional regularization term to encourage the smoothness of ϕ to ensure the topology of I_M.

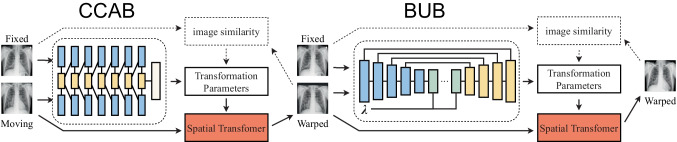
To achieve the aim of large deformation registration of lung X-ray, we divided our network into two parts, CCAB and BUB, as shown in the dashed box in Fig. 2. The pair of the fixed images and moving images are input into CCAB together. The warped images which are the output of CCAB are paired with the same fixed images and then input into the BUB together.

Fig. 2.

Cascading affine and B-splines network

Cross-stitch Convolutional Affine Block

Affine transformation is commonly used as a rigid registration method to calibrate deformation caused by different photographing positions. Affine transformation is a combination of a series of linear transformations which can maintain the parallelism of lines on the image. Using affine registration at the beginning can help simplify the subsequent optimization steps and improve the overall registration accuracy. So, it is often the first step in image registration.

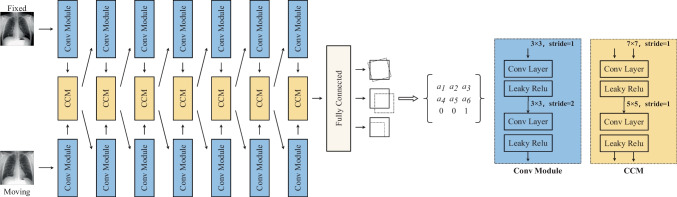
To extract the global information better, we introduced the cross-stitch module to improve affine registration. Cross-stitch module helps to enable two different independent networks to learn knowledge from each other. Coincidentally, the affine network used in DLIR is a parallel dual-channel structure. Therefore, the cross-stitch units can be used in an affine network to improve affine accuracy which was realized in cross-stitches affine network [24] (CAN). In CAN, the pair of input feature images are flattened and then concatenated to form a matrix. After that, this matrix will be multiplied by another parameter-learnable square matrix and re-split into a flattened form of the pair of two feature images. Nevertheless, when we tried to reproduce their experiment on our datasets, it is hard to be applied to affine registration of two high-resolution images which is commonly used in medicine, because the parameter-learnable square matrix in CAN will occupy a lot of computing resources. For example, if the shape of both feature images is 512 × 512, then the shape of this image will be 524,288 × 524,288 (512 × 512 × 2). Therefore, we replace the matrix multiplication operation with convolutional operation of several different kernel sizes, which not only retains the ability to learn the optimal combination of the feature maps obtained from the previous layer but also can effectively reduce computing costs and be applied to most size images. We refer to it as a convolutional cross-stitched module (CCM), and it is combined with our CCAB.

Despite affine transformation having been applied in many registration networks based on deep learning, most of them only regress the affine transformation matrix A and do not calculate the transformation parameters, including rotation, two translations, two scaling, and two shearing transformation parameters. For example, there are seven parameters with spatial meanings for 2D transformation including one for rotation (θ), two for translations (t_x, t_y), two for scaling (sc_x, sc_y), and two for shearing (sh_x, sh_y). The 2D affine transformation matrix is:

$$A=\left[\begin{array}{ccc}{a}_1& a_2& a_3\\ a_4& a_5& a_6\\ 0& 0& 1\end{array}\right],$$ 4

where a₁–a₆ are the six parameters used for interpolation. And the translation matrix M_t, the scaling matrix M_sc, the shearing matrix M_sh, and the rotation matrix M_r can be represented as:

$$\begin{array}{cc}\hfill M_t=& \left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right],M_r=\left[\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right],\hfill \\ \hfill & M_{\mathit{sc}}=\left[\begin{array}{ccc}{\mathit{sc}}_x& 0& 0\\ 0& {\mathit{sc}}_y& 0\\ 0& 0& 1\end{array}\right],M_{\mathit{sh}}=\left[\begin{array}{ccc}1& {\mathit{sh}}_x& 0\\ {\mathit{sh}}_y& 1& 0\\ 0& 0& 1\end{array}\right].\hfill \end{array}$$ 5

Thus, from these seven spatial parameters, the six parameters in 2D transformation matrix A can be easily calculated by:

$$A=M_t·M_{\mathit{sc}}·M_{\mathit{sh}}·M_r=\left[\begin{array}{ccc}{\mathit{sc}}_{x}cos\theta +{\mathit{sh}}_x{\mathit{sc}}_{x}sin\theta & -{\mathit{sc}}_{x}sin\theta +{\mathit{sh}}_x{\mathit{sc}}_{x}cos\theta & t_x\\ {\mathit{sh}}_y{\mathit{sc}}_{y}cos\theta +{\mathit{sc}}_{y}sin\theta & -{\mathit{sh}}_y{\mathit{sc}}_{y}sin\theta +{\mathit{sc}}_{y}cos\theta & t_y\\ 0& 0& 1\end{array}\right].$$ 6

After affine registration, the pixels whose coordinates are (x, y) on the moving images will become (x’, y’) on the warped images by the formula:

$$\left[\begin{array}{c}{x}^{,}\\ y^{,}\\ 1\end{array}\right]=A\left[\begin{array}{c}x\\ y\\ 1\end{array}\right].$$ 7

Considering that our task is to complete the large deformation registration of the lung, which is mainly caused by the contraction and expansion of the lung and the shift of the shooting position, therefore, we choose to remove the shearing transformation from the affine transformation, which can reduce the calculation cost and make the network converge faster.

In our CCAB, as shown in Fig. 3, the fixed image I_F and the moving image I_M are fed into two separate convolutional modules. The two convolutional layers and two activation layers in convolutional modules (Conv Module) can extract the feature maps and down-sample them for the enhancement of the receptive field. After that, the two feature maps of I_F and I_M are concatenated and put into the CCM to enable the relevant information between the two images that can be learned effectively. The CCM used in our network consists of a 7 × 7 convolution kernel and a 5 × 5 convolution kernel. The two different kernel sizes can extract features of multiple scales. With the down sampling operation in the network, the receptive field of CCM gradually increases, which contributes to capture the features of a larger size. The output feature map of the last CCM will go through the fully connected layer and turn into the spatial parameters. According to Eq. (6), these six parameters in matrix A can be calculated to warp I_M.

Fig. 3.

Convolutional cross-stitches affine block

B-splines U-Net-Like Block

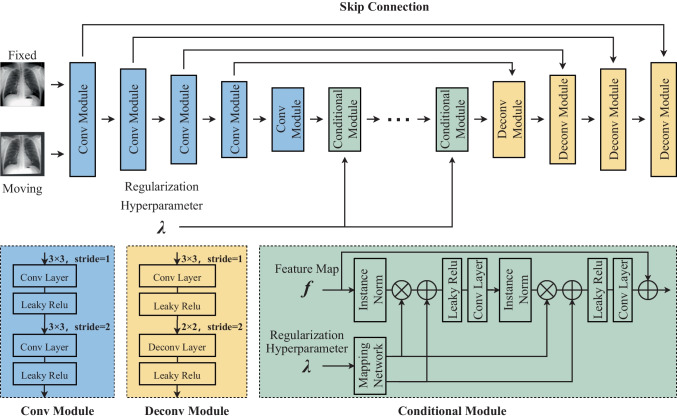
Many deformable models can deal with local deformation. However, we prefer to use cubic B-splines because different from dense deformation field such as VoxelMorph, cubic B-splines deform an object by manipulating an underlying mesh of control points. The basic idea of cubic B-splines is to deform an object by manipulating an underlying mesh of control points. According to the different intervals between control points, B-splines can realize the registration of deformation in different ranges. The resulting deformation controls the shape of the object and produces a smooth and continuous transformation. The main target of BUB is to learn the offsets of each control point through the designed U-net-like network sketched in Fig. 4. Therefore, BUB is designed to output the offset of each control point in the x and y directions. In the following, it will be introduced how to realize the nonlinear deformation of the whole image through the offset of each control point.

Fig. 4.

B-splines U-net-like block

In addition, searching for regularization parameters in the registration network is often a time-consuming and difficult task. To solve this problem, we introduced the conditional module proposed by Mok and Chung [25]. This module can learn the conditional features that are correlated with the regularization hyperparameter by shifting the feature statics. It enables the network to learn the features in different cases of regularization parameter. This will help to find the optimal regularization parameter without tedious multiple training and grid searching.

Firstly, a certain amount of control points with the intervals d as a hyperparameter need to be set on the image. A large interval of control points allows modeling of global non-rigid deformation, while a small interval of control points allows modeling of highly local non-rigid deformation. And the resolution of the control point mesh determines the number of degrees of freedom and the computational complexity. Referring to the paper [22], we use 16 control points in 4 rows and 4 columns to control the offset of a pixel. Then, the offsets of these control points are optimized through the back-propagation of the network. In our algorithm, the rows R_cp and columns C_cp of the control points are calculated from:

$$R_{\mathit{cp}}=\mathit{ceil}\left(R,/,d\right)+3,C_{\mathit{cp}}=\mathit{ceil}\left(C,/,d\right)+3,$$ 8

where R and C are the rows and cols of pixels on the image, and ceil(∙) denotes rounding-up operation. It is important to note that there will be several control points outside the image to ensure that every pixel on the image is controlled by 16 control points. Therefore, R_cp and C_cp ought to be added 3. In order to obtain the registration field, it is ought to calculate the offsets of each pixel on the image. For each pixel with coordinate (x, y), the offset (∆x, ∆y) can be calculated from:

$$\left(\mathrm{\Delta },x,,,\mathrm{\Delta },y\right)=\sum _{l=0}^3\sum _{m=0}^3{B}_l\left(u\right)·B_m\left(v\right)·{\phi }_{i+l,j+m},$$ 9

where i and j are calculated from:

$$i=\mathit{floor}\left(x,/,d\right),j=\mathit{floor}\left(y,/,d\right),$$ 10

where floor(∙) denotes the rounding-down operation.

In addition, in Eq. (9), φ_i+l,j+m is the offset of the control points dominating the offset of pixels, and B_k(t) is the B-spline interpolation formula:

$$B_k\left(t\right)=\left\{\begin{array}{c}\left(-,t^3,+,3,t^2,-,3,t,+,1\right)/6\\ \left(3,t^3,-,6,t^2,+,4\right)/6\\ \left(-,3,t^3,+,3,t^2,+,3,t,+,1\right)/6\\ \left(t^3\right)/6\end{array},\begin{array}{c},k=0\\ ,k=1\\ ,k=2\\ ,k=3\end{array}\right).$$ 11

As shown in Fig. 4, the fixed image and the moving image are first concatenated and put into the U-net-like network. The convolutional module (Conv Module) includes two convolutional layers and two activation layers, while the deconvolutional module (Deconv Module) consists of one convolutional layer, one deconvolutional layer, and two activation layers. These convolutional layers inside assist in extracting feature maps; at the same time, the convolutional layer and deconvolutional layer can realize up sampling and down sampling of feature map respectively. At the bottleneck layer of the network, we use 5 conditional modules to help to search for the optimal regularization hyperparameter λ. The conditional module is designed as a residual structure. At the end of the network, there is a convolutional layer that converts the output into the offsets of the control points with the size of R × C × 2, where R and C represent the number of rows and columns of the control points, respectively.

Loss Function

In many deformable image registration methods [7, 11, 18, 26], negative local normalized cross-correlation (NCC) is successfully utilized to be a similarity metric for gradient descent optimization. NCC is a statistic of corresponding correlation, obtained by calculating the correlation of the pixels between two images [27]. Therefore, we use NCC as the similarity measure L_sim to evaluate the results of registration in our experiments. Let f and m(ϕ) denote the pixel in fixed images and warped images, and Ω is the image domain. The formula of NCC is:

$$L_{\mathit{sim}}\left(f,,,m,,,\varphi \right)=-NCC\left(f,,,m,,,\varphi \right)=-\frac{\frac{1}{\mathrm{\Omega }}\sum \left(f,-,\widehat{f}\right)\left(m,\left(\varphi \right),-,\widehat{m},\left(\varphi \right)\right)}{\sqrt{\frac{1}{\mathrm{\Omega }}\sum {\left(f,-,\widehat{f}\right)}^2}\sqrt{\frac{1}{\mathrm{\Omega }}\sum {\left(m,\left(\varphi \right),-,\widehat{m},\left(\varphi \right)\right)}^2}}.$$ 12

Furthermore, in non-rigid registration, minimizing L_sim will encourage m(ϕ) to approximate f, but may generate a discontinuous displacement vector field ϕ. To solve this problem, we introduced the L2 gradient loss proposed by Rueckert et al. [20] as a regular term L_smooth to encourage a smooth displacement vector field:

$$L_{\mathit{smooth}}\left(\varphi \right)=\sum {\Vert \mathrm{\nabla }\varphi \left(p\right)\Vert }^2.$$ 13

We approximate spatial gradients using differences between neighboring pixels. The complete loss of our method is defined as:

$$L\left(I_F,,,I_M,,,\varphi \right)=L_{\mathit{sim}}\left(I_F,,,I_{M\left(\varphi \right)}\right)+\lambda L_{\mathit{smooth}}\left(\varphi \right).$$ 14

Considering our network consists of rigid registration CCAB and non-rigid registration BUB, the value of the regularization parameter λ is 0 in CCAB. And the selection of λ in BUB will be discussed in the following experiments.

Results

Implement Details

To evaluate the registration performance of the proposed method, we conduct our experiments on two datasets. One was from a hospital in Shandong province, containing 39 X-ray images taken from 12 patients at different time. The resolution of chest X-ray images is about 3000 × 3000 pixels. Here we refer it as Test12 dataset. The other is a public dataset ChestX-ray8 [28] extracted from the clinical PACS database at the National Institutes of Health Clinical Center, which contains 112,120 frontal-view chest X-ray PNG images with 14 disease labels from 30 K patients [29]. This dataset is for disease detection on chest X-rays, so some patients only have a single visit record, which is not suitable for medical image registration tasks. Therefore, we screened the dataset to fit the condition that all enrolled patients must have at least two medical records. After that, we obtained a total of 823 eligible pairs of chest X-rays from 280 patients. Since the size of each chest X-ray is different, the filtered images have been uniformly resampled to 512 × 512 in the preprocessing. The difference between them is that Test12 is the dataset without lung lesions, and ChestX-ray8 is the dataset with lung lesions. In the experiment of CCAB, we use affine based on the traditional registration toolbox Elastix and ANTs to compare with the proposed method to illustrate the registration performance. In addition, because of the similar model structure, the deep learning method DLIR and GlobalNet [17] are also compared with our method. While in the experiment of BUB, two state-of-art conventional registration methods, SyN [30] and FFD [31, 32], based on B-splines are compared with the proposed method to illustrate the registration performance. Besides, RCN [18] and RNN [19] are also chosen because of their ability to deal with large deformation. In order to evaluate the registration performance, the visualization of warped images and subtraction of fixed images and moving images are used in our paper. Note that the gray value of all the input in deep learning networks was normalized into 0–1 in preprocessing, and the output gray value will be restored to the original range. Besides, in CCAB, there is a limited range of the obtained spatial parameters. So that according to the prior knowledge, we will normalize each spatial parameter to its specific range. This part is added after the full connection layer.

As for the parameters of the baseline methods, we run SyN, affine in ANTs and FFD, and affine in Elastix with the parameters recommended in VTN [33]. The parameters of both RCN and RRN are set according to their papers. The number of RCN cascades is set to 10. NCC is selected as the loss function in all deep learning methods. For better comparison, the parameter settings of affine methods in GlobalNet and DLIR are consistent with those of CCAB, and the number of convolutional layers other than CCM is also consistent.

The evaluation metrics in our experiment include mean square error (MSE), mutual information (MI), and dice. For the parameter setting of the registration network, the batch size was 2 due to the limitation of GPU memory, the learning rate was 0.0001, and the training epoch was 5000. Our code was developed using Pytorch 1.9.0. It was run on a Windows server and a Ubuntu server with a GPU NVIDIA RTX 2060 Super and a CPU Intel Core i5-10,500. We divided the whole dataset into training set, validation set, and test set, accounting for 70%, 15%, and 15% respectively. We used the training set to train the registration model. The model might be overfitting, so we utilized the validation set to choose the best model. The test set was used to test the registration model and obtain the registration results.

CCAB Registration Results

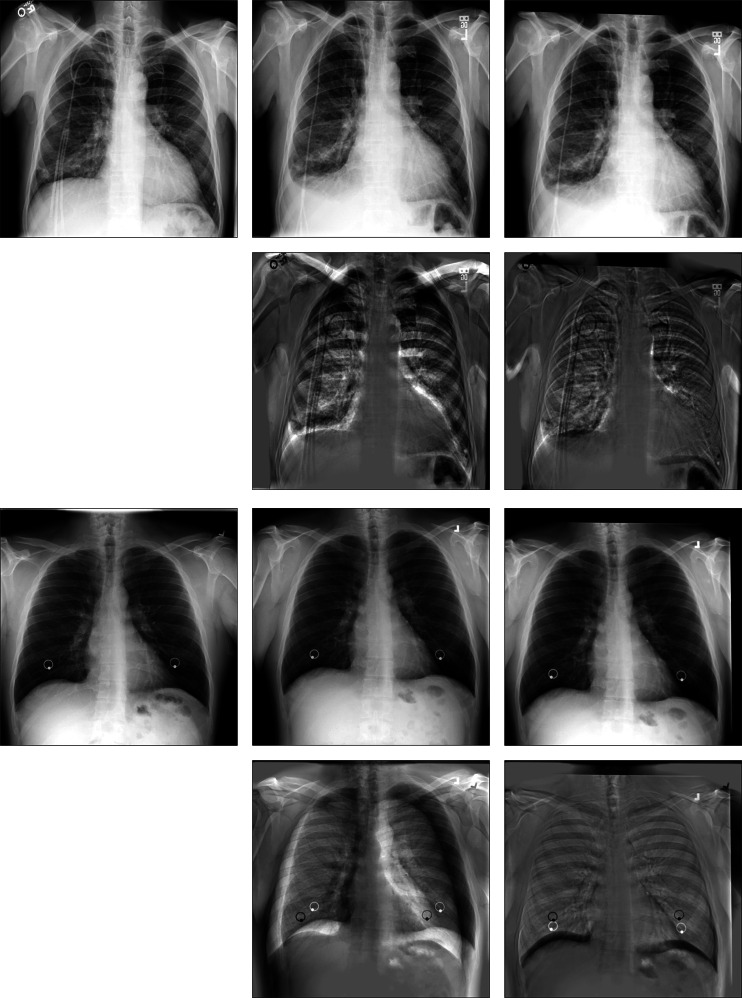
Figures 5 and 6 display the subtraction images including before registration and after registration. We can see that the gray value of our method’s result near the lung contour is more uniform. It means that CCAB can achieve better registration results. From Table 1, we can also see that the MSE, MI, and dice of our method are comparable to those of the conventional affine registration method in both ANTs and Elastix. Furthermore, it is also 23 times faster than the conventional affine registration method in CPU time and is 35 times faster when it comes to GPU time. In addition, we also compare our method with the deep learning method of similar models: GlobalNet and DLIR. The result shows that with the help of the cross-stitches convolutional module, our model can improve the registration results better which proves the effectiveness and necessity of the cross-stitches convolutional module. In the ChestX-ray8 dataset, the dice of the proposed network increases by 0.43%, compared to the second-best approaches. And in the Test12 dataset, the increment of dice is also 0.43%. The experimental result benefits from the CCM which can combine the information of different scales of two characteristic maps at each layer of the network. As the size of the feature maps decreases, the receptive field of CCM also gradually increases, which enables it to better capture the global information related to the two, helping to improve the accuracy of rigid registration. Figure 7 shows the results of CCAB for the data of two other patients.

Fig. 5.

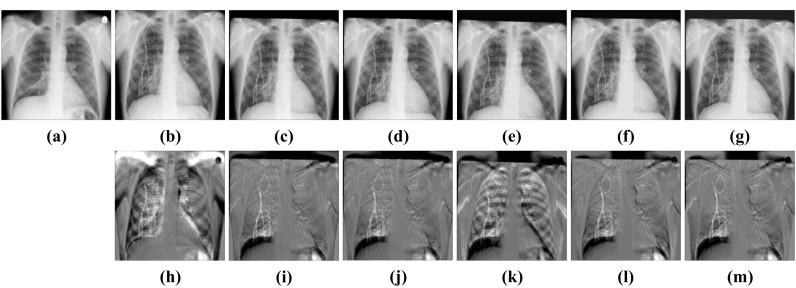
Visual rigid registration results of ChestX-ray8. a Fixed image. b Moving image. c Elastix-affine. d ANTs-affine. e DLIR. f GlobalNet. g CCAB. h Subtraction image before registration. Sub-images (i–m) correspond to the subtraction images of the above algorithm in turn

Fig. 6.

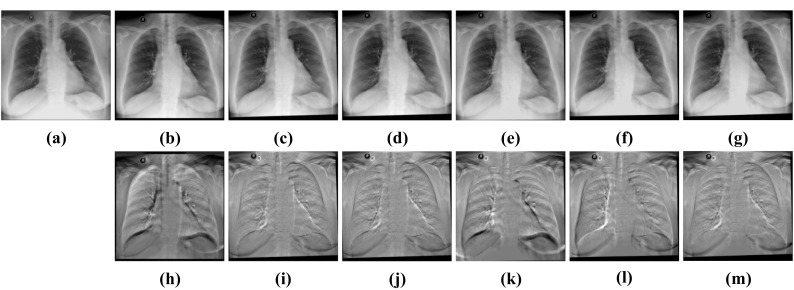
Visual rigid registration results of Test12. a FIXED image. b Moving image. c Elastix-affine. d ANTs-affine. e DLIR. f GlobalNet. g CCAB. h Subtraction image before registration. Sub-images (i–m) correspond to the subtraction images of the above algorithm in turn

Table 1.

Comparison of different rigid registration methods. Standard deviation is provided in the brackets. The best performances are shown in bold

Methods	ChestX-ray8
	MSE	MI	Dice	CPU time/s	GPU time/s
Before	0.048 (0.017)	0.719 (0.206)	0.833 (0.076)	-	-
Elastix-affine	0.029 (0.020)	1.020 (0.194)	0.921 (0.030)	0.767 (0.055)	-
ANTs-affine	0.032 (0.018)	1.038 (0.188)	0.922 (0.029)	0.622 (0.114)	-
DLIR	0.041 (0.034)	0.915 (0.172)	0.914 (0.054)	0.025 (0.003)	0.005 (0.002)
GlobalNet	0.035 (0.041)	1.005 (0.198)	0.920 (0.034)	0.022 (0.003)	0.004 (0.003)
CCAB	0.028 (0.015)	1.032 (0.204)	0.926 (0.028)	0.025 (0.002)	0.018 (0.002)
Methods	Test12
	MSE	MI	Dice	CPU time/s	GPU time/s
Before	0.048 (0.012)	0.916 (0.199)	0.876 (0.045)	-	-
Elastix-affine	0.036 (0.021)	1.187 (0.103)	0.923 (0.045)	0.805 (0.041)	-
ANTs-affine	0.038 (0.043)	1.235 (0.113)	0.924 (0.042)	0.627 (0.102)	-
DLIR	0.043 (0.024)	1.088 (0.130)	0.917 (0.029)	0.024 (0.002)	0.005 (0.003)
GlobalNet	0.041 (0.021)	1.162 (0.120)	0.921 (0.029)	0.020 (0.002)	0.004 (0.002)
CCAB	0.030 (0.020)	1.256 (0.119)	0.928 (0.032)	0.027 (0.003)	0.006 (0.002)

Fig. 7.

Visual rigid registration results of other two patients’ data. From left to right are respectively fixed images, moving images, and CCAB results. The images in the second line correspond to the subtraction images of the above images in turn

BUB Registration Results

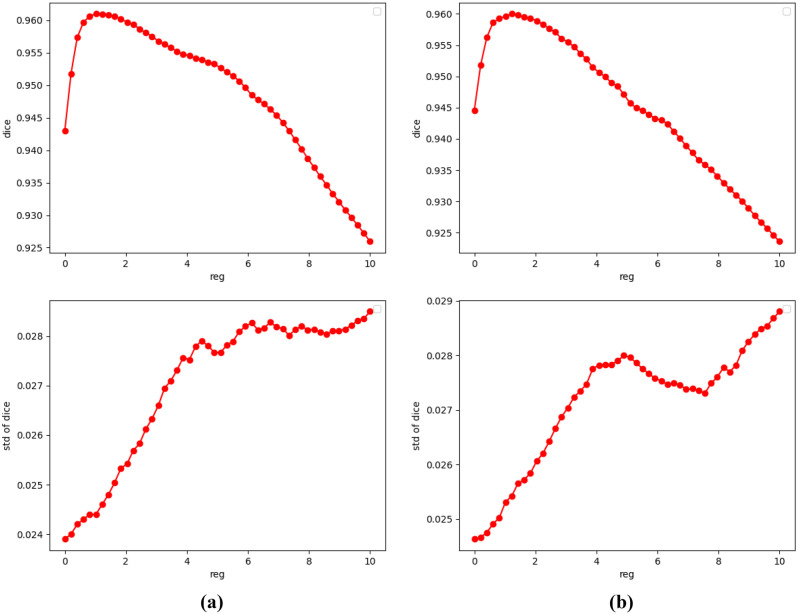
As shown in Figs. 5 and 6, there are still many lung deformations caused by respiratory movement to be aligned by deformable registration. For most deformable registration networks, it is time-consuming and difficult to analyze the influence of hyperparameters and search for the optimal regularization parameters. Therefore, we utilize the conditional module to assist in searching for the regularization parameters. As shown in Fig. 8, the abscissa of the curves is the different values of regularization parameters, and the ordinate is the average dice scores calculated from the warped images and the fixed images. The dice scores vary slowly in the range where λ is 1 to 2 on both datasets. So, we will choose λ = 1.5 in the following experiment.

Fig. 8.

Dice-regularization parameters curve of two datasets. a ChestX-ray8. b Test12. First row: mean value of dice scores. Second row: std of dice scores

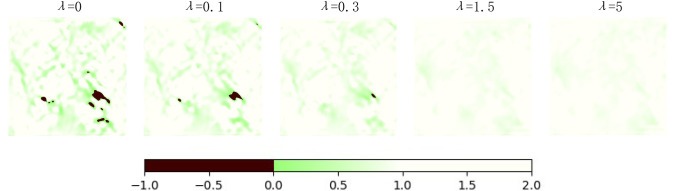
In addition, we also observed the Jacobian determinant of the deformation fields, as shown in Fig. 9. If the pixel color is close to green, it indicates that the deformation field here tends to shrink. The black part means that the deformation field in this region overlaps, which is detrimental to the maintenance of the topology. We can see that with the increment of λ, the overlap in the deformation field decreases gradually, which means the maintenance of the topology. Therefore, combined with the curve in Fig. 8, we take 1.5 as the value of λ in the experiments of BUB.

Fig. 9.

Jacobian determinant of the deformation fields

Besides, we also tested the influence of different intervals d of control points on both datasets. The results in Table 2 show that when d = 8, the dice score will achieve the best value. The reason is that the larger values of d will enable the cubic B-spline model to perform larger deformation registration; however, it may cause an inability to achieve fine registration. The smaller values of d will complete fine registration at the cost of large deformation registration. From Table 2, we can know that setting d to a value of 8 is an option that accommodates both fine registration and large deformation registration. In summary, we set the hyperparameters in the experiments of BUB as λ = 1.5 and d = 8.

Table 2.

Comparison of the results of different intervals d on both datasets. Standard deviation is provided in the brackets. The best performances are shown in bold

d	ChestX-ray8			Test12
	MSE	MI	Dice	MSE	MI	Dice
4	0.024 (0.018)	1.298 (0.213)	0.955 (0.018)	0.032 (0.035)	1.557 (0.142)	0.952 (0.041)
8	0.021 (0.020)	1.346 (0.204)	0.970 (0.023)	0.028 (0.037)	1.570 (0.138)	0.960 (0.054)
16	0.023 (0.018)	1.294 (0.205)	0.953 (0.016)	0.033 (0.033)	1.547 (0.136)	0.949 (0.050)
32	0.023 (0.019)	1.282 (0.205)	0.945 (0.020)	0.039 (0.031)	1.516 (0.126)	0.940 (0.042)

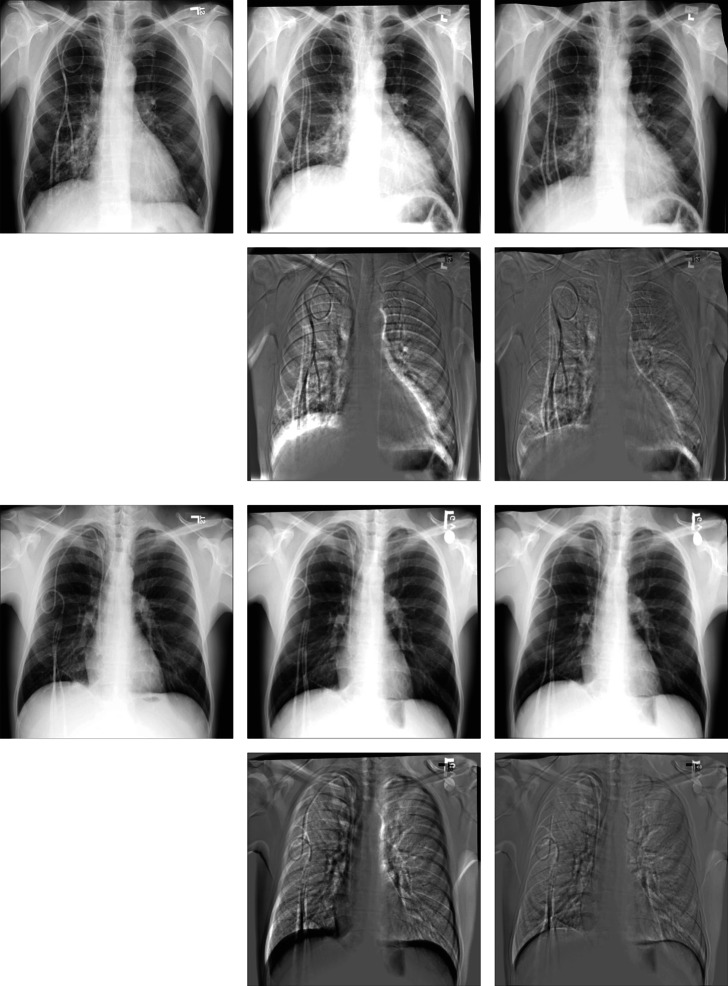
We can see from (g–i) subtraction images in Figs. 10 and 11 that there is less black part below the lung caused by the structural difference in the subtraction images of our method. In addition, the grayscale of the ribs in the images is also uniform than other methods. It indicates that the images after registration of our methods match better with the fixed images. From Table 3, we can see that the performance of BUB outperforms other methods on both datasets. In the ChestX-ray8 dataset, the dice of our proposed method increases by 0.84% compared to the second-best method. And in the Test12 dataset, it increases by 0.63%. Notably, FFD also provided a better registration result than other methods when dealing with large deformation. It proved that it is effective to apply FFD to the task of X-ray chest registration. In addition, BUB is also about 8 times faster than these two conventional methods in CPU time. When it comes to GPU time, our method is faster than 173 times the speed of them. It shows that our method can achieve deformable registration more quickly. Meanwhile, our method can achieve better results than conventional methods. Figure 12 shows the results of BUB for the data of two other patients.

Fig. 10.

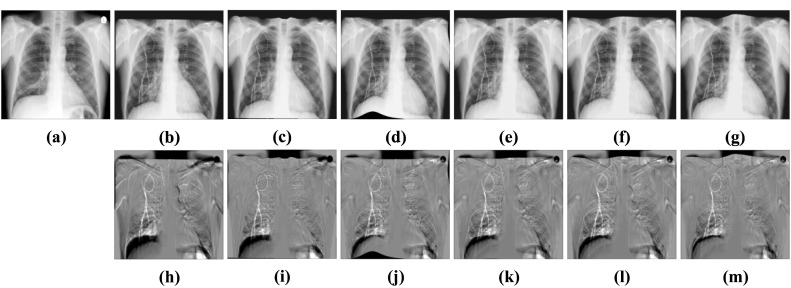
Visual deformable registration results of ChestX-ray8. a Fixed image. b Moving image. c Affine + SyN. d Affine + FFD. e Affine + RCN. f Affine + RRN. g Affine + BUB. h Subtraction image before registration. Sub-images (i–m) correspond to the subtraction images of the above algorithm in turn

Fig. 11.

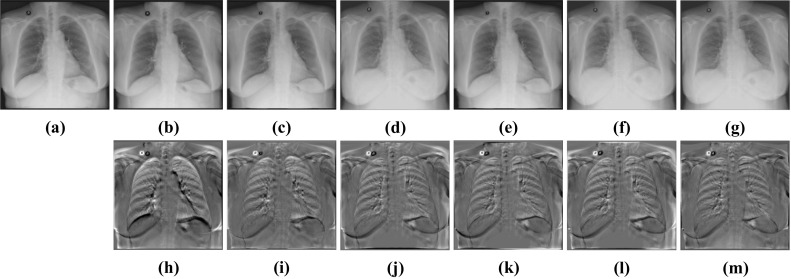
Visual deformable registration results of Test12. a Fixed image. b Moving image. c Affine + SyN. d Affine + FFD. e Affine + RCN. f Affine + RRN. g Affine + BUB. h Subtraction image before registration. Sub-images (i–m) correspond to the subtraction images of the above algorithm in turn

Table 3.

Comparison of different deformable registration methods. Standard deviation is provided in the brackets. The best performances are shown in bold

Methods	ChestX-ray8
	MSE	MI	Dice	CPU time/s	GPU time/s
Affine	0.032 (0.018)	1.038 (0.188)	0.922 (0.029)	-	-
Affine + SyN	0.033 (0.014)	1.317 (0.226)	0.945 (0.056)	2.300 (0.042)	-
Affine + FFD	0.023 (0.016)	1.331 (0.196)	0.953 (0.030)	2.358 (0.109)	-
Affine + RCN	0.024 (0.020)	1.323 (0.129)	0.951 (0.024)	0.781 (0.052)	0.030 (0.002)
Affine + RRN	0.025 (0.017)	1.313 (0.198)	0.942 (0.020)	0.541 (0.163)	0.022 (0.002)
Affine + BUB	0.021 (0.020)	1.346 (0.204)	0.961 (0.023)	0.284 (0.011)	0.012 (0.001)
Methods	Test12
	MSE	MI	Dice	CPU time/s	GPU time/s
Affine	0.038 (0.043)	1.235 (0.113)	0.923 (0.042)	-	-
Affine + SyN	0.034 (0.025)	1.553 (0.106)	0.947 (0.025)	2.245 (0.052)	-
Affine + FFD	0.026 (0.026)	1.562 (0.192)	0.954 (0.030)	2.278 (0.143)	-
Affine + RCN	0.034 (0.046)	1.560 (0.031)	0.949 (0.010)	0.840 (0.206)	0.031 (0.002)
Affine + RRN	0.035 (0.043)	1.547 (0.043)	0.950 (0.032)	0.457 (0.006)	0.023 (0.001)
Affine + BUB	0.028 (0.037)	1.570 (0.138)	0.960 (0.054)	0.280 (0.011)	0.013 (0.001)

Fig. 12.

Visual deformable registration results of other two patients’ data. From left to right are respectively fixed images, affine results, and Affine + BUB results. The images in the second line correspond to the subtraction images of the above images in turn

CABN Registration Results

CCAB and BUB have shown their advantages in rigid registration and deformable registration respectively. Then, we cascade CCAB and BUB into CABN and complete comparative experiments with other algorithms. The results in Table 4 and Figs. 13 and 14 show that compared with other algorithms, CABN can better handle large deformation and effectively reduce the difference between images. With the help of a separate rigid registration module, CABN outperforms both two datasets. The dice of CABN increases by 1.26% and 1.47% in the ChestX-ray8 and Test12 datasets, respectively, compared to the second-best results. Figure 15 shows the results of CCAB for the data of two other patients.

Table 4.

Comparison of CABN with other methods. Standard deviation is provided in the brackets. The best performances are shown in bold

Methods	ChestX-ray8
	MSE	MI		Dice	CPU time/s	GPU time/s
Before	0.048 (0.017)	0.719 (0.206)		0.833 (0.076)	-	-
SyN	0.022 (0.019)	1.271 (0.197)		0.954 (0.024)	2.762 (0.034)	-
FFD	0.023 (0.018)	1.266 (0.206)		0.940 (0.037)	2.803 (0.113)	-
RCN	0.031 (0.010)	1.212 (0.214)		0.933 (0.033)	0.812 (0.036)	0.032 (0.006)
RRN	0.026 (0.010)	1.231 (0.217)		0.935 (0.031)	0.525 (0.020)	0.023 (0.008)
CABN	0.015 (0.011)	1.376 (0.219)		0.966 (0.024)	0.378 (0.014)	0.012 (0.001)
Methods	Test12
	MSE		MI	Dice	CPU time/s	GPU time/s
Before	0.048 (0.012)		0.916 (0.199)	0.876 (0.045)	-	-
SyN	0.026 (0.026)		1.492 (0.103)	0.940 (0.029)	2.489 (0.120)	-
FFD	0.024 (0.020)		1.537 (0.091)	0.952 (0.019)	2.453 (0.152)	-
RCN	0.027 (0.018)		1.483 (0.140)	0.944 (0.022)	0.863 (0.021)	0.032 (0.005)
RRN	0.029 (0.020)		1.473 (0.135)	0.943 (0.028)	0.512 (0.015)	0.028 (0.010)
CABN	0.020 (0.014)		1.642 (0.149)	0.966 (0.029)	0.284 (0.011)	0.013 (0.001)

Fig. 13.

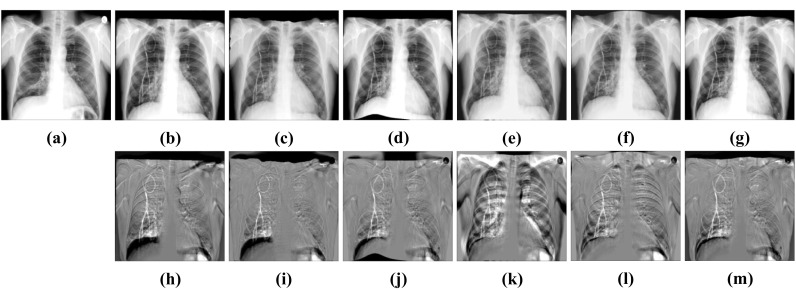
Visual deformable registration results of ChestX-ray8. a Fixed image. b Moving image. c SyN. d FFD. e RCN. f RRN. g CABN. h Subtraction image before registration. Sub-images (i–m) correspond to the subtraction images of the above algorithm in turn

Fig. 14.

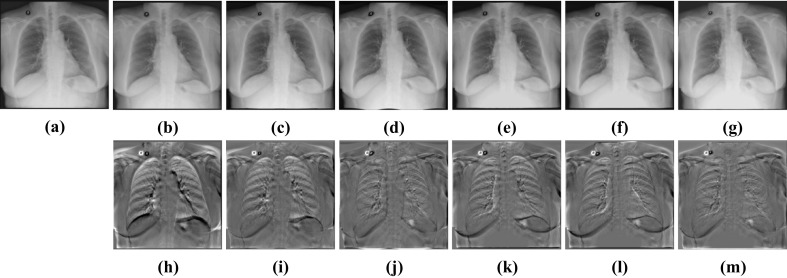
Visual deformable registration results of Test12. a Fixed image. b Moving image. c SyN. d FFD. e RCN. f RRN. g CABN. h Subtraction image before registration. Sub-images (i–m) correspond to the subtraction images of the above algorithm in turn

Fig. 15.

Visual deformable registration results of other two patients’ data. From left to right are respectively fixed images, CCAB, and CABN result. The images in the second line correspond to the subtraction images of the above images in turn

Ablation Study

To confirm the universality of CCAB, we replaced the affine used in the pretreatment in non-rigid registration experiment with CCAB. As shown in Figs. 16 and 17, and Table 5, we can see that BUB still maintains a good registration result among these registration methods. Comparing these results with Figs. 10 and 11 and Table 3, we can find that replacing the traditional affine method with CCAB can not only reduce the time required for registration, but also better help to improve the registration accuracy as a pre-processing operation before the deformable registration. The dice of the results also increase 0.97% and 0.57% in average, compared to the combination of affine and BUB as shown in Table 3. Therefore, our method CABN outperforms other traditional methods and deep learning methods in dealing with large deformation of lung X-ray.

Fig. 16.

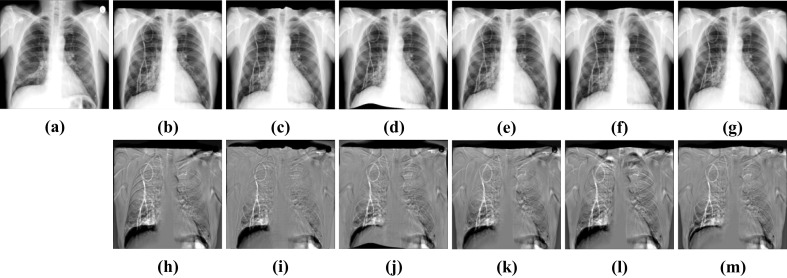
Visualization results of different algorithms of ChestX-ray8. a Fixed image. b CCAB. c CCAB + SyN. d CCAB + FFD. e CCAB + RCN. f CCAB + RRN. g CABN. h Subtraction image before registration. Sub-images (i–m) correspond to the subtraction images of the above algorithm in turn

Fig. 17.

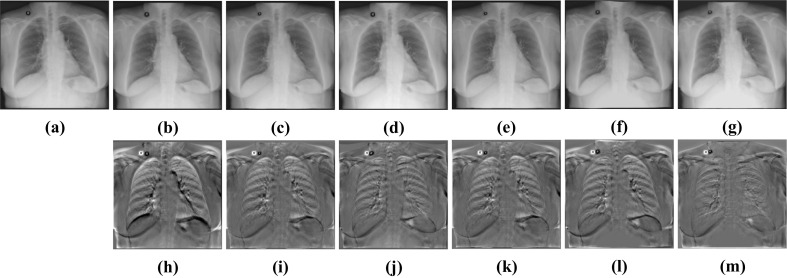
Visualization results of different algorithms of Test12. a Fixed image. b CCAB. c CCAB + SyN. d CCAB + FFD. e CCAB + RCN. f CCAB + RRN. g CABN. h Subtraction image before registration. Sub-images (i–m) correspond to the subtraction images of the above algorithm in turn

Table 5.

Comparison of different deformable registration methods. Standard deviation is provided in the brackets. The best performances are shown in bold

Methods	ChestX-ray8
	MSE	MI	Dice	CPU time/s	GPU time/s
CCAB	0.028 (0.015)	1.032 (0.204)	0.926 (0.028)	-	-
CCAB + SyN	0.023 (0.024)	1.350 (0.212)	0.958 (0.037)	2.200 (0.048)	-
CCAB + FFD	0.017 (0.016)	1.370 (0.172)	0.963 (0.018)	2.376 (0.187)	-
CCAB + RCN	0.022 (0.015)	1.348 (0.172)	0.956 (0.014)	0.808 (0.136)	0.025 (0.002)
CCAB + RRN	0.023 (0.014)	1.354 (0.138)	0.955 (0.023)	0.488 (0.013)	0.025 (0.018)
CCAB + BUB (CABN)	0.015 (0.011)	1.376 (0.219)	0.966 (0.024)	0.378 (0.014)	0.012 (0.001)
Methods	Test12
	MSE	MI	Dice	CPU time/s	GPU time/s
CCAB	0.030 (0.020)	1.256 (0.119)	0.928 (0.032)	-	-
CCAB + SyN	0.028 (0.041)	1.629 (0.111)	0.953 (0.029)	2.267 (0.081)	-
CCAB + FFD	0.024 (0.023)	1.632 (0.092)	0.959 (0.037)	2.362 (0.161)	-
CCAB + RCN	0.025 (0.010)	1.626 (0.128)	0.956 (0.019)	0.785 (0.021)	0.028 (0.004)
CCAB + RRN	0.029 (0.029)	1.621 (0.129)	0.953 (0.028)	0.487 (0.012)	0.027 (0.010)
CCAB + BUB (CABN)	0.020 (0.014)	1.642 (0.149)	0.966 (0.029)	0.284 (0.011)	0.013 (0.001)

Discussion

The registration of X-ray chest radiographs often faces the problem that the position and shape of the lungs in the two images are very different and it is difficult to register. Generally, for these large deformations, the fairly method is to deal with rigid deformation and non-rigid deformation in cascade. We proposed corresponding networks for the two tasks.

In rigid deformation registration, we choose affine based on the traditional registration toolbox ANTs and Elastix, and GlobalNet and DLIR as comparative experiments. From the subtraction images in Figs. 5 and 6, we can see that the result of DLIR is obviously inaccurate. This is because its structure is to extract the features of the moving map and the fixed map separately and combine them at the end of the network. Although this makes it possible to deal with the case where the size of the two input images is inconsistent, it cannot extract the correlation information between the images well. GlobalNet’s method of concatenating two images and extracting features using a single channel can achieve better registration results. However, this will lead to insufficient utilization of the internal information of the image. In contrast, CCAB can not only take advantage of the dual channel structure to extract the internal information of images, but also adds CCM to fuse the large-scale information between images. The results are visually similar to those of the conventional affine methods. The quantitative data in Table 1 can also demonstrate that. In addition, our method outperforms the conventional methods in running time. Furthermore, we also performed ablation experiments. We compared the two cases that choosing the affine based on the traditional method and choosing CCAB as the pretreatment before non-rigid registration. The experimental results show that choosing CCAB as the pretreatment can help the non-rigid deformation registration method to improve the accuracy.

In non-rigid deformation registration, we choose RRN and RCN, which are also good at handling large deformation, and SyN and FFD, which are commonly used in conventional methods, as comparative experiments. As shown in Figs. 10 and 11, the visual results show that these results are approximately the same. However, when focusing on the lung contour, we can find that there are still structural differences between the fixed images and moved images of SyN, RRN, and RCN. When it comes to FFD and BUB, the black part of the lower side of the right lung is less, which means that the lung structures in the two images are more similar and the registration results are better. The quantitative data in Table 3 can also demonstrate that.

Then, we compare CABN with other algorithms. The experimental results of Table 4 and Figs. 13 and 14 have demonstrated that CABN can generate more accurate registration results. We have also completed the ablation experiment. In the non-rigid deformation registration experiment, we use CCAB instead of affine to complete the preprocessing operation. It can be found in Table 5 and Figs. 16 and 17 that after the replacement, the visualization results and quantitative indicators are improved compared with those before the replacement, which indicates that the CCAB module has a wide range of applications and can be used for preprocessing before non-rigid registration.

Conclusion

In this paper, we have proposed a deep learning–based fast registration network CABN on lung X-ray images. CABN which consists of CCAB and BUB provides a high degree of flexibility to model the lung motion. In BUB, we also introduce the conditional module to efficiently select regularization parameters. This avoids the tedious operation of training different hyperparametric models multiple times. The experimental results show that CCM in CCAB can help extract and learn the relevant long-distance information among the fixed images and the moving images, which contributes to more accurate registration results. The results have also demonstrated that BUB can effectively reduce the structural differences between the two images with the help of applying the idea of cubic B-splines. Through the cascade of CCAB and BUB, CABN can achieve more accurate results compared with other conventional and deep learning registration methods which are good at dealing with large deformation.

Funding

This work was supported by the National Natural Science Foundation of China under award number 61976091.

Data Availability

The data that support the findings of this study are available at 10.1109/CVPR.2017.369.

Declarations

Ethics Approval

This is an observational study.

Conflict of Interest

The authors declare no competing interests.