Abstract
Medical imaging has acquired more attention due to the emerging design of wireless technologies, the internet, and data storage. The reflection of these technologies has gained attraction in medicine and medical sciences facilitating the diagnosis and treatment of different diseases in an effective manner. However, medical images are vulnerable to noise, which can make the image unclear and perplex the identification. Thus, denoising of medical images is imperative for processing medical images. This paper devises a novel optimal deep convolution neural network–based vectorial variation (ODVV) filter for denoising medical computed tomography (CT) images and Lena images. Here, the input medical images are fed to a noisy pixel map identification module wherein the deep convolutional neural network (Deep CNN) is adapted for discovering noisy pixel maps. Here, Deep CNN training is done with the Adam algorithm. Once noisy pixels are identified, it is further given to noise removal module which is performed using the proposed optimization algorithm, namely Feedback Artificial Lion (FAL). Here, the FAL is devised by combining the FAT and Lion algorithm. After noise removal, the pixel enhancement is performed using the vectorial total variation norm to get final pixel-enhanced image. The proposed FAL algorithm offered enhanced performance in contrast to other techniques with the highest peak signal-to-noise ratio (PSNR) of 24.149 dB, highest second-derivative-like measure of enhancement (SDME) of 32.142 dB, highest structural index similarity (SSIM) of 0.800, and Edge Preserve Index (EPI) of 0.9267.
Keywords: Medical image denoising, Deep convolutional neural network, Vectorial total variation norm, Pixels
Introduction
Medical images are extensively adapted in diagnosing clinical diseases due to the arrival of digital imaging technologies. The medical image plays an imperative role in carrying information regarding the brain, heart, and nerves for acquiring interior vision of the human body. Several mathematical operations are adapted to medical images for deducing the infection of healthy tissue. However, the loss of specific region in medical imaging resulted in a disaster like death. The major issue in medical imaging is to generate an image without losing any imperative information. It is reliable that the images generated can be corrupted due to the occurrence of noise and artifacts during acquisition or further processing phases [1]. However, the acquired images become contaminated due to noise issue and suffer from various issues, like occlusion and low exposure to radiation [2]. The noise can be defined as an arbitrary change of the original value of the pixel. Here, the noise minimizes the quality of the image, and is particularly imperative when objects being imaged are diminutive and have comparatively less contrast. In contrast to classical images, the medical images have generally low contrast. In general, the noise elevates radiation amount. Thus, an imperative pre-processing step must be included for enhancing the medical images’ quality. In addition, denoising is enviable for analyzing the medical image [3]. For providing precise decisions, the images are collected from different medical imaging modalities that are free of noise [4]. Thus, the medical image denoising is crucial and obligatory pre-processing phase in medical imaging systems [1].
Image denoising is a major issue in computer vision and has acquired the attention of several researchers. In general, there exist two techniques for denoising medical images. The first one is devised on the basis of capturing various types of images, and takes average on them for obtaining enhanced image as outcome, and the second technique is devised on the basis of post-processing for minimizing noise [2, 5]. There is balance between image denoising and losing edges. Hence, handling the edges in procedure of denoising is a major concern [5]. The denoising of an image provides a trade-off among noise removal and preservation of image details. The contemporary image acquisition tools are becoming more perceptive to noise. Thus, there exists a huge reliability on image denoising techniques for minimizing impact of noise in resultant image. Noise can be termed as an arbitrary variation in color information or intensity values of image pixels. The widespread modalities of medical imaging involve positron emission tomography (PET), magnetic resonance imaging (MRI), CT, and ultrasound images. Other than natural images, the majority of medical images contains signal-dependent noises, and thus, it is complex to eliminate noises by using classical natural image denoising methods [1, 6].
Various image denoising methods are devised until now. The utilization of sparse and superfluous representations for denoising image has gained the attention of many researchers in the previous decades. The sparse representation model considers clean units in noisy images, which are sparsely presented by superfluous dictionary while the dictionary cannot present noisy regions sparsely, and thus, one can eliminate noise. The technique based on dictionary has major significance while using a sparse representation model. Presently, two methods about this problem are extensively used. The method based on orthogonal base and technique relies on learning. The dictionaries of initial technique involve wavelets [7], neural network [8], and contourlet [9], which typically have effective executions, but are deficient of adaptability. The second technique utilizes learning algorithms for training dictionary with series of instances. The techniques of this kind involve method of optimal directions (MOD) and K-means singular value decomposition (K-SVD). The trained dictionaries are more adaptive and had attained exceptional concert in different domains. However, it arrives with expenditure of elevated computational complexity [10]. The classical denoising algorithms, like wavelet soft threshold, median filter, and Wiener filter, are adapted on noisy image for enhancing image quality. The Wiener filter is devised by Norbert Wiener and reduces mean square error (MSE) by evaluating statistical estimate of unknown signal with a random process. The dynamic nature of the Wiener filter offers point estimation whereas it poses issue to eliminate multiplicative noise. The median filter is edge preservative and non-linear, and thus is extensively adapted in image processing for removing noise [11, 12].
The goal is to design a novel optimal deep convolution neural network–based vectorial variation (ODVV) filter for denoising medical images. In this method, the medical images are considered input and are subjected to a noisy pixel map detection phase wherein deep convolutional neural network (Deep CNN) is utilized for discovering noisy pixel maps. Here, Deep CNN training is done using the Adam algorithm. After identifying noisy pixels, it is further subjected to a noise removal phase, which is carried out using the proposed FAL algorithm. Here, the proposed FAL is devised by combining the FAT and Lion algorithm. Once the noise removal is completed, the pixel enhancement is carried out using vectorial total variation norm for getting final pixel-enhanced image.
The key contributions of the paper are:
Proposed FAL for denoising medical images: The removal of noise from medical images is performed using the proposed FAL, and is devised by integrating the FAT and Lion algorithm.
The remainder of the paper is arranged as follows: the “Motivations” section provides a literature survey of classical medical image denoising techniques. The “Proposed ODVV Filter with the FAL Algorithm for Medical Image Denoising” section portrays the medical image denoising model using the proposed FAL algorithm. The “Results and Discussion” section describes the effectiveness of the proposed method in contrast to classical techniques. The “Conclusion” section elaborates the conclusion.
Motivations
The modern medicines generate massive information present in medical databases. Hence, the mining of precious knowledge and decision-making for diagnosis has increasingly turned into a necessity for attaining effectual diagnosis. However, the issues like occlusion and low radiation are certain issues that destroy the images due to noise. The aforementioned issues and the challenges faced by the classical techniques are considered a motivation to devise a novel medical image denoising model.
Literature Survey
The literature review of eight classical methods devised on the basis of denoising medical image is presented. Jifara et al. [2] devised deep feed forward denoising convolutional neural networks by adapting deep framework for medical image denoising. Here, the residual learning and batch normalization were employed in deep model. In addition, the residual learning learned the noise from noisy images. In addition, the batch normalization was combined with residual learning for improving accuracy and time of training. However, the method failed to examine compression artifact reduction of images using an influential convolutional neural network model. Ji et al. [3] devised a geometric regularization technique for denoising medical images. The method aimed at reconstructing surface by reducing approximation error and gradient error for suppressing noise from medical images. The method comprises two phases; one is for giving a basic estimate. The surface was devised by splitting the coefficients into two sets. The first group was used to reduce gradient of surface, and another group was to reduce estimate accuracy. However, the method failed to improve real-time performance of the technique. Aravindan et al. [13] devised a technique for denoising a high-noise density image in an effective manner with minimal computation cost. Here, an image denoising method using Social Spider Optimization (SSO) and Discrete Wavelet Transform (DWT) was devised. Initially, the salt and pepper, Gaussian, and speckle noises were added, and then, the DWT was adapted. Here, the wavelet coefficient optimization was carried out to optimize coefficient value using SSO. Thereafter, inverse DWT (IDWT) was adapted in wavelet-optimized parameter. The method significantly minimized noise from the image, but the method was not applicable with other datasets. Rani et al. [14] devised a steepest descent (SD)–based learning algorithm and was utilized in artificial neural networks (ANN) for minimizing noise from images in an adaptive manner. Moreover, soft thresholding function was devised as an activation function of ANN. However, the method failed to consider high-order derivatives for handling numerical properties. Laves et al. [15] devised randomly initialized convolutional network for medical image denoising. The method included Bayesian approach using Monte Carlo’s dropout for quantifying both aleatoric and epistemic uncertainty. The method offered improved predictive uncertainty and correlated with predictive error. However, the method failed to adapt deformable registration or other inverse image tasks for improved performance. Kumar and Nagaraju [16] designed a filter for restoring the corrupted digital image. Here, the filter incorporated type II fuzzy system and the cuckoo search optimization algorithm (T2FCS) for restoring noise from images. The noisy pixels from images are determined with the circular-based searching scheme and identified corrupt pixels were removed with the cuckoo search algorithm. The method was adaptable to different noisy conditions, but failed to provide proper exploration. Bai et al. [10] devised a denoising method that integrated sparse dictionary learning and cluster ensemble for medical image denoising. The method exploited both intrinsic self-similarity and sparsity on image patches. Initially, the image feature set was constructed by utilizing steering kernel regression. Thereafter, a cluster ensemble was used for gaining class label. The trained dictionary was more adaptive and was helpful for improving recovered image quality, but the method suffered from huge computational complexity. Miri et al. [5] devised a technique for eliminating Gaussian noise from medical images with the ant colony optimization (ACO) algorithm and two-dimensional discrete cosine transform (2DDCT). Here, the method identified imperative frequency coefficients using ACO and eliminated the impacts of noise by deleting high-frequency parts. However, the method failed to adapt deep learning technique for improved performance.
Proposed ODVV Filter with the FAL Algorithm for Medical Image Denoising
The denoising of images is an imperative part in analyzing medical images. In addition, the image denoising is a procedure whose goal is to remove noise that may corrupt an image during transmission. The medical images are affected by noise during the process of image collection. Thus, the occurrence of noise generates undesired visual quality and minimizes the contrast of objects. Hence, the removal of noise is an imperative part in imaging applications for improving the image and retaining fine details from the image. This research devises a hybrid optimization algorithm, namely the FAL algorithm, for medical image denoising. The steps involved in medical image denoising are noisy pixel map identification, noise removal, and the pixel enhancement. At first, the input image is given to the noisy pixel map identification module where the Deep CNN is adapted for identifying the noisy pixel maps. After that, the identified noisy pixel maps are given to the noise removal module. Here, the noise is removed using the proposed optimization algorithm, termed the FAL algorithm. Here, the FAL algorithm is devised newly by integrating the FAT [17] and Lion algorithm [18]. Once the noise removal is done, the enhancement of pixels is performed using vectorial total variation norm [19] to get final pixel-enhanced image. The schematic view of medical image denoising using the FAL algorithm is depicted in Fig. 1.
Fig. 1.
Architecture of medical image denoising model with the proposed FAL algorithm
Assume an input medical dataset be given as D and is expressed as,
| 1 |
where denotes the image, and M specifies total images.
Each image presented in the database is given to the noise pixel map generation phase wherein the noisy pixels are identified using Deep CNN. The briefer illustration of the noisy pixel map generation process is described below.
Noisy Pixel Map Generation
In this section, the noisy pixel map generation is carried out using Deep CNN using the input images. The training of Deep CNN is carried out using the Adam algorithm to detect the noisy pixels. Kingma and Ba [20] is a first-order stochastic gradient-based optimization which is extensively applied to the objective function that alters in contrast to the attributes. The major implication of the technique is computational efficiency and less memory requirements. In addition, the issues linked with the non-stationary objectives and the existence of noisy gradients are managed in an effective manner. Moreover, the Adam poses the following benefits. Here, the magnitudes of updated parameters are invariant in contrast to rescaling of gradient and step size is managed using hyperparameter that works with sparse gradients. Furthermore, the Adam algorithm is effectual for performing step size annealing. The architecture of Deep CNN and the steps of the Adam algorithm are portrayed below.
Structural Design of Deep CNN
The design and illustration of the Deep CNN [21, 22] are described in Fig. 2. The Deep CNN comprises pooling (POOL) layers, convolutional (conv) layers, and fully connected (FC) layers in which each layer is liable to perform a specific task. The goal of conv layers is to form feature maps using sensed data and feature maps are sampled down and subjected to pool layers, which is the second layer in Deep CNN. At last, the FC layer led to classification. The classification accuracy is enhanced considering huge conv layers in Deep CNN.
Fig. 2.
Structural design of Deep CNN
Convolutional Layers
It is utilized for producing features and provides extraction of pattern using feature vector, which is produced with sensed objects. The neurons are associated using trainable weights which are convoluted with inputs to devise feature maps. The convolution layer input is sensed data and the count of the conv layers [21] is expressed as,
| 2 |
where i refers to the total conv layers and represents the conv layer in Deep CNN. The units positioned at derive the output [21] expressed as,
| 3 |
where * signifies the conv operator that facilitates mining of pattern with outputs generated from adjacent conv layers, represents fixed feature maps, signifies total feature maps, and signifies weights which is trained with Adam’s algorithm.
ReLU and POOL Layers
ReLU ensures high efficiency and straightforwardness and the implication of the ReLU layer is that it works in rapid manner and is capable of handling huge networks. The output with ReLU, when subjected to feature maps [21], is expressed as,
| 4 |
where signifies the activation function in the uth layer.
FC Layers
The patterns generated from POOL and conv layers are fed as an input to FC to initiate classification of sensed data [21]. The output produced from the FC layers is expressed as,
| 5 |
where signifies weight associated with in the feature map of layer and fth unit in layer u Here, weights are optimally tuned with the Adam technique.
Training of Deep CNN Using the Adam Algorithm
The training of Deep CNN [21, 22] is performed using the Adam algorithm [20] which assists to determine best weights for tuning Deep CNN for noisy pixel identification. The briefer elaboration of algorithmic steps in the Adam algorithm is illustrated. The optimum weights are obtained from the Adam technique that assists to tune Deep CNN for producing optimum outcomes. The model employs Deep CNN to detect noisy pixels by providing optimal detection. The steps of Adam are given as follows:
Step 1: Initialization
The first step is initialization of bias [20] corrections where signifies corrected bias of first-moment estimate and symbolizes corrected bias of second-moment estimate.
Step 2: Computation of the Fitness
The fitness of bias is evaluated to choose optimum weight for training the Deep CNN model. Here, the fitness function is termed as the error function which yields to global optimum solution. The function is termed as a minimization function and is expressed as,
| 6 |
where r signifies the total data samples, symbolizes the output generated from the Deep CNN classifier, and denotes the ground truth value.
Step 3: Determination of Updated Bias
Adam is used to improve optimization and behavior of convergence. This technique generates smoother variation with effectual computational efficiency and less memory requirements. As per Adam [20], the bias is expressed as,
| 7 |
where signifies the step size, represents the corrected bias, symbolizes the bias-corrected second-moment estimate, denotes constant, and represents the parameter at previous time instant. The corrected bias of first-order moment is expressed as,
| 8 |
| 9 |
The corrected bias of second-order moment is represented as,
| 10 |
| 11 |
| 12 |
where
Step 4: Finding Optimal Solution
The optimum solution is determined using error measure and solution with the best solution is employed for finding the noisy pixels.
Step 5: Stopping Criterion
The optimal weights are obtained repeatedly until maximal iterations are attained.
Noise Removal Using the Proposed FAL Algorithm
The noise removal is an obligatory step in medical image denoising process. In addition, the preservation of fine features from an image is imperative during the noise removal process. The presence of noise may destroy the quality of an image and may adversely affect the processing. Here, the noise removal [16] is performed by selecting an optimal threshold, which is achieved by the proposed FAL algorithm. Initially, the noisy pixels are obtained and then, the new pixel values are evaluated for equivalent noisy pixels. Whenever center pixel is determined as noisy, it must be enhanced for eliminating the noisy pixel which is done by,
| 13 |
where indicates new pixel image value. The chosen noisy pixel is only adapted for computing the new pixel value. At first, the window is produced around detected noisy pixel. Thereafter, the noisy pixels of window are matched with input image .
Whenever the value of is higher than the threshold value, the new pixel value is produced, else the noisy pixels are replaced using an original image in that chosen window.
Here, the generation of new pixel is performed with function using three parameters like that can be modeled as follows:
| 14 |
where B represents the absolute function of window considering neighboring pixel value as,
| 15 |
Thereafter, the value of is obtained from absolute outcomes of above value B using prefixed window. At first, the value of is set to 0 wherein the value of j varies using the selected number of prefix window .
| 16 |
Thereafter, the rounding procedure is carried out for the evaluated value of as, which is expressed as t . Then, the sorting is carried out for outcomes wherein the first value is selected as D.
| 17 |
The resultant output is compared with threshold. Whenever the value of is higher than threshold value, the new function is produced as,
| 18 |
where symbolizes the mean of neighboring pixel and standard deviation is expressed as. In this method, the value of is adapted as constant where. The evaluation of the mean value is expressed as,
| 19 |
Whenever the produced new function outcome is higher than threshold, the generation of new pixel value is performed with a formula represented as,
| 20 |
The pseudo code for evaluating new pixel considering noise pixels is stated in Table 1.
Table 1.
Pseudo code of new pixel evaluation
| Input: |
|---|
| Output: |
| Parameter: represent threshold value computed with the proposed FAL algorithm |
| Procedure: |
| Begin |
| Select window by adapting noise pixel as center pixel |
| Match noisy pixel using input image |
| Determine the count of similar matched pixel count |
| If |
| Discover |
| If |
| Determine |
| else |
| If |
| else |
| Determine new pixel values for noisy pixels |
| else |
| End |
Proposed FAL Algorithm for Discovering Optimal Threshold
For performing effective evaluation of new pixel values, the optimum choice of threshold is essential. Here, the proposed FAL algorithm is newly devised for computing optimal threshold value on the basis of promising efficiency. Moreover, the proposed FAL algorithm is devised by combining the FAT and Lion algorithm. The FAT algorithm [17] is motivated from the organic matter’s transportation and update theories of branches. Here, the transport of organic matters is devised with feedback method of moistures. Here, dispersive propagation operator and self-propagating operator are incorporated for solving huge optimization issues effectively. Moreover, the FAT algorithm is effective in handling various types of optimization issues. It can adaptively control the parameter for improving the efficiency of search. On the other hand, the Lion algorithm [18] is motivated from unique social behavior of lion. The lion algorithm tends to be competing in contrast to other evolutionary computation techniques while addressing multimodal functions. The stability of performance is guaranteed which maintained better tradeoff between mean performance and standard deviation. The Lion algorithm tends to be effective in contrast to other swarm algorithms and is effective on solving design issues. The method solved unimodal and multimodal functions with several local minima. The steps considered in the proposed FAL algorithm are given below.
Step 1: Initialization
The initial step is solution initialization [18] that is expressed as R with total solutions such that
| 21 |
where is the total solution, and signifies the solution.
Step 2: Determination of Fitness Function
Here, the fitness value of both new solutions and randomly chosen solution is computed. The fitness of each solution is determined by adapting statistical model provided in the “Noise Removal Using the Proposed FAL Algorithm” section to produce restored image.
Step 3: Evaluation of Update Equation
The FAT algorithm helps to solve wide range of optimization issues in an effective manner. According to the FAT algorithm [17], the update equation is given as,
| 22 |
where indicates the best branch position at the eth dimension, represents random number between 0 and 1, and signifies the position of self-evolution operator at branch b at the eth dimension and iteration.
| 23 |
| 24 |
The fertility evaluation can assist for skipping from local optimal solutions. According to the Lion algorithm [18], the update position of lion is expressed as,
| 25 |
where signifies the current position of lion, symbolize random numbers, and represents the best position of lion.
| 26 |
| 27 |
Substitute Eq. (24) in Eq. (27),
| 28 |
| 29 |
The final update equation of the proposed FAL algorithm is given by,
| 30 |
Step 4: Determination of Optimal Solution
The optimal solution is discovered with fitness measure and solution with the best solution is employed for removing the noisy pixels using optimal threshold.
Step 5: Stopping Criterion
The optimal weights are obtained repeatedly until maximal iterations are attained.
Pixel Enhancement Using Vectorial Total Variation Norm
Here, the briefer illustration of an image enhancement procedure is illustrated and is utilized for modifying input image by changing visual impacts. The outcomes of enhancing image are more apposite for particular application in contrast to the original image. The image enhancement offers detailed information regarding different features like boundaries or edges by maximizing its dynamic ranges. Here, the process of enhancement is done using noisy pixels. Once the location of noisy pixel is determined, then the pixels are applied for enhancement process. In this method, the pixel enhancement process is performed using total variation norm [19]. Here, the discrete gradient operator adapted to a function y at point is expressed as,
| 31 |
where symbolizes divergence operator, and signifies grid point.
| 32 |
| 33 |
The iterative process is stopped if where R refers to the given residual and evokes that. Here, initial values are selected to be and the residual .
Results and Discussion
The effectiveness of the proposed FAL using Lena and CT images considering PSNR, SDME, SSIM, and EPI parameters is illustrated. Here, the noise level is varied for performing the analysis.
Experimental Setup
The implementation of the proposed technique is performed in MATLAB 2020a considering PC with Windows 10 OS, 4 GB RAM, and Intel i3 processor. Table 2 shows the experimental setup of the proposed method.
Table 2.
Experimental setup
| Parameter | Value |
|---|---|
| Input size | 256 × 256 × 3 |
| Number of channels in batch normalization | 32 |
| Training epoch | 25 |
| Learning rate | 0.01 |
| Number of conv layer | 10 |
Dataset Description
The analysis of the proposed medical denoising method using hybrid filter utilizes Lena image and medical images. Here, the Lena images are utilized in uncompressed TIF format and pose size of 512 * 512. The medical images are obtained from NIH Clinical Center [23] donated by Summers, Ronald. The dataset is named as the DeepLesion dataset, which includes 32,120 axial CT slices obtained from 10,594 CT scans of 4427 patients. Here, every image contains 1–3 lesions with related size measurements and bounding boxes, including up to 32,735 lesions together.
Performance Metrics
The metrics adapted to analyze techniques involve PSNR, SDME, SSIM, and EPI.
Experimental Results
The experimental results of the proposed T2FCS + FAL considering Lena images are shown in Fig. 3. Here, Fig. 3a presents the input Lena images. Figure 3b depicts the Gaussian noise added Lena image, random noise added Lena image, salt and pepper added Lena image, and uniform noise added Lena image. Figure 3c presents the output after denoising Gaussian noise added Lena image, random noise added Lena image, salt and pepper added Lena image, and uniform noise added Lena image.
Fig. 3.
Experimental results of the proposed T2FCS + FAL using a input Lena images; b Gaussian noise added Lena image, random noise added Lena image, salt and pepper added Lena image, and uniform noise added Lena image; and c output after denoising Gaussian noise added Lena image, random noise added Lena image, salt and pepper added Lena image, and uniform noise added Lena image
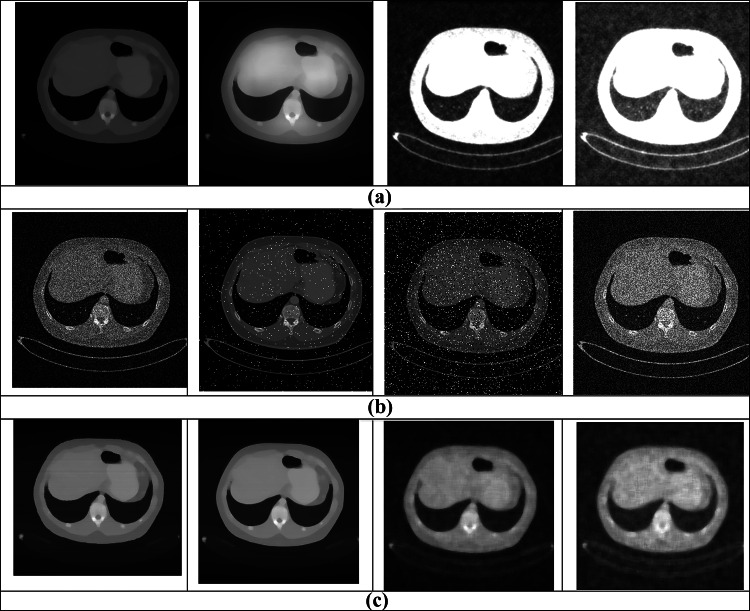
Figure 4 depicts the experimental results of the proposed T2FCS + FAL considering CT image. Here, the input CT image is given in Fig. 4a. The noises, such as Gaussian noise, random noise, salt and pepper, and uniform noise added CT images, are given in Fig. 4b, and the output of these noises added images is shown in Fig. 4c.
Fig. 4.
Experimental results of the proposed T2FCS + FAL using a input CT image; b Gaussian noise added CT image, random noise added CT image, salt and pepper added CT image, and uniform noise added CT image; and c output after denoising Gaussian noise added CT image, random noise added CT image, salt and pepper added CT image, and uniform noise added CT image
Comparative Methods
The techniques adapted for the evaluation involve the following: adaptive fuzzy-based switching weighted average (AFSWA) [24], Modified Decision Based Unsymmetric (MDBU) [25], Decision-Based Algorithm for Removal of High-Density Impulse Noises (DBAIN) [26], boundary discriminative noise detection (BDND) [27], and the proposed T2FCS + FAL.
Comparative Analysis
The assessment of the proposed FAL algorithm with classical techniques based on PSNR, SDME, SSIM, and EPI is evaluated. The analysis is carried out by varying noise levels.
Analysis Using Lena Image
The analysis using Lena image with PSNR, SDME, SSIM, and EPI parameters by varying noise levels is presented below.
-
Analysis considering random noise
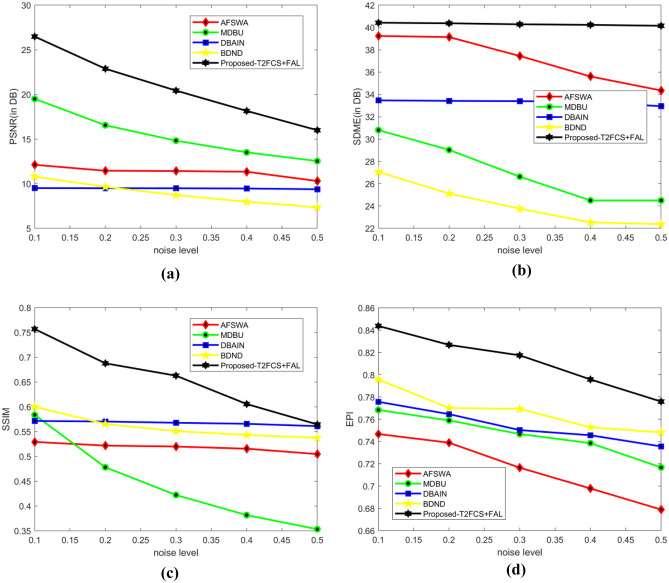
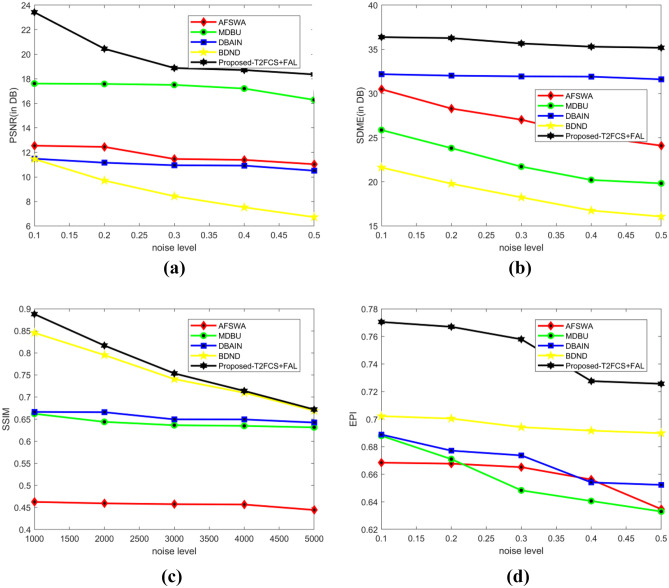
Figure 5 presents the analysis of techniques considering random noise considering PSNR, SDME, SSIM, and EPI using Lena image. The analysis of methods using PSNR is displayed in Fig. 5a. When noise level is 1000, the PSNR values computed by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 11.519 dB, 19.511 dB, 16.855 dB, 7.026 dB, and 12.155 dB. The analysis of methods using SDME is portrayed in Fig. 5b. When noise level is 1000, the SDME values computed by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 40.724 dB, 30.808 dB, 18.756 dB, 27.029 dB, and 41.618 dB. The analysis of methods using SSIM is displayed in Fig. 5c. When noise level is 1000, the SSIM values computed by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL filter are 0.544, 0.584, 0.712, 0.530, and 0.617. The EPI analysis is shown in Fig. 5d. When noise level is 2000, the EPI values computed by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL filter are 0.7128, 0.7380, 0.7475, 0.7607, and 0.8255.
-
Analysis considering salt and pepper noise
Figure 6 presents the analysis of methods by adding salt and pepper noise considering PSNR, SDME, SSIM, and EPI using Lena image. The analysis of methods using PSNR is displayed in Fig. 6a. When noise level is 0.1, the PSNR values computed by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 12.120 dB, 18.672 dB, 16.422 dB, 9.517 dB, and 10.802 dB. The analysis of methods using SDME is depicted in Fig. 6b. When the noise level is 0.1, the corresponding SDME values measured by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 39.244 dB, 45.542 dB, 38.270 dB, 33.567 dB, and 27.058 dB. The analysis of methods using SSIM is depicted in Fig. 6c. When the noise level is 0.1, the SSIM values measured by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 0.529, 0.831, 0.524, 0.573, and 0.600. The EPI analysis is depicted in Fig. 6d. When noise level is 0.2, the EPI values computed by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL filter are 0.7390, 0.7589, 0.7646, 0.7702, and 0.8267.
-
Analysis considering Gaussian noise
Figure 7 presents the analysis of methods by adding Gaussian noise considering PSNR, SDME, SSIM, and EPI using Lena image. The analysis of methods using PSNR is displayed in Fig. 7a. When the noise level is 0.1, the PSNR values evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 11.539 dB, 28.140 dB, 9.517 dB, 14.144 dB, and 11.066 dB. The analysis of methods using SDME is displayed in Fig. 7b. When noise level is 0.1, the SDME values evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 41.180 dB, 38.549 dB, 33.474 dB, 16.496 dB, and 40.678 dB. The performance improvement of AFSWA in contrast to the proposed T2FCS + FAL using SDME is 100%. The analysis of methods using SSIM is depicted in Fig. 7c. When noise level is 0.1, the corresponding SSIM values measured by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 0.535, 0.832, 0.572, 0.503, and 0.460. In Fig. 7d, the EPI analysis is depicted. When noise level is 0.3, the EPI values computed by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL filter are 0.7057, 0.7256, 0.7298, 0.7365, and 0.7790.
-
Analysis in the presence of uniform noise
Figure 8 presents the analysis of methods by adding uniform noise considering PSNR, SDME, SSIM, and EPI using Lena image. The analysis of methods using PSNR is displayed in Fig. 8a. When the noise level is 10, the PSNR values computed by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 14.289 dB, 26.487 dB, 29.476 dB, 21.341 dB, and 21.520 dB. The analysis of methods using SDME is displayed in Fig. 8b. When noise level is 10, the SDME computed by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 21.827 dB, 40.432 dB, 41.811 dB, 59.644 dB, and 55.511 dB. The analysis of methods using SSIM is displayed in Fig. 8c. When the noise level is 10, the SSIM computed by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 0.699, 0.757, 0.899, 0.770, and 0.874. In Fig. 8d, the EPI analysis is shown. When noise level is 30, the EPI values computed by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL filter are 0.6836, 0.7567, 0.7646, 0.7860, and 0.8866.
Fig. 5.
Analysis of methods considering random noise. a PSNR. b SDME. c SSIM. d EPI
Fig. 6.
Analysis of methods in the presence of salt and pepper noise. a PSNR. b SDME. c SSIM. d EPI
Fig. 7.
Analysis of methods considering Gaussian noise. a PSNR. b SDME. c SSIM. d EPI
Fig. 8.
Analysis of methods in the presence of uniform noise. a PSNR. b SDME. c SSIM. d EPI
Analysis Considering CT Image
The analysis with CT image using PSNR, SDME, SSIM, and EPI by altering noise levels from 1000 to 5000 is presented below.
-
Analysis considering random noise
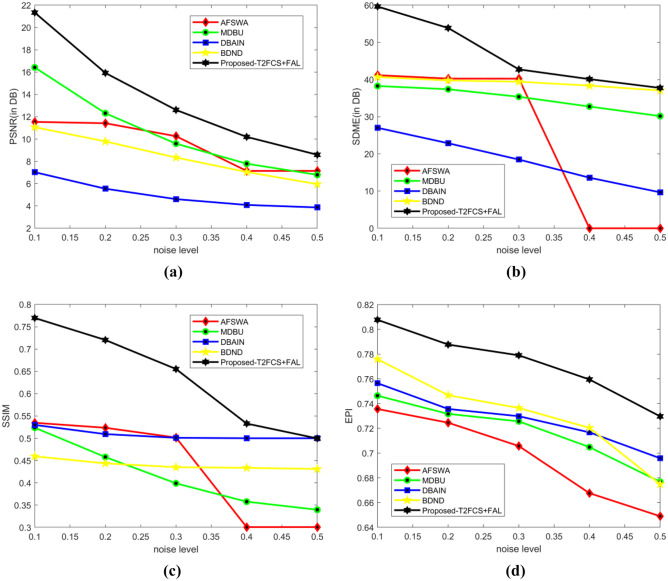
Figure 9 presents the analysis of techniques considering random noise with PSNR, SDME, SSIM, and EPI using CT image. The analysis of methods using PSNR is displayed in Fig. 9a. When noise level is 1000, the PSNR values evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 17.642 dB, 17.613 dB, 22.267 dB, 8.307 dB, and 13.864 dB. The analysis of methods using SDME is displayed in Fig. 9b. When the noise level is 1000, the SDME evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 29.784 dB, 25.869 dB, 20.212 dB, 28.153 dB, and 32.498 dB. The analysis of methods using SSIM is displayed in Fig. 9c. When the noise level is 1000, the SSIM evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 0.463, 0.669, 0.712, 0.482, and 0.846. The EPI analysis is shown in Fig. 9d. When noise level is 3000, the EPI values computed by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL filter are 0.6749, 0.7029, 0.7426, 0.7340, and 0.7810.
-
Analysis considering salt and pepper noise
Figure 10 presents the analysis of methods by adding salt and pepper noise considering PSNR, SDME, SSIM, and EPI using CT image. The analysis of methods using PSNR is displayed in Fig. 10a. When the noise level is 1000, the PSNR values evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 12.549 dB, 16.281 dB, 17.095 dB, 11.503 dB, and 11.455 dB. The analysis of methods using SDME is depicted in Fig. 10b. When the noise level is 1000, the corresponding SDME values measured by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 30.482 dB, 30.810 dB, 23.849 dB, 32.257 dB, and 21.627 dB. The analysis of methods using SSIM is displayed in Fig. 10c. When noise level is 3000, the SSIM evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 0.602, 0.781, 0.598, 0.666, and 0.467. The analysis of methods using SSIM is displayed in Fig. 10c. When noise level is 3000, the SSIM evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 0.602, 0.781, 0.598, 0.666, and 0.467. The EPI analysis is displayed in Fig. 10d. When noise level is 0.2, the EPI evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 0.6677, 0.6710, 0.6771, 0.7004, and 0.7670.
-
Analysis considering Gaussian noise
Figure 11 presents analysis of methods by adding Gaussian noise considering PSNR, SDME, SSIM, and EPI using CT image. The analysis of methods using PSNR is depicted in Fig. 11a. When the noise level is 0.1, the PSNR evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 19.136 dB, 11.459 dB, 11.487 dB, 12.025 dB, and 12.420 dB. The analysis of methods using SDME is displayed in Fig. 11b. When the noise level is 0.1, the SDME evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 27.435 dB, 28.592 dB, 32.189 dB, 17.824 dB, and 26.924 dB. The analysis of methods using SSIM is displayed in Fig. 11c. When the noise level is 0.1, the corresponding SSIM evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 0.529, 0.662, 0.561, 0.604, and 0.525. The EPI analysis is displayed in Fig. 11d. When noise level is 0.3, the EPI evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 0.7197, 0.7418, 0.7635, 0.7893, and 0.8558.
-
Analysis in the presence of uniform noise
Figure 12 presents analysis of methods by adding uniform noise considering PSNR, SDME, SSIM, and EPI using CT image. The analysis of methods using PSNR is displayed in Fig. 12a. When the noise level is 10, the PSNR evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 18.372 dB, 23.423 dB, 13.061 dB, 12.923 dB, and 24.149 dB. The analysis of methods using SDME is displayed in Fig. 12b. When the noise level is 10, the SDME evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 19.442 dB, 36.384 dB, 33.971 dB, 31.154 dB, and 32.142 dB. The analysis of methods using SSIM is displayed in Fig. 12c. When the noise level is 10, the SSIM evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 0.713, 0.765, 0.888, 0.780, and 0.800. The EPI analysis is displayed in Fig. 12d. When noise level is 40, the EPI evaluated by AFSWA, MDBU, DBAIN, BDND, and the proposed T2FCS + FAL are 0.7361, 0.7677, 0.7743, 0.8004, and 0.8291.
Fig. 9.
Analysis of methods considering random noise. a PSNR. b SDME. c SSIM. d EPI
Fig. 10.
Analysis of methods in the presence of salt and pepper noise. a PSNR. b SDME. c SSIM. d EPI
Fig. 11.
Analysis of methods considering Gaussian noise. a PSNR. b SDME. c SSIM. d EPI
Fig. 12.
Analysis of methods in the presence of uniform noise. a PSNR. b SDME. c SSIM. d EPI
Comparative Discussion
Table 3 describes the analysis of the proposed T2FCS + FAL with existing methods considering PSNR, SDME, SSIM, and EPI parameters. Here, the analysis is performed by using Lena image and CT image by varying noise levels. Using Lena image, the maximal PSNR of 21.520 dB is computed by the proposed T2FCS + FAL whereas the PSNR computed by existing AFSWA, MDBU, DBAIN, and BDND are 14.289 dB, 26.487 dB, 29.476 dB, and 21.341 dB. The maximal SDME of 55.511 dB is computed by the proposed T2FCS + FAL while the SDME computed by AFSWA, MDBU, DBAIN, and BDND are 21.827 dB, 40.432 dB, 41.811 dB, and 59.644 dB. The maximal SSIM of 0.874 is measured by the proposed T2FCS + FAL while the SSIM of AFSWA, MDBU, DBAIN, and BDND are 0.699, 0.757, 0.899, and 0.770. Using CT image, the maximal PSNR of 24.149 dB, maximal SDME of 32.142 dB, and maximal SSIM of 0.800 are computed by the proposed T2FCS + FAL.The maximum EPI attained by the proposed T2FCS + FAL is 0.9267 for uniform noise by considering Lena images.
Table 3.
Comparative analysis
| Images | Noise type | Metrics | AFSWA | MDBU | DBAIN | BDND | Proposed T2FCS + FAL |
|---|---|---|---|---|---|---|---|
| Lena image | Random noise | PSNR | 11.519 | 19.511 | 16.855 | 7.026 | 12.155 |
| SDME | 40.724 | 30.808 | 18.756 | 27.029 | 41.618 | ||
| SSIM | 0.544 | 0.584 | 0.712 | 0.530 | 0.617 | ||
| EPI | 0.7379 | 0.7482 | 0.7576 | 0.7760 | 0.8358 | ||
| Salt and pepper noise | PSNR | 12.120 | 18.672 | 16.422 | 9.517 | 10.802 | |
| SDME | 39.244 | 45.542 | 38.270 | 33.567 | 27.058 | ||
| SSIM | 0.529 | 0.831 | 0.524 | 0.573 | 0.600 | ||
| EPI | 0.7468 | 0.7683 | 0.7756 | 0.7957 | 0.8438 | ||
| Gaussian noise | PSNR | 11.539 | 28.140 | 9.517 | 14.144 | 11.066 | |
| SDME | 41.180 | 38.549 | 33.474 | 16.496 | 40.678 | ||
| SSIM | 0.535 | 0.832 | 0.572 | 0.503 | 0.460 | ||
| EPI | 0.7356 | 0.7464 | 0.7565 | 0.7759 | 0.8077 | ||
| Uniform noise | PSNR | 14.289 | 26.487 | 29.476 | 21.341 | 21.520 | |
| SDME | 21.827 | 40.432 | 41.811 | 59.644 | 55.511 | ||
| SSIM | 0.699 | 0.757 | 0.899 | 0.770 | 0.874 | ||
| EPI | 0.7646 | 0.7857 | 0.8058 | 0.8245 | 0.9267 | ||
| CT image | Random noise | PSNR | 17.642 | 17.613 | 22.267 | 8.307 | 13.864 |
| SDME | 29.784 | 25.869 | 20.212 | 28.153 | 32.498 | ||
| SSIM | 0.463 | 0.669 | 0.712 | 0.482 | 0.846 | ||
| EPI | 0.6980 | 0.7380 | 0.7472 | 0.7446 | 0.8042 | ||
| Salt and pepper noise | PSNR | 12.549 | 16.281 | 17.095 | 11.503 | 11.455 | |
| SDME | 30.482 | 30.810 | 23.849 | 32.257 | 21.627 | ||
| SSIM | 0.602 | 0.781 | 0.598 | 0.666 | 0.467 | ||
| EPI | 0.6684 | 0.6879 | 0.6888 | 0.7022 | 0.7705 | ||
| Gaussian noise | PSNR | 19.136 | 11.459 | 11.487 | 12.025 | 12.420 | |
| SDME | 27.435 | 28.592 | 32.189 | 17.824 | 26.924 | ||
| SSIM | 0.529 | 0.662 | 0.561 | 0.604 | 0.525 | ||
| EPI | 0.7330 | 0.7660 | 0.7728 | 0.8038 | 0.8624 | ||
| Uniform noise | PSNR | 12.372 | 23.423 | 32.061 | 21.523 | 24.149 | |
| SDME | 19.442 | 36.384 | 33.971 | 31.154 | 32.142 | ||
| SSIM | 0.713 | 0.765 | 0.888 | 0.780 | 0.800 | ||
| EPI | 0.7665 | 0.7898 | 0.8085 | 0.8247 | 0.8655 |
The performance of the proposed method is improved due to the following reasons:
In the devised method, for noisy pixel map generation is done by Deep CNN, which is trained by the Adam optimization. It boosts computational efficiency and reduces the memory requirements. The optimum weights are obtained from the Adam technique that assists to tune Deep CNN for producing optimum outcomes. Moreover, the noise removal is done by the proposed FAL algorithm, which is devised for computing optimal threshold value on the basis of promising efficiency. Besides, the image enhancement provides detailed information regarding different features like boundaries or edges by maximizing its dynamic ranges. Thus, the proposed method attains maximum performance than the conventional approaches.
Statistical Analysis
The statistical analysis of the methods is expressed in Table 4. This analysis is done with the evaluation metrics, such as PSNR, SDME, SSIM, and EPI, based on the best value, mean, and variance.
Table 4.
Statistical analysis
| Metrics/methods | PSNR | SDME | SSIM | EPI | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | Mean | Variance | Best | Mean | Variance | Best | Mean | Variance | Best | Mean | Variance | ||
| Lena image | |||||||||||||
| Random noise | |||||||||||||
| AFSWA | 11.519 | 11.515 | 0.004 | 40.724 | 40.721 | 0.003 | 0.544 | 0.541 | 0.003 | 0.7379 | 0.7375 | 0.0004 | |
| MDBU | 19.511 | 19.508 | 0.003 | 30.808 | 30.804 | 0.004 | 0.584 | 0.581 | 0.003 | 0.7482 | 0.7479 | 0.0003 | |
| DBAIN | 16.855 | 16.852 | 0.003 | 18.756 | 18.754 | 0.003 | 0.712 | 0.710 | 0.002 | 0.7576 | 0.7573 | 0.0003 | |
| BDND | 7.026 | 7.023 | 0.003 | 27.029 | 27.026 | 0.003 | 0.530 | 0.527 | 0.003 | 0.7760 | 0.7757 | 0.0003 | |
| Proposed T2FCS + FAL | 12.155 | 12.153 | 0.002 | 41.618 | 41.617 | 0.001 | 0.617 | 0.615 | 0.002 | 0.8358 | 0.8356 | 0.0002 | |
| Salt and pepper noise | |||||||||||||
| AFSWA | 12.120 | 12.117 | 0.003 | 39.244 | 39.240 | 0.004 | 0.529 | 0.526 | 0.003 | 0.7468 | 0.7464 | 0.0004 | |
| MDBU | 18.672 | 18.668 | 0.004 | 45.542 | 45.540 | 0.002 | 0.831 | 0.829 | 0.002 | 0.7683 | 0.7680 | 0.0003 | |
| DBAIN | 16.422 | 16.419 | 0.003 | 38.270 | 38.267 | 0.003 | 0.524 | 0.520 | 0.004 | 0.7756 | 0.7753 | 0.0003 | |
| BDND | 9.517 | 9.513 | 0.004 | 33.567 | 33.563 | 0.004 | 0.573 | 0.570 | 0.003 | 0.7957 | 0.7953 | 0.0004 | |
| Proposed T2FCS + FAL | 10.802 | 10.800 | 0.002 | 27.058 | 27.052 | 0.002 | 0.600 | 0.599 | 0.001 | 0.8438 | 0.8436 | 0.0002 | |
| Gaussian noise | |||||||||||||
| AFSWA | 11.539 | 11.535 | 0.004 | 41.180 | 41.177 | 0.003 | 0.535 | 0.532 | 0.003 | 0.7356 | 0.7353 | 0.0004 | |
| MDBU | 28.140 | 28.138 | 0.002 | 38.549 | 38.545 | 0.004 | 0.832 | 0.830 | 0.002 | 0.7464 | 0.7460 | 0.0003 | |
| DBAIN | 9.517 | 9.515 | 0.002 | 33.474 | 33.470 | 0.004 | 0.572 | 0.570 | 0.002 | 0.7565 | 0.7561 | 0.0003 | |
| BDND | 14.144 | 14.140 | 0.004 | 16.496 | 16.493 | 0.003 | 0.503 | 0.500 | 0.003 | 0.7759 | 0.7756 | 0.0004 | |
| Proposed T2FCS + FAL | 11.066 | 11.065 | 0.001 | 40.678 | 40.676 | 0.002 | 0.460 | 0.459 | 0.001 | 0.8077 | 0.8075 | 0.0002 | |
| Uniform noise | |||||||||||||
| AFSWA | 14.289 | 14.285 | 0.004 | 21.827 | 21.825 | 0.002 | 0.699 | 0.696 | 0.003 | 0.7646 | 0.7642 | 0.0004 | |
| MDBU | 26.487 | 26.485 | 0.002 | 40.432 | 40.430 | 0.002 | 0.757 | 0.755 | 0.002 | 0.7857 | 0.7853 | 0.0004 | |
| DBAIN | 29.476 | 29.473 | 0.002 | 41.811 | 41.808 | 0.003 | 0.899 | 0.896 | 0.003 | 0.8058 | 0.8055 | 0.0003 | |
| BDND | 21.341 | 21.338 | 0.003 | 59.644 | 59.640 | 0.004 | 0.770 | 0.767 | 0.003 | 0.8245 | 0.8242 | 0.0003 | |
| Proposed T2FCS + FAL | 21.520 | 21.518 | 0.002 | 55.511 | 55.510 | 0.001 | 0.874 | 0.872 | 0.002 | 0.9267 | 0.9265 | 0.0002 | |
| CT image | |||||||||||||
| Random noise | |||||||||||||
| AFSWA | 17.642 | 17.640 | 0.002 | 29.784 | 29.780 | 0.004 | 0.463 | 0.460 | 0.003 | 0.6980 | 0.6975 | 0.0005 | |
| MDBU | 17.613 | 17.610 | 0.003 | 25.869 | 25.866 | 0.003 | 0.669 | 0.665 | 0.004 | 0.7380 | 0.7376 | 0.0004 | |
| DBAIN | 22.267 | 22.263 | 0.004 | 20.212 | 20.209 | 0.003 | 0.712 | 0.709 | 0.003 | 0.7472 | 0.7470 | 0.0002 | |
| BDND | 8.307 | 8.303 | 0.004 | 28.153 | 28.150 | 0.003 | 0.482 | 0.479 | 0.003 | 0.7446 | 0.7442 | 0.0004 | |
| Proposed T2FCS + FAL | 13.864 | 13.862 | 0.002 | 32.498 | 32.496 | 0.002 | 0.846 | 0.844 | 0.002 | 0.8042 | 0.8040 | 0.0002 | |
| Salt and pepper noise | |||||||||||||
| AFSWA | 12.549 | 12.545 | 0.004 | 30.482 | 30.480 | 0.002 | 0.602 | 0.599 | 0.003 | 0.6684 | 0.6680 | 0.0004 | |
| MDBU | 16.281 | 16.278 | 0.003 | 30.810 | 30.807 | 0.003 | 0.781 | 0.777 | 0.004 | 0.6879 | 0.6875 | 0.0004 | |
| DBAIN | 17.095 | 17.090 | 0.005 | 23.849 | 23.845 | 0.004 | 0.598 | 0.593 | 0.005 | 0.6888 | 0.6885 | 0.0003 | |
| BDND | 11.503 | 11.500 | 0.003 | 32.257 | 32.254 | 0.003 | 0.666 | 0.662 | 0.004 | 0.7022 | 0.7019 | 0.0003 | |
| Proposed T2FCS + FAL | 11.455 | 11.453 | 0.002 | 21.627 | 21.625 | 0.002 | 0.467 | 0.466 | 0.001 | 0.7705 | 0.7703 | 0.0002 | |
| Gaussian noise | |||||||||||||
| AFSWA | 19.136 | 19.131 | 0.005 | 27.435 | 27.431 | 0.004 | 0.529 | 0.526 | 0.003 | 0.7330 | 0.7326 | 0.0004 | |
| MDBU | 11.459 | 11.454 | 0.005 | 28.592 | 28.590 | 0.002 | 0.662 | 0.660 | 0.002 | 0.7660 | 0.7657 | 0.0003 | |
| DBAIN | 11.487 | 11.484 | 0.003 | 32.189 | 32.185 | 0.004 | 0.561 | 0.558 | 0.003 | 0.7728 | 0.7724 | 0.0004 | |
| BDND | 12.025 | 12.021 | 0.004 | 17.824 | 17.820 | 0.004 | 0.604 | 0.600 | 0.004 | 0.8038 | 0.8034 | 0.0004 | |
| Proposed T2FCS + FAL | 12.420 | 12.418 | 0.002 | 26.924 | 26.923 | 0.001 | 0.525 | 0.523 | 0.002 | 0.8624 | 0.8622 | 0.0002 | |
| Uniform noise | |||||||||||||
| AFSWA | 12.372 | 12.370 | 0.002 | 19.442 | 19.439 | 0.003 | 0.713 | 0.710 | 0.003 | 0.7665 | 0.7660 | 0.0005 | |
| MDBU | 23.423 | 23.420 | 0.003 | 36.384 | 36.380 | 0.004 | 0.765 | 0.761 | 0.004 | 0.7898 | 0.7895 | 0.0003 | |
| DBAIN | 32.061 | 32.057 | 0.004 | 33.971 | 33.968 | 0.003 | 0.888 | 0.884 | 0.004 | 0.8085 | 0.8080 | 0.0005 | |
| BDND | 21.523 | 21.520 | 0.003 | 31.154 | 31.150 | 0.004 | 0.780 | 0.777 | 0.003 | 0.8247 | 0.8244 | 0.0003 | |
| Proposed T2FCS + FAL | 24.149 | 24.147 | 0.002 | 32.142 | 32.140 | 0.002 | 0.800 | 0.798 | 0.002 | 0.8655 | 0.8653 | 0.0002 | |
Conclusion
This paper presents a novel ODVV filter with hybrid optimization technique, namely the FAL algorithm, for medical image denoising. Here, the input medical images are subjected to noisy pixel map identification module in which the Deep CNN is employed to identify noisy pixel maps. Here, Deep CNN training is carried out with the Adam technique. After the identification of noisy pixels, it is further subjected to a noise removal phase which is performed with the proposed hybrid optimization technique, namely the FAL algorithm. Here, the proposed FAL is obtained by integrating the FAT and Lion algorithm. Once the noise removal phase is done, the enhancement of pixel is carried out using vectorial total variation norm in order to get final pixel-enhanced image. The proposed FAL outperformed other techniques with the highest PSNR of 24.149 dB, highest SDME of 32.142 dB, highest SSIM of 0.800, and highest EPI of 0.9267. The proposed method is used to denoise the image without losing any imperative information. Also, the proposed method is useful in various applications, such as visual tracking, image restoration, image segmentation, image registration, and image classification. In future, other medical data classification datasets can be adapted for evaluating the competence of the proposed technique. Moreover, sophisticated optimization methods can be explored to reveal effectiveness of classical techniques. Also, the performance will be evaluated by considering other medical images, such as MRI and X-ray images.
Data Availability
Dataset is available on online web portal of NIH clinical centre and accessible to everyone.
Declarations
Conflict of Interest
The author declares no competing interests.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Sameera, V., Sagheera, Mand Georgeba, S.N. A review on medical image denoising algorithms, Biomedical Signal Processing and Control, vol. 61, no. 102036, 2020.
- 2.Jifara, W., Jiang, F., Rho, S., Cheng, Mand Liu, S., Medical image denoising using convolutional neural network: a residual learning approach, The Journal of Supercomputing, vol.75, no.2, pp.704–718, 2019.
- 3.Ji, L., Guo, Qand Zhang, M., Medical image denoising based on biquadratic polynomial with minimum error constraints and low-rank approximation, IEEE Access, vol.8, pp.84950–84960, 2020.
- 4.Raj, V.N.P and Venkateswarlu, T., Denoising of medical images using image fusion techniques, Signal and Image Processing: An International Journal (SIPIJ), vol.3, no.4, August 2012.
- 5.Miria A, Sharifianb S, Rashidib S, Ghods M. Medical image denoising based on 2D discrete cosine transform via ant colony optimization. Optik. 2018;156:938–948. doi: 10.1016/j.ijleo.2017.12.074. [DOI] [Google Scholar]
- 6.Mohana J, Krishnaveni V, Guo Y. A survey on the magnetic resonance image denoising methods. Biomedical Signal Processing and Control. 2014;9:56–69. doi: 10.1016/j.bspc.2013.10.007. [DOI] [Google Scholar]
- 7.Binh, N.T and Khare, A., Adaptive complex wavelet technique for medical image denoising, In Proceedings of Third International Conference on the Development of Biomedical Engineering in Vietnam, Springer, Berlin, Heidelberg.pp. 196–199,2010.
- 8.Chithra RS. Jagatheeswari. P, Enhanced WOA and modular neural network for severity analysis of tuberculosis, Multimedia Research. 2019;2(3):43–55. [Google Scholar]
- 9.Do, M.N and Vetterli, M., The contourlet transform: an efficient directional multiresolution image representation, IEEE transactions on image processing, vol. 14, no. 12, December 2005. [DOI] [PubMed]
- 10.Bai J, Song S, Fan T, Jiao L. Medical image denoising based on sparse dictionary learning and cluster ensemble. Soft Computing. 2018;22(5):1467–1473. doi: 10.1007/s00500-017-2853-7. [DOI] [Google Scholar]
- 11.Dogra, A., and Goyal, B., Medical image denoising, Austin Journal of Radiology, October 2016.
- 12.Satapathy LM, Das P, Shatapathy A, Patel AK. Bio-medical image denoising using wavelet transform. International Journal of Recent Technology and Engineering (IJRTE) 2019;8(1):2277–3878. [Google Scholar]
- 13.Aravindan, T.E., Seshasayanan, Rand Vishvaksenan, K.S., Medical image denoising by using discrete wavelet transform: neutrosophic theory new direction, cognitive Systems Research, cogsys, vol.27, 2018.
- 14.Rani, M.L.P., Rao, G.S and Rao, B.P., ANN application for medical image denoising, In Soft Computing for Problem Solving, pp. 675–684, Springer, Singapore, 2019.
- 15.Laves, M-H., Tolle, Mand Ortmaier, T., Uncertainty estimation in medical image denoising with Bayesian deep image prior, arXiv preprint arXiv:2008.08837, 2020.
- 16.Kumar, S.V and Nagaraju, C., T2FCS filter: type 2 fuzzy and cuckoo search-based filter design for image restoration, Journal of Visual Communication and Image Representation, vol.58, pp.619–641, 2019.
- 17.Li, Q.Q., He, Z.C and Li, E., The feedback artificial tree (FAT) algorithm, Soft Computing, pp.1–28, 2020.
- 18.Boothalingam, R., Optimization using lion algorithm: a biological inspiration from lion’s social behavior, Evolutionary Intelligence, vol.11, pp.1–2, pp.31–52, 2018.
- 19.Bresson X, Chan TF. Fast dual minimization of the vectorial total variation norm and applications to color image processing. Inverse problems and imaging. 2008;2(4):455–484. doi: 10.3934/ipi.2008.2.455. [DOI] [Google Scholar]
- 20.Kingma, D.P. and Ba, J., Adam: a method for stochastic optimization, arXiv preprint arXiv:1412.6980, 2014.
- 21.Tu, F., Yin, S., Ouyang, P., Tang, S., Liu, Land Wei, S., Deep convolutional neural network architecture with reconfigurable computation patterns, IEEE Transactions on Very Large-Scale Integration (VLSI) Systems, vol.25, no.8, pp.2220–2233, 2017.
- 22.Babu, G.S., Zhao, P and Li, X-L., Deep Convolutional Neural Network Based Regression Approach for Estimation of Remaining Useful Life, International Conference on Database Systems for Advanced Applications (DASFAA), pp. 214–228, 2016.
- 23.National Institutes of Health - Clinical Center taken from, https://nihcc.app.box.com/v/DeepLesion/folder/50715173939, Accessed on December 2020.
- 24.Varghese J, Ghouse M, Subash S, Siddappa M, Khan MS, Hussain OB. Efficient adaptive fuzzy-based switching weighted average filter for the restoration of impulse corrupted digital images. IET Image Processing. 2014;8(4):199–206. doi: 10.1049/iet-ipr.2013.0297. [DOI] [Google Scholar]
- 25.Esakkirajan, S., Veerakumar, T., Subramanyam, A.N and PremChand, C.H., Removal of high-density salt and pepper noise through modified decision based unsymmetric trimmed median filter, IEEE Signal processing letters, vol.18, no.5, pp.287–290, 2011.
- 26.Kannan, K. and Perumal, S.A., Combined denoising and fusion of multi focus images, Int. J. Adv. Res. Comput. Sci. Softw. Eng, vol.2, no.2, 2012.
- 27.Ng PE, Ma KK. A switching median filter with boundary discriminative noise detection for extremely corrupted images. IEEE Transactions on image processing. 2006;15(6):1506–1516. doi: 10.1109/TIP.2005.871129. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Dataset is available on online web portal of NIH clinical centre and accessible to everyone.