Emerging Trends of Computational Chemistry and Molecular Modeling in Froth Flotation: A Review

Abstract

Froth flotation is the most versatile process in mineral beneficiation, extensively used to concentrate a wide range of minerals. This process comprises mixtures of more or less liberated minerals, water, air, and various chemical reagents, involving a series of intermingled multiphase physical and chemical phenomena in the aqueous environment. Today’s main challenge facing the froth flotation process is to gain atomic-level insights into the properties of its inherent phenomena governing the process performance. While it is often challenging to determine these phenomena via trial-and-error experimentations, molecular modeling approaches not only elicit a deeper understanding of froth flotation but can also assist experimental studies in saving time and budget. Thanks to the rapid development of computer science and advances in high-performance computing (HPC) infrastructures, theoretical/computational chemistry has now matured enough to successfully and gainfully apply to tackle the challenges of complex systems. In mineral processing, however, advanced applications of computational chemistry are increasingly gaining ground and demonstrating merit in addressing these challenges. Accordingly, this contribution aims to encourage mineral scientists, especially those interested in rational reagent design, to become familiarized with the necessary concepts of molecular modeling and to apply similar strategies when studying and tailoring properties at the molecular level. This review also strives to deliver the state-of-the-art integration and application of molecular modeling in froth flotation studies to assist either active researchers in this field to disclose new directions for future research or newcomers to the field to initiate innovative works.

1. Introduction

Froth flotation is a widely used mineral processing method that can be custom designed to recover valuable minerals from a wide range of ores. With a century-long technological tradition in the field, it is undoubtedly the “via regia” of mineral separation.¹ In this process, desirable minerals are separated from undesirable ones by direct or reverse flotation based on inherent differences in wettability, although these are often artificially induced by the addition of chemical reagents to force the emergence of hydrophobic contrasts. However, this contrast is elicited, it is the introduction of tiny air bubbles into the pulp that provides the hydrophobic mineral carrier and enables mineral separation. The interfacial chemistry that governs flotation involves numerous complex phenomena, including adsorption and desorption of reagents, conformation and rearrangement of reagents on the mineral surface, translocation, dissolution, surface modification and reconstruction, precipitation, and so on.^2,3 These interactions between water, air, and minerals make the process a multifaceted and intrinsically complex phenomenon.^2,3

As in any engineering field, the evolutionary dynamics of knowledge that helped to establish flotation as a distinct discipline has essentially and traditionally relied on macroscopic experimental observations, empirical recipes, and more or less reliable analytical protocols, long before the modern “atomistic” view as we manipulate it today could open up new breaches and perhaps initiate a paradigm shift.^1,2 As insightful as these traditional approaches have been, they cannot keep up with the increasing complexity of today’s exploitable resources. This is primarily due to the ever-decreasing amounts and quality of target minerals in the matrices of newly discovered and mined deposits. Direct measurement of the microphenomena at the interfaces of these mineral matrices, which are confined to the immediate atomic neighborhood of the target elements, is difficult, if not impossible, without first having an atomic resolution to map flotation phenomena at the Angstrom or nanometer scale.⁴ Ores containing trace amounts of rare earth elements, gold in arsenopyrite solid solutions, niobium in pyrochlore or columbite are some prominent examples, to name a few.⁵⁻⁸

A notable advance in mineral froth flotation studies to date has been the popularity of tools such as computational chemistry and molecular modeling to represent the minute geometric details at the atomic scale that can account for the specificity of thermodynamic, (electro)kinetic, and colloidal phenomena of mineral surfaces.^4,9,10 Since its first application to mineral froth flotation in 1993,¹¹ this tool has contributed to a better understanding of reagent adsorption on mineral surfaces, reagent conformation and desorption, mineral crystal and surface chemistry, mineral surface modification and dissolution, and interfacial phenomena at mineral/water/gas interfaces.^4,9,12−18 However, advances in the near future are also a priority, as easily processed ores are rapidly depleted, leaving only very complex ores that are much more difficult to beneficiate.¹⁹ In addition to the depletion of high-grade deposits, the negative environmental impact of reagents used in ore beneficiation has become a concern that can no longer be ignored. Therefore, developing highly selective reagents is essential for the sustainable development of mineral beneficiation processes. Just as the advent of computational fluid dynamics tools has benefited chemical reactors and separations to simulate as many different scales of flow as possible with sufficient spatial and temporal resolution,²⁰ molecular modeling is emerging as an indispensable tool for atomic resolution simulations needed to control and understand fluid-mineral interface phenomena and, ultimately, to tailor environmentally friendly reagents.⁴

Despite a large number of papers and several recent reviews on flotation, there are many conceptual and practical gaps in the coverage of the application of molecular modeling approaches in this field. From available literature it is clear that mineral processing community has not yet benefited from the advantages of molecular modeling techniques to the extent that other fields, such as pharmaceutical and polymer sciences, have. The advent of commercial packages has reduced attention to the fundamental aspects of molecular modeling and limited the level of postprocessing to those available in the graphical user interface. Worryingly, even in some applications, the basic theories and statistical concepts have been overlooked, and the interpretation of results has been fraught with many uncertainties. Scrutiny in the recent review papers further revealed a lack of emphasis on the postprocessing scenarios applicable to flotation processes, particularly within the molecular dynamics (MD) framework.¹⁴⁻¹⁷ For example, the recent review by Liu et al.¹⁴ focused on the theory behind various molecular modeling techniques and a recension of published work on the design of flotation collectors. Zhao et al.¹⁵ assessed the theories and characterization approaches of first-principle calculations, chiefly density functional theory (DFT), in adsorption studies of organic molecules on mineral surfaces at liquid–solid or gas–solid interfaces. Foucaud et al.¹⁶ reviewed the recently published articles using molecular modeling techniques in an illustrative-themed, focusing on liquid–solid adsorption phenomena. The most recent review article that comprehensively addressed the role of molecular modeling was limited exclusively to low-rank coal flotation, targeting coal-water, coal-reactive, coal-bubble, and coal-clay interactions, but without details for postanalysis.¹⁷ In this presentation, it was deemed appropriate to devote a review of the advanced approaches and critical postprocessing concepts and methods that are widely applicable in the flotation field. Further, we enumerate the molecular modeling approaches that have been applied in flotation studies to date, with emphasis on their potential from a practical point of view. Knowledge of the directions, prospects, and challenges for future applications of molecular modeling in mineral processing needs further attention to maximize the benefits from the development of computational approaches.

To this end, this contribution aims to provide froth flotation researchers with the insight needed to use molecular modeling to address the challenges of this discipline and to identify new research directions. To this end, this review is organized as a diptych. In the first part, we provide the descriptive framework of the principles underlying the molecular modeling approaches used in flotation by focusing on the types of data mining strategies related to flotation. In the second part, several representative examples of molecular modeling applications in froth flotation studies are discussed under the five headings reflecting current research priorities. Our presentation strategy in this section is more illustrative, but critical comments and suggestions are also included whenever necessary for clarification. Finally, we conclude this review with a brief summary and outlook on open problems in the field of flotation related to minerals computation.

2. Molecular Modeling Approaches Emphasizing Flotation Studies

Molecular modeling techniques and their rise in popularity have taken a quantum leap over the past two decades. Nowadays, several techniques and software (both commercial or open-source) are available to perform computational chemistry calculations,¹⁵ and advances in high-performance computing (HPC) infrastructure have expanded their applications. Molecular modeling approaches, in general, are proving to be powerful tools to shed light on different ranges of structural and dynamic properties, starting from the fundamental physics associated with a given microstructure.

Froth flotation involves three phases, namely, liquid, gas, and solid, as well as interfacial phenomena governing the solid–liquid and gas–liquid interfaces.¹ In the flotation process, it is mainly the interfacial interactions between the dissolved reagents and minerals on the one hand, and the bubbles, on the other hand, that are at the center of the modeling at the molecular or atomic scale. The simulation results provide practical guidance for identifying the most effective mechanisms and facilitate the development of chemicals with improved performance rationally and systematically (applications discussed in depth in section 3).

The most common classification of molecular modeling methods labels them according to the time and length scales they are designed to represent. Figure 1 schematically aggregates the categories of simulation methods at the corresponding length and time scales.

Figure 1.

Schematic representation of the various molecular modeling techniques and the corresponding length and time scales (QM = Quantum Mechanics, HF = Hartree–Fock, DFT = Density Functional Theory, AIMD = Ab initio Molecular Dynamics, ReaxFF = Reactive Force field, MM = Molecular Mechanics, MD = Molecular Dynamics, MC = Monte Carlo).

Not surprisingly, the more accurate the method, the higher the computational cost, the smaller the accessible size scale, and the shorter the time scale. Quantum mechanical (QM) methods, particularly density functional theory (DFT), which includes electronic structure calculations, can routinely handle a few hundred atoms in the simulation. In contrast, methods that do not explicitly include electrons, such as force field methods like classical molecular dynamics (MD), can be applied to thousands of atoms and track their evolution over a few hundreds of nanoseconds.

The molecular modeling methods can be further classified according to the type of properties they can handle. QM methods provide nearly exact descriptions of system energy, adsorption energy, chemical bond cleavage/formation, band structure, bond population, etc., taking into account the electronic structure of constituent atoms.²¹ In contrast, in force field approaches, intra- and intermolecular interactions are expressed by analytical functions, taking into account the energy contributions of valence and nonbond interactions.^4,21 Broadly speaking, molecular mechanics (MM) is well suited to the study of dynamic processes such as thermal properties, adhesion, diffusion, and wettability. Compared to QM methods, the effect of charge transfer, polarization, and bond breakage/formation cannot be modeled in classical MM techniques.

Hybrid atomistic methods were introduced to include the advantages of both QM and MM theories in a simulation. Ab initio molecular dynamics (AIMD)²²⁻²⁶ and the hybrid QM/MM algorithm²⁷⁻²⁹ are the two well-known methods in this category. The former method falls in the QM region, while the latter includes the overlap region between QM and MM simulations (Figure 1). Combining DFT and MD in AIMD, chemical molecular processes and reactions, as well as the effect of finite temperature and pressure, can be included in the simulations.^25,26 For the QM/MM method, the general idea is to encompass the merits of both QM and MM so that the electronically important region (i.e., reactive region) of the system is treated with the more accurate QM methods, while for the surrounding region, lower-level simulation methods (e.g., classical MD) are allowed.²⁷ These assumptions would considerably speed up the simulation.²⁷

The reactive molecular dynamics method (also called ReaxFF) is another route to bridge the gap between QM and MM approaches.³⁰⁻³⁵ In the ReaxFF method, dynamic bonds and polarization effects are incorporated into the force field formulations through preset ab initio calculations and stored in the force field file.^30,35 As a result, the bond formation/breakage can be modeled continuously in ReaxFF simulations. The primary challenge here is the accessibility of an efficient and scalable reactive force field for the system of interest. Otherwise, the ReaxFF method is limited to significantly larger lengths and time scales than the QM techniques.

This section briefly summarizes molecular modeling related to the flotation process, including DFT, MD (classical and reactive), and some hybrid methods. For hybrid simulation methods, AIMD and QM/MD techniques would be targeted. Without dwelling on the founding theories described competently elsewhere,³⁶ the primary focus here is to discuss and compare the general features, application areas, and advantages/disadvantages of each technique.

2.1. Quantum Mechanical Calculations: Density Functional Theory

In quantum mechanical calculations, the nuclei and the (multi)electron interactions, and the system’s energy are described by the well-known Schrödinger equation.^37,38 The complete solution of Schrödinger’s equation, if it is computable at all, is equivalent to a formidable complex many-body problem.^39,40

Two independent steps are often used to ease the computational burden instead of solving the Schrödinger equation. The first, known as the Born–Oppenheimer approximation,⁴¹ assumes that the nuclei are immobile, given that the mass of a proton is 3 orders of magnitude greater than that of an electron. The nuclei merely act as a source of electrostatic potential for the electrons in the electronic structure calculations. The second, which in practice is a combination of several approximations, is often classified as a first principle or ab initio method.²¹ The ab initio approaches can be divided into two main branches, including wave function-based methods, which all start from the Hartree–Fock method,^42,43 and density-based methods, which are mainly based on density functional theory.⁴⁴ Density-based methods are the most commonly used electronic structure methods.

2.1.1. Simulation Setups in DFT

In all molecular modeling approaches, constructing the initial simulation box is a crucial step that must be handled with careful consideration. The simulation cell must be large enough to (a) freely allow all necessary changes in the structure (e.g., surface reconstruction) and (b) eliminate any undesirable interactions between the periodic images of any asymmetrical feature in the structure (e.g., defects). In most cases, the simulation cell consists of a slab model representing a surface of the adsorbate. In slab models, additional precautions must be taken in the nonperiodic direction by considering sufficient atomic layers in the surface and vacuum size. Verification of the system size (including slab surface area, number of atomic layers, and vacuum size) is an essential step in the preprocessing, usually performed by monitoring the convergence of the surface energy and/or the energy change caused by the nonperiodic feature (e.g., defect formation energy).

Previous investigations revealed that the initial arrangements of a complex system also directly affect the adsorption studies in DFT problems.⁴⁵⁻⁵¹ In order to find the most stable adsorption mode in a complex, combinations of all potential initial relative positions of adsorbents and adsorbates must be constructed and evaluated. For small linear molecules, a manual initialization is possible.⁴⁷ However, for complexes containing larger adsorbate molecules and/or surfaces with local disorder (such as a deficiency), it is highly plausible to miss a key initial mode, leading to inaccurate prediction of the globally optimized adsorption configuration. Alizadeh Sahraei and Larachi⁴⁹⁻⁵¹ suggested that the grand canonical Monte Carlo (GCMC) method could be a robust framework for searching all the potential initial configurations in DFT calculations. Their procedure was tested on the adsorption of a molecule, a monolayer and a multilayer of water, and a solvated or nonsolvated amino acid on sphalerite surfaces with and without defects. It should be noted that the reliability of GCMC simulations depends on the availability of accurate force fields for the system; otherwise, the GCMC pretreatment would converge to unrealistic configurations.

The key to the DFT method is to combine the nuclei and the effective potentials into a single external potential for each electron, known as the exchange-correlation functional.^40,52 Among the simulation parameters, the choice of the exchange-correlation functional is key for the accuracy of DFT calculations. The main difficulty with DFT is that there is no exact mathematical expression for the exchange-correlation functionals, so some approximations are needed in the first place. The local density approximation (LDA) is the simplest approximation for the exchange-correlation functional. It assumes that the energy is only related to the value of the electronic density at each point in space.⁵³ Previous investigations have shown that LDA does not produce reliable results for structures with chemical bond breakage/formation (as this is a crucial topic in flotation modeling).^54,55 The electron density gradient is included in the exchange-correlation functional by introducing a new family of functionals known as generalized gradient approximation (GGA).⁵⁶ The most popular functionals in the GGA class are Perdew–Burke–Enzerhof (PBE), PBEsol, PW91, and BLYP. Meta-GGA and hybrid functionals are the next-generation functionals⁵⁶⁻⁶⁰ (i.e., further discussion and the amendments the exchange-correlation functionals continually undergo can be found in the literature.)^40,44 In general, the richer a function is in terms of physical description, the more expensive the simulation is in terms of computation, although the results are more accurate. Perdew and Schmidt have suggested the idea of “Jacob’s Ladder” to select functionals in DFT problems.⁶¹ The ladder starts with LDA and then gradually rises in accuracy to GGA, meta-GGA, hybrid, and ultimate exact functionals.

In standard DFT, dispersion or van der Waals interactions are not accurately taken into account by the exchange-correlation functional. One efficient solution is to add an analytical correction term to the exchange-correlation functional.⁶²⁻⁶⁵ Although this comes at the expense of a more laborious calculation, the results indicate that the corrections would include the physics necessary for capturing most phenomena reliably.⁶⁶⁻⁶⁹

The choice of the basis set and k-points should also be considered carefully.^21,40 Basis sets are the representation of wave functions, and their quality is determined by the number and type of basis functions in their formulations. The k-points are defined for periodic systems and are the sampling points in the first Brillouin zone of the model in reciprocal space. The widely used method for k-point sampling is the Monkhorst–Pack mesh. In general, it is essential to pre-evaluate the convergence of the energy, electronic structure, and target properties of the system based on different functionals, basis sets, and k-point sizes. Parameter verification tests can be very time-consuming; however, the prejudice of rerunning all simulations caused by choosing inappropriate input parameters will be much greater. Finally, it is important to emphasize that there is no prescription for parameter selection in DFT, and caution against blind reliance on the recommendations of others or the default values offered by simulation codes is to be exercised. Overall, a lack of understanding or the likening of modern simulation codes to a black box can be tendentious, but if the results are apparently convergent.

2.1.2. DFT Analysis

Energy Calculations in DFT

Depending on the system, many different relative energies can be calculated and applied to interpret the results. The apparent adsorption energy or affinity is frequently used to comment on the most stable adsorption configuration in a complex after DFT geometry optimization (applications discussed in section 3.1). On the basis of the definition:

1

where E_total is the total energy of the system containing both the adsorbent and the adsorbates, E_adsorbent represents the energy of the optimized bare adsorbent surface, and E_adsorbate is the optimized energy of an isolated adsorbate molecule(s). Note that the energy calculations for all the systems and subsystems must be performed with the same convergence parameters. The relative energy obtained by eq 1 is called “interaction energy” when E_adsorbent and E_adsorbate are the single point energy of the naked adsorbent surface and the adsorbate, retaining the structure as in the adsorbed situation.^49,50 The more negative values of E_ads suggest stronger adsorption of the adsorbate on the adsorbent surface.

Vacancies and dislocations are common defects within bulk materials, especially minerals⁷⁰⁻⁷² (applications discussed in section 3.5.2). The defect formation energy per defect can be calculated as²¹

2

where E_defective is the energy of the system with the defect, E_{vacant_atom} represents the energy of the isolated atom removed to create the defect, and E_defect-free is the energy of the defect-free system. It is suggested to calculate the defect formation energy in two stages: (1) without further relaxation and (2) after relaxation of the defective surface. By comparing these two energies, the contribution of the relaxation to defect stabilization can be characterized.

The surface formation energy, or in short, the surface energy, is typically calculated with the intention of classifying the cleavage plane of a crystal structure. The surface energy in a vacuum is defined as^73,74

3

where E_slab is the energy of the slab with two surfaces, A is the surface area, E_bulk is the energy of the bulk unit cell structure, and N represents the number of unit cells in the slab. To build a surface, the starting bulk structure should be thick enough to guarantee the convergence of the surface energy.

In the case of a hydrated surface, the surface energy of the surface is calculated as follows:^75,76

4

where E_slab^N_H2O is the energy of the optimized slab in the presence of explicit water molecules on the surface, N_H2O is the number of water molecules on the surface, and E_H2O is the energy of a single water molecule using the same calculation parameters. G_corr = −H_vap – TS_liq is the experimental free energy correction for the reference state of bulk water, where H_vap is the water evaporation enthalpy and S_liq^° is the absolute entropy of liquid water. In most cases, the entropy of strongly adsorbed water can be ignored.^75,76

The activation energy determines the minimum energy to be supplied to the reactants for a chemical reaction to occur, and it cannot be evaluated on the sole basis of the total energies of the products and reactants. A transition state calculation is required to find the transition state configuration. The activation energy is then calculated as the energy difference between the reactants and the obtained transition state.⁴⁰ The activation Gibbs free energy and, consequently, the reaction rate constant can also be obtained through transition state simulations.

Population Analysis in DFT

Population analysis, also known as charge distribution, is a postprocessing approach often included in DFT studies. However, one must be aware of differences in the formulations used to predict atomic partial charges. Ambiguity in the methods stems from how regions of space to atoms are assigned and how areas of overlap between atoms are treated.²¹ The two best-known methods are the Hirshfeld⁷⁷ and Becke⁷⁸ schemes, which operate based on devising the overlapping area between atoms by assigning them different weights. The weights in the Hirshfeld scheme are assigned according to the contribution of each atom in the charge density, while for the Becke scheme, the atomic region shares are defined by a generalization of Voronoi polyhedra.⁷⁹

The atoms-in-molecules Bader approach is another widely used method,⁸⁰ which determines the position of transitions between atoms by analyzing the charge density topology. This method is more computationally expensive than the first two methods since it requires a full electron density analysis to calculate the atomic partial charges. The Mulliken method,⁸¹ which is applicable with localized basis sets, is also commonly used for charge calculations. The Mulliken method, in particular, is highly dependent on the basis set; thus, the output can be overly unreliable. Overall, extra caution would be warranted when implementing the Mulliken method for population analysis.⁷⁹

Bond population analysis is further implemented to quantify the possibility of bond formation/breakage in a system, considering the overlap of charge density between atom pairs. The higher the bond population value, the higher the bond covalency levels. Note that most visualization codes can predict bonds in a system using a heuristic algorithm based on the distance between atoms and their van der Waals radii. One has to be aware however that the method is a purely distance-based prediction, so care must be taken to avoid misinterpretations.

Atom Reactivity in DFT

The most important orbitals for the reactivity of molecules are the frontier orbitals, called the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO).^21,40 The energy difference between the HOMO and LUMO is termed the band gap or HOMO–LUMO gap. In general, molecules with a larger band gap are less reactive. Note that functionals suffering from a self-interaction error do not provide an accurate result for the calculation of the HOMO–LUMO gap.²¹ The Fukui functions further characterize the reactivity of atoms in DFT calculations.⁸²⁻⁸⁶ In this description, the distribution of electron densities in the HOMO and LUMO is recognized as the factor defining the reactivity of an atom. The explicit expression of Fukui indices, using finite difference approximation, is given by

5

6

where f⁺ and f^– functions measure the reactivity per nucleophilic and electrophilic attacks, respectively, and ρ_K(r) (K = N – 1, N, N + 1) denotes the electron density at a point r of a K-electron system. The value of f⁺ reflects the ability of an atom to accommodate an extra electron while f^– signifies the ability of an atom to cope with the loss of an electron.⁸⁶ The larger the values of f⁺ and f^–, the more reactive the region during electrophilic and nucleophilic attacks, respectively.

The density of states (DOS) measures the proportion of states to be occupied in an energy window. DOS results can be applied to characterize the valence bandwidth and energy gap in insulators and to qualitatively interpret the reactivity by comparing the location and intensity of orbital peaks.²¹ For systems with local discontinuities, such as surfaces and defects, the DOS of the whole system is often not informative.²¹ In these cases, the projected density of states (PDOS) of a particular atom or group of atoms would be more instructive, although one should be aware of the illusory character of projecting the DOS onto atoms due to the delocalized nature of the wave functions in DFT.

Vibrational Spectroscopy in DFT

Vibrational spectroscopies, such as infrared (IR), Raman, and NMR, can also be extracted from DFT calculations. In DFT, the calculated frequencies are sometimes rescaled for convenience of comparisons with experimental spectra, as provided by Alecu et al.⁸⁷ Frequency analysis is also included in the transition state search, in which a configuration with only one imaginary frequency manifests the genuine transition state mode. In geometry optimization, the absence of imaginary frequencies confirms the obtained structure as a globally optimized structure. Optical spectroscopies could be addressed by time-dependent DFT (TD-DFT) simulation,⁸⁸⁻⁹⁰ which is outside the scope of this review.

2.2. Molecular Dynamics Simulations

Molecular dynamics (MD) is a simulation of a time-dependent motion of the particles, atoms, or molecules dynamically framed according to Newton’s equation of motion under different ensembles, each fixes some thermodynamic variables in order to simulate the process that occurs in reality.⁹¹ The number of atoms, volume, pressure, temperature, and energy are variables that can be fixed at the cost of additional equations coupled to the equations of motion. Fixing thermodynamic variables relates to a specific ensemble like NVT, NVE, NPT, etc.

This computational approach ignores the explicit presence of electrons in the calculation and assigns the properties to the nucleus of the atoms. Therefore, classical molecular dynamics is not able to estimate the properties that contribute to the electron effect. Newton’s equation of motion requires the force between the atoms in the simulation box, which brings us to the core of molecular dynamics: the force field.⁹²⁻⁹⁴

Force fields are known as the engine of MD simulations and are sets of (analytical) equations that can describe the potential energy between constituent atoms.⁹³ There are different types of force fields, and each has advantages and disadvantages that need to be considered. Each force field has bonded and nonbonded parts comprised of different sets of interactions. The bonded terms in the force field attempt to incorporate covalent bonds into the calculations by defining the potential energy contributed to the stretching of two-atom bonds, the bending of three-atom angle, and the deformation of four-atom dihedra. Nonbonded force field terms cover electrostatic and van der Waals interactions between atoms. van der Waals interaction occurs at a much shorter distance between the atoms. A cutoff radius is assigned to the van der Waals interaction to ignore the force calculation beyond this distance. For long-range electrostatic forces, more complicated approaches such as Ewald summation and particle–particle particle-mesh (PPPM) are employed to calculate electrostatic forces at much larger distances.⁹³ Other potential interactions, especially bonded potential, have been proposed, taking into account the cross-terms of bond–bond, bond-angle, etc. COMPASS⁹⁵ and PCFF⁹⁶ are examples of this family of force fields. By adding more terms to the force field formulation, the accuracy of the force calculation is expected to increase, as well as the computational cost. CHARMM,⁹⁷ OPLS,^98,99 GROMOS,¹⁰⁰ and AMBER¹⁰¹ are also among the well-known force fields used in molecular simulation methods.

In contrast to the rich availability of force fields for organic molecules, inorganic compounds (e.g., silicates, oxides, aluminates, metals, etc.) suffer from a lack of accurate and compatible force field parameters. Even if they existed, the simulation of organic–inorganic interfaces is hardly feasible when the energy expressions of the compound are dissimilar. In this regard, an early attempt to develop specialized force fields was modifying CSHFF or ClayFF¹⁰² to be compatible with harmonic energy expressions in PCFF, CHARMM, AMBER, COMPASS, and OPLS-AA, which allowed reliable MD simulations of interfaces of chemical admixtures and cement-related minerals.^103−106 However, the energy expressions were limited in transferability and could not apply to the large, diverse family of minerals. More recently, Heinz et al.^107,108 introduced a collection of all-atom parameters for more than 20 common minerals and metals within the INTERFACE force field compatible with PCFF, CVFF, and CHARMM. With all their achievements, developing a universal and concerted force field to describe the inorganic–organic systems has remained a work in progress.

Among all the substances and materials, the aforementioned force fields could be applied to, special attention must be given to water as the working fluid in the flotation process. There are numerous models of water, each attempting to describe the properties of water in a more realistic way. The existing water force fields attempt to model the molecules based on assumptions such as rigidity, partial atomic charge, and the number of sites. Among the water models, SPC/E, TIP3P, 4-site models, and higher accuracy models are the most recommended ones.^109,110

All the force fields mentioned above are classical, meaning that they are not able to describe bond breaking/formation during the simulation. In this regard, reactive force fields (ReaxFF) were developed for a narrower range of atom types and molecules to overcome this limitation. Reactive force fields can be categorized as methods that lie between quantum calculation and classical molecular dynamics.³⁴ First introduced by Van Duin³⁰ in 2001, reactive force fields have opened up promising glades in the approach to molecular simulations. ReaxFF potentials incorporate more electron-based behaviors into the force field, making it more robust in monitoring systems that include bond dissociation/formation phenomena. More details about the force field and its contributed equations can be found in ref.³⁰ Implementing MD simulations with reactive force fields would increase the computational cost because the force field needs a much shorter time step for convergence. To date, many parameter sets are published for different types of atoms and materials (such as silica)^111−113 that could also be applicable to mineral flotation simulations.^114−116 Note that since the ReaxFF parameters are found based on DFT calculations and fit with predefined equations, the transferability of the force field to any other system of interest should be checked according to the phenomena studied.

2.2.1. MD Analysis

Wettability (Contact Angle)

The quality of mineral separation in the flotation process depends strongly on the adsorption phenomena and, thus, on the properties of the mineral surfaces.¹ Contact angle measurements are a simple and convenient way to infer valuable details about surface characteristics.¹¹⁷ Liquid–solid interaction, roughness, surface functional groups and their polarity, and surface hydrophobicity/hydrophilicity all contribute to the contact angle.¹¹⁸ It is customary to relate hydrophobicity/hydrophilicity to the measurement of the contact angle of water on a surface or to the free energy of hydration.¹¹⁹ The contact angle results are translated into the degree of hydrophobicity/hydrophilicity of the materials, providing some insight into the total solvent-solid interaction at the macroscopic scale.¹²⁰ In contrast, doing the same in nanoscale surface probing still faces experimental and instrumental limitations.¹²⁰ To this end, atomistic simulations can overcome such limitations by identifying events occurring at the nanoscale that are reflected in the contact angle calculation. Computational efforts to calculate contact angle can be categorized into two general approaches.^121,122 The first approach, which is easy to implement, is known as sessile droplet. In this approach, a water nanodroplet is placed on the material’s surface, and the droplet equilibrates by adapting its shape during the simulation time. The second approach is based on free energy calculations, which may not be as easy as the first approach, but provides a more accurate contact angle determination.

The calculation of the contact angle in both theoretical and experimental approaches is based on Young’s fundamental equation of a planar geometry¹²³ given as follows:

7

where θ is the contact angle of the droplet on the surface and γ_SV, γ_SL, and γ_VL are, respectively, the solid–vapor, solid–liquid, and vapor–liquid surface tensions. Some challenges have been addressed in the sessile droplet approach regarding the equilibration time for reshaping the droplet, the size of droplet, and systematic errors in contact angle calculation. In this approach, the isochoric vapor–liquid interface is needed for the calculation of the contact angle, which is the contour whose density is equal to half the bulk density.^124,125 The contact angle is determined by drawing, from a point on the triple line, a tangent to the liquid–vapor interface and taking the angle inside the body of the drop bearing on the solid surface.¹²¹ Furthermore, contact angle calculation can be performed by fitting a spherical shape to the droplet¹²⁴ or comparing the center of mass of the droplet with the ideal droplet on the surface.^126,127 Both methodologies deal with the droplet geometry, which requires the droplet to be well equilibrated. However, some recent investigations suggest that droplet formation may take a much longer simulation time (∼100 ns) than is usually taken for granted (∼4–5 ns).^128,129 Another issue with the sessile droplet simulation technique is the use of the macroscopic Young’s equation for the microscopic droplet. In this case, the modified Young’s equation is used, which includes the line tension terms in the original equation. In that case, one needs to simulate the system for different sizes of droplets and extrapolate the modified equation to an infinite size. However, the inadequacy of the approach for small nanodroplets continues to be debated.¹³⁰ Thus, the contribution of system size to line tension values is not fully understood, and additional work is needed to further clarify what is happening at this scale.¹²⁵ Some systematic precautions addressed in ref (122) must be considered when the sessile droplet is chosen as the primary method for contact angle determination.

The second simulation approach employs free energy calculation to determine the contact angle by forming a vapor–liquid interface, where the grand canonical transition-matrix Monte Carlo method is used. In this method, the vapor–liquid interfacial surface tension is calculated with and without the surface. The fluid is sandwiched between the surface and a hard wall that may have an attractive or repulsive affinity with the solvent. The determination of the contact line is no longer followed in this approach, and all calculations are based on the drying/spreading of the solvent on the surface. Drying potentials (attractive walls) are helpful for solvophobic surfaces, while spreading potentials (repulsive walls) are used for solvophilic surfaces. The GCMC is used to investigate the dry/spreading potentials in which the number of molecules and chemical potential of the system can be tuned. Then, the values are related to the modified version of Young’s contact angle equation.^131−134 Errington and co-workers recently proposed the same methodology based on the MC/MD combination, which gave good results for drying potentials, but not for spreading interface potentials.¹³⁵

A similar approach devised in molecular dynamics simulation is introduced as the phantom-wall method.¹³⁶ In this approach, a liquid film is placed above the solid surface, while a repulsive hard wall lies between the liquid film and the solid. Removing the hard wall will make a gap or vacuum between the solid and liquid. The vacuum free energy can be approximated as solid–vapor free energy difference, which is valid only for weak solid–vapor interactions. In the calculations, the free energy is studied relative to the film thickness of the solvent in the system. The difference between the minimum free energy at the small thickness and the free energy plateau at the higher solvent thickness will be directly related to the vapor–liquid surface tension and contact angle. Free energy calculation can be performed using GCMC and MD. MD is computationally efficient for large and complex systems, but more simulations are needed for different densities of the solvent to construct the profile of free energy-thickness. For a simple system, the GCMC is more straightforward because it can change its number of molecules and its chemical potential, while it may not be efficient for large and complex systems.¹²²

Another promising approach for contact angle calculation is based on enhanced sampling methods, which could be implemented through MD or GCMC. This efficient method uses the biased potential to change the number of solvent molecules to gradually wet the surface. The free energy difference relative to the wetting change is calculated and related to the contact angle. The approach simulates the Wilhelmy plate method of exposing two plates to the solvent but calculates the free energy rather than the capillary force.¹³⁷ This approach also allows accurate calculation of the vapor–liquid surface tension for a given contact angle.¹³⁷ The introduction of hydrophobic and hydrophilic patches is an alternative to grasp the mineral surface-reagent contact, especially in the context of hydrophobicity/hydrophilicity of complex molecules such as proteins.¹³⁸

Surface Tension

In addition to measuring the contact angle, surface tension can also play a key role in the flotation and solvation of reagents, especially frothers, by helping to simulate the phenomenon on the vapor–liquid interface side.¹³⁹ This section provides an alternative mechanical and thermodynamic insight into the above section on the calculation of wettability.

The surface tension can also be viewed as a quantity emerging from the mechanical equilibrium of forces at the interface known as the Irvin-Kirkwood equation:¹⁴⁰

8

where P_N and P_T are the normal and tangential pressure tensors relative to the normal direction of the interface (z-direction) when the system is in a state of equilibrium. The main drawbacks of the method are the large fluctuation of the surface tension and its limitation of implementation at high temperatures.

The thermodynamic approach for surface tension calculation is based on the following fundamental equation:

9

where F is the Helmholtz free energy and A denotes the interfacial area. In essence, the variation of the free energy or potential energy relative to the variation of the interfacial area at a constant number of molecules, volume, and temperature gives the interfacial surface tension.^141,142 The primary challenge of the method is the calculation of the Helmholtz free energy, which is far from trivial in molecular dynamics simulation. The test-area method is based on the perturbation of the interfacial area by then calculating the change in the free energy of the system as follows:¹⁴³

10

In this method, rescaling is done at constant volume while each dimension of the simulation box can change. Similar concepts with different implementations for surface tension calculation are described elsewhere.¹⁴⁴

Hydrogen Bonding

Interactions induced by water molecules are a factor that should not be ignored when describing aqueous mineral pulps in froth flotation processes. For instance, hydrogen bonding with the water itself, the reactant, and polar sites on mineral surfaces is about 5 to 10 times stronger than van der Waals interactions.¹¹⁸ In molecular dynamics simulation, geometrical criteria are used to detect hydrogen bonds between polar atoms (N, O, F, and Cl) connected to at least one hydrogen atom. A hydrogen bond is comprised of a donor atom (D) (i.e., the polar atom connected to a hydrogen atom), a hydrogen atom (H), and an acceptor (A) (i.e., the polar atom interacting with the hydrogen atom). The hydrogen bond forms when the donor–acceptor distance (DA) and angle are lower than critical values, respectively, called cutoff distance and maximum angle. For water, the cutoff distance on DA is 3.5 Å and the maximum 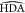angle is 30°,^145,146 but slightly different values can be found in other works for different molecules.¹⁴⁷ The number of hydrogen bonds can change the solvation of reagents or prevent their adsorption on the mineral surface due to competition with water hydrogen bonds and minerals. The dynamics of the hydrogen bond and its lifetime is also a feature to be accounted for. Usually, such dynamics is evaluated by the normalized temporal autocorrelation function (C_HB):¹⁴⁸

11

where h_ij is 1 or 0 depending on whether or not there is a hydrogen bond between a pair of atoms i and j. Two formulations exist for the hydrogen bond autocorrelation function: one for continuous and another for intermittent hydrogen bond lifetimes. In the first case, only if the H-bond breaks does the function cancel; otherwise, the lifetime is quantified as the continuous time of hydrogen bonds between atoms. In the second, intermittent hydrogen bonding considers a different time window of H-bond formation, regardless of whether H-bonds are broken beforehand. Obviously, a continuous lifetime would be shorter than an intermittent one.¹⁴⁹ Fitting the hydrogen bond autocorrelation function by an exponential gives access to the retardation time, i.e., how long a hydrogen bond lasts between specific pairs of atoms. The case of a nonexponential behavior is interpreted by the contribution of molecular diffusion in the hydrogen bonding dynamics.¹⁴⁵

Hydrogen Shell

The hydrophobic regions do not form hydrogen bonds with the water molecules, which instead cluster as hydration shells.¹⁵⁰ The number of hydration shells around ions, reagents, or minerals is estimated using the radial distribution function. The first minimum of the radial distribution function of water-solvated molecules or ions gives the thickness of the first or primary hydration shell.¹⁵¹ The other detected hydration shells are of lesser intensity than the first one. Since the number of water molecules around the solvated species allows estimation of the degree of molecule solvation, the lifetime of water molecules remaining in the shell should be considered. To calculate the lifetime of water molecules remaining in the hydration shell, the normalized autocorrelation function is used:¹⁵⁰

12

where N is the hydration number, with f_i = 1 or 0 depending on whether or not the water molecule i is in the hydration shell. The average lifetime of the water molecules in the hydration shell is calculated by integrating R until the function approaches to 0.99. Through residence time calculations, if the molecules do not return to the hydration shell for 2 ps, they are considered noncontributing to the hydration residence time.

Although the effects of ion charge and diameter on the hydration shell are well established, the new flotation bioreagents can be better characterized by examining their solvation and adhesion to the mineral surface.¹⁵²

Diffusion Coefficient

The mobility of the reagent and ion in the solution or close to the mineral reflects their interaction with the solvent and the solid-solvent interface. The stronger the affinity of a molecule with a mineral, the more reduced its normal mobility at the expense of diffusion, mainly on the plane parallel to the solid surface. The mean square displacement (MSD) is used to calculate the diffusion coefficient as follows:

13

where r_i(t) is the coordinate vector for species i at the specific time of simulation and d is the diffusion dimension (3 for bulk and 2 for surface diffusion).

2.3. Hybrid Methods

Classified as hybrid methods, they stem: (1) in the temporal sense by combining QM and MM, and (2) in the spatial sense by applying QM and MM methods to different physical regions of a system. The AIMD simulation is an example of the first category, while the QM/MM method belongs to the second class. In what follows, these two methods are introduced with their application scenarios.

2.3.1. Ab Initio Molecular Dynamics

The description of the interatomic interaction forces in a given system is at the heart of MD simulations. In classical MD, these forces are computed from predefined force fields or interatomic potentials. However, the available force fields are often unable to afford acceptable accuracy, and, more importantly, chemical reactions cannot be modeled by MD.

The advent of ab initio molecular dynamics (AIMD) has provided a new route to calculate the interatomic forces directly from electronic structure and reduce its dependence on force fields.²²⁻²⁴ In AIMD, finite-temperature dynamical trajectories are obtained by including the forces collected from the “on the fly” electronic structure calculations as MD simulation proceeds.²³ Therefore, the effect of temperature-induced thermal agitation, on the one hand, and electronic polarization and bond formation/cleavage, on the other hand, can be described in AIMD.

Ab initio electronic structure calculations are exceedingly computationally expensive; therefore, the electronic calculation portion of AIMD is usually DFT-coded to trade off accuracy and computational cost.^24,25 In this case, the quality of the exchange-correlation functional is the key control on the overall accuracy of the simulation.

To date, AIMD has been successfully applied to a wide variety of problems and is already beginning to percolate through the mineral community as well.^{8,72,153−156} With the help of this tool, new physical phenomena could be unveiled, taking a new step forward compared to classical MD or ground-state DFT calculations. With advances in HPC, AIMD simulations can routinely reach total simulation times of a few hundred picoseconds for systems comprising a few hundred atoms.

2.3.2. Quantum Mechanics (QM)/Molecular Mechanics (MM) Method

The first step in the QM/MM method is to divide the input system into two distinct regions. The smaller “active site” region, where the force field parameters are unknown or where chemical reactions or polarization effects play an important role, must be treated by QM calculations. The remaining region is described by lower-class MM methods.²⁷ In practice, due to a favorable trade-off between computational cost and accuracy, many problems are solved using DFT and classical MD to, respectively, represent the QM and MM components.

The various QM/MM approaches differ in the way they: a) describe the interaction between the QM and MM regions and b) compute the system energy.²⁷⁻²⁹ Interactions between QM and MM comprise long-range electrostatic interactions and local short-range ones (e.g., binding and van der Waals interactions). Electrostatic interactions are usually dominant; accordingly, depending on the treatment between QM and MM, QM/MM schemes can be classified as mechanical or electronic embedding.¹⁵⁷ In the mechanical embedding scheme, the QM calculation is performed without considering the polarization effect caused by the atoms in the MM region. However, for the MM simulation, the Coulombic interactions of the QM region are accounted for by providing partial charges for the atoms in the QM region at the force field level. In the electronic embedding, the QM region is polarized by the atomic charges of the MM region, and similarly, the Coulomb forces on the MM atoms include the QM density share acting on the MM point partial charges. Of course, the electronic embedding provides a more accurate description with increased computational demands.²⁷

In many cases, it is inevitable to split a molecule to clarify the QM and MM domains. With cleavage bonds at the boundary, a modification of the QM and MM calculations is necessary since the unpaired electrons caused by the broken bonds significantly influence the electronic structure in the QM region.¹⁵⁸ A typical solution is the so-called link atom approach, in which the dangling bonds at the boundary are saturated by introducing capping (hydrogen) link atoms to the QM system. Regardless of the type of embedding, the total system total energy cannot be calculated simply as the sum of the subsystem energies due to the strong QM-MM interactions.^27−29,157 Therefore, the energy expressions in QM/MM can be evaluated under different assumptions, either by an additive or subtractive expression.

In the subtractive schemes, the QM/MM energy is given by

14

where E_MM and E_QM are the energy values calculated by MM and QM methods, respectively. In eq 14, S represents the entire system, and C corresponds to a combination of QM regions and the link atom region. It should be noted that the subtractive embedding scheme requires proper force field parameters for the atoms of the entire system, which limits the overall range of applicability of the approach.¹⁵⁹

Additive approaches for energy description, on the other hand, avoid MM calculation on the whole system and region C. This makes these methods particularly attractive since the unavailability of force field parameters for QM region would not be a concern. The total energy of the system is calculated as

15

As can be seen in eq 15, the MM calculation is performed only on the MM region. E_QM–MM refers to an explicit coupling term, which collects the interaction terms between MM and QM subsystems. The E_QM–MM coupling energy term is the most elaborate term in the additive formulation and includes bonded, van der Waals, and electrostatic interactions between QM and MM atoms.

QM/MM approaches are now widely established for modeling biomolecular, inorganic/organometallic, and solid-state systems, as well as for studying processes in explicit solvents.^27,28 In mineral processing, QM/MM applications are still a relatively untouched area of research, while increased attention to these approaches can enrich future investigations.

2.4. Summary

In this section, the most important simulation techniques within the category of molecular modeling have been reviewed. The basic theories have been initially described for each method, while the primary focus has been on property calculations relevant to the flotation process. Representative examples of flotation applications will be reviewed in section 3. Before jumping in, and to get a better overview of the pros and cons of various simulation techniques, brief descriptions of all the methods reviewed are listed in Table 1. The motivation for performing every simulation should start with a straightforward question and clearly stated expectations. To select an appropriate simulation method, the ability of the different techniques to calculate the desired properties should be considered while accounting for the limitations and computational cost.

Table 1. Comparison of Different Molecular Modeling Techniques.

molecular modeling techniques	merit	limitations
DFT	• more accurate calculation based on the electronic state	• high computational cost
	• capable of simulating:	• small simulation size
	- charge polarization/transfer	• incapable of calculating dynamic properties
	- bond formation/cleavage	• incapable of including temperature effect (all simulations are performed at 0 K)
	- electronic-based properties, e.g., band structure, DOS, etc.
	- chemical reactions
	- transition state
AIMD	• includes finite temperature effect in DFT calculations	• high computational cost
		• small simulation size
QM/MM	• takes advantage of both DFT and MM methods	• complexity in the implementation, especially at QM-MM boundary region
	• suitable for larger systems
ReaxFF	• includes charge polarization to the classical force field	• force field availability and transferability
	• adds bond formation/cleavage simulation into MD	• shorter time- and length scales than MD
MD	• includes the effect of temperature, pressure, volume, etc. in the simulations	• incapable of simulating chemical reactions and bond formation/cleavage
	• larger time (up to μs) and length (up to μm) scale	• lower accuracy compared to DFT calculations
	• capable of calculating:	• accuracy and feasibility depend on the availability of proper force fields
	- dynamic properties, e.g. wettability, diffusion, etc.
	- thermodynamic properties

In general, from a technical point of view, the unavailability of accurate force fields and atomic partial charges for complex mineral systems is the most critical limitation in the application of MD simulations in flotation systems. The danger of oversimplifying the interactions by applying generic force fields comes to the fore, which inevitably leads to underestimating the properties of interest. Even if all technical shortcomings are overcome, the limitations of molecular modeling techniques, mainly the size of the system and the length of the possible simulation, are still prohibitive. The computational cost of molecular simulations overgrows with the system size and is limited to a few hundred atoms for DFT calculations and several tens of thousands of atoms for MD simulations. The routine MD simulation time is currently in the order of a few hundred of nanoseconds. While this is adequate to address some scientific challenges, it is not for many others, especially those involving biological phenomena such as protein folding or crystal growth in mineral systems, which occur on the time scale of seconds in the real world. The nanosecond time limit further restricts the configurational sampling space accessible to MD, which is critical for calculating thermodynamic properties. It is worth mentioning, however, that with the rapidly growing HPC facilities, substantial headway toward larger scales and longer time scales is expected. As evidence, we already find in the literature DFT and MD simulations of systems with millions of atoms.^160−165

3. Applications of Molecular Modeling to Froth Flotation

Once the ore is milled, the minerals of which it is composed, released with a sufficient degree of liberation, are separated from each other by exploiting the natural or artificial propensity of their surfaces to be wetted by water. The degree of hydrophobicity/aerophobicity of the mineral determines whether it ends up in the overflow (hydrophobic) or the underflow (aerophobic/hydrophilic) depending on the reagents, e.g. collectors, used. Therefore, all phenomena that alter or adjust the surface properties of minerals significantly contribute to the efficiency of the mineral separation procedure.¹⁶⁶ A nonexhaustive sketch (Figure 2) of these phenomena focuses on the mineral surface and the interface with the bubble, namely, surface hydration, adsorption of reagents and their consequence on the hydrophilic/hydrophobic split at the gas–liquid interface, surface modification by the dissolution of leachable entities or (re)precipitation of species, and to some extent, the presence of surface defects or impurities. Having summarized in the foregoing section some of the principles of molecular modeling relevant to our topic, let us now turn to its applications in flotation by unpicking some of the phenomena illustrated in the preceding figure.

Figure 2.

General picture of the phenomena that govern the froth flotation of minerals.

3.1. Mineral-Reagent Interactions in Froth Flotation and Molecular Modeling Insights

As Wills and Finch mentioned: “true flotation exploits the differences in surface properties of particles of various minerals. After treatment with reagents, such differences in surface properties between the minerals within the flotation pulp become apparent.”¹⁶⁶ Therefore, the mineral-reagent interaction is one of the key features of flotation, through which the surface properties of minerals can be tuned in a targeted way. Notably, the overwhelming majority of molecular modeling studies on froth flotation fall under the characterization of mineral-reagent interactions.

3.1.1. Principle Features of Interactions

In this section, the application of molecular modeling techniques to reveal the nature of the interaction (physical and chemical adsorptions) and the conformations of reagents on the mineral surface is reviewed.

Interaction Mechanism and Adsorption Conformation

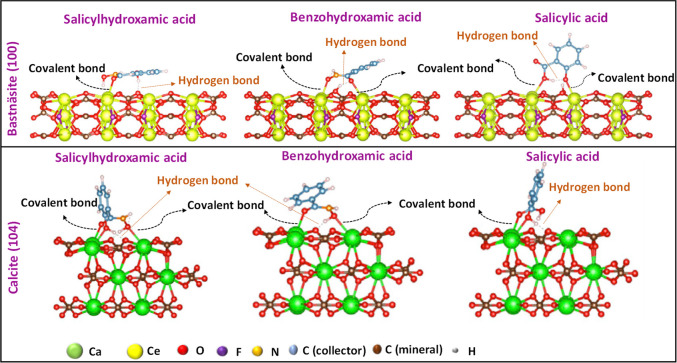
While it is possible to infer the nature of the interactions by quantum computation, predictions of the covalent mechanism by MD simulations are always fraught with uncertainty. As an example in the rare earth element (REE) category, Chapleski et al.¹⁶⁷ analyzed the adsorption mechanism and configuration of several salicylic (SA), salicylhydroxamic (SHA), and benzohydroxamic (BHA) acid–based collectors on bastnäsite (100) and calcite (104) surfaces using DFT calculations (Figure 3). For bastnäsite, the aromatic ring moieties of BHA and SHA (SA) are predominantly oriented face parallel (face perpendicular) to the mineral surface. While for the calcite surface, all dominant conformations are oriented almost normally with minimal shadowing on the surface. The orientation maximizing the shadowing of the aromatic rings (BHA, SHA) on the bastnäsite surface promotes multilayer adsorption of the collector. On the contrary, carboxylic collectors would lack this property suggesting a lower efficiency in promoting the increased accumulation of bastnäsite in the overflow.¹⁶⁸ The uptake of the collector on the bastnäsite and calcite surfaces occurs either by the formation of covalent bonds (bidentate or monodentate) with the metal cations or by hydrogen bonding involving the reagent hydroxyl groups and the carbonates (Figure 3).¹⁶⁷

Figure 3.

DFT structures of the most stable adsorption configurations of various hydroxamic bearing collectors on bastnäsite (100) and calcite (104) surfaces adapted from ref (167).

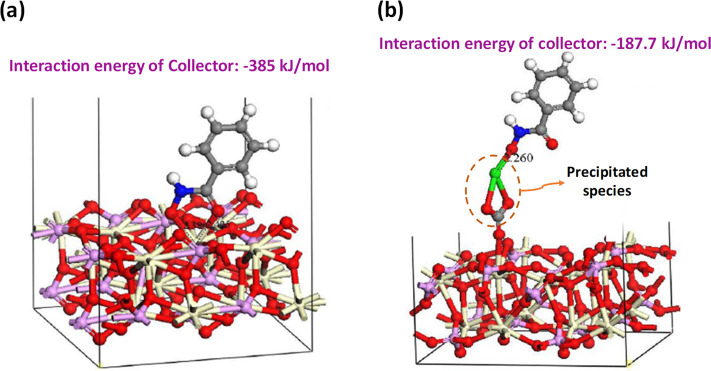
Wanhala et al.¹⁶⁹ employed a combined experimental-computational approach to clarify the alkyl hydroxamic collector adsorption behavior on the bastnäsite surface. The study showed that the effect of collector concentration is bivalent. First, it affects the inclination of the collector alkyl chains relative to the surface, ranging from tight/straight to almost lying down. Second, the covalent bond can evolve from monodentate to bidentate. In another study, Sarvaramini et al.¹⁷⁰ investigated the adsorption mechanism of alkyl-hydroxamic acids on monazite and bastnäsite surfaces by emphasizing the interactions between the collector and solvated REE species susceptible to leach and consisting of Ce(OH)₂⁺ and Ce(OH)²⁺. Despite the intriguing findings, one should be aware that excluding solvation and surface complexation in an aqueous environment could cause uncertainties in the results, thereby compromising their practical applicability.^50,51

Sutton et al.¹⁷¹ ranked the interactions of 20 bis-phosphinate ligands toward calcite (104) and Ce-bastnäsite (100) surfaces using a combination of DFT and MD calculations. Covalent bonds were revealed for four ligand-surface configurations, namely, bidentate, repeated monodentate, staggered monodentate, and neighboring monodentate. The prediction of Ce-bastnäsite-selective ligands was experimentally verified by vibrational sum-frequency (vSFG) spectroscopy, attenuated total reflectance Fourier transform infrared (ATR-FTIR) spectroscopy, and isothermal titration calorimetry (ITC).

Based on DFT and AIMD calculations and diffuse reflectance infrared Fourier-transform (DRIFT) measurements, Foucaud et al.^172,173 examined the adsorption conformations of carboxylate collectors on the fluorite surface. The results indicate that the adsorption of the carboxylate anion takes place through monodentate or bidentate covalent bonds with the fluorite or fluorapatite¹⁷⁴ surface, while the sodium carboxylate counterion plays a role in the adsorption sequence of the collector. These studies demonstrate the power of molecular modeling when combined with experimental analysis to facilitate material characterization and improve the interpretation of experimental observations, ultimately leading to a more complete understanding of the phenomena under study.

Kumar et al.¹⁷⁵ confirmed by DFT calculations the observed selectivity of 2-mercaptobenzothiazole (MBT) toward pyrite at the expense of chalcopyrite. This result is explained by stronger MBT adsorption on pyrite due to the formation of two Fe–S bonds with the endo- and exocyclic S atoms of MBT with Fe of the pyrite (110) surface. The MBT interactions with the chalcopyrite surfaces involve a single Cu-exocyclic bond. These different mechanisms would account for the greater MBT selectivity toward pyrite.

Molecular modeling techniques can also help shed light on the influence of depressants on minerals in flotation systems. As an example, the adsorption mechanism of pyrogallol (a tannic derivative), as an eco-friendly depressant, in the flotation of bismuth–molybdenum sulfide ore was studied by DFT.¹⁷⁶ Chemisorption of pyrogallol on the bismuthinite surface involves its alcohol group in covalent bonds (monodentate and bidentate) with the mineral surface. Similar calculations on the adsorption of a new m-nitrobenzoate depressant with arsenopyrite,¹⁷⁷ suggest the involvement of the -NOO residue of the depressant and not its −COO residue. The adsorption mechanism of sodium hexametaphosphate (NaHMP) depressant from the kaolinite surface was analyzed by combining DFT, MD, and Monte Carlo simulations.¹⁷⁸ The anionic form of NaHMP adsorbs through hydrogen binding, although the effect of water molecules and solution pH was neglected. Neglecting the inclusion of counterions would not lead to an infinite charge of the simulation box in DFT calculations since the overall electroneutrality can be preset in the calculations; however, the partial charges assigned and, consequently, the electrostatic interactions would forcibly deviate from reality. This shortcoming could also affect the predictability of surface species, as shown by MD simulations of sylvite (KCl) and halite (NaCl) surfaces during flotation of potash ores by cationic collectors if water molecules were to be ignored in the phenomenology.¹⁷⁹ More recently, Alizadeh Sahraei and Larachi⁵¹ revealed the importance of explicit water modeling in the DFT calculations. Their results suggest that implicit water modeling fails to predict the formation of solvated mineral-reagent complexes. The critical role of the explicit water model over implicit models was further highlighted in the DFT calculations of Chapleski et al.¹⁸⁰ for separating rare-earth elements from gangue materials. For the description of such complexes, the inclusion in the simulations of water molecules in the form of a multilayer is essential and highly recommended.

Effect of pH on Reagent Interactions

Some researchers also highlighted the capability of molecular modeling to determine the effect of pH on collector–mineral interaction. For this purpose, they considered different species of collectors corresponding to a specific range of pH.^181−184 Liu et al.¹⁸⁴ used MD and a semiempirical quantum chemical method to compare the interactions with the bastnäsite surface of three possibly occurring species of lauryl phosphate, namely, C₁₂H₂₅OPO₃H^–, C₁₂H₂₅OPO₃H_2, and C₁₂H₂₅OPO₃^2–. Adsorption of carboxylic acid-bearing collector species on spodumene in proton-impoverished solutions at pH 8 was DFT-simulated¹⁸⁵ to examine the plausible interactions of ionic–molecular complexes consisting of (a) head–head, (b) head–middle, but not (c) head–tail on the spodumene surface.

At this stage, the value of these simulations of the pH and its impact on the speciation of the collector and, thus, on the reagent-mineral interactions is to be taken cum grano salis because all the criteria to account for the pH in the flotation are not there. The consideration of protonation/deprotonation states of adsorbates with pH-sensitive functional groups at different pK_a is not sufficient to model adsorption phenomena at different pHs.¹⁸⁶ For solid molecular modeling (particularly molecular dynamics simulations) at different pH, the mineral surface and solution must also be carefully constructed. The type and area density of surface groups upon solvation, the likely ionization degree as a function of pH, the ionic strength and type of cations, etc. are crucial parameters that must be considered in model constructions for accurate modeling of flotation systems. Knowledge is typically provided by experimental characterization via BET adsorption isotherms, spectroscopies (e.g., solid-state NMR, infrared, Raman, and X-ray photoelectron spectroscopy), potentiometric titration, and ζ-potential measurements. For instance, a fairly comprehensive database already exists for the silica family at different pH levels.^{108,187−189}

In DFT calculations, however, the construction of the realistic formulation of the solution at different pHs is prohibitive due to the size limitation of the system. In this regard, the (de)protonation state of the adsorbate per pK_a values of the functional groups should include the appropriate counterions to ensure that the physical system is neutral. While the explicit solvent model is not affordable for routine DFT calculations, one alternative is to use a cluster model. In this approach, the adsorbate molecule and counterions are surrounded by several water molecules to explicitly include the solvent effect, and an implicit solvation model (i.e., replacing the explicit solvent with a dielectric continuum) is applied for the remaining space. When the cluster model is not affordable, implicit models based on the polarized continuum solvation model are recommended for (de)protonated systems at different pHs.¹⁹⁰

Interaction of Reagent Mixtures

Molecular modeling is proven to be instructive in developing a microscopic picture of mixed surfactants at mineral/water/gas interfaces. Chemisorption (covalent bonds) with the hematite surface is predicted by DFT upon adsorption of oleate alone or starch alone on iron oxide. On the other hand, in the presence of an oleate-starch-hematite system, starch inhibits the adsorption of oleate, leading to a significant reduction in its recovery by flotation.¹⁹¹ The mechanism of interaction of mixed cationic/anionic surfactants or polar/nonpolar collectors with the surface of low-rank coals can be further analyzed by means of MD simulations based on the ratio of their concentrations and the ability of their hydrophobic carbon chain to repel water molecules from adsorption on the coal surface.^192−195 Sequential adsorption of cationic surfactants onto deprotonated oxygen functional groups dangling from the carbon surface, followed by adsorption of anionic surfactants onto preadsorbed cationic molecules, has been presented as a dominant mechanism for these surfactant systems. Experimental observations revealed that the process leads to a significant reduction in collector consumption and an improvement in flotation efficiency.¹⁹⁶ In another study, MD simulations showed that mixed anionic/cationic collectors could significantly boost the hydrophobicity of the muscovite surface. The interaction between polar groups of cationic and anionic collectors helps reduce the electrostatic repulsion if cationic collectors were to act alone, improving the adsorption of the mixed collectors on the muscovite surface.^197,198 Similar findings have been reported in the case of galena flotation using MD simulations.¹⁹⁹

Wang et al.²⁰⁰ took advantage of MD simulations to shed insight into the adsorption behavior of mixed dodecylamine (DDA)/sodium oleate (NaOL) (cationic/anionic collectors) in quartz flotation. Prior to this study, it was assumed that adsorption of most DDA on the surface occurs first, and then NaOL can adsorb via hydrophobic interaction among alkyl chains. The MD results, however, demonstrated that most DDA and NaOL species form hydrophilic spherical-like micelles near the quartz surface (Figure 4a), and only a few DDA molecules adsorb directly on the quartz via hydrogen binding bridging the spherical micelles and the mineral surface (Figure 4a). On the contrary, using MD simulations, Shen et al.²⁰¹ captured a different adsorption mechanism for the same reagent mixture in the case of kaolinite flotation. The computational results suggested that coadsorption of DDA and NaOL on the surface of (001) kaolinite may take place via hydrogen binding (Figure 4b), where the anionic molecules were intertwined among NaOL ions via a hydrophobic interaction between the alkyl chains on the mineral surface.²⁰¹ Thus, MD simulations predict two different types of assembly for the same DDA/NaOL couple on quartz (Figure 4a) and kaolinite (Figure 4b) surfaces.

Figure 4.

Different adsorption behaviors of mixed cationic/anionic collectors (DDA/NaOL) on the surface of (a) quartz (promoting depression effect) and (b) kaolinite (promoting activation effect). Adapted with permission from refs (200) (a) and (201) (b). Copyright 2016 and 2017, respectively, Elsevier.

The muscovite (001) surface exposed to mixed DDA/NaOL collectors was also simulated using MD simulations.²⁰² Alone, DDA adsorbs as an organized monolayer on the muscovite surface, while NaOL alone is unable to hold attached to the surface. However, for the DDA/NaOL surfactants mixture, the ammonium head groups of DDA remain adhered to the surface, and the NaOL molecules intertwine among the DDA molecules instead of being repelled by the muscovite surface (a mechanism similar to that discussed in the case of kaolinite²⁰¹). The electrostatic interaction between the ionic head groups of the collectors as well as the hydrophobic interaction between their tails, was recognized as the dominant adsorption mechanism in this system.²⁰² Other studies have also confirmed the possibility of forming micelle-like spherical structures (Figure 4a) in mixed surfactant systems, while such manifestation in single-surfactant systems is rare.^202,203

When mixed with monohydric alcohols, DDA adsorption on magnesite and dolomite surfaces can be increased according to simulations.²⁰⁴ MD simulations with COMPASS force field²⁰⁵ elucidated the adsorption mechanism of mixed surfactants of citric acid, pregelatinized starch, and NaOL on hematite, quartz, and siderite surfaces. Coadsorption of all three surfactants occurs on the siderite surface (Figure 5). Citric acid and pregelatinized starch are densely distributed over the entire hematite surface preventing the adsorption of NaOL directly onto the mineral (Figure 5b). Neither pregelatinized starch nor NaOL is able to adsorb onto the quartz surface (Figure 5c), in contrast to citric acid. Such behaviors suggest that siderite, easily flocculated, is then separable by flotation, as the experimental results corroborate.²⁰⁵

Figure 5.

Adsorption patterns and relative concentration profiles of citric acid, pregelatinized starch, and NaOL during their interactions with (a) siderite, (b) hematite, and (c) quartz. Adapted with permission from ref (205). Copyright 2020 Elsevier.

MD simulations using COMPASS have examined the effects of mixing aluminosilicate polymorphs (andalusite, sillimanite, kyanite) with cationic (octadecylamine) and anionic (sodium hexadecanesulfonate) collectors.²⁰⁶ The two collectors acted according to different adsorption mechanisms. For the former, electrostatic attraction and hydrogen binding between the amine cation and the surface oxygens predominated. For the second, the chemisorption of sulfonate anions on Al atoms prevailed. Because classical MD cannot model chemical interactions, X-ray photoelectron spectroscopy (XPS) has validated this last mechanism. A clathrate-type interaction between DDA and starch was simulated by MD in a vacuum and aqueous solution using the generic Universal force field.²⁰⁷ This rationalized the observed decrease in the contact angle with water on the quartz surface by concealing the hydrophobic tail of DDA (Figure 6).

Figure 6.

Snapshot of a six glucose ring starch molecule and DDA before and after clathrate interaction, resulting in masking the DDA hydrophobic tail. Adapted with permission from ref (207). Copyright 2017 Elsevier.

Section Outlook

Overall, the molecular-scale representation afforded by molecular modeling provides first-hand information about mineral-reactant interactions. This knowledge is crucial for the design, control, and operation of flotation chemistry to improve process performance. A myriad of similar molecular modeling studies (by DFT and MD) have recently been performed to unveil the interaction mechanisms of various reagents with pure gold,^208−212 hydrophobic mineral surfaces (e.g., talc, graphite),^213,214 aluminas,^215−218 sulfide minerals,^{175,219−223} Ca and Mg bearing minerals,^224−229 and more. Such a wide range of case studies using molecular modeling is a testimony to the versatility of the tool that can address just about any mineral system of interest for froth flotation. Proportionally, however, there are fewer studies based on molecular dynamics simulations due to a lack of appropriate force fields for the various mineral families. Even in the case of using class II force fields (e.g., COMPASS and PCFF), the accuracy of the force field parameters of the minerals remain indecisive. Presently, the simulations implemented with the INTERFACE or specialized force fields produce the most reliable MD results.

3.1.2. Minerals–Reagents Adsorption Energy and Affinity

The apparent adsorption energy of a reactant on a mineral surface is a valuable indicator for the affinity ranking of reagent-mineral pairs in flotation systems. The affinity calculation provides insight into the magnitude of surface-reactant interactions and the feasibility of adsorbate configurations.

Different definitions in use have been explained in section 2.1.2, e.g., adsorption or interaction energy, and many more defined according to the requirements of the problem. Mineral surfaces offer a vast diversity of atomic termination and electronic structures depending on the cleavage directions (especially in oxide minerals). Therefore, one has to expect different interactions between the reagents and cleavage planes. In simulation studies, these interactions are often determined for the most stable cleavage plane. In theory, the lower energy surface has a higher probability of occurrence on particle facets. However, other cleavage directions also exist on the mineral facets to form a particle. In this regard, for more accurate simulation of reagent-mineral interactions, it is preferable to apply adsorption studies on a set of cleavage planes rather than a single stable plane. The Wulff construction theory²³⁰ is an effective tool for recognizing the preferential cleavage planes of minerals and for predicting their crystal morphology. Therefore, performing surface energy calculations of the different cleavage planes of the mineral and subsequently searching for the Wulff construction would be a preliminary step before initiating adsorption studies. Note that Wulff’s theory of surface construction is founded on thermodynamic equilibrium assumptions,²³¹ whereas grinding prior to froth flotation could be an out-of-equilibrium process, especially for high-energy grinding.^232,233 Therefore, expecting further disagreements between simulation models and reality is not exaggerated.²³¹Table 2 summarizes the studies involving adsorption energy calculations, highlights as well as limitations found in these studies.

Table 2. Examples of Molecular Modeling Applications to Compare Interaction Affinity of Various Reagent–Mineral Systems.

minerals	reagents (type and name)	molecular modeling approach	comparative results	main limitations	refs
bastnäsite, calcite	collector: salicylhydroxamic acid (SHA), benzohydroxamic acid (BHA), salicylic acid (SA)	DFT (GGA/PBE functional)	collector affinity toward bastnäsite: BHA > SHA > SA	1. mineral surface charges and protonation states of surface ligands at studied pH not defined specified; 2. explicit water-solvated forms of models not studied	(167)
			collector affinity toward calcite: SHA > SA > BHA
sylvite (KCl), halite (NaCl) (potash ores)	collector: octadecylamine	MD (COMPASS force field)	mineral affinity toward collector: KCl > NaCl	1. mineral surface complexations at the studied pH not considered in the simulations; 2. simulation box size too small for an MD simulation; 3. number of water molecules in the model very low, preventing collector solvation to occur	(234)
magnesite, calcite, dolomite	collector: potassium cetyl phosphate	MD (COMPASS and Universal, force fields)	mineral affinity toward phosphate-based collector: magnesite > calcite and dolomite	1. mineral surface complexation at the studied pH not considered in the simulations; 2. no verification of reaching equilibrium state; 3. no verification of the force field parameters, particularly when using a generic force field like Universal	(235), (236)
quartz, magnesite, dolomite	Collector: isopropanol amine	MD (force field unknown)	mineral affinity toward amine-based collectors: quartz > dolomite > magnesite	1. mineral surface complexation at studied pH not considered in the simulations; 2. number of water molecules in the model very low, preventing collector solvation to occur; 3. no information on force field parameters reported, so the accuracy of parameters cannot be verified	(237)
bastnäsite, calcite	collector: bisphosphinate ligands	DFT (PBEsol-D3) + AIMD (γ point)	1. mineral affinity toward reagents: bastnäsite > calcite		(171)
brucite, kaolinite, quartz	flocculant: hydrolyzed polyacrylamides	MD (AMBER + CLAYFF-MOH force field)	mineral affinity toward reagents: brucite > kaolinite > quartz		(238)
kaolinite, montmorillonite	depressant: nine types of organic carboxylates	DFT (GGA/PBE functional)	1. depressant affinity toward kaolinite: hydrogen phthalate > acetate > hydrogen succinate > hydrogen citrate > gallate > salicylate > hydrogen oxalate > bitartrate > lactate	1. calculations carried out in gas phase, no water effect included; 2. effect of initial configurations of adsorbates not comprehensively investigated	(239)
			2. depressant affinity toward montmorillonite: hydrogen phthalate > acetate > hydrogen succinate > hydrogen citrate > gallate > salicylate > hydrogen oxalate > bitartrate > lactate
chalcopyrite: (100) and (110) cleavage planes	collector: thiophosphorus collector, including diethyl dithiophosphate (DEDTPA), diethyl dithiophosphinate (DEDTPI), diethyl monothiophosphate (DEMTPA), and diethyl monothiophosphinate (DEMTPI)	DFT (GGA/RBPE functional)	1. collector affinity toward (100) surface: DEDTPI > DEDTPA > DEMTPI > DEMTPA	1. effect of water molecules not considered	(240)
			2. collector affinity toward (100) surface: DEDTPI > DEDTPA > DEMTPI > DEMTPA
			3. (110) surface more strongly adsorbs collectors than (100) surface
calcite, dolomite, ankerite	collector: alkyl hydroxamic acid bearing collector; depressant: sodium silicate	DFT (GGA/PBEsol functional)	1. collector affinity toward minerals: ankerite > calcite > dolomite	1. water effect not included in the calculations; 2. effect of initial configurations on adsorption modes not comprehensively investigated	(241)
			2. depressant affinity toward minerals: ankerite > dolomite > calcite
			3. interaction energy of collector with minerals higher than depressant
fluorapatite, dolomite	collector: N-hexadecanoylglycine	DFT (GGA/PBE functional)	collector affinity toward minerals: fluorapatite > dolomite	1. water effect not included in the calculations; 2. effect of initial configurations on adsorption modes not comprehensively investigated	(242)
sphalerite, pyrite	collector: tert-dodecyl mercaptan (TDM)	DFT (GGA/PBE functional)	collector affinity toward mineral: sphalerite > pyrite	1. water effect not included in the calculations; 2. vacuum thickness not tuned for DFT calculations: 10 Å vacuum insufficient to prevent relatively long reagent from seeing other slab side	(243)

3.2. Flotation Reagents

“Without reagents, there would be no flotation, and without flotation, the mining industry, as we know it today, would not exist”.¹³⁹ Numerous types of reagents and surfactants are used in froth flotation, including collectors (which selectively make mineral surfaces hydrophobic), depressants (which prevent flotation of unwanted minerals), modifiers (which deliberately change the properties of mineral surfaces), activators (which activate mineral surfaces for reagents uptake) and frothers (which prevent bubble coalescence).^139,166 The selection of appropriate reagents for flotation has always been a challenge, especially for complex orebodies. As will be seen through the following examples, the advent of molecular modeling puts more than one arrow in the quiver to help deliberately tune flotation reagents’ properties.

3.2.1. Structure–Property Relationships

Effect of Polar and Nonpolar Groups

Liu et al.²⁴⁴ took advantage of DFT calculation to investigate the relationship between the structure of mercaptobenzoheterocyclic compounds and their potential to interact with the pyrite surface for flotation separability. Not unexpectedly, it is the O, N, and S heterocycle atoms that induce chemical bonding with the iron atoms on the pyrite surface. In particular, the surface complexes induced by the thione tautomers exhibit higher reactivity than the thiol tautomers. In another study on the selective separation of pyrite and sphalerite, thiophosphorus collectors were analyzed using a similar molecular modeling approach to reveal the chemical reactivity of their P = S group and affinity toward surfaces depending on the solvent-mediated ionization of their thione and thiol functions.²⁴⁵ The hydrophobic tail of collectors is another concerning issue. This aspect was addressed with fatty acid collectors adsorbing on the surface of fluorapatite (0 0 1), specifically in terms of carbon chain length and isomerism and number of C=C bonds.²⁴⁶ Several highlights emerge. First, the strongest interactions with the mineral surface stem from the collectors with the longest chains. Second, the number of C=C double bonds has a negligible impact on the collectors’ reactivity. Third, the isomerism of the collector carbon chains significantly modifies the adsorption energies.²⁴⁶

If polar groups are the crux of flotation collectors, their multiplication in a single collector should contribute to improving the collection capacity, as confirmed by DFT simulations when increasing the number of polar groups of hemimorphite-carboxylic acid collectors.²⁴⁷ A combination of DFT and AIMD simulations further underlined the importance of the number of polar groups in the bastnäsite flotation system using bis- and monophosphinate collectors.¹⁷¹ Indeed, the former would outperform the latter due to overall surface coverage and adsorption interactions.

MD simulations were employed to elucidate the role of secondary amino groups on the adsorption behavior of amine-based reagents on the quartz surface by comparing N-dodecylethylenediamine (ND) and dodecyl amine (DDA) adsorption configurations.²⁴⁸ ND, comprising both primary (−NH₂) and secondary (−NH) amino groups in its structure, develops a stronger interaction with quartz as compared to DDA with only one primary amino group. Similarly, another MD simulation²⁴⁹ indicated that bis(2-hydroxyethyl)dodecyl amine (BHDA), a tertiary amine surfactant, has better selectivity toward quartz than DDA due to the weaker polar group electronegativity and stronger steric hindrance of BHDA. The superior adsorption behavior of BHDA compared to DDA was ascribed to the presence of the – CH₂CH₂OH group in BHDA, increasing the possibility of hydrogen binding with the quartz surface. The interactions of three amine-based collectors, including DDA, N-dodecyliso-propanolamine (DIPA, with one iso-propanol substituent group), and N,N-dodecyl-diiso-propanolamine (DDIPA, with two iso-propanol substituent groups) with quartz and magnesite were also compared within MD framework.²⁵⁰ The presence of isopropanol substituents in the structure of DIPA and DDIPA improves selectivity by enhancing the spatial position barrier effect and increasing the hydrogen binding site on the collector.

The influence of the number of ethylene oxide (EO) groups in the nonionic dodecyl ethoxyl ethers (C₁₂EO_n) on the efficiency of low-rank coal flotation was investigated using a combination of DFT and MD calculations.²⁵¹ The simulation results confirmed the greater selectivity of the surfactant toward coal than the (gangue mineral) kaolinite upon increasing the EO number in C₁₂EO_n. Based on a more recent MD study,²⁵² the polarity of a nonionic surfactant was shown to have a substantial role in its selectivity performance during the flotation of low-rank coal and kaolinite.

MD simulations on muscovite (001) by Xu et al.²⁵³ demonstrate that the nature of the interaction and the adsorption conformation of primary ammonium ions are not a function of the collector alkyl chain length. This is unlike the carbon chain length in low molecular weight carboxylic collectors where this would affect the adsorption of the collector on muscovite.²⁵⁴ The adsorption energy of carboxylic acid collectors with longer carbon chains (C₄) is higher than the (C₁, C₂, and C₃) ones, primarily due to the improvement in carboxylic acid diffusion at the water-muscovite interface.²⁵⁴ DFT simulations on the affinity of carboxylic acid collectors for smithsonite or of xanthate collectors for pyrite demonstrate similar behavior in terms of (alkyl) chain length.^255,256

Reagent Mixtures

NaOL/alcohol mixtures by varying the alcohol carbon number have been studied in the flotation of dolomite and magnesite.²⁵⁷ Two key observations emerged from the MD results: first, the mixture of collectors works better than if NaOL acted alone; second, the higher the carbon number of the alcohol, the higher the flotation efficiency. The effect of carbon chain length and isomeric structure of monohydric alcohols was further investigated by DFT for the same system of the magnesite–dolomite system when coadsorbed with DDA.²⁵⁸ By compressing the hydration layer on mineral surfaces and diluting it, the adsorption of mixed collectors with longer alcohol chains is more stabilized on mineral surfaces.

The flotation of quartz with DDA assisted by nonpolar oil in an aqueous pulp was examined using MD simulations.²⁵⁹ The interaction between the hydrophobic alkyl tail of DDA and the nonpolar oil improves the diffusivity of the latter contributing to a greater thickness of the interface. The addition of DDA expands the oil–water interface by spontaneous cross displacement: the oil components by the DDA hydrophobic tail and the water molecules by its hydrophilic headgroup. On the other hand, the performance of quartz flotation with DDA–aromatic hydrocarbon mixtures seems to outperform that with (un)saturated aliphatic hydrocarbons.

A mixture of dodecane/2-octanol and dodecane/ether alcohol reagents were tested by MD simulations for improved performance in coal flotation systems. The results suggested that while low concentrations of 2-octanol and ether frothers would promote synergism in both the spreading and adsorption of dodecane and frothers on the coal surface, the excessive frother concentration would not show a synergistic effect, thus deteriorating dodecane adsorption on the surface.²⁶⁰

3.2.2. Reagents Rational Design

Molecular modeling techniques provide a powerful framework for upgrading common, time-consuming, and costly trial-and-error experimental methodologies for reagent design to a more robust, rational approach for the design and development of new, high-performance reagents for froth flotation. In recent years, the gradual depletion of easy-to-process ores has been accentuated in large part by the shift to mineral sources from complex and highly disseminated ore deposits. Without detailed knowledge of such complex ores, it is almost certain that the beneficiation of target minerals contained therein would be doomed to failure if one were to rely solely on recipes that have worked in the past, such as conventional chemicals and flotation methodologies. Indeed, conventional flotation reagents have shown low efficiency in the flotation of these complex ores since they have been designated for less refractory ore deposits.^261,262 It becomes necessary to develop new reagents adapted to the flotation of complex ores but also to the urgency of sustainable development; otherwise, the development of the mining and metals sectors could be seriously compromised in the near future.^261,262 Molecular modeling approaches would be a promising pathway toward the discovery and development of these new flotation reagents.^{10,13−15,121,263−267}

Five different azolethione derivatives as novel collectors for copper mineral flotation were evaluated by DFT.²⁶⁸ The heptyl-substituted derivatives demonstrated exceptional recovery for chalcopyrite and malachite due to the chemisorption of azolethione at the Cu site. A new synthetic collector, S-benzoyl-N,N-diethyldithiocarbamate (BEDTC), was compared by DFT to conventional thio collectors, e.g., sodium diethyl dithiocarbamate (SEDTC) and sodium isobutyl xanthate (SIBX), for the selective flotation of galena over sphalerite.²⁶⁹ The DFT simulation predicts a bidentate chemisorption complex involving the BEDTC thiol group sulfur and carbonyl oxygen with the lead surface atoms of galena. The experiments confirmed the superior selectivity of the new synthetic collector as compared to the conventional ones.

Glucan, as a new depressant for the flotation separation of pyrite and pyrophyllite, was the subject of MD simulations.²⁷⁰ Due to its hydrophilic −OH group, the depressant prefers to act differentially with respect to the Al atoms of pyrophyllite and Fe of FeS₂.

An AIMD-assisted design has resulted in new hydroxamate-based collectors for the flotation separation of rare earth minerals.²⁷¹ The surface lanthanides associated with bastnäsite and xenotime form bi- and monodentate surface complexes with the hydroxamate ligands, respectively. Therefore, the emerging strategy for improving the selectivity of, for example, xenotime over gangue minerals is to design a collector in which a single chelating group is replaced by multiple monodentate groups to complement and encompass the simultaneous interactions of the collector with multiple adjacent sites on the surface.

Overall, the application of computational chemistry to the development of new reagents for various flotation systems is a trending topic in the mineral community, as summarized in Table 3.

Table 3. Examples of Molecular Modeling Investigations Focusing on Rational Design of Various Reagents for Mineral Froth Flotation.

molecular modeling approach	reagent type and application	key findings	ref
DFT (B3LYP/6-3 functional)	polyamine-based cationic collector for goethite and kaolinites system	1. design and synthesis of novel amine-based collector by DFT following lab-scale verification; 2. selectivity and collecting capability of collectors determined by interaction energy calculation	(272)
MD (Universal force field)	sodium hexametaphosphate (SHMP) dispersant for serpentine	1. anionic components of SHMP adsorbed on Mg and Si surface sites; 2. dispersant interact with serpentine through chemi/physisorption; 3. SHMP dominantly adsorbed on basal plane of serpentine rather than edge surface due to presence of rich Mg atoms with broken bonds	(273)
MD (COMPASS force field)	butane-3-heptyloxy-1,2-diamine (BHLD) collector for quartz flotation	1. electrostatic and hydrogen bond formation recognized as dominant binding mechanism of BHLD to quartz; 2. BHLD cations outperformed BHDL molecule as indicated by higher interaction energy values	(274)
DFT (B3LYP functional)	sodium O-benzythioethyl xanthate (SBEX) collector for chalcopyrite flotation	1. SBEX features higher affinity toward chalcopyrite compared to conventional xanthate sodium isobutyl xanthate (SIBX) and sodium phenylethyl xanthate (SPEX); 2. superior performance of SBEX collector ascribed to presence of thioether structure in structure	(275)
DFT (GGA/PW91 functional)	polymaleamide-propyl dithiocarbamate (PMA-PDTC) depressant for galena	1. study compared interactions and selectivity of DTC (depressant) and O-isopropyl-N-ethyl thionocarbamate (IPETC) (collector) with galena surface; 2. DTC shown to have higher affinity to galena surface; 3. based on DFT calculations, DTC (as galena-avid group) attach to hydrophilic PMA to form a new depressant for galena	(276)
DFT (B3LYP-D3 functional)	2-cyano-N-ethylcarbamoyl acetamide (CEA) collector for fluorite, calcite, and scheelite flotation	1. CEA collector outperform BHA and fatty acid collectors in mineral flotation due to presence of two functional groups interacting with both cations and anions on mineral surface; 2. based on DFT results, CEA affinity to minerals followed the order fluorite > calcite > scheelite	(277)
DFT (GGA/PBEsol functional)	2-(carbamoylamino) lauric acid (2-CLA) collector for quartz flotation	1. adsorption energy of main species in the flotation solution follows the order Ca2+ > Ca (OH)+ > OH– > H2O > 2-CLA–, meaning that quartz surfaces should be activated by metal cations or hydroxyl group prior to collector adsorption (especially in the case of 2-CLA–); 2. DFT calculations revealed superior performance of 2-CLA– due to chemical bonding and hydrogen binding abilities of amide group −CONH2	(278)
DFT (GGA/PBE functional)	Evodiae fructus oil (EV-1) collector for fluorite flotation	1. results suggest oleic acid anion/oleamide anion mixture result in stronger interaction with fluorite surface	(279)
DFT (GGA/PBE functional)	Rhodanine-3-acetic acid (3-Rd) as chalcopyrite depressant in molybdenite flotation	1. DFT results reveal that 3-Rd collector prefers to adsorb on Fe rather than on Cu for chalcopyrite surface; 2. dominant binding mechanism in 3-Rd-chalcopyrite is chemisorption of – COO– and −CSS– groups of 3-Rd bind with Fe sites on chalcopyrite surface; 3. 3-Rd-molybdenite interactions mainly through physisorption via hydrogen bonding and electrostatic interactions	(280)
DFT (GGA/PBE functional)	l-cysteine as chalcopyrite depressant in molybdenite flotation	1. l-cysteine dominantly adsorbed on chalcopyrite surface via chemisorption of −SH and/or −NH2 groups of cysteine with Cu atoms rather than Fe sites on the surface; 2. based on DFT results, formation of l-cysteine dimer is predominant species on chalcopyrite surface	(281)
MD (COMPASS force field)	dodecyltrimethylammonium bromide (DTAB) collectors for flotation of low-rank coal	1. DTAB adsorption on coal surface improves hydrophobicity of coal by excluding water molecules from surface and reducing adsorption thickness; 2. adsorption configuration of DTAB, in which its headgroup faces coal surfaces and alkyl chain is exposed to water phase, is favorable for repelling water molecules	(282)
DFT (GGA/PBEsol functional)	ethylenediamine tetra(methylene phosphonic acid) sodium (EDTMPS) as magnesite depressant for quartz reverse flotation	1. DFT result suggests that preadsorption of EDTMPS weakens DDA-magnesite interactions due to favorable adsorption of EDTMPS on magnesite surface; 2. preadsorption of EDTMPS showed negligible effect of DDA adsorption on quartz surface	(283)
DFT (GGA/PBEsol functional)	O-butyl S-(1 chloroethyl)carbonodithioate (GC-1) collector for flotation of copper sulfide ore	1. DFT results confirm GC-1 interactions with chalcopyrite and pyrite are through chemi/physisorption, respectively; 2. adsorption energy calculations show that GC-1 collector forms more stable and stronger interactions with chalcopyrite compared to butyl xanthate collector	(284)
DFT (GGA/PBEsol functional) MD (COMPASS force field)	N-dimethyl-N′-dodecyl-1,3-propanediamine (DPDA) collector for quartz flotation in hematite–quartz systems	1. DFT and MD simulation results confirm DPDA has better collectivity and selectivity toward quartz than conventional amine-based collectors (e.g., DDA); 2. DPDA-quartz interactions predominantly tuned by electrostatic attraction and hydrogen bonding	(285)
DFT (GGA/PBE functional)	Cupferron collector for cassiterite flotation in cassiterite–quartz systems	1. DFT results confirm selective adsorption of Cupferron on cassiterite surface than quartz before activating surface by Pb2+; 2. Pb2+ activation shown to be more energetically favorable on cassiterite than quartz surface; 3. Interaction study further suggests that Pb2+ activation promotes Cupferron adsorption on hydrated quartz surface, and Cupferron interacts slightly more stronger with activated quartz than with cassiterite surface; 4. based on simulation results, for efficient separation of cassiterite from quartz, dosage of Pb2+ should be strictly controlled to prevent quartz activation	(286)
DFT (GGA/BFGS functional)	N-(carboxymethyl)-N-tetradecylglycine (NCNT) collector for fluorapatite flotation	1. Based on DFT study, NCNT has stronger interaction with fluorapatite than oleic acid collector; 2. adsorption configurations suggest that NCNT adsorption mechanism on fluorapatite is through bidentate covalent bond with surface-exposed Ca atoms	(174)

3.2.3. Rational Design of Novel Ecofriendly Collectors

Peptide-Based Collectors

Molecular modeling approaches have been put forward to develop a new family of environmentally friendly reagents by rationally tuning peptides for application in froth flotation as novel green collectors.^{49,51,287−290} In one of the earliest efforts to model peptide–mineral interactions, DFT calculations were utilized to determine the interaction between acetic acid and methylamine on clay mineral surfaces.²⁹¹ The study revealed that the formation of the clay mineral-peptide bond occurs via an asynchronous mechanism by initiating a dative N–C bond, followed by proton transfer from N to O atoms. Another AIMD-MD study investigated the adsorption mode and mechanism of alanine and two dipeptides, including alanine-glutamic acid and alanine-lysine, on the rutile (110) surface.²⁹² Chemisorption involves a bidentate complex by the two carboxyl O atoms of the amino acids with two adjacent Ti atoms on the rutile surface.²⁹² Similarly, molecular modeling studies on the interaction nature of various peptide structures with minerals and metal surfaces, including gold,^210,293,294 palladium,²⁹³ calcium oxalate monohydrate,¹⁵⁴ platinum,²⁹⁵ hydroxyapatite,^296,297 and rutile⁴⁶ further confirmed that peptide-mineral interactions would predominantly occur as chemisorption. Lately, the promising potential of peptides as collectors in the flotation of sulfidic minerals was scrutinized through systematic molecular modeling studies on the amino acids, as the peptides’ building blocks. The combination of DFT calculation and Monte Carlo simulations has allowed examining the adsorption mechanism of alanine on the sphalerite surface.^49,51 The interaction of all 20 natural amino acids on pyrite, chalcopyrite, and sphalerite surfaces has been studied recently.²⁸⁸ PDOS and Hirshfeld population charge analyses, site density calculations of the mineral surfaces, HOMO and LUMO distributions, and interaction energies were used to rank the amino acids against these model sulfides over a wide pH range. The affinity of pyrite toward amino acids is higher than that of chalcopyrite and sphalerite, with in all cases, the amino acids being adsorbed by chemisorption. The amino acid acid–base speciation as a function of pH also plays a role in their level of interaction with the sulfide surfaces. Very recently, a robust simulation scheme combining classical MD, replica exchange MD, and steered MD was synergized to characterize the quartz-selective peptide sequences initially identified by phage display at pH 9 as alternative reagents for direct flotation of quartz mineral.¹⁸⁶ The simulation results revealed that the simultaneous presence of positively and negatively charged residues in peptide sequences are favorable for stronger binding of peptides to the surface due to two main reasons. First, the negatively charged residues have strong affinities toward abundant positively charged moieties on quartz surface at basic pH, and second, the repulsive self-interactions in the peptide chain containing dissimilarly charged residues keep the extended conformation of the peptide, guaranteeing the accessibility of peptide side groups to the surface. The investigation further highlighted the capability of molecular modeling to study mechanistic details and to accelerate the rational design of novel reagents for mineral processing applications.

Ionic Liquid-Based Collectors

The extension of ionic liquids (ILs) has not gone unnoticed by the molecular modeling field, which has been sharpened by the interest in new “green” collectors in minerals’ flotation. Although traditionally considered “designer solvents,” ILs have recently found applications in froth flotation^{168,298−300} because of virtually limitless possibilities for combining cationic and anionic moieties,³⁰¹ allowing them to tailor a new range of collectors. The potential application of quaternary ammonium-based ILs (C4–C12 NR4+) as flotation collectors would suggest, according to MD simulations, that the adsorption mechanism on the surface (101) is mainly controlled by electrostatic and van der Waals forces. A more localized look by DFT on the interactions of phosphonium/ammonium-based ILs with semisoluble minerals such as calcite, bastnäsite, and monazite allowed researchers to differentiate the roles of the anions and cations associated with these ILs: if the first one adsorbs directly on the metallic active centers of the minerals, the second one is rather involved in weak solvophobic interactions.^302,303

3.3. Properties of Mineral Crystals and Surfaces in Flotation

Interfacial phenomena at the gas–solid–liquid interfaces control the separation efficiency, but where the mineral solid phase plays an essential role in the flotation process.^1,9,166,304 In contrast to fluid mechanics of amorphous media, the success of molecular modeling approaches owes much to solid-state physics, which has made possible the calculation of crystalline and surface properties of minerals useful for mineral flotation.^{10,15−17,121,264} This section shows how molecular modeling approaches can describe the inherent properties of mineral structures and compositions in terms of mineral surface reactivity and then floatability.

3.3.1. Mineral Surfaces: Structure–Property Relationships

Molecular modeling can provide atomic-scale information on mineral surfaces and crystal structures. In an early attempt, Kundu et al.³⁰⁵ conducted DFT calculations to study the electronic properties of seven different wollastonite cleavage planes. Surface energy calculations revealed that the (100) plane is the most energetically favorable surface in wollastonite. Similarly, Kundu et al.²²⁷ carried out the same procedure to recognize the lowest energy cleavage planes of magnesite and reported that the (110) and (111) directions are the predominant growth planes for magnesite.

DFT was utilized to elucidate the surface reconstruction and relaxation of chalcopyrite surfaces with different terminations.^306,307 Three mechanisms were captured: (1) surfaces with metal-exposed atoms form several metal–metal bonds, (2) those directions with relatively close sulfur atoms with lower coordination numbers form an S–S bond on the outermost layer, and (3) in some directions (e.g., (101), (110), and (112)), only a relaxation of metal atoms occurs by moving the metal atoms downward. The three DFT-reconstruction mechanisms of chalcopyrite surfaces are illustrated in Figure 7.²⁴⁰ The different surface speciations would lead to significant variations in the chemical reactivity of chalcopyrite surfaces in terms of mineral-collector interactions.

Figure 7.

Schematic of surface reconstruction evolution of different chalcopyrite surfaces: (a) metal-exposed (100) surface, (b) sulfur-exposed (100) surface, and (c) (110) surface (Fe: purple, Cu: red, S: yellow). Adapted with permission from ref (240). Copyright 2017 Elsevier.

DFT calculations were employed to disclose more information about the surface reactivity of bastnäsite, considering its complex surface chemistry behavior in flotation.^298,308 DFT was able to successfully capture the reconstruction and hydration behavior of different cleavage directions (as suggested by Wulff’s construction theory) in aqueous media as a crucial step to explain the complex flotation behavior of bastnäsite. Molecular modeling has provided insight into the flotation behavior observed with aluminosilicates (e.g., spodumene and albite) by specifying the directional reactivities of the minerals’ surfaces.³⁰⁴ The surface energy calculated by DFT was related to the cleavage properties of spodumene and albite and their impact on the reactivity of their surface atoms as well as their flotation behavior.³⁰⁹ The broken bond density was used to account for the differences in reactivity of different cleavage directions. As an example, the number of broken bonds on different cleavage planes of feldspar was determined after surface optimization (Figure 8).³¹⁰ Three types of broken bonds, including Si–O, Na–O, and Al–O, are present on the various cleaved surfaces but differ in number on each surface. The feldspar (110), (001), and (110) cleaved planes have 4 (Figure 8a), 8 (Figure 8b), and 10 (Figure 8c) broken bonds, respectively. Al atoms, as the most favorable sites for chemisorption of the collectors on feldspar,^311,312 are more abundant on the (001) and (110) surfaces. Similar work has been done on fluorite and spodumene.^313−315 This information could be put to good use by controlling the grinding conditions to generate mineral particles that favor particular reactive cleavage planes.

Figure 8.

Schematic illustration of the broken bonds presents on different crystal planes of feldspar: (a) (110), (b) (001), and (c) (100). (O: red, Si: yellow, Al: pink, Na: purple). Adapted with permission from ref (310). Copyright 2017 Elsevier.

In the case of the bastnäsite surface, bond population analysis by DFT calculations showed that the C–O bonds in the mineral structure feature covalent bonds, while the Ce–O and Ce–F consist of strong ionic bonds. Consequently, Ce–O and Ce–F bonds are more prone to be ruptured from the bastnäsite cleaved planes, leaving ≡Ce³⁺, ≡CO₃^2-, and ≡F^– dangling bonds to interact with water molecules in the solution, thus resulting in high hydrophilicity of bastnäsite.^298,316

DFT calculations were carried out to characterize the hydrophilicity level of coal as a function of surface functional groups.³¹⁷ X-ray photoelectron spectroscopy (XPS) of the samples revealed the existence of four oxygen-containing functional groups, namely, −OH, C–O, C=O, and −COOH, on the coal surface. The hydrogen binding energy between these functional groups with water molecules was DFT-calculated to be in the order −COOH > −OH > −O– > C=O, where more hydrophilic −COOH groups form two hydrogen bonds. The observations suggest that the complexity of lignite flotation is predominately due to the availability of hydrophilic oxygen-containing function groups on its surfaces. Shen et al.³¹⁸ investigated the effect of surface porosity on the flotation of low-rank coal using the MD framework. The results showed that surface porosity would stabilize the hydration layer on the coal surface, thus disrupting bubbles-surface attachment. On the contrary, the reduction in pore content would lead to a decrease in water-surface interactions and would possibly facilitate the expulsion of water molecules from the surface by bubbles. The coalification degree of low-rank coal, and thus its wettability, was qualified by MD simulations as being controlled by the amount of hydrogen binding between water molecules and coal surfaces.³¹⁹ These atomic/molecular level insights into the wettability of coal surfaces provide significant guidance toward improving the flotation efficiency of coal slime.

3.3.2. Effect of Surface Vacancy on Mineral Surface Properties

Real minerals almost always contain defects in the form of impurities or vacancies in their crystal lattice or surfaces. Quantum-based molecular modeling techniques are able to describe the electronic properties of deficient mineral surfaces.^{49−51,69,175,320−328} The role of vacancies on the wettability of sphalerite depends on the type of surface vacancies (Zn or S) as demonstrated by DFT calculations integrated with the GCMC method on the (110) cleavage plane of sphalerite (Figure 9).⁴⁹⁻⁵¹ The S (Zn) vacancy produces a hydrophobic (hydrophilic) region around the deficient site, thereby potentially changing the dominant adsorption pattern of a reagent on the surface.⁴⁹ Nonstochiometric sites on the pyrite surface would also be involved in the chemical evolution of glycine from zwitterionic form to an ionic species, according to a DFT study.³²⁵

Figure 9.

Optimized structures of ZnS (110) slab with (a) no defect, (b) single sulfur vacancy defect, (c) single zinc vacancy defect, and (d) with double congruent vacancies (Zn: purple and S: yellow). Adapted with permission from ref (49). Copyright 2021 Elsevier.

Atomistic details about the evolution of O₂ by DFT calculations captured distinct dominant adsorption configurations on defect-free and defective pyrite surfaces.³²² While dioxygen dissociative chemisorption on sulfur atoms was more favorable than on iron atoms for a defect-free surface, molecular oxygen adsorption on sulfur vacancies predominantly took place on defective pyrite surfaces. More recently, a DFT study further confirmed that the dissociative adsorption of water on the sulfur-deficient pyrite surface is less favorable.³²⁹ Zn-vacancies repressed water adsorption on the smithsonite surface;³²⁷ i.e., pure molecular adsorption on the Zn-deficient surface replaced the energetically more favorable dissociative adsorption of H₂O on the defect-free surface.

3.3.3. Effect of Lattice Impurities on Mineral Properties

The presence of impurities in the natural mineral crystal lattice is another common phenomenon modulating reagent adsorption in froth flotation, chiefly in the case of solid solutions.^330−332 In this regard, Chen et al.³³³ conducted DFT calculations to determine the effect of lattice impurities on the electronic structures and floatability of sphalerite. Their results indicated that the lattice parameter, semiconductor type, Fermi level, and density of state of sphalerite can significantly vary in the presence of various elemental impurities such as Cd, Hg, Ga, Ge, In, Ag, Sn, Pb, and Sb. Furthermore, the HOMO/LUMO analysis shows that the impurities would even alter the electrophilicity of the sphalerite surface, so that the presence of Mn, Fe, Co, Ni, Cu, Hg, and Pb would increase the affinity of the sphalerite toward the xanthate collector, thus improving its flotation recovery. The sensitivity to oxygen and xanthate during flotation of pyrite when it contains impurities such as As, Se, Te, Co, or Ni can be well understood in light of a DFT calculation.³³⁴ By means of frontier orbitals, while the tendency of pyrite is to oxidize when it contains As, Co, or Ni compared to Se and Te, it has a greater affinity for xanthate in the presence of Co or Ni. DFT calculations further confirmed the possible occurrence of Au in the structure of pyrite and captured the changes in electronic properties and reactivity of pyrite, as already reported by experiments.^335,336

The influence of impurity incorporation on minerals’ wettability and adsorption properties was also studied through MD simulations. For instance, using the sessile drop contact angle measurement concept, it was revealed that replacing Si⁴⁺ with Al³⁺ in the talc crystal structure can reduce talc’s natural hydrophobicity.³³⁷ MD simulations were utilized to compare the swelling pattern of Na- and Ca-montmorillonites and suggested that Ca-montmorillonites have a stronger hydration swelling than Na-montmorillonites, most probably due to a larger hydration radius of Ca²⁺.³³⁸ The isomorphous substitution effect of Fe, Cr, and Mn for Al and Mn for Si in the spodumene structure was investigated with respect to the wetting characteristics and NaOL adsorption using DFT and MD simulations.³³⁹ The results showed that spodumene would keep its natural hydrophilicity with and without elemental substitution; however, such impurities would promote NaOL adsorption on the surface. Based on DFT calculations, the surface with Mn substituting for Si showed the highest affinity toward NaOL. The molecular-scale insights would provide beneficial information for interpreting the complex flotation of spodumene as a solid-solution mineral occurring in pegmatite ores.³⁴⁰

3.3.4. Effect of Mineral–Mineral Close Contacts on Mineral Properties

Galvanic Contacts in Sulfidic Minerals

In addition to impurities in the crystal structure, mineral–mineral close contacts encompass changes in mineral reactivities and electronic properties. In this regard, galvanic coupling in sulfide–sulfide systems would significantly affect the floatability of sulfide minerals.^341−343 DFT was implemented to determine the galvanic interactions between pyrite and galena surfaces, as well as the xanthate electrochemical adsorption on galena.^344,345 Galvanic coupling prompts electron transfer from galena to pyrite, as a result, the collector-surface adsorption modes would differ from the single mineral-collector complexes. DFT calculations revealed that pyrite–arsenopyrite contacts decrease the band gap at the interface, thus facilitating electron transfer and curbing the pyrite oxidation rate.³⁴⁶

Nonsulfide Minerals Contacts

DFT calculations were implemented to shed insights into the coating mechanism of kaolinite on low-rank coal.³⁴⁷ The results divulged that van der Waals attraction between low-rank coal and the kaolinite (001) surface causes kaolinite coating on low-rank coal flotation. The finding is in line with the results reported by Chen et al.³⁴⁸ for the kaolinite interactions with fine coal particles.

3.4. Mineral Surface Modification and Activation in Flotation

Mineral surface modification and activation are critical subjects in mineral flotation, routinely used to promote mineral-reagent interactions. Surface alterations may also occur by some uncontrolled phenomena (e.g., surface precipitation and dissolution) within the process, sometimes resulting in a reduction of flotation recovery.^1,166 Molecular modeling techniques, however, are capable of evaluating mineral-reagent interactions, foreseeing surface speciations, and assessing mineral surface reactivity as part and parcel of tackling the challenges of froth flotation.

3.4.1. Surface Activation by Metal Cations

Metal cations and metal complex species, intervening deliberately or not on minerals’ surfaces, alter the surface properties via surface-reagent interactions. Precipitation of Ca(OH)⁺ and Ca(OH)₂ hydroxide species on the spodumene surface boosts surface activation and mineral-reagent interactions, according to a DFT study.³⁴⁹ Ca atoms of the hydroxide species form covalent bonds with O atoms on the mineral surface, yielding new active sites on the spodumene (110) surface. DFT-simulated Ca(OH)⁺ are shown to act as a bridge for α-bromolauric acid (α-BLA^–) anionic collectors to interact with quartz (101) surfaces,³⁵⁰ while α-BLA^– is unable to adsorb on the quartz surface due to a shielding hydration shell. Quartz surface activation with Ca²⁺ or Ca(OH)⁺ repels water molecules from the surface, bridging α-BLA^– to it and leading to a significant promotion of quartz floatability. DFT calculations further revealed that the preactivation of hydroxylated quartz surface with Ca²⁺ introduces favorable active sites for subsequent adsorption of sodium oleate, making direct flotation of quartz industrially feasible.³⁵¹

MD simulations based on the Universal force field parameters and Mulliken partial charges were conducted to assess the hydrophilicity of Cu²⁺ activated sphalerite surface.³⁵² The wettability of the pristine and the Cu²⁺-activated sphalerite was compared by calculating the contact angle, water number density distribution, water dipole orientation, and water residence time, among other things. Although using a generic force field combined with Mulliken partial charges should be treated cautiously, the MD results confirmed that activating the sphalerite surface with Cu²⁺ increases the mineral hydrophobicity due to decreased surface polarity. The different hydrophobic characteristic between the naked and the Cu-activated sphalerite was confirmed by DFT calculations.⁴⁸

A DFT study of the activation of stibnite (010) surface by Pb²⁺ indicated that lead cation cannot substitute to lattice Sb³⁺ on the stibnite surface;³⁵³ Pb-surface interactions of covalent nature being more likely. Five energetically favorable Pb²⁺-adsorption configurations enable activating as many adsorptions for xanthate on the stibnite (010) surface (Figure 10). Adsorption energy calculations confirmed that xanthate adsorption on the Pb-activated stibnite surface was more favorable than on the inactivated surface. Tian et al.³⁵⁴ discerned the importance of sequential activation for the sake of higher flotation efficiencies for oxide minerals. Their DFT calculations confirmed that the complexation of benzohydroxamic acid (BHA) collector with Pb²⁺ hydroxide species prior to its introduction in the flotation solution is remarkably more energetically favorable than activating mineral surface (cassiterite in this case) in the first place and using BHA afterward. A similar improving mechanism was also reported by DFT calculations for the complexation of BHA with Fe (III) for the flotation of cassiterite mineral.³⁵⁵

Figure 10.

Stibnite (010) surface activation by Pb²⁺ at five different possible surface sites as well as butyl xanthate collector interaction with activated surfaces at these five Pb-activated sites. Adapted with permission from ref (353). Copyright 2018 Elsevier.

The adsorption of different alkali and earth-alkali cations on the spodumene surface can be followed by MD/DFT integrated surface charge simulations to change the reactivity of the mineral surface with respect to surfactants.³⁵⁶ Below the zero-charge point, adsorption of anionic collectors occurs primarily via electrostatic interactions with the abundant cations on the spodumene surface. However, above the zero-charge point, the anionic collectors continue to adsorb onto the spodumene cationic sites albeit with lesser numbers on the surface, leading to more negative potential ζ values.

3.4.2. Surface Sulfidization and Oxidation

Surface Sulfidization

Surface sulfidization is a surface modification approach in froth flotation to promote recovery, especially in the case of oxide minerals.³⁵⁷ A density functional based tight binding (DFTB+) study was performed to clarify the sulfidization-amine flotation mechanism of the smithsonite surface.³⁵⁸ The study demonstrated two different mechanisms based on the concentration of hydrosulfide (HS^–) on the surface: (1) per lower concentrations of HS^–, Zn-SH-SH structure is formed on the surface, preventing the N atom of amine collectors from interacting with Zn on the surface but rather with the S atom in the HS^–, and (2) per higher HS^– concentrations, ZnS is formed on the surface, promoting the adsorption of amine collectors on the Zn atoms of the smithsonite surface. In another study, DFT calculations of cerussite (PbCO₃) surface sulfidization revealed that HS^– ions can readily adsorb onto the surface through hybridization of S atom of HS^– and the surface-exposed Pb atoms on the PbCO₃ surface.³⁵⁹ DFTB+ calculations of the sulfidization of the same PbCO₃ mineral suggest that Pb²⁺ on the activated surface interacts more readily with xanthate but less with water, based on the adsorption energy values.³⁶⁰ Surface sulfidization, however, is not always favorable for collector adsorption. For instance, a DFT study showed that chalcopyrite and galena surface sulfidization by Na₂S prevents the adsorption of xanthate collectors on the mineral surfaces and thus reduces flotation recovery.³⁶¹ The higher interaction of sodium sulfide with the chalcopyrite and galena surfaces was introduced as an indication of a significant reagent-removal effect of Na₂S in the chalcopyrite-xanthate and galena-xanthate systems.

Surface Oxidation

Surface oxidations (i.e., surface–oxygen interaction) would strongly modify the electronic properties of mineral surfaces, leading to a different adsorption behavior of collectors.^{47,322,362,363} Liu et al.³⁶⁴ applied DFT to determine how O₂ adsorption alters the reactivity of gold (211) surface. A transition state study captured four possible pathways for surface activations of the gold surface, all give almost equivalent free energy barriers in an aqueous environment, indicating the substantial role of surface H and H₂O coverage on the reaction mechanism. Another DFT study implied that the adsorption of water molecules on galena (100) favorably occurs upon coadsorption with O₂ or after galena surface oxidation.³⁶⁵

3.4.3. Surface Precipitation of Solution Components

The presence of a whole “fauna” of ions in the real solutions of flotation pulps makes the controlled solutions studied in the laboratory more the exception than the norm. These species can precipitate on the mineral surfaces, altering their surface properties and, ultimately, the flotation behavior of the minerals. DFT/experimental studies have shown that the presence in the flotation solution of species from gangue leaching (e.g., calcite, dolomite) present together with the rare earth minerals would spoil the efficiency of the hydroxamic collectors through complex formation, negatively affecting the flotation recovery of rare earth (RE) minerals.^366,367 Specifically, the DFT results revealed two dominant decaying mechanisms for the lower floatability of RE-minerals in these complex systems: (1) adsorption energy calculation confirmed that the complexation of dolomite supernatant species with the hydroxamic collector is energetically favorable, causing the depletion of free collectors in the solution and, subsequently, the reduction of collector adsorption on the target minerals, and 2) dissolved dolomite and calcite species, including Ca(OH)₂, Mg(OH)₂, CaCO_3, and MgCO_3, can readily be precipitated on the RE-minerals’ surfaces (through chemisorption), reducing the surface affinity toward hydroxamic acid collectors by preventing the collector from directly interacting with the mineral surface (Figure 11). As seen in Figure 11, ion surface precipitation would critically change the adsorption mode of hydroxamic acid on the RE-mineral: bidentate adsorption of hydroxamic acid on rare-earth atoms on the monazite surface would change to monodentate adsorption with Ca when CaCO₃ has been priorly precipitated on the surface. The adsorption energy of the former configuration was calculated to be more than two times lower than the latter one.

Figure 11.

Interaction of benzohydroxamic collector with (a) directly monazite (100) surface and (b) CaCO₃ species precipitated on monazite (100) surface, (Ce: beige, O: red, P: purple, C: gray, Mg: orange, H; white, Ca; green, N: blue). Adapted with permission from ref (367). Copyright 2018 Elsevier.

3.5. Minerals/Water/Gas Interfaces in Flotation

The froth flotation process is a three-phase system bounded by up to as many interfaces (Figure 2). In this section, we will discuss complementary aspects of molecular modeling techniques to those covered in the previous sections but with an emphasis on the interfaces themselves.

3.5.1. Mineral/Water Interface

Mineral Surface Electronic Properties and Reagent Adsorption

The electronic properties and reactivity of minerals’ surfaces can readily be altered in an aqueous environment, leading to different adsorption properties compared to dry surfaces.^{50,73−75,173,363−365,368−372} For instance, DFT calculations showed that the water hydration layer on the smithsonite weakens the hybridization of s and p orbitals and lowers the electrophilicity of Zn atoms on the outermost mineral layer, subsequently reducing the interaction levels of smithsonite with carboxyl collectors.²⁵⁵ As further confirmed by DFT, hydration of sphalerite significantly alters the mineral surface properties through localization of Zn 3d, 4s, and 4p orbitals, resulting in a reduction in the reactivity of Zn atoms and, ultimately, the Zn-xanthate collector interactions.³⁷³ The multilayer hydration of the hydrophobic galena and hydrophilic pyrite surfaces via DFT calculations captured different dominant interaction mechanisms for each surface; while water-surface interactions in hydrophobic surfaces mainly occur through hydrogen bonds, covalent bonding between surface-exposed metal atoms and oxygens of water molecules dominantly occurs for hydrophilic surfaces.³⁷²

Ai et al.²³⁴ used MD simulations to compare the flotation separation of KCl and NaCl in the presence of a hydration layer using the octadecylamine (ODA) collector. The ODA collector is able to cross the hydration layer to adsorb on the KCl surface. This is due to the adsorption energy of ODA/KCl being greater than the cohesive energy between water molecules in the hydration layer. On the contrary, the cohesive energy in the hydration layer is higher than that of the ODA/NaCl, preventing the collector from interacting with the NaCl surface. Thus, only KCl would be collected from the potash ores upon addition of ODA collectors.

DFT-simulated adsorption of BHA on the hydrated cassiterite (110) surface demonstrated that direct adsorption of BHA on the tin sites of the pristine surface is not favorable.³⁷⁴ However, activation of the cassiterite surface by Pb²⁺ was shown to assist in the selective adsorption of BHA by allowing the departure of two water molecules from the lead ion coordination shell. Other studies confirmed that Pb²⁺ activation of cassiterite,³⁷⁴ and smithsonite surface sulfidization by means of HS^– and S^2– would repel the hydration-layer water molecules,³⁷⁵ facilitating collector uptake by the mineral surface. A DFT study on the adsorption of alanine on the ZnS surface further suggested that solvated alanine cannot be chemically adsorbed on the defect-free ZnS surface, while surface sulfur vacancy prompts alanine adsorption on the ZnS surface through the formation of monodentate bond with the undercoordinated Zn atoms around the vacancy site.⁵¹ Alteration of the adsorption modes, from chemisorption in the vacuum to physisorption in the presence of water molecules, was also reported in the case of sodium dimethyl dithiocarbamate (SDD) and butyl xanthate (BX) collectors adsorption on the sphalerite (110) surface.³⁶⁸ All of these examples emphasize the need to consider water molecules to reflect true interactions in modeling flotation systems.

Mineral Surface Wettability

The microscopic wettability characteristics of a surface are mainly inferred from contact angle determinations using MD simulations.^{216,313,376−381} For an accurate prediction of the contact angle, the vapor–liquid border on the outer surface of the water droplet must be carefully recognized (see section 2.2.1 for explanations and references therein). The literature review points to a gap in MD simulations of the water-vapor boundary and determination of the contact angle on mineral surfaces of interest for flotation. The degree of hydrophobicity of the bastnäsite surface was simulated by MD from the viewpoint of a change in the concentration of hydroxamate collectors.³⁸² Snapshots of the simulation after introducing a water droplet on the bastnäsite surface show this concentration effect for octyl hydroxamate: 8.3% (Figure 12a), 25% (Figure 12b), and 50% (Figure 12c). The contact angle or, in other words, the hydrophobicity of the surface increases with the concentration of the collector.

Figure 12.

MD simulation snapshot of the initial configuration (0 ps) and the configuration after 40 ps for a water droplet on the bastnäsite surface with different levels of octyl hydroxamate coverage: (a) 8.3% hydroxamate coverage, (b) 25% hydroxamate coverage, and (c) 50% hydroxamate coverage (red: oxygen; blue: cerium; green: fluorine; cyan: carbon; white: hydrogen, pink: hydroxamate oxygen; gray: nitrogen). Adapted with permission from ref (382). Copyright 2014 Elsevier.

As an alternative to estimating the contact angle, the wettability of a mineral surface can be assessed qualitatively by means of the hydration energy, hydration shell, orientation, degree of segregation of water molecules, and radial distribution of water molecules on the surface.^{308,383−389} Combining DFT with Wulff’s construction theory for the calculation of water adsorption energy demonstrates that a Ca-bearing bastnäsite surface is more hydrophilic than the same surface but bearing La.³⁸⁴

3.5.2. Water/Gas Interface

Frother at the Interface

Chong et al.³⁹⁰ employed MD simulations to simulate the frothers/air/oily saltwater interface with three surfactant frothers, namely, methyl isobutyl carbinol (MIBC), terpineol, and ethyl glycol butyl ether (EGBE), through a binary combination of liquid–air and liquid–liquid interfaces. The MIBC, terpineol, and EGBE molecules were representative of the alcohol, cyclic alcohol, and glycol ether chemical classes of common flotation frothers. The surface tension calculation at the frother/air interfaces provided good agreement with experimental results for MIBC and terpineol. While for EGBE, the value was lower than experimentally measured, possibly due to the reduced charges assigned to EGBE molecules. The authors further extended the work to study the effect of frother on saltwater/air interfaces.³⁹¹ Simulation results indicate that the polar alcohol groups of the frother molecules orient themselves to adsorb onto the saltwater. Surface tensions were found to decrease upon the addition of MIBC and terpineol, while for the EGBE, comparatively small changes in surface tensions were observed.

Collector at the Interface

MD simulations were utilized to better understand the adsorption and packing of octadecylamine hydrochloride (ODA) collector molecules at the air/water interface in the presence of various ions in the solution.³⁹² Some anions (e.g., I^– and SO₄^2–) are shown to penetrate the ODA monolayer at the air/water interface due to their larger size and greater polarizability and disrupt the arrangement of the ODA molecule. Furthermore, the interactions between the anions and the -NH₃ headgroup of the ODA revealed that the SO₄^2– anion has a denser distribution around ODA, while no anion layer for NO₃^– and SCN^– was observed. Wang et al.³⁹³ investigated the surface activity and self-aggregation behavior of DDA and four alcohol mixtures at the water/air interface using MD simulations. Tighter surfactant aggregation takes place at the water/air interface for longer alkyl chain alcohols. Comparison of the radial distribution function (RDF) between the DDA and alcohol headgroups pairs revealed that the alcohol positions between the DDA headgroups leading to an increased rigidity of the surfactants’ adsorbed monolayer. The new configuration reduces the surface tension of water, confirming the auxiliary role of alcohols in DDA/alcohol mixture.

Effect of External Electric Field

The MD method has also demonstrated its ability to simulate the effect of an external electric field on water/mineral/gas interfaces.^394−397 Air flotation of hydrophobic particles immersed in saline solutions with different concentrations of NaCl and in the presence of an electric field³⁹⁶ shows that the latter would deteriorate the adhesion of bubbles to hydrophobic particles. The application of an external electric field could also lead to a reduction in the size of the bubbles, thus promoting better attachment of hydrophobic particles during flotation.³⁹⁵ Furthermore, the application of an electric field can weaken the restriction of the aqueous solvent on the surfactant (e.g., dodecyl trimethylammonium chloride, DTAC), reduce the surface tension, inhibit the coalescence of small bubbles, and thus promote the adsorption of DTAC at the gas–liquid interface.³⁹⁷ Controlling the direction of the electric field would also manipulate the distribution of the DTAC surfactant helping to improve the stability and adsorption capacity of the bubbles.

3.5.3. Mineral/Gas Interface

The mineral-air bubble attachment is the main objective that must be achieved for an efficient flotation process (Figure 2).¹⁷ Scrutiny of the dynamics of bubble attachment at the molecular scale would be an undeniable asset to the scope of MD simulations. The mechanism of nitrogen nanobubble attachment on molybdenite and quartz surfaces has been recently unraveled.³⁹⁸ The chain of events on a hydrophobic surface unfolds through thinning the water film on the mineral surface, rupturing the thinned water film, film displacement, and, finally, direct bubble-surface interactions. Water film rupture does not occur at the (hydrophilic) quartz surface, keeping a stable hydration layer (Figure 13a). Film thinning and breakup are clearly reproduced by simulation on the molybdenite face surface (Figure 13d), forming a hemispherical gas bubble at the interface. The nitrogen bubble retains its spherical shape for zigzag- and armchair-edged molybdenite surfaces (Figure 13c, b), while thinning and rupture of the film occur to a lesser degree. These surfaces show a more modest hydrophobic character compared to the molybdenite face surface. Specifically, analysis of the interfacial water region captures a “water exclusion zone” at the hydrophobic molybdenite face surfaces, promoting spontaneous attachment of bubbles to the surface by attractive van der Waals forces. This exclusion zone is relatively smaller on the zigzag-edge and armchair-edge molybdenite surfaces, restricting surface interactions with gas molecules.

Figure 13.

Thin sections of initial and final states (after 1 ns) of nitrogen bubbles at (a) quartz (001), (b) molybdenite zigzag-edge, (c) molybdenite armchair-edge, and (d) molybdenite face surfaces, adopted from ref (398).

Implementing the same approach to study the thinning and breakage of the wetting film during bubble attachment on charcoal surfaces with different degrees of coalifaction demonstrates a higher rate of bubble attachment on surfaces with higher hydrophobicity.³⁹⁹ During film thinning, the decay rate of hydrogen bond number is the fastest on the bituminous coal (BC) surface and the slowest on the low-rank coal (LRC) surface.

4. Summary, Outlook, and Recommendations

This review of molecular modeling applied to flotation attests to the extent to which this tool contributes to advancing fundamental knowledge in mineral processing. Perhaps if Fuerstenau, Jameson, and Yoon were to write a new edition of their book “Froth Flotation: A Century of Innovation,”¹ they would endorse the important role of molecular modeling approaches in the ongoing rational design of flotation chemicals. In order for this review to be useful, we felt it was necessary to highlight directions in the study of flotation using molecular modeling for researchers who are actively using this tool in their flotation studies or for those new to the research field who have begun to use this tool. Hence, the first part (section 2) aimed to review the key principles of a wide range of molecular modeling approaches, whereas emerging trends of their applications to the froth flotation process were the subject of the second part (section 3).

Considering the promising avenue depicted in this review, it can be concluded that molecular modeling techniques are applicable to support or refute hypotheses that are difficult to prove through experimentation alone. Thus, this tool must be seen for what it is, i.e. to complement the analytical and experimental work on froth flotation. As highlighted throughout this review, molecular modeling techniques are capable of providing scientists with first-hand atomic information at solid–liquid, solid–gas, and liquid–gas interfaces. The quest for the Holy Grail in the application of molecular modeling simulations is to build a rational framework to (i) describe the reactivity of the mineral surface and its interactions with different classes of flotation reagents and (ii) use the accumulated knowledge to design suitable reagents based on the mimicry of the phenomena occurring at the atomic scale at mineral/water/gas interfaces. However, the authors caution researchers to carefully study the theory and technical details before embarking on hands-on practice and to consult the available references in other disciplines to familiarize themselves with standard implementation and analysis approaches. This comprehensive review shows remarkable excitement about the application and implementation of molecular modeling in the mineral processing community. However, the road remains somewhat bumpy in some respects; for example, the majority of published work on water contact angle evaluation has neglected the basic statistical concepts of molecular modeling.

The following is a collection of key recommendations for future directions of molecular studies in the field of froth flotation:

• The next step would be to address the dynamic behaviors occurring during flotation. The reagent adsorption and surface hydration are dynamic behaviors, meaning that the adsorption could occur with different molecular configurations and the effect of temperature is nontrivial. Adding temperature to the simulation would decrease the energy barrier between multiple minima, most probably leading to different stable adsorption configurations overlooked by geometry optimizations at 0 K. Dynamic simulations allow us to explain the reagent solubility, the (self)diffusion of the adsorbates, the orientational parameters, the configurational transition, and the phenomenological and mechanistic details of the adsorption phenomena in the process. The competitive adsorptions of adsorbates (i.e., reagents, water, and solution ions) are also trackable with dynamic simulations. Hereupon, investigating dynamic properties is inevitable for the sake of more realistic conclusions.

• Extra attention must be given to developing accurate force fields for mineral systems. The scarcity of concerted force fields, particularly for minerals with transition metals, is the most critical bottleneck in the application of MD simulations in flotation studies. More recently, the INTERFACE force field has been developed for several minerals, but the development remains a work in progress for the large portfolios of mineral classes.

• A key step toward the reliability of atomistic models of flotation systems is the accurate definition of solution environments and mineral surface complexations in contact under different pH levels and ionic strengths. To this end, systematic attempts comprising coupled experiments and ab initio calculations for various minerals at different pH must be pursued to (i) build realistic surface models that are essential for predictive simulations and (ii) find entry into molecular models to resolve the shortcomings of conventional force fields.

• Despite the lack of accurate force fields, AIMD and QM/MM techniques have demonstrated descriptive power to simulate dynamic behaviors in mineral systems. AIMD simulations still cannot afford a swarm of water molecules required for appropriate solvation of reagents; however, QM/MM is capable of modeling larger-size systems, where the solid/reagent/water are taken care of with quantum calculations, and beyond that, molecular mechanics plays a role. The applications of these two methods are still relatively unknown; attention to these dynamic processes would benefit from being studied in order to fertilize and enrich future research.

• Rather than using commercially available simulation software, open-source packages should be further employed to perform MD simulations at higher length scales along with more prolonged simulation time to explore the dynamics of the system thoroughly.

• More attention must be paid to important flotation topics that remain unexplored by molecular modeling tools. For example, the number of studies on the characteristics of water/mineral/gas interfaces (in particular, the gas–mineral interface) remains limited, while the accumulated knowledge could be beneficial in the rational design of flotation reagents.

• The environmental risks of flotation have been critically brought to the fore by pointing fingers at the broad portfolio of nonbenign and biohazardous reagents used in industrial processes. In this situation, principles of green chemistry in terms of designing biodegradable and sustainable alternatives must become an imperative part of future studies. Along with the rapid advances in green synthetic methodologies and computational toxicology, molecular modeling techniques can significantly accelerate the transition toward greener solutions, i.e., designing ecofriendly and nontoxic reagents with improved efficiency and selectivity.

Author Contributions

CRediT: Abolfazl Alizadeh Sahraei conceptualization (equal), data curation (equal), formal analysis (equal), writing-original draft (equal); Dariush Azizi conceptualization (equal), data curation (equal), formal analysis (equal), writing-original draft (equal); Abdol Hadi Mokarizadeh conceptualization (equal), data curation (equal), formal analysis (equal), writing-original draft (equal); Daria C. Boffito funding acquisition (equal), project administration (equal), supervision (equal), writing-review & editing (supporting); Faïçl Larachi funding acquisition (equal), project administration (equal), supervision (equal), writing-review & editing (supporting).

The authors declare no competing financial interest.