Molecular-Induced Chirality Transfer to Plasmonic Lattice Modes

Abstract

Molecular chirality plays fundamental roles in biology. The chiral response of a molecule occurs at a specific spectral position, determined by its molecular structure. This fingerprint can be transferred to other spectral regions via the interaction with localized surface plasmon resonances of gold nanoparticles. Here, we demonstrate that molecular chirality transfer occurs also for plasmonic lattice modes, providing a very effective and tunable means to control chirality. We use colloidal self-assembly to fabricate non-close packed, periodic arrays of achiral gold nanoparticles, which are embedded in a polymer film containing chiral molecules. In the presence of the chiral molecules, the surface lattice resonances (SLRs) become optically active, i.e., showing handedness-dependent excitation. Numerical simulations with varying lattice parameters show circular dichroism peaks shifting along with the spectral positions of the lattice modes, corroborating the chirality transfer to these collective modes. A semi-analytical model based on the coupling of single-molecular and plasmonic resonances rationalizes this chirality transfer.

Introduction

Chiral plasmonics is one of the fascinating topics in nanophotonics, which simultaneously raises fundamental questions on light–matter interactions and promises for future applications to address real-life challenges.¹⁻¹² Chiral molecules are abundant yet crucially important in nature.¹³ The handedness of a molecule underpins its function in biological systems, despite having an otherwise identical chemical nature as the enantiomeric counterpart. On a larger length scale, encoding chirality into plasmonic materials has enabled the manipulation of electromagnetic fields, and thus tailoring light–matter interactions,^{1−3,5,7,9−12} and enhancing the sensitivity of chiral molecule detection,^2,6−8,14 with the potential to enable early disease detection in tissues.¹⁵ The potential to use chiral nanophotonic sensors to enhance molecular signals is appealing. However, the accurate measurement of molecular circular dichroism (CD) spectra in the ultraviolet region requires sensitive and expensive instrumentation.¹⁶ Furthermore, the fabrication of suitable plasmonic systems for such chiral detection is complex and requires sophisticated infrastructure.¹⁷⁻²⁰

Chiral plasmonic metamaterials exhibit much larger CD signals compared to chiral molecules.¹⁶ The dominant chiral signal of such metamaterials might screen the intrinsic chiral information from the molecule, thus necessitating background subtraction and alignment.²²⁻²⁶ These difficulties can be overcome by using racemic metamaterial structures, which do not exhibit an overall intrinsic far-field CD signal and thus do not shield the molecular signal.^22,27−31

A conceptually much simpler alternative can take advantage of plasmonic resonances in isotropic, achiral nanoparticles to detect the handedness of a molecular analyte. Such nanoparticles can become optically active by a chirality transfer from the molecules in their vicinity (see Figure 1a, green line and Figure S1), relying on induced chirality.^{16,19,25,32−34} A particular appealing aspect of this mechanism is that the observation of chirality occurs at the plasmonic resonance in the visible range, while the initial molecular signal can be located at lower wavelengths, i.e., in the UV.³⁵ However, this transfer may come at the cost of losing some information of the molecular CD spectrum as, in general, helicity is not preserved by plasmonic nanoparticles. This molecular chirality transfer has so far solely been demonstrated for localized surface plasmon resonances (LSPRs).³⁶⁻⁴⁴

Figure 1.

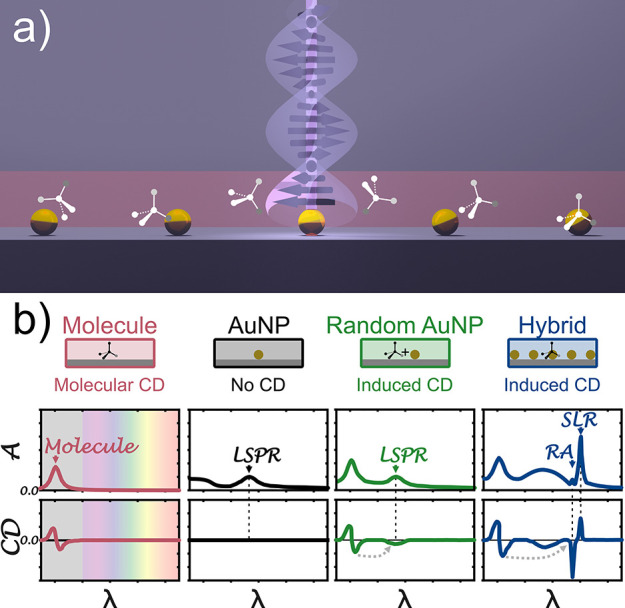
Hypothesis of induced chirality in individual achiral plasmonic gold nanoparticles and their arrays. (a) A chiral film (red) consists of randomly oriented chiral molecules embedded in a thin layer of polymer (PMMA). This chiral film is sandwiched between a glass substrate and immersion oil of similar real refractive indices. (b) This configuration exhibits circular dichroism (CD ≠ 0) around the molecular resonance as shown in the schematic spectra (red). This means the absorption is different for the left- and right-handed circularly polarized light. Randomly arranged achiral gold nanoparticles added to a chiral film can show induced chirality at the LSPR (green). An assumed array of spherical gold nanoparticles will excite, in addition to a broad LSPR, also sharp surface lattice resonances (SLRs) and Rayleigh anomalies (RA). In this work, we extend the effect of induced chirality to lattice modes. We assume these coherent resonances can also show optical activity when chiral molecules are present around the nanoparticle arrays. Besides the LSPR, one can see that the RAs and SLRs show non-zero CD signals (blue). No actual data, schematic representation for illustrative visualization.

The chirality transfer between molecules and LSPRs of plasmonic structures^{16,19,25,26,32−34} is complex and remains subject to current research.⁴⁵⁻⁵² Using individual nanoparticles seems straightforward but shows certain limitations. Single nanoparticles show relatively weak near-fields and broad resonance features. These near-fields can be enhanced in hotspots formed by dimers or chains of nanoparticles to improve the induced chirality. However, their mode volume remains strongly confined to a small region.³⁶⁻⁴⁴ Surface lattice resonances (SLRs) may provide solutions to these drawbacks. SLRs occur in periodic plasmonic nanoparticle arrays and result from electromagnetic coupling of LSPRs and diffractive modes. This coupling reduces losses, leading to sharper, spectrally tunable modes.⁵³⁻⁶¹ Characteristically, the enhanced near-fields in SLRs^53−55,57 are much more delocalized throughout the volume between the particles as compared to that in LSPRs.^62,63

Here, we demonstrate the molecular chirality transfer to lattice resonances, using arrays of spherical gold nanoparticles, as the simplest possible realization of such systems. We hypothesize that randomly arranged molecules covering these substrates (Figure 1a) can successfully couple with the achiral plasmonic particles in the array. Thus, both LSPRs and SLRs in such a “hybrid” system will show an induced chirality (Figure 1b, blue line) if the chiral molecules surround them. This demonstration of chirality transfer to collective plasmonic modes opens possibilities to harvest the attractive properties of lattice resonances, like spectral tunability and narrow features, toward molecular chirality detection. Importantly, this new approach avoids using intrinsic chiral surface lattice modes, which were predicated to improve chiral sensing⁶⁴ and were recently applied in enantiomeric sensing,⁴ but require more complex nanostructure design.

Results and Discussion

Design of the Experimental System

We experimentally realize the proposed systems (Figure 1a) to examine our hypothesis (Figure 1b). We fabricate large-area nanoparticle arrays on a substrate via colloidal self-assembly^63,65 (Figure 2a). We use core–shell microgels with plasmonic NP cores (AuNPs; D_TEM = 99 nm) surrounded by soft poly(N-isopropylacrylamide) (PNiPAm) shells (bulk diameter D_{h,core–shell} = 367 nm). These core-shell particles are spread at the air–water interface until the interface is fully covered and a homogeneous particle monolayer in hexagonal arrangement is formed. The monolayer is then transferred to a glass slide (Figure S2). After the first deposition, the remaining interfacial particle monolayer relaxes into a hexagonal array with increased lattice constant D_hex, which again can be transferred to a solid substrate.^63,65 After transfer, the organic PNiPAm shell is removed by oxygen plasma, revealing the hexagonal array of AuNPs on the glass substrate (Figure 2b). Using this method, we prepare samples with two different lattice constants, where the cores are separated by D_hex ∼ 450 nm and D_hex ∼ 550 nm (exemplarily shown for D_hex ∼ 450 nm in Figure 2b). Due to fabrication imperfections and a reduced coupling strength between the plasmonic resonance and the Rayleigh anomaly (RA), the latter results in broader SLRs. A detailed correlation between experimental parameters of the interfacial self-assembly of the used Au@PNiPAm core-shell particles, the structural properties of the formed arrays, and the resultant quality of the SLRs in the system has been previously established.^64,66.

Figure 2.

Realization of the experimental system to investigate induced chirality in surface lattice resonances. (a) Core–shell microgels (99 nm AuNP@367 nm PNiPAm) were assembled at the air–water interface and transferred to glass substrates. The organic shells of the resulting monolayers were removed, revealing the hexagonal arrays of AuNPs. A ∼200 nm PMMA film with 40 mM riboflavin was spin-coated on top. The RI environment was matched with immersion oil and a glass cover. (b) Top: photograph of a typical sample after the transfer of the interfacial colloidal monolayer to the solid substrate with structural coloration arising from the periodic nature of the two-dimensional array. Bottom: SEM image of the arrays of AuNPs taken after shell removal. The fast Fourier transformation (FFT) (inset) reveals the hexagonal symmetry of the assembly. (c) Representative AFM image of a sample with D_hex ∼ 450 nm. Note that the organic shells are still present in this sample. (d) Side-view SEM images at two different magnifications of a sample with arrays of AuNPs and a chiral film on top (without immersion oil).

As the chiral molecule, we use riboflavin embedded in a poly(methyl methacrylate) (PMMA) film to allow comparison with previous experiments.³⁷ We modify the established protocol (details in Methods section) to create a chiral polymer film of ∼200 nm thickness. The side-view images (Figure 2d) reveal that the AuNPs remain assembled on the substrate. We produce a set of two reference samples, one with arrays of AuNPs in plain PMMA films without riboflavin and a second one having a riboflavin-containing PMMA film without the AuNPs. All substrate films were covered with immersion oil and a cover slide (Figures S2 and S3) to match the refractive index (RI), and thus, we effectively excite SLRs.⁵³⁻⁵⁷ The homogeneous RI environment also prevents scattering, so that the surface roughness of the PMMA film does not compromise the optical properties. A smoother PMMA interface may be obtained from employing a different solvent used for similar coatings.^66,67 The coating with a PMMA film did not disturb the positions of the individual NP in the arrays, as evidenced by the persistence of SLRs with similar quality compared to reference measurements using only index-matching oils.^63,65

The large area covered by the AuNP array allows us to measure the samples in a commercial CD spectrometer (Jasco J-815a) under normal illumination with a simple, custom-built sample holder (Figure S3).

Experimental Demonstration of Molecular Chirality Transfer to Lattice Modes

We optically characterize the prepared samples by illumination with circularly polarized light at normal incidence. We measure absorption under left and right circularly polarized (LCP, RCP) illumination in transmission mode to obtain the CD spectra. First, in Figure 3a,b, we show the absorption and CD spectra for all references, the pure chiral riboflavin molecules embedded in PMMA (red line), and two AuNP array samples without any chiral molecules (black and gray lines). The bare molecular film shows spectral features between 350 and 500 nm, both in absorption and in CD. Note that the used glass substrate is not transmissive below 350 nm. Our measured molecular signals are comparable in spectral position and intensity with the previous study of induced chirality using the same molecule.³⁷ The bare AuNP arrays (without molecules) show two resonances each, an LSPR located at around 575 nm and SLRs with resonances at ∼630 and ∼720 nm for the samples with D_hex ∼ 450 nm (SLR1) and D_hex ∼ 550 nm (SLR2), respectively (see also Figure S4). Assuming that the SLRs result from coupling to the <1,0> diffraction mode, we expect RAs at 592 and 724 nm, respectively, for the two interparticle spacings (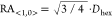, Figure S5).⁵³⁻⁵⁸ The spectra agree with previous results obtained from periodic arrays of similar, spherical AuNPs.^63,65 Note that the broadening of the SLRs arises from fabrication imperfections typical of self-assembled structures^62−64,68 and limitations in coherency and collimation of the commercial CD spectrometer.⁵⁸ If needed, the structural order of the plasmonic lattice formed from the interfacial two-dimensional self-assembly of the Au@PNiPAm CS particles and, thus, the optical quality of the SLRs can be improved using thermal annealing,⁶⁹ or more sophisticated fabrication resulting in lattices with sharp and defined band structures.⁶⁹⁻⁷¹ As anticipated, for achiral, plain arrays of AuNPs, there are no signatures of chirality present in the CD spectra (black and gray lines in Figure 3b; see also Figure S4).

Figure 3.

Optical response of isotropic, achiral AuNP arrays embedded in plain and riboflavin-loaded PMMA films to circularly polarized light. (a) Mean absorbance and (b) circular dichroism spectra of two reference systems with only the riboflavin/PMMA layer (red line) and only the AuNP arrays (black and gray lines; D_hex ∼ 450 and ∼550 nm). Only the riboflavin-loaded film shows chirality, while the plasmonic arrays remain achiral at the positions of the LSPRs and SLRs. (c) Mean absorption and (d) circular dichroism spectra of the two hybrid samples with AuNP arrays embedded in the chiral riboflavin-loaded film. The absorption spectra appear as additions of the individual contributions. Both samples show CD peaks at the positions of the respective surface lattice resonances (SLR1 and SLR2, indicated by arrows). Black and gray lines for D_hex ∼ 450 and ∼550 nm, respectively; red, dashed line shows molecular CD spectra.

The combination of chiral molecules and achiral AuNP arrays (“hybrid” system) changes the chiroptical response. Figure 3c,d shows the spectra for these hybrid systems (blue and yellow lines). The absorption spectra of the hybrid systems show the spectral features of the individual constituents (Figure 3c). In particular, both samples show a common molecular feature at 350–500 nm and SLRs at ∼645 nm (SLR1) and ∼693 nm (SLR2), for the lattice parameters D_hex ∼ 450 nm and D_hex ∼ 550 nm, respectively. In contrast, the CD spectra are seemingly not a mere addition of the two component signals (Figure 3d). The CD signals in the molecular region change sign and shape, presumably because interactions with the AuNPs prevent the preservation of the helicity.⁵⁰ Importantly, the CD spectra show several additional features not observed in the reference systems. Positive CD signals at ∼575 nm, corresponding to the position of the LSPRs (gray arrow), are found in both samples and result from molecular chirality transfer to the LSPRs, corroborating results from literature.³⁷

The sample with D_hex ∼ 450 nm additionally shows a CD peak at ∼650 nm. This positive CD peak nearly coincides with the spectral position of the SLR1 peak (Figure 3d, blue arrow), indicating that the molecular chirality signal is transferred to the SLR of the array. Corroborating this interpretation, the CD peak shifts along with the SLR for the sample with a larger lattice spacing (D_hex ∼ 550 nm) to ∼700 nm, which spectrally coincides with the SLR2 (Figure 3d, yellow arrow). Together, these observations provide experimental demonstration of plasmon-induced chirality transfer to SLRs.

Theoretical Description of the Plasmon-Induced Chirality Transfer to Surface Lattice Modes

We systematically investigate the chirality transfer to SLRs via full-wave electromagnetic simulations (COMSOL Multiphysics).⁷² We set up an array of gold nanospheres (D = 90 nm) positioned at the bottom of a 200 nm-thick chiral film, where the chiral response is introduced as specified below. We consider a square array of spherical gold nanoparticles with a variable lattice spacing D_squ. The surrounding environment is assumed to be a homogenous medium with RI n_eff = 1.518 matching the experiment. We include the isotropic, homogenous chirality by modifying the constitutive relations for the electric displacement field and the magnetic induction 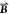in the response of the chiral film and incorporate it into the COMSOL solver through the Pasteur parameter κ, as^35,52

2-1

2-2

with ε being the permittivity, μ the permeability, 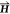the magnetic field, and the electric field.³⁵ The complex chirality parameter κ describes the molecular chiroptical response, modeled by a frequency-dependent Lorentzian function, associated with a molecular electronic transition (see Methods for details).³⁵

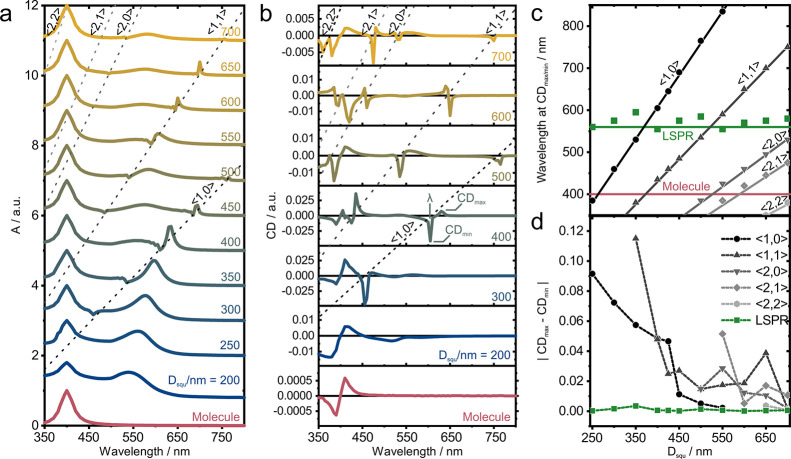
Figure 4a shows the average absorption of LCP and RCP light for a bare chiral film (red line) and that of a bare array of AuNPs for a selected lattice spacing of D_squ = 425 nm (black line). We assume a single molecular resonance at λ₀ = 400 nm. The absorption spectrum of the bare AuNP array shows an LSPR peak around 570 nm, as well as RAs and SLRs, marked with arrows. For this lattice parameter, we obtain the <1,0> RA to be at RA = n_eff · D_squ = 646 nm, and the <1,1> RA at 457 nm. The <1,0> RA couples with the LSPR, resulting in a pronounced SLR at around 660 nm. The chiroptical response of both reference systems is shown in Figure 4b. As expected, no chiral activity is observed for the bare particle array (black line), whereas the chiral film (red line) shows a bisignated (i.e., having a negative and positive peak around the resonance position⁷³) Lorentzian-like peak centered at 400 nm.

Figure 4.

Simulated chiroptical response of arrays of spherical AuNPs with and without the presence of chiral molecules. (a) Calculated mean absorbance of randomly oriented molecules in a chiral film for right and left circularly polarized (red line) and for the achiral square array of AuNP spheres (D = 90 nm) embedded in a homogeneous achiral medium with n_eff = 1.518 (black line). The molecular response shows a pronounced resonance peak at 400 nm, and the particle array exhibits a surface lattice resonance (SLR) at 660 nm, localized surface plasmon resonance (LSPR) at 570 nm, and RAs at 426 and 645 nm. (b) The differential absorption (CD) shows a chiral signature for the molecular resonance, while the plain plasmonic arrays remain achiral (flat line at CD = 0). (c) The mean absorption for the hybrid system combining the chiral film (blue line) exhibits all spectral features of the individual components. (d) The circular dichroism (CD) shows strong absorption differences at the plasmonic resonances (LSPR, SLR1) and the RAs. (e) Amplitude of the electric field enhancement at the wavelengths of interest for the hybrid system from the top (i–iii) and side (iv–vi) views. Cuts are through the center of the sphere; dashed lines indicate the position of the AuNP and the substrate/chiral film.

We analyze the absorbance and chirality of the hybrid system in Figure 4c and d, respectively. Similar to the experimental case, the average absorption spectrum (blue lines) appears as additions of the spectral features of the chiral film and the AuNP array. All resonances can be clearly identified, and their near-fields show the expected localized (LSPR) and delocalized (SLR) nature (Figure 4e). In contrast, the differential absorbance, CD, of the hybrid system in Figure 4d shows clear features associated with all plasmonic resonances of the achiral AuNPs (Figure 4c), not found in the spectra of the individual components (Figure 4b). In particular, beside a Lorentzian-like feature at the spectral position of the LSPR centered around 570 nm, distinctive and pronounced resonances around the spectral positions of the RA and SLR are observed.

Moreover, the chiral fingerprint of the molecular film seems to be modified by the influence of the plasmonic modes of the AuNP array. As in the experimental case, we hypothesize that the original shape of the molecular signal is not preserved because plasmonic AuNPs are not helicity preserving.⁵⁰

All spectral features of the experimental hybrid system (Figure 3) are thus reproduced by the simulations (Figure 4). Our simulations are also consistent with recent theoretical work^52,74−76 and delocalized chiral fields of intrinsic chiral lattice modes⁶⁴ recently used for highly sensitive chiral sensing.⁴

We now systematically vary the lattice parameters and investigate the occurrence and efficiency of the chirality transfer to the SLR modes. In Figure 5a, we show the simulated absorbance for the different lattices in the presence of the molecular chiral film (hybrid system). As expected, the system shows multiple higher-order RAs for large enough lattice parameters (D_squ) appearing as dips in the absorption spectra. To quantify the chiroptical effect on these resonances, we show the differential absorbance (CD) for selected values of D_squ in Figure 5b (full set in Figure S6). Similar to the case of D_squ = 425 nm (Figure 4c,d), we observe strong induced CD signatures around the <1,0> RA. This spectral shift demonstrates that the induced chirality mechanism results from the lattice modes interacting with the molecules. This chirality transfer can even be extended to higher-order modes (<1,1>, <2,0>, <2,1>, <2,2>) for very large spacing D_squ. In Figure 5c, we plot the expected positions of the RAs (solid lines) together with the points of maximum chiral signal (CD_min/max). A closer look reveals that the induced CD appears with a typical bisignated shape around the RA, i.e., resulting in a minima and maxima around the resonance position. To extract the maximum, we used the strongest of both peaks. As a result, we see that the optical activity coincides with the RAs for all lattice parameters. As expected for such large particle separation, the chiral signal at the position of the LSPRs is fairly weak compared to the values around the RAs (Figure 5b). To emphasize this effect more clearly, in Figure 5d, we show the CD contrast, defined as the difference between the CD maxima and minima at the position of an RA (|CD_max – CD_min|). This contrast exposes an effective and relatively large chirality transfer to the RAs through their coupling with the molecular CD. In spite of a smaller detuning to the molecular response, the LSPRs do not show such an effective chirality transfer for large AuNP separations (green squares in Figure 5d); therefore, one can conclude that RAs are more effective in the process of induced chirality transfer compared to the LSPRs in the system.

Figure 5.

Simulated absorbance and differential absorbance for different lattice spacings of the hybrid system. (a) Absorbance of randomly oriented molecules in a 200 nm-thickness chiral film (bottom) for hybrid systems with different lattice parameter D_squ, embedded in a matrix with n_eff = 1.518 illuminated by circularly polarized light. Dashed lines crossing diagonally are guides to the eye to indicate in-plane RAs of different order. (b) Differential absorbance (CD) for selected hybrid systems. (c) RAs as function of the lattice parameter D_squ. Solid diagonal lines represent the different in-plane diffractive orders, as labeled. The data points are the peak positions extracted from the individual CD spectra. Horizontal lines mark the spectral position of the LSPR and the molecular resonance. (d) CD contrast, defined as the difference between the maxima and the minima of the calculated differential absorbance at the different RAs and at the LSPR.

Insights into the Mechanism of Chirality Transfer

Electromagnetic interactions are known to be relevant in chirality transfer phenomena in hybrid systems composed of chiral molecules and plasmonic nanoparticles.^75,77,78 In particular, the electromagnetic coupling between the nanoparticles and the chiral molecules can induce differential dissipative currents in the plasmonic particles.⁷⁹ These currents can induce a prominent CD response at the plasmonic resonance frequencies even if the plasmonic system is achiral, a phenomenon known as the plasmon-induced CD effect. The full-wave simulations of the array of gold nanospheres surrounded by a chiral film shown in Figure 4 naturally capture this effect. With the aim of qualitatively understanding the phenomenon of chirality transfer to the lattice modes, we developed a semi-analytical model based on the coupling of a dipolar chiral molecule to a generic optical resonator described through a dipolar polarizability, which mimics the spectral properties of the plasmonic array under study (see the Supporting Information). The interaction between the chiral molecule and the plasmonic resonator is described within the dyadic Green’s tensor formalism under the coupled dipole approximation.⁷⁷

Figure 6 summarizes the results of this phenomenological model. Figure 6a shows both the extinction cross section of a chiral molecule (red line) and the polarizability mimicking the optical response of the nanoparticle array (black line). The extinction cross section of the molecule presents a Lorentzian line-shape resonance at λ = 400 nm similar to the simulated molecular resonance in Figure 4a (red line). The optical response of the plasmonic array is characterized by three Lorentzian resonances, one for each lattice resonance and another one for the LSPR. This reproduces the LSPR around 550 nm, the SLR at 650 nm, and RAs at 460 and 645 nm.

Figure 6.

Phenomenological model of a dipolar chiral molecule coupled to an optical resonator with spectral properties similar to the plasmonic array. (a) Calculated extinction cross section of the dipolar chiral molecule and the polarizability mimicking the optical response of the plasmonic nanoparticle array. (b) Calculated extinction CD spectra of the dipolar chiral molecule and the plasmonic nanoparticle array. (c) Calculated extinction cross section of the hybrid system consisting of a single molecular dipole and the plasmonic array. Note that the single molecular resonance is absent in the spectra due to the weak oscillator strength. (d) Calculated extinction CD spectra of the hybrid system spatially averaged for all possible molecular locations.

Figure 6c presents the extinction cross section of the hybrid system. Since we consider the resonator strength of a single molecule, the molecular polarizability is substantially weaker than the plasmonic resonances and is thus not resolved in the spectra. Also note that different positions and orientations of the molecular dipole were averaged to capture the effect of the random distribution of molecules in the experimental system. The CD spectra for both the bare molecule and the plasmonic array are shown in Figure 6b. As expected, only a feature corresponding to the chiral molecular resonance is observed. The CD spectrum of the hybrid system (Figure 6d) shows clear chiral signals at the spectral positions of all plasmonic modes, in agreement with experiment (Figure 3) and full numerical simulations (Figure 4). It is remarkable that the polarizability of a single molecule, hardly detectable in direct extinction spectra, is able to produce such a large chiral signature at other, tunable spectral regions. The qualitative agreement provided by the coupled-dipole model points toward the basic mechanism of chirality transfer. A molecular chiral signal, even if largely detuned from the plasmonic resonance, is able to transfer its chirality via the overlapping of the spectral tail of the molecular signal with the plasmonic resonance. This overlap, even if small, is actually the only form of coupling considered in our model. The coupling is particularly pronounced if the plasmonic resonance exhibits spectrally narrow resonances, as it occurs in lattice modes. This is also the reason why the chirality transfer to the LSPR, even though spectrally less detuned, is less efficient. Note that considering the chiral molecule under the influence of the near-field created by the plasmonic array, without considering the coupling, does not reproduce the observed chirality transfer in the hybrid system. As a plasmonic system cannot sustain electric and magnetic dipoles at the same time,^26,31,50 we observe that the plain electromagnetic CD enhancement of our achiral arrays contributes equally to both handedness. Thus, we observe no efficient contribution to the resulting hybrid CD when considering passively the near-field enhancement (details in the Supporting Information, Figure S7). From this insight and the results of the semi-analytical model that includes the self-interaction of the chiral molecules with the plasmonic array, one can conclude that this coupling is the predominant mechanism governing the efficiency of chirality transfer in our system.

Conclusions

In summary, we experimentally demonstrate a molecular chirality transfer to plasmonic lattice resonances. In the presence of a chiral molecular film, achiral AuNP arrays exhibit clear CD peaks at the position of their lattice modes despite the low-quality factor of the presented arrays. Numerical simulations using AuNPs with systematically varying lattice constants embedded in a chiral film corroborate the experimental results and show chiral signals that spectrally coincide with the RAs and SLRs. A phenomenological model based on coupled dipoles including full electromagnetic interactions identifies the electromagnetic coupling, through the spectral overlap, as responsible for the chirality transfer. This model demonstrates that the polarizability of single molecules, hardly detectable in direct extinction spectra, is able to produce a large chiral signature at a different, tunable spectral region, underlining the efficient enhancement. These findings suggest that an effective chirality transfer is possible even without intrinsic chiral plasmonic platforms.^4,64

Chirality transfer to SLRs offers an exciting possibility to tailor the spectral position of a detected chiral signal simply by changing the interparticle distance. Hence, such systems may be tuned to specific wavelengths to match desired light sources (LED, lasers) and detectors with optimized single-wavelength polarizing components. This makes such a platform suitable for in-line quality control measurements in (pharmaceutic) production sites, chromatographic sensors, or highly sensitive microfluidic devices. More sophisticated fabrication processes, providing SLRs with very high Q-factors⁵⁸ may significantly enhance the induced CD signal. Local functionalization strategies⁸⁰ or specifically targeted molecular motives^81,82 may improve sensitivity and selectivity of the chiral response and possibly provide control of the orientation of the chiral molecules with respect to the particle array to further enhance the chirality transfer. Our work demonstrates that chiral SLRs⁶⁴ can be efficiently obtained by molecular chirality transfer to initially achiral lattices, avoiding the need for intrinsic chiral plasmonic lattices⁴ and thus opening the question of the role of structural chirality in enantiomeric sensing.

Methods

Materials

All chemicals were used as received without further purification unless specified otherwise. Chemicals for synthesis, assembly, and sensing were all purchased by Sigma-Aldrich or Carl Roth in synthesis or chromatography grade unless otherwise specified. Ultrapure water was from a Milli-Q system (18.2 MΩ·cm, Elga PURELAB Flex). All substrates were glass substrates (microscopy slides, Objektträger) from Menzel/Carl Roth. Immersion oil (n = 1.518) was purchased from Cargille (type LDF, very low autofluorescence). Plasmonic Au-PNiPAm CS microgels were synthesized according to the protocol published elsewhere.^63,65

Induced Chirality Samples

The assembly at the air–water interface and synthesis of the Au-PNiPAm CS microgels (d_Core ∼ 99 nm) are based on established protocols from our groups and are described in more detail in refs (63, 65). The polymeric shells were removed by oxygen plasma treatment (4 sccm O₂, 100 W, 5–10 min) without affecting the gold nanoparticle assembly. To ensure comparability with literature, the functionalization with a chiral test molecule and a homogenous RI environment, samples were prepared following a modified literature protocol.³⁷ PMMA (5 wt %) was dissolved in dimethyl sulfoxide at 60 ° C under constant stirring (350 rpm) overnight. No filtering or purification was applied at any point. Note that conventional atactic PMMA was used in this study. Using defined, isotactic PMMA may induce a chiral signal from the polymer matrix itself, which may compromise the detection of the analyte signal. After cooling to ambient, riboflavin (40 mM) was added and stirred in a dark place for 4 h. The slim substrates containing AuNP arrays were attached to a sacrificial cover slip (26 × 26 mm²) with double-sided carbon tape for spin-coating. The polymeric solutions (400 μL) were spin-coated (30 s, 3400 rpm, 400 μL) on the mounted samples within reduced ambient light (dark room). Samples were placed in a desiccator to remove the solvent by vacuum (∼60 min). The backsides of the samples were cleaned with EtOH and Kimwipes prior to measuring CD spectra. A small drop of immersion oil was sandwiched between the substrate and a cover slip (same as the substrate here; see Figures S2 and S3).

Characterization

Microscopy

SEM images were taken using a GeminiSEM 500 (Zeiss, Germany) at 1 kV using the in-lens detector. AFM images (original size 10 × 10 μm²) were measured with a NanoWizard 4 (JPK Instruments) in intermittent contact mode using OTESPA-R3 tips (Bruker) and analyzed with ImageJ software.

Spectroscopy

UV–vis–NIR spectra (only in the SI) were measured using a conventional spectrometer (Lambda 950, Perkin-Elmer) with a Glan-Thompson polarizer drive (Perkin-Elmer, B050-5284), typically in the range between 400 and 2500 nm in 2 nm steps and 0.48 s integration time. Molecular CD and absorption spectra for circularly polarized light with high sensitivity were recorded using a commercial CD spectrometer (Jasco J-815) with 1 s integration time at 50 nm/min. The substrates were attached in a custom-built substrate holder (Figure S3), allowing normal illumination and fitting into the temperature-controlled (N₂ flow, 21 °C) cuvette compartment.

Electrodynamic Simulations

Differential absorbance ΔA = A_RCP – A_LCP (RCP and LCP referred to as right and left circularly polarized light, respectively) shown throughout the paper and representing the optical response of the chiral slab/gold NP system upon interaction with circularly polarized light at normal incidence was obtained by numerically solving the full set of Maxwell’s equations for a bi-anisotropic media by performing the finite element method (FEM) implemented in the commercial software COMSOL Multiphysics⁷² using the radiofrequency (RF) module in the frequency domain.

The complete system consisting of an array of gold NPs and a chiral film containing chiral molecules (riboflavin) was modeled using the lumped port formulation and imposing periodic (Floquet) boundary conditions at the in-plane directions of a squared unit cell (x- and y-axes) and scattering boundary conditions in the out-of-plane direction (z-axis). To represent the experimental conditions, a single gold spherical nanoparticle (R = 45 nm) was assumed to be deposited at the bottom part of a 200 nm-thick slab representing the chiral film. Both gold NPs and the chiral slab were placed in the middle of a sufficiently long (∼1–2 μm) z-directed environment, representing the simulation unit cell. Accordingly, the physical domains were placed in regular square array arrangements with corresponding lattice parameters. Finally, perfectly matched layers (PMLs) with thickness T_PML = 500 nm were placed at the bottom and top parts of the simulation unit in addition to the scattering boundary conditions in the out-of-plane axis in order to avoid spurious reflections coming from the interfaces along this direction.

All domains in the simulation box were meshed by using tetrahedral elements maintaining a maximum element size mesh below λ/10, where λ is the wavelength of the incident light. For the elements corresponding to both the sphere and the slab domains, the size was 10 times finer than the largest element size until convergence. A homogeneous RI n_eff = 1.518 was used for all the simulation boxes, except for the gold sphere and for the chiral film. For the former, the optical functions were taken from experimental data available in ref (83), and for the latter, we used the theoretical scheme followed, among others, in refs (35, 42, 52). The dispersive chirality parameter κ(ω) of the chiral film used in the electromagnetic calculations was modeled by a frequency-dependent Lorentzian function κ(ω) = A(f(ω) + ig(ω)) associated with molecular electronic transitions with f(ω) and g(ω) given, respectively, by and . The parameter A relates to the density of chiral molecules, ω₀ represents the angular frequency of resonance, and Γ is the broadening of this resonance. All numerical calculations used a single molecular resonance, numerically set at ω₀ = 3.1 eV (λ₀ = 400 nm) with a damping parameter Γ = 0.2 eV.

Data Availability Statement

Raw data and images are accessible from the corresponding authors upon reasonable request.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphotonics.3c00174.

• Further details on the introduced concept, the experimental setup, additional CD, and reference measurements; further theory details about the chirality transfer (PDF)

Author Present Address

^# NanoPhotonics Centre, Cavendish Laboratory, University of Cambridge, Cambridge CB3 0HE, U.K

Author Contributions

E.S.A.G. developed the idea and experimental concept with the help of M.K. and N.V. E.S.A.G. and N.V. conceived the study. E.P. and D.F. synthesized the core-shell microgels, and fabricated and characterized the self-assembled monolayers with AFM. E.S.A.G. fabricated the final samples; performed electron microscopy, photography, and chiroptical investigations; performed renderings, compiled figures; and developed a preliminary theory. M.Z.-H. performed the numerical calculations and analyzed and discussed the results with J.A. and A.G.-E.; M.Z.-H., A.G.-E., and J.A. applied the chirality transfer theory. All authors discussed the results and contributed to the final version of the manuscript. E.S.A.G., M.Z.-H., A.G.-E., J.A and N.V. wrote the manuscript with corrections from all authors. N.V., M.K., and J.A. supervised the project.

This project received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement no. 861950, project POSEIDON. N.V. acknowledges support from Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)– Project-ID 416229255 – SFB 1411. A.G.-E. acknowledges support from the Spanish Ministerio de Ciencia e Innovación (PID2019-109905GA-C2), from Programa de Red Guipuzcoana de Ciencia, Tecnología e Innovación 2021 (Grant No. 2021-CIEN-000070-01), from Eusko Jaurlaritza Elkartek Program KK-2021/00082, and from IKUR Strategy under the collaboration agreement between Ikerbasque Foundation and DIPC on behalf of the Department of Education of the Basque Government, Programa de ayudas de apoyo a los Agentes de la Red Vasca de Ciencia, Tecnología e Innovación acreditados en la categoría de Centros de Investigación Básica y de Excelencia (Programa BERC), Departamento de Universidades e Investigación del Gobierno Vasco and the Centros Severo Ochoa AEI/CEX2018-000867-S from the Spanish Ministerio de Ciencia e Innovación. M.K. acknowledges the German Research Foundation (DFG) for funding under grant KA3880/6-1. D.F. acknowledges the Luxembourg National Research Fund (FNR), Project Reference 15688439. J.A. and M. Z-H acknowledge financial support from Spanish Ministry of Science and Innovation MICIN, project nr. PID2019-107432GB-I00 and from the Department of Education of the Basque Government under Project IT1526-22. E.S.A.G. acknowledges support from the German National Academy of Sciences Leopoldina (No. LPDS 2022-01).

The authors declare no competing financial interest.