Optimization in the Space Domain for Density Compensation with the Nonuniform FFT

Abstract

The non-uniform Discrete Fourier Transform algorithm has shown great utility for reconstructing images from non-uniformly spaced samples in the Fourier domain in several imaging modalities. Due to the non-uniform spacing, some correction for the variable density of the samples must be made. Common methods for generating density compensation values are either sub-optimal or only consider a finite set of points in the optimization. This manuscript presents an algorithm for generating density compensation values from a set of Fourier samples that takes into account the point spread function over an entire rectangular region in the image domain. We show that the reconstructed images using the density compensation values of this method are of superior quality when compared to other standard methods. Results are shown with a numerical phantom and with magnetic resonance images of the abdomen and the knee.

1. Introduction

In several imaging modalities including Magnetic Resonance Imaging (MRI) [1], Computed Tomography (CT) [2], Spectral Domain Optical Coherence Tomography (SD-OCT) [3], and radio astronomy [4], a formalism exists to represent the collected data as samples in the Fourier domain. When the samples are unique and located on a Cartesian grid, e.g. spin-warp imaging with MRI, then the image can be reconstructed with the inverse Discrete Fourier Transform (DFT). However, when the samples are not located on a uniform grid, a non-uniform DFT must be used; this is a problem of type I, as defined in [5]: a discrete conversion from a non-Cartesian sample set in the Fourier domain to a Cartesian sample set in the space domain).

When the Fourier values do not lie on a uniform grid, one must compensate for the varying density of samples. Effectively, the density compensation values determine the point spread function of the non-uniform transformation. Several methods have been proposed to determine density compensation values¹. A thorough review of existing techniques is presented in [8]. The most intuitive method is to calculate the Voronoi cell of each point and set the density compensation values equal to the areas of the corresponding cells (with some exception made for the points on the convex hull) [9, 10, 11]. This corresponds to estimating the inverse Fourier transform with a Riemann sum where the partition of the sum is the set of Voronoi cells. This is an intuitive and computationally efficient approach but is not generally optimal (i.e., it does not optimize a quality metric). And the density compensation value assigned to outer most points is arbitrary. The methods of [12, 13, 7, 14, 15, 16] require the use of a convolution kernel; notably, there is not a convolution kernel inherent to the Riemann summation. Moreover, these methods as well as that of [17] only consider a finite set of points of the point spread function in the space domain; thus, there is some propensity for larger errors on points that were not considered.

In what follows, we present a density compensation algorithm for a general set of samples that takes into account the point spread function over an entire rectangular region in the space domain (rather than on a set of arbitrary points), and we show that the images reconstructed with this method are of superior quality when compared to density compensation values determined in other ways. Importantly, these density compensation weights have utility beyond an implementation of a non-uniform DFT; they can be used for preconditioning with iterative reconstruction algorithms [18] or as part of a system model in an neural network [19, 20, 21].

2. Background

A set of samples consists of a vector of frequencies $\mathit{\text{k}}=\left(k_1,k_2,\dots ,k_M\right)\in {ℝ}^{M\times D}$ (called the sample coordinates) and a corresponding vector of Fourier values at those frequencies: $\mathit{\text{G}}=\left(G\left(k_1\right),G\left(k_2\right),\dots ,G\left(k_M\right)\right)\in {ℂ}^M$. Here, $D$ represents the number of dimensions of the source and destination domains. Reconstruction estimates the values of $\mathit{\text{g}}=\left(g\left(x_1\right),g\left(x_2\right),\dots ,g\left(x_N\right)\right)\in {ℂ}^N$ for a vector of space domain locations $\mathit{\text{x}}=\left(x_1,x_2,\dots ,x_N\right)\in {ℝ}^{N\times D}$. Here, $g={ℱ}^{-1}G$ where the symbol ${ℱ}^{-1}$ represents the inverse Fourier transform². For this paper, we make the assumption that the support of $g$ is a subset of $\mathit{N}=\left[-N_1/2,N_1/2\right]\times \cdots \times \left[-N_D/2,N_D/2\right]$. (Here, set multiplication represents the Cartesian cross product.) The rectangle $\mathit{N}$ is called the field of view. If the frequencies $\mathit{k}=(k_1,\dots ,k_M)$ and coordinates $\mathit{x}=(x_1,\dots ,x_N)$ are equally spaced with $M=N$ (where the spacings between adjacent $k$ frequencies are inversely related to the spacings between adjacent $x$ coordinates), then the image can be reconstructed with the inverse DFT, which can be derived as a Riemann sum approximation to the Fourier transform [22]. When the frequencies $\mathit{k}$ do not lie on a uniform grid, then the inverse DFT is no longer an appropriate reconstruction algorithm.

A simple (though computationally inefficient) reconstruction algorithm is to calculate the following sum directly [22]:

$$\widehat{g}\left(x_n\right)=\sum _{m=0}^{M-1}{w}_{m}G\left(k_m\right)\text{exp}\left(i2\pi k_m\cdot x_n\right),$$ (1)

where, $k_m\in {ℝ}^D$, $x_n\in {ℝ}^D$, and · represents the dot product. The elements of the vector $w=\left(w_1,\dots ,w_M\right)\in {ℝ}^M$ are called the density compensation values; their values can dramatically affect the quality of the reconstructed image [23]. Note that (1) can be expressed as $\widehat{g}={ℱ}^{-1}\left\{G{S}_w\right\}=g*S_w$, where * represents continuous convolution, $S_w={\sum }_{m=0}^{M-1}{w}_m\delta \left(k-k_m\right)$, $\delta$ represents the Dirac delta function, and $s_w={ℱ}^{-1}\left\{S_w\right\}$.

3. Theory

If $s_w=\delta$ then $\widehat{g}\approx g$. As previously stated, we further assume that $g$ has compact support, which is a subset of $\mathit{N}$. In this case, $s_w$ only need approximate the Dirac delta function well over $2\mathit{\text{N}}={\prod }_{d=1}^D\left[-N_d,N_d\right]$ in order for $\widehat{g}\approx g$, where $\Pi$ represents a product over a set of indices. This motivates our approach; we will attempt to find a density compensation vector $\mathit{w}$ such that $s_w\left(x\right)\approx \delta \left(x\right)$ for all $x\in {\prod }_{d=1}^D\left[-N_d,N_d\right]$.

3.1. Forming an Optimization Problem

Note that $s_w$ is a true function (as opposed to a distribution) and takes a finite value at all locations in the domain. This differs from the Dirac delta, which is not a function but a distribution; thus, $s_w$ could never equal the Dirac delta over any domain that includes 0. Our hope, then, is that we can find some function that approximates the Dirac delta well in the sense that it is a steep function centered at the origin that integrates to 1 [24].

An algorithm that optimized over $2\mathit{N}$ could yield a point spread function with large positive values near the origin and with large negative values away from the origin. The resulting point spread function would integrate to 1, but it would not represent a delta function well. To prevent this from happening, we have created an optimization function that forces $s_w$ to approximate a dirac delta well in a subset of the domain near the origin, and to make its values small outside of that subset. Let $\mathit{\eta }={\prod }_{d=1}^D\left[-{\eta }_d/2,{\eta }_d/2\right]$, a small rectangular region centered on the origin, be this subset. Then the density compensation values can be determined by solving the following optimization algorithm:

$$\begin{gathered} \underset{w,r^{\prime }}{\text{minimize}}\int \int \underset{2\mathbf{\text{N}}}{\cdots }\int \text{exp}\left(-\sum _{d=1}^D\frac{\left|x_d\right|}{{\gamma }_d{N}_d}\right){\left|s_w(x)\right|}^{2}d\mathit{\text{x}} \\ \text{subject to }{s}_w(0)=r^{\prime }>0,w_m\ge 0\text{ for all }m \\ ,\text{and }\int \int \underset{\eta }{\cdots }\int s_w(x)d\mathit{\text{x}}=1. \end{gathered}$$ (2)

The objective function attempts to make the values of the point spread function small throughout $2\mathit{N}$. Because the value at the origin is constrained to $r\prime$, and because the resulting $s_w$ function is continuous, it will be more difficult to make values close to the origin small than it is to make values distant from the origin small. The $\text{exp}\left(-{\sum }_{d=1}^D|\cdot |/\left({\gamma }_d{N}_d\right)\right)$ function is a weighting that places more emphasis on the values near the origin and less emphasis on those values distant from the origin. This weighting permits the user (through the use of the parameter ${\gamma }_d>0$, a fraction of the length of the domain $N_d$) to trade off between some additional error in areas more distant from the origin for improvements in those values close to the origin.

The density compensation values are constrained to be non-negative to make the interpolation process of (1) more stable. Moreover, the non-negativity constraint permits interpretation of the density compensation values as areas of an unknown partition such that (1) is a Riemann sum approximation of the Inverse Fourier Transform.

3.2. Solving the Optimization Problem

We now present a method for numerically solving problem (2). Consider the relaxed problem of (3) for an arbitrary value of $r>0$ (where the integration constraint of (2) has been removed and $r$ is not necessarily equal to $r\prime$):

$$\begin{gathered} \underset{w}{\text{minimize}}\int \int \underset{2\mathbf{\text{N}}}{\cdots }\int \text{exp}\left(-\sum _{d=1}^D\frac{\left|x_d\right|}{{\gamma }_d{N}_d}\right){\left|s_w(x)\right|}^{2}d\mathit{\text{x}} \\ \text{subject to }{s}_w(0)=r>0\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{w}_m\ge 0\text{ for all }m\text{. } \end{gathered}$$ (3)

The $s_w\left(0\right)=r$ constraint of (3) sets the value of the point spread function at $x=0$ to be $r$; together with the objective function the problem attempts to find values that yield a peak near the origin and small values away from the origin. However, solving problem (3) does not yield a point spread function that integrates to 1, which is the remaining requirement of a good approximation of a Dirac delta function.

Problem (3) is a convex optimization problem that can be solved with known algorithms, as detailed in section 4. Importantly, if we find the solution to (3), we can find a solution to (2).

Note that if (3) is solved with two different values of $r$, the effect is to simply scale the determined weights. So problem (3) can be solved with $r=1$ and then scaled to attain the solution for other values of $r$. There is a unique value of $\kappa =1/r^{\prime }$ such that the integral over $\mathit{\eta }$ is 1:

$$\int \int \underset{\mathit{\eta }}{\cdots }\int s_{\kappa w^{\star }}(x)d\mathit{\text{x}}=1.$$ (4)

where $w^{\star }$ is the solution of problem (3). Thus, to find the density compensation values, one solves problem (3) with $r=1$ and then scales the weights by $\kappa =1/r^{\prime }$ such that (4) is satisfied. The expression for $\kappa$, derived in Appendix B, is

$$\kappa =\sum _{j=1}^M{w}_j{\Pi }_{d=1}^D\left(\frac{\text{sin}\left(\pi k_{j,d}{\eta }_d\right)}{\pi k_{j,d}}\right).$$

4. Algorithm

In this section, we review the family of gradient projection algorithms that can be used to solve problem (3). We then present an algorithm that reduces the number of gradient computations required to attain a valuable solution.

4.1. Gradient Projection Algorithm

To solve problem (3) for $r=1$, we convert it into a form that can be solved with a gradient-projection algorithm. Let $f_0$ denote the objective function of the problem, and let ${\mathbb{I}}_{Pr}$ denote the indicator function of the probability simplex (equal to 0 when the argument is an element of the probability simplex and equal to infinity otherwise). Then problem (3) is equivalent to

$$\underset{w}{\text{minimize}}{f}_0(w)+{\mathbb{I}}_{Pr}(w).$$

The gradient-projection algorithm requires an implementation of the gradient of $f_0$, denoted $\nabla f_0$, and an implementation of the Euclidean projection onto the probability simplex, denoted ${\Pi }_{\mathit{Pr}}$ (which is the proximal operator of the corresponding indicator function [25]). We use the computationally efficient algorithm of Wang and Carreira-Perpinán for this projection operator [26].

The gradient of the objective function, derived in appendix Appendix C, is $\nabla f_0\left(w\right)=Aw$ where

$$A_{lj}=2\prod _{d=1}^D\frac{2{\gamma }_d{N}_d}{1+{\gamma }_d^2{v}_d^2{N}_d^2}\left[1-e^{\left(-1/{\gamma }_d\right)}\left(\text{cos}\left(v_d{N}_d\right)-{\gamma }_d{v}_d{N}_d\text{\hspace{0.17em}sin}\left(v_d{N}_d\right)\right)\right],$$ (5)

and $v_d=2\pi \left(k_{l,d}-k_{j,d}\right)$.

With the above definitions, problem (3) can be solved by alternating between an iteration of gradient descent and a Euclidean projection onto the probability simplex, as shown in Alg. 1, where ${\Pi }_{\mathit{Pr}}$ represents projection onto the probability simplex.

Here, $K$ is the number of iterations and $\mu$ is the step size of gradient descent. For reference, we call the results of this algorithm (and its variants) applied to problem (2) the Gradient Projection (GP) density compensation values.

Rather than using gradient-projection, we use the fast iterative shrinkage threshold algorithm (FISTA) [27]. To improve the speed further still, we used an adaptive restart algorithm based on the gradient [28]. In addition to limiting the maximum number of optimization iterations, we also incorporated a dynamic stopping criteria based on the relative difference between successive results. The complete algorithm is presented in Alg. 2. For this algorithm, · represents the dot product, $\delta$ represents the relative difference, and $G$ represents the generalized gradient scaled by $\mu$.

5. Experiments

We present results for three experiments with two-dimensional data: (1) a numerical phantom, (2) multi-coil magnetic resonance (MR) data from the 2010 reconstruction challenge of the International Society of Magnetic Resonance in Medicine (ISMRM) [29], and (3) MR data of a slice of a knee. Fourier domain data was normalized to lie in the [−0.5,0.5]² square. The true images of the experiments can be seen in Fig. 1. To reconstruct the image once the density compensation values were determined, rather than calculating the sum of (1) directly, we use the more efficient algorithm of [2, 12, 30] with a Kaiser-Bessel kernel and an oversampling ratio of 1.5. Unless otherwise specified, the value of $\gamma$ used with the gradient projection algorithm was 0.25% of the size of the image; this value was chosen to ensure that there was significant weighting near the center of the point spread function and to ensure that the weightings near the boundary of $2\mathit{N}$ were non-negligible. For all experiments, $\eta$ was set to 5% of the length of the side of the image (approximately 15 pixels) and ${\delta }_{\text{thresh}}$ was set to 10⁻⁴. The sizes of the images of the phantom, the abdomen, and the knee were, 208×208, 190×305, and 300×270, respectively. Correspondingly, the values of (${\gamma }_1,{\gamma }_2$) were (52, 52), (47.5, 76.25), and (75, 67.5) pixels, respectively. For the gradient projection algorithm, the values of $x^{\left(0\right)}$ are initialized to the result of the Voronoi algorithm, the value of $\Vert A\Vert$ is estimated using power iteration, and the initial step size of the optimization algorithm is set to $0.99/‖A‖$.

Figure 1:

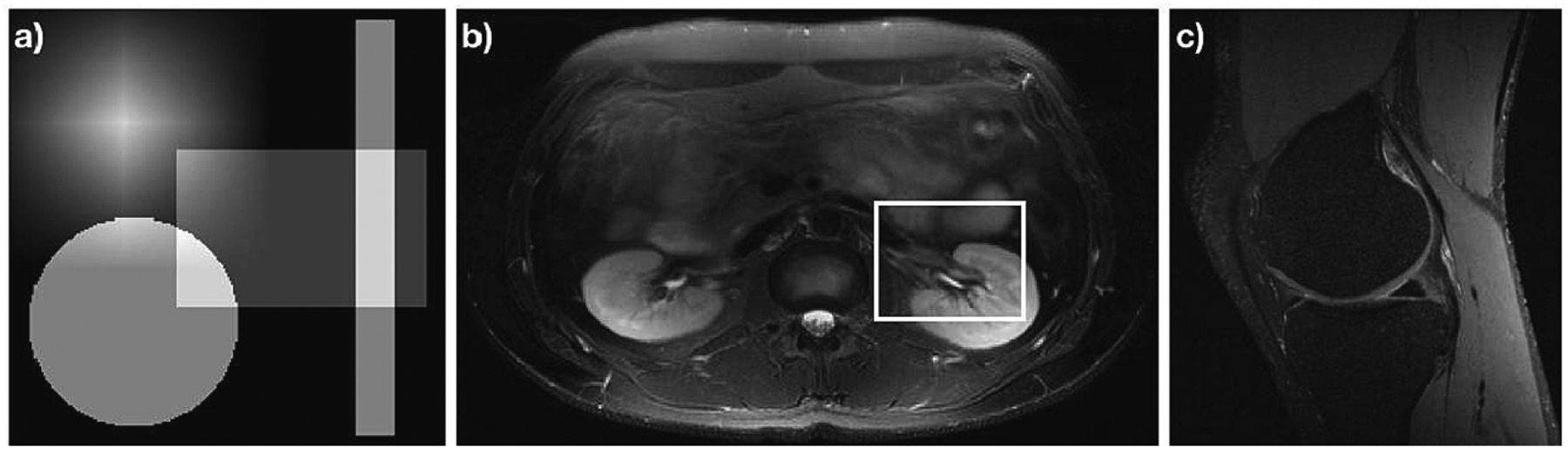
Accurate images for data analyzed in this manuscript. (a) A numerical phantom consisting of the sum of a separable tri function, a circ function, and two separable stretched rect functions, each translated from the origin. (b) Slice 6 of the Double Vision dataset from the 2010 reconstruction challenge of the ISMRM. (c) A slice of a knee acquired from mridata.org. The white box in (b) shows a region zoomed into when presenting the results in Fig. 4.

The numerical phantom, shown in Fig. 1a, consists of a separable tri function, a circ function, and two separable scaled rect functions all offset from the origin and summed together. The Fourier values of this phantom are known. (The Fourier transform of a tri function is sinc², the Fourier transform of a circ is a jinc, and the Fourier transform of a rect is a sinc. When these facts are combined with the Fourier shift and scaling theorems, the Fourier values of the numerical phantom can be determined analytically.) The sample coordinates used with this phantom are radial with 360 spokes, 150 points per spoke. An image of every sixth spoke from this sample set is shown in Fig. 2a.

Figure 2:

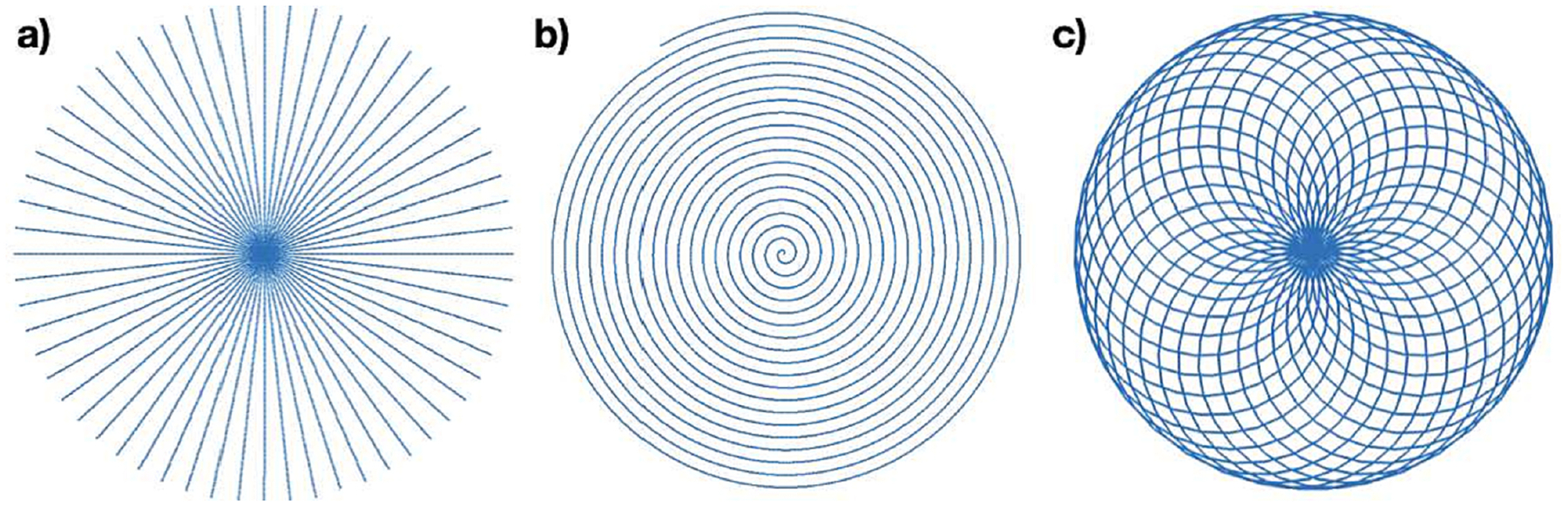
Subsets of the sample coordinates used for the data of Fig. 1. Sub-image (a) shows every 6^th radial line for the radial sample set used with the numerical phantom Fig. 1a. Sub-image (b) shows 1 of the eight spiral interleaves from the sample set used with Fig. 1b. Sub-image (c) shows one cycle of the rosette trajectory used with Fig. 1c.

The image shown in Fig. 1b consists of an axial slice of an abdomen with an 8 coil acquisition from the 2010 reconstruction challenge of the International Society of Magnetic Resonance in Medicine [29]. (Slice 6 of the 12 slice acquisition is used in this manuscript.) The method of Roemer et al. is used to combine the individual images of each coil into a single image for display [31]. The spiral trajectory created by Craig Meyer for the challenge was used, which consists of 8 spiral interleaves with 19 revolutions per interleave. However, to increase the difficulty of attaining a quality solution and better show the differences between the density compensation weights determined, only every 5^th sample of the readout was retained for a total of 4000 points per interleave. A single interleave of this set of sample coordinates is shown in Fig. 2b.

The image shown in Fig. 1c consists of a sagittal slice of a knee acquired from mridata.org. The coordinates of the sample set used for analysis consists of 30 evenly spaced rotations of the the rosette trajectory [32, 33] with an inner frequency of 17 cycles and an outer frequency of 30 cycles. Figure 2c shows the Rosette trajectory that gets rotated.

For the images of the abdomen and the knee, a type II non-uniform DFT (where the input is a set of Fourier values that do not lie on a Cartesian grid and the output is a set of space-domain values that do lie on a Cartesian grid) was used to estimate the Fourier values given the images [34]. In the case of the abdomen, the type II non-uniform DFT was applied to the image from each coil separately.

Reconstructions were done with density compensation values determined using the Voronoi cell based algorithm of [10], the fixed point (FP) algorithm of [13, 7] with a Kaiser-Bessel kernel, the LSQR algorithm of [6], and the proposed gradient projection (GP) algorithm. For FP, the kernel was normalized so that it integrates to 1 in order to scale the reconstructed image correctly. The mean square error (MSE) metric and the structural similarity metric (SSIM) were calculated for the difference between the reconstruction and the true image. All code was written in Matlab R2019b and computations were performed by a 16-core 2019 Mac Pro with 112 gigabytes of memory. The creation of the $A$ matrix for the GP method and the $C$ matrix for the Fixed point and LSQR methods were each parallelized across 30 workers.

6. Results

Figures 3, 4, and 5 show magnitude reconstructions for the phantom, the abdomen, and the knee, respectively. In Fig. 3, the top row shows the reconstructions of each algorithm and the bottom row shows the error image in decibels. All reconstruction algorithms generated the most significant errors at the edges of the circ and rect functions. Overall, the GP algorithm has less error than the other methods, as evidenced by the dark regions in the difference image. The MSE and SSIM values are reported in table 1.

Figure 3:

Reconstructions of the phantom with the radial trajectory depicted in Fig. 2(a) and with density compensation values determine using (left) the areas of Voronoi cells, (center) the fixed-point iteration algorithm, and (right) the gradient projection algorithm. The first row shows the reconstructed images, the second row shows the error of each pixel in decibels. The gradient projection algorithm has lower error in more portions of the image than the other techniques.

Figure 4:

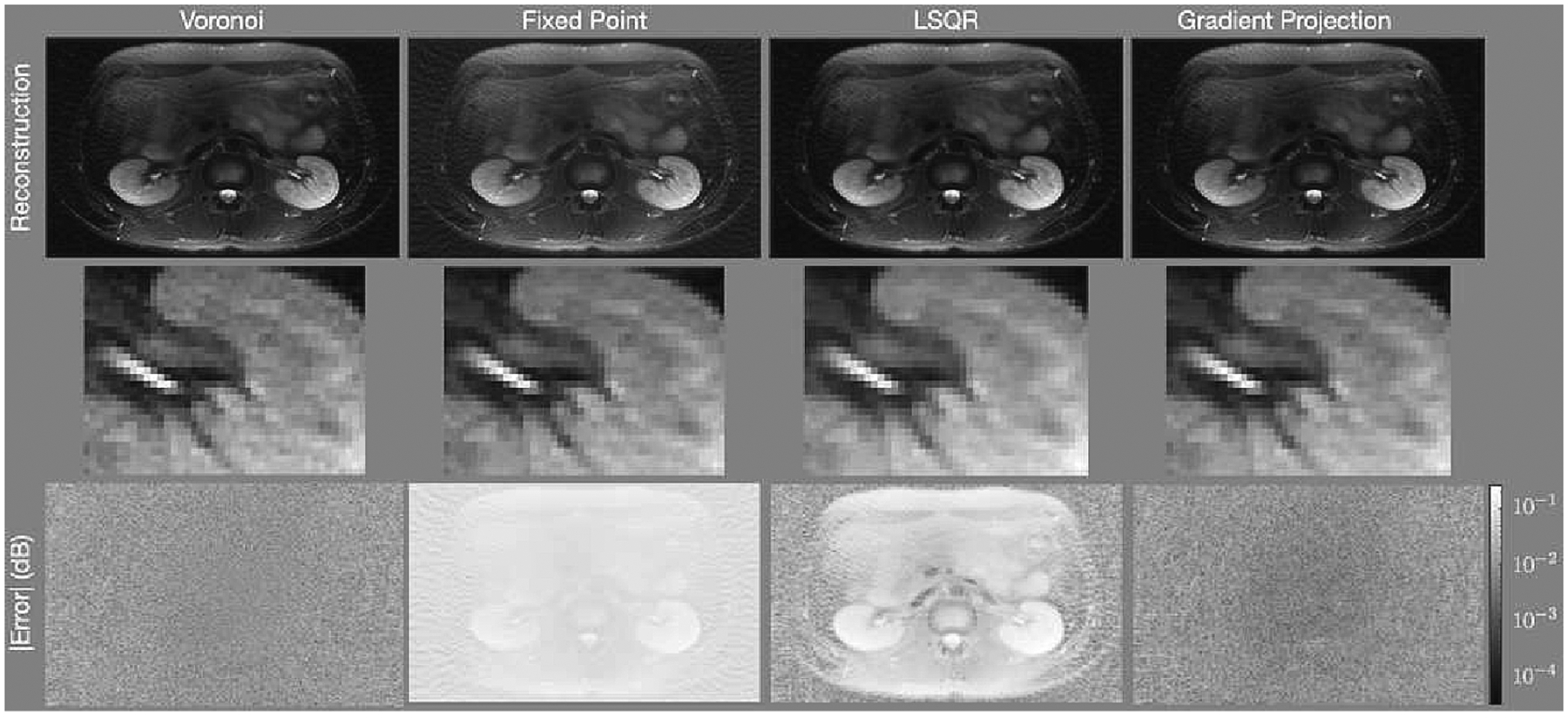
Reconstructions of the abdomen with the spiral trajectory depicted in Fig. 2(b) and density compensation values determine using (left) the areas of Voronoi cells, (center) the fixed-point iteration algorithm, and (right) the gradient projection algorithm. The first row shows the reconstructed images, the second row shows a zoomed into a portion of the image centered on the left kidney indicated by the white rectangle shown in Fig. 1b, and the third row shows the error of each pixel in decibels. The gradient projection algorithm has lower error in more portions of the image than the other techniques.

Figure 5:

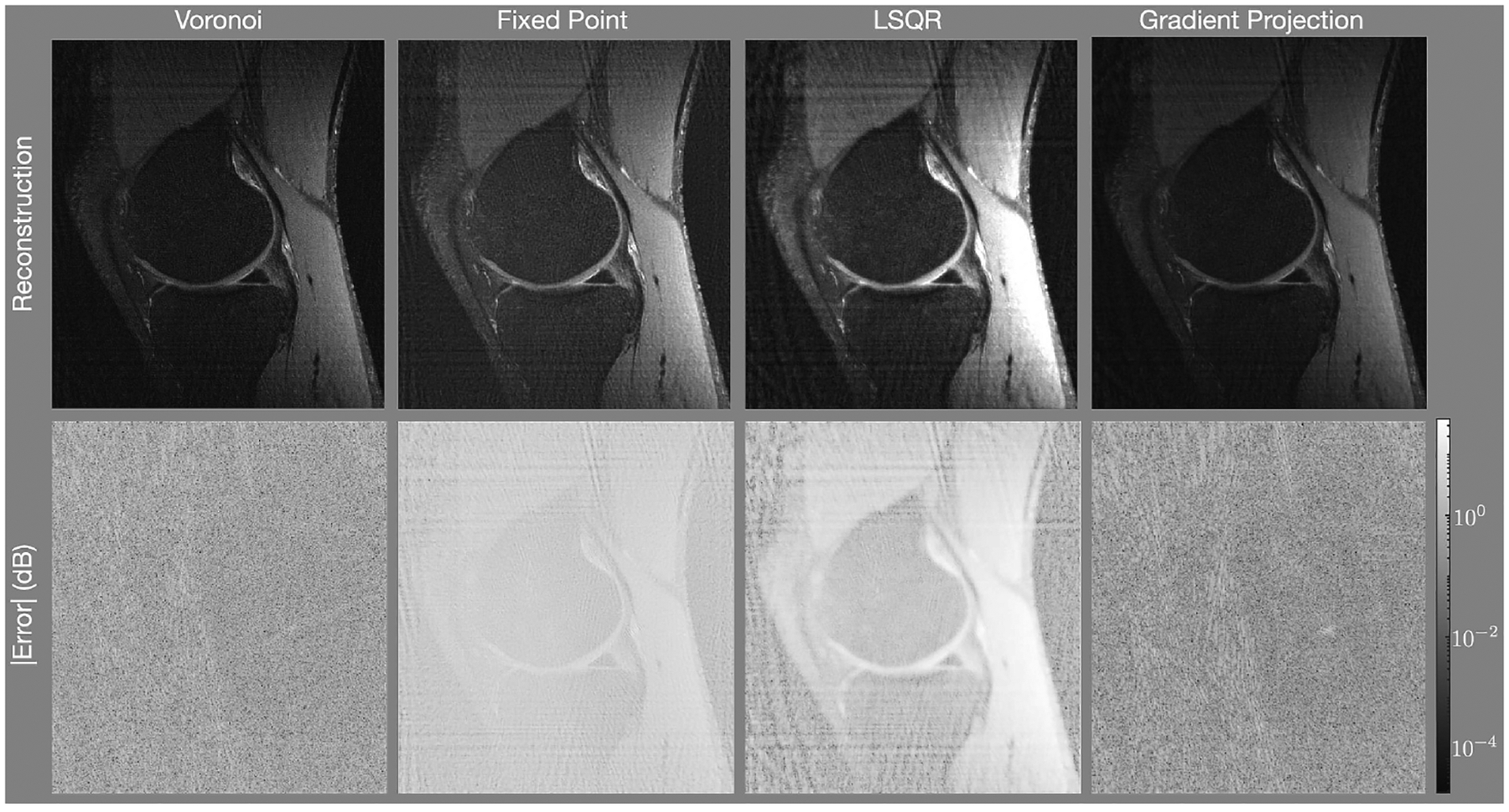
Reconstructions of the knee with the rosette trajectory depicted in Fig. 2(c) and a density compensation values determine using (left) the areas of Voronoi cells, (center) the fixed-point iteration algorithm, and (right) the gradient projection algorithm. The first row shows the reconstructed images (each individually scaled) and the second row shows the error of each pixel on a logarithmic scale. The gradient projection algorithm has lower error than the other techniques.

Table 1:

Mean square error and structural similarity metric of each reconstruction

	Voronoi	Fixed Point	LSQR	Gradient Projection
	Mean Square Error
Phantom	0.028	0.15	0.45	0.024
Abdomen	0.0010	0.079	0.034	0.00067
Knee	0.0026	0.062	0.110	0.0011
	Structural Similarity Metric
Phantom	0.986	0.937	0.863	0.988
Abdomen	0.985	0.644	0.730	0.991
Knee	0.962	0.594	0.423	0.984
	Runtime (seconds)
Phantom	1.1	10.8	6.1	586
Abdomen	3.6	1.7	1.3	190
Knee	1.9	1.4	1.1	775

Figure 4 shows results for the abdomen. The top row shows the reconstructed images, the middle row shows a region centered near the left kidney zoomed into the white rectangle shown in Fig. 1b, and the bottom row shows the difference images. As with the numerical phantom, there are regions of the image with less error when using the gradient projection algorithm than when using the competing algorithms. The FP reconstruction yields an image that is too bright. Additionally, it alters the contrast of the image significantly, making regions of the center of the image much brighter than the true image. In the zoomed-in images, note that there is an erroneous high frequency block pattern super-imposed on the reconstruction with the Voronoi cell based weights that is significantly reduced in the GP reconstruction.

Figure 5 shows the reconstructions of the knee with the rosette trajectory of Fig. 2(c). The Voronoi and GP methods present the lowest errors, with the GP method presenting a slightly lower error than that of Voronoi. The FP and LSQR methods present significantly higher error. This is likely due to the scaling of the convolution kernel employed with these methods. Without explicitly constraining the point spread function to mimic a delta function, as is done with GP, the scaling of the point spread function is a result of the convolution kernel chosen. This leads to the errors depicted in the FP and LSQR reconstructions.

Table 1 shows the mean square error, the structural similarity metric [35], and the runtimes for generating the density compensation values. In all cases, the gradient projection algorithm yields the lowest (best) mean square error and the highest (best) structural similarity value. The Voronoi method is the fastest method. The GP method takes dramatically longer the other methods.

Figure 6 shows the density compensation values determined when ${\gamma }_1={\gamma }_2=0.25$ for each of the four methods (Voronoi, fixed point, LSQR, and gradient projection) for the results presented in Table 1. Notably, the Voronoi method includes some values that are very high. While the values of those sampling points on the interior of the sampling pattern are defined with the Voronoi method, the values for those points on the convex hull are not defined as an area of a Voronoi cell. In the method of [10], utilized in this work, the values for those points are determined according to a heuristic method, and that method yields values that are very high. This may partially explain the high frequency artifacts that accompany the Voronoi method.

Figure 6:

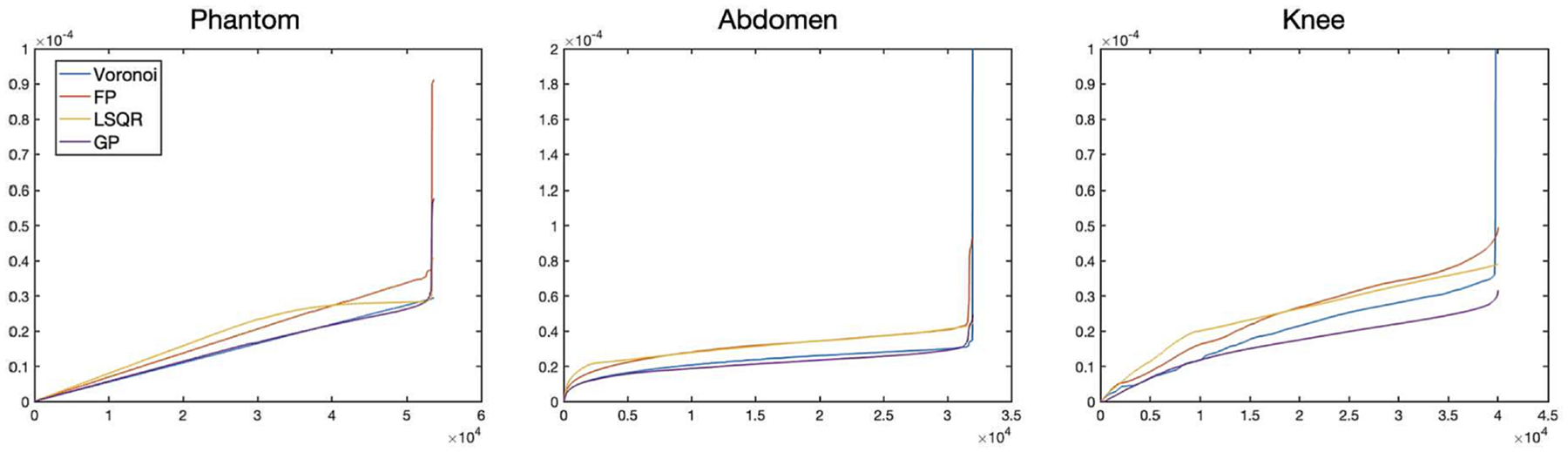
Density compensation values determined when $\gamma =0.25$ using the Voronoi, Fixed Point, LSQR, and Gradient-Projection algorithms for the (left) numerical phantom with radial trajectory, (center) abdomen with spiral trajectory, and (right) knee with rosette trajectory.

The value of $\gamma ={\gamma }_1={\gamma }_2$ was chosen empirically. Figure 7 shows how the reconstruction of the knee with density compensation values determined using GP changes as the value of $\gamma$ changes between 01. to 0.4. Table 2 shows how the mean square error and the structural similarity metric change with as the value of $\gamma$ changes for all the data studied. The effect is minor, which indicates that the density compensation values determined are not sensitive to changes in $\gamma$.

Figure 7:

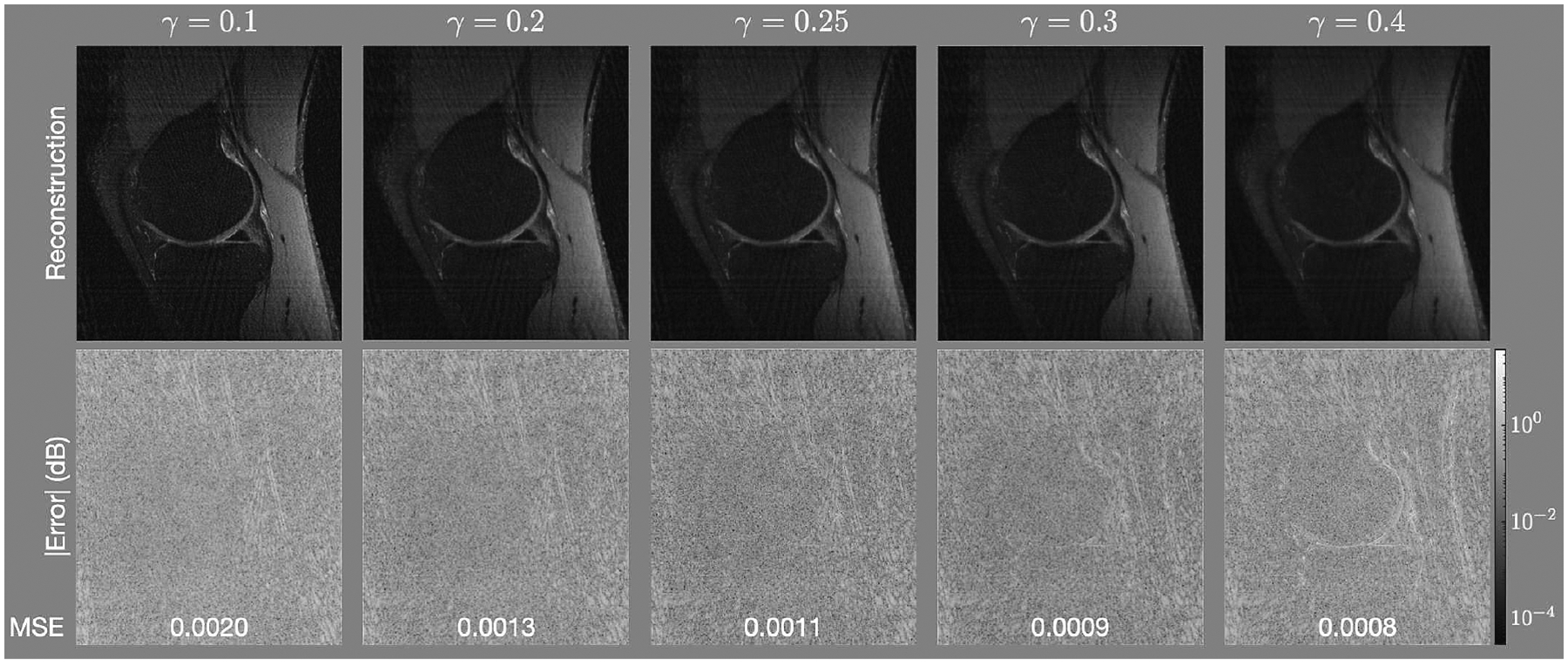
(Top) reconstructions and (Bottom) error (in decibels) for the knee for $\gamma ={\gamma }_1={\gamma }_2$ equal to 0.1, 0.2, 0.25, 0.25, 0.3 and 0.4.

Table 2:

Mean square error and structural similarity metric for different values of $\gamma$

γ	0.1	0.2	0.25	0.3	0.4	∞
	Mean Square Error
Phantom	0.026	0.024	0.024	0.023	0.024	0.021
Abdomen	0.0011	0.0007	0.0007	0.0006	0.0005	0.0022
Knee	0.0020	0.0013	0.0011	0.0009	0.0008	0.0014
	Structural Similarity Metric
Phantom	0.986	0.987	0.988	0.988	0.988	0.989
Abdomen	0.983	0.990	0.991	0.991	0.992	0.952
Knee	0.972	0.984	0.982	0.985	0.984	0.950

It is often the case that the overall scale of the image is irrelevant; e.g., this is the case with MRI. We scaled the intensities of the reconstruction of the abdomen with each algorithm from 0.1 to 1.5 in steps of 0.1 and found the scaling that minimized the mean squared error. Figure 8 shows the reconstructions of the best scaling along with the corresponding error images. Table 3 shows the Mean Squared Error (MSE), Mean Absolute Error (MAE), and the SSIM for each reconstruction. Much of the error was eliminated, especially for the LSQR algorithm. Even in this case, though, the error metrics show that the GP algorithm yields the image with the best error metrics. The error images show significantly more structure in the Voronoi, FP, and LSQR reconstructions; e.g., the kidneys are clearly visible in the error images. The error image for the GP algorithm does not obviously reveal any anatomical structure.

Figure 8:

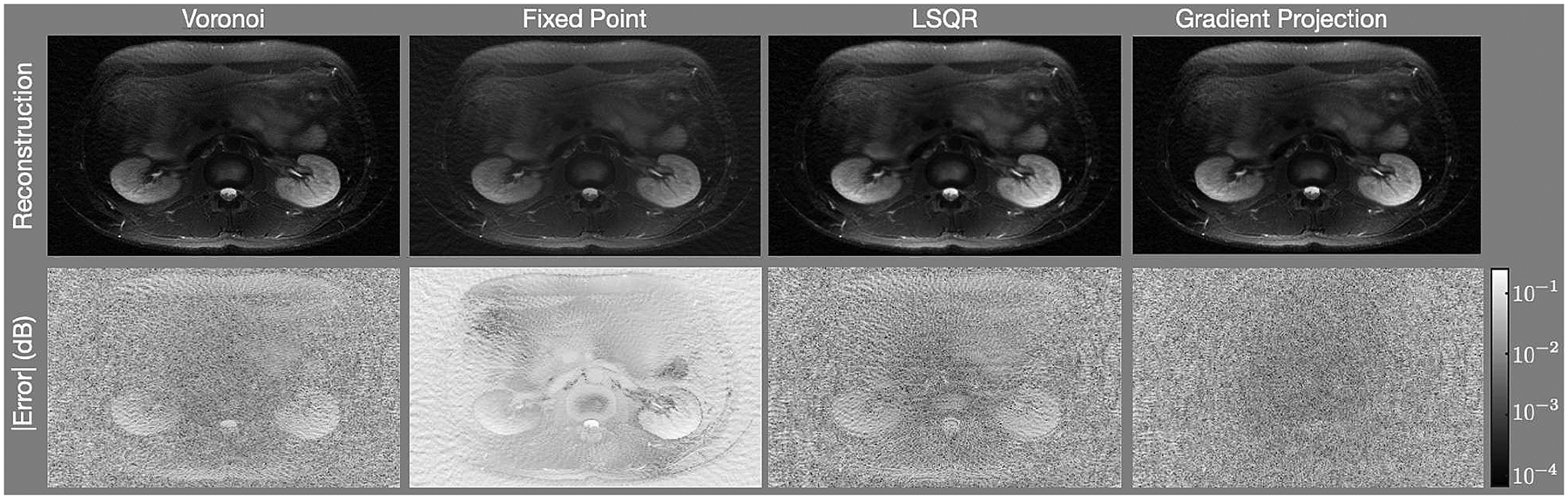
Reconstructions of the abdomen after scaling the image intensities to minimize the MSE.

Table 3:

Error Metrics for Reconstructions of the Abdomen after Scaling the Intensities

	Voronoi	Fixed Point	LSQR	Gradient Projection
Best Scaling	0.9	0.5	0.6	1.0
MSE (×10−3)	1.0	6.7	0.8	0.7
MAE (×10−2)	2.6	7.0	2.3	2.1
SSIM	0.985	0.88	0.988	0.991

7. Discussion

The results show that the quality of the reconstruction is improved when the gradient projection method is used to determine the density compensation values, as opposed to the Voronoi method or the fixed point method. As previously stated, the density compensation values of the points that lie on the convex hull of the sample coordinates is arbitrary with Voronoi. This may lead to the high frequency noise observed in Fig. 4. The fixed point method is not, generally, guaranteed to converge to a set of values. Since there is no constraint, the values may increase to large magnitudes due to instabilities. Early stopping of 8 iterations is employed to prevent this from happening. However, this would yield sub-optimal values. This, along with the scaling ambiguity of the convolution kernel, may explain the significantly higher error of the fixed point iteration observed in Fig. 4b.

The gradient projection algorithm proposed is more computationally intensive than either of the others. The maximum number of iterations for the GP algorithm was limited to 250, but the dynamic stopping criteria based on the relative difference tends to prevent the maximum number from being reached, though it still conducts many more iterations than 8 (always over 100). Despite the long runtime, the gradient projection method is useful for systems where the sample coordinates are known prior to imaging (e.g. MRI or CT), or where the time required to collect the data is so long that the computation time is negligible in comparison (e.g. radio astronomy). If the sample coordinates are known, the density compensation values can be computed prior to imaging and stored for future use. In this case, the time required to determine the density compensation weights does not alter the time between data acquisition and reconstruction. If the acquisition time is so long that the computation time is negligible in comparison (as is often the case with radio astronomy), then perhaps the gradient projection method is appropriate to get the highest quality image possible from a reconstruction. Finally, the runtimes presented were from an implementation in Matlab, an interpreted language. If speed is greatly desired, the GP algorithm can be implemented in a compiled language and/or run on specialized hardware (e.g., a Graphics Processing Unit).

The algorithm, as presented, requires that the image have compact support. For many applications, this assumption is met due to the limits of the sensing equipment. For example, with CT, the image must be of a person that fits within the machine. With MRI, the antennas have negligible sensitivity outside of the machine (and therefore the images that are reconstructed have compact support.

Aside from reconstructing the image directly for viewing, the result can be used to initialize an iterative model based reconstruction algorithm [36, 37] such as compressed sensing [38, 39, 40]. This is especially important for non-convex model based reconstruction algorithms, such as ENLIVE [41] or MCCS [42], since a closer initial guess reduces the probability of yielding a final answer from an erroneous local minima. Finally, the density compensation weights can also be used for pre-conditioning with iterative reconstruction algorithms that include regularization [18]. When used for this purpose, they can actually reduce the time between data collection and reconstruction.

Though results are shown for two-dimensional data, the straightforward modification to three-dimensional data may be useful for non-Cartesian three-dimensional MRI datasets where the trajectories do not lie in a single plane, such as cones [43, 44] or yarn ball [45].

Though this approach has been demonstrated on non-uniform discrete Fourier transform problems of type I, it may be more general. The approach may be valid for problems of type III, where the points of both the source and the destination domain do not lie on a uniform grid. This possibility comes from the fact that a discrete set of points in the destination domain was never used when determining the density compensation values. The relevant change may simply be to alter the set $\left\{x_n:n=1,2,\dots ,N\right\}$ where the summation of (1) is calculated. We leave this pursuit as future work.

8. Conclusions

In this work, we present a method to determine the density compensation values of the non-uniform DFT of type I. The method for determining the density compensation values results from an optimization problem that considers twice the field of view of the object to be imaged. To the best knowledge of the authors, this is the first method for determining the density compensation values that is optimized over a set of non-zero measure.

Appendix A. Fourier Transform Definitions

For this document, the Fourier Transform and Inverse Fourier Transform are defined as

$$\begin{gathered} F(k)=ℱ\left\{f\right\}(k)={\int }_{-\infty }^{\infty }f(x)\text{\hspace{0.17em}exp}(-i2\pi kx)dx, \\ f(x)={ℱ}^{-1}\left\{F\right\}(x)={\int }_{-\infty }^{\infty }F(k)\text{\hspace{0.17em}exp}(i2\pi kx)dk. \end{gathered}$$

The DFT and Inverse DFT are defined as

$$\begin{gathered} V[m]=DFT(v)[m]=\sum _{n=0}^{N-1}v[n]\text{\hspace{0.17em}exp}\left(-i2\pi \frac{mn}{N}\right), \\ v[n]={\text{DFT}}^{-1}(V)[n]=\frac{1}{N}\sum _{m=0}^{M-1}V[n]\text{\hspace{0.17em}exp}\left(i2\pi \frac{mn}{N}\right). \end{gathered}$$

Appendix B. Expression for Scaling

Here we derive the expression for the scalar multiple that satisfies constraint (4) as explained in section 3. Let $\tilde{w}$ be the solution to problem (3) when $r=1$. Starting from constraint (4),

$$\begin{gathered} 1=\int \int \underset{\eta }{\cdots }\int s_{w^{\star }}(x)d\mathit{\text{x}}=\int \int \underset{\eta }{\cdots }\int r^{\prime }{s}_{\tilde{w}}(x)d\mathit{\text{x}} \\ =r^{\prime }\int \int \underset{\eta }{\cdots }\int \sum _{j=1}^M{\tilde{w}}_j\text{\hspace{0.17em}exp}\left(-i2\pi k_j\cdot x\right)dx \\ =r^{\prime }\sum _{j=1}^M{\tilde{w}}_j\prod _{d=1}^D{\int }_{-{\eta }_d/2}^{{\eta }_d/2}\text{exp}\left(-i2\pi k_{j,d}{x}_d\right)d{x}_d. \\ \text{Therefore, }\kappa =1/r^{\prime }=\sum _{j=1}^M{\tilde{w}}_j\prod _{d=1}^D\left(\frac{\text{sin}\left(\pi k_{j,d}{\eta }_d\right)}{\pi k_{j,d}}\right)\text{. } \end{gathered}$$

Appendix C. Gradient of the Objective function

Consider the objective function $f_0\left(w\right)=\int \cdots {\int }_{2N}h\left(x,w\right)d\mathit{x}$, where

$$h(x,w)=\text{exp}\left(-\sum _{d=1}^D\frac{\left|x_d\right|}{{\gamma }_d{N}_d}\right){\left|s_w(x)\right|}^2=\text{exp}\left(-\sum _{d=1}^D\frac{\left|x_d\right|}{{\gamma }_d{N}_d}\right)s_w(x)\overline{s_w(x)}.$$

Here, · denotes the complex conjugate. Then $\nabla f_0\left(w\right)=\int \cdots {\int }_{2\mathit{N}}{\nabla }_{w}h\left(x,w\right)d\mathit{x}$. By the product rule of differentiation,

$$\begin{gathered} \frac{\partial }{\partial w_l}h(x,w)=\text{exp}\left(-\sum _{d=1}^D\frac{\left|x_d\right|}{{\gamma }_d{N}_d}\right)\left[\left(\frac{\partial }{\partial w_l}{s}_w(x)\right)\left(\overline{s_w(x)}\right)+\left(s_w(x)\right)\left(\frac{\partial }{\partial w_l}\overline{s_w(x)}\right)\right] \\ =\text{exp}\left(-\sum _{d=1}^D\frac{\left|x_d\right|}{{\gamma }_d{N}_d}\right)\left[\sum _{j=1}^M{w}_j\text{\hspace{0.17em}exp}\left(i2\pi \left(k_j-k_l\right)\cdot x\right)+\sum _{j=1}^M{w}_j\text{\hspace{0.17em}exp}\left(-i2\pi \left(k_j-k_l\right)\cdot x\right)\right] \\ =2\text{\hspace{0.17em}exp}\left(-\sum _{d=1}^D\frac{\left|x_d\right|}{{\gamma }_d{N}_d}\right)\sum _{j=1}^M\text{cos}\left(2\pi \left(k_j-k_l\right)\cdot x\right). \end{gathered}$$

With this expression, we can now find an analogous expression for the partial derivative of the objective function:

$$\frac{\partial }{\partial w_l}{f}_0(w)=2\sum _{j=1}^M{w}_j\int \int \underset{2\mathit{\text{N}}}{\cdots }\int \text{cos}\left(2\pi \left(k_j-k_l\right)\cdot x\right)\text{exp}\left(-\sum _{d=1}^D\frac{\left|x_d\right|}{{\gamma }_d{N}_d}\right)d\mathit{\text{x}}=a_l\cdot w,$$

where $a_l$ is the vector such that the $j^{\text{th}}$ component is

$$a_{lj}=2\int \int \cdots {\int }_{2\mathit{\text{N}}}\text{cos}\left(2\pi \left(k_j-k_l\right)\cdot x\right)\text{exp}\left(-\sum _{d=1}^D\frac{\left|x_d\right|}{{\gamma }_d{N}_d}\right)d\mathit{\text{x}}.$$

We are left to determine $a_l$:

$$\begin{gathered} a_{lj}=\text{exp}\left(-\sum _{d=1}^D\frac{\left|x_d\right|}{{\gamma }_d{N}_d}\right)\int \int \underset{2\mathit{\text{N}}}{\cdots }\int \text{exp}\left(i2\pi \left(k_j-k_l\right)\cdot x\right)d\mathit{\text{x}}+\text{exp}\left(-\sum _{d=1}^D\frac{\left|x_d\right|}{{\gamma }_d{N}_d}\right)\int \int \underset{2\mathit{\text{N}}}{\cdots }\int \text{exp}\left(-i2\pi \left(k_j-k_l\right)\cdot x\right)d\mathit{\text{x}} \\ =\prod _{d=1}^D{\int }_{-N_d}^{N_d}\text{exp}\left(i2\pi \left(k_{j,d}-k_{l,d}\right)x_d-\frac{\left|x_d\right|}{{\gamma }_d{N}_d}\right)d{x}_d+\prod _{d=1}^D{\int }_{-N_d}^{N_d}\text{exp}\left(-i2\pi \left(k_{j,d}-k_{l,d}\right)x_d-\frac{\left|x_d\right|}{{\gamma }_d{N}_d}\right)d{x}_d \\ =2\text{Real}\left\{\prod _{d=1}^D{\int }_{-N_d}^{N_d}\text{exp}\left(i2\pi \left(k_{j,d}-k_{l,d}\right)x_d-\frac{\left|x_d\right|}{{\gamma }_d{N}_d}\right)d{x}_d\right\}. \end{gathered}$$

Consider

$$t_d={\int }_{-N_d}^{N_d}\text{exp}\left(i2\pi \left(k_{j,d}-k_{l,d}\right)x_d-\left|x_d\right|/\left({\gamma }_d{N}_d\right)\right)d{x}_d.$$

If $k_{j,d}=k_{l,d}$ , then $t_d=2{\gamma }_d{N}_d\left(1-\text{exp}\left(1-1/{\gamma }_d\right)\right)$. Otherwise,

$$\begin{gathered} t_d={\int }_0^{N_d}\text{exp}\left(i2\pi \left(k_{l,d}-k_{j,d}\right)x_d-\frac{x_d}{{\gamma }_d{N}_d}\right)+{\int }_{-N_d}^0\text{exp}\left(i2\pi \left(k_{l,d}-k_{j,d}\right)x_d+\frac{x_d}{{\gamma }_d{N}_d}\right) \\ =\frac{1}{i{v}_d-1/\left({\gamma }_d{N}_d\right)}\text{exp}\left(i{v}_d{N}_d-1/{\gamma }_d\right)-\frac{1}{i{v}_d-1/\left({\gamma }_d{N}_d\right)}+\frac{1}{i{v}_d+1/\left({\gamma }_d{N}_d\right)}-\frac{1}{i{v}_d+1/\left({\gamma }_d{N}_d\right)}\text{exp}\left(-i{v}_d{N}_d-N_d^2{\gamma }_d\right) \\ =2\text{Real}\left\{\frac{-1/\left({\gamma }_d{N}_d\right)-i{v}_d}{{\left(1/\left({\gamma }_d{N}_d\right)\right)}^2+v_d^2}\text{exp}\left(i{v}_d{N}_d-1/{\gamma }_d\right)+\frac{1/\left({\gamma }_d{N}_d\right)-i{v}_d}{{\left(1/\left({\gamma }_d{N}_d\right)\right)}^2+v_d^2}\right\} \\ =\frac{2}{\left(1+{\gamma }_d^2{N}_d^2{v}_d^2\right)}\left[\text{exp}\left(-1/{\gamma }_d\right)\left(-{\gamma }_d{N}_d\text{\hspace{0.17em}cos}\left(v_d{N}_d\right)+{\gamma }_d^2{N}_d^2{v}_d\text{\hspace{0.17em}sin}\left(v_d{N}_d\right)\right)+{\gamma }_d{N}_d\right], \end{gathered}$$

where $v_d=2\pi \left(k_{l,d}-k_{j,d}\right)$.

Therefore, $a_{l,j}=2{\prod }_{d=1}^D{t}_d$ where $t_d=2{\gamma }_d{N}_d\left(1-\text{exp}\left(-1/{\gamma }_d\right)\right)$ if $k_{j,d}=k_{l,d}$ and otherwise,

$$t_d=\frac{2}{1+{\gamma }_d^2{N}_d^2{v}_d^2}\left[\text{exp}\left(-1/{\gamma }_d\right)\left(-{\gamma }_d{N}_d\text{\hspace{0.17em}cos}\left(v_d{N}_d\right)+{\gamma }_d^2{N}_d^2{v}_d\text{\hspace{0.17em}sin}\left(v{N}_d\right)\right)+{\gamma }_d{N}_d\right]$$

With this expression of $a_l$, $\left(\partial /\partial w_l\right)f_0\left(w\right)=a_l\cdot w$. Let $A$ be the matrix such that the $l^{\text{th}}$ row of $A$ is $a_l$. Then $\nabla f_0\left(w\right)=Aw$.