Abstract
We develop new quasi-experimental tools to measure disparate impact, regardless of its source, in the context of bail decisions. We show that omitted variables bias in pretrial release rate comparisons can be purged by using the quasi-random assignment of judges to estimate average pretrial misconduct risk by race. We find that two-thirds of the release rate disparity between white and Black defendants in New York City is due to the disparate impact of release decisions. We then develop a hierarchical marginal treatment effect model to study the drivers of disparate impact, finding evidence of both racial bias and statistical discrimination.
Keywords: C26, J15, K42
1. Introduction
Racial disparities are pervasive throughout much of the U.S. criminal justice system. Black individuals are, for example, more likely than white individuals to be searched by the police, charged with a serious crime, detained before trial, convicted of an offense, and incarcerated.1 Such racial disparities are often taken as evidence of discrimination, driven by racially biased preferences or stereotypes. But this interpretation overlooks at least two alternative explanations. First, the observed disparities may reflect legally relevant differences in criminal behavior that are partially observed by police officers, prosecutors, and judges but not by the econometrician. Second, the observed disparities may be driven by statistical discrimination, instead of or alongside racially biased preferences and stereotypes.2 Distinguishing between these explanations for racial disparities and correctly measuring racial discrimination remains difficult, hampering efforts to formulate appropriate policy responses.
This paper develops new quasi-experimental tools to estimate disparate impact, a broad and legally based definition of discrimination encompassing both racial bias and statistical discrimination. We develop these tools in the context of bail, where the sole legal objective of judges is to allow most defendants to be released before trial while minimizing the risk of pretrial misconduct (such as failing to appear in court or being arrested for a new crime). Bail judges thus risk violating U.S. anti-discrimination law if they release white and Black defendants with the same objective misconduct potential at different rates.3 Correspondingly, we measure disparate impact as the difference in a judge’s release rates between white and Black individuals with identical misconduct potential. This measure is consistent with the legal theory of disparate impact, as well as economic notions of discrimination that compare white and Black individuals with the same productivity (Aigner and Cain, 1977) and notions of algorithmic discrimination that compare equally “qualified” white and Black individuals (Berk et al., 2018).
Estimating the disparate impact of release decisions among white and Black defendants is fundamentally challenging. Observed disparities do not adjust for unobserved misconduct potential and can therefore suffer from omitted variables bias (OVB) when there are unobserved racial differences in misconduct risk.4 Observational comparisons can also suffer from included variables bias (IVB) when they adjust for non-race characteristics, such as criminal history and crime type, that can mediate disparate impact. Randomized audit studies (e.g., Bertrand and Mullainathan, 2004; Ewens, Tomlin and Choon Wang, 2014) can test whether decision-makers treat fictitious white and Black individuals with the same non-race characteristics in the same way, but do not capture disparate impact that arises via non-race characteristics and are infeasible in high-stakes and face-to-face settings such as bail decisions. Outcome-based tests can detect one potential driver of disparate impact—racial bias at the margin of release decisions (e.g., Arnold, Dobbie and Yang, 2018; Marx, Forthcoming)—but cannot detect accurate statistical discrimination or measure the overall extent of disparate impact.
Our primary methodological contribution is to show that disparate impact in bail decisions, regardless of its source, can be measured by leveraging the quasi-random assignment of decision-makers (such as bail judges) to white and Black individuals. This approach proceeds in two steps. First, we show that to purge OVB from observational release rate comparisons we need only to measure average white and Black misconduct risk. Intuitively, the OVB in observational comparisons comes from the correlation between defendant race and unobserved misconduct potential in each judge’s defendant pool. When judges are as-good-as-randomly assigned, this correlation is common to all judges and is furthermore a simple function of misconduct risk (i.e., average misconduct potential) by race. We can therefore use estimates of race-specific misconduct risk to rescale observational release rate comparisons in such a way that makes released white and Black defendants comparable in terms of misconduct potential within each as-good-as-randomly assigned judge’s defendant pool. The rescaled comparisons avoid OVB by revealing the rates at which each judge releases white and Black defendants with the same objective misconduct potential. Our rescaling approach further avoids IVB by conditioning on pretrial misconduct potential directly, instead of conditioning on non-race characteristics that can mediate disparate impact. The key econometric challenge is then to estimate the average misconduct risk parameters, which is difficult since misconduct outcomes are only selectively observed among the subset of defendants who a judge endogenously releases before trial.
In the second step of our approach, we estimate the required average misconduct risk inputs from quasi-experimental variation in pretrial release and misconduct rates. To build intuition for this step, consider an idealized setting with an as-good-as-randomly assigned bail judge who is supremely lenient in that she releases nearly all defendants assigned to her. The supremely lenient judge’s release rates among white and Black defendants are close to one, meaning (by as-good-as-random assignment) that the misconduct rates among her released white and Black defendants are close to the average misconduct risk inputs. In practice, we do not observe such a supremely lenient judge. Instead, we estimate average misconduct risk by extrapolating observed release misconduct rates across observed quasi-randomly assigned judges with high release rates. Importantly, we do not require a model of judge decision-making for either our approach to extrapolating pretrial misconduct risk or to estimating discrimination from these extrapolations. Our model-free approach to measuring disparate impact only requires that the statistical extrapolations and judges’ legal objective are well-specified.
We use our quasi-experimental approach to measure the disparate impact of release decisions in New York City (NYC), home to one of the largest pretrial systems in the country. Our most conservative estimates show that approximately two-thirds of the average release rate disparity between white and Black defendants is due to the disparate impact of release decisions (62 percent, or 4.2 percentage points out of 6.8 percentage points), with the remaining one-third attributable to OVB. The average release rate disparity due to disparate impact shrinks by 17 percent (0.7 percentage points out of 4.2 percentage points) when we condition on observable characteristics such as criminal history and crime type, additionally highlighting the importance of IVB in this setting. Our main finding applies to most defendant subgroups and is robust to different extrapolations of average misconduct risk, specifications of pretrial misconduct, classifications of pretrial release, and definitions of defendant race. Judge-specific estimates further show that the vast majority of bail judges make decisions with nonzero disparate impact (87 percent, by our most conservative estimate), with higher levels among more stringent judges, judges assigned a lower share of cases with Black defendants, and judges who are not newly appointed in our sample period.
Our second methodological contribution is to develop a hierarchical marginal treatment effect (MTE) model that imposes additional structure on the quasi-experimental variation to investigate the drivers of disparate impact in NYC bail decisions. The model allows us to decompose disparate impact into components due to racial bias and statistical discrimination, two drivers that have historically been the focus of the economics literature. The model specifies a joint distribution of judge preferences for releasing defendants of a given race and judge skill at inferring misconduct potential by race. The distributions of judge preferences and skill imply a distribution of judge- and race-specific MTE curves that can be used to test for racial bias at the margin of release and measure racial differences in average risk or signal quality that generate statistical discrimination. The model also allows racial disparities in the quality of misconduct signals to generate indirect (or “systemic”) discrimination, in the absence of racial bias or statistical discrimination (Bohren, Hull and Imas, 2022).
We estimate the distribution of judge MTE curves using a tractable simulated minimum distance (SMD) procedure that matches moments of the quasi-experimental variation in pretrial release and misconduct rates. Model estimates show evidence of both racial bias and statistical discrimination in NYC, with the latter coming from a higher level of average risk (that exacerbates disparate impact) and less precise risk signals (that alleviates disparate impact) for Black defendants. The finding of statistical discrimination implies that outcome-based tests of racial bias (as in Arnold, Dobbie and Yang (2018)) would miss important sources of disparate impact in this setting.
We conclude by using our MTE model to investigate whether disparate impact can be reliably targeted, and potentially reduced, with existing data. We simulate counterfactuals in which judges can be subjected to race-specific release rate quotas that eliminate the disparate impact in release decisions, as estimated by a policymaker. We find that targeting the most discriminatory NYC judges with a quota based on our quasi-experimental estimates can reduce the average level of disparate impact by 36 percent, and that targeting all judges with such a quota can essentially eliminate disparate impact despite the noise in our estimation procedure. By comparison, targeting judges with a quota based on observational release rate disparities can lead to a small but non-zero level of disparate impact against white defendants, due to the OVB in observed release rates.
This paper complements a recent empirical literature that uses quasi-experimental variation to test for racial bias in the criminal justice system, which is one potential driver of the disparate impact we measure. Arnold, Dobbie and Yang (2018) use the release tendencies of quasi-randomly assigned bail judges to test for racial bias using a conventional MTE framework, while Marx (Forthcoming) uses a similar approach to test for racial bias at the margin of police stops under a weaker first-stage monotonicity assumption. The outcome-based tests developed by Arnold, Dobbie and Yang (2018) and Marx (Forthcoming) detect racial bias from taste-based discrimination or inaccurate stereotypes, but cannot detect accurate statistical discrimination or measure the magnitude of any disparate impact. Our primary contribution to this literature is to show how quasi-experimental judge assignment can be used to measure these magnitudes and detect all possible disparate impact violations of U.S. anti-discrimination law, regardless of their source. Our secondary contribution is to show how to investigate the drivers of disparate impact by imposing alternative structure on the quasi-experimental variation, providing a way to quantify the relative importance of the racial bias detected in the outcome-based tests of Arnold, Dobbie and Yang (2018) and Marx (Forthcoming).5
Methodologically, this paper builds on a recent literature on estimating average treatment effects (ATEs) and MTEs with multiple discrete instruments (Kowalski, 2016; Brinch, Mogstad and Wiswall, 2017; Mogstad, Santos and Torgovitsky, 2018; Hull, 2020). An important feature of our approach is that we do not impose the usual first-stage monotonicity assumption, which has received scrutiny both in general (Mogstad, Torgovitsky and Walters, 2020) and in the specific context of so-called “judge designs” (Mueller-Smith, 2015; Frandsen, Lefgren and Leslie, 2019; Norris, 2019). Our extrapolation-based solution to estimating mean misconduct risk (which can be viewed as an ATE) without imposing monotonicity is most closely related to Hull (2020), who considers non-parametric extrapolations of quasi-experimental moments in the spirit of “identification at infinity” in sample selection models (Chamberlain, 1986; Heckman, 1990; Andrews and Schafgans, 1998). Our hierarchical MTE framework is closely related to the contemporaneous work of Chan, Gentzkow and Yu (2021), who use a similar model to study variation in physician preferences and skill when making pneumonia diagnoses.
The remainder of the paper is organized as follows. Section 2 describes how U.S. anti-discrimination laws motivate our approach and provides an overview of the NYC pretrial system. Section 3 outlines the conceptual framework underlying our analysis. Section 4 describes our data and documents pretrial release rate differences for Black and white defendants. Section 5 develops and implements our quasi-experimental approach to measuring disparate impact in bail decisions. Section 6 develops and estimates our hierarchical MTE model to explore the drivers of disparate impact and conduct policy counterfactuals. Section 7 concludes.
2. Setting
2.1. Disparate Impact and U.S. Anti-Discrimination Law
The two main legal doctrines of discrimination in the United States are disparate impact and disparate treatment, with each requiring distinct statistical and non-statistical evidence. In this section we first discuss disparate impact and motivate an idealized statistical measure, which we formalize and estimate in this paper. We then compare disparate impact to disparate treatment, which generally requires non-statistical evidence to establish or strongly suggest discriminatory intent under the law. We emphasize that our empirical analysis draws on the legal doctrine of disparate impact and not alternative definitions that use the same terminology to refer to, for example, unconditional disparities in treatments or outcomes between groups.
The disparate impact doctrine concerns the discriminatory effects of a policy or practice, rather than a decision-maker’s intent. Under this doctrine, a policy or practice is discriminatory if it leads to an adverse impact on a protected class and either the decision-maker cannot offer a substantial legitimate justification or if it can be shown that such a justification could be reasonably achieved by less disparate means. The disparate impact standard was formalized in the landmark U.S. Supreme Court case of Griggs v. Duke Power Co. (1971). This case began in 1965, when the Duke Power Company instituted a policy requiring employees to have a high school diploma in order to be considered for promotion. The policy had the effect of drastically limiting the eligibility of Black employees, despite being race-neutral. The Court found that these promotion disparities reflected illegal discrimination, since having a high school diploma had little to no relationship to a worker’s productivity at Duke Power (the “legitimate justification” in this setting). Notably, the employer’s motivation for instituting the diploma requirement was irrelevant to the Court’s decision, as was the fact that the policy was applied equally to white and Black employees.6 Subsequent court decisions, such as Albemarle Paper Co. v. Moody (1975), have clarified that policies like the diploma requirement in the Griggs v. Duke Power Co. case remain illegal even when they are related to a worker’s productivity—provided there is an alternative policy that could reasonably achieve the same goal by less disparate means.
An important question in interpreting the disparate impact doctrine, both in general and in our specific context of pretrial decisions, is how to define a legitimate justification for potential disparities. In the employment context, the U.S. Supreme Court has consistently found that an employer charged with a disparate impact must show that their hiring practices “bear a demonstrable relationship to successful performance of the jobs for which it was used” (Griggs v. Duke Power Co., 1971). In the lending context, guidance issued by various U.S. banking regulators has similarly explained that legitimate justifications are typically related to cost, profitability, soundness, or other measurable objectives of the lender (see, e.g., the Interagency Fair Lending Examination Procedures). We interpret these decisions as saying that the legitimate justification that defines disparate impact is based on objective potential outcomes, such as worker productivity in an employment context, profits in a lending context, or (as we discuss more below) pretrial misconduct in the pretrial context.
The ideal statistical test for disparate impact would therefore compare the treatment of different protected groups with identical potential for achieving a given relevant outcome. In the context of bail decisions, discussed further below, this means that we would like to compare the release decisions of white and Black defendants with identical pretrial misconduct potential. The finding of disparities conditional on misconduct potential would likely be necessary (though perhaps not sufficient) evidence to win a disparate impact case—depending on, for example, whether or not it can be shown that there is a decision rule yielding less of a conditional disparity while achieving similar or better outcomes.
By design, the ideal statistical test will measure disparate impact coming from both “direct” discrimination on the basis of race itself and “indirect” discrimination from non-race characteristics—as with the race-neutral policy considered in Griggs v. Duke Power Co. (1971). For example, a bail judge using defendant criminal history to accurately predict pretrial misconduct potential in a race-neutral way may make release decisions with disparate impact because she fails to take into account existing racial disparities in criminal history (e.g., due to discrimination in policing).7 The statistical measure of disparate impact we develop below captures such indirect discrimination by comparing the release rates of white and Black defendants with identical pretrial misconduct potential, without conditioning on other non-race characteristics like criminal history. Our measure also quantifies the extent of such disparate impact, not just its presence, allowing for the comparisons of different decision-making rules (e.g., bail judges vs. algorithmic decision rules) that may serve as the basis for disparate impact litigation.
The disparate treatment doctrine contrasts with disparate impact by prohibiting polices or practices motivated by a “discriminatory purpose” and thus requiring proof of intent.8 There are two competing views on the ideal statistical test for disparate treatment, with broad agreement that statistical evidence alone is insufficient because of the need to show intent. The first view is that one would still like to compare the treatment of different groups with identical potential outcomes, as in a disparate impact case, but augment this comparison with non-statistical evidence showing or strongly suggesting intent.9 The second view is that we would like to compare the treatment of different groups with identical observable characteristics using, for example, a well-designed audit study or observational analysis that controls for all observable differences between groups. Such a test would reveal whether the decision-maker is impartial with respect to protected attributes such as race (i.e., is “race-blind”) and may, along with proof of intent, be enough to establish disparate treatment.
2.2. The New York City Pretrial System
We study disparate impact in the New York City pretrial system, which is one of the largest pretrial systems in the country. U.S. pretrial systems are meant to allow most criminal defendants to be released from legal custody while minimizing the risk of pretrial misconduct. Bail judges in both NYC and the country as a whole are granted considerable discretion in determining which defendants should be released before trial, but they cannot discriminate against minorities and other protected classes even when membership in a protected class contains information about the underlying risk of criminal misconduct (Yang and Dobbie, 2020). Judges are also not meant to assess guilt or punishment when determining which individuals should be released from custody, nor are they meant to consider the political consequences of their bail decisions.
In NYC, bail conditions are set by a judge at an arraignment hearing held shortly after an arrest. These hearings usually last a few minutes and are held through a videoconference to the detention center. The judge typically receives detailed information on the defendant’s current offense and prior criminal record, as well as a release recommendation based on a six-item checklist developed by a local nonprofit (New York City Criminal Justice Agency Inc., 2016). The judge then has several options in setting bail conditions. First, she can release defendants who show minimal risk on a promise to return for all court appearances, known broadly as release on recognizance (ROR) or release without conditions. Second, she can require defendants to post some sort of bail to be released. The judge can also send higher-risk defendants to a supervised release program as an alternative to cash bail. Finally, the judge can detain defendants pending trial by denying bail altogether. Cases such as murder, kidnapping, arson, and high-level drug possession and sale almost always result in a denial of bail, for example, though these cases make up only about 0.8 percent of our sample.
We exploit three features of the pretrial system in our analysis. First, the legal objective of bail judges is both narrow and measurable among the set of released defendants for whom pretrial misconduct outcomes are observed (although not among detained defendants, for whom such outcomes are unobserved). This narrow legal objective yields a natural approach to measuring disparate impact from the difference in a judge’s release rates between white and Black defendants with identical misconduct potential. Second, bail judges can be effectively viewed as making binary decisions, releasing low-risk defendants (generally by ROR or setting a low cash bail amount) and detaining high-risk defendants (generally by setting a high cash bail amount). We explore alternative characterizations of bail decisions in our analysis, such as viewing judges as deciding between release without conditions and any cash bail amount. Third, the case assignment procedures used in most jurisdictions, including NYC, generate quasi-random variation in judge assignment for defendants arrested at the same time and place. The quasi-random variation in judge assignment, in turn, generates quasi-experimental variation in the probability that a defendant is released before trial which we exploit in our analysis.
There are two differences between the NYC pretrial system and other pretrial systems around the country that are potentially relevant for our analysis. First, New York instructs judges to only consider the risk that defendants will not appear for a required court appearance when setting bail conditions (a so-called failure to appear, or FTA), not the risk of new criminal activity as in most states (§510.10 of New York Criminal Procedure Law). We explore robustness to this narrower definition of pretrial misconduct in our analysis. Second, many defendants in NYC will never have bail set, either because the police gave them a desk appearance ticket that does not require an arraignment hearing or because the case was dismissed or otherwise disposed at the arraignment hearing before bail was set. However, the decision of whether or not to issue a desk appearance ticket is made before the bail judge is assigned, and cases should only be dismissed or otherwise disposed at arraignment if there is a clear legal defect in the case (Leslie and Pope, 2017). We show below that there is no relationship between the assigned bail judge and the probability that a case exits our sample due to case disposal or dismissal at arraignment, and exclude these cases from our analysis.
3. Conceptual Framework
3.1. Formalizing Disparate Impact
We formalize the disparate impact standard in a setting where a set of decision-makers j make binary decisions Dij ∈ {0, 1} across a population of individuals i. Each decision-maker’s goal is to align Dij with a latent binary state which captures the legitimate justification for setting Dij = 1.10 In the context of bail decisions, Dij = 1 indicates that judge j would release defendant i if assigned to her case (with Dij = 0 otherwise) while indicates that the defendant would subsequently fail to appear in court or be rearrested for a new crime if released (with otherwise). Each judge’s objective is to release individuals without misconduct potential and detain individuals with misconduct potential, but may differ in their predictions of which individuals fall into which category. We note that Dij is defined as the potential decision of judge j for defendant i, setting aside for now the judge assignment process which yields actual release decisions from these latent variables.
We measure disparate impact, both overall and for each judge, by the average release rate disparity between white and Black defendants with identical misconduct potential. To build up to this measure, let Ri ∈ {w, b} index the race of white and Black defendants and define:
| (1) |
as the release rate disparity among white and Black defendants without misconduct potential and:
| (2) |
as the release rate disparity among white and Black defendants with misconduct potential. Each Δjy parameter can be understood as capturing racial differences in the tendency of judge j to correctly and incorrectly classify individuals by their misconduct potential. The average level of disparate impact in judge j’s decisions is then given by:
| (3) |
with weights given by the average misconduct risk in the population, . The system-wide level of disparate impact is given by the case-weighted average of Δj across all judges.
We say that judge j discriminates against Black defendants when Δj > 0, that she discriminates against white defendants when Δj < 0, and that she does not discriminate against either Black or white defendants when Δj = 0, again recognizing that the Dij capture a judge’s potential release decisions. By holding the potential defendant population fixed, estimates of Δj can be used to calculate both the average level of disparate impact in a bail system as well as any variation in the level of disparate impact across judges. We choose the weights such that Δj captures the expected level of disparate impact in a pool of defendants where pretrial misconduct potential is unknown. We explore robustness to other weighted averages of Δj0 and Δj1 below.
By design, our measure of disparate impact, Δj, captures the discriminatory effects of judge j’s release decisions rather than any discriminatory intent underlying her decisions. As noted in Section 2.1 the disparate impact measured by Δj can arise from direct discrimination, via the conscious or unconscious use of defendant race, as well as indirect discrimination through the conscious or unconscious use of non-race characteristics that are correlated with race. Importantly, this measure is not meant to test whether judges treat fictitious white and Black individuals with the same non-race characteristics in the same way, as in a randomized audit study measuring such direct discrimination. As we discuss more below, conditioning on non-race characteristics beyond pretrial misconduct potential can bias our measure when disparate impact arises through these characteristics.11
The economics literature has historically focused on two potential drivers of racial discrimination, though it has not always been clear on how they can manifest as disparate impact. The first driver is racial bias, in which judges discriminate against Black defendants at the margin of pretrial release due to either racial preferences (Becker, 1957) or some form of inaccurate beliefs or stereotypes (Bohren et al., 2020; Bordalo et al., 2016). The second theoretical driver is statistical discrimination, in which judges act on accurate risk predictions but discriminate due to racial differences in average risk or the precision of received risk signals (Phelps, 1972; Arrow, 1973; Aigner and Cain, 1977). In Section 6, we formalize these potential drivers of Δj with a simple decision-making model. The model further allows disparate impact to arise from systemic differences in the distribution of non-race characteristics judges use to form misconduct predictions—a channel not usually considered in economic analyses of direct discrimination (Bohren, Hull and Imas, 2022). Estimates of this model allow us to quantify the role of each channel in driving our main estimates of disparate impact.
We emphasize that our analysis of disparate impact is not premised on the idea that the differences in misconduct potential which we condition on are innate or unaffected by discrimination at other points of the criminal justice system (or society as a whole). Differences in could, for example, be driven by various systemic factors such as the over-policing of Black neighborhoods relative to white neighborhoods, discrimination in the types of crimes that are reported to and investigated by the police, discrimination in local housing and labor markets, and so on. Thus a finding of Δj = 0 need not suggest pretrial release decisions are unaffected by disparate impact, only that there is no disparate impact conditional on these other potentially discriminatory systems and conditions. A finding of Δj ≠ 0 in turn isolates only one form of disparate impact in bail decisions, which may be reliably targeted and potentially reduced by policy, holding fixed other potentially harder to quantify forms of discrimination.
3.2. Empirical Challenges
Observational disparity analyses, whether in bail decisions or another area of the criminal justice system, often come from “benchmarking” regressions of decisions (such as pretrial release) on an indicator for an individual’s race and potentially other controls for the observed non-race characteristics (e.g., Gelman, Fagan and Kiss, 2007; Abrams, Bertrand and Mullainathan, 2012). Since such analyses cannot control for unobserved misconduct potential, they may suffer from omitted variables bias (OVB) when viewed as a measure of disparate impact. They may further suffer from included variables bias (IVB) when controlling for non-race characteristics through which disparate impact arises.
We formalize these empirical challenges in an idealized version of our setting with complete random assignment of judges to defendants. Let Zij = 1 if defendant i is assigned to judge j, let indicate the defendant’s release status, and let indicate the observed pretrial misconduct outcome. The expression for observed misconduct reflects the fact that an individual who is detained (Di = 0) cannot fail to appear in court or be rearrested for a new crime, such that Yi = 0 when Di = 0 regardless of individual i’s misconduct potential . The econometrician observes (Ri, Zi1, …, ZiJ, Di, Yi) for each defendant, and records whether the defendant is white in an indicator Wi = 1[Ri = w]. Under complete random assignment, each Zij is independent of .
We first formalize the OVB challenge by considering a simple judge-specific benchmarking regression of release decisions on judge-by-race interactions and judge main effects:
| (4) |
We omit the constant term from this regression in order to include all judge fixed effects, and for now abstract away from other controls. The interaction coefficients measure differences in judge release rates for white defendants relative to Black defendants, and under random judge assignment:
| (5) |
The difference between these regression coefficients and our disparate impact measure, ξj = αj−Δj, measures OVB in the simple benchmarking analysis. To unpack ξj, note first that we can write:
| (6) |
where gives the race- and judge-specific release rate of defendants with or without misconduct potential and gives the average misconduct risk among individuals of race r. In contrast, with Δj0 = δjw0 −δjb0 and Δj1 = δjw1 −δjb1, the disparate impact of judge j’s decisions given by Equation (3) can be written:
| (7) |
where is the average misconduct risk across all defendants, with pr = Pr(Ri = r) denoting racial shares. The difference in these expressions shows OVB can be written:
| (8) |
where the second line follows by definition of the population risk . The regression coefficient αj will be biased upward for Δj when ξj > 0 and biased downward when ξj < 0.
Two key insights follow from the OVB formula in Equation (8). First, the simple benchmarking regression (4) will generally yield biased estimates of disparate impact. The exception is when either judge release decisions are uncorrelated with misconduct potential (so δjr0 = δjr1 for each race r) or when misconduct potential is uncorrelated with defendant race (so μb = μw). Both scenarios are unlikely in practice.12 Second, Equation (8) suggests a potential avenue for addressing OVB and measuring disparate impact when bail judges are as-good-as-randomly assigned, using familiar econometric objects. One of the terms driving the bias of each αj is the difference in race-specific misconduct risk in the population, μb − μw, which is common to all judges. With capturing defendant i’s potential for pretrial misconduct when released and Yi = 0 for all detained individuals, each can be understood as an average treatment effect (ATE) of pretrial release on pretrial misconduct among individuals of race r. We show in Section 5 how such ATEs can be estimated from quasi-experimental judge assignment and used to purge OVB from benchmarking estimates, recovering estimates of Δj.
We can similarly formalize the potential for IVB in observational analyses by considering a simple case where white and Black misconduct risk are equal, μw = μb, so there is no OVB in the simple benchmarking regression: αj = Δj. Appendix B.2 shows how adjusting for some binary non-race characteristic Xi (such as an indicator for crime type) in this scenario yields an analogous formula for bias in the “overcontrolled” disparity :
| (9) |
where δjr,X=x = E[Dij | Ri = r,Xi = x] gives the race- and X-specific release rate of judge j and gives the race-specific average of Xi. Here, IVB arises whenever the judge’s decisions are correlated with the included non-race characteristic (so δjw,X=0 ≠ δjw,X=1 and this characteristic is correlated with race (so ). Similar IVB formulas can be derived when μw ≠ μb but when the econometrician has adjusted for so white and Black misconduct risk are conditionally comparable. We avoid IVB in our empirical strategy by making such an adjustment but not conditioning on non-race characteristics like crime type or criminal history.
4. Data and Observational Comparisons
4.1. Sample and Summary Statistics
Our analysis of disparate impact in bail decisions is based on the universe of 1,458,056 arraignments made in NYC between November 1, 2008 and November 1, 2013. The data contain information on a defendant’s gender, race, date of birth, and county of arrest, as well as the (anonymized) identity of the assigned bail judge. In our primary analysis, we categorize defendants as white (including both non-Hispanic and Hispanic white individuals), Black (including both non-Hispanic and Hispanic Black individuals), or neither. We explore alternative categorizations of race in robustness checks below.
In addition to detailed demographics, our data contain information on each defendant’s current offense, history of prior criminal convictions, and history of past pretrial misconduct (both rearrests and FTA). We also observe whether the defendant was released at the time of arraignment and whether this release was due to release without conditions or some form of money bail. We categorize defendants as either released (including both release without conditions and with paid cash bail) or detained (including cash bail that is not paid) at the first arraignment, though we again explore robustness to other categorizations of the initial pretrial release decision below. Finally, we observe whether a defendant subsequently failed to appear for a required court appearance or was subsequently arrested for a new crime before case disposition. We take either form of pretrial misconduct as the primary outcome of our analysis, but again explore robustness to other measures below.
We make four key restrictions to arrive at our estimation sample. First, we drop cases where the defendant is not charged with a felony or misdemeanor (N=26,057). Second, we drop cases that were disposed at arraignment (N=364,051) or adjourned in contemplation of dismissal (N=230,517). This set of restrictions drops cases that are likely to be dismissed by virtually every judge: Appendix Table A1 confirms that judge assignment is not systematically related to case disposal or case dismissal. Third, we drop cases in which the defendant is assigned a cash bail of $1 (N=1,284). This assignment occurs in cases in which the defendant is already serving time in jail on an unrelated charge; the $1 cash bail is set so that the defendant receives credit for served time, and does not reflect a new judge decision. Fourth, we drop defendants who are non-white and non-Black (N=45,529). Finally, we drop defendants assigned to judges with fewer than 100 cases (N=3,785) and court-by-time cells with fewer than 100 cases, only one unique judge, or only Black or only white defendants for a given judge (N=191,647), where a court-by-time cell is defined by the assigned courtroom, shift, day-of-week, month and year (e.g., the Wednesday night shift in Courtroom A of the Kings County courthouse in January 2012). The final sample consists of 595,186 cases, 367,434 defendants, and 268 judges.13
Table 1 summarizes our estimation sample, both overall and by race. Panel A shows that 73.0 percent of defendants are released before trial. A defendant is defined as released before trial if either the defendant is released without conditions (ROR) or the defendant posts the required bail amount before disposition. The vast majority of these releases are without conditions, with only 14.4 percent of defendants being released after being assigned money bail. White defendants are more likely to be released before trial than Black defendants, with a 76.7 percent release rate relative to a 69.5 percent release rate. Among released defendants, however, the distribution of release conditions (e.g., the ROR share) is virtually identical across race.
Table 1:
Descriptive Statistics
| All Defendants | White Defendants | Black Defendants | |
|---|---|---|---|
|
|
|||
| Panel A: Pretrial Release | (1) | (2) | (3) |
|
|
|||
| Released Before Trial | 0.730 | 0.767 | 0.695 |
| Share ROR | 0.852 | 0.852 | 0.851 |
| Share Money Bail | 0.144 | 0.144 | 0.145 |
| Share Other Bail Type | 0.004 | 0.004 | 0.004 |
| Share Remanded | 0.000 | 0.000 | 0.000 |
| Panel B: Defendant Characteristics | |||
| White | 0.478 | 1.000 | 0.000 |
| Male | 0.821 | 0.839 | 0.804 |
| Age at Arrest | 31.97 | 32.06 | 31.89 |
| Prior Rearrest | 0.229 | 0.204 | 0.253 |
| Prior FTA | 0.103 | 0.087 | 0.117 |
| Panel C: Charge Characteristics | |||
| Number of Charges | 1.150 | 1.184 | 1.118 |
| Felony Charge | 0.362 | 0.355 | 0.368 |
| Misdemeanor Charge | 0.638 | 0.645 | 0.632 |
| Any Drug Charge | 0.256 | 0.257 | 0.256 |
| Any DUI Charge | 0.046 | 0.067 | 0.027 |
| Any Violent Charge | 0.143 | 0.124 | 0.160 |
| Any Property Charge | 0.136 | 0.127 | 0.144 |
| Panel D: Pretrial Misconduct, When Released | |||
| Pretrial Misconduct | 0.299 | 0.266 | 0.332 |
| Share Rearrest Only | 0.499 | 0.498 | 0.499 |
| Share FTA Only | 0.281 | 0.296 | 0.269 |
| Share Rearrest and FTA | 0.220 | 0.205 | 0.232 |
|
| |||
| Total Cases | 595,186 | 284,598 | 310,588 |
| Cases with Defendant Released | 434,201 | 218,256 | 215,945 |
Notes. This table summarizes the NYC analysis sample. The sample consists of bail hearings that were quasi-randomly assigned judges between November 1, 2008 and November 1, 2013, as described in the text. Information on demographics and criminal outcomes is derived from court records as described in the text. Pretrial release is defined as meeting the bail conditions set by the first assigned bail judge. ROR (released on recognizance) is defined as being released without any conditions. FTA (failure to appear) is defined as failing to appear at a mandated court date.
Observed release rate disparities will generally not measure disparate impact when white and Black defendants have different misconduct rates. Suggestive evidence of such OVB is found in Panel B of Table 1. Black defendants are, for example, 4.9 percentage points more likely to have been arrested for a new crime before trial in the past year compared to white defendants, as well as 3.0 percentage points more likely to have a prior FTA in the past year. Panel C further shows that Black and white defendants tend to have different crime types. Black defendants are 1.3 percentage points more likely to have been charged with a felony compared to white defendants, as well as 3.6 percentage points more likely to have been charged with a violent crime. Finally, Panel D shows that Black defendants who are released are 6.6 percentage points more likely to be rearrested or have an FTA than white defendants who are released (though the composition of such misconduct is similar). Importantly, and in contrast to the other statistics in Table 1, the risk statistics in Panel D are only measured among released defendants. Pretrial misconduct potential is, by definition, unobserved among detained individuals despite being the key legal objective for bail judges.
4.2. Quasi-Experimental Judge Assignment
Our empirical strategy exploits variation in pretrial release from the quasi-random assignment of judges who vary in the leniency of their bail decisions. There are three features of the NYC pretrial system that make it an appropriate setting for this research design.
First, NYC uses a rotation calendar system to assign judges to arraignment shifts in each of the five county courthouses in the city, generating quasi-random variation in bail judge assignment for defendants arrested at the same time and in the same place. Each county courthouse employs a supervising judge to determine the schedule that assigns bail judges to the day (9 a.m. to 5 p.m.) and night arraignment shift (5 p.m. to 1 a.m.) in one or more courtrooms within each courthouse. Individual judges can request to work certain days or shifts but, in practice, there is considerable variation in judge assignments within a given arraignment shift, day-of-week, month, and year cell.
Second, there is limited scope for influencing which bail judge will hear any given case, as most individuals are brought for arraignment shortly after their arrest. Each defendant’s arraignment is also scheduled by a coordinator, who seeks to evenly distribute the workload to each open courtroom at an arraignment shift. Combined with the rotating calendar system described above and the processing time required before the arraignment, it is unlikely that police officers, prosecutors, defense attorneys, or defendants could accurately predict which judge is presiding over any given arraignment.
Finally, the rotation schedule used to assign bail judges to cases does not align with the schedule of any other actors in the criminal justice system. For example, different prosecutors and public defenders handle matters at each stage of criminal proceedings and are not assigned to particular bail judges, while both trial and sentencing judges are assigned to cases via different processes. As a result, we can study the effects of being assigned to a given bail judge as opposed to, for example, the effects of being assigned to a given set of bail, trial, and sentencing judges.
Appendix Table A3 verifies the quasi-random assignment of judges to bail cases in the estimation sample. Each column reports coefficient estimates from an ordinary least squares (OLS) regression of judge leniency on various defendant and case characteristics, with court-by-time fixed effects that control for the level of quasi-experimental bail judge assignment. We measure leniency using the leave-one-out average release rate among all other defendants assigned to a defendant’s judge. Following the standard approach in the literature (e.g., Arnold, Dobbie and Yang, 2018; Dobbie, Goldin and Yang, 2018), we construct the leave-one-out measure by first regressing pretrial release on court-by-time fixed effects and then using the residuals from this regression to construct the leave-one-out residualized release rate. By first residualizing on court-by-time effects, the leave-one-out measure captures the leniency of a judge relative to judges assigned to the same court-by-time cells. Most coefficients in this balance table are small and not statistically significantly different from zero, both overall and by defendant race. A joint F-test fails to reject the null of quasi-random assignment at conventional levels of statistical significance, albeit only marginally in certain specifications, with a p-value equal to 0.300 among white defendants and 0.101 among Black defendants.14
Appendix Table A4 further verifies that the assignment of different judges meaningfully affects the probability an individual is released before trial. Each column of this table reports coefficient estimates from an OLS regression of an indicator for pretrial release on judge leniency and court-by-time fixed effects. A one percentage point increase in the predicted leniency of an individual’s judge leads to a 0.96 percentage point increase in the probability of release, with a somewhat smaller first-stage effect for white defendants and a somewhat larger effect for Black defendants.
4.3. Observational Comparisons
Table 2 investigates the system-wide level of observed racial disparity in NYC pretrial release rates. We first estimate OLS regressions of the form:
| (10) |
where Di is an indicator equal to one if defendant i is released, Wi is an indicator for the defendant being white, and Xi is a vector of controls. Column 1 of Table 2 omits any controls in Xi, column 2 adds court-by-time fixed effects to adjust for unobservable differences at the level of quasi-experimental bail judge assignment to Xi, and column 3 further adds the defendant and case observables from Table 1. Such regressions generally follow the conventional benchmarking approach from the literature (e.g., Gelman, Fagan and Kiss, 2007; Abrams, Bertrand and Mullainathan, 2012), where we again note that because of potential of both OVB and IVB the defendant and case observables included in column 3 can lead us to either over- or understate the true level of disparate impact in bail decisions.
Table 2:
Observational Release Rate Disparities
| (1) | (2) | (3) | |
|---|---|---|---|
|
|
|||
| White | 0.072 (0.005) | 0.068 (0.005) | 0.052 (0.004) |
| Male | −0.092 (0.004) | ||
| Age at Arrest | −0.005 (0.000) | ||
| Prior Rearrest | −0.068 (0.004) | ||
| Prior FTA | −0.208 (0.005) | ||
| Felony Charge | −0.171 (0.005) | ||
| Any Drug Charge | −0.057 (0.007) | ||
| Any DUI Charge | 0.119 (0.004) | ||
| Any Violent Charge | −0.146 (0.007) | ||
| Any Property Charge | −0.072 (0.005) | ||
|
| |||
| Court × Time FE | No | Yes | Yes |
| Case/Defendant Observables | No | No | Yes |
| Mean Release Rate | 0.730 | 0.730 | 0.730 |
| Cases | 595,186 | 595,186 | 595,186 |
Notes. This table reports OLS estimates of regressions of an indicator for pretrial release on defendant characteristics. The regressions are estimated on the sample described in the notes to Table 1. Robust standard errors, two-way clustered at the individual and the judge level, are reported in parentheses.
Table 2 documents both statistically and economically significant release rate disparities between white and Black defendants in NYC. The unadjusted white-Black release rate difference α is estimated in column 1 at 7.2 percentage points, with a standard error (SE) of 0.5 percentage points. This release rate gap is around 10 percent of the mean release rate of 73 percent. The release rate gap falls slightly, to 6.8 percentage points (SE: 0.5), when we control for court-by-time fixed effects. The gap falls by an additional 24 percent, to 5.2 percentage points (SE: 0.4), when we add defendant and case observables. These estimates are similar in magnitude to the association, reported in column 3, between the probability of release and having an additional drug charge (−5.7 percentage points) or pretrial arrest (−6.8 percentage points) in the past year.
Figure 1 summarizes the distribution of judge-specific release rate disparities across the 268 bail judges in our sample. We estimate judge-specific disparities from OLS regressions of the form:
| (11) |
where Di is again an indicator equal to one if defendant i is released, WiZij is the interaction between an indicator for the defendant being white and the fixed effects for each judge, Zij are the noninteracted fixed effects for each judge, and Xi is again a control vector. We estimate Equation (11) with Xi demeaned, such that αj captures the regression-adjusted difference in release rates for white and Black individuals assigned to judge j. Figure 1 then plots empirical Bayes estimates of the posterior distribution of αj across judges, using the posterior average effect approach of Bonhomme and Weidner (2020) (see Appendix B.3 for details). We show the distribution when adjusting only for the main judge fixed effects and court-by-time fixed effects, following column 2 of Table 2, as well as the distribution when we add both defendant and case observables and court-by-time fixed effects, following column 3 of Table 2. We also report estimates of the prior mean and standard deviation of αj across judges, as well as the fraction of judges with positive αj (again following the posterior average effect approach of Bonhomme and Weidner (2020)).
Figure 1:
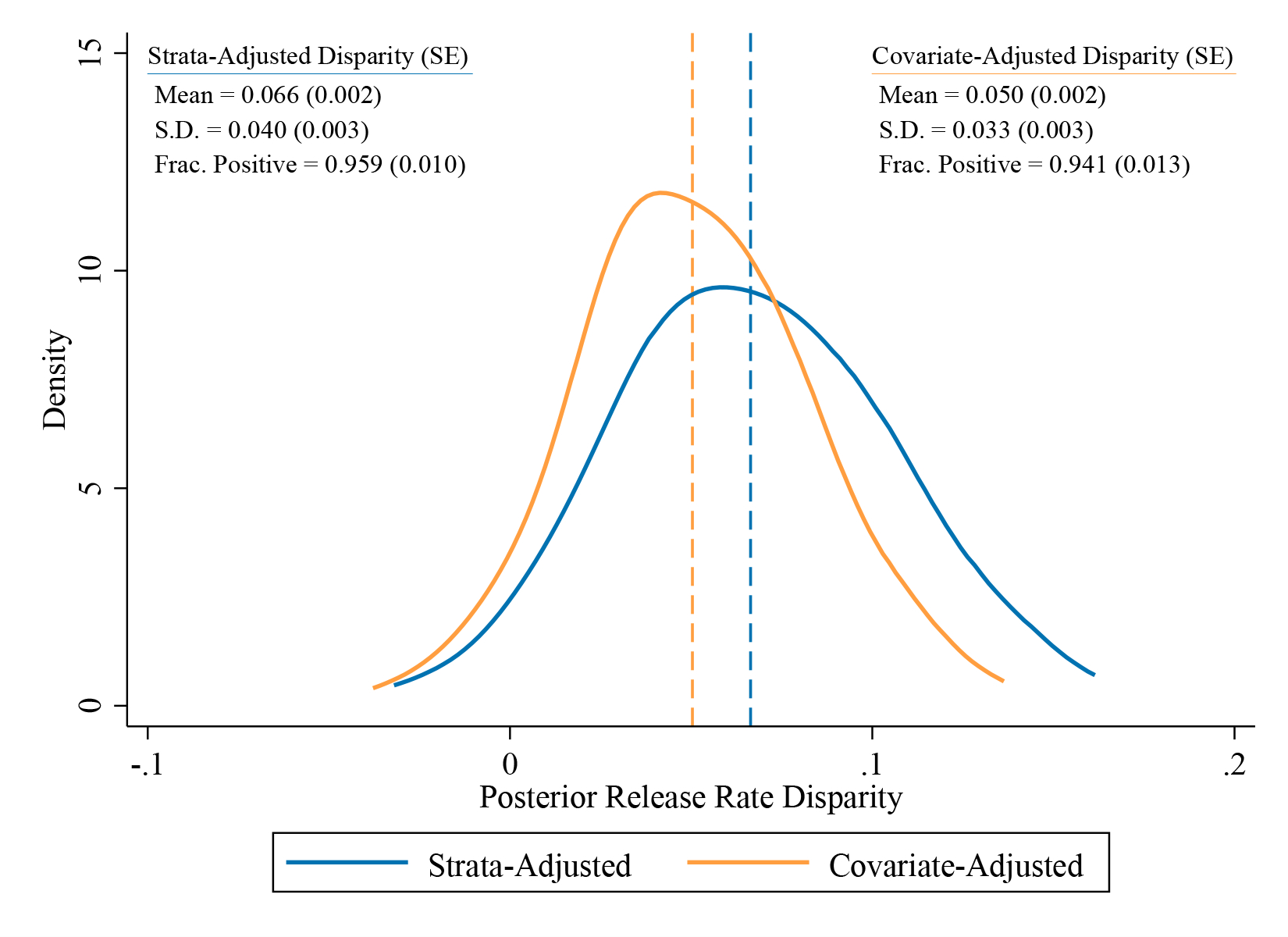
Observational Release Rate Disparities
Notes. This figure plots the posterior distribution of observational release rate disparities for the 268 judges in our sample. We estimate disparities by OLS regressions of an indicator for pretrial release on white×judge fixed effects, controlling for judge main effects. The strata-adjusted disparity regression controls only for the main judge fixed effects and court-by-time fixed effects. The covariate-adjusted disparity regression adds the baseline controls from Table 2. The distribution of judge disparities, and fractions of positive disparities, are computed from these estimates as posterior average effects; see Appendix B.3 for details. Means and standard deviations refer to the estimated prior distribution.
The posterior distributions of release rate disparities in Figure 1 are both located well above zero, revealing that nearly all judges in our sample release white defendants at a higher rate than Black defendants. We estimate that 95.9 percent (SE: 1.0) of judges in our sample release a larger share of white defendants in the specification that adjusts for court-by-time fixed effects, while 94.1 percent (SE: 1.3) are estimated to release a larger share of white defendants when we additionally adjust for defendant and case observables. Figure 1 nevertheless shows considerable variation in the magnitude of the release rate disparities across judges. The standard deviation of αj is estimated at 4.0 percentage points (SE: 0.3) when we adjust for court-by-time fixed effects, and 3.3 percentage points (SE: 0.3) when we additionally adjust for defendant and case observables. The average judge-specific disparities, which differ from the system-wide averages in Table 2 due to differences in weighting, are 6.6 percentage points (SE: 0.2) when we adjust for court-by-time fixed effects, and 5.0 percentage points (SE: 0.2) when we additionally adjust for defendant and case observables.
Together, the results from Table 2 and Figure 1 confirm large and pervasive racial disparities in NYC release decisions, both in the raw data and after accounting for observable differences between white and Black defendants. These observational estimates suggest that there may be a disparate impact of release decisions, but are not conclusive as we cannot directly adjust for unobserved misconduct potential and could thus either over- or understate the true level and distribution of disparate impact across judges in the NYC pretrial system. We next develop and apply a quasi-experimental approach to adjust for unobserved misconduct potential directly and measure disparate impact.
5. Quasi-Experimental Estimates of Disparate Impact
5.1. Methods
We estimate the disparate impact in NYC pretrial release decisions by rescaling the observational release rate comparisons in Figure 1 using quasi-experimental estimates of average white and Black misconduct risk. This quasi-experimental approach does not require a model of judge decision-making, only that average misconduct risk among white and Black defendants can be accurately extrapolated from the quasi-experimental data.
The first key insight underlying our approach is that when judges are as-good-as-randomly assigned, the problem of measuring disparate impact in release decisions for individual judges reduces to the problem of estimating the average misconduct risk among the full population of Black and white defendants. The source of OVB in an observational benchmarking comparison is the correlation between race and unobserved misconduct potential among a given judge’s pool of white and Black defendants. Under quasi-random judge assignment, this correlation is common to all judges and captured by race-specific population misconduct risk. Thus, given estimates of these race-specific risk parameters, observed release outcomes can be appropriately rescaled to make released white and Black defendants comparable in terms of their unobserved misconduct potential.
The rescaling that purges OVB from observational comparisons is given by expanding the conditional release rates from the definition of disparate impact in Equation (7):
| (12) |
| (13) |
where the third equalities in both lines follow from quasi-random judge assignment and the definition of mean risk . Substituting these expressions into Equation (7) yields:
| (14) |
where:
| (15) |
The rewritten definition in Equation (14) shows that the disparate impact in judge j’s release decisions Δj is given by the αj coefficients in a simple benchmarking regression, where the release decisions Di of each individual are rescaled by a positive factor Ωi. This Ωi reweights the sample to make released white and Black defendants comparable in terms of their unobserved misconduct potential. It therefore reveals the extent to which each judge discriminates against white and Black defendants with identical misconduct potential, even though misconduct potential is unobserved and cannot be directly conditioned on.15 Equation (15) shows that Ωi is a function of observed misconduct outcomes Yi and the unobserved average race-specific misconduct risk parameters μr, where again . The key econometric challenge is therefore to estimate average misconduct risk μr among the full population of white and Black defendants.
The second key insight underlying our approach is that the average race-specific misconduct risk parameters that enter Equation (14) can be estimated from quasi-experimental variation in pretrial release and misconduct rates. To build intuition for this approach, consider a setting with as-good-as-random judge assignment and a supremely lenient bail judge j∗ who releases nearly all defendants regardless of their race or potential for pretrial misconduct. This supremely lenient judge’s race-specific release rate among both Black and white defendants is close to one:
| (16) |
making the race-specific misconduct rate among defendants she releases close to the race-specific average misconduct risk in the full population:
| (17) |
where the first equality in both expressions follows by quasi-random assignment. Without further assumptions, the decisions of a supremely lenient and quasi-randomly assigned judge can therefore be used to estimate the average misconduct risk parameters needed for our disparate impact measure.
In the absence of such a supremely lenient judge, the required average misconduct risk parameters can be estimated using model-based or statistical extrapolations of release and misconduct rate variation across quasi-randomly assigned judges. This approach is conceptually similar to how average potential outcomes at a treatment cutoff can be extrapolated from nearby observations in a regression discontinuity (RD) design, particularly “donut RD” designs in which data in some window of the treatment cutoff is excluded. Here, released misconduct rates are extrapolated from quasi-randomly assigned judges with high leniency to the release rate cutoff of one given by a hypothetical supremely lenient judge. Mean risk estimates may, for example, come from the vertical intercept, at one, of linear, quadratic, or local linear regressions of estimated released misconduct rates on estimated release rates E[Dij | Ri = r] across judges j within each race r. As we show below, extrapolations may also come from a model of judge behavior. Absent any extrapolations, conservative bounds on mean risk may be obtained from the released misconduct rates of highly (but not supremely) lenient judges. Each of these approaches build on recent advances in ATE estimation with multiple discrete instruments (e.g., Brinch, Mogstad and Wiswall, 2017; Mogstad, Santos and Torgovitsky, 2018; Hull, 2020) and a long literature on “identification at infinity” in sample selection models (e.g., Chamberlain, 1986; Heckman, 1990; Andrews and Schafgans, 1998).16
A further practical complication arises in our setting, with NYC bail judges only quasi-randomly assigned conditional on court-by-time effects. Some adjustment for these strata is generally needed to estimate the potential judge- and race-specific release rates E[Dij | Ri = r] and released misconduct rates that enter our mean risk estimation. We use linear regression adjustment, which tractably incorporates the large number of court-by-time effects under an auxiliary linearity assumption. Specifically, we estimate release rates from the earlier benchmarking regression in Equation (11) and estimate released misconduct rates from the analogous OLS regression:
| (18) |
among released individuals (Di = 1), where again Xi contains demeaned court-by-time fixed effects. Here, ζj and ρj + ζj estimate and , respectively, just as ϕj and αj + ϕj estimate E[Dij | Ri = w] and E[Dij | Ri = b] in Equation (11).
The linear covariate adjustment in Equation (11) is appropriate when release rates are linear in the court-by-time effects for each judge and race, with constant coefficients: i.e., when . Similarly, a sufficient condition for Equation (18) to consistently estimate released misconduct rates is . Intuitively, both conditions require the court-by-time effects to shift judge actions similarly across the judges j and two races r. A judge who is lenient for a given race in one courtroom and time period is thus restricted to still be lenient in different courtrooms and time periods.17 Below, we relax this restriction in robustness checks that allow the control coefficients, β and γ, to vary flexibly by judge and race. We do this by separating the estimation of Equations (11) and (18) by borough and by interacting the judge effects with linear and quadratic functions of time.
5.2. Results
Mean Risk by Race
Figure 2 illustrates our extrapolation-based estimation of the mean risk parameters in NYC. The horizontal axis plots estimates of the regression-adjusted judge- and race-specific release rates. We find sizable variation across judges within each race, with several judges releasing a high fraction of white or Black defendants.18 Released misconduct rates, plotted on the vertical axis, tend to increase with judge leniency for both races—as would be predicted by a behavioral model in which the more lenient judges release riskier defendants at the margin. This pattern is shown by the two solid lines in Figure 2, representing the race-specific lines-of-best-fit through the first-step estimates. The lines-of-best-fit are obtained by OLS regressions of judge-specific released misconduct rate estimates on judge-specific release rate estimates, with the judge-level regressions weighted inversely by the variance of misconduct rate estimation error. We also plot curves-of-best-fit from judge-level quadratic and local linear specifications as dashed and dotted lines, respectively, with both specifications again weighted inversely by the variance of misconduct rate estimation error. The simple linear specification fits the local IV variation well, with quadratic and local linear specifications yielding similar fits across much of the leniency distribution.
Figure 2:
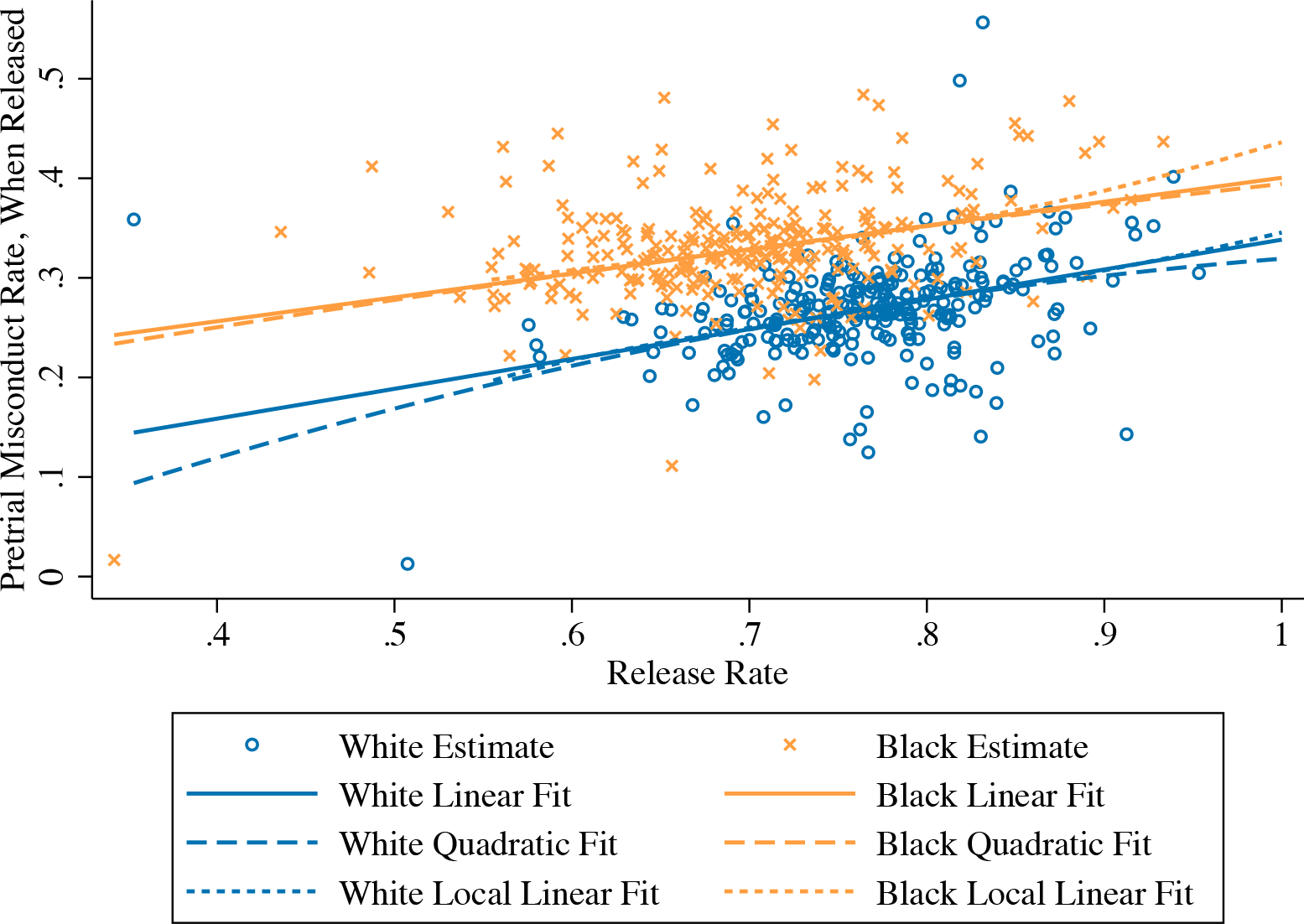
Judge-Specific Release Rates and Conditional Misconduct Rates
Notes. This figure plots race-specific release rates for the 268 judges in our sample against rates of pretrial misconduct among the set of released defendants. All estimates adjust for court-by-time fixed effects. The figure also plots race-specific linear, quadratic, and local linear curves of best fit, obtained from judge-level regressions that inverse-weight by the variance of the estimated misconduct rate among released defendants. The local linear regressions use a Gaussian kernel with a race-specific rule-of-thumb bandwidth.
The vertical intercepts of the different curves-of-best-fit, at one, provide different estimates of the race-specific mean risk parameters μr. These estimates and associated SEs are reported in Panel A of Table 3 (all SEs in this and subsequent sections are obtained from a bootstrap procedure which accounts for the first-step estimation of the judge- and race-specific release rates and released misconduct rates). The simplest linear extrapolation, summarized in column 1, yields precise mean risk estimates of 0.338 (SE: 0.007) for white defendants and 0.400 (SE: 0.006) for Black defendants. This extrapolation suggests that the average misconduct risk within the population of potential Black defendants is 6.2 percentage points higher than among the population of potential white defendants in NYC. Per Section 3.2, such a racial gap in misconduct risk is likely to generate OVB in observational release rate comparisons.
Table 3:
Mean Risk and Disparate Impact Estimates
| Linear Extrapolation | Quadratic Extrapolation | Local Linear Extrapolation | |
|---|---|---|---|
|
|
|||
| Panel A: Mean Risk by Race | (1) | (2) | (3) |
|
|
|||
| White Defendants | 0.338 (0.007) | 0.319 (0.021) | 0.346 (0.014) |
| Black Defendants | 0.400 (0.006) | 0.394 (0.021) | 0.436 (0.016) |
| Panel B: System-Wide Disparate Impact | |||
| Mean Across Cases | 0.054 (0.002) | 0.054 (0.007) | 0.042 (0.006) |
| Panel C: Judge-Level Disparate Impact | |||
| Mean Across Judges | 0.054 (0.003) | 0.054 (0.007) | 0.042 (0.006) |
| Std. Dev. Across Judges | 0.038 (0.003) | 0.037 (0.003) | 0.037 (0.003) |
| Fraction Positive | 0.929 (0.016) | 0.931 (0.036) | 0.873 (0.036) |
|
| |||
| Judges | 268 | 268 | 268 |
Notes. This table summarizes estimates of mean risk and disparate impact from different extrapolations of the variation in Figure 2. Panel A reports estimates of race-specific average misconduct risk, Panel B reports estimates of system-wide (case-weighted) disparate impact, and Panel C reports empirical Bayes estimates of summary statistics for the judge-level disparate impact prior distribution. To estimate mean risk, column 1 uses a linear extrapolation of the variation in Figure 2, while column 2 uses a quadratic extrapolation and column 3 uses a local linear extrapolation with a Gaussian kernel and a rule-of-thumb bandwidth. Robust standard errors, two-way clustered at the individual and judge level, are obtained by a bootstrapping procedure and appear in parentheses.
The quadratic and local linear extrapolations of the quasi-experimental variation yield similar race-specific mean risk estimates, as can be seen from Figure 2. The quadratic fit suggests a slight nonlinearity in the relationship between judge leniency and released misconduct rates, with a slightly concave dashed curve for white defendants and a more linear dashed curve for Black defendants. Column 2 of Table 3 shows that the former nonlinearity translates to a somewhat lower estimate of white mean risk, at 0.319 (SE: 0.021), with a similar estimate of Black mean risk, at 0.394 (SE: 0.021). Near one, the local linear fit of Figure 2 coincides with the linear fit for white defendants and is above both the quadratic and linear fit for Black defendants, yielding mean risk estimates in column 3 of 0.346 (SE: 0.014) and 0.436 (SE: 0.016), respectively. The implied racial gap in risk—and thus the potential for OVB—rises with these more flexible extrapolations, to 7.5 percentage points in column 2 and 9.0 percentage points in column 3. We take the most flexible local linear extrapolation as our baseline specification in NYC, which we show below gives the most conservative estimate of average disparate impact. We explore robustness to a wide range of alternative mean risk estimates below.
The extrapolations in Figure 2 yield accurate mean risk estimates when judge release rules are accurately parameterized or when there are many highly lenient judges. Appendix Figure A1 validates our extrapolations by plotting race-specific extrapolations of average predicted misconduct outcomes, among released defendants, in place of actual released misconduct averages in Figure 2. We first construct predicted misconduct outcomes using the fitted values from an OLS regression of actual pretrial misconduct on the controls in column 3 of Table 2 in the subsample of released defendants. Appendix Figure A1 then plots estimates of and E[Dij = 1 | Ri = r], constructed as in Figure 2. Since can be computed for the entire sample, we also include in this figure the overall averages that are analogous to the race-specific mean risk parameters of interest. Figure A1 shows that each of the linear, quadratic, and local linear extrapolations of predicted misconduct rates yields similar and accurate estimates of the overall actual averages. The 95 percent confidence intervals of the local linear extrapolations, for example, include the actual Black average and only narrowly exclude the actual white average. These results build confidence for the extrapolations of actual pretrial misconduct outcomes in this setting.19
Disparate Impact
Panels B and C of Table 3 summarize the estimates of disparate impact Δj given the corresponding ATE estimates in Panel A. These estimates are obtained from the sample analogue of Equation (7), noting that a judge’s release rate conditional on no misconduct potential can be written:
| (19) |
and similarly for her release rate condition on misconduct potential δjr1. We use the regression-adjusted estimates of E[Dij | Ri = r] and from Figure 2 and the sample share of Black defendants to complete the formula for Δj. Case-weighted averages of the resulting Δj estimates, reported in Panel B, estimate system-wide disparate impact. We also compute empirical Bayes posteriors of the distribution of Δj, again following Bonhomme and Weidner (2020). Summary statistics for the judge-level prior distribution (estimated as in Figure 1) are given in Panel C.
We find that approximately two-thirds of the system-wide release rate disparity between white and Black defendants in NYC is explained by disparate impact in release decisions, with about one-third explained by unobserved differences in pretrial misconduct risk (i.e., OVB). The local linear extrapolations yield the most conservative estimate of system-wide disparate impact in Table 3, implying that 62 percent (4.2 percentage points) of the case-weighted average disparity of 6.8 percentage points in Table 2 can be explained by disparate impact in release decisions. By comparison, both the linear and quadratic extrapolation-based estimates of race-specific mean risk imply that 79 percent (5.4 percentage points) of the average benchmarking disparity can be explained by disparate impact. We thus find that unobservable differences in defendant risk can explain 21 to 38 percent (1.4 to 2.6 percentage points) of the average disparity that remains after adjusting for court-by-time fixed effects.
We also find that IVB has a meaningful role in observational comparisons that adjust for non-race characteristics. Panels B and C of Appendix Table A8 show that adjusting the estimated release rates and released misconduct rates by the defendant and case characteristics in column 3 of Table 2 leads to smaller disparate impact estimates.20 With the local linear extrapolation, for example, the average disparate impact estimate shrinks by 17 percent (0.7 percentage points, out of 4.2 percentage points) compared to our baseline specification in Table 3. The reduction in the disparate impact estimate suggests that some of the findings in Table 3 are mediated by these defendant or case observables. As discussed above, our rescaling approach avoids such IVB concerns by conditioning on pretrial misconduct potential itself, rather than conditioning on these types of non-race characteristics.
Figure 3 plots the full posterior distribution of judge-level disparate impact, paralleling Figure 1, again using the most conservative local linear estimates of mean risk and returning to the baseline court-by-time fixed effect adjustment. For comparison, we also include the posterior distribution of observed racial disparities from our benchmarking model that adjusts only for the court-by-time fixed effects. The former distribution is shifted evenly to the left of the latter distribution, consistent with nontrivial OVB across the judge-specific estimates. Around 62 percent of the judge-weighted average benchmarking disparity (4.2 percentage points, out of 6.6 percentage points) is found to be due to disparate impact in release decisions, the same as the case-weighted decomposition from Panel B of Table 3. The standard deviation of judge-specific disparate impact estimates remains large, at 3.7 percentage points, though it shrinks somewhat from the 4.0 percentage point standard deviation of observed release rate disparities. The clear majority of NYC judges have positive Δj, at 87.3 percent, though this share is also smaller than the 95.9 percent predicted by the benchmarking model. Panel C of Table 3 shows that these statistics are similar across different mean risk estimates.
Figure 3:
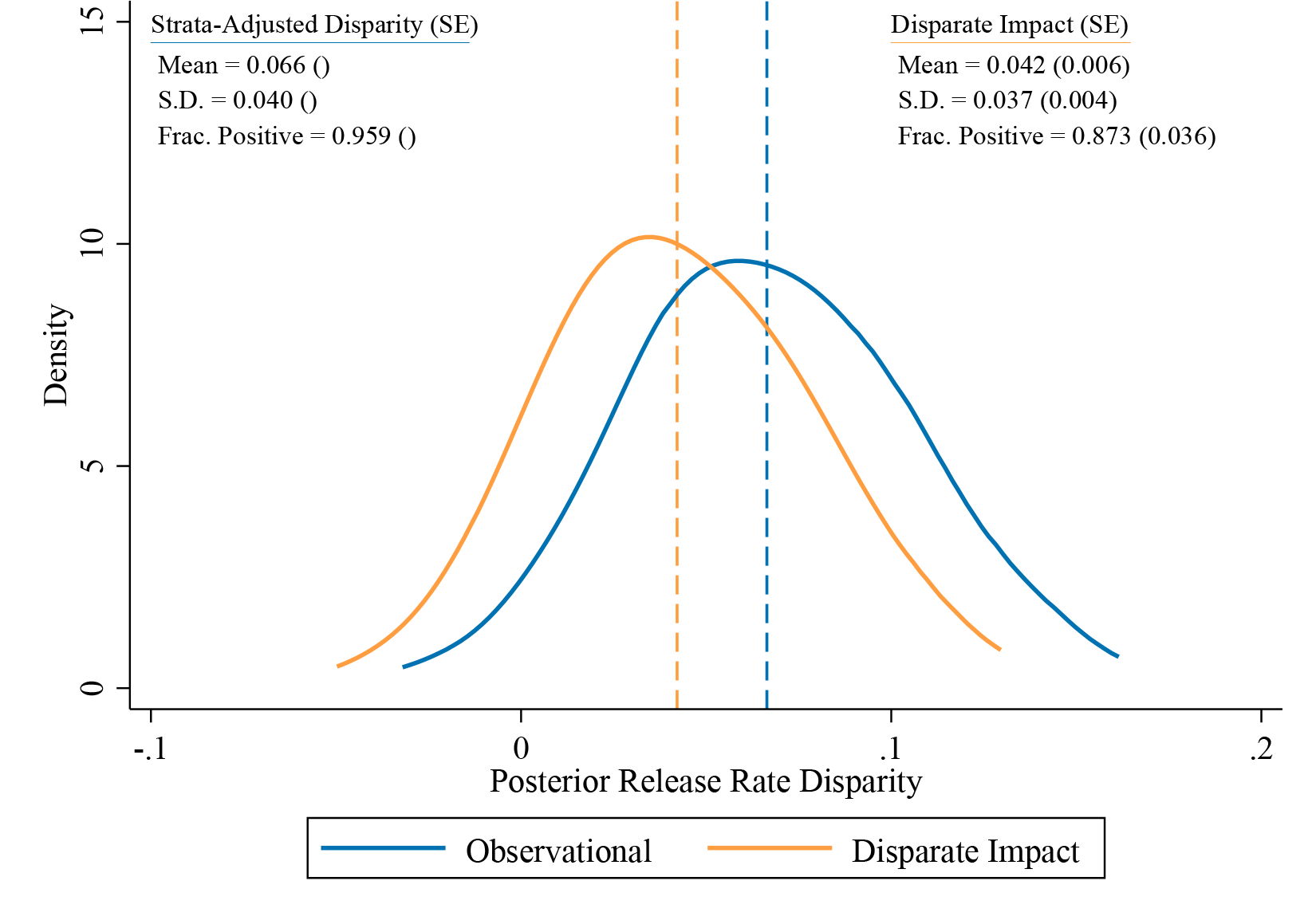
Observational Disparities and Disparate Impact Estimates
Notes. This figure plots the posterior distribution of observational disparities and disparate impact estimates for the 268 judges in our sample. Strata-adjusted disparities are estimated by the coefficients of an OLS regression of an indicator for pretrial release on white×judge fixed effects, controlling for judge main effects and court-by-time fixed effects. Disparate impact is estimated as described in Section 5, using the local linear extrapolations from Figure 2 to estimate the mean risk of each race. The distribution of judge disparities and disparate impact estimates, and fractions of positive disparities and disparate impact estimates, are computed from these estimates as posterior average effects; see Appendix B.3 for details. Means and standard deviations refer to the estimated prior distribution.
We explore patterns in this heterogeneity by regressing the judge-level disparate impact estimates on judge observables. Specifically, in columns 1–5 of Appendix Table A9 we regress the Δj estimates on indicators for whether a judge is newly appointed during our sample period, exhibits above-average leniency, or has an above-median share of Black defendants (as measured before the adjustment for court-by-time fixed effects, which makes Black defendant shares balanced across judges). We weight all regressions by estimates of the inverse variance of the disparate impact estimates, with similar results obtained from weighting by judge caseload. We find significantly lower levels of disparate impact among newly appointed judges, more lenient judges, and judges with a higher share of Black defendants. We also find that judges who primarily see cases in the Manhattan, Queens, and Richmond county courtrooms tend to exhibit higher levels of disparate impact, while those who primarily see cases in Brooklyn (the omitted category) and the Bronx have lower levels of disparate impact. Columns 6–7 of Appendix Table A9 further investigate the persistence of our disparate impact measure over time by computing separate Δj estimates in the first and second half of cases that each judge sees in our sample period, recomputing the race-specific mean risk estimates in each half, and estimating OLS regressions of current disparate impact estimates on lagged disparate impact posteriors and judge observables. We compute posteriors via a conventional empirical Bayes “shrinkage” procedure, detailed in Appendix B.3, and again weight by estimates of the inverse variance of the disparate impact estimates. We find that the judge-specific disparate impact estimates are highly correlated over time, with an autoregressive coefficient of 0.86. Lagged disparate impact alone explain about 29 percent of the variation in current disparate impact, with the lagged disparity and observable judge characteristics explaining about 43 percent.21
We further explore heterogeneity in the disparate impact estimates across defendants, using a conditional version of our baseline local linear approach that restricts to defendants with a particular criminal record or charge. For this more fine-grained analysis we restrict attention to judges who see at least 25 cases involving defendants with the indicated criminal record or charge in each specification. Appendix Table A10 shows we find disparate impact against Black defendants in each subgroup, with point estimates for the extent of disparate impact ranging from 1.0 percentage points for defendants charged with a property offense and 2.4 percentage points for defendants charged with a DUI and defendants without a prior criminal charge, to 3.0 percentage points for defendants charged with a felony, 4.6 percentage points for defendants charged with a misdemeanor, 5.5 percentage points for defendants charged with a drug offense, and 10.7 percentage points for defendants charged with a violent offense. The estimates are generally precisely estimated, with the exception of felony offenses and violent offenses where we obtain noisy estimates of the mean risk inputs.
Overall, our estimates show that there are both statistically and economically significant disparities in the release rates of Black and white defendants with identical potential for pretrial misconduct. The most conservative estimate in Table 3, for example, implies that the disparate impact in release rates could be closed if NYC judges released roughly 2,609 more Black defendants each year (or detained roughly 2,609 more white defendants). Using an estimate from Dobbie, Goldin and Yang (2018), releasing this many defendants would lead to around $78 million in recouped earnings and government benefits annually. We can also compare the average disparate impact in release rates to other observed determinants of pretrial release. Table 2 shows, for example, that the most conservative 4.2 percentage point disparate impact estimate corresponds to more than half of the decreased probability in release associated with having an additional pretrial arrest in the past year (−6.8 percentage points).
5.3. Robustness and Extensions
We verify the robustness of our main results to several deviations from the baseline specification, exploring alternative estimates of mean risk, weighting schemes, adjustments for court-by-time strata, definitions of pretrial misconduct, classifications of pretrial release, and definitions of defendant race.
Mean Risk Estimates:
Figure 4 examines the sensitivity of our main results to different values of the mean misconduct risk inputs, showing that our finding of pervasive disparate impact does not depend on any particular extrapolation of the released misconduct rates in Figure 2. We first compute the range of possible mean risk parameters given the observed misconduct and release rates in the sample. Since , a lower bound on is given by race r’s unconditional average misconduct rate . Similarly, an upper bound on is given by . Plugging the rates from Table 1 into these formulas, we obtain white and Black mean risk bounds of μw ∈ [0.204, 0.437] and μb ∈ [0.231, 0.536]. We then plot in Figure 4 the range of system-wide disparate impact obtained from different pairs of white and Black mean risk in these bounds.
Figure 4:
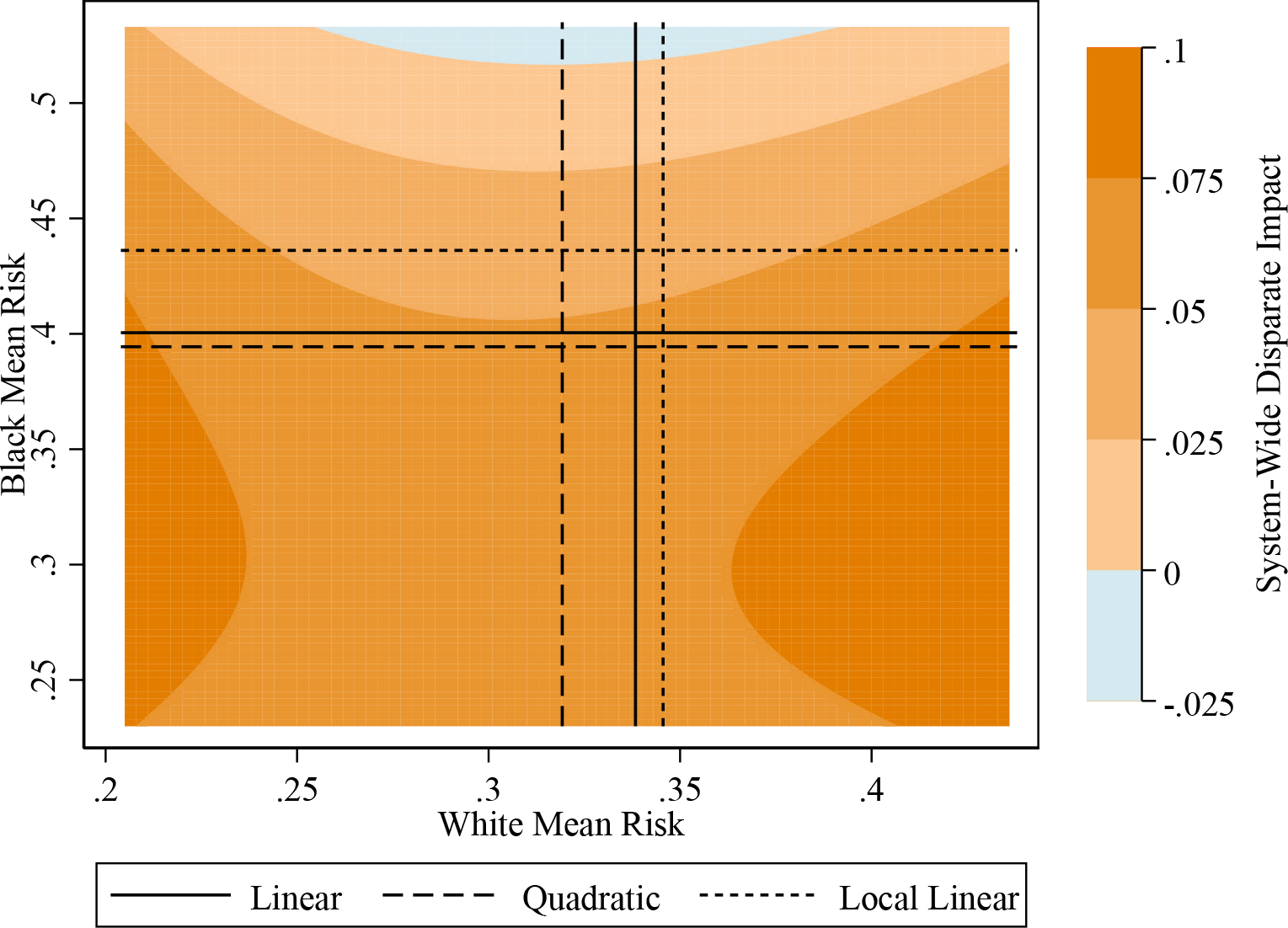
Sensitivity Analysis
Notes. This figure shows how our estimate of system-wide disparate impact changes under different estimates of white and Black mean risk. The mean risk estimates obtained from the linear, quadratic, and local linear extrapolations in Figure 2 are indicated by solid, dashed, and dotted lines. The ranges of white and Black mean risk reflect the bounds implied by average misconduct and release rates.
The estimated level of disparate impact against Black defendants generally decreases as the assumed value of Black misconduct risk increases, holding fixed the assumed value of white misconduct risk. Racial differences in misconduct risk would have to be extremely large, however, before we could conclude there is no average disparate impact. For example, at our baseline white mean risk estimate of 0.346 (indicated by the dotted vertical line), Black misconduct risk would need to be 0.516 for system-wide disparate impact to be zero. This is near the upper bound of Black misconduct risk computed above, and it would imply a Black-white misconduct risk gap of 17 percentage points—nearly twice the size of our most conservative estimate (9 percentage points).
Tighter bounds on the mean risk parameters, and thus on disparate impact, can be obtained from the misconduct and release rates of judges with above-average leniency. Panel A of Appendix Table A11 reports mean risk bounds from calculations similar to the full-sample formulas, which again exploit the fact that is binary (see Appendix B.5 for details). Panels B and C report corresponding bounds on the disparate impact statistics in Table 3 by finding the pair of mean risk estimates which minimize and maximize each statistic in these ranges. The bounds on each statistic narrow as a higher release rate is used, since a narrower range of mean risk parameters are consistent with less selected released misconduct rates. For example, moving from a release rate of 0.80 to a release rate of 0.90 brings the possible range of system-wide disparate impact from [0.02, 0.09] to [0.04, 0.07] by halving the length of both mean risk bounds.
Weighting Schemes:
Our baseline measure of disparate impact averages the conditional release rate disparities Δj0 and Δj1 by the average misconduct rate in the population. This weighting scheme makes Δj capture judge j’s expected level of disparate impact in a pool of defendants where pretrial misconduct potential is unknown. However, we show in Appendix Table A12 that our finding of system-wide disparate impact is not sensitive to the choice of weighting scheme. The average Δj0 and Δj1 estimates across judges are both positive in each of our three mean risk extrapolations, implying any convex average of these conditional release rate disparities will be positive. While imprecise, these estimates suggest judges set higher release rates for white defendants than Black defendants in both the and subpopulations.
Strata Adjustment:
Our baseline analysis uses linear regression to adjust for the court-by-time fixed effects that control for the level of quasi-experimental judge assignment. Regression adjustment is tractable given the large number of strata, but may lead to biased disparate impact estimates when the effects of court or time are heterogeneous across judges or defendant race. In Appendix Table A13, we relax the restriction of homogeneity across courts by estimating versions of Equations (11) and (18) separately for each NYC borough (while still adjusting linearly for time and arraignment part effects within boroughs). We then use these separate release and released misconduct rate estimates to separately estimate mean risk and disparate impact by borough and average the resulting estimates by borough case share. We omit Richmond in this calculation since only a small number of judges serve in this borough. We obtain similar (though less precise) estimates of all the disparate impact statistics from this stratified estimation procedure, suggesting minimal bias is introduced by the baseline linear adjustment.
Similarly relaxing the homogeneity restriction across time is challenging because of the large number of time effects. We instead explore sensitivity to this restriction in Appendix Table A14 by interacting flexible parameterizations of time with judge and race indicators and adding these interactions to the borough-stratified versions of Equations (11) and (18). For example, columns 1 and 2 add a linear and quadratic function of year-month time interacted with the judge effects, respectively, while column 3 adds separate linear interactions of year and month with the judge effects. Columns 4–6 include additional interactions of all the same functions of time with race.22 We estimate similar levels of system-wide disparate impact across all specifications, though the standard errors increase due to the large number of added interactions—to the point where we cannot reject the null hypothesis of no disparate impact in these robustness checks. Still, the similarity in point estimates suggest the baseline linear adjustment of court-by-time effects introduces minimal bias to our mean risk and disparate impact estimates.
Misconduct Outcome:
Our baseline measure of disparate impact assumes that the sole legal objective of bail judges is to target pretrial misconduct, and not other objectives or outcomes. When the legal objective of judges is misspecified, our estimates may suffer from what Kleinberg et al. (2018) refer to as “omitted payoff bias.” Such bias may arise when, for example, bail judges consider new crime to be more important than a failure to appear, or if they only target new violent crime. We explore the empirical relevance of omitted payoff bias in Appendix Table A15, which presents estimates given these different definitions of the judge’s legal objective. We find similar results when using a measure of pretrial misconduct that only includes FTA (column 2 of Appendix Table A15) or only includes new arrests (column 3 of Appendix Table A15). We also find a slightly higher case-weighted average of disparate impact, at 6.8 percentage points, when using a measure of pretrial misconduct that only includes new arrests for a violent crime (column 4 of Appendix Table A15). These results are consistent with Kleinberg et al. (2018) and Arnold, Dobbie and Yang (2018), who find similar evidence of prediction errors and racial bias in bail decisions, respectively, using different measures of the pretrial misconduct outcome.
A related concern is that measurement error in the judge’s legal objective is systematically correlated with race. This could be an issue if, for example, judges seek to minimize all new crime, not just new crime that results in an arrest, and if the police are more likely to rearrest Black defendants conditional on having committed a new crime. Gelman, Fagan and Kiss (2007), for example, find that the NYC Stop, Question, and Frisk program disproportionately targeted minority residents. With discriminatory policing, we will tend to overestimate the misconduct risk for Black defendants compared to white defendants and underestimate the total amount of disparate impact in bail decisions. It is therefore possible that our estimates reflect a lower bound on the true amount of disparate impact in NYC, at least under the plausible assumption that the police are more likely to rearrest Black defendants conditional on having committed a new crime. Reassuringly, column 2 of Appendix Table A15 shows a similar level of disparate impact when we measure pretrial misconduct using just FTA, which is less subject to this measurement concern.
Release Decision:
Our baseline specification abstracts away from the fact that bail judges may set different levels of monetary bail, taking into account a defendant’s ability to pay, by specifying the judge’s decision as a binary release indicator. One possibility is that the disparate impact we find is partly driven by judges over-predicting the relative ability of Black defendants to pay cash bail, causing fewer Black defendants to be released than white defendants of identical misconduct risk. We explore racial differences in the ability to pay cash bail in Appendix Table A16, which replaces our baseline definition of the judge’s release decision with an indicator for the judge releasing a defendant on recognizance, without setting cash bail. We find very similar results with this new specification, with disparate impact explaining about 55 percent (3.2 percentage points) of the court-by-time adjusted white-Black ROR rate difference of 5.8 percentage points. These results suggest that the disparate impact we find in bail decisions is not driven by judges over-predicting the relative ability of Black defendants to pay cash bail, which is consistent with the fact that the vast majority of released white and Black defendants are released on recognizance (see Table 1).
Defendant Race:
Our baseline results categorize defendants as either white (including both non-Hispanic and Hispanic white individuals) or Black (including both non-Hispanic and Hispanic Black individuals), but judges may also discriminate against Hispanic white defendants. We explore this possibility in Appendix Table A17, which presents estimates with defendants categorized as either non-Hispanic white or any racial minority (including Hispanic white individuals and both non-Hispanic and Hispanic Black individuals). Under this alternative categorization, we find larger estimates of case-weighted average disparate impact, for example, 11.2 percentage points for the local linear extrapolation in column 3.
Taken together, the results from this section robustly show that there is substantial disparate impact in NYC bail decisions, both on average and for most defendants and judges, and that judge-specific estimates of disparate impact are both predicted by observable characteristics and correlated over time. However, these results do not speak to whether such disparate impact is driven by racial bias or statistical discrimination, nor whether we can reliably target and potentially reduce disparate impact using existing data. We next develop a framework to answer these questions.
6. Model Estimates of Bias and Statistical Discrimination
6.1. Judge Decisions and MTE Frontiers
We quantify the drivers of disparate impact in NYC bail decisions by fitting a hierarchical marginal treatment effect (MTE) model to the quasi-experimental variation in judge release rates and released misconduct rates. The model allows us to decompose disparate impact into components associated with racial bias and statistical discrimination, two drivers of discrimination that have historically been the focus of the economics literature. The model also allows us to conduct policy counterfactuals in which disparate impact is minimized or eliminated. We first develop a model of individual judge release decisions and show how it equivalently parameterizes a set of judge- and race-specific MTE frontiers, features of which capture racial bias and statistical discrimination. We then develop and apply a simulated minimum distance (SMD) estimator to recover these features from the distribution of quasi-experimental estimates in Figure 2.
Our model of judge decisions follows Aigner and Cain (1977) in assuming each judge j observes a noisy signal of pretrial misconduct potential , with conditionally normally distributed noise: . We allow the “quality” (i.e., precision) of risk signals τjr = 1/σjr to vary both by defendant race r and by the identity of the judge j. Judges with higher τjr can be thought of as being more skilled at inferring pretrial misconduct potential, either by having a richer information set or by being more adept at inferring true misconduct potential from a common information set. We assume judges form accurate posterior risk predictions pj(νij, Ri) from the signal and the defendant’s race, satisfying . Finally, we assume each judge has a subjective benefit of releasing individuals of race r, given by πjr ∈ (0, 1). Judges release all defendants whose benefit exceeds the posterior risk cost, yielding potential release decisions:
| (20) |
Appendix B.6 derives the specific form of the posterior function pj(·), and shows how equivalent models are obtained when judges have inaccurate risk beliefs (instead of accurate pj(νij, Ri)) or minimize race-specific costs of misconduct classification errors (instead of having explicit πjr thresholds).
Racial bias in the sense of Becker (1957) arises when a judge perceives a different benefit from releasing Black defendants than white defendants with the same risk posterior, so that πjb < πjw. By applying different thresholds to posterior risk, the judge generally makes different decisions for white and Black defendants with the same misconduct potential , thereby leading to disparate impact against the group with the lower benefit from release.23 Inaccurate racial stereotyping can similarly result in disparate impact and tends to be observationally equivalent to such racial animus (Arnold, Dobbie and Yang, 2018; Hull, 2021). Inaccurate beliefs on the riskiness of white or Black defendants can lead judges to effectively set different release standards by race despite intending to apply the same threshold (Bohren et al., 2020).
Statistical discrimination in the sense of Aigner and Cain (1977) arises when judges set race-neutral thresholds on accurate race-specific risk predictions, but discriminate because the risk predictions are affected by racial differences in either the average misconduct risk μr or signal quality τjr. Differences in average misconduct risk will tend to lead to lower release rates for defendants in the group with higher average misconduct risk, thereby resulting in disparate impact against that group.24 Statistical discrimination due to differences in signal quality has an ambiguous effect on disparate impact. If, for example, a judge’s release threshold πjr is higher than the average level of misconduct risk in the population μr for each race r then noisier risk signals will lead to fewer defendants of that race being detained given true misconduct potential, as judges place more weight on the mean risk μr which falls below the threshold.
Importantly, our model allows both racial bias and statistical discrimination to arise indirectly from non-race characteristics like criminal history or crime type—as with disparate impact itself. A judge may, for example, indirectly set race-specific thresholds by penalizing defendants charged with certain crimes (such as the possession of crack versus powdered cocaine) that are correlated with defendant race but do not predict pretrial misconduct potential.25 Similarly, signal quality differences may reflect innate differences in the predictiveness of non-race characteristics or indirect differences in how a judge weighs equally predictive characteristics. Our model does not parameterize such relationships between non-race characteristics and effective judge risk thresholds or signal quality, but it allows them to drive our findings and policy counterfactuals.
To bring this model to data, we first reframe it in terms of familiar econometric objects. Note that we can equivalently write Equation (20) as with conditionally uniformly distributed Uij | Ri by applying a conditional probability integral transform to the judge’s posteriors pj(νij, Ri). This reformulation defines a conditional MTE frontier of:
| (21) |
Here μjr(t) gives the effect of release on pretrial misconduct for race-r defendants who judge j perceives to be at the (t×100)th percentile of risk. In this MTE representation, Πjr = E[Dij | Ri = r] parameterizes the race-r release rate of judge j and is the corresponding released misconduct rate.
Racial differences in a judge’s MTE curves, evaluated at her release thresholds Πjr, yield a marginal outcome test for racial bias in her release decisions (Arnold, Dobbie and Yang, 2018; Hull, 2021). This follows from the fact that misconduct effects at the margin of release capture a judge’s race-specific release benefits:
| (22) |
using the law of iterated expectations in the second equality and the fact that in the third equality. The race-specific MTEs, μjr(Πjr), should therefore be equal when the judge is racially unbiased (πjw = πjb), but marginal white defendants should have higher misconduct outcomes if the judge is racially biased against Black defendants (πjw > πjb).
This framework makes clear that outcome-based tests of racial bias can detect only one potential driver of disparate impact, and thus cannot be used to rule out all potential violations of anti-discrimination law. A judge who “passes” a marginal outcome test, with πjw = πjb, may still have Δj > 0 because of statistical discrimination, and the level of such disparate impact is generally not knowable from πjw and πjb. Once Δj is established, however, a finding of πjw ≠ πjb rejects accurate statistical discrimination as the sole reason for disparate impact.
The framework also shows how the judge- and race-specific MTE frontiers, if known, could be used to quantify statistical discrimination. The mean risk of each race r is given by integrating the MTE frontier of any judge: . The slopes of these curves furthermore capture the quality of a judge’s risk signals: a judge with τjw > τjb will, for example, have a steeper-sloping μjw(·) than μjb(·) as we illustrate below. More generally, the judge- and race-specific MTE frontiers can be used to calculate the extent of disparate impact in counterfactual calculations where a judge’s release rate Πjr is set to eliminate racial bias by equalizing the marginal released outcomes.
In using this framework to quantify racial bias and statistical discrimination in NYC, however, we face a fundamental underidentification challenge. The parameterization of judge skill and preferences in the model is very flexible, to the point where the equivalent MTE frontiers are not uniquely recoverable from the quasi-experimental variation in judge release rates and released misconduct rates absent further restrictions. The flexibility of the model is formalized in Appendix B.7, which shows there exist judge- and race-specific parameters fitting any pair of conditional-on- release rates satisfying . This result implies the judge-level model can be imposed without loss on the race-specific decision rule of any judge whose decisions are better-than-random. However, with unobserved, this model cannot be fit directly; the observable quasi-experimental variation in release rates and released misconduct rates only reveals a single point on each judge-by-race MTE frontier, not the frontier itself. Formally, the underidentification challenge can be seen from the fact that with J judges there are 1+2J race-specific model parameters (mean risk μr and the J pairs of skill and preference parameters τjr and πjr) and only 2J race-specific moments (the J pairs of release rates and released misconduct rates). At least one additional restriction is needed to satisfy the order condition for identification.
We consider two approaches to overcoming the underidentification challenge. First, following Arnold, Dobbie and Yang (2018), we consider restricting the race-specific MTE curves to be common across judges by assuming uniformity of judge skill within race, i.e., τjr = τr for each j. This restriction amounts to an assumption of first-stage monotonicity when viewing the as-good-as-randomly assigned bail judges as instruments for pretrial release.26 While tractable, this restriction is potentially strong in our setting as it implies the observed variation in judge release rates only reflects differences in risk thresholds πjr. An implication of the restriction is that, absent estimation error, the race-specific release rates and released misconduct rates plotted in Figure 2 will lie on a single curve determined by the common MTE frontier. Given the relatively large sample size in NYC, the sizable dispersion in released misconduct rates among judges with similar release rates suggests this restriction fails.
Our second, preferred approach avoids the potentially strong assumption of uniform judge skill by instead modeling the heterogeneity in signal quality, and thus the distribution of MTE curves, across judges. This approach leads to a hierarchical MTE model, the higher-level parameters of which quantify the drivers of system-wide disparate impact in terms of racial bias and statistical discrimination. We next develop this estimation procedure.
6.2. SMD Estimator
Our hierarchical MTE model parameterizes the distribution of signal quality τjr and release benefits πjr across judges, separately by race. The parameterization uses the fact, proved in Appendix B.6, that each judge’s posterior function pj(ν, r) is strictly increasing in the risk signal ν and is therefore invertible for each race. Applying this fact shows that judge decisions follow a probit model conditional on defendant race and misconduct potential:
| (23) |
where is a normalized signal threshold and . We model κjr and ln τjr as being joint-normally distributed, independently across judges conditional on race, with the log-normality of τjr imposing the constraint of positive signal precision. This yields a higher-level parameter vector Θ containing the mean risk parameters μr and the means and variances/covariances of (κjr, ln τjr) across judges for each race r. Appendix B.7 shows how this hierarchical approach can be viewed as parameterizing differences in how judges weigh different defendant characteristics, such as demeanor or prior arrest record.
Figure 5 builds intuition for this parameterization by showing how different values of the higher-level parameters in Θ manifest in the estimable reduced-form moments. We construct this figure by first simulating draws of ln τjr for a given race r across a large population of judges j with widely varying κjr, for some choice of mean risk μr, average log signal quality ln τjr, variance of ln τjr, and correlation of ln τjr and κjr. The wide variation in signal thresholds leads to a wide variation in model-implied judge release rates E[Dij | Ri = r], while the choice of the other higher-level parameters change the distribution of model-implied released misconduct rates . We plot this distribution as in Figure 2, abstracting away from moment estimation error. Panels A and B set the variance of signal quality across judges to zero, satisfying the uniformity (or first-stage monotonicity) restriction and ensuring that the judge moments fall on a common frontier. Panels C and D then relax monotonicity by allowing signal quality to vary across judges.
Figure 5:
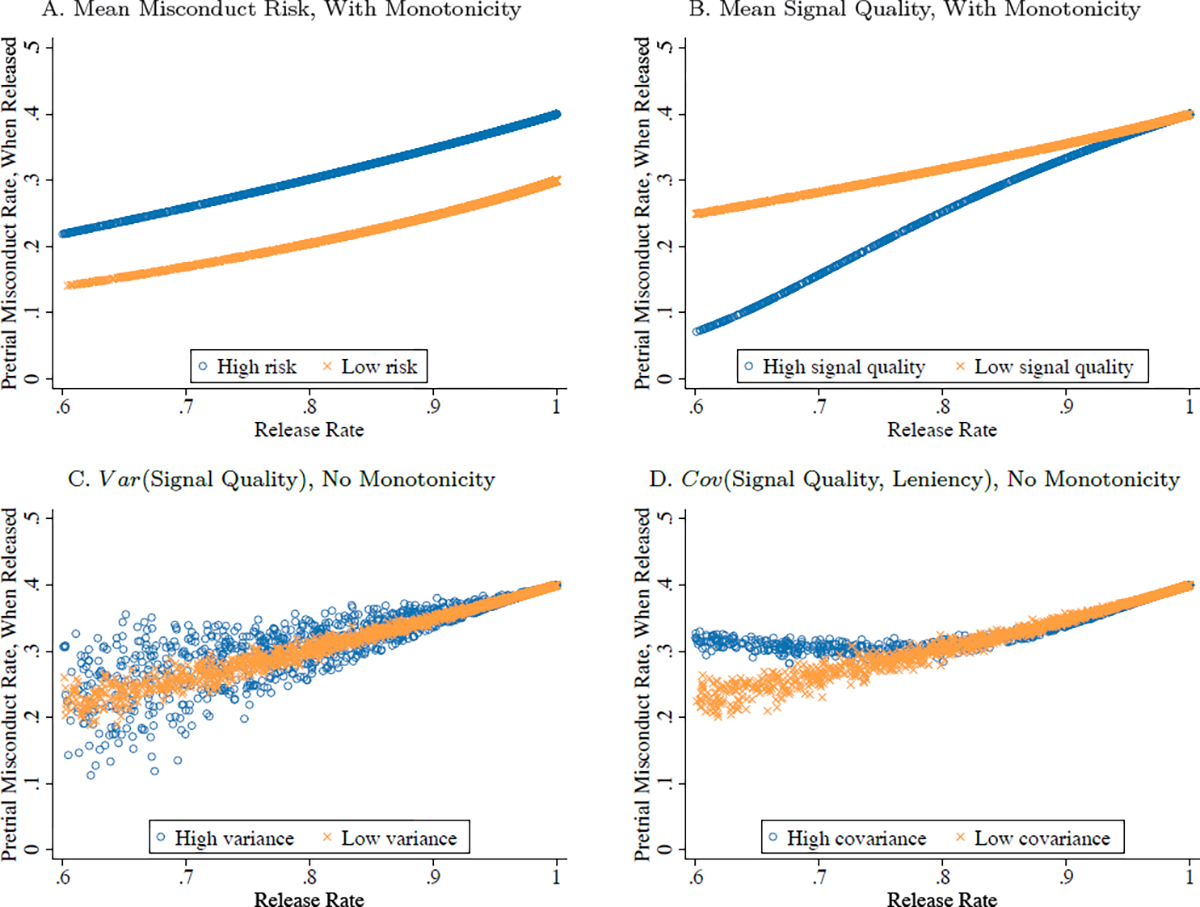
Identification of Hierarchical MTE Model Parameters
Notes. This figure plots simulated race- and judge-specific release rates against rates of pretrial misconduct among the set of released defendants under different parameterizations of the hierarchical MTE model described in the text. Panel A plots differences in mean misconduct risk (μ = 0.4 vs. μ = 0.3) when conventional MTE monotonicity holds (ψ = 0). Panel B plots differences in mean signal quality (α = 1 vs. α = 0) when conventional MTE monotonicity holds (ψ = 0). Panel C plots differences in signal quality variance (ψ = 0.4 vs. ψ = 0.1). Panel D plots differences in the covariance between judge signal quality and judge leniency (β = 2 vs. β = 0.1). The default parameterization is μ = 0.4, α = 0.2, ψ = 0.1, β = 0, γ = 1.3, and δ = 1.
Panel A of Figure 5 shows how differences in mean misconduct risk μr lead to differences in the vertical intercept of the model-implied moment curve at one, or (per the discussion in Section 5.1) the release rate of a hypothetical supremely lenient judge. These vertical intercepts correspond to model-based extrapolations of the quasi-experimental data, in contrast to the data-driven extrapolation used previously in Section 5. Panel B further shows how differences in mean signal quality lead to different slopes of the model-implied curves, with a higher mean ln τjr resulting in a steeper relationship between the share of defendants that a judge releases and the extent of pretrial misconduct among the released. When we relax first-stage monotonicity in Panels C and D, the quasi-experimental variation no longer falls on a common frontier (even without estimation error). Panel C shows that a higher variance in signal quality manifests as more dispersion in released misconduct rates among judges with similar release rates. Finally, Panel D shows that the trend in this distribution of points becomes more nonlinear when judge signal quality is more highly correlated with the signal thresholds.
We estimate the hierarchical MTE model by a minimum distance procedure based on this intuition. Specifically, we find the values of Θ which can best match key features of the distribution of model-implied release and released misconduct rates, simulated as in Figure 5, to the corresponding features of estimated release and released misconduct rates in Figure 2. Following the above intuition, the features we match are the race-specific mean and variance of judge release rates and the race-specific intercept, slope, curvature, and residual variation from quadratic regressions of judge released misconduct rates on judge release rates. Appendix B.8 details this SMD procedure, showing it is just-identified and deriving the necessary correction for estimation error in the Figure 2 estimates. Appendix B.8 further shows how SMD estimates of Θ can be combined with the Figure 2 estimates to form empirical Bayes predictions of individual judge κjr and ln τjr, following the approach of Angrist et al. (2017). These predictions in turn give individual judge measures of marginal released outcomes and signal quality for each defendant race, heterogeneity in which we explore below.
As with the model-free analysis of disparate impact in Section 5, our model-based analysis of racial bias and statistical discrimination requires adjustment for the court-by-time effects that ensure as-good-as-random judge assignment. The adjustment allows us to model differences in average judge decisions Dij as being due to judge preferences and skill, averaging over the court-by-time heterogeneity. We again adjust for court-by-time effects using linear regression, which is justified under the linearity assumption discussed in Section 5.27
6.3. Results
Table 4 reports SMD estimates of the race-specific moments we use to investigate racial bias and statistical discrimination in NYC bail decisions: namely, the mean misconduct risk μr and the first and second moments of marginal released outcomes μjr(Πjr) and signal quality τjr across judges. Underlying parameter estimates are reported in Appendix Table A18.28 Columns 1–3 of Table 4 impose a conventional monotonicity assumption by restricting judge signal quality to be constant among defendants of a given race: τjr = τr. Columns 4–6 relax this restriction, allowing judges to differ in their skill at ranking white and Black defendants by their appropriateness for pretrial release. Figure 6 illustrates the fit of this second preferred specification by plotting the model-implied average released misconduct rate across races and judges of different leniencies against the reduced-form estimates of release rates and released misconduct rates from Figure 2.
Table 4:
Hierarchical MTE Model Estimates
| With Monotonicity | Without Monotonicity | |||||
|---|---|---|---|---|---|---|
|
|
|
|||||
| White Defendants | Black Defendants | Diff. | White Defendants | Black Defendants | Diff. | |
|
|
|
|||||
| (1) | (2) | (3) | (4) | (5) | (6) | |
|
|
||||||
| Mean Misconduct Risk | 0.346 (0.008) | 0.423 (0.009) | −0.077 (0.012) | 0.391 (0.007) | 0.441 (0.007) | −0.050 (0.010) |
| Mean Marginal Released Outcome | 0.616 (0.057) | 0.511 (0.030) | 0.105 (0.061) | 0.651 (0.033) | 0.576 (0.021) | 0.074 (0.038) |
| Mean Signal Quality | 1.712 (0.219) | 0.963 (0.141) | 0.749 (0.271) | 1.385 (0.104) | 0.970 (0.073) | 0.416 (0.128) |
| Marginal Outcome Std. Dev. | 0.211 (0.029) | 0.094 (0.022) | 0.117 (0.037) | 0.080 (0.009) | 0.064 (0.005) | 0.016 (0.010) |
| Signal Quality Std. Dev. | 0.196 (0.038) | 0.163 (0.017) | 0.033 (0.041) | |||
| Covariance of Signal Quality and Marginal Released Outcomes | 0.013 (0.005) | 0.007 (0.002) | 0.006 (0.005) | |||
|
| ||||||
| Judges | 268 | 268 | – | 268 | 268 | – |
Notes. This table reports simulated minimum distance estimates of moments of the MTE model described in Section 6. See Table A18 for underlying hyperparameter estimates. Columns 4–6 estimate the baseline model, while columns 1–3 impose conventional monotonicity. Robust standard errors, two-way clustered at the individual and the judge level, are obtained by a bootstrapping procedure and appear in parentheses.
Figure 6:
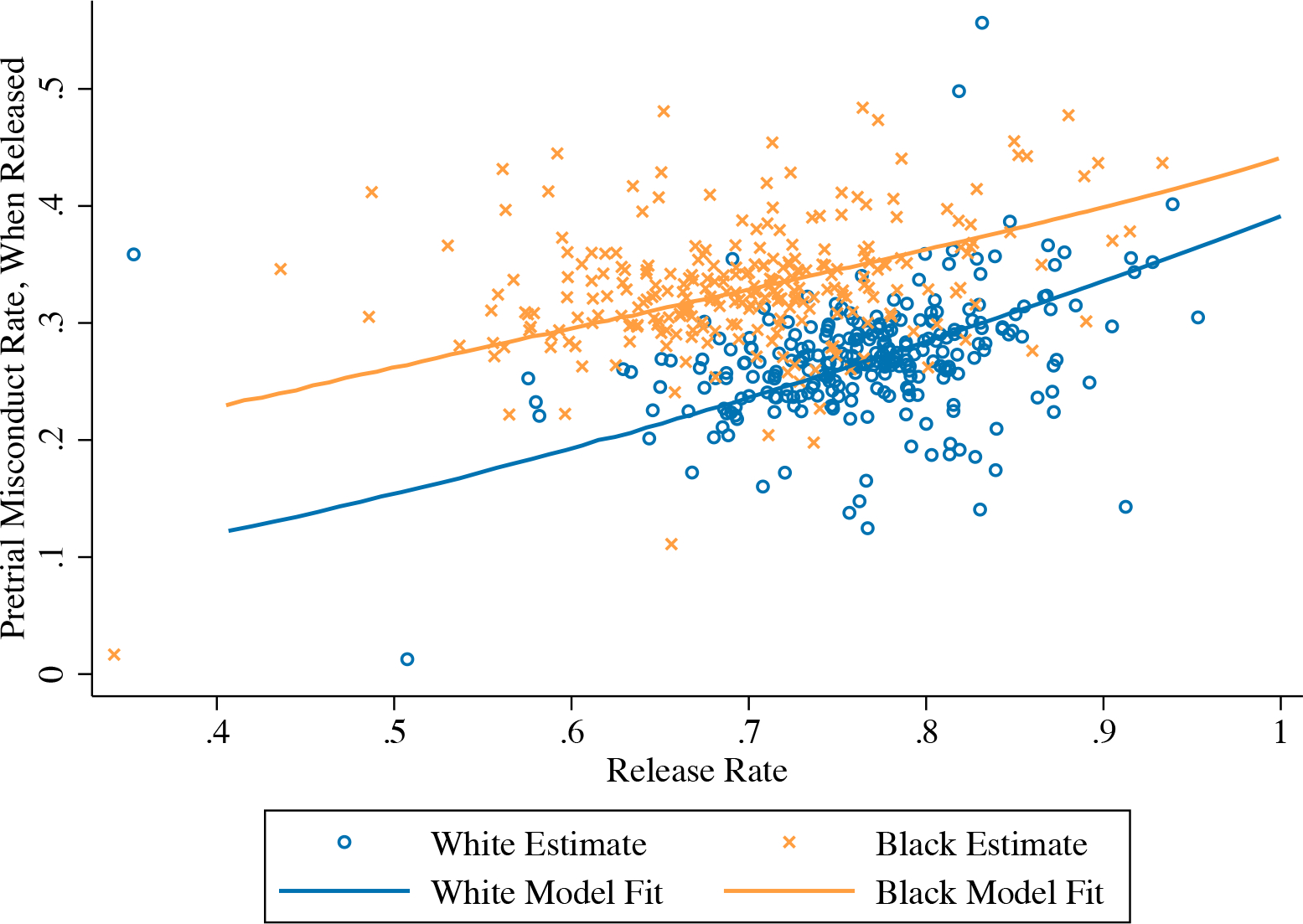
Hierarchical MTE Model Fit
Notes. This figure plots race-specific release rates for the 268 judges in our sample against rates of pretrial misconduct among the set of released defendants. All estimates adjust for court-by-time fixed effects. The figure also plots race-specific curves of best fit implied by our baseline hierarchical MTE model hyperparameter estimates.
In both sets of model estimates we find higher mean marginal released outcomes among white defendants, implying racial bias per the discussion in Section 6.1. This finding of bias is suggested by Figure 6, where judge release rates are concentrated around a section of the model-fit released misconduct rate curve that is steeper for white defendants than for Black defendants. Judges who choose to release defendants at rates where the misconduct rate gradient is relatively higher are interpreted by the model as receiving a relatively higher benefit for releasing these defendants. In Figure 6, judges appear equally willing to marginally increase white and Black release rates, even though white misconduct rates would increase by a larger amount. In the preferred specification this pattern translates to a higher estimate of mean misconduct risk among marginal white defendants of 0.651 (SE: 0.033) compared to 0.576 (SE: 0.021) among marginal Black defendants. The difference in these mean marginally released outcomes is a statistically significant 7.4 percentage points (SE: 3.8).
We also find higher mean risk and less precise risk signals for Black defendants, implying statistical discrimination per the discussion in Section 6.1. As illustrated in Panel A of Figure 5, mean risk differences manifest empirically as differences in the released misconduct rates of highly lenient judges. Figure 6 shows how the model extrapolates the generally higher released misconduct rates of Black defendants to a higher estimate of Black mean risk, as with the model-free extrapolations in Figure 2. In the preferred specification we find that Black defendants have a 5.0 percentage points higher mean misconduct risk than white defendants (SE: 1.0), similar to the 6.0 percentage point gap from our linear extrapolation in Table 3. As illustrated in Panel B of Figure 5, signal quality differences manifest empirically as overall slope differences in the relationship between released misconduct rates and release rates. Figure 6 shows how the model finds an overall steeper gradient for white defendants, as with the model-free lines-of-best-fit in Figure 2. In the preferred specification we find an average signal quality of 1.385 (SE: 0.104) for white defendants and 0.970 (SE: 0.073) for Black defendants, implying the typical noise in Black risk signals is around 30 percent more dispersed. These racial differences in mean risk and signal quality imply that outcome-based tests of racial bias (as in Arnold, Dobbie and Yang (2018)) miss two potentially important sources of disparate impact in this setting.
The SMD estimates further suggest that the first-stage monotonicity restriction is inconsistent with judge behavior in this setting. As illustrated in Panel C of Figure 5, monotonicity violations manifest empirically as variation in released misconduct rates across judges with similar release rates. Figure 6 shows sizable variation for both white and Black defendants, though unlike in Figure 5 some of this variation reflects estimation error. Columns 4 and 5 of Table 4 show that after accounting for estimation error our preferred specification interprets the variation in released misconduct rates as significant variation in judge signal quality, with standard deviations of 0.196 (SE: 0.038) for white defendant signal quality and 0.163 (SE: 0.017) for Black defendant signal quality.29 This variation in judge skill is highly correlated with variation in judge release preferences, with covariances between judge signal quality and marginal released outcomes of 0.013 for white defendants and 0.007 for Black defendants (implying respective correlation coefficients of 0.83 and 0.67). While point estimates of the mean parameters with and without conventional monotonicity are qualitatively similar, the precision is higher without. The standard error on average racial bias, for example, falls by 17 percent from column 3 to column 6. These precision gains also suggest that the model which allows variation in signal quality provides a better fit to the quasi-experimental data. At the same time, the similarity of the estimates in Table 4 suggests that imposing an invalid assumption of first-stage monotonicity in this setting does not qualitatively affect our other findings. This finding in turn suggests prior MTE-based tests of racial bias (as in Arnold, Dobbie and Yang (2018)) may be valid even though a conventional monotonicity assumption is a priori unlikely to hold.
Table 5 uses the preferred model estimates to quantify the joint role of racial bias and statistical discrimination in driving disparate impact in NYC bail decisions. Column 1 summarizes the baseline degree of disparate impact, racial bias, and differences in signal quality implied by the model estimates. We obtain these by simulating draws of the judge-level parameters (κjr, ln τjr) from the estimated distribution, computing discrimination and bias for each judge from these draws (see Appendix B.6 for exact formulas), and averaging across simulated judges. In column 2, we counterfactually raise or lower each simulated judge’s Black or white release rate to equalize marginal released outcomes and thus eliminate bias. In column 3, we instead counterfactually raise or lower each simulated judge’s Black or white signal quality. Column 4 combines these counterfactuals by eliminating both racial bias and differences in signal quality across white and Black defendants.
Table 5:
Disparate Impact Decompositions
| Baseline | No Racial Bias | Equal Signal Quality | Both | |
|---|---|---|---|---|
|
|
||||
| Panel A: Change Black Parameters | (1) | (2) | (3) | (4) |
|
|
||||
| Disparate Impact | 0.047 | −0.042 | 0.095 | 0.039 |
| Release Rates (W/B) | 0.768 / 0.703 | 0.768 / 0.795 | 0.768 / 0.652 | 0.768 / 0.709 |
| Racial Bias | 0.074 | 0.000 | 0.074 | 0.000 |
| Marginal Outcomes (W/B) | 0.650 / 0.577 | 0.650 / 0.650 | 0.650 / 0.577 | 0.650 / 0.650 |
| Signal Quality (W/B) | 1.386 / 0.970 | 1.386 / 0.970 | 1.386 / 1.386 | 1.386 / 1.386 |
| Panel B: Change White Parameters | ||||
| Disparate Impact | −0.006 | 0.136 | 0.062 | |
| Release Rates (W/B) | 0.716 / 0.703 | 0.853 / 0.703 | 0.781 / 0.703 | |
| Racial Bias | 0.000 | 0.074 | 0.000 | |
| Marginal Outcomes (W/B) | 0.577 / 0.577 | 0.650 / 0.577 | 0.577 / 0.577 | |
| Signal Quality (W/B) | 1.386 / 0.970 | 0.970 / 0.970 | 0.970 / 0.970 | |
|
| ||||
| Judges | 268 | 268 | 268 | 268 |
Notes. Column 1 of this table reports average disparate impact and racial bias across judges and 250 simulations of the hierarchical MTE model, along with average release rates, marginal released outcomes, and signal quality of Black and white defendants. Simulations are based on the estimates from columns 2 and 4 of Appendix Table A18. Column 2 recomputes the statistics for a counterfactual in which Black (Panel A) or white (Panel B) release rates are set to eliminate racial bias, while column 3 adjusts Black (Panel A) or white (Panel B) signal quality to equalize signal quality across race. Column 4 applies both counterfactuals simultaneously.
Both bias and statistical discrimination drive disparate impact, with the latter due both to the higher level of average risk (that exacerbates disparate impact) and less precise signals (that alleviates disparate impact) for Black defendants. The model-based estimate of average disparate impact in column 1, at 4.7 percentage points, is similar to our most conservative estimate in Table 3. Column 2 shows that average disparate impact significantly declines when judge leniency is counterfactually raised or lowered to eliminate bias: the system-wide measure falls from 4.7 percentage points to −4.2 percentage points in Panel A (where Black release rates are generally raised) and −0.6 percentage points in Panel B (where white release rates are generally lowered). This result shows that, absent racial bias, the average disparate impact is reversed, with white defendants becoming less likely to be released than Black defendants of identical misconduct potential. Columns 3 and 4 show that this reversal is driven by the relatively higher signal quality for white defendants: equalizing signal quality across races for each judge, with and without racial bias, again results in average disparate impact against Black defendants. Intuitively, the lower precision of risk signals for Black defendants means judges place relatively more weight on the mean risk level when forming Black posteriors. Because this mean level of risk falls below the threshold for release, lower signal quality acts as a force to increase Black release rates relative to white release rates. The remaining statistical discrimination in column 4, which solely due to mean risk differences, yields a mean disparate impact of 3.9 percentage points when Black release rates and signal quality are counterfactually set, and a mean disparate impact of 6.2 percentage points when adjusting the corresponding white parameters.
We conduct additional model-based analyses in Appendix Tables A20–A22 and Appendix Figure A3. First, we confirm in Appendix Table A20 and Appendix Figure A3 that our conclusions about the distribution and correlates of judge-level disparate impact continue to hold with the model-based estimates of mean risk. Second, we explore variation in judge-specific estimates of racial bias and signal quality differences in Appendix Tables A21–A22, following our analysis of the disparate impact estimates in Section 5.2 and using an empirical Bayes posterior calculation detailed in Appendix B.8. We find significantly lower levels of racial bias among newly appointed judges and less lenient judges, as well as lower signal quality among newly appointed judges. Variation in racial bias and signal quality are both strongly correlated with differences in overall disparate impact across judges.
6.4. Policy Simulations
Lastly, we use our hierarchical MTE model estimates to investigate whether disparate impact can be reliably targeted and potentially reduced with existing data. The model-free analysis in Section 5 shows that judge-specific disparate impact measures are relatively stable over time, suggesting that identifying and targeting judges with high measures for an appropriate intervention could help reduce future disparate impact. This analysis also shows that approximately one-third of the observed release rate disparity between white and Black defendants is explained by unobserved differences in misconduct risk, suggesting that observational regressions may also be useful for targeting judge-specific disparate impact even in the absence of our quasi-experimental analysis. By linking unobserved differences in misconduct risk, racial bias, and statistical discrimination in the release decisions of each judge, the model provides the necessary structure to simulate the effects of reducing disparate impact using existing observational and quasi-experimental data. Here we focus on the more general analytic question of whether disparate impact can be reliably targeted using existing data, abstracting away from the legal status of any particular policy reform.
Table 6 summarizes simulations that target both disparate impact posteriors (columns 2 and 3) and observational disparities (columns 4 and 5), relative to the status quo in column 1. The counterfactuals suppose that individual bail judges can be subjected to race-specific release rate quotas that eliminate racial disparities, as estimated by a policymaker using either an observational or quasi-experimental analysis. The simulation based on the disparate impact posteriors gauges the reliability of the individual predictions given the noise in our estimation procedure. The simulation based on observational disparities further tests whether conventional benchmarking regressions may be useful for targeting disparate impact despite OVB. To simulate both sets of policies, we redraw all judge-specific parameters for each race from the estimated hierarchical MTE model 250 times, along with draws of appropriate estimation error. We use these to simulate 250 draws of the quasi-experimental variation plotted in Figure 2. We then re-estimate the MTE model in each draw and compute empirical Bayes posteriors, as in our analysis of the true data. Finally, we force all or a subset of simulated judges to adjust their race-specific leniencies to the point where their racial disparities are expected to be eliminated given the simulated model estimates and posteriors. Panel A simulates closing the targeted disparities for all judges, while Panel B simulates closing the targeted disparities only for judges in the top quintile of the estimated disparities.
Table 6:
Policy Simulations
| Baseline | Target Disparate Impact Posteriors | Target Observational Disparity Posteriors | |||
|---|---|---|---|---|---|
|
|
|
||||
| Increase Leniency | Decrease Leniency | Increase Leniency | Decrease Leniency | ||
|
|
|
|
|||
| Panel A: Close All Disparities | (1) | (2) | (3) | (4) | (5) |
|
|
|||||
| Mean Disparate Impact | 0.047 [0.037] | 0.000 [0.020] | 0.000 [0.026] | −0.017 [0.020] | −0.019 [0.026] |
| Mean Observational Disparity | 0.065 [0.038] | 0.017 [0.020] | 0.019 [0.026] | 0.000 [0.019] | −0.000 [0.026] |
| Racial Bias | 0.074 [0.078] | 0.039 [0.068] | 0.013 [0.055] | 0.025 [0.070] | −0.011 [0.053] |
| Panel B: Close Top-Quintile Disparities | |||||
| Mean Disparate Impact | 0.030 [0.035] | 0.030 [0.037] | 0.026 [0.038] | 0.026 [0.041] | |
| Mean Observational Disparity | 0.047 [0.035] | 0.048 [0.037] | 0.044 [0.039] | 0.043 [0.040] | |
| Racial Bias | 0.062 [0.075] | 0.051 [0.076] | 0.059 [0.076] | 0.045 [0.080] | |
|
| |||||
| Observations | 268 | 268 | 268 | 268 | 268 |
Notes. This table reports the results from a series of policy simulations. Column 1 reports the mean disparate impact, observational disparity, and racial bias across judges and 250 simulations of the hierarchical MTE model. Average standard deviations across judges are included in brackets. Simulations are based on the estimates from columns 2 and 4 of Appendix Table A18. Column 2 of Panel A recomputes the statistics for a counterfactual in which the lower of the Black or white release rate of each judge is raised to equalize disparate impact posteriors, while column 3 of Panel A does the same by lowering one of the two release rates. Columns 4 and 5 of Panel A instead adjust release rates to equalize observational disparity posteriors. Panel B conducts the counterfactual exercises only on judges ranked in the top quintile of disparate impact estimates (columns 2 and 3) or observational (columns 4 and 5) disparity posteriors. Estimates of the model hyperparameters and empirical Bayes posteriors of all judge-specific parameters are recomputed in each simulation draw via the SMD procedure outlined in the text, using moments simulated according to the estimated distribution of reduced-form estimates in Figure 2.
The simulations suggest that disparate impact can be reliably targeted using our posteriors, despite estimation error. Targeting the disparities of all judges using our posteriors results in the virtual elimination of disparate impact (columns 2 and 3 of Table 6, Panel A), while only targeting judges in the top quintile results in a 36 percent reduction in the average level of disparate impact (columns 2 and 3 of Panel B). These simulated reductions are essentially unchanged when the targeted judges are forced to increase their leniency (typically for Black defendants) in column 2 or decrease their leniency (typically for white defendants) in column 3. The average standard deviation of disparate impact across judges, reported in brackets, is also reduced from around 3.7 percentage points to 2.0 percentage points in column 2 and 2.6 percentage points in column 3. Observational release rate disparities still remain when eliminating disparate impact, however, as the higher level of mean risk for Black defendants leads to OVB in the policy target.
Targeting judges with observational disparities can also reduce discrimination, as they are highly correlated with the disparate impact posteriors. Appendix Figure A4 shows, for example, that we obtain a coefficient close to one (0.903, SE: 0.010) from regressing estimated judge-specific disparate impact posteriors on observational disparity posteriors. Consequently, we find in Table 6 that targeting all judges with simulated observational disparity posteriors reduces average disparate impact by 6.4 percentage points in column 4 and 6.6 percentage points in column 5. The resulting average disparate impact of −1.7 and −1.9 percentage points reflects the fact that the level of observed disparities is too high on average because of OVB. When targeting just the observational disparity posteriors in the top quintile of judges, average disparate impact is reduced by 45 percent but not reversed (columns 4 and 5 of Panel B). This finding, that observational benchmarking regressions can be useful for monitoring and targeting disparate impact despite OVB, mirrors a result in the education and healthcare setting on the utility of biased observational measures of school and hospital quality (e.g., Angrist et al., 2017; Hull, 2020). There, as here, observational rankings prove to be highly predictive of policy-relevant parameters despite non-zero OVB.30
7. Conclusion
Large racial disparities exist at every stage of the criminal justice system, but it is unclear whether these disparities reflect racial bias, statistical discrimination, or omitted variables bias. This paper shows that disparate impact in bail decisions can be measured, regardless of its source, using observational comparisons of white and Black release rates that are rescaled with quasi-experimental estimates of average white and Black misconduct risk. Our most conservative estimates from NYC show that approximately two-thirds of the observed racial disparity in release decisions is due to disparate impact, with around one-third due to unobserved racial differences in misconduct risk. Using a novel hierarchical MTE model, we show that this disparate impact is driven by both racial bias and statistical discrimination, with the latter due to a higher level of average risk (that exacerbates disparate impact) and less precise risk signals (that offsets disparate impact) for Black defendants. Outcome-based tests of racial bias therefore omit an important source of disparate impact in NYC bail decisions, and cannot be used to rule out all possible violations of U.S. anti-discrimination law.
We conclude by noting that the methods we develop to study disparate impact in bail decisions may prove useful for measuring racial disparities in several other high-stakes settings, both within and outside of the criminal justice system. One key requirement is the quasi-random assignment of decision-makers, such as judges, police officers, employers, government benefits examiners, loan officers, or medical providers. A second requirement is that the objective of these decision-makers is both known and well-measured among the subset of individuals that the decision-maker endogenously selects. Mapping these settings to the quasi-experimental methods in this paper can help distinguish between different explanations for observed racial disparities and form appropriate policy responses.
Supplementary Material
Acknowledgments
We thank Josh Angrist, Tim Armstrong, Leah Boustan, Sydnee Caldwell, Raj Chetty, John Donohue, Joseph Doyle, Matt Gentzkow, Ed Glaeser, Paul Goldsmith-Pinkham, Felipe Goncalves, Damon Jones, Chinhui Juhn, Scott Michelman, Conrad Miller, Derek Neal, Scott Nelson, Sam Norris, Evan Rose, Jesse Shapiro, Megan Stevenson, Alex Torgovitsky, Crystal Yang, four anonymous referees, and numerous seminar participants for helpful comments. Emily Battaglia, Nicole Gandre, Jared Grogan, Ashley Litwin, Alexia Olaizola, Bailey Palmer, Elise Parrish, Emma Rackstraw, and James Reeves provided excellent research assistance. The data we analyze are provided by the New York State Division of Criminal Justice Services (DCJS) and the Office of Court Administration (OCA). The opinions, findings, and conclusions expressed in this publication are those of the authors and not those of DCJS or OCA. Neither New York State, DCJS or OCA assumes liability for its contents or use thereof.
Footnotes
A large recent literature documents racial disparities in the criminal justice system. See, for example, Gelman, Fagan and Kiss (2007), Antonovics and Knight (2009), Anwar, Bayer and Hjalmarsson (2012), Abrams, Bertrand and Mullainathan (2012), McIntyre and Baradaran (2013), and Rehavi and Starr (2014), among many others.
The observed disparities may also be driven by systemic, or indirect, discrimination, as formalized by Bohren, Hull and Imas (2022). For example, racial disparities in prior criminal histories due to discrimination in policing can lead to different pretrial release rates for equally risky white and Black defendants despite a race-neutral release rule. We describe how such systemic factors are included in our analysis below.
Section 2 describes how U.S. anti-discrimination laws apply in our context. As we discuss there in greater detail, finding different release rates among white and Black individuals with identical misconduct potential would likely be necessary, but perhaps not sufficient, to win a disparate impact case. We also compare disparate impact to disparate treatment, which generally requires additional non-statistical evidence of discriminatory intent.
Our analysis, and use of OVB terminology, is not premised on the view that differences in misconduct risk are innate or unaffected by discrimination at other points of the criminal justice system (or society as a whole). Differences in misconduct risk and subsequent OVB in observational analyses could, for example, be driven by the over-policing of Black neighborhoods relative to white neighborhoods, discrimination in the types of crimes that are reported to and investigated by the police, discrimination in housing and labor markets, and so on. We measure the disparate impact of release decisions holding fixed these other potential sources of discrimination, isolating by design one particular set of racial disparities that may be reliably targeted and potentially reduced by policy.
Other recent related work includes Rose (2021) and Feigenberg and Miller (2021). Rose (2021) shows that a policy reform that sharply reduced prison punishments for technical probation violations nearly eliminated the racial disparity in incarceration without significantly increasing the disparity in reoffending rates, suggesting that technical probation violations may convey less precise risk signals for Black individuals on probation. Feigenberg and Miller (2021) show that Black motorists in Texas are stopped at higher rates than white motorists without any commensurate increase in contraband hit rates, suggesting that the racial disparity in search rates is inefficient.
The disparate impact standard only applies in certain contexts, since it stems from statutory rules rather than constitutional law. Examples include employment via Title VII of the 1964 Civil Rights Act and housing via the Fair Housing Act of 1968. The disparate impact standard may also apply to all programs and activities receiving federal financial assistance via Title VI of the 1964 Civil Rights Act, which includes the state and local courts considered in our analysis of the pretrial setting (e.g., United States v. Maricopa County 2012).
The consideration of indirect discrimination aligns the disparate impact doctrine, and our measure, with notions of discrimination in sociology, psychology, and related fields that account for unconscious or implicit biases and systemic or structural racism in seemingly race-neutral decisions (Bohren, Hull and Imas, 2022). Notably, the Supreme Court has explained that disparate impact liability under various civil rights laws “permits plaintiffs to counteract unconscious prejudices and disguised animus that escape easy classification as disparate treatment” (Texas Department of Housing & Community Affairs v. Inclusive Communities Project, 2015).
The disparate treatment doctrine derives its force from the Equal Protection Clause of the U.S. Constitution’s Fourteenth Amendment. It was formalized in the landmark U.S. Supreme Court case Washington v. Davis (1976), where the Supreme Court explained that the “basic equal protection principle that the invidious quality of a law claimed to be racially discriminatory must ultimately be traced to a racially discriminatory purpose.” Later, in McCleskey v. Kemp (1987), the Court similarly rejected a challenge to Georgia’s capital punishment scheme—despite statistical evidence showing large racial disparities in death penalty rates—because the evidence was “clearly insufficient to support an inference that any of the decisionmakers in [the defendant’s] case acted with discriminatory purpose.”
This view is consistent with the Supreme Court’s ruling in Washington v. Davis, where the Court explained that a law or official governmental practice must have a “discriminatory purpose,” not merely a disproportionate effect on one race, to constitute “invidious discrimination” under the Fifth Amendment Due Process Clause or the Fourteenth Amendment Equal Protection Clause. Of course, a disproportionate impact may be relevant as “evidence” of a “discriminatory purpose.”
Appendix B.1 discusses how our approach can be extended to multi-valued or continuous .
Comparing the treatment of white and Black defendants with the same objective potential for pretrial misconduct aligns Δj with economic notions of labor market discrimination that compare white and Black workers with the same objective productivity (e.g., Aigner and Cain, 1977), measures of algorithmic discrimination that compare equally “qualified” white and Black individuals (e.g., Berk et al., 2018), and a long literature in sociology and related fields that considers systemic forces which drive discrimination through non-race characteristics (e.g., Pincus, 1996). By comparison, Phelps (1972) suggests measuring labor market discrimination by comparing white and Black workers with the same subjective signal of labor market productivity. Canay, Mogstad and Mountjoy (2020) similarly suggest measuring racial bias (one potential driver of discrimination) by comparing marginal white and Black individuals with the same non-race characteristics (see also Ayres (2010)). Measures that condition on either subjective signals or non-race characteristics may be helpful for estimating disparate treatment or understanding the most likely drivers of disparate impact, but as we discuss in Section 2.1 are generally unsuitable for estimating disparate impact per se.
The OVB formula also shows that simple benchmarking analyses generally yield biased estimates of the relative differences in the extent of racial discrimination across judges, even though here judges are as-good-as-randomly assigned. This is because the extent of OVB generally varies across judges, so differences in benchmarking coefficients αj −αk = Δj − Δk + ξj − ξk need not equal (or even have the same sign as) differences in disparate impact Δj − Δk.
Appendix Table A2 compares the full sample of NYC bail cases to our estimation sample. By construction, our estimation sample has a somewhat lower release rate, although the ratio of release rates by race is similar. Our estimation sample is also broadly representative in terms of defendant and charge characteristics, with a slightly higher share of defendants with prior FTAs and rearrests, and a lower share of defendants charged with drug and property crimes.
Even with the quasi-random assignment of bail judges, the exclusion restriction in our framework could be violated if judge assignment impacts the probability of pretrial misconduct through channels other than pretrial release. While the assumption that judges only systematically affect defendant outcomes through pretrial release is fundamentally untestable, we join Arnold, Dobbie and Yang (2018) in viewing it as reasonable here. Bail judges only handle one decision, limiting the potential channels through which they could affect defendants. Pretrial misconduct is also a relatively short-run outcome, further limiting the role of alternative channels. In a similar setting, Dobbie, Goldin and Yang (2018) and Ouss and Stevenson (2021) find that there are no independent effects of the assigned money bail amount on defendant outcomes. We explore the robustness of our findings to such effects below.
Appendix Table A5 illustrates the rescaling solution with a simple numerical example. Appendix Table A6 illustrates how rescaling yields our finding of significant disparate impact in NYC bail decisions. See Appendix B.4 for details.
Our approach can be justified without a conventional monotonicity assumption, in contrast to some of the recent literature. To see why, consider a simple model in which each judge’s release decisions are given by Dij = 1[κj ≥ vij] where vij | κj, λj ~ U(0, 1) without loss and . This model violates conventional monotonicity, since judges differ both in their orderings of individuals by the appropriateness of release (vij) and their relative skill at predicting misconduct outcomes (λj). Nevertheless, when E[λj | κj] is constant (linear) in κj, average released misconduct rates are linear (quadratic) in release rates E[Dij] = κj, so that these extrapolations identify the ATE μ. More flexible extrapolations accommodate a broader range of judge decision-making models by leveraging richer quasi-experimental variation.
This restriction is especially strong when Xi is continuously distributed with full support. A straightforward argument shows in that case that judges with equal release rates for particular races must also have equal misconduct rates, such that there is no difference in judge skill. We do not impose this sharp restriction here, since Xi is a vector of group indicators.
We emphasize that the release rates plotted in Figure 2 adjust for courtroom-by-time fixed effects. Points above 0.9, for example, may correspond to a judge with a lower raw release rate who primarily serves courtrooms or time periods with riskier-than-average defendants. We account for such differences in cases across courtrooms and periods with a linear adjustment, as discussed above.
Appendix Table A7 explores the sensitivity of our extrapolations to estimation error in judge release rates, which may attenuate their estimated relationship with released misconduct rates. We do so by first applying empirical Bayes shrinkage to the release rate estimates, separately by race (see Appendix B.3 for details). This exercise yields very similar results, suggesting negligible bias from first-step estimation error. Negligible estimation error is consistent with the fact that we observe many (at least 100) cases per judge.
See Appendix Figure A2 for the corresponding covariate-adjusted version of Figure 2.
The average disparate impact in the second half of judge cases is somewhat larger, at 6.1 percentage points, suggesting disparate impact may increase with judge experience.
We demean the functions of time before interacting them in order to include all judge main effects. Interacting all demeaned covariates with judge and race effects would yield a specification similar to one proposed by Imbens and Wooldridge (2009) for estimating ATEs by regression. In practice we restrict estimation to judges handling cases across at least two years when adding the judge-specific linear time effects and across at least three years when adding the judge-specific quadratic effects. These restrictions cause the number of judges to vary across the columns of Appendix Table A14.
If, for example, πjb < πjw but mean risk μr and signal quality τjr are the same across race (implying a common distribution of pj(νij, Ri) given ), the judge will release fewer Black defendants conditional on such that Δj > 0.
Suppose, for example, that signal quality and release benefits are the same across race (τjb = τjw and πjb = πjw) but mean risk is higher for Black defendants (μb > μw). The judge’s posterior pj(νij, Ri) will then be higher among Black defendants given νij, making Black defendants less likely to be released conditional on and so Δj > 0.
This notion of racial bias thus differs from that of Canay, Mogstad and Mountjoy (2020), who consider a judge as biased only if she sets a higher release threshold for white defendants conditional on all non-race characteristics that are observed by each judge. See Hull (2021) for a discussion of the difference in these definitions.
Technically, the τjr = τr restriction is weaker than conventional monotonicity, which would restrict judges to have a common ordering of defendants by their appropriateness for release. Imposing τjr = τr allows random violations of monotonicity in the sense of ηij ≠ ηik for j ≠ k, so long as ηij and ηik have the same variance. Similar relaxations of conventional monotonicity have been considered in Frandsen, Lefgren and Leslie (2019) and Marx (Forthcoming).
An alternative approach would explicitly model the heterogeneity in defendant risk across courtrooms and time and derive appropriate adjustments from the resulting model of judge decisions. This alternative approach would be more coherent from a structural point of view, as heterogeneity in judge risk signals may lead to heterogeneous effects of courtroom and time on release rates that can violate the linearity assumption underlying our preferred regression adjustment. An advantage of the regression adjustment is that it is computationally tractable, given the large number of court-by-time effects and nonlinear decision model. The regression adjustment also aligns our analyses of disparate impact, racial bias, and statistical discrimination as being based on the same reduced-form variation in Figure 2.
The estimates in columns 1–3 of Table 4 are derived from the parameter estimates in columns 1 and 4 of Appendix Table A18, while columns 4–6 of Table 4 come from columns 2 and 5 of Appendix Table A18. The latter specification assumes log signal quality and release thresholds are uncorrelated. A richer specification that allows for such correlation is estimated in columns 3 and 6 of Appendix Table A18. This model produces estimates that are very similar to columns 2 and 5, but which are considerably less precise.
Frandsen, Lefgren and Leslie (2019) propose model-free tests of monotonicity in the context of quasi-randomly assigned judges that also account for such error. Appendix Table A19 shows that applying these tests to our data yields decisive rejections, in both samples of white and Black defendants, consistent with our model estimates.
Our simulations also highlight the impossibility of simultaneously eliminating disparate impact (on average) and racial bias (at the margin) when either mean misconduct risk or the risk signal quality differ for white and Black defendants (Kleinberg, Mullainathan and Raghavan, 2017). The simulation based on the disparate impact posteriors, for example, results in non-zero racial bias against Black defendants of between 1.3 and 3.9 percentage points.
References
- Abrams David, Bertrand Marianne, and Mullainathan Sendhil. 2012. “Do Judges Vary in Their Treatment of Race?” Journal of Legal Studies, 41(2): 347–383. [Google Scholar]
- Aigner Dennis, and Cain Glen. 1977. “Statistical Theories of Discrimination in Labor Markets.” Industrial and Labor Relations Review, 30(2): 175–187. [Google Scholar]
- Andrews Donald, and Schafgans Marcia. 1998. “Semiparametric Estimation of the Intercept of a Sample Selection Model.” Review of Economic Studies, 65(3): 497–517. [Google Scholar]
- Angrist Joshua, Hull Peter, Pathak Parag, and Walters Christopher. 2017. “Leveraging Lotteries for School Value-Added: Testing and Estimation.” Quarterly Journal of Economics, 132(2): 871–919. [Google Scholar]
- Antonovics Kate, and Knight Brian. 2009. “A New Look at Racial Profiling: Evidence from the Boston Police Department.” Review of Economics and Statistics, 91(1): 163–177. [Google Scholar]
- Anwar Shamena, Bayer Patrick, and Hjalmarsson Randi. 2012. “The Impact of Jury Race in Criminal Trials.” Quarterly Journal of Economics, 127(2): 1017–1055. [Google Scholar]
- Arnold David, Dobbie Will, and Yang Crystal. 2018. “Racial Bias in Bail Decisions.” Quarterly Journal of Economics, 133(4): 1885–1932. [Google Scholar]
- Arrow Kenneth J. 1973. “The Theory of Discrimination.” In Discrimination in Labor Markets. ed. Ashenfelter Orley and Rees Albert, 3–33. Princeton, NJ:Princeton University Press. [Google Scholar]
- Ayres Ian. 2010. “Testing for Discrimination and the Problem of Included Variable Bias.” Yale Law School Mimeo. [Google Scholar]
- Becker Gary S. 1957. The Economics of Discrimination. Chicago: University of Chicago Press. [Google Scholar]
- Berk Richard, Heidari Hoda, Jabbari Shahin, Kearns Michael, and Roth Aaron. 2018. “Fairness in Criminal Justice Risk Assessments: The State of the Art.” Sociological Methods & Research, 1–42. [Google Scholar]
- Bertrand Marianne, and Mullainathan Sendhil. 2004. “Are Emily and Greg More Employable than Lakisha and Jamal? A Field Experiment on Labor Market Discrimination.” American Economic Review, 94(4): 991–1013. [Google Scholar]
- Bohren J Aislinn, Haggag Kareem, Imas Alex, and Pope Devin G. 2020. “Inaccurate Statistical Discrimination: An Identification Problem.” NBER Working Paper No. 25935. [Google Scholar]
- Bohren J, Aislinn Peter Hull, and Imas Alex. 2022. “Systemic Discrimination: Theory and Measurement.” NBER Working Paper No. 29820. [Google Scholar]
- Bonhomme Stephane, and Weidner Martin. 2020. “Posterior Average Effects.” Unpublished Working Paper. [Google Scholar]
- Bordalo Pedro, Coffman Katherine, Gennaioli Nicola, and Shleifer Andrei. 2016. “Stereotypes.” Quarterly Journal of Economics, 131(4): 1753–1794. [Google Scholar]
- Brinch Christian, Mogstad Magne, and Wiswall Matthew. 2017. “Beyond LATE with a Discrete Instrument.” Journal of Political Economy, 125(4): 985–1039. [Google Scholar]
- Canay Ivan, Mogstad Magne, and Mountjoy Jack. 2020. “On the Use of Outcome Tests for Detecting Bias in Decision Making.” NBER Working Paper No. 27802. [Google Scholar]
- Chamberlain Gary. 1986. “Asymptotic Efficiency in Semiparametric Models with Censoring.” Journal of Econometrics, 32(2): 189–218. [Google Scholar]
- Chan David, Gentzkow Matthew, and Yu Chuan. 2021. “Selection with Variation in Diagnostic Skill: Evidence from Radiologists.” NBER Working Paper No. 26467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobbie Will, Goldin Jacob, and Yang Crystal. 2018. “The Effects of Pre-Trial Detention on Conviction, Future Crime, and Employment: Evidence from Randomly Assigned Judges.” American Economic Review, 108(2): 201–240. [Google Scholar]
- Ewens Michael, Tomlin Bryan, and Wang Liang Choon. 2014. “Statistical Discrimination or Prejudice? A Large Sample Field Experiment.” Review of Economics and Statistics, 96(1): 119–134. [Google Scholar]
- Feigenberg Benjamin, and Miller Conrad. 2021. “Would Eliminating Racial Disparities in Motor Vehicle Searches Have Efficiency Costs?” Quarterly Journal of Economics. [Google Scholar]
- Frandsen Brigham, Lefgren Lars, and Leslie Emily. 2019. “Judging Judge Fixed Effects.” NBER Working Paper No. 25528. [Google Scholar]
- Gelman Andrew, Fagan Jeffrey, and Kiss Alex. 2007. “An Analysis of the New York City Police Department’s “Stop-and-Frisk” Policy in the Context of Claims of Racial Bias.” Journal of the American Statistical Association, 102(479): 813–823. [Google Scholar]
- Heckman James J. 1990. “Varieties of Selection Bias.” American Economic Review Papers and Proceedings, 80(2): 313–318. [Google Scholar]
- Hull Peter. 2020. “Estimating Hospital Quality with Quasi-Experimental Data.” Unpublished Working Paper. [Google Scholar]
- Hull Peter. 2021. “What Marginal Outcome Tests Can Tell Us About Racially Biased Decision-Making.” NBER Working Paper No. 28503. [Google Scholar]
- Imbens Guido W, and Wooldridge Jeffrey M. 2009. “Recent Developments in the Econometrics of Program Evaluation.” Journal of economic literature, 47(1): 5–86. [Google Scholar]
- Kleinberg Jon, Lakkaraju Himabindu, Leskovec Jure, Ludwig Jens, and Mullainathan Sendhil. 2018. “Human Decisions and Machine Predictions.” Quarterly Journal of Economics, 133(1): 237–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleinberg Jon, Mullainathan Sendhil, and Raghavan Manish. 2017. “Inherent Trade-Offs in Algorithmic Fairness.” Proceedings of the 8th Conference on Innovations in Theoretical Computer Science. [Google Scholar]
- Kowalski Amanda. 2016. “Doing More When You’re Running LATE: Applying Marginal Treatment Effect Methods to Examine Treatment Effect Heterogeneity in Experiments.” NBER Working Paper No. 22363. [Google Scholar]
- Leslie Emily, and Pope Nolan. 2017. “The Unintended Impact of Pretrial Detention on Case Outcomes: Evidence from NYC Arraignments.” Journal of Law and Economics, 60(3): 529–557. [Google Scholar]
- Marx Philip. Forthcoming. “An Absolute Test of Racial Prejudice.” Journal of Law, Economics, and Organization. [Google Scholar]
- McIntyre Frank, and Baradaran Shima. 2013. “Race, Prediction, and Pretrial Detention.” Journal of Empirical Legal Studies, 10(4): 741–770. [Google Scholar]
- Mogstad Magne, Torgovitsky Alexander, and Walters Christopher. 2020. “The Causal Interpretation of Two-Stage Least Squares with Multiple Instrumental Variables.” NBER Working Paper No. 25691. [Google Scholar]
- Mogstad Magne, Santos Andres, and Torgovitsky Alexander. 2018. “Using Instrumental Variables for Inference About Policy-Relevant Treatment Parameters.” Econometrica, 86(5): 1589–1619. [Google Scholar]
- Morris Carl. 1983. “Parametric Empirical Bayes Inference: Theory and Applications.” Journal of the American Statistical Association, 78(381): 47–55. [Google Scholar]
- Mueller-Smith Michael. 2015. “The Criminal and Labor Market Impacts of Incarceration.” Unpublished Working Paper. [Google Scholar]
- New York City Criminal Justice Agency Inc. 2016. “Annual Report 2015.”
- Norris Sam. 2019. “Examiner Inconsistency: Evidence from Refugee Appeals.” Unpublished Working Paper. [Google Scholar]
- Ouss Aurelie, and Stevenson Megan. 2021. “Bail, Jail, and Pretrial Misconduct:The Influence of Prosecutors.” SSRN Working Paper No. 3335138. [Google Scholar]
- Pakes Ariel, and Pollard David. 1989. “Simulation and the Asymptotics of Optimization Estimators.” Econometrica, 57(5): 1027–1057. [Google Scholar]
- Phelps Edmund S. 1972. “The Statistical Theory of Racism and Sexism.” American Economic Review, 62(4): 659–661. [Google Scholar]
- Pincus Fred L. 1996. “Discrimination Comes in Many Forms: Individual, Institutional, and Structural.” American Behavioral Scientist, 40(2): 186–194. [Google Scholar]
- Rehavi M. Marit, and Starr Sonja B.. 2014. “Racial Disparity in Federal Criminal Sentences.” Journal of Political Economy, 122(6): 1320–1354. [Google Scholar]
- Rose Evan. 2021. “Who Gets a Second Chance? Effectiveness and Equity in Supervision of Criminal Offenders.” Quarterly Journal of Economics, 136(2): 1199–1253. [Google Scholar]
- Yang Crystal, and Dobbie Will. 2020. “Equal Protection Under Algorithms: A New Statistical and Legal Framework.” Michigan Law Review, 119(2): 291–396. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


