Abstract
The cubic phase of CsNbO3 (CNO) perovskite has been hypothesized to investigate the elastic, electronic, photocatalytic, and optical properties for various technological applications using first-principles method. The pressure dependent structural stability has been confirmed from computed elastic constants. Relatively high value of elastic moduli, large hardness and toughness suggested that CNO would be applicable to design industrial machineries. The ductile to brittle transition is noticed at 20 GPa. The indirect bandgap of CNO proclaims its suitability for photovoltaic and IR photodetector applications. The total and partial density of states are calculated to show in evidence the contribution of individual atomic orbitals in the formation of bands. The pressure changes orbitals hybridization which can be substantiated by the change in the bandgap. Strong covalency of the Nb–O bond and antibonding character of Cs–O have been anticipated by the Mulliken population analysis and by the contour maps of electron charge density. The low carrier effective mass and high mobility carriers predict the good electrical conductivity of the material. The calculated values of conduction and valance band edge potential illustrate the excellent water-splitting and environmental pollutants degradation properties of CNO.
Subject terms: Materials for devices, Theory and computation
Introduction
ABO3-type perovskites, a large family of ternary oxides, continue to draw significant attention as materials for solid oxides fuel cells1, catalytic2 and electrochemical applications3, hydrogen membranes4, actuators, sensors5, etc. Such types of materials are found of great interest because of their adaptable material characteristics and tunable physical properties. These compounds exhibit structural distortions as well as various spin orderings6 depending on temperature and pressure. Furthermore, the perovskite’s structural phase transitions7, which are crucial for understanding the quantum fluctuations that are driven by the characteristics of the materials may result in fascinating ferroelectrics phenomenon. The perovskite materials also display extraordinary physical properties in electronic devices, like diodes, transistors, integrated circuits1, thin-film transistors for flat-panel displays8, spin-dependent transport9, strong electron lattice couplings10, etc.
Recently, new catalysts and photocatalyst materials have gained a lot of attention in wastewater treatment in an effort to reduce some significant challenges connected to heavy ions, dyes, and emerging contaminants. Researchers have been working consistently over the past few decades to create photocatalysts that are stable, effective, affordable, and non-toxic for use in water splitting and environmental remediation. The exceptional stability of ABO3-type oxide photocatalysts, which is the most fundamental and crucial prerequisite of photocatalysts for practical application, makes them highly valuable for study2. However, the wide bandgap, which were typically brought on by the low valence bands and were composed of O-2p orbitals with low potential vs NHE (Normal Hydrogen Electrode), frequently served as an intrinsic restriction on the ability of oxide photocatalysts to utilize visible light11. Additionally, the generated visible light driven oxide photocatalytic activity remained modest12. The improvement of visible light driven photocatalytic activity and the expansion of light response ranges should therefore be the main research areas for oxide photocatalysts13. A number of theoretical and experimental research have been done to look at the different characteristics of perovskite systems such as niobates, titanates, cuprates, etc. Very recently, pressure-dependent theoretical investigations on mechanical, electronic, and optical properties of BaCuO314, CaCuO3 and SrCuO315 have been explored which shows their utility for several optoelectronic applications. The improvement of visible light driven photocatalytic activity and the expansion of light response ranges should therefore be the main research areas for oxide photocatalysts13. For the construction of lasers and detectors, many semiconducting materials are used16. Recent researches have shown the structural, magnetic, and magnetocaloric properties of niobates under pressure17. Materials must be customized for individual application since their qualities determine how effective they are in field service.
Nowadays, many theoretical investigations have been performed on niobate oxides such as LiNbO3, NaNbO3, KNbO3, SrNbO3, and RbNbO318, RbSr2Nb3O1019 etc. as well as the temperature-dependent investigations of different properties of CsNbO3 have also been demonstrated17. These explorations are proved to be essential to the material engineering sectors. These oxides exhibit structural phase transitions at various pressures20 and have a high dielectric constant21, high breakdown strength22, wide bandgap23, and low current leakage current density24. As a function of temperature, pressure, and particle size, NaNbO3 displays a very intricate sequence of structural phase changes25. Under light illumination, KNbO3 is very stable and nontoxic26. Due to its accessibility, low toxicity, and ability to exhibit strong polarization at high electric fields, AgNbO327 is another alluring lead-free ferroelectric material. Cs shows the greater ionic radius, low first ionization energy, and electronegativity, while relatively average density and melting temperature among the A-site cations of niobates. Therefore, in the current study, we choose CsNbO3 (CNO) for additional pressure dependent analysis among different niobates. Very recently, pressure dependent vibrational, electronic, thermoelectronic, and optical properties of CNO have been reported28. However, the value of reported energy gap was quite low due to the use of conventional exchange correlational functional28. Despite the fact of very intriguing results, there is still a serious lack of knowledge regarding important aspects such as elastic properties, electronic band structure using advanced exchange correlation functional, charge density, and photocatalytic efficiency that must be addressed in order to take full advantages of CNO for potential technological applications.
In view of above circumstances, we explore structural, elastic, electronic, and photocatalytic properties of CNO. Investigating the effect of pressure on the aforementioned physical characteristics of CNO at low and high pressures is the main objective of this research.
Methodology
Using the CASTEP algorithm, the first principles calculations of CNO were performed within the framework of density functional theory (DFT)29 using the plane wave pseudopotential approximation. Perdew-Burke-Ernzerhof (PBE)30 form of generalized gradient approximation (GGA) was used to calculate the exchange correlation energy generated by the electrical interaction of core ions and valance electrons in order to optimize the shape of the material. It is well known that the GGA-PBE approximation underestimates bandgap values, therefore, the electronic calculations were also performed using hybrid approaches such as sx-LDA31. After evaluating numerous cut-off points (where the energy is least), 400 eV was chosen as the plane-wave cut-off energy for the calculations. For Brillouin zone sampling, a Monkhrost-pack grid32 of 15 × 15 × 15 k-points was used. The calculation of the ground state atomic configuration were performed using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) approach33,34 with the ultrasoft pseudopotential method35. The ultrasoft pseudopotential approach carries out the calculations of the materials by treating the electron density in the valance as the soft portion and the core region as the hard part, where the cut-off energy is significantly decreased and the computational efficiency noticeably improves. The stress–strain method included in the CASTEP code was used to determine the bulk modulus, shear modulus, and single crystal independent elastic constants. To execute the pseudo-atomic calculations, the following electronic configurations were taken into consideration: 5s25p66s1 for the Cs, 4s24p64d45s1 for the Nb atom, and 2s22p6 for the O atom. At the time of the geometry optimization, the energy convergence of the total energy, 0.5 × 10−5 eV/atom, the maximum interatomic force, 0.01 eV/Å, the maximum stress, 0.02 GPa, and the ionic displacement, 5 × 10−4 Å were set. CNO belongs to the cubic (space group ) crystal structure. The atomic positions for the Cs, Nb, and O atoms in the unit cell are (0, 0, 0), (0.5, 0.5, 0.5), and (0, 0.5, 0), respectively36.
Results and discussions
Structural properties
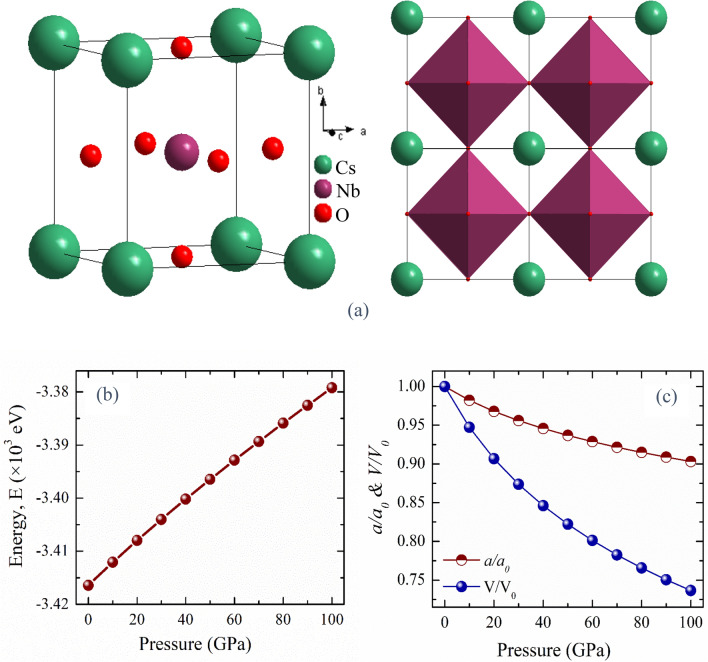
Figure 1a shows the 3D and 2D schematic illustration of cubic CNO crystal structure. By fitting the reduced total energy of the crystal with respect to the volume of the unit cell using the Birch–Murnaghan equation of state15, the geometry optimizations were carried out to find the lattice constants, isothermal bulk moduli, and pressure derivatives. The obtained value of a = 4.15 Å, which is very close to the reported data of CNO17 that asserts the authenticity of the present calculation.
Figure 1.
(a) 3D and 2D view of CsNbO3 (b) Pressure dependent ground state energy (E), and (c) Pressure dependent normalized lattice parameter, a/a0 and volume, V/V0 of CsNbO3.
In order to investigate the pressure-dependent properties of CNO, the pressure dependent stability was checked. The calculated negative values of ground state energy of CNO reflects the stability of CNO up to 100 GPa. Figure 1b displays the pressure-dependent ground state energy of CNO. From Fig. 1b, it is seen that the minimum energy of CNO increase with increasing hydrostatic pressure. The rise in the ground state energy announces that the applied pressure drives the structure to be unstable and more energy is needed to stabilize the compound37.
Figure 1c demonstrates the fluctuation of the lattice constant and unit cell volume with hydrostatic pressures up to 100 GPa. From graph, it is realized that the normalized lattice constant and unit cell volume gradually decrease with increasing hydrostatic pressure. As the pressure rises, the structure's relative compression reduces as a result of the inter-atomic repulsive interaction.
Stiffness constants and elastic moduli
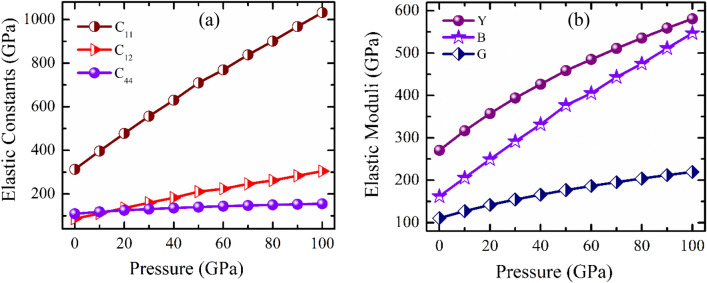
The "strain–stress" approach, which was used in earlier investigations33,34, was used to perform the calculations of elastic constants. The three independent elastic stiffness constants C11, C12, and C44 are obtained for CNO due to its cubic crystal structure. The pressure dependent fluctuations of Cij’s (i, j = 1, 2 & 4) which are shown in Table 2, and displayed in Fig. 2a.
Table 2.
Elastic stiffness constants, Cij in GPa, Elastic moduli (B, G, Y) in GPa, Pugh’s ratio (G/B), Poisson’s ratio (ν), Cauchy pressure (C12–C44) in GPa, Kleinman parameter (ξ) and Vickers hardness (HV) in GPa of CsNbO3 under pressure, P (GPa).
| P | C11 | C12 | C44 | B | Y | G | G/B | ν | C12–C44 | ξ | HV |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 312 | 87 | 109 | 162 | 271 | 111 | 0.683 | 0.221 | − 22 | 0.426 | 17.10 |
| 10 | 396 | 110 | 118 | 206 | 317 | 127 | 0.619 | 0.243 | − 7 | 0.427 | 16.45 |
| 20 | 478 | 135 | 125 | 249 | 357 | 142 | 0.568 | 0.261 | 10 | 0.432 | 15.71 |
| 30 | 556 | 159 | 131 | 292 | 394 | 155 | 0.530 | 0.275 | 29 | 0.434 | 15.16 |
| 40 | 630 | 183 | 136 | 331 | 427 | 166 | 0.500 | 0.286 | 47 | 0.438 | 14.68 |
| 50 | 710 | 211 | 140 | 377 | 459 | 177 | 0.469 | 0.297 | 71 | 0.444 | 14.03 |
| 60 | 769 | 223 | 144 | 405 | 486 | 186 | 0.460 | 0.301 | 79 | 0.439 | 14.18 |
| 70 | 838 | 246 | 147 | 444 | 511 | 195 | 0.441 | 0.308 | 99 | 0.441 | 13.78 |
| 80 | 901 | 262 | 150 | 475 | 536 | 204 | 0.430 | 0.312 | 112 | 0.439 | 13.72 |
| 90 | 968 | 284 | 153 | 512 | 559 | 212 | 0.415 | 0.318 | 131 | 0.441 | 13.40 |
| 100 | 1032 | 305 | 154 | 547 | 581 | 220 | 0.401 | 0.323 | 150 | 0.443 | 13.11 |
Figure 2.
Pressure dependence of (a) Elastic stiffness constants and (b) Elastic Muduli of CsNbO3.
The mechanical stability can be confirmed from the positively defined quadric form of energy density, where the coefficients obtained from DFT calculations (elastic stiffness) fulfill the cubic structure's fundamental minors and these are (C11–C12 > 0), (C11 + 2C12 > 0) and C44 > 032. It is noticed that the elastic constants of CNO totally satisfy the aforementioned stability criteria for the entire range of applied hydrostatic pressure. Thus, CNO shows mechanical stability under pressure and the estimated elastic stiffness constant go under monotonous increase with increasing pressure.
The various elastic parameters, such as Y, B, G, and Poisson’s ratio (ν) and hardness (HV) were determined using the acquired elastic constants, Cij. By averaging the upper and lower bounds of Voigt's and Reuss's techniques, B and G have been calculated using the Voigt–Reuss–Hill approximation by the following equations:
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
where, BR and GR indicate the Reuss approximation, BV and GV represent the Voigt approximation, and B and G have been calculated following the Voigt–Reuss–Hill approximation38.
Additionally, Y, ν and HV are the function of B and G and can be calculated from the following equations
| 6 |
| 7 |
| 8 |
The calculated values of Y, B, and G under different pressure have been reported in Table 2. According to Table 1, the CNO has a large value of Y among the three elastic moduli (B, Y, and G) across the whole range of pressure. As the elastic tensor is directly proportional to Y, hence, the relatively large value of Y indicates that the CNO possesses a high elastic tensor. It can be also noticed that the elastic tensile resistance is getting increases with the increase of pressure and suggest the applicability of CNO at very high pressure.
Table 1.
The lattice parameter (a) and unit cell volume (V) of CsNbO3.
Again, Y is inversely proportional to the critical thermal shock coefficient inside the elastic limit, which has an impact on a solid's thermal shock resistance39. Better thermal shock resistance is represented by a lower value of Y. The value of Y for LiNbO340, NaNbO341 and KNbO342 are 356, 272 GPa and 298 GPa respectively, whereas the obtained value for CNO is 271 GPa. As a result, CNO can be more suitable for thermal barrier coatings in comparison with above mentioned niobates. As demonstrated in Fig. 2b, it can be seen that G is less than B at all the pressure, and hence, rather than the volume change, shape deforming stress should be used to control the mechanical failure mechanism of CNO when pressure is applied.
Ductility and hardness
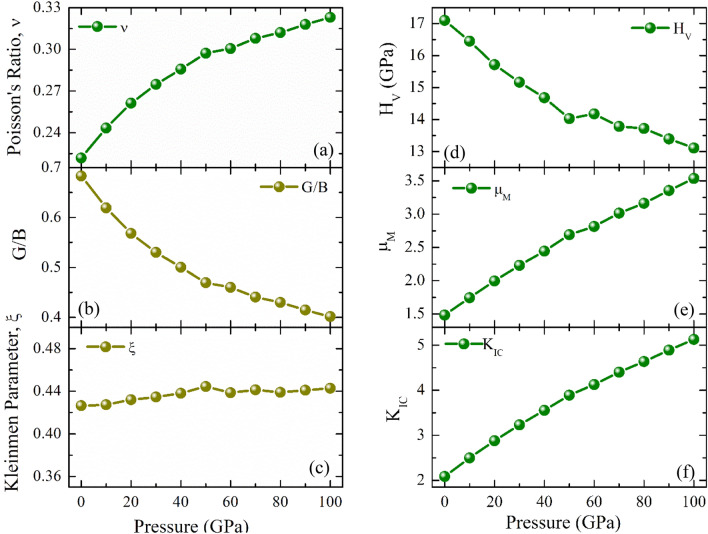
The hardness of materials can be accurately predicted with significant support from Pugh's (G/B), Poisson's (ν) ratio and Cauchy Pressure (CP). Frantsevich et al.43 first reported the separation of ductility from brittleness of materials on the basis of Poisson’s ratio. Frantsevich rule suggested that ν ~ 0.26 as the border line which separates the brittle from ductile character. If the Poisson’s ratio is greater than 0.26 then the material will go under plastic deformation (ductile) otherwise the material will fracture having no plastic deformation (brittleness). On the other hand, Niu et al.44 have shown that one can draw a line on the basis of the Pettifor’s criterion45, that intersects the Pugh’s criterion at G/B = 0.571. The value of Pugh’s ratio less than 0.571 predict the ductile nature while the G/B is greater than 0.571 suggest the brittle nature. For cubic crystals, the difference between (C12–C44) is known as Cauchy pressure. If the value of C44 has a value greater than C12, according to Pettifor’s rule45, the materials with negative Cauchy pressure have covalence bonds and thus become brittle in nature. Otherwise, the materials have ionic bonding and thus become ductile. The values of ν, G/B and CP (Table 2) predicted that the material possesses ductile nature below 20 GPa, and its shows brittleness for ≥ 20 GPa which are shown in Fig. 3a and b. The Kleinman parameter (ξ) defied by and essential parameter to determines the substantial contribution of the bond bending and bond stretching to minimize the external pressure effect whose value ranges from 0 to 146. All the calculated values of ξ as shown in Fig. 3c forecast that CNO displays prominent bond bending over bond stretching at all external pressure.
Figure 3.
Changes of (a) Poison’s ratio, (b) Pugh’s ratio, (c) Kleinman parameter, (d) Vickers (e) machinability index, μM, and (f) fracture toughness, KIC hardness under pressure of CsNbO3.
The pressure dependent calculated values of Vickers Hardness of CNO have been listed in Table 2 and shown in Fig. 3d. A decreasing trend of hardness can be observed for the increasing pressure because the lower value of G/B and the larger value of Poisson’s ratios are the indication of less hardness of the material and vice-versa47. The high value of HV predicts the CNO is a hard material and useful for mechanical applications.
The stress intensity factor KIC can be used to calculate the quantitative value at which a tiny break in the material starts to spread. A reliable model of fracture toughness was proposed by Niu et al.44 and used the following empirical formula to calculate KIC:
| 9 |
where V0 is the volume per atom.
From the calculation, it can be seen that CNO possesses a high value of KIC in the whole range of pressure (Fig. 3f) i.e., the material can show high resistance to fracture propagation or micro cracks.
The machinability index, μM (= B/C44)48 is important for determining how lubricating and plastic a solid is49. Figure 3e shows that the value of μM increases in accordance with increasing pressure that proves the high-pressure applicability of CNO. In comparison to other materials, CNO48 shows a greater value of μM, which indicates excellent lubricating qualities and a reduced friction value that may be useful to design industrial machineries.
Electronic properties
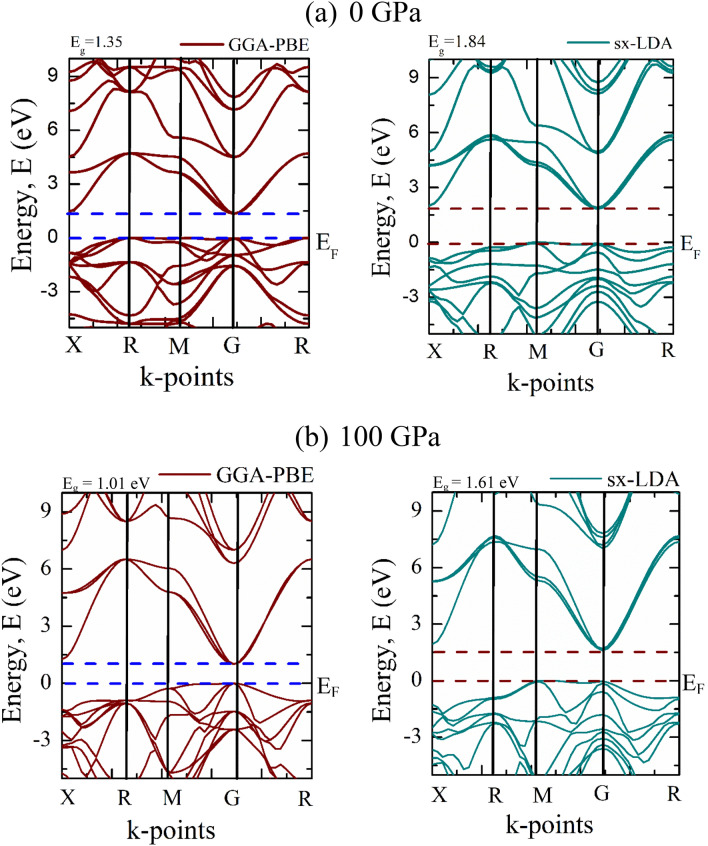
We investigate the electronic band structure of CNO (Fig. 4) that describes the state of electrons in terms of their energy, E, and momentum, k. Figure 4 shows that CNO exhibits semiconducting nature with an indirect bandgap. In general, indirect bandgap semiconductors are utilized for photovoltaic device applications17.
Figure 4.
Electronic band structures of CsNbO3 calculated by using GGA-PBE, and sx-LDA approximations at (a) zero pressure and (b) 100 GPa.
This simulated bandgap is found to be fitting well with the prior theoretical value13. As it is well known that the GGA-PBE approach underestimates the bandgap values, therefore, we have performed the calculation using hybrid approaches such as sx-LDA since it gives the bandgap value close to the experimental results31. Interestingly, the bandgap value is enhanced significantly to 1.84 eV due to the use of sx-LDA (Fig. 4). Unfortunately, there is no available experimental data to compare the present result. The bandgap of CNO predicts the IR photodetector applications and substantiates the photoactive characteristics.
The electronic band structure also determines the dispersion relation for electrons in a material. The G–R direction shows the larger energy dispersion in comparison with X–R, R–M, and M–G directions for CNO. Consequently, it is believed that the band dispersion in the G–R direction controls the charge density50. Highly dispersive bands correspond to higher electrical conductivity due to their low carrier effective mass and higher charge mobility51.
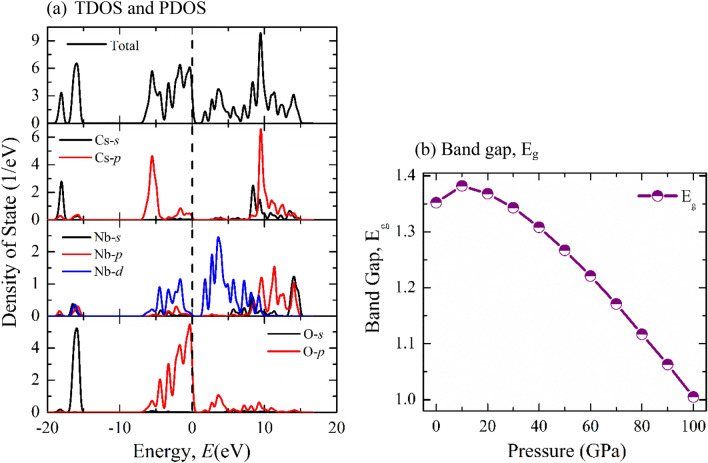
Figure 5a depicts the total and partial density of states of CNO to analyze the orbital contribution close to the Fermi level. As displayed in Fig. 5a, below the Fermi level (0 to − 6.9 eV), the valance band (VB) arises mainly from the contribution of 2p orbital of O atom, which is well-known for oxide-based semiconductor52. Strong hybridization among Cs-5p, Nb-4d, and O-2p orbitals is also observed in the top of VB. Besides, O-2p, and Nb-4d orbitals are mainly attributed to the bottom of the conduction band (CB). Cs-5p, Nb-4p orbitals also contribute to the upper CB.
Figure 5.
Graphical representation of (a) Total and partial DOS at zero pressure, and (b) Pressure dependent change of bandgap of CsNbO3.
The bandgap, preferred orientation, and thermoelectric characteristics of CNO are all significantly changes with the external pressure. The obtained values of Eg using conventional GGA method at 0 and 100 GPa are 1.35 eV and 1.01 eV, respectively. On the other hand, when we use the hybrid functional like sx-LDA, the bandgap values at 0 and 100 GPa are 1.84 eV and 1.61 eV, respectively. The change of Eg for GGA and sx-LDA are 0.34 eV and 0.23 eV which is very closed. However, it is well known that the hybrid functional gives more accurate value (closed to experimental result) of bandgap compared to conventional functional. A material to be a narrow bandgap semiconductor, the value of the bandgap should be near the infrared region. The obtained value of the bandgap using hybrid functional suggests that CNO can not be a narrow bandgap semiconductor at 100 GPa.
It can be seen from Fig. 5b that the bandgap of CNO increases up to 10 GPa and after that it begins to decrease with increasing pressure. Because electron–hole pairs become closer under pressure and their Coulomb interaction cannot be overlooked initially, the bandgap widens, leading to increase kinetic energy. Further increased pressure with increasing kinetic energy, causing the change in electron/hole-ion potential, makes the material able to neglect the Coulomb interaction and impose the electronic state to be closer. As a result, the Eg decreases later with the increasing pressure. This observation is well agreed with recent theoretical report28, however, the authors do not describe the phenomena below 10 GPa.
Mulliken population analysis provides details on the charge, bond length, and bond population in a solid crystalline system, which aids in figuring out how charges are distributed among the bonds as well as ionicity and covalency of a material. The bonding and antibonding states, respectively, are responsible for the positive and negative bond overlap populations. The calculated data of charge, population, and bond length under pressure of CNO have been reported in Table 3.
Table 3.
Calculated pressure dependent values of Mulliken effective charge (e), bond population and bond length (Å) of CsNbO3.
| P (GPa) | Mulliken effective charge (e) | Bond population | Bond length (Å) | ||||
|---|---|---|---|---|---|---|---|
| O | Nb | Cs | O–Nb | O–Cs | O–Nb | O–Cs | |
| 0 | − 0.77 | 0.93 | 1.38 | 1.26 | − 0.38 | 2.07 | 2.93 |
| 10 | − 0.79 | 1.04 | 1.32 | 1.20 | − 0.35 | 2.04 | 2.88 |
| 20 | − 0.80 | 1.13 | 1.26 | 1.14 | − 0.33 | 2.01 | 2.84 |
| 40 | − 0.82 | 1.29 | 1.17 | 1.03 | − 0.28 | 1.96 | 2.77 |
| 60 | − 0.84 | 1.42 | 1.09 | 0.93 | − 0.24 | 1.93 | 2.72 |
| 80 | − 0.85 | 1.54 | 1.01 | 0.82 | − 0.20 | 1.90 | 2.68 |
| 100 | − 0.85 | 1.67 | 0.92 | 0.72 | − 0.16 | 1.87 | 2.65 |
The reported data in Table 3 predicted that in CNO the Nb (0.93) shows a lower atomic charge contribution to form an atomic bond with the O atom. The Nb–O (1.26) bond also provides the higher value of bond populations than that of the Cs–O bond. The Nb–O (2.07 Å) bond length is also shorter than the Cs–O bond length. These observation refer to the strong covalent characteristics of the Nb–O bond. The antibonding situation of the Cs–O bond can be confirmed by the reported (− 0.38) value. The applied pressure bring change to the hybridization, charge, and bond population along with the bond length. From Table 3, it can be seen that with increasing pressure the covalency of Nb–O bond is decreased. In contrast, the antibonding character of the Cs–O bond is becoming weaker as the applied pressure give rise to the bond populations and reduces the charge of the Cs atom.
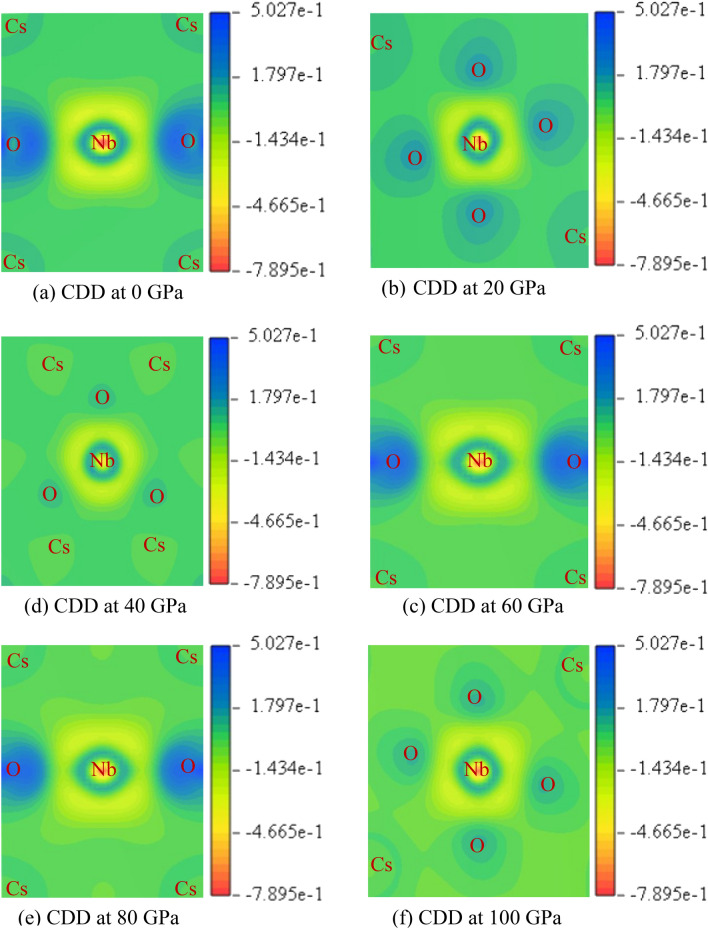
Understanding the type of atomic bonding in a compound can be done by looking at the contour map of the electron charge distribution among the atoms that make up the compound. Figure 6a–d show the contour color map of CNO at 0, 20, 40, 60, 80 and 100 GPa. The electron cloud that has been generated by the charge distributions around the atoms is almost spherical, and its intensity controls how much charge is accumulating. In Fig. 6a, it can be seen that the maximum electron density has been grown around the O-atom that exhibits strong electron localization. With increasing pressure the electron density increase around the O-atom that consistent with Mulliken Population analysis that gives rise to the antibonding character of the O–O bond. This increased electron density is also responsible for the lowering strength of the covalent Nb–O bond. As the positive charge density around the Cs atom decreases, the antibonding character of the Cs–O bond becomes weaker.
Figure 6.
The electronic charge density (CDD) map of CsNbO3 at (a) zero pressure, (b) 20 GPa, (c) 40 GPa (d) 60 GPa (e) 80 GPa and (f) 100 GPa.
The antibonding nature can be explained from the correlation of DOS, band structure and CDD map. In the band structure, it is seen that the dispersion curve in the valence band is flat at a finite wave vector. It indicates the valance band to be occupied by the electrons with same wave vector and in CNO, electrons of Cs-5p, O-2p orbitals are responsible which are observed from partial density of states (Fig. 5). With the same wave vector, the wave functions of the electrons from different orbital interfere each other. From the Pauli’s exclusion principal, if two electrons try to share an identical set of quantum numbers, their probability functions cancel (destructive interference) and create zero electron probability density between the orbitals. As a result, from CDD, we observe the antibonding nature of Cs-5p and O-2p orbitals. On the other hand, due to the constructive interference of the wave functions of Nb-4d and O-2p suggest the bonding nature.
Effective mass and photocatalytic activity
To expand light absorption into the visible area and effectively use the solar energy, an efficient photocatalyst needs a bandgap energy less than 3 eV53. The bandgap of the semiconducting CNO proves that it can absorb a wide range of solar radiation. In Fig. 7, Eph represents the energy of the photon and the Eph needs to be greater than Eg. The indirect bandgap (Fig. 4) may be more advantageous for photocatalytic applications because it may lower the radiative recombination rate due to the momentum mismatch between the CBM and VBM, which is advantageous for a longer carrier lifetime and therefore, photocatalytic activity54. The band structures in Fig. 4 also make it clear that the CBM of CNO is more parabolic (highly dispersive) than the VBM. This suggests that the photogenerated electron may have a lower effective mass than the hole effective mass.
Figure 7.
Schematic illustration of photoactivation and charge carriers transfer in CsNbO3.
The rate of diffusion and separation efficiency of the photogenerated carriers have a significant impact on a material's photocatalytic activity55. A high ratio of electron () to hole () effective mass, results a low recombination rate and a large difference between electron–hole mobility. “The E–k relation at the conduction band minimum can be well fitted by a parabolic relation of the form:
| 10 |
where, E is the band-edge energy and k is the amplitude of reciprocal lattice vector. After calculating the second order derivative from the minimum of the conduction band of E–k diagram, the effective mass of electron is obtained.” From the band diagram of GGA-PBE approximation, the is estimated at G-point to be 0.67 me in CBM, whereas the at R-point is estimated to be 2.63 me in VBM. Usually is positive, while is negative. For sx-LDA approach, the has been calculated at G-point in the CBM is 0.61 me whereas the estimated values of at M-point is 4.40 me in CBM. It is noted that electron and hole effective masses of CNO is close to ZnO56, BaTiO32 and RbSr2Nb3O1019 and lower than TiO257 and In2O358 semiconductor photocatalysts. In present work, the low values of and imply that it has high electrical conductivity. The photogenerated carriers can quickly transfer to the surface of CNO, which is crucial for photocatalytic activity. Nevertheless, the low value of hole carrier effective mass (2.63me for GGA-PBE) has a great impact on catalytic efficiency. The low value of carrier effective mass of the hole causes the highest rate of H2 production. In addition, relatively high ratio of electron () to hole () effective mass is associated with easy separation of photogenerated electrons from their associated holes, which lowers the probability of their recombination and increases their availability to perform catalytic processes. This is because a decrease in carrier mass results in a corresponding increase in carrier mobility. Therefore, the reduction of recombination of the electron–hole carrier of CNO enhances its photocatalytic efficiency.
In order to clarify the separation of photogenerated electron–hole pairs over the CNO, it is necessary to find out the conduction and valence band edge potentials of the component. In the case of water splitting, the valence band edge potential should be more positive than the potential needs for oxygen evolution (1.23 eV vs. NHE) and the conduction band potential should be more negative than the potential corresponding to the hydrogen evolution reaction (0 eV vs. NHE). These energy band potentials are calculated using the following empirical equations59:
| 11 |
| 12 |
where, χ is the absolute electronegativity of CNO and the ECB and EVB indicate the band edge potentials of CB and VB, respectively. The Mulliken electronegativity of an atom is determined by the average value of its electron affinity and its first ionization energy60. Eg denotes the acquired electronic bandgap, while Ee resembles the energy of free electrons on the hydrogen scale (4.5 eV).
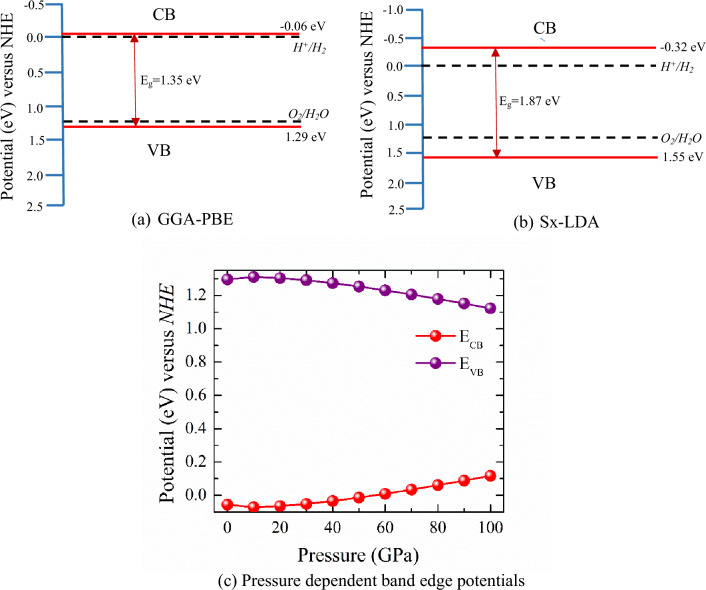
The CNO has an estimated electronegativity, χ of 5.12 eV. Figure 8a and b show the band edge potentials of VB and CB in CNO for the GGA-PBE, and sx-LDA approximations. The thermodynamic aspect of the CBM potential of CNO, which is negative, demonstrates that H+ to H2 reduction will occur which could delay the electron–hole recombination process. As the dilation in the recombination process enhances the photocatalytic efficiency, the negative value of CB potential substantiates the CNO to be a good photocatalytic material. The evolution of O2 from water is revealed by the VBM potential, which is higher than O2/H2O (1.23 eV) in all approaches. The larger value of the VBM potential of CNO indicates the possibility of a spontaneous photocatalytic reaction. Therefore, the VBM potential also proves the CNO is good for water splitting applications.
Figure 8.
Calculated potentials for conduction band minimum, ECB, and valence band maximum, EVB using the band structures and bandgap values calculated by (a) GGA-PBE, and (b) sx-LDA, and (c) Pressure dependent changes of ECB and EVB for CsNbO3.
The band edge potentials that characterize the photocatalytic activity are greatly influenced by the bandgap as shown in Fig. 8c. With increasing pressure, the CB potential initially decreases (becomes more negative) and then increase (after 10 GPa) and exits the potential of hydrogen evaluation reaction i.e., the CNO losses its photocatalytic efficiency. The change of VB potential under pressure also displays a similar effect on photocatalytic activity. The change in the bandgap, Eg is responsible for these changes. However, from these calculations, it can be confirmed that at 10 GPa CNO shows the highest photocatalytic efficiency and at high pressure, it stops functioning as a photocatalyst.
Conclusions
Using the state of art density functional theory, we investigate the effect of hydrostatic pressure on the structural, elastic, electronic, and photocatalytic properties of CsNbO3. The values of Pugh’s ratio, Poisson’s ratio, Cauchy pressure, and Kleinman parameter confirmed the ductile nature below 20 GPa. The obtained high value of fracture toughness and machinability index revealed the good mechanical application against micro-cracks and excellent lubricating qualities. The electronic band structure discloses the semiconducting character of the compound. Two different approaches provide variety in bandgap energy of 1.35 and 1.87 eV for GGA-PBE, and sx-LDA, respectively. The estimated indirect bandgap suggests the good photoactive character of CsNbO3. Under pressure, the bandgap energy increases initially till 10 GPa and then decreases gradually with pressure. The calculated Mulliken effective charge, bond population and bond length revel the good covalency and antibonding character of Nb–O and Cs–Nb, respectively. The calculation of electron charge density was in good agreement with the Mulliken population analysis. Low value of carrier effective mass assert that CsNbO3 has to be good electrical conductivity as well as photocatalytic activity. The calculated band edge potentials revealed the CNO would exhibit excellent water splitting efficiency. The result of the current computations are expected to serve as a foundation for future experimental and theoretical investigations of the suitability of CsNbO3 in various device applications.
Acknowledgements
This study was supported in part by research grant from Begum Rokeya University, Rangpur. Authors are thankful to Department of Physics, Begum Rokeya University, Rangpur for providing computer facility.
Author contributions
M.M.: Conceptualization, data curation and formal analysis, methodology, investigation, writing original draft. M.A.H.: Conceptualization, review & editing, formal analysis, writing original draft, funding acquisition, supervision. M.N.H.L.: Methodology, formal analysis, review & editing, visualization. M.K.: Review & editing. S.K.: Formal analysis, review & editing.
Data availability
The authors ensure that the data supporting the findings of the study are available to M. Monira (muniramarjanum@gmail.com) and can be provided if needed.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
M. Monira, Email: muniramarjanum@gmail.com
M. A. Helal, Email: helalphy82@gmail.com
References
- 1.Baek S-W, Kim JH, Bae J. Characteristics of ABO3 and A2BO4 (A = Sm, Sr; BCo, Fe, Ni) samarium oxide system as cathode materials for intermediate temperature-operating solid oxide fuel cell. Solid State Ion. 2008;179:1570–1574. doi: 10.1016/j.ssi.2007.12.010. [DOI] [Google Scholar]
- 2.Chakraborty A, Liton MNH, Sarker MSI, Rahman MM, Khan MKR. A comprehensive DFT evaluation of catalytic and optoelectronic properties of BaTiO3 polymorphs. Physica B. 2023;648:414418. doi: 10.1016/j.physb.2022.414418. [DOI] [Google Scholar]
- 3.Kreuer KD, et al. Proton conducting alkaline earth zirconates and titanates for high drain electrochemical applications. Solid State Ion. 2001;145:295–306. doi: 10.1016/S0167-2738(01)00953-5. [DOI] [Google Scholar]
- 4.Hashim SS, et al. Perovskite-based proton conducting membranes for hydrogen separation: A review. Int. J. Hydrog. Energy. 2018;43:15281–15305. doi: 10.1016/j.ijhydene.2018.06.045. [DOI] [Google Scholar]
- 5.Lantto V, Saukko S, Toan NN, Reyes LF, Granqvist CG. Gas sensing with perovskite-like oxides having ABO3 and BO3 structures. J. Electroceramics. 2004;13:721–726. doi: 10.1007/s10832-004-5182-z. [DOI] [Google Scholar]
- 6.Zhao YX, et al. Observation of novel charge ordering and spin reorientation in perovskite oxide PbFeO3. Nat. Commun. 2021;12:1917. doi: 10.1038/s41467-021-22064-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ruf F, et al. Temperature-dependent studies of exciton binding energy and phase-transition suppression in (Cs, FA, MA)Pb(I, Br)3 perovskites. APL Mater. 2019;7:031113. doi: 10.1063/1.5083792. [DOI] [Google Scholar]
- 8.Kimura M. Emerging applications using metal-oxide semiconductor thin-film devices. Jpn. J. Appl. Phys. 2019;58:090503. doi: 10.7567/1347-4065/ab1868. [DOI] [Google Scholar]
- 9.Sun B, et al. ABO3 multiferroic perovskite materials for memristive memory and neuromorphic computing. R. Sci. Chem. 2021;6:939–970. doi: 10.1039/d1nh00292a. [DOI] [PubMed] [Google Scholar]
- 10.Konsin P, Sorkin B. Electron-phonon mechanism of mixed displacive and order-disorder phase transitions in oxide perovskites and photoferroelectricity. Feroelectrics. 2007;353:63–69. doi: 10.1080/00150190701367077. [DOI] [Google Scholar]
- 11.Kudo A, Miseki Y. Heterogeneous photocatalyst materials for water splitting. Chem. Soc. Rev. 2009;38:253–278. doi: 10.1039/B800489G. [DOI] [PubMed] [Google Scholar]
- 12.Zou ZG, Ye JH, Sayama K, Arakawa H. Direct splitting of water under visible light irradiation with an oxide semiconductor photocatalyst. Nature. 2001;414:625–627. doi: 10.1038/414625a. [DOI] [PubMed] [Google Scholar]
- 13.Joshi UA, Palasyuk A, Arney D, Maggard PA. Semiconducting oxides to facilitate the conversion of solar energy to chemical fuels. J. Phys. Chem. Let. 2010;1:2719–2726. doi: 10.1021/jz100961d. [DOI] [Google Scholar]
- 14.Helal MA, Farid Ul-Islam AKM, Liton MNH, Kamruzzaman M. Hydrostatic pressure dependent structural, elastic, vibrational, electronic, and optoelectronic properties of superconducting BaCuO3: A DFT insight. J. Phys. Chem. Solids. 2022;161:110452. doi: 10.1016/j.jpcs.2021.110452. [DOI] [Google Scholar]
- 15.Monira M, et al. Effect of hydrostatic pressure on mechanical and optoelectronic properties of ACuO3 (A = Ca, Sr) Jpn. J. Appl. Phys. 2022;61:111001. doi: 10.35848/1347-4065/ac95e7. [DOI] [Google Scholar]
- 16.Lianwei C, Hong M. Laser surface structuring of semiconductors and functionalization. Handb. Laser Micro- Nano-Eng. 2021;1:1017–1061. doi: 10.1007/978-3-030-63647-0_20. [DOI] [Google Scholar]
- 17.Berri S, Bouarissa N. First-principle calculations to investigate structural, electronic, optical, thermodynamic, and thermoelectric properties of ABO3 (A = Cs, Rb and B = Ta, Nb) compounds. Compd. Emerg. Mater. 2022;5:1831–1847. doi: 10.1007/s42247-021-00324-0. [DOI] [Google Scholar]
- 18.Grabowska E. Selected perovskite oxides: Characterization, preparation and photocatalytic properties: A review. Appl. Catal. B. 2016;186:97–126. doi: 10.1016/j.apcatb.2015.12.035. [DOI] [Google Scholar]
- 19.Liton MNH, et al. Electronic, mechanical, optical and photocatalytic properties of perovskite RbSr2Nb3O10 compound. J. Alloys Compd. 2021;867:159077. doi: 10.1016/j.jallcom.2021.159077. [DOI] [Google Scholar]
- 20.Wang W, Wang S, He D, Xu J. Pressure induced phase transition of PbNiO3 from LiNbO3-type to perovskite. Solid State Commun. 2014;18420140:8–12. doi: 10.1016/j.ssc.2014.06.022. [DOI] [Google Scholar]
- 21.Kim E, Kim J, Min K. Prediction of dielectric constants of ABO3-type perovskites using machine learning and first-principles calculations. Phys. Chem. Chem. Phys. 2022;24:7050–7059. doi: 10.1039/D1CP04702G. [DOI] [PubMed] [Google Scholar]
- 22.Zha JW, Yao SC, Qiu Y, Zheng MS, Dang ZM. Enhanced dielectric properties and energy storage of the sandwich-structured poly (vinylidene fluoride-co-hexafluoropropylene) composite films with functional BaTiO3 @Al2O3 nanofibres. IET Nanodielectr. 2009;2:103–108. doi: 10.1049/iet-nde.2019.0010. [DOI] [Google Scholar]
- 23.Putilov LP, Tsidilkovski VI. The role of deep acceptor centers in the oxidation of acceptor-doped wide-band-gap perovskites ABO3. J. Solid State Chem. 2017;247:147–155. doi: 10.1016/j.jssc.2017.01.010. [DOI] [Google Scholar]
- 24.Wu T, Pisula W, Rashid MYA, Gao P. Application of perovskite-structured materials in field-effect transistors. Adv. Electron. Mater. 2019;5:1900444. doi: 10.1002/aelm.201900444. [DOI] [Google Scholar]
- 25.Wang XB, et al. High temperature Raman study of phase transitions in antiferroelectric NaNbO3. J. Mol. Struct. 1996;385:1–6. doi: 10.1016/S0022-2860(96)09397-0. [DOI] [Google Scholar]
- 26.Yan L, et al. Crystalline phase-dependent photocatalytic water splitting for hydrogen generation on KNbO3 submicro-crystals. Int. J. Hydrog. Energy. 2013;38:3554–3561. doi: 10.1016/j.ijhydene.2013.01.028. [DOI] [Google Scholar]
- 27.Zhao L, Liu Q, Zhangb S, Li JF. Lead-free AgNbO3 anti-ferroelectric ceramics with an enhanced energy storage performance using MnO2 modification. J. Mater. Chem. C. 2016;4:8380–8384. doi: 10.1039/C6TC03289C. [DOI] [Google Scholar]
- 28.Fadhali MM, Bakar A, Ali S, Afaq A, Hegazy HH. Effect of pressure on structural, electronic dispersion relations, optical and thermoelectric properties of CsNbO3 perovskite for photovoltaic and energy applications. Polyhedron. 2023;230:116217. doi: 10.1016/j.poly.2022.116217. [DOI] [Google Scholar]
- 29.Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965;140:A1133–A1138. doi: 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
- 30.Bensaid D, Benkhettou NE, Kourdassi A. Structural and electronic properties of BiXO3 (X = Mn, Fe, Cr) J. Mod. Phys. 2011;2:8665. doi: 10.4236/jmp.2011.27075. [DOI] [Google Scholar]
- 31.Clark SJ, Robertson J. Screened exchange density functional applied to solids. Phys. Rev. B. 2010;82:085208. doi: 10.1103/PhysRevB.82.085208. [DOI] [Google Scholar]
- 32.Dujana WA, et al. Structural, electronic, mechanical, thermal, and optical properties of UIr3 under pressure: A comprehensive DFT study. AIP Adv. 2021;11:105205. doi: 10.1063/5.0064021. [DOI] [Google Scholar]
- 33.Helal MA, Ara IE, Islam AKMFU, Rahman MM, Kamruzzaman M. A comparative study based on the first principles calculations of ATiO3. Indian J. Phys. 2016;90:1105–1113. doi: 10.1007/s12648-016-0848-3. [DOI] [Google Scholar]
- 34.Helal MA, Islam AKMA. Elastic, electronic, and optical properties of hypothetical SnNNi3 and CuNNi3 in comparison with superconducting ZnNNi3. Physica B. 2011;406:4564–4568. doi: 10.1016/j.physb.2011.09.018. [DOI] [Google Scholar]
- 35.Mattsson TR, et al. Validating density-functional theory simulations at high energy-density conditions with liquid krypton shock experiments to 850 GPa on Sandia's Z machine. Phys. Rev. B. 2014;90:184105. doi: 10.1103/PhysRevB.90.184105. [DOI] [Google Scholar]
- 36.Jain A, et al. Commentary: The materials project: A materials genome approach to accelerating materials innovation. APL Mater. 2013;1:011002. doi: 10.1063/1.4812323. [DOI] [Google Scholar]
- 37.Agrawal A, Meredig B, Wolverton C, Choudhary A. A formation energy predictor for crystalline materials using ensemble data mining. IEEE. 2016;1:1276–1279. [Google Scholar]
- 38.Zuo L, Hambert M, Esling C. Elastic properties of polycrystals in the Voigt–Reuss–Hill approximation. J. Appl. Crystallogr. 1992;25:751–755. doi: 10.1107/S0021889892004874. [DOI] [Google Scholar]
- 39.Arikawa J, Shiono T. Evaluation of thermal shock resistance for ceramic materials by Young’s modulus. Key Eng. Mater. 2018;766:170–174. doi: 10.4028/www.scientific.net/KEM.766.170. [DOI] [Google Scholar]
- 40.Moazzem Hossain Md. First-principles study on the structural, elastic, electronic and optical properties of LiNbO3. Heliyon. 2019;5:e01436. doi: 10.1016/j.heliyon.2019.e01436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mohanty SK, et al. Influence of NaNbO3 on the structural, optical and dielectric properties of 0.05(K0.5Bi0.5TiO3)–0.95(NaNbO3) composites ceramics. J. Mater. Sci. Mater. Electron. 2019;30:5833–5844. doi: 10.1007/s10854-019-00881-5. [DOI] [Google Scholar]
- 42.Faridi MA, et al. Pressure induced band-gap tuning in KNbO3 for piezoelectric applications: Quantum DFT-GGA approach. Chin. J. Phys. 2018;56:1481–1487. doi: 10.1016/j.cjph.2018.06.003. [DOI] [Google Scholar]
- 43.Frantsevich IN, Voronov FF, Bokuta SA. Elastic Constants and Elastic Moduli of Metals and Insulators Handbook. Naukova Dumka; 1983. pp. 60–180. [Google Scholar]
- 44.Niu H, et al. Extra-electron induced covalent strengthening and generalization of intrinsic ductile-to-brittle criterion. Sci. Rep. 2012;2:71. doi: 10.1038/srep00718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pettifor DG. Theoretical predictions of structure and related properties of inter- metallics. Mater. Sci. Technol. 1992;8:345–349. doi: 10.1179/mst.1992.8.4.345. [DOI] [Google Scholar]
- 46.Kleinman L. Deformation potentials in silicon. I. Uniaxial Strain. Phys. Rev. 1962;128:2614. [Google Scholar]
- 47.Ziati MB, Zahraouy HE. Mechanical stability, electronic, and optical properties of bulk and (001)-surfaces of Sr2RuO4−xFx quaternary alloy. Surf. Sci. 2022;721:122071. doi: 10.1016/j.susc.2022.122071. [DOI] [Google Scholar]
- 48.Majumder R, Mitro SK, Bairagi B. Influence of metalloid antimony on the physical properties of palladium-based half-Heusler compared to the metallic bismuth: a first-principle study. J. Alloys Compos. 2020;836:155395. doi: 10.1016/j.jallcom.2020.155395. [DOI] [Google Scholar]
- 49.Vitos L, Korzhavyi PA, Johansson B. Stainless steel optimization from quantum mechanical calculations. Nat. Mater. 2003;2:25–28. doi: 10.1038/nmat790. [DOI] [PubMed] [Google Scholar]
- 50.Riane R, Matar SF, Hammerelaine L. Ab initio calculations of electronic band structure and charge densities of zinc blende-type GaN, BN and their solid solution B0.5Ga0.5N. Z. Naturforsch. 2008;63:1231–1237. doi: 10.1515/znb-2008-1015. [DOI] [Google Scholar]
- 51.Ziati M, Bekkioui N, Zahraouy HE. Correlation between carrier mobility and effective mass in Sr2RuO4–xFx (x = 2) under uniaxial strain using the Yukawa screened PBE0 hybrid functional. J. Phys. Chem. Solids. 2022;161:110409. doi: 10.1016/j.jpcs.2021.110409. [DOI] [Google Scholar]
- 52.FaridUlIslam AKM, Liton MNH, Islam HMT, Helal MA, Kamruzzaman M. Mechanical and thermodynamical stability of BiVO4 polymorphs using first-principles study. Chin. Phys. B. 2017;26:036301. doi: 10.1088/1674-1056/26/3/036301. [DOI] [Google Scholar]
- 53.Katwal R, Kothari R, Pathania D. An overview on degradation kinetics of organic dyes by photocatalysis using nanostructured electrocatalyst. Deliv. Low Carbon Biofuels Bioproduct Recov. 2021;10:195–213. doi: 10.1016/B978-0-12-821841-9.00005-0. [DOI] [Google Scholar]
- 54.Zhang X, Shen JX, Wang WN, de Walle V. First-principles analysis of radiative recombination in lead-halide perovskites. ACS Energy Lett. 2018;3:2329–2334. doi: 10.1021/acsenergylett.8b01297. [DOI] [Google Scholar]
- 55.Chen X, Shen S, Guo L, Mao SS. Semiconductor-based photocatalytic hydrogen generation. Chem. Rev. 2010;110:6503–6570. doi: 10.1021/cr1001645. [DOI] [PubMed] [Google Scholar]
- 56.Liton MNH, Rani A, Khan MKR, Sarker MSI, Rahman MM, Kamruzzman M. Insight of the role of F-impurity on the structural, electro-optical properties of ZnO: DFT and experiment. Mater. Sci. Semicond. 2023;154:107223. doi: 10.1016/j.mssp.2022.107223. [DOI] [Google Scholar]
- 57.Tang H, Prasad K, Sanjines R, Schmid P, Levy F. Electrical and optical properties of TiO2 anatase thin films. J. Appl. Phys. 1994;75:2042–2047. doi: 10.1063/1.356306. [DOI] [Google Scholar]
- 58.Walsh A, Da Silva JLF, Wei S-H. Origins of band-gap renormalization in degenerately doped semiconductors. Phys. Rev. B. 2008;78:075211. doi: 10.1103/PhysRevB.78.075211. [DOI] [Google Scholar]
- 59.Liu J, Chen S, Liu Q, Zhu Y, Zhang J. Correlation of crystal structures and electronic structures with visible light photocatalytic properties of NaBiO3. Chem. Phys. Lett. 2013;572:101–105. doi: 10.1016/j.cplett.2013.04.040. [DOI] [Google Scholar]
- 60.Casteli IE, et al. Computational screening of perovskite metal oxides for optimal solar light capture. Energy Environ. Sci. 2012;5:5814–5819. doi: 10.1039/C1EE02717D. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The authors ensure that the data supporting the findings of the study are available to M. Monira (muniramarjanum@gmail.com) and can be provided if needed.