Leveraging multi-tier healthcare facility network simulations for capacity planning in a pandemic

Abstract

The COVID-19 pandemic has placed severe demands on healthcare facilities across the world, and in several countries, makeshift COVID-19 centres have been operationalised to handle patient overflow. In developing countries such as India, the public healthcare system (PHS) is organised as a hierarchical network with patient flows from lower-tier primary health centres (PHC) to mid-tier community health centres (CHC) and downstream to district hospitals (DH). In this study, we demonstrate how a network-based modelling and simulation approach utilising generic modelling principles can (a) quantify the extent to which the existing facilities in the PHS can effectively cope with the forecasted COVID-19 caseload; and (b) inform decisions on capacity at makeshift COVID-19 Care Centres (CCC) to handle patient overflows. We apply the approach to an empirical study of a local PHS comprising ten PHCs, three CHCs, one DH and one makeshift CCC. Our work demonstrates how the generic modelling approach finds extensive use in the development of simulations of multi-tier facility networks that may contain multiple instances of generic simulation models of facilities at each network tier. Further, our work demonstrates how multi-tier healthcare facility network simulations can be leveraged for capacity planning in health crises.

1. Introduction

The SARS-CoV-2 (COVID-19) pandemic has resulted in severely stressed healthcare systems across the world, and in many countries, the capacity of existing infrastructure has proven to be inadequate for managing the COVID-19 caseload [1], [2]. To meet this demand-capacity imbalance, makeshift facilities for COVID-19 have been set up around the world - for example, Nightingale hospitals in the UK and COVID-19 Care Centres (CCCs) in India. In this context, there is a need for analytical tools capable of providing quantitative assessments of the extent to which the existing healthcare infrastructure, which are often composed of multiple tiers, in a given region can respond adequately to pandemic caseloads. This is important for planning the capacities of makeshift COVID-19 care facilities.

Generating capacity estimates, along with their distributional information, requires a tool capable of handling the complex interplay of the multiple operational elements associated with the pandemic response strategy (many of which are stochastic in nature) of a multi-tier public health network (PHN). It is evident that the use of a computational technique such as discrete-event simulation (DES), which is capable of handling the above complexities, including the stochasticities associated with the operational element of the pandemic response strategy, becomes necessary. The flexibility of DES makes it among the most frequently used techniques in operations research and management science, including in the healthcare domain [3], [4].

In the literature, there is growing work that discusses DES modelling for resource planning in the context of COVID-19.  Garcia-Vicuña et al. [5] aim at predicting short-term bed requirements in the ICUs and general wards due to the outbreak of COVID-19 in the Navarre region of Spain. VanDeusen et al. [6] use a DES model and a colonoscopy case study to illustrate the effect of capacity reduction, brought about by the pandemic outbreak, on wait time and other operational metrics for non-emergency patients. Allen et al. [7] model a network of nine hospitals in the South of England delivering dialysis services during the COVID-19 outbreak. In this work, a DES modelled the patient flow and a Monte Carlo simulation was used to estimate COVID patients’ travel time. In more recent work, Bovim et al. [8] used DES models to estimate the number of beds required in the emergency department of a hospital during the pandemic for patients awaiting COVID-19 screening reports and also for patients unable to find a bed in upstream COVID-19 wards. Other studies considered the operational performance of individual hospital departments such as radiology [9] and the outpatient laboratory [10] under various COVID-19 related operational protocols. In more recent work, using a systems dynamics simulation, Kamran et al. [11] redesign a vaccine supply chain network by minimizing the costs of the multi-commodity supply chain using simulation–optimization methods.

To the best of our knowledge, a comprehensive DES-based analysis of the operational response to the pandemic in a multi-tier hierarchical PHN has yet to be reported in the literature. Towards this, our study demonstrates how DESs of PHNs can be leveraged to conduct capacity planning for both the existing PHN and augmentative makeshift CCCs. Public healthcare infrastructures are often composed of multiple tiers. The Indian public healthcare system, for example, consists largely of three levels of formal medical care: (a) the primary health centre (PHC, for the provision of primary care), (b) the community health centre (CHC, for the provision of primary and limited secondary care), and (c) the district hospital (DH, for provision of secondary and limited tertiary care) [12]. In this research, we developed a discrete-event simulation (DES) of a network of public health facilities using the ‘generic modelling’ approach [13], which is typically required when multiple instances of a facility type operate within a healthcare delivery system. The model was applied to a multi-tier public health network (PHN) in an Indian district comprising 10 PHCs, 3 CHCs, and one DH. We worked with a clinical expert - a pulmonologist (co-author) directly involved with COVID-19 care at one of the largest public hospitals in India - to formulate a COVID-19 response scenario that can plausibly be implemented across the PHN in the case study district. The study helped us determine the capacity of the makeshift CCCs while also ensuring adequate utilisation of the existing PHN and makeshift CCCs.

Given the ubiquity of multi-tier PHNs, our work will be of interest to public health programme managers and planning authorities associated with regional public or private health systems. Our work provides a comprehensive accounting of the different operational elements that must be integrated into a decision support tool capable of answering key operational questions regarding both the patient as well as provider experiences associated with the pandemic response of a multi-tier PHN.

The remainder of the paper is organized as follows. In Section 2, a discussion of the relevant extant research is presented. Section 3 then details the development of the multi-tier PHN simulation model using the generic modelling approach, along with the estimation of the model input parameters. Following this, Section 4 presents the formulation of the simulated COVID-19 response scenario, including the case and testing load estimation, and the formulation of clinical and operational pathways for COVID-19 patients across the PHN. In Section 5, the simulation experiments and their outcomes are described. Finally, in Section 6, a discussion of key study findings and their potential impact is presented. This section also outlines study limitations and future directions of research.

2. Modelling of healthcare networks using DES: A review of the literature

Our review of the literature has identified that DES-based healthcare network modelling can be classified into: (a) single-tier network modelling, (b) multi-tier network modelling, (c) generic modelling of healthcare facilities, and (d) Application of DES in the context of infectious disease outbreaks. Single-tier network simulation models consist of all the units or facilities delivering care at a specific level, for example, a network of primary care hospitals or a network of general physician clinics. In comparison, multi-tier network simulation models incorporate the interconnected structure of healthcare delivery networks. Multiple patient classes, complex patient pathways, and a multitude of tier-specific resource configurations make modelling such networks challenging. Given that a healthcare network consists of several tiers, with each tier comprising operational units that largely perform similar functions, a generic modelling approach for network modelling can reduce complexity and lower the time for model implementation. Generic modelling proposes building reusable models when systems being modelled exhibit operational commonalities. Relevant literature is presented below, along with a tabular summary ( Table 1).

Table 1.

Literature review: classification and summary of key studies.

Study	Research overview	Type of study
Abe [33 ]	DES of primary care facility for staffing level determination	Single-tier (ST), Primary (P), Multi-patient (MP), Developing country (D)
Allen et al. [16 ]	DES model of neonatal network to aid in capacity, service, and location planning,	Secondary (S), Single patient (SP), Single-tier network (STN)
Allen et al. [7 ]	Network simulation for dialysis in England in pandemic outbreak	SP, STN, COVID-19 (C)
Bayer et al. [34 ]	Patient flow modelling in case of a stroke across hospitals	ST, T, MP
Fatma et al. [14 ]	PHC network simulation using stochastic metamodels	P, MP, STN, D, Generic modelling (G)
Ferreira et al. [35 ]	Surgical centre of a large hospital was simulated to analyze effect of increase of PABs	ST, S, MP
Fetter and Thompson [36 ]	Whole hospital simulation	Multi-tier (MT), S, MP
Fialho et al. [37 ]	Simulation on PHCCs and effect of upgradation to higher level facilities (FHUs)	ST, P, MP, D
Garcia-Vicuña et al. [5 ]	Short term bed planning at ICUs and general wards in Spain	MP, MT, C
Gunal and Pidd [22 ]	Conceptual simulation models of a hospital	MP, MT, G
Harper [24 ]	Modelled operational resources using genereic modelling	MP, MT, G
Hung et al. [38 ]	DES of a pediatric emergency department for staffing analyses in over-crowding scenario	ST, S, MP
Konrad et al. [39 ]	Patient flow for mental health clinic	ST, P, SP
Landa et al. [40 ]	DES of internal medicine department for resource utilisation	ST, S, MP
Le Lay et al. [41 ]	DES model that predicts bed and staff requirement in France	MP, MT, C
Matta and Patterson [17 ]	Patient pathways in an Oncology department of a hospital	T, SP, Multi-tier network (MTN)
Mustafee et al. [18 ]	DES model of a supply chain. Showed distributed simulation for rum time reduction	MTN
Zeltyn et al. [42 ]	Multi-class single facility simulation of an ED for short-, medium- and long-term staffing level planning	MP, T, ST
McClean et al. [43 ]	Stroke care system modelling using analytical as well as simulation approaches	SP, ST, T
Mustafee et al. [15 ]	DES model of the hematology outpatient clinics operating in four different hospitals	T, SP, STN
Ortiz-Barrios et al. [44 ]	Gynecological outpatient unit simulated to evaluate improvement strategies	ST, S, MP
Patrick et al. [19 ]	Capacity planning for LTCs and SHs	S, MP, MTN
Pitt [23 ]	DES for bed utilisation in a hospital	MP, MT, G
Revankar et al. [45 ]	Pathways of skin care patients in emergency, inpatient and outpatient units of a hospital	MT, T, SP
Shi et al. [46 ]	Simulation analysis of patients visiting primary care clinics	ST, P, MP
Steins and Walther [26 ]	Planning critical care resources in intensive care units	MP, ST, G
Swisher et al. [47 ]	Visual DES model of family physician clinic. Used OOP for reusable models	ST, P, SP, G
VanBerkel and Blake [25 ]	Generic simulation in general surgery department to reduce waiting time and capacity planning	MP, MT, G
VanDeusen et al. [6 ]	Effect of reduced capacity due to COVID-19 outbreak on non-emergency patients	SP, ST, C

(a) Single-tier network simulation models. Research which explicitly models a network of primary healthcare centres in an Indian district was presented by Fatma et al. [14]. The major highlight of the work was the development of a stochastic metamodel - simplified versions of the full-featured facility simulation models (parent model) – which yields computational gains in runtimes versus the parent simulation model. Mustafee et al. [15] created a DES model of the haematology outpatient clinics operating in four different hospitals. Further, Allen et al. [16] developed a DES model of neonatal network to support capacity, types of services, and location planning. The model predicted the number of cots, nurses, and units required to meet the guidelines and estimated travel time for parents to reach the hospitals. A separate piece of research by Allen et al. [7], discussed earlier in Section 1, models a single-tier network of hospitals delivering dialysis services during the COVID-19 outbreak.

(b) Multi-tier network simulation models. Our literature search found only a few studies that modelled a multi-tier healthcare network. In the study by Matta and Patterson [17], a large oncology department of a hospital that comprised three major oncology clinics, fourteen separate diagnostic testing centres, and one large treatment centre was simulated using DES methodology. The authors designed a stratification framework that evaluated clinical performance and presented an approach to evaluate performance measures. Mustafee et al. [18] developed a DES model of the UK National Blood Service (NBS) supply chain to explore blood unit ordering policies. The authors demonstrated the use of distributed simulation to decrease simulation execution time. Patrick et al. [19] presented work on the capacity planning of a small network of facilities using DES. The network consisted of community healthcare hospitals and long-term care facilities (LTCs) and supportive housing (SH). They built a model representing patients’ flow to the SHs and LTCs from the hospitals and the community and conducted capacity analyses.

(c) Generic modelling studies. There are several examples of the use of a generic modelling approach in healthcare, for example, blood supply chain [20] and the modelling of ambulance systems [21]. In healthcare facility operations, which is the subject of our paper, Gunal and Pidd [22] described the conceptual development of generic DES models of a hospital with an accident and emergency department (A&E) and outpatient clinics. Pitt [23] described a generic simulation system of modelling to assess bed utilisation in a hospital. For modelling operational resources in a hospital, Harper [24] proposed a generic modelling framework. The authors demonstrated the framework’s usability through case studies on theatre capacity and general surgery bed needs. VanBerkel and Blake [25] developed a simulation by adopting the generic modelling approach for the general surgery department division at Capital District Health Authority in Canada. The objective was the reduction of waitlisted patients via capacity planning. To plan critical care resources in intensive care units (ICUs), Steins and Walther [26] developed generic DES models. They modelled patient pathways in the ICU and reported bed occupancy, coverage (patients admitted upon arrival), and transfer (referred to other ICUs for resource shortage). Next, we discuss DES Models of operational response to epidemics/pandemics other than COVID-19.

(d) Application of DES in the Context of Infectious Disease Outbreaks.Multiple studies in the literature use DES models to analyse the response of health systems in the context of infectious disease outbreaks/pandemics. Broadly, such studies focus on (a) the response of multi-facility health systems to infectious disease (viral influenza pandemics) and bioterrorism attacks [27], [28], [29] (b) capacity planning of single facility healthcare facilities [30], [31] and (c) capacity planning for large vaccination centers in terms of wait times for vaccination, staff levels, and throughput (e.g., number of persons that can be vaccinated in a day) [30], [31], [32]. Several studies that consider multi-facility health systems also use infectious disease spread models (e,g., SIR models) to simulate the patient load.

Studies which considered a single facility focused on capacity planning for drug (antibiotic) distribution centers in terms of the number of staff [32], oxygen requirements in a developing country health facility when faced with a childhood pneumonia outbreak [31], and staff capacity and patient flow planning for drug and vaccine dispensaries (clinics) [30].

We now discuss in more detail the studies that consider multi-facility health systems. Miller et al. [27] show a hypothetical spread of smallpox infection due to a bioterrorism attack and employ two DES models to study the spread of the disease and the delivery of care. The first model simulates the spread of the infection, and the second simulates the care provision process for infected patients at multiple facilities, all of which are of the same type – i.e., a single-tier network of facilities. Miller et al. [28] adapt this approach to pandemic influenza as well, where they conclude that a mix of strategies such as social distancing, targeted vaccination, and dispensation of medication may prevent patient demand from exceeding available health system capacity. The authors estimate the number of beds and acute care nurses required under each pandemic mitigation strategy. Woodul et al. [29] also considered the response of a hospital system in a region to the increase in demand during an influenza pandemic. They simulated bed availability in twelve hospitals in the network – no other operational aspects or resources were included in their models, as available bed numbers were linked to provider and space availability as well.

Our work contributes in the following ways. (a) We developed a DES of a PHN using the principles of ‘generic modelling’ [13]. From a generic modelling standpoint, our work is the first to demonstrate the implementation of the archetypal ‘generic’ models and their modifications (A.1, A.2) within a multi-tier PHN simulation. (b) To the best of our knowledge, our work is the first DES study to comprehensively consider the capacity planning of a multi-tier PHN, including augmentative makeshift facilities, in the context of an infectious disease pandemic. (c) Our DES model of a PHN considers multiple patient types (in addition to COVID-19 patients). In our knowledge, multi-tier healthcare facility network simulations (e.g., the work by Matta and Patterson [17], who consider oncology patients) do not consider more than one patient or medical care type.

3. Development of the multi-tier PHN model using a generic modelling approach

This section introduces the readers to the three tiers of an Indian PHN (PHC, CHC and DH). The generic modelling approach for the development of the PHN and CHC models is also discussed. The section concludes with an outline of the makeshift COVID-19 Care Facility (CCC) model that is linked to the PHN model for the case study district in question.

The PHN simulation was developed on the Python programming platform, using the open-source discrete event simulation library salabim [48]. The computational modelling was performed on a workstation with an Intel i7 four-core processor having 8 GB of random access memory. Internal validation of the model involved verifying the logical consistency of the outcomes of the model with respect to the operational pathways and the input parameter estimates used in the model. External model validation of the individual facilities in the network was also performed. These have previously been described in Shoaib and Ramamohan (2022) [49] (PHCs) and in Shoaib and Ramamohan (2021) [50] (CHCs). For example, wait times for outpatients from the PHC simulations were validated against outpatient wait times in a similar facility in an urban region; for CHCs, wait times for outpatients and utilisation estimates for doctors were found to agree with in situ observations for these outcomes (ibid).

3.1. Primary Health Centre (PHC) model

In the Indian public healthcare system, the first call for patients is the Primary Health Centre (PHC). The PHC primarily provides outpatient and antenatal care; however, inpatient care on a limited basis for minor conditions and childbirth care are also provided [12]. The facilities are staffed by one or two general physicians who are present primarily during outpatient hours. Nursing staff include a nurse dedicated to providing care to inpatients and childbirth patients, and a second nurse to perform lifestyle disease checks and counselling for outpatients. PHCs typically also house a small inpatient section with four to six beds and a childbirth room capable of serving one patient at a time. An in-house clinical laboratory for routine investigations and a pharmacy, which also handles patients’ registration, are also present. Doctors attend to both inpatients, childbirth patients and outpatients during outpatient hours, whereas staff nurses work in shifts so that childbirth patients and inpatients can avail care around the clock. COVID-19 clinical and operational pathways pertaining to PHCs are discussed in Section 4.2. Implementation-specific details on COVID-19 pathways and model parameters are included in Appendix A.1.

Generic Modelling Approach:We surveyed multiple facilities and developed a generic or ‘archetypal’ model that represented the operational aspects common to most facilities [51]. To account for the differences in the services offered and staff levels, we grouped the PHCs into three configurations. The first configuration represents the ‘archetypal’ PHC model as it was closest to the configuration described in the government guidelines [12]. We modified the archetypal model to represent the operations of the other two PHCs. Further details regarding each configuration (configuration 1 represents the archetypal configuration) are provided in Table A.6 in Appendix A.1.

3.2. Community health clinic (CHC) model

CHCs are designed to provide secondary care and also act as referral units for up to four PHCs. They serve as intermediate-level hospitals, offer more extensive services, and attend to more complex cases; however, they do not provide tertiary and specialised care. Services offered include routine surgical procedures, childbirth, antenatal care, and both general and specialised outpatient care in gynaecology and obstetrics, paediatrics, and dental care. CHCs have a relatively large inpatient section, typically with 20–30 beds, and also contain facilities for general surgery (an operating room), childbirth (a labour room), and emergency care (3–6 beds). Further, they house a diagnostic laboratory for routine assay-based investigations as well as for conducting X-ray, ultrasound and electrocardiogram-based investigations. COVID-19 clinical and operational pathways for the CHC are discussed in Section 4.2, and their implementation for CHCs and simulation model parameters are included in Appendix A.2.

Generic modelling approach: Given that CHCs were established according to guidelines published by the Indian government [12] that outline staffing and resource levels, CHCs across the country are likely to have similar operational patterns. This was evident from our visits to the CHCs and further backed up by the literature [52]. The commonalities in staffing, resource levels and operational patterns enabled the development of an ‘archetypal’ generic model for CHCs. These were subsequently modified to account for the different configurations encountered in practice. Similar to PHCs, we determined that the CHCs could also be grouped into three configurations, with the first configuration being the archetypal ‘generic’ one. Each of the CHCs we include in the model represents a different operational configuration - that is, CHCs 1, 2 and 3 in Table A.7 in Appendix A.2 represent configurations 1, 2 and 3, with configuration 1 representing the archetypal CHC configuration. Input parameters associated with non-COVID-19 patients for the CHC models were estimated based on the data collected during our visits and from the literature [52].

3.3. District hospital (DH) model

District hospitals (DHs) are relatively large hospitals established to provide secondary care on a comprehensive basis and, to some extent, tertiary care. According to government guidelines for DHs, each district will have a DH with 75–500 beds depending upon the population and the geographical terrain of the catchment - for example, sparsely populated mountainous regions may have smaller DHs [53]. Services offered are grouped as essential, such as general medicine, general surgery, ophthalmology, intensive care units (ICUs), and radiology; and desirable, which include general specialities (dermatology, radiotherapy, dialysis service, etc.) and super specialities (such as neurology). Given the size and complexity of DHs, developing a comprehensive model of its operations, including both COVID-19 and non-COVID-19 patient flow, would be outside the scope of this study. Therefore, we model only the COVID-19-related services in the DH under the pandemic response scenario detailed in Section 4. Further description of the development of the COVID-19 pathway for the DH Model can be found in Appendix A.3.

The following aspects of COVID-19 care are included in the DH model: (1) testing and triaging, (2) general ward care, (3) ICU care with supplemental oxygen, and (4) ICU care with ventilator support. A patient can access the DH in one of two ways: (1) by approaching the DH directly for testing and triaging, and (2) by referral or transfer from a PHC or a CHC (for patients of types B and C, see Table 2). Given the relatively large proportion of patients who lack home isolation facilities in India, it is immediately apparent that the inpatient capacity at the CHCs and the DH is insufficient. Therefore, we simulate a CCC facility, offering inpatient COVID-19 care facilities similar to that provided in the DH, and include it in the network simulation.

Table 2.

Clinical pathways simulated for COVID-19 patients.

Triage categories	Patient subclassification	Inpatient resources involved	Pathway, with lengths of stay (days)
Mild (94%)	Not applicable	None at DH; isolation ward at CCC	Home isolation (90%) or isolation ward (10%) at the CCC, with LOS = U[7,14]
Moderate (4%)	Type A (90%)	General ward	Admission to the general ward. LOS = U[4,5]
	Type B (8%)	General ward, ICU with supplemental oxygen support	Admission to the general ward, LOS = U[3,4]; followed by ICU bed with supplemental oxygen support, LOS = U[5,7]; then general ward, LOS = U[2,3]
	Type C (2%)	General ward, ICU with ventilator support	Admission to the general ward, LOS = U[3,4]; followed by ICU bed with ventilator support, LOS = U[5,10]; then general ward (75%) with LOS = U[4,7], else patient exits via death (25%).
Severe (2%)	Type D (25%)	ICU with ventilator support	Admission to the ICU with ventilator support, LOS = U[2,3]; followed by exit via death
	Type E (25%)	General ward, ICU with ventilator support	ICU with ventilator support, LOS = U[5, 10]; followed by treatment at the general ward U[4, 7] (90%), 10% transition to Type F pathway at this point
	Type F (50%)	General ward, ICU with supplemental oxygen support	ICU with ventilator support, LOS = U[5, 10]; followed by treatment at the general ward U[2, 3] (90%), 10% transition to Type E pathway at this point

LOS = length of stay. DH = district hospital. CCC = COVID-19 care centre. ICU = intensive care unit. U[x, y] = discrete uniform distribution with parameters x and y.

3.4. COVID-19 care centre (CCC) model

The CCC offers the following components of COVID-19 care: (a) isolation facilities for patients with mild COVID-19 that do not have adequate home isolation facilities; (b) general ward care, (c) ICU care with supplemental oxygen, and (d) ICU care with ventilator support. The CCC does not offer testing and triaging because it is a facility that patients access only via referral; thus, following the triage at PHC/CHC/DH and only in cases where an appropriate bed in either CHC or DH is not expected to be available, are patientsreferred to the CCC.

COVID-19 clinical and operational pathways pertaining to DH and CCCs are discussed in Section 4.2. Implementation-specific details on DH/CCC COVID-19 patient flow and model parameters are included in Appendix A.3.

We end this section with a list of the overarching modelling assumptions used in developing the PHN simulation.

• •All resources (beds, equipment, etc.) and staff are available throughout their duration of service - in other words, we assume no interruptions of service occur.
• •The medical staff at PHCs, CHCs, and the DH are trained in COVID-19 testing and clinical management protocols.
• •All tests for COVID-19 (especially for patients arriving newly to PHCs, CHCs and the DH) are conducted only during outpatient hours.
• •Information on bed availability at the DH and the CCC is accessible at facilities that offer testing and triaging (PHC, CHCs and DH).
• •There is sufficient transportation capacity at each facility in the network for transferring patients from one facility to another.
• •In facilities where inpatient capacity (the number of beds) is reduced under the pandemic response scenario, we assume the non-COVID-19 patient load also reduces proportionally. This is relevant for the CHCs and the DH, where under the pandemic response scenario described in Section 4, 50% of the inpatient capacity is reserved for COVID-19 care. More specifically, because we do not have information regarding non-COVID-19 patient loads at the DH, this could imply that inpatient care provided to non-COVID-19 patients is also reduced by half. However, the fact that non-COVID-19 patient loads have decreased across the world, including in India, either due to fears of infection at healthcare facilities on the part of patients or because said facilities are deferring treatment due to stresses placed on resources by the pandemic [54] may provide support for this assumption.

4. COVID-19 response scenario for experimentation

In this section, we describe the formulation of the COVID-19 response scenario that we simulate, including (a) the testing and treatment pathways operationalised across the multi-tier PHN and the classification of patients into different categories of inter-related clinical and operational pathways depending upon their severity of illness (Section 4.1), and (b) determining the case and test load to simulate and the types of patients to include in the model for testing and treatment (Section 4.2).

4.1. COVID-19 clinical and operational pathways

We worked with a clinical expert - a pulmonologist directly involved with COVID-19 care at one of the largest public hospitals in India - to formulate a COVID-19 response scenario that can plausibly be implemented across the PHN. The pandemic response scenario that we formulate involves two key aspects: (a) for the PHC, its operationalisation primarily as a testing and triaging centre; and (b) for the CHCs and DH, in addition to their operationalisation for testing and triaging, reserving a certain proportion of the inpatient care resources for COVID-19 patients. Due to limited medical staffing levels in these centres, we assume that doctors, nurses and laboratory technicians are shared between COVID-19 and non-COVID-19 resources; however, in the DH, we assume that the same set of resources are exclusively assigned to provide COVID-19 care.

When a patient is diagnosed at a PHC, CHC or DH with COVID-19, they undergo a triaging procedure where the doctor classifies them as having a mild, moderate or severe case of COVID-19. This is consistent with the COVID-19 clinical management guidelines published by the World Health Organization [55]. The proportions of patients diagnosed as having mild, moderate or severe disease may be determined from the literature [55]; however, we opted to base these estimates on the experience of our clinical collaborator. To obtain these estimates and other relevant modelling information such as clinical pathways for each of these patient types, length of stay estimates in different hospital units for each patient type, test sample collection times, triage times, service times of doctors and nurses for patients of each type in various hospital units (for example, the general ward, and intensive care unit beds with supplemental oxygen support) etc., we designed a detailed questionnaire to be filled by our clinical collaborator. The expert’s responses to the questionnaire are reflected in the input parameter estimates for the network simulation shown in Table 2. Our engagement with the healthcare expert also enabled us to map patient subclassifications and associated clinical pathways for patients with mild, moderate and severe COVID-19 (summarised in Table 2).

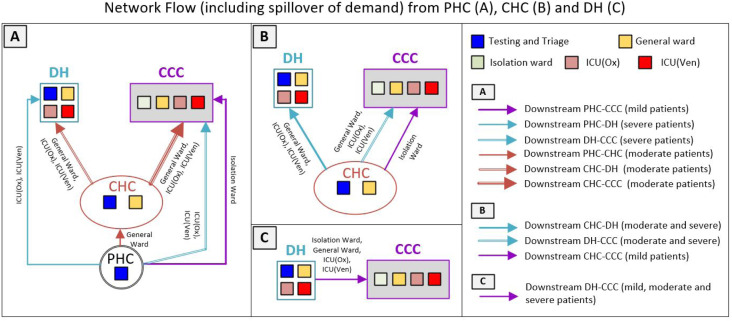
Patient subclassifications and associated clinical pathways. Patients with mild COVID-19 are advised to isolate at home, failing which they are transferred to the isolation ward at the CCC. In the Indian context, these comprise the majority of COVID-19 patients. Those requiring rigorous monitoring either due to the severity of their symptoms or other risk factors are categorised as moderately ill. Most of these patients are admitted to the inpatient ward of the CHC, the general ward of the DH, or the CCC (patient Type A). We define two other clinical pathways (Type B and Type C in Table 2) for patients judged to have moderate disease, which accounts for the possibility that their condition can deteriorate, including succumbing to death. For patients categorised as having severe COVID-19, we define specific pathways to account for the following possibilities: (a) critically ill patients presenting in severe distress requiring immediate ventilator support, whose condition worsens and results in death (Type D); (b) patients presenting with breathing difficulties requiring supplemental oxygen, whose condition then deteriorates (Type E); and (c) patients presenting with breathing difficulties requiring supplemental oxygen, whose condition then improves (Type F). We also account for possible transitions between pathways, particularly between Types E and F. The operational pathways for the PHN network are illustrated in Fig. 1.

Fig. 1.

Facility types, associated resources/services and overarching patient flow in the modelled public healthcare facility network. ICU = intensive care unit. ICU (Ox) = ICU with supplemental oxygen support. ICU (Ven) = ICU with ventilator support.

The wait time threshold and patient transfer. The wait time thresholds before which patients are transferred to another facility - 6 h for moderately ill patients and 30 min for severely ill patients - were determined based on discussions with our clinical collaborator. However, these can be modified to suit the thresholds used within the PHN of interest to the analyst. The threshold for severely ill patients is implemented only if the patient is waiting for the resource in the same hospital (e.g., a patient admitted to the general ward of the DH is waiting for an ICU bed in the same DH). If they are waiting for the resource in another facility (e.g., a patient who has been triaged in a CHC requiring an ICU bed in the DH), they are transferred to the first downstream facility where a bed is available or to the CCC, where wait times are likely to be substantially lower than in the DH because of its significantly higher resource levels. A key point here is that other than for patients categorised as moderately ill at the PHC, all patients whose wait times exceed the appropriate threshold (where applicable) are transferred to the next downstream facility (e.g., a DH or a CCC) only if a bed is available. This check is performed at the facility where they are currently located. For example, a patient triaged to be severely ill at the PHC is transferred to a DH only after determining from the PHC whether there is an ICU bed available at the DH. If a bed is unavailable, the patient is transferred to the CCC. Patients categorised as moderately ill at the PHC are immediately transferred to the CHC, where they wait for up to 6 h before a second transfer to a DH or a CCC is considered. This is because the caseload we simulate is not high enough that a large proportion of patients transferred to the CHC require a second transfer; further, CHCs are likely to be better equipped to handle any sudden deterioration in a moderately ill patient’s health than a PHC.

4.2. COVID-19 case and test load estimation

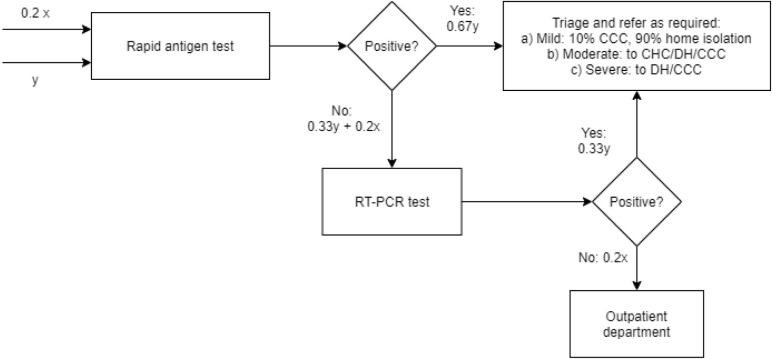
We envision that the PHN simulation can be used by stakeholders such as the district or state public health administration for capacity planning and evaluation of response scenarios given a short- to medium-term forecast (e.g., up to a month or two months that encompasses the beginning, peak and subsequent waning of a wave) of the COVID-19 case load that may be generated by district- or city-level COVID-19 dynamic transmission models such as the study by Agrawal et al. [56]. For this study, given that actual COVID-19 caseloads are available in the form of daily records, we utilised the COVID-19 district-level surveillance data published by the district health administration [57]. Taking the example of September 2020, the summary data shows that 8,586 COVID-19 cases were recorded for this month in the district. We assumed that the caseload would be distributed equally across the different facilities that comprise the PHN: one DH, three CHCs and ten PHCs. Thus, one-third of the daily caseload would be handled by the DH, one-third equally distributed between the three CHCs and the remainder equally distributed across the ten PHCs. Once the number of COVID-19 cases arriving on a given day to a facility is estimated, then their interarrival times were determined assuming Poisson arrivals.

With regard to determining the COVID-19 testing load at each facility, we assumed that the tests conducted at each facility would be for symptomatic COVID-19 patients seeking care, including a certain proportion of non-COVID-19 patients who present with COVID-like symptoms and hence undergo testing. We considered using the actual number of tests conducted on a given day in the district (reported by the district public health administration) and apportioning the testing load across the facilities in a manner similar to the COVID-19 caseload. However, tests are conducted not only for symptomatic patients but also for the close contacts of each symptomatic case per the test protocol established by the government. A large number of tests (an average of 3,120 per day) - relative to the average daily caseload of approximately 300 - were conducted on average in September 2020 in the district under consideration. These ‘extra’ tests likely represent tests conducted for close contacts of symptomatic COVID-19 patients, persons seeking testing due to travel, or uninfected persons seeking testing because they may display COVID-like symptoms (e.g., fever due to a non-COVID-19 condition), etc. These tests, particularly those for close contact with symptomatic COVID-19 patients, are generally conducted by contact tracing and surveillance teams. We assumed that most of the tests conducted at the DH, PHCs and CHCs in our pandemic response scenario would consist of tests conducted for symptomatic patients seeking care at these facilities. This is consistent with a scenario wherein symptomatic patients seeking tests at public health facilities are responding to public health awareness campaigns advising persons displaying typical symptoms of COVID-19 to undergo testing. However, patients without COVID-19 who display similar symptoms may also seek testing; for example, a patient who develops a fever or a cough due to a non-COVID-19 condition may present at the public health facility seeking testing. We estimate this number to be 20% based on the prevalence of fevers, coughs, and other COVID-19-like symptoms as a proportion of the set of conditions for which patients commonly seek care at PHCs [58]. Therefore, we estimated that approximately 20% of non-COVID-19 patients visiting the PHC/CHC/DH also undergo testing because they display one or more COVID-like symptoms.

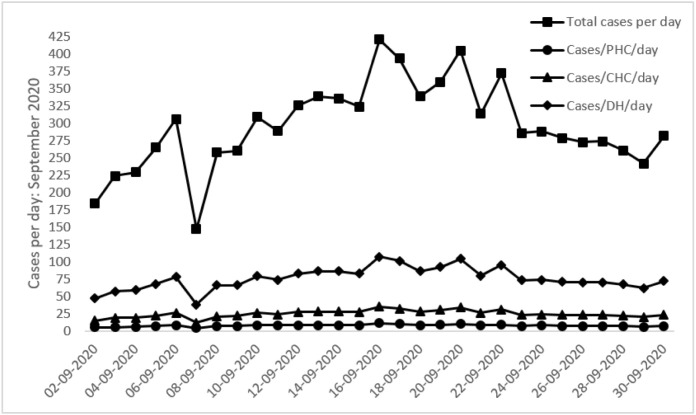
We also account for asymptomatic cases of COVID-19. There is substantial variation in the literature regarding the proportion of COVID-19 cases that are asymptomatic, with a systematic literature review and meta-analysis reporting a range between 20%–70% [59]. Given this wide range, we have conservatively assumed that 25% of COVID-19 cases are asymptomatic, and have correspondingly adjusted the caseload simulated in the model. The daily total caseload and the caseload by facility across the month are depicted in Fig. 2 below. The daily total caseload plot in Fig. 2 represents the actual data maintained by the district administration [57]. The plots depicting facility-wise estimates are obtained by apportioning daily total caseloads to each facility. The apportionment technique was necessary since caseload data is available only at the district level. However, if facility-level caseload projections based on actual facility-level data are available in the future, they can be used directly in the DES model.

Fig. 2.

Daily total caseloads and caseload by facility type. Note: the total cases per day plot represents the actual number of COVID-19 cases detected in the district, whereas the cases per facility (PHC/CHC/DH) per day plots are estimated using the total cases per day records for use in the model.

The testing protocol we implement at each facility is described in Appendix A.1, where we discuss how we model testing and triaging at the PHCs. The detailed clinical and operational pathways for COVID-19 patients in our network simulation is provided in algorithmic form in Appendix B.

5. Network simulation outcomes for the pandemic response scenario

A key objective of this study is to demonstrate the application of a healthcare network simulation for analysing pandemic response strategies for capacity planning. The network simulations may be constructed during periods of routine healthcare delivery by identifying key facilities, developing and validating individual models and integrating their instances into a network simulation. Further to routine operational analysis, such models can be readily modified in a crisis such as the COVID-19 pandemic to plan credible response strategies.

The validation of the network simulation is discussed next, followed by the presentation of the network simulation outcomes for the pandemic response scenario developed in Section 4.

A validation approach that compares the model outcomes, namely, waiting times for resources and resource utilisation estimates, with primary data from the healthcare facilities would be feasible only if we simulated the actual COVID-19 response strategy implemented in the PHN. However, we were unable to visit the PHCs, CHCs and DH facilities due to pandemic restrictions. While a few aspects of the pandemic response strategy currently implemented in the public healthcare system can be determined from publicly available internet sources, in-person visits and data collection at the individual facilities in the network becomes essential because many PHCs and CHCs are located in relatively remote rural regions. These facilities typically do not maintain digitised information relevant from a simulation modelling and validation standpoint. For example, data points on patient arrival, resource allocation, and exit times are not generally recorded due to the lack of automated patient flow systems. As such, operational outcomes such as patient wait times, lengths of stay (especially for outpatients) and resource utilisation could only be estimated by collecting data and observing processes through on-site visits. However, as our coauthor is a clinician with extensive experience in respiratory diseases and the clinical and administrative management of COVID-19, their clinical expertise helped us estimate model parameters such as lengths of stay and service times. The coauthor’s domain knowledge also enabled us to establish the face validity of our network model. Establishing face validity with domain experts has been widely reported in the literature. For example, a recent review of hybrid simulation studies revealed that from a total of 35 papers that reported model validation, 11 studies had an element of face validity being established with domain expertise [60].

5.1. Simulation outcomes by facility type

Simulation outcomes reported in this section are estimated from 50 replications, each requiring approximately 2 min of computational runtime. The number of replications were determined by conducting an analysis of the simulation output variance associated with key outputs – for example, the variance in the ICU ventilator bed utilization estimate. The variance values were plotted against the number of replications, and it was observed that the variances of these outputs stabilized at a threshold of approximately 30 replications. Therefore, as a conservative measure, we chose to conduct 50 replications for this study based on the above simulation output variance analysis.

The outcomes were recorded for the PHN’s simulated response under the pandemic response strategy to the caseload described in Section 4. The caseload was introduced in the simulation after it had reached a steady-state during a warm-up period of 180 days. During the warm-up period, the model was simulated using a constant COVID-19 caseload, which equalled the caseload for the first day in the 30-day period of interest. The warm-up period was estimated by observing the period after which key simulation outcomes, such as the utilisation of ICU beds with ventilators at the DH, stabilised. We observed that this stabilisation occurred after approximately 120 days of simulation time; however, we conservatively chose a warm-up period of 180 days based on this observation.

As discussed in Fig. 2 , we executed the model for a 30 day period given that generating forecasts for longer than 3–4 weeks from a dynamic transmission model for diseases such as COVID-19, where the public health situation can rapidly evolve due to interventions such as lockdowns, is not recommended [61]. We note here that while the results we generate are not ‘steady state’ results in a queueing-theoretic sense, neither can they strictly be considered to generated from the ‘transient’ state of the simulation. This is because the question of whether the simulation period of interest with a time-varying caseload corresponds to the steady state or transient period depends on how ‘steady state’ would be defined for the simulation in this situation. For the COVID-19 case, the number of cases appears to vary with time as a wave, and during the course of the pandemic, multiple waves of varying amplitude and frequency are likely to occur before the pandemic wanes. Thus, the steady state for such situations can be considered as the period when the pandemic wanes and the number of cases per time unit dwindles to zero or a low, approximately constant number. However, such a steady state is not very interesting from an operational planning standpoint, and hence we consider a ‘wave’ of the pandemic as the duration of interest.

However, as described earlier, we also ensure that the simulation achieves steady state in the queueing theoretic sense with a constant caseload before we introduce the time-varying caseload corresponding to the period that encompasses a ‘wave’ of COVID-19 cases. Therefore, given this nuance, we prefer not to define the simulation period from which we extract outcomes as either steady state or transient in the queueing theoretic sense. Instead, we just indicate that steady state during the warm-up period is achieved with a constant caseload, and the time-varying caseload for outcomes generation is introduced after this warm-up period.

We now discuss outcomes at each tier of the PHN.

(A) Outcomes at the PHC. The time series on caseloads for 30 days (model input) yields an average daily COVID-19 caseload of 7.5 patients at each of the 10 PHCs and a maximum of 11 cases per day. For every PHC, we have outcomes on outpatient wait times (this includes wait times for COVID-19 patients waiting for triage) and utilisation of outpatient doctors, inpatient beds, the laboratory and nurses. We also report the daily average and maximum proportions of severely ill patients referred to the CCC from the PHC due to the unavailability of ICU beds at the DH. We do not report similar outcomes for moderately ill patients because, per the operational pathways in Fig. B.6, these patients are immediately transferred to CHCs. Table 3 lists the simulation outcomes relevant to the PHCs. The patient wait times are negligible (under three minutes in each PHC). Resource utilisation of doctors across all configurations is between 30%–55%, with the highest utilisation observed in configurations 2 and 3 with one doctor each. Nurse utilisations across configurations (each configuration has four nurses) are 15%–36%. Laboratory technician utilisations reach a maximum of approximately 50%. The laboratory technician’s utilisation remains relatively low because even though the time required to generate the RAT test report is 15 min, the time needed to conduct a test and certify the report is significantly lower (1 to 2 min). The nurse and laboratory technician utilisation estimates indicate that significantly more COVID-19 tests can be performed at the PHCs, potentially including those of direct contacts of symptomatic patients, with triaging required only for patients testing positive. Our analysis of the PHC simulation results shows that irrespective of the configuration, the existing capacity at the PHC is sufficient under the pandemic response scenario to handle the simulated patient load effectively.

Fig. B.6.

Operational pathways for COVID-19 patients in the healthcare network - divided in parts (a), (b) and (c). PHC = primary health centre, CHC = community health centre, DH = district hospital, CCC = COVID-19 care centre, ICU = intensive care unit, ICU (ven) = ICU with ventilator support unit, ICU (ox) = ICU with supplemental oxygen support.

Table 3.

PHC outcomes from the simulation.

PHC	Outpatient wait time (min)	Outpatient doctor utilisation	Inpatient bed utilisation	Laboratory utilisation	Nurse utilisation	Maximum and average proportion referred to CCC (among severely ill patients)
PHC 1	2.506 (0.274)	0.319 (0.014)	0.089 (0.016)	0.483 (0.015)	0.361 (0.030)	0.733 (0.450) & 0.309 (0.317)
PHC 2	2.476 (0.296)	0.320 (0.014)	0.091 (0.016)	0.485 (0.014)	0.365 (0.027)	0.633 (0.490) & 0.310 (0.310)
PHC 3	2.430 (0.213)	0.320 (0.012)	0.090 (0.014)	0.484 (0.013)	0.364 (0.026)	0.817 (0.382) & 0.354 (0.232)
PHC 4	1.256 (0.134)	0.505 (0.017)	0.004 (0.002)	0.319 (0.011)	0.185 (0.004)	0.650 (0.476) & 0.352 (0.336)
PHC 5	0.826 (0.097)	0.461 (0.015)	0.011 (0.003)	0.224 (0.009)	0.189 (0.005)	0.711 (0.453) & 0.295 (0.269)
PHC 6	2.477 (0.248)	0.324 (0.013)	0.089 (0.017)	0.485 (0.013)	0.361 (0.030)	0.617 (0.486) & 0.289 (0.265)
PHC 7	0.876 (0.106)	0.464 (0.013)	0.004 (0.002)	0.224 (0.009)	0.178 (0.003)	0.743 (0.660) & 0.369 (0.475)
PHC 8	1.208 (0.147)	0.538 (0.02)	0.054 (0.011)	0.334 (0.011)	0.278 (0.017)	0.700 (0.466) & 0.326 (0.308)
PHC 9	2.477 (0.248)	0.319 (0.013)	0.089 (0.015)	0.486 (0.014)	0.363 (0.028)	0.683 (0.464) & 0.282 (0.261)
PHC 10	2.423 (0.240)	0.322 (0.014)	0.090 (0.013)	0.483 (0.011)	0.362 (0.025)	0.550 (0.497) & 0.241 (0.289)

All outcomes reported in the table are average values, with standard deviations in parentheses.

Network flow outcomes at the PHC. Before discussing results specific to the flow of COVID-19 patients from the PHC to the other centres of care, we briefly remind the readers of the clinical and operational pathways of patients across the network (refer to Section 4.1, Table 2, and Fig. B.6 for further information). From the network simulation standpoint, what is interesting is the outcome related to the number of patients transferred to the CCC from the PHC due to the lack of beds in DH and the CHCs. The results of the simulation ( Table 3) show that the proportions of severely ill patients - average and maximum - referred to the CCC are significant, with average values ranging from 24%–36%, and maximum values reaching 82%. This outcome is calculated as follows: the proportion of severely ill patients triaged at the PHC on a given day that are transferred to the CCC because of unavailability of an ICU bed at the DH is recorded, and then averaged across all 30 days. The average and standard deviation reported in Table 3 is the average of this within replication outcome across all replications. The maximum value is calculated similarly. The high variance in these outcome measures is primarily due to the relatively low number of severely ill patients arriving daily at a PHC (e.g., 1–3), and hence even a single referral to a CCC substantially increases the value of the parameter. Further, it is not uncommon to have zero patients referred to a CCC over the course of a single 30-day replication. Overall, the need for a CCC is immediately apparent from this outcome measure at this caseload, even though resource utilisations at the PHC indicate the availability of sufficient capacity to handle testing and triaging of significantly more patients. The high variance in the proportion of severely ill patients referred to CCCs underscores the need for more capacity - especially for ICU beds - on days when the patient overflow is particularly high at the DH. This is further supported by the outcomes at the CHCs and the DH, which we describe next.

(B) Outcomes at the CHC. Given the larger set of services modelled at the CHC, we report on a more extensive range of outcomes for this healthcare facility (Table 4). Simulation results show that providing COVID-19 care significantly impacts operational outcomes at the CHCs more than the PHCs. The utilisation of doctors is the highest at CHC-2 because it houses only a single general physician involved in COVID-19 care provision. However, the utilisation estimates for the nurse, the laboratory technician, and the inpatient ward remain low because CHC-2 has a minimal non-COVID-19 patient load compared with CHC-1 and CHC-3. At CHCs with two general physicians, we see that while there is a substantial increase in utilisation compared to non-COVID-19 conditions, it remains below 50%. This may mean that there is scope for handling a more significant test plus triage as well as inpatient care (especially for moderately ill patients of types A, B and C) load, provided the number of inpatient beds is increased. This is supported by the fact that laboratory technician and nurse utilisation estimates are also lower than 50%. However, this is primarily due to the relatively low patient loads we model at CHCs under routine operating conditions. Given that utilisation estimates for doctors and nurses double, and in some cases nearly triple, when COVID-19 care is included, if patient loads at other CHCs under routine operating conditions are relatively higher to begin with (e.g., with utilisation estimates $>$ 50% for doctors and nurses), then it may be a challenge for the CHCs to serve the caseload that we simulate effectively.

Table 4.

Outcomes at the CHCs from the network simulation.

Resource/Patient type	CHC 1	CHC 2	CHC 3
Wait time (min): mean (standard deviation)
Outpatients	0.328 (0.037)	3.312 (0.291)	0.303 (0.035)
Inpatient bed	33.33 (12.36)	0.190 (0.000)	12.812 (3.132 )
Laboratory	4.717 (0.613)	1.188 (0.118)	1.661 (0.153)
COVID-19 bed	81.114 (24.047)	75.001 (23.010)	100.548 (19.537)
Resource utilisation: mean (standard deviation)
Doctor: outpatients	0.480 (0.011)	0.927 (0.048)	0.444 (0.008)
Doctor: inpatients	0.119 (0.006)	0.054 (0.003)	0.150 (0.006)
Laboratory	0.38 (0.006)	0.199 (0.006)	0.246 (0.006)
Nurse	0.349 (0.009)	0.192 (0.007)	0.306 (0.014)
Inpatient bed	0.779 (0.038)	0.408 (0.043)	0.82 (0.063)
COVID-19 bed	0.756 (0.07)	0.808 (0.062)	0.828 (0.054)
Maximum and average proportion referred to CCC: mean (standard deviation)
Type A	0.000 (0.00) & 0.000 (0.00)	0.000 (0.00) & 0.000 (0.00)	0.000 (0.00) & 0.000 (0.00)
Type B	0.067 (0.25) & 0.013 (0.05)	0.233 (0.50) & 0.048 (0.11)	0.067 (0.26) & 0.013 (0.05)
Type C	0.000 (0.00) & 0.000 (0.00)	0.000 (0.00) & 0.000 (0.00)	0.000 (0.00) & 0.000 (0.00)
Type D	0.800 (0.41) & 0.439 (0.31)	0.833 (0.38) & 0.472 (0.32)	0.733 (0.45) & 0.438 (0.34)
Type E	0.750 (0.43) & 0.472 (0.34)	0.767 (0.41) & 0.407 (0.30)	0.800 (0.41) & 0.368 (0.27)
Type F	0.700 (0.45) & 0.209 (0.20)	0.700 (0.43) & 0.174 (0.15)	0.733 (0.43) & 0.183 (0.15)
Maximum and average proportion referred to DH: mean (standard deviation)
Type A	0.959 (0.13) & 0.187 (0.07)	0.975 (0.10) & 0.250 (0.07)	0.992 (0.05) & 0.215 (0.06)
Type B	0.333 (0.55) & 0.078 (0.14)	0.400 (0.55) & 0.114 (0.18)	0.300 (0.43) & 0.077 (0.14)
Type C	0.417 (0.49) & 0.173 (0.24)	0.333 (0.48) & 0.208 (0.34)	0.500 (0.49) & 0.242 (0.40)

Network flow outcomes at the CHC. From an operational standpoint, it is evident that inpatient beds at the DH are likely to be the critical cause for concern - particularly those in the ICU due to the expected longer lengths of stay (LOS) of severely ill patients. Even at the CHC, COVID-19 beds have utilisation estimates exceeding 75%. Thus, although doctors and nurses are likely to be sufficiently resourced under the current patient loads at the CHCs (similar to PHCs), even moderate increases in COVID-19 caseload may lead to waiting times increasing substantially for moderately ill patients seeking admission at CHCs. At the caseload that we simulate, we see that 75%–92% of moderately ill patients are admitted to the CHC within six hours of arrival. We see that at most 25% of Type A patients are referred to the DH from CHC-2 on average, and very few moderately ill patients (Type A-C) are referred from the CHCs to the CCC. However, as in the case of the PHCs, the need for a CCC becomes immediately apparent, with significant proportions of severely ill patients (Type D-F) requiring transfer to CCCs because of ICU bed unavailability at the DH. For example, 47%, 40% and 17% of patients of types D, E and F were transferred from CHC-2 to the CCC. Note that the proportions referred to the DH from the CHC are reported only for moderately ill patients when they present at the CHC for testing and triaging (they reflect those patients who are transferred because of bed unavailability at the CHC). However, the proportions transferred to the CCC are reported for all moderately and severely ill patient types because they reflect those who are referred to the CCC due to beds being unavailable at both the CHC and the DH (for moderately ill patients) and at the DH (for severely ill patients). Simulation outcomes from the DH and the CCC are discussed next.

(C) Outcomes at the DH and the CCC. The DH and the CCC outcomes from the network simulation are listed in Table 5. Patients arriving at these facilities have three paths into the systems: (a) moderately ill patients transferred from the CHCs (to the DH or the CCC) or the DH (to the CCC) due to the unavailability of general ward beds, (b) severely ill patients transferred from the PHCs and the CHCs (to the DH or the CCC) or the DH (to the CCC) because of unavailability of ICU beds, and (c) patients arriving directly at the DH for testing and triaging. Note that we do not report patient wait times in the DH/CCC in Table 5 because, with respect to the first two patient pathways into these facilities, the transfers occur only after verifying bed availability at the DH/CCC, implying that patients are admitted almost immediately upon approval. In the third case, wait times for admission are negligible because of these facilities’ substantially higher resource levels. Concerning the operational outcomes in both the DH and the CCC, we see trends similar to those observed for the PHCs and the CHCs. For example, the DH and CCC simulation outcomes show relatively low utilisation estimates for medical personnel than significantly higher utilisation for the ICU beds. This is more so in the case of the DH. The disparity between the general ward and ICU ward utilisation estimates at the DH indicates that the current pandemic response scenario, which reserves 50% of the inpatient bed capacity at the DH, can be improved. For example, converting additional general ward beds to ICU beds with supplemental oxygen and/or ventilator support may reduce the need for transfers to the CCC. Furthermore, a dynamic resource allocation policy that stipulates that a percentage (e.g., 25%) of inpatient and medical staff capacity is reserved for COVID-19 care and then adding beds and staff as necessary may also be worth exploring as a pandemic response scenario. However, such a strategy can potentially handle unexpected caseload spikes and cases requiring emergency care only if a set of beds and staff is held in reserve for emergency COVID-19 care, which is over and above the current fraction allocated for such care based on the caseload forecast (for example, 5% beds held as a contingency resource set over and above the 25% allocated based on default). We do not investigate such a scenario due to page length restrictions.

Table 5.

Simulation outcomes at the DH and CCC.

Resource utilisation/Patient type	DH: mean (SD)	CCC: mean (SD)
General ward doctor	0.264 (0.005)	0.003 (0.001)
ICU (ox) ward doctor	0.277 (0.015)	0.017 (0.007)
ICU (ven) ward doctor	0.283 (0.013)	0.083 (0.018)
General ward nurse	0.087 (0.005)	0.006 (0.002)
ICU (ox) ward nurse	0.246 (0.014)	0.016 (0.006)
ICU (ven) ward nurse	0.377 (0.017)	0.110 (0.024)
General ward bed	0.419 (0.024)	0.021 (0.006)
ICU (ox) ward bed	0.769 (0.037)	0.063 (0.02)
ICU (ven) ward bed	0.889 (0.029)	0.239 (0.048)
Isolation ward	NA	0.434 (0.016)
Maximum and average proportion referred to CCC: mean (standard deviation)
Type A	0.000 (0.00) & 0.000 (0.00)	NA
Type B	0.000 (0.00) & 0.000 (0.00)	NA
Type C	0.000 (0.00) & 0.000 (0.00)	NA
Type D	1.000 (0.00) & 0.299 (0.09)	NA
Type E	0.983 (0.09) & 0.242 (0.10)	NA
Type F	0.766 (0.27) & 0.079 (0.05)	NA

ICU = intensive care unit. ICU (ox) = ICU with supplemental oxygen support. ICU (ven) = ICU with ventilator support. SD = standard deviaton. NA = not applicable.

Note: the proportions referred to the CCC are associated with patients referred to the CCC from the DH.

Simulation outcomes at the DH and the CCC are provided in Table 5 below.

Network flow outcomes at the DH and the CCC. From the proportion of severely ill patients referred to the CCC from the DH (approximately 25%–30% on average, Table 5), it is clear that ICU bed capacity at the DH may not be sufficient for the simulated caseload. As expected, the highest utilisation estimates (nearly 90%) are reported for the ICU ward with ventilator support. This is reflected in the proportions of Type D and Type E patients transferred to the CCC. From the utilisation estimates associated with CCC resources, and specifically that of the isolation ward, the need for CCC resources other than ICU beds is evident. However, this is not a surprising outcome, given that 10% of all patients with mild COVID-19 lack isolation facilities at home. We do not discuss CCC outcomes in detail because the capacity of the CCC is assumed. Instead, we believe a demonstration of how this PHC-CHC-DH network simulation can be used to estimate the CCC’s capacity would be of more interest.

Overall, the key insight that emerges from the simulation outcomes observed at facilities comprising the existing PHN involve the fact that personnel capacity (e.g., doctors, nurses) is relatively less utilized than the resource capacity (e.g., CHC and DH beds) at the facilities. PHCs, however, appear to be sufficiently resourced for their testing and triaging role in the PHN for the simulated COVID-19 wave as well as for higher caseloads. The above outcomes are driven largely by the higher lengths of stay for patients of moderately and severely ill COVID-19 patients relative to the service time parameters of personnel for COVID-19 cases. This is consistent with the experience of our clinical collaborator as well as experiences documented in the literature [62], [63], who found that the demand for beds far outstripped the demand for personnel. However, even personnel capacities become severely stretched depending upon the extent of the surge in cases, as was observed in the 2021 ‘Delta’ COVID-19 variant wave in India [63].

5.2. Healthcare network capacity planning under a pandemic response scenario

Capacity planning for the PHN under a pandemic response strategy involves two aspects: (a) determining the COVID-19 caseload at which the capacity of the existing healthcare infrastructure is fully utilised, and (b) determining an appropriate capacity of the makeshift CCC such that it is utilised at a reasonable level while ensuring care is delivered to all patient types within appropriate wait time thresholds. In the previous section, we quantified how the existing PHN responds to the simulated COVID-19 caseload. It is evident that a CCC is required to serve the patient overflow. Therefore, we address the second aspect of capacity planning by considering CCC capacity. We then describe how the PHN described in Section 3 responds to increases in COVID-19 caseload.

We would like to note that while we discuss the capacity caseload for a single CCC, this approach can be extended for multiple CCCs. This may be relevant for the PHNs in large urban metropolitan areas in India.

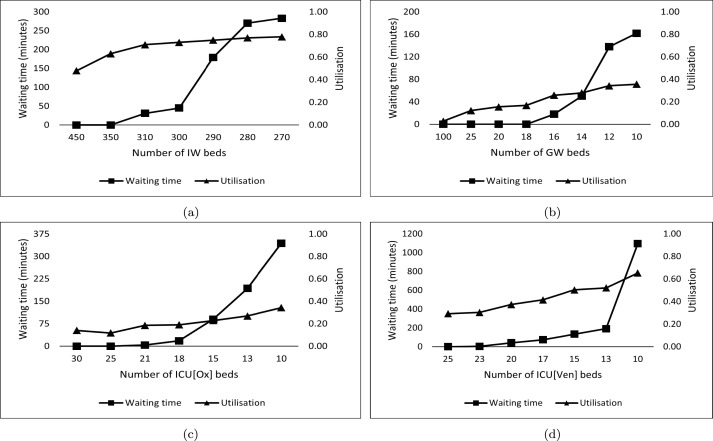
The CCC provides resources for different levels of COVID-19 inpatient care: isolation wards (IW) for mildly ill patients; general wards (GW) for moderately ill patients (Type A); ICUs with supplemental oxygen (ICU[Ox]) and ventilator support (ICU[Ven]) for the severely ill patients. Moderately ill patients whose conditions might have deteriorated in the GW will also be moved to ICU[Ox] or ICU[Ven]. Under the COVID-19 caseload described in Section 4.2, we vary the number of beds in each of the four units (IW, GW, ICU[OX] and ICU[Ven]), while keeping the number of doctors and nurses constant. We measure two key operational outcomes concerning bed capacity changes: bed utilisation and patient wait times before admission. The results are shown in Fig. 3 below. Our experiment parameters are based on the simulation outcomes in Section 5.1, which indicate medical staff capacity as adequate and inpatient bed capacity (in particular, ICU beds) to be the likely bottleneck in providing effective COVID-19 care.

Fig. 3.

CCC capacity planning outcomes. Average wait times to admission and average bed utilisation estimates for (a) isolation ward (IW), (b) general ward (GW), (c) ICU with supplemental oxygen support (ICU[Ox]), and (d) ICU with ventilator support (ICU[Ven]).

Fig. 3(a) indicates that at approximately 300 isolation beds, wait times for the IW drop below 50 min, with the utilisation of the ward close to 80%. In the case of the GW (Fig. 3(b)), with an allocation of only ten beds, the wait time before admission is approximately 160 min (compared to the wait time threshold of six hours assumed for moderately ill patients seeking admission at GW). At this capacity level, the utilisation of the GW is less than 40%. This shows that the capacity for GW beds is nearly sufficient at the CHCs and the DH, as seen in Table 4, Table 5. For the ICU[Ox] and ICU[Ven] units, reducing wait times to the extent possible becomes important. We see from Fig. 3(c) that wait times to admission become negligible once the number of beds crosses 20; similarly, from Fig. 3(d), we see that having approximately 25 beds serves this purpose for the ICU[Ven]. In these cases, utilisation estimates remain between 30%–40%.

The results show our network simulation model’s applicability in determining the appropriate capacity levels for CCC resources like IW, GW, ICU[Ox] and ICU[Ven]. Our caseload is derived from secondary data published by the district administration. Equally, these could have been projections based on expert input or forecasts from epidemiological and agent-based models. A public health administration can thus input the caseload distributions specific to their area and use the network simulation to determine the appropriate capacity levels based on a combination of locally agreed wait time metrics and acceptable utilisation levels. For example, an appropriately scaled convex combination of wait times (e.g., the ratio of average wait time to maximum allowable wait time) and utilisation levels can be constructed and optimised (via discrete simulation optimisation methods) to determine an optimal capacity level for the CCC under consideration. The analyst can adjust the weights of each operational performance measure based on its importance (e.g., higher weights assigned for wait times in ICU[Ox] and ICU[Ven], compared to GW and IW).

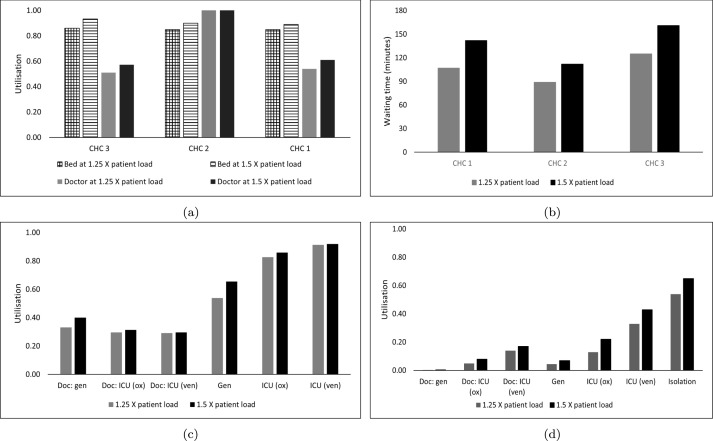
We now demonstrate the broader applicability of the model by increasing the caseload to 1.25 and 1.5 times the original caseload (subsequently referred to as 1.25X and 1.5X respectively) and investigate its impact on the PHN. It can be seen from Fig. 4(a) that bed utilisation estimates for both 1.25X and 1.5X at all CHCs approach 90%, which is reflected in increases in the average wait times up to nearly 160 min for CHC-3 at 1.5X (Fig. 4(b)) . Similar to the original outcomes but amplified with increases in caseload, we see that ICU units are the most affected at the DH, with ICU(ox) and ICU(ven) utilisation estimates approaching 90% at the lower 1.25X (Fig. 4(c)). The results indicate that caseloads exceeding 1.25X will not be viable at the current capacity, especially in relation to the ICU section at the DH and inpatient section capacities at the CHCs, respectively.

Fig. 4.

COVID-19 case load sensitivity analysis results. (a) Average utilisation at the CHC. (b) Average wait times at the CHC for moderately ill patients. (c) Average utilisation estimates at the DH. (d) Average utilisation estimates at the CCC.

Doc = doctor; gen = general ward; ICU (ox): ICU with supplemental oxygen support; ICU (ven): ICU with ventilator support; Isolation: isolation ward.

6. Conclusion

In this section, we summarise the main results of this study. Next, we outline the relevance of our work in terms of the broader applicability of the network simulation approach and developing such models by considering the principles of generic modelling and model reuse. We then discuss the limitations of our study and potential avenues for future research.

Summary of the main results. This study presents operational performance measures for facilities at different tiers within the PHN under a simulated COVID-19 pandemic response scenario developed in conjunction with a clinical collaborator. In this pandemic response scenario, each facility at a given tier plays a specific role in delivering COVID-19 care in a given region. The outcomes reported include the average patient waiting time to receive care at each tier, resource utilization levels and network flow outcomes, including the average and maximum proportion of cases referred to higher tiers from each applicable facility. At the PHC tier, where facilities focus on testing and triaging COVID-19 patients under this pandemic response scenario, the existing capacity appeared to be sufficient to manage the COVID-19 caseload across a ‘wave’ of the pandemic. However, even at the PHC level, simulation outcomes associated with the referral of severely ill patients highlighted the necessity for the establishment of a dedicated makeshift CCC within the PHN. At the CHC tier, which in addition to testing and triaging also admitted moderately ill patients, the impact of the COVID-19 caseload on operational performance measures was more significant, and was reflected in the elevated doctor and nurse utilisation levels. Thus CHCs may struggle to deliver COVID-19 care if further increases in patient load are encountered. With regard to the outcomes at the DH and CCC, the general ward and isolation ward bed capacities appeared to be adequate. However, at the DH, the high utilisation of ICU wards with Oxygen and Ventilator support and a significantly large referral rate to CCCs highlighted inadequate capacity. This could potentially be addressed by converting underutilised general ward beds into ICU beds assuming availability of supplemental oxygen and ventilators. Overall, the results emphasize the need for the establishment of makeshift CCCs to not only improve the quality of care for severely ill patients in terms of reducing wait times to admission but also assist with the operational load on existing facilities in the PHN. Finally, the study demonstrated the use of the PHN simulation to estimate the capacity of the CCC for each resource type (e.g., general ward beds, ICU beds) it may house.

Relevance.Publicly-funded healthcare systems comprise of multiple-tiers with established patient flow mechanisms. For example, the UK NHS has primary, secondary and tertiary care; in India, the public healthcare network (PHN) comprises the PHCs, CHCs and the DH. As the current pandemic has shown, it may also be necessary to create makeshift capacity (like the CCCs in India and the Nightingale Hospitals in the UK) and link them to the existing tiers. The ideal capacity of these makeshift facilities may depend on the expected patient flows between the existing PHN tiers and the makeshift facility, as well as an understanding of how the capacity of the existing PHN facilities responds to the patient flow mechanisms under consideration. Considering the interplay of these complex flows (illustrated in Table 2 and Fig. B.6) and factors such as the trajectory of this caseload, stochastic patient care requirements and lengths of stay, multiple service level criteria from the patient and facility administration perspectives, etc., the task of estimating the ideal capacity of a makeshift facility can be challenging. A computational technique such as Discrete-event Simulation (DES) can handle such complexities and can help in the planning of such facilities. In this paper, using the COVID-19 pandemic as a case study, we have shown how capacity planning of the PHN for a public health crisis can be accomplished through a DES model.

While we have used the COVID-19 pandemic as a case study, a network simulation such as this, in conjunction with caseload forecasts generated using compartmental or agent-based models of infectious disease transmission dynamics, offers the potential to aid in the planning of other outbreaks. For example, the infectious season in India is reasonably well-established for vector-borne diseases such as dengue or malaria. As such, a network simulation would allow for experimenting with public health strategies before a dengue or malaria outbreak. Our work thus provides a comprehensive proof-of-concept for how multi-tier PHN simulations, including an accounting of the different modelling elements that must be integrated with such an analysis, can be leveraged to plan operational aspects of infectious disease outbreak response strategies.

The network model’s implementation required considerable effort. Reflecting on the experience, it would be challenging to develop such detailed multi-tier network models de novo upon the onset of a public health emergency. Further, such emergencies may trigger restrictions on access to healthcare facilities, thus impacting primary data collection and observation of process flow (as has happened with this case). The development of distinct models of the facility types at each tier would enable the routine analysis of specific elements of the network (e.g., the use of the PHC models for the operational analysis of non-COVID-19 workflows can be seen in the studies of Shoaib and Ramamohan [49], Fatma et al. [14] and Fatma and Ramamohan [64], whilst also providing opportunities for model reuse. Existing models representing different healthcare network tiers could also be joined-up to create an overarching network simulation model [15]. However, in any such network, it is unlikely that every instance of a facility type will have an identical configuration. Hence the generic modelling approach becomes important since, (a) at the conceptual level, it helps identify the commonalities and differences between operational configurations among facilities that may belong within the same network tier, and (b) at the model development level, the generic approach enables the development of an ‘archetypal’ or ‘generic’ model which can subsequently be modified to represent its various network instances (for example, we implemented three different PHC configurations). Thus, from a facility network simulation standpoint, our study highlights how a generic modelling approach is vital for developing network simulations that contain multiple instances of facility types within the network.

Limitations. The COVID-19 restrictions affected primary data collection for the model. Additionally, our observation of the COVID-19 process flows at the healthcare networks’ different tiers was only partly complete. We overcame this limitation by collaborating with a clinical expert directly involved with clinical and administrative aspects of COVID-19 care at one of India’s largest public research hospitals. The clinical expert’s domain knowledge also enabled us to validate our network simulation model. External validation of the simulation outcomes was challenging as we did not have access to the specific pandemic response strategy across the public health network in our case study district. Thus, a key avenue of future research could involve surveying the pandemic response strategies implemented across the various districts, simulating and comparing their operational viability, and concomitantly also performing a comprehensive external validation of the network simulation.

Future research. Our future work will research the application of network simulation and optimisation for the optimal location of the CCC. There is also the opportunity to augment the DH element of the network model. Unlike the PHC and CHC models, the DH model currently simulates only the flow of COVID-19 patients. A DH model, such as the one presented in Gunal and Pidd [22], could also include non-COVID-19 flows like outpatient clinics and elective surgeries. Waiting times for elective procedures are projected to increase significantly post-COVID-19 [65], [66]. Thus, an improved DH model could be used to experiment with strategies for reducing waiting lists locally (whilst also ensuring sufficient resources are available for COVID-19 patients), which would mean that the system experiences less stress in meeting waiting list targets post-pandemic.

Funding

The work was funded through a Newton Bhabha grant award (grant agreement- 547641913) with the Indian Institute of Technology Delhi and the University of Exeter Business School, UK .

CRediT authorship contribution statement

Mohd Shoaib: Methodology, Data curation, Formal analysis, Software, Investigation, Visualization, Writing – original draft, Writing – review & editing. Navonil Mustafee: Methodology, Validation, Writing – original draft, Writing – review & editing. Karan Madan: Methodology, Data curation, Validation. Varun Ramamohan: Conceptualization, Project administration, Supervision, Methodology, Investigation, Formal analysis, Data curation, Visualization, Writing – original draft, Writing – review & editing.

Biographies

Mohd Shoaib is a research scholar at the Department of Mechanical Engineering at the Indian Institute of Technology Delhi, New Delhi, India. His email address is mez178322@mech.iitd.ac.in.

Navonil Mustafee is a Professor of Analytics and Operations Management at the University of Exeter Business School, Exeter, United Kingdom. His email address is n.mustafee@exeter.ac.uk.

Karan Madan is an Additional Professor of Pulmonology, Critical Care and Sleep Medicine at the All India Institute of Medical Sciences, New Delhi, India. His email address is drkaranmadan@gmail.com.

Varun Ramamohan is an Assistant Professor in the Department of Mechanical Engineering at the Indian Institute of Technology Delhi, New Delhi, India. His email address is varunr@mech.iitd.ac.in.

Appendix A. PHN simulation development: PHC, CHC and DH/CCC Tiers

In this section, we describe the PHC, CHC and DH/CCC simulation model development.

A.1. PHC simulation development

PHC COVID-19 patient flow. As part of the pandemic response scenario, PHCs are used primarily as testing and triaging centres for COVID-19 patients. This implies that COVID-19 patients are seen only during outpatient hours, with the assumption that COVID-19 patients requiring emergency care are seen directly at CHCs, or the DH. We assume that only symptomatic COVID-19 patients are tested and triaged at the PHC; more details regarding the rationale underlying this assumption are provided in the pandemic response scenario description in Section 4. Based on inputs from our clinical collaborator, and given (a) the limited number of doctors, nurses and laboratory technicians in the PHCs, and (b) our observation of testing and triaging operations for COVID-19 patients at an urban equivalent of a PHC, we model a scenario wherein both COVID-19 and non-COVID-19 patients are seen by the same medical staff, albeit in different locations in the same facility and with personal protective equipment (PPE) protocols in place.

When a symptomatic patient seeking to undergo a COVID-19 test arrives in the PHC, they report to the nurse who collects their test sample and completes their registration process. The test sample is then sent to the laboratory where it is analyzed and the report is generated. Based on the testing protocol recommended by the Indian government at the time of development of this model [67], rapid antigen tests (RAT) are first performed, and because RATs have relatively low sensitivities [68], symptomatic patients with negative test results undergo confirmatory RT-PCR tests cases (assumed to be the gold standard). The rationale underlying this testing protocol is that RATs are cheaper, easier to deploy (for example, tests can be conducted at the point of sample collection itself) and have much shorter turnaround times when compared to RT-PCR tests. Further, given their higher specificities, a positive test result for symptomatic patients can be considered to be reliable, while negative test results warrant confirmation with the RT-PCR. This approach may not be suitable for asymptomatic contacts of confirmed COVID-19 patients, however, and for these patients, RT-PCR tests are conducted. The RATs deployed in the Indian context were found to have a specificity of 99.6% and a sensitivity in the range 50.6–84.1% [68]; hence we assumed a sensitivity of 67% and a specificity of 100% for the RAT in the model.

All facilities in the network follow the same testing protocol. RAT test reports become available approximately 15 min after the sample is collected, and RT-PCR test reports become available approximately 24 h after sample collection. We assume that the RT-PCR test is conducted in a separate clinical laboratory and not in the PHC (i.e., the collected samples are transported to said laboratory). This is consistent with testing practice in urban areas as well, as observed in primary urban health centres. COVID-positive cases are categorised as having a mild, moderate or severe case of COVID-19. 90% of mild patients isolate at home, with the remainder referred to the CCC for institutional quarantine (this caters for patients who do not have exclusive access to a bedroom or a bathroom at home). Patients with moderate and severe cases of COVID-19 are either referred to the CHCs or the DH. If beds are not available at CHCs/DH, then they are referred to the CCC. This testing and triaging process at the PHCs is described in Fig. A.5 below.

Fig. A.5.

Testing and triaging process at the PHC. $x$ = Number of non-COVID-19 patients, 20% of whom present with COVID-like symptoms and hence seek testing; $y$ = number of symptomatic COVID-19 patients.

PHC parameters for the model. The resource levels - doctors, nurses, beds - and non-COVID-19 outpatient, inpatient and childbirth patient interarrival times at each PHC in the PHN are provided in Table A.6. Note that the consultation times of the doctors for non-COVID-19 outpatients, COVID-19 patient triage times, and the test sample collection times for the nurse are provided in Table A.7. Estimates of these parameters are the same for both PHCs and CHCs.

Table A.6.

PHC parameters.

PHC	Doctors	Nurses	Beds	Outpatient IAT	Inpatient IAT	ANC patient IAT	Childbirth patient IAT
PHC 1 (C1)	2	4	6	4	2880	1440	1440
PHC 2 (C1)	2	4	6	4	2880	1440	1440
PHC 3 (C2)	1	4	6	4	2880	1440	1440
PHC 4 (C3)	1	4	6	6	2880	NA	NA
PHC 5 (C3)	1	4	6	9	2880	NA	NA
PHC 6 (C1)	2	4	6	4	2880	1440	1440
PHC 7 (C3)	1	4	6	9	2880	NA	NA
PHC 8 (C2)	1	4	6	6	2880	2880	2880
PHC 9 (C1)	2	4	6	4	2880	1440	1440
PHC 10 (C1)	2	4	6	4	2880	1440	1440

C1/C2/C3 = Configuration 1/2/3. IAT = interarrival time. All interarrival times are in minutes.

Notes. 1. Configuration 3 PHCs do not offer antenatal or childbirth care. 2. The nurses work in 8-hour shifts, with one nurse available per shift.

A.2. CHC simulation development

CHC COVID-19 patient flow. CHCs conduct testing and triaging for symptomatic COVID-19 patients as described for PHCs (Appendix A.1), and in addition they provide inpatient care for moderately ill patients of type A (see Table 2). COVID-19 patients can directly approach a CHC for testing and triaging, or moderately ill patients can be referred to the CHC from a PHC for inpatient care. We assume that the rationale for allocation of COVID-19 testing and triaging duties in the PHC (described in Appendix A.1) is applicable in the CHCs as well, and hence testing and triaging in CHCs is conducted in the same manner as in PHCs. This means that we assume that general physicians in the CHC are responsible for the triaging, and that these physicians attend to both COVID-19 and non-COVID-19 patients. The staff nurse in charge of the inpatient ward attends to both non-COVID-19 inpatients, COVID-19 inpatients as well as test sample collection. Assigning these multifarious roles to the staff nurse is possible only because of the generally low non-COVID-19 inpatient load at CHCs, and the relatively short service times for type A COVID-19 patients admitted to the CHC and for COVID-19 test sample collection. As the number of samples to be collected increases (i.e., the COVID-19 case load increases), this resource use pattern may become infeasible, and an alternative duty allocation to staff nurses may be required. In such a situation, auxiliary nurse midwives (ANMs), who often assist the staff nurses with childbirth patients and on an informal basis with other duties, may be tasked with COVID-19 sample collection and other COVID-19 care related duties. We do not consider ANMs explicitly in our models because they are typically associated primarily with sub-centres and play a significant role in public health outreach, and are not involved with patient care on a full-time basis.

If a test report for a patient is positive, and the attending physician categorises this patient as a moderately ill patient of type A, the patient is admitted to the inpatient ward dedicated to COVID-19 care in the CHC. As mentioned in Section 4, under this pandemic response strategy, fifty percent of the inpatient ward bed capacity is reserved for moderately ill type A COVID-19 patients. CHCs do not have intensive care facilities, and hence all other COVID-19 patient types except those of type A are referred to the DH or the CC. The referral process is described in Fig. B.6. We assume that patients of type A wait for up to six hours at the CHC for admission before they are transferred to the DH or the CCC, subject to bed availability. In the CHC, COVID-19 patients are attended to by nurses and doctors twice a day, with each individual service duration equal to half the service time mentioned in Table A.7.

CHC parameters for the model. Input parameters associated with COVID-19 care in the CHCs were estimated based on inputs from our collaborating clinical expert provided via the questionnaire described in Section 4, and provided in Table A.7. In Table A.7, the majority of the input parameter estimates provided are those directly associated with COVID-19 care. We also provide some parameter estimates associated with non-COVID-19 outpatients and inpatients also in Table A.7 because the wait times for these patients before receiving care are also affected by the COVID-19 care process.

In the following section, we describe the DH and the CC simulation development.

Table A.7.

COVID-relevant CHC resource levels and service times.

Parameter	CHC 1	CHC 2	CHC 3	Source
Number of general physicians	2	1	2	Shoaib and Ramamohan [50 ]
Number of nurses	11	8	8	Shoaib and Ramamohan [50 ]
Number of non-COVID-19 inpatient beds under pandemic response scenario	9	7	9	Assumed
Number of COVID-19 inpatient beds under pandemic response scenario	8	7	8	Assumed
Non-COVID-19 outpatient consultation time with doctorsa (mean, SD) (min)	N(0.87, 0.21)	N(0.87, 0.21)	N(0.87, 0.21)	Shoaib and Ramamohan [49 ]
Nurse service times for non-COVID-19 inpatients (min)	U(20,30)	U(20,30)	U(20,30)	Shoaib and Ramamohan [50 ]
COVID-19 patient triage timesa (min)	U(5,10)	U(5,10)	U(5, 10)	Clinical expert input
Doctor service times for COVID-19 inpatient (min)	U(3, 6)	U(3, 6)	U(3, 6)	Clinical expert input
Nurse service times for COVID-19 inpatients (min)	U(5,10)	U(5,10)	U(5,10)	Shoaib and Ramamohan [50 ]
Length of stay, COVID-19 inpatients (days)	U(4 ,5)	U(4 ,5)	U(4 ,5)	Clinical expert input
COVID-19 test sample collection timea (min)	U(1, 2)	U(1, 2)	U(1, 2)	Clinical expert input
Outpatient interarrival time (min)	1.2	3	1.4	Shoaib and Ramamohan [50 ]
Childbirth patient interarrival time (min)	550	1440	1200	Shoaib and Ramamohan [50 ]
Inpatient interarrival time (min)	222	618	414	Shoaib and Ramamohan [50 ]
Surgery patient interarrival time (min)	1470	4722	230	Shoaib and Ramamohan [50 ]

SD = Standard deviation. N = normal distribution. U[$x$, $y$] = discrete uniform distribution with parameters $x$ and $y$.

^aInput parameter estimates applicable for resources in both PHCs and CHCs.

A.3. District hospital and COVID-19 Care Centre Simulation Development

According to the DH guidelines, a minimum of 5%–10% of the beds in a DH must be intensive care unit (ICU) beds, and a minimum of 34 doctors and 90 staff nurses across all its departments should be employed in the DH [53]. The DH in the district that we model has 200 beds across all departments, and hence we assumed that 100 beds are reserved for COVID-19 care. We assumed that 10% of these beds (10 in number) are ICU beds with ventilator support, and assumed that an additional 20 beds will be converted to ICU beds with supplemental oxygen support given that the DH is the preferred public care provider for patients requiring respiratory support. Creating ICU beds with supplemental oxygen support is substantially easier to facilitate than creating beds with ventilator support, and hence this appeared to be a reasonable assumption given the pandemic situation. This implies that the remaining 70 beds are general ward beds reserved for COVID-19 patients. We emphasize that while we have attempted to make these resource use assumptions as reasonable and realistic as possible (including vetting by our collaborating clinical expert), the goal of this study is to demonstrate the use of a public healthcare facility network simulation such as this to evaluate and optimise aspects of pandemic response strategies, and not to prescribe specific response strategies based on the input parameter estimates and COVID-19 care patterns represented in our model. Therefore, as we demonstrate in the analyses that we conduct to estimate the CCC resource levels given the COVID-19 case load, the specific input parameter estimates and patient flow assumptions can be modified as required within the framework that we construct based on in-field information that a stakeholder can access.

DH/CCC COVID-19 patient flow. Patient flow in the DH and CCC are similar. Patients who arrive at the DH directly undergo testing and triaging in the same manner as in the PHC and the CHC. However, at the DH, we assume that a dedicated nurse is present for patient registration and sample collection. This is because the staffing levels at the DH are significantly higher and also because the COVID-19 case load at the DH is also significantly higher than at the CHCs and the PHCs (equal to total case load across all PHCs or CHCs). The doctors in charge of the general ward for COVID-19 care also handle the triaging for patients testing positive. The clinical and operational patient pathways for those admitted in the DH and in the CCC (patients of types A, B, C, D, E and F) have already been described in Section 4.1.

DH/CCC Parameters for the model. Input parameters, including doctor and nurse service times for various categories of patients and the staffing levels for each unit (the ICUs and the general ward) for the DH and CCC have largely been derived based on inputs from our collaborating clinical expert, based on their experience in managing COVID-19 care in a large hospital setting. The process of obtaining these parameter estimates via a questionnaire is described in Section 4. Input parameters related to resource and staffing levels are shown in Table A.8, and service time distributions are provided in Table A.9. Note that the resource levels at the CCC are assumed; in Section 5, we describe the process of estimating the capacity of the CCC given a COVID-19 case load forecast.

Table A.8.

Resource and staffing levels at the DH and CCC.

Resources	CCC	DH
Number of isolation beds	500	NA
Number of general ward beds	150	70
ICU (supplemental oxygen support) beds	50	20
ICU (ventilator support) beds	30	10
General ward doctors/shifta (one per 50 beds)	3	2
ICU (ox) ward: doctors/shift (one per 10 beds)	5	2
ICU (ven) ward: doctors/shift (one per 10 beds)	3	1
General ward nurses/shift (one per 50 beds)	3	2
ICU (ox) ward: nurses/shift (one per 7 beds)	7	3
ICU (ven) ward: nurses/shift (one per 5 beds)	6	2

NA = not applicable. ICU = intensive care unit. ICU (ox): ICU with supplemental oxygen support. ICU (ven) = ICU with ventilator support.

All parameter estimates obtained via the questionnaire filled by our collaborating clinical expert.

^aThree shifts per day of 8 h each.

Table A.9.

Doctor and nurse service times for inpatient COVID-19 care.

Service time per bed (min)	Distribution
General ward doctor	U(3, 6)
General ward nurse	U(5, 10)
ICU (supplemental oxygen support) ward: doctor	U(30, 60)
ICU (supplemental oxygen support) ward: nurse	U(40, 80)
ICU (ventilator support) ward: doctor	U(30, 60)
ICU (ventilator support) ward: nurse	U(80, 160)

All parameter estimates were obtained via the questionnaire filled out by our collaborating clinical expert. U[$x$, $y$] = discrete uniform distribution with parameters $x$ and $y$.

Appendix B. Operational pathways for COVID-19 patients

The detailed operational pathway corresponding to the clinical pathways described in Table 2 is provided in Fig. B.6.

Data availability

Data will be made available on request.