Conceptual and analytical approaches for modelling the developmental origins of inequality

Abstract

In many species, individuals that experience harsh conditions during development have poor health and fitness outcomes in adulthood, compared with peers that do not. These early-life contributions to inequality are often attributed to two classes of evolutionary hypotheses: Developmental Constraints (DC) models, which focus on the deleterious effects of low-quality early-life environments, and Predictive Adaptive Response (PAR) hypotheses, which emphasize the costs individuals incur when they make incorrect predictions about conditions in adulthood. Testing these hypotheses empirically is difficult for conceptual and analytical reasons. Here, we help resolve some of these difficulties by providing mathematical definitions for DC, PAR (particularly focusing on ‘external’ PAR) and related concepts. We propose a novel, quadratic regression-based statistical test derived from these definitions. Our simulations show that this approach markedly improves the ability to discriminate between DC and PAR hypotheses relative to the status quo approach, which uses interaction effects. Simulated data indicate that the interaction effects approach often conflates PAR with DC, while the quadratic regression approach yields high sensitivity and specificity for detecting PAR. Our results highlight the value of linking verbal and visual models to a formal mathematical treatment for understanding the developmental origins of inequitable adult outcomes.

This article is part of the theme issue ‘Evolutionary ecology of inequality’.

1. Introduction

Early-life adversity is associated with a wide variety of negative outcomes in adulthood, including poor health, short lifespans, and low evolutionary fitness. These ‘early-life effects’ are believed to contribute to inequalities in adult outcomes and thus have generated strong interest from many fields, including ecology and evolution [1–3], public health and medicine [4–7], psychology and psychiatry [8,9], sociology [10] and economics [11].

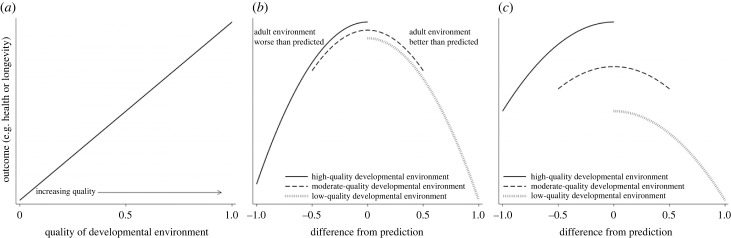
The widespread observation of early-life effects across species [12] has given rise to two broad classes of hypotheses that seek to explain the evolution of such effects (reviewed in [13–15]). The first class, often termed Developmental Constraints (DC) or ‘silver spoon’ hypotheses [16,17], posits that harsh conditions in early life decrease later-life phenotypic quality (and thus, evolutionary fitness), perhaps because organisms make tradeoffs in harsh developmental environments that promote immediate survival but compromise long-term outcomes [15]. The second class, Predictive Adaptive Response (PAR) hypotheses, proposes that there is selection for organisms to use their early-life conditions to predict characteristics of their adult environment and adjust their responses to the early environment accordingly [17,18]. Under this model, incorrect ‘guesses’ about the future lead to poor outcomes during adulthood. Organisms may predict something about their external environment (referred to as an external PAR), or the quality of their own somatic state (an internal PAR) [18,19]). A key difference between the DC and PAR hypotheses is whether the early environment per se is the primary determinant of later-life outcomes (figure 1a), or whether the accuracy of an organism’s prediction about some aspect of its future is the determining factor [20,21] (figure 1b).

Figure 1.

Visualizations of the predictions of the Developmental Constraints (DC) hypothesis (a), external Predictive Adaptive Reponse (PAR) hypothesis (b) and a co-occurrence of the two (c). If environmental quality is a continuous variable bounded by 0 (worst) and 1 (best), (a) the DC hypothesis predicts that low-quality developmental environments will result in worse adult outcomes (e.g. health or longevity) than high-quality environments. (b) The external PAR hypothesis predicts that, controlling for other factors, bigger differences between an organism’s prediction about its adult environment and its actual adult environment lead to worse adult outcomes. The centre of the x-axis (0) represents a perfect match between prediction and realized adult environment. Negative x-axis values (bounded by −1) represent an organism that predicted that its adult environment would be worse than it actually ended up being; i.e. it predicted a high-quality adult environment but ended up in a low-quality one. Positive x-axis values (bounded by 1) represent an organism that predicted that some feature of its adult environment would be worse than it ended up being; i.e. it predicted a low-quality environment and ended up in a high-quality one. An organism that predicted some intermediate outcome in adulthood (a moderate-quality environment) can experience either a negative or positive prediction error (bounded by −0.5 and 0.5 in our figure). (c) The DC and external PAR hypotheses, as defined in §2, can be true simultaneously. An organism that experienced a low-quality developmental environment can have worse outcomes relative to what its outcomes would have been had it experienced a high-quality developmental environment, and can fare worse the greater the error in its prediction about its future environment.

As conceptualized above, the DC and PAR hypotheses are not mutually exclusive, as many people have noted [14,22–24]. Adult outcomes can simultaneously be determined by the quality of the developmental environmental and how well organisms predict some feature of adulthood [21,25]. For example, depending on the size of the effects of DC, an organism that starts off in a low-quality environment may always fare worse than if it had started in a high-quality environment, even if it would also fare worse if its prediction about the future was wrong (figure 1c). In parallel, higher-quality adult environments may also yield better outcomes independent of the developmental environment or an organism’s predictive accuracy [23,26]. This conceptually related idea, termed the Adult Environment Quality (AEQ) hypothesis [17], is implicit in tests of the relationship between adult environment and fitness that do not consider early life.

Currently, in humans and other long-lived mammals, the DC hypothesis has stronger empirical support than PAR hypotheses (reviewed in [14]). However, it is difficult to know what conclusions to draw from this pattern because the ubiquitous verbal and visual models used for testing these hypotheses create uncertainty about precisely what is being evaluated. Explicit mathematical definitions for DC, PAR and AEQ models can help remedy these problems and resolve ambiguity in interpreting the empirical data [27,28]. Here, we provide definitions of DC, external PAR and AEQ, and use those definitions to motivate a quadratic regression model and tests for these hypotheses. Using simulations, we demonstrate substantial improvements in the sensitivity and specificity of tests of these hypotheses with our quadratic regression approach over a commonly used interaction regression model [17,29]. We show that a key reason for this improvement is that, unlike the interaction regression approach, the quadratic regression method avoids conflating DC with external PAR. In addition, we discuss conceptual issues that continue to constrain formal tests of DC and PAR models, and provide guidance on practical implementation of tests for these hypotheses.

2. Mathematical definitions and predictions

In this section, we propose formal mathematical definitions for DC, PAR and the related AEQ hypothesis. We then outline the theoretical predictions that follow from these definitions, and make explicit assumptions that are often left implicit in studies of the early-life origins of inequality. Our definitions and predictions are summarized in table 1.

Table 1.

Formal definitions and derived predictions of theories for the relationship between the quality of developmental environments and inequalities in adult outcomes. The variables we use here align with the numbered causal chain in §2b that focuses on external environments. However, one can substitute other inputs for external environment e, as described in our first, non-numbered causal chain in §2b. Here, y₀ is outcome during development; y₁ is outcome during adulthood; e₀ is developmental environment; e₁ is adult environment; E(e₁) is adult environment the organism expects; Δe = e₁ − e₀ is the difference between developmental and adult environments; and p is a phenotypic adaptation to a given environment. Definitions assume a differentiable function that maps from environment, or from discrepancy between environment and adapted-to environment, to outcomes. Refer to §2 for details on all theories.

theory	definition	observable variation	prediction or test (eqn no.)
Developmental Constraints (DC)	$\mathrm{\partial }{y}_1/\mathrm{\partial }{e}_0>0$	(y1, e0)	$\mathrm{\partial }{y}_1/\mathrm{\partial }{e}_0>0$ (2.1)
Predictive Adaptive Response (PAR)	E(e1) = e0
	$\mathrm{\partial }p/\mathrm{\partial }\mathrm{E}(e_1)<0$
	${\mathrm{\partial }}^2{y}_1/\mathrm{\partial }p\hspace{0.17em}\mathrm{\partial }{e}_1<0$
phenotypic adaptation test		(e0, p)	$\mathrm{\partial }p/\mathrm{\partial }{e}_0<0$ (2.5)
prediction error test		(y1, |Δe|)	$\mathrm{\partial }{y}_1/\mathrm{\partial }|\mathrm{\Delta }e|<0$ (2.7)
Adult Environmental Quality (AEQ)	$\mathrm{\partial }{y}_1/\mathrm{\partial }{e}_1>0$	(y1, e1)	$\mathrm{\partial }{y}_1/\mathrm{\partial }{e}_1>0$ (2.8)

We note three conceptual points about our definitions. Firstly, they posit what would happen if, for a given organism, its developmental environment were to be different from what it is, or if it made a different prediction about its adult environment. A useful way to phrase the inquiry is: How would a given individual’s outcome differ if, in a parallel universe, its environment were different? In the real world, some studies of identical twins attempt to approximate this hypothetical scenario. Therefore, another way to conceptualize this is to ask: What would happen if identical twins were separated and raised in two different environments?

It is also helpful to clarify what our definitions are not. Our definitions are not about the distributions of environments and outcomes across individuals in a given population. For example, we will not define DC as a claim that organisms with better outcomes tend to have been born in better environments. These clarifications are required because, though our definitions are intra-individual (in the sense that they compare an individual with itself in another hypothetical world), the DC and PAR hypotheses are often empirically tested with data that relies on inter-individual comparisons. That is, tests of the theories we define often rely on data that compare one individual with another (e.g. [30,31]), though there are situations (especially when doing experimental work, either in the lab or with wild animals) where it is possible to observe the same individual under a range of prediction error or adult environmental quality conditions (e.g. [32–34]). Whether it is appropriate to use inter-individual data to test intra-individual hypotheses is a methodological question concerning causation that is beyond the scope of this article. We recommend [35,36] for a detailed discussion of such issues.

Secondly, our definitions constitute theories or hypotheses about the influence of early environment on an organism’s outcome, and they generate (testable) predictions about how environments affect outcomes. In some cases, the theory and the prediction are the same: the prediction of the theory is mathematically identical to the statement of the theory. An example is DC, where the theory says low-quality early environments cause poor adult outcomes and the prediction is that low-quality early environments cause poor adult outcomes. In other cases, such as PAR, the definitions and the predictions are not the same.

Thirdly, our definitions assume that developmental and adult environments are continuous variables and that one can take derivatives of the mathematical functions that relate those environments to outcomes. Our conclusions can be extended to categorically coded variables if some technical modifications are used. We will by default use partial derivatives, indicated by the symbol ∂, because we are typically examining the impact of changing input into a function, holding all other inputs into that function constant.

(a) . Developmental Constraints hypothesis

The Developmental Constraints (DC) hypothesis proposes that lower-quality developmental environments will lead to worse outcomes in adulthood, relative to higher-quality developmental environments [17]. For example, Drosophila melanogaster larvae that are nutritionally stressed become smaller adults and have lower egg viability in adulthood than larvae that are not [37].

DC can be described by a simple, within-individual causal chain:

Mathematically, this can be represented as follows:

$$y_1=f(e_0),\hspace{0.17em}\mathrm{where}\hspace{0.17em}\frac{\mathrm{\partial }{y}_1}{\mathrm{\partial }{e}_0}>0,$$ 2.1

where y₁ represents adult outcomes (e.g. health or longevity), f is an increasing function and e₀ is the developmental environment. (This definition is also stated in row 1 of table 1.) Higher values of y₁ and e₀ indicate better outcomes and higher-quality environments, respectively. The expression ∂y₁/∂e₀ > 0 can be restated as follows: an improvement in early-life environment (the denominator e₀) causes an improvement in adult outcomes (the numerator y₁). We use a partial derivative ∂ because we are holding all else constant. DC can be directly tested with empirical data, assuming that the developmental environment is independent from other factors that predict adult health and fitness. Our definition of DC is evolutionary in the sense that it proposes that early-life adversity is potentially a selective force, but it takes no stance on the mechanism(s) by which early adversity is connected to worse adult outcomes.

(b) . Predictive Adaptive response hypothesis

Predictive Adaptive Response (PAR) hypotheses propose that an organism adopts a phenotype optimized for something that it expects to experience in adulthood [18,38]. The within-individual causal chain that motivates PAR has four steps:

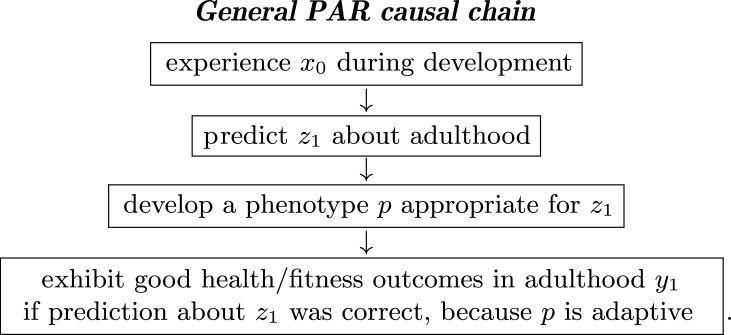
The subscripts indicate aspects of early life (0) or adult life (1). The definitions of x and z can accommodate a range of inputs. The variable y always refers to some outcome, such as fitness. To shorten our exposition, we will specifically focus on a version of PAR known as external PAR, where organisms base their predictions about the future on cues in the external environment (e.g. temperature or rainfall). The definitions of x and z can accommodate a range of inputs (see electronic supplementary material, §SA for a brief discussion of potential variants of PAR. This requires naming variables in the aforementioned causal chain in a manner that is consistent with external PAR. Specifically, x₀ will be developmental environment and renamed e₀, and z₁ will be adult environment and renamed e₁. These substitutions generate the following causal chain:

The aforementioned numbered chain assumes that all else is held constant, and that there is an analogous causal chain for high-quality environments.

This causal chain has clear similarities to the developmental mismatch hypothesis, which is ubiquitous in the evolutionary health literature [19,39].¹ It posits that the more closely the environment at life-history stage m matches the environment to which the organism adapted at some prior stage, m − k (for k > 0), the better an organism’s outcomes at stage m will be.

Each step in the aforementioned numbered chain is necessary. The proximate mechanism underlying PAR is captured by steps 2 to 3: the organism makes a prediction about its adult environment, and that prediction must lead it to adjust to cope with that predicted future environment. Step 4 is required to complete the evolutionary logic of PAR (i.e. the ‘ultimate’ mechanism): this response evolves because adopting a phenotype optimized to a low-quality adult environment improves fitness outcomes for an organism in adulthood relative to the outcomes it would have experienced if it had not adopted that phenotype.

Steps 1 and 4 typically correspond to things that can be observed and measured directly. For example, step 1 can be captured by measures of environmental variation where some values are thought to be high-quality/benign (e.g. abundant food, favourable temperature) and some low-quality/adverse (e.g. restricted food, unfavourable temperatures). Step 4 can be captured by measures of health- or fitness-related outcomes. Step 3 is theoretically observable, if the relevant, optimizable phenotypic response is known (e.g. smaller body size if the environment is food-restricted). However, step 2, an organism’s prediction, is not typically observable, so step 1 serves as a proxy for an organism’s prediction:

$$E(e_1)=e_0.$$ 2.2

In other words, an organism expects (the function E( · )) that its adult environment will be the same as its developmental environment. Equation (2.2) is critical for making the PAR hypothesis falsifiable.

The steps outlined earlier can be mapped to mathematical expressions. PAR is defined by two claims. The first captures steps 2 to 3:

$$p=f(E(e_1)),\mathrm{where}\hspace{0.17em}\frac{\mathrm{\partial }f}{\mathrm{\partial }E(e_1)}=\frac{\mathrm{\partial }p}{\mathrm{\partial }E(e_1)}<0,$$ 2.3

where p is the value of a given phenotype (e.g. the weight or length of an organism if body size is the phenotype of interest) that is protective in low-quality environments. The variable e₁ represents the quality of the adult environment. (Our choice to define the adaptation to high e₁ to be low p, i.e. to suppose that it is a bad environment that needs an adaptation, is arbitrary. We could have assumed that high p is better suited for high e₁ so long as we also reversed the sign of ∂p/∂E(e₁).) The derivative (∂p/∂E(e₁)) < 0) in equation (2.3) says that predicting a higher-quality environment (i.e. the expectation of e₁, or E(e₁)) reduces the degree to which an organism adopts a phenotype suited for a low-quality environment.

The second claim captures steps 3 to 4:

$$y_1=g(p,e_1),\mathrm{where}\hspace{0.17em}\frac{\mathrm{\partial }}{\mathrm{\partial }{e}_1}(\frac{\mathrm{\partial }{y}_1}{\mathrm{\partial }p})=\frac{{\mathrm{\partial }}^2{y}_1}{\mathrm{\partial }p\mathrm{\partial }{e}_1}<0,$$ 2.4

where y₁ is the outcome of interest, measured in adulthood. Note that y₁ must be an outcome that can be ordered to represent better or worse outcomes (e.g. good versus poor health). The derivative in equation (2.4) says that adopting a phenotype that is adaptive in a bad adult environment (i.e. a phenotype where ∂y₁/∂p > 0 when e₁ is low) leads to worse outcomes when the adult environment improves (∂(∂y₁/∂p)/∂e₁ < 0), assuming all else is held constant. Equation (2.4) is written as a derivative of a derivative, i.e. a cross-derivative, because a cross-derivative provides information about how a derivative changes when other variables are changed. Together, these two propositions (equations (2.3) and (2.4)) formalize steps 2 to 4. This definition of PAR, including equations (2.2), (2.3) and (2.4), is also stated in row 2 of table 1.

To illustrate the logic of the last two paragraphs, suppose that low-quality environment (low e₀) maps onto a cold environment and that growing a thick coat (p) is a phenotypic adaptation to the cold environment. An organism that predicts that the adult environment will be warm (higher E(e₁), as predicted by high e₀) will grow a thinner coat (less fur p). If the adult environment is indeed warm as predicted, then this phenotype (less fur) is likely to improve adult outcomes (e.g. less fur p means less overheating, so higher y₁).

See the electronic supplementary material for related information about the relationship between PAR and the developmental adaptive response hypothesis, which posits that an organism adapts to its developmental, rather than its predicted adult environment (electronic supplementary material, §SB).

(i) . Tests for Predictive Adaptive Response

In this section, we explain the tests that are implied by our definition of PAR. Two basic tests are used in the literature (e.g. [32,41]), which we will refer to as ‘phenotypic adaptation tests’ and ‘prediction error tests’. Both of these strategies are appropriate for our mathematical models.

Phenotypic adaptation tests focus on the mechanism of PAR, i.e. the phenotypic ‘choice’ an organism makes during development based on some input that it receives. We refer to the phenotypic adaptation (e.g. butterflies developing a specific wing spot pattern, or voles developing thick coats [42,43]) as a mechanism because developmental ‘choices’ about these phenotypes are how an organism gets from a prediction to a fitness outcome. To understand the two-part test implied by this phenotype-focused strategy, we can collapse the three equations that capture PAR (equations (2.2), (2.3) and (2.4)) into two expressions. The first expression is

$$p=f(e_0),\mathrm{where}\hspace{0.17em}\frac{\mathrm{\partial }f}{\mathrm{\partial }{e}_0}=\frac{\mathrm{\partial }p}{\mathrm{\partial }{e}_0}<0,$$ 2.5

which is obtained by plugging equation (2.2) (which describes steps 1 to 2 of our causal chain) into equation (2.3) (steps 2 to 3). This inequality says that low-quality developmental environments cause phenotypic adaptations to low-quality adult environments. The second expression is simply equation (2.4). That equation describes steps 3 and 4 of our causal chain and says that a phenotypic adaptation to a low-quality environment improves adult outcomes if adult environment is indeed low-quality. Each of these two expressions offers a separate test for PAR that makes use of data on phenotypic adaptations.

The second strategy for testing for PAR, prediction error tests, ignores information about specific phenotypes and instead focuses on the difference between an organism’s prediction and its realized adulthood. Prediction error tests evaluate whether an organism does better, on a given health or fitness measure, if its prediction about the future was correct. In steps 1–4 above, the organism would have predicted its adult environment based on its developmental environment. The implication is that it will do better if its developmental and adult environments more closely ‘match’ than if they do not (i.e. the mismatch hypothesis) (e.g. [23,32]). This strategy plugs the inequality from equation (2.5) into steps 3 to 4 (equation (2.4)) to connect developmental and adult environment, without reference to any specific phenotypic adaptation:

$$y_1=g(f(e_0),e_1),\mathrm{where}\hspace{0.17em}\frac{{\mathrm{\partial }}^2{y}_1}{(-\mathrm{\partial }{e}_0)\mathrm{\partial }{e}_1}=\frac{{\mathrm{\partial }}^2{y}_1}{(-\mathrm{\partial }p)\mathrm{\partial }{e}_1}\frac{\mathrm{\partial }p}{\mathrm{\partial }{e}_0}<0.$$ 2.6

This inequality gives both the definition and the test of the mismatch hypothesis. To see why, it helps to evaluate the function at the point where e₀ = e₁ (i.e. simply assign e₀ the same value as e₁, so that an organism’s developmental and adult environments match perfectly). A concomitant decrease in developmental environmental quality (−∂e₀) and increase in adult environmental quality (∂e₁), or vice versa, increase the mismatch between developmental and adult environments, leading to worse outcomes (∂²y₁ < 0).² While mathematically useful, this definition of the mismatch hypothesis is awkward because it relies on a cross-derivative (i.e. taking the partial derivative of the function with respect to developmental environment, and then the partial derivative of that result with respect to adult environment), as well as potentially placing restrictions on e₀ and e²₁. However, we can simplify the mismatch hypothesis to be more user-friendly as follows:

$$\frac{\mathrm{\partial }{y}_1}{\mathrm{\partial }|e_1-e_0|}=\frac{\mathrm{\partial }{y}_1}{\mathrm{\partial }|\mathrm{\Delta }e|}<0.$$ 2.7

From this point forward, we will define Δe = e₁ − e₀ and |Δe|=|e₁− e₀|. Now, the hypothesis states that adult outcomes decline as the difference between developmental and adult environments increases.

There is nothing about the prediction error testing strategy that precludes also using a phenotypic adaptation testing strategy. Indeed, the latter can complement prediction error tests by providing more specific information about the mechanism(s) by which organisms arrive at outcomes, which is information that prediction error tests do not provide. For more on the phenotypic adaptation test strategy, refer to electronic supplementary material, §SC. Going forward, we will focus on prediction error tests, which are commonly invoked in the literature (e.g. [23,29,32]).

(c) . Adult Environmental Quality hypothesis

Finally, we define the Adult Environmental Quality (AEQ) hypothesis, which says that a higher-quality adult environment will result in better adult outcomes, i.e.

$$\frac{\mathrm{\partial }{y}_1}{\mathrm{\partial }{e}_1}>0.$$ 2.8

This equation says that an improvement in adult environment (∂e₁) causes an improvement in adult outcomes (∂y₁ > 0). This definition of the AEQ hypothesis is restated in row 6 of table 1.

The AEQ hypothesis is not a primary focus of the literature on understanding the early-life drivers of inequality. We include it here to facilitate the discussion of conceptual issues surrounding the DC and PAR hypotheses in the next section.

3. Conceptual issues in testing models

Four conceptual issues are central to any empirical tests of the DC, PAR and AEQ hypotheses. We discuss two of these issues below. The other two (overlapping predictions generated by the theories, and the difficulty of testing intra-individual theories with inter-individual data) are discussed in electronic supplementary material, §SD.

(a) . Issue 1: non-independence of e₀, e₁ and Δe

Testing DC depends on variation in e₀; the prediction error test of PAR depends on Δe; and testing AEQ depends on e₁. Because these variables are not independent (varying e₀ or e₁ by necessity changes Δe), testing the DC, PAR and AEQ hypotheses independently is challenging. For instance, if we hold e₀ constant but increase e₁, we cannot determine if observed changes in outcomes are associated with an increase in e₁ or an increase in the change in environment (Δe). This means that researchers testing for DC and for PAR must make additional assumptions to also test the AEQ hypothesis. For example, one must define PAR as having equally deleterious effects regardless of whether the adult environment is better or worse than the developmental environment (‘symmetric’ rather than ‘asymmetric’ PAR; see electronic supplementary material, §§SA and SE and figure S1). Because symmetric PAR posits that changes in environment have the same effect on outcomes whether the change is positive or negative, a smaller reduction in outcomes with positive changes than with negative changes suggests AEQ, but also could, in theory, be consistent with asymmetric PAR.³

To deal with this issue (called an identification problem in many literatures) in a way that does not arbitrarily prioritize testing one hypothesis over another, we recommend (i) explicitly stating the relationships among developmental environment, adult environment and the difference between the two, and (ii) deciding which of these is/are independent of the theoretical model (i.e. exogenous to the model’s structure), and which a byproduct of the model’s structure (i.e. not independent of the model’s structure, but simply a byproduct of the exogenous variation). Only hypotheses that concern the independent variation are testable [45].

The process that we feel best represents the phenomenon of interest here is that e₀ and Δe are independent, and that these collectively generate e₁ via the formula e₁ = e₀ + Δe. An alternative assumption—that Δe is simply a byproduct—seems less defensible, because time moves linearly: e₀ and Δe come before e₁, so it is unlikely e₁ causes either e₀ or Δe. Imagine an adult baboon living through a drought. It has already experienced e₀, and the drought it is now experiencing is familiar (i.e. matches prior experience, a low Δe), or unfamiliar (i.e. does not match prior experience, a high Δe). The baboon does not experience e₁ independently of what it experienced during development. One could assume a different process, but it is still the case that only two of the three hypotheses will be testable.

(b) . Issue 2: non-mutually exclusive theories

A second difficulty is that the DC, PAR and AEQ theories, as we have chosen to define them, are not mutually exclusive. Any combination of them could be true at the same time [46,47], and indeed meta-analyses suggest that more than one may often be at work [48]. This means that univariate models without higher-order polynomial terms (e.g. interacting and squared variables) may not be able to distinguish which theories are true. Consider the following simple model:

$$y_1=F(|\mathrm{\Delta }e|)=\beta |\mathrm{\Delta }e|+e.$$ 3.1

The goal of this model is to correlate adult outcomes with the mismatch between early-life and adult environments. We distinguish this model from the theoretical models in the previous section by using capital letters to define the function. Suppose, however, that both DC and PAR are true. The model described earlier (equation (3.1)) does not simply control for or eliminate the influence of DC just by excluding a separate e₀ term. The functional consequence of this is that the model will mistakenly attribute the effect of e₀ to Δe = e₁ − e₀ (something that is often referred to in the statistics and economics literature as omitted variable bias [36]). The result is that the estimated coefficient will not equal the partial derivative of adult outcomes with respect to mismatch (∂y₁/∂|Δe|):

$$E(\hat{\beta })=\beta +{\gamma }_0{\delta }_{0d},$$ 3.2

where γ₀ is equal to ∂y₁/∂e₀ and δ_0d is the coefficient from a regression of |Δe| on e₀. Put simply: the coefficient may be biased. A similar problem will afflict any regression equation that does not allow all plausible models to be true, a difficulty that has been noted before [48]. At best, effect sizes are likely to be over- or under-estimated; at worst, such models will generate answers that are the opposite of the real-world truth (e.g. concluding that DC or PAR do not exist when in fact they do). Moreover, simply including an e₀ (or e₁) term in such a model does not solve the problem, for reasons we will explain in §6.

4. Issues with a common visualization and testing strategy

One common approach for implementing a prediction error test for PAR (§2b) relies on running a regression that contains a term for an interaction between the developmental and adult environments (e.g. [23,32,49–53]), i.e.

$$y_1=\beta +{\beta }_0{e}_0+{\beta }_1{e}_1+{\beta }_{01}{e}_0{e}_1+u,$$ 4.1

where u is a regression error term. We refer to this equation as ‘the interaction regression’.

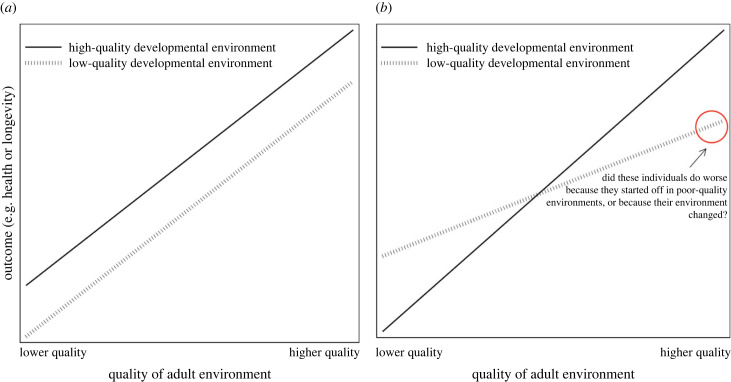
Testing for DC with the interaction regression focuses on the coefficient on e₀, while the test for PAR focuses on the coefficient on the interaction term β₀₁. We believe that this strategy is partly motivated by visualizations like the one depicted in figure 2, which plot adult outcomes against adult environmental quality separately for organisms that experienced different developmental environments (e.g. [17,23]). Rejecting the hypothesis that β₀ = 0 (i.e. the null, that low-quality developmental environments do not lead to worse adult outcomes) is interpreted as evidence for DC, while rejecting the hypothesis that β₀₁ = 0 is interpreted as preliminary evidence for a PAR (so long as β₀ < 0 is also true, as in figure 2a, regardless of what β₀ is, as shown in figure 2b).

Figure 2.

Commonly used depictions of empirical evidence for the Developmental Constraints (DC; §2a) and Predictive Adaptive Response (PAR; §2b) hypotheses. (a) As adult environmental quality improves, health and fitness outcomes improve. However, organisms that started in low-quality developmental environments always fare worse than peers that started in high-quality environments. (b) Organisms that experienced similar-quality developmental and adult environments have better outcomes than organisms that experienced ‘mismatched’ developmental and adult environments. These depictions manipulate both the starting point (e₀ in table 1, the variable that DC theory is concerned with) and how well the developmental and adult environments match (Δe in table 1, the variable that PAR theory is concerned with) simultaneously. This approach makes it difficult to distinguish between these two hypotheses. Moreover, the x-axis shows variation in the adult environment, which is the key variable of interest for the Adult Environmental Quality (AEQ) hypothesis (e₁ in table 1).

To interpret the direction of the effect of the interaction term β₀₁, researchers often use visualizations. In these visualizations, if the line for organisms with high-quality developmental environments crosses from below the line for organisms with low-quality developmental environments (as shown in figure 2b), this is interpreted as evidence for PAR, because organisms whose developmental and adult environments ‘match’ do better than those whose environments do not match.⁴ Figure 2b is indeed consistent with predictions derived from the PAR hypothesis: organisms do better in adult environments that are more similar to their developmental environments. It is also consistent with the AEQ hypothesis (equation (2.8)), since all organisms do better as their adult environmental quality improves.

However, any visualization with the axes in figure 2 is manipulating two variables simultaneously—the developmental environment (implicitly, DC) and differences between the developmental and adult environment (PAR). This makes it hard to determine which one is responsible for the observed effect. For example, on the right-hand sides of figure 2a,b (where adult environmental quality is high), the organisms represented by the dashed line began their lives in a low-quality environment, which may account for their worse outcomes relative to the organisms that began their lives in a high-quality environment (those represented by the solid line). However, the organisms that began in a low-quality environment are also in an adult environment that does not match their developmental environment (i.e. they predicted their adult environment poorly), while the organisms that began in a high-quality developmental environment are in an adult environment that matches their developmental environment (i.e. they predicted their adult environment accurately). It is not clear whether the individuals with high-quality developmental environments have better outcomes because they started their lives on top or because their developmental and adult environments match. This conceptual issue (i.e. the inability to distinguish between DC and PAR when limiting comparisons to individuals that end up in high-quality adult environments) has been noted repeatedly in the literature (e.g. [14,32,50,54]).

Comparing individuals from low- and high-quality developmental environments in low-quality adult environments (the left-hand side of the x-axis in figure 2a,b) is essential to executing the prediction error test for PAR, something that has been referred to as the ‘fully factorial’ version of this test (e.g. [32]). However, this approach still does not cleanly separate the effects of starting point from the effects of prediction error, because it is manipulating two different variables (e₀ and Δe) while embedding information about a third (e₁) (see electronic supplementary material, §SF for additional discussion). As such, it fails to place the independent variable of primary interest on the x-axis, making these plots difficult to interpret. When visualizing DC, we recommend creating figures with an x-axis that represents the developmental environment (figure 1a), and when visualizing prediction error tests for PAR, creating figures with an x-axis that reflects difference-from-prediction (in our particular use case, how well the developmental and adult environments match (figure 1b,c)). This allows separate visual identification of DC and/or PAR, as well as determination of how a negative change in environment might be different from a positive one (see also [32] for another visualization strategy).

5. Constructing theoretically derived tests of the Developmental Constraints and Predictive Adaptive Response models

Here, we derive the empirical tests that follow from our formal definitions of DC and PAR. The definitions of DC and PAR are compatible with a very general mathematical function where outcomes are proposed to be the result of both developmental environment and the difference between developmental and adult environments:

$$\hspace{0.17em}{y}_1=F(e_0,|\mathrm{\Delta }e|),$$ 5.1

where capital F indicates a continuous empirical function (i.e. a curve) involving observed data. We do not include adult environment in the function (and thus the AEQ hypothesis) for the reasons given in §3a.

Testing these theories with data requires a regression equation that we can estimate. A simple example of such a regression equation, where y₁ varies linearly with Δe, would be

$$\hspace{0.17em}{y}_1=\beta +{\beta }_0{e}_0+{\beta }_d|\mathrm{\Delta }e|+u.$$ 5.2

β_d is the marginal effect of the absolute value of the mismatch between developmental and adult environments (i.e. the effect of prediction error when all else is held constant). While equation (5.1) is too general to directly estimate via regression analysis, equation (5.2) is specific enough to estimate. Equation (5.2) is a useful example, but assuming a linear relationship between y₁ and Δe is likely to be too simple to capture many possible patterns in the data. In the next section, we present a regression equation that is both mathematically connected to equation (5.1), and also flexible enough to allow for diverse real-world relationships between environment and outcomes.

(a) . Regression model derived from mathematical definitions

To obtain a more flexible regression model than equation (5.2), we assume F (the function describing the relationship between early environments (e₀) and the difference between early and adult environments (Δe)) is differentiable (i.e. that it is possible for us to take the derivative of the function) and take a Taylor expansion. A Taylor expansion is a mathematical method for approximating a section of a curve like equation (5.1) as the sum of different powers of its inputs in that section of the curve. The Taylor Series theorem says that as this sum grows to include infinitely different powers of the function’s inputs, i.e. e₀ and |Δe| for F, the sum will converge to the relevant section of the function F. Of course, one cannot use an infinite sum for a regression because more explanatory variables reduce power for any given sample. So we must choose a cutoff on the number of powers in our series to balance power and precision. Moreover, we must choose a section of the curve to approximate.

We choose a second-order expansion around e₀ = e₁ = |Δe| = 0, i.e. a sum of only first and second powers of the inputs in F. Estimating a regression model with only first-order terms cannot capture both DC and PAR. Moreover, it would be difficult to relate to the interaction regression (equation (4.1)), since an interaction term requires a second-order (or higher) expansion. A higher than second-order expansion is possible, but requires more data to be adequately powered relative to a model with fewer terms. Sample sizes in the real world often cannot accommodate this requirement. A second-order expansion implies the following regression model:

$$\begin{array}{r}{y}_1=\gamma +{\gamma }_0{e}_0+{\gamma }_d|\mathrm{\Delta }e|+{\gamma }_{00}{e_0}^2+{\gamma }_{\mathrm{dd}}|\mathrm{\Delta }e{|}^2+{\gamma }_{0d}{e}_0|\mathrm{\Delta }e|+u,\end{array}$$ 5.3

where the subscript 0 on γ indicates the coefficient is on e₀, d indicates it is on |Δe|, 0d indicates it is on e₀|Δe| and so on. The error term u captures factors that influence the observed outcomes in a given dataset but which were omitted (presumably unintentionally) from the model. The first three terms are included in a first-order Taylor expansion; the last three terms, including the interaction term (equation (4.1)), are added by a second-order expansion.

Equation (5.3) is the primary regression model that we recommend and evaluate in the remainder of this paper. It balances capturing important elements that are omitted from the interaction model (which we discuss in the next section) with the power limitations of real-world datasets. Researchers with larger datasets may attempt to estimate higher-order polynomials and apply the appropriate tests implied by the definitions of DC and PAR. For simplicity’s sake, the version of the regression in the main text assumes ‘symmetrical’ prediction error effects (i.e. that the costs of erroneously predicting that the adult environment will be better than it really is, are the same as the costs of erroneously predicting that the adult environment will be worse than it really is). One can modify the regression to accommodate asymmetric prediction error costs; see electronic supplementary material, §§SA and SE for more details.

Before proceeding, we should note that this article does not have much to say about the domain of y₁ and (e₀, e₁), the distribution of the error term and the method one uses for estimation. Our focus is on the use of an interaction term in the interaction model. Our recommendation is to use the same units, distribution of u, and method of estimation as one would have used in an interaction regression model. If the researcher would ordinarily conduct an interaction regression in log units, using logy₁ and (loge₀, loge₁), then we would recommend using logy₁ and (loge₀, log|Δe|) in the quadratic regression. Likewise, if y₁ is binary and one would use a logit model, where $y_1=\Lambda (f\hspace{0.17em}(e_0,e_1)$ to account for the distribution of the error term, where the function f is an interaction model, then our recommendation is to replace the f with a quadratic function but keep the logit structure. Finally, if one would like to estimate the model with maximum likelihood or generalized method of moments [55], there is no reason not to do so. The key constraint the quadratic regression adds is replacing e₁ with |Δe| and adding squared terms of these two inputs to the regression model.

(b) . Testing for Developmental Constraints and Predictive Adaptive Response with a quadratic regression

The quadratic regression (equation (5.3)) implies specific and different statistical tests for DC and PAR. The test for DC can be derived by taking the derivative of equation (5.3) for adult outcomes y₁ with respect to early-life environment e₀, i.e. seeing how adult outcomes would change (∂y₁) with a change in early environment (∂e₀). According to our mathematical definition of DC, the change should be positive. This implies the following test for DC:

$$\frac{\mathrm{\partial }{y}_1}{\mathrm{\partial }{e}_0}={\gamma }_0+{2\gamma }_{00}{e}_0+{\gamma }_{0d}|\mathrm{\Delta }e|>0.$$ 5.4

If one cannot reject that ∂y₁/∂e₀ = 0 in favour of the aforementioned inequality, then one cannot reject the null hypothesis that DC is false.

The test for PAR can be derived in a similar manner: take the derivative of the regression model of adult outcomes in equation (5.3) with respect to a greater difference between early-life and adult environments (i.e. greater |Δe|), and then apply the definition of the PAR hypothesis from equation (2.7). The test that emerges is:

$$\frac{\mathrm{\partial }{y}_1}{\mathrm{\partial }|\mathrm{\Delta }e|}={\gamma }_d+2{\gamma }_{\mathrm{dd}}|\mathrm{\Delta }e|+{\gamma }_{0d}{e}_0<0.$$ 5.5

If one cannot reject ∂y₁/∂|Δe| = 0 in favour of the aforementioned inequality, then one cannot reject the null hypothesis that PAR is false.

6. Implications for the interaction regression model

Although the interaction regression (equation (4.1)) is commonly used to test for PAR and also may be used to test for DC (via the coefficient on e₀), we have identified two main problems with using that regression to test these hypotheses. In this section, we show why the interaction regression is mathematically incompatible with the existence of PAR as we formally define it. In electronic supplementary material, §SG we also show why (i) the test for DC in an interaction model may yield a different result compared with the simple test for a correlation between developmental environment and adult outcomes, and, (ii) if the interaction regression does not accurately describe reality, the coefficients estimated from that regression are likely to be misleading.

Why is the interaction regression mathematically incompatible with our definition of PAR in table 1? In short, the reason is that this regression does not allow for the possibility that positive and negative prediction errors could both be harmful, which is a key prediction of the PAR hypothesis. For the interaction regression to test the mismatch prediction of PAR, it must be the case that either positive errors are harmful or negative errors are harmful, but not both. We demonstrate this problem in two steps: first, we show how outcomes must change with increased prediction error, assuming the interaction model is correct, and second, we show that that change is not feasible.

The first step requires us to manipulate the interaction regression model. Equation (4.1) posits that adult outcomes are a function of early-life and adult environments (including the interaction of the two), but not of the mismatch in environments. However, because the PAR hypothesis says that a mismatch between early and adult environment is bad for outcomes, we want to manipulate the interaction model to express adult outcomes as a function of early-life environment and the mismatch between early and adult environments.

To accomplish this manipulation, we do two things. Firstly, we can re-write adult environment e₁ as a function of early environment e₀ and change in environment |Δe| as follows: e₁ = e₀ + (e₁ − e₀) = e₀ + Δe. If we plug this equation for e₁ into the interaction model, that model can express the relationship between early environment and change in environment:

$$y_1=\beta +{\beta }_0{e}_0+{\beta }_1(e_0+\mathrm{\Delta }e)+{\beta }_{01}{e}_0(e_0+\mathrm{\Delta }e)+u.$$ 6.1

Importantly, PAR as we have defined it focuses on the impact of mismatch (|Δe| = |e₁ − e₀|), not just the differences between early and adult environments (Δe = e₁ − e₀). Therefore, we complete our manipulation using tools from calculus that enable us to take the derivative of the last equation with respect to mismatch, even though that equation does not have mismatch in it. The first tool is the chain rule: the derivative of y₁ with respect to |Δe| is equal to the derivative of y₁ with respect to Δe times the derivative of Δe with respect to |Δe|. The second tool is that ∂Δe/∂|Δe| = |Δe|/Δe, i.e. the effect of the mismatch on the difference in outcomes depends on whether the difference is positive or negative.

To see what the interaction model says about how outcomes must change with increasing mismatch, we take the derivative of equation (6.1) with respect to mismatch:

$$\begin{array}{r}\frac{\mathrm{\partial }{y}_1}{\mathrm{\partial }|\mathrm{\Delta }e|}=(\frac{\mathrm{\partial }{y}_1}{\mathrm{\partial }(e_1-e_0)})\hspace{0.17em}\frac{\mathrm{\partial }(e_1-e_0)}{\mathrm{\partial }|\mathrm{\Delta }e|}=({\beta }_1+{\beta }_{01}{e}_0)\hspace{0.17em}\frac{|\mathrm{\Delta }e|}{(e_1-e_0)}<0.\end{array}$$ 6.2

Equation (6.2) now reflects the prediction of the PAR hypothesis in equation (2.7), which is that PAR exists if this derivative is negative. In other words, on average, bigger gaps between developmental and adult environments lead to worse outcomes when all else is held constant.

Our second step is to show that the inequality in equation (6.2) cannot hold if the interaction regression was correct. Our PAR definition requires that the derivative must be negative when Δe is both positive and negative, i.e. when the adult environment turned out to be better than was predicted, as well as when it was worse than was predicted. This is required even if the environment is coded as a binary variable. For example, coding a low-quality environment as e = 0 and a high-quality environment as e = 1 yields mismatch if Δe is 1 or −1 or, equivalently, |Δe| > 0.

Regardless of how environments are coded, it is not possible for the derivative to be negative both when environment improves and when it worsens between development and adulthood. If Δe > 0, then Δe/|Δe| > 0, and if Δe < 0, then Δe/|Δe| < 0. So, for the inequality in equation (6.2) to hold, β₁ + β₀₁e₀ has to be negative for positive Δe and positive for negative Δe. However, if we start from a given developmental environment e₀, this is impossible: the β₁ + β₀₁e₀ term is constant and does not flip signs.

Importantly, and by contrast, the mismatch prediction of PAR is not a theoretical impossibility with the quadratic regression because it includes a |Δe| term that the interaction model does not. The derivative in the quadratic regression equation (5.5) can theoretically be negative regardless of whether the adult environment was better or worse than predicted (i.e. for the full range of Δe).

Strictly speaking, the interaction regression will only fail to find evidence of PAR if researchers test for PAR based on the prediction in equation (2.7) (adult outcomes decline as the difference between developmental and adult environments increases). The interaction regression cannot generate results that pass that test. However, this impossibility likely also undermines the two-part test that supplements the interaction regression with a visualization of the interaction. That two-part test can be thought of as an effort to approximate testing the prediction in equation (2.7). However, if directly testing that prediction with the interaction regression cannot find evidence for mismatch, then the approximation that combines the interaction regression with a visualization is also unlikely to find it.

7. Simulations of alternative tests fors Developmental Constraints and Predictive Adaptive Response

We conducted simulations to determine how often the interaction regression (equation (4.1)), as compared with the quadratic regression (equation (5.3)), correctly finds or rejects the predictions generated by DC or PAR. Our process has five steps. We provide a brief overview of our simulation design below, but provide additional details in electronic supplementary material, §SI.

(a) . Simulation design

Step 1: Generate a large number of different virtual realities. Each simulation posits a virtual reality where, by assumption, a third-order polynomial perfectly describes the effect of (a) an organism’s developmental environment and (b) the mismatch between its developmental and adult environments on adult outcomes. We chose a third-order polynomial because it is the lowest-order polynomial that allows both the interaction and quadratic regression models to generate erroneous test results and compare error rates.

However, a third-order polynomial can have infinitely different coefficient values and thus describe infinitely different realities. To reduce these possibilities, we pared those possible realities down to five evenly spaced values of e₀ ∈ [0, 1] and of Δe ∈ [ − 1, 1], and excluded realities where at any allowed value of e₀ or Δe generated an outcome outside the range of [0, 1]. This left 130 201 ‘pruned’ realities where each reality is defined by a third-order polynomial and a 10 × 1 vector of parameters for that polynomial.

Step 2: Determine whether PAR or DC is true in each reality. Each of the 130 201 realities was evaluated for PAR and DC by applying the tests in equations (2.7) and (2.1), respectively. Of all the pruned realities, 2697 (2.07%) were truly positive for PAR, 2697 (2.07%) were truly positive for DC and 58 (0.04%) were truly positive for both. These feasible and true positive realities are the benchmark against which tests based on each regression model are evaluated.

Step 3: Simulate a dataset for each reality. For each pruned reality, we generated a simulated dataset for estimating regressions by adding noise to the outcomes that are generated in that reality for 16 different combinations of developmental and adult environments. Each dataset included 2000 observations on the variables (${\hat{y}}_1,e_0,\mathrm{\Delta }e$). For each observation, e₀ is drawn uniformly from four evenly spaced points between 0 and 1; Δe from a normal distribution with mean −0.03 and standard deviation 0.21⁵ but truncated at −1 and 1; and an error term v from a normal distribution with mean 0 and variance equal to that of the outcome at the mean value of (e₀, Δe) in each reality. The observed outcome ${\hat{y}}_1$ is generated by adding v to the true outcome in that pruned reality at the drawn (e0, Δe).

Step 4: Apply different empirical tests for PAR and DC on simulated data for each reality. We applied tests that researchers currently use (based on the interaction regression) and tests we recommend (based on the quadratic regression) to determine if each test finds that there is PAR and DC in each virtual reality. Specifically, we generated four test results for PAR in each reality:

• 1. PAR test 1: Visualization test for PAR using the interaction regression (equation (4.1)). This test finds evidence for PAR if (i) β₀₁ ≠ 0, and (ii) the visualization shows that the fit line depicting the adult environment/adult outcomes relationship for organisms from low-quality developmental environments (the dotted line in figure 2b) intersects from above the same line for organisms from high-quality developmental environments (the solid line in figure 2b).
• 2. PAR test 2: ‘Relaxed’ version of the visualization test with the interaction regression (equation (4.1)). In the presence of DC, the fit line for the relationship between adult environment and adult outcomes for organisms from low-quality developmental environments may be shifted downwards relative to organisms from medium- and high-quality developmental environments (as depicted in figure 1c). In this case, PAR might exist even if the lines for low- and high-quality developmental environments do not cross. This suggests a relaxed visualization test which finds evidence for PAR if (i) β₀₁ ≠ 0 and (ii) the visualization shows that the fit line depicting the relationship between adult environment and adult outcomes for organisms from low-quality developmental environments has a lower slope than the same line for organisms from high-quality developmental environments.
• 3. PAR test 3: Theoretically motivated test (equation (2.7)) applied to the interaction regression (equation (4.1)). This test finds evidence for PAR if the derivative of the interaction regression with respect to |Δe| is negative (i.e. equation (6.2)). We implement this test notwithstanding the fact that the mismatch prediction of the PAR hypothesis cannot be true if the interaction regression is a correct specification of reality.
• 4. PAR test 4: Theoretically motivated test (equation (2.7)) applied to the quadratic regression (equation (5.3)). This test finds evidence for PAR if the derivative of the quadratic regression with respect to |Δe| is negative (equation (5.5)).

We also generated three tests for DC in each reality:

• 1. DC test 1: Naive test for DC with the interaction regression (equation (4.1)). This test finds evidence for DC if β₀ in equation (4.1) is positive.
• 2. DC test 2: Theoretically motivated test (equation (2.1)) applied to the interaction regression (equation (4.1)). This test finds evidence for DC if the derivative of the interaction regression with respect to e₀ is positive, i.e. β₀ + β₀₁e₁ is positive.
• 3. DC test 3: Theoretically motivated test (equation (2.1)) applied to the quadratic regression (equation (5.3)). This test finds evidence for DC if the derivative of the quadratic regression with respect to e₀ is positive. This test is presented in equation (5.4).

(b) . Evaluating empirical tests

Finally, we computed the rate at which each test correctly concludes there is PAR or DC and correctly concludes there is no PAR or DC. The upper part of table 2 provides the sensitivity and specificity of each of the four methods of testing for PAR across all feasible realities (sensitivity is the percentage of the 2755 realities where PAR was true in which PAR was correctly detected; specificity is the percentage of the remaining 127 504 realities where PAR was not true in which it was correctly not detected). The second column shows the performance of a coin-flip test, which we use as a benchmark of a data-uninformed test (i.e. a test with performance equal to chance).

Table 2.

Percentage of simulated realities where Predicitive Adaptive Response (PAR) and Developmental Constraints (DC) were correctly detected (sensitivity) and correctly not detected (specificity) using different tests.

Predictive Adaptive Response (PAR)
regression	none	interaction	interaction	interaction	quadratic
test	coin flip	β01 ≠ 0 in (4.1) and strict visual test (test 1)	β01 ≠ 0 in (4.1) and relaxed visual test (test 2)	theory-motivated test in (6.2) (test 3)	theory-motivated test in (5.5) (test 4)
sensitivity	51.54	58.84	79.24	9.76	90.74
specificity	50.13	72.40	56.64	73.67	71.45
Developmental Constraints (DC)
regression	none		interaction	interaction	quadratic
test	coin flip		naive test (β0 > 0) (test 1)	theory-motivated test (β0 + β01e1 > 0) (test 2)	theory-motivated test in (5.4) (test 3)
sensitivity	49.43		93.21	100.00	100.00
specificity	50.09		10.11	56.76	66.57

The interaction regression has poor or imbalanced performance across a range of tests. For instance, the interaction regression with the visualization approach to testing for PAR has sensitivity that is only slightly better than a coin flip (58.84%). A relaxed visual test has higher sensitivity (79.24%) but specificity that is only marginally better than a coin flip (56.64%); in other words, it incorrectly detected PAR 43.46% of the time. The interaction regression showed even worse performance with the theoretically motivated test for PAR: sensitivity (9.76%) was much worse than a coin flip. This very poor sensitivity is to be expected. If the interaction regression is a correct description of reality, we demonstrated that one theoretically cannot find PAR. The visualization test using the interaction regression actually gets the right answer more often than the theoretically motivated version precisely because the former is not testing the prediction generated by the PAR hypothesis (equation (2.7)). This allows it to perform the same as or marginally better than a coin flip, while a theoretically motivated use of the interaction regression is specifically biased against finding the mismatch prediction of PAR even when it exists.

The quadratic regression combined with a theoretically motivated test performs best of all. Sensitivity (90.34%) is higher than any test using an interaction regression and specificity is roughly the same (71.61%) as the best tests under the interaction model. This test is not perfectly sensitive and specific because it too suffers from bias due to omitted variables, since the realities it approximates also have third-order terms.

The lower part of table 2 provides the sensitivity and specificity of three methods of testing for DC across feasible realities. The interaction model performed poorly relative to the quadratic regression. The naive test using the interaction regression has good sensitivity, but much worse specificity than a coin-flip. The test often finds DC whether or not it is true. The interaction regression combined with a theoretically motivated test has perfect sensitivity, but specificity that is only marginally better than a coin flip. Switching to a quadratic regression and using a theoretically motivated test for DC performs best of all. It too has perfect sensitivity, and somewhat better specificity (66.57%).

8. Discussion

DC and PAR are currently the most commonly invoked evolutionary explanations for early-life determinants of inequality in adult health and fitness outcomes. However, these theories lack precise and consistent definitions. Further, different forms of DC and PAR make their own assumptions, assumptions that need to be made explicit rather than left implicit. Making definitions and assumptions explicit has the benefit of clarifying where different flavours of hypotheses do and do not generate differentiating predictions, what steps researchers must take to differentiate between them, and under what conditions it is possible to do so.

In this article, we have chosen to focus on one specific consequence of the lack of formal definitions for DC and PAR, namely, that a common test meant to disentangle these hypotheses—linear regression models with interaction effects—ends up conflating the two theories. Testing a key prediction generated by the PAR hypothesis requires researchers to detect the effects of prediction errors—in our use case here, of environmental mismatches. Doing so with any accuracy is difficult with an interaction model and its complementary data visualization strategy. Indeed, such an interaction model is theoretically incapable of testing the mismatch prediction of PAR. A test that applies the mismatch prediction to the quadratic regression does not suffer from a basic mathematical incompatibility problem. Similar arguments justify the use of a reasonable, formal definition of DC along with a quadratic regression. Our simulations show that using the theoretical predictions of PAR and DC specified in table 1, together with the quadratic regression, dramatically improved sensitivity/specificity tradeoffs (relative to any use of an interaction model) when testing for PAR and DC. Critically, there is no downside to using the quadratic specification, beyond requiring slightly larger sample sizes. It will produce reliable answers even in a world where an interaction regression is an accurate representation of the biological reality, a possibility we discuss in more detail below. The reverse is not true, for the many reasons discussed earlier.

Currently, support for PAR in the literature is mixed, especially in mammals [14]. The definitional and testing issues highlighted here raise the question of whether this is because of flaws in the methods used to detect them. Our results show that statistical tests derived from mathematical definitions of the DC and PAR concepts, along with more flexible regression models, provide clearer answers and will improve our ability to compare results across studies.

Because there is already a literature that employs visualizations such as figure 2 and the interaction regression in equation (4.1) to test for PAR, it is useful to know if there are conditions under which this approach is a valid test. Sufficient conditions for the interaction regression to be valid are if (a) prediction errors in only one direction reduce health/longevity/fitness (so to avoid the problem we highlight in §6), and (b) the relationship between outcome, developmental environment and the change in environment over a lifetime is quadratic, but with certain parameter restrictions that cause the quadratic model to be identical to the interaction model. For example, focusing on a positive change in environment, so that the quadratic regression can be written as follows:

$$y={\beta }_0{e}_0+{\beta }_{\mathrm{\Delta }}(e_1-e_0)+{\beta }_{00}{e}_0^2+{\beta }_{\mathrm{\Delta }\mathrm{\Delta }}{(e_1-e_0)}^2+{\beta }_{0\mathrm{\Delta }}{e}_0(e_1-e_0)+u,$$ 8.1

condition (b) implies the following restrictions on the coefficients in this equation: β_ΔΔ = 0, β₀₀ = −β_0Δ and β_0Δ ≠ 0. If these restrictions are plugged into the equation above, then that equation collapses to the interaction model in equation (4.1). One problem with this approach is that the required coefficient restrictions have no biological meaning. A second problem is that it is difficult to know ex ante whether condition (b) is satisfied without first estimating a quadratic regression.

Given the high rates of both false positives and false negatives generated by the interaction model plus visual test strategy (table 2), it is reasonable to infer that somewhere between 20 and 40% of the PAR-related results in the literature that rely on the tests described here are false negatives, 30–45% are false positives, and that it may contain a significant number of false positives for DC. Of course, this assumes that researchers are equally likely to publish null results and results in which they found evidence for PAR and/or DC. Assuming the ‘file drawer’ effect applies to this literature [57], then false positives may be over-represented relative to false negatives.

The DC and PAR hypotheses appear in the literature of many academic fields [5,18,19,21,32,44]. Significant human and financial resources are being devoted to untangling their effects because of their important implications for public health and policy [59], and for our understanding of if and how variation in early environments explains inequality in adult outcomes [60]. Clear, careful definitions and appropriate statistical tests are absolutely essential for forward progress in this important research area. We recommend that researchers take the following steps when testing the DC and PAR hypotheses:

• 1. Rely on statistical tests that are derived from mathematical definitions, to avoid conflating different phenomena being evaluated in the same model.
• 2. Avoid using interaction or first-order polynomial models to test for prediction error (a.k.a. mismatch) effects; instead, use a quadratic or higher-order regression model. We provide Stata and R code at https://github.com/anup-malani/PAR.git to assist with implementation of quadratic models and the associated statistical tests for DC and PAR.
• 3. Verify that data visualizations cleanly separate the concept(s) of interest. It is better to use multiple visualizations that each address a single phenomenon than a single visualization that potentially conflates different phenomena.
• 4. Keep in mind that the overlapping predictions made by DC and PAR, their non-mutually exclusive nature, and the non-independence of the variables under consideration mean that separately identifying the effects of developmental and adult environments, alongside the effects of prediction error, is frequently not possible.

Data accessibility

The code for the simulation is available at https://github.com/anup-malani/PAR/blob/main/PAR_simulation_220117b.do.

Supplementary material is available online [58].

Authors' contributions

A.M.: conceptualization, formal analysis, methodology, visualization, writing—original draft, writing—review and editing; E.A.A.: conceptualization, funding acquisition, methodology, writing—review and editing; S.R.: conceptualization, formal analysis, methodology, project administration, visualization, writing—original draft, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed herein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

We gratefully acknowledge the support of the NIH, especially the National Institute on Aging, particularly NIH grant nos R01AG053330, R01AG053308, R01HD088558 and P01AG031719. A.M. acknowledges the support of the Barbara J. and B. Mark Fried Fund at the University of Chicago Law School.