Smart manufacturing inspired approach to research, development, and scale-up of electrified chemical manufacturing systems

Derek Richard; Joonbaek Jang; Berkay Çıtmacı; Junwei Luo; Vito Canuso; Prakashan Korambath; Olivia Morales-Leslie; James F Davis; Haresh Malkani; Panagiotis D Christofides; Carlos G Morales-Guio

doi:10.1016/j.isci.2023.106966

. 2023 May 29;26(6):106966. doi: 10.1016/j.isci.2023.106966

Smart manufacturing inspired approach to research, development, and scale-up of electrified chemical manufacturing systems

Derek Richard ¹, Joonbaek Jang ¹, Berkay Çıtmacı ¹, Junwei Luo ¹, Vito Canuso ¹, Prakashan Korambath ², Olivia Morales-Leslie ^2,³, James F Davis ^1,², Haresh Malkani ³, Panagiotis D Christofides ^1,⁴, Carlos G Morales-Guio ^1,^∗

PMCID: PMC10291476 PMID: 37378322

Summary

As renewable electricity becomes cost competitive with fossil fuel energy sources and environmental concerns increase, the transition to electrified chemical and fuel synthesis pathways becomes increasingly desirable. However, electrochemical systems have traditionally taken many decades to reach commercial scales. Difficulty in scaling up electrochemical synthesis processes comes primarily from difficulty in decoupling and controlling simultaneously the effects of intrinsic kinetics and charge, heat, and mass transport within electrochemical reactors. Tackling this issue efficiently requires a shift in research from an approach based on small datasets, to one where digitalization enables rapid collection and interpretation of large, well-parameterized datasets, using artificial intelligence (AI) and multi-scale modeling. In this perspective, we present an emerging research approach that is inspired by smart manufacturing (SM), to accelerate research, development, and scale-up of electrified chemical manufacturing processes. The value of this approach is demonstrated by its application toward the development of CO₂ electrolyzers.

Subject areas: Chemistry, Chemical engineering, Engineering, Electrical engineering, Catalysis

Graphical abstract

Chemistry; Chemical engineering; Engineering; Electrical engineering; Catalysis

Introduction

A growing coalition of countries, cities, businesses, and other institutions are pledging to achieve net-zero emissions by 2050 or earlier. Meeting this ambitious goal will require cutting greenhouse gas emissions as close to zero as possible, while also implementing carbon offset technologies to capture persistent emissions from the atmosphere to close the carbon cycle. A major factor enabling this shift to a carbon-neutral economy is the emergence of cost-effective renewable energy sources such as photovoltaics and wind turbines that harvest renewable energy in the form of electricity. The energy landscape in 2050 is expected to be dominated by renewable energy technologies. To enable the transition to an electric-based energy landscape, Power-to-X and X-to-Power technologies will be needed to decouple power from the electricity sector for use in other sectors of the economy: such as transportation fuels, industrial chemical production, grid-scale energy storage, and eventually carbon capture (Figure 1A). The development and scale-up of Power-to-X and X-to-Power technologies is viewed as a promising solution to meet strong decarbonization targets while enabling the high penetration of renewables into the different sectors of the economy.¹

Application of AI and ML to electrolyzer Scale-up can enable a net-zero carbon future

(A) Vision of a net-zero carbon future.

(B) AI and ML for scale-up of CO₂ electrolyzers.

Great progress has been made in the electrification of residential and commercial heating, as well as the electrification of industrial furnaces and the use of green hydrogen for metal refining.²^,³^,⁴^,⁵^,⁶ However, progress in the scale-up of emerging technologies for the electrification and decarbonization of hard-to-abate sectors, such as the production of fuels and chemicals, has been slow due to the inherent complexity of these systems.⁷^,⁸^,⁹^,¹⁰^,¹¹^,¹² Electrochemical systems involve many simultaneously interacting phenomena drawn from various aspects of physics and chemistry, and require a disciplined learning of the multiple variables affecting the process.¹³ Understanding the underlying effects of thermodynamics, reaction kinetics, and transport phenomena occurring inside an electrochemical system, and how they interact across different length and time scales, is one of the greatest engineering challenges inhibiting the Research, Development, and Deployment (RD&D) of industrial-scale electrified chemical manufacturing systems. Current research methods attempt to extrapolate an understanding of these complex phenomena from small, simple datasets.¹⁴^,¹⁵^,¹⁶^,¹⁷ This approach has so far prevented a holistic understanding of the system. Instead, large datasets that are commensurate to the complexity of the system should be used. This will require the development of new techniques to enable efficient handling of large datasets, the extraction of useful relationships, and the development of descriptive multi-scale models. Successful application of these techniques in research will be crucial in accelerating the scale-up of electrosynthesis technologies from bench-scale reactors operating at the watt scale to industrially relevant systems operating on the terawatt scale in a timely manner (Figure 1B).

In the following sections, we will examine the research challenges that have thus far prevented the scale-up of electrochemical reactors for CO₂ reduction, and discuss why traditional research methodology may prove to be unsuccessful in providing the understanding that is necessary to scale these systems. Having identified the challenges of using traditional research methodology, we then discuss how the inspiration for a more efficient approach can be taken from smart manufacturing (SM) methods that have been applied successfully to complex industrial processes. The framework of the SM-inspired research methodology is presented, followed by detailed examples of how it has been applied in efforts toward the scale-up of electrochemical CO₂ reduction devices. In this perspective, we highlight how techniques such as automation, connectivity, and advanced modeling methods can be seamlessly integrated with experimental processes to accelerate the scale-up of electrochemical systems.

The discussion of challenges toward the scale-up of electrochemical reactors for CO₂ reduction presented in this perspective is not exhaustive. Learning curves for water electrolyzer technologies have shown that high cost across the entire value chain have limited their rapid deployment. Electricity is the dominant cost for on-site production of green hydrogen, but the journey to lower renewable costs is already underway. Efforts are shifting to the second largest cost for green hydrogen: electrolysers. Green hydrogen production as well as electrolyzer manufacturing benefit from economies of scale. However, the lack of infrastructure and a skilled workforce to sustain gigawatt (GW) scale manufacturing have limited the current electrolyzer manufacturing capacity to under 8 GW/year.¹⁸ In comparison, solar modules manufacturing capacity in 2021 was already 240 GW/year. The same challenges in the scale-up of manufacturing capacity are expected to limit CO₂ electrolyzer manufacturing, even if all the fundamental research challenges presented in this perspective were suddenly resolved.

Challenges in existing approach to RD&D of CO₂ electrolyzers

The production of fuels and chemicals from carbon dioxide, water, and renewable electricity in an electrochemical reactor has been proposed as a viable approach to the reduction of CO₂ emissions associated with the chemical manufacturing sector.¹⁹ Most importantly, when paired with carbon capture technologies and renewable energy sources, electrochemical CO₂ reduction offers the unique possibility of closing the carbon cycle by recycling carbon from the atmosphere as feedstock that supports chemical manufacturing industries.²⁰ Industrial scale adoption of CO₂ electrolysis would enable many existing processes based on carbon feedstocks to continue operation while minimizing the need for new chemical production and distribution infrastructures. Most notable examples include production of fuels for transportation, base chemicals for production of plastics, and grid-scale liquid-fuel energy storage for intermittent renewable energy sources. As such, interest in developing this technology has been increasing steadily for the last decade. While high current densities as high as 3.37 A cm⁻² have been reported,¹³ durability remains low with current density decreasing quickly after tens of hours, and when the scale of the system is increased. To achieve efficient and low-cost production of chemicals at large scales, CO₂ electrolysis technologies will need further improvements in durability, efficiency, conversion, product selectivity, and overall system design as well as the development of efficient direct air capture technologies to provide carbon feedstocks. One of the key roadblocks to understanding how to scale-up these systems is the development of a practical kinetics-transport model of electrochemical CO₂ reduction. The development of such a model has thus far eluded the scientific community due to the convolution of different interactions within CO₂ electrolyzer systems.

Many complications preventing these improvements arise from the chemistry itself. While various transition metals have been shown to effectively reduce CO₂ to CO or formate, Cu is the only known single-element metal to enable conversion to C₂₊ products such as olefins and liquid alcohols at an appreciable rate. Because Cu offers the potential for one-step production of valuable precursors such as ethylene, ethanol, and propanol, Cu-based catalysts have been the main material of interest for electrochemical CO₂ reduction. A total of 16 different chemicals have been identified as products, with CO and hydrocarbons (CH₄ and C₂H₄) observed in the gas phase, and oxygenates such as formate, ethanol, n-propanol, acetate, and aldehydes observed in the liquid phase.²¹ CO is the key intermediate formed via two electron transfer steps and can be further reduced to CH₄, methanol, and C₂₊ products. However, the kinetics associated with each intermediate step and the species involved in the reactions are difficult to elucidate conclusively, and various mechanistic pathways have been proposed without collective agreement on a detailed mechanism within the research community.²²

The existence of competing reactions further complicates understanding the electrochemical CO₂ reduction mechanism. Hydrogen evolution reaction (HER) is inherent in the nature of aqueous electrochemistry, as proton sources are required to reduce CO₂. In aqueous electrolytes, the proton sources can be hydronium ions, molecular water, and buffers that relay protons to the surface of the electrode. Formate is another product pathway that proceeds in parallel to the CO production pathway. The production of hydrogen and formate is affected by the CO₂ and bicarbonate buffer chemistry, in which bicarbonate can act as a proton donor and buffer in the bulk electrolyte.²³ This homogeneous buffering chemistry makes mass transport characteristics nonlinear for key reaction species including CO₂, bicarbonate, and hydroxide, creating an additional layer of complexity in describing the electrochemical environment near the electrode surface. Even the formation of the simplest two electron transfer products (H₂, formate, and CO) consists of at least three elementary steps (i.e., adsorption, two-electron-proton transfer steps, and desorption) which cannot be readily described by the Butler-Volmer equation, especially when concentrations of reactive species in the vicinity of the reaction front are unknown.

While the products of electrochemical CO₂ reduction were first analyzed completely by Hori and co-workers,²⁴ this process did not gain mainstream attention until the last decade. In the time since Hori’s results were published, the majority of research has been performed using an H-cell configuration with low current density. These experiments were conducted with the intention of investigating the fundamental relationships governing electrochemical CO₂ reduction. Early reports suggested that mass transport significantly affects the selectivity and rates of CO₂ reduction.²⁵^,²⁶ To overcome mass transfer limitations, flow cell-type reactors and high-pressure CO₂ electrolyzers were investigated early on. Systems showing high current density near 1 A cm⁻² were demonstrated as early as the 1990s.²⁶ Flow cells, in particular, have consistently shown current density significantly higher than other cell types due to the improved mass transport of CO₂ to the catalyst near the three-phase boundary. These systems are better used for benchmarking catalysts in the sense that their activity can be studied under reduced mass transport limitations. However, scaling these reactor types remains difficult due to the lack of fundamental understanding of the underlying relationships governing CO₂ reduction rates and selectivity as the conversion of CO₂ increases along the flow path. One example that clearly demonstrates this issue is circled in the top right corner of Figure 2A. Three data points show the current densities obtained for three flow cells with the same catalyst when the geometric surface area of the electrode is increased from 1 to 10 and then 100 cm².¹³ The 1 cm² electrode reaches current densities of 3.37 A cm⁻². However, when the system is scaled to an electrode area of 10 and 100 cm², the current densities quickly decrease to below 1 A cm⁻². Research in electrochemical CO₂ reduction is still very much in the fundamental research stage, as demonstrated by the fact that nearly all research is still conducted with electrode surface areas of less than 10 cm² (Figure 2B) and that attempts of scaling these systems typically resulted in significant performance losses. To move beyond this stage, the development of selective and efficient electrochemical processes will require advances in both catalyst and device/process design.²²^,²⁷ At large, the research community has generally focused on the design of catalysts or devices separately, and rarely on understanding the coupling of both.

Data highlighting the difficulty in CO₂ electrolyzer scale-up and the significance of mass transport

(A) Current densities for select experimental electrochemical CO₂ reduction studies since Hori’s initial reports.

(B) Cathode geometric areas for the same studies shown in (A). Cell types listed in (A) and (B) are primarily categorized as identified in their respective publication. However, H-cell and compression cell classification is not entirely clear, so the following criteria were considered for classification. H-cell is a two or three compartment cell where high electrode area to electrolyte volume ratio is not a priority, and where the cross section area of the membrane separating cathode and anode is small relative to the cathode compartment cross section area. The compression cell is a small form factor reactor targeting high electrode area to electrolyte volume ratio, where the components of the cell are sandwiched together with compressive force to provide gas and liquid-tight connections. References for H-cell,²⁴^,²⁸^,²⁹^,³⁰^,³¹^,³²^,³³^,³⁴^,³⁵^,³⁶^,³⁷ compression cell,²¹^,³⁸^,³⁹^,⁴⁰ high pressure,²⁶^,⁴¹ polymer electrolyte membrane (PEM) type flow cell,¹³^,⁴²^,⁴³^,⁴⁴^,⁴⁵^,⁴⁶^,⁴⁷^,⁴⁸^,⁴⁹ microfluidic flow cell,⁵⁰^,⁵¹^,⁵² solid oxide electrolyzer (SOEC) flow cell,⁵³^,⁵⁴^,⁵⁵ differential electrochemical mass spectrometry (DEMS) cell,⁵⁶^,⁵⁷ and the rotating cylinder electrode (RCE) reactor.²⁷

(C) A ternary plot showing that the data collected in common reactors used for electrochemical CO₂ reduction falls in the region representative of stagnant flow conditions inside the RCE, suggesting that mass transport is poorly defined in these reactors.²³^,⁵⁸^,⁵⁹^,⁶⁰

The widespread adoption of compression-type H-cell reactors highlights this trend. The introduction of the compression cell²¹ ushered in a flood of fundamental research due to the ease of experimentation and improvement in the sensitivity for detecting C₂₊ liquid products. However, this reactor is limited in the fact that it does not provide control over mass transport. Because of this, the electrochemical conditions near the electrode surface are poorly defined. The implications of this limitation are apparent when data generated in this electrochemical reactor is compared with results from a rotating cylinder electrode (RCE) reactor, in which mass transport can be controlled. Figure 2C shows a ternary plot for product selectivity to CO, C₁, and C₂₊ products denoted as S_CO, S_C1, and S_C2+, respectively. These selectivities relate to the fractions of CO₂ molecules consumed in producing the three groups of products (data extracted from Jang et al.²⁷). The purple and the pink curves show data collected with the RCE cell using 0.2 and 0.1 M potassium bicarbonate electrolytes, respectively, at a constant potential of −1.41 V vs. the standard hydrogen electrode (SHE) while varying the electrode rotation speed. As the rotation speed decreases from 800 to 100 rpm, the mass transport coefficient of all species to and from the electrode surface decreases. This decrease in the mass transport coefficient also applies to the intermediate CO, slowing down the removal of CO generated on the surface of the electrode and increasing the residence time of CO (τ_CO). The increase in τ_CO increases the probability of further reducing CO to C₁ or C₂₊ products, and reduces the probability of the intermediate CO being released as a final product.²⁷ This trend in the selectivity shift is clearly shown for data obtained in the RCE cell. On the other hand, in electrochemical reactors with poor mass transport characteristics, τ_CO is likely very long, although this cannot be well-defined, resulting in a high conversion of CO to its further reduced products (X_CO). The selectivity curves from these reactors populate only the bottom-right corner of the ternary diagram (Figure 2C) under electric potentials similar to experiments from the RCE cell, in the range of −1.38 to −1.44 V vs. SHE. This brings up an important realization that what we measure experimentally is reactor kinetics, not reaction kinetics. Thus, the use of Tafel analysis to study reaction mechanism in CO₂ reduction experiments on copper electrodes, for example, does not have any scientific foundation. Gregoire and co-workers have also recently shown how hydrodynamics in the electrochemical cell determine the apparent Tafel slope measured during electrochemical CO₂ reduction on a copper electrode, further demonstrating that mass transport is on equal footing with catalyst active sites in determining reaction mechanisms and the ensuing product distribution.⁶¹ Thus, the importance of collecting data across a large operational parameter space under well-controlled transport characteristics in electrocatalytic reactors cannot be understated, as this is the only manner in which we will be able to extract intrinsic kinetics from reactor kinetics.

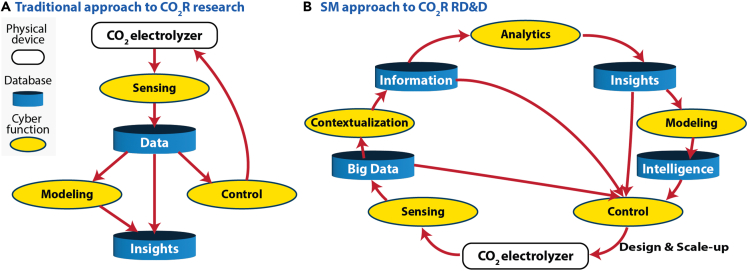
In addition to the effect that reactor selection has on the quality of data collected in experimental CO₂ electrolyzers, it becomes apparent that the traditional research approach taken to the study of CO₂ electrolyzers may be inadequate to fully parameterize the kinetics for electrochemical CO₂ reduction reactions. For comparison, a generalization of the traditional approach is presented in Figure 3A. In this approach, data is collected from an experimental reactor, using various sensors, and insights are extracted from relatively small datasets. However, these insights often do not translate readily to larger-scale systems, as is becoming evident in the CO₂ electrolyzer research community. In CO₂ electrolysis, this is primarily because the results collected in experimental systems are specific to the reactor properties rather than reaction properties. This is demonstrated by the fact that identical catalysts will often show differing performances in different experimental reactors. Frequently, density functional theory (DFT) or microkinetic modeling is used to explain the results or to try to better understand what is happening at time and length scales that are inaccessible to experiments in the real system. Multi-scale modeling can be a powerful tool for understanding what is happening in a reactor. However, accurate, high-fidelity experimental data and an excellent understanding of the experimental conditions in the reactor are required to fully parameterize these multi-scale models. In many instances, there is a disconnect between modeling and experimental groups that prevents this from happening, leading to models that simply fit the data. As shown here, difficulty in collecting high quality data and the typical method of conducting research, make it difficult to conclusively understand the fundamental relationships governing the performance of CO₂ electrolyzers. Accelerating the scale-up of these systems requires an adjustment to the current research approach.

Comparing the traditional research workflow to smart manufacturing (SM)

(A) A visual representation of how research is traditionally conducted, showing how control over the electrochemical CO₂ reduction reaction is attempted based on results from small datasets and modeling is often conducted separate from data interpretation.

(B) A visual representation of the SM approach, showing how connectivity of information from all stages of the RD&D process aid in providing the knowledge necessary to develop the control of CO₂ electrolysis necessary to scale-up.

Smart manufacturing background and context for applications in scale-up research

SM refers to a holistic approach to process optimization, where advanced sensing techniques are paired with robust data handling and modeling strategies to provide rationally optimized system operations, improved safety and security, and reduced waste.⁶²^,⁶³^,⁶⁴^,⁶⁵ Application of SM is built on the idea that optimal control can be achieved through the integration of advanced operations technologies (OT) and information technologies (IT) to develop streamlined data acquisition, handling, and interpretation processes that interconnect the individual parts of a process.⁶²^,⁶⁶^,⁶⁷^,⁶⁸^,⁶⁹ While implementation of SM can look very different between two systems,⁷⁰ the approach can be generalized by Figure 3B. Here we see that optimal control with SM begins with sensing that allows for the collection of large datasets. Sensors for a given process should be chosen to provide useful and reliable data that can be collected in an automated fashion. Sensors applied in this way enable the collection of large datasets for modeling and frequent input updates for real-time system control.⁶⁵ For example, a thermocouple senses the temperature and produces a voltage signal that is recorded as data. However, for these data to be useful, they need to be contextualized. By tying the data to the sensor type and the characteristics of the process, information can be extracted to improve control of the system. An example of this would be taking the data from the thermocouple and contextualizing it with the knowledge that the thermocouple is located in a liquid-filled vessel, and that a certain voltage signal correlates with a specific temperature. By contextualizing these data with knowledge of the process and the sensor, we gain the information: in this case, the temperature of the fluid in the vessel. Next, analytics provide insights to further optimize control of the process. Using the thermocouple example again, we could analyze the change in temperature over a period of time to gain insight about the trajectory of the fluid temperature with time. Fluid temperature could also be tied to other sensor types, such as pressure sensors, to further evaluate the performance or safety of the overall system using a combination of hundreds or thousands of sensors across a manufacturing process. With the immense dataset provided by these sensors, modeling can provide an added degree of intelligence by building on the knowledge from past data to predict the system’s future behavior. Models can also provide information about the current state of the system that cannot be sensed directly. Examples of how advanced modeling can be applied industrially include the prediction of catalyst lifetime or equipment failure,⁷¹ adjusting for external factors such as changes in real-time feedstock, product and utility pricing,⁷² or setting optimized system control set-points based on predicted performance.⁷³^,⁷⁴^,⁷⁵ Benefits of implementing SM in the industry have been demonstrated for a wide range of applications,⁷⁶ and industrial adoption has been successful for improving efficiency and safety in large scale industrial applications.⁷⁷ It stands to reason that similar benefits might be gained by applying the same principles and methodologies to RD&D of emerging electrosynthesis technologies.

Additionally, using SM techniques at the research stage can help enable SM implementation when the technology is scaled-up.⁷⁸ Many chemical manufacturing processes utilize aging infrastructure, and were not designed with SM in mind. Even though the technology and methods have been available for decades, the industry has been surprisingly slow to adopt SM regardless of the proven benefits. Hesitancy to adopt SM remains, primarily, due to the technical debt that must be repaid before legacy systems can be converted to an SM infrastructure.⁷⁹^,⁸⁰ In the context of this discussion, technical debt can be separated into two main components, intellectual and physical, that describe the costs associated with upgrading existing systems to SM systems. First, the intellectual component of technical debt comes from a lack of trained individuals who are educated on SM methods and know how to implement and maintain them in the industry. Time, energy, and financial backing are required to train personnel in SM practices, and educational institutions along with industry partners must develop programs to supply this workforce.⁸¹ As such, technical debt is not only associated with the cost of hiring a technically skilled labor force, but also a shift in the education system to supply skilled individuals.⁷⁷ Second, the physical component of technical debt includes the hardware and software upgrades necessary to implement SM techniques. This may include costs associated with adding sensors and the infrastructure to collect data from them or purchasing software to process data and the equipment to run the software. In many cases, the cost associated with implementing SM may simply be too high to justify retrofitting an existing process, especially for smaller businesses that lack the necessary financial backing. However, the physical component of technical debt can be eliminated for new processes if they are designed from the start with SM in mind. This provides an exciting opportunity for the development of electrochemical manufacturing technologies that will utilize SM industrially. Not only can the implementation of SM techniques in research of advanced reactor technologies accelerate the experimental process by streamlining data acquisition and interpretation, but implementation at early stages of development and scale-up can enable systems to be designed from the start to utilize SM once commercialized.

Framework for a smart manufacturing inspired approach to RD&D

As an example of how the SM approach can be applied in research, the framework developed for electrochemical CO₂ reduction research is provided in Figure 4.⁸² The individual steps defined in Figure 3B are shown at the top of the framework in Figure 4 for direct comparison, while the parts of the process involved in each step are defined below. This framework can be separated into four distinct phases that are highlighted by the background color.

The smart manufacturing (SM) inspired framework for research

A framework for the application of the SM approach to accelerate scale-up and development of CO₂ electrolyzers. Adapted,⁸² Copyright 2022, with permission from Elsevier.

Blue indicates Phase I where the experimental reactor is adapted to automate data collection and improve connectivity to enhance experimental throughput, data accessibility, and data collection. This requires the selection of a reactor that can provide high-fidelity data suitable for modeling. That is, a reactor with well-defined transport characteristics. Phase II is highlighted in orange, where machine learning (ML) and artificial intelligence (AI) are utilized along with dimensional analysis to accelerate data processing and enable the extraction of underlying relationships between inputs and outputs. These relationships are used to design real-time control schemes and build predictive models for the reactor. Real-time control of the reactor is used to validate the extracted relationships, as control will not be possible without an adequate understanding of the relationships governing the reactor performance. Green highlights Phase III, where multi-scale modeling techniques utilize first principle relationships and the relationships extracted in Phase II to build predictive models of the reactor. This step develops modeling methods to capture the local phenomena occurring at the gas/liquid, liquid/solid, and gas/liquid/solid interfaces that will be used in parameterizing improved reactor designs.⁸³ Finally, red highlights the last step, where insights gained from the aforementioned modeling methods are utilized to guide the rational design of prototype reactors. These designs can then be tested in silico using the methods developed in Phase III before actual construction, reducing cost and time requirements. This is an iterative process that can then be applied to the prototype reactor at each scale and used to accelerate further scale-up to more industrially relevant systems over multiple iterations. Multi-scale models are also key for the workforce training of electrochemical engineers. The following sections will discuss in detail how this framework has accelerated progress toward the goal of enabling the scale-up of electrochemical CO₂ reduction technologies.

Lab-scale reactor selection for CO₂ reduction research

The first step in applying the SM framework to RD&D of CO₂ electrolyzers is the identification of process-relevant variables. Significant variables that are common to most fuel and chemical manufacturing processes include pressures, temperatures, flow rates, and composition. However, electrochemical systems require additional variables to be fully characterized, including electric potential, current, and impedance. Other factors that must be considered in the design of larger-scale electrochemical reactors include the effects of chemical and electrical interfaces, charge, heat and species transport, the presence of multiphase interfaces, and the composition of the electrolyte.⁸⁴ While the complexity of these systems makes them ideally suited for utilization of an SM inspired approach, application of the framework requires a lab-scale system designed to allow individual manipulation of each relevant process variable and efficient collection of large datasets.

Several experimental electrochemical reactors exist for investigating electrocatalysis, but many of these systems have limitations that make them less than ideal for investigating CO₂ electrolysis. The compression cell was introduced to improve product detection of liquid products by increasing the electrode-to-electrolyte ratio compared to traditional H-cell reactors. However, the compression cell lacks control over hydrodynamics and mass transport conditions. Flow cells are utilized to overcome mass transport limitations, but are too complex to extract a fundamental understanding of the underlying phenomena. Rotating disk electrode (RDE) reactors have been widely adopted for the investigation of electrocatalysis because of the well-understood mass transport effects provided by the Levich equation. However, RDE electrodes are restricted to diameters of less than 5 mm and laminar flow conditions. In this case, the small electrode area prevents liquid product quantification.

A promising alternative reactor type that provides control over mass transport while also maintaining a high electrode area to electrolyte volume ratio is the gastight rotating cylinder electrode (RCE) reactor. While the current system is limited to a small range of temperatures and pressure, it is uniquely suited to decouple transport effects from intrinsic electrode kinetics. The main advantages provided by the RCE can be attributed to the high degree of symmetry. Symmetry ensures that all points on the electrode surface are exposed to the same hydrodynamics, resulting in a uniform and controllable mass and heat transport across the entire surface. This is especially true for the hydrodynamics in the electrocatalytically active region of the reactor, within a few micrometers of the electrode surface. Furthermore, the mass and heat transport can be controlled by simply adjusting the cylinder rotation speed. Changing the rotation speed increases the velocity gradient and reduces the boundary layer thickness, enhancing mass and heat transport to and from the electrode surface.⁸³ By controlling the rotation speed and evaluating the change in rates and selectivity, the timescales of the intrinsic kinetics and transport processes can be decoupled from each other. This allows the determination of the intrinsic reaction kinetics rather than the reactor kinetics that have been measured in other reactor configurations. Additionally, the symmetry of the RCE means that the hydrodynamics of the RCE is independent of the cylinder length, which enables the use of a large surface area electrode while ensuring uniform mass transport conditions and current densities. This enables the system to attain high total reaction rates, resulting in more easily detectable liquid products. The RCE is ideally suited to experimental studies that require mass and heat transport effects to be decoupled from kinetics, thus providing the information necessary to optimize the conditions in larger-scale designs. However, it should be noted that the RCE is not intended to represent the design of a larger-scale system, and other specialized reactor designs may be needed to investigate relevant phenomena other than mass and heat transport as these systems are scaled-up.

Application of automation and connectivity for enhanced data collection and processing

After identifying an appropriate reactor, the next step is to integrate automation and data connectivity in the reactor system. At the lab scale, data collection can be tedious and time-consuming. As such, automation efforts should be focused on two results: elimination of time-consuming, human-performed tasks and improvement of data collection reliability and accessibility. Process-relevant variables, identified in the initial analysis of the system, should be used here to identify what data can be collected through automated methods. This will support the efficient collection and management of large datasets to cover a wide parameter space. Recently, efforts have been growing to automate workflows in the lab using high-throughput screening and experimentation, as well as to develop self-driven laboratories that use ML to guide automated test systems.⁸⁵ Although primarily developed for material discovery,⁸⁶ drug and vaccine development,⁸⁷ and optimization of synthesis techniques,⁸⁸ a general push in the field to increase throughput through automated techniques will be beneficial for a wide range of applications. Indeed, it can be argued that most efforts in the automation of data collection, digestion, contextualization, and modeling can be mapped out eventually against the SM approach to RD&D in Figure 3B.

There are three modes of data collection: fully automated, semi-automated, and manually recorded. Examples of easily automated data types for electrochemical CO₂ reduction reactors⁸² are displayed in green in Figure 5. These include potential, current, electrode rotation speed, temperature, and CO₂ gas flow rates. Other data types, such as product concentrations, may require a degree of manual interaction for data collection or interpretation. Establishing automation and data connectivity with experimental systems requires an initial time investment, but will quickly pay for itself when collecting large datasets.

Automation of the experimental CO₂ electrolyzer

An overview of data collection, interpretation, and utilization within the experimental electrochemical RCE system showing how automation was incorporated for different data types.

An example where automation significantly improved the workflow in CO₂ electrolysis research, is the automation of data collected using a gas chromatograph (GC). Before automation efforts, GC results were manually integrated using GC-specific software. In a typical experiment, four GC injections were measured approximately 20 min apart. While the physical task of integrating and logging the data from an injection only took 5–10 min, the intermittency of this task and the short length of time between each injection made it difficult to conduct outside work during experiments. To automate the GC data collection, a Python-based script was used to automatically baseline the GC spectra, identify peaks, and extract product concentrations (orange path in Figure 5). This Python script was connected with a LabVIEW user interface that would upload data in real-time to the Clean Energy Smart Manufacturing Innovation Institute (CESMII) Smart Manufacturing Innovation Platform (SMIP) for centralized data storage, as explained by Çitmaci et al.⁸² With the help of OT/IT specialists, these data collected through the LabVIEW interface were also connected with equipment profiles in the SMIP that connected the data to information about the individual sensor they were collected from, thus providing context for the data generated. From this platform, data can be easily accessed in a centralized location and in a standardized format along with relevant sensor information, which is very important when building models of the reactor performance. This setup has been demonstrated in the real-time control of ethylene concentration in the RCE reactor effluent using proportional integral (PI) control⁷² and multi-input-multi-output (MIMO) control of ethylene and CO concentrations.⁸⁹

Data types that are typically collected manually include tasks such as recording sample preparation methods or material properties. These types of data are often recorded once at the beginning of the experiment. However, models may need to access these data for contextualization, so they should be tied to real-time data collected during experiments. This data type can also be integrated with the online data collection with a centralized user interface like LabVIEW. Data such as electrolyte pH, pressure, impedance, electrolyte concentration, and the unique identifier for the reference electrode can be entered once at the beginning of the experiment and automatically connected to the real-time data when transferred to the SMIP. In the CO₂ electrolyzer system, the only data type not automated is nuclear magnetic resonance (NMR) measurements of the liquid product composition. Since these data are processed ex situ, the data must later be entered manually (black path in Figure 5). However, data collection for liquid products could be automated using high-performance liquid chromatography in the future.

The principles of automation and connectivity are broadly applicable for accelerating research by enabling more efficient data collection and accessibility. Many demonstrations of this principle have proven useful, especially in the discovery of catalysts and development of new materials.⁹⁰^,⁹¹^,⁹² Automation of data collection and storage has shown promise in basic research and should be implemented when possible to reduce the need for human interaction and the possibility of human error, to streamline the process of data collecting, and to improve management of large experimental datasets.

Application of machine learning to lab-scale reactor modeling and control

ML allows modeling, control, and optimization in CO₂ electrolyzer development. The collection and structuring of data must be designed well and should be pre-processed before the models are built. For both a dynamic and steady-state model, experimental conditions for generating training data should be comprehensive. Training data should include data from the highest and lowest operational limits, and safety can be increased by adding data points from slightly higher and lower operational input regions. For example, the electric current values of an electrolyzer might be higher than the training data limits, depending on surface potential. Furthermore, the data collection points should be well-distributed. If the training set is considerably more populated around a specific operational region and sparsely sampled around other operational regions, the model is not expected to generalize well to all conditions. Thus, a more balanced dataset is the objective of designing experiments. On the other hand, preprocessing encompasses, but is not limited to, techniques such as outlier detection and correlation extraction. A correlation matrix is an effective way of exploring linear relations between experimental parameters. By checking covariance and standard deviation for two parameters, it is possible to gain intuition about the process. However, it is important to keep in mind that a correlation matrix might not be efficient in very nonlinear processes. Jensen and co-workers⁹³ automated an experimental flow reactor system for nucleophilic aromatic substitution of morpholine onto 2,4-dichloropyrimidine reactions to estimate kinetic parameters. A correlation matrix approach was used on the effects of pre-exponential factors and activation energies of 4 kinetic constants to comprehend the uncertainties in kinetic parameter predictions. An example of a correlation matrix for CO₂ electrolysis in the RCE reactor is shown in Figure 6A. This correlation matrix is based on steady-state data for two process inputs (surface potential and catalyst rotation speed) and nine products. The intuition about process variable correlations provided by relative gain array (RGA) can be used at early stages to inform the building of models.

Examples of successful applications of ML techniques to CO₂ electrolyzer scale-up

(A) Correlation matrix showing the degree of linear correlation between the production rates of nine CO₂ reduction products and the surface potential, rotation speed, and electric current.

(B and C) Expected concentration for ethanol and formate at different operational points. Continuous lines show predictions at different rotation speeds, and solid markers show averaged experimental data.

(D and E) Relative gain arrays that demonstrate the coupled values. (D) Shows that coupling production rates of ethylene with potential and carbon monoxide with rotation speed works well for controlling the system with two PI controllers since RGA values are close to 1 across all conditions. However, (E) has varying RGA values at different operational regions, indicating that two PI controllers can control the process only in a small region of the parameter space between −1.18 and −1.23 V vs. SHE and 100 to 500 rpm where RGA values are close to 1. For the remaining operational ranges, an MPC is needed.

An ML method that might be used for building steady-state operational models is feedforward neural networks (FNN), due to their ability to capture complex nonlinear relationships. Since FNNs are high-fidelity models, they can easily overfit data, especially for small datasets. In the electrochemical CO₂ reduction, FNN was used to model the steady-state production of thirteen product species and oxygenate selectivity.⁹⁴ Given the large number of product species and reactor variability, an FNN was chosen for this model because the steady-state performance of the reactor is assumed to be independent of time. The inputs to the FNN are the applied potential and rotation speed since these are independent variables that quantify the kinetic and mass-transfer rates, respectively. To improve model prediction, the FNN loss function was designed to account for the statistical variability of the data. This FNN is trained to maximize the probability that the model predicts the data. Specifically, the loss function is the mean-squared error, but each term is weighted by the standard deviation of the data point generated by repeating experiments at specific inputs three times. The FNN model is described in more detail by Luo et al.⁹⁴ Figure 6B shows the concentration predictions of ethanol, one of the most valuable products in this electrochemical reactor, and Figure 6C shows the formic acid model without an overfit in the operational range described.⁸⁹ Additionally, this model can be used for management-level control and optimization. The energy consumption of the reactor is related to the applied potential, so set-points can be selected by solving a nonlinear optimization problem that maximizes the energy efficiency or profitability of the reactor. This approach was demonstrated by selecting cost-optimal set-points to conduct multivariable control experiments.⁷²^,⁸⁹

Another step up in complexity is the use of recurrent neural network (RNN) models. RNNs are a class of deep learning neural networks that are specifically suited for handling a series of data points, such as time-series data. To capture the time dependencies, the RNNs feed the neural network output of the previous states as an additional input to the next unit. This recursive nature of the RNN is usually explained as its memory of the previous data in the series. The more advanced RNN structure is the long short-term memory (LSTM) unit.⁹⁵ For process data regression, LSTMs check the time-dependent relations between two respective inputs and learn how the process should dynamically develop for the next time steps. Specifically, LSTMs check a specific time window from the past data and learn the inherent relations from this time window.

RCE cell dynamics vary depending on specific operating conditions. For example, the dead time in the RCE cell depends on the specific rotation speed or the amount of change in rotation speed.⁸⁹ RNN models were shown to adapt to variable dynamics and are able to capture the dynamic behavior of the RCE well. Alternatively, the transient behavior of product concentrations in the effluent of the RCE cell can be approximated using a continuous stirred tank reactor (CSTR) approximation.⁷² However, this type of approximation is not an accurate description of the real reactor and adds error to predictions. Thus, a model built only with electrochemical cell data can represent inherent reactor dynamics better than hybrid model approximations. However, to build a deep learning model such as RNN, voluminous datasets are required. Although the applied potential, current, and rotation speed values are recorded at per-second basis, the output gas concentrations are measured via GC, which only provides results in long discrete time intervals (e.g., 20 min). To overcome the scarcity of the GC data, the dataset was augmented using polynomial fits to approximate a probable dynamic experimental trajectory between GC data points.⁸⁹ After enriching the dataset with the polynomial fits, more than a hundred thousand artificially generated data points were generated from the initial hundreds of GC data points. This increase in the amount of data enables training of a dynamic deep learning model and can be useful in the dynamic modeling of any electrochemical process with gas products. RNNs have been shown to model the dynamic behavior of chemical reactors and to make robust models for use with model predictive control (MPC) or multiple PI controllers, even when faced with data variability.⁹⁵^,⁹⁶ For example, two PI controllers were used for multi-input-multi-output (MIMO) control using feedback from the LSTM models of the RCE⁸⁹ and Xavier and Trimboli used MPC in an electrochemical system to charge a lithium-ion battery in the shortest time under voltage constraints using a circuit model.⁹⁷

Benefits of machine learning for scale-up research

A black-box ML model itself can be operationally very useful, yet would not be very informative about the underlying mechanisms. Efforts to discover the first-principle equations of electrochemical CO₂ reduction can be accelerated and supported by black-box steady-state models. A candidate kinetics model can be derived from a proposed reaction mechanism, and this mechanism can be validated by experimental data at various operational regions. However, in complex processes such as CO₂ electrolysis, there are many possible candidate reaction mechanisms, and it would be very costly and time-consuming to experimentally validate each model. Instead, the results of a proposed kinetic model can be compared to the predictions of steady-state ML models at numerous operational conditions. Thus, a strong generalizer model built with well-distributed data from experiments can produce infinitely many accurate predictions within the operational range and replace a myriad amount of physical experiments.

Additionally, due to the non-linear nature and high degree of complexity in developing electrochemical synthesis processes, new control schemes may be necessary to control these devices effectively when scaled-up. Thus, the development of robust, system-specific models and control techniques alongside the development of the reactor provides an integrated approach to developing both the reactor and the methods of controlling it. The control strategy of a system can be decided based on an RGA. In RGA, one of the process inputs is coupled with one of the process outputs for each input and output. The RGA results for a nanoporous copper cylinder electrode in the RCE are presented in Figure 6. If the RGA results are close to one in a broad range of operation regions, then multiple PI controllers can be implemented for feedback control. On the other hand, if the RGA array consists of a broad range of values including negative numbers and values greater than 1, a more advanced controller scheme such as MPC should be implemented.

The objective of showing successful control in RCE is to develop control strategies and intuition for a scaled-up system. Model-based control may be particularly useful for nonlinear system scale-up efforts, as in the implementation of MPC. If there is a dynamic model available, an MPC scheme can be constructed, and ML methods have been proven to build accurate dynamic models in the absence of first principles. In the context of scale-up, an MPC control system can leverage information from multi-scale models of the reactor and external factors in its control actions. For example, the controller can stabilize the system while simultaneously minimizing the energy consumption, maximizing selectivity of desired products, avoiding unsafe operating regions, etc. Likewise, this multi-scale modeling and optimization approach could allow better integration of complex reactor interactions and be used to guide the optimized design of industrial reactors, as well as implement control for nonlinear electrochemical reactors once constructed.

Understanding underlying relationships through dimensional analysis

In addition to the black-box-type ML models discussed in the previous section, dimensional analysis is a powerful, reduced-order modeling method for understanding underlying relationships in electrochemical reactors. When used properly, dimensional analysis enables the description of intrinsic relationships between variables in a system using dimensionless numbers: i.e., groups of physical variables that reduce to dimensionless descriptors for specific phenomena. By establishing scale-invariant relationships between physical variables, the same characteristics can be defined for systems of different scales by ensuring that the dimensionless value that describes that characteristic is the same in both systems.⁹⁸^,⁹⁹ Additionally, these dimensionless numbers can provide an effective way of investigating the influences of physical variables on a process by reducing the order of parameters to be studied. For example, changing temperature has multiple effects on the electrochemical CO₂ reduction process including the diffusion coefficients of species, the viscosity and density of electrolytes, the solubility of CO₂ in the bulk electrolyte, the kinetics of homogeneous buffer reactions, and the kinetics of heterogeneous electrochemical reduction reactions on the electrode surface. Among the aforementioned effects, the temperature effect on diffusion with respect to changes in material properties can be segregated using the Schmidt number (Sc). As defined in Table 1, the Schmidt number reduces three parameters (diffusivity, viscosity, and density) down to a single grouped parameter, simplifying the tracking of temperature effects. Since it is a material property, Sc can also normalize the effects of diffusing species and electrolyte media on the overall mass transport characteristics represented using another dimensionless number, the Sherwood number (Sh).

Table 1.

Dimensionless numbers used in research with the RCE reactor

Name	Description	Symbol and Equation
Reynolds number	$\frac{I n e r t i a l f o r c e s}{V i s c o u s f o r c e s}$	$R e = \frac{ρ U_{c y l} d_{c y l}}{μ}$
Schmidt number	$\frac{V i s c o u s t r a n s p o r t}{D i f f u s i v e t r a n s p o r t}$	$S c = \frac{μ}{ρ D_{i}}$
Sherwood number	$\frac{C o n v e c t i v e t r a n s p o r t}{D i f f u s i v e t r a n s p o r t}$	$S h = \frac{k_{m}}{D_{i} / d_{c y l}} = 0.204 {R e}^{0.59} {S c}^{0.33}$
Damkhöhler number	$\frac{R e a c t i o n r a t e}{M a s s t r a n s f e r r a t e}$	$D a = \frac{r_{i}}{k_{m} C_{i, b}}$

Open in a new tab

Here ρ is the electrolyte density, U_cyl is the surface velocity of the electrode, d_cyl is the cylindrical electrode diameter, μ is the electrolyte viscosity, D_i is the diffusivity of species i, r_i is the rate of reaction for species i, and C_i,b is the bulk concentration of species i in solution. k_m is the mass transfer coefficient derived from the limiting current (j_lim) by j_lim= zFk_mC_i,b where z is the number of electrons involved in the reaction, and F is Faraday’s constant.

In the RCE reactor, when Sc and Sh are characterized as a function of rotation speed (non-dimensionalized as the Reynolds number, Re) using simple reactions with facile kinetics producing a single product, a universal relationship can be extracted from mass transport limited reaction rates (Figure 7) as demonstrated by Jang et al.²⁷ and Richard et al.⁸³ This dimensionless correlation is useful in three ways. First, once established using facile and simple reactions, convective mass transfer rates of species involved in more complicated reactions can be quantified since all the species are affected by the same hydrodynamics. This is particularly useful in understanding mass transport in CO₂ electrolyzers where mass transport limited reaction rates cannot be readily extracted from experimental data, and homogeneous reactions occur involving multiple buffering species. Second, this relationship can be used to evaluate whether a specific reaction or reaction step is mass transfer limited. If a reaction is mass transfer limited, the rates will align with the universal correlation, while if it is kinetically limited, the rates may be lower and will not scale with Re. Lastly, the correlation between Sh and Re is empirically derived and will only hold for the specific reactor geometry and flow pattern in which it was developed. However, when paired with multi-scale modeling techniques such as computational fluid dynamics (CFD) this correlation can be tied to specific physical phenomena such as the hydrodynamic or diffusion boundary layer thicknesses.⁸³ Knowing this relationship between Sh and the phenomena governing it can then enable the same correlations developed in the RCE to be applied in systems with different geometry, enabling rational decisions to be made when selecting new reactor configurations.

The dimensionless universal correlation for mass transport limited reactions in the rotating cylinder electrode (RCE) reactor

The dimensionless correlation between mass transfer and rotation speed for the RCE reactor showing CFD simulation results overlaying experimental data. This correlation applies to any reaction occurring under mass transport limited conditions inside the RCE reactor. Copied with permission, Elsevier copyright 2022.

The Damköhler number (Da) is another dimensionless parameter that has been useful in evaluating the mechanisms driving reaction and selectivity for CO₂ reduction products. Da represents the ratio of timescales for reaction and convective mass transport, and is used to evaluate if a reaction is kinetically or transport limited at given conditions. In the RCE reactor, Da has revealed that CO₂ reduction is not limited by the convective transfer of CO₂ from the bulk to the electrode surface (Da_CO2< 1) at −1.41 V vs. SHE for electrode rotation speeds within 100 and 800 rpm. On the other hand, the residence time of CO near the electrode surface, which decreases with Sh², has been identified as a critical parameter in determining the selectivity of reactions toward products involving transfer of more than two electrons (>2e⁻) or toward the intermediate CO. As the Sherwood number decreases, longer residence time of CO leads to higher Da _{> 2e}- and conversion of CO.²⁷^,⁶¹ This relationship between Da _{> 2e}- and Sh has significant implications in the design and scale-up of CO₂ electrolyzers, since the rate of production for > 2e⁻ products can now be estimated by the production rate of the intermediate CO and Sh, representing the local mass transport around the catalyst. Further details on thedevelopment of a model capturing this relationship and demonstrating the application of this estimation will be covered in a follow-up report.

In addition to the traditional approach discussed so far, dimensional analysis has the potential to be integrated with the ML approach. There is an analogy between dimensional analysis and ML in the sense that they remove the variance in dimensions to better capture the underlying relationships. Recently, there have been attempts to incorporate or replace the traditional Buckingham Pi theorem using the physics-informed neural network (PINN) to identify independent dimensionless parameters that are significant to the system. PINN could incorporate principles of the Buckingham Pi theorem directly in the training algorithm,¹⁰⁰ or replace the theorem by iteratively solving for both the physical dimensional constraints and exponents of the governing equations.¹⁰¹ This makes the PINN a powerful tool since the traditional Buckingham Pi theorem does not provide information on the dominance and power-law exponents of each independent dimensionless number.¹⁰¹ Another approach to implementing dimensional analysis in PINN is through solving physical laws in the form of dimensionless partial differential equations. There are several advantages to non-dimensionalizing equations and unknown variables. Such an approach reduces the computational pressure on neural networks and is less sensitive to simulation instabilities arising from changes in the scales of physical parameters (e.g., diffusivity, mass transfer coefficient, rate constants, etc.).¹⁰⁰^,¹⁰²

This perspective has focused primarily on issues related to mass transport. The principles of similarity for mass and heat transfer establish that the level of turbulence experienced by a particle as it traces out similar paths in reactors at multiple scales should be kept constant so that mass and heat transfer rates are similar at all scales. This is key for reactor scale-up. The reader is directed to the chapter on “Principles of similarity and their application for scale up” in “Design of multiphase reactors”⁸⁴ for a review of dimensionless analysis in process scale-up from model to prototype scales. When scaling up electrolyzers from a model scale, it will not be sufficient to maintain the similarity of mass and heat. Rather, chemical similarity (rate of product formation to the rate of bulk flow, and rate of product formation to the rate of convective mass/heat transfer) must be maintained. In practice, it is very difficult to maintain chemical similarity between a model and a prototype. These challenges are become more significant in electrochemical systems where charge transport between the working and counter electrode also becomes important as this affects concentration polarization and ionic resistance, which in turn affect energy efficiency and heat generation in the cell. The different mass, heat, and charge transport phenomena must be controlled and optimized at each scale during reactor scale-up, and here is where extraction of relationships in a bench-scale system using dimensionless numbers can be powerful, as dimensionless correlations can be useful in determining the similarity principles that are most relevant to the performance of the system. Combined with multi-scale models, dimensional analysis can be further integrated into the optimal design, control, and operation of pilot scale systems using SM methods. This is very similar to what has been shown in industry. Undoubtedly, heat and charge transport management will likely become more important at larger scales and will need to be optimized to control selectivity and rates for desired products while minimizing overpotential.

Multi-scale modeling aided research and design

The previous modeling techniques using AI and dimensional analysis are powerful tools for understanding how the process-relevant variables in a system affect its performance, but can be difficult to connect with the underlying phenomena in complex systems. To overcome this difficulty, well-parameterized, physics-based, multi-scale models can be developed to tie these reduced order relationships to physical phenomena and allow the design of optimized larger scale systems. Multi-scale modeling incorporates physics-based modeling techniques to capture local phenomena in detail that cannot be evaluated experimentally. These models can be used to identify the local conditions that correspond to specific experimental results, and then to ensure that the desired local conditions are present in a larger-scale design. By building these multi-scale models based on first principle relationships and ensuring that experimental behavior is replicated, these models can help to generate rational designs that can be tested in silico with multi-scale models before construction.

An example of how multi-scale modeling can be used to better understand the local conditions governing reactor performance is in the evaluation of boundary layer conditions at the RCE surface. As mentioned previously, this small region governs the rates at which species move to and from the electrode surface. The universal relationships between Sh and Re discussed in the previous section help us understand the effect of rotation speed on the rate of mass transfer, but only apply to systems where similar definitions of Sh and Re can be used. While we know that the boundary layer is responsible for this behavior, we cannot easily observe this phenomenon during experiments. To probe the boundary layer region, a CFD simulation of the RCE reactor was constructed that is capable of replicating the experimental behavior of the cell under well-defined mass transfer limited reaction conditions.⁸³ This model was developed to capture both the transient and steady-state behavior to ensure that both the average and variations in local conditions could be evaluated. With this simulation, not only can a connection be made between mass transfer rates and the rotation speed, but the physical conditions in the boundary layer region can be defined for the mass transport rates observed. These include the velocity and concentration gradients at the wall, the velocity and concentration boundary layer thicknesses, and the influence of small vortexes near the boundary layer region (Figure 8A). With this information, local conditions in other systems can be identified, and the mass transport rates can be predicted regardless of geometry.

Multi-scale modeling can provide insights across the relevant length and timescales to guide intelligent design of advanced electrochemical synthesis reactors

(A) CFD provides information about the system effects, like boundary layer conditions. Reprinted, Copyright 2023, with permission from Elsevier.⁸³

(B) MD can provide information about the local environment at the electrode interface. Reprinted with permission,¹⁰³ Copyright 2020, American Chemical Society.

(C) DFT provides information about the energetics of different reaction pathways. Springer Nature, 2022, reproduced with permission from SNCSC.¹⁰⁴

(D) Models can provide information for each other to span various scales and guide intelligent system design.

Further efforts are being directed at adding complex reaction schemes involving both heterogeneous and homogeneous reactions to these simulations. These simulations will help to understand how the local concentration and residence time of species in the boundary layer affect selectivity in the multi-step reaction mechanisms of CO₂ electrolysis. Together, this information will enable the extraction of intrinsic reaction kinetics from experimental data, by revealing the local conditions at the electrode surface and removing the bulk characteristics that are influenced by the reactor geometry. Finally, the kinetics and simulation techniques used to describe the existing system can be applied to developing new reactor designs that optimize rates and selectivity for desired products.

In the case of CO₂ electrolysis, mass transport has a significant influence over the product distribution and reaction rates. Once this influence is accounted for, other effects may require further investigation to achieve industry-relevant performance. Molecular dynamics (MD) simulations can provide insight into phenomena occurring at the electrode surface near the electrical double layer, where hydrodynamics are essentially stagnant (Figure 8B).¹⁰³ DFT can provide insight into the energetics of specific reaction pathways on the electrode surface (Figure 8C), guiding the development of more selective catalysts.¹⁰⁴ Typically, modeling methods such as CFD, MD, and DFT are individually investigated, but each can provide complimentary information for each other (Figure 8D).¹⁰⁵ CFD can provide continuum scale information about the concentrations of species near the electrode surface. MD can incorporate this information to evaluate the local environment within nanometers of the electrode surface to capture stochastic processes relevant to catalysis. DFT provides the energetics of different reaction pathways, but utilizing information from the MD and CFD models can help to determine if a species is available to react on the electrode. Additionally, AI and ML techniques can be incorporated into these modeling methods to reduce the computational cost and increase the accuracy of these models.¹⁰⁶ At larger scales, these techniques can be further integrated into the optimal control and operation of pilot scale systems using SM methods. For example, heat management will likely become more important at larger scales and will need to be optimized to control selectivity and rates for desired products. Industrial applications for controlling temperature distributions in a steam methane reformer have shown how the integration of advanced sensing, data management, ML, and multiscale modeling can be utilized to optimize such operations.⁷⁵ Likewise, the techniques discussed here could be applied to similar problems in the operation of larger scale electrochemical systems. Only through a coordinated incorporation of these models across multiple scales with high-fidelity experimental data can intelligent designs be developed to bring complex electrochemical conversions to industrial scales.

Conclusions

Emerging CO₂ electolyzer technologies have proven to be particularly difficult to scale-up due to the convoluted interactions of mass, charge, and heat transport with complex reaction pathways. Tackling the difficult task of scaling up electrochemical synthesis methods requires a more holistic scientific approach that incorporates high-fidelity experimental results with big data and advanced modeling techniques spanning from the atomic to the reactor scale. In this perspective, we evaluate an approach to accelerate research targeted at the scale-up of complex electrochemical reactors that is inspired by the same techniques used to apply SM in the industry to tackle complex process optimizations. This approach not only provides an improved research methodology but also provides a pathway for the parallel development of strategies to apply SM in industrial electrosynthesis processes.

In summary, this approach is divided into four phases. In Phase I, automation of data collection and handling is applied to the experimental reactor system to accelerate the data collection process and enable easy access to the data when building models. Next, AI and ML techniques along with dimensional analysis are used in Phase II to interpret the large datasets and extract useful relationships governing the reactor performance. For example, RGA provides insights into the dependency of product concentrations on the potential or rotation speed of the electrode, and dimensional analysis reveals a universal correlation between the rotation speed and mass transport rates. These relationships are used in Phase III to inform the development of physics-based multi-scale models that cover a spectrum of time and length scales relevant to the reaction process. Additionally, these models allow phenomena that cannot be directly observed experimentally to be quantified and tied to the relationships developed in Phase II. The same modeling techniques can be applied in Phase IV to evaluate the performance of scaled-up reactor designs in silico before materials are committed to construction. Finally, these four phases can be applied iteratively at each new scale to address additional challenges as they arise.

When applied independently, each of these steps can provide limited insight into how to improve an electrochemical synthesis process. However, when incorporated as part of this holistic approach, the use of these tools can efficiently accelerate the development of industrial-scale electrochemical reactors. To show the utility of this approach, we have provided an example of how it has been applied so far to RD&D of CO₂ electrolyzers. While CO₂ electrolysis has been the focus of this demonstration, the same methodology can be applied to RD&D of any electrosynthesis technology, as the same underlying phenomena will be influential in the scale-up of any electrosynthesis process. Each step of the approach presented in this perspective provides key advantages in accelerating the research necessary to scale up electrochemical systems, and we hope such an approach will be applied by others to accelerate new discoveries in the field of electrochemistry.

Acknowledgments

We would like to gratefully acknowledge financial support from the U.S. Department of Energy, through the Office of Energy Efficiency and Renewable Energy (EERE), under the Advanced Manufacturing Office Award Number DEEE0007613.

Author contributions

P.D.C. and C.G.M.-G. conceived of and initiated the project. The article was written through the contributions of all authors.

Declaration of interests

The authors declare no competing interests.

Inclusion and diversity

We support inclusive, diverse, and equitable conduct of research. One or more of the authors of this paper self-identifies as an underrepresented ethnic minority in their field of research or within their geographical location. One or more of the authors of this paper self-identifies as a gender minority in their field of research.

References

1.Rego de Vasconcelos B., Lavoie J.-M. Recent advances in power-to-X technology for the production of fuels and chemicals. Front. Chem. 2019;7:392. doi: 10.3389/fchem.2019.00392. [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Perkin R.M. John Wiley & Sons, Ltd; 2000. Electrically Generated Heat. Ullmann's Encyclopedia of Industrial Chemistry. [DOI] [Google Scholar]
3.Wismann S.T., Engbæk J.S., Vendelbo S.B., Bendixen F.B., Eriksen W.L., Aasberg-Petersen K., Frandsen C., Chorkendorff I., Mortensen P.M. Electrified methane reforming: a compact approach to greener industrial hydrogen production. Science. 2019;364:756–759. doi: 10.1126/science.aaw8775. [DOI] [PubMed] [Google Scholar]
4.Madeddu S., Ueckerdt F., Pehl M., Peterseim J., Lord M., Kumar K.A., Krüger C., Luderer G. The CO2 reduction potential for the European industry via direct electrification of heat supply (power-to-heat) Environ. Res. Lett. 2020;15:124004. doi: 10.1088/1748-9326/abbd02. [DOI] [Google Scholar]
5.Brockway A.M., Delforge P. Emissions reduction potential from electric heat pumps in California homes. Electr. J. 2018;31:44–53. doi: 10.1016/j.tej.2018.10.012. [DOI] [Google Scholar]
6.Gielen D., Saygin D., Taibi E., Birat J.-P. Renewables-based decarbonization and relocation of iron and steel making: a case study. J. Ind. Ecol. 2020;24:1113–1125. doi: 10.1111/jiec.12997. [DOI] [Google Scholar]
7.Yuan S., Li Y., Peng J., Questell-Santiago Y.M., Akkiraju K., Giordano L., Zheng D.J., Bagi S., Román-Leshkov Y., Shao-Horn Y. Conversion of methane into liquid fuels—bridging thermal catalysis with electrocatalysis. Adv. Energy Mater. 2020;10:2002154. doi: 10.1002/aenm.202002154. [DOI] [Google Scholar]
8.Richard D., Huang Y.-C., Morales-Guio C.G. Recent advances in the electrochemical production of chemicals from methane. Curr. Opin. Electrochem. 2021;30:100793. doi: 10.1016/j.coelec.2021.100793. [DOI] [Google Scholar]
9.Arnarson L., Schmidt P.S., Pandey M., Bagger A., Thygesen K.S., Stephens I.E.L., Rossmeisl J. Fundamental limitation of electrocatalytic methane conversion to methanol. Phys. Chem. Chem. Phys. 2018;20:11152–11159. doi: 10.1039/C8CP01476K. [DOI] [PubMed] [Google Scholar]
10.Zhu C., Hou S., Hu X., Lu J., Chen F., Xie K. Electrochemical conversion of methane to ethylene in a solid oxide electrolyzer. Nat. Commun. 2019;10:1173. doi: 10.1038/s41467-019-09083-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Latimer A.A., Kakekhani A., Kulkarni A.R., Nørskov J.K. Direct methane to methanol: the selectivity–conversion limit and design strategies. ACS Catal. 2018;8:6894–6907. doi: 10.1021/acscatal.8b00220. [DOI] [Google Scholar]
12.Garagounis I., Vourros A., Stoukides D., Dasopoulos D., Stoukides M. Electrochemical synthesis of ammonia: recent efforts and future outlook. Membrane. 2019;9:112. doi: 10.3390/membranes9090112. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Wen G., Ren B., Wang X., Luo D., Dou H., Zheng Y., Gao R., Gostick J., Yu A., Chen Z. Continuous CO2 electrolysis using a CO2 exsolution-induced flow cell. Nat. Energy. 2022;7:978–988. doi: 10.1038/s41560-022-01130-6. [DOI] [Google Scholar]
14.Chanussot L., Das A., Goyal S., Lavril T., Shuaibi M., Riviere M., Tran K., Heras-Domingo J., Ho C., Hu W., et al. Open catalyst 2020 (OC20) dataset and community challenges. ACS Catal. 2021;11:6059–6072. doi: 10.1021/acscatal.0c04525. [DOI] [Google Scholar]
15.Mou T., Pillai H.S., Wang S., Wan M., Han X., Schweitzer N.M., Che F., Xin H. Bridging the complexity gap in computational heterogeneous catalysis with machine learning. Nat. Catal. 2023;6:122–136. doi: 10.1038/s41929-023-00911-w. [DOI] [Google Scholar]
16.Margraf J.T., Jung H., Scheurer C., Reuter K. Exploring catalytic reaction networks with machine learning. Nat. Catal. 2023;6:112–121. doi: 10.1038/s41929-022-00896-y. [DOI] [Google Scholar]
17.Esterhuizen J.A., Goldsmith B.R., Linic S. Interpretable machine learning for knowledge generation in heterogeneous catalysis. Nat. Catal. 2022;5:175–184. doi: 10.1038/s41929-022-00744-z. [DOI] [Google Scholar]
18.Taibi E., Miranda R., Carmo M., Blanco H. International Renewable Energy Agency; Abu Dhabi: 2020. Green Hydrogen Cost Reduction: Scaling up Electrolysers to Meet the 1.5 oC Climate Goal. [Google Scholar]
19.Xia R., Overa S., Jiao F. Emerging electrochemical processes to decarbonize the chemical industry. JACS Au. 2022;2:1054–1070. doi: 10.1021/jacsau.2c00138. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Vogel G.H. John Wiley & Sons, Ltd; 2011. Process Development, 1. Fundamentals and Standard Course. Ullmann's Encyclopedia of Industrial Chemistry. [DOI] [Google Scholar]
21.Kuhl K.P., Cave E.R., Abram D.N., Jaramillo T.F. New insights into the electrochemical reduction of carbon dioxide on metallic copper surfaces. Energy Environ. Sci. 2012;5:7050–7059. doi: 10.1039/C2EE21234J. [DOI] [Google Scholar]
22.Nitopi S., Bertheussen E., Scott S.B., Liu X., Engstfeld A.K., Horch S., Seger B., Stephens I.E.L., Chan K., Hahn C., et al. Progress and perspectives of electrochemical CO2 reduction on copper in aqueous electrolyte. Chem. Rev. 2019;119:7610–7672. doi: 10.1021/acs.chemrev.8b00705. [DOI] [PubMed] [Google Scholar]
23.Resasco J., Lum Y., Clark E., Zeledon J.Z., Bell A.T. Effects of anion identity and concentration on electrochemical reduction of CO2. Chemelectrochem. 2018;5:1064–1072. doi: 10.1002/celc.201701316. [DOI] [Google Scholar]
24.Hori Y., Kikuchi K., Suzuki S. Production of CO and CH4 in electrochemical reduction of CO2 at metal electrodes in aqueous hydrogencarbonate solution. Chem. Lett. 1985;14:1695–1698. doi: 10.1246/cl.1985.1695. [DOI] [Google Scholar]
25.Kim J.J., Summers D.P., Frese K.W. Reduction of carbon dioxide and carbon monoxide to methane on copper foil electrodes. J. Electroanal. Chem. Interfacial Electrochem. 1988;245:223–244. doi: 10.1021/acs.jpclett.0c01261. [DOI] [Google Scholar]
26.Hara K., Tsuneto A., Kudo A., Sakata T. Electrochemical Reduction of CO2 on a Cu Electrode under high pressure: factors that determine the product selectivity. J. Electrochem. Soc. 1994;141:2097–2103. doi: 10.1149/1.2055067. [DOI] [Google Scholar]
27.Jang J., Rüscher M., Winzely M., Morales-Guio C.G. Gastight rotating cylinder electrode: toward decoupling mass transport and intrinsic kinetics in electrocatalysis. AIChE J. 2022;68:e17605. doi: 10.1002/aic.17605. [DOI] [Google Scholar]
28.Sobkowski J., Wieckowski A., Zelenay P., Czerwiński A. Electrochemical reduction of CO2 and oxidation of adsorbed species on the rhodium electrode. J. Electroanal. Chem. Interfacial Electrochem. 1979;100:781–790. doi: 10.1016/S0022-0728(79)80197-7. [DOI] [Google Scholar]
29.Hori Y., Suzuki S. Electrolytic reduction of carbon dioxide at mercury electrode in aqueous solution. BCSJ. 1982;55:660–665. doi: 10.1246/bcsj.55.660. [DOI] [Google Scholar]
30.Hori Y., Wakebe H., Tsukamoto T., Koga O. Electrocatalytic process of CO selectivity in electrochemical reduction of CO2 at metal electrodes in aqueous media. Electrochim. Acta. 1994;39:1833–1839. doi: 10.1016/0013-4686(94)85172-7. [DOI] [Google Scholar]
31.Hori Y., Takahashi I., Koga O., Hoshi N. Electrochemical reduction of carbon dioxide at various series of copper single crystal electrodes. J. Mol. Catal. Chem. 2003;199:39–47. doi: 10.1016/S1381-1169(03)00016-5. [DOI] [Google Scholar]
32.Lu Q., Rosen J., Zhou Y., Hutchings G.S., Kimmel Y.C., Chen J.G., Jiao F. A selective and efficient electrocatalyst for carbon dioxide reduction. Nat. Commun. 2014;5:3242. doi: 10.1038/ncomms4242. [DOI] [PubMed] [Google Scholar]
33.Kas R., Kortlever R., Milbrat A., Koper M.T.M., Mul G., Baltrusaitis J. Electrochemical CO2 reduction on Cu2O-derived copper nanoparticles: controlling the catalytic selectivity of hydrocarbons. Phys. Chem. Chem. Phys. 2014;16:12194–12201. doi: 10.1039/C4CP01520G. [DOI] [PubMed] [Google Scholar]
34.Kortlever R., Peters I., Koper S., Koper M.T.M. Electrochemical CO2 reduction to formic acid at low overpotential and with high faradaic efficiency on carbon-supported bimetallic Pd–Pt nanoparticles. ACS Catal. 2015;5:3916–3923. doi: 10.1021/acscatal.5b00602. [DOI] [Google Scholar]
35.Yang H.B., Hung S.-F., Liu S., Yuan K., Miao S., Zhang L., Huang X., Wang H.-Y., Cai W., Chen R., et al. Atomically dispersed Ni (I) as the active site for electrochemical CO2 reduction. Nat. Energy. 2018;3:140–147. doi: 10.1038/s41560-017-0078-8. [DOI] [Google Scholar]
36.Jiang K., Sandberg R.B., Akey A.J., Liu X., Bell D.C., Nørskov J.K., Chan K., Wang H. Metal ion cycling of Cu foil for selective C–C coupling in electrochemical CO2 reduction. Nat. Catal. 2018;1:111–119. doi: 10.1038/s41929-017-0009-x. [DOI] [Google Scholar]
37.Pan F., Li B., Deng W., Du Z., Gang Y., Wang G., Li Y. Promoting electrocatalytic CO2 reduction on nitrogen-doped carbon with sulfur addition. Appl. Catal. B. 2019;252:240–249. doi: 10.1016/j.apcatb.2019.04.025. [DOI] [Google Scholar]
38.Manthiram K., Beberwyck B.J., Alivisatos A.P. Enhanced electrochemical methanation of carbon dioxide with a dispersible nanoscale copper catalyst. JACS. 2014;136:13319–13325. doi: 10.1021/ja5065284. [DOI] [PubMed] [Google Scholar]
39.Hatsukade T., Kuhl K.P., Cave E.R., Abram D.N., Jaramillo T.F. Insights into the electrocatalytic reduction of CO2 on metallic silver surfaces. Phys. Chem. Chem. Phys. 2014;16:13814–13819. doi: 10.1039/C4CP00692E. [DOI] [PubMed] [Google Scholar]
40.Lee S.Y., Jung H., Kim N.-K., Oh H.-S., Min B.K., Hwang Y.J. Mixed copper states in anodized Cu electrocatalyst for stable and selective ethylene production from CO2 reduction. JACS. 2018;140:8681–8689. doi: 10.1021/jacs.8b02173. [DOI] [PubMed] [Google Scholar]
41.Kas R., Kortlever R., Yılmaz H., Koper M.T.M., Mul G. Manipulating the hydrocarbon selectivity of copper nanoparticles in CO2 electroreduction by process conditions. Chemelectrochem. 2015;2:354–358. doi: 10.1002/celc.201402373. [DOI] [Google Scholar]
42.Hara K., Sakata T. Large current density CO2 reduction under high pressure using gas diffusion electrodes. BSCJ. 1997;70:571–576. doi: 10.1246/bcsj.70.571. [DOI] [Google Scholar]
43.Narayanan S.R., Haines B., Soler J., Valdez T.I. Electrochemical conversion of carbon dioxide to formate in alkaline polymer electrolyte membrane cells. J. Electrochem. Soc. 2011;158:A167. doi: 10.1149/1.3526312. [DOI] [Google Scholar]
44.Albo J., Beobide G., Castaño P., Irabien A. Methanol electrosynthesis from CO2 at Cu2O/ZnO prompted by pyridine-based aqueous solutions. J. CO2 Util. 2017;18:164–172. doi: 10.1016/j.jcou.2017.02.003. [DOI] [Google Scholar]
45.Salvatore D.A., Weekes D.M., He J., Dettelbach K.E., Li Y.C., Mallouk T.E., Berlinguette C.P. Electrolysis of gaseous CO2 to CO in a flow cell with a bipolar membrane. ACS Energy Lett. 2017;3:149–154. doi: 10.1021/acsenergylett.7b01017. [DOI] [Google Scholar]
46.Dinh C.-T., Burdyny T., Kibria M.G., Seifitokaldani A., Gabardo C.M., García de Arquer F.P., Kiani A., Edwards J.P., De Luna P., Bushuyev O.S., et al. CO2 electroreduction to ethylene via hydroxide-mediated copper catalysis at an abrupt interface. Science. 2018;360:783–787. doi: 10.1126/science.aas9100. [DOI] [PubMed] [Google Scholar]
47.Ren S., Joulié D., Salvatore D., Torbensen K., Wang M., Robert M., Berlinguette C.P. Molecular electrocatalysts can mediate fast, selective CO2 reduction in a flow cell. Science. 2019;365:367–369. doi: 10.1126/science.aax4608. [DOI] [PubMed] [Google Scholar]
48.Lee J., Lim J., Roh C.-W., Whang H.S., Lee H. Electrochemical CO2 reduction using alkaline membrane electrode assembly on various metal electrodes. J. CO2 Util. 2019;31:244–250. doi: 10.1016/j.jcou.2019.03.022. [DOI] [Google Scholar]
49.García de Arquer F.P., Dinh C.-T., Ozden A., Wicks J., McCallum C., Kirmani A.R., Nam D.-H., Gabardo C., Seifitokaldani A., Wang X., et al. CO2 electrolysis to multicarbon products at activities greater than 1 A cm-2. Science. 2020;367:661–666. doi: 10.1126/science.aay4217. [DOI] [PubMed] [Google Scholar]
50.Whipple D.T., Finke E.C., Kenis P.J.A. Microfluidic reactor for the electrochemical reduction of carbon dioxide: the effect of pH. Electrochem. Solid State Lett. 2010;13:B109. doi: 10.1149/1.3456590. [DOI] [Google Scholar]
51.Rosen B.A., Salehi-Khojin A., Thorson M.R., Zhu W., Whipple D.T., Kenis P.J.A., Masel R.I. Ionic liquid–mediated selective conversion of CO2 to CO at low overpotentials. Science. 2011;334:643–644. doi: 10.1126/science.1209786. [DOI] [PubMed] [Google Scholar]
52.Ma S., Sadakiyo M., Luo R., Heima M., Yamauchi M., Kenis P.J. One-step electrosynthesis of ethylene and ethanol from CO2 in an alkaline electrolyzer. J. Power Sources. 2016;301:219–228. doi: 10.1016/j.jpowsour.2015.09.124. [DOI] [Google Scholar]
53.Zhan Z., Kobsiriphat W., Wilson J.R., Pillai M., Kim I., Barnett S.A. Syngas production by coelectrolysis of CO2/H2O: the basis for a renewable energy cycle. Energy Fuels. 2009;23:3089–3096. doi: 10.1021/ef900111f. [DOI] [Google Scholar]
54.Xie K., Zhang Y., Meng G., Irvine J.T.S. Electrochemical reduction of CO2 in a proton conducting solid oxide electrolyser. J. Mater. Chem. 2011;21:195–198. doi: 10.1039/C0JM02205E. [DOI] [Google Scholar]
55.Yu L., Wang J., Hu X., Ye Z., Buckley C., Dong D. A nanocatalyst network for electrochemical reduction of CO2 over microchanneled solid oxide electrolysis cells. Electrochem. Commun. 2018;86:72–75. doi: 10.1016/j.elecom.2017.11.019. [DOI] [Google Scholar]
56.Clark E.L., Singh M.R., Kwon Y., Bell A.T. Differential electrochemical mass spectrometer cell design for online quantification of products produced during electrochemical reduction of CO2. Anal. Chem. 2015;87:8013–8020. doi: 10.1021/acs.analchem.5b02080. [DOI] [PubMed] [Google Scholar]
57.Clark E.L., Bell A.T. Direct observation of the local reaction environment during the electrochemical reduction of CO2. JACS. 2018;140:7012–7020. doi: 10.1021/jacs.8b04058. [DOI] [PubMed] [Google Scholar]
58.Murata A., Hori Y. Product selectivity affected by cationic species in electrochemical reduction of CO2 and CO at a Cu electrode. BCSJ. 1991;64:123–127. doi: 10.1246/bcsj.64.123. [DOI] [Google Scholar]
59.Resasco J., Chen L.D., Clark E., Tsai C., Hahn C., Jaramillo T.F., Chan K., Bell A.T. Promoter effects of alkali metal cations on the electrochemical reduction of carbon dioxide. JACS. 2017;139:11277–11287. doi: 10.1021/jacs.7b06765. [DOI] [PubMed] [Google Scholar]
60.Hahn C., Hatsukade T., Kim Y.-G., Vailionis A., Baricuatro J.H., Higgins D.C., Nitopi S.A., So- riaga M.P., Jaramillo T.F. Engineering Cu surfaces for the electrocatalytic conversion of CO2: controlling selectivity toward oxygenates and hydrocarbons. Proc. Natl. Acad. Sci. USA. 2017;114:5918–5923. doi: 10.1073/pnas.1618935114. [DOI] [PMC free article] [PubMed] [Google Scholar]
61.Watkins N.B., Schiffer Z.J., Lai Y., Musgrave C.B., Atwater H.A., Goddard W.A., Agapie T., Peters J.C., Gregoire J.M. Hydrodynamics change tafel slopes in electrochemical CO2 reduction on copper. ACS Energy Lett. 2023;8:2185–2192. doi: 10.1021/acsenergylett.3c00442. [DOI] [Google Scholar]
62.Leiva C. First principles of smart manufacturing. J. Adv. Manuf. Process. 2022;4:e10123. doi: 10.1002/amp2.10123. [DOI] [Google Scholar]
63.Tuptuk N., Hailes S. Security of smart manufacturing systems. J. Manuf. Syst. 2018;47:93–106. doi: 10.1016/j.jmsy.2018.04.007. [DOI] [Google Scholar]
64.Burnak B., Diangelakis N.A., Katz J., Pistikopoulos E.N. Integrated process design, scheduling, and control using multiparametric programming. Comput. Chem. Eng. 2019;125:164–184. doi: 10.1016/j.compchemeng.2019.03.004. [DOI] [Google Scholar]
65.Soroush M., Baldea M.M., Edgar T.F. Elsevier; Oxford: 2020. Smart Manufacturing: Concepts and Methods. [Google Scholar]
66.Davis J. In: Encyclopedia of Sustainable Technologies. Abraham M.A., editor. Elsevier; Oxford: 2017. Smart manufacturing; pp. 417–427. [Google Scholar]
67.Phuyal S., Bista D., Bista R. Challenges, opportunities and future directions of smart manufacturing: a state of art review. Sus. Fut. 2020;2:100023. doi: 10.1016/j.sftr.2020.100023. [DOI] [Google Scholar]
68.Burnak B., Diangelakis N.A., Pistikopoulos E.N. Towards the grand unification of process design, scheduling, and control - utopia or reality? Processes. 2019;7:461. doi: 10.3390/pr7070461. [DOI] [Google Scholar]
69.Lin Y.-J., Wei S.-H., Huang C.-Y. Intelligent manufacturing control systems: the core of smart factory. Procedia Manuf. 2019;39:389–397. doi: 10.1016/j.promfg.2020.01.382. [DOI] [Google Scholar]
70.Prior J., Bartelt M., Sinnemann J., Kuhlenkötter B. Investigation of the automation capability of electrolyzers production. Procedia CIRP. 2022;107:718–723. doi: 10.1016/j.procir.2022.05.051. [DOI] [Google Scholar]
71.Bogojeski M., Sauer S., Horn F., Müller K.R. Forecasting industrial aging processes with machine learning methods. Comput. Chem. Eng. 2021;144:107123. doi: 10.1016/j.compchemeng.2020.107123. [DOI] [Google Scholar]
72.Çıtmacı B., Luo J., Jang J.B., Canuso V., Richard D., Ren Y.M., Morales-Guio C.G., Christofides P.D. Machine learning-based ethylene concentration estimation, real-time optimization and feedback control of an experimental electrochemical reactor. Chem. Eng. Res. Des. 2022;185:87–107. doi: 10.1016/j.cherd.2022.06.044. [DOI] [Google Scholar]
73.Kumar A.S., Ahmad Z. Model predictive control (MPC) and its current issues in chemical engineering. Chem. Eng. Commun. 2012;199:472–511. doi: 10.1080/00986445.2011.592446. [DOI] [Google Scholar]
74.Ding Y., Wang L., Li Y., Li D. Model predictive control and its application in agriculture: a review. Comput. Electron. Agric. 2018;151:104–117. doi: 10.1016/j.compag.2018.06.004. [DOI] [Google Scholar]
75.Kumar A., Baldea M., Edgar T.F., Ezekoye O.A. Smart manufacturing approach for efficient operation of industrial steam-methane reformers. Ind. Eng. Chem. Res. 2015;54:4360–4370. doi: 10.1021/ie504087z. [DOI] [Google Scholar]
76.Malkani H., Korambath P. Clean energy smart manufacturing innovation institute (CESMII) special issue. J. Adv. Manuf. Process. 2022;4:e10146. doi: 10.1002/amp2.10146. [DOI] [Google Scholar]
77.Brunner Z. NIST; 2022. Manufacturing USA Highlights Report 2022. [Google Scholar]
78.Arden N.S., Fisher A.C., Tyner K., Yu L.X., Lee S.L., Kopcha M. Industry 4.0 for pharmaceutical manufacturing: preparing for the smart factories of the future. Int. J. Pharm. 2021;602:120554. doi: 10.1016/j.ijpharm.2021.120554. [DOI] [PubMed] [Google Scholar]
79.Vogel-Heuser B., Rösch S., Martini A., Tichy M. 2015 IEEE 7th International Workshop on Managing Technical Debt (MTD) 2015. Technical Debt in Automated Production Systems; pp. 49–52. [DOI] [Google Scholar]
80.Martini A., Bosch J. Chapter 4. John Wiley & Sons, Ltd; 2019. pp. 77–103. (Architectural Technical Debt in Embedded System). [DOI] [Google Scholar]
81.Kravchenko A. Workforce training and management challenges in the contemporary smart manufacturing (SM) Intel. Arch. 2019;8:59–65. doi: 10.32370/IA_2019_02_9. [DOI] [Google Scholar]
82.Çıtmacı B., Luo J., Jang J.B., Korambath P., Morales-Guio C.G., Davis J.F., Christofides P.D. Digitalization of an experimental electrochemical reactor via the smart manufacturing innovation platform. Digit. Chem. Eng. 2022;5:100050. doi: 10.1016/j.dche.2022.100050. [DOI] [Google Scholar]
83.Richard D., Tom M., Jang J., Yun S., Christofides P.D., Morales-Guio C.G. Quantifying transport and electrocatalytic reaction processes in a gastight rotating cylinder electrode reactor via integration of computational fluid dynamics modeling and experiments. Electrochim. Acta. 2023;440:141698. doi: 10.1016/j.electacta.2022.141698. [DOI] [Google Scholar]
84.Pangarkar V.G. Chapter 5: Principles of similarity and their application for scale up. John Wiley & Sons, Ltd.; 2014. Design of Multiphase Reactors; pp. 93–105. [DOI] [Google Scholar]
85.Abolhasani M., Kumacheva E. The rise of self-driving labs in chemical and materials sciences. Nat. Synth. 2023:1–10. doi: 10.1038/s44160-022-00231-0. [DOI] [Google Scholar]
86.Vriza A., Chan H., Xu J. Self-driving laboratory for polymer electronics. Chem. Mater. 2023;35:3046–3056. doi: 10.1021/acs.chemmater.2c03593. [DOI] [Google Scholar]
87.Mennen S.M., Alhambra C., Allen C.L., Barberis M., Berritt S., Brandt T.A., Campbell A.D., Castañón J., Cherney A.H., Christensen M., et al. The evolution of high-throughput experimentation in pharmaceutical development and perspectives on the future. Org. Process Res. Dev. 2019;23:1213–1242. doi: 10.1021/acs.oprd.9b00140. [DOI] [Google Scholar]
88.Tao H., Wu T., Kheiri S., Aldeghi M., Aspuru-Guzik A., Kumacheva E. Self-driving platform for metal nanoparticle synthesis: combining microfluidics and machine learning. Adv. Funct. Mater. 2021;31:2106725. doi: 10.1002/adfm.202106725. [DOI] [Google Scholar]
89.Çıtmacı B., Luo J., Jang J.B., Morales-Guio C.G., Christofides P.D. Machine learning-based ethylene and carbon monoxide estimation, real-time optimization, and multivariable feedback control of an experimental electrochemical reactor. Chem. Eng. Res. Des. 2023;191:658–681. doi: 10.1016/j.cherd.2023.02.003. [DOI] [Google Scholar]
90.Goldsmith B.R., Esterhuizen J., Liu J.-X., Bartel C.J., Sutton C. Machine learning for heterogeneous catalyst design and discovery. AIChE J. 2018;64:2311–2323. doi: 10.1002/aic.16198. [DOI] [Google Scholar]
91.Angulo A., Yang L., Aydil E.S., Modestino M.A. Machine learning enhanced spectroscopic analysis: towards autonomous chemical mixture characterization for rapid process optimization. Digit. Discov. 2022;1:35–44. doi: 10.1039/D1DD00027F. [DOI] [Google Scholar]
92.MacLeod B.P., Parlane F.G.L., Morrissey T.D., Häse F., Roch L.M., Dettelbach K.E., Moreira R., Yunker L.P.E., Rooney M.B., Deeth J.R., et al. Self-driving laboratory for accelerated discovery of thin-film materials. Sci. Adv. 2020;6:eaaz8867. doi: 10.1126/sciadv.aaz8867. [DOI] [PMC free article] [PubMed] [Google Scholar]
93.Reizman B.J., Jensen K.F. An automated continuous-flow platform for the estimation of multistep reaction kinetics. Org. Process Res. Dev. 2012;16:1770–1782. doi: 10.1021/op3001838. [DOI] [Google Scholar]
94.Luo J., Canuso V., Jang J.B., Wu Z., Morales-Guio C.G., Christofides P.D. Machine learning-based operational modeling of an electrochemical reactor: handling data variability and improving empirical models. Ind. Eng. Chem. Res. 2022;61:8399–8410. doi: 10.1021/acs.iecr.1c04176. [DOI] [Google Scholar]
95.Wu Z., Tran A., Rincon D., Christofides P.D. Machine learning-based predictive control of nonlinear processes Part I: Theory. AIChE J. 2019;65:e16729. doi: 10.1002/aic.16729. [DOI] [Google Scholar]
96.Wu Z., Luo J., Rincon D., Christofides P.D. Machine learning-based predictive control using noisy data: evaluating performance and robustness via a large-scale process simulator. Chem. Eng. Res. Des. 2021;168:275–287. doi: 10.1016/j.cherd.2021.02.011. [DOI] [Google Scholar]
97.Xavier M.A., Trimboli M.S. Lithium-ion battery cell-level control using constrained model predictive control and equivalent circuit models. J. Power Sources. 2015;285:374–384. doi: 10.1016/j.jpowsour.2015.03.074. [DOI] [Google Scholar]
98.Denn M. Prentice-Hall; 1980. Process Fluid Mechanics. [Google Scholar]
99.Santhanagopalan S. Electrochemical Systems - Scaling, Dimensionless Groups; Springer New York: 2014. Encyclopedia of Applied Electrochemistry; pp. 634–640. [DOI] [Google Scholar]
100.Oppenheimer M.W., Doman D.B., Merrick J.D. Multi-scale physics-informed machine learning using the Buckingham Pi theorem. J. Comput. Phys. 2023;474:111810. doi: 10.1016/j.jcp.2022.111810. [DOI] [Google Scholar]
101.Xie X., Samaei A., Guo J., Liu W.K., Gan Z. Data-driven discovery of dimensionless numbers and governing laws from scarce measurements. Nat. Commun. 2022;13:7562. doi: 10.1038/s41467-022-35084-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
102.Chen H., Batchelor-McAuley C., Kätelhön E., Elliott J., Compton R.G. A critical evaluation of using physics-informed neural networks for simulating Voltammetry: strengths, weaknesses and best practices. J. Electroanal. Chem. 2022;925:116918. doi: 10.1016/j.jelechem.2022.116918. [DOI] [Google Scholar]
103.Tu Y.-J., Delmerico S., McDaniel J.G. Inner layer capacitance of organic electrolytes from constant voltage molecular dynamics. J. Phys. Chem. C. 2020;124:2907–2922. doi: 10.1021/acs.jpcc.0c00299. [DOI] [Google Scholar]
104.Kong S., Lv X., Wang X., Liu Z., Li Z., Jia B., Sun D., Yang C., Liu L., Guan A., et al. Delocalization state-induced selective bond breaking for efficient methanol electrosynthesis from CO2. Nat. Catal. 2022;6:6–15. doi: 10.1038/s41929-022-00887-z. [DOI] [Google Scholar]
105.Micale D., Ferroni C., Uglietti R., Bracconi M., Maestri M. Computational fluid dynamics of reacting flows at surfaces: methodologies and applications. Chem. Ing. Tech. 2022;94:634–651. doi: 10.1002/cite.202100196. [DOI] [Google Scholar]
106.Zhu L.-T., Chen X.-Z., Ouyang B., Yan W.-C., Lei H., Chen Z., Luo Z.-H. Review of machine learning for hydrodynamics, transport, and reactions in multiphase flows and reactors. Ind. Eng. Chem. Res. 2022;61:9901–9949. doi: 10.1021/acs.iecr.2c01036. [DOI] [Google Scholar]

[bib1] 1.Rego de Vasconcelos B., Lavoie J.-M. Recent advances in power-to-X technology for the production of fuels and chemicals. Front. Chem. 2019;7:392. doi: 10.3389/fchem.2019.00392. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib2] 2.Perkin R.M. John Wiley & Sons, Ltd; 2000. Electrically Generated Heat. Ullmann's Encyclopedia of Industrial Chemistry. [DOI] [Google Scholar]

[bib3] 3.Wismann S.T., Engbæk J.S., Vendelbo S.B., Bendixen F.B., Eriksen W.L., Aasberg-Petersen K., Frandsen C., Chorkendorff I., Mortensen P.M. Electrified methane reforming: a compact approach to greener industrial hydrogen production. Science. 2019;364:756–759. doi: 10.1126/science.aaw8775. [DOI] [PubMed] [Google Scholar]

[bib4] 4.Madeddu S., Ueckerdt F., Pehl M., Peterseim J., Lord M., Kumar K.A., Krüger C., Luderer G. The CO2 reduction potential for the European industry via direct electrification of heat supply (power-to-heat) Environ. Res. Lett. 2020;15:124004. doi: 10.1088/1748-9326/abbd02. [DOI] [Google Scholar]

[bib5] 5.Brockway A.M., Delforge P. Emissions reduction potential from electric heat pumps in California homes. Electr. J. 2018;31:44–53. doi: 10.1016/j.tej.2018.10.012. [DOI] [Google Scholar]

[bib6] 6.Gielen D., Saygin D., Taibi E., Birat J.-P. Renewables-based decarbonization and relocation of iron and steel making: a case study. J. Ind. Ecol. 2020;24:1113–1125. doi: 10.1111/jiec.12997. [DOI] [Google Scholar]

[bib7] 7.Yuan S., Li Y., Peng J., Questell-Santiago Y.M., Akkiraju K., Giordano L., Zheng D.J., Bagi S., Román-Leshkov Y., Shao-Horn Y. Conversion of methane into liquid fuels—bridging thermal catalysis with electrocatalysis. Adv. Energy Mater. 2020;10:2002154. doi: 10.1002/aenm.202002154. [DOI] [Google Scholar]

[bib8] 8.Richard D., Huang Y.-C., Morales-Guio C.G. Recent advances in the electrochemical production of chemicals from methane. Curr. Opin. Electrochem. 2021;30:100793. doi: 10.1016/j.coelec.2021.100793. [DOI] [Google Scholar]

[bib9] 9.Arnarson L., Schmidt P.S., Pandey M., Bagger A., Thygesen K.S., Stephens I.E.L., Rossmeisl J. Fundamental limitation of electrocatalytic methane conversion to methanol. Phys. Chem. Chem. Phys. 2018;20:11152–11159. doi: 10.1039/C8CP01476K. [DOI] [PubMed] [Google Scholar]

[bib10] 10.Zhu C., Hou S., Hu X., Lu J., Chen F., Xie K. Electrochemical conversion of methane to ethylene in a solid oxide electrolyzer. Nat. Commun. 2019;10:1173. doi: 10.1038/s41467-019-09083-3. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib11] 11.Latimer A.A., Kakekhani A., Kulkarni A.R., Nørskov J.K. Direct methane to methanol: the selectivity–conversion limit and design strategies. ACS Catal. 2018;8:6894–6907. doi: 10.1021/acscatal.8b00220. [DOI] [Google Scholar]

[bib12] 12.Garagounis I., Vourros A., Stoukides D., Dasopoulos D., Stoukides M. Electrochemical synthesis of ammonia: recent efforts and future outlook. Membrane. 2019;9:112. doi: 10.3390/membranes9090112. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib13] 13.Wen G., Ren B., Wang X., Luo D., Dou H., Zheng Y., Gao R., Gostick J., Yu A., Chen Z. Continuous CO2 electrolysis using a CO2 exsolution-induced flow cell. Nat. Energy. 2022;7:978–988. doi: 10.1038/s41560-022-01130-6. [DOI] [Google Scholar]

[bib14] 14.Chanussot L., Das A., Goyal S., Lavril T., Shuaibi M., Riviere M., Tran K., Heras-Domingo J., Ho C., Hu W., et al. Open catalyst 2020 (OC20) dataset and community challenges. ACS Catal. 2021;11:6059–6072. doi: 10.1021/acscatal.0c04525. [DOI] [Google Scholar]

[bib15] 15.Mou T., Pillai H.S., Wang S., Wan M., Han X., Schweitzer N.M., Che F., Xin H. Bridging the complexity gap in computational heterogeneous catalysis with machine learning. Nat. Catal. 2023;6:122–136. doi: 10.1038/s41929-023-00911-w. [DOI] [Google Scholar]

[bib16] 16.Margraf J.T., Jung H., Scheurer C., Reuter K. Exploring catalytic reaction networks with machine learning. Nat. Catal. 2023;6:112–121. doi: 10.1038/s41929-022-00896-y. [DOI] [Google Scholar]

[bib17] 17.Esterhuizen J.A., Goldsmith B.R., Linic S. Interpretable machine learning for knowledge generation in heterogeneous catalysis. Nat. Catal. 2022;5:175–184. doi: 10.1038/s41929-022-00744-z. [DOI] [Google Scholar]

[bib18] 18.Taibi E., Miranda R., Carmo M., Blanco H. International Renewable Energy Agency; Abu Dhabi: 2020. Green Hydrogen Cost Reduction: Scaling up Electrolysers to Meet the 1.5 oC Climate Goal. [Google Scholar]

[bib19] 19.Xia R., Overa S., Jiao F. Emerging electrochemical processes to decarbonize the chemical industry. JACS Au. 2022;2:1054–1070. doi: 10.1021/jacsau.2c00138. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib20] 20.Vogel G.H. John Wiley & Sons, Ltd; 2011. Process Development, 1. Fundamentals and Standard Course. Ullmann's Encyclopedia of Industrial Chemistry. [DOI] [Google Scholar]

[bib21] 21.Kuhl K.P., Cave E.R., Abram D.N., Jaramillo T.F. New insights into the electrochemical reduction of carbon dioxide on metallic copper surfaces. Energy Environ. Sci. 2012;5:7050–7059. doi: 10.1039/C2EE21234J. [DOI] [Google Scholar]

[bib22] 22.Nitopi S., Bertheussen E., Scott S.B., Liu X., Engstfeld A.K., Horch S., Seger B., Stephens I.E.L., Chan K., Hahn C., et al. Progress and perspectives of electrochemical CO2 reduction on copper in aqueous electrolyte. Chem. Rev. 2019;119:7610–7672. doi: 10.1021/acs.chemrev.8b00705. [DOI] [PubMed] [Google Scholar]

[bib23] 23.Resasco J., Lum Y., Clark E., Zeledon J.Z., Bell A.T. Effects of anion identity and concentration on electrochemical reduction of CO2. Chemelectrochem. 2018;5:1064–1072. doi: 10.1002/celc.201701316. [DOI] [Google Scholar]

[bib24] 24.Hori Y., Kikuchi K., Suzuki S. Production of CO and CH4 in electrochemical reduction of CO2 at metal electrodes in aqueous hydrogencarbonate solution. Chem. Lett. 1985;14:1695–1698. doi: 10.1246/cl.1985.1695. [DOI] [Google Scholar]

[bib25] 25.Kim J.J., Summers D.P., Frese K.W. Reduction of carbon dioxide and carbon monoxide to methane on copper foil electrodes. J. Electroanal. Chem. Interfacial Electrochem. 1988;245:223–244. doi: 10.1021/acs.jpclett.0c01261. [DOI] [Google Scholar]

[bib26] 26.Hara K., Tsuneto A., Kudo A., Sakata T. Electrochemical Reduction of CO2 on a Cu Electrode under high pressure: factors that determine the product selectivity. J. Electrochem. Soc. 1994;141:2097–2103. doi: 10.1149/1.2055067. [DOI] [Google Scholar]

[bib57] 27.Jang J., Rüscher M., Winzely M., Morales-Guio C.G. Gastight rotating cylinder electrode: toward decoupling mass transport and intrinsic kinetics in electrocatalysis. AIChE J. 2022;68:e17605. doi: 10.1002/aic.17605. [DOI] [Google Scholar]

[bib27] 28.Sobkowski J., Wieckowski A., Zelenay P., Czerwiński A. Electrochemical reduction of CO2 and oxidation of adsorbed species on the rhodium electrode. J. Electroanal. Chem. Interfacial Electrochem. 1979;100:781–790. doi: 10.1016/S0022-0728(79)80197-7. [DOI] [Google Scholar]

[bib28] 29.Hori Y., Suzuki S. Electrolytic reduction of carbon dioxide at mercury electrode in aqueous solution. BCSJ. 1982;55:660–665. doi: 10.1246/bcsj.55.660. [DOI] [Google Scholar]

[bib29] 30.Hori Y., Wakebe H., Tsukamoto T., Koga O. Electrocatalytic process of CO selectivity in electrochemical reduction of CO2 at metal electrodes in aqueous media. Electrochim. Acta. 1994;39:1833–1839. doi: 10.1016/0013-4686(94)85172-7. [DOI] [Google Scholar]

[bib30] 31.Hori Y., Takahashi I., Koga O., Hoshi N. Electrochemical reduction of carbon dioxide at various series of copper single crystal electrodes. J. Mol. Catal. Chem. 2003;199:39–47. doi: 10.1016/S1381-1169(03)00016-5. [DOI] [Google Scholar]

[bib31] 32.Lu Q., Rosen J., Zhou Y., Hutchings G.S., Kimmel Y.C., Chen J.G., Jiao F. A selective and efficient electrocatalyst for carbon dioxide reduction. Nat. Commun. 2014;5:3242. doi: 10.1038/ncomms4242. [DOI] [PubMed] [Google Scholar]

[bib32] 33.Kas R., Kortlever R., Milbrat A., Koper M.T.M., Mul G., Baltrusaitis J. Electrochemical CO2 reduction on Cu2O-derived copper nanoparticles: controlling the catalytic selectivity of hydrocarbons. Phys. Chem. Chem. Phys. 2014;16:12194–12201. doi: 10.1039/C4CP01520G. [DOI] [PubMed] [Google Scholar]

[bib33] 34.Kortlever R., Peters I., Koper S., Koper M.T.M. Electrochemical CO2 reduction to formic acid at low overpotential and with high faradaic efficiency on carbon-supported bimetallic Pd–Pt nanoparticles. ACS Catal. 2015;5:3916–3923. doi: 10.1021/acscatal.5b00602. [DOI] [Google Scholar]

[bib34] 35.Yang H.B., Hung S.-F., Liu S., Yuan K., Miao S., Zhang L., Huang X., Wang H.-Y., Cai W., Chen R., et al. Atomically dispersed Ni (I) as the active site for electrochemical CO2 reduction. Nat. Energy. 2018;3:140–147. doi: 10.1038/s41560-017-0078-8. [DOI] [Google Scholar]

[bib35] 36.Jiang K., Sandberg R.B., Akey A.J., Liu X., Bell D.C., Nørskov J.K., Chan K., Wang H. Metal ion cycling of Cu foil for selective C–C coupling in electrochemical CO2 reduction. Nat. Catal. 2018;1:111–119. doi: 10.1038/s41929-017-0009-x. [DOI] [Google Scholar]

[bib36] 37.Pan F., Li B., Deng W., Du Z., Gang Y., Wang G., Li Y. Promoting electrocatalytic CO2 reduction on nitrogen-doped carbon with sulfur addition. Appl. Catal. B. 2019;252:240–249. doi: 10.1016/j.apcatb.2019.04.025. [DOI] [Google Scholar]

[bib37] 38.Manthiram K., Beberwyck B.J., Alivisatos A.P. Enhanced electrochemical methanation of carbon dioxide with a dispersible nanoscale copper catalyst. JACS. 2014;136:13319–13325. doi: 10.1021/ja5065284. [DOI] [PubMed] [Google Scholar]

[bib38] 39.Hatsukade T., Kuhl K.P., Cave E.R., Abram D.N., Jaramillo T.F. Insights into the electrocatalytic reduction of CO2 on metallic silver surfaces. Phys. Chem. Chem. Phys. 2014;16:13814–13819. doi: 10.1039/C4CP00692E. [DOI] [PubMed] [Google Scholar]

[bib39] 40.Lee S.Y., Jung H., Kim N.-K., Oh H.-S., Min B.K., Hwang Y.J. Mixed copper states in anodized Cu electrocatalyst for stable and selective ethylene production from CO2 reduction. JACS. 2018;140:8681–8689. doi: 10.1021/jacs.8b02173. [DOI] [PubMed] [Google Scholar]

[bib40] 41.Kas R., Kortlever R., Yılmaz H., Koper M.T.M., Mul G. Manipulating the hydrocarbon selectivity of copper nanoparticles in CO2 electroreduction by process conditions. Chemelectrochem. 2015;2:354–358. doi: 10.1002/celc.201402373. [DOI] [Google Scholar]

[bib41] 42.Hara K., Sakata T. Large current density CO2 reduction under high pressure using gas diffusion electrodes. BSCJ. 1997;70:571–576. doi: 10.1246/bcsj.70.571. [DOI] [Google Scholar]

[bib42] 43.Narayanan S.R., Haines B., Soler J., Valdez T.I. Electrochemical conversion of carbon dioxide to formate in alkaline polymer electrolyte membrane cells. J. Electrochem. Soc. 2011;158:A167. doi: 10.1149/1.3526312. [DOI] [Google Scholar]

[bib43] 44.Albo J., Beobide G., Castaño P., Irabien A. Methanol electrosynthesis from CO2 at Cu2O/ZnO prompted by pyridine-based aqueous solutions. J. CO2 Util. 2017;18:164–172. doi: 10.1016/j.jcou.2017.02.003. [DOI] [Google Scholar]

[bib44] 45.Salvatore D.A., Weekes D.M., He J., Dettelbach K.E., Li Y.C., Mallouk T.E., Berlinguette C.P. Electrolysis of gaseous CO2 to CO in a flow cell with a bipolar membrane. ACS Energy Lett. 2017;3:149–154. doi: 10.1021/acsenergylett.7b01017. [DOI] [Google Scholar]

[bib45] 46.Dinh C.-T., Burdyny T., Kibria M.G., Seifitokaldani A., Gabardo C.M., García de Arquer F.P., Kiani A., Edwards J.P., De Luna P., Bushuyev O.S., et al. CO2 electroreduction to ethylene via hydroxide-mediated copper catalysis at an abrupt interface. Science. 2018;360:783–787. doi: 10.1126/science.aas9100. [DOI] [PubMed] [Google Scholar]

[bib46] 47.Ren S., Joulié D., Salvatore D., Torbensen K., Wang M., Robert M., Berlinguette C.P. Molecular electrocatalysts can mediate fast, selective CO2 reduction in a flow cell. Science. 2019;365:367–369. doi: 10.1126/science.aax4608. [DOI] [PubMed] [Google Scholar]

[bib47] 48.Lee J., Lim J., Roh C.-W., Whang H.S., Lee H. Electrochemical CO2 reduction using alkaline membrane electrode assembly on various metal electrodes. J. CO2 Util. 2019;31:244–250. doi: 10.1016/j.jcou.2019.03.022. [DOI] [Google Scholar]

[bib48] 49.García de Arquer F.P., Dinh C.-T., Ozden A., Wicks J., McCallum C., Kirmani A.R., Nam D.-H., Gabardo C., Seifitokaldani A., Wang X., et al. CO2 electrolysis to multicarbon products at activities greater than 1 A cm-2. Science. 2020;367:661–666. doi: 10.1126/science.aay4217. [DOI] [PubMed] [Google Scholar]

[bib49] 50.Whipple D.T., Finke E.C., Kenis P.J.A. Microfluidic reactor for the electrochemical reduction of carbon dioxide: the effect of pH. Electrochem. Solid State Lett. 2010;13:B109. doi: 10.1149/1.3456590. [DOI] [Google Scholar]

[bib50] 51.Rosen B.A., Salehi-Khojin A., Thorson M.R., Zhu W., Whipple D.T., Kenis P.J.A., Masel R.I. Ionic liquid–mediated selective conversion of CO2 to CO at low overpotentials. Science. 2011;334:643–644. doi: 10.1126/science.1209786. [DOI] [PubMed] [Google Scholar]

[bib51] 52.Ma S., Sadakiyo M., Luo R., Heima M., Yamauchi M., Kenis P.J. One-step electrosynthesis of ethylene and ethanol from CO2 in an alkaline electrolyzer. J. Power Sources. 2016;301:219–228. doi: 10.1016/j.jpowsour.2015.09.124. [DOI] [Google Scholar]

[bib52] 53.Zhan Z., Kobsiriphat W., Wilson J.R., Pillai M., Kim I., Barnett S.A. Syngas production by coelectrolysis of CO2/H2O: the basis for a renewable energy cycle. Energy Fuels. 2009;23:3089–3096. doi: 10.1021/ef900111f. [DOI] [Google Scholar]

[bib53] 54.Xie K., Zhang Y., Meng G., Irvine J.T.S. Electrochemical reduction of CO2 in a proton conducting solid oxide electrolyser. J. Mater. Chem. 2011;21:195–198. doi: 10.1039/C0JM02205E. [DOI] [Google Scholar]

[bib54] 55.Yu L., Wang J., Hu X., Ye Z., Buckley C., Dong D. A nanocatalyst network for electrochemical reduction of CO2 over microchanneled solid oxide electrolysis cells. Electrochem. Commun. 2018;86:72–75. doi: 10.1016/j.elecom.2017.11.019. [DOI] [Google Scholar]

[bib55] 56.Clark E.L., Singh M.R., Kwon Y., Bell A.T. Differential electrochemical mass spectrometer cell design for online quantification of products produced during electrochemical reduction of CO2. Anal. Chem. 2015;87:8013–8020. doi: 10.1021/acs.analchem.5b02080. [DOI] [PubMed] [Google Scholar]

[bib56] 57.Clark E.L., Bell A.T. Direct observation of the local reaction environment during the electrochemical reduction of CO2. JACS. 2018;140:7012–7020. doi: 10.1021/jacs.8b04058. [DOI] [PubMed] [Google Scholar]

[bib58] 58.Murata A., Hori Y. Product selectivity affected by cationic species in electrochemical reduction of CO2 and CO at a Cu electrode. BCSJ. 1991;64:123–127. doi: 10.1246/bcsj.64.123. [DOI] [Google Scholar]

[bib59] 59.Resasco J., Chen L.D., Clark E., Tsai C., Hahn C., Jaramillo T.F., Chan K., Bell A.T. Promoter effects of alkali metal cations on the electrochemical reduction of carbon dioxide. JACS. 2017;139:11277–11287. doi: 10.1021/jacs.7b06765. [DOI] [PubMed] [Google Scholar]

[bib60] 60.Hahn C., Hatsukade T., Kim Y.-G., Vailionis A., Baricuatro J.H., Higgins D.C., Nitopi S.A., So- riaga M.P., Jaramillo T.F. Engineering Cu surfaces for the electrocatalytic conversion of CO2: controlling selectivity toward oxygenates and hydrocarbons. Proc. Natl. Acad. Sci. USA. 2017;114:5918–5923. doi: 10.1073/pnas.1618935114. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib61] 61.Watkins N.B., Schiffer Z.J., Lai Y., Musgrave C.B., Atwater H.A., Goddard W.A., Agapie T., Peters J.C., Gregoire J.M. Hydrodynamics change tafel slopes in electrochemical CO2 reduction on copper. ACS Energy Lett. 2023;8:2185–2192. doi: 10.1021/acsenergylett.3c00442. [DOI] [Google Scholar]

[bib62] 62.Leiva C. First principles of smart manufacturing. J. Adv. Manuf. Process. 2022;4:e10123. doi: 10.1002/amp2.10123. [DOI] [Google Scholar]

[bib63] 63.Tuptuk N., Hailes S. Security of smart manufacturing systems. J. Manuf. Syst. 2018;47:93–106. doi: 10.1016/j.jmsy.2018.04.007. [DOI] [Google Scholar]

[bib64] 64.Burnak B., Diangelakis N.A., Katz J., Pistikopoulos E.N. Integrated process design, scheduling, and control using multiparametric programming. Comput. Chem. Eng. 2019;125:164–184. doi: 10.1016/j.compchemeng.2019.03.004. [DOI] [Google Scholar]

[bib65] 65.Soroush M., Baldea M.M., Edgar T.F. Elsevier; Oxford: 2020. Smart Manufacturing: Concepts and Methods. [Google Scholar]

[bib66] 66.Davis J. In: Encyclopedia of Sustainable Technologies. Abraham M.A., editor. Elsevier; Oxford: 2017. Smart manufacturing; pp. 417–427. [Google Scholar]

[bib67] 67.Phuyal S., Bista D., Bista R. Challenges, opportunities and future directions of smart manufacturing: a state of art review. Sus. Fut. 2020;2:100023. doi: 10.1016/j.sftr.2020.100023. [DOI] [Google Scholar]

[bib68] 68.Burnak B., Diangelakis N.A., Pistikopoulos E.N. Towards the grand unification of process design, scheduling, and control - utopia or reality? Processes. 2019;7:461. doi: 10.3390/pr7070461. [DOI] [Google Scholar]

[bib69] 69.Lin Y.-J., Wei S.-H., Huang C.-Y. Intelligent manufacturing control systems: the core of smart factory. Procedia Manuf. 2019;39:389–397. doi: 10.1016/j.promfg.2020.01.382. [DOI] [Google Scholar]

[bib70] 70.Prior J., Bartelt M., Sinnemann J., Kuhlenkötter B. Investigation of the automation capability of electrolyzers production. Procedia CIRP. 2022;107:718–723. doi: 10.1016/j.procir.2022.05.051. [DOI] [Google Scholar]

[bib71] 71.Bogojeski M., Sauer S., Horn F., Müller K.R. Forecasting industrial aging processes with machine learning methods. Comput. Chem. Eng. 2021;144:107123. doi: 10.1016/j.compchemeng.2020.107123. [DOI] [Google Scholar]

[bib72] 72.Çıtmacı B., Luo J., Jang J.B., Canuso V., Richard D., Ren Y.M., Morales-Guio C.G., Christofides P.D. Machine learning-based ethylene concentration estimation, real-time optimization and feedback control of an experimental electrochemical reactor. Chem. Eng. Res. Des. 2022;185:87–107. doi: 10.1016/j.cherd.2022.06.044. [DOI] [Google Scholar]

[bib73] 73.Kumar A.S., Ahmad Z. Model predictive control (MPC) and its current issues in chemical engineering. Chem. Eng. Commun. 2012;199:472–511. doi: 10.1080/00986445.2011.592446. [DOI] [Google Scholar]

[bib74] 74.Ding Y., Wang L., Li Y., Li D. Model predictive control and its application in agriculture: a review. Comput. Electron. Agric. 2018;151:104–117. doi: 10.1016/j.compag.2018.06.004. [DOI] [Google Scholar]

[bib75] 75.Kumar A., Baldea M., Edgar T.F., Ezekoye O.A. Smart manufacturing approach for efficient operation of industrial steam-methane reformers. Ind. Eng. Chem. Res. 2015;54:4360–4370. doi: 10.1021/ie504087z. [DOI] [Google Scholar]

[bib76] 76.Malkani H., Korambath P. Clean energy smart manufacturing innovation institute (CESMII) special issue. J. Adv. Manuf. Process. 2022;4:e10146. doi: 10.1002/amp2.10146. [DOI] [Google Scholar]

[bib77] 77.Brunner Z. NIST; 2022. Manufacturing USA Highlights Report 2022. [Google Scholar]

[bib78] 78.Arden N.S., Fisher A.C., Tyner K., Yu L.X., Lee S.L., Kopcha M. Industry 4.0 for pharmaceutical manufacturing: preparing for the smart factories of the future. Int. J. Pharm. 2021;602:120554. doi: 10.1016/j.ijpharm.2021.120554. [DOI] [PubMed] [Google Scholar]

[bib79] 79.Vogel-Heuser B., Rösch S., Martini A., Tichy M. 2015 IEEE 7th International Workshop on Managing Technical Debt (MTD) 2015. Technical Debt in Automated Production Systems; pp. 49–52. [DOI] [Google Scholar]

[bib80] 80.Martini A., Bosch J. Chapter 4. John Wiley & Sons, Ltd; 2019. pp. 77–103. (Architectural Technical Debt in Embedded System). [DOI] [Google Scholar]

[bib81] 81.Kravchenko A. Workforce training and management challenges in the contemporary smart manufacturing (SM) Intel. Arch. 2019;8:59–65. doi: 10.32370/IA_2019_02_9. [DOI] [Google Scholar]

[bib82] 82.Çıtmacı B., Luo J., Jang J.B., Korambath P., Morales-Guio C.G., Davis J.F., Christofides P.D. Digitalization of an experimental electrochemical reactor via the smart manufacturing innovation platform. Digit. Chem. Eng. 2022;5:100050. doi: 10.1016/j.dche.2022.100050. [DOI] [Google Scholar]

[bib83] 83.Richard D., Tom M., Jang J., Yun S., Christofides P.D., Morales-Guio C.G. Quantifying transport and electrocatalytic reaction processes in a gastight rotating cylinder electrode reactor via integration of computational fluid dynamics modeling and experiments. Electrochim. Acta. 2023;440:141698. doi: 10.1016/j.electacta.2022.141698. [DOI] [Google Scholar]

[bib84] 84.Pangarkar V.G. Chapter 5: Principles of similarity and their application for scale up. John Wiley & Sons, Ltd.; 2014. Design of Multiphase Reactors; pp. 93–105. [DOI] [Google Scholar]

[bib85] 85.Abolhasani M., Kumacheva E. The rise of self-driving labs in chemical and materials sciences. Nat. Synth. 2023:1–10. doi: 10.1038/s44160-022-00231-0. [DOI] [Google Scholar]

[bib86] 86.Vriza A., Chan H., Xu J. Self-driving laboratory for polymer electronics. Chem. Mater. 2023;35:3046–3056. doi: 10.1021/acs.chemmater.2c03593. [DOI] [Google Scholar]

[bib87] 87.Mennen S.M., Alhambra C., Allen C.L., Barberis M., Berritt S., Brandt T.A., Campbell A.D., Castañón J., Cherney A.H., Christensen M., et al. The evolution of high-throughput experimentation in pharmaceutical development and perspectives on the future. Org. Process Res. Dev. 2019;23:1213–1242. doi: 10.1021/acs.oprd.9b00140. [DOI] [Google Scholar]

[bib88] 88.Tao H., Wu T., Kheiri S., Aldeghi M., Aspuru-Guzik A., Kumacheva E. Self-driving platform for metal nanoparticle synthesis: combining microfluidics and machine learning. Adv. Funct. Mater. 2021;31:2106725. doi: 10.1002/adfm.202106725. [DOI] [Google Scholar]

[bib89] 89.Çıtmacı B., Luo J., Jang J.B., Morales-Guio C.G., Christofides P.D. Machine learning-based ethylene and carbon monoxide estimation, real-time optimization, and multivariable feedback control of an experimental electrochemical reactor. Chem. Eng. Res. Des. 2023;191:658–681. doi: 10.1016/j.cherd.2023.02.003. [DOI] [Google Scholar]

[bib90] 90.Goldsmith B.R., Esterhuizen J., Liu J.-X., Bartel C.J., Sutton C. Machine learning for heterogeneous catalyst design and discovery. AIChE J. 2018;64:2311–2323. doi: 10.1002/aic.16198. [DOI] [Google Scholar]

[bib91] 91.Angulo A., Yang L., Aydil E.S., Modestino M.A. Machine learning enhanced spectroscopic analysis: towards autonomous chemical mixture characterization for rapid process optimization. Digit. Discov. 2022;1:35–44. doi: 10.1039/D1DD00027F. [DOI] [Google Scholar]

[bib92] 92.MacLeod B.P., Parlane F.G.L., Morrissey T.D., Häse F., Roch L.M., Dettelbach K.E., Moreira R., Yunker L.P.E., Rooney M.B., Deeth J.R., et al. Self-driving laboratory for accelerated discovery of thin-film materials. Sci. Adv. 2020;6:eaaz8867. doi: 10.1126/sciadv.aaz8867. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib93] 93.Reizman B.J., Jensen K.F. An automated continuous-flow platform for the estimation of multistep reaction kinetics. Org. Process Res. Dev. 2012;16:1770–1782. doi: 10.1021/op3001838. [DOI] [Google Scholar]

[bib94] 94.Luo J., Canuso V., Jang J.B., Wu Z., Morales-Guio C.G., Christofides P.D. Machine learning-based operational modeling of an electrochemical reactor: handling data variability and improving empirical models. Ind. Eng. Chem. Res. 2022;61:8399–8410. doi: 10.1021/acs.iecr.1c04176. [DOI] [Google Scholar]

[bib95] 95.Wu Z., Tran A., Rincon D., Christofides P.D. Machine learning-based predictive control of nonlinear processes Part I: Theory. AIChE J. 2019;65:e16729. doi: 10.1002/aic.16729. [DOI] [Google Scholar]

[bib96] 96.Wu Z., Luo J., Rincon D., Christofides P.D. Machine learning-based predictive control using noisy data: evaluating performance and robustness via a large-scale process simulator. Chem. Eng. Res. Des. 2021;168:275–287. doi: 10.1016/j.cherd.2021.02.011. [DOI] [Google Scholar]

[bib97] 97.Xavier M.A., Trimboli M.S. Lithium-ion battery cell-level control using constrained model predictive control and equivalent circuit models. J. Power Sources. 2015;285:374–384. doi: 10.1016/j.jpowsour.2015.03.074. [DOI] [Google Scholar]

[bib98] 98.Denn M. Prentice-Hall; 1980. Process Fluid Mechanics. [Google Scholar]

[bib99] 99.Santhanagopalan S. Electrochemical Systems - Scaling, Dimensionless Groups; Springer New York: 2014. Encyclopedia of Applied Electrochemistry; pp. 634–640. [DOI] [Google Scholar]

[bib100] 100.Oppenheimer M.W., Doman D.B., Merrick J.D. Multi-scale physics-informed machine learning using the Buckingham Pi theorem. J. Comput. Phys. 2023;474:111810. doi: 10.1016/j.jcp.2022.111810. [DOI] [Google Scholar]

[bib101] 101.Xie X., Samaei A., Guo J., Liu W.K., Gan Z. Data-driven discovery of dimensionless numbers and governing laws from scarce measurements. Nat. Commun. 2022;13:7562. doi: 10.1038/s41467-022-35084-w. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib102] 102.Chen H., Batchelor-McAuley C., Kätelhön E., Elliott J., Compton R.G. A critical evaluation of using physics-informed neural networks for simulating Voltammetry: strengths, weaknesses and best practices. J. Electroanal. Chem. 2022;925:116918. doi: 10.1016/j.jelechem.2022.116918. [DOI] [Google Scholar]

[bib103] 103.Tu Y.-J., Delmerico S., McDaniel J.G. Inner layer capacitance of organic electrolytes from constant voltage molecular dynamics. J. Phys. Chem. C. 2020;124:2907–2922. doi: 10.1021/acs.jpcc.0c00299. [DOI] [Google Scholar]

[bib104] 104.Kong S., Lv X., Wang X., Liu Z., Li Z., Jia B., Sun D., Yang C., Liu L., Guan A., et al. Delocalization state-induced selective bond breaking for efficient methanol electrosynthesis from CO2. Nat. Catal. 2022;6:6–15. doi: 10.1038/s41929-022-00887-z. [DOI] [Google Scholar]

[bib105] 105.Micale D., Ferroni C., Uglietti R., Bracconi M., Maestri M. Computational fluid dynamics of reacting flows at surfaces: methodologies and applications. Chem. Ing. Tech. 2022;94:634–651. doi: 10.1002/cite.202100196. [DOI] [Google Scholar]

[bib106] 106.Zhu L.-T., Chen X.-Z., Ouyang B., Yan W.-C., Lei H., Chen Z., Luo Z.-H. Review of machine learning for hydrodynamics, transport, and reactions in multiphase flows and reactors. Ind. Eng. Chem. Res. 2022;61:9901–9949. doi: 10.1021/acs.iecr.2c01036. [DOI] [Google Scholar]

PERMALINK

Smart manufacturing inspired approach to research, development, and scale-up of electrified chemical manufacturing systems

Derek Richard

Joonbaek Jang

Berkay Çıtmacı

Junwei Luo

Vito Canuso

Prakashan Korambath

Olivia Morales-Leslie

James F Davis

Haresh Malkani

Panagiotis D Christofides

Carlos G Morales-Guio

Summary

Graphical abstract

Introduction

Figure 1.

Challenges in existing approach to RD&D of CO2 electrolyzers

Figure 2.

Figure 3.

Smart manufacturing background and context for applications in scale-up research

Framework for a smart manufacturing inspired approach to RD&D

Figure 4.

Lab-scale reactor selection for CO2 reduction research

Application of automation and connectivity for enhanced data collection and processing

Figure 5.

Application of machine learning to lab-scale reactor modeling and control

Figure 6.

Benefits of machine learning for scale-up research

Understanding underlying relationships through dimensional analysis

Table 1.

Figure 7.

Multi-scale modeling aided research and design

Figure 8.

Conclusions

Acknowledgments

Author contributions

Declaration of interests

Inclusion and diversity

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Challenges in existing approach to RD&D of CO₂ electrolyzers

Lab-scale reactor selection for CO₂ reduction research