Data-driven choice of a model selection method in joinpoint regression

Abstract

Selecting the number of change points in segmented line regression is an important problem in trend analysis, and there have been various approaches proposed in the literature. We first study the empirical properties of several model selection procedures and propose a new method based on two Schwarz type criteria, a classical Bayes Information Criterion (BIC) and the one with a harsher penalty than BIC ( ${\text{BIC}}_3$). The proposed rule is designed to use the former when effect sizes are small and the latter when the effect sizes are large and employs the partial $R^2$ to determine the weight between BIC and ${\text{BIC}}_3$. The proposed method is computationally much more efficient than the permutation test procedure that has been the default method of Joinpoint software developed for cancer trend analysis, and its satisfactory performance is observed in our simulation study. Simulations indicate that the proposed method performs well in keeping the probability of correct selection at least as large as that of ${\text{BIC}}_3$, whose performance is comparable to that of the permutation test procedure, and improves ${\text{BIC}}_3$ when it performs worse than $\text{BIC}.$ The proposed method is applied to the U.S. prostate cancer incidence and mortality rates.

1. Introduction

An important question in trend analysis is to determine if there are changes in the trend, their locations, and the direction and magnitude of the trend changes. To identify changes in cancer incidence and mortality trends, Kim et al. [11] considered a piecewise linear regression model to describe continuous changes in cancer trends and proposed the permutation procedure where the permutation tests were sequentially conducted to determine the number of changes in the trend, that is, the number of segments or change-points. Another model selection procedure widely used in practice is the approach based on information criteria. Akaike Information Criterion (AIC) of Akaike [1] and Bayes (or Bayesian) Information Criterion (BIC) proposed by Schwarz [24] are the two classical information-based selection criteria, and various types of modifications have been proposed in the literature. In the context of change-point problems, Liu et al. [18], Pan and Chen [23], Zhang and Siegmund [39] and Lee and Chen [16] proposed modified Schwarz type criteria and studied their empirical and asymptotic properties. For further details on selecting the number of change-points, see Haccou and Meelis [9] and Bai and Perron [2] for hypothesis testing approaches, and Yao [38], Tiwari et al. [29], Wu [37], Lu et al. [19], Hannart and Naveau [10], Ciuperca [5], and Ninomiya [22] for various approaches based on information-based criteria.

The model selection method proposed in Kim et al. [11] and related inference procedures are implemented in Joinpoint software, developed by a team at the U.S. National Cancer Institute (NCI) and first released in 1998. The permutation test procedure has been the default model selection method of Joinpoint software and various BIC type procedures have been implemented in later versions to determine the number of change-points, called joinpoints in Kim et al. [11]. The permutation test procedure has been successfully applied in cancer trend analysis, where our goal is often to find a most parsimonious model, but its main drawback was the intensive computation needed in a series of resampling tests, especially for long series data. Various BIC type methods have been introduced as more efficient model selection procedures, but detailed comparisons of these model selection procedures in the context of segmented regression have not been available in the literature. More importantly, a need to develop an automated procedure to internally determine a selection method has arisen to assist users for more efficient model selection.

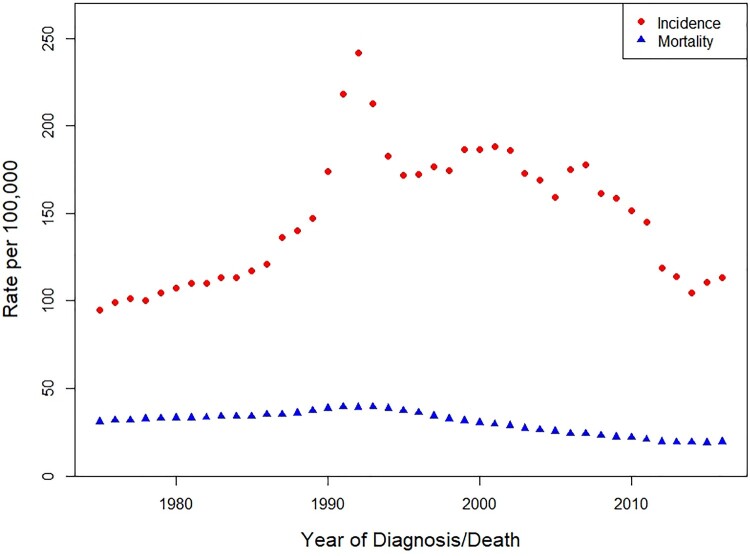
Figure 1 shows prostate cancer incidence and mortality rates during the period of 1975–2016 for males in the United States. The incidence rates are obtained from the Surveillance, Epidemiology, and End Results (SEER) population-based cancer registry program of the U.S. NCI, and Figure 1 shows the delay-adjusted incidence rates based on the nine SEER registries that cover approximately 9.4% of the U.S. population [36]. The U.S. mortality rates presented in Figure 1 are from the U.S. National Center for Health Statistics. In 2012, the U.S. Preventive Services Task Force concluded that, although there are potential benefits of screening for prostate cancer, these benefits do not outweigh the expected harms enough to recommend routine screening (D recommendation) [8,21]. Probably as a result of this recommendation, the proportion of men getting a Prostate Specific Antigen (PSA) test fell in 2013 from the 2010 proportion [31]. There was an intense interest in the impact of this fall in PSA testing on prostate cancer incidence and mortality, and the data in Figure 1 show signs that changes are occurring, but objective criteria are needed.

Figure 1.

Prostate incidence (SEER 9 delay-adjusted) and US mortality rates: 1975–2016.

As to be shown in the simulation study and the example section, the numbers of the segments estimated by various methods are not all equal and the performance of each method depends on data characteristics. Motivated by such findings, our aim in this paper is to study the empirical properties of several model selection procedures in joinpoint regression, the segmented line regression model with continuity constraints, and propose a new procedure that combines two Schwarz type criteria, BIC and ${\text{BIC}}_3$, based on the characteristics of data. The proposed data-driven selection procedure will be computationally less intensive than the permutation procedure, while its performance (in terms of correctly determining the number of change-points in simulation examples) is competitive as ${\text{BIC}}_3$ that performs similarly as the permutation procedure and it improves ${\text{BIC}}_3$ when the performance of ${\text{BIC}}_3$ is not satisfactory. More specifically, for the cases where the procedures have practically reasonable power, the new procedure will be shown to perform well in terms of the probability of correct selection while it controls the over-fitting probability as the permutation procedure does.

In Section 2, we introduce the joinpoint regression model and summarize several model selection methods that have been available in Joinpoint software, the permutation test procedure, BIC, ${\text{BIC}}_3$, and a modified BIC. Section 3 summarizes the simulation study to compare the performance of these model selection methods and considers a measure that can guide a data-driven choice of a model selection method. In Section 4, we propose a weighted BIC that combines $\text{BIC}$ and ${\text{BIC}}_3$ based on the data characteristics and present the results from further simulation studies. Section 5 includes examples, followed by concluding remarks in Section 6.

2. Model and selection procedures

Consider the n pairs of observations, $(x_1,y_1),\dots ,(x_n,y_n)$, and the joinpoint regression model such that for $i=1,\dots ,n$,

$$y_i={\mathrm{\text{β}}}_0+{\mathrm{\text{β}}}_1{x}_i+{\delta }_1(x_i-{\tau }_1{)}^{+}+\cdots +{\delta }_{\kappa }(x_i-{\tau }_{\kappa }{)}^{+}+{ϵ}_i,$$

where $a^{+}=max(a,0),$ the τ's are unknown joinpoints, κ is the unknown number of joinpoints, and the ${ϵ}_i$ are independent and identically distributed errors with mean zero and variance ${\sigma }^2$. Typically in trend analysis, the $x_i$ are the equally spaced time points.

Kim et al. [11] used the least-squares method to fit the model with a given number of joinpoints, say k, first by minimizing $\sum _{i=1}^n(y_i-{\mathrm{\text{β}}}_0-{\mathrm{\text{β}}}_1{x}_i-{\delta }_1(x_i-t_1{)}^{+}-\cdots -{\delta }_k(x_i-t_k){)}^2$ at given $\text{t}=(t_1,\dots ,t_k{)}^{\prime }$ and then by searching for the minimum sum of squared errors over all possible locations of joinpoints $t$, and proposed the permutation test procedure (Perm) to select the number of joinpoints. The model fitting and inference procedures were implemented in Joinpoint software that has been widely used for trend analyses and is available at the U. S. NCI website [35]. The default method of Joinpoint to estimate the joinpoints at given k, ${\tau }_k=({\tau }_1,\dots ,{\tau }_k{)}^{\prime }$, is the grid search originally proposed by Lerman [17], and Joinpoint software provides the confidence intervals of the model parameters and relevant p-values using both parametric and resampling approaches ([13,14]). The permutation test procedure that has been the default model selection method of Joinpoint software starts with testing the null hypothesis that there are ${\text{JP}}_{min}$ joinpoints against the alternative hypothesis that there are ${\text{JP}}_{max}$ joinpoints for pre-determined values of ${\text{JP}}_{min}$ and ${\text{JP}}_{max}$. Then, it conducts the test of ${\text{JP}}_{min}$ joinpoints versus ${\text{JP}}_{max}-1$ joinpoints if the null hypothesis is not rejected and proceeds to the test of ${\text{JP}}_{min}+1$ joinpoints versus ${\text{JP}}_{max}$ joinpoints otherwise. The procedure repeatedly conducts the test of $k_0$ joinpoints against $k_1$ joinpoints, where $k_1>k_0$, until we reach to the test of k joinpoints versus k + 1 joinpoints for some k, ( ${\text{JP}}_{min}\le k<{\text{JP}}_{max}$). The P-value of each test in this multiple testing procedure is estimated by using the permutation distribution of the F-type statistics under the null hypothesis because classical asymptotic theory is not applicable. Also, the significance level of the test where the null hypothesis states $k_0$ joinpoints is set at $\alpha /({\text{JP}}_{max}-k_0)$, which would control the over-fitting probability under α. See Kim et al. [11,15] for further details.

Bayes or Bayesian Information Criterion (BIC) and a modified version of BIC have been considered/implemented in later versions of Joinpoint software. The BIC is first proposed by Schwarz [24] as a large sample version of Bayes procedure, and its basic idea is to choose the model that maximizes $\log \left(M_j\right)-\frac{k_j}{2}\log n$, where $M_j$ is the maximized likelihood function and $k_j$ is the dimension for the jth model. Under the normal distribution and using that the number of unknown parameters for the joinpoint regression model with k joinpoints is $2k+3,$ the following BIC can be considered as a classical form of the BIC:

$$\text{BIC}\left(k\right)=\log \left(\frac{{\text{RSS}}_k}{n}\right)+\frac{2k}{n}\log n,$$

where ${\text{RSS}}_k$ denotes the residual sum of squares for the model fit with k joinpoints, and the model that minimizes $\text{BIC}\left(k\right)$ will be selected. Kim et al. [15] applied BIC in the context of joinpoint regression and their simulation study indicated that BIC is more liberal (i.e. choose a model with more joinpoints) than the permutation test procedure with an overall significance level of 0.05. As discussed in Ding et al. [7] and presented in Shao [26] for a variable selection in linear models, BIC is known to select the model consistently when the true model belongs to a set of candidate models and is often recommended as a model selection method in a parametric framework. Zhang and Siegmund [39], however, noted that ‘the classical BIC does not work well’ in change-point problems where ‘the likelihood functions do not satisfy the required regularity conditions’ and proposed a modified BIC to detect multiple changes in means of a sequence of random variables. They noted that the penalty term of their criterion derived by approximating the Bayes factor reflects one dimension for each mean change and between one and two dimensions for each change-point based on the change-point locations. The penalty term of their modified BIC for a model with k change-points is ‘maximized when the change-points are equally spaced and minimized when the change-points are as close as possible’. Pan and Chen [23] also indicated that the locations of change-points play a role in assessing the model complexity and proposed a modification of the traditional BIC that incorporates the spacing between the change-points. They considered that ‘the model is unnecessarily complex’ when the change-points are clustered, which is due to some of the parameters becoming redundant and incorporated an additional penalty corresponding to the locations of change-points. For multi-phase regression, Liu et al. [18] proposed a modified information criterion (MIC) with a penalty much harsher than that of the traditional BIC and the logarithm of the mean squared error as the first term, and proved its consistency under mild assumptions on non-Gaussian errors.

Motivated by such findings mentioned above, a modified BIC (MBIC) was derived for the selection of a joinpoint regression model following the similar arguments of Zhang and Siegmund [39] and implemented in Joinpoint software. The MBIC reflects the adjustment corresponding to the locations of the joinpoints, and its detail can be found at the U.S. NCI Joinpoint Help site [34]. Kim and Kim [12] studied the asymptotic properties of these Schwarz type model selection criteria in selecting the number of change-points in segmented line regression with normally distributed errors. When the neighboring segments are not constrained to be continuous at the change-point (i.e. the number of parameters is 3k + 3 for the model with k change-points) Kim and Kim [12] proved that the number of change-points estimated by ${\text{BIC}}_4,$ defined by ${\text{BIC}}_4\left(k\right)=\log \left(\frac{{\text{RSS}}_k}{n}\right)+\frac{4k}{n}\log n,$ is a consistent estimator of the true number of change-points. For the situation where the segments are assumed to be continuous at the change-point (i.e. the number of parameters is 2k + 3 for the model with k change-points) they provided empirical evidence that ${\text{BIC}}_3,$ defined by ${\text{BIC}}_3\left(k\right)=\log \left(\frac{{\text{RSS}}_k}{n}\right)+\frac{3k}{n}\log n,$ performs similarly as MIC of Liu et al. [18] and is expected to work as a consistent model selection rule. Based on such empirical properties and that the penalty term of MBIC is asymptotically equivalent to (respectively, smaller than) $\frac{3k}{n}\log n$ for k greater than or equal to (respectively, smaller) the true number of joinpoints under some conditions on the spacings of the x's, ${\text{BIC}}_3$ is also considered in this paper.

3. Comparison of model selection procedures

Simulation studies were conducted to compare the performance of the model selection procedures reviewed in Section 2, and the results are summarized in this section. Table 1 summarizes the performance of Perm, BIC, ${\text{BIC}}_3$, and MBIC for various cases. The simulations were conducted for $\kappa =1,\dots ,5$ with various values of ${\tau }_{\kappa }=({\tau }_1,\dots ,{\tau }_{\kappa }{)}^{\prime }$, ${\delta }_{\kappa }=({\delta }_1,\dots ,{\delta }_{\kappa }{)}^{\prime }$ and σ, and the following common setting was used: ${\mathrm{\text{β}}}_0=1$, ${\mathrm{\text{β}}}_1=0.01,$ $n=30,$ and $x=1,2,\dots ,30$. This moderate size of the sample, n = 30, was used considering the number of time points often observed in cancer trend analysis, and the parameter settings are also chosen based on examples in cancer incidence and mortality trend changes. In the simulation study, data are generated with the ϵ independent and identically distributed according to the normal distribution with mean zero and variance ${\sigma }^2$, and the model selection was conducted with ${\text{JP}}_{min}$ set as 0 and ${\text{JP}}_{max}$ set as 5. The number of simulations was 1600, and the number of permutations for the permutation procedure was 319, which was chosen according to the suggestion of Boos and Zhang [3].

Table 1.

Probability of Correct Selection.

Case	$({\tau }_1,\dots ,{\tau }_{\kappa })$	$({\delta }_1,\dots ,{\delta }_{\kappa })$	σ	Perm	MBIC	BIC	${\text{BIC}}_3$	WBIC	${\mathrm{\Delta }}^{\ast }$	$min\left|{\delta }_i\right|/\sigma$
$\kappa =1$
1-1-i-a	5	−0.02	0.03	0.379	0.089	0.643	0.456	0.644	8.248	0.67
1-1-i-b			0.01	0.973	0.997	0.863	0.973	0.967	74.231	2
1-2-i-a	10	−0.02	0.03	0.969	0.911	0.864	0.963	0.950	40.593	0.67
1-2-i-b			0.01	0.976	1	0.836	0.963	0.947	365.339	2
1-3-i-a	15	−0.02	0.03	0.976	0.992	0.841	0.966	0.934	62.43	0.67
1-3-i-b			0.01	0.971	1	0.81	0.956	0.939	561.869	2
1-4-i-a	25	−0.02	0.03	0.638	0.259	0.785	0.709	0.837	13.398	0.67
1-4-i-b			0.01	0.974	1	0.849	0.968	0.961	120.578	2
$\kappa =2$
2-1-i-a	(10, 20)	(0.02, 0.03)	0.03	0.619	0.202	0.744	0.717	0.788	18.471	0.67
2-1-i-b			0.01	0.975	1	0.782	0.95	0.933	166.241	2
2-1-ii-a		(−0.02, 0.03)	0.03	0.823	0.338	0.822	0.882	0.884	18.471	0.67
2-1-ii-b			0.01	0.979	0.999	0.791	0.949	0.935	166.241	2
2-2-i-a	(5,10)	(0.02, 0.03)	0.03	0.057	0.002	0.22	0.083	0.130	2.29	0.67
2-2-i-b			0.01	0.748	0.314	0.81	0.844	0.863	20.606	2
2-2-ii-a		(−0.02, 0.03)	0.03	0.082	0.014	0.286	0.113	0.171	2.29	0.67
2-2-ii-b			0.01	0.818	0.477	0.833	0.899	0.905	20.606	2
2-3-i-a	(20, 25)	(0.02, 0.03)	0.03	0.098	0.009	0.318	0.151	0.207	5.151	0.67
2-3-i-b			0.01	0.954	0.8	0.836	0.951	0.947	46.364	2
2-3-ii-a		(−0.02, 0.03)	0.03	0.326	0.006	0.524	0.263	0.384	5.151	0.67
2-3-ii-b			0.01	0.975	0.984	0.824	0.957	0.957	46.364	2
2-4-i-a	(10, 15)	(0.02, 0.03)	0.03	0.112	0.006	0.351	0.173	0.285	6.31	0.67
2-4-i-b			0.01	0.958	0.807	0.801	0.954	0.944	56.786	2
2-4-ii-a		(−0.02, 0.03)	0.03	0.305	0.059	0.558	0.378	0.495	6.31	0.67
2-4-ii-b			0.01	0.973	0.99	0.806	0.957	0.952	56.786	2
$\kappa =3$
3-1-i-a	(7, 15, 23)	(−0.02, −0.03, 0.04)	0.03	0.211	0.023	0.505	0.287	0.392	7.467	0.67
3-1-i-b			0.01	0.966	0.979	0.76	0.941	0.932	67.2	2
3-1-ii-a		(−0.03, 0.04, −0.02)	0.03	0.471	0.043	0.706	0.566	0.567	7.881	0.67
3-1-ii-b			0.01	0.964	0.999	0.741	0.939	0.924	70.933	2
3-2-i-a	(10, 20, 23)	(−0.02, −0.03, 0.04)	0.03	0.121	0.001	0.313	0.122	0.194	3.922	0.67
3-2-i-b			0.01	0.968	0.893	0.813	0.955	0.944	35.297	2
3-2-ii-a		(−0.03, 0.04 −0.02)	0.03	0.092	0.003	0.269	0.121	0.129	0.98	0.67
3-2-ii-b			0.01	0.744	0.334	0.76	0.853	0.831	8.824	2
3-3-i-a	(7, 10, 20)	(−0.02, −0.03, 0.04)	0.03	0.034	0.003	0.199	0.064	0.085	1.772	0.67
3-3-i-b			0.01	0.366	0.071	0.654	0.569	0.574	15.952	2
3-3-ii-a		(−0.03, 0.04, −0.02)	0.03	0.156	0	0.371	0.139	0.190	3.988	0.67
3-3-ii-b			0.01	0.957	0.851	0.809	0.951	0.943	35.891	2
$\kappa =4$
4-1-i-a	(6, 12,	(−0.05, 0.02,	0.03	0.068	0.001	0.263	0.094	0.111	3.97	0.67
4-1-i-b	18, 24)	0.03, 0.04)	0.01	0.946	0.74	0.801	0.946	0.936	35.734	2
4-1-ii-a		(−0.02, 0.05,	0.03	0.201	0.001	0.451	0.2	0.230	3.97	0.67
4-1-ii-b		-0.04, 0.03)	0.01	0.948	0.84	0.798	0.941	0.933	35.734	2
4-2-i-a	(7, 14,	(−0.05, 0.02,	0.03	0.033	0.001	0.188	0.051	0.061	3.526	0.67
4-2-i-b	21, 28)	0.03, 0.04)	0.01	0.935	0.768	0.813	0.943	0.933	31.733	2
4-2-ii-a		(−0.02, 0.05,	0.03	0.084	0.001	0.237	0.089	0.100	1.983	0.67
4-2-ii-b		−0.04, 0.03)	0.01	0.817	0.454	0.797	0.881	0.874	17.85	2
4-3-i-a	(3, 10,	(−0.05, 0.02,	0.03	0.126	0.001	0.331	0.108	0.131	6.128	0.67
4-3-i-b	17, 24)	0.03, 0.04)	0.01	0.956	0.7	0.779	0.948	0.937	55.152	2
4-3-ii-a		(−0.02, 0.05,	0.03	0.067	0.001	0.216	0.086	0.094	0.98	0.67
4-3-ii-b		−0.04, 0.03)	0.01	0.432	0.103	0.656	0.564	0.559	8.824	2

Table 1 lists the probability of correct selection (PCS) by each selection method under given parameter settings, and the case number ‘k-l-m-a’ indicates the case with ‘k’ joinpoints, the joinpoint location setting of ‘l’, the $\delta$ setting of ‘m’, and the σ setting of ‘a’. More cases were considered in our simulation study, but to save a space, Table 1 does not include the cases whose results imply similar findings as those included in Table 1 as well as those with $\kappa =5$ where over-fitting is not allowed. The table also includes the values of ${\mathrm{\Delta }}^{\ast }$ and $min|{\delta }_i|/\sigma ,$ which are the measures of effect sizes, i.e. sizes of slope changes adjusted for the variability in data, and whose details will be provided below. The full result available upon request includes 195 cases for $\kappa =1,2,3,4,$ and 5 and 159 cases for $\kappa =1,2,3$ and 4, and it indicates the followings:

1. BIC performs better than other procedures when the effect size, measured by $|{\delta }_i|/\sigma$ and/or ${\mathrm{\Delta }}^{\ast }$, is small, while Perm, ${\text{BIC}}_3$, and MBIC work better to correctly detect changes of relatively larger effect sizes. When the effect size is large enough to have the PCS by BIC larger than 0.8 among the 159 cases, the PCS values of Perm and ${\text{BIC}}_3$ are greater than those of BIC in general.

2. MBIC is most conservative with a tendency to choose a smaller model and works best when the effect size is very large. In the 16 cases where MBIC has the highest PCS, the performance of ${\text{BIC}}_3$ and/or Perm is usually satisfactory enough with its PCS larger than 0.94.

3. ${\text{BIC}}_3$ is most comparable to Perm, with the median difference of their PCS values being 0.008 over the 159 differences, PCS( ${\text{BIC}}_3$)-PCS(Perm). When either Perm has the highest PCS (15 such cases) or PCS(Perm) $>0.7$ and PCS(Perm)>PCS( ${\text{BIC}}_3$) (30 such cases), the difference between their PCS values, i.e. PCS( ${\text{BIC}}_3$)-PCS(Perm), is in the range of -0.043 and -0.003.

4. The performances of the selection procedures, in terms of PCS, depend on the locations of the joinpoints, and MBIC seems to depend more heavily, compared to other selection methods, which is expected from the penalty term of MBIC that reflects the locations of the joinpoints.

5. Although not reported in Table 1, BIC showed a tendency to overestimate the number of joinpoints when the effect size is relatively large, and BIC produced the highest PCS in most cases with $\kappa =5$, which can be explained by that the over-estimation was not possible with the maximum number of joinpoints set at 5.

Thus, it would be ideal to use BIC when effect sizes are small and use Perm/ ${\text{BIC}}_3$ when effect sizes are large, but the estimation of effect size depends on the model, i.e. the number of joinpoints. Our goal in this paper is to develop an automated and computationally efficient procedure to internally choose one of these selection methods or combine these methods based on the characteristics of data. Because Perm is computationally intensive and the performance of MBIC does not seem to be consistent in our simulation studies, our focus of the study to propose a data-driven selection procedure would be on BIC and ${\text{BIC}}_3$.

In order to study further details of BIC and ${\text{BIC}}_3$, we note that the probability of correct selection depends on the effect size, and the following measure of effect size, $\mathrm{\Delta }\left(k\right),$ is considered as a minimum effect size of the model with k joinpoints. This measure is motivated by the measure on which the power of the test to detect a slope change of δ from a simple linear regression model depends. More specifically, consider the test of the null hypothesis that there is no change in the regression mean function, $H_0:E\left(y\right)=X\mathrm{\text{β}}$, against the alternative hypothesis that there is one joinpoint at known τ, $H_a:E\left(y\right)=X\mathrm{\text{β}}+\delta z$, where $y=(y_1,\dots ,y_n{)}^{\prime },$ $\mathrm{\text{β}}=({\mathrm{\text{β}}}_0,{\mathrm{\text{β}}}_1{)}^{\prime },$ $z=\left(\right(x_1-\tau {)}^{+},\dots ,(x_n-\tau {)}^{+}{)}^{\prime },$ and $X=\left(\begin{array}{cc}1& x_1\\ ⋮& ⋮\\ 1& x_n\end{array}\right).$ And, consider the F-type statistic,

$$F=\frac{{\text{RSS}}_0-{\text{RSS}}_a}{{\text{RSS}}_a/(n-3)},$$

where ${\text{RSS}}_0$ and ${\text{RSS}}_a$ are the residual sums of squares under $H_0$ and $H_a$, respectively. Under $H_a$, we see that ${\text{RSS}}_a/(n-3)$ converges to ${\sigma }^2$ and $E\left[{\text{RSS}}_0\right]-E\left[{\text{RSS}}_a\right]={\sigma }^2+{\delta }^2{z}^{\prime }(I-X(X^{\prime }X{)}^{-1}{X}^{\prime })z$ (See Seber and Lee [25, P 229]) which motivated the use of

$$\mathrm{\Delta }=\frac{{\delta }^2{\mathit{z}}^{\prime }(\mathit{I}-\mathit{X}({\mathit{X}}^{\prime }\mathit{X}{)}^{-1}{\mathit{X}}^{\prime })\mathit{z}}{{\sigma }^2}$$

as an effect size. Now, we consider a sample measure of Δ over the two segments of a joinpoint regression fit and propose the minimum of those values as the observed effect size. Suppose that a model with k joinpoints is selected by BIC (or ${\text{BIC}}_3$) for which the parameters are estimated as ${\hat{\tau }}_1,\dots ,{\hat{\tau }}_k$, ${\widehat{\mathrm{\text{β}}}}_0,{\widehat{\mathrm{\text{β}}}}_1,{\hat{\delta }}_1,\dots ,{\hat{\delta }}_k.$ For the observations in the i-th and $(i+1)$-st segments, that is, those observations whose x values are in $({\hat{\tau }}_{i-1},{\hat{\tau }}_{i+1}]$ where ${\hat{\tau }}_0=min{x}_i-1$ and ${\hat{\tau }}_{k+1}=max{x}_i$, call such x's as $x_{j_1+1},\dots ,x_{j_2}$ and let $X_0=\left(\begin{array}{cc}1& x_{j_1+1}\\ ⋮& ⋮\\ 1& x_{j_2}\end{array}\right)$, $z_i=\left(\begin{array}{c}(x_{j_1+1}-{\hat{\tau }}_i{)}^{+}\\ ⋮\\ (x_{j_2}-{\hat{\tau }}_i{)}^{+}\end{array}\right)$, and $H_0=X_0(X_0^{\prime }{X}_0{)}^{-1}{X}_0^{\prime }$. Let ${\mathrm{\Delta }}_{i,i+1}={\hat{\delta }}_i^2{z}_i^{\prime }(I-H_0)z_i/{\tilde{\sigma }}^2,$ where ${\tilde{\sigma }}^2$ is the mean squared error estimated for $\kappa ={\text{JP}}_{max}$ and define

$$\mathrm{\Delta }\left(k\right)=\underset{i=1,\dots ,k}{min}{\mathrm{\Delta }}_{i,i+1}.$$

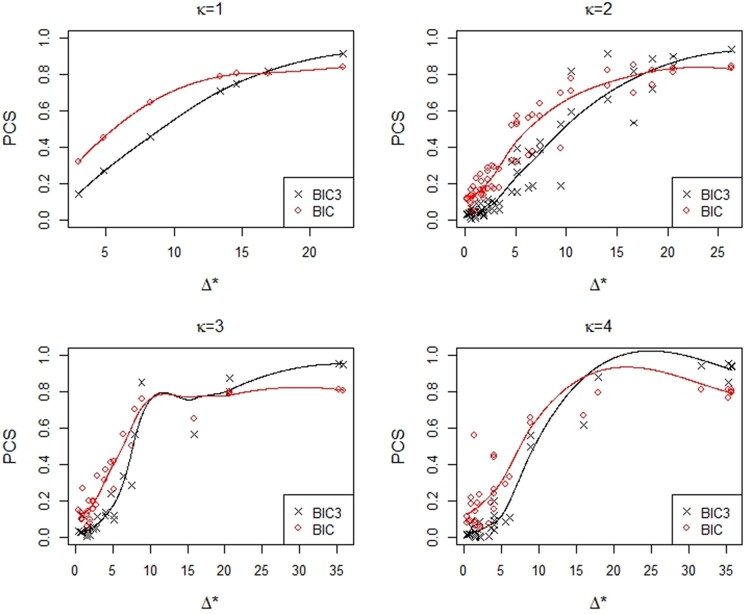
If $k^{\ast }$ is the true number of joinpoints and ${\mathrm{\Delta }}^{\ast }$ is the value of $\mathrm{\Delta }\left(k^{\ast }\right)$ with the true parameter values given for the model with $k^{\ast }$ joinpoints, then the rule to use BIC when ${\mathrm{\Delta }}^{\ast }\le 10$ and ${\text{BIC}}_3$ when ${\mathrm{\Delta }}^{\ast }>20$ was observed to perform satisfactorily in our simulation study. This observation is based on the 159 simulation cases with $\kappa =1,2,3$ or 4, a part of which is summarized in Table 1, and the cut-off values of 10 and 20, which can be adjusted to numbers between 10 and 20, are based on the empirical data shown in Figure 2. Figure 2 presents the PCS values of BIC and ${\text{BIC}}_3$ for the 131 cases where ${\mathrm{\Delta }}^{\ast }<40.$ For the remaining 28 cases with ${\mathrm{\Delta }}^{\ast }\ge 40$, their PCS values by ${\text{BIC}}_3$ were all higher than those of BIC and so these cases are not included in Figure 2 for a clearer comparison of the results when ${\mathrm{\Delta }}^{\ast }<40.$ Note that Figure 2 also includes smoothed curves of the PCS values for each selection method, BIC and ${\text{BIC}}_3,$ which can be helpful in visualizing how the PCS depends on ${\mathrm{\Delta }}^{\ast }.$ Although ${\mathrm{\Delta }}^{\ast }$ provides a useful guideline to choose between $\text{BIC}$ and ${\text{BIC}}_3$, ${\mathrm{\Delta }}^{\ast }$ is not known in practice and the accuracy of its estimation will play an important role in correctly selecting the model. In the next section, we propose a weighted BIC which combines $\text{BIC}$ and ${\text{BIC}}_3$ based on a measure similar to ${\mathrm{\Delta }}_{i,i+1}$ and also include a brief discussion of the model selection method based on the estimated ${\mathrm{\Delta }}^{\ast }$.

Figure 2.

Probability of correct selection (PCS) by BIC and ${\text{BIC}}_3$ for 131 cases with the number of joinpoints, $\kappa =1,2,3,$ and 4.

4. Weighted BIC

4.1. Definition

In this section, we consider the partial $R^2$ in fitting a model with one joinpoint over the i-th and $(i+1)$-st segments:

$$R_{i,i+1}^2=\frac{\left\{{\mathit{y}}_i^{\prime }\right(\mathit{I}-{\mathit{H}}_0){\mathit{z}}_i{\}}^2}{\left({\mathit{y}}_i^{\prime }\right(\mathit{I}-{\mathit{H}}_0\left){\mathit{y}}_i\right)\left({\mathit{z}}_i^{\prime }\right(\mathit{I}-{\mathit{H}}_0\left){\mathit{z}}_i\right)}$$

where $y_i$ is the vector of the y-values in the i-th and $(i+1)$-st segments and $H_0$ and $z_i$ are introduced earlier to define ${\mathrm{\Delta }}_{i,i+1}.$ We note that $R_{i,i+1}^2$ and ${\mathrm{\Delta }}_{i,i+1}$ are related in the following way:

$$R_{i,i+1}^2\approx \frac{1}{1+\frac{n_i-3}{{\mathrm{\Delta }}_{i,i+1}}},$$

where $n_i$ denotes the number of observations in the i-th and $(i+1)$-st segments, and thus $R_{i,i+1}^2$ tends to be large for a situation with a large effect size. Differently from ${\mathrm{\Delta }}_{i,i+1}$ (and thus $\mathrm{\Delta }\left(k\right)$) that does not have any specific range, however, $0\le R_{i,i+1}^2\le 1$, and this motivates us to consider the following weighted BIC (WBIC):

$$\text{WBIC}\left(k\right)=\log \left(\frac{{\text{RSS}}_k}{n}\right)+(2+R_{max}^2(k\left)\right)\frac{k\log n}{n},$$

where $R_{max}^2\left(k\right)=\underset{i=1,\dots ,k}{max}{R}_{i,i+1}^2.$ For WBIC, more weight will be given to ${\text{BIC}}_3$ when effect sizes are larger, while $\text{WBIC}$ will be close to $\text{BIC}$ when effect sizes are small.

Remark 4.1

The weight used in WBIC, $R_{max}^2\left(k\right)$, incorporates the locations of joinpoints. Compared to the penalty term in Equation (5) of Zhang and Siegmund [39], this weight function depends on the locations of joinpoints in a much more complex way, and also the spacings of the independent variable x as well as the sizes of slope changes play a role in determining the value of the weight. The larger the effect size, which depends on the sizes of slope changes and segment lengths, is, the heavier weight is assigned. The weight being between 0 and 1, it is similar to the modified BIC of Zhang and Siegmund [39] in that the penalty term of WBIC reflects between one and two dimensions for each joinpoint.

Remark 4.2

When the weighted least squares fitting to handle heteroscedastic errors is implemented with the appropriately chosen weight matrix $W$, $R_{i,i+1}^2$ needs to be revised accordingly: $X_0,$ $z_i$, and $y_i$ need to be updated with $W^{1/2}{X}_0$, $W^{1/2}{z}_i$, and $W^{1/2}{y}_i$.

4.2. Performance comparison

Further simulations have been conducted to assess the performance of $\text{WBIC}$. The simulations to examine the performance of $\text{WBIC}$ were conducted with 5,000 replications and the results for these cases are summarized in Tables 2 and 3. The PCS values of BIC and ${\text{BIC}}_3$ used to construct Tables 2 and 3 are obtained with 5,000 replications as well, and they were very close to those reported in Table 1 based on the 1,600 replications. Considering that our goal in trend analysis is often to find a most parsimonious model and ‘Perm,’ the default selection method of Joinpoint software, and ${\text{BIC}}_3$ perform comparably in selecting a parsimonious model, we investigate the performance of $\text{WBIC}$ by comparing the PCS of $\text{WBIC}$ and ${\text{BIC}}_3$. More specifically, our goal is to see whether (i) $\text{WBIC}$ performs as well as ${\text{BIC}}_3$ when ${\text{BIC}}_3$ works better than BIC and (ii) $\text{WBIC}$ improves ${\text{BIC}}_3$ when BIC performs better than ${\text{BIC}}_3$.

Table 2.

Number/Proportion of cases where $\text{PCS}\left(\text{WBIC}\right)>\text{PCS}\left({\text{BIC}}_3\right)-\zeta$.

		$\text{PCS(WBIC)}>\text{PCS}\left({\text{BIC}}_3\right)-\zeta$ given
n	ζ	$\text{PCS}\left({\text{BIC}}_3\right)<0.4$		$0.4\le \text{PCS}\left({\text{BIC}}_3\right)<0.7$		$\text{PCS}\left({\text{BIC}}_3\right)\ge 0.7$		Total
		All κ ${}^a$	$\kappa \ne 5$	All κ	$\kappa \ne 5$	All κ	$\kappa \ne 5$	All κ	$\kappa \ne 5$
30	0	111	94	15	12	25	17	151	123
		(94.1%)	(100%)	(100%)	(100%)	(40.3%)	(32.1%)	(77.4%)	(77.4%)
	0.01	118	94	15	12	54	45	187	151
		(100%)	(100%)	(100%)	(100%)	(87.1%)	(84.9%)	(95.9%)	(95.0%)
	0.03	118	94	15	12	61	52	194	158
		(100%)	(100%)	(100%)	(100%)	(98.4%)	(98.1%)	(99.5%)	(99.4%)
	Total	118	94	15	12	62	53	195	159
		All κb	$\kappa \ne 2$	All κ	$\kappa \ne 2$	All κ	$\kappa \ne 2$	All κ	$\kappa \ne 2$
15	0	93	20	12	5	11	6	116	31
		(100%)	(100%)	(100%)	(100%)	(52.4%)	(54.5%)	(92.1%)	(86.1%)
	0.01	93	20	12	5	18	8	123	33
		(100%)	(100%)	(100%)	(100%)	(85.7%)	(72.7%)	(97.6%)	(91.7%)
	0.03	93	20	12	5	21	11	126	36
		(100%)	(100%)	(100%)	(100%)	(100%)	(100%)	(100%)	(100%)
	Total	93	20	12	5	21	11	126	36

${}^a$ $\kappa =1,2,3,4,5$

${}^b$ $\kappa =1,2$

Table 3.

(i) Number/Proportion of cases where $\text{WBIC}$ performs at least as well as ${\text{BIC}}_3$ when ${\text{BIC}}_3$ works better than BIC and (ii), (iii) Number/Proportion of cases where $\text{WBIC}$ improves ${\text{BIC}}_3$ when BIC works better than ${\text{BIC}}_3$.

	$\text{PCS (WBIC)}$
	(i) $>\text{PCS }\left({\text{BIC}}_3\right)-\zeta$			(ii) $>\text{PCS }\left({\text{BIC}}_3\right)-\zeta$		(iii) $>\frac{\text{PCS}\left(\text{BIC}\right)+\text{PCS}\left({\text{BIC}}_3\right)}{2}$
	given			given		given
n	$\text{PCS}\left({\text{BIC}}_3\right)>\text{PCS}\left(\text{BIC}\right)$			$\text{PCS}\left({\text{BIC}}_3\right)\le \text{PCS}\left(\text{BIC}\right)$		$\text{PCS}\left({\text{BIC}}_3\right)\le \text{PCS}\left(\text{BIC}\right)$
	ζ	All κ ${}^a$	$\kappa \ne 5$	All κ	$\kappa \ne 5$	All κ	$\kappa \ne 5$
30	0	13	13	141	110
		(26.5%)	(26.5%)	(96.6%)	(100%)
	0.01	41	41	146	110	20	20
		(83.7%)	(83.7%)	(100%)	(100%)	(13.7%)	(18.2%)
	0.03	48	48	146	110
		(98.0%)	(98.0%)	(100%)	(100%)
	Total	49	49	146	110	146	110
	ζ	All κ ${}^b$	$\kappa \ne 2$	All κ	$\kappa \ne 2$	All κ	$\kappa \ne 2$
15	0	4	4	116	27
		(44.4%)	(44.4%)	(99.1%)	(100%)
	0.01	6	6	117	27	29	27
		(66.7%)	(66.7%)	(100%)	(100%)	(24.8%)	(100%)
	0.03	9	9	117	27
		(100%)	(100%)	(100%)	(100%)
	Total	9	9	117	27	117	27

${}^a$ $\kappa =1,2,3,4,5$

${}^b$ $\kappa =1,2$

The number of cases where $\text{PCS}\left(\text{WBIC}\right)>\text{PCS}\left({\text{BIC}}_3\right)-\zeta$ (i.e. $\text{WBIC}$ performs at least as well as ${\text{BIC}}_3$ allowing a small margin of error of $\zeta =0,0.01,0.03$) is reported according to the value range of $\text{PCS}\left({\text{BIC}}_3\right)$ in Table 2 and for the cases where $\text{PCS}\left({\text{BIC}}_3\right)>\text{PCS}\left(\text{BIC}\right)$ in Table 3-(i). Table 3 also reports the number of cases where $\text{PCS}\left(\text{WBIC}\right)>\frac{\text{PCS}\left(\text{BIC}\right)+\text{PCS}\left({\text{BIC}}_3\right)}{2}$ given $\text{PCS}\left({\text{BIC}}_3\right)\le \text{PCS}\left(\text{BIC}\right)$ (i.e. $\text{WBIC}$ improves ${\text{BIC}}_3$ when ${\text{BIC}}_3$ performs worse than BIC). When $n=30,$ based on 195 and 159 cases as before, the numbers under the column heading of ‘ $\kappa \ne 5$’ represent the cases for $\kappa =1,2,3,$ and 4, not considering the extreme case with $\kappa =5$ where over-fitting is not allowed with ${\text{JP}}_{max}=5$. Also, the corresponding percentages are reported in parentheses. When ${\text{BIC}}_3$ is performing well, either with $\text{PCS}\left({\text{BIC}}_3\right)\ge 0.7$ in Table 2 or $\text{PCS}\left({\text{BIC}}_3\right)>\text{PCS}\left(\text{BIC}\right)$ in Table 3-(i), the results indicate that $\text{WBIC}$ performs well in maintaining the power of ${\text{BIC}}_3$. For the goal of improving ${\text{BIC}}_3$ when ${\text{BIC}}_3$ performs worse than BIC, it was observed in Table 3-(iii) that $\text{WBIC}$ improves ${\text{BIC}}_3$ by picking up cases where BIC selects the correct model, in addition to be more powerful than ${\text{BIC}}_3$ as shown in Table 3-(ii). In summary, $\text{WBIC}$ improves ${\text{BIC}}_3$ in almost all cases with relatively small effect sizes and maintains its power close to that of ${\text{BIC}}_3$ when effect sizes are relatively large. Note that the PCS values of $\text{WBIC}$ used in Tables 2 and 3 are also reported in Table 1.

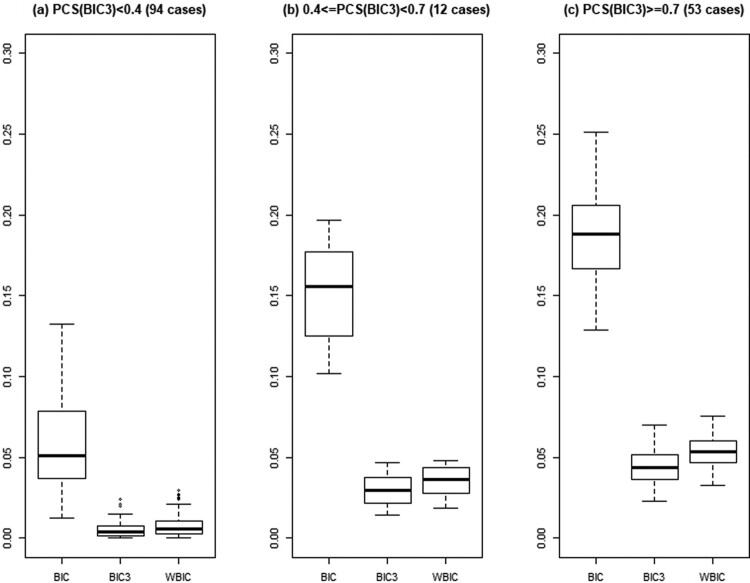
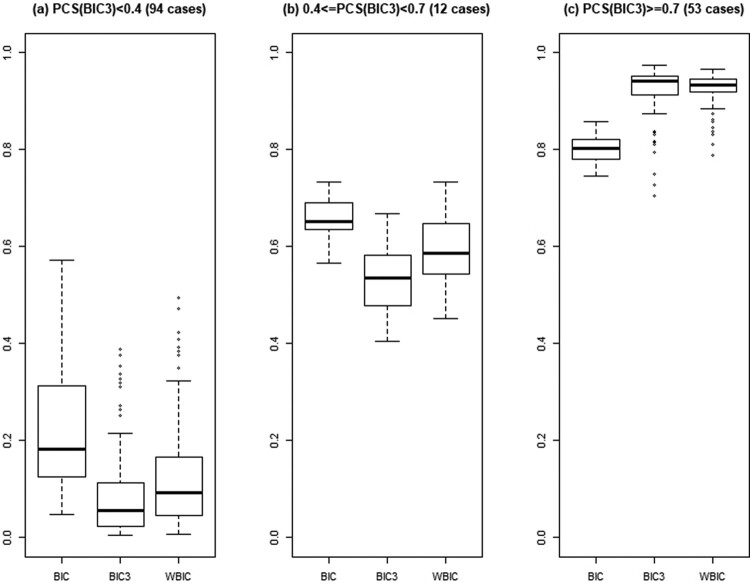
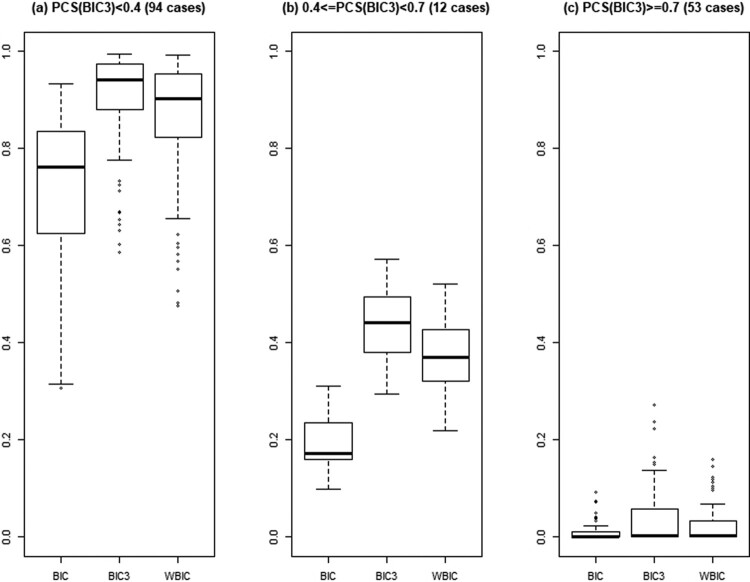
Further details of BIC, ${\text{BIC}}_3$, and WBIC are illustrated in Figures 3–5, where the probabilities of correct selection, over-fitting, and under-fitting are summarized via box-plots according to the range of $\text{PCS}\left({\text{BIC}}_3\right).$ Figures 3–5 indicate that $\text{WBIC}$ performs at least as well as ${\text{BIC}}_3$ with its median PCS values being close to or higher than those of ${\text{BIC}}_3$, the median under-fitting probabilities being smaller than those of ${\text{BIC}}_3$, and the median over-fitting probabilities being smaller than those of $\text{BIC}$. Especially when the effect sizes are practically large enough to have the PCS of ${\text{BIC}}_3$ being greater than or equal to 0.7 (i.e. (c) in Figures 3–5), $\text{WBIC}$ achieves our aim of maintaining the power of ${\text{BIC}}_3$ and keeping the over and under-fitting probabilities low. Also, when we compared the performance of WBIC to that of the permutation test, which is the default selection method of Joinpoint software, PCS(WBIC) $\ge$PCS(Perm) in 122 cases while PCS(WBIC)<PCS(Perm) in 37 cases among the 159 cases presented in Figures 3–5. Except for two cases with very small effect sizes, PCS(WBIC) was at least 0.88 for the 35 cases where PCS(WBIC)<PCS(Perm).

Figure 4.

Over-fitting probabilities of BIC, ${\text{BIC}}_3$, and WBIC for 159 cases with $n=30$ and $\kappa =1,2,3,4$.

Figure 3.

Probability of correct selection by BIC, ${\text{BIC}}_3$, and WBIC for 159 cases with $n=30$ and $\kappa =1,2,3,4$.

Figure 5.

Under-fitting probabilities of BIC, ${\text{BIC}}_3$, and WBIC for 159 cases with $n=30$ and $\kappa =1,2,3,4$.

Motivated by that SEER 21 data available in the SEER database of the U.S. NCI [36] summarize data during the relatively short period of 2000-2016, we have also conducted simulations to assess the performance of the proposed procedure with short series data, whose results are summarized in the lower parts of Tables 2 and 3. There were 126 cases where 36 cases with different parameter settings were considered under the true model with one joinpoint and 90 cases were generated under the true model with two joinpoints. For these results, the maximum number of joinpoints was set as 2, and thus only the numbers under $\kappa \ne 2$, which are the cases with the true model of one joinpoint, reflect situations where over-fitting could occur. Although there are only 36 cases with one joinpoint and n = 15, similar findings as in the case with n = 30 are found.

Remark 4.3

We have considered other types of weighted BIC using $R_{min}^2\left(j\right)=\underset{i=1,\dots ,j}{min}{R}_{i,i+1}^2,$ and examined the performances of the weighted BIC whose penalty terms are $(2+R_{min}^2(k\left)\right)\frac{k\log n}{n}$ and $(2k+\sum _{j=1}^k{R}_{min}^2(j\left)\right)\frac{\log n}{n}.$ For both types of weighted BIC, we observed in our simulations not reported here that their performances are much worse than the WBIC introduced above in maintaining the power of ${\text{BIC}}_3$ for the cases with medium and large effect sizes although they perform better in improving ${\text{BIC}}_3$ when effect sizes are relatively small. Considering that the permutation method with the over-fitting probability controlled to be under 0.05 has been known to perform well to select a parsimonious model in cancer trend analysis and also that ${\text{BIC}}_3$ and the permutation test perform comparably, we only presented WBIC given above, but other types of weighted BIC can be considered depending on one's goal.

Remark 4.4

Although not reported in this paper, we have considered another type of data-dependent model selection procedure, called DDS at the NCI Joinpoint website [32], whose idea is to estimate ${\mathrm{\Delta }}^{\ast }$ discussed in Section 3. The DDS method uses BIC or ${\text{BIC}}_3$ for the model selection when the sample selection measures indicate a higher likelihood of ${\mathrm{\Delta }}^{\ast }$ being relatively smaller or larger, respectively. In our simulation study, the performance of DDS was sometimes better than that of WBIC, but due to its main drawback that its implementation, i.e. the determination of the cut-off values, is rather ad-hoc, this paper focuses only on WBIC.

4.3. Large sample properties

Simulation results summarized in Section 4.2 indicate that the WBIC maintains its power when ${\text{BIC}}_3$ performs good (i.e. when effect sizes are relatively large) and improves ${\text{BIC}}_3$ when BIC outperforms ${\text{BIC}}_3$ (i.e. when effect sizes are relatively small). Recall that the simulation study of Kim and Kim [12] indicated the consistency of $\hat{\kappa }$ estimated by ${\text{BIC}}_3$, while the consistency of ${\text{BIC}}_4$ has been theoretically proved for the segmented regression model without continuity constraint. In this section, we report a simulation study where we investigate how the performances of these selection methods, BIC, ${\text{BIC}}_3$, and WBIC, change as the number of observations, n, increases, which is expected to provide insights on the consistency of WBIC. For this study, we consider the parameter settings used in the first two cases for each of the κ values in Table 1: Cases 1-1-i, 2-1-i, 3-1-i, and 4-1-i with $\sigma =0.03$ and 0.01. Then, we estimated $P(\hat{\kappa }=k)$ for $k=0,1,\dots ,5$ and $n=30,50,$ and 100, where the locations of joinpoints were adjusted so that the proportions of the segment lengths stay constant. That is, we set $\tau =n\ast 5/30$ for $\kappa =1$, $({\tau }_1,{\tau }_2)=(n\ast 10/30,n\ast 20/30)$ for $\kappa =2$, $({\tau }_1,{\tau }_2,{\tau }_3)=(n\ast 7/30,n\ast 15/30,n\ast 23/30)$ for $\kappa =3$, and $({\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4)=(n\ast 6/30,n\ast 12/30,n\ast 18/30,n\ast 24/30)$ for $\kappa =4$. The slope parameter of each segment stayed the same as in Table 1. For each of these cases, Table 4 reports the probability of under-fitting (PUF), the probability of correct selection (PCS), and the probability of over-fitting (POF) observed for BIC, ${\text{BIC}}_3$ and WBIC. Note that PUF= $P(\hat{\kappa }<k^{\ast })$, PCS= $P(\hat{\kappa }=k^{\ast })$, and POF= $P(\hat{\kappa }>k^{\ast })$, where $\hat{\kappa }$ is the estimated number of joinpoints and the $k^{\ast }$ is the true number of joinpoints.

Table 4.

Probability of Under-Fitting, Correct Selection, and Over-Fitting.

			n = 30			n = 50			n = 100
Case	σ	prob	BIC	${\text{BIC}}_3$	WBIC	BIC	${\text{BIC}}_3$	WBIC	BIC	${\text{BIC}}_3$	WBIC
$\kappa =1$
1-1-i-a	0.03	PUF ${}^a$	0.262	0.528	0.328	0.000	0.005	0.000	0.000	0.000	0.000
		PCS ${}^b$	0.636	0.458	0.644	0.919	0.983	0.977	0.961	0.995	0.986
		POF ${}^c$	0.102	0.073	0.028	0.081	0.012	0.023	0.039	0.005	0.014
1-1-i-b	0.01	PUF	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
		PCS	0.858	0.974	0.967	0.910	0.988	0.979	0.955	0.994	0.988
		POF	0.142	0.026	0.033	0.090	0.012	0.021	0.045	0.006	0.012
$\kappa =2$
2-1-i-a	0.03	PUF	0.075	0.238	0.161	0.000	0.000	0.000	0.000	0.000	0.000
		PCS	0.746	0.727	0.788	0.862	0.977	0.959	0.935	0.993	0.991
		POF	0.179	0.036	0.051	0.138	0.023	0.041	0.065	0.007	0.009
2-1-i-b	0.01	PUF	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
		PCS	0.770	0.942	0.933	0.846	0.973	0.970	0.914	0.989	0.988
		POF	0.230	0.058	0.067	0.154	0.027	0.030	0.086	0.011	0.012
$\kappa =3$
3-1-i-a	0.03	PUF	0.372	0.668	0.583	0.005	0.032	0.024	0.000	0.000	0.000
		PCS	0.506	0.311	0.392	0.839	0.940	0.937	0.914	0.991	0.990
		POF	0.123	0.021	0.025	0.156	0.028	0.039	0.086	0.009	0.010
3-1-i-b	0.01	PUF	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
		PCS	0.752	0.935	0.932	0.827	0.971	0.969	0.908	0.989	0.989
		POF	0.248	0.065	0.067	0.173	0.029	0.031	0.092	0.011	0.011
$\kappa =4$
4-1-i-a	0.03	PUF	0.679	0.897	0.883	0.087	0.280	0.249	0.000	0.000	0.000
		PCS	0.260	0.098	0.111	0.767	0.695	0.721	0.899	0.986	0.985
		POF	0.061	0.005	0.006	0.146	0.025	0.029	0.101	0.014	0.015
4-1-i-b	0.01	PUF	0.000	0.008	0.007	0.000	0.000	0.000	0.000	0.000	0.000
		PCS	0.799	0.937	0.936	0.820	0.968	0.967	0.886	0.984	0.984
		POF	0.201	0.055	0.057	0.180	0.032	0.033	0.114	0.016	0.016

${}^a$ PUF: Probability of Under-Fitting, $P(\hat{\kappa }<k^{\ast })$ where $\hat{\kappa }$ is the number of joinpoints estimated and $k^{\ast }$ is the true number of joinpoints

${}^b$ PCS: Probability of Correct Selection, $P(\hat{\kappa }=k^{\ast })$

${}^c$ POF: Probability of Over-Fitting, $P(\hat{\kappa }>k^{\ast })$

The following summarizes the results:

1. As the effect size increases from $\sigma =0.03$ to $\sigma =0.01$, we observe that allowing the maximum simulation margin of error of 0.014, (i) the PUF decreases for all of BIC, ${\text{BIC}}_3$ and WBIC regardless of n, (ii) the PCS of BIC increases only when n = 30 while the PCS values of ${\text{BIC}}_3$ and WBIC are the same/increasing for all of n = 30, 50 and 100, and (iii) the POF of BIC shows a larger increase from the case with $\sigma =0.03$ to that with $\sigma =0.01$, compared to ${\text{BIC}}_3$ and WBIC, for all of n = 30, 50 and 100, while the POF changes of ${\text{BIC}}_3$ and WBIC between $\sigma =0.03$ and 0.01 are all within the margin of error when n = 50 and 100.

2. As the number of observations n increases, (i) the PUF decreases for all of BIC, ${\text{BIC}}_3$ and WBIC, (ii) the PCS increases for all of BIC, ${\text{BIC}}_3$ and WBIC, and (iii) the POF decreases for all of BIC, ${\text{BIC}}_3$ and WBIC when $\sigma =0.01,$ and for the cases with $\sigma =0.03$, the POF when n = 100 is the smallest in general.

3. For large n, smaller POF values are observed for ${\text{BIC}}_3$ and WBIC than for BIC. For n=100, the ranges of the POF values are (0.045, 0.114), (0.005, 0.016) and (0.009, 0.016) for BIC, ${\text{BIC}}_3$ and WBIC, respectively. For n=50, the ranges are (0.081, 0.180), (0.012, 0.032), and (0.021, 0.041) for BIC, ${\text{BIC}}_3$ and WBIC, respectively. That is, when $n=50$ and 100, the POF values of ${\text{BIC}}_3$ and WBIC are under 5% while the POF of BIC is as large as 18%. It is also observed that the over-fitting tendency of BIC relative to WBIC, in terms of POF(BIC)/POF(WBIC), gets worse as n increases in the majority cases of Table 4.

In summary, as the number of observations increases, the under-fitting probability of WBIC approaches zero and its probability of correct selection is very close to 1. The performance of ${\text{BIC}}_3$ is comparable to that of WBIC when n = 50 and 100, but WBIC shows higher PCS in general when n = 30. BIC also shows a similar tendency, but its over-fitting probability is much larger than those of ${\text{BIC}}_3$ and WBIC even when n=100.

5. Examples

In this section, we apply the model selection methods discussed in the previous sections to prostate cancer incidence and mortality rates for males in the United States. For the analysis, we used the delay-adjusted incidence rates during the period of 1975–2016 obtained from the SEER 9 program of the U. S. National Cancer Institute [27] and U. S. mortality rates collected by states and compiled by the National Center for Health Statistics [28]. Cancer incidence data is typically first released approximately two years after the end of the year when the cases were diagnosed. Delay-adjusted rates make an adjustment in the current incidence rates to account for anticipated future additions and deletions to the case count (due to additional cases found or modifications to the data, e.g. a case originally thought to be brain cancer is eventually identified as ovarian cancer that metastasized to the brain) in each subsequent annual release. More accurate trend analysis can be conducted with delay-adjusted rates [6,20] and more information can be found in Ref. [30]. To fit a joinpoint regression model, Joinpoint Version 4.7 is used with the default setting that includes the annual grid search, the log-linear model with the weighted least squares fitting using the standard errors provided by the SEER program, and 4499 permutations for the permutation procedure. Note that 4499 is the default number of permutations in Joinpoint software, which was recommended to achieve the desired level of accuracy for the P-value estimation, but recall that the number of permutations used in our simulations was 319, which was chosen to manage a computational limitation in simulations while preserving the accuracy of the simulation results. The maximum number of joinpoints, ${\text{JP}}_{max}$, is set at 7 considering that the length of the data is relatively long over the forty two year period.

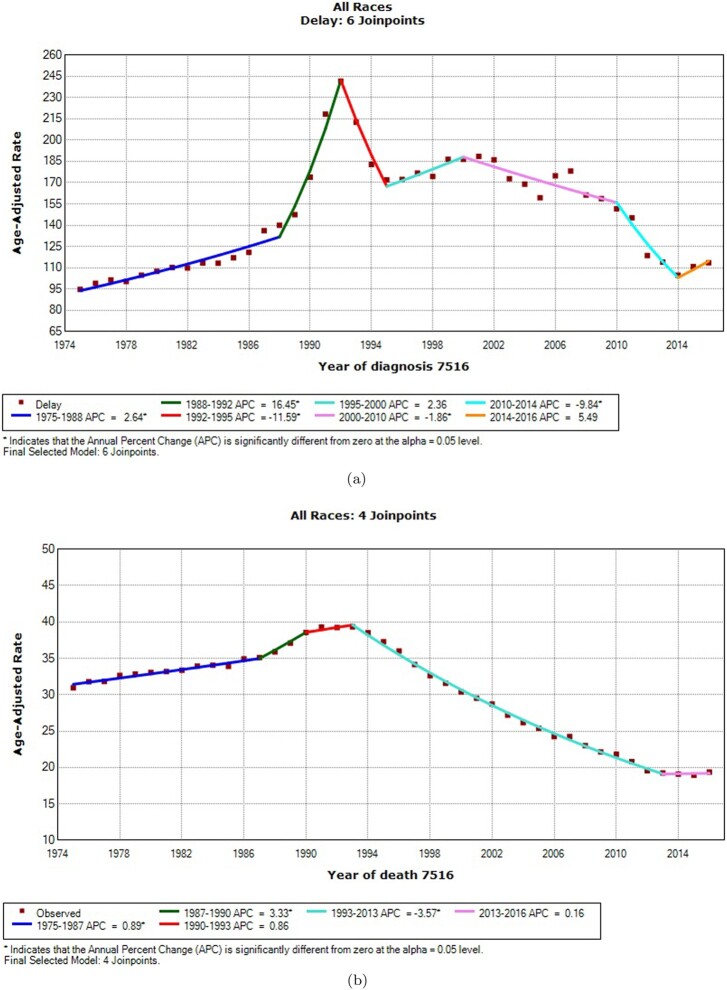
We report the model selection results for the prostate cancer incidence and mortality rates in Table 5. For the prostate cancer incidence rates for all races combined, all of the Perm, ${\text{BIC}}_3$, and WBIC methods selected the model with six joinpoint, while BIC selected the one with seven joinpoints and MBIC selected the one with four joinpoints. Figure 6(a) shows the six joinpoint model fit selected by most of the selection methods along with the annual percent change (APC) for each segment. Note that the APC for the segment with a slope of β in the log-linear model is defined as $100\left(\text{Exp}\right(\mathrm{\text{β}})-1)$. For the incidence data, the permutation test produced the p-value of 0.130 in testing the null model with six joinpoints versus the alternative model with seven joinpoints under ${\text{JP}}_{max}=7$, which supports the six joinpoint model chosen by Perm, ${\text{BIC}}_3$, and WBIC.

Table 5.

Final model ( $\hat{\kappa }$) selected.

Data	Perm	BIC	${\text{BIC}}_3$	MBIC	WBIC
Prostate Incidence ${}^a$	6	7	6	4	6
(All races)	$P_{6\text{ vs }7}=0.130$ ${}^b$
	${\hat{\mathit{\tau }}}_6=(1988,1992,1995,2000,2010,2014)$
	${\hat{\mathit{\tau }}}_7=(1985,1989,1992,1995,2000,2010,2014)$
Prostate Mortality ${}^c$	4	5	4	3	4
(All races)	$P_{4\text{ vs }5}=0.018$
	${\hat{\mathit{\tau }}}_4=(1987,1990,1993,2013)$
	${\hat{\mathit{\tau }}}_5=(1987,1991,1994,1998,2013)$

${}^a$ SEER 9 delay-adjusted incidence rates, 1975–2016

${}^b$ $P_{k_0\text{vs }{k}_1}$ is the P-value of the permutation test of $H_0:k_0$ joinpoints versus $H_a:k_1$ joinpoints under ${\text{JP}}_{max}=7$.

${}^c$ U.S. mortality, 1975-2016

Figure 6.

Prostate cancer incidence and mortality rates.(a) SEER 9 delay-adjusted incidence: 1975–2016. (b) US mortality: 1975–2016.

Figure 6(b) shows the prostate cancer mortality rates for all races combined during 1975–2016 with the fit made for the four joinpoint model. For this data, four joinpoint model is selected by Perm, ${\text{BIC}}_3$, and WBIC, while the model with five joinpoints is selected by BIC and the one with three joinpoints by MBIC. In this case, the p-value of the permutation test of the null model with four joinpoints versus the alternative model with five joinpoints was 0.018 under ${\text{JP}}_{max}=7$, which is much smaller than 0.130 of the incidence case but not small enough to lead to a significant result when multiple testings are conducted.

As indicated by the simulation study, the MBIC is shown to be extremely conservative, and it did not pick up the change in the incidence rates during the last three years, while MBIC detected a change in mortality at 2013 when its decreasing trend stopped and progressed to a plateau. Also, BIC is shown to be the most liberal, as indicated in the simulation study, and the additional joinpoints estimated by BIC are at 1985 for the incidence trend and at 1998 for the mortality trend, which certainly make for better fits but may just be adding noise as analysts try to relate changes in trends to modifications in how prostate cancer is diagnosed or treated. Although most of the methods, except MBIC in the incidence rate analysis, identified changes from their decreasing trends during the recent several years, the last segment APCs are not statistically significant which might be due to very short lengths of the last segment, three years for incidence and four years for mortality, and the generally low power to determine whether short segment APCs are significantly different from zero.

As noted in the introduction, these trend changes in prostate cancer incidence and mortality rates observed during the recent years have received great attention in the cancer surveillance community, especially related to a recommendation by the U. S. Preventive Services Task Force against the use of the PSA screening and the subsequent drop in testing rates [21]. It seems illogical that the joinpoint for incidence could occur one year after the joinpoint for mortality (2014 and 2013, respectively), when changes in screening rates should logically impact cancer incidence before mortality. However, it must be kept in mind that these joinpoints are measured with error, especially the rather gradual changes in slope for mortality. The 95% resampling confidence intervals for these joinpoints produced by Joinpoint software ((2013, 2014) for the sixth joinpoint in the incidence rates and (2012, 2014) for the fourth joinpoints in the morality rates; Kim et al. [13]) indicate that they are not different when considering their variability. Given the controversies surrounding the value of the PSA screening, there is considerable interest in interpretation of these trends and it is critically important that a single objective method be applied to characterize the trends. The U. S. Preventive Services Task Force recommendations changed again in 2018 [8], this time to a C recommendation indicating that ‘For men aged 55 to 69 years, the decision to undergo periodic prostate-specific antigen (PSA)-based screening for prostate cancer should be an individual one. Before deciding whether to be screened, men should have an opportunity to discuss the potential benefits and harms of screening with their clinician and to incorporate their values and preferences in the decision.’ Such changes will certainly further complicate future analyses of trends.

6. Discussion

In this paper, we have studied the empirical properties of several model selection methods to determine the number of joinpoints in a joinpoint regression model, and proposed a data-driven selection method, the weighted BIC, which is computationally much more efficient than the permutation procedure and is shown to maintain the probability of correct selection while keeping the over-fitting probability close to that of the permutation procedure. Each selection method has its own strengths as well as weaknesses as we have discussed in the previous sections, and we recommend one to use the proposed method, WBIC, as an automated selection procedure considering his/her goal. As summarized in the Joinpoint help site [33],

‘our overall recommendations are to use the permutation test if one prefers the method that has the longest track record in trend analysis and generally produces parsimonious results, use ${\text{BIC}}_3$ if one would like to produce results similar to the permutation test procedure but computation time is an issue, use WBIC if one prefers a method that on average performs best across a wide range of situations. While Perm, BIC, and ${\text{BIC}}_3$ might perform better in some specific situations, WBIC is most flexible in adapting to different situations.’

Based on its conceptual justification and its adaptable performance under a number of different conditions, there is consideration of making WBIC the default method in the Joinpoint software.

As indicated in the Introduction, our aim in this paper was to propose an automated model selection procedure and to provide empirical evidence for its satisfactory performance in cancer trend analysis with a moderate size of observations. Also, it was noted in the Introduction that theoretical and conceptual work previously conducted on the performance of BIC type selection measures in change-point problems suggested modifications of traditional BIC type measures, and our simulation study in this paper supports such findings in the context of joinpoint regression. In terms of large sample properties, our simulation study in Section 4.3 indicated the consistency of the model selected by the proposed method, WBIC. More rigorous study on the consistency of the model selected by WBIC requires further work.

Another related research project is to compare the performances of BIC type selection measures discussed in this paper with those of fully Bayesian procedures as in Tiwari et al. [29]. Tiwari et al. proposed to use the Bayes factor and ‘Bayesian’ version of BIC to select the model and also to obtain the posterior distribution of the model parameters. They used Markov chain Monte Carlo simulations to compute the posterior distributions of the model parameters as well as competing models, and also compared the performances of their Bayesian approaches with the permutation test procedure discussed in this paper. Although MBIC discussed in Zhang and Siegmund [39] and this paper is based on the Bayes factor, its main use was for the model selection, and fully Bayesian approaches such as those of Tiwari et al. [29] can be used to obtain posterior probabilities of the model parameters.

And the performance measure that we used in this paper is the probability of correct selection, which is an important measure to identify a consistent selection method that will justify subsequent inferences in segmented line regression. Another frequently used accuracy measure is the prediction accuracy, and such a study could provide useful information for projection. In Chen et al. [4], various models and methods have been investigated in predicting cancer mortality rates, and it has been observed that the joinpoint regression model selected by a relatively conservative method performs better. Thus, it would be another interesting research topic to investigate how and why a better performance in the prediction is achieved by a relatively conservative model selection.

Funding Statement

H.-J. Kim's research was partially supported by U. S. National Institute of Health Contract HHC 26120150003B and also a part of the research was conducted while H.-J. Kim was visiting the U.S. National Cancer Institute under the support of the Intergovernmental Personnel Act program.

Disclosure statement

No potential conflict of interest was reported by the authors.