The minimum work requirements for atmospheric water harvesting

Abstract

Idealized cycles for the three most common methods of atmospheric water harvesting, membrane, desiccant, and condenser, are analyzed. It is found that they all have substantially the same efficiency as a function of water removal fraction. In addition, for small removal fractions they all approach the minimum thermodynamic work requirement. This minimum is shown to come from the entropy of mixing at the water-atmosphere boundary. For larger removal fractions, additional work is required, which is shown to come from mixing the drier output air with ambient air.

1. Introduction

Extracting water from the atmosphere for the purposes of drinking, irrigation or household use is attracting increased attention as concerns about water availability mount. The process is usually called atmospheric water harvesting (AWH). The academic work in the field has been reviewed recently by several authors [[1], [2], [3]]. These papers explore the many different approaches researchers have taken. Much of the early work in the field addressed passive approaches such as fog nets [4] or solar distillation of water captured in desiccants [5]. More recent work has focused on new desiccants based on metal-organic-framework materials [6,7].

For active systems, which typically use electric power to provide the required energy, a natural question is “how much energy is required to extract say a kilogram of water from the atmosphere?” This question has been explored recently by Rao et al., using tabulated humid air thermodynamic properties [8].

This paper uses approximate analytical forms for the thermodynamic properties of humid air. We show that the minimum required energy as work follows from the simple relation derived in Section 2, ${W/M_f=R}_v{T}_a\ln \left(1/\mathcal{H}\right)$ where $W$ is the work, $M_f$ the mass of extracted water, $R_v$ the gas constant of water vapor, $T_a$ the ambient temperature, and $\mathcal{H}$ the relative humidity (Equation (2.2)). It is shown that this required work comes from the need to overcome the lost work of mixing of the water source (ocean) and atmosphere.

Inserting the constants from Appendix A into the above equation gives $W/M_f=$ 95 kJ/kg water for 50% relative humidity and 25 °C atmospheric temperature. This is equivalent to a productivity of 38 L/kWh, which is considerably more than typical commercial units achieve. For example, the most efficient whole-home dehumidifier certified by Energy Star has a productivity of 2.35 L/kWh.1 Bagheri measured the energy efficiency of three commercially available AWH units under laboratory test conditions and found that they all produced less than 1.2 L/kWh [9]. These examples are less than 5% of the theoretical maximum. Most well-developed thermodynamic systems such as heat pumps and heat engines operate at 30 to 80% of their thermodynamic limit. It seems there may be considerable room for improvement.

The paper organization is as follows. Section 2 provides a simple explanation of where the minimum work equation above comes from (Equation (2.2)). Section 3 uses an exergy analysis to compute the minimum work of a flow through system that takes in atmospheric air, extracts some of its water, and expel the reminder. The minimum work occurs when there is no internal entropy production. Flow through processes consume more energy than the minimum of Equation (2) and (2). The additional work is shown to come from the lost work of the output air, which has lost some water vapor, mixing with ambient air.

The exergy analysis is silent on actual extraction process. Section 4, 5, 6 analyze the membrane, desiccant and condenser processes respectively using ideal cycles. These require additional work compared to the minimum-work flow-through process due to internal entropy production. The details of relevant calculations are relegated to appendices so as not to interrupt the presentation flow with unnecessary detail.

One of the conclusions is that the three approaches studied, membrane harvesting, desiccant harvesting, and condenser harvesting, all have essentially the same ideal cycle efficiency as a function of their water removal fraction. Also, they all approach Equation (2.2) for small removal fractions (as does the minimum work of Section 3). Thus, there is little to recommend one over the other based on theoretical efficiency potential. The choice will depend on practical engineering and implementation factors.

An ancillary finding is that terms in the thermodynamic state functions involving the liquid water specific volume, $v_f$, which are often ignored because of their small value compared to other terms, must be included in multiple places for the results to be strictly true. This includes in integrating the Clapeyron equation to find the saturation vapor pressure. It is shown that the Clapeyron equation can be integrated in closed form without assuming $v_f=0$, as is usually done. In the end all the terms involving $v_f$ cancel and don't appear in the final results. But this is true only if they are properly included at every step.

2. Simple compression analysis with membrane separation

The minimum work required to extract liquid water from an air-water vapor mixture can be found by a simple ideal cycle analysis. Fig. 1 shows a piston-cylinder arrangement coupled to the atmosphere through valve A and an ideal membrane. This membrane is assumed to have infinite permeability to water vapor and zero to the other constituents of the atmosphere. Therefore, the pressure in the cylinder is the water vapor pressure in the atmosphere, $p_v$. The total atmospheric air pressure is $p_{atm}$, which is equal to the sum of the water vapor partial pressure and the partial pressure of dry air, $p_a$. Everything is assumed to be at the ambient air temperature, $T_a$. $M_w$ is the mass of water in the cylinder. Throughout this paper we assume that gaseous constituents obey the ideal gas law, have constant specific heats, and that air-water vapor is an ideal mixture. Thus, $p_{atm}=p_v+p_a$, and when the water in the cylinder is in the vapor state, $p_{v}V=M_w{R}_v{T}_a$. Here $V$ is the cylinder volume, which varies during the cycle, and $R_v$ is the water vapor gas constant. By moving the piston we do work, $W$, where

$$\Delta W=-\left(p_v-p_{atm}\right)dV\text{.}$$

Fig. 1.

Expander-compressor cylinder coupled to the atmosphere through an ideal water vapor permeable membrane and valve A, and to a water storage reservoir through valve B. The meaning of the symbols is explained in the text.

To extract water from the ambient we take the system through the cycle in Fig. 2. The steps are as follows. Note that water is conserved in this process and the total mass of water, $M_w$, is the sum of that in the vapor and liquid form, or

$$M_w=M_v+M_f$$

Where $M_v$ is the mass of water in vapor form, and $M_f$ that in liquid form.

Fig. 2.

Cycle to remove water from ambient. The steps are described in the text.

Starting at 1 we open valve A and expand the volume to $V_T$ at 2. The total pressure on the piston is constant during this process so the work on the piston for this step is

$$W_{\mathrm{1,2}}=-\left(p_v-p_{atm}\right)V_T\text{.}$$

In this process we extract a mass of water equal to $M_v$ where $p_v{V}_T=M_v{R}_v{T}_a$. We assume that the reservoir is very large and so the extraction process does not change its pressure. No heat is transferred to the cylinder in this step. Next, we close valve A and isothermally compress the water vapor from $p_v$ to $p_{sat}$, where $p_{sat}$ is the saturation vapor at $T_a$. The work for this step is

$$W_{\mathrm{2,3}}=-{\int }_{V_T}^{V_{sat}}\left(p_v-p_{atm}\right)dV=-M_v{R}_v{T}_a{\int }_{V_T}^{V_{sat}}\frac{1}{V}dV+p_{atm}\left(V_{sat}-V_T\right)$$

$$={-M}_v{R}_v{T}_a\ln \left(V_{sat}/V_T\right)+p_{atm}\left(V_{sat}-V_T\right)$$

$$=M_v{R}_v{T}_a\ln \left(p_{sat}^0/p_v\right)+p_{atm}\left(V_{sat}-V_T\right)$$

where we have used the fact that during the compression $p_{v}V=M_v{R}_v{T}_a$. Here, $M_v$ and $T_a$ are constants during this process, and so $p_v{V}_T=p_{sat}{V}_{sat}$. In this relation the first term is the work done on the vapor. Since this is an iso-thermal process, and the internal energy of the vapor depends only on temperature, then heat, $Q_{\mathrm{2,3}}$, must be extracted from the vapor

$$Q_{\mathrm{2,3}}=M_v{R}_v{T}_a\ln \left(p_{sat}/p_v\right)+p_{atm}\left(V_{sat}-V_T\right)$$

Next, we compress the saturated vapor until it is all liquid. At this point it occupies a volume of $V=V_f=M_f{v}_f$ where $v_f$ is the specific volume of liquid water. This is a constant pressure compression so that

$$W_{\mathrm{3,4}}=p_{sat}\left(V_{sat}-V_f\right)-p_{atm}\left(V_{sat}-V_f\right)$$

The heat of condensation must be removed from the liquid water which is

$$Q_{\mathrm{3,4}}=M_f{h}_{fg}$$

We now have liquid water, but it is at a pressure $p_{sat}$ and needs to be expelled to the storage reservoir which is at $p_{atm}$, the last step in Fig. 2. We open valve B and the work for this is clearly

$$W_{\mathrm{4,1}}={-(p}_{atm}-p_{atm})V_f=0$$

This is 0 because the pressure on both sides of the piston is equal. Also, there is no heat flow involved in this step. The total work around the cycle is then

$$W=W_{\mathrm{1,2}}+W_{\mathrm{2,3}}+W_{\mathrm{3,4}}+W_{\mathrm{4,1}}=M_f{R}_v{T}_a\ln \left(p_{sat}/p_v\right)+\left(p_{atm}-p_{sat}\right)V_f$$

where we have used the relation $p_v{V}_T=p_{sat}{V}_{sat}$ and $M_v$ in the above equation for work becomes $M_f$ (all the vapor is compressed to liquid).

We will be most interested in the required work per mass of extracted water, which is

$${\frac{W}{M_f}=R}_v{T}_a\ln \left(p_{sat}/p_v\right)+\left(p_{atm}-p_{sat}\right)v_f$$ Eq. 2.1

where $v_f=V_f/M_f$. The last term is the work required to expel the water to ambient. At this point it is tempting to define the atmosphere's relative humidity, $\mathcal{H}$, as $\mathcal{H}=p_v/p_{sat}$ so we can write Equation (2.1) as

$${\frac{W}{M_f}=R}_v{T}_a\ln \left(1/\mathcal{H}\right)+\left(p_{atm}-p_{sat}\right)v_f\left(\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\right)$$

This would be incorrect, however, because the saturation pressure in the atmosphere is different than that in the cylinder due to the Poynting effect [10, p. 344]. If $p_{sat}$ is the water saturation pressure as pure vapor over water, then the effect of the remaining atmospheric constituents is to raise the saturation pressure in the atmosphere, $p_{sat}^a$, by (see Equation B13)

$$\mathit{ln}\left(\frac{p_{sat}^a}{p_{sat}}\right)=\frac{v_f}{R_v{T}_a}\left(p_{atm}-p_{sat}\right)=\ln \left(\frac{p_{sat}^a}{p_v}\frac{p_v}{p_{sat}}\right)$$

The actual relative humidity is $=p_v/p_{sat}^a$ so the above equation becomes

$$\ln \left(\frac{p_{sat}}{p_v}\right)=\ln \left(1/\mathcal{H}\right)-\frac{v_f}{R_v{T}_a}\left(p_{atm}-p_{sat}\right)$$

Thus, we have

$${\frac{W}{M_f}=R}_v{T}_a\ln \left(1/\mathcal{H}\right)$$ Eq.2.2

It is seen that the work to expel the water is offset by the increased saturation vapor pressure, which upon reflection comes from the increased enthalpy, and hence chemical potential, of the source water due to atmospheric pressure.

Likewise, the heat removed from the device is

$$Q=Q_{\mathrm{2,3}}+Q_{\mathrm{3,4}}={M_f{h}_{fg}+M}_f{R}_v{T}_a\ln \left(p_{sat}/p_v\right)+p_{atm}\left(V_{sat}-V_T\right)={M_f{h}_{fg}+M}_f{R}_v{T}_a\ln \left(1/\mathcal{H}\right)-M_f\left(p_{atm}-p_{sat}\right)v_f{+M}_f\left(p_{atm}-p_{sat}\right)v_f$$

and the heat per mass of water is given by Equation (2.3),

$$\frac{Q}{M_f}={h_{fg}+R}_v{T}_a\ln \left(1/\mathcal{H}\right)$$ Eq.2.3

It should be noted that the terms involving $v_f$ in the above equations are very small, and negligible from an engineering viewpoint. We keep them throughout in this paper so that the results are consistent with the assumed thermodynamic properties, as well as the First and Second Laws.

At first glance it may be surprising that the heat of vaporization does not appear explicitly in Equation (2.2). Indeed, no work at all is required to harvest water when $\mathcal{H}=1$. One can see that this must be the case, however, by noting that if you have two bodies of water near each other with saturated air above them, then if one body has an infinitesimal lower temperature, water will migrate from the warmer to lower body. Since the temperature difference can be infinitesimal, then a reversible heat engine can supply the heat with infinitesimal work. The work and heat flows are quite different indeed.

When $\mathcal{H}<1$ work is required, as given by Equation (2.2). It is instructive to examine where this comes from. At the surface of the source reservoir (oceans and lakes) humid air at the surface will mix irreversibly with dryer air above without generating work. Following the methodology and terminology of Keesling [11] this is the lost work from the irreversible mixing of water vapor at the source reservoir surface, where it is at $p_v=p_{sat}^a$, (i.e., $\mathcal{H}=1)$ with air where $\mathcal{H}<1$. It is also equal to the entropy of mixing. This work could in principle be recovered by a reversible engine covering the entire source that works from humidity differences. Of course, covering all the earth's water surface with such a device is unthinkable, so this work is truly lost. Thus, we are left with the result of Equation (2.2) being the minimum work required to remove water vapor from air and turn it into liquid. The following sections explore more realistic cycles for comparison to Equation (2.2).

One thing to note is that if the atmosphere is in equilibrium with salt water, then $\mathcal{H}$ is necessarily less than unity due to vapor pressure lowering. In this case, Equation (2.2) can be shown to yield the same result as the minimum required work for desalination.

Another thing of note is that the process of Fig. 2 is reversible. The process could equally be run backwards and generate energy as work. In his case water is vaporized and injected into the atmosphere yielding the same work as in Equation (2.2), but with a negative sign. Paraphrasing the argument of Carnot that all reversible heat engines operating between two temperature reservoirs must have the same efficiency, else a perpetual motion machine could be constructed, it is clear that all reversible machines that extract water vapor from the atmosphere having relative humidity $\mathcal{H}$ must require the same work. Thus Equation (2.2) is indeed the minimum possible work regardless of the process employed.

3. Exergy analysis and the minimum required work

3.1. Analyzing a reversible flow-throw process

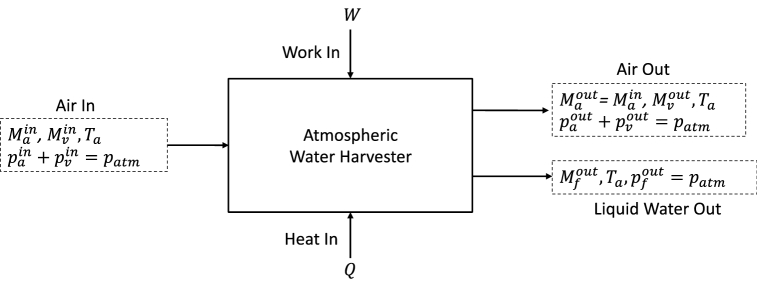
The analysis of Section 2 suffers from the assumption that the water vapor partial pressure is constant as it is pulled through the membrane. This will not be strictly true as diffusive transport through the ambient air will result in a decrease in water partial pressure as water is drawn into the compressor. A more realistic model of the process is represented by a flow-through system where air is drawn into a system and expelled with some water removed. This is shown in Fig. 3. The symbols are given in Appendix A. The harvester is treated as a control volume.

Fig. 3.

Water harvesting system showing input and output flows. For this case we assume that heat, $Q$, is exchanged with the ambient at ambient temperature, $T_a$.

Since we are focused on the work requirements, and not the heat flow to and from ambient, this system is most easily modeled using an exergy analysis using the concept of available work [10, p. 80]. For a given mass the exergy, $ℇ$, is defined as $ℇ=E+p_{atm}V-T_{a}S$, Equation B2. For a given process on a control volume it is shown in Appendix B that when there are no chemical reactions involved and heat is exchanged only with the ambient at a temperature $T_a$, the work on the volume is given by Equation (B4),

$$W=T_a\Delta {\mathcal{P}}_s+\Delta ℇ+B^{out}-B^{in}\text{.}$$ Eq.B4

where $\Delta {\mathcal{P}}_s$ is the entropy production in the volume, $\Delta ℇ$ is the change in the exergy of the volume, and $B^{in}$ and $B^{out}$ are the flow work availability of mass entering and leaving the volume (our harvester in this case) during the process. These are given by

$$B^{in}={\sum }_i^{in}{M}_i\left(h_i-T_a{s}_i\right)$$

and

$$B^{out}={\sum }_i^{out}{M}_i\left(h_i-T_a{s}_i\right)$$

Here $W$ includes all forms of work on the control volume except for that due to the ambient pressure acting on control volume change. In Appendix B it is shown that the work availability of an air water mixture at temperature $T_a$ and pressure $p_{atm}$ is

$$B-B_0=M_a{R}_a{T}_a\ln \left(p_a/p_{a,sat}\right)+M_v{R}_v{T}_a\ln \left(\mathcal{H}\right)$$ Eq.B14

In Equation (B14) $p_{a,sat}$ is the partial pressure of dry air in the presence of saturated water vapor. $B_0$ is the so-called dead state work availability, which in this case is the availability of saturated air and water, i.e., when $\mathcal{H}=1$. Note that the liquid water does not contribute to availability in this formulation as its availability is zero (i.e., is at the dead state). The only subtility in this relation is that the partial pressure of air, $p_a$, varies with water content through the relation $p_a+p_v=p_{atm}$ so that $p_{a,sat}=p_{atm}-p_{sat}^a$.

The second law requires that $\Delta {\mathcal{P}}_s\ge 0$, and is 0 for a reversible process. For the calculation below in this section we assume that the process is reversible, as we are looking at the minimum required work, $W_{\mathit{min}}$. We also assume a steady state process so $\Delta ℇ=0$ so that Equation B2 becomes $W=B^{out}-B^{in}$. This gives the result in Equation (B15) below which is derived in Appendix B.

$$W_{\mathit{min}}=M_v^{in}{R}_v{T}_a\ln \left(1/{\mathcal{H}}^{in}\right)-M_v^{out}{R}_v{T}_a\ln \left({1/\mathcal{H}}^{out}\right)+M_a{R}_a{T}_a\ln \left(p_a^{out}/p_a^{in}\right)$$ Eq.B15

Note that the output dry air mass is equal to the input mass, assuming no accumulation of air in the harvester, so no superscripts are needed for $M_a$. The work elements are pretty clear here. The first term in Equation 3.2 is the work required to remove water as liquid from the ambient at ${\mathcal{H}}^{in}$ (Equation (2.2)), whereas the second term is the work gained in adding liquid water to the ambient at the output humidity, and the third term is the work required to compress the dry air from $p_a^{in}$ to $p_a^{out}$. This is a positive number since $p_a^{in}<p_a^{out}$. It is interesting to note that when ${\mathcal{H}}^{in}\cong 0.5$, and when half the input water is removed giving ${\mathcal{H}}^{out}\cong 0.25$, then the first two terms in Equation (B15) cancel. Curiously, in this case nearly all the required work comes from the air compression term.

Appendix C1 covers the development of Equation (B15) into the form most useful here, giving the result in Equation (3.1).

$$W_{\mathit{min}}=M_f^{out}{R}_v{T}_a\left[\ln \left(1/{\mathcal{H}}^{in}\right)+\left(1-\frac{p_{atm}}{f{p}_v^{in}}\right)\ln \left(1-\frac{f{p}_v^{in}}{p_{atm}}\right)-\frac{1-f}{f}\ln \left(\frac{1}{1-f}\right)\right]$$ Eq.3.1

we have defined the recovery factor, as

$$f=\frac{M_f^{out}}{M_v^{in}}=1-\frac{M_v^{out}}{M_v^{in}}$$

where $f$ is the fraction of input water that is removed as liquid. The result now depends explicitly only on the input humidity, the recovery factor, and $p_v^{in}$. It is interesting to note that, when $p_v\ll p_{atm}$, i.e., well below the boiling point, the logarithm in the second term of 3.1 can very reasonably expressed by its first order expansion. So, to a good approximation, 3.1 becomes

$$W=M_f^{out}{R}_v{T}_a\left[\ln \left(1/{\mathcal{H}}^{in}\right)+1-\frac{1-f}{f}\ln \left(\frac{1}{1-f}\right)\right]$$

Except for its presence in ${\mathcal{H}}^{in}$, the dependence on $p_v^{in}$ and $p_{atm}$ is quite negligible assuming that $p_v\ll p_{atm}$.

As discussed in Section 2, the first term in Equation (3.1) is the minimum work needed because of the input mixing of air and water at the source (Equation (2.2)). The remaining terms are therefore the added work needed because of the flow-through process. The nature of this is explored in Section 3.2 below.

The sum of the last two terms in parentheses in Equation 3.3 approaches 0 for small f. In other words, for small removal fractions the exergy difference approaches the minimum possible of Equation (2.2). Thus, the device is reversible for small f. We will see that the idealized cycles for the cases considered below have the same characteristic; they are all reversible for small f.

When $f=1$ the last two terms sum to $1\text{.}$ Surprisingly, the work requirement does not approach infinity for complete vapor removal, but rather $M_f^{out}{R}_v{T}_a\left[\ln \left(1/{\mathcal{H}}^{in}\right)+1-{fp}_v^{in}/p_{atm}\right]$.

3.2. Lost work due to output mixing

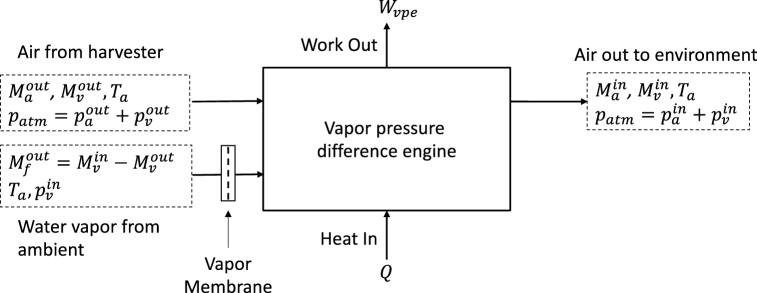
Since the ejected air has less water vapor than the input air, this suggest that the last terms in Equation (3.1) may be due to the lost work of mixing the output with ambient. It is simple to show this is the case by imagining a vapor pressure engine that works between airmasses of different humidity. This engine is coupled to the ambient air via a water permeable membrane as shown in Fig. 4. The output work of this machine, $W_{vpe}\text{,}$ can be found using the same procedures as for the harvester in Section 2.1. It is more easily seen, however, by realizing that if such an engine is combined with the harvester, then the output air-water vapor availability equals the input air-water vapor availability.

Fig. 4.

Vapor pressure difference engine with input from the harvester of Fig. 3, and output to ambient. Water from the ambient is input as vapor at $p_v^{in}$ with mass sufficient to make up the harvested water, $M_f^{out}$. The work is shown as output so that it is a positive number.

In this case the output air availability is the same as the input air availability, and so the input availability is just the vapor availability and the output is that of the fluid water, which is zero. The work of the combined system, $W_{comb}$, is

$$W_{combined}=B^{out}-B^{in}=M_f^{out}{R}_v{T}_a\ln \left(1/{\mathcal{H}}^{in}\right)\text{.}$$

This is of course just Equation (2.2), so the work from the vapor pressure engine cancels the term

$$W_{vpe}=M_f^{out}\left[\left(1-\frac{p_{atm}}{f{p}_v^{in}}\right)\ln \left(1-\frac{f{p}_v^{in}}{p_{atm}}\right)-\frac{1-f}{f}\ln \left(\frac{1}{1-f}\right)\right]$$

in Equation (3.1). If we don't have an output vapor pressure engine, this work is not recovered. For the combined harvester-vapor pressure engine we thus can write

$$W_{combined}=M_f^{out}{R}_v{T}_a\ln \left(1/{\mathcal{H}}^{in}\right)+W_{vpe}-W_{vpe}\text{.}$$

For the case of the harvester alone we don't recover the output of the vapor pressure engine, so the work potential of the output mixing is lost. Thus

$$W=M_f^{out}{R}_v{T}_a\ln \left(1/{\mathcal{H}}^{in}\right)+W_{vpe}$$

In practice it would be very difficult to recover $W_{vpe}$ . The same issue that drove us to imagine a flow through device would limit the vapor pressure engine to needing to be flow-through and we would be back to the starting point with output mixing loss.

Based on the discussion in Section 1, we can define the following terms

$$W_{inputmixing}^{lost}={M_f^{out}R}_v{T}_a\ln \left(1/H^{in}\right)$$

$$W_{outputmixing}^{lost}={M_f^{out}R}_v{T}_a\left[\left(1-\frac{p_{atm}}{f{p}_v^{in}}\right)\ln \left(1-\frac{f{p}_v^{in}}{p_{atm}}\right)-\frac{1-f}{f}\ln \left(\frac{1}{1-f}\right)\right]$$

So that

$$W=W_{inputmixing}^{lost}+W_{outputmixing}^{lost}$$

This result is illustrated in Fig. 5 for the case of ${\mathcal{H}}^{in}=0.5$. Other cases will be presented in later sections.

Fig. 5.

Minimum required work for harvesting liquid water from air at a relative humidity of 50% and temperature 25 °C as a function of recovery factor. The contributions from lost work of input air mixing with the water reservoir and output air mixing with ambient are shown. As discussed in the text, the output mixing loss is recoverable in principle by using a vapor pressure difference engine.

Equation (3.1) is plotted in Fig. 6 to quantify the impact of varying humidity.

Fig. 6.

Impact of ambient relative humidity in the minimum required work. The ambient temperature is 25 °C.

3.3. Discussion

The method of this section gives the minimum necessary work to harvest atmospheric water; however, it is opaque as to what sort of physical cycle could perform the function. Appendix D analyzes three cycles which are reversible and meet the minimum work requirement. These are a) a batch process, b) isothermal compression of the air-water mixture, and c) adiabatic expansion cooling followed by condensation with heat removal by means of a heat pump. They all give the same result, as expected. Unfortunately, none of these cycles appear to be models for a practical approach. The following Sections 4, 5, 6 analyze cycles which are closer to being models of a practical system. They all have some irreversibility, and hence require more than the minimum work.

4. Flow through membrane system

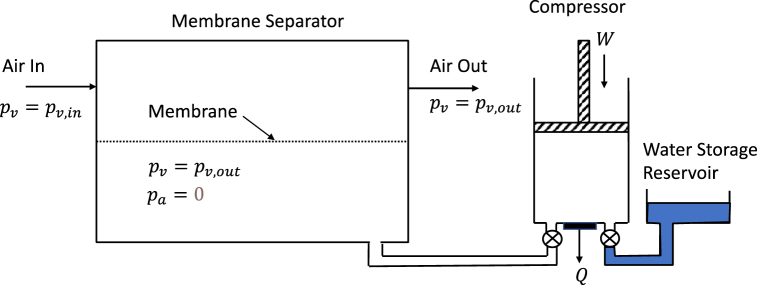
In this section we analyze an idealized flow-through water harvester incorporating a membrane separator. Air enters the separator at one end and exits at the other. A water permeable membrane separates the air from a vacuum region where water vapor is compressed back to liquid water. The process is illustrated in Fig. 7. Entering air has the ambient water vapor pressure and humidity. As it passes by the membrane separator it loses water until the exit, where the air is assumed to have a vapor pressure equal to that in the pumped vacuum side. In actuality, the exit air will have a slightly higher vapor pressure, but we assume that the separator is sufficiently long that equilibrium is achieved between the water vapor on both sides of the membrane by the exit. This approach has been proposed and analyzed by Claridge et al. [12]. A similar approach using a condenser on the vacuum side to recover water has been developed by Bergmair et al. [13].

Fig. 7.

Flow through process with membrane separation.

This is not a minimum work process because vapor is transported across the membrane with varying pressure differences, starting at $p_{v,in}-p_{v,out}$ at the input and ending at zero. Thus, potential work is lost through diffusive transport.

This system is easy to analyze using the piston compressor of Section 2. In his case the compressor is receiving water vapor at a pressure $p_{v,out}$ instead of the atmosphere pressure of $p_v=p_{v,in}$. From Equation (2.1) the work per mass of water is

$${\frac{W}{M_f}=R}_v{T}_a\ln \left(p_{sat}/p_{v,out}\right)+\left(p_{atm}-p_{sat}\right)v_f$$

Defining the output relative humidity as ${\mathcal{H}}^{out}=p_{v,out}/p_{sat}^a$ this becomes

$${\frac{W}{M_f}=R}_v{T}_a\ln \left(1/{\mathcal{H}}^{out}\right)$$ Eq.4.1

Instead of the input atmospheric humidity, as in Equation (2.2), it is the output humidity that determines the minimum work. To compare this with the minimum work of Section 3, Equation 3.3, we need to know the output humidity in terms of input humidity and removal fraction. In Appendix C, we found that

$$\frac{p_v^{out}}{p_v^{in}}=\frac{{\mathcal{H}}_{out}}{{\mathcal{H}}_{in}}=\frac{1-f}{1-{fp}_v^{in}/p_{atm}}$$ Eq.C1

So that

$${\frac{W}{M_f}=R}_v{T}_a\left[\ln \left(1/{\mathcal{H}}_{in}\right)+\ln \left(\frac{1}{1-f}\right)+\ln \left(1-\frac{{fp}_v^{in}}{p_{atm}}\right)\right]$$ Eq.4.2

This is plotted in Fig. 8 and compared with the minimum work result of Section 3. The work approaches the input mixing result as the recovery factor approaches zero, just as the minimum work does. In contrast, it becomes infinite for complete recovery, unlike the minimum work.

Fig. 8.

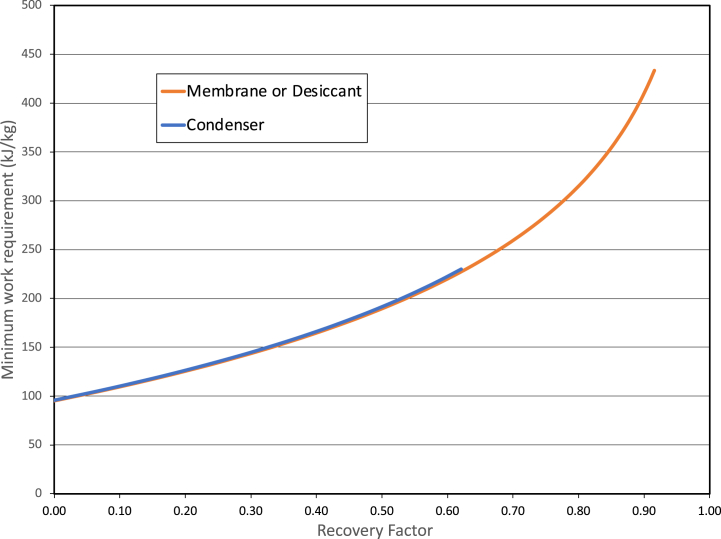
Required work for flow-through membrane harvester at 50% relative humidity and 25 °C ambient temperature as a function of recovery factor (orange line). Also shown is the minimum work for a system that produces no internal entropy as discussed in Section 3 (blue line) as well as for a system as in Section 2 that has no output mixing (dashed line). (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

5. Desiccant-based water harvester

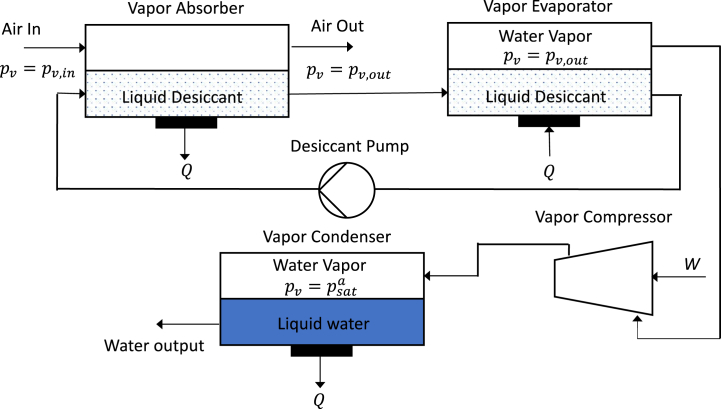
A desiccant harvester system is illustrated in Fig. 9. Air is passed through an absorber where it is in contact with a desiccant that absorbs water vapor from the air. Desiccants can be either liquid or solid. We analyze a liquid system based on water-salt mixtures such as water-CaCl₂ because the absorption process can be reversible in this case. If the vapor pressure near the liquid interface is greater than the equilibrium value, water will be absorbed at a high rate, and vice versa. This will not be significantly impacted by the finite vapor transport rate. It is also assumed that the diffusion constant of solute in the desiccant is sufficiently high that the surface salt concentration is not diluted by the water absorption.

Fig. 9.

Desiccant-based water harvester diagram. All components are at ambient temperature.

Solid desiccants, on the other hand, can have additional irreversible transport losses as water diffuses into and out of the material. These are not considered here; however, it can be assumed that the additional transport losses will imply additional work requirement. This has been analyzed using experimental desiccant properties by Rao et al. [8].

Note that the heat of condensation must be removed from the absorber. This heat can be transferred to ambient via a heat exchanger, but more commonly it is carried off by the air flow. This will reduce the amount of recovery because the desiccant temperature increases resulting in higher equilibrium vapor pressure. In the idealized process discussed here it is assumed that the desiccant temperature is kept at ambient. Liquid desiccant is pumped to the evaporator where the newly acquired water is removed by an isothermal vapor compressor. The heat of vaporization must be supplied in the evaporator. The compressed vapor is condensed in the vapor condenser. The necessary heat of condensation can be used to supply the evaporator requirement. In essence the evaporator, compressor, condenser combination is the same as in a mechanical vapor compression desalination system with isothermal compression [14].

This system is easy to analyze when one notices that the required work to compress vapor from $p_{v,out}$ to $p_{sat}^a$ is the same as that in for the membrane separator of Section 4. In fact, the desiccant basically performs the same function as the membrane. Thus, the required work is

$${\frac{W}{M_f}=R}_v{T}_a\left[\ln \left(1/{\mathcal{H}}_{in}\right)+\ln \left(\frac{1}{1-f}\right)+\ln \left(1-\frac{{fp}_v^{in}}{p_{atm}}\right)\right]$$ Eq.5.1

which is the same as Equation (4.1). Equation (5.1) is plotted in Fig. 10.

Fig. 10.

Required work for flow-through desiccant process at 50% relative humidity (orange line). The result is the same as for the membrane process of Section 4. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

The harvest process is the same as that required to regenerate the desiccant in a dehumidification system. In this analysis a vapor compression method was used; however, there are other ways to do this. Alternatives include thermal [15], reverse osmosis [16], and electrodialysis [17]. Ren provides a comprehensive overview of these methods [18].

6. Condenser-based harvester

The final method analyzed is the condenser harvester. This is the basis of most commercially available units, and a common method of dehumidifying air. We analyze the idealized condensing cycle in this section.

The flow diagram of an idealized process is illustrated in Fig. 11. Atmospheric air enters a counter-flow heat exchanger at 1, losing heat to the exit streams 4. It then enters the condenser heat exchanger which is at a temperature $T_c$. We assume that it exits the condenser at a temperature equal to $T_c$. In other words, the condenser heat exchanger is assumed to have unity effectiveness. This case is different than that considered in Rao et al., who did not use a heat exchanger to pre-cool the incoming air [8].

Fig. 11.

Condenser separator flow diagram. The process is described in the text, and the flow states are shown in the table.

It is readily shown that the heat capacity of the effluent air stream is less than the input stream because the effluent is missing some water vapor, plus there is some condensation of input air in the heat exchanger. Thus, the limiting capacity comes from the exit stream. The effluent will exit at temperature $T_a$ given that the heat exchanger's effectiveness is also assumed to be unity (NTU→∞). Under this assumption $T_2$ will be greater than $T_c$; however, we don't need an explicit formula for that using the control volume of Fig. 11. Heat of value $Q_c$ is removed from the condenser at temperature $T_c$ and pumped to ambient temperature where it is rejected. The heat pump is assumed reversible and so has a coefficient of performance of $COP=Q_c/W=T_c/\left(T_a-T_c\right)$.

Doing a First Law analysis on the components in the dotted line of Fig. 11 gives

$$Q_c=H_1-H_4-H_5$$

Using the thermodynamic relations in Appendix B it is straightforward to find that

$$\frac{Q_c}{M_w}=h_{fg}\left(T_a\right)-\left[p_{atm}-p_{sat}\left(T_a\right)\right]v_f+c_f\left(T_a-T_c\right)$$

Note that the relevant heat of vaporization is that at ambient temperature, not the condenser temperature. The source of the term $\left[p_{atm}-p_{sat}\left(T_a\right)\right]v_f$ is perhaps not immediately obvious but will prove necessary as seen below.

Incorporating the work required to pump heat $Q_c$ from the condenser to ambient temperature using the ideal heat pump with a COP of $T_c/\left(T_a-T_c\right)$ gives

$$\frac{W_{hp}}{M_w}=\frac{Q_c/M_w}{COP}=\left\{h_{fg}\left(T_a\right)-\left[p_{atm}-p_{sat}\left(T_a\right)\right]v_f+c_f\left(T_a-T_c\right)\right\}\left(\frac{T_a}{T_c}-1\right)$$ Eq.6.1

At this point there is a residual heat demand of $c_f\left(T_a-T_c\right)$ caused by the water exiting at the cold temperature. Since this term is much less than $h_{fg}\left(T_a\right)$ there is little penalty in simply dumping the cold water into the ambient. For a typical system at ${\mathcal{H}}^{in}=0.5$, $T_a-T_c$ is of order 15 C, and the additional loss is 2.6% of $h_{fg}\left(T_a\right)$. In commercial systems this is a reasonable compromise compared to trying to extract energy from the cold water. For our ideal cycle, however, we can imagine extracting the available energy of the cold water. The available work, denoted $W_f$ here, is simply the availability of the water effluent, which is

$$\frac{W_f}{M_f}=\frac{\Delta ℇ}{M_f}=c_f\left(T_a-T_c\right)-{c_{f}T}_a\ln \left(\frac{T_a}{T_c}\right)$$

With the sign convention used here, $W_f$ is negative and subtracts from the required work. (Alternately, a real system might be able to extract value from the cold water stream without attempting to provide work, but that is not considered here.)

Adding $W_f$ to $W_{hp}$ in Equation (6.1) gives the total work $W$.

$$\frac{W}{M_w}=\left[h_{fg}\left(T_a\right)-\left[p_{atm}-p_{sat}\left(T_a\right)\right]v_f\right]\left(\frac{T_a}{T_c}-1\right)+{c_{f}T}_a\left[\left(\frac{T_a}{T_c}-1\right)-\ln \left(\frac{T_a}{T_c}\right)\right]$$ Eq.6.2

The amount of water harvested will depend on the condenser temperature, $T_c$. Since we know the vapor partial pressure at the exit is $p_{sat}^a\left(T_c\right)\text{,}$ and at the input is $p_v^{in}={\mathcal{H}}^{in}{p}_{sat}^a\left(T_a\right)$, we can use the equations of Appendix C (Equation (C1) shown here as Equation (6.3)) to yield the recovery fraction as

$$f=\frac{1-p_{sat}^a\left(T_c\right)/({\mathcal{H}}^{in}{p}_{sat}^a\left(T_a\right)}{1-p_{sat}^a\left(T_c\right)/p_{atm}}$$ Eq.6.3

We have everything needed to compute the work except for $p_{sat}^a\left(T_a\right)$ and $p_{sat}^a\left(T_c\right)$; i.e., we need to know the vapor pressure as a function of temperature. This has not been needed until considering the condenser approach. There are many formulations for this in the literature. See for example the compendium of Vomel at the National Center for Atmospheric research, http://cires1.colorado.edu/∼voemel/vp.html. Most of these are parameter fits of Antonine-type equations fit to empirical data such as that of the IAPWS [19]. A recent example is that of [20] which will be used here. This is

$$p_{sat}\left(T\right)=6.112\exp \left\{17.62T/\left(243.12+T\right)\right\}$$ Eq.6.4

where pressure is in Pascals and temperature in degrees Celsius.

This, of course, is the vapor pressure of pure water over liquid water. It needs to be corrected to get $p_{sat}^a\left(T\right)$ through Equation (B13),

$$R_v{T}_a\ln \left(p_{sat}^a/p_{sat}\right)=\left(p-p_{sat}\right)v_f$$ Eq.B13

The heat exchanger and condenser are all at atmospheric pressure, $p=p_{atm}$, so from Equation B13

$$p_{sat}^a\left(T_a\right)=p_{sat}\left(T_a\right)\exp \left\{\left(p_{atm}-p_{sat}\left(T_a\right)\right)v_f/R_v{T}_a\right\}$$

and

$$p_{sat}^a\left(T_c\right)=p_{sat}\left(T_c\right)\exp \left\{\left(p_{atm}-p_{sat}\left(T_c\right)\right)v_f/R_v{T}_a\right\}$$

The required work can be computed by picking a condenser temperature, $T_c$, computing $p_{sat}\left(T_a\right)$ via Equation (6.4) and inserting these into Equation (6.2) for work. After computing $p_{sat}^a\left(T_a\right)$ and $p_{sat}^a\left(T_c\right)$ the resulting removal fraction comes from solving Equation (6.3).

Note that the dew point, $T_{dp}$, occurs when

$$p_{sat}^a\left(T_c\right)=p_{sat}^a\left(T_{dp}\right)=H^{in}{p}_{sat}^a\left(T_a\right)=p_v^{in}$$

For condenser temperatures greater than the dew point the removal fraction of Equation (6.2) becomes negative. This is not non-physical. It simply means that water on the condenser is evaporating, and the device is running backwards (${\dot{M}}_w<0$) as an atmospheric heat engine fueled by evaporating water.

The results of this calculation are in Fig. 12. Also included are the results for membrane and desiccant harvesters presented in Sections 4, 5. For the given relative humidity and ambient temperature the condenser plot ends at just over 60% recovery factor where the condenser is at freezing temperature. For this calculation the value for $h_{fg}\left(T_a\right)$ is from Equation (B10), and the numerical values are from Table A2. This analysis is not valid below freezing because the heat of fusion is not included and the assumed formula for vapor pressure is no longer appropriate, although the unit could in principle operate below freezing with periodic defrosting.

Figure 12.

Required work for a flow through condensing harvester with heat exchanger recovery at 50% relative humidity and 25 °C ambient temperature as a function of recovery factor.

It is remarkable that there is very little difference between the condenser work and membrane/desiccant work even though there is no obvious relation between Equation (6.2) and Equation (4.2) for the case for a membrane or desiccant. The difference becomes discernible only at the highest recovery factors. Of course, this is not just an amazing coincidence. The reason for this is explored in the next subsection, Section 6.1.

6.1. Relation between humidity and work requirement

The remarkable similarity in results between the condenser and membrane/desiccant harvesters deserves some inspection. In Ref. [21] it is shown that the Clausius-Clapeyron equation

$$\frac{d{p}_{sat}\left(T\right)}{dT}=\frac{s_{fg}}{v_{fg}}=\frac{h_{fg}}{T\left(v_f-v_g\right)}$$

implies that between any two temperatures, such as $T_a$ and $T_c$,

$$\ln \left(\frac{p_{sat}\left(T_a\right)}{p_{sat}\left(T_c\right)}\right)=-\frac{h_{fg}\left(T_a\right)}{R_v{T}_a}+\frac{h_{fg}\left(T_c\right)}{R_v{T}_c}-\frac{\left(c_f-c_{p,v}\right)}{R_v}\ln \left(\frac{T_a}{T_c}\right)$$

or

$$R_v{T}_a\ln \left(\frac{p_{sat}\left(T_a\right)}{p_{sat}\left(T_c\right)}\right)=-h_{fg}\left(T_a\right)+h_{fg}\left(T_c\right)\frac{T_a}{T_c}-\left(c_f-c_{p,v}\right)T_a\ln \left(\frac{T_a}{T_c}\right)$$

Inserting Equation (B10) into the above equation gives

$$R_v{T}_a\ln \left(\frac{p_{sat}\left(T_a\right)}{p_{sat}\left(T_c\right)}\right)=h_{fg}\left(T_a\right)\left(\frac{T_a}{T_c}-1\right)+\left(c_f-c_{p,v}\right)T_a\left[\left(\frac{T_a}{T_c}-1\right)-\ln \left(\frac{T_a}{T_c}\right)\right]+\left(p_{sat}\left(T_a\right)-p_{sat}\left(T_c\right)\right)v_f\frac{T_a}{T_c}$$

The left side of the above equation is related to the output humidity but must be corrected by the Poynting effect as follows.

$$\ln \left(\frac{1}{{\mathcal{H}}^{out}}\right)=\ln \left(\frac{p_{sat}^a\left(T_a\right)}{p_{sat}^a\left(T_c\right)}\right)=\ln \left(\frac{p_{sat}\left(T_a\right)}{p_{sat}\left(T_c\right)}\frac{p_{sat}^a\left(T_a\right)}{p_{sat}\left(T_a\right)}\frac{p_{sat}\left(T_c\right)}{p_{sat}^a\left(T_c\right)}\right)$$

$$=\ln \left(\frac{p_{sat}\left(T_a\right)}{p_{sat}\left(T_c\right)}\right)+\frac{\left(p_{atm}-p_{sat}\left(T_a\right)\right)v_f}{R_v{T}_a}-\frac{\left(p_{atm}-p_{sat}\left(T_c\right)\right)v_f}{R_v{T}_c}$$

Inserting this into Equation (6.2) for the total work gives, after some manipulation,

$$\frac{W}{M_w}=R_v{T}_a\ln \left(\frac{1}{{\mathcal{H}}^{out}}\right)+{c_{p,v}T}_a\left[\left(\frac{T_a}{T_c}-1\right)-\ln \left(\frac{T_a}{T_c}\right)\right]$$ Eq.6.4a

It is interesting to note that, once again, all terms in $v_f$ have cancelled out when the result is expressed in terms of relative humidity.

Equation (6.4) is nearly the same as Equation (4.1) for the membrane and desiccant separators, depending mainly on the output relative humidity. There is, however, and additional term in $c_{p,v}$. This term is quite small. In fact, it is easy to show that it is zero to first order in $T_a-T_c$. That this result is slightly larger than the membrane harvester is perhaps not surprising, as there is likely some added entropy production in the unbalanced heat exchanger having unequal flow capacities. In any case, we see that the differences between the three flow-through ideal cycles are negligible from a practical point of view. This difference is just discernible in Fig. 11.

7. Conclusions

The main conclusion from this work is that the three most common flow-through atmospheric water harvesting approaches, membrane, desiccant, and condenser, all have substantially the same idealized cycle efficiency and work requirement as a function of water removal fraction. In addition, for small removal fractions they all approach the minimum thermodynamic work requirement and hence are reversible devices. Thus, the issue of which approach will be most cost-effective rests on practical engineering and implementation issues. It is also shown that the minimum work requirement comes from overcoming the lost work due to the entropy of mixing at the water source and atmosphere, and the increased work for an ideal flow-through system is shown to come from the lost work of the dryer output mixing with ambient air.

Author contribution statement

Richard M. Swanson: conceived and designed the experiments; performed the experiments; analyzed and interpreted the data; contributed reagents, materials, analysis tools or data; wrote the paper.

Data availability statement

No data was used for the research described in the article.

Declaration of competing interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:Richard M. Swanson reports a relationship with BB&Y LLC that includes: board membership and equity or stocks.

Appendix A. Symbols and values

Table A1.

Symbols

Symbol	Unit	Description
$c_f$	J/kgK	Specific Heat capacity of saturated liquid water
$c_{p,v}$	J/kgK	Constant pressure heat capacity of water vapor
$c_{p.a}$	J/kgK	Constant pressure heat capacity of dry air
$c_{v,v}$	J/kgK	Constant volume heat capacity of water vapor
$h_{fg}$	J/kg	Specific heat of vaporization, $h_f-h_g$
$L^0$	J/kg	Extrapolated specific heat of vaporization
$M_a$	kg	Mass of dry air
$M_f$	kg	Mass of liquid water
$M_v$	kg	Mass of water vapor
$M_w$	kg	Mass of water, $M_v+M_f$
$p_a$	Pa	Dry air partial pressure
$p_{atm}$	Pa	Ambient air pressure
${\mathcal{P}}_s$	J/K	Entropy production
$p_{sat}^a$	Pa	Saturation pressure of atmospheric water vapor
$p_{sat}$	Pa	Saturation pressure of pure water
$p_v$	Pa	Water vapor partial pressure
$R_a$	J/kgK	Dry air gas constant
$R_v$	J/kgK	Water vapor gas constant
$s_{fg}$	J/kgK	$s_f-s_g$
$T_a$	K	Ambient temperature
$T_a$	K	Ambient air temperature
$T_c$	K	Condenser temperature
$T_c$	K	Water vapor condenser temperature
$T_R$	K	Reference temperature
$V_f$	m3	Volume of fluid water
$v_f$	m3/kg	Specific volume of liquid water
$B$	J	Flow availability
COP		Heat pump coefficient of performance
$ℇ$	J	Exergy
$f$		Water removal fraction
$\mathcal{H}$		Relative humidity
$H$	J	Enthalpy
$h$	J/kg	Specific enthalpy
$k$		$c_{p,v}/c_{v,v}$
$Q$	J	Heat
$S$	J/K	Entropy
$s$	J/kgK	Specific entropy
$u$	J/kg	Specific internal energy
$V$	m3	Volume
$W$	J	Work
$\omega$		$M_v/M_a$

Table A2.

Property values

Symbol	Value	Unit
$c_f$	4195	J/kgK
$c_{p,v}$	1850	J/kgK
$c_{p.a}$	1004.6	J/kgK
$c_{v,v}$	1388	J/kgK
$h_{fg}\left(T_R\right)$	2.501 × 106	J/kg
$p_{atm}$	101325	Pa
$p_{sat}\left(T_R\right)$	611	Pa
$R_a$	287.05	J/kgK
$R_v$	461.52	J/kgK
$T_R$	273.15	K
$v_f$	0.001	kg/m3

Appendix B. Exergy and the thermodynamic relations of air-water mixtures

This section outlines the methodology used for finding the thermodynamic parameters of air-water mixtures. In all cases we assume gasses are ideal with constant specific heats and that liquid water is incompressible. The thermodynamic parameters come from standard textbooks on thermodynamics. They are analyzed here to clarify the role of certain parameters. The symbols are standard but are grouped in Appendix A for clarity.

B1. Exergy approach

We consider a control volume with input work and heat along with entering and exiting mass streams. It is assumed that no chemical reactions occur. In this case, for a given process the First Law for the control volume is,

$$\Delta E=W_{cv}+{\sum }_j{Q}_j+{\sum }_i^{in}{M}_i{h}_i-{\sum }_i^{out}{M}_i{h}_i$$

where the sum over $i$ is over all input and output mass constituencies and streams, and the sum over j is the different points where energy enters as heat. Here $W_{cv}$ includes all forms of work done on the control volume. The Second Law gives

$$\Delta S={\mathcal{P}}_s+{\sum }_j\Delta Q_j/T_j+{\sum }_i^{in}{M}_i{s}_i-{\sum }_i^{out}{M}_i{s}_i$$

Where the entropy production ${\mathcal{P}}_s$ must be zero or greater. It is zero for a reversible process. Multiplying this by the ambient temperature gives

$$T_a\Delta S=T_a{\mathcal{P}}_s+{{\sum }_j{Q}_j\frac{T_a}{T_j}+T}_a{\sum }_i^{in}{M}_i{s}_i-T_a{\sum }_i^{out}{M}_i{s}_i$$

Subtracting this from the First Law gives

$$W_{cv}=T_a{\mathcal{P}}_s+\Delta E-T_a\Delta S+{\sum }_j{Q}_j\left(\frac{T_a}{T_j}-1\right)-{\sum }_i^{in}{M}_i\left(h_i-T_a{s}_i\right)+{\sum }_i^{out}{M}_i\left(h_i-T_a{s}_i\right)$$

We will be interested in the work needed by an external agent for the process. The atmosphere can also supply work through volume changes, but this work is free from our perspective. So we define $W$ as the work required by this agent. The atmospheric work, $-p_{atm}\Delta V$, is added to this giving

$$W_{cv}=W-p_{atm}\Delta V$$

Henceforth we will be concerned only with $W$. In terms of this the above relation becomes

$$W=T_a{\mathcal{P}}_s+\Delta E+p_{atm}\Delta V-T_a\Delta S+{\sum }_j{Q}_j\left(\frac{T_a}{T_j}-1\right)-{\sum }_i^{in}{M}_i\left(h_i-T_a{s}_i\right)+{\sum }_i^{out}{M}_i\left(h_i-T_a{s}_i\right)$$ Eq.B1a

We define the exergy of the control volume exergy, $ℇ$, as

$$ℇ=E+p_{atm}V-T_{a}S=H-T_{a}S+\left(p_{atm}-p\right)V$$ Eq.B2a

The relation in terms of $H$ is added because many of the thermodynamic variables will be expressed in terms of $H$ rather than $E$. We also define

$$B^{in}={\sum }_i^{in}{M}_i\left(h_i-T_a{s}_i\right)$$ Eq. B3a

often called the flow availability of the input stream, and likewise for the output stream

$$B^{out}={\sum }_i^{out}{M}_i\left(h_i-T_a{s}_i\right)$$ Eq. B3b

Note that when $p=p_{atm}$ the work availability, $B$, of a mass is equal to its exergy, $ℇ$, through Equation (B1).

Using Equation (B1), B2, B3a, and B3b, the equation for work then becomes

$$W=T_a{\mathcal{P}}_s+\Delta ℇ+{\sum }_j{Q}_j\left(\frac{T_a}{T_j}-1\right)+B^{out}-B^{in}$$ Eq.B4a

Accordingly, we compute the parameters needed in equation B4. The following approach to developing suitable state equations follows the methodology in Swanson [22].

B2. Enthalpy

• a.Liquid Water.

The specific enthalpy of liquid (fluid) water, $h_f$, is

$$h_f\equiv u_f+p{v}_f$$ Eq.B5a

where $u_f$ is the specific internal energy, $v_f$ the specific volume, and $p$ the pressure. We will need the temperature and pressure dependence of $h_f$. In principle for this simple compressible substance all the terms in the above equation are functions of $T$ and $p$.

In looking at the vapor enthalpy below, we will need the enthalpy along the liquid-vapor saturation line where $p=p_{sat}\left(T\right)$, and so $u_f$, $v_f$, and $h_f$ depend only on $T$. In other words, under saturated conditions

$$h_f\left(T\right)=u_f\left(T\right)+p_{sat}\left(T\right)v_f\left(T\right)$$

If we assume that the internal energy at the saturation pressure is linearly dependent on temperature change for small changes, and that the specific volume is independent of temperature and pressure, the saturation enthalpy of the fluid is then

$$h_f\left(T\right)=c_f\left(T-T_R\right)+p_{sat}\left(T\right)v_f$$ Eq.B6a

where $c_f$ and $v_f$ are constants and $T_R$ is the reference temperature about which small changes obtain.

This raises the question of what commonly defined specific heat best approximates $c_f$. Since the fluid is incompressible, its internal energy is independent of pressure. For small changes in temperature and pressure

$$d{u}_f={\left(\frac{\partial u_f}{\partial T}\right)}_{p}dT+{\left(\frac{\partial u_f}{\partial p}\right)}_{T}dp={\left(\frac{\partial u_f}{\partial T}\right)}_{p}dT\equiv c_{p.f}dT$$

So, except for very small factors related to the compressibility of liquid water, $c_f$ in Equation 4 is indistinguishable from constant pressure specific heat of the fluid, $c_{p.f}$. For the purposes here it is merely required that $u_f$ vary linearly with temperature along the saturation line. $c_f$ for water can, of course be found from the saturated steam tables [19]. It differs negligibly from $c_{p,f}$, but substantially from $c_{p,v}$.

In the case where the fluid is at a pressure other than $p_{sat}$ we can assume from the above that the internal energy is unaffected by the pressure so Equation (B5) and B6 imply that

$$h_f\left(T\right)=c_f\left(T-T_R\right)+p{v}_f$$ Eq.B7a

• b.Water vapor

If we have pure water with saturated vapor above it, then the specific enthalpy of the saturated vapor is, using Equation B6

$$h_v\equiv h_f+h_{fg}=c_f\left(T-T_R\right)+p_{sat}{v}_f+h_{fg}$$ Eq.B8a

where $p_{sat}$ is the saturated water vapor pressure over liquid water, i.e., when there are no other air constituents present. Since the enthalpy of an ideal gas depends only on temperature, the above equation is valid at pressures other than saturation. Of course, the vapor pressure must be equal to or less than $p_{sat}$.

In Equation (B8) we have included the term proportional to $v_f$ from Equation (B6) for $h_f$, which is $p_{sat}{v}_f$. Because the fluid specific volume is small, this term can be, and usually is, neglected. The terms in $v_f$ appear at many points in the analysis, however, and if not included at each point inconsistent results are obtained. Of course, it is also consistent to set $v_f=0$, even if that is not strictly true for water. Equation (B4) and B6 for the enthalpy of liquid and vapor are often referred to in the literature as the Wepfer approximations [23].

$h_{fg}$ is temperature dependent and we will have need of finding $h_v$ at varying temperatures. This temperature dependence can be found by taking another path to the vapor enthalpy; first vaporizing the water at ${T=T}_R$ and then heating the vapor to temperature $T$.

$$h_v=h_f\left(T_R\right)+h_{fg}\left(T_R\right)+c_{p,v}\left(T-T_R\right)=p_{sat}\left(T_R\right)v_f+h_{fg}\left(T_R\right)+c_{p,v}\left(T-T_R\right)$$ Eq.B9a

$h_{fg}\left(T_R\right)$ is the heat of vaporization at $T_R$ which is assumed to be 0 °C for this work. Comparing Equation (B8) and B9 yields

$$h_{fg}\left(T\right)=h_{fg}\left(T_R\right)-\left(c_f-c_{p,v}\right)\left(T-T_R\right)-\left(\left(p_{sat}\left(T\right)-p_{sat}(T_R\right)\right)v_f\text{.}$$ Eq.B10a

Sometimes the last term in Equation (B10) is bundled into the $c_f$ term making it like the partial derivative of $c_{p,f}=\partial h_f/\partial T$ so that

$$h_{fg}\left(T\right)=h_{fg}\left(T_R\right)-\left(c_{p,f}-c_{p,v}\right)\left(T-T_R\right)$$

however, this is not strictly true because pressure and temperature cannot be independently varied under saturation conditions, as well as the fact that $p_{sat}$ is a rapidly varying function of $T$. There is admittedly little difference because the $\left(p_{sat}\left(T\right)-p_{sat}\left(T_R\right)\right)v_f$ term is quite small.

A form which we will find useful in Section 6 is to write this as

$$h_{fg}\left(T\right)=L^0-\left(c_f-c_{p,v}\right)T-p_{sat}\left(T\right)v_f$$ Eq.B11a

Where $L^o=h_{fg}\left(T_R\right)+\left(c_f-c_{p,v}\right)T_R+p_{sat}\left(T_R\right)v_f$. $L^o$ is often called the “extrapolated heat of vaporization.”

• c.Dry air

The specific enthalpy of dry air is taken to be

$$h_a=c_{p,a}\left(T-T_R\right)\text{.}$$

• d.Total enthalpy

We assume the water-air mixture is ideal so that the total enthalpy of the air-water mixture is

$$H=M_a{h}_a+M_f{h}_f+M_v{h}_v\text{.}$$

Here $M_a$ is the mass of dry air, $M_f$ is the mass of liquid water, and $M_v$ is the mass of water vapor in the mixture.

B3. Entropy

Using the standard expressions, the corresponding specific entropies are as follows.

• a.Fluid Water

The specific entropy of liquid water, still assumed incompressible, is

$$s_f=c_f\ln \left(T/T_R\right)$$

• b.Water vapor

For water vapor

$$s_v=c_f\ln \left(T/T_R\right)-R_v\ln (p_v/p_{sat})+h_{fg}/T\text{.}$$ Eq.B12a

The last term Equation (B12) is from the standard relation $s_g-s_f=h_{fg}/T$, while the second accounts for changes in pressure from $p_{sat}$. The reference entropy for liquid water at $T=T_R$ has been set to zero.

There is some subtilty regarding the $p_{sat}$ term that needs exploration. It turns out that the equilibrium vapor pressure depends slightly on the air pressure when the other constituents of air are present. We denote this equilibrium pressure $p_{sat}^a$. This dependence is as follows. When the vapor in the air and liquid water are in equilibrium, then their chemical potentials must be equal. Since chemical potential $\mu$ is given by

$$\mu =\left(h-Ts\right)$$

Using the above relations, for liquid water this is

$${\mu }_f=c_f\left(T-T_R\right)+p{v}_f-c_{f}T\ln \left(T/T_R\right)$$

and for vapor

$${\mu }_v=c_f\left(T-T_R\right)+p_{sat}{v}_f+h_{fg}-c_{f}T\ln \left(T/T_R\right)+R_{v}T\ln (p_{sat}^a/p_{sat})-h_{fg}$$

Here $p_{sat}^a$ is the vapor pressure in equilibrium with liquid water. Equating ${\mu }_f$ and ${\mu }_v$ we get

$$R_{v}T\ln \left(p_{sat}^a/p_{sat}\right)=\left(p-p_{sat}\right)v_f$$ Eq.B13a

This is known as the Poynting relation [10, p. 344].

It is convenient and natural to define the relative humidity $\mathcal{H}$ as $\mathcal{H}=p_v/p_{sat}^a$ so that the above equation for entropy, Equation (B12), becomes

$$s_v=c_f\ln \left(T/T_R\right)+R_v\ln \left(1/\mathcal{H}\right)-\left(p-p_{sat}\right)v_f/T{+h}_{fg}/T$$

• c.Dry air

For dry air

$$s_a=c_{p,a}\ln \left(T/T_R\right)-R_a\ln \left(p_a/p_{atm}\right)$$

where we have assumed the reference pressure for entropy is 1 atm. Again, the last term can arise when air is mixed with vapor so that $p_a<p_{atm}$.

• d.Total entropy

The total entropy for a mixture of air, liquid water, and water vapor is then

$$S=M_a{s}_a+M_f{s}_f+M_v{s}_v$$

B4. Minimum work of water harvesting

In this analysis we assume that all mass entering and leaving the water harvester is at ambient temperature and pressure. Using the state equations given above the flow availability of an air-water mixture is

$$B=M_a\left[c_{p,a}\left(T_a-T_R\right){-c}_{p,a}{T}_a\ln \left(T_a/T_R\right)+R_a{T}_a\ln \left(p_a/p_{atm}\right)\right]$$

$$+M_v\left[c_f\left(T_a-T_R\right)-c_f{T}_a\ln \left(T_a/T_R\right)+R_v{T}_a\ln \left(\mathcal{H}\right)+p_{atm}{v}_f\right]$$

$$+M_f\left[c_f\left(T_a-T_R\right)+p_{atm}{v}_f-c_f{T}_a\ln \left(T_a/T_R\right)\right]$$

Note that the terms involving $h_{fg}$ and $p_{sat}{v}_f$ cancel out in the availability.

Here $p_a+p_v=p_{atm}$, so $p_a$ depends on $p_v$. Both the mass of the air and the total mass of water, $M_v+M_f$, are conserved in this process. This allows the above to be written

$$B=M_a\left[c_{p,a}\left(T_a-T_R\right){-c}_{p,a}{T}_{amb}\ln \left(T_a/T_R\right)+R_a{T}_a\ln \left(p_a/p_{atm}\right)\right]$$

$$+\left(M_v+M_f\right)\left[c_f\left(T_a-T_R\right)-c_f{T}_{amb}\ln \left(T_a/T_R\right)+p_{atm}{v}_f\right]$$

$$+M_v\left[R_v{T}_a\ln \left(\mathcal{H}\right)\right]$$

We will be interested in the differences in availability and so we can subtract a constant $B_0$ from this. The following is a convenient constant,

$$B_0=M_a\left[c_{p,a}\left(T_a-T_R\right){-c}_{p,a}{T}_a\ln \left(T_a/T_R\right)+R_a{T}_a\ln \left(p_{a,sat}/p_{atm}\right)\right]$$

$$+\left(M_v+M_f\right)\left[c_f\left(T_a-T_R\right)-c_f{T}_a\ln \left(T_a/T_R\right)+p_{atm}{v}_f\right]$$

where $p_{a,sat}=p_{atm}-p_{sat}^a$ is the air partial pressure under saturated conditions. $B_0$ is the availability of a saturated air-water mixture at $T_a$ where $\mathcal{H}=1$ and $p_v=p_{sat}^a$. Sometimes this is called the “dead state.” Thus,

$$B-B_0=M_a{R}_a{T}_a\ln \left(p_a/p_{a,sat}\right)+M_v{R}_v{T}_a\ln \left(\mathcal{H}\right)$$ Eq.B14a

There is no term in liquid water because it has zero work availability with this reference. The dead state here is for the mass in equilibrium with saturated air ($\mathcal{H}=1$). Some care is needed in selecting the dead state. For a discussion of this see Ref. [24]. In addition, the terms involving $v_f$ conveniently cancel.2

At this point all the effort to incorporate the temperature dependence of the input and output streams seems pointless because everything was assumed to be at one uniform temperature, $T_a$. The temperature dependence of $h$ and $s$ will prove critical, however, for analyzing the condensation harvester of Section 6.

We now have the elements needed to compute the harvester work requirement given by Equation B2. For the calculations in this section, we also assume that the process is reversible (${\mathcal{P}}_s=0)$, as we are looking at the minimum required work, the process is in steady state so that $\Delta ℇ=0$, and the heat is exchanged externally with the ambient at temperature $T_a$. Under these conditions Equation (B2a) becomes $W_{\mathit{min}}=B^{out}-B^{in}$. And so, realizing that air is conserved so that $M_a^{in}=M_a^{out}=M_a$ we have finally

$$W_{\mathit{min}}=M_v^{in}{R}_v{T}_a\ln \left(1/{\mathcal{H}}^{in}\right)-M_v^{out}{R}_v{T}_a\ln \left({1/\mathcal{H}}^{out}\right)+M_a{R}_a{T}_a\ln \left(p_a^{out}/p_a^{in}\right)$$ Eq.B15a

This result is used in Section 2, where the work is examined more fully.

Appendix C. Derivations of Equation 3.1

This appendix covers the details of deriving Equation (3.1). Two approaches are presented. The first concentrates on the water in the system, and the second on the humid air. They are equivalent, of course, but the former seems more transparent. The latter approach is that taken in most psychometric and HVAC studies. It will, however, prove useful in deriving the batch process of Appendix D.

C1: approach 1 to deriving Equation 3.1

The desired product, $M_f^{out}$ , is given by $M_f^{out}=M_v^{in}-M_v^{out}$. It is also useful to define the recovery factor, $f$, as the fraction of input water as vapor to the output as liquid,

$$f=\frac{M_f^{out}}{M_v^{in}}$$

with these definitions Equation (B15) becomes, after adding and subtracting

$${M_f^{out}R}_v{T}_a\ln \left(1/{\mathcal{H}}^{in}\right)\text{,}$$

$$W=M_f^{out}{R}_v{T}_a\left[\ln \left(1/{\mathcal{H}}^{in}\right)+\frac{M_a}{{fM}_v^{in}}\frac{R_a}{R_v}\ln \left(\frac{p_{atm}-p_v^{out}}{p_{atm}-p_v^{in}}\right)+\frac{1-f}{f}\ln \left(p_v^{out}/p_v^{in}\right)\right]$$

$p_v^{in}$ is known though $p_v^{in}=p_{sat}^a{\mathcal{H}}^{in}$ , so what is needed is $p_v^{out}$. This is found as follows. The total volume of the mixture is given by

$$M_a{R}_a{T}_a+M_v{R}_v{T}_a=p_{atm}V$$

or

$$V=\frac{M_a{R}_a{T}_a+M_v{R}_v{T}_a}{p_{atm}}$$

So that

$$p_v=\frac{M_v{R}_v{T}_a}{V}=p_{atm}\frac{M_v{R}_v}{M_a{R}_a+M_v{R}_v}$$

This gives the following needed relations.

$$p_v^{in}=p_{atm}\frac{M_v^{in}{R}_v}{M_a{R}_a+M_v^{in}{R}_v}$$

$$p_v^{out}=p_{atm}\frac{M_v^{out}{R}_v}{M_a{R}_a+M_v^{out}{R}_v}$$

Also

$$M_v^{in}=M_a\frac{R_a}{R_v}\frac{p_v^{in}/p_{atm}}{1-p_v^{in}/p_{atm}}$$

$$\frac{p_v^{out}}{p_v^{in}}=\frac{{\mathcal{H}}_{out}}{{\mathcal{H}}_{in}}=\frac{1-f}{1-{fp}_v^{in}/p_{atm}}$$ Eq.C1a

and

$$\frac{p_{atm}-p_v^{out}}{p_{atm}-p_v^{in}}=\frac{1}{1-{fp}_v^{in}/p_{atm}}$$

Inserting these into the above equation for work yields Equation (3.1),

$$W_{\mathit{min}}=M_f^{out}{R}_v{T}_a\left[\ln \left(1/{\mathcal{H}}^{in}\right)+\left(1-\frac{p_{atm}}{f{p}_v^{in}}\right)\ln \left(1-\frac{f{p}_v^{in}}{p_{atm}}\right)-\frac{1-f}{f}\ln \left(\frac{1}{1-f}\right)\right]$$ Eq.3.1a

Interestingly, both $M_a$ and $R_a$ disappear from Equation (3.1) in this formulation.

C2: approach 2 to deriving Equation 3.3

In psychometric work, where one is most concerned with moist air, a common is to define the humidity ratio, $\omega$, as the ratio of water vapor mass to dry air mass in a given volume

$$\omega \equiv \frac{M_v}{M_a}$$

for a given volume of air plus vapor, $M_v{R}_{v}T=p_{v}V$, $M_a{R}_{a}T=p_{a}V$, and $p_a+p_v=p_{atm}$,

which gives

$$\omega \equiv \frac{M_v}{M_a}=\frac{R_a}{R_v}\frac{p_v}{p_a}=\frac{R_a}{R_v}\frac{p_v}{{p_{atm}-p}_v}$$

and so

$$p_a={p_{atm}-p}_v=p_{atm}\left(\frac{1}{1+\frac{R_v}{R_a}\omega }\right)$$

and

$$p_v={p_{atm}-p}_a=p_{atm}\left(\frac{\frac{R_v}{R_a}\omega }{1+\frac{R_v}{R_a}\omega }\right)$$

$$\mathcal{H}=\frac{p_v}{p_{sat}^a}=\frac{\omega }{{\omega }_{sat}}\frac{1+\frac{R_v}{R_a}{\omega }_{sat}}{1+\frac{R_v}{R_a}\omega }$$

${\omega }_{sat}$ is $\omega$ when $p_v=p_{sat}^a\text{.}$.

Assuming there is no accumulation of water in the harvester, then

$$M_f^{out}=M_v^{in}-M_v^{out}$$

It is also useful to define the recovery factor, $f$, as the fraction of input water as vapor to the output as liquid,

$$f=\frac{M_f^{out}}{M_v^{in}}$$

in terms of $\omega$, the recovery factor, $f$, is

$$f=\frac{M_f^{out}}{M_v^{in}}=1-\frac{{\omega }^{out}}{{\omega }^{in}}$$

Inserting these into Equations (3.1) and (3).2 gives

$$ℇ-{ℇ}_0=M_a{R}_a{T}_a\left[\left(1+\frac{R_v}{R_a}\omega \right)\ln \left(\frac{1+\frac{R_v}{R_a}{\omega }_{sat}}{1+\frac{R_v}{R_a}\omega }\right)+\frac{R_v}{R_a}\mathrm{\omega }\ln \left(\frac{\omega }{{\omega }_{sat}}\right)\right]$$ Eq.C2a

and

$$W=M_a{R}_a{T}_a\left[\ln \left(\frac{1+\frac{R_v}{R_a}{\omega }^{in}}{1+\frac{R_v}{R_a}{\omega }^{out}}\right)+\frac{R_v}{R_a}{\omega }^{in}\ln \left(\frac{{\omega }_{sat}}{{\omega }^{in}}\frac{1+\frac{R_v}{R_a}{\omega }^{in}}{1+\frac{R_v}{R_a}{\omega }_{sat}}\right)-\frac{R_v}{R_a}{\omega }^{out}\ln \left(\frac{{\omega }_{sat}}{{\omega }^{out}}\frac{1+\frac{R_v}{R_a}{\omega }^{out}}{1+\frac{R_v}{R_a}{\omega }_{sat}}\right)\right]$$ Eq.C3a

Equation C2 and C3 are the forms most often seen in textbooks covering psychometric

processes [25, p. 440]. This gives the work explicitly in terms of humidity ratios but is focused on dry air mass and so not too helpful (They will prove convenient in Appendix D, however.). This is remedied by noting that

$$\frac{M_f^{out}}{M_a}=\frac{M_v^{in}}{M_a}-\frac{M_v^{out}}{M_a}={\omega }^{in}-{\omega }^{out}$$

so that

$$W=M_f^{out}{R}_v{T}_a\left[\frac{R_a/R_v}{{\omega }^{in}-{\omega }^{out}}\ln \left(\frac{1+\frac{R_v}{R_a}{\omega }^{in}}{1+\frac{R_v}{R_a}{\omega }^{out}}\right)+\frac{{\omega }^{in}}{{\omega }^{in}-{\omega }^{out}}\ln \left(\frac{{\omega }_{sat}}{{\omega }^{in}}\frac{1+\frac{R_v}{R_a}{\omega }^{in}}{1+\frac{R_v}{R_a}{\omega }_{sat}}\right)-\frac{{\omega }^{out}}{{\omega }^{in}-{\omega }^{out}}\ln \left(\frac{{\omega }_{sat}}{{\omega }^{out}}\frac{1+\frac{R_v}{R_a}{\omega }^{out}}{1+\frac{R_v}{R_a}{\omega }_{sat}}\right)\right]$$

adding and subtracting $\ln \left(1/{\mathcal{H}}^{in}\right)$ inside the brackets gives

$$W=M_f^{out}{R}_v{T}_a\left[\ln \left(1/{\mathcal{H}}^{in}\right)+\frac{R_a/R_v}{{\omega }^{in}-{\omega }^{out}}\ln \left(\frac{1+\frac{R_v}{R_a}{\omega }^{in}}{1+\frac{R_v}{R_a}{\omega }^{out}}\right)+\frac{{\omega }^{out}}{{\omega }^{in}-{\omega }^{out}}\ln \left(\frac{{\omega }^{out}}{{\omega }^{in}}\frac{1+\frac{R_v}{R_a}{\omega }^{in}}{1+\frac{R_v}{R_a}{\omega }^{out}}\right)\right]$$

Some considerable manipulation gives the form presented in Equation (3.1),

$$W=M_f^{out}{R}_v{T}_{amb}\left[\ln \left(1/{\mathcal{H}}^{in}\right)+\left(1-\frac{p_{atm}}{f{p}_v^{in}}\right)\ln \left(1-\frac{f{p}_v^{in}}{p_{atm}}\right)-\frac{1-f}{f}\ln \left(\frac{1}{1-f}\right)\right]$$ Eq.3.1b

C3: an alternative derivation of the minimum work

A different approach to Equation (3.1) is presented in this section. If we remove water as liquid from a specific mass of air and water vapor, then $d\omega =-d{M}_w/M_a$. (Removing water decreases $\omega$). Doing work on the mass increases its exergy, so that the minimum required work for this incremental change is $dW=dℇ$. Specifically

$$dW=\frac{dℇ}{d{M}_w}d{M}_w=-\frac{1}{M_a}\frac{dℇ}{d\omega }d{M}_w$$

Computing $dℇ/d\omega$ from Equation (B4) we get

$$dℇ/d\omega =M_a{R}_v{T}_{amb}\ln \left(\mathcal{H}\right)$$

so that

$$dW=R_v{T}_{amb}\ln \left(1/\mathcal{H}\right)d{M}_w$$

This is, of course, just Equation (2.2). This makes sense in that when removing an incremental amount of water from a volume we don't much affect the relative amount of water, just as in the case with the atmosphere as was assumed in deriving Equation (2.2).

This does suggest an alternative view of the minimum work requirement. Instead of a flow through device, imagine we bring in a volume of air at ambient conditions. We then extract water from this volume using a device such as the membrane and piston in Section 2, starting at an initial mass of vapor, $M_v^{in}$, and ending at $M_v^{out}$ all at a pressure $p_{atm}$. We thereafter eject that volume, which requires no work.

Thus

$$W={\int }_{M_v^{in}}^{M_v^{out}}{R_{v}T}_{amb}\ln \left(1/\mathcal{H}\right)d{M}_w$$

plugging in the value of $\mathcal{H}$ in terms of $\omega$ and using the fact that $d\omega =-d{M}_w/M_a$ gives

$$W={{M_{a}R}_{v}T}_{amb}{\int }_{{\omega }^{in}}^{{\omega }^{out}}\ln \left(1/\mathcal{H}\right)d\omega$$

Plugging in the value of $\mathcal{H}$ in terms of $\omega$ and performing the integration yields the minimum work of Equation (C3) which was shown equal to Equation (3.1).

Appendix D. Ideal cycle examples

The exergy analysis of Section 3 does give the required work for a flow-through process; however, it is opaque on what sort of physical cycles might actually produce this result. In other words, what sort of idealized cycles have zero internal entropy production. This appendix presents three such examples. None appears particularly practical; however, they do point to how such a machine could be made in principle.

D1: batch process

The first example is that of a batch process. This was already explored in Section C3, where it was shown to have the minimum work. This should be of no surprise as there was no internal entropy production. The batch approach is analogous to batch reverse osmosis for liquid water purification. Unfortunately, it is not very practical due to the large volume of air needed per volume of liquid water produced, as well as the need to keep the air well mixed to avoid diffusive losses.

D2: isothermal compression

Another approach would be to draw air-water mixture into an isothermal compressor, compress the mixture until the water vapor pressure equals the saturation pressure, remove water, and then expand the volume back to atmospheric pressure. This must yield the same result as there is no entropy production. It is instructive, however, to do the calculation much as in Section 2, but this time with air included (no membrane).

In this case, during the compression and expansion process there is no input or output mass flow. Thus, also assuming no entropy production, Equation (B4) becomes,

$$W=\Delta ℇ$$

The work on the system is just the change in its exergy under an isothermal and reversible process.

We define state 1 as the point after inputting the air-water vapor mass at atmospheric pressure, state 2 as after compressing to condense some water, and state 3 after expanding back to atmospheric pressure. Then from Equation B2a the compression work is

$$W_{12}=\left(H_2+\left(p_{atm}-p_2\right)V_2-T_a{S}_2\right)-\left(H_1+\left(p_{atm}-p_{atm}\right)V_1-T_a{S}_1\right)$$

Next, we recover some of the compression work by expanding back to atmospheric pressure. This work is

$$W_{23}=\left(H_3+\left(p_{atm}-p_{atm}\right)V_3-T_a{S}_3\right)-\left(H_2+\left(p_{atm}-p_2\right)V_2-T_a{S}_2\right)$$

The total cycle work is

$$W=W_{12}+W_{23}=\left(H_3-T_{amb}{S}_3\right)-\left(H_1-T_{amb}{S}_1\right)$$

This is just the difference of the ending and beginning available work, which was given by Equation (B15),

$$W_{\mathit{min}}=M_v^{in}{R}_v{T}_a\ln \left(1/{\mathcal{H}}^{in}\right)-M_v^{out}{R}_v{T}_a\ln \left({1/\mathcal{H}}^{out}\right)+M_a{R}_a{T}_a\ln \left(p_a^{out}/p_a^{in}\right)$$ Eq.B15b

So, the required work is, not surprisingly, the same as the minimum required work. Note that the beginning and ending volumes are not the same, as some water is condensed, but that does not matter in the total exergy change because we begin and end at atmospheric pressure. Note also that there is no work requirement to remove the water as the system is at atmospheric pressure when that is done. Some method must be arranged, however, to prevent the water from re-vaporizing during the expansion.

Besides providing another concrete example of a reversible water harvesting cycle, the purpose doing this calculation is to compute the compression work separately from the total work, i.e.,

$$W_{12}=\left(H_2-T_{amb}{S}_2\right)-\left(H_1-T_{amb}{S}_1\right)+\left(p_{atm}-p_2\right)V_2$$

All the parameters for computing $W_{12}$ are given Appendix B. Only the results of this calculation are presented here. The purpose is to show that the compression work, $W_{12}$, is much larger than $W$. The ratio of these is shown in Figure D1. For a typical humidity of 50%, the ratio is over 80. That means that a very efficient compressor-expander is needed to approach the minimum work. A 99% isentropic efficiency for the expansion and compression would roughly double the work required. This is not withstanding the fact that isothermal compression is assumed, which also presents practical implementation issues. More realistic adiabatic compression followed by cooling to atmospheric temperature would further increase the work.

A similar approach, but with adiabatic rather than isothermal expansion and compression, is to do the expansion first, which lowers the temperature below the dewpoint causing condensation. The condensed water is then removed, and the air recompressed adiabatically to atmospheric pressure for discharge. This approach also requires very high compressor-expander efficiencies, however. It can be shown that it is not reversible because when the expanded air is recompressed to atmospheric pressure for discharge, its temperature is above ambient.

Fig. D1.

Ratio of compression work to minimum required work as a function of humidity and removal fraction.

D3: adiabatic expansion cooling

Another approach, but with adiabatic rather than isothermal compression and expansion, is to do the expansion first, which lowers the temperature below the dewpoint causing condensation. The condensed water is then removed and the air recompressed adiabatically to atmospheric pressure for discharge. This approach also requires very high compressor-expander efficiencies, however. It can be shown that it is not reversible because when the expanded air is recompressed to atmospheric pressure for discharge, its temperature is above ambient. A similar approach has been proposed, but in this case the work of recompression is not recovered because the exhaust valve is opened after expansion, causing an inrush of atmospheric air [26].

Here we show that if a membrane is used to extract water vapor from air, followed by adiabatic isentropic expansion cooling to reach the dew point, followed by condensation using a heat pump to remove the heat of condensation, the process has the minimum work of Section 2. All the above examples involve isothermal processes, so this will test our temperature dependent properties, particularly the vapor pressure which was derived in Section 6.

The process follows a path similar to that shown in Fig. 2. The steps are as follows.

Step 1–2

: Draw water vapor from the atmosphere through a water vapor permeable membrane into a cylinder, as in Fig. 2, starting at zero volume to a final volume $V_2$.

Step 2–3

Expand the vapor adiabatically and isentropically, lowering the temperature to the condensation point, $T_c$ where the volume is $V_3$.

Step 3–4

Compress the vapor isothermally condensing the water while withdrawing the heat of condensation via an ideal heat pump operating between $T_c$ and ambient, $T_a$. The process is continued until all the vaper is converted to liquid. The volume is now $V_4=V_f=M_w{v}_f$.

Step 4–5

Expel the liquid water from the cylinder so that the volume is $V_5=0$.

Step 5–6

The liquid water is at temperature $T_c$, so its exergy is extracted as work, as in

Section 6.

The work for these steps is as follows. The work of the atmosphere is neglected as it will cancel out over the whole cycle.

$$W_{\mathrm{1,2}}=-p_v{V}_2={-M}_w{R}_v{T}_a$$

$$W_{\mathrm{2,3}}=-{\int }_{V_2}^{V_3}pdV=-p_2{V}_2^k{\int }_{V_2}^{V_3}\frac{1}{V^k}dV=\frac{p_2{V}_2}{k-1}\left[{\left(\frac{V_2}{V_3}\right)}^{k-1}-1\right]$$

$$=\frac{M_w{R}_v{T}_a}{k-1}\left(\frac{T_c}{T_a}-1\right)={-M}_w\left(c_{p,v}-R_v\right)\left(T_a-T_c\right)$$

These manipulations follow from the perfect gas relations ${pV=M}_w{R}_{v}T$, $k=c_{p,v}/c_{v,v}\text{,}$.

$c_{p,v}-c_{p,v}=R_v$, and $p{V}^k=constant$ for the expansion.

$$W_{\mathrm{3,4}}=p_s\left(T_c\right)\left(V_3-V_f\right)+{M_{w}h}_{fg}\left(T_c\right)\left(\frac{T_a}{T_c}-1\right)$$

$$=M_w{R}_v{T}_c-M_w{p}_s\left(T_c\right)v_f+{M_{w}h}_{fg}\left(T_c\right)\left(\frac{T_a}{T_c}-1\right)$$

The last term comes from the heat extracted by the reversible heat pump, which has a COP of $T_c/\left(T_a-T_c\right)$.

$$W_{\mathrm{4,5}}=M_w{p}_{atm}{v}_f$$

The change in specific exergy of the effluent water is $c_f\left(T_a-T_c\right)-c_f{T}_a\ln \left(T_a/T_c\right)$, which is negative and reduces the work requirement. So

$$W_{\mathrm{5,6}}=M_w\left[c_f\left(T_a-T_c\right)-c_f{T}_a\ln \left(T_a/T_c\right)\right]$$

Summing these gives the total work which is

$$\frac{W}{M_w}=h_{fg}\left(T_c\right)\left(\frac{T_a}{T_c}-1\right)+\left(c_f-c_{p,v}\right)\left(T_a-T_c\right)-c_f{T}_a\ln \left(T_a/T_c\right)+p_{atm}{v}_f-p_{sat}\left(T_c\right)v_f$$

The temperature dependence of $h_{fg}$ can be brought in through Equation B11.

$$h_{fg}\left(T_c\right)=L^0-\left(c_f-c_{p,v}\right)T_c-p_{sat}\left(T_c\right)v_f$$

Inserting this into the above equation for work gives

$$\frac{W}{M_w}=L^0\left(\frac{T_a}{T_c}-1\right)-c_f{T}_a\ln \left(T_a/T_c\right)+p_{atm}{v}_f-p_{sat}\left(T_c\right)v_f\frac{T_a}{T_c}$$

We can bring in the temperature dependence of the saturation pressures by Equation E5 taken between $T_a$ and $T_c$.

$$\ln \left(\frac{p_{sat}\left(T_a\right)}{p_{sat}\left(T_c\right)}\right)=-\frac{L^0}{R_v}\left(\frac{1}{T_a}-\frac{1}{T_c}\right)-\frac{\left(c_f-c_{p,v}\right)}{R_v}\ln \left(\frac{T_a}{T_c}\right)+\frac{p_{sat}\left(T_a\right)v_f}{R_v{T}_a}-\frac{p_{sat}\left(T_R\right)v_f}{R_v{T}_c}$$

or

$$R_v{T}_a\ln \left(\frac{p_{sat}\left(T_a\right)}{p_{sat}\left(T_c\right)}\right)=L^0\left(\frac{T_a}{T_c}-1\right)-\left(c_f-c_{p,v}\right)T_a\ln \left(\frac{T_a}{T_c}\right){+p}_{sat}\left(T_a\right)v_f-p_{sat}\left(T_c\right)v_f\frac{T_a}{T_c}$$

Solving this for $L^0\left(\frac{T_a}{T_c}-1\right)$ and inserting into the above equation for work gives

$$\frac{W}{M_w}=R_v{T}_a\ln \left(\frac{p_{sat}\left(T_a\right)}{p_{sat}\left(T_c\right)}\right)-c_{p,v}{T}_a\ln \left(T_a/T_c\right)+\left(p_{atm}-p_{sat}\left(T_a\right)\right)v_f$$

Note that the terms in $p_{sat}\left(T_c\right)v_f$ cancel out. To finish, we need to compute $T_c$. In step 2 to 3 we have for the isentropic process

$$\frac{T_a}{T_c}={\left(\frac{p_v}{p_{sat}\left(T_c\right)}\right)}^{R_v/c_{p,v}}$$

or

$$c_{p,v}{T}_a\ln \left(\frac{T_a}{T_c}\right)=R_v\ln \left(\frac{p_v}{p_{sat}\left(T_c\right)}\right)$$

Inserting this into the work equation above we get

$$\frac{W}{M_w}=R_v{T}_a\ln \left(\frac{p_{sat}\left(T_a\right)}{p_v}\right)+\left(p_{atm}-p_{sat}\left(T_a\right)\right)v_f$$

This is the same result of Section 2, and can be converted in the same way to refer to relative humidity using the Poynting effect correction so that as before

$${\frac{W}{M_f}=R}_v{T}_a\ln \left(1/\mathcal{H}\right)$$ Eq.2.2a