Abstract
Cu0.5Fe2.5O4 nanoparticles were synthesized by the self-combustion method whose XRD and FTIR analyzes confirm the formation of the desired spinel phase. The thermal evolution of conduction shows a semiconductor behaviour explained by a polaronic transport mechanism governed by the Non-overlapping Small Polaron Tunnelling (NSPT) model. DC conductivity and hopping frequency are positively correlated. The scaling of the conductivity leads to a single universal curve where the scaling parameter α has positive values, which testifies to the presence of Coulomb interactions between the mobile particles. Conduction and relaxation processes are positively correlated by similar activation energies. Nyquist diagrams are characterized by semicircular arcs perfectly modeled by an equivalent electrical circuit (R//C//CPE) indicating the contribution of the grains. The dielectric behaviour shows a strong predominance of conduction by the phenomenological theory of Maxwell-Wagner. The low values of electrical conductivity and dielectric loss and the high value of permittivity, make our compound a promising candidate for energy storage, photocatalytic and microelectronic applications.
Keywords: Copper ferrite, Self-combustion method, Conduction phenomenon, Scaling law, Dielectric behaviour
1. Introduction
The ferrite nanomaterials are widely used in various categories of technological applications such as recording heads [1], microwave devices [2], magnetic data storage [3], automotive [4], targeted drug delivery [5], electrical devices [6], ferrofluids [7], photo-catalytic applications [8], medical imaging [9], gas sensing [10] etc. These nanoparticles have been studied extensively because of their potential applications and their particular properties such as high resistivity, semiconducting properties and structural phase change with sintering temperature [11]. Also, these materials are recognized as soft magnetic materials due to their low coercivity and low eddy current loss [12] when it comes to high frequency applications such as EMI filters [13] and multilayer chip inductors [14]. The dielectric behaviour of a ferrite material is indicative of the nature of the electrical charge carriers located in it and leads to an understanding of the phenomenon of dielectric polarization. Furthermore, the properties of ferrite depend on many parameters such as the stoichiometric ratio [15], the preparation method and conditions [16] which are of great interest to control the distribution of cations, grain size, crystal phases and to understand their correlation with physical properties. Among these materials, copper ferrite represents a remarkable and very interesting versatile material [17]. Typically, copper ferrite can be presented as a tetragonal or cubic crystallographic phase depending on the distribution of cations between the tetrahedral and octahedral sites of its spinel lattice [18]. The cubic structure has a stronger magnetic moment than the tetragonal structure due to the number of Cu ions occupying the tetrahedral sites in the cubic structure [19]. The physical properties of this compound are basically correlated to the distribution of iron and copper ions on the octahedral and tetrahedral sites as follows: [Cu1−xFex] (CuxFe2−x) O4, where the square brackets and parentheses denote the tetrahedral [A] and octahedral (B) sites, respectively, and “x” is the inversion parameter which varies between 0 and 1.
Prabhu et al. [20] reported that the reduction in grain size of CuFe2O4 is accompanied by a tetragonal to cubic phase transition. Furthermore, Amer et al. [21] reported that increasing the annealing temperature induces a cubic-tetragonal-cubic phase transition in CuFe2O4 nanoparticles grown by the coprecipitation method. Copper ferrite has been widely synthesized by different methods, such as sol-gel [22], autocombustion [23], sonochemistry [24], hydrothermal [25], co-precipitation [26], solvothermal [27] and so on. Among these synthetic processes, the combustion method has been particularly appreciated for the synthesis of metal oxides due to its simplicity, short preparation time and inexpensive precursors. This method leads to homogeneous and non-agglomerated multi-component nanoparticles. This method is based on the mixture of an oxidizing agent (metal nitrates) and a reducing agent (fuel). The latter plays a very important role as it determines the crystal structure, grain size and morphology. It is clear that green synthesis processes offer a simple and efficient alternative to physical and chemical synthesis methods.
After a thorough study in the literature on this compound, we found the absence of precise and thorough study on all the physical properties (structural, morphological, electric and dielectric) of this compound substituted by copper with this percentage. Thus, the aim of this work is to systematically study the effect of the substitution of iron by copper on the physical properties of spinel ferrites and its usefulness for multidomain such as energy storage, photocatalytic and microelectronic applications. The results indicate that this compound has excellent electrical and dielectric properties, including low conductivity, high permittivity at room temperature and low frequencies, which makes them extremely attractive for the fabrication of electrical and microwave devices.
2. Experimental section
2.1. Synthesis
The reagents used are Fe(NO3)3⋅9H2O, Cu(NO3)2⋅6H2O and analytical grade glycine, purchased from Sigma Aldrich.
In a typical synthesis, stoichiometric amounts of Fe(NO3)3⋅9H2O, Cu(NO3)2⋅6H2O and glycine were dissolved in distilled water to give a mixed solution. This solution was placed on a hot plate at 80 °C under continuous magnetic stirring. As the excess distilled water evaporated, the solution was transformed into a viscous gel. This gel was then heated to 300 °C to initiate the combustion reaction and the resulting powder was carefully ground for 30 min and heated to 350 °C in an oven under an air atmosphere for 2 h. Eq. (1) shows that the reaction is:
| (1) |
2.2. Characterization
The microstructure study was carried out using a BRUKER D8 diffractometer in (θ-2θ) geometry between 20° and 70° at a step size of 0.02°/min and with a CuKα radiation source λ = 1.5406 Å. FTIR spectroscopy was performed using a Thermo Scientific Nicolet 6700 FTIR spectrometer operating between 400 and 4000 cm−1. In addition, dielectric measurements were performed in the frequency range of 1 Hz–5 MHz and the temperature range 300 K–600 K using an Agilent 4294 A dielectric impedance analyzer, a Lakeshore thermal controller and a Janis VPF-800 cryostat. The pellet made from the powder was 2.39 mm in diameter and 2.09 mm thick.
3. Results and discussion
3.1. Microstructure study
The X-ray diffractograms represented in Fig. 1a shows the formation of the spinel phase of our compound which crystallizes in the face-centered cubic structure with space group Fd-3m. The Miller indices (hkl) are indexed in Fig. 1. The lattice parameter, a, was calculated from the diffraction peak using Eq. (2) [28]:
| (2) |
where λ is the wavelength, θ is the diffraction angle and hkl are the Miller indices of the plan. For an accurate calculation of the lattice constant, the lattice parameter was calculated for each peak of the XRD pattern and then the average of these values is determined, a = 8.3541 Å which is in agreement with the previously reported results [29,30]. Also, it shows the presence of a secondary phase α-Fe2O3 with a percentage of 0.29. This percentage is determined using Eq. (3):
| (3) |
with and are the intensities of the most intense peak of α-Fe2O3 and respectively. A bibliographic study shows that it is almost impossible to get rid of the αFe2O3 phase. Indeed, Bergstein et al. [31] have shown that the α-Fe2O3 phase is present in compounds with a spinel ferrite structure and whose sintering temperature is lower than 1280 °C. Moreover, Hwang et al. [32] and Zahi et al. [33] have explained the presence of this phase by the incomplete reaction according to Eq. (4):
| MO + Fe2O3 → MFe2O4 | (4) |
where M is a divalent metal ion (like Cu2+ in our compound).
Fig. 1.
(a) X-ray diffractogram and (b) Fourier transformation infrared spectrum in the 400–1000 cm−1 ranges for Cu0.5Fe2.5O4.
To confirm the formation of the spinel phase of our compound we plot the Fourier transform infrared (FTIR) absorption spectra in Fig. 1b. It shows the presence of two broad absorption bands around 431 and 519 cm−1. The first band is attributed to the Metal-Oxygen stretching vibration in the octahedral site (νB) while the second is attributed to the Metal-Oxygen stretching vibration in the tetrahedral site (νA) [34,35]. The appearance of these two absorption bands in a frequency range below 1000 cm−1 is a characteristic of all spinel materials [36] which confirms the formation of the desired spinel phase in our compound.
The morphological study was performed using Scanning Electron Microscopy (SEM) as shown in Fig. 2a. In this figure, irregularly shaped grain agglomerations and inhomogeneous grain sizes are clearly visible, resulting in a rough and microporous surface morphology. Indeed, these agglomerations are not only due to the magnetic moments, but also, to the large surface of the particles and their interaction by the weak Van der Waals force [37]. It is therefore necessary to qualitatively describe the surface of the reaction products obtained by the self-combustion synthesis method which allowed us to obtain particles of nanometric size. Therefore, from a chemical point of view, a large surface area of particles tends to coalesce to form larger particles [38]. Moreover, the TEM image shown in Fig. 2b shows that the particles are more or less spherical. Although the distribution is inhomogeneous, they appear to be clumped together due to the magnetic property of the nanoparticles within the material. Using ImageJ software, an average size distribution of 1.93 μm was found. See Fig. 2c.
Fig. 2.
(a and b) SEM and TEM images respectively and (c) the corresponding average particle size histograms of Cu0.5Fe2.5O4.
3.2. Optical analysis
The absorbance in the UV–vis range was used to determine the optical properties of this sample. Fig. 3a shows the presence of six (6) absorption bands for the following wavelengths: 327, 365, 460, 550, 576, 626 nm. The first band is attributed to the inter-band transition i.e. the migration of electrons from the valence band to the conduction band while the other bands are associated with the intra-band transition i.e. excitonic transition [39]. The optical band gap can be estimated by linear extrapolation of ()2 as a function of photon energy (hν) using Eq. (5) [40]:
| (5) |
where α is the absorption coefficient, hυ represents the energy of the incident wave, A is a constant and n is a parameter related to the nature of the transition. In the case of a direct or indirect transition, it corresponds to 1/2 or 2 respectively. Fig. 3 shows that the gap energy value is 3.7 eV which indicates the semiconducting behaviour of this sample and makes it a promising candidate for various optoelectronic and photocatalytic applications. This gap value is consistent with the literature [41,42]. The results of our study demonstrate that this sample has bandgap energy values higher than the theoretical value required for water separation (λ > 1.23 eV). This observation is of great importance in the context of photocatalysis of sunlight. As a photocatalyst, this sample can absorb photons from sunlight thanks to their specific properties related to the high band gap. When photons are absorbed, they exceed the band gap energy and generate electron-hole pairs. These electron-hole pairs constitute the reactive species responsible for photocatalysis reactions. In the case of water splitting, these reactive species can break water down into oxygen and hydrogen, helping to produce clean, renewable energy [43].
Fig. 3.
(a) absorption spectra in the UV–Visible range and (b) the variation of (αhv)2 versus (hv) of Cu0.5Fe2.5O4.
3.3. Conductivity analysis
The variation of the conductivity as a function of frequency for different temperatures is shown in Fig. 4a. Analysis of these spectra shows the presence of two distinct regimes: a static regime at low frequencies which results in a plateau irrespective of the increase in frequency and the conductivity in this region is called the continuous conductivity. With increasing frequency, the conductivity moves away from this static regime towards a dispersive regime and the conductivity in this region is called the AC conductivity. This evolution of the conductivity is in accordance with the universal law for all oxides which is known as Jonscher’s law expressed by Eq. (6) [44].
| (6) |
where σdc represents the steady state conductivity, A is a temperature dependent factor, ω is the angular frequency and the exponent s is a temperature dependent parameter. Depending on the thermal variation of this exponent, several conduction models can be addressed to study the charge hopping mechanisms. Electronic exchange can take place by two transport processes, either by hopping over the potential barrier or by the tunnelling effect [45]. In the former case the exponent “s” decreases continuously with increasing temperature and the model responsible for the conduction is the correlated barrier hopping (CBH) model [46]. Then, in the case of a transport process by tunnel effect, this exponent shows a multiple variation with temperature. When s is independent of temperature, the conduction is dominated by the quantum mechanical tunnelling (QMT) model [47] whereas when “s” increases with temperature it is dominated by the non-overlapping small polaron tunnelling (NSPT) model [48]. In the case where “s” decreases with temperature until it reaches a minimum and then increases the overlapping large polaron tunnelling MODEL (OLPT) is responsible for the conduction process [49].
Fig. 4.
(a) Frequency response of ac conductivity at several temperatures and (b) Temperature dependence of s and 1-s of Cu0.5Fe2.5O4.
The thermal variation of the exponent “s" is illustrated in Fig. 4b. As clearly shown in this figure “s” increases with increasing temperature and therefore the transport process is of polaronic type and governed by the NSPT model. In this model “s” can be expressed by Eq. (7) [48].:
| (7) |
with KB is the Boltzmann constant, i.e., 8.617 × 10−5 eV K−1, WH represents the potential barrier to be crossed and τ0 defines the characteristic time of the relaxation. For large values of WM/kBT, the parameter “s” can be reduced and expressed by Eq. (8):
| (8) |
It is clear that from the variation of “1-s" as a function of temperature, one can deduce the value of the height of the potential barrier. As shown in Fig. 4b this height decreases with increasing temperature from 684 meV to 101 meV indicates the reduction of defect centres with increasing temperature [50].
The results of the Jonscher conductivity fit are used to define the jump frequency νH expressed by Eq. (9) [51]:
| (9) |
The variation of the dc conductivity σdc and the jump frequency νH as a function of temperature shown in Fig. S1a shows an increasing trend and as shown in Fig. S1b, they are positively correlated by a slope very close to 1. Generally, the study of the electrical transport properties requires the study of the temperature dependence of the conductivity allowing the understanding of the dynamics of the charge carriers inside the materials. Knowing that the electrical conductivity of ferrites depends on many parameters including the microstructure, the existence of a mixed valence (Fe2+/Fe3+) and the density of the charge carriers, it depends considerably on the temperature which influences the mobility and the number of charge carriers available for conduction. Under the effect of the increase in temperature, the electrical conductivity increases, which is justified by the improvement in mobility and the exponential variation in the number of charge carriers. Among the most used transport models, we applied the small polaron jump conduction model and the variable distance jump conduction model. These two modes of transport will take place near the Fermi level between the most favorable conductive sites in terms of distances and energies. The temperature dependence of the conductivity shows that it increases continuously with increasing temperature indicating a semiconducting behaviour. This behaviour is attributed to the increase in the concentration of free carriers and the enhancement of their mobility with increasing temperature which strongly reduces the barriers crossed by these charge carriers [52]. Furthermore, as the temperature increases, the moving charge carriers acquire more thermal energy to easily overcome the potential barriers encountered [53]. The study of the dynamics of these charges is done by two models of conduction processes, namely, the small polaron hopping (SPH) model and the variable distance hopping (VRH) model [54]. To determine the type of conduction mechanism in this sample, we fitted the experimental conductivity data by these two models. The variation of log(σdcT) as a function of 1000/T is shown in Fig. 5a which shows that in the high temperature region, the data are well fitted by the SPH model mathematically represented by Eq. (10) [46]:
| (10) |
where σ0 is a pre-exponential coefficient, Ea represents the energy needed to activate the conduction. This energy is 309 meV which indicates that the conduction is electronic. This value is comparable with other values reported in the literature associated with similar compounds [55,56]. On the other hand, the variation of log(σdc) as a function of T1/4 is shown in Fig. 5b which shows that in the low temperature region the conductivity spectra are perfectly fitted by the variable distance hopping (VRH) model mathematically expressed by Eq. (11) [57]:
| (11) |
where T0 is the Mott temperature which is of the order of 2.14 × 108 K.
Fig. 5.
(a) Variation of log (σdc T) versus 1000/T and (b) variation of log (σdc) versus (1/T) ¼ of Cu0.5Fe2.5O4.
These results indicate that at low temperatures the jump in charge carriers can be explained by the presence of localised trapping centres involving varying activation energies. Whereas at high temperatures these trapping centres emit short range carriers due to the thermally activated energy and conduction is governed by the SPH mechanism.
In order to gain a deeper understanding of the charge dynamics and the factors that influence the electrical transport process, we have implicated the scaling law in the conductivity spectra. In general, several scaling approaches have been proposed in the literature and are grouped by Eq. (12) [58]:
| (12) |
where F is the scaling function which is independent of temperature and νs is the scaling parameter which can be (i) νs = νH (Taylor and Isard approach), (ii) νs = σdcT. (Summerfield approach), and (iii) νs = σdcT/(T/T0) α (Baranovskii and Cordes approach).
In order to study the behaviour of frequency hopping and to determine the correlation between the two conduction regimes, we examine the validity of scaling the frequency axis by the hopping frequency (νH) [59]. The variation of σac/σdc as a function of ν/νH shown in Fig. S2a shows the tendency of these conductivity spectra to overlap over the entire temperature range explored. However, this superposition is not perfect, which may be attributed to changes in the number of possible voices for electrical transport and/or to changes in the density of thermally activated charge carriers. To examine the origin of the failure of the Taylor and Isard formalism, we introduce Summerfield’s formalism which consists in normalising the axis of the frequency by the quantity (σdcT) [60]. The variation of σac/σdc as a function of ν/(σdcT) shown in Fig. S2b shows that these spectra are perfectly superposed at low and high frequencies, whereas at intermediate frequencies they diverge from the main curve. This divergence of the spectra is probably attributed to the coexistence of different types of conduction mechanisms. In this frequency region, the transport of charge carriers is assisted by the thermal activation of various conduction processes with charge carriers of different radii. These changes are the main factors contributing to the failure of the superposition of conductivity spectra. To investigate the origin of the failure of the Summerfield formalism at intermediate frequencies, Baranovskii and Cordes [61] proposed the introduction of a parameter (T/T0) α to correct the Summerfield approach. Where T0 is the initial temperature of the measurement (in our case T0 = 300 K) and α is a factor that depends on the cationic disorder, the structural defects [62] and the strength of the coulombic interactions between the mobile charges [63]. According to Baranovskii et al. [61] and Roling et al. [63], the superposition of the conductivity spectra occurs for α = −1.3 in the absence of Coulomb interactions between the particles. Other studies have confirmed that 'α' can deviate from the value α = −1.3 and can take on positive numbers [64,65]. A quick inspection of Fig. S3 which plots the variation of σac/σdc versus ((ν/σdcT)/(T/T0)−1.3) reveals the divergence of these spectra from the intermediate frequencies onwards, indicating the presence of coulombic interactions between the moving charges. In order to obtain the optimal value of α, we applied numerous scaling tests for all isothermal curves. Fig. S3b shows the variation of σac/σdc as a function of ((ν/σdcT)/(T/T0) α) and demonstrates a perfect convergence of all conductivity spectra to a single spectrum along the temperature and frequency range. The thermal variation of α represented in Fig. S3c shows that this factor is between 1.3 ≤ α ≤ 1.66 indicating a strong coulombic interaction mechanism between the particles.
3.4. Impedance analysis
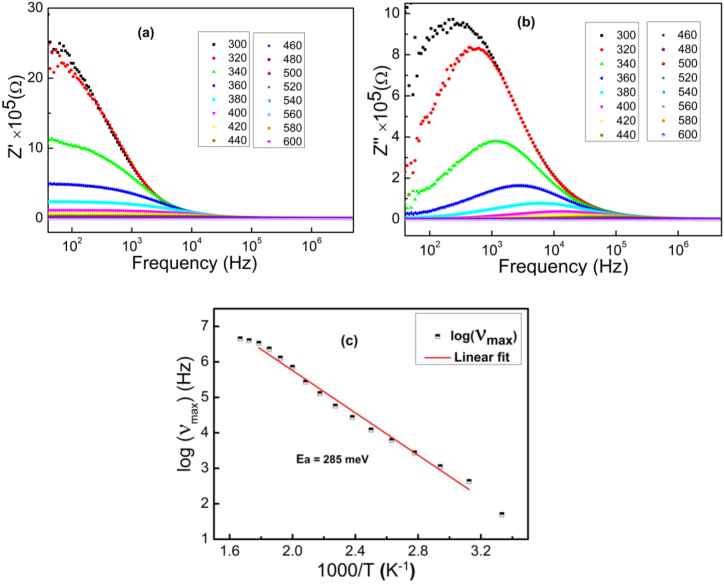
The variation of the real part of the impedance as a function of frequency for different temperatures is shown in Fig. 6a. Initially in the low frequency and high temperature region, Z′ has typically high values and then it gradually decreases with increasing temperature and frequency. This variation in the real part of the impedance could be due to the increase in the mobility of free charges and the decrease in the density of trapped carriers [66]. However, in the high frequency region, the real part of the impedance curves seems to merge independently with increasing temperature and frequency, possibly suggesting the presence of space charges [67]. This behaviour is due to the reduction of the trapping centres as the temperature increases which could be a factor responsible for the dispersion of the conductivity at high frequencies [66]. The variation of the imaginary part of the impedance as a function of frequency (50 Hz −5 MHz) for different temperatures is shown in Fig. 6b. It shows the existence of a single relaxation peak for each temperature indicating the beginning of the process of an electrical relaxation phenomenon in this compound [68]. These humps are explained by Koop’s phenomenological theory and the interfacial polarization model [69,70]. According to these models, the spinel ferrite structure is considered to be formed of two layers: a layer of highly conductive grains, separated by a layer of relatively thin and poorly conductive grain boundaries. It is known that grain boundaries are more effective at low frequencies, unlike grains which are effective at high frequencies. Therefore, these humps indicate a change in charge carrier dynamics from long-range mobility (left of peak) to short-range mobility (right of peak).
Fig. 6.
(a and b) The frequency dependence of the real and imaginary parts of impedance at several temperatures respectively and (c) the variation of ln(νmax) as a function of 1000/T.
It is clear that the frequency of these peaks shifts towards the high frequencies and that their heights decrease with increasing temperature, which demonstrates that the charge carriers involved in electrical conduction are thermally activated and confirms the semiconducting nature of this sample [71,72]. This behaviour is in agreement with that previously reported in the literature for different ferrite systems [67,73]. In the high frequency region, the convergence of the Z″ (f) spectra over the whole temperature range confirms the presence of space charges in this compound [68]. Furthermore, the frequency values of these peaks (νmax) are used to determine the activation energy of the relaxation mechanisms using Eq. (13) [72]:
| (13) |
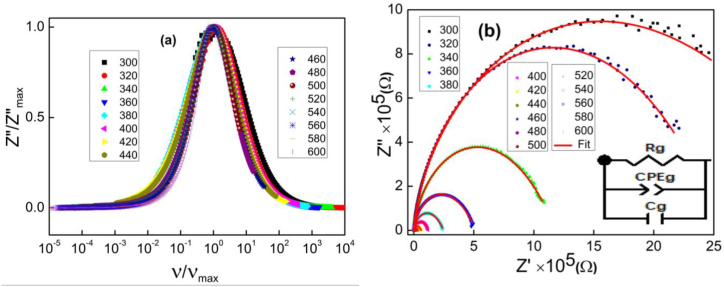
The logarithmic variation of the relaxation frequency as a function of the inverse of the temperature is shown in Fig. 6c. Note that the linear fit of these data leads to an activation energy of 285 meV which is very close to that derived from the analysis of steady state conduction. This indicates the presence of some common species involved in relaxation and electrical conduction and suggests that the charge carriers involved in both processes cross the same potential barrier [71]. In order to study the temperature dependence of relaxation mechanisms we have plotted the variation of Z″/Z″max as a function of ν/νmax in Fig. 7a. The convergence of all impedance spectra to a single universal spectrum (superposition) reflects that the increase in temperature has not induced any change in the relaxation process [74]. The impedance plot in the complex plane (i.e., Z″ vs. Z′) for the temperature range is shown in Fig. 7b. These plots are characterized by semi-circular arcs whose diameter decreases with increasing temperature. The maintenance of a single semicircle at each temperature proves that the electrical mechanism obeys a single relaxation process and the decrease in diameter with increasing temperature refers to the sharp increase in the DC conductivity [75]. In order to analyse such a diagram, it is essential to fit these impedance curves using the Zview software. The best fit of these data (red lines) leads to the sample being modeled as a single electrical circuit consisting of a parallel combination of a resistor (R), capacitor (C) and a fractal capacitor (CPE) whose equivalent configuration is [R//C//CPE]. The value of the equivalent impedance (Z*eq) is expressed by Eq. (14) [76]:
| (14) |
where C represents the capacitance and α indicates the exponent of the CPE factor. Indeed, for this equivalent circuit, the real (Z′) and imaginary (Z″) components of the impedance are expressed by Eqs. (15), (16):
| (15) |
| (16) |
Fig. 7.
(a) the variation of Z″/Z″max as a function of ν/νmax and (b) the Nyquist diagram at several temperatures of Cu0.5Fe2.5O4.
3.5. Modulus analysis
The variation of the real part of the modulus as a function of frequency for different temperatures is shown in Fig. 8a. Initially, at low frequencies, M′ is practically zero (very close to zero), which means that the electronic polarization is negligible [77].With increasing frequency, M′ is found to increase strongly with frequency, until it reaches a maximum value where it becomes insensitive to frequency. This evolution indicates a change in charge carrier dynamics (a change in charge mobility) induced by spatial confinement [78,79]. The variation of the imaginary part of the impedance as a function of frequency for different temperatures is shown in Fig. 8b. The presence of a single peak for each temperature confirms the unique process of relaxation pre-reported in the impedance analysis [80]. These peaks also confirm the change in the distance of the charge carrier jump from short distance to long distance at a particular frequency (fmax) for each temperature. In the left side of this peak the charge carrier hopping occurs at long distance while in the other side the charge carrier hopping occurs at short distance due to spatial confinement [80]. Furthermore, as shown in Fig. 9a, the linear fit of the log(νmax) variation as a function of 1000/T, leads to an activation energy of 274 meV which is similar to those deduced from the conductivity and impedance analysis [81]. In order to confirm the temperature independence of the relaxation mechanisms we have plotted the variation of M″/M″max as a function of ν/νmax in Fig. 9b. This figure shows the tendency of these curves to converge to a single universal curve in accordance with impedance scaling [74].
Fig. 8.
(a and b) The frequency dependence of the real and imaginary parts of modulus M′ at several temperatures respectively.
Fig. 9.
(a) the variation of ln(fmax) as a function of 1000/T and (b) the variation of M″/M″max as a function of ν/νmax respectively of Cu0.5Fe2.5O4.
3.6. Permittivity analysis
The analysis of the dielectric response is an additional method to understand the conduction phenomena. Based on Mott's theory, the complex dielectric constant is defined by Eq. (17) [82]:
| (17) |
where is the real part of the permittivity which characterises, the energy stored in the material, while is the imaginary part which characterises the dissipated energy.
The variation of the real part of the relative permittivity as a function of frequency for different temperatures is shown in Fig. 10a. It is clearly noticed that at low frequencies the real relative permittivity has very large values associated with the existence of various types of polarization [83]. With increasing frequency, a rapid decrease in permittivity has been observed up to a certain frequency where it slowly decreases with frequency. This decrease can be interpreted either as an increase in the concentration of free charges which induces a decrease in polarization, or as a result of the stresses faced by the dipole as it follows the field orientation [84]. For a given frequency, the permittivity is strongly dependent on temperature suggesting that both dipolar (rotational) and interfacial polarization are responsible for the permittivity [84]. The variation of the imaginary part of the relative permittivity as a function of frequency for different temperatures is shown in Fig. 10b. It shows that the increase in frequency leads to a rapid decrease in until it reaches a static value at high frequencies. In this region, the electronic exchange between the electric dipoles no longer follows the increase in the frequency of the external electric excitation, hence the slow decrease in permittivity [19]. This evolution of the dielectric behaviour is explained by the phenomenological theory of Maxwell-Wagner [69] and the Koop theory [70]. The dielectric structure of ferrite materials is composed by grains of conductive nature separated by grain boundaries of resistive nature. Consequently, the large value of the dielectric constant is due to the polarization of the space charge generated by the grain boundaries [85]. The polarization process is based on the exchange of electrons between two ions of the same mixed valence element and irregularly distributed between identical interstitial sites [86]. In this context, the electrons must necessarily pass through the grains, which are more conductive and effective at high frequencies, and the grain boundaries, which are more resistive and effective at low frequencies. As a result, the imaginary relative permittivity decreases rapidly at low frequencies due to the resistivity of the grain boundaries, whereas at high frequencies, the effects of the grains become apparent and thus the electron exchange can no longer keep up with the increase in frequency of the alternating field. This explains the slow decrease in permittivity at high frequencies. On the other hand, we notice that εr″ increases with temperature due to the fact that the charge jump is thermally activated. The dielectric loss Tan (δ) of our sample is determined from the ratio of the imaginary and real component of the permittivity as shown in Eq. (18):
| (18) |
Fig. 10.
(a and b) Variation of the real, imaginary part of the relative permittivity respectively and (c) the dielectric loss with frequency at different temperatures of Cu0.5Fe2.5O4.
The variation of the dielectric loss with frequency (50 Hz–5 MHz) for different temperatures shown in Fig. 10c, shows a similar variation of the permittivity. On the one hand, the evolution of the loss as a function of frequency can be interpreted by the fact that at low frequencies, the charge carriers require more energy to cross the joints of the resistive grains. At high frequencies, however, the charges require less energy to pass through the grains. On the other hand, the increase of the loss with increasing temperature is justified by the thermal activation of the charge carriers. As the temperature increases, the concentration of charge carriers increases, requiring more activation energy, which is reflected in the dielectric loss.
The ability of a material to store electrical energy is assessed by measuring its dielectric constant when subjected to an electric current. Higher values of dielectric constant indicate a greater charge storage capacity. On the other hand, dielectric loss represents the energy dissipated as heat when a material is subjected to an alternating electric field. Lower values of dielectric loss indicate better energy efficiency of the material, which is important in microelectronic applications where energy consumption needs to be minimized. Therefore, the dielectric results of this sample of ferrite materials, with a high dielectric constant and low dielectric loss at high frequencies, suggest that these materials can be advantageously used in energy storage applications.
4. Conclusion
In this work, we have described the electrical and dielectric properties of a spinel ferrite compound Cu0.5Fe2.5O4 prepared by the autocombustion method. The ac conductivity is interpreted by Jonscher’s universal law. The conduction mechanism is successfully explained by the NSPT model. Scaling using the Taylor and Isard approach leads to an imperfect superposition of the conductivity spectra. At the same time, using the Summerfield approach, a strong deviation of these spectra is observed. To correct this deviation, the approach of Baranovskii and Cordes was applied, which leads to a single universal curve indicating the presence of Coulombic interactions between the moving charges. The processes of conduction and relaxation are positively correlated by similar activation energies. The Nyquist diagrams reveal the presence of an arc of the circle whose diameter decreases with increasing temperature indicating that the transport process is thermally activated. The dielectric behaviour shows a strong predominance of conduction by the Maxwell-Wagner phenomenological theory.
Author contribution statement
I. El Heda: Conceived and designed the experiments; Wrote the paper.
R. Dhahri, F. Bahri, K. khirounic: Analyzed and interpreted the data.
J. Massoudi: Performed the experiments.
E. Dhahri: Contributed reagents, materials, analysis tools or data.
B. F. O. Costa: Conceived and designed the experiments.
Data availability statement
No data was used for the research described in the article.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.heliyon.2023.e17403.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- 1.Sodaee T., Ghasemi A., Paimozd E., Paesano A., Jr., Morisako A. The role of terbium cation substitution on the magnetic properties of cobalt ferrite nanoparticles. J. Magn. Magn Mater. 2013;330:169–173. [Google Scholar]
- 2.Kuanr B.K., Veerakumar V., Lingam K., Mishra S.R., Kuanr A.V., Camley R.E., Celinski Z. Size dependent microwave properties of ferrite nanoparticles: application to microwave devices. J. Appl. Phys. 2009;105 [Google Scholar]
- 3.Chakradhary V.K., Ansari A., Akhtar M.J. Design, synthesis, and testing of high coercivity cobalt doped nickel ferrite nanoparticles for magnetic applications. J. Magn. Magn Mater. 2019;469:674–680. [Google Scholar]
- 4.Praveena K., Chen H.-W., Liu H.-L., Sadhana K., Murthy S.R. Enhanced magnetic domain relaxation frequency and low power losses in Zn2+ substituted manganese ferrites potential for high frequency applications. J. Magn. Magn Mater. 2016;420:129–142. [Google Scholar]
- 5.Nigam A., Pawar S.J. Structural, magnetic, and antimicrobial properties of zinc doped magnesium ferrite for drug delivery applications. Ceram. Int. 2020;46:4058–4064. doi: 10.1016/j.ceramint.2019.10.243. [DOI] [Google Scholar]
- 6.Kumbhar V.S., Jagadale A.D., Shinde N.M., Lokhande C.D. Chemical synthesis of spinel cobalt ferrite (CoFe2O4) nano-flakes for supercapacitor application. Appl. Surf. Sci. 2012;259:39–43. [Google Scholar]
- 7.Gomes J. de A., Sousa M.H., Tourinho F.A., Aquino R., da Silva G.J., Depeyrot J., Dubois E., Perzynski R. Synthesis of core- shell ferrite nanoparticles for ferrofluids: chemical and magnetic analysis. J. Phys. Chem. C. 2008;112:6220–6227. [Google Scholar]
- 8.Sundararajan M., Sailaja V., Kennedy L.J., Vijaya J.J. Photocatalytic degradation of rhodamine B under visible light using nanostructured zinc doped cobalt ferrite: kinetics and mechanism. Ceram. Int. 2017;43:540–548. [Google Scholar]
- 9.Liu J., Deng M., Huang Z., Yin G., Liao X., Gu J. Preparation of ZnFe2O4 nanoparticles in the template of silk-fibroin peptide and their neuro-cytocompability in PC12 cells. Colloids Surf. B Biointerfaces. 2013;107:19–26. doi: 10.1016/j.colsurfb.2013.01.072. [DOI] [PubMed] [Google Scholar]
- 10.Sandu I., Presmanes L., Alphonse P., Tailhades P. Nanostructured cobalt manganese ferrite thin films for gas sensor application. Thin Solid Films. 2006;495:130–133. doi: 10.1016/j.tsf.2005.08.318. [DOI] [Google Scholar]
- 11.Yadav R.S., Kuřitka I., Vilcakova J., Havlica J., Masilko J., Kalina L., Tkacz J., Hajdúchová M., Enev V. Structural, dielectric, electrical and magnetic properties of CuFe2O4 nanoparticles synthesized by honey mediated sol–gel combustion method and annealing effect. J. Mater. Sci. Mater. Electron. 2017;28:6245–6261. doi: 10.1007/s10854-016-6305-4. [DOI] [Google Scholar]
- 12.Jalili H., Aslibeiki B., Varzaneh A.G., Chernenko V.A. The effect of magneto-crystalline anisotropy on the properties of hard and soft magnetic ferrite nanoparticles. Beilstein J. Nanotechnol. 2019;10:1348–1359. doi: 10.3762/bjnano.10.133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Batoo K.M., Hadi M., Chauhan A., Verma R., Singh M., Aldossary O.M., Bhargava G.K. High-frequency applications of bismuth-doped Co–Zn ferrite nanoparticles for electromagnetic interference filter and multilayer inductor chip fabrication. Appl. Phys. A. 2022;128:1–17. [Google Scholar]
- 14.Batoo K.M., Ansari M.S. Low temperature-fired Ni-Cu-Zn ferrite nanoparticles through auto-combustion method for multilayer chip inductor applications. Nanoscale Res. Lett. 2012;7:1–14. doi: 10.1186/1556-276X-7-112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cobos M.A., de la Presa P., Llorente I., García-Escorial A., Hernando A., Jiménez J.A. Effect of preparation methods on magnetic properties of stoichiometric zinc ferrite. J. Alloys Compd. 2020;849 [Google Scholar]
- 16.El-Shobaky G.A., Turky A.M., Mostafa N.Y., Mohamed S.K. Effect of preparation conditions on physicochemical, surface and catalytic properties of cobalt ferrite prepared by coprecipitation. J. Alloys Compd. 2010;493:415–422. [Google Scholar]
- 17.Manikandan V., Vanitha A., Kumar E.R., Chandrasekaran J. Effect of in substitution on structural, dielectric and magnetic properties of CuFe2O4 nanoparticles. J. Magn. Magn Mater. 2017;432:477–483. [Google Scholar]
- 18.Stewart S.J., Tueros M.J., Cernicchiaro G., Scorzelli R.B. Magnetic size growth in nanocrystalline copper ferrite. Solid State Commun. 2004;129:347–351. [Google Scholar]
- 19.Nedkov I., Vandenberghe R.E., Marinova T., Thailhades P., Merodiiska T., Avramova I. Magnetic structure and collective Jahn–Teller distortions in nanostructured particles of CuFe2O4. Appl. Surf. Sci. 2006;253:2589–2596. [Google Scholar]
- 20.Prabhu D., Narayanasamy A., Shinoda K., Jeyadeven B., Greneche J.-M., Chattopadhyay K. Grain size effect on the phase transformation temperature of nanostructured CuFe2O4. J. Appl. Phys. 2011;109 [Google Scholar]
- 21.Amer M.A., Meaz T., Hashhash A., Attalah S., Fakhry F. Structural phase transformations of as-synthesized Cu-nanoferrites by annealing process. J. Alloys Compd. 2015;649:712–720. [Google Scholar]
- 22.Yadav R.S., Havlica J., Hnatko M., Šajgalík P., Alexander C., Palou M., Bartoníčková E., Boháč M., Frajkorová F., Masilko J. Magnetic properties of Co1- xZnxFe2O4 spinel ferrite nanoparticles synthesized by starch-assisted sol–gel autocombustion method and its ball milling. J. Magn. Magn Mater. 2015;378:190–199. [Google Scholar]
- 23.Chauhan L., Shukla A.K., Sreenivas K. Properties of NiFe2O4 ceramics from powders obtained by auto-combustion synthesis with different fuels. Ceram. Int. 2016;42:12136–12147. [Google Scholar]
- 24.Almessiere M.A., Slimani Y., Korkmaz A.D., Guner S., Sertkol M., Shirsath S.E., Baykal A. Structural, optical and magnetic properties of Tm3+ substituted cobalt spinel ferrites synthesized via sonochemical approach. Ultrason. Sonochem. 2019;54:1–10. doi: 10.1016/j.ultsonch.2019.02.022. [DOI] [PubMed] [Google Scholar]
- 25.Paramasivan P., Venkatesh P. Controllable synthesis of CuFe2O4 nanostructures through simple hydrothermal method in the presence of thioglycolic acid. Phys. E Low-dimens. Syst. Nanostruct. 2016;84:258–262. [Google Scholar]
- 26.Salavati-Niasari M., Mahmoudi T., Sabet M., Hosseinpour-Mashkani S.M., Soofivand F., Tavakoli F. Synthesis and characterization of copper ferrite nanocrystals via coprecipitation. J. Cluster Sci. 2012;23:1003–1010. [Google Scholar]
- 27.Solano E., Perez-Mirabet L., Martinez-Julian F., Guzmán R., Arbiol J., Puig T., Obradors X., Yañez R., Pomar A., Ricart S. Facile and efficient one-pot solvothermal and microwave-assisted synthesis of stable colloidal solutions of MFe2O4 spinel magnetic nanoparticles. J. Nanoparticle Res. 2012;14:1–15. [Google Scholar]
- 28.El Heda I., Massoudi J., Dhahri R., Dhahri E., Bahri F., Costa B.F.O. Physical properties of substituted M0. 5Fe2. 5O4 ferrite spinels with M=(Mn and Zn) J. Alloys Compd. 2023;931 [Google Scholar]
- 29.Satheeshkumar M.K., Kumar E.R., Srinivas C., Prasad G., Meena S.S., Pradeep I., Suriyanarayanan N., Sastry D.L. Structural and magnetic properties of CuFe2O4 ferrite nanoparticles synthesized by cow urine assisted combustion method. J. Magn. Magn Mater. 2019;484:120–125. [Google Scholar]
- 30.El Heda I., Massoudi J., Dhahri R., Dhahri E., Bahri F., Omari L.H., Mariano J.F. The effect of transition metal substitution on the structural, elastic, optical, electrical and dielectric properties of M0.5Fe2.5O4 (M= Co and Mg) synthesized by the auto combustion method. Mater. Chem. Phys. 2023 [Google Scholar]
- 31.Bergstein A. Formation of the spinel Cu0.5Fe2.5O4 from CuFe2O4 and αFe2O3. Mater. Res. Bull. 1968;3:787–796. [Google Scholar]
- 32.Hwang C.-C., Tsai J.-S., Huang T.-H., Peng C.-H., Chen S.-Y. Combustion synthesis of Ni–Zn ferrite powder—influence of oxygen balance value. J. Solid State Chem. 2005;178:382–389. [Google Scholar]
- 33.Zahi S., Hashim M., Daud A.R. Synthesis, magnetic properties and microstructure of Ni–Zn ferrite by sol–gel technique. J. Magn. Magn Mater. 2007;308:177–182. [Google Scholar]
- 34.Henderson C.M.B., Charnock J.M., Plant D.A. Cation occupancies in Mg, Co, Ni, Zn, Al ferrite spinels: a multi-element EXAFS study. J. Phys. Condens. Matter. 2007;19 doi: 10.1088/0953-8984/19/7/076214. [DOI] [PubMed] [Google Scholar]
- 35.Ansari M.M.N., Khan S. Structural, electrical and optical properties of sol-gel synthesized cobalt substituted MnFe2O4 nanoparticles. Phys. B Condens. Matter. 2017;520:21–27. [Google Scholar]
- 36.Waldron R.D. Infrared spectra of ferrites. Phys. Rev. 1955;99:1727. [Google Scholar]
- 37.Kurian M., Thankachan S., Nair D.S., EK A., Babu A., Thomas A., Krishna KT B. Structural, magnetic, and acidic properties of cobalt ferrite nanoparticles synthesised by wet chemical methods. J. Adv. Ceram. 2015;4:199–205. [Google Scholar]
- 38.Dabagh S., Ati A.A., Ghoshal S.K., Zare S., Rosnan R.M., Jbara A.S., Othaman Z. Cu2+ and Al3+ co-substituted cobalt ferrite: structural analysis, morphology and magnetic properties. Bull. Mater. Sci. 2016;39:1029–1037. [Google Scholar]
- 39.Sharma R., Bansal S., Singhal S. Tailoring the photo-Fenton activity of spinel ferrites (MFe2O4) by incorporating different cations (M= Cu, Zn, Ni and Co) in the structure. RSC Adv. 2015;5:6006–6018. [Google Scholar]
- 40.Kislov N., Srinivasan S.S., Emirov Y., Stefanakos E.K. Optical absorption red and blue shifts in ZnFe2O4 nanoparticles. Mater. Sci. Eng. B. 2008;153:70–77. [Google Scholar]
- 41.El Heda I., Massoudi J., Dhahri R., Dhahri E., Bahri F., Costa B.F.O. Physical properties of substituted M0.5Fe2.5O4 ferrite spinels with M=(Mn and Zn) J. Alloys Compd. 2023;931 [Google Scholar]
- 42.El Heda I., Massoudi J., Dhahri R., Dhahri E., Bahri F., Omari L.H., Mariano J.F. The effect of transition metal substitution on the structural, elastic, optical, electrical and dielectric properties of M0.5Fe2.5O4 (M= Co and Mg) synthesized by the auto combustion method. Mater. Chem. Phys. 2023;296 [Google Scholar]
- 43.Bouokkeze D., Massoudi J., Hzez W., Smari M., Bougoffa A., Khirouni K., Dhahri E., Bessais L. Investigation of the structural, optical, elastic and electrical properties of spinel LiZn2Fe3O8 nanoparticles annealed at two distinct temperatures. RSC Adv. 2019;9:40940–40955. doi: 10.1039/c9ra07569k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Jonscher A.K. Dielectric relaxation in solids. J. Phys. Appl. Phys. 1999;32:R57. [Google Scholar]
- 45.Thijssen J.M., Van der Zant H.S. Charge transport and single-electron effects in nanoscale systems. Phys. Status Solidi (b) 2008;245:1455–1470. [Google Scholar]
- 46.Amghar M., Bougoffa A., Trabelsi A., Oueslati A., Dhahri E. Structural, morphological, and electrical properties of silver-substituted ZnAl2O4 nanoparticles. RSC Adv. 2022;12:15848–15860. doi: 10.1039/d2ra01800d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ghosh A. Frequency-dependent conductivity in bismuth-vanadate glassy semiconductors. Phys. Rev. B. 1990;41:1479. doi: 10.1103/physrevb.41.1479. [DOI] [PubMed] [Google Scholar]
- 48.Ghosh A. Transport properties of vanadium germanate glassy semiconductors. Phys. Rev. B. 1990;42:5665. doi: 10.1103/physrevb.42.5665. [DOI] [PubMed] [Google Scholar]
- 49.Kotkata M.F., Abdel-Wahab F.A., Maksoud H.M. Investigations of the conduction mechanism and relaxation properties of semiconductor Sm doped a-Se films. J. Phys. Appl. Phys. 2006;39:2059. [Google Scholar]
- 50.Massoudi J., Bouekkeze D., Bougoffa A., Khirouni K., Dhahri E., Bessais L. Structural, elastic, optical and dielectric properties of Li0.5Fe2.5O4 nanopowders with different particle sizes. Adv. Powder Technol. 2020;31:4714–4730. [Google Scholar]
- 51.Gharbi S., Dhahri A., Dhahri E., Barille R., Rguiti M., Omari L.H., Mariano J.F. 2022. Impact of Ca Substitution on Structural, Optical, and the Colossal Permittivity Dielectric Properties of La1-xCaxNi0.5Ti0.5O3 (x= 0 and x= 0.2) Nanomaterial's for Energy Storage Devices. [Google Scholar]
- 52.Benamara M., Dahman H., Massoudi J., Dhahri E., El Mir L., Ly A., Debliquy M., Lahem D. 2021. High Performances Room Temperature NO2 Gas Sensor Based on ZnO Nanoparticles with Oxygen Vacancies Prepared by Auto Combustion Method. [Google Scholar]
- 53.Hajlaoui M.E., Dhahri R., Hnainia N., Benchaabane A., Dhahri E., Khirouni K. Conductivity and giant permittivity study of Zn0.5Ni0.5Fe2O4 spinel ferrite as a function of frequency and temperature. RSC Adv. 2019;9:32395–32402. doi: 10.1039/c9ra06589j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Hadded A., Massoudi J., Dhahri E., Khirouni K., Costa B.F.O. Structural, optical and dielectric properties of Cu1.5Mn1.5O4 spinel nanoparticles. RSC Adv. 2020;10:42542–42556. doi: 10.1039/d0ra08405k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hosseini S.N., Enayati M.H., Karimzadeh F., Sammes N.M. Formation mechanism, crystallite growth and electrical conductivity of nano-crystalline CuxFe3-xO4 (0.75 ≤ x ≤ 1.25) spinels prepared by glycine-nitrate process. Thermochim. Acta. 2016;639:91–97. doi: 10.1016/j.tca.2016.07.001. [DOI] [Google Scholar]
- 56.Hemeda O.M., Tawfik A., Henaish A.M.A., Salem B.I. Spectral, electrical, thermoelectrical and dielectric properties of (Zn,Zr) Co-doped CuFe2O4. J. Supercond. Nov. Magnetism. 2018;31:3733–3752. doi: 10.1007/s10948-018-4582-2. [DOI] [Google Scholar]
- 57.Dhahri N., Dhahri A., Dhahri J., Hlil E., Dhahri E. Structure, magnetic and electrical transport properties of the perovskites La0.67-xEuxSr0.33MnO3. J. Magn. Magn Mater. 2013;326:129–137. [Google Scholar]
- 58.Singh D.P., Shahi K., Kar K.K. Superlinear frequency dependence of AC conductivity and its scaling behavior in xAgI-(1-x) AgPO3 glass superionic conductors. Solid State Ionics. 2016;287:89–96. [Google Scholar]
- 59.Moualhi Y., Rahmouni H., Gassoumi M., Khirouni K. Summerfield scaling model and conduction processes defining the transport properties of silver substituted half doped (La–Ca) MnO3 ceramic. Ceram. Int. 2020;46:24710–24717. [Google Scholar]
- 60.Summerfield S. Universal low-frequency behaviour in the ac hopping conductivity of disordered systems. Phil. Mag. B. 1985;52:9–22. [Google Scholar]
- 61.Baranovskii S.D., Cordes H. On the conduction mechanism in ionic glasses. J. Chem. Phys. 1999;111:7546–7557. [Google Scholar]
- 62.Mahesh Kumar M., Yee Z.G. Scaling of conductivity spectra in acceptor–doped ferroelectric SrBi2Ta2O9. Phys, Rev. B. 2005;72 [Google Scholar]
- 63.Roling B., Happe A., Funke K., Ingram M.D. Carrier concentrations and relaxation spectroscopy: new information from scaling properties of conductivity spectra in ionically conducting glasses. Phys. Rev. Lett. 1997;78:2160. [Google Scholar]
- 64.Moualhi Y., M’nassri R., Nofal M.M., Rahmouni H., Selmi A., Gassoumi M., Chniba-Boudjada N., Khirouni K., Cheikhrouhou A. Magnetic properties and impedance spectroscopic analysis in Pr0.7Ca0.3Mn0.95Fe0.05O3 perovskite ceramic. J. Mater. Sci. Mater. Electron. 2020;31:21046–21058. [Google Scholar]
- 65.Roling B., Martiny C., Murugavel S. Ionic conduction in glass: new information on the interrelation between the “jonscher behavior” and the “nearly constant-loss behavior” from broadband conductivity spectra. Phys. Rev. Lett. 2001;87 doi: 10.1103/PhysRevLett.87.085901. [DOI] [PubMed] [Google Scholar]
- 66.Lily K., Prasad K., Choudhary R.N.P. Impedance spectroscopy of (Na0.5Bi0.5)(Zr0.25Ti0.75)O3 lead-free ceramic. J. Alloys Compd. 2008;453:325–331. [Google Scholar]
- 67.Omri A., Bejar M., Dhahri E., Es-Souni M., Valente M.A., Graça M.P.F., Costa L.C. Electrical conductivity and dielectric analysis of La0.75(Ca, Sr)0.25Mn0.85Ga0.15O3 perovskite compound. J. Alloys Compd. 2012;536:173–178. [Google Scholar]
- 68.Hcini S., Oumezzine E., Baazaoui M., Rahmouni H., Khirouni K., Hlil E.K., Oumezzine M. Electrical conductance and complex impedance analysis of La0.6Pr0.1Ba0.3Mn1-xNixO3 nanocrystalline manganites. Appl. Phys. A. 2015;120:1453–1459. [Google Scholar]
- 69.Bougoffa A., Amghar M., Trabelsi A., Dhahri E., Graça M.P.F., Almeide Valente M., Costa B.F.O. New structural and dielectric phase transitions in Nanbo3 material at room temperature. 2022. Available at: SSRN 4005975. [Google Scholar]
- 70.Hajlaoui M.E., Gharbi S., Dhahri E., Khirouni K. Impedance spectroscopy and giant permittivity study of ZnFe2O4 spinel ferrite as a function of frequency and temperature. J. Alloys Compd. 2022;906 [Google Scholar]
- 71.Rahmouni H., Selmi A., Khirouni K., Kallel N. Chromium effects on the transport properties in La0.7Sr0.3Mn1-xCrxO3. J. Alloys Compd. 2012;533:93–96. [Google Scholar]
- 72.Jemai R., M’nassri R., Selmi A., Rahmouni H., Khirouni K., ChnibaBoudjada N., Cheikhrouhou A. Composition dependence of physical properties in Pr0.7Ca0.3Mn1-xNixO3. J. Alloys Compd. 2017;693:631–641. [Google Scholar]
- 73.Das P.R., Behera S., Padhee R., Nayak P., Choudhary R.N.P. Dielectric and electrical properties of Na2Pb2La2W2Ti4Ta4O30 electroceramics. J. Adv. Ceram. 2012;1:232–240. [Google Scholar]
- 74.Williams G., Watts D.C. Non-symmetrical dielectric relaxation behaviour arising from a simple empirical decay function. Trans. Faraday Soc. 1970;66:80–85. [Google Scholar]
- 75.Benali E.M., Benali A., Bejar M., Dhahri E., Graca M.P.F., Valente M.A., Costa B.F.O. Structural, morphological, Raman, dielectric and electrical properties of La1-2xBaxBixFeO3 (0.00≤x≤0.20) compounds. RSC Adv. 2021;11:36148–36165. doi: 10.1039/d1ra05299c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Bougoffa A., Massoudi J., Smari M., Dhahri E., Khirouni K., Bessais L. Study of the effect of Mn substitution on the electrical and dielectric behavior of Spinel structured materials. J. Mater. Sci. Mater. Electron. 2019;30:21018–21031. [Google Scholar]
- 77.Zaouali A., Dhahri A., Boughariou A., Dhahri E., Barillé R., Costa B.F.O., Khirouni K. High electrical conductivity at room temperature of MnCo2O4 cobaltite spinel prepared by sol–gel method. J. Mater. Sci. Mater. Electron. 2021;32:1221–1232. [Google Scholar]
- 78.Padmasree K., Kanchan D., Kulkarni A. Impedance and Modulus studies of the solid electrolyte system 20CdI2–80[xAg2O–y(0.7V2O5–0.3B2O3)], where 1≤x/y≤3. Solid State Ionics. 2006;177:475–482. doi: 10.1016/j.ssi.2005.12.019. [DOI] [Google Scholar]
- 79.Badapanda T., Sarangi S., Parida S., Behera B., Ojha B., Anwar S. Frequency and temperature dependence dielectric study of strontium modified Barium Zirconium Titanate ceramics obtained by mechanochemical synthesis. J. Mater. Sci. Mater. Electron. 2015;26:3069–3082. [Google Scholar]
- 80.Dhahri A., Rhouma F.I.H., Dhahri J., Dhahri E., Valente M.A. Structural and electrical characteristics of rare earth simple perovskite oxide La0.57Nd0.1Pb0.33Mn0.8Ti0.2O3. Solid State Commun. 2011;151:738–742. [Google Scholar]
- 81.Charguia R., Hcini S., Boudard M., Dhahri A. Microstructural properties, conduction mechanism, dielectric behavior, impedance and electrical modulus of La0.6Sr0.2Na0.2MnO3 manganite. J. Mater. Sci. Mater. Electron. 2019;30:2975–2984. doi: 10.1007/s10854-018-00575-4. [DOI] [Google Scholar]
- 82.Amghar M., Bougoffa A., Trabelsi A., Oueslati A., Dhahri E. Optical and dielectric properties of silver-substituted ZnAl2O4 spinels synthesized using a sol-gel auto-combustion method. RSC Adv. 2022;12:20348–20359. doi: 10.1039/d2ra02555h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Kakade S.G., Ma Y.-R., Devan R.S., Kolekar Y.D., Ramana C.V. Dielectric, complex impedance, and electrical transport properties of erbium (Er3+) ion-substituted nanocrystalline, cobalt-rich ferrite (Co1.1Fe1.9–xErxO4) J. Phys. Chem. C. 2016;120:5682–5693. [Google Scholar]
- 84.Lahouli R., Massoudi J., Smari M., Rahmouni H., Khirouni K., Dhahri E., Bessais L. Investigation of annealing effects on the physical properties of Ni0.4Co0.4Mg0.2Fe2O4 ferrite. RSC Adv. 2019;9:19949–19964. doi: 10.1039/c9ra02238d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Selmi A., Hcini S., Rahmouni H., Omri A., Bouazizi M.L., Dhahri A. Synthesis, structural and complex impedance spectroscopy studies of Ni0.4Co0.4Mg0.2Fe2O4 spinel ferrite. Phase Transit. 2017;90:942–954. doi: 10.1080/01411594.2017.1309403. [DOI] [Google Scholar]
- 86.Yang H., Pan L., Wang X., Deng H.-X., Zhong M., Zhou Z., Lou Z., Shen G., Wei Z. Mixed-valence-driven quasi-1D SnIISnIVS3 with highly polarization-sensitive UV–vis–NIR photoresponse. Adv. Funct. Mater. 2019;29 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
No data was used for the research described in the article.