In silico optimization of heparin microislands in microporous annealed particle (MAP) hydrogel for endothelial cell migration

Abstract

Biomaterials capable of generating growth factor gradients have shown success in guiding tissue regeneration, as growth factor gradients are a physiologic driver of cell migration. Of particular importance, a focus on promoting endothelial cell migration is vital to angiogenesis and new tissue formation. Microporous Annealed Particle (MAP) scaffolds represent a unique niche in the field of regenerative biomaterials research as an injectable biomaterial with an open porosity that allows cells to freely migrate independent of material degradation. Recently, we have used the MAP platform to heterogeneously include spatially isolated heparin-modified microgels (heparin microislands) which can sequester growth factors and guide cell migration. In in vitro sprouting angiogenesis assays, we observed a parabolic relationship between the percentage of heparin microislands and cell migration, where 10% heparin microislands had more endothelial cell migration compared to 1% and 100%. Due to the low number of heparin microisland ratios tested, we hypothesize the spacing between microgels can be further optimized. Rather than use purely empirical methods, which are both expensive and time intensive, we believe this challenge represents an opportunity to use computational modeling. Here we present the first agent-based model of a MAP scaffold to optimize the ratio of heparin microislands. Specifically, we develop a two-dimensional model in Hybrid Automata Library (HAL) of endothelial cell migration within the unique MAP scaffold geometry. Finally, we present how our model can accurately predict cell migration trends in vitro, and these studies provide insight on how computational modeling can be used to design particle-based biomaterials.

1. INTRODUCTION

A key challenge limiting the translation of biomaterial scaffolds is the ability to promote angiogenesis[1,2]. Angiogenesis is a coordinated process controlled by heparin-binding growth factors, most notably vascular endothelial growth factor (VEGF)[3–5]. This has inspired biomaterials design to control growth factor presentation in efforts to promote angiogenesis and new tissue formation[6–9].

Microporous annealed particle (MAP) scaffold is composed of an injectable slurry of individual hydrogel microspheres (microgels), which are annealed after injection to form a structurally stable scaffold with cell-scale microporosity[10]. A unique aspect of MAP scaffolds is that they allow for development of heterogenous environments through controlled ratiometric mixing of different microgel populations. Recently, we have developed heparin microislands, which are spatially limited heparin-modified microgels that can sequester and release growth factors[11,12]. We have used the MAP scaffold with heparin microislands to control the spatial organization of endogenous growth factors[11]. In published in vitro work, we observed a parabolic relationship between percentage of heparin microgels and cell migration, where 10% heparin microislands performed better than 1% and 100%[11]. Subsequently, 10% heparin microislands provided accelerated angiogenesis in a mouse model of diabetic wound healing[11]. However, the in vitro study was limited in the number of formulations that could be tested experimentally to determine the impact of microgel spacing on cell migration. Ratiometric mixtures of heparin microgels present a unique optimization challenge as we have found that changing the microisland ratio subsequently changes cellular response (Fig. 1A). This challenge represents an opportunity to use computational modeling to identify the optimal heparin microisland ratio for efficiently vascularizing MAP scaffolds.

Figure 1. Model Overview.

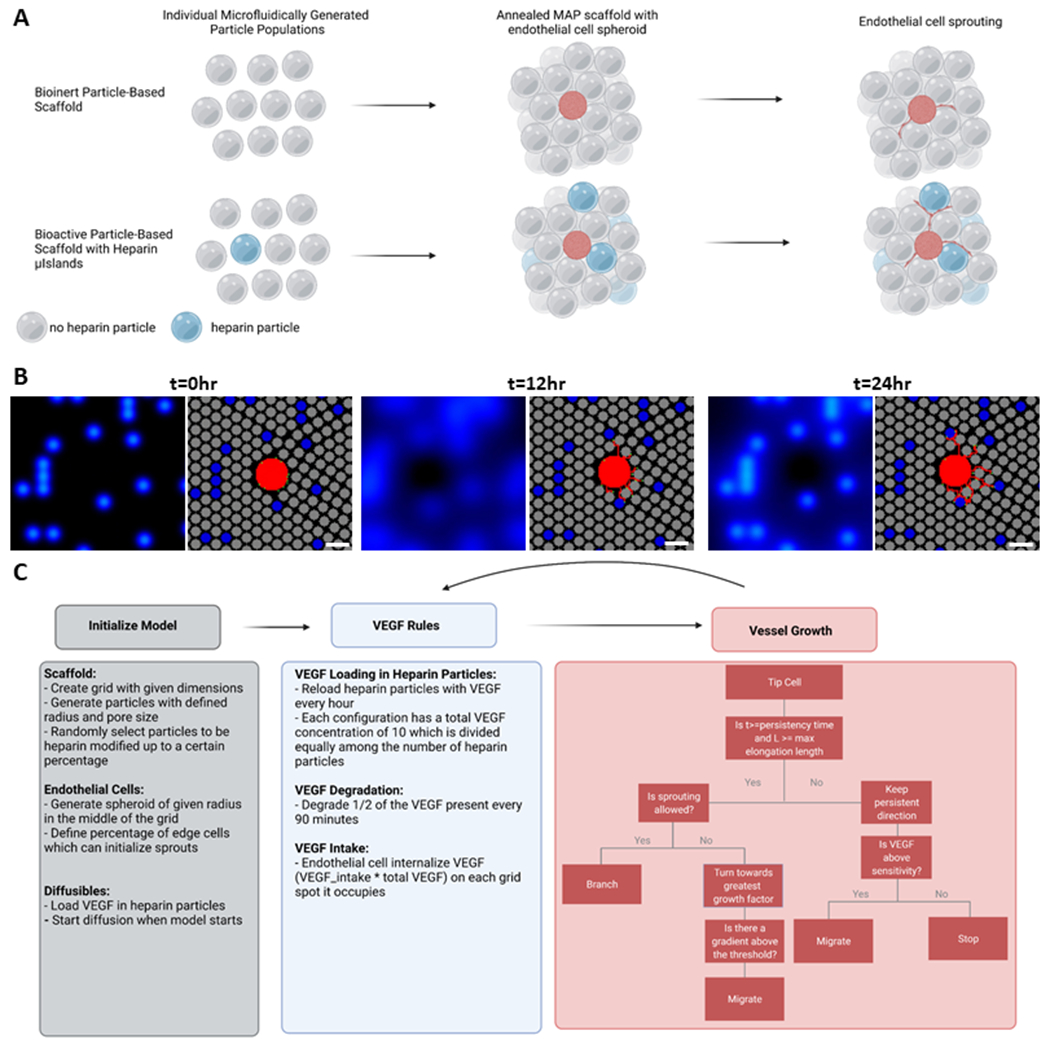
A) Schematic of a MAP scaffold with and without heparin microislands and the predicted results for an endothelial cell sprouting assay. B) Snapshots from the 2D hybrid ABM across 24 hours for the 10% heparin microislands condition. The left panel shows the diffusibles (VEGF), and the right panel is the 2D sprouting angiogenesis ABM. In the right panel, heparin particles are blue, no heparin particles are grey, and the endothelial cells are in red. Scale bar: 200μm. C) Flowchart outlining the literature-derived rules of the model.

Computational modeling of biomaterials can provide a tool for rapidly screening formulations and determining the best approaches to evaluate experimentally[13]. Experimental and computational approaches are increasingly being used in combination to gain a better understanding of angiogenesis [14–16]. Mathematical modeling has often been utilized to understand angiogenesis in wound healing[16], using ordinary or partial differential equations, with applications including identification of protein targets[17] and predictive modeling of growth factor delivery[18] to accelerate angiogenesis and wound closure. Additionally, agent-based modeling (ABM) specifically has been used to model angiogenesis, which is a rule-based modeling useful for complex spatial environments[16]. Multiple ABMs have been developed to understand angiogenesis in porous biomaterials[13,14,19,20], however these biomaterials these materials present significantly different porous geometry than MAP gel (i.e., they are not composed of spherical microparticle building blocks). Despite these models, biomaterials design influenced by in silico experiments is still a very underdeveloped field.

Importantly, this is the first demonstration of hybrid agent-based modeling of MAP scaffold vascularization to optimize material properties of the scaffold (Fig. 1B). Here we present a two-dimensional model of sprouting angiogenesis in a MAP scaffold with varying percentages of heparin microislands to predict the optimal formulation. Specifically, we chose to use hybrid modeling, which combines diffusible elements represented by partial differential equations with agent-based modeling. Diffusion is not accurately represented in traditional agent-based modeling software (e.g. NetLogo), justifying the use of Hybrid Automata Library[21]. This paper demonstrates the ability to use hybrid modeling to optimize biomaterial properties and provides a basis for future studies focused on designing the properties of microporous annealed particle (MAP) scaffolds to achieve specific cellular responses.

2. METHODS

2.1. Model Creation

2.1.1. Hybrid Agent-Based Model

A hybrid agent-based model was developed to simulate endothelial cell migration from a spheroid in a MAP scaffold. A two-dimensional ABM was developed using Hybrid Automata Library (HAL), which is a Java-based library that couples a spatial ABM with partial differential equation components to model diffusion. In this system agents are the endothelial cells (EC), which are governed by a set of literature derived rules (Fig. 1C) to control behavior. EC agent rules are defined to mimic angiogenesis including elongation, migration, and branching. In this system the diffusible is assumed to be VEGF, which is an important growth factor in angiogenesis[22].

2.1.2. Endothelial Cell Rules

The ECs start as a spheroid of a defined radius (CULTURE_RADIUS). Once the model starts running, ECs can start sprouting. Tip cells are only located at the edge of the spheroid, and a defined probability (INIT_PERCENT_HEAD) determines the likelihood that any perimeter cell will be a tip cell. During each action, each tip cell internalizes a set value of VEGF on the grid space it occupies (VESSEL_VEGF_INTAKE). A tip cell grows and elongates at a defined migration rate (MIGRATION_RATE) consistent with literature values until it reaches the maximum elongation length (MAX_ELONGATION_LENGTH). Tip cells migrate in the direction of the greatest growth factor they can sense (SIGHT_RADIUS). For a tip cell to change migration direction, it must have reached its elongation length and passed its persistency time (PERSISTENCY_TIME). Tip cells can also branch into two new tip cells, and this is governed by the amount of VEGF present. The higher the VEGF concentration, the higher probability of branching (BRANCHING_PROBABILITY) assuming the tip cell has passed its branching delay time (BRANCH_DELAY_TIME). ECs can only migrate if there is enough VEGF present (VEGF_SENSITIVITY); otherwise, they stay quiescent. ECs can only grow in the pores of the scaffold. The EC diameter is 1 grid unit, which is equivalent to 10μm. Any parameters listed with relative units are due to this model not having absolute values of growth factors and concentrations. Endothelial cell parameter values and justification are listed in Table 2.

Table 2:

Endothelial Cell Parameters

Parameter Name	Definition	Value	Justification
CULTURE_RADIUS	Spheroid radius	140 μm	Estimated from experiments
SIGHT_RADIUS	Distance an EC can sense	20 μm	[14]
PERSISTENCY_TIME	Minimum time between direction changes	3 hrs	[14]
MAX_ELONGATION_LENGTH	Required elongation length before a cell can proliferate	40 μm	[14]
MIGRATION_RATE	Chemotactic migration rate	30 μm/hr	[43]
BRANCH_DELAY_TIME	Minimum time between branching actions	6 hrs	Estimated from [14]
VEGF_SENSITIVITY	VEGF threshold necessary for endothelial cells to migrate	0.025 relative units	Manual parameter fitting
VESSEL_VEGF_INTAKE	Amount of VEGF internalized from the location an endothelial cell occupies	0.001 relative units	Manual parameter fitting
INITIAL_PERCENT_HEAD_CELLS	Percentage of initial spheroid head cells	7%	Estimated from experiments
REQUIRED_VEGF_GRADIENT	Required difference between the amount of VEGF at the new location compared to the current location	0.005 relative units	Estimated
BRANCHING_PROBABILITY	Probability of branching based on GF concentration	GF Conc.   Probability <0.05 relative units  0.4 0.05-0.25 relative units 0.55 >0.25 relative units  0.9	Estimated from [14]

2.1.3. Diffusion

VEGF diffusion from heparin particles is modeled using a calculated diffusion coefficient for VEGF in 37°C through PBS, based on the VEGF molecular weight of 45 kDa[23]. VEGF diffusion is implemented using the alternating direction implicit method in HAL. VEGF half-life is 90 minutes[24]; therefore every 90 minutes half of the VEGF was depleted from everywhere on the grid (VEGF_DEGRADATION_RATE). Heparin microislands act as a constant source of VEGF and are updated every hour (MEDIA_EXCHANGE_SCHEDULE). The total VEGF concentration within each particle configuration is 0.1 to start, and it is equally distributed between heparin particles (ex. 10% heparin microislands are loaded with a starting VEGF concentration of 1, 100% heparin microislands are loaded with a starting VEGF concentration of 0.1). The variable to represent the starting VEGF concentration in the heparin microislands is HEP_MAP_VEGF_RELEASE.

2.1.4. Scaffold Rules

The 2D scaffold is represented as equal sized particles (MAP_RADIUS) spaced by a pore diameter (MAP_SPACING), which is defined as the distance between the edges of two particles. The particles are placed in hexagonal close packing. All heparin particles (blue, Fig. 1B) are loaded with growth factor to start the model and are assumed as the only sources of VEGF. The percentage of heparin particles (HEPARIN_PERCENTAGE) is a variable. Heparin particles are distributed randomly during each simulation run. Scaffold parameter values and justification are listed in Table 1.

Table 1:

Scaffold and Diffusible Parameters

Parameter Name	Definition	Value	Justification
MAP_RADIUS	Radius of each microgel	40μm	[11]
MAP_SPACING	Approximate pore size of MAP scaffolds with 80μm particles	15μm	[10]
DIFFUSION_COEFFICIENT	Diffusion coefficient of VEGF from MAP particles	0.733	Calculated using MW of VEGF for PBS in 37°C[42]
MEDIA_EXCHANGE_SCHEDULE	How often heparin particles are loaded with VEGF	1 hr	Consistent with heparin microislands sequestering growth factors for 48hr[11]
HEP_MAP_VEGF_RELEASE	Amount of VEGF loaded in each heparin particle	0.1 relative units /HEPARIN_PERCENTAGE	Same amount of VEGF loaded per configuration
VEGF_DEGRADATION_RATE	Fraction of VEGF degraded every 90 min	0.5	Consistent with the half-life of VEGF being 90 min[24]
X_MICRONS, Y_MICRONS	Size of MAP scaffold	2000μm by 2000μm	Estimated from experiments
HEPARIN_PERCENTAGE	Percentage of heparin particles	0 - 1

2.1.5. Sensitivity Analysis

Four parameters (VEGF_SENSITIVITY, VESSEL_VEGF_INTAKE, GRID_SIZE, and VEGF_GRADIENT_DIFFERENCE) were not able to be fitted via experimental data or determined via literature values. A sensitivity analysis was conducted to determine which of these four parameters were most influential in determining model outputs. Each parameter was perturbed either 50%, 30%, or 10% above or below the baseline values to conduct a local sensitivity analysis. A sensitivity coefficient[25] was calculated using the equation $S=\frac{y_b-y_p}{{|x}_b-x_p|}*\frac{x_p}{y_p}$ where $x$ is the input value, $y$ is the output, $b$ is baseline, and $p$ is perturbed. Sensitivity coefficients were calculated for the following outputs: total blood vessel length and fold change in area over 24 hours. The mean sensitivity value was determined from 100 model runs. The most influential parameters were defined as the parameters with the highest $S$ values.

2.1.6. Manual Parameterization

Due to computational constraints, the two most influential parameters were manually fit to experimental data. A seven-by-seven matrix of possible parameter values for VEGF_SENSITIVITY and VESSEL_VEGF_INTAKE was generated, and simulations of every combination of the two parameters were run 100 times for both 10% and 100% heparin microislands. The output mean fold changes were generated, and the differences between the model and experimental outputs (Section 2.2.4) were calculated. The parameter combination with the least combined error relative to the experimental value was used in all the subsequent simulations.

2.1.7. Model Simulations

Once the model was parameterized, the values displayed in Table 1 and Table 2 were used, with heparin percentage (HEPARIN_PERCENTAGE) and the amount of VEGF loaded (HEP_MAP_VEGF_RELEASE) as the only variables. To start, 100 simulations of every 5% increment heparin microislands from 5% to 100% was run. The best 10% range was determined from these simulation runs. From there, every 1% increment in that 10% range was run 500 times to determine the best percentage to test for experimental validation. The outputs were fold change and total blood vessel lengths. If the model did not run (i.e., blood vessel length=0), the measurement was removed from the dataset. The best condition was defined as the percentage of heparin which resulted in the longest total blood vessel length.

2.1.8. Computational Framework

The simulation runs were conducted using the Java-based library, Hybrid Automata Library (HAL). The IDE IntelliJ IDEA Community Edition 2021.2.3 was used to implement the model using Java SDK 16 version 16.0.1. Model data was exported to a .CSV file for further analysis. A 16GB RAM Lenovo Yoga laptop was used to run all simulations. Each simulation took between 10 and 30 seconds to run. The model is available for public use in the following GitHub repository: https://github.com/lpruett/2DHybridABMHeparinMAP.

2.2. In Vitro Experiments

2.2.1. Sources of Materials and Cells

PEG-maleimide (10kDa) was purchased from Nippon Oil Foundry. A MMP-2 sensitive crosslinker (GCGPQGIAGQDGCG) and RGD peptide (RGDSPGC) were purchased from WatsonBio Sciences. A custom annealing macromer was synthesized as previously described[26]. Heparin sodium salt from porcine intestinal mucosa was purchased from EMD Millipore with an approximate molecular weight of 15,000 Da. Human Dermal Microvascular Endothelial Cells (HDMVECs) were purchased from ATCC (PCS-110-010). Cells were cultured and passaged according to manufacturer’s guidelines with Vascular Cell Basal Media (PCS-100-030) supplemented with Microvascular Endothelial Cell Growth Kit- VEGF (PCS-100-041).

2.2.2. Heparin Thiolation

Heparin was thiolated as previously described[11]. Briefly, a 20mg/mL solution of heparin was mixed with a 25% equivalency of PDPH and the pH was adjusted to pH=1.5. DMTMM was added in each day at a 1:1 ratio to heparin repeat units for a total of 3 days. The reaction proceeded at room temperature. After 72 hours, the heparin was dialyzed with 1M NaCl for 3 days followed by 0.01M NaCl for six one-hour washes. Next, the heparin was lyophilized and then deprotected with TCEP to expose a free thiol for linkage into the MAP network. Heparin thiolation was quantified using a PDPH absorbance assay following manufacturer’s protocol. This batch of heparin had a thiol content of 2.74e-04 mmol SH/ mg heparin.

2.2.3. Microgel Creation

A 3.2wt% no heparin formulation was created with a PEG-maleimide backbone, MMP-2 sensitive crosslinker, RGD cell adhesive peptide, and a custom annealing macromer[26] as previously described[11]. A 2.2wt% formulation was created with the same components in addition to 6mg/mL of heparin as previously described[11]. Microgels were created using a high-throughput microfluidic device and purified and sterilized as previously described. Microgels were sized as previously described using a Molecular Devices Confocal (ImageXpress) (Supplemental Figure 1).

2.2.4. Parameterization Experiment

A spheroid sprouting angiogenesis assay[11,27] was conducted to get experimental fold change values for the 10% and 100% heparin microislands conditions, to prevent model overfitting[28,29]. Briefly human dermal microvascular endothelial cells (HDMVECs) were cultured and passaged according to manufacturer’s guidelines (ATCC). For all cell studies, passage 5 cells were used. HDMVECs were labeled with CellTracker 488 and formed into spheroids using the hanging drop method as previously described[11] with 20% methylcellulose to assist with spheroid formation. Spheroids were incubated for 72 hours before starting a migration study. Heparin and no heparin microgels were incubated with complete medium and 0.2mM lithium phenyl-2,4,6-trimethylbenzoylphosphinate (LAP) at a 1:1 ratio for a minimum of 4 hours prior to starting the migration assay. Microgels were centrifuged at 18,000g for 10 minutes and excess LAP was removed. The 10% heparin microislands group was prepared by mixing 10% heparin microgels with 90% no heparin microgels. 40μL pucks were pipetted into a 48-well low-binding plate and annealed for 30 seconds using UV light (440mA, 365nm). Following annealing spheroids were pipetted on top of the scaffold. Spheroids were imaged after 30 minutes and then again at 24 hours with brightfield and fluorescent imaging on an EVOS microscope. Fold change in area was calculated by tracing of spheroids using ImageJ as previously described[11]. N=5.

2.2.5. Validation Experiment

A second spheroid sprouting angiogenesis assay was conducted to compare the computationally determined best condition to 10% and 100% heparin microisland conditions. The experiment was the same as described above, with the addition of the computational best microisland group and a no heparin microisland group as a control. The 26% heparin microisland condition was made by mixing 26% heparin microgels and 74% no heparin microgels. Spheroid area was traced using ImageJ at 24 hours, and fold change from Day 0 was calculated. N=8.

2.3. Statistics

Statistics were performed using GraphPad Prism. All model simulations are reported as mean +/− 95% confidence interval. Experimental sprouting assay results are represented as mean +/− standard deviation. Experiment results were analyzed with ANOVA followed by Tukey HSD to determine statistical differences between groups. All graphs were produced using GraphPad Prism.

3. RESULTS

3.1. Creation of 2D hybrid agent-based model of sprouting angiogenesis

We developed a 2D hybrid agent-based computational model based on literature-derived rules to predict endothelial cell sprouting from a spheroid on a MAP scaffold with heparin microislands, where the percentage of heparin microislands in the scaffold was altered (Fig. 1A,B). The choice of representing the 3D MAP environment as a 2D computational model was intentional, as it was a necessary simplifying assumption that permitted us to conduct sensitivity analyzes and further characterize the model in a manner that was computationally feasible[30]. We designed this model to mimic an in vitro spheroid migration assay that is frequently used to measure migration on biomaterial scaffolds[27]. Importantly, in this system the spheroid is placed on top of the hydrogel making the most of the early migration on a single plane, justifying the use of a 2D model.

3.2. Manual parameterization to match experimental results for two heparin microislands conditions

We conducted a univariate sensitivity analysis of the four parameters that could not be predicted from literature in order to determine how parameter perturbations affected model output. Grid size was not sensitive (S<0.05); therefore, it was not parameterized. The VEGF sensitivity, VEGF gradient difference, and VEGF intake were determined to be the three most influential parameters, with VEGF sensitivity and VEGF intake being the most influential of both total blood vessel length (Fig. 2A) and fold change in surface area (Fig. 2B). These 2 parameters were also determined to be influential when varying the parameter by 10% or 30% above or below baseline values (Supplemental Figure 2). We anticipated that these two parameters would be important because they relate to the ability of the endothelial cells to sense and impact their microenvironment as they migrate. Importantly, these two parameters are also difficult values to quantify experimentally due to an inability to confidently measure the absolute spatio-temporal values of VEGF, so we used estimates in our model.

Figure 2. Sensitivity Analysis and Model Parameterization.

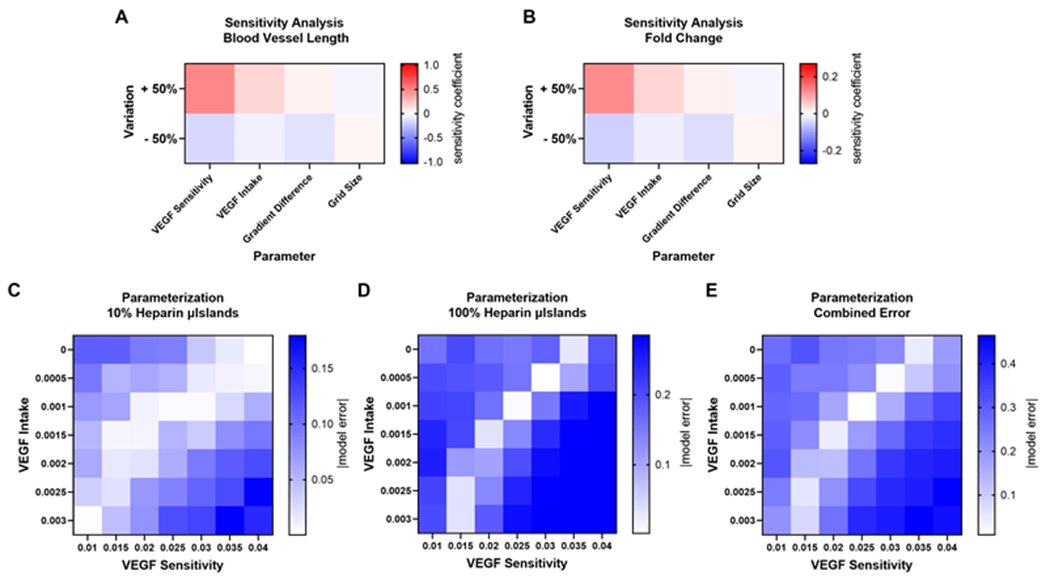
Sensitivity analysis was performed by calculating a sensitivity coefficient for each parameter by varying each parameter above or below the baseline value 50% for the A) blood vessel length output and B) surface area fold change from t=0hr output. The two most influential parameters were VEGF sensitivity and VEGF intake, which were manually parameterized to fit experimental results. Heat maps representing the difference between model and experimental results for a 7 by 7 matrix of the two most influential parameters varied for the C) 10% microislands conditions and D) 100% microislands. E) The combined error was determined by adding the two model errors, and the parameter values that produce model results closest to experimental results are determined as the parameter values.

The two most influential parameters, VEGF sensitivity and VEGF intake, were manually fitted to minimize the error between simulated and experimental results. We chose to minimize error for two of the experimental microislands conditions that we had previously investigated[11]: 10% and 100% heparin microislands. We varied these two parameters simultaneously to calculate the difference in fold change between model and experimental results for 49 different combinations. For both heparin microislands conditions, there were several parameter values that predicted experimental results well (Fig. 2C–D). To determine the values for VEGF sensitivity and VEGF intake, the model error was added for both percentages and the parameter combinations that had the minimum difference from experimental results were used, which were 0.025 and 0.001 respectively (Fig. 2E).

3.3. Optimization of heparin microislands using a 2D hybrid ABM

After parameter fitting, simulations were conducted to predict the effects of varying the percentage of heparin microislands from 5% to 100% (in increments of 5%). The model outputs included total blood vessel length and surface area fold change from day 0, which followed similar trends. We chose total blood vessel length to be the primary metric for success as we believe this output to be of greater translational impact (i.e., ability to achieve more complete biomaterial vascularity) and this output was used as the primary indicator for success in prior ABM studies of biomaterials[14]. Surface area fold change was chosen as a second metric as this is the output metric for the sprouting spheroid angiogenesis assay we are using for parameterization and validation.

Each simulation was run 100 times, and we observed a parabolic relationship between percentage of microislands and total blood vessel length (Fig. 3A–B), aligning with our previously published experimental results[11]. The model predicted that the greatest total blood vessel length occurred when heparin microislands ranged from 20% to 30%. Next, we simulated the percentage of heparin microislands in 1% increments between 20% and 30% (500 times each), and the model predicted that a configuration with 26% heparin microislands was an optimal condition which resulted in a blood vessel length of 2557μm and fold change in surface area of 1.49 (Fig.3C–D, Supplemental Figure 3).

Figure 3. Model Results.

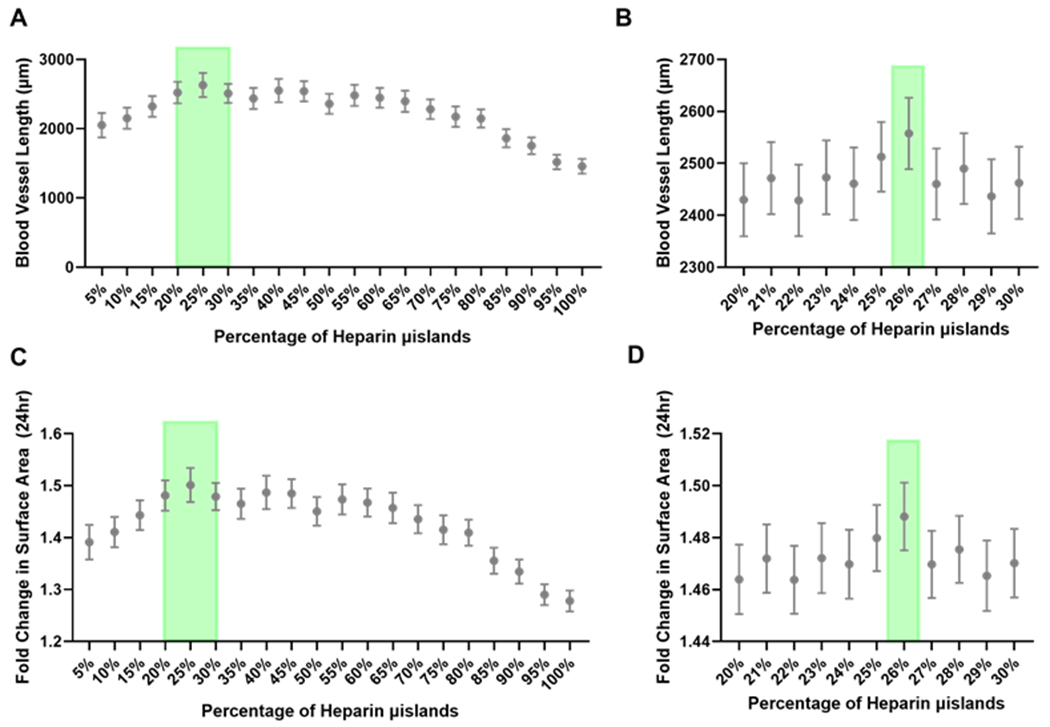
A) The heparin microislands ratio was varied from 5-100%, and the total blood vessel length was the highest in the 20-30% heparin microislands range (green shading). N=100 simulations. B) In the 20-30% range, 26% heparin microislands (green shading) resulted in the highest total blood vessel length. N=500 simulations. These same trends were seen for the fold change in surface area for the C) full range from 5-100% heparin microislands. N=100 simulations. D) In the 20-30% range, 26% (green shading) is the best microislands ratio. N=500 simulations. Mean ± 95% confidence interval is represented in graphs.

3.4. Model results accurately predict in vitro trends

To validate the model, we compared endothelial sprouting from a spheroid for 0%, 10%, 26%, and 100% heparin microisland conditions. The model trends accurately recapitulated the experimental trends, where 26% microislands induced the most endothelial migration (Fig. 4, Supplemental Figure 4). Due to the model assumption that heparin microislands are the only source of growth factor, 0% heparin microislands cannot be tested using the model; however, it is an important control to compare to heparin microislands.

Figure 4. Model Validation.

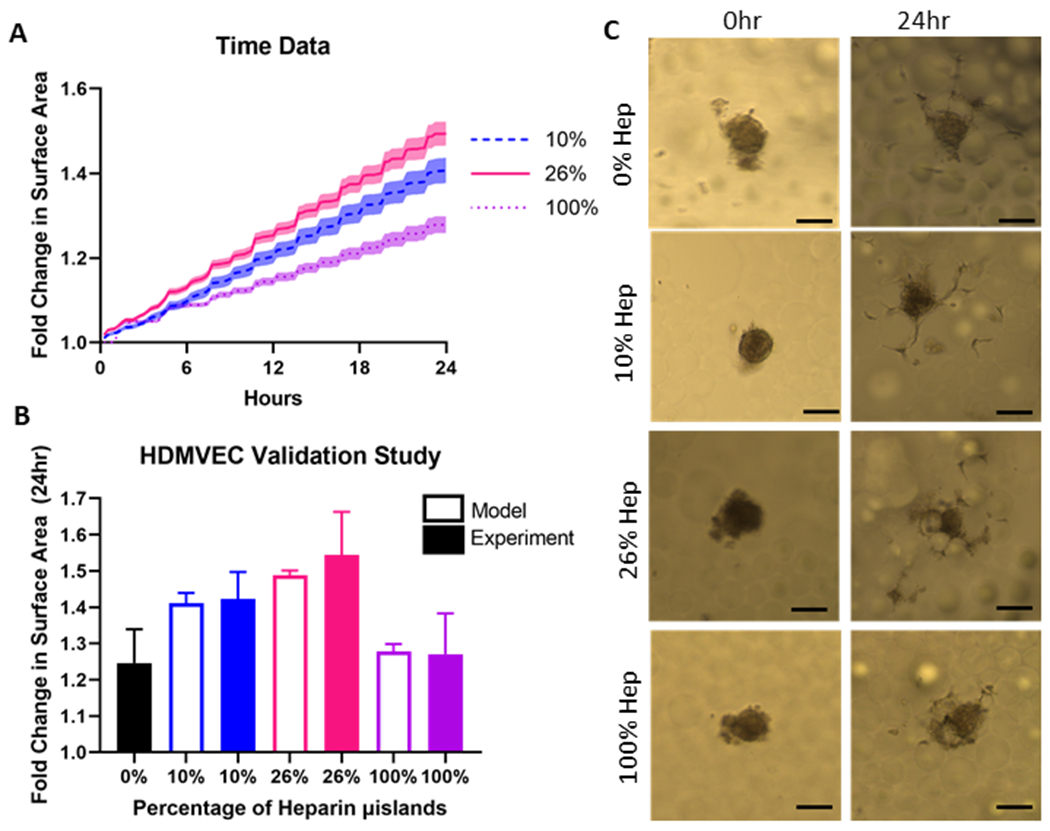
A) Time course data from the 2D hybrid ABM to compare the computational best heparin microisland percentage (26%) to the two previously investigated heparin microisland percentages (10% and 100%). Shading represents 95% confidence interval. B) Sprouting assay results to validate the model and compare experimental and model results. Experimental data is represented as mean ± standard deviation and model generated data is represented by mean ± 95% confidence interval. C) Representative endothelial cell migration images for each group at 0 and 24 hours. Scale Bar: 100μm.

3.5. Extension of the model to look at the effect of particle size on sprouting angiogenesis

We also used the model to explore how MAP scaffolds containing different particle sizes impact scaffold vascularization, as this is another tunable parameter of our scaffold (Fig 5B–D). We tested three particle sizes (30, 60, 90μm)[10] that have well characterized pore diameters (Fig. 5A). Prior to running these conditions, we conducted a sensitivity analysis for the particle radius and pore diameter similar to Figure 2, where particle size and pore size were each independently perturbed 50% above and below their baseline values. This sensitivity analysis revealed that the model was very sensitive to these parameters (Fig. 5A–B), with even higher sensitivity coefficient values than the parameters that had to be manually fitted. This aligns well with the literature showing that pore size dictates cellular behavior[31,32]. Interestingly, 30μm diameter particles induced the most endothelial cell migration (Fig. 5E–F).

Figure 5. Pore Size Variation.

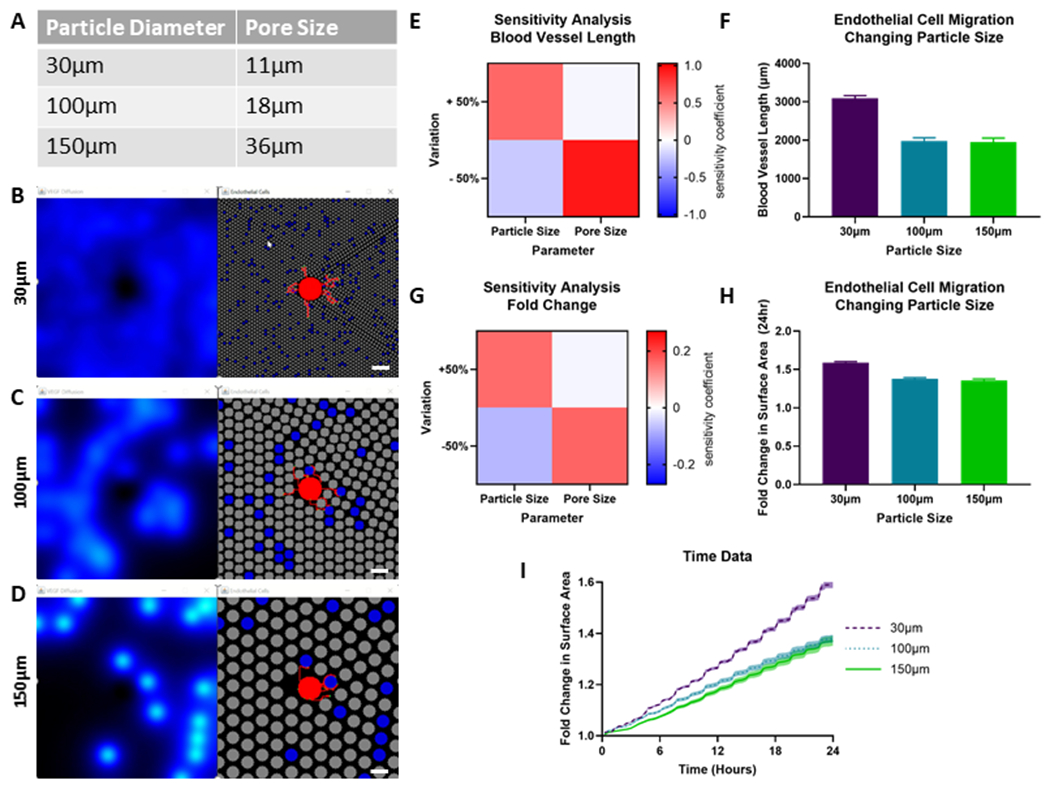
A) Particle and pore diameters tested in this model. Simulation at day 0 for the B) 30μm, C) 100μm, and D) 150μm particle diameters. The left panel represents the VEGF diffusion profiles from heparin microislands. The right panel represents the heparin particles in blue, no heparin particles in grey, and the endothelial cell spheroid and blood vessels in red. Scale Bar: 200μm. E) Sensitivity analysis and F) model results for the blood vessel length output. G) Sensitivity analysis and H) model results for the fold change in surface area output. I) Time course data for the three different particle sizes for the fold change in area output. Error bars and shading represents 95% confidence interval.

4. DISCUSSION

Computational modeling of biomaterial scaffolds has the potential to be a powerful tool to help design biomaterials with optimized properties with a decreased amount of time, resources, and effort. After we observed the parabolic relationship between percentage of heparin microislands and cell migration, we hypothesized this percentage could be optimized with hybrid agent-based modeling to achieve maximal endothelial cell migration, which is an important attribute of successful regenerative biomaterials. In this paper, we demonstrate the first hybrid agent-based model of MAP hydrogel and show it can accurately predict cell migration trends with heparin microislands in vitro.

Importantly, we chose to represent the 3D MAP environment using a 2D computational model, as this allowed us to characterize the model in a manner that was computationally feasible[30]. Further, our choice to validate this model with a spheroid sprouting assay was intentional because the early migration behavior in these experiments is typically confined to a 2D-plane[27]. We expected that a higher percentage than 10% heparin microislands would result in the greatest migration in a 2D setting due to the heparin microislands being spaced farther apart, which was consistent with our findings that 26% heparin microislands promoted the most migration (Fig. 3). In future studies, we plan to expand this model to 3D and see how this added dimension impacts the optimal percentage of heparin microislands and size of particles.

While future studies are needed to confirm that these modeling results are consistent with experimental results, our subsequent use of our model to examine different particle and pore sizes demonstrates the potential of hybrid agent-based modeling to refine particle-based scaffold parameters. We were surprised to see that the 30μm particles promoted the most migration and hypothesize that this is due to the closer proximity of the heparin microislands and growth factor production, but this mechanism needs further exploration. MAP scaffolds have numerous parameters which can be easily tuned including stiffness, degradation rate, particle size, and heterogeneity[33,34].

Agent-based modeling presents an opportunity to refine scaffold parameters while decreasing experimental time and expenses typically associated with biomaterial scaffold development. There is a clear benefit to employing computational techniques to drive biomaterials design[35,36], including reducing resource waste and removing financial barriers to exploring possible new directions. While we investigated promoting endothelial cell migration in this model, other groups have also used ABMs of porous scaffolds to predict stem cell differentiation[37], bone regeneration[38] and tissue remodeling[39], which represents opportunities for future applications expanding to projects beyond heparin microislands.

Another exciting future direction would be to further expand this hybrid ABM into a multi-scale model by integrating the hybrid ABM with a differential equations-based approach to simulate intracellular signaling networks with a higher degree of resolution than can be done using ABM alone[40]. This approach has been previously used to combine cell-signaling models with agent-based models to study angiogenesis[41]; however, this is a very underdeveloped field in biomaterials design. This approach could be leveraged with our model to depict heparin-growth factor interactions and downstream intracellular signaling more accurately in combination with the spatial details that agent-based modeling provides to create a more physiologically relevant model.

The creation of this model included several simplifying assumptions that we acknowledge as limitations to be removed in future work. First, this is 2D model of 3D geometry of a MAP scaffold, which does not fully recapitulate the porous environment the cells sense. Additionally, we have implemented very simplified growth factor interactions. In this model, we are assuming the heparin microislands are the only source of growth factor, so we cannot run the model in a scenario where there is no heparin present. We also are assuming a simplified method of keeping heparin microislands as constant sources of growth factors and degrading half of the VEGF every 90 minutes. Diffusion is the only mechanism of transport within the model, without accounting for the VEGF-heparin binding interactions. Finally, the growth factor concentrations are neither known nor absolute values, so the parameters that were based on growth factor concentrations had to be estimated and manually parameterized. This model was still able to accurately predict trends in vitro, indicating that it is useful despite these limitations.

Moving forward, this paper demonstrates the benefit of combining experimental and computational techniques to design biomaterial scaffolds. We have observed enhanced vascularization in vivo from 10% heparin microislands[11], and further improving this scaffold could have translational implications for applications requiring accelerated blood vessel growth, such as diabetic wound healing.

5. CONCLUSIONS

In conclusion, our work represents the first hybrid agent-based model for the optimization of MAP hydrogel designs, with a specific focus on the ratio of heparin microislands in the scaffold. We demonstrate that the model can accurately predict cell migration trends in vitro, including an accurate prediction of an iteration of MAP hydrogel (26% heparin microislands) with improved spheroid outgrowth over our previously published scaffold[11] (10% heparin microislands). This study generates insight on how computational modeling can be used to assist the design of particle-based biomaterials, making this a promising avenue to accelerate biomaterials development.

Table 3:

Rules Overview and Justification

Rule	Justification
Endothelial cells migrate towards highest concentration of VEGF	[43]
Endothelial cells internalize VEGF	[44]
Branching probability increases with increasing VEGF concentration	[14]
Heparin microgels are a constant source of growth factor	[11]

Statement of Significance.

While the combination of experimental and computational approaches is increasingly being used to gain a better understanding of cellular processes, their combination in biomaterials development has been relatively limited. Heparin microislands are spatially isolated heparin microgels; when located within a microporous annealed particle (MAP) scaffold, they can sequester and release growth factors. Importantly, we present the first agent-based model of MAP scaffolds to optimize the ratio of heparin microislands within the scaffold to promote endothelial cell migration. We demonstrate this model can accurately predict trends in vitro, thus opening a new avenue of research to aid in the design of MAP scaffolds.