A meta-analysis approach for evaluating the effectiveness of complex multisite programs

Abstract

The National Institutes of Health (NIH) created the Building Infrastructure Leading to Diversity (BUILD) initiative to incentivize undergraduate institutions to create innovative approaches to increasing diversity in biomedical research, with the ultimate goal of diversifying the NIH-funded research enterprise. Initiatives such as BUILD involve designing and implementing programs at multiple sites that share common objectives. Evaluation of initiatives like this often includes statistical analyses that combine data across sites to estimate the program’s impact on particular outcomes. Meta-analysis is a statistical technique for combining effect estimates from different studies to obtain a single overall effect estimate and to estimate heterogeneity across studies. However, it has not been commonly applied to evaluate the impact of a program across multiple different sites. In this chapter, we use the BUILD Scholar program—one component of the broader initiative—to demonstrate the application of meta-analysis to combine effect estimates from different sites of a multisite initiative. We analyze three student outcomes using a typical “single-stage” modeling approach and a meta-analysis approach. We show how a meta-analysis approach can provide more nuanced information about program impacts on student outcomes and thus can help support a robust evaluation.

INTRODUCTION

The Building Infrastructure Leading to Diversity (BUILD) initiative is one of the main components of the Diversity Program Consortium (DPC), which was funded by the National Institutes of Health (NIH) to increase diversity in the study of biomedical research and, ultimately, in NIH-funded research. BUILD focuses on the undergraduate experience and involves implementing a range of interventions at 10 diverse, primarily undergraduate institutions across the United States. Evaluation of the BUILD initiative is part of the consortium-wide evaluation effort described in Chapter 1 by Guerrero et al.

As part of the consortium-wide evaluation, the DPC developed Hallmarks of Success that correspond to the three levels of program impact—the student, faculty/mentor, and institutional levels. These are key indicators at critical training and career transition points toward a scientific research career. Hallmarks for undergraduate students include the intent to pursue a biomedical research career, high self-efficacy as a science researcher, and high science identity.

The plan for evaluation of the multisite BUILD initiative includes statistical analyses of the Hallmarks of Success, comparing students with and without exposure to BUILD programs. We were especially interested in understanding outcomes for students referred to as BUILD Scholars—undergraduate students with the highest levels of exposure to BUILD on each campus. BUILD Scholars were admitted into research training and mentorship programs at their institutions that were aimed at supporting their research career training and persistence into biomedical graduate study and/or the biomedical workforce.

Statistical analyses evaluating the impact of BUILD on the student Hallmarks of Success are facilitated by several advantages, including common measures across sites and longitudinal data on student outcomes through annual survey data collection (McCreath et al., 2017). There are, however, important challenges. Each of the 10 BUILD institutions designed activities for its BUILD Scholar program, leading to substantial program heterogeneity. Additionally, each site had its process for selecting students for participation in BUILD Scholar programs, leading to heterogeneity in baseline characteristics of BUILD-exposed students at each site as well as baseline differences between BUILD-exposed students and their non-BUILD counterparts. Each BUILD institution also represents a different educational context, with the schools varying in institutional type, size, minority-serving-institution status, and racial and ethnic demographic composition. This considerable heterogeneity reflects the diversity of the educational landscape and thus can be viewed as a strength; however, it also creates a challenge to select appropriate statistical methods to estimate the impact of BUILD and assess its generalizability. Ideally, the utilized statistical methods for program evaluation must account for the multi-program, multisite context.

Many evaluations of multisite programs have used a regression model fit to the combined data from all sites for quantitative analysis. For example, Kitchen, Sonnert, and Sadler (2018) examined the impact of college-run high school summer programs on students’ end-of-high-school STEM career aspirations. They combined student data from programs at 27 colleges and universities into a single propensity-weighted logistic regression model. In contrast, some authors have advocated for using a meta-analysis approach (Mumford, Steele, & Watts, 2015). Meta-analysis is a two-stage statistical modeling technique; estimates of intervention or program effects are obtained for individual studies or sites and then these estimates are combined to yield a synthesized result.

For a quantitative multisite program evaluation, a meta-analysis approach has several potential advantages over fitting a regression model to the combined data, which we call a single-stage modeling approach. For instance, in a multisite evaluation where several sites have implemented a similar program, but with site-level differences in study design, eligibility criteria for participants, or data collected, such factors can make it difficult to combine the data into a single dataset and single analysis model. However, in a meta-analysis, if individual participant data are available, evaluators can conduct customized site-specific analyses, obtain site-specific estimates, and then combine the estimates across all sites into a single summary estimate. Another advantage is that meta-analysis also has formalized methods for characterizing heterogeneity in the treatment (program) effect. Since some degree of heterogeneity is expected for a complex multisite program, having established methods for quantifying the heterogeneity can add rigor to an analysis.

Although meta-analysis has potential advantages for quantitative evaluation of a multisite program, it is rarely cited as a statistical approach in evaluation literature and likely underutilized. In this chapter, we use student-level survey data from the BUILD evaluation to demonstrate the use of meta-analysis as a quantitative modeling framework for evaluating a complex multisite program and discuss the advantages and disadvantages of the approach compared to a single-stage statistical model. The question we explore through this use of meta-analysis is: What was the impact of participation as a BUILD Scholar during a student’s first undergraduate year on three outcomes: intent to pursue a biomedical career, research self-efficacy, and science identity? We note that because the analysis in this chapter was conducted for pedagogical purposes, we have made various simplifications to it; thus, the results here are not intended to be interpreted as the final quantitative evaluation for these outcomes.

METHODS

Our goal was to apply and compare a single-stage modeling approach and a meta-analysis approach for estimating the effect of participation in the BUILD Scholar program on three Hallmarks of Success outcomes at the end of participants’ freshman year. Our analyses involved comparing outcomes between BUILD Scholars and comparison students not involved in BUILD at the same institutions, controlling for potential confounders.

BUILD Scholars

BUILD Scholars are the most intensely treated and supported group of undergraduate students at each BUILD site. Involvement includes financial support, research training, academic support, extensive advising and mentoring, and other supports and resources. Compulsory and structured participation in a host of BUILD activities is common for this group. Additional information on BUILD activities can be found in Chapter 5 by Maccalla et al. Each institution designed its own Scholar program, creating variation by site in the extent to which each program component was delivered. Additionally, selection criteria varied from site to site, but generally involved an interest in science and research and a minimum high school grade-point average.

Sample

Among the 10 BUILD sites, four decided to open their BUILD Scholar program to first-year students; the other sites enrolled students in their junior and senior years into the BUILD Scholar program. BUILD staff at each site reviewed applications and selected candidates. All first-year BUILD Scholars were full-time, first-time college students entering college directly from high school and planning to obtain a bachelor’s degree or above. The present analysis involves students at the four sites that offered the BUILD Scholar program to first-year students, which we refer to as Sites A, B, C and D. To help ensure comparability with BUILD Scholars, the pool of non-BUILD-Scholar comparison students was restricted to those who were full-time, first-time college students who were entering college directly from high school and planning to obtain a bachelor’s degree or above.

Data sources

Student survey data were collected through the Higher Education Research Institute’s (HERI) Freshman Survey (TFS) and the DPC’s Student Annual Follow-Up Survey (SAFS). The TFS was administered to incoming first-year students before they started their first-semester classes. The SAFS was administered to continuing undergraduate students at BUILD sites and was open for responses from mid-spring to early summer. By the time they responded to the SAFS, most BUILD Scholars had received several months of BUILD Scholar interventions. We used data from students who entered college in the fall of 2016, 2017, 2018, and 2019, and who completed both the TFS and the SAFS.

Outcomes

The outcome variables were: (a) intent to pursue a biomedical career, measured by the survey item “Will you pursue a science-related research career?” (response categories “definitely no,” “possibly no,” “uncertain,” “possibly yes,” and “definitely yes,” scored 1 to 5); (b) research self-efficacy, a construct measured by a scale of six items (responses on a 5-point scale from “not confident at all” to “absolutely confident”); and (c) science identity, a construct measured by a scale of four items (responses on a 5-point scale from “strongly disagree” to “strongly agree”). These variables were collected on both the TFS and the SAFS.

Covariates

Participation in the BUILD Scholar program was not randomly assigned; rather, students were selected to participate in the program, creating nonequivalent comparison groups of BUILD Scholars and students without BUILD participation. To address selection bias, for both analytic approaches we used propensity weighting to balance covariates. The covariates used in the propensity weighting, which were collected on the TFS (baseline), were: (a) the outcome variable at baseline; (b) race/ethnicity, coded as Asian, Black, Hispanic, White, or other (including two or more race/ethnicities); (c) gender identity, coded as man, woman, or other; (d) first-generation college student (yes/no); (e) receipt of a Pell grant (yes/no); (f) high school GPA; and (g) intended major, coded as biomedical natural sciences, biomedical social/behavioral sciences, or non-biomedical. The propensity score models also included site and cohort.

Propensity weighting

Propensity weighting uses propensity scores to construct weights for individuals such that the weighted data are balanced on covariates. We estimated propensity scores using the twang package in R (Griffin et al., 2014). The twang package implements gradient boosted modeling, a machine learning method, to estimate propensity scores and associated weights. We used the propensity score weights to estimate the average effect of treatment on the treated (ATT). The ATT is the effect of the treatment (program) on the population potentially exposed to the treatment. This is contrasted with the average treatment effect, which estimates the potential effect of the treatment on the wider population (Guo & Fraser, 2015). Given that our focus is meta-analysis, we do not provide further details on the propensity score methods.

Single-stage modeling approach

For comparison with the meta-analysis approach, we obtained an estimate of the effect of the BUILD Scholar program on each outcome using single-stage models that combined data across all sites. This consisted of a simple linear regression model with the outcome variable at follow-up (SAFS during spring of freshman year) as the dependent model and BUILD Scholar (yes/no) as the predictor, fit using propensity weights to balance covariates. Site was included as a fixed effect. The regression coefficient for BUILD Scholar from this model provides an estimate of the mean difference in the outcome at follow-up that is attributable to the BUILD Scholar program, which is assumed to be the same at each site—that is, the program effects are not heterogeneous.

Meta-analysis approach

The meta-analysis was conducted in two stages. First, we obtained site-specific estimates of program effects by fitting models to the data at each site. These models followed the same procedure as the single-stage modeling approach described above except that the data were site-specific. After obtaining the site-specific estimates, we meta-analyzed the estimated mean differences for each site and their standard errors using a random effects model. We conducted the meta-analysis using the metaphor package in R (Viechtbauer, 2010).

RESULTS

Table 1 shows the number of BUILD Scholars and potential comparison students at each site. The number of BUILD Scholars ranged from nine to 80 at the four sites; the number of comparison students was much larger, ranging from 255 to 904.

TABLE 1.

Sample sizes of BUILD Scholars and comparison students at the four sites

Site	BUILD Scholars	Comparison students
A	9	255
B	80	904
C	66	872
D	15	543
Total	170	2574

Single-stage modeling approach

The top section of Table 2 provides program effect estimates from the single-stage modeling approach, which fits a single model to data from all sites combined. Program effects are estimated as mean differences in each outcome variable for BUILD Scholars compared to comparison students. We present mean differences, both unadjusted for any covariates and after propensity weighting to balance covariates. The mean differences are statistically significant (p < 0.0001) for all three outcomes in unadjusted analysis and are attenuated after propensity weighting but remain significant (all p < 0.05). The propensity-weighted mean differences range from 0.22 for Intent to Pursue to 0.29 for Science Identity. The single-stage model assumes these effects are the same across sites.

TABLE 2.

Results of single-stage modeling and meta-analysis approaches

	Intent to pursue	Research self-efficacy	Science identity
Single-stage modeling results
Unadjusted mean difference (SE)	0.74 (0.11)	0.39 (0.08)	0.69 (0.07)
p-value	<0.0001	<0.0001	<0.0001
Propensity-weighted mean difference (SE)	0.22 (0.09)	0.25 (0.08)	0.29 (0.06)
p-value	0.011	0.002	<0.0001
Meta-analysis results
Summary effect estimate (SE)	0.27 (0.08)	0.18 (0.15)	0.32 (0.14)
p-value	0.001	0.25	0.002
Heterogeneity, I2	3.1%	64.4%	76.5%
p-value	0.37	0.045	0.002

Abbreviation: SE, standard error

Meta-analysis approach

The bottom section of Table 2 summarizes key results from the random effects meta-analysis model for each outcome. All results use propensity weighting to adjust for covariates in the site-specific analysis. The summary effect estimates are somewhat higher for two outcomes and lower for the third compared to those obtained from the single-stage models. In contrast to the single-stage models, which found statistical significance at the 0.05 level for all three outcomes, in the meta-analysis, statistical significance is not evident for Research Self-Efficacy (p = 0.25).

Figure 1 presents forest plots showing the site-specific estimates as well as the summary-effect estimates. Variability in the effect estimates across sites is evident for all three outcomes. A useful statistic for quantifying heterogeneity is the I² statistic, which describes the percentage of the total variability in effect estimates that is due to real differences in effect sizes rather than sampling variability. Table 2 reports the I² statistics for each outcome as well as p-values for tests of the null hypothesis that heterogeneity is zero. The p-values depend strongly on the number of sites, which is small here. The I² values vary considerably among the outcomes. A rough guide to interpretation is that values of 25%, 50%, and 75% might be considered low, moderate, and high heterogeneity, respectively (Higgins, Thompson, Deeks, & Altman, 2003). In these data, there is very little heterogeneity for Intent to Pursue (I² = 3.1%), moderate to high heterogeneity for Research Self-Efficacy (I² = 64.4%) and high heterogeneity for Science Identity (I² = 76.5%).

FIGURE 1.

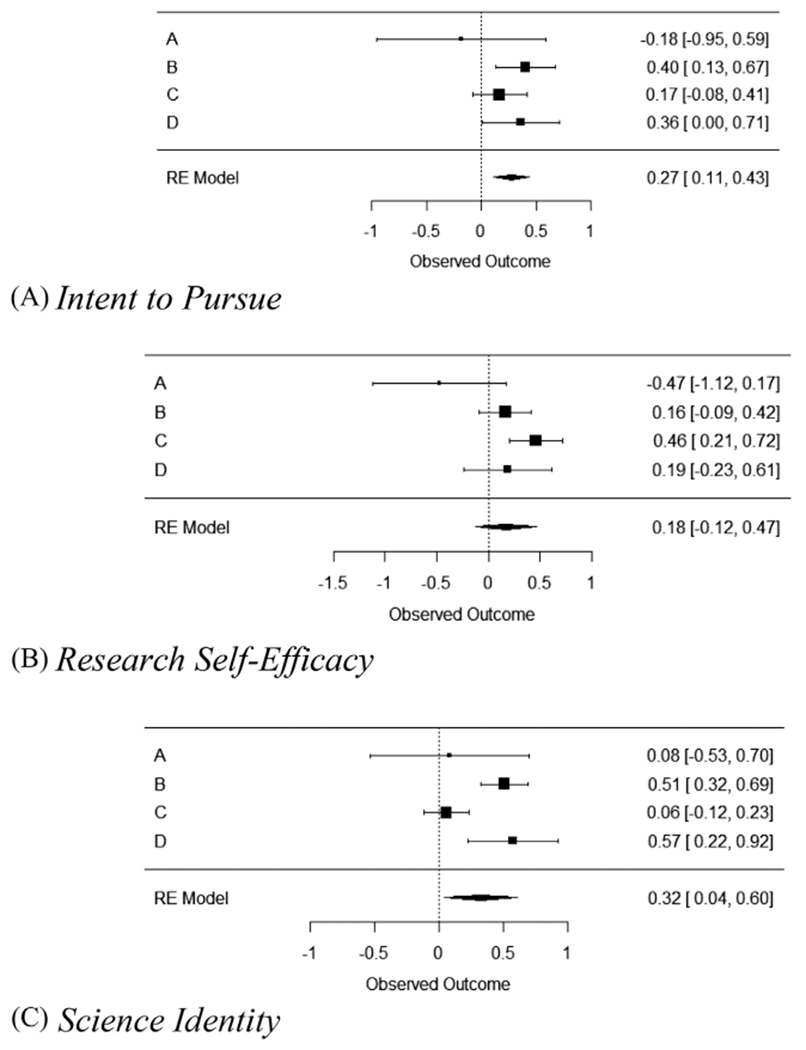
Meta-analysis forest plots for the three outcomes of interest

DISCUSSION

We have demonstrated the application of meta-analysis for evaluating multisite programs such as the BUILD initiative. In particular, we applied a meta-analysis approach to compare three outcomes for first-year students in the BUILD Scholar program compared to first-year students at the same campuses who did not participate in the program. This represents an application of meta-analysis to aggregate effects across sites, rather than across independent studies, which is the more common use of meta-analysis.

The single-stage modeling and the meta-analysis approaches found slightly different overall estimates of the effect of the BUILD Scholar program on the three outcomes. Mathematically, this can be attributed to differences in the weight given to each site in the two different approaches. The meta-analysis weights each site’s contribution to the overall effect estimate by the inverse of the variance (squared standard error) of its site-specific estimate. These variances reflect site-specific factors, including sample size and propensity score weighting for that site. In contrast, the single-stage method has a more opaque weighting scheme involving both individual and site factors, and it is not easily interpretable.

Meta-analysis has the advantage of including formal methods for quantifying heterogeneity in the treatment (program) effect. While some variability in effect estimates between sites is expected due to chance (i.e., sampling variability), heterogeneity exists when the true effects differ between sites (i.e., the differences are not just due to chance). Heterogeneity in the effect of an intervention is important in that it partly determines the extent to which generalizable conclusions can be drawn. When using a single-stage approach, heterogeneity in program effects across sites can be explored by including interactions between sites and the treatment indicator variable in the model. This approach may be adequate when the number of sites is small; however, if the number of sites is large, this approach may be impractical.

In our analysis, heterogeneity was very low for Intent to Pursue, suggesting that the effects of the various first-year BUILD Scholar programs on this outcome were quite similar across the four sites. In contrast, the effects on Research Self-Efficacy and Science Identity differed across sites. Inspection of the forest plot suggests that Site A had little effect on heterogeneity (or the overall effect estimate) due to its wide confidence interval; Sites B and D had similar effects on all three outcomes; and thus Site C was driving the observed heterogeneity.

When heterogeneity is present, one can seek explanations for it, and this can offer new insights. Programs can differ in design and conduct as well as in participants, interventions, and settings. Such diversity in program implementation and site context may or may not be responsible for observed discrepancies in the results of the studies. In-depth case studies are important for understanding such differences. (See Chapter 2 by Cobian et al. to discuss how case studies fit into the DPC evaluation.) Other potential options are to conduct subgroup analyses or a meta-regression. In a meta-regression, the units of observation are the studies, the outcome variable is the effect estimate (e.g., mean difference), and the explanatory variables are characteristics of the studies that might influence the size of the effect. For a multisite program, meta-regression could be applied to estimates from different sites. The meta-regression model allows one to assess these characteristics as potential effect modifiers (Thompson & Sharp, 1999). Derzon et al. (2012) provided an example of the effective use of meta-regression in their series of meta-regression analyses as part of the evaluation of the Safe Schools/Healthy Students Initiative.

An advantage of meta-analysis over a single-stage modeling approach is that it can more easily handle situations in which there are differences in the variables collected across sites. Although this was not the case for BUILD, which coordinated data collection across sites, in many complex multisite programs the covariates collected from participants may differ from site to site, rendering it more difficult to analyze data across sites in a single model. When using a meta-analysis approach, one can use different covariates in the models for each site to account for differences in the covariates that are available or are relevant. Different groups of investigators could even conduct the site-specific analyses. This underscores how meta-analysis allows site-specific analyses to be decoupled from each other for added flexibility.

When conducting any statistical analysis, it is important to understand the underlying statistical assumptions and ensure that they are reasonably met. When conducting a meta-analysis, this applies to both the site-specific analyses and the meta-analysis. For example, the normal distribution assumption is used extensively in meta-analyses, often in ways that are not readily apparent (Jackson & White, 2018). Furthermore, if effect estimates from individual studies are biased, the summary effect estimate from the meta-analysis may also be biased. Thus, it is important to understand the potential pitfalls and limitations before embarking on a meta-analysis.

A potential limitation of conducting a meta-analysis as compared with a single-stage model is that some sites may have small sample sizes, making it difficult to obtain the site-specific estimates needed for a meta-analysis. However, we were able to obtain site-specific estimates for all of our sites, including one with only nine program participants.

The outcome variables in our analyses are five-level ordinal variables, but we opted to model them as normal, continuous variables. In general, the ramifications of such choices should be evaluated using sensitivity analyses, for example, repeating the analyses using ordinal regression.

In summary, meta-analysis can be a useful tool for quantitative evaluation of multisite programs due to its flexibility in obtaining site-specific estimates and characterizing heterogeneity in program effects among sites. It should be considered along with other tools and approaches for achieving a robust evaluation.

AUTHOR BIOGRAPHIES

Catherine M. Crespi, PhD, is a professor of biostatistics at the UCLA Fielding School of Public Health and serves as a co-investigator for the Evaluation Core of the Coordination and Evaluation Center for the Diversity Program Consortium.

Krystle P. Cobian, PhD, is a research analyst for the Coordination and Evaluation Center of the Diversity Program Consortium.