Density functional theory and ab initio molecular dynamics reveal atomistic mechanisms for carbonate clumped isotope reordering

Abstract

Carbon (¹³C) and oxygen (¹⁸O) isotopes in carbonates form clumped isotope species inversely correlated with temperature, providing a valuable paleothermometer for sedimentary carbonates and fossils. However, this signal resets (“reorders”) with increasing temperature after burial. Research on reordering kinetics has characterized reordering rates and hypothesized the effects of impurities and trapped water, but the atomistic mechanism remains obscure. This work studies carbonate-clumped isotope reordering in calcite via first-principles simulations. We developed an atomistic view of the isotope exchange reaction between carbonate pairs in calcite, discovering a preferred configuration and elucidating how Mg²⁺ substitution and Ca²⁺ vacancies lower the free energy of activation (ΔA^‡) compared to pristine calcite. Regarding water-assisted isotopic exchange, the H⁺-O coordination distorts the transition state configuration and reduces ΔA^‡. We proposed a water-mediated exchange mechanism showing the lowest ΔA^‡ involving a reaction pathway with a hydroxylated four-coordinated carbon atom, confirming that internal water facilitates clumped isotope reordering.

A molecular view of the oxygen isotope exchange informs the mechanisms behind the carbonate clumped isotope geothermometer.

INTRODUCTION

Carbonate-clumped isotope thermometry is one of the most important developments in geochemistry in the past two decades, greatly affecting research in paleoclimates (1, 2), oxygen isotope evolution of Phanerozoic seawater (2–5), paleoaltitudes and tectonics (6), sedimentary basin history, and petroleum geology (7). This is because the carbonate-clumped isotope concentration, the measure of the preferential enrichment of ¹³C─¹⁸O bonds, relative to the stochastic distribution, has an inverse relationship with temperature and serves as a paleothermometer independent of the isotopic composition of the precipitating fluid (8, 9). However, the primary clumped isotope signature undergoes solid-state reequilibration (“reordering”) at high temperatures (e.g., >125°C), compromising the integrity of the original signal (10–14).

Clumped isotope reordering proceeds in a closed system through ¹⁸O and possibly ¹³C exchange and diffusion reactions in the carbonate crystal lattice. Equation 1 describes the exchange reaction between two carbonate groups, where M is the metal cation (M = Ca, Mg, Ba, Sr, etc.).

$${\mathbf{M}}^{13}{\mathrm{C}}^{18}{\mathrm{O}}^{16}{\mathrm{O}}_2+{\mathbf{M}}^{12}{\mathrm{C}}^{16}{\mathrm{O}}_3\leftrightarrow {\mathbf{M}}^{13}{\mathrm{C}}^{16}{\mathrm{O}}_3+{\mathbf{M}}^{12}{\mathrm{C}}^{18}{\mathrm{O}}^{16}{\mathrm{O}}_2$$ (1)

To constrain the time-temperature domain within which carbonates can preserve the original Δ₄₇ signals, heating experiments have been performed to study the clumped isotope reordering kinetics for natural calcite (10–12), dolomite (15), and aragonite (16, 17). A unique feature of all these experimental results is that the clumped isotope reordering does not follow a first-order exponential decay but is characterized by an initial fast reordering rate followed by reordering at a slower rate. To account for this observation, previous studies proposed several reordering kinetics models. The rapid reordering during the initial heating period was first attributed to the efficacy of nonequilibrium defects that decrease in concentration and decelerate reordering after annealing (10). This mechanism led to the establishment of the transient/equilibrium defect model that adds the contribution of transient defects to the reordering kinetics caused by equilibrium defects (11). The paired diffusion model states that rapid reordering arose from the fast ¹⁸O exchange between a clumped carbonate ion (¹³C¹⁸O¹⁶O₂²⁻) and a neighboring common carbonate ion (¹²C¹⁶O₃²⁻), followed by the slow solid-state diffusion of carbonate ions (12). Most recently, the disordered kinetic model proposed this non–first-order reordering as a superposition of parallel pseudo–first-order declumping reactions with different rates (18). The authors hypothesized that the ¹³C─¹⁸O bond reordering proceeds through random-walk ¹⁸O diffusion in the lattice. This concept allows ¹⁸O atoms to diffuse in every particular pathway with a probability proportional to the zero-point energy change and inversely proportional to the squared distance between neighboring carbonate groups. In this framework, the change in the overall reordering rate eventually arises from the evolution of the activation energy distribution of the system; the reordering kinetic models mentioned previously represent specific cases of disordered kinetics subject to certain constraints.

These kinetic models have had partial success in explaining the general behavior of carbonate clumped isotope reordering; however, discrepancies in the reordering rates of different calcite materials suggest that there exist composition- and structure-specific factors not addressed in existing phenomenological kinetic models. The discrepancy is illustrated in Fig. 1A, the Arrhenius plots of multiple calcite materials compilated from different studies (18, 19), where calcites that reorder rapidly appear toward the upper-right corner. Notably, the mean reordering rate at 360°C for belemnite rostral calcite (L23) is two to three orders of magnitude faster than all other calcites at 385°C. The authors attribute this behavior to a fast initial resetting resulting from oxygen isotope exchange with internal skeletal water present as fluid inclusions or organic-derived water based on the δ¹⁸O decrease observed during heating experiments (19), which is in agreement with other works excluding the presence of external water as the primary origin (20, 21). In particular, this belemnite also shows a calcium substitution concentration (Mg/Ca, Mn/Ca, Sr/ Ca, and Fe/Ca) up to 32 times higher compared to optical calcite. However, spar calcite with greater Mn and Mg contents reordered slower than optical calcite under the same experimental conditions (10). Hence, a key knowledge gap pertains to the atomistic mechanisms for water-mediated clumped isotope reordering in a manner that accounts for the specifics of crystal structure, chemical composition, and defect density. Elucidation of the atomistic dynamics underpinning clumped isotope reordering and the structures of transition states and reaction intermediates can help aid development of a more general model for clumped isotope reordering. For instance, Eq. 2 denotes a potential reordering pathway with the presence of water

$${\mathbf{M}}^{\mathbf{13}}{\mathbf{C}}^{18}{\mathrm{O}}^{16}{\mathrm{O}}_2+{{\mathrm{H}}_2}^{16}\mathrm{O}\leftrightarrow {\mathbf{M}}^{\mathbf{13}}{\mathbf{C}}^{16}{\mathrm{O}}_3+{{\mathrm{H}}_2}^{18}\mathrm{O}$$ (2)

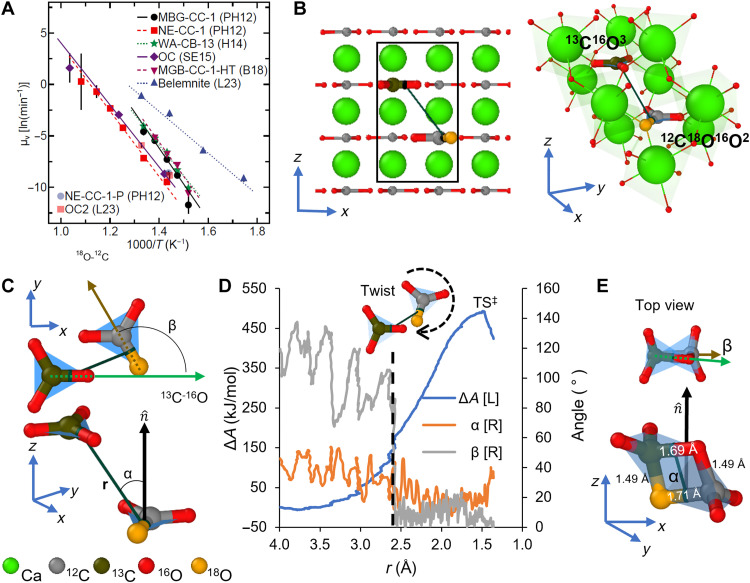
Fig. 1. Transition state for ¹⁶O and ¹⁸O isotope exchange between two proximal carbonate groups in calcite.

(A) Arrhenius plots of carbonate reordering compiled from other works (18, 19); the slope is −E_a/R, where E_a is the mean activation energy and R is the molar gas constant. A clear separation is observed between belemnite calcite (dark blue triangles), and remaining calcites, pointing to the acceleration of reordering by incorporated water (10, 12, 15, 20). (B) Calcite supercell with proximal carbonate groups ¹³C¹⁶O₃ and ¹²C¹⁸O¹⁶O₂ along the (010) plane. Heavier isotopes (¹⁸O and ¹³C) are represented in different colors than common isotopes (¹⁶O and ¹²C). The three-dimensional view to the right side in (B) shows the two proximal carbonates and the semitransparent green polyhedra depict Ca²⁺O₆ octahedra. (C) Reaction coordinates for studying isotope exchange shown in (A) and (B). r is the distance to centroids between bonds ¹³C─¹⁶O and ¹⁸O─¹²C, α is the angle between the vector r and the vector $\hat{\mathit{n}}$ normal to the plane that crosses the oxygen species in carbonate ¹²C¹⁸O¹⁶O₂, and β is the angle between the vectors ¹³C─¹⁶O (green arrow) and ¹⁸O─¹²C (brown arrow). The semitransparent blue polyhedra depict the trigonal planar geometry of the proximal carbonate groups. (D) Free energy change (ΔA) plotted for isotope exchange between the two proximal carbonates is shown in (A) to (C). Free energy change at the transition state (TS^‡) is the free energy of activation (ΔA^‡) (E) Bitetrahedral transition state (TS^‡) for isotope exchange of ¹⁶O and ¹⁸O exchange in proximate carbonates shown in (A) to (C).

This mechanism can be accompanied by changes in carbonate morphology and mineralogy if carbonate dissolution-reprecipitation reactions occur at the carbonate-fluid interface. Alternatively, reordering may be facilitated by dissociated water incorporated in the crystal lattice as interstitial or substitutional H⁺/OH⁻ ions. Highly mobile H⁺ may weaken C─O bonds and lower the energy barrier for the exchange between two carbonate groups. Ignoring cation substitution or structural water in choosing reordering parameters could lead to incorrect reconstruction of paleotemperatures or basin thermal histories. While numerous studies have proposed these factors as an influence on reordering rates in carbonate minerals, none have applied atomistic simulations to evaluate their impact.

In this study, we examine the atomistic mechanisms, transition states, and origins of defect modification of free energy barriers of clumped isotope reordering in calcite via density functional theory (DFT) and constrained ab initio molecular dynamics (cAIMD). First, we calculate the free energy of activation (ΔA^‡) of the thermodynamically favored clumping reaction (reverse of Eq. 1) via thermodynamic integration of the free-energy gradient (22–26) for calcite with no defects (“pristine”), with a substitutional Mg²⁺ impurity, and with a Ca²⁺ vacancy following the exchange mechanism in Eq. 1. On the basis of microscopic reversibility and the knowledge of the equilibrium constant (12), models for the clumping reaction enable evaluation of energy barriers for the reverse reaction (clumped isotope reordering) denoted in Eq. 1. Second, we address the impact of interstitial protons and hydroxyl ions on the exchange reaction, and last, we quantify ΔA^‡ for isotope exchange between an H₂¹⁸O molecule and a ¹³C¹⁶O₃ group following the mechanism proposed in Eq. 2. We identify the critical role of a “bitetrahedral” transition state and demonstrate that the reordering dynamics are governed not just by interatomic/interlayer separation but also by the rotational offsets between clumped and common carbonate moieties. Interstitial protons, substitution in the cation lattice, vacancies, or incorporated water activate more facile reaction trajectories by reducing the magnitude of structural distortions needed to access the transition state and can thus substantially reduce the free energy barriers for declumping. While first-principles simulations of reaction kinetics are currently intractable (vide infra), the simulations show excellent quantitative agreement with experimental results. Our proposed water-mediated mechanism shows a 59% ΔA^‡ reduction compared to the free energy change observed for pristine calcite, which is in quantitative agreement with the 63% reduction in the Arrhenius regression activation energy (μ_E) of belemnite rostral calcite compared to the “all other calcites” average from Fig. 1A. These atomistic mechanisms explain previous observations of faster reordering rates and oxygen diffusion in calcite associated with water (Fig. 1) and are an important step toward developing a universal kinetic model for carbonate clumped isotope reordering based on atomistic understanding of reaction mechanisms.

RESULTS

Isotope exchange between carbonate pairs in pristine calcite

Table S1 summarizes the lattice parameters calculated for calcite, showing a less than 2% variation as compared to experimental data. Before including isotope effects, ab initio molecular dynamics (AIMD) calculations were performed on a cubic 270-atom CaCO₃ supercell at 900°C. Figure S1 shows a slight off-centering of atoms from their ground-state positions induced by this thermal annealing; however, the elevated temperature is insufficient to promote dissociation and reordering of carbonate groups within the simulation window. The dimensions of the 270-atom cubic supercell, 15.15 Å × 17.49 Å × 17.30 Å, affords a single pair of ¹³C¹⁶O₃ and ¹²C¹⁸O¹⁶O₂ carbonate groups surrounded by ¹²C¹⁶O₃ groups. On the basis of natural abundances, the likelihood of finding a ¹³C¹⁶O₃ group paired with a ¹²C¹⁸O¹⁶O₂ closest neighbor is only 6% in calcite (12). However, our focus here was not to quantify the probability for this exchange to happen but to understand the exchange dynamics once the pair forms using a supercell that is tractable at a reasonable computational cost.

Figure 1 (B and C) outlines the isotope exchange reaction between two proximal carbonate groups ¹³C¹⁶O₃ and ¹²C¹⁸O¹⁶O₂ in calcite. The reaction coordinates r, α, and β represent the relative orientation between the two carbonates. r is the distance to centroids between bonds ¹³C─¹⁶O and ¹⁸O─¹²C, α is the angle between the vector r and the vector $\hat{\mathbf{n}}$ normal to the plane that crosses the oxygen species in carbonate ¹²C¹⁸O¹⁶O₂, and β is the angle between the vectors ¹³C─¹⁶O (green arrow) and ¹⁸O─¹²C (brown arrow). The exchange reaction proceeds after the SHAKE algorithm drives together the atom pairs ¹³C and ¹⁸O and ¹⁶O and ¹²C from each carbonate. Figure 1D shows the free energy profile for the isotope exchange. The initial |r| magnitude, 4.00 Å, decreases as the two carbonates approach each other, triggering a rotational reconfiguration after twisting of the ¹²C¹⁸O¹⁶O₂ moiety when |r| approaches 2.59 Å, beyond which the β angle decreases to approximately 0°. Movie S1 closely captures this reconfiguration process. The increasing proximity of the two carbonates drives the α angle to 20° and stabilizes the condensed TS^‡ state at |r| equal to 1.49 Å. A grand challenge in understanding reaction mechanisms and their activation energy barriers is elucidation of the structure of the transition state. The TS^‡ state in Fig. 1E shows the two carbonate groups distorted into a tetrahedral pair sharing an edge, herein called the bitetrahedral configuration. The distances ¹³C-¹⁶O and ¹⁸O-¹²C elongate to 1.69 and 1.71 Å, respectively, whereas the pairs ¹³C-¹⁸O and ¹⁶O-¹²C both shorten to 1.49 Å. This TS^‡ state leads to the formation of carbonates ¹²C¹⁶O₃ and ¹³C¹⁸O¹⁶O₂. The rotation required for this particular exchange configuration makes the ΔA^‡ equal to 493.57 kJ/mol.

Figure S2 plots the entropy change throughout the exchange process outlined above. The structural distortion resulting from twisting and rotational reconfiguration drives the observed increase in entropy. However, the increase in entropy decreases again upon completion of the rotation. The initial slow linear decrease corresponds to the two carbonates drifting into each other without suffering a substantial structural distortion in their internal coordinates. However, a second stage with a faster linear entropy decrease is coincident with the formation of the TS^‡. The rapid entropy loss at this stage derives from the strong coupling between the two carbonates close to the TS^‡ state that restricts their translational and rotational displacements. An earlier work proposes a similar explanation for proton exchange between an alkane and a Bronsted acid site in acidic chabazite (26).

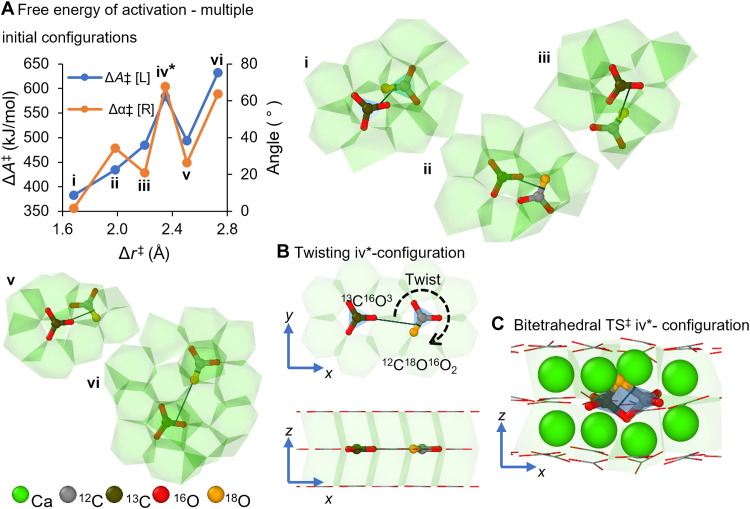
Figure 2A summarizes the free energy of activation across six different carbonate pair configurations and provides the initial configuration for each carbonate pair configuration. The shorter the displacement toward the transition state (Δr^‡) and the smaller the angular change (Δα^‡), the lower the ΔA^‡. Notably, high ΔA^‡ values do not rule out a particular exchange path but make it less likely to proceed. In this way, isotope reordering occurs as a superposition of multiple elementary exchange reactions whose probability of occurrence is proportional to the energy cost. The *-marked singularity showing a sudden increase in ΔA^‡ indicates a relationship more complex than the mere separation between the two proximal carbonates and ΔA^‡ suggested in earlier works (18) and points the key role of rotational reconfiguration. Figure 2 (B and C) shows the initial and TS^‡ configurations for the iv*-marked exchange. For this configuration, the two carbonate groups involved in the exchange drift closer within the same “carbonate layer,” whereas the ¹²C¹⁸O¹⁶O₂ group rotates to align its ¹²C─¹⁸O bond parallel to the ¹³C─¹⁶O bond of the other ¹³C¹⁶O₃ carbonate group. Movie S2 details this ¹²C¹⁸O¹⁶O₂ rotation. This behavior suggests that isotope exchange reactions occur preferentially between neighboring carbonate groups wherein the O─C bonds involved in the exchange are aligned parallel to each other (β = 0°), as in fig. S3. Figure S4A shows the initial state for the most favorable configuration for isotope exchange (ΔA^‡ = 382 kJ/mol); the angular changes Δα^‡ and Δβ^‡ are 1.68 and 4.45°.

Fig. 2. Comparison of free energy change for isotope exchange across six different carbonate pair configurations in calcite.

(A) Free energy of activation (ΔA^‡), angular change among carbonate pairs (Δα^‡) plotted against the displacement toward the transition state (Δr^‡). The iv *-marked singularity shows a deviation from the direct correlation of ΔA^‡ and Δr^‡ between the two proximal carbonates and highlights the importance of carbonate alignment. (B) Initial carbonate pair configuration for the iv*-marked exchange reaction. The semitransparent green polyhedra depict the Ca²⁺O₆ octahedra in the calcite supercell. The semitransparent blue polyhedra depict the trigonal planar geometry of the proximal carbonate groups (¹³C¹⁶O₃ and ¹²C¹⁸O¹⁶O₂). The bitetrahedral TS^‡ and isotope exchange for this configuration is captured in movie S2. (C) Bitetrahedral TS^‡ configuration for the *-marked exchange reaction. After the TS^‡ forms, the semitransparent blue polyhedra depict the tetrahedral local coordination environments ¹³C¹⁶O₃¹⁸O and ¹²C¹⁸O¹⁶O₃. Atom coloring palette provided at the bottom.

Influence of imperfections on clumped isotope reordering

Crystal defects and impurities have been hypothesized to lower the ΔA^‡ of activation in isotope exchange reactions in calcite (10, 11, 21). A recent report shows that a belemnite rostral calcite, with a concentration of calcium substitutions up to 32 times higher than optical calcites (Mg, Mn, Sr, Fe), shows reordering rates notably faster than other forms of calcite (19). To provide insights on this behavior, we studied the isotope exchange with a substitutional impurity (Mg²⁺) and with a Ca²⁺ vacancy. The concentration of these defects in the simulation cell is low and does not demand a total structural reconstruction. Figure S4 (B and C) shows the initial and TS^‡ states most favorable for the exchange reaction in both cases, and Table 1 lists the corresponding displacement and angular changes to the transition state, together with their ΔA^‡ of activation. The initial configurations are similar regardless of the substitutional impurity and the Ca²⁺ vacancy; the exchange is most favorable between the closest carbonate groups from adjacent “carbonate planes” in parallel orientation (β ~ 0°). However, the energy change ΔA^‡ decreases to 366.41 and 360.95 kJ/mol for the Mg²⁺ substitution and Ca²⁺ vacancy, respectively, compared to 382.48 kJ/mol for pristine calcite. Thus, on a molar basis, a Ca²⁺ vacancy will increase reordering rates to a greater extent than Mg²⁺ substitution.

Table 1. Free energy activations and total displacements and angular variations toward the TS^‡ state.

Case	Δr‡ (Å)	Δα‡ (°)	Δβ‡ (°)	ΔA‡ (kJ/mol)
CaCO3	1.68	1.68	4.45	382.48
CaCO3/Mg2+	1.78	1.78	13.27	366.41
CaCO3/Ca2+ vac.	2.08	10.58	4.81	360.95

To understand how changes in structural distortions at the transition state affect the ΔA^‡ of activation, we have performed integrated projected crystal orbital Hamilton population (IpCOHP) analyses (27–31). This IpCOHP parameter provides a measure of the bonding strength between two atoms. The more negative the parameter, stronger the bonding interaction. The calculation proceeded using Bunge’s local basis functions (32) and the orbitals included are 2s and 2p for carbon and oxygen; 3s, 4s, and 3p for calcium; and 2s, 3s, and 2p for magnesium. The absolute charge spilling was <1.63% in all cases (30).

Figure 3 shows the transition states for pristine calcite, calcite with the substitutional Mg²⁺ impurity, and the Ca²⁺ vacancy, together with the IpCOHP values quantifying the strength of oxygen interactions with their surrounding cations. The transition state is stabilized by a structural distortion that brings the two carbonate groups close enough to adopt the bitetrahedral configuration. In pristine calcite, the ground-state O-Ca distances and corresponding IpCOHP parameter are 2.39 Å and −0.725 eV, respectively. However, in the transition state, the O─Ca bond is elongated, which is accompanied by less negative IpCOHP parameters that indicate a weakened bonding interaction. This structural distortion is local and is a major contributor to the free energy of activation of the transition state.

Fig. 3. Role of Mg²⁺ dopant and Ca²⁺ vacancy in lowering free energy change for isotope exchange.

Atomistic representation of Ca-O interactions in transition state configuration together with their corresponding IpCOHP (measure of bond strength) versus O─M bond length distribution plots in (A) pristine calcite, (B) calcite with Mg²⁺ substitution, and (C) a Ca²⁺ vacancy. M denotes Ca or Mg. Selected bond distances are noted on the TS^‡ configurations to aid discussion. Atom coloring palette provided at the bottom.

Upon Mg²⁺ substitution, the average O-Mg distance and IpCOHP parameter at the ground state are 2.19 Å and −0.880 eV, respectively. These values indicate a stronger bonding interaction compared to Ca²⁺, and this trend survives upon stabilization of the transition state, which shows the Mg²⁺ ion interacting with two oxygen species from each carbonate group at separations of 2.08 and 2.37 Å; both of these values are shorter than the average O-Ca distance in the ground state (2.41 Å). The IpCOHP values for these two interactions (−0.949 and −0.597 eV, respectively) are comparable or more negative than the average O-Ca IpCOHP parameter in the ground state (−0.615 eV). This analysis indicates that O-Mg interactions are stronger than O-Ca interactions. In this configuration, the Mg²⁺ ion serves to bring together the two carbonate groups to create the TS^‡ configuration; the stabilizing effect of Mg²⁺ substitution partially explains the lower free energy of activation (and consequently faster reordering rates) as compared to pristine calcite.

The Ca²⁺ vacancy in calcite lowers the free energy of activation even further to 360.95 kJ/mol (Table 1). The TS^‡ state in Fig. 3C shows fewer O-Ca interactions after Ca²⁺ removal. Fewer O-Ca distortions imply a lower energetic cost to bringing together the two carbonate groups to proceed with isotope exchange. The IpCOHP plot shows three O-Ca interactions at the transition state, ranking very close to the ground-state average values; moreover, the variance in O-Ca distances is decreased as compared to pristine calcite. This behavior explains the lower free energy of activation; because fewer O-Ca distortions need to be induced to reach the transition state, there is a relatively lower energetic penalty for bringing together the two carbonate groups to proceed with isotope exchange (and clumped isotope reordering).

Water-mediated clumped isotope reordering

Recent studies have explored the role of water in promoting resetting of clumped isotope compositions, either by oxygen exchange with water in fluid inclusions or by enhancing oxygen mobility in the solid state (20, 21). It has long been known that the presence of water enhances oxygen diffusion in calcite (fig. S5 sketches a line drawing of a water-mediated oxygen isotope exchange through a tetrahedral intermediate) (33–35). Heating experiments with aragonite have led to the proposal that oxygen exchange between trapped water and carbonate cause overestimation of reordering rates in aragonite and perhaps calcite fossils. On the other hand, water in the carbonate lattice, either as nondissociated H₂O or dissociated H⁺/OH⁻, may weaken C─O bonds and lower activation energies for solid-state exchange. For example, a H⁺ released after water dissociation is highly mobile and weakens C─O bonds as a result of bonding interactions with oxygen species, arguably lowering the free energy of activation for the exchange reaction.

Our nudged elastic-band (NEB) calculations reveal that the barrier for H⁺ migration from one carbonate group to another is ~1 to 2 kJ/mol (fig. S6). Figure 4 expands on Eq. 2 and presents a proposed mechanism for the addition of a water molecule or dissociated interstitial proton and hydroxyl species in calcite. A bicarbonate group is stabilized by the protonation of a carbonate in the calcite structure. The hydroxyl group close to the bicarbonate displaces itself and preferentially binds to the bicarbonate group. The overall addition of water to a calcite structure leads to the formation of calcium hydroxide and bicarbonate, which can facilitate declumping and isotopic exchange by weakening carbonate bonds. The structures in Fig. 4 (B and C) capture a proposed Ca(OH)(HCOO₂) tetrahedral intermediate with two bicarbonate bonds and the subsequent carbonate bond cleavage to accommodate an oxygen from the water molecule.

Fig. 4. A two-dimensional depiction of a water-mediated oxide diffusion mechanism proposed for calcite.

(A) A water molecule approaches a calcite supercell. (B) The stabilization of water in the calcite lattice leads to the tetrahedral intermediate with two bicarbonate bonds. (C) The cleavage of carbonate bonds inserts an oxygen from the water molecule in the calcite lattice. (D) A water molecule containing an oxygen dissociated from calcite lattice drifts away.

A viable scenario for water-mediated oxide diffusion and isotopic exchange can thus be put forth and modeled with AIMD simulations. To analyze this hypothesis and understand the effect of proton and hydroxyl addition on the carbonate group, ground structure relaxations are performed for the structural motifs shown in Fig. 4B. Figure S7A shows that the formation of bicarbonate (protonation of carbonate) lengthens the carbonate bond from 1.299 to 1.383 Å. Relaxation of the hydrated structure in Fig. 4B yields the structure in Fig. 4C, which shows a tetrahedral intermediate with two ─OH groups (fig. S7B). The carbonate bond is further elongated to 1.514 Å.

AIMD simulations are performed to explore declumping mechanisms with a particular emphasis on the role of hydroxyl and bicarbonate species stabilized within the structures that possibly serve as reaction intermediates (fig. S8). AIMD simulations at 300°C on the structure containing the tetrahedral intermediate in Fig. 4C and fig. S7B revealed the cleavage of C─O bonds (fig. S8, A to D). The dissociation of a C─O linkage from the tetrahedral intermediate declumps an oxygen that is intrinsic to the pristine carbonate structure and instead generates a carbonate that has one oxygen derived from the dissociated water molecule.

We further elaborated this model to account for isotopic effects and understand isotopic exchange in the calcite structure in the presence of protons and water molecules. We inserted dissociated H⁺, as well as a OH⁻ group to maintain charge balance, into interstitial sites of a pristine calcite supercell and calculated the isotope exchange reaction between two adjacent carbonate moieties in the presence of H⁺. Figure 5 (A and B) shows the ground-state and TS^‡ configurations for this process. The average O-C distance and IpCOHP parameter are 1.299 Å and −12.823 eV, respectively. However, lattice phonons enable the interstitial H⁺ to approach the ¹³C¹⁶O₃ carbonate; the O─C bond elongates to 1.374 Å, and the IpCOHP parameters lower to −10.938 eV, consistent with the reduced electron density in the C─O bond. Following the isotopic exchange with the neighboring ¹²C¹⁸O¹⁶O₂ group, the free energy of activation (ΔA^‡) for the TS^‡ formation is 314.6 kJ/mol, notably lower than the cases for pristine calcite and calcite incorporating Mg²⁺ substitution or a Ca²⁺ vacancy. Figure 5B shows that the H⁺-O coordination distorts the bitetrahedral configuration such that the ¹²C-O and O-¹³C interatomic separations are 2.04 and 2.30 Å, respectively. These interactions are longer than in the equivalent TS^‡ configuration for pristine calcite (see Fig. 1E) and confirm the role of H⁺ in weakening the C-O interaction and decreasing the ΔA^‡ barrier. Movie S3 provides a magnified view of this exchange.

Fig. 5. Role of H⁺ and H₂O in mediating isotope exchange reaction in calcite.

(A) Ground-state configuration of H⁺-mediated isotope exchange in a calcite supercell viewed along the (010) plane. The semitransparent green polyhedra depict the Ca²⁺O₆ octahedra in the calcite supercell. (B) Orthographic view of transition state (TS^‡) configuration for H⁺-mediated isotope exchange in a calcite supercell. The exchange reaction is visualized in movie S3. (C) Thermally equilibrated H₂¹⁸O molecule in pristine calcite. (D) Reaction coordinates describing the global reaction coordinate, where the three interatomic distances r₁ and r₂ are the distances from the H₁ and H₂ atoms to the ¹⁶O species, and r₃ is the distance from the ¹⁸O isotope to the ¹³C atom. Oxygen isotope exchange (¹⁸O and ¹⁶O) reaction between the H₂¹⁸O and a ¹³C¹⁶O₃ group based on Eq. 2. (E) Free energy profile for the ¹⁸O and ¹⁶O exchange reaction between the H₂¹⁸O and a ¹³C¹⁶O₃ group as calculated through cAIMD simulation. (F) Selected frames throughout the oxygen exchange reaction between H₂¹⁸O and a ¹³C¹⁶O₃ group referenced along the free energy profile with roman numerals. Atom coloring palette provided at the bottom.

We further studied the water-mediated mechanism proposed in Eq. 2 and sketched in Fig. 5 (C to F) by adding a water molecule into an interlayer site in pristine calcite. Figure 5C shows the thermally equilibrated H₂¹⁸O in pristine calcite. The surrounding carbonates are distorted to accommodate the water molecule, and indeed, the local structural distortion drives isotopic exchange with a relatively lower activation energy barrier. The global reaction coordinate consists of three interatomic distances outlined in Fig. 5D ξ = (r₁, r₂, r₃); the distances from the H₁ and H₂ atoms to the ¹⁶O species, and the distance from the ¹⁸O isotope to the ¹³C atom.

The free energy profile and the selected frames in Fig. 5 (E and F) summarize the reaction progress. The H₂¹⁸O molecule vibrates around the ¹³C¹⁶O₃ group until reaching a relatively low-energy orientation that stabilizes the H-¹⁶O interaction that ultimately triggers ¹⁸O-H scission (Fig. 5F, frames I and II). The ¹⁸O-H group thus released ends up coordinating with the ¹³C atom from the carbonate group, resulting in formation of a TS^‡ configuration (frame III) before the formation of the ¹³C¹⁸O¹⁶O₂ group and the H₂¹⁶O molecule pictured in frame IV. The free energy change for this process is 221.7 kJ/mol, substantially lower compared to the H⁺-mediated exchange (314.6 kJ/mol). This notable reduction in the free energy change compares directly to the Arrhenius regression activation energies (μ_E) from the experimental data compiled in Fig. 1A. For example, the μ_E for belemnite rostral calcite (167.7 kJ/mol) is only 63% of the “all other calcites” average (266.1 kJ/mol). Similarly, the free energy change for our proposed water-mediated mechanism (221.7 kJ/mol) is about 59% of the average of free energy changes for pristine calcite, calcite with a Mg²⁺ impurity, and calcite with a Ca²⁺ vacancy (369.9 kJ/mol).

This exchange mechanism differs from the other ones studied here because it only involves one carbonate group, but the exchange proceeds with H₂¹⁸O instead of a neighboring carbonate. The need for only one carbonate group instead of two as in Eq. 1 affords an altogether different reaction pathway with reduced local structural distortions, which, when coupled with the need to break fewer C─O bonds, lowers the ΔA^‡ of activation of this exchange mechanism and confirms the experimental observations in Fig. 1A that internal water facilitates facile isotope reordering in carbonate minerals.

DISCUSSION

Experimental data for clumped isotope reordering highlight substantial variations in clumped isotope reordering rates (i) as a function of structure type for the same composition (contrasting calcite and aragonite); (ii) as a function of composition across similar structure types (contrasting dolomite to calcite and aragonite); and (iii) as a function of cation substitution and water inclusion for the same composition and structure type (calcite of different origins). Current phenomenological kinetic models are unable to fully account for these differences, which clearly originate in differences in atomistic reaction trajectories. The absence of first-principles atomistic understanding of these rare events remains a critical knowledge gap that has substantial implications for the accuracy and generalizability of paleothermometers. The first-principles quantum chemical models developed here provide the first atomistic reaction trajectory descriptions and frameworks for diffusive reordering, which have thus far remained elusive. Just as pioneering studies of isotope fractionation required statistical thermodynamic models to ground-truth experimental data, experimental determinations of clumped isotope reordering require first-principles simulations to disentangle the competing influences of structure-, composition-, and defect-dependent reaction rates and to develop a means of composition- and structure-calibrated paleothermometry.

Atomistic simulations provide a molecular view of multiple mechanisms driving clumped isotope reordering in calcite, and suggest that isotope reordering works as a superposition of multiple elementary exchange reactions whose free energies of activation depends on (i) the relative geometric orientation of adjacent carbonate groups, (ii) substitutional impurities and vacancies, and (iii) the presence of water. We demonstrate that reordering follows a more complex mechanism than a mere random-walk ¹⁸O diffusion. The relative geometric orientation between carbonate groups, defined by a twist angle, strongly affects the reordering dynamics. The most favorable configuration for isotope exchange between a pair of carbonates is that which positions the interacting C─O bonds in a parallel configuration, allowing two carbonates to approach each other to stabilize a bitetrahedral configuration that represents the lowest energy transition state. The presence of defects such as substitutional Mg²⁺ ions and Ca²⁺ vacancies lower the free energy of activation by reducing the magnitude of structural distortions needed to access the transition state as compared to the pristine calcite structure. However, the most notable reduction of the activation energy is observed in a water-assisted isotopic exchange. In the case of dissociated water, the highly mobile H⁺ ions that can migrate between interstitial sites weaken C─O bonds and distort the transition state configuration to lower the free energy of activation. In the case of nondissociated water, an altogether different reaction pathway becomes accessible. In this scenario, the water molecule interacts with a carbonate moiety resulting in dissociation of a HO─H bond. A tetrahedral transition state configuration is stabilized with a hydroxyl moiety; proton diffusion followed by C─O bond scission facilitates declumping. This mechanism shows the most notable reduction in the free energy of activation for isotopic exchange in calcite.

Deciphering atomistic mechanisms for isotopic exchange through molecular dynamics simulations provides a means of understanding elementary reactions and structural/compositional parameters governing the activation energy barriers to clumped isotope reordering. Our focus in this work is to identify the lowest energy reaction trajectories resulting in isotope exchange between neighboring carbonates and to decipher the effects of water and substituted cations and anions on clumped isotope reordering. Our cAIMD method successfully captures trends in reordering rates between calcite minerals with and without water reported in experimental work. However, first-principles derivation of the equivalent of kinetic rates for isotope reordering requires the evaluation of the Eyring-Polanyi equation, which necessitates calculation of a dynamic transmission coefficient that captures the efficiency of the transition from the initial to the TS^‡ states and their corresponding quasi-partition functions (36). For strongly diffusive condensed-phase reactions such as the mechanisms considered here, transmission coordinates deviate considerably from ideality. Multiconfiguration time-dependent first-principles models with exhaustive sampling schemes that accurately capture the thermal distribution of the initial states required for accurate assessment of transmission functions in the reactive flux correlation function formalism remain intractable for systems of the dimensions considered here (37). Development of analytical and semiclassical approximation models for carbonate-clumped isotope reordering and examination of the extent to which such models capture transmission coefficients in highly diffusive rare-event scenarios to enable direct comparison with experiment is a focus of ongoing research. A parallel focus is elaboration of the framework developed here to other carbonate minerals to enable comparison of trends in activation energy barriers where once again quantitative differences are observed in experimental work and are accessible through first-principles simulations.

THEORETICAL METHODS

Electronic structure calculations and proton migration barriers

The geometry optimizations apply the DFT method implemented in the Vienna Ab initio Simulation Package (VASP, version 5.4.4) (38–41). The Perdew-Burke-Ernzerhof (PBE) functional addresses the exchange-correlation energy approximation, and the projector augmented wave method deals with the electron interactions with a plane-wave basis expansion up to 400 eV (42, 43). The modeling of partial occupancies uses the Gaussian smearing method set to 0.05 eV, and the Monkhorst-Pack scheme samples the Brillouin zone with a grid density determined according to the size of the simulation cells (42, 44, 45). The geometry relaxation uses the conjugate gradient algorithm set to a stopping criterion equal to 0.05 eV/Å, while the break condition for the electronic self-consistent loop is 10⁻⁴ eV. The NEB method implemented in VASP was used to calculate proton migration barriers using a series of images calculated along the minimum energy path (46).

Molecular dynamics simulations and thermodynamic integration of free-energy gradients

The Verlet algorithm integrates Newton’s equations during the AIMD simulations performed with the NVT ensemble. The time step is 1.5 fs except for those calculations with hydrogen atoms that require a shorter 1.0-fs time step. In addition, the Nose-Hoover thermostat controls the temperature around 698 K. This temperature choice comes from heating experiments performed on calcite samples (12); the Δ₄₇ evolution shows a distinctively “kinked” shape that might come from a superposition of multiple reordering mechanisms that become relevant to this temperature and most likely easier to follow by modeling.

The cAIMD method implemented in VASP enables calculation of the free energy change based on thermodynamic integration of the free-energy gradient (25, 47); a user-defined set of coordinates describes the reaction, and the SHAKE algorithm constrains the system onto the reaction path (48). Isotope reordering is a transition process between stable carbonate configurations that occur by infrequent activated events of short duration; the cAIMD method enables us to model these processes within a time simulation window accessible with molecular dynamics (22, 48).

A geometry optimization with the DFT method precedes the molecular dynamics simulation, which starts with a 2-ps AIMD thermal equilibration and finishes with a cAIMD calculation to perform the transformation toward the TS^‡ state. We applied an 0.002 Å/step increment throughout the calculation for the collective variables to drive the exchange reaction. The free-energy gradient integration uses the trapezoid rule, and the TS^‡ location is at the point where the free-energy gradient vanishes.

Supplementary Materials

This PDF file includes:

Legends for movies S1 to S3

Table S1

Figs. S1 to S8

References

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S3