Optical and electronic spin properties of fluorescent micro- and nanodiamonds upon prolonged ultrahigh-temperature annealing

Abstract

High-temperature annealing is a promising but still mainly unexplored method for enhancing spin properties of negatively charged nitrogen-vacancy (NV) centers in diamond particles. After high-energy irradiation, the formation of NV centers in diamond particles is typically accomplished via annealing at temperatures in the range of 800–900 °C for 1–2 h to promote vacancy diffusion. Here, we investigate the effects of conventional annealing (900 °C for 2 h) against annealing at a much higher temperature of 1600 °C for the same annealing duration for particles ranging in size from 100 nm to 15 μm using electron paramagnetic resonance and optical characterization. At this high temperature, the vacancy-assisted diffusion of nitrogen can occur. Previously, the annealing of diamond particles at this temperature was performed over short time scales because of concerns of particle graphitization. Our results demonstrate that particles that survive this prolonged 1600 °C annealing show increased NV T₁ and T₂ electron spin relaxation times in 1 and 15 μm particles, due to the removal of fast relaxing spins. Additionally, this high-temperature annealing also boosts magnetically induced fluorescence contrast of NV centers for particle sizes ranging from 100 nm to 15 μm. At the same time, the content of NV centers is decreased fewfold and reaches a level of <0.5 ppm. The results provide guidance for future studies and the optimization of high-temperature annealing of fluorescent diamond particles for applications relying on the spin properties of NV centers in the host crystals.

I. INTRODUCTION

Fluorescent diamond particles (FDPs) containing nitrogen-vacancy centers have shown utility as contrast agents due to strong photostability and the capability for background-free fluorescence imaging based on microwave or magnetic field induced fluorescence contrast. FDPs have also been identified as a promising candidate for nanoscale quantum sensing applications.¹ Many of these emerging technologies are based on unique optical and electron spin properties of the negatively charged nitrogen vacancy (NV) center that have been discussed exhaustively in the literature.^{2, 3} It was shown that the optical manipulation of the individual electronic spins⁴ or spin ensembles⁵ of NV centers at or around room temperature can be used for the sensing of electric^{6, 7} and magnetic fields,^{8, 9} mechanical stress,¹⁰ and temperature.^11–13 Up until now, many of these demonstrations employed NV centers in bulk diamond plates. Unfortunately, the size and geometry of macroscopic plates impose limitations for the use of such quantum sensors in biological systems such as tissues or inside the cells. The use of FDPs for monitoring intracellular temperature¹¹ and activity in neuronal cell networks¹⁴ have already been reported. Applications of FDPs outside the biomedical fields are also growing. For example, Foy et al. demonstrated the use of FDPs for wide field simultaneous magnetic field and temperature mapping of gallium nitride high electron mobility transistors (GaN HEMTs).¹⁵ Dou and co-workers employed FDPs to monitor temperature fluctuations during dendrite formation in the electrochemical deposition of Zn.¹⁶ Such fluctuations could have significant implications for battery performance. FDPs were also used as non-bleaching fluorescent markers in conventional¹⁷ and background-free fluorescence imaging^{18, 19} utilizing magnetic and/or microwave manipulation of the NV fluorescence intensity.²⁰ A proof-of-principle demonstration of FDPs as dual mode fluorescence and ¹³C MRI contrast agents was provided by Lv and co-workers.²¹ Specifically, the optical pumping of NV centers was used to hyperpolarize ¹³C nuclear spins in the diamond lattice²² to enable direct high sensitivity inductive detection by conventional MRI, while FDPs were simultaneously imaged by NV fluorescence. Notably, MRI and fluorescence data can be collected in Fourier reciprocal spaces, which can be leveraged to enhance sensitivity, resolution, and imaging speed.²¹ Polarization transfer from optically pumped NV electronic spins to ¹³C can be a useful strategy for novel sensing technologies such as nanoscale NMR and magnetometry, since the considerably longer relaxation and coherence times of nuclear spins would allow for the monitoring of processes occurring over a broader timescale as compared to electronic spins relaxing on much shorter time scales.^{23, 24}

The majority of the aforementioned applications are enabled by NV centers with long electron spin relaxation and coherence times formed in high quality crystal lattices such as those of diamond plates. Comparatively, the crystal lattices of diamond particles are typically more distorted and may contain significant amounts of other paramagnetic defects such as surface spins and dangling bonds induced from mechanical damage from milling of larger diamond particles. Those paramagnetic centers together with the surface defects are the likely reason that NV centers of FDPs typically exhibit much shorter spin coherence and spin-lattice relaxation times compared to the diamond plates. Thus, the development and optimization of synthesis and processing techniques to enhance electron spin properties of NV centers in FDPs are essential prerequisites for the further development of particle-based quantum sensing and imaging with NV centers.

One of the processing techniques affecting defects in the crystal structure is thermal annealing. For diamond, annealing temperatures have to be sufficiently high—typically above ∼800 °C—to promote the diffusion of vacancies to form NV centers. In addition to color center formation, annealing can remove radiation-induced lattice damage. Recently, it has been shown that a rapid (e.g., 1–10 min) thermal annealing (RTA) at very high temperatures (∼1500–2000 °C) promotes the formation of green emitting nitrogen-vacancy-nitrogen (NVN) centers in synthetic type Ib particles by enabling vacancy assisted nitrogen diffusion that occurs in this temperature range.²⁵ This led to the fabrication of diamond particles containing both NV and NVN centers.²⁶ Typically, RTA also improves spin-coherence and spin-lattice relaxation times based on estimates obtained from continuous wave (CW) electron paramagnetic resonance (EPR),^{27, 28} magnetic field induced fluorescence contrast,²⁷ and ¹³C NMR signal enhancement upon optical hyperpolarization.²⁹

Here, we report on a continuing investigation of effects of high-temperature annealing (1600 °C) on electron spin and optical properties of FDPs. In contrast to the previous efforts of the high-temperature annealing of diamond particles for ∼10 min or less, the duration was extended to ≥2h using a conventional vacuum tube furnace. The impacts of this long ultrahigh-temperature annealing (LUHTA) on fluorescence, magnetically modulated fluorescence contrast, and spin dynamics of paramagnetic species in the diamond particles as observed by CW and pulsed EPR, optically detected magnetic resonance (ODMR), and ¹³C lifetimes from NV induced optical hyperpolarization are reported.

II. EXPERIMENT

A. Materials

Synthetic type Ib HPHT diamond particles of three different nominal sizes of 15 μm, 1 μm, and 100 nm were provided by Adámas Nanotechnologies, Inc. (Raleigh, NC, USA). The particles were irradiated with 3 MeV electrons to a fluence of ∼1 × 10¹⁹ e⁻/cm². All other chemicals were purchased from Thermo Fisher Scientific (Waltham, MA, USA) unless specified otherwise.

B. Annealing

The particles were annealed under vacuum (∼10⁻⁶ Torr) using a cylindrical tube furnace (Carbolite, UK) under two different regimes denoted as “standard” (ST) and “ultra-high temperature (UHT).” ST annealing was at 900 °C for 2h and UHT annealing at 1600 °C for 2h. Due to the slow cooling rate of the furnace, the time the samples spent at high temperatures for the UHT series should not be neglected: as a rough estimate, the UHT samples experienced several more hours above 1000 °C.

C. Post-anneal cleaning

ST annealed particles were oxidized in air at 500 °C for 2h using a Linberg/Blue M furnace (Thermo Fisher Scientific). Due to more significant graphitization, the UHT annealed particles were cleaned using a multistep process. The 15 μm UHT particles were oxidized in molten potassium nitrate (KNO₃, 99+%, Acros Organics, Belgium), which is similar to a reported procedure.³⁰ The particles were combined with 1.5–3 g of KNO₃ in a round bottom glass test tube, which was immersed in a sand bath and treated at 520 °C for 1 h in air (Barnstead Thermolyne 62700, Thermo Fisher Scientific). After cooling, the particles were washed with de-ionized water until all residual potassium salts were removed and then dried.

For the 1 μm and 100 nm UHT particles, four consecutive steps were used for cleaning. The reasons for choosing the multiple steps were a greater surface area of the smaller particles and an empirical observation of an apparently more violent reaction taking place for these particles when treated directly in KNO₃ first. First, the particles were subjected to wet oxidation in KMnO₄ (ACS grade) and H₂SO₄ (98%, ACS Reagent Grade). For this step, a saturated solution of KMnO₄ was prepared (∼65–70 g/l) in de-ionized water. Separately, the graphitized diamond powder was added to a 500 ml round bottom flask with 100 ml of de-ionized water. Next, 100 ml of concentrated sulfuric acid was added to the flask. Finally, 200 ml of the saturated KMnO₄ solution was added dropwise using a funnel with a stopcock. The mixture was stirred at 130 °C for 2 h, after which, 30% hydrogen peroxide (Avantor Inc., Radnor Township, PA, USA) was added dropwise to reduce unreacted permanganate. The particles were washed with de-ionized water to neutral pH and then dried back to a powder.

Next, the particles were combined with KNO₃ and treated at similar conditions described above for the 15 μm particles (520 °C, 20 min for 100 nm particles, 520 °C, 45 min for 1 μm particles). The shorter time was chosen for the smaller 100 nm particles in efforts to avoid complete combustion. Afterward, the particles were cleaned in a 1:3 (v:v) mixture of nitric acid (70%, ACS Plus Grade) and hydrochloric acid (37%, Fisher, ACS Plus Grade) overnight (≈16 h) at 70 °C to ensure the removal of metal contaminants. Finally, the particles were additionally wet oxidized for 72 h in a 1:3 (v:v) mixture of HNO₃ and H₂SO₄ at 130 °C under reflux. Finally, the particles were washed with deionized water to neutral pH, dried, and collected for further characterization.

To verify the removal of amorphous carbon formed during annealing, the Raman characterization of 100 nm and 1 μm with a 442 nm laser line on a Horiba Jobin Yvon LabRAM ARAMIS system (Horiba Scientific, Japan).

D. Electron paramagnetic resonance

CW and pulsed EPR were utilized for the characterization of spin ensembles in the diamond particles. X-band (9.5–9.8 GHz) CW EPR measurements were carried out at room temperature (RT) using either a Bruker Elexsys-II E500 X-band spectrometer (Bruker Biospin, Billerica, MA USA) installed at North Carolina State University (Raleigh, NC USA) or a Bruker EMX-220 spectrometer installed at the Ben Gurion University of the Negev (Beersheba, Israel). The E500 spectrometer was equipped with a super high sensitivity probe head. Pulsed EPR measurements were performed at room temperature with an Elexsys E580 FT-EPR spectrometer installed at North Carolina State University and configured for Q-band (≈34 GHz) measurements. Data visualization and fitting was carried out using either matlab^® (The MathWorks, Inc., Natick, MA, USA) or originlab^® (OriginLab Corp., Northampton, MA) software.

Spin concentrations were determined from the double integration of unsaturated main field (g ≈ 2 region) and half-field (g ≈ 4 region) CW X-band EPR spectra and comparing with the reference spectra from a previously reported purified detonation nanodiamond containing substitutional nitrogen (P1) at a concentration N_s = 6.3 × 10¹⁹ spins/g³¹ and a fluorescent microdiamond sample containing NV⁻ at a concentration N_NV= 5.4 × 10¹⁷ spins/g.³² For power saturation experiments, CW EPR spectra in the g ≈ 2 region were collected by varying the incident microwave power from 60 to 0 dB attenuation in 2 dB increments.

Pulsed EPR was employed to directly measure ensemble spin–lattice T₁ and spin–spin T₂ relaxation times for both the center line hyperfine component of the P1 signal and the high field allowed component of the NV⁻ center (for the UHT series, this line was only detectable in the 15 μm UHT sample) using 3-pulse (π–π/2–π, inversion recovery) and 2-pulse (π/2–π, Hahn echo decay) sequences. Biexponential or monoexponential fits (as specified in subsequent sections) were used to assess spin–lattice and spin–spin relaxation times, where the fast and slow relaxing components of either T₁ or T₂ are denoted as T_fast and T_slow, respectively.

E. Single particle optical NV⁻ spin characterization

Characterization of the spin properties of single diamond particles was performed using a home-built confocal microscope installed at the City College of New York (CCNY, NY, USA). Samples were prepared by drop casting a solution containing particles on a glass coverslip. The coverslip was then fixed to a PCB board patterned with an omega-shaped antenna designed to generate a microwave magnetic field over the sample. The microwave signal was generated by an R&S SMB100A synthesizer (Rohde & Schwarz USA, Inc., Columbia, MD, USA) and amplified by a ZHL-16W-43-S+ high power amplifier (Mini-Circuits/Scientific Components Corp., New York, NY, USA). A typical 250 μW power of green laser excited NV centers through a NA = 0.42 microscope objective (Mitutoyo 50× M Plan Apo, Mitutoyo Corp., Kawasaki, Japan), and the collected photoluminescence (PL) was filtered using a high pass 650 nm filter, coupled into a multimode fiber, and detected by a single-photon (SPD) SPCM-AQRH-14 detector (PerkinElmer, Waltham, MA, USA). For brighter diamonds, neutral density filters (OD 0.5, 3, 4) were used to prevent the saturation of the SPD.

Single crystals were identified by performing a scan of the coverslip using a galvanometer-based confocal scanning system. Once an emission spot was found on the coverslip, an optically detected magnetic resonance (ODMR) measurement was performed under a magnetic field of ∼50 G generated by a neodymium magnet. The magnetic field was rotated until the ODMR spectra exhibited eight or fewer lines to confirm that the PL was coming mostly from a single crystal.

Pulsed measurements were then performed on each single crystal to determine the Rabi oscillation frequency and contrast, the longitudinal relaxation time (T₁), the inhomogeneous transverse relaxation time (or dephasing time, T₂*) using a Ramsey sequence, and the coherence time (T₂) using a Hahn echo sequence with a single rephasing pulse. The curves obtained were fitted by an exponential decay for T₁, a gaussian decay for T₂*, and a stretch exponential decay (stretch coefficient b constrained between 1 and 3) for T₂.³³ For these measurements, an acousto-optic modulator was used to switch off the laser, while a ZASWA-2-50DR+ microwave switch (Mini-Circuits) placed between the synthesizer and the amplifier was used to control microwave. The spins were typically initialized and read out using a 100 μs laser pulse and a 5 μs gate of the single-photon detector (SPD). For Rabi oscillation experiments, a reference signal without any microwave applied was measured. For T₁, Ramsey, and Hahn echo sequences, every data acquisition was repeated with an additional π-pulse before the measurement; the two signals were subsequently subtracted and divided by a reference in order to minimize errors arising from slow system instabilities (see the supplementary material⁴¹ for an example of these measurements and additional information on the pulse protocols used for the various measurements).

F. Photoluminescence and magnetically modulated NV⁻ photoluminescence intensity

Photoluminescence spectra of particles were collected using an inverted epifluorescence microscope (Olympus IX71, Olympus Corp., Tokyo, Japan) with a xenon-arc lamp excitation and a 535/50 nm band pass filter and a 562 nm long pass emission filter. Spectra were acquired with an HR2000 USB spectrometer (Ocean Insight Inc., Orlando, FL, USA).

Modulation of NV⁻ PL was measured using a methodology described elsewhere.²⁷ In brief, 20 μl droplets of 10 mg/ml suspensions of 100 nm and 1 μm particles were placed on glass coverslips and dried in air before the measurement. For 15 μm particles, a small pile of dry powder was placed on a coverslip. NV fluorescence was modulated by placing neodymium magnets to provide a magnetic field of approximately of 20 mT (±2 mT) at the sample. The magnetic field was measured with a GM2 Gaussmeter (AlphaLab, Inc., Salt Lake City, UT, USA). Error in the magnetic field was determined by repeating the placement of the magnets 10 times and calculating the standard deviation. For each particle size and treatment (UHT or ST annealing), five modulation measurements were performed, where a single modulation is defined as switching between a magnet-off and magnet-on configuration, or a magnet-on and magnet-off configuration. The fluorescence intensity at 680 nm was recorded in each of the magnet configurations, and the modulation was calculated as

$$\mathrm{PL}\mathrm{Modulation}\mathrm{at}680\mathrm{nm}(\text{\%})=100\times {\displaystyle \frac{I_{\mathrm{off}}-I_{\mathrm{on}}}{I_{\mathrm{off}}},}$$

where $I_{\mathrm{off}}$ and $I_{\mathrm{on}}$ are the intensities of the PL spectra at 680 nm in the “magnet off” and “magnet on” configurations, respectively. The 680 nm wavelength was selected as this is approximately the peak of NV-emission.³⁴ In addition to PL modulation at a single wavelength, the modulation as a function of wavelength is also determined by using the same equation for each wavelength recorded on the PL spectra for two spectra where the magnet is applied in one spectrum and removed in another spectrum.

G. ¹³C transverse lifetime measurements (T₂′)

The ¹³C transverse lifetimes (T₂′) serve as the relevant interrogation time for quantum sensing experiments using the ¹³C nuclear spins as magnetometers.²³ The ¹³C T₂′ values were measured using the following procedure. The ¹³C spins were first hyperpolarized at low field (≈36 mT) at room temperature via the optical pumping of the NV centers. Their transverse lifetime is then probed at high field (7 T) while subjecting the spins to a train of spin-locking pulses of a flip angle θ (close to pi/2) that lock them along a transverse axis on the Bloch sphere. In windows between the pulses, the Larmor precession of the spins was digitized every 1 ns. Typically, the pulses were spaced 100 μs apart and over 1 million pulses were applied. After digitizing the precession signal, a Fourier transform was performed to extract the amplitude and phase information at the precise Larmor frequency. T₂′ values were estimated from the 1/e intercept of the signal decay trace. In the absence of the spin-locking train, the native ¹³C dephasing time is T₂*∼1.5 ms. The ¹³C signal for the 100 nm (both ST and UHT) particles was too weak to detect at room temperature, and, therefore, no data were obtained.

III. RESULTS AND DISCUSSION

A. Yield of particles after UHT annealing

Mass loss during the oxidation of UHT annealed particles ranged from 46% for the 15 μm particles to 74% for the 100 nm particles (Table I). The yield of UHT annealed diamond postoxidation ranged from approximately 25%–30% for the 100 nm and 1 μm particles to 46% for the 15 μm particles. The majority of the mass lost (≈60%) from the 100 nm UHT sample occurred during cleaning after annealing. The remaining ≈14% of losses may be attributed to the sample handling losses or losses incurred during the annealing treatment. For the 15 μm UHT sample, losses during postannealing oxidation accounted for approximately 34% of the 46% total losses. An important observation is that after 2h annealing at 1600 °C, it was possible to recover diamond particles even from the 100 nm starting material. Furthermore, the postannealing treatment in molten potassium nitrate was extremely effective in removing the graphitized material for all three particle sizes. This is additionally illustrated in Fig. 1 showing the photographs of 15 μm particles at various treatment stages. Additionally, Raman analysis did not indicate the substantial amounts of amorphous carbon (see the supplemental material⁴¹ for Raman spectra). From our prior experience in removing amorphous carbon from diamond, this treatment protocol is significantly more efficient than just air oxidation at similar temperatures and is considerably more effective than a typical wet oxidation process based on mixtures of nitric and sulfuric acid.

TABLE I.

Mass loss of diamond particles during the oxidation of sp² carbon after UHT annealing at 1600 °C for 2 h. Peak to peak linewidths of the central line component of X-band EPR spectra of diamond particles recorded at 2 μW incident microwave power. Spin concentrations determined from the double integration of main field (primary defects, S = 1/2, 3/2, P1 centers) and half-field (g = 4.24) signals. Error in spin concentrations does not exceed 15%.

Sample	% Mass lost during oxidation	ΔBp-p (Gauss)	Primary defects (ppm)	P1 (ppm)	NV (ppm)	P1/Total primary ratio
15 μm ST	—	1.32	34	29	4.78	0.85
15 μm UHT	46	0.94	40	33	<0.5	0.83
1 μm ST	—	1.25	64	45	4.66	0.70
1 μm UHT	69	0.86	52	37	<0.5	0.71
100 nm ST	—	2.58	78	30	3.03	0.38
100 nm UHT	79	2.50	46	15	<0.5	0.33

FIG. 1.

Photographs of initial 15 μm diamond particle powder (a), after UHT annealing (b), and after KNO₃ oxidation (c).

Note that the annealing temperature of 1600 °C is close to a threshold separating two different mechanistic regions of graphitization as assessed in an early work by Fedoseev and co-workers. One of the conclusions of the latter study was that surface graphitization is a size-independent phenomenon at temperatures below ∼1630 °C.³⁵ While our data may indicate some size dependence, it could be also related to different post annealing oxidation treatments. We note here that detailed studies of the size-dependent graphitization of the diamond particle upon high-temperature annealing fall outside of the scope of this report.

B. Electron paramagnetic resonance

1. Continuous wave EPR (X-band, 9.5–9.8 GHz)

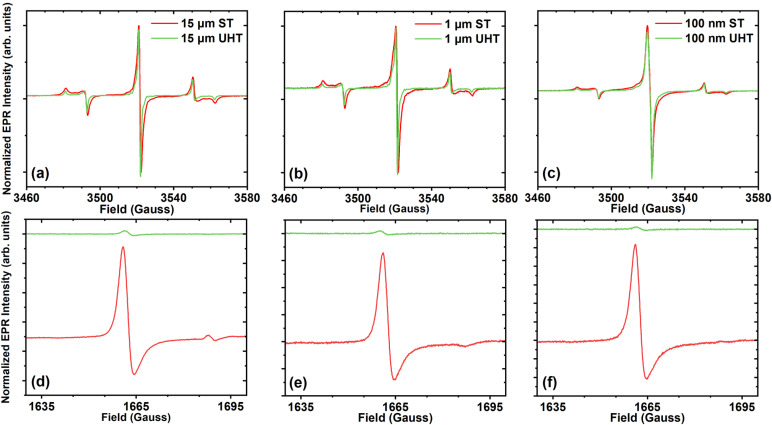
Figure 2 shows the representative main field and half-field EPR spectra for each particle size and treatment. EPR signals at the main field are consistent with substitutional nitrogen (P1) centers [Figs. 2(a)–2(c)]. This signal consists of overlapping spin components; these additional components, such as S = 1/2 dangling bonds and S = 3/2 negatively charged vacancies (V⁻), contribute to the broadening of the central line, leading to complexity in spectral interpretation due to unresolved inhomogeneously broadened lines. We denote these combined signal contributions from the main field defects as “primary” defect centers. Traces of the UHT annealed samples all indicate the narrowing of the central line spectra [Figs. 2(a)–2(c)]. The measured peak–peak linewidths of the central line are shown in Table I.

FIG. 2.

Continuous wave EPR main field (a)–(c) and half-field (d)–(f) spectra recorded at X-band (9.87 GHz), room temperature. ST annealed particles are shown with red traces, and UHT annealed particles with green traces. The 15 μm, 1 μm, and 100 nm main field and half-field spectra are shown in (a) (d), (b) (e), and (c) (f), respectively. Main field spectra were recorded at 2 μW incident power with 1 G modulation and five averages. Half-field spectra were recorded at 126.3 μW incident power with 3 G modulation and 200 averages.

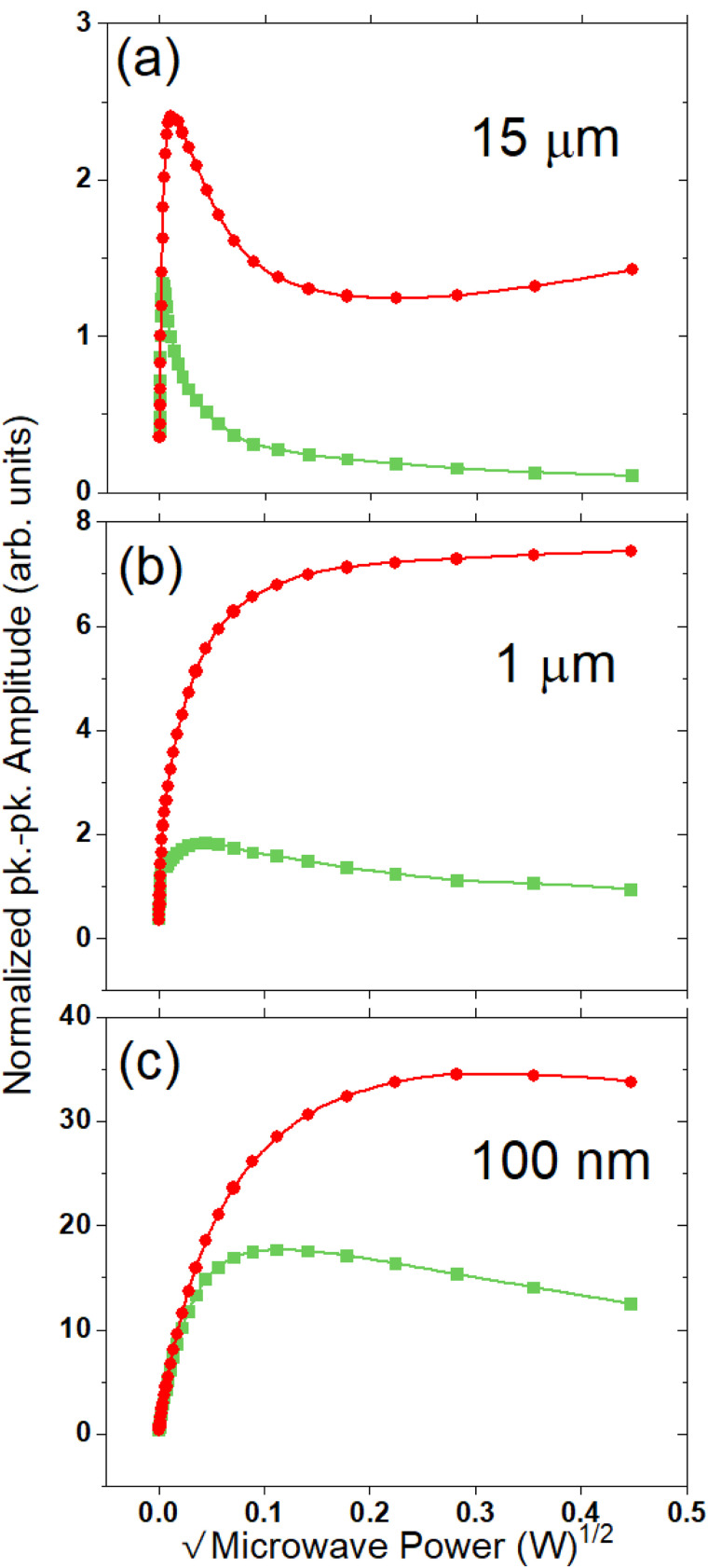
This narrowing of linewidths is indicative of the removal of spectral components, which would contribute to inhomogeneous line broadening. Figure 3 shows the 2D microwave power sweep traces recorded from 0 to 60 dB power attenuation. The combination of reduced linewidth and observed saturation at lower power indicates the removal of fast relaxing spin components in all three particle sizes. The impact of annealing is most significant for the 15 μm particle sizes due to the minimized impact of the surface at this size.

FIG. 3.

2D microwave power saturation spectra for ST annealed (circles) and UHT annealed (squares) particles for 15 μm (a), 1 μm (b), and 100 nm (c) sizes. The peak–peak amplitude of the central line component of the main field CW spectra [see Figs. 2(a)–2(c)] is recorded vs the square root of incident microwave power. Spectra were recorded at X-band (9.87 GHz) at room temperature. The peak-peak amplitudes are normalized to the peak–peak amplitude at 2 μW incident power. Spectra were recorded from 0 dB attenuation (200 mW) to 60 dB (200 nW) in 2 dB increments.

2. Spin concentrations

Double integration of main field (g = 2) and half-field (g = 4) spectra in comparison with a known reference sample allows for the determination of P1, total primary defects (P1 + other half-integer primary spins), and NV spin concentrations. Measured spin concentrations for these centers are summarized in Table I. UHT annealing reduces the NV⁻ spin concentration from ∼3–5 ppm to <0.5 ppm for all particle sizes. This is also indicated by the significant reduction of the half-field signal in the UHT particles as compared to the ST particles [Figs. 2(d)–2(f)]. It should be noted that the half-field transition for the UHT particles is nearly at noise level, and the calculated double integral value could be erroneous for these weak signals; our detection limit is approximately 0.5 ppm, so, for these samples, we denote them as simply having <0.5 ppm of NV⁻.

It is useful to consider the ratio of P1 centers relative to other S = 1/2 contributions; this is shown in Table I. This percentage is not impacted by UHT annealing; however, it is a function of particle size. The percentage of P1 relative to all other spin-1/2 defects drops from ∼80% for 15 μm particles to ∼30%–40% for 100 nm particles. This additionally confirms the greater impact of paramagnetic spins such as surface defects and dangling bonds at smaller particle sizes. It should be noted that the measured P1 concentrations in these samples are lower than the typical ∼100 ppm in type Ib particles. A drop in the P1 concentration is a consistent observation following irradiation and was the focus of a separate recent study.³⁶

3. Pulsed EPR (Q-band, 34 GHz)

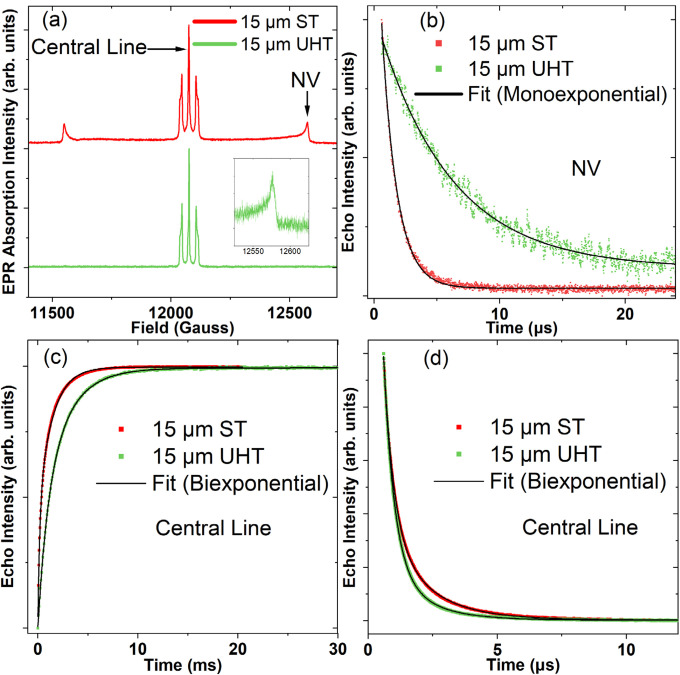
Figure 4 shows the representative echo detected field-sweep EPR spectra as well as Hahn echo decay and inversion recovery traces for the 15 μm particles. The echo-detected spectra are similar to those of FDPs reported earlier.³⁷ As noted above with the CW EPR spectra, the central line is the superposition of spectra arising from P1 (N⁰, substitutional nitrogen) and other paramagnetic defects with half-integer spin, while the outer components are attributed to allowed transitions of the NV⁻ ground state.³²

FIG. 4.

(a) Echo detected field sweep spectra of 15 μm UHT and ST annealed particles. Inset shows the high field allowed NV transition in the UHT particles, which was significantly reduced in the intensity after annealing. The “central line” and “high NV allowed” transition lines are labeled for clarity. The inset is an additional narrow field sweep taken of the NV allowed transition line at high field on the UHT sample. Hahn Echo decay traces from 2pESEEM (2-pulse electron spin echo envelope modulation) experiments for the high NV allowed transition (b) and the central component of the P1 (d) for the 15 μm particles. Inversion recovery for the central component of the P1 spectrum for the 15 μm particles (c).

The NV T₂ time in the 15 μm UHT particles is extended approximately fivefold as compared to their ST annealed counterparts [Fig. 4(b)]. Interestingly, the concentrations of P1 were mostly unchanged by annealing (Table I), and since substitutional nitrogen is known to be a major source of decoherence in diamond,³⁸ this suggests that paramagnetic centers other than P1 are responsible for a significant amount of decoherence for the NV centers in these particles. Based on 2D saturation measurements at X-band, fast relaxing spins are significantly suppressed after annealing (see Fig. 3).

Another consideration is the spatial distribution of NV centers in the particles. It is known that nitrogen is inhomogeneously distributed in HPHT diamond.³⁹ This could lead to a higher density of NV centers in nitrogen rich regions, which may be readily annealed out at 1600 °C. However, there may still be isolated P1 centers, which can facilitate the formation of NV centers after irradiation and annealing. These isolated NV centers may not anneal out readily and could be responsible for the observed behavior in the 15 μm particles. However, at the moment, this is only a tentative explanation, and further investigations into the spatial distributions of NV centers and P1 centers in these particles are warranted.

While the effects on the T₂ times are negligible for the central P1 line component [Fig. 4(d), Table II], the T₁ relaxation times are extended in the 1 and 15 μm particles, probably due to the removal of bulk lattice defects induced during irradiation or those resulting from fragmentation after synthesis. As the particle size decreases, there is a significant reduction in the T₁ times. Considering only the slowest relaxing component of the UHT series, the T₁ values drop from 2.6 ms in the 15 μm particles, to about 0.6 ms in the 100 nm particles. This is likely due to the prevalence of surface spins in the 100 nm particles, which are not removed via annealing.

TABLE II.

Measured relaxation times of the P1 central line and NV allowed of the echo detected field swept EPR absorption spectra (see Fig. 4). Measurements were performed at room temperature at the Q-band (∼34 GHz). The values reported in the table are the fitted T₂ values multiplied by 2. Standard error of fit values is shown in parentheses next to the reported values.

Spectral line	P1 center line (biexponential fit)				High NV allowed (monoexponential fit)
Procedure	T1 by Inversion recovery		T2 by Hahn echo decay		T2 by Hahn echo decay
Sample	T1 (fast) (μs)	T1 (slow) (μs)	T2 (fast) (μs)	T2 (slow) (μs)	T2 (μs)
100 nm ST	57.8 (2.0)	636.1 (10.5)	0.73 (0.0037)	3.0 (0.025)	—
100 nm UHT	29.6 (0.74)	646.4 (6.6)	0.70 (0.0036)	2.6 (0.036)	—
1 um ST	185.1 (2.9)	1291.2 (7.1)	0.77 (0.0026)	4.2 (0.022)	—
1 um UHT	441.7 (13.1)	2017.5 (14.9)	0.82 (0.0032)	3.3 (0.032)	—
15 um ST	191.9 (3.0)	1414.7 (7.2)	0.78 (0.0024)	3.2 (0.011)	2.43 (0.034)
15 um UHT	993.2 (24.5)	2609.1 (36.1)	0.82 (0.0025)	2.8 (0.019)	11.70 (0.15)

C. Single particle optical NV⁻ spin characterization

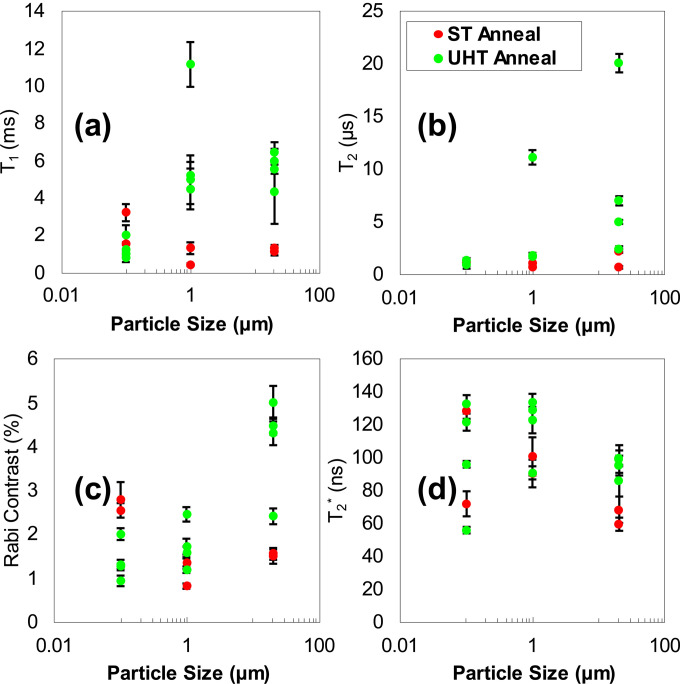
The analysis of T₁, T₂, T₂*, and Rabi contrast for the NV spins of 18 single particles is recorded in Figs. 5(a)–5(d). The major conclusion of single particle analysis is that UHT annealing has the most positive impact on the spin properties of NV centers in 15 and 1 μm particles, with only marginal impact on NV centers in 100 nm particles. This is due to surface defects, which would be more pronounced on the 100 nm particles.

FIG. 5.

Summarized analysis of the single particle spin characterization for ST annealed and UHT annealed particles. (a) Values of T₁ relaxation determined from exponential decay fit. (b) T₂ spin-coherence determined from stretched exponential decay fit. (c) Rabi contrast vs particle size. (d) T₂* determined from Gaussian fits as a function of particle size.

D. Photoluminescence and magnetically modulated NV⁻ photoluminescence

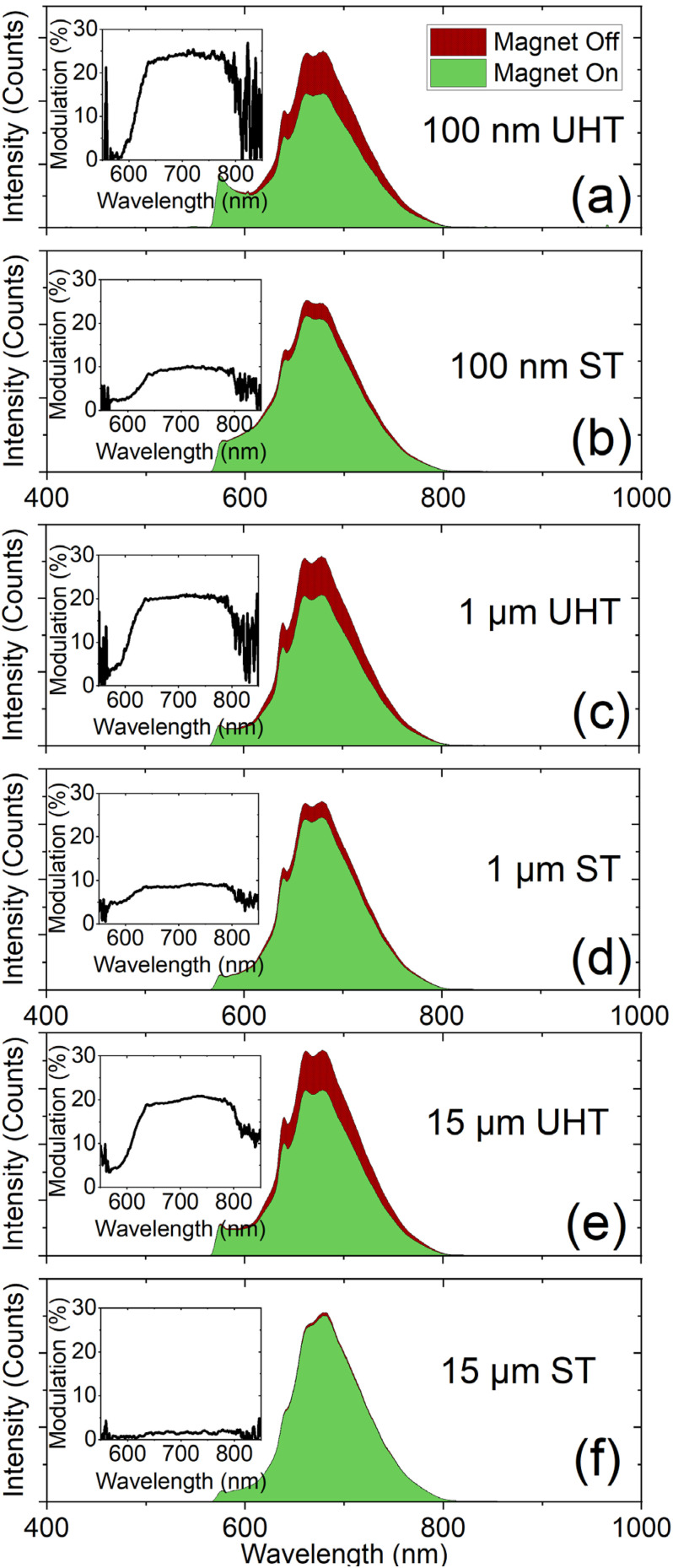
Extended UHT annealing results in enhanced magnetic field induced fluorescence contrast, which is in agreement with prior observations’ rapid high-temperature annealing.²⁷ All particle sizes exhibit an enhancement of magnetic field induced NV⁻ fluorescence modulation following UHT annealing [Figs. 6(a)–6(c)]. Tabulated modulation values are summarized in Table III. The UHT annealing process leads to a ∼2.5× enhancement in the magnetic field induced fluorescence contrast for the 100 nm and 1 μm particles, and a 10× enhancement for the 15 μm particles. After UHT annealing, all of the particles exhibited a ∼20% contrast, which is independent of particle size.

FIG. 6.

Static magnetic field (∼200 G) induced NV⁻ fluorescence modulation at 680 nm for the 100 nm (a), (b), 1 μm (c), (d), and 15 μm particles (e), (f) for the UHT and ST annealing treatments. The PL spectra shown are representative spectra from the modulation experiments (see Sec. II). Insets show the wavelength dependent modulation for each particle size and annealing treatment.

TABLE III.

Summarized magnetic modulation data for all particle sizes from N = 5 modulation cycles (see Sec. II). The contrast enhancement is calculated by ratioing the UHT modulation for a given size to the ST annealed for the same sized particles.

Particle size and annealing	Modulation at 680 nm, % (standard deviation)	Contrast enhancement relative to ST anneal
15 μm ST	1.96 (0.559)	—
15 μm UHT	20.3 (0.931)	10.3
1 μm ST	8.55 (0.340)	—
1 μm UHT	19.8 (0.361)	2.32
100 nm ST	9.51 (0.338)	–
100 nm UHT	23.7 (0.163)	2.49

There is still not a definitive explanation for this observed enhancement. In the previous study,²⁷ it was speculated that the improvement in contrast was due to the removal of NV centers in damaged portions of the lattice. Since this observed modulation effect results from the mixing of electron spin states in the ground and excited levels, which increases the probability of non-radiative decay through the singlet via intersystem crossing,⁴⁰ it is possible that the high-temperature annealing removes fast relaxation pathways for the NV centers. A more definitive answer to this question will likely require the use of single crystals with well controlled NV spatial distribution.

E. ¹³C transverse lifetime measurements (T₂′)

Table IV reports the measured ¹³C transverse lifetimes (T₂′) measured via pulsed spin-locking trains for the 15 and 1 μm particle sizes. High-temperature annealing appeared to have a substantial benefit for the 15 μm particles, but the opposite trend was observed for the 1 μm particles.

TABLE IV.

Measured ¹³C T₂′ transverse lifetimes from the NV optical polarization experiments.

Sample	13C T2′ (ms)
15 μm ST	102.6
15 μm UHT	233.6
1 μm ST	96
1 μm UHT	26

IV. SUMMARY AND CONCLUSIONS

High-temperature annealing treatments of diamond particles at temperatures in excess of 1500 °C are still an emerging approach for the optimization of spin properties of NV centers in FDPs. It is shown here that even with relatively long treatment times at 1600 °C, it is possible to recover diamond down to ∼100 nm particle sizes. Hence, these treatments can be performed if rapid annealing is not an available option. Annealing at this high temperature generally improves the spin properties of paramagnetic centers in the diamond via the removal of fast relaxing spins, which can promote decoherence. These positive benefits are more pronounced in larger particles, where surface effects are less pronounced; however, a proper combination of high-temperature annealing with optimized surface chemistry may be a means of enhancing the spin properties of smaller particles. We observe an approximate fivefold improvement in the NV T₂ times for 15 μm particles (∼10–11 μs with high-temperature annealing at 1600 °C versus ∼2–3 μs with standard annealing at 900 °C) as measured in EPR, and these results are in reasonable agreement with the optical characterization of NV T₂ times. Notably, the high-temperature annealing boosts the static magnetic modulation of the NV-fluorescence significantly in all particle sizes. The achieved ∼20% contrast after annealing is apparently independent of particle sizes, but the mechanisms behind this improvement are speculative at the moment. In a future study, we will examine temperature dependent effects in an effort to maximize the spin properties of NV centers while also preserving as many NVs as possible to ensure high brightness. Overall, the approach of high-temperature annealing is a viable means of improving the spin properties of paramagnetic centers in particulate diamond, and this study provides a template for future studies in this direction and that optimized annealing treatments will be an integral part of future production methodologies for FPDs in sensing applications.

AUTHOR DECLARATIONS

Conflict of Interest

M.D.T. is an employee of Adamas Nanotechnologies, Inc.; O.A.S. is the founder and president of Adamas Nanotechnologies, Inc., a for profit commercial entity that manufactures diamond materials.

Author Contributions

Nicholas Nunn: Conceptualization (equal); Formal analysis (lead); Investigation (lead); Methodology (lead); Visualization (lead); Writing – original draft (lead); Writing – review & editing (equal). Sergey Milikisiyants: Formal analysis (supporting); Supervision (equal). Marco D. Torelli: Formal analysis (equal); Writing – review & editing (equal). Richard Monge: Formal analysis (equal); Writing – original draft (equal). Tom Delord: Formal analysis (equal); Supervision (equal); Writing – original draft (equal). Alexander I. Shames: Formal analysis (equal); Writing – review & editing (equal). Carlos A. Meriles: Funding acquisition (equal); Supervision (equal); Writing – review & editing (equal). Ashok Ajoy: Formal analysis (equal); Funding acquisition (equal); Writing – review & editing (equal). Alex I. Smirnov: Funding acquisition (equal); Supervision (equal); Writing – review & editing (equal). Olga A. Shenderova: Conceptualization (equal); Funding acquisition (equal); Project administration (equal); Writing – review & editing (equal).

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon reasonable request.