基于共空间模式算法和支持向量机二重分类的癫痫发病预测

Abstract

目前癫痫患者的发病预测手段十分耗时且易受主观因素干扰，因此文中提出了一种基于共空间模式算法（CSP）和支持向量机（SVM）二重分类的癫痫发病自动预测方法。此方法将提取空域特征的共空间模式算法应用到癫痫脑电信号检测中，但是该算法未考虑信号的非线性动力学特征且忽略了其时频信息，所以在特征提取阶段选取了标准差、熵和小波包能量这几种互补特征来进行组合。分类过程采取一种基于支持向量机的全新二重分类模式，即将癫痫患者正常期、发作间期和发作期三个阶段分成正常期和准发病期（包括发作间期和发作期）两类进行支持向量机识别，然后对属于准发病期的样本进行发作间期和发作期的分类，最终实现三个时期的分类识别。实验数据来自德国波恩大学的癫痫研究数据库。实验结果显示，第一重分类平均识别率为 98.73%，第二重分类平均识别率可达 99.90%。结果表明，引入空域特征和二重分类模式能够有效解决众多文献中发作间期和发作期识别率不高的问题，提升各个时期的识别效率，为癫痫患者的发病预测提供有效的检测手段。

引言

癫痫是一种常见的神经系统疾病，全世界约有 6 500 万的癫痫患者，发病人群涉及各个年龄阶段。癫痫发病的危险因素有：癫痫病家族史、颅脑损伤、热性惊厥、新生儿疾病和孕期危险因素^[1]。目前我国在抗癫痫药物^[2]以及添加治疗、微创手术和共病防治等^[3]治疗手段方面都进行了深入研究。这种疾病具有反复发作和发作前无固定征兆的特点。据统计，约 80% 癫痫患者的脑电图（electroencephalogram，EEG）在发作间期会表现异常，因此目前监控脑电图是判断癫痫患者发病情况的主要手段。癫痫种类繁多且脑电图具有非直观性，所以仅依靠专业医师主观经验进行判断,效率低下，易发生误判。因此癫痫患者脑电信号的实时检测和高精度分类识别是当前研究的主要方向。

几十年来，为了提高脑电图的诊断性能，学者们从时域、频域和非线性动力学等方面提取了脑电信号中的有效信息^[4]。Gotman^[5]在 1982 年最早提出了癫痫脑电时域特征的提取方法，用信号的波峰幅度、斜率和变异系数等参数作为表征脑电信号的时域特征。功率谱（power spectral density，PSD）为最常用的频域特征，在 2010 年 Naghsh-Nilchi 等^[6]采用了基于谱值的特征提取方法，从每个子带的功率谱中提取相应的均值、标准差、熵等参数，成功地将时域特征融于频域特征。之后考虑到脑电信号的非平稳特性和单方面特征的局限性，人们开始进行时频分析，主要方法有短时傅里叶变换（short-time Fourier transform，STFT）^[7]、小波变换（wavelet transform，WT）^[8-9]、Hilbert-Huang 变换^[10]、经验模态分解（empirical mode decomposition，EMD）^[11]等。随着研究深入，人们发现大脑可看作一个非线性动力系统，于是引入基于熵的特征提取方法。Pincus 从衡量时间序列复杂性角度提出近似熵（approximation entropy，ApEn）的概念，其缺点是易受数据长度的影响^[12]。随后 Richman 等^[13]提出样本熵的概念，弥补了近似熵的缺陷。文献[14]应用排列熵特征进行癫痫脑电信号的识别，从而取得了显著效果。

分类效果较好的方法有支持向量机（support vector machine，SVM）（不同情况可选择不同的核函数）^[15]、人工神经网络（artificial neural network，ANN）^[16]、K-最近邻分类器^[17]以及 Boosting 算法^[18]。目前分类识别效果较好的方法中多是时频域和非线性动力学的组合，没有考虑到信号的空域特征，未能达到高精度的分类识别率。分类过程多是二分类或者直接进行三分类，忽略了癫痫发作（由正常期到发作间期再到发作期）的连续性。

本文结合以上文献中的方法，针对癫痫脑电信号的三分类问题提出一种全新的检测模式。首先利用共空间模式（common spatial model，CSP）算法提取多通道癫痫脑电信号的空域特征，然后结合时频域和非线性动力学方面的特征，共同送入不同核函数的 SVM 中进行二重分类。第一重是对正常期和准发病期（包括发作间期和发作期）进行分类，第二重是对属于准发病期的样本进行发作间期和发作期的分类，最终实现正常期、发作间期和发作期三个时期的检测。整个实验流程如图 1 所示。

图 1.

Automatic detection process of epileptic electroencephalogram signal

癫痫脑电信号自动检测流程

1. 方法

1.1. 实验数据

本文利用德国波恩大学的癫痫研究数据进行了有效性验证^[19]。数据分 A、B、C、D、E 五组，分别为患者正常时期清醒睁眼、正常时期清醒闭眼、发作间期致痫灶外、发作间期致痫灶内和发作期。每组数据集有 100 段脑电信号，每段总计 4 097 个数据，采样频率 173.6 Hz。本文进行分类的三个时期分别为：A、B 组正常期，C、D 组发作间期，E 组发作期。本文假定脑电信号为五通道采集，则每组数据集包含 20 组五通道数据，因每段脑电数据点过多，使用前将每段第一个点舍弃，然后等分为 4 段，最终五组数据集共得到 400 个五通道样本。

1.2. 共空间模式算法

CSP 算法最早由 Fukunage 等提出^[20]，目前在运动想象脑电信号识别和情感脑电信号分类中应用较多，考虑到癫痫发作过程中也会伴随一些身体上的行为，和运动想象过程有一定的相关度，所以本文尝试将 CSP 算法应用于癫痫患者三个时期的检测。CSP 算法的核心思想是利用矩阵的对角化找出最佳空间滤波器，使得脑电信号矩阵滤波后，方差值差异最大化，从而得到具有较高区分度的特征向量。其算法具体流程如下：假设 X₁ 和 X₂ 为两类脑电信号矩阵，它们的维数为 N·T，N 为脑电通道数，T 为每个通道所采集的样本数，则 X₁ 和 X₂ 可以分别写为：

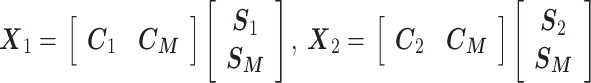1

归一化后的协方差矩阵 R₁ 和 R₂ 分别为：

2

分别使用 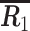和 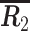代表两类脑电信号的空间协方差矩阵，则混合空间协方差矩阵为：

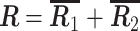3

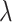而 R 可以表示为 ，其中 U 是矩阵的特征向量， 是对应的特征值。然后对特征值进行降序排列，利用主成分分析法求出白化矩阵：

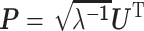4

则协方差矩阵 R₁ 和 R₂ 可变换为：

5

然后对 S₁ 和 S₂ 做主分量分解，得到：

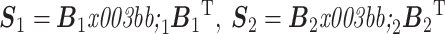6

通过上面的式子可以证明两个矩阵的特征向量是相等的，即 B₁ = B₂ = V，同时，两个特征值的对角矩阵 和 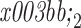之和为单位矩阵，即 ，所以 S₁ 的最大特征值所对应的特征向量使 S₂ 有最小的特征值，反之亦然。将白化后的脑电信号投影到特征向量 B的前 m 和后 m 列特征向量，便可得到最佳的分类特征，投影矩阵可表示为 W = B^TP，单次脑电信号的采集数据 X_i 可变换为 Z_i = W·X_i。

构造好空间滤波器后，对原始数据进行空间滤波便可选取出特征向量 f_i：

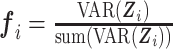7

1.3. 互补特征的选取

空间滤波很适合处理多维的脑电信号，它能够同步利用脑电信号的空间相关性，有效提取出不同通道上脑电信号的空域特征。鉴于单一特征难以全面地反映信号携带的信息，为获得更好的分类识别效果，本文采用多特征结合的方式，共选取 4 个互补特征如表 1 所示。其中标准差属于时域特征，样本熵和排列熵属于非线性动力学的典型特征，小波包能量是时频分析中基于小波变换的进一步处理^[18]。特征之间的互补信息如表 2 所示。

表 1. Feature numbers and the corresponding name.

特征编号及分别对应的名称

特征编号	特征名称
1	标准差
2	样本熵
3	排列熵
4	前 7 级小波包能量

表 2. Feature complementary information.

特征互补信息

特征属性	优势	劣势
标准差	理论成熟，指标意义明确	特异性较低，无法刻画非线性信号
小波变换	多分辨率，可以提高信号的隐藏特征	依赖先验知识，算法不够灵活
熵方法	分析数据少，算法稳定，运算量小	无法反映信号的时频特征
CSP	不需要预先确定特异频段	需要多通道分析且易受噪声干扰

传统的小波变换对信号分解后的低频成分能够再次分解，但是对于高频成分却无法分析，因此并不能充分地提取信号特征。所以本文选取能够对高频成分做进一步分析的小波包分解来提取时频特征。频带 j 的小波包能量可定义为：

8

其中 N 为对应频带系数个数，n_i 为小波包系数。

经典的三种熵方法是近似熵、样本熵和排列熵，因样本熵是文献[21]提出来的一种近似熵的改进算法，故本文仅选择了样本熵和排列熵。样本熵可表示为：

9

其中 m 为嵌入维度，r 称为相似容限，是一个给定值，取值范围为r = 0.1～0.25 std（std 代表序列的标准差）。

排列熵是文献[21]提出来的一种动力学突变检测方法，能够方便准确地定位系统突变的时刻，并对信号的微小变化具有放大作用。其定义式为：

10

其中 m 为嵌入维度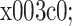， 为一种排列方式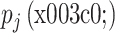， 为对应每个 i 值 出现的概率。

1.4. 基于 SVM 的二重分类

本文首次提出一种基于 SVM 的二重分类模式。其分类流程如下：

（1）第一重分类：将发作间期和发作期定义为准发病期，然后对正常期和准发病期进行 SVM 分类识别；

（2）第二重分类：对准发病期的样本进行发作间期和发作期的 SVM 识别。

传统三分类法需将脑电信号进行三次比对，本文分类模式着眼于正常期到发作间期、发作间期到发作期的转化过程，只需对患者脑电信号进行两次比对即可完成分类识别。与传统三分类法相比，有效节省了识别时间，使得医疗介入更加及时。对比分类流程如图 2 所示。

图 2.

Flow diagram of traditional triple classification and double classification model

传统三分类法与二重分类模式流程对比图

SVM 有着简单的拓扑结构和良好的泛化能力，被广泛应用于分类、函数拟合和时间序列预测等领域。其主要思想是通过合适的非线性映射将输入向量映射到高维的特征空间，从而使得数据总能被一个超平面分割。为了将两类数据正确分开，且分类间隔达到最大，需要找到一个最优分类面W^TX + b = 0，进而可转换为求解以下二次规划问题：

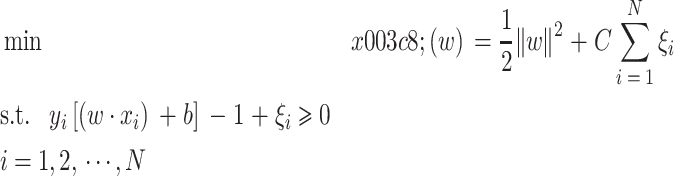12

利用拉格朗日对偶和 KKT 条件继续推导，并引入核函数和正则化项，模型最终变为求解：

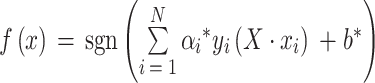13

对于非线性问题，相应的最优决策函数变为：

14

2. 实验结果与讨论

脑电原始数据波形如图 3 所示，从上到下依次为患者正常时期清醒睁眼、正常时期清醒闭眼、发作间期致痫灶外、发作间期致痫灶内和发作期。由图 3 可看出三个时期的脑电波形存在一定差异，但是依靠人工判读，难以满足实时性要求，因此需要对三个时期的脑电信号进行有效特征提取，进而完成癫痫脑电信号的自动检测。

图 3.

EEG waveform of each dataset

各数据集脑电信号波形

特征提取阶段，首先利用 CSP 算法对 400 个五通道脑电数据进行空域滤波和特征提取，空域特征在三个时期的分布规律如图 4 所示。

图 4.

Distribution of CSP values in three periods

CSP 值在三个时期的分布情况

然后提取脑电数据的互补特征：标准差、样本熵、排列熵和小波包能量。宏观上，样本熵和排列熵对非线性序列有较强的表征能力，当样本熵参数m = 2、r = 0.2 × std 时能够达到最佳的分类效果^[22]；当参数m = 5 时，排列熵取得最佳嵌入维度^[14]。小波包能量特征提取时最优的小波基函数为 Daubechies4 小波，最佳的级数为前 7 级小波包能量。

五个特征全部提取完毕，其中标准差、样本熵、排列熵和 CSP 提取的空域特征均为单一特征值，前 7 级小波包能量为 7 维特征向量，将五个特征采用并行组合的方式，构成 11 维特征向量，送入 SVM 进行分类。本文共采用六种核函数的 SVM^[23]，第一重的分类结果如图 5 所示。Cubic SVM 对正常期和准发病期的分类效果最好，与文献[18]相比正常期的识别率提高了 0.77%。Cubic SVM 详细分类情况如图 6 所示，其中左图为正常期和准发病期两类样本分布图，横纵坐标分别为空域特征和标准差（特征组合中任意两个特征值均可作为横纵坐标），蓝色点和红色点分别代表正常期与准发病期；正常期和准发病期样本分类结果统计图中，“1”和“2”分别代表正常期与准发病期。

图 5.

The first average recognition rate of SVM with different kernel functions

第一重不同核函数 SVM 下的平均识别率

图 6.

Cubic SVM classification results of normal and paroxysmal periods

正常期与准发病期的 Cubic SVM 分类结果

第二重的分类结果如图 7 所示。其中 Coarse Gaussian SVM 能够稳定达到 99.90% 及以上的高识别率，因此本文选取 Coarse Gaussian SVM。其详细分类情况如图 8 所示。发作间期和发作期两类样本分布图中，蓝色点和红色点分别代表发作间期与发作期；发作间期和发作期样本分类结果统计图中，“1”和“2”分别代表发作间期与发作期。分类结果与文献[18]相比，发作间期和发作期的识别率分别提高了 3.90% 和 1.50%，大幅度提高了癫痫患者发病的预测准确率。

图 7.

The second average recognition rate of SVM with different kernel functions

第二重不同核函数 SVM 下的平均识别率

图 8.

Coarse Gaussian SVM classification results of interictal and ictal periods

发作间期与发作期的 Coarse Gaussian SVM 分类结果

为了证明将空域特征和上述互补特征组合的有效性，本文对仅采用 CSP 算法、仅采用互补特征、采用 CSP+互补特征三种分类情况进行了对比，如图 9 所示。结果表明，当空域特征与其他方面特征组合时能够达到更好的分类效果。

图 9.

Recognition rate of different features

不同特征下的识别率

同时为了证明本文二重分类算法的有效性，将提取到的组合特征送入 SVM 直接进行三分类。分类结果最好的为 Cubic SVM，识别率为 98.00%，而二重分类两个阶段的识别率均高于该值（详见图 9 中的绿色柱形图），因此我们可以证明二重分类模式在癫痫三个时期的识别分类中发挥了重要作用。

采用同一数据集的其他相关文献的分类效果如表 3 所示。与文献[16]相比，本文在特征方面进一步添加了空域特征，使得脑电信号的信息提取更加充分，从而产生了更高的识别率；同时，本文的二重分类模式仅需运用 2 次 SVM 分类，而文献[9]中的传统 SVM 分类方法则需运用 3 次 SVM 分类。实验证明本文方法在癫痫脑电数据的多分类问题上，不仅减少了时间开销，在分类识别率上也有了较大提升。

表 3. Method and accuracy of similarity research.

相似研究采用的方法与最终识别率

特征提取方法	分类方法	数据集分类	识别率
连续小波变换+高阶谱+纹理[9]	基于径向基核函数的 SVM	A, C, E	96.00%
样本熵+小波包能量[18]	Real AdaBoost+纠错编码	AB, CD, E	96.78%
经验模态分解 [11]	SVM	ABCD, E	97.66%
近似熵+递归定量分析[12]	卷积神经网络	AB, CD, E	98.15%
本文方法（第一重分类）	Cubic SVM	AB, CDE	98.73%
本文方法（第二重分类）	Coarse Gaussian SVM	CD, E	99.90%

3. 结论

为提高癫痫患者正常期、发作间期和发作期的识别率和识别效率，本文引入 CSP 算法提取的空域特征，并在特征提取阶段选取了标准差、熵和小波包能量这几种互补特征来进行组合，最后采用 SVM 二重分类模式实现三个时期的高精度分类。实验证明，当空域特征与其他特征进行结合时，识别率能够得到有效提升。此外，SVM 的二重分类模式充分考虑了癫痫患者由正常到发作的连续性，优化了分类识别流程，提升了识别效率，同时对分类识别率也起到了积极作用。与既往的癫痫脑电数据的多分类方法相比，本文方法在癫痫患者的实时检测中具有更高的可靠性，能够更好地应用于临床实践，同时也为心电分类和情绪分类等研究提供了可借鉴的方法。但是该算法在第一重分类上仍存在较大的提升空间，今后我们可考虑选取不同的特征组合以及优化特征组合方式等途径，来提高正常期与准发病期的识别率，另外可尝试在更多的数据集中验证此方法的有效性，使得本文方法能够得到更加广泛的应用。

利益冲突声明：本文全体作者均声明不存在利益冲突。

Funding Statement

山东省重大科技创新项目 (2017CXGC1503)

Natural Science Foundation of Shandong Province