使用二分支卷积神经网络识别第一心音与第二心音

Abstract

心音听诊是一种重要的用于心脏疾病诊断的方法。心音中可以听见的部分主要为第一心音（S1）和第二心音（S2）。在一个心动周期中，不同阶段的杂音往往对应不同的心脏疾病，因此心音分割是利用心音进行疾病诊断的前提。S1 和 S2 分别出现在心脏收缩期和舒张期的开始阶段，准确定位 S1 和 S2 有利于心音的正确分割。本文研究了一种不利用收缩期和舒张期的时间特征，而仅使用 S1 和 S2 本身特性的分类方法。将训练集中带有标注的 S1 和 S2 进行短时傅里叶变换得到时频图，然后构建有分支的双层卷积神经网络，使用时频图对卷积神经网络进行训练，得到可用于 S1 和 S2 分类的神经网络。神经网络对测试集中 S1 和 S2 的分类准确率最高为 91.135%，高于传统的方法。神经网络的敏感性和特异性最高分别为 91.156% 和 92.074%。该方法无需预先提取心音的特征，计算简单，有利于心音的实时分割。

引言

心血管疾病在我国是一种较为常见的疾病，尽早发现此类疾病对于提高人们的健康状况具有非常重大的意义。虽然有超声心动图^[1]、心脏磁共振^[2]、心脏计算机断层显像^[3]等方法可用于心脏的检查，但这些设备通常价格昂贵，操作复杂，不利于普及化。由于心音中包含了大量关于心脏和心血管的重要信息^[4-5]，因此可以被用于判断心脏的健康状况。心音听诊是一种非侵入式的利用心音进行心脏疾病诊断的方法，该方法易于操作，成本低廉，适合大规模推广。

典型的心音波形如图 1 所示。一个心音周期通常可以分为收缩期和舒张期。普通人的心音中，容易听见的成分主要有第一心音（S1）和第二心音（S2）。S1 是由二尖瓣（mitral valve，MV）和三尖瓣（tricuspid valve，TV）的关闭引起的，产生于心脏的收缩期，是心室收缩的标志，其频率范围主要分布于 50～150 Hz。S2 是由主动脉瓣（aortic valve，AV）和肺动脉瓣（pulmonary valve，PV）的关闭引起的，产生于舒张期的开始阶段，主要成分的频率范围为 50～200 Hz^[6-7]。在基于心音的计算机辅助诊断中，一个心动周期通常被分割为四个阶段：S1、S1～S2、S2 和 S2～S1^[8]。当心脏出现异常时，心音中可能会有杂音的出现，有效利用此杂音可以实现心脏疾病的诊断^[9-10]。

图 1.

Segmentation of the heart sound

心音的分段

由于一个心动周期中不同阶段的杂音对应的疾病往往是不同的，心音的准确分割对于心脏疾病的诊断具有非常重大的意义。S1 和 S2 的定位在心音分割中非常重要。目前常用的识别 S1 和 S2 的方法大多利用了收缩期和舒张期的时间特性，然而一些患者心脏的收缩期和舒张期时长大小关系不固定，此时利用收缩期和舒张期的时长特性来识别 S1 和 S2 是不准确的^[11]。为了解决上述问题，研究人员提出仅用 S1 和 S2 本身的特征来对其进行区分。Kumar 等^[12]计算心音的高频包络，并设定了一个阈值。由于 S2 的频率上限通常高于 S1，作者将包络超过该阈值的心音段判定为 S2。这种方法对于阈值的选择非常敏感。另外，有时 S1 与 S2 的频率分布非常接近，此时该方法的准确率有限。Moukadem 等^[11]提出了基于心音 S 矩阵奇异值分解（singular value decomposition，SVD）提取心音特征，并使用 k 最近邻（k-nearest neighbor，KNN）算法对其进行分类。但 KNN 算法需要将待测样本与数据库中全部样本进行对比，当数据库中样本较多时，计算耗时太长，不利于实时分类^[13]。侯雷静^[14]提取了心音的梅尔倒谱系数（Mel-frequency cepstral coefficients，MFCCs），并使用深度神经网络（deep neural network，DNN）对 S1 和 S2 进行分类，平均准确率为 88.63%。Chen 等^[15]先将心音转换为 MFCC 的序列，然后使用 K-means 算法将每一个心音段的声学特征聚类为两组，计算每个组的中心向量，合并上述两个中心向量为一个超向量，然后使用该超向量训练深度神经网络，进而对心音中的 S1 和 S2 进行分类。该模型准确率可达到 91%，但计算过程较为繁琐。Tsao 等^[16]提出使用谱重建算法（spectral restoration algorithm，SRA）以减小心音中的噪声成分，并使用多重训练策略（multi-style training strategy，MTS）来训练稳健的 DNN 对 S1 和 S2 进行分类，但是该方法也存在提取特征过程繁琐以及训练流程复杂的不足。

本文提出了一种基于卷积神经网络（convolutional neural network，CNN）的 S1 和 S2 识别方法。对心音数据进行短时傅里叶变换（short-time Fourier transform，STFT），将其转换为时频图，再由专业医生对时频图中 S1 和 S2 数据段进行标注。使用训练集中已标注的 S1 和 S2 时频图训练不同深度的 CNN。当训练完成后，使用该神经网络对测试集中的 S1 和 S2 进行分类。本方法无须预先提取心音信号的特征，免去了繁琐的计算过程，具有较高的实用价值。

1. 算法介绍

1.1. 短时傅里叶变换

STFT 是一种常用的时频分析方法，它是 Gabor 于 1946 年提出的，其表达式为^[17]：

1

其中x（τ）为待变换的时域信号，h（·）为窗函数，需要足够窄以确保窗内的信号是平稳的。对于具体的时刻t₀，S（t₀，f）可以看成是信号在该时刻的瞬时频谱^[18]。当心音进行 STFT 之后，就被转成类似图像的二维信号，可以反映出心音频率分布的特征。

1.2. 卷积神经网络

近年来，随着高性能 GPU 的出现，计算机的运算能力得到了很大提高，这使得 DNN 得到了大规模应用^[19]。CNN 作为 DNN 的一种，被广泛应用于自然语言处理^[20]、语音信号处理^[21]、目标识别^[22]、医学信号和图像分析^[23-26]等领域。传统的图像模式识别方法需要预先提取图像的特征，但是这严重依赖于使用者的经验。通过使用大量数据进行训练，CNN 可以学习到自动提取图像特征的方法，这对于降低处理流程的复杂性和提高识别准确率都是有益的^[27-28]。此外，CNN 使用了共享权重机制，需要计算的参数比传统全连接 DNN 少^[29-31]。在语音识别中，部分研究人员将语音信号转换为语谱图送入 CNN 中^[32]，这在某种程度上与图像识别类似。而心音也是一种音频信号，由于 S1 和 S2 的频率分布不同，其 STFT 变换后得到的时频图也是不同的，因此可以使用 CNN 对 S1 和 S2 进行识别。

在 CNN 中，比较具有代表性的有 AlexNet^[33]、GoogLeNet^[34]、VGGNet^[35]和 ResNet^[36]等，这些网络在计算机视觉任务中有突出的表现。然而上述网络都是为复杂的分类任务而设计的，参数较多，需要使用大量的数据训练。当训练数据不足时，很容易出现过拟合的现象。此外，这些复杂网络占用计算机的资源较多。在本文中，我们没有直接使用这些复杂的网络，而是构建了一个带分支的小型双层 CNN 网络用于实现 S1 和 S2 的分类。

本文所使用的分支 CNN 的结构如图 2 所示，它由输入层、卷积层、池化层、全连接层和输出层组成。在本文中，输入层为 S1 和 S2 的时频图。卷积层用于训练输入图像局部的感受野，进而可以提取图像的抽象特征。抽象特征的矩阵由输入图像与卷积核卷积运算之后生成，其计算公式为：

图 2.

Structure of two-stream convolutional neural network used in this paper

本文所用分支卷积神经网络的结构

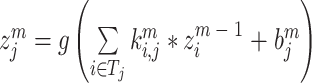2

其中g（·）为激活函数，m为当前层，k_i，j为滤波器，b_j为偏置，*表示卷积操作，T_j表示输入特征矩阵的集合。激活函数中常用的有 tanh、sigmoid 和 ReLU 等^[37]。考虑到 ReLU 激活函数计算速度较快，且可以有效地避免训练时的过饱和与梯度消失^[38-39]，本文选用 ReLU 激活函数，其表达式为：

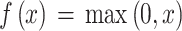3

池化层（pooling layer）也被称为减采样（sub-sampling）层，通常用于对卷积之后的特征图进行减采样。常用的池化方式有两种：最大值池化（max pooling）和平均值池化（average pooling）。最大值池化计算局部特征图的最大值，而平均值池化计算局部特征图中的平均值^[40]。本研究采用最大值池化。

本文所用的模型第一层使用了分支的卷积神经网络，两个分支的卷积核大小分别固定为 3 × 3 和 5 × 5，这有利于提取输入心音时频图不同层次的特征。经过分支卷积后，需要将结果合并，然后送到第二层卷积神经网络中。由于本文研究的是分类问题，训练时选用交叉熵误差（cross entropy error）损失函数^[41]。

2. 实验过程

2.1. 实验数据

本文的研究使用 PhysioNet/Computing in Cardiology Challenge 心音数据库（https://www.physionet.org/challenge/2016/）^[42]，它包含了真实临床环境下多种类型的心音传感器采集到的心音，心音中存在呼吸音和肠鸣音等因素的干扰，有较高的普适性。该数据库包含从 training-a 到 training-f 的六个文件夹，每个文件夹中都有一定数量的 wav 格式心音文件。我们将这六个文件夹中的心音分为训练集和测试集（见表 1）。

表 1. Heart sound waves in training dataset and testing dataset.

训练集和测试集的心音文件

文件夹名	训练集中的文件名	测试集中的文件名
training-a	a0001～a0368	a0369～a0409
training-b	b0001～b0441	b0442～b0490
training-c	c0001～c0028	c0029～c0031
training-d	d0001～d0050	d0051～d0055
training-e	e00001～e01927	e01928～e02141
training-f	f0001～f0103	f0104～f0114

在表 1 中，训练集和测试集分别有 2 917 和 323 个心音文件。由于心音的频率范围通常低于 500 Hz^[43]，根据奈奎斯特采样定理，我们将训练集和测试集中的心音都由 4 kHz 减采样至 1 kHz。图 3 所示为一个典型的心音周期的时域波形和对应的 STFT 之后的时频图。我们选出心音中的 S1 和 S2（如图中白线包围的部分）送入 CNN 中进行训练和测试。数据库的训练集中 S1 有 83 754 个，S2 有 83 631 个，测试集中 S1 有 9 181 个，S2 有 9 172 个。

图 3.

A heart sound cycle

一个心音周期

a. 时域波形；b. 短时傅里叶变换后的时频图

a. waveform; b. time-frequency diagram after short-time Fourier transform

2.2. 神经网络构建与计算

为了对比不同结构 CNN 的效果，本文构建了五种 CNN，其结构如表 2 所示。其中 Conv1a 和 Conv1b 分别表示第一层中两个分支所使用的卷积滤波器数量，Dropout1a 和 Dropout1b 分别表示第一层中两个分支的随机 dropout 比例。

表 2. Structures of two-stream convolutional neural networks.

分支卷积神经网络的结构

层名	Model 1	Model 2	Model 3	Model 4	Model 5
Conv1a	16 ×（3 × 3）	32 ×（3 × 3）	64 ×（3 × 3）	128 ×（3 × 3）	128 ×（3 × 3）
Dropout1a	0.4
Conv1b	16 ×（5 × 5）	32 ×（5 × 5）	64 ×（5 × 5）	128 ×（5 × 5）	128 ×（5 × 5）
Dropout1b	0.4
Conv2	128 ×（3 × 3）	128 ×（3 × 3）	128 ×（3 × 3）	128 ×（3 × 3）	256 ×（3 × 3）
Maxpooling2	2 × 2
Dropout2	0.4
Dense1	256
Dropout3	0.4
Dense2	512
Dropout4	0.4
Softmax	2

本研究使用 Keras 和 Tensorflow 构建 CNN 网络，利用相同的数据训练和测试上述五种 CNN 模型。计算机主要配置如下：操作系统为 Ubuntu 18.04，CPU 为 Intel i5 8400，主板为 GIGABYTE B360-HD3，显卡为 GTX1060 6 GB，内存为 DDR4 2400（共 24 GB）。训练 300 个 epoches。训练过程中的 Loss 曲线和 Accuracy 曲线如图 4 所示。

图 4.

Loss curves and accuracy curves of different models

不同模型训练时的 Loss 曲线和 Accuracy 曲线

3. 分类结果分析

本文使用准确率（accuracy）、敏感性（sensitivity）和特异性（specificity）来衡量不同 CNN 模型的分类性能。其计算公式为

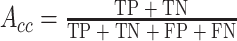4

5

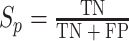6

其中A_cc、S_e、S_p分别表示准确率、敏感性和特异性，TP 表示真阳性（本来是阳性，被正确分类为阳性）的样本个数，FP 表示假阳性（本来不是阳性，被错误分类为阳性）的样本个数，TN 表示真阴性（本来是阴性，被正确分类为阴性）的样本个数，FN 表示假阴性（本来不是阴性，被错误分类为阴性）的样本个数。在本文中为了便于说明，我们假定 S1 为阳性，S2 为阴性。因此，TP 表示的是 S1 的正确检出数，TN 表示的是 S2 的正确检出数。

3.1. 在公开数据集上的结果

表 3 给出了不同的模型对表 1 中测试集数据的分类结果。作为对比，表 1 中也列出了使用文献[14-16]分类方法的准确率。

表 3. Classification results of different methods.

多种方法分类结果

指标	Model 1	Model 2	Model 3	Model 4	Model 5	文献[14]	文献[15]	文献[16]
TP	8 257	8 317	8 294	8 256	8 369	8 248	8 286	8 305
TN	8 409	8 397	8 432	8 445	8 356	8 389	8 393	8 410
FP	763	775	740	727	816	783	779	762
FN	924	864	887	925	812	933	895	876
S e	89.936%	90.589%	90.339%	89.925%	91.156%	89.838%	90.252%	90.459%
S p	91.681%	91.550%	91.932%	92.074%	91.103%	91.463%	91.507%	91.692%
A cc	90.808%	91.070%	91.135%	90.999%	91.130%	90.650%	90.879%	91.075%

对比表 3 中 Model 1 到 Model 3 的结果可以看出，随着第一层卷积滤波器数量的增加（依次为 16、32、64），预测准确率A_cc会上升。这表明卷积滤波器数量的增加使得 CNN 具备更强大的特征提取能力。然而对比 Model 3 和 Model 4 可以发现，继续增加第一层卷积滤波器的数量反而导致A_cc下降。此时如果增加第二层的滤波器数量，可以发现A_cc有所提升（对比 Model 4 和 Model 5）。 Model 5 的参数数量比 Model 3 多，但其 A_cc 略低于 Model 3。这可能是由于训练时出现了过拟合的情况。在本文所述模型中，A_cc最高的模型为 Model 3，为 91.135%，其对应的S_e为 90.339%，S_p为 91.932%。这表明在我们研究的范围内，CNN 第一层的两个分支均使用 64 个卷积核，而第二层使用 128 个卷积核，可以达到最优的总体分类效果。

对比表中S_e和S_p可以发现，Model 5 的S_e最高（91.156%），而 Model 3 和 Model 4 的S_p相对较高（分别为 91.932% 和 92.074%）。这表明如果想要达到较高的 S1 检出率，需要在 CNN 的第一层使用 128 个卷积核，在第二层使用 256 个卷积核。若想达到较高的 S2 检出率，则第一层可以使用 64 或 128 个卷积核，第二层使用 128 个卷积核。

综合来看，上文所提出的 Model 3 虽然S_e低于文献[16]所描述的结果，但其A_cc高于文献[14-16]的效果，这证明了本文所述方法有利于提高 S1 和 S2 识别的分类准确率。此外，本文所述方法无须繁琐的特征提取步骤，而是由 CNN 自动提取特征，这使得模型构建流程的复杂性进一步降低。

3.2. 对实际采集心音的分类结果

为了验证本文所提出模型实际应用的效果，我们在中国医学科学院阜外医院采集了 20 例患者的心音，其中窦性心律和心律不齐的患者各 10 例，采集的心音包括主动脉瓣听诊区和二尖瓣听诊区的心音，每段心音采集时长为 40 s。其中心律不齐的患者包括 3 例室性早搏、3 例房性早搏、2 例左束支传导阻滞和 2 例右束支传导阻滞的病例。心音数据采集符合医学伦理学原则，在采集数据前已经征得被测试人员同意，且采集时未损害被测试者人体。使用 Model 3 对上述心音中的 S1 和 S2 进行分类，结果如表 4 所示。

表 4. Classification results of S1 and S2 in sinus rhythm heart sounds and arrhythmia heart sounds.

窦性心律与心律不齐心音的 S1 和 S2 分类结果

指标	窦性心律			心律不齐
	主动脉瓣听诊区	二尖瓣听诊区		主动脉瓣听诊区	二尖瓣听诊区
TP	434	470		459	467
TN	442	451		463	455
FP	29	35		42	47
FN	38	23		48	44
S e	91.949%	95.335%		90.533%	91.389%
S p	93.843%	92.798%		91.683%	90.637%
A cc	92.895%	94.076%		91.107%	91.017%

从表 4 中可以看出，Model 3 对于窦性心律心音的 S1 和 S2 分类准确率高于心律不齐心音的 S1 和 S2。这可能是由于窦性心律的心音的频谱特征与用于训练模型的样本更加相似。此外，在主动脉瓣听诊区采集的心音，S2 检出率高于 S1，而在二尖瓣听诊区采集的心音，S1 检出率高于 S2。这是由于主动脉瓣听诊区 S2 强度较高，S1 更容易受噪声所影响，而二尖瓣听诊区则 S1 强度高于 S2。可见，如果想要实现更加精确的 S1 和 S2 分类，需要多个听诊区同步采集心音。

为了展示本模型对不同心律不齐疾病心音中 S1 和 S2 的识别效果，我们在表 5 和表 6 中分别给出本模型对采集于四类心律不齐患者主动脉瓣听诊区和二尖瓣听诊区的心音的详细识别结果。可以看出，在上述两个听诊区采集的心音中，右束支传导阻滞心音的 S1 和 S2 分类准确率相对较低，其他三类心律失常心音中 S1 和 S2 的分类准确率大致相同。其原因有待于进一步探究。

表 5. Classification results of S1 and S2 in arrhythmia heart sounds acquired at aortic valve auscultation area.

主动脉瓣听诊区采集的四种心律不齐心音的 S1 和 S2 分 类结果

指标	室性早搏	房性早搏	左束支传导阻滞	右束支传导阻滞
S e	91.724%	91.391%	90.816%	88.182%
S p	91.216%	91.216%	91.919%	92.035%
A cc	91.468%	91.304%	91.371%	90.135%

表 6. Classification results of S1 and S2 in arrhythmia heart sounds acquired at mitral valve auscultation area.

二尖瓣听诊区采集的四种心律不齐心音的 S1 和 S2 分类 结果

指标	室性早搏	房性早搏	左束支传导阻滞	右束支传导阻滞
S e	92.000%	92.715%	91.667%	88.596%
S p	90.845%	91.034%	91.176%	89.381%
A cc	91.438%	91.892%	91.414%	88.987%

值得注意的是，本文所用的分支卷积神经网络是基于经典的卷积计算方法，计算量相对较大。未来如果需要将该方法应用于嵌入式设备中，则可以借鉴 MobileNet 的思想，采用深度可分离卷积（depth-wise separable convolution）代替传统卷积，即将标准卷积分解为深度卷积和逐点卷积（pointwise convolution）。如此可以在准确率损失不大的情况下大幅度降低 CNN 的参数数量，同时将每次卷积的计算量减少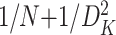（其中N为输入特征图的大小，D_K为标准卷积核的大小）。同时，也可以尝试 ShuffleNet 的思路，将输入层的不同特征图分组，然后使用不同卷积核对各个组进行卷积，以降低计算量。文献[44]表明分组之后计算量可以降低到原来的 1/g（g为输入输出的组数）。

4. 总结

不使用时间信息的心音分割长期以来是一个难点，此时无法利用收缩期短于舒张期这一特性确定第一心音（S1）和第二心音（S2）。本文提出了一种 S1 和 S2 的识别方法，该方法在对心音信号进行短时傅里叶变换的基础上，使用训练好的分支卷积神经网络对 S1 和 S2 进行分类。对比不同的卷积神经网络模型，我们发现本文所提出的模型的分类准确率最高可以达到 91.135%，分类敏感性和特异性最高分别可达到 91.156% 和 92.074%。此后将训练出来的模型用于我们采集到的窦性心律和心律不齐的心音，采集区域为主动脉瓣听诊区和二尖瓣听诊区。结果表明对于主动脉瓣听诊区采集到的心音，S2 检出率较高，而对于二尖瓣听诊区采集到的心音，S1 检出率较高。本文所述方法无须预先提取复杂的特征，计算较为简单，能够迅速识别 S1 和 S2，有利于实现不依赖时间间隔特征的心音分割。下一步我们将改进本文所述模型，减小计算量，以移植到嵌入式系统中；另外，我们计划研究进一步提高识别准确率的方法，例如多听诊区同时采集心音等。同时，考虑到实际采集到的心音经常包含各种类型的噪声，我们将研究使用卷积神经网络识别包含噪声的 S1 和 S2，以扩大该方法的适用范围。

利益冲突声明：本文全体作者均声明不存在利益冲突。

Funding Statement

国家自然科学基金（61527811，11564006，11864007）

The National Natural Science Foundation of China