Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2023 Jun 12;8(25):23024–23031. doi: 10.1021/acsomega.3c02195

Density Functional Theory Computation and Machine Learning Studies of Interaction between Au3 Clusters and 20 Natural Amino Acid Molecules

Jiao Peng †, Li Wang †, Pu Wang †, Yong Pei †,‡,§,*
PMCID: PMC10308543  PMID: 37396243

Abstract

graphic file with name ao3c02195_0008.jpg

The optimal adsorption sites and the binding energies of neutral Au3 clusters with 20 natural amino acids under the gas phase and water solvation were systematically investigated based on density functional theory (DFT) calculations. The calculation results showed that in the gas phase Au3 tends to bind with N atoms of amino groups in amino acids, except methionine, which tends to bind with Au3 through S atoms. Under water solvation, Au3 clusters tended to bind to N atoms of amino groups and N atoms of side chain amino groups in amino acids. However, methionine and cysteine bind more strongly to the gold atom through the S atom. Based on the binding energy data of Au3 clusters and 20 natural amino acids under water solvation calculated by DFT, a machine learning model (gradient boosted decision tree) was proposed to predict the optimal binding Gibbs free energy (ΔG) of the interaction between Au3 clusters and amino acids. The main factors affecting the strength of the interaction between Au3 and amino acids were uncovered by the feature importance analysis.

1. Introduction

Gold nanoparticles (AuNPs) have been widely used in medical diagnosis and medical therapy because they can be used as intermediates in the fabrication of nanoscale devices and as carriers for drug delivery.1−3 The AuNPs can be quickly absorbed by the human body due to their extremely small size and surface characteristics. Once it enters the blood, proteins will easily be adsorbed on AuNPs to form protein crowns.4 Furthermore, due to their optical properties (e.g., fluorescence) and biocompatibility with biomolecules (peptides, amino acids (AAs), and proteins), some human proteins can retain their function in the presence of AuNPs and coat the protein layer to regulate surface properties, which provides a means for intracellular interactions and imaging.5−7 Therefore, studying AuNPs and protein interactions is crucial for understanding the protein corona and regulating protein surface engineering.

It is well known that proteins are composed of AAs, so the study of the interaction between AuNPs and proteins can be simplified as the study of the interaction between Au nanoclusters (AuNCs) and AAs. Over the past few years, there has been growing interests in studies to elucidate the interactions of AuNCs with different AAs. For example, Xie et al. reported the interaction of Aun clusters (n = 3 and 4) with cysteine and glycine, and found that the best site for Au3 to interact with cysteine and glycine was the amine group.8 Pakiari et al. investigated the binding mode and binding energy of Au3 and Ag3 clusters to AAs (glycine and cysteine) using density functional theory (DFT) calculations and demonstrated that the interaction of AAs with gold and silver clusters is governed by two main factors, including the anchoring N–Au(Ag), O–Au(Ag), and S–Au(Ag) bonds and the unconventional N–H–Au(Ag) and O–H–Au(Ag) hydrogen bonds.9 Rai et al. studied the interaction of proline with Au3 by DFT calculations and found the tendency to bind to Au clusters through the amide terminals.10 Buglak et al. reported the binding of the gold ion Au+ and diatomic neutral Au2 to the full set of AAs using DFT and the RI-MP2 computation.11 The studies demonstrated that the interaction of gold cations and neutral gold clusters with protonated and deprotonated AA residues is not much different. The binding affinity of AAs to Au2 clusters was determined in the following order: Cys(H+) > Asp(H+) > Tyr(H+) > Glu(H+) > Arg > Gln, His, Met [Asn, Pro, Trp] > Lys, Tyr, Phe > His(H+) > Asp > Lys(H+) > Glu, Leu > Arg(H+) > Ile, Val, Ala > Thr, Ser > Gly, Cys.11 There are also many studies on the interaction of larger size AuNCs with AAs. For example, Srivastava studied the interaction between cysteine and gold clusters and found that the binding strength between gold clusters and cysteine was positively correlated with the S–Au bond order and negatively correlated with the S–Au bond length.12 Abdalmoneam et al. reported the stability and electronic properties of Aun (n = 8 and 20) clusters interacting with alanine (Ala) and tryptophan (Trp) in their canonical and zwitterionic configurations.13 They found that the geometry of the gold clusters and the polarity of the AAs determined the nature of the interactions in the gas and solvation phases. To design asymmetric nanocatalytic materials, the enantiospecific interactions of cysteine with chiral Au55 clusters were investigated. It was found that the driving force for enantioselectivity was related to the finite size of the adsorption “substrate”, which in this case corresponded to the cluster facet.14−16 In order to understand the relative interaction strength between the AAs and the Au surface, Feng and colleagues used molecular dynamics (MD) simulations to study the Gibbs free energy of adsorption of 20 different AAs on the Au(111) surface,17 and the order of their interactions is found to be aromatic < cationic < polar < aliphatic. Interestingly, Kruger et al. demonstrated that the optimal size of gold clusters bound to organic molecules consists of three to four bonded gold atoms by ab initio molecular dynamics simulations. This indicated that Au clusters with n = 3 or n = 4 were very easy to interact with organic molecules (AAs, peptides, and proteins).18 However, despite the efforts of researchers on the interaction of Au clusters with AAs,10,19−25 the interaction of AuNCs with the full set of protein AAs (20 species) in the gas phase and solvated environments has not been systematically studied. The main influencing factor affecting the binding strength between gold clusters and AAs is not clear.

Inspired by recent reports and the needs to gain insight into the interaction of small-sized Aun clusters with AA, in this work we systematically studied the interaction of Au3 with 20 natural AAs in the gas phase and water solvation by DFT calculations. On the basis of DFT energy calculation results, we propose an efficient machine learning model to search the main factors affecting the binding affinity between Au3 clusters and AAs. In our model, we only use the properties of the 20 natural AAs as descriptors and not the structural/electronic properties of the Au3–AA complex (which requires performing many additional DFT calculations). The main factor to affect the interaction of Au3 with AAs was revealed by feature importance analysis. To the best of our knowledge, this is the first machine learning study done for the interaction of AuNCs with AAs.

2. Computational Methods and Details

2.1. DFT Computations

The geometry structure of the Au3, 20 natural AAs (arginine, histidine, lysine, asparagine, glutamine, tryptophan, methionine, cysteine, alanine, phenylalanine, tyrosine, valine, isoleucine, serine, leucine, glycine, aspartic acid, threonine, glutamic acid, and proline) and Au3–AAs complexes were optimized by DFT with the M06-2X functional in Gaussian 09 software.26,27 The cc-pVTZ basis set was used for atoms in AAs, while for Au atoms the Los Alamos effective core potential (ECP) def2-QZVP basis set was applied.28,29 The initial structure of Au3–amino acid complexes was constructed by placing gold clusters near the active sites of AAs, in which the active sites of AAs considered include amino groups, thiols, benzene rings, and hydroxyl and carbonyl groups. Binding Gibbs free energy (ΔG) between Au3 and 20 natural AAs can be calculated via the formula: ΔG = G(Au3–AAs) – G(Au3) – G(AAs), where G(Au3–AAs) is the free energy of Au3 AA complexes, G(Au3) and G(AAs) are the free energy of Au3 and AA molecules at 298.15 K and 1.0 atm, respectively.

2.2. Machine Learning Method and Details

To uncover the main factors affecting the strength of Au3–AA interactions with the Au3 cluster, we trained a machine learning model based on the results of DFT calculation.30 The structure and physical chemistry properties of AAs are used as the feature set, and the optimal ΔG is used as the target value. Since the useful features in the data set only account for a small part of the entire data set, in order to reduce the redundancy of features and speed up the model convergence, we need to perform feature selection on the feature set before training. In addition, before training the machine learning model, we also need to randomly split the entire data set into training and test sets in a ratio of 8:2. Three machine learning methods were used to train the data in the training set, including gradient boosted decision tree (GBDT), K-nearest neighbors (KNN), and lasso regression.31−33 Meanwhile, in order to evaluate the performance of these algorithms, the root mean square error (RMSE) and coefficient of determination (R2) are used as evaluation criteria.34 When training the model and adjusting the parameters to achieve the minimum RMSE and the maximum coefficient of determination (R2), the feature importance of the model can be counted in different ways, such as the feature output GBDT35 and SHapley Additive exPlanations (SHAP).36

Feature importance in GBDT is specific to the model and is calculated based on the number of times a feature is used to split the data in the trees of the model.35 The importance of a feature is proportional to the reduction in impurity (e.g., Gini impurity) achieved by splitting on that feature. SHAP is a model agnostic method that provides global and local feature importance values.36 It is based on game theory and provides a unified framework for interpreting the output of any machine learning model. The SHAP value of a feature measures the contribution of that feature to the prediction of a specific instance, while the global SHAP value of a feature measures its importance across all instances in the data set. One advantage of SHAP over feature importance in GBDT is that SHAP values provide a more nuanced understanding of how each feature contributes to the prediction for each specific instance. This can help identify interactions between features and potential confounding factors that may not be captured by global feature importance. The GBDT model used in this work comes with an output of feature importance, but considering the understanding of each specific instance in the data set, we chose the SHAP method. In this way, the importance relationship between each feature and the predicted value of machine learning can be obtained, and the main factors affecting the interaction strength of Au3 and AAs can be identified.

3. Results and Discussion

3.1. Interaction between Au3 Cluster and 20 Natural AAs

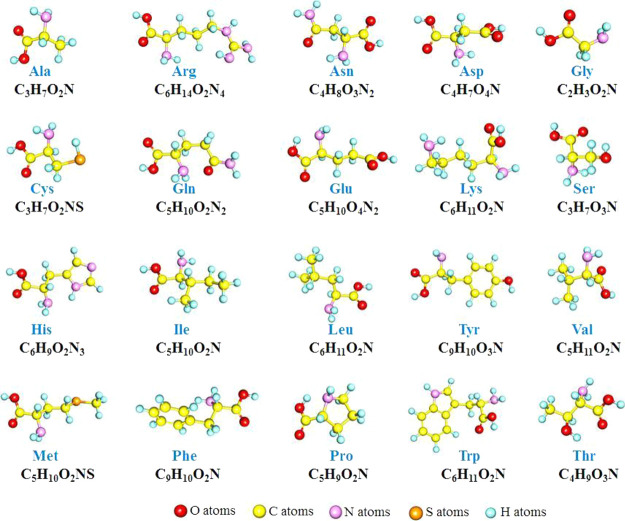
Studying AuNPs and protein interactions is critical for understanding protein corona formation and regulating protein surface engineering. Human proteins are mainly composed of 20 natural AAs. As shown in Figure 1, the structures of these 20 natural AAs are different, but most of them have carboxyl groups, amino groups, and individual thiol groups and hydroxyl groups. Since carboxyl, amino, thiol, and hydroxyl groups are electron-rich groups, S atoms, N atoms, and O atoms can be regarded as the active adsorption sites for the interaction of Au3 with AAs.

Figure 1.

Figure 1

Open in a new tab

Structure and molecular formulas of 20 natural AAs.

Among the 20 kinds of natural AAs, only the methionine (Met) and cysteine (Cys) contain carboxyl, amino, thiol, and hydroxyl groups at the same time, so their interaction with Au3 is discussed first. The configuration of Au3·Met and Au3·Cys complexes was comprehensively sampled. The optimal binding configuration was determined by DFT energy calculation. As shown in Figure 2, when Au3 interacts with Met and Cys, the Au atom can bind with the N, S, and O atom, respectively, forming three different Au3·Met complexes (Au3·Met_1, Au3·Met_2, and Au3·Met_3) and Au3·Cys complexes (Au3·Cys_1, Au3·Cys_2, and Au3·Cys_3), respectively. As shown in Table 1, for the interaction between Au3 and Met, Au3·Met_1 is the most stable complex under the gas phase and water solvation. Au3 is bonded to the S atom and the ΔG is −17.09 and −12.80 kcal/mol in the gas phase and water solvation, respectively. For the interaction between Au3 and Cys, under water solvation, the S atom is the most favorable binding site to Au3. However, in the gas phase, the N atom of the amino group is the most favorable binding site to Au3. The ΔGg and ΔGaq are −17.01 and −10.95 kcal/mol for Au3·Cys_1, and the ΔGg and ΔGaq are −11.91 and −11.31 kcal/mol for Au3·Cys_2, respectively.

Figure 2.

Figure 2

Open in a new tab

Interaction of the Au3 with methionine (Met) and cysteine (Cys).

Table 1. ΔG of Interaction between Au3 with Met and Cys in the Gas Phase (g) and Water Solvation (aq).

complex adsorption site ΔGg (kcal/mol) ΔGaq (kcal/mol)
Au3·Met_1 S atom –17.09 –12.80
Au3·Met_2 N atom –14.28 –11.02
Au3·Met_3 O atom –6.80 –1.29
Au3·Cys_1 S atom –17.01 –10.95
Au3·Cys_2 N atom –11.90 –11.31
Au3·Cys_3 O atom –8.67 –0.14
Open in a new tab

Phenylalanine (Phe), tryptophan (Trp), and tyrosine (Tyr) contain benzene rings, which also can act as an active site to bind with Au3 clusters. Figure 3 shows the optimized binding molecular structure of Au3·Phe, Au3·Trp, and Au3·Tyr, respectively. It is found that Au3 tends to bind with N atoms of AAs in both the gas phase and water solvation and the binding affinity of Au3 to the benzene ring is much weaker (Table 2).

Figure 3.

Figure 3

Open in a new tab

Interaction of Au3 with Phe, Trp, and Tyr.

Table 2. ΔG of the Interaction between Au3 and Phe, Trp, and Tyr in the Gas Phase (g) and Water Solvation (aq).

complex adsorption site ΔGg (kcal/mol) ΔGaq (kcal/mol)
Au3·Phe_1 N atom –15.87 –12.97
Au3·Phe_2 C atom –4.55 –3.09
Au3·Phe_3 C atom –4.40 –3.70
Au3·Phe_4 O atom –5.18 –2.38
Au3·Phe_5 O atom –1.62 –1.10
Au3·Trp_1 N atom –17.29 –13.78
Au3·Trp_2 N atom 0.58 0.13
Au3·Trp_3 C atom –2.81 1.01
Au3·Trp_4 O atom –9.69 –7.09
Au3·Trp_5 O atom –5.29 –3.90
Au3·Tyr_1 N atom –14.11 –9.60
Au3·Tyr_2 C atom –9.71 –6.17
Au3·Tyr_3 O atom –0.90 2.01
Au3·Tyr_4 O atom –5.88 –3.40
Au3·Tyr_5 O atom –0.69 –0.81
Open in a new tab

For the remaining 15 AAs, including alanine (Ala), serine (Ser), glycine (Gly), arginine (Arg), aspartic acid (Asp), histidine (His), glutamic acid (Glu), glutamine (Gln), asparagine (Asn), threonine (Thr), proline (Pro), leucine (Leu), isoleucine (Ile), leucine (Leu), and valine (Val), they only contain two kinds of active sites (N atom and O atom) for the interaction with Au3. Therefore, we only considered two adsorption modes for each Au3–AA interaction. Figures S1–S4 show the different bonding structures of Au3 with 15 kinds of AAs and their ΔG. It was seen that Au3 is more likely to bind with the N atom no matter in the gas phase or water solvent.

Table 3 summarizes the ΔG and optimal adsorption sites for the interaction between Au3 and 20 natural AAs under the gas phase and water solvation. Comparing the interaction strength of Au3 with 20 natural AAs, it was found that the binding affinities of 20 natural AAs to the Au3 cluster can be ranked in the following order: Arg > His > Lys > Asp > Gln > Trp > Met > Cys > Ala > Phe > Tyr > Val > Ile > Ser > Leu > Gly > Asp > Thr > Glu > Pro. The situation in water solvation is somewhat different from that in the gas phase, the difference is that cysteine prefers to bind with Au3 through the S atom, while in the gas phase, the N atom of the amino group binds with Au3 more favorably in energy. Under aqueous solvation, the binding affinities of 20 AAs to Au3 clusters was ranked in a different order: Arg > Lys > Trp > His > Ala > Phe > Met > Asn > Ile > Cys > Val > Asp > Gln > Ser > Thr > Leu > Tyr > Gly > Glu > Pro. Moreover, under solvation, the optimal adsorption site of AAs with Au3 is basically the N atom of amino groups, but their ΔG is different. These results indicate the ΔG value depends on the properties of the AAs themselves but what properties is not clear. It is worth noting that our work only considered the case of single site adsorption and the actual solution environment was not taken into consideration.

Table 3. Optimal Adsorption Sites of Au3 with 20 Natural AAs in the Gas Phase and Water Solvation and the Computed ΔG.

complex optimal adsorption site (g) optimal adsorption site (aq) ΔGg (kcal/mol) ΔGaq (kcal/mol)
Au3·Tyr N atom in NH2 N atom in NH2 –14.11 –9.60
Au3·Val N atom in NH2 N atom in NH2 –13.77 –11.31
Au3·Ile N atom in NH2 N atom in NH2 –13.52 –11.98
Au3·Ser N atom in NH2 N atom in NH2 –12.88 –9.93
Au3·Leu N atom in NH2 N atom in NH2 –12.73 –9.77
Au3·Gly N atom in NH2 N atom in NH2 –12.59 –9.33
Au3·Asp N atom in NH2 N atom in NH2 –12.06 –10.74
Au3·Thr N atom in NH2 N atom in NH2 –10.71 –9.56
Au3·Glu N atom in NH2 N atom in NH2 –9.87 –7.71
Au3·Pro N atom in NH N atom in NH –8.58 –6.18
Au3·Arg N atom in NH N atom in NH –21.04 –16.16
Au3·His N atom in imidazolyl N atom in NH2 –20.09 –13.37
Au3·Lys N atom in NH2 N atom in NH2 –19.17 –15.12
Au3·Asn N atom in NH2 N atom in NH2 –19.13 –12.36
Au3·Gln N atom in NH2 N atom in NH2 –17.87 –10.35
Au3·Trp N atom in NH2 N atom in NH2 –17.29 –13.78
Au3·Met S atom S atom –17.09 –12.80
Au3·Cys N atom in NH2 S atom –17.01 –11.31
Au3·Ala N atom in NH2 N atom in NH2 –16.96 –13.08
Au3·Phe N atom in NH2 N atom in NH2 –15.87 –12.97
Open in a new tab

3.2. Factors Affecting the Interaction Strength of Au3 and AAs

To quickly find the main factors affecting the interaction strength between Au3 and AAs, the machine learning method is used. The structure and physical chemistry properties of AAs are used as the descriptors. The descriptor and definition of descriptors are listed in Table 4. Previous theoretical studies have shown that the strength of the interaction between gold clusters and AAs is related to the size and polarity of AAs.13−16 At present, in addition to the molecular polarity index of AAs (MPI) and relative molecular mass of AAs (M) being used as descriptors, the atomic charge (q), the HOMO–LUMO gap of AA molecules (H–L), the dipole moment of AA molecules (μ), volume of fragments after removing HOOC–CH–NH2 or HOOC–CH–NH1 units of AA molecules (V), chain lengths of AA molecules (L), the proportion of S, O, C, and N atoms in AAs (PS, PO, PC, and PN), the number ratio of N atoms and O atoms (RN/O) and the C atoms and O atoms (RC/O) in AAs, and the number of O, S, C, and N atoms in the AA molecule (nO, nS, nC, and nS) are adopted as well.

Table 4. Descriptor and Definition of Descriptors.

descriptor the definition of descriptors
MPI the molecular polarity index of AA molecules
μ the dipole moment of AA molecules
V volume of fragments after removing HOOC–CH–NH2/1 of AA molecules
L chain length of AA molecules
M relative molecular mass of AA molecules
q the charge of the N, S, or O atom connected to Au3
H–L the HOMO–LUMO gap of AA molecules
PS the proportion of S atoms in AA molecules
PO the proportion of O atoms in AA molecules
PC the proportion of C atoms in AA molecules
PN the proportion of N atoms in AA molecules
nO the number of O atoms in AA molecules
nN the number of N atoms in AA molecules
nS the number of S atoms in AA molecules
nC the number of C atoms in AA molecules
RN/O the number ratio of N atoms and O atoms in AA molecules
RC/O the number ratio of C atoms and O atoms in AA molecules
Open in a new tab

In order to reduce the redundant features and speed up the model convergence, the feature–feature correlation was first analyzed before machine learning training. As shown in Figure 4, we found high correlations between many features, such as the feature correlations between PS and nS, RN/O and nN, PN, M, and V, L, PC, and nC, and MPI and μ, are as high as 0.8. To ensure that two features with a correlation higher than 0.8 do not appear simultaneously in the data set, we choose to retain the features PS, RN/O, M, PC, and MPI, and delete features nS, nN, PN, L, M, nC, and μ. It is worth mentioning that the correlation between PS and q is also as high as 0.8, and theoretically, one of the features should be deleted. However, considering that only two of the 20 AA molecules have S atoms, we choose to retain these two features. Features with a feature correlation below 0.8 do not require additional processing, so features H–L, nO, PO, and RC/O can be retained.

Figure 4.

Figure 4

Open in a new tab

Feature–feature correlation map of the top features.

After analyzing feature–feature correlations, 10 features of AAs (q, M, H–L, PO, PC, MPI, RN/O, RC/O, PS, and nO) were used as input, and machine learning was trained to predict the optimal ΔG value. Since deep learning techniques suffer from black boxes, it is difficult to figure out the physical relationship between features and target values, so different machine learning methods are adopted. As shown in Figure 5, it shows that three models (GBDT, lasso, and KNN) obtained by three different machine learning methods (GBDT, lasso linear regression, and KNN) are used in the same data set prediction results. The results of the GBDT model show that the R2 of the training set (train_set) and test set (test_set) are 0.992 and 1.000, respectively. This result indicates that the GBDT model fits optimal ΔG values very well. Another result obtained by the lasso method shows that the R2 of the training set (train_set) and the test set (test_set) are 0.169 and 0.204, respectively (Table 5), which means that the lasso model is not suitable for fitting the optimal ΔG value. This may be because there is no linear relationship between ΔG and eigenvalues. Therefore, we can consider more nonlinear models in our predictions or improve the linear models. The result of the KNN model is that the R2 of the training set (train_set) and the test set (test_set) are 0.162 and 0.483, respectively, which means that the KNN model fits the most stable ΔG value poorly. Although the KNN model is nonlinear, it does not perform well for predicting the optimal ΔG value for the data set. By evaluating these three models, we found that the GBDT model was the best fit for this sample. On the one hand, the RMSE of the train_set and test_set of the GBDT model are 0.231 and 0.001, respectively, and on the other hand, the gap between the actual and predicted most stable ΔG values is small. Therefore, the GBDT method is the best machine learning method to predict the most stable ΔG for this sample. It is worth mentioning that it has been shown that the t-distributed stochastic neighbor embedding (t-SNE) method can obtain better results than the KNN method for clusters. For example, Zhou et al. showed that both one-dimensional (1D) and two-dimensional (2D) models of the t-SNE approach are advantageous in distinguishing important functional states of the model heteromeric protein system.37 Raza et al. showed that the t-SNE method is extremely efficient in predicting defluorination of per- and polyfluoroalkyl substances (PFS) for their efficient treatment and removal.38

Figure 5.

Figure 5

Open in a new tab

Comparison of ΔG between DFT calculation and machine learning prediction; the left is calculated by GBDT regression, the middle is obtained by lasso regression, and the right is obtained by KNN regression.

Table 5. Train_RMSE, Train_R2, Test_RMSE, and Test_R2 of Various Machine Learning Models.

model Train_RMSE Train_R2 Test_RMSE Test_R2
GBDT 0.231 0.992 0.001 1.000
lasso 2.368 0.169 0.956 0.204
KNN 2.378 0.162 0.771 0.483
Open in a new tab

On basis of the best model GBDT, we ranked the feature importance of the models to find out the main factors affecting interactions of Au3 with AAs. Figure 6 shows the top 10 important features selected by the SHAP method and the 10 features in a descending order. Surprisingly, the simple characteristic ratio of the number of N atoms to the number of O atoms (RN/O) had the greatest impact on the predicted ΔG, while the number of O atoms in the amino acid (nO) had the least impact on the predicted ΔG. Notably, the molecular polarity index of AAs (MPI) and AA relative molecular mass (M) of AAs are among the highest three characteristics. This indicates that the main factors affecting the interaction strength of Au3 with AAs are RN/O, MPI, and M, which is somewhat similar to the conclusion reached by Abdalmoneam et al.13 That is, the polarity of the amino acid determines the properties of the interaction between the gold clusters and the AA in the gas phase and the solvent phase. Since M and RN/O are closely related to the size and steric hindrance of AAs and the number of functional groups amino and oxygen-containing groups, the interaction of gold clusters with AAs can be regulated by modulating the size of AAs and crown energy groups, thus affecting the formation of protein crowns as well as regulating the surface formation of proteins. This is essential for regulating the formation of protein crowns and for regulating the surface engineering of proteins.

Figure 6.

Figure 6

Open in a new tab

Highest ranking important features selected by SHAP and the corresponding Pearson correlation coefficient and mutual information values.

4. Conclusions

Overall, the ΔG of Au3 interacting with 20 natural AAs under the gas phase and water solvation conditions was computed by DFT. On the basis of the computed ΔG and optimal absorption configuration, a machine learning model (GBDT) based on the GBDT method is proposed for predicting the ΔG value of Au3 interacting with AAs under water solvation conditions. Based on the GBDT model and feature importance analysis, it is found that the ratio of the number of N atoms to the number of O atoms of AAs (RN/O), the molecular polarity index of AAs (MPI), and the relative molecular mass (M) of AAs are the main factors that affect the strength of the interaction between Au3 and AAs. This suggests that the interaction of gold clusters with AAs can be regulated by modulating the size of the protein and the number of amino and oxygen-containing groups in protein. Our work not only addresses the question of optimal sites for Au clusters to react with AAs but also proposes the main factors affecting the strength of their interactions.

Acknowledgments

This work is supported by the Natural Science Foundation of China (Grant Nos. 91961121 and 22003054), the project of innovation team of the ministry of education (IRT_17R90), the Guangdong Basic and Applied Research Foundation (No. 2019A1515110181), and the Natural Science Foundation of Hunan Province of China (No. 2020JJ5533).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c02195.

  • Interaction energies of Au3 with 15 natural AAs and the descriptor used for exploring the factors affecting the strength of the interaction between Au3 and AAs (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao3c02195_si_001.pdf (589.1KB, pdf)

References

  1. Mathew A.; Pradeep T. Noble metal clusters: applications in energy, environment, and biology. Part. Part. Syst. Charact. 2014, 31, 1017–1053. 10.1002/ppsc.201400033. [DOI] [Google Scholar]
  2. Bindhu M. R.; Umadevi M. Silver and gold nanoparticles for sensor and antibacterial applications. Spectrochim. Acta, Part A 2014, 128, 37–45. 10.1016/j.saa.2014.02.119. [DOI] [PubMed] [Google Scholar]
  3. Ghosh P.; Han G.; De M.; Kim C. K.; Rotello V. M. Gold nanoparticles in delivery applications. Adv. Drug Delivery Rev. 2008, 60, 1307–1315. 10.1016/j.addr.2008.03.016. [DOI] [PubMed] [Google Scholar]
  4. Chen D.; Ganesh S.; Wang W.; Amiji M. Protein Corona-Enabled Systemic Delivery and Targeting of Nanoparticles. AAPS J. 2020, 22, 83. 10.1208/s12248-020-00464-x. [DOI] [PubMed] [Google Scholar]
  5. Shang L.; Nienhaus G. U. Small fluorescent nanoparticles at the nano–bio interface. Mater. Today 2013, 16, 58–66. 10.1016/j.mattod.2013.03.005. [DOI] [Google Scholar]
  6. Sych T. S.; Polyanichko A. M.; Plotnikova L. V.; Kononov A. I. Luminescent silver nanoclusters for probing immunoglobulins and serum albumins in protein mixtures. Anal. Methods 2019, 11, 6153–6158. 10.1039/C9AY02054C. [DOI] [Google Scholar]
  7. Jin R. Atomically precise metal nanoclusters: stable sizes and optical properties. Nanoscale 2015, 7, 1549–1565. 10.1039/C4NR05794E. [DOI] [PubMed] [Google Scholar]
  8. Xie H. J.; Lei Q. F.; Fang W. J. Intermolecular interactions between gold clusters and selected amino acids cysteine and glycine: a DFT study. J. Mol. Model. 2012, 18, 645–652. 10.1007/s00894-011-1112-6. [DOI] [PubMed] [Google Scholar]
  9. Pakiari A. H.; Jamshidi Z. Interaction of Amino Acids with Gold and Silver Clusters. J. Phys. Chem. A 2007, 111, 4391–4396. 10.1021/jp070306t. [DOI] [PubMed] [Google Scholar]
  10. Rai S.; Suresh-Kumar N. V.; Singh H. A theoretical study on interaction of proline with gold cluster. Bull. Mater. Sci. 2012, 35, 291–295. 10.1007/s12034-012-0314-6. [DOI] [Google Scholar]
  11. Buglak A. A.; Kononov A. I. Comparative study of gold and silver interactions with amino acids and nucleobases. RSC Adv. 2020, 10, 34149–34160. 10.1039/D0RA06486F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Srivastava R. Interaction of cysteine with Aun (n = 8, 10, 12) even neutral clusters: A theoretical study. ChemistrySelect 2017, 2, 2789–2796. 10.1002/slct.201700041. [DOI] [Google Scholar]
  13. Abdalmoneam M. H.; Waters K.; Saikia N.; Pandey R. Amino-Acid-Conjugated Gold Clusters: Interaction of Alanine and Tryptophan with Au8 and Au20. J. Phys. Chem. C 2017, 121, 25585–25593. 10.1021/acs.jpcc.7b09108. [DOI] [Google Scholar]
  14. López-Lozano X.; Pérez L. A.; Garzón I. L. Enantiospecific Adsorption of Chiral Molecules on Chiral Gold Clusters. Phys. Rev. Lett. 2006, 97, 233401 10.1103/PhysRevLett.97.233401. [DOI] [PubMed] [Google Scholar]
  15. De Jesús Pelayo J.; Valencia I.; Díaz G.; López-Lozano X.; Garzón I. L. Enantiospecific adsorption of cysteine on a chiral Au34 cluster. Eur. Phys. J. D 2015, 69, 277. 10.1140/epjd/e2015-60562-0. [DOI] [Google Scholar]
  16. Pérez L. A.; López-Lozano X.; Garzón I. L. Density functional study of the cysteine adsorption on Au nanoclusters. Eur. Phys. J. D 2009, 52, 123. 10.1140/epjd/e2008-00289-5. [DOI] [Google Scholar]
  17. Feng J.; Pandey R. B.; Berry R. J.; Farmer B. L.; Naik R. R.; Heinz H. Adsorption mechanism of single amino acid and surfactant molecules to Au(111) surfaces in aqueous solution: Design rules for metal-binding molecules. Soft Matter 2011, 7, 2113–2120. 10.1039/c0sm01118e. [DOI] [Google Scholar]
  18. Kruger D.; Fuchs H.; Rousseau D.; Marx D.; Parrinello M. Pulling Monatomic Gold Wires with Single Molecules: An Ab Initio Simulation. Phys. Rev. Lett. 2002, 89, 186402 10.1103/PhysRevLett.89.186402. [DOI] [PubMed] [Google Scholar]
  19. Abdalmoneam M. H.; Saikia A.; Abd El-Mageed H. R.; Pandey R. First principles study of the optical response of Au8 cluster conjugated with methionine, tryptophan, and tryptophyl-methionine dipeptide. J. Phys. Org. Chem. 2021, 34, e4201 10.1002/poc.4201. [DOI] [Google Scholar]
  20. Buglak A. A.; Ramazanov R. R.; Kononov A. I. Silver cluster–amino acid interactions: a quantum-chemical study. Amino Acids 2019, 51, 855–864. 10.1007/s00726-019-02728-z. [DOI] [PubMed] [Google Scholar]
  21. Abd El-Mageed T. R.; Taha M. Exploring the intermolecular interaction of serine and threonine dipeptides with gold nanoclusters and nanoparticles of different shapes and sizes by quantum mechanics and molecular simulations. J. Mol. Liq. 2019, 296, 111903 10.1016/j.molliq.2019.111903. [DOI] [Google Scholar]
  22. Taha M.; Abd El-Mageed H. R.; Lee M. J. DFT study of cyclic glycine-alanine dipeptide binding to gold nanoclusters. J. Mol. Graphics Modell. 2021, 103, 107823 10.1016/j.jmgm.2020.107823. [DOI] [PubMed] [Google Scholar]
  23. Nhat P. V.; Si N. T.; Tien N. T.; Nguyen M. T. Theoretical Study of the Binding of the Thiol-Containing Cysteine Amino Acid to the Silver Surface Using a Cluster Model. J. Phys. Chem. A 2021, 125, 3244–3256. 10.1021/acs.jpca.0c11182. [DOI] [PubMed] [Google Scholar]
  24. Denys B.; Zdenek F. Adsorption of Amino Acids at the Gold/Aqueous Interface: Effect of an External Electric Field. J. Phys. Chem. C 2021, 125, 7856–7867. 10.1021/acs.jpcc.0c11248. [DOI] [Google Scholar]
  25. Chall S.; Mati S. S.; Das I.; Kundu A.; De G.; Chattopadhyay K. Understanding the Effect of Single Cysteine Mutations on Gold Nanoclusters as Studied by Spectroscopy and Density Functional Theory Modeling. Langmuir 2017, 33, 12120–12129. 10.1021/acs.langmuir.7b01789. [DOI] [PubMed] [Google Scholar]
  26. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09, Revision E.01; Gaussian, Inc.; Wallingford, CT, 2009. [Google Scholar]
  27. Sure R.; Brandenburg J. G.; Stefan G. Small Atomic Orbital Basis Set First-Principles Quantum Chemical Methods for Large Molecular and Periodic Systems: A Critical Analysis of Error Sources. ChemistryOpen 2016, 5, 94–109. 10.1002/open.201500192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Grant-Hill J.; Peterson K. A. Gaussian basis sets for use in correlated molecular calculations. XI. Pseudopotential-based and all-electron relativistic basis sets for alkali metal (K–Fr) and alkaline earth (Ca–Ra) elements. J. Chem. Phys. 2017, 147, 244106–244112. 10.1063/1.5010587. [DOI] [PubMed] [Google Scholar]
  29. Weigend F.; Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
  30. Panapitiya G.; Avendaño-Franco G.; Ren P.; Wen X.; Li Y.; James P. Lewis Machine-Learning Prediction of CO Adsorption in Thiolated, Ag-Alloyed Au Nanoclusters. J. Am. Chem. Soc. 2018, 140, 17508–17514. 10.1021/jacs.8b08800. [DOI] [PubMed] [Google Scholar]
  31. Dong W.; Cao X.; Wu X.; Dong Y. Examining pedestrian satisfaction in gated and open communities: An integration of gradient boosting decision trees and impact-asymmetry analysis. Landscape Urban Plann. 2019, 185, 246–257. 10.1016/j.landurbplan.2019.02.012. [DOI] [Google Scholar]
  32. Uddin S.; Haque I.; Lu H.; Moni M. A.; Gide E. Comparative performance analysis of K-nearest neighbour (KNN) algorithm and its different variants for disease prediction. Sci. Rep. 2022, 12, 6256. 10.1038/s41598-022-10358-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Tibshirani R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. B 1996, 58, 267–288. 10.1111/j.2517-6161.1996.tb02080.x. [DOI] [Google Scholar]
  34. Chicco D.; Warrens M. J.; Jurman G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623 10.7717/peerj-cs.623. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Friedman J. H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. 10.1214/aos/1013203451. [DOI] [Google Scholar]
  36. Dickinson Q.; Meyer J. G. Positional SHAP (PoSHAP) for Interpretation of machine learning models trained from biological sequences. PLoS Comput. Biol. 2022, 18, e1009736 10.1371/journal.pcbi.1009736. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Zhou H.; Wang F.; Tao P. t-Distributed Stochastic Neighbor Embedding Method with the Least Information Loss for Macromolecular Simulations. J. Chem. Theory Comput. 2018, 14, 5499–5510. 10.1021/acs.jctc.8b00652. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Raza A.; Bardhan S.; Xu L.; Yamijala S.; Lian C.; Kwon H.; Wong B. M. A Machine Learning Approach for Predicting Defluorination of Per- and Polyfluoroalkyl Substances (PFAS) for Their Efficient Treatment and Removal. Environ. Sci. Technol. Lett. 2019, 6, 624–629. 10.1021/acs.estlett.9b00476. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao3c02195_si_001.pdf (589.1KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES