APLUS: A Python library for usefulness simulations of machine learning models in healthcare

Abstract

Despite the creation of thousands of machine learning (ML) models, the promise of improving patient care with ML remains largely unrealized. Adoption into clinical practice is lagging, in large part due to disconnects between how ML practitioners evaluate models and what is required for their successful integration into care delivery. Models are just one component of care delivery workflows whose constraints determine clinicians’ abilities to act on models’ outputs. However, methods to evaluate the usefulness of models in the context of their corresponding workflows are currently limited. To bridge this gap we developed APLUS, a reusable framework for quantitatively assessing via simulation the utility gained from integrating a model into a clinical workflow. We describe the APLUS simulation engine and workflow specification language, and apply it to evaluate a novel ML-based screening pathway for detecting peripheral artery disease at Stanford Health Care.

1. Introduction

While the development of models in healthcare via machine learning (ML) continues at a breakneck pace [1–4], deployment of models into practice remains limited [5–7]. As an example, a recent survey found evidence of adoption for only a small fraction of over 250,000 published clinical risk prediction systems [8]. The primary reason for limited adoption is that models are only one component of the care delivery workflows that they are designed to improve [6,9–11]. Healthcare workflows are complex: successful care delivery often depends on the coordination of several providers across multiple departments to execute many steps in highly specific, context-dependent sequences [12]. Their ability to execute is impacted by resource constraints, patient needs, and existing protocols [13,14]. Asking a clinician to incorporate information output by an ML model may require redesigning workflows or altering behavior. For example, a workflow mapping exercise done at Kaiser to understand how an early deterioration model fit into care delivery identified 44 different states and 6 different departments needed to act upon the model’s output [10], while process mapping at Stanford Hospital revealed 21 steps and 7 handoffs necessary to put an ML model for advance care planning into practice [15].

Traditional metrics for evaluating ML models are insufficient for assessing their usefulness in guiding care [6,7,16–19]. Popular metrics such as Area Under the Receiver Operating Characteristic curve (AUROC), F1 Score, and Accuracy ignore a workflow’s capacity constraints as well as the variable costs of misprediction. For example, the cost of administering an unnecessary cancer screening (false positive) may be much lower than the cost of failing to detect cancer (false negative). The outcomes that actually matter to a health system – namely, cost-effectiveness and net benefit to patients – are not captured by these traditional metrics [6,7,16–19]. An approach which does take these factors into account is utility analysis. There has been extensive research on using utility as a north-star metric for predictive models. Vickers et al. 2006 introduced decision curves as an improved method for comparing predictive models [17], and Baker et al. 2009 introduced a similar concept called relative utility [20]. While these utility-based metrics complement traditional ML metrics like AUROC, they still suffer from an important underlying limitation – namely, they estimate theoretical rather than achievable utility gained from using a model [6,9,14]. They assume that every model prediction gets acted upon, and thus ignore the structure and constraints of the relevant workflow (e.g. budget, staffing, data acquisition delays, human error, etc.) [6,9,21].

Because deploying an ML model into a healthcare setting has a cost in terms of time, money, and potential risk of harm to patients [14,22,23], proactively assessing the overall benefit of using a model to guide care is essential for two reasons. First, deciding which models to implement – even a simple tool can cost hundreds of thousands of dollars [23]. Second, for deciding how best to integrate a chosen model’s output into a care delivery workflow.

In the remainder of this paper, we refer to this process of conducting a utility-based analysis of a model within the context of the workflow into which it will be deployed as a usefulness assessment. In essence, a usefulness assessment aims to quantitatively answer the question: If I use this ML model to guide this workflow, will the benefits outweigh the costs, and by how much? Prior work has used simulations to identify potential changes to clinical workflows that can reduce operational inefficiencies in healthcare settings [24–28], but efforts to quantify the usefulness of model-guided care delivery workflows are limited. Existing approaches rely on bespoke simulation pipelines that are specific to the workflow being evaluated and are not designed for reuse [9,29–33].

To bridge this gap in tooling, we have developed APLUS, a simulation framework for systematically conducting usefulness assessments of ML models in triggering care management workflows. Of the various aspects of clinical decision support systems that merit study, our framework is specifically focused on measuring the integration and evaluation of ML models prior to their deployment [11]. Our framework can simulate any workflow that can be represented as a set of states and transitions, and includes the ability to incorporate individual-level utility analyses [29], heterogeneous treatment effects and costs, and preferential allocation of shared resources. We make APLUS available as a Python library and demonstrate its use by conducting a usefulness assessment of a classification model for identifying patients with peripheral artery disease (PAD) [34].

2. Methods

In this section, we describe the design of APLUS including its simulation engine, workflow specification language, and the analyses it supports. The code for APLUS is available on Github at https://github.com/som-shahlab/aplus.

2.1. Simulation engine

Inspired by prior work to develop simulation tools for patient flow [25–28], we take a patient-centric, discrete-event approach to workflow simulation. Specifically, we developed a synchronous, time-driven discrete-state simulator [35]. Given a set of patients and a workflow (defined via the specification language described below in 2.1.2 Workflow Specification Language), the simulation engine progresses all patients through the workflow and tracks their state history, transitions taken, and utilities achieved. We model each individual patient’s journey through the workflow as an ordered sequence of states occurring over a set of evenly spaced time steps, where cycles are permitted. Each state and transition is associated with a non-negative integer duration which represents the number of time steps that it takes to complete. Within a single timestep, states are unordered, with two exceptions: (i) states that are dependent on the completion of previous states will always occur after those prior dependencies have been completed, (ii) patients who reach a state which has at least one transition that depends on a shared resource will be sequentially processed based on an end-user-defined function that preferentially ranks patients for access to that shared resource. This enables modeling of a limited resource that is allocated based on a patient’s predicted risk – e.g. Stage IV cancer patients getting first access to a novel therapy.

When there are multiple possible transitions that a patient can take from a state, there are two possible ways that a specific transition can be selected by the simulation engine. Transitions can be associated with (i) a probability of occurrence or (ii) a conditional expression. For transitions associated with a probability (e.g. patients have a 30 % chance of going down the “high-risk” pathway and a 70 % chance of going down the “low-risk” pathway), the simulation engine samples from the set of possible transitions proportional to their specified probabilities. This is best suited for workflows in which one might have a rough sense of what proportion of patients go down each treatment pathway, but it is difficult to articulate more precise criteria. For transitions associated with a conditional expression (e.g. patients with attributes X and Y are “high-risk”, patients with attributes W and Z are “low-risk”) the simulation engine sequentially evaluates each expression and selects the transition whose expression evaluates to True, thus allowing APLUS to generalize to essentially any situation that can be expressed as a set of Boolean conditions. For example, heterogeneous treatment effects and costs can be simulated via a conditional expression predicated on a patient-level property variable, as defined below in 2.2 Workflow Specification Language. A gene therapy workflow might take a patient to the “treatment succeeded” state if the patient has a specific gene mutation, and otherwise send the patient to a “treatment failed” state. Patients belonging to different “context groups” (i.e. subpopulations) can have different workflow trajectories applied to them via these conditional transitions [36]. Transitions can also be conditioned on the availability of system-level resources to model the impact of resource constraints.

The simulation engine is written in Python. The outputs that it generates are a set of Python dictionaries and objects which are subsequently analyzed via the methods described below in 2.1.3 Utility Analyses.

2.2. Workflow specification language

Building on previous work on mapping healthcare workflows [9,37,38] and clinical guidelines [39–41] into machine comprehensible representations [42], we created a lightweight workflow specification language for APLUS. Our language was designed with three key points of differentiation in mind. First, our target end user is an informatician with intermediate programming skills, rather than a clinician or business operations analyst. Thus, we prioritized the ability to easily modify workflows programmatically over concerns like user interfaces or integrations with clinical ontologies. Second, we wanted to enable fast iteration over many workflow variations. Thus, we prioritized simplicity and speed of writing over support for edge cases that would add significant complexity. Third, we wanted APLUS’s core simulation engine to support a broad range of workflows without modification. Thus, our language prioritizes expressive flexibility. A detailed schema is available at the APLUS GitHub repository.

We represent a care delivery workflow as a state machine consisting of a set of states and transitions. We take a “patient-centric” view, i.e. the state machine represents the journey of an individual patient through the workflow. We represent our specification language using YAML, a popular markup language that aims to be both human- and machinereadable [43]. Thus, the only dependency for creating a workflow specification is a basic text editor (e.g. vim, TextEdit, Notepad). Concretely, an APLUS workflow specification has three sections: metadata, variables, and states.

The metadata section contains information needed to initialize the simulation. This includes the name of the workflow, the locations of relevant files that will be imported (e.g. a CSV containing predictions from a relevant model), and column mappings for tabular data (e.g. which column in a CSV corresponds to patient IDs).

The variables section contains a list of all of the variables that will be used in the simulation. Variables can be referenced in the definition of any state or transition in the states section. There are four main types of variables that are currently supported: (1) Simulation-Level Variables are tracked by the simulation engine itself and measure the progression of time within the simulation. Examples include: the number of timesteps the simulation has already run, the duration of time that a patient has spent in the hospital, the duration of time that a patient has before being discharged, etc. (2) Patient-Level Properties represent unique, individual-level properties associated with each patient. Examples include model predictions, ground truth labels, age, stage of cancer, etc. (3) System-Level Resources represent attributes of the overall system (e.g. hospital, department, outpatient clinic, etc.). As such, they are shared across all patients. When one patient depletes a system-level resource, that change will be reflected across all other patients. Examples include budget, MRI availability, specialist capacity, etc. (4) Constants are variables in the purest sense – they are not directly associated with the overall workflow or any individual patient. They can be any primitive Python type (integer, float, string, or boolean) or basic Python data structure (list, dict, set). Examples include: 0.98, [1–3], True, etc.

The states section describes the structure of the workflow. We represent a workflow as a state machine, and thus the states section contains a list of all states in the workflow, as well as the possible transitions between them. There are three types of states: start, end, and intermediate. All patients begin their journey at the same start state, pass through 0 + intermediate state(s) over the course of the simulation, and finish their journey at one of the end states. A patient moves between states via transitions. If only one transition is specified for a state, then every patient who reaches that state will take that transition. If a state has multiple transitions, however, the simulator will follow whatever rules were specified for each transition to decide which one to take.

In order to measure the outcomes from executing a workflow, utilities must be associated with each state and/or transition. Utilities are grouped by their unit of measurement, so multiple distinct types of utilities can be simultaneously tracked. This permits the assessment of a model across a wide range of performance indicators of interest to a health system, including time-related (e.g. length-of-stay), clinical (e.g. patient outcomes), financial (e.g. monetary cost), or resource-related (e. g. staff utilization) [44]. Utility values can also be conditioned on arbitrary expressions. This allows for conducting individual-level utility analyses by including patient-level variables in a utility’s associated conditional expression [29]. This tends to be the most difficult step of specifying a workflow, as the end user must obtain these utility values via literature review, expert interviews, or financial modeling [32]. For example, a usefulness assessment that had been previously conducted on an advance care planning workflow derived utilities from a previously published randomized controlled trial [9].

In order to represent the temporal nature of workflows, durations of time can be associated with each state and transition. These durations represent the number of discrete time steps that a patient waits after reaching a state or taking a transition. For example, if we have a workflow where patients stay in a hospital for multiple days post-surgery and are evaluated once a day for additional treatment, then we could set up two states named “rest” and “evaluation”, where the transition between “rest” and “evaluation” takes 0 timesteps since they occur on the same day, but the transition between “evaluation” and “rest” takes 1 timestep since after evaluating a patient, we progress to the next day.

In order to model how resource constraints change over time, resource deltas can be associated with each state and transition. A resource delta encodes how a system-level resource changes after a transition is taken. For example, a transition which directs a patient to an MRI machine might have a resource delta of “−1” for the resource “MRI capacity.” This setting allows for fine-grained control over the depletion and augmentation of shared resources which influence the delivery of care.

2.3. Utility analyses

APLUS conducts three categories of analyses to assess a model’s usefulness: predictive performance, theoretical utility, and achievable utility under workflow constraints. The analysis outputs automatically generated by APLUS (with examples in Appendix A) are as follows:

1. Plots which summarize the model’s predictive performance, including Receiver Operating Characteristic (ROC) curve, Precision-Recall curve, Calibration curve, Work v. PPV/TPR/FPR, and Model Cutoff Threshold v. PPV/TPR/Work. Work is defined as the proportion of model predictions that are positive, PPV is the model’s positive predictive value, TPR is the true positive rate, FPR is the false positive rate, and model cutoff threshold is the value above which we consider a model’s probabilistic output to be a positive prediction. These standard measurements of model performance gauge the ability of an ML model to make accurate predictions.

2. Plots which summarize the model’s theoretical utility, i.e. the outcomes achieved by following the model’s predictions after weighting them by their corresponding utilities. The plots that we generate include ROC curve with utility indifference curves, Precision-Recall curve with utility indifference curves, Decision curve, Relative Utility curve, PPV v. Mean Utility Per Patient, Model Cutoff Threshold v. Mean Utility Per Patient, and Work v. Mean Utility Per Patient. A decision curve is a plot of a model’s net benefit across different risk thresholds. Net benefit is defined as the difference between the TPR and FPR of a model, where the FPR is translated onto the same scale as the TPR via an “exchange rate” which depends on the relative utility of true v. false positives [17]. As an analogy, one can imagine net benefit being the “profit” of using a model, where the “revenue” is generated in one currency (true positives) while the “costs” are generated in another currency (false positives), and thus there is an intermediary step in which the currency of costs (false positives) are “exchanged” into the currency of revenue (true positives) [45]. Risk threshold is defined as the cutoff value above which a model’s probabilistic output is considered to be a positive prediction. Thus, a decision curve allows a reader to quickly compare different models’ expected utilities across various risk thresholds. A slight variation is the relative utility curve [46]. The relative utility of a model at a given risk threshold is the maximum net benefit achieved by the model divided by the net benefit achieved by a perfect classifier [46].

3. Plots which summarize the model’s achievable utility within the context of its workflow, i.e. how much utility we expect the model to achieve given the constraints of the overall care delivery pathway that it impacts. The plots that we generate include Model Cutoff Threshold v. Mean Achieved Utility Per Patient, Mean Achieved Utility Per Patient v. Optimistic Baseline, and Mean Achieved Utility Per Patient under Workflow Variant #1 v. Mean Achieved Utility Per Patient under Workflow Variant #2. We define Optimistic Baseline as the case in which all of a model’s predictions get acted upon. Note that these evaluation metrics integrate information about the entirety of the workflow, and can also relax some of the assumptions made in generating the theoretical utility plots. For example, decision curve analyses assume that utilities are uniform across all patients, an assumption that does not need to be enforced within an APLUS simulation [19]. Additionally, theoretical utility analyses ignore the possibility of downstream constraints turning positive predictions into true/false negatives, or turning negative predictions into true/false positives (e.g. if alternative tests or clinicians determine that a patient originally assigned a negative prediction should be treated as a positive case).

3. Application of APLUS to risk models for PAD screening

In this section, we present a case study of conducting a novel usefulness assessment via APLUS of ML models for the early detection of PAD.

3.1. Clinical background of PAD

To demonstrate APLUS in action, we applied it to a novel usefulness assessment scenario – identifying patients with PAD via a state-of-the-art ML model for further screening [34] – and show that our framework can be used to select the optimal model and workflow combination to maximize the model’s usefulness to patients. PAD is a chronic condition which occurs when the arteries in a patient’s limbs are constricted by atherosclerosis, thereby reducing blood flow [47]. A total of 8–12 million people in the US have PAD [48], costing the US healthcare system over $21 billion annually [49]. Left untreated, PAD is associated with a higher risk of mortality, serious cardiovascular events, and lower quality of life [50]. Despite these risks, PAD is often missed by healthcare providers. Roughly half of all PAD patients are asymptomatic [50], and one study showed that even when a previous PAD diagnosis was documented in a patient’s medical record, only 49 % of primary care physicians were aware [48]. A broad suite of treatment options is available to patients suffering from PAD, ranging from lifestyle changes to drugs to surgery [50,51]. The earlier that a patient is diagnosed, the better the chances of preventing disease progression and thus avoiding the need for costlier interventions [32,34]. The low-risk and non-invasive ankle-brachial index (ABI) is the primary test used to diagnose PAD today [32,52]. However, the most recent guidance from the US Preventive Services Task Force cited “inadequate evidence” on the usefulness of population-wide ABI testing to identify asymptomatic PAD patients who might benefit from further treatment [53].

3.2. Previously developed ML models for PAD screening

Ghanzouri et al. 2022 developed three ML models to classify patients for PAD based solely on EHR data: a deep learning model, a random forest, and a logistic regression with respective AUROCs of 0.96, 0.91 and 0.81 [34]. Each model assigns a probabilistic risk score to each visiting patient which indicates their likelihood of having PAD. Patients with risk scores above a certain threshold (chosen to be 0.5 in their study) are classified as having PAD and recommended for follow-up ABI testing [34]. We extend this prior work by conducting a usefulness assessment on incorporating a PAD classification model’s predictions into clinical decision making at Stanford Health Care.

3.3. Specification of the PAD screening workflows

To apply APLUS to this use case, we first mapped out the states, transitions, and utilities of possible model-guided PAD screening workflows. Based on interviews with practitioners (chiefly, co-author ER, who is a practicing vascular surgeon), we identified two workflows to consider: (1) a nurse-driven workflow which assumes the existence of a centralized team of nurses reviewing the PAD model’s predictions for all patients visiting their clinic each day; and (2) a doctor-driven workflow which assumes that the PAD model’s predictions appear as a real-time alert in a patient’s EHR during their visit to the clinic. These interviews yielded natural language descriptions of both workflows, which we then translated into the APLUS specification language.

In both the nurse-driven and doctor-driven workflows, our experiments assumed that there were 3 possible end outcomes for patients: “Untreated”, “Medication”, or “Surgery.” These roughly capture the spectrum of treatment options available for patients with PAD – either the patient’s visit is concluded without treatment, the patient is prescribed medication to reduce the risk of cardiovascular disease, or the patient undergoes a procedure like angioplasty or bypass [50,51]. We assume that patients who end up in the “Surgery” state have also been given medication prior to their procedures. The utility of each of these outcomes depends on the ground truth PAD status for a specific patient. For example, “Untreated” is the best option for patients without PAD but has the largest cost for patients with PAD. “Medication” is the ideal outcome for patients with moderate PAD but is undesirable for patients without PAD. “Surgery” is the costliest outcome for all patients, but the relatively best option for patients with severe PAD. We combined clinician input with utility estimates from Itoga et al. 2018 to define the utilities associated with the end outcomes of each workflow in terms of a multiplier on remaining years living to reflect quality-adjustment on lifespan [32]. Given that a healthy patient with no PAD has a baseline utility of 1, we used the following relative utilities for various outcomes: 0.95 for patients without PAD who are prescribed medication, 0.9 for patients with PAD who are prescribed medication, 0.85 for patients with moderate PAD not prescribed medication, 0.7 for patients without PAD who undergo surgery, 0.68 for patients who have severe PAD and undergo surgery, and 0.6 for patients with severe PAD who do not undergo surgery [32]. The corresponding YAML workflow specification files are available in the APLUS Github repository.

In both workflows, we also assume the existence of a cardiovascular specialist who can evaluate patients after they are referred by a doctor or nurse. We assume that the specialist has a set capacity for how many patients she can see per day. However, once a patient reaches the specialist, we assume that the specialist makes the optimal treatment decision for that patient. Thus, prioritizing which patients use up the limited capacity of the specialist is the key driver of our simulated workflow’s achieved utility.

The doctor-driven workflow assumes that model predictions will appear as an alert within the EHR of a patient during their visit to the clinic. If the attending physician notices this alert, she can choose to either ignore the alert or act on it. We assume that physicians ignore alerts at random. If a physician decides to act on an alert, she will either administer treatment herself or refer the patient to a specialist. The main constraints on this workflow are the probability that the attending physician reads the alert (previous studies have shown that up to 96 % of alerts are overridden [54–56]) and the specialist’s schedule.

The nurse-driven workflow assumes the existence of a centralized team of nurses tasked with reviewing the predictions of the PAD model for each patient who visits the clinic on a given day. Based on these predictions, the nursing staff decides which patients to directly refer to the specialist, thus cutting out any intermediate steps with a non-specialist physician. The main constraints on this workflow are the capacity of the nursing staff and the specialist’s schedule. We assume that the nursing staff does not suffer from alert fatigue, i.e. they will not randomly ignore predictions from the PAD model. This is an assumption we have made in this study, and we acknowledge that nurses might suffer from alert fatigue as well. This is an example of a potentially significant assumption which can be easily changed within APLUS by anyone interested in replicating our experiments under a different set of nurse-driven workflow constraints (e.g. including a probability that nurses ignore alerts).

One important distinction between these two workflows is that the nurse-driven workflow is centralized whereas the doctor-driven workflow is decentralized. In other words, the nurse-driven workflow batches together all model predictions for each day before patients are chosen for follow-up, while in the doctor-driven workflow each doctor decides whether to act on a PAD alert immediately upon receipt of the alert independently from the decisions of other doctors. Thus, specific to the nurse-driven workflow with a daily capacity of K, we consider two possible strategies that the nurses can leverage for processing this batch of predictions: (1) ranked screening, in which the nursing staff follows up with the K patients with the highest PAD risk scores; or (2) thresholded screening, in which a random subset of K patients are selected from the batch of predictions whose predicted PAD risk score exceeds some cutoff threshold.

3.4. Simulation parameters for the PAD workflows

We acquired a dataset of 4,452 patients (henceforth referred to as the “dataset”) who had both ground-truth labels of PAD diagnosis and risk score predictions from all three ML models developed in Ghanzouri et al. 2022 [34]. This data was directly sourced from the authors of Ghanzouri et al. 2022 [34], who had previously run their models on this cohort of patients at Stanford Hospital and who share two co-authors with this paper (ER and NHS). For each combination of model/workflow that we evaluated, we simulated 500 consecutive days of patient visits. For each simulated day, the number of visiting patients was determined by randomly sampling from a Poisson distribution with a mean of 35 (this distribution was chosen to reflect historical patterns of the rate at which patients who would trigger the PAD model visit Stanford clinics). Then, given the number of patients visiting on a given day, we randomly sampled (with replacement) that number of patients from our dataset. The same set of sampled patients was used across all simulations to ensure comparability of results.

Based on clinician interviews and a literature review, we identified the following parameters for our simulation. First, we assumed that patients with PAD have an ABI sampled from a normal distribution with a mean of 0.65 and standard deviation of 0.15, while patients without PAD have an ABI sampled from a normal distribution with a mean of 1.09 and standard deviation of 0.11 [47]. We used an ABI of 0.90 as the cutoff threshold between PAD and no PAD [57]. Our simulated ABI test showed roughly 95 % sensitivity and 95 % specificity on our simulated patients, which is consistent with previous estimates for the accuracy of an ABI test [32,47,52]. To simulate the increased risk of serious complications from untreated PAD, we assumed that if a PAD patient saw a specialist, then they would need surgery only if their ABI score was < 0.45, whereas a PAD patient who did not see a specialist would eventually require surgery if their ABI score was < 0.55. The overall proportion of simulated patients with an ABI score < 0.45 was 9 %, while the proportion of simulated patients with an ABI score < 0.55 was 26 %, which emulates the fact that roughly 7 % of patients with PAD will require surgical intervention [48], and that 26 % of patients with symptomatic PAD should eventually progress to needing some form of surgery to manage their PAD [32]. We also assumed that an ABI score > 0.8 was moderate enough to be treated by a non-specialist physician, but that a score < 0.8 must be referred to a specialist [57].

For the doctor-driven workflow specifically, we assumed that only patients who have a PAD risk score ≥ 0.5 will generate an alert, which is consistent with the threshold used in Ghanzouri et al. 2022 (42). The representations of these two workflows in the APLUS specification language, as well as visualizations of their states and transitions, can be found in our Github repository: https://github.com/som-shahlab/aplus. The specifications can be viewed in any basic text editor, but for ease of visualization we recreate diagrams of the nurse-driven and doctor-driven workflows in Fig. 1.

Fig. 1.

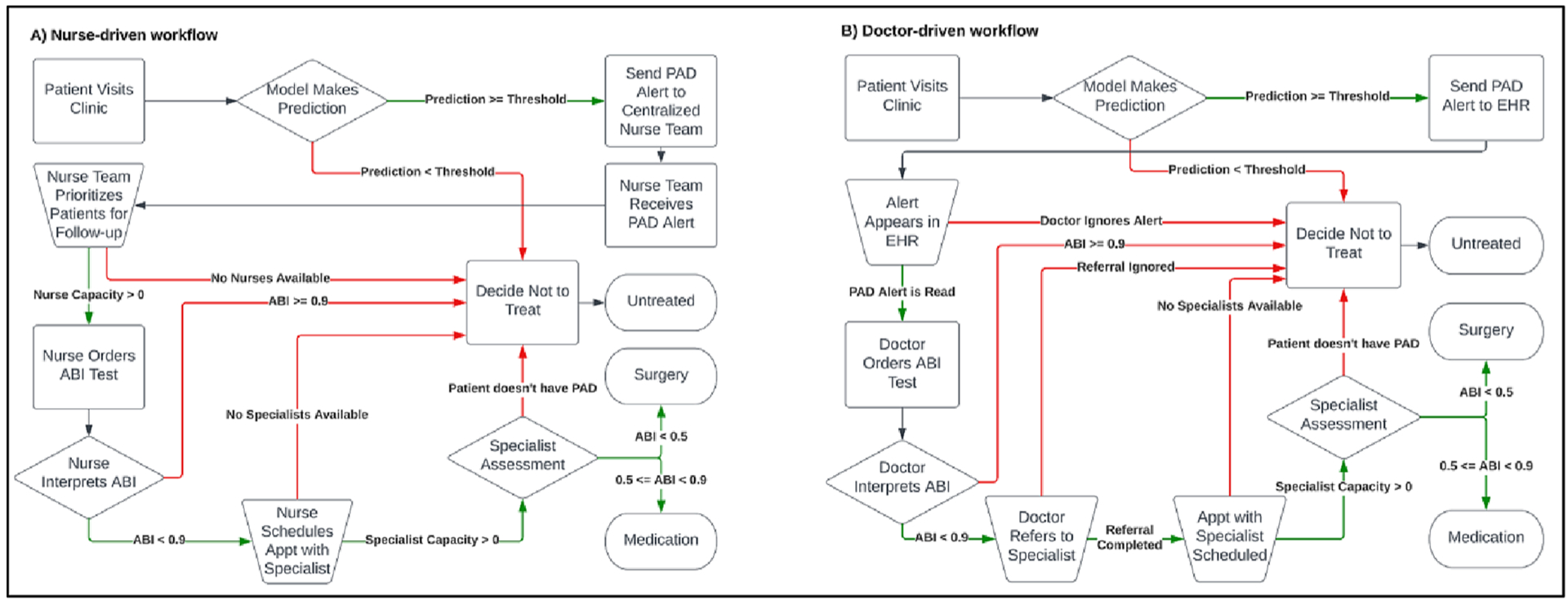
States, transitions, and transition conditions for the (a) nurse-driven workflow and (b) doctor-driven workflow. All patients begin at the “Patient Visits Clinic” state in the top left of the charts. Then, patients progress according to their individual-level properties, and end at one of 3 treatment options: “Untreated”, “Medication”, or “Surgery”. Trapezoids represent capacity constraints, diamonds represent decision points, squares are intermediate states, and pills are end states.

We evaluated the doctor-driven and nurse-driven workflows across ranges of possible values for two constraints: (1) nurse capacity for the nurse-driven workflow and (2) probability that a PAD alert is read for the doctor-driven workflow. Nurse capacity is defined as the total number of patients per day that the nursing team can follow-up with for an ABI test. Probability that a PAD alert is read (also referred to as probability alert is read or simply alert fatigue) is the chance that a doctor acts on an alert generated when a patient is classified by a model as having PAD.

3.5. Usefulness assessment of the PAD workflows

We evaluated each PAD model’s utility relative to three baselines: Treat None, where the model simply predicts a PAD risk score of 0 for all patients; Treat All, where the model predicts a PAD risk score of 1 for all patients; and Optimistic, where there were no workflow constraints or resource limits on model predictions. Concretely, we measured each model’s expected utility achieved per patient above the Treat None baseline as a percentage of the utility achieved under the Optimistic scenario. In other words, we measured how much of the total possible utility gained from using a model was actually achieved under each workflow’s constraints. The Treat None baseline should therefore always have a relative achieved utility of 0 %, while all models should have a utility value of 100 % in the Optimistic setting (as all patients are simply sent to the specialist for screening). For clarity, we do not show the Treat None baseline in any of the following plots, as it is always trivially set to 0 %.

4. Results

In this section, we summarize the results of conducting our APLUS usefulness assessment on the doctor-driven and nurse-driven PAD workflows under realistic capacity constraints.

4.1. Simulating unlimited downstream specialist capacity

For our first set of experiments, we assumed that the capacity of the downstream specialist was infinite to isolate the impact of nurse capacity on the nurse-driven workflow and alert fatigue on the doctor-driven workflow.

(A). Nurse-driven workflow:

As detailed below, APLUS revealed that the choice of model for a nurse-driven workflow mattered only under the medium- and high-capacity settings, and certain screening strategies. This was because the three models had similar top-K precision (i.e. they were all able to identify the most obvious PAD cases), and thus in low-capacity settings where only the top few model predictions could be acted upon, the choice of model does not matter. In higher-resource settings, however, the deep learning model offered a significant boost in utility.

To determine this, we first used APLUS to evaluate the thresholded screening strategy, in which a random subset of K patients is selected from the batch of patients whose predicted PAD risk score exceeds the cutoff threshold. As shown in Fig. 2a, the deep learning ML model (purple line) achieves the highest expected utility per patient across all treatment strategies under this thresholded screening regime. A nursing staff which leverages the deep learning model to prioritize patients can achieve roughly 50 % of the total possible utility under the optimistic scenario with a screening capacity of only 5 patients per day, and almost 80 % of the total possible utility with a screening capacity of 10 patients per day. As the nursing capacity increases, we see the difference between the relative utility achieved by the deep learning model and the random forest model (blue line) increasing from 4 absolute percentage points under a capacity of 3 patients/day to 13 percentage points under a capacity of 6 patients/day.

Fig. 2.

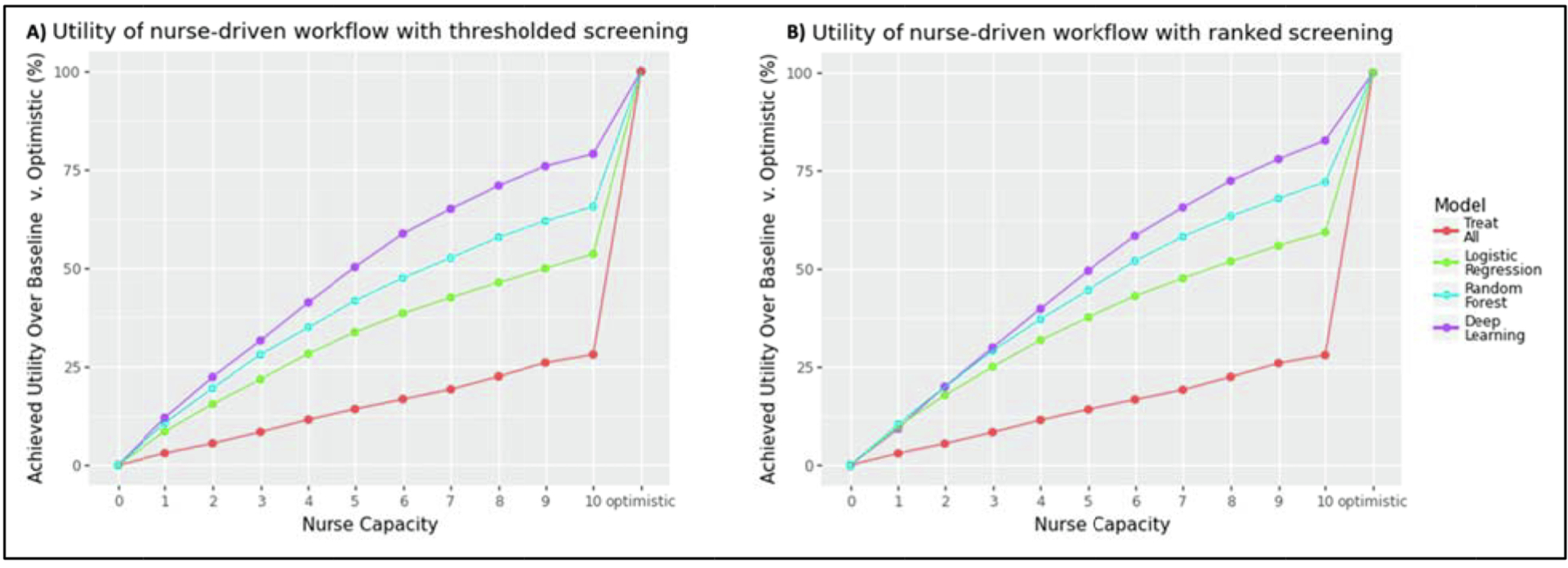
(a) Utility achieved by the nurse-driven workflow under thresholded screening across different nurse capacities using the optimal model cutoff threshold. (b) Utility achieved by the nurse-driven workflow under ranked screening across different nurse capacities. The deep learning model is most differentiated under a thresholded screening strategy, and only at high nurse capacity levels. All plots assume unlimited specialist capacity.

We observe similar overall trends in Fig. 2b when simulating a ranked screening strategy in which the nursing staff follows up with the K patients with the highest PAD risk scores. However, APLUS reveals slightly different results in low resource settings (i.e. nurse capacity < 4). In a low-capacity setting, all three ML models achieve relatively similar utilities. This makes sense, as nurses are only able to act on each model’s most confident prediction under this constrained setting, and thus the achieved utility of the model depends only on the accuracy of its top-3 highest scoring predictions, rather than its overall predictive performance across all patients. The difference between the achieved utility of the deep learning model (purple line) and random forest model (blue line) is smaller than it is under the thresholded screening strategy, ranging from only 1 absolute percentage points with a capacity of 3 patients/day to 7 percentage points with a capacity of 6 patients/day.

Using APLUS, we can now conclude the following: For workflows with a nurse capacity ≥ 4, a deep-learning-guided ranked screening approach, rather than a thresholded screening approach, yields the highest expected achieved utility. For workflows with a nurse capacity < 4, however, the results are mixed – the three ML models do not appear to be differentiated from a utility standpoint, and the ranked screening approach does not yield a consistently higher utility than the thresholded screening approach. This indicates that there are enough additional steps and constraints in the nurse-driven workflow under these low resource settings that the choice of model or patient prioritization does not make a tangible difference.

As an additional experiment, we were curious about the impact of varying the cutoff threshold used for each of the ML models on their expected achievable utility. The results shown in Fig. 3 provide a hint for why the deep learning model showed superior utility in our previous analysis – the probability distribution it learned more accurately reflected the binary prediction task it was given than either of the other two models. This can be seen in the significantly sharper, immediate jump in expected utility that the deep learning model (far left) experiences as its cutoff threshold increases from 0 compared to the more gradual slope in the utility curves of the random forest (middle) and logistic regression (far right).

Fig. 3.

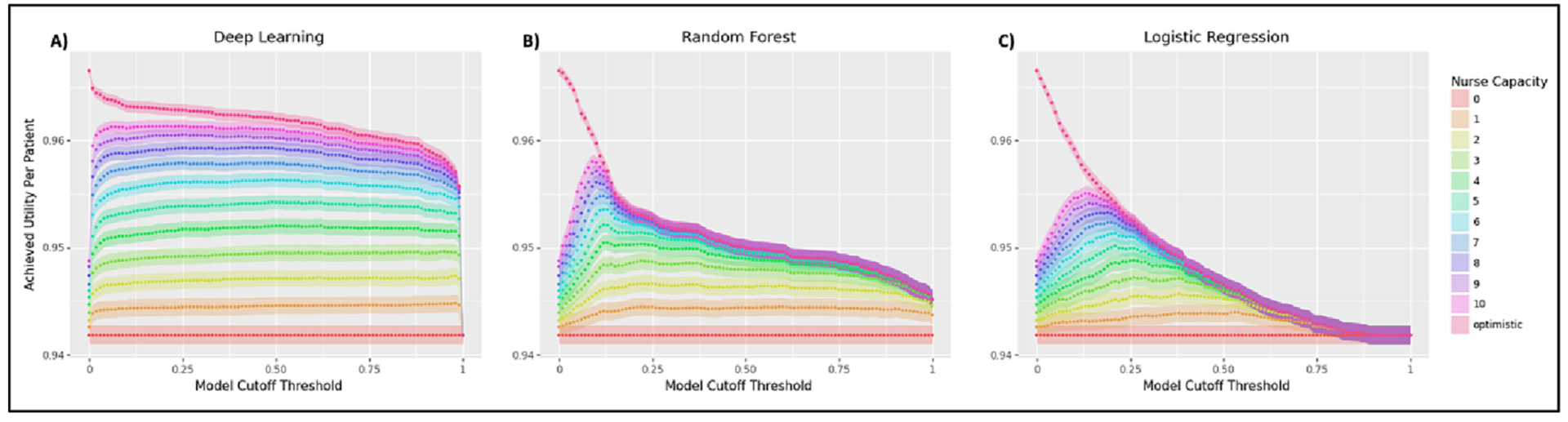
Utility achieved by the (a) deep learning model, (b) random forest model, and (c) logistic regression across various model cutoff thresholds. The sharper peaks in the random forest and logistic regression plots indicate that the probability distributions they learn have more dispersion than that learned by the deep learning model. All plots assume unlimited specialist capacity and a thresholded screening strategy.

This reflects the better calibration and accuracy of the deep learning model, as its predictions have a highly bimodal distribution clustered around 0 and 1 (of its total set of probabilistic predictions, 63 % are < 0.01 while 16 % are > 0.99). As shown in Fig. 3, this makes the deep learning model highly sensitive to increases in cutoff threshold around 0 and 1, whereas the more dispersed probability distributions learned by the random forest and logistic regression cause their cutoff thresholds to have a more gradual impact on their achieved utilities. By making these types of differences more readily apparent, APLUS can help to debug and compare models.

(B). Doctor-driven workflow:

We simulated a doctor-driven workflow in which we assumed that every physician who sees a patient with a predicted risk score ≥ 0.5 would receive an EHR alert recommending follow-up [34]. The one exception was the Treat All case, in which an alert was automatically sent for all patients. Again, this simulation assumed that the capacity of the specialist was infinite to isolate the impact of the probability that an alert is read. We see in Fig. 4 that a strategy of Treat All (red line) uniformly generates the highest expected utility under this doctor-driven workflow, with alerts triggered by the deep learning model (purple line) coming in a distant second. This was expected, as our workflow assumed that patients assessed by a specialist would always have better outcomes than patients who were not. Thus, any increase in the number of alerts that we simulated would also increase the number of patients referred to a specialist, and since the specialist had unlimited capacity under this experimental setting, this would always result in better outcomes for patients.

Fig. 4.

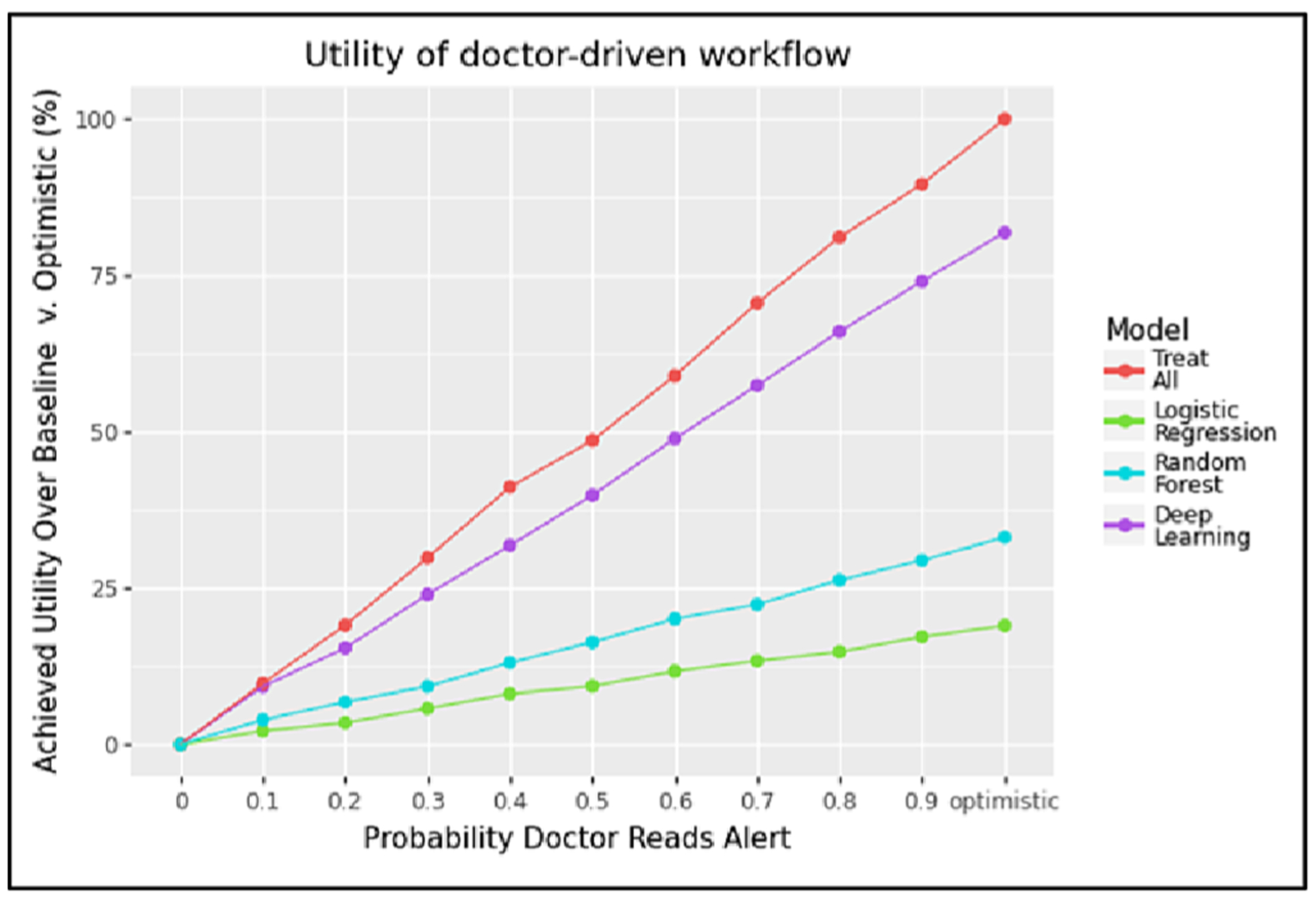
This plot shows the utility achieved by the doctor-driven workflow across different levels of alert fatigue using a model cutoff threshold of 0.5, assuming unlimited specialist capacity.

4.2. Simulating finite downstream specialist capacity

A more realistic setting is a downstream cardiovascular specialist with finite capacity. Thus, we repeated the above experiments under the assumption that our specialist could see a maximum of 2 referred patients per day.

(A). Nurse-driven workflow:

Though the deep learning model still shows the strongest performance of all treatment strategies across all nursing capacity levels, its achievable utility caps out at a nurse capacity of 3 patients per day. This is because the downstream specialist’s capacity is the limiting factor capping the achievable utility of the model. Thus, a policymaker deciding how to staff a nursing-driven workflow in which the downstream cardiovascular specialist can only see 2 patients per day could feel comfortable with staffing to a capacity of 3 patients per day, regardless of how many patients might be flagged by the model.

We see this clearly in Fig. 5. The thresholded screening strategy is shown in the far-left panel and shows that the deep learning model (purple line) yields high improvements in utility over alternative treatment strategies. However, this difference quickly becomes negligible at higher nurse capacity levels (e.g. > 3 patients per day). This is the opposite of the conclusion that we had previously reached under an unlimited capacity setting. There, we found that the deep learning model’s advantage grew as the nursing team’s capacity grew. This example illustrates the importance of factoring in capacity constraints when evaluating models, as they can substantially distort the incremental gain of increasing resource allocation to act on a model’s output.

Fig. 5.

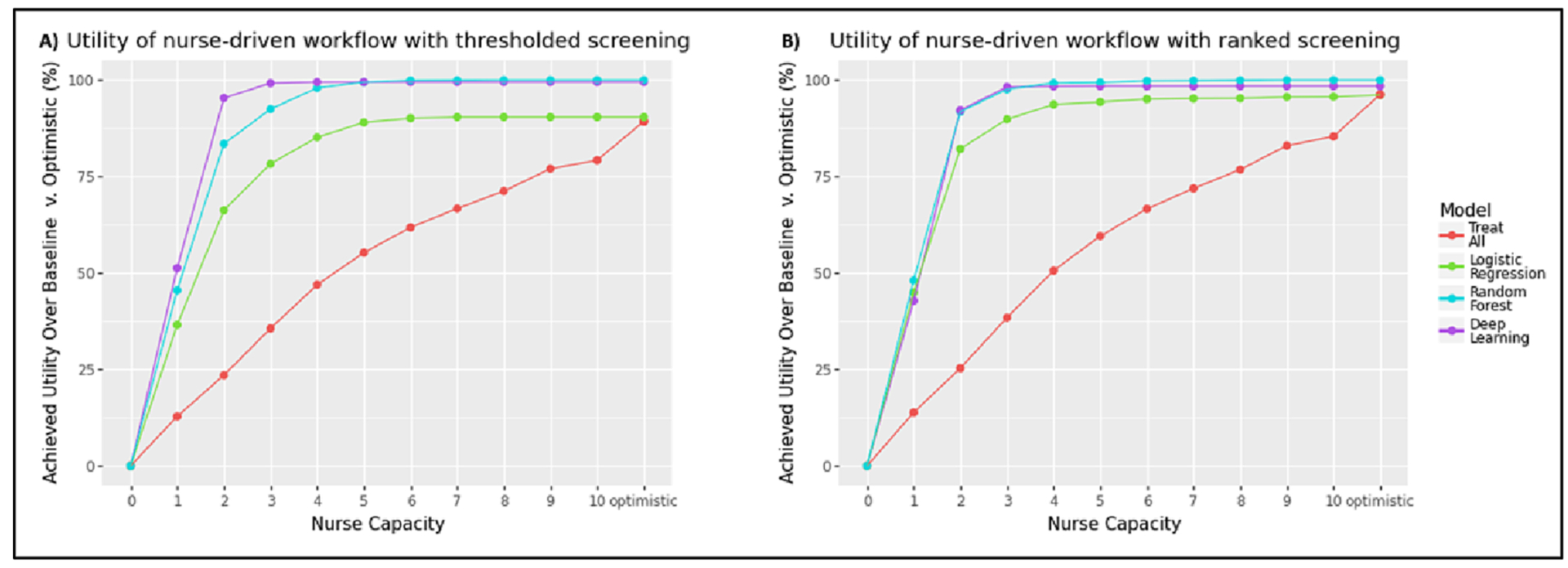
(a) Utility achieved by the nurse-driven workflow under thresholded screening across different nurse capacities using the optimal model cutoff threshold. (b) Utility achieved by the nurse-driven workflow under ranked screening across different nurse capacities. We see that the achievable utility of all models is unaffected by increases in nurse capacity beyond 3–4 nurses. All plots assume a specialist capacity of 2 patients/day.

This result is replicated under the ranked screening strategy in Fig. 5b which shows that the ML models do not exhibit substantially different achieved utility across potential nurse capacities. This is similar to the parity across models that we observed in our analysis of unlimited specialist capacity when considering low-resource nursing teams.

(B). Doctor-driven workflow:

In the case of the doctor-driven workflow, Fig. 6 shows strong differentiation across all three ML models in the limited specialist setting. However, we now see that the deep learning model (purple line) achieves a higher relative utility than the Treat All (red line) strategy once the probability of an alert being read is above 0.4. This can be explained as follows. When doctors are more likely to respond to alerts, more patients will be referred to the specialist, but the specialist will have to turn people away because of the specialist’s limited capacity (set to 2 patients/day in this experiment). Thus, ensuring that we only send patients who are likely to have PAD to the specialist becomes more important as doctors become increasingly willing to act on the alerts they see (and thus exceed the capacity of the specialist to handle referrals). The accuracy of the model therefore has more influence on the workflow’s utility as the probability increases that a doctor reads an alert. In our case, the deep learning model had the best predictive performance, hence the utility when using this model was greatest at higher levels of alert responsiveness.

Fig. 6.

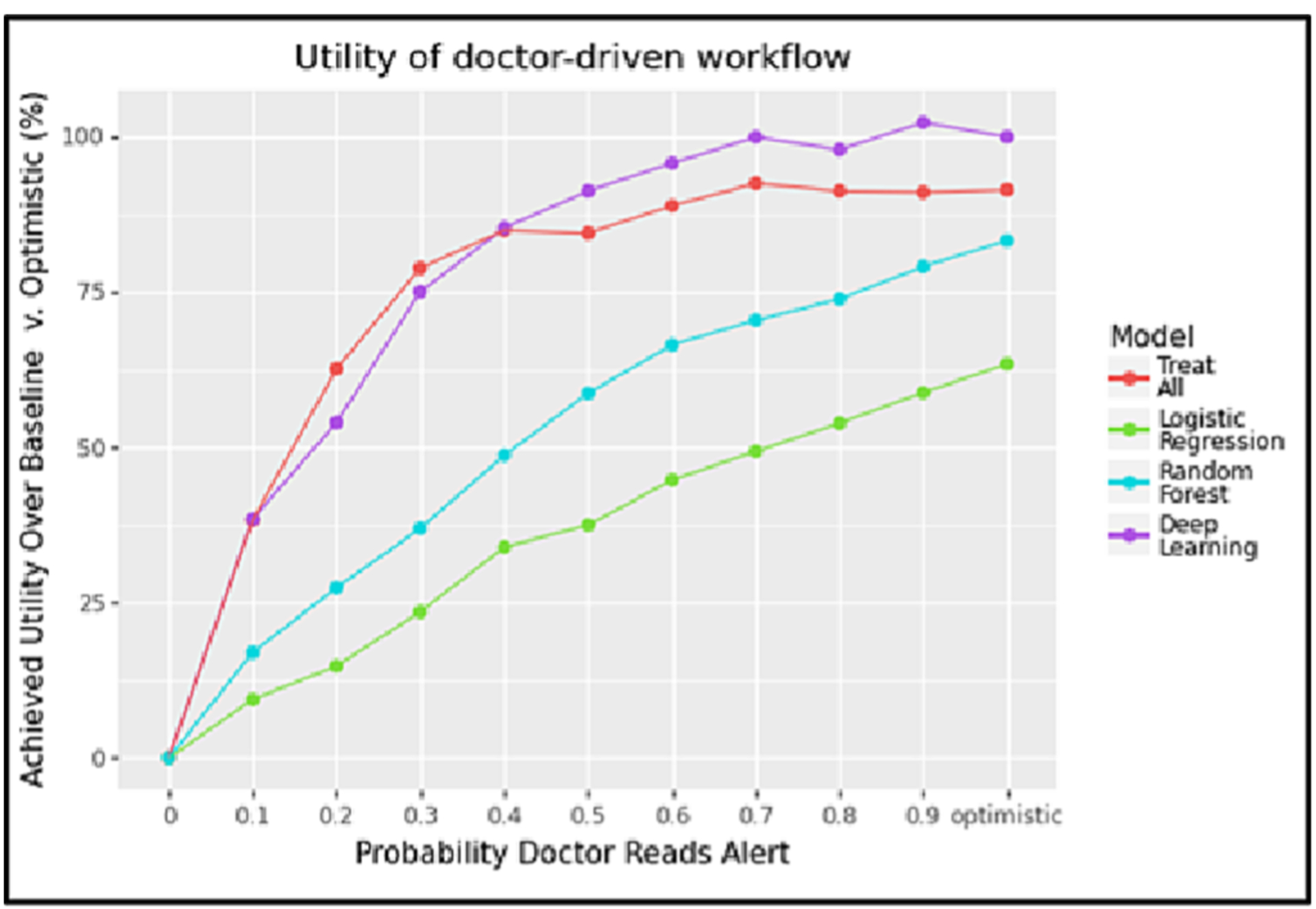
This plot shows the utility achieved by the doctor-driven workflow across different levels of alert fatigue using a model cutoff threshold of 0.5, assuming a specialist capacity of 2 patients/day.

4.3. Comparing the two proposed integration pathways

Given the results of our first two analyses, which demonstrated the superiority of the deep learning model, the next question we aimed to answer was which of the two workflows offered the optimal deployment strategy for the model. For this experiment, we focused on quantifying the trade-off between nursing capacity and alert fatigue, as this was the primary question that came up in our conversations with clinicians. Our guiding question was as follows: How many patients would a staff of nurses need to screen per day to have the nurse-driven workflow yield the same expected utility as a doctor-driven workflow with a given level of alert fatigue?

To answer this question, we used APLUS to measure the deep learning model’s achieved utility under different nurse capacities (using a ranked screening strategy) and compared this against the utility achieved under the doctor-driven workflow as the probability that doctors read alerts increased (where an alert was generated if the predicted probability of PAD for a patient was ≥ 0.5). We then subtracted the latter from the former to calculate the incremental gain in achievable utility that could be expected by adopting the nurse-driven workflow at that capacity level over a doctor-driven workflow at that alert fatigue level. We plotted the results as a heatmap in Fig. 7, under the assumption that the downstream specialist can see 5 patients per day. The y-axis is the nursing capacity that a cell’s utility value is calculated at, while the x-axis shows the level of alert fatigue in the doctor-driven workflow that corresponding to that cell’s measurement. Red squares (positive numbers) indicate that the nurse-driven workflow is expected to yield more utility at that capacity level than the corresponding doctor-driven workflow, while blue squares (negative numbers) indicate that the doctor driven workflow should be preferred. This allows a policymaker to quickly determine what nurse capacity is required for the nurse-driven workflow to have a greater expected utility than the doctor-driven workflow with a given level of PAD alert acceptance.

Fig. 7.

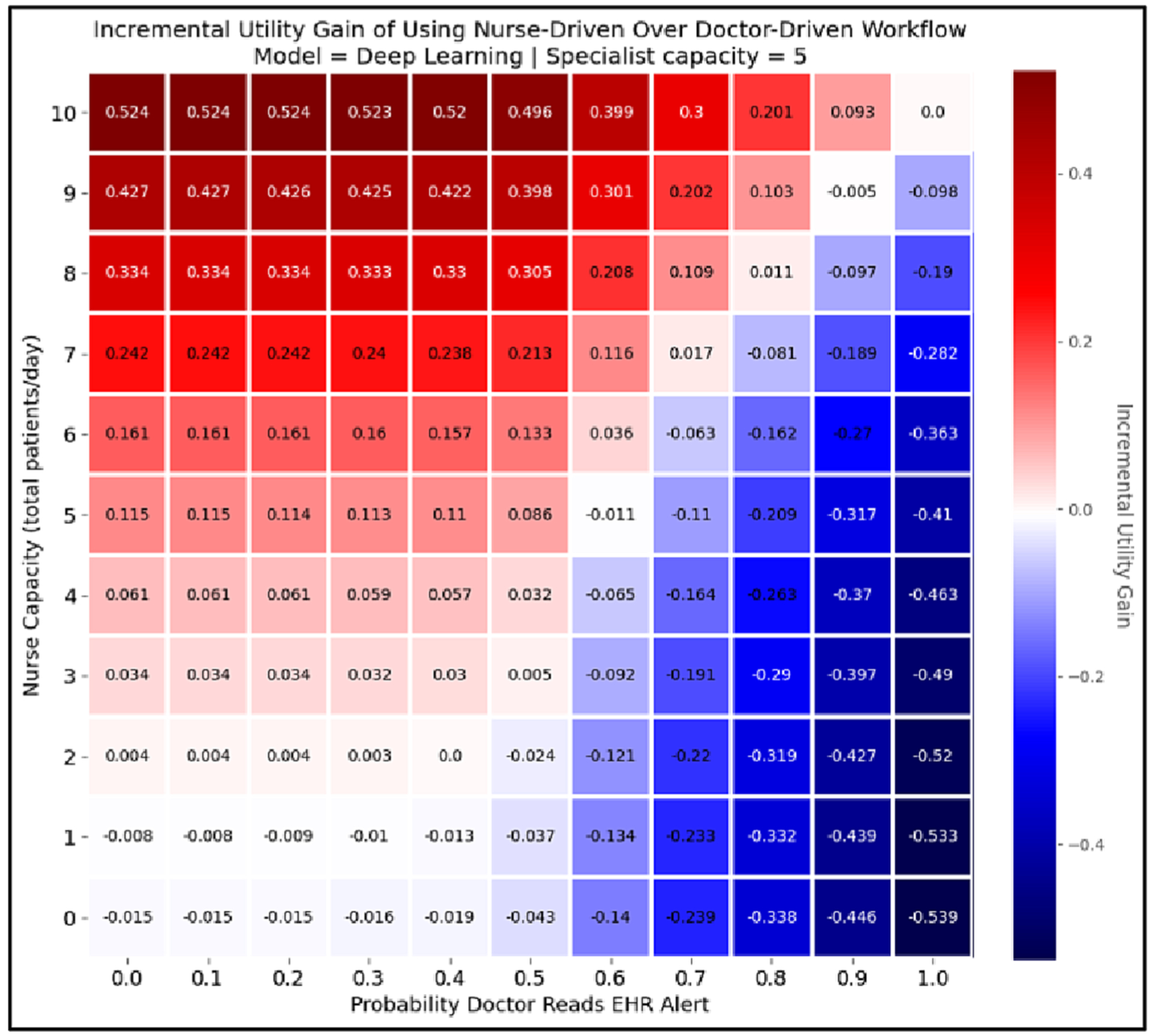
This heatmap shows the incremental gain from using the nurse-driven workflow over a doctor-driven workflow at a given capacity level for each workflow, assuming a specialist capacity of 5 patients/day. The y-axis represents capacity for the nurse-driven workflow, and the x-axis represents the probability that a doctor reads an EHR alert in the doctor-driven workflow. The value of the cell at coordinates (i, j) in the heatmap shows the incremental gain in achievable utility that can be expected by using a nurse-driven workflow with capacity i instead of a doctor-driven workflow with an alert fatigue level of j. Thus, positive numbers (i.e. red cells) indicate that the nurse-driven workflow is preferable to the doctor-driven workflow at their corresponding capacity levels, while negative numbers (i.e. blue cells) are situations in which the doctor-driven workflow should be preferred. That is why the top rows, which show nurse capacity at its highest, are dark red, while the farright rows, which represent the highest probability that doctors read their EHR alerts, are dark blue.

5. Discussion

We have demonstrated the use of APLUS to quantify the relative utility achieved by using the three ML models proposed in Ghanzouri et al. 2022 to drive two possible workflows for PAD screening [34]. In our evaluation of these models, we factored in the consequences of the downstream patient care decisions that they enabled, as well as the impact of resource constraints on their usefulness. Our results affirm that the deep learning model results in the largest gains in relative utility compared to the other proposed models under certain workflow settings, but we also found that constraints on the capacity of a cardiovascular specialist to handle referrals can create a hard bound on the achievable utility of a model-guided screening workflow. Our simulations also helped to quantify the trade-off between choosing a nurse-driven v. doctor-driven workflow for model implementation. Specifically, we investigated the impact of screening capacity on the nurse-driven workflow and the impact of alert fatigue on the doctor-driven workflow. We identified the conditions under which one of these integration pathways yields higher expected utilities, and thus greater usefulness, via a sensitivity analysis of nurse capacity and alert fatigue.

The plots generated by APLUS can help to quantify the expected utility that can be achieved by deploying each of the three ML models into one of the two workflows considered. This yielded insights that were not readily apparent by simply looking at ROC curves – namely, the parity across models in low-capacity settings for the nurse-driven workflow (in which case the simpler/more explainable model, logistic regression, may be preferable given its identical performance to the opaque deep learning model), the significantly higher utility unlocked by the deep learning model in the doctor-driven workflow (especially at lower levels of alert fatigue), and the incremental value of using one workflow over the other at different capacity levels as shown in the heatmap of Fig. 7. All of these utility-based results depended on simulating both the model and its surrounding workflow via APLUS, and could not have been determined via traditional ML evaluation metrics like AUROC.

Though we focus on PAD screening as a case study, APLUS generalizes to a broader range of ML models and decision support situations. APLUS can simulate any scenario involving a machine learning model to classify or predict patient state that meets two conditions: (i) the clinical workflow of interest can be represented as a set of states and transitions (i.e. a finite state machine), and (ii) there is a cohort of patients with their associated ML model outputs available as input to APLUS.

To assess the generalizability of our approach, we also conducted APLUS usefulness simulations for another care delivery workflow that had been previously evaluated in terms of clinical utility – a model-guided workflow for prioritizing advance care planning (ACP) consultations [9]. We were able to successfully replicate the results of the previous study’s analyses (for brevity, results are not shown; the code is available at the APLUS GitHub repository). The primary differences between the ACP use case and the PAD screening use case are that the model used for the ACP use case is a mortality prediction model (its output is a probability of death 3–12 months in the future for an individual patient) rather than a PAD classification model, and the clinical workflow triggered by model output differs as well (see [9] for ACP workflow details).

The process for conducting the ACP usefulness assessment was very similar to that for the PAD screening use case. The ACP workflow, defined via interviews with clinicians, was converted into the APLUS specification language, utilities were sourced from the palliative care literature, and a dataset of patients and their associated mortality model predictions were acquired from the original authors of the ACP machine learning model. Any one of these steps may present a challenge when simulating other workflows using APLUS: utilities can be hard to quantify, workflow steps may be vaguely defined, or the ML model may be inaccessible to researchers.

Additionally, we performed custom analyses to evaluate the effect of alternative care pathways for ACP on the model’s usefulness. For an informatician applying APLUS to their own model-guided workflow, writing such custom analyses will likely require additional effort. This is both a limitation and strength of APLUS – APLUS can support arbitrary downstream analyses because it imposes minimal assumptions on the workflow simulations, which comes with the tradeoff of requiring additional custom tuning to support specific use cases.

The design of our workflow specification language has several key strengths. First, unlike prior usefulness assessments which directly hardcoded the structure of the workflow into the simulation and analysis logic [9,31,32], APLUS explicitly separates the act of defining a workflow from the act of simulating and analyzing it. This facilitates interoperability between APLUS and existing analysis pipelines with minimal code refactoring. Additionally, APLUS logs the entirety of each patient’s trajectory such that their journeys can be reconstructed post hoc, which enables arbitrary downstream analyses without the need to re-run the simulation. Second, our simulation engine can simulate virtually any workflow that can be represented as a set of states and transitions in which a patient can only ever be in one state concurrently. The ability to specify many types of transition conditions allows APLUS to handle intricate branching logic within a workflow. Third, because APLUS simulates the actual trajectories of patients rather than simply representing patients/workflows as a set of equations, it supports more complex workflows, branching conditions, and probability distributions than would be feasible to analytically describe. Fourth, our specification language takes advantage of the expressivity that YAML enables, including human-readability, straightforward version control, minimal dependencies (e.g. just a text editor), and a simple interface for programmatically manipulating the settings of a workflow (e.g. any of the existing YAML-parsing libraries for Python). This allows an analyst to quickly generate and test many workflow variations. Fourth, APLUS supports the specification of variables (i.e. utilities and resource constraints) that have varying units. This enables the end user to simultaneously measure how quantities such as QALYs and dollars are impacted by a model-guided workflow, rather than having to conduct two separate simulations focused on each unit of measurement in isolation. This also helps to increase replicability by forcing the end user to be precise in how they define the properties of their workflow. Beyond the software that we have developed, another unique aspect of our work is our close collaboration with a clinician partner (ER) who was directly involved in designing the workflows that we simulated. This ensured that our experiments accurately reflected real-world care delivery pathways.

There are several limitations of our work. First, an analyst is still required to do the preliminary legwork of mapping out a care workflow’s steps. This is an inherently non-technical task which can represent a large bottleneck in the usefulness assessment process, because it requires either actively scheduling and conducting interviews with stakeholders and operations personnel [9], or automated process mining of clinical pathway patterns which requires detailed analysis of previously collected data/event logs [44,58]. To aid in this process mapping step, we recommend that analysts partner with members of a hospital’s operations, quality improvement, or business management offices. Second, because our framework makes minimal assumptions about the structure/length/design of the workflow being simulated, the end user must specify many detailed aspects of their workflow. While we do provide plausible defaults, this task can be time consuming for complex workflows and requires the informatician to decide on the proper level of simplification. Third, our choice of time-driven discrete-event-based simulation suffers from several known computational inefficiencies, such as a lack of parallelizability and inefficient modeling of longer time intervals, that can be addressed through further algorithmic refinement of our core simulation engine [35,59,60].

Our framework is general enough to assess a wide range of workflows, and we look forward to demonstrating the full depth of APLUS’s capabilities by applying it to future usefulness assessments. By reducing the need to write bespoke scripts, our work can help to accelerate and systematize this process across health systems. At Stanford Health Care, this work is one component of a larger effort to develop a delivery science for fair, useful, and reliable adoption of models to guide care management workflows [61]. Accomplishing this goal requires automated methods such as APLUS.

More broadly, we aim for our research to be useful for both large health systems with expertise in ML deployments, as well as health systems without much experience. At academic medical centers which aim to conduct usefulness assessments across dozens of models, our tool can help to systematize and scale this evaluation process [61,62]. For health systems with more limited resources and less expertise in ML, the availability of an off-the-shelf tool like APLUS which can readily quantify the benefit of investing in the implementation of an ML model may encourage funding its development.

6. Conclusion

We have presented APLUS, a framework for conducting usefulness assessments of ML models that considers the properties of the care workflows that they drive. We applied APLUS to yield implementation insights for a new care delivery workflow – the early screening of PAD via machine learning. More broadly, our simulation engine can assist in understanding the usefulness of model-guided care prior to committing to deployment. We hope that our library enables other researchers to study a wide range of workflows, thereby deepening our field’s understanding of the impact of workflow constraints on ML model usefulness in healthcare.

Statement of Significance.

Problem	The adoption of ML models into clinical workflows is lacking because traditional ML evaluation metrics fail to accurately assess how useful a model will be in practice.
What is Already Known	Prior work has simulated individual model impact in the context of specific care delivery workflows. However, these efforts have limited generalizability to other models/workflows and exhibit overreliance on non-modifiable assumptions.
What This Paper Adds	Our contribution builds on prior work through the development of a flexible, reusable set of methods that allow for the systematic quantification of the usefulness of ML models by simulating their corresponding care management workflows. The APLUS library can help hospitals to better evaluate which models are worthy of deployment and identify the best strategies for integrating such models into clinical workflows.

Appendix A.

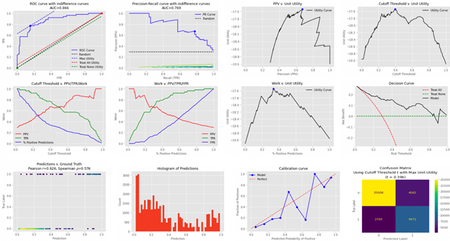
A set of plots that are automatically generated by APLUS to measure a 12-month all-cause mortality model’s predictive performance and theoretical utility.