Quantifying the fraction of new mutations that are recessive lethal

Abstract

The presence and impact of recessive lethal mutations have been widely documented in diploid outcrossing species. However, precise estimates of the proportion of new mutations that are recessive lethal remain limited. Here, we evaluate the performance of Fit∂a∂i, a commonly used method for inferring the distribution of fitness effects (DFE), in the presence of lethal mutations. Using simulations, we demonstrate that in both additive and recessive cases, inference of the deleterious nonlethal portion of the DFE is minimally affected by a small proportion (<10%) of lethal mutations. Additionally, we demonstrate that while Fit∂a∂i cannot estimate the fraction of recessive lethal mutations, Fit∂a∂i can accurately infer the fraction of additive lethal mutations. Finally, as an alternative approach to estimate the proportion of mutations that are recessive lethal, we employ models of mutation–selection–drift balance using existing genomic parameters and estimates of segregating recessive lethals for humans and Drosophila melanogaster. In both species, the segregating recessive lethal load can be explained by a very small fraction (<1%) of new nonsynonymous mutations being recessive lethal. Our results refute recent assertions of a much higher proportion of mutations being recessive lethal (4%–5%), while highlighting the need for additional information on the joint distribution of selection and dominance coefficients.

Introduction

Since the early days of genetics, it was noted that it was often not possible to make a chromosome homozygous in a Drosophila cross. This inability to make a chromosome homozygous was taken as evidence that it carried a recessive lethal mutation in the heterozygous state that resulted in death or sterility when made homozygous (Dobzhansky et al., 1954; Dubinin, 1946). Through further study, approximately 20%–40% of Drosophila melanogaster autosomes sampled from natural populations could not be made homozygous, implying approximately 1.6 recessive lethal mutations per diploid genome (Lynch & Walsh 1998; Simmons & Crow, 1977). Similar estimates of ~1–2 recessive lethals per diploid genome have also been obtained from natural zebrafish and bluefin killifish populations, despite these species having genome sizes an order of magnitude larger than D. melanogaster (Halligan & Keightley, 2003; McCune et al., 2002). Together, these studies suggest that the recessive lethal load may be relatively constrained across species.

Obtaining estimates of the number of segregating recessive lethals in humans has required more indirect approaches, given that humans are not amenable to experimentation. In the 1950s, Morton et al. found that the rate of juvenile mortality in humans increased with increasing relatedness between an individual’s parents (Morton et al., 1956). Such studies have revealed that humans typically carry 1.4 diploid lethal equivalents or mutations that would result in a genetic death if made homozygous (Bittles & Neel, 1994). This estimate may therefore represent an upper bound on the number of recessive lethals, as the total number of lethal equivalents in a genome represents the cumulative effect of all recessive deleterious mutations in a genome (Morton et al., 1956). More recently, an elegant study combined the observed incidence of recessive lethal disease in a founder population with pedigree records and simulations to more directly estimate the number of recessive lethal mutations carried by the founders (Gao et al., 2015). They inferred that each founder carried ~0.6 recessive lethal mutations; however, they note that this may be a slight underestimate (Gao et al., 2015). Thus, available evidence suggests that humans have a recessive lethal load that is similar to estimates from other species.

Separately from this work, a growing number of studies have attempted to use genetic variation data to estimate the distribution of fitness effects of new mutations (DFE) in humans and other species. This distribution quantifies the expected effects on fitness of new mutations entering a population, including lethal mutations. In other words, it is the distribution of selection coefficients (s) for new mutations at sites of a particular type in the genome (e.g., nonsynonymous mutations). This approach has been implemented in a number of software programs (Boyko et al., 2008; Eyre-Walker et al., 2006; Keightly & Eyre-Walker, 2007; Tataru et al., 2017), including Fit∂a∂i (Kim et al., 2017). Fit∂a∂i relies on genetic variation data from resequencing of individuals from natural populations, which is summarized by the site frequency spectrum (SFS), that is, the numbers of variants with particular frequencies in the sample. The parameters of the DFE are then estimated using population genetic models of mutation, selection, and demography that match this observed SFS. Methods based on the SFS have been used to infer the DFE from numerous taxa including prokaryotes (Cavassim et al., 2021), C. elegans (Gilbert et al., 2022), yeast (Elyashiv et al., 2010; Huber et al., 2017; Koufopanou et al., 2015), Drosophila (Campos et al., 2014; Castellano et al., 2015; Huang et al., 2021; Huber et al., 2017; Keightley & Eyre-Walker, 2007), Arabidopsis (Huber et al., 2018; Moutinho et al., 2019), primates (Castellano et al., 2019; Galtier, 2016; Hvilsom et al., 2012; Ma et al., 2013), and humans (Eyre-Walker & Keightley, 2009; Boyko et al., 2008; Eyre-Walker et al., 2006; Huang et al., 2021; Kim et al., 2017; Li et al., 2010). Estimates of the DFE for nonsynonymous mutations in humans suggest that there are many nearly neutral mutations (e.g., 32% of mutations were estimated to have s > −10⁻⁴ by Kim et al., 2017). The proportion of strongly deleterious mutations (s < −10⁻²) has varied across studies, ranging from ~25% to 35% of mutations (Boyko et al., 2008; Eyre-Walker et al., 2006; Kim et al., 2017). Importantly, recent studies using larger sample sizes have suggested that the proportion of very strongly deleterious mutations (s < −0.1) is very small (e.g., Kim et al., 2017 estimated ~3%).

Studies of the DFE from approaches like Fit∂a∂i that use genetic variation from natural populations summarized by the SFS have several limitations. First, inferences conducted to date typically assume that the effects of deleterious mutations, including strongly deleterious ones, are additive (h = 0.5, though see Huber et al., 2018). This is largely due to computational convenience and the challenges in separately inferring dominance and the DFE using data from a single population as the SFS may not contain sufficient information regarding both parameters (Boyko et al., 2008; Ragsdale, 2022). Second, the genetic variation data in a sample of hundreds or fewer individuals from the population largely consists of weakly deleterious or neutral variation, as strongly deleterious mutations are unlikely to be segregating in samples of modest size (Kim et al., 2017). Instead, the inferences made about the proportions of strongly deleterious mutations are informed by the absence of genetic variation expected under the particular mutation rate and demographic history and the functional form of the DFE assumed (Bank et al., 2014). Indeed, recent studies have suggested that the proportion of strongly deleterious mutations may have been underestimated by SFS-based approaches applied to data sets of less than thousands of individuals (Dukler et al., 2022; Galtier & Rousselle, 2020; but also see Charmouh et al., 2022). Thus, the SFS-based methods to infer the DFE may not give a complete picture of the proportion of lethal and near-lethal mutations.

The extent to which these limitations impact inference of the DFE and the proportion of recessive lethal mutations from molecular population genetic data remains unclear. Indeed, several studies have questioned the accuracy of DFE inference methods from population genetic data using samples from hundreds of individuals. It has been claimed (Kardos et al., 2021; Pérez-Pereira et al., 2022) that not only are strongly deleterious mutations missed by the molecular genetic approaches, but also the proportion of weakly deleterious and nearly neutral mutations has been overestimated in studies of the DFE (Kim et al., 2017). Furthermore, studies have claimed that there may be a higher proportion of lethal or near-lethal new mutations in a variety of organisms. For example, Kardos et al. (2021) proposed a DFE where 5% of deleterious mutations are recessive lethal and ~21% have s < −0.1. Similarly, Pérez-Pereira et al. (2022) proposed a DFE where ~4% of deleterious mutations are recessive lethal and ~41% have s < −0.1. Importantly, both of these DFEs were not directly estimated from data, but were instead loosely based on results from mutation accumulation experiments in Drosophila (Kardos et al., 2021; Pérez-Pereira et al., 2022). Moreover, recent work has found that the models proposed by Kardos et al. (2021) and Pérez-Pereira et al. (2022) are not consistent with patterns of genetic variation or estimates of the number of segregating recessive lethals in humans (Kyriazis et al., 2022).

Given these disparate claims regarding the proportion of strongly deleterious and lethal mutations, there is a critical need to test the performance of molecular estimates of the DFE and to develop better estimates. Here we take two steps in that direction by first testing the performance of one SFS-based approach, Fit∂a∂i (Kim et al., 2017), in the presence of lethal mutations using simulated genetic variation data, and second, developing an alternative approach for quantifying the fraction of new mutations that are recessive lethal. We find that Fit∂a∂i is unable to accurately infer the simulated fraction of recessive lethals when performing inference under an additive model, as expected, given the misspecification of the dominance model. However, we find that Fit∂a∂i can accurately estimate the simulated fraction of additive lethal mutations. Moreover, in both the recessive and additive case, a small proportion (<10%) of lethal mutations does not greatly affect inference of the nonlethal portion of the DFE. Finally, mutation–selection–drift balance models in concert with estimates of segregating recessive lethals in humans and D. melanogaster suggest that a very small fraction of mutations (<1%) in humans and D. melanogaster are likely to be recessive lethal. Our work suggests limits on the proportion of mutations that are recessive lethal, which has implications for studying inbreeding depression in a variety of species.

Materials and methods

Simulations

We used the forward-in-time simulator SLiM 3 (Haller & Messer, 2019) to generate genetic variation data sets (Supplementary Figure S1). For each simulation replicate, we modeled a 100 Mb chromosomal segment with randomly placed genic regions comprising ~1.5% (or ~1.5 Mb) of the total chromosome. The length of intervening noncoding regions was modeled using a uniform distribution between 500 and 50,000 bp. Within each coding region, we modeled deleterious (nonsynonymous) and neutral (synonymous) mutations occurring at a ratio of 2.31:1 (Huber et al., 2017). To maintain computational efficiency, we did not model neutral mutations occurring in noncoding regions.

We simulated from a bimodal DFE for deleterious mutations, with nonlethal mutations arising from a gamma distribution and lethal mutations arising with a fixed selection coefficient s = −1.0. The parameters of the gamma distribution were based on estimates from the 1000G European population consisting of a mean s = −0.0131 (where s here reflects the reduction in fitness in the homozygote) and shape parameter of 0.186 (Kim et al., 2017). We assumed varying levels of lethal mutations of 0%, 1%, 5%, and 10%. For example, in the case of 5% lethals, selection coefficients for 95% of nonsynonymous mutations were drawn from the gamma distribution and the remaining 5% were set to have a selection coefficient s = −1.0 (see Supplementary Table S1). All mutations arising from the gamma distribution were assumed to be additive (h = 0.5), whereas lethal mutations were assumed either to be additive or fully recessive (h = 0.0). Assuming nonlethal mutations are additive is a reasonable first approximation as evidence suggests more strongly deleterious mutations are the ones that are more likely to be most recessive and more weakly deleterious mutations tend to have more additive effects on fitness (Agrawal & Whitlock, 2011). For all simulations, we assumed a mutation rate of 1.5 × 10⁻⁸ per site per generation as in Ségurel et al. (2014) and uniform recombination rate of 1.0 × 10⁻⁸ crossover events per site per generation (Kong et al., 2010). We assumed a constant effective population size (N_e) of 10,000 diploid individuals for all simulations. We ran burn-ins for 10 ×N_e generations to attain equilibrium prior to outputting the SFS.

From each simulation, we computed both deleterious (nonlethal and lethal) and neutral site frequency spectra (SFS) from sample sizes of 10, 100, and 1,000 haploid genomes independently. To obtain SFS with a sufficient number of SNPs and to mimic a human exome, we ran 30 simulation replicates for each set of parameters and summed the SFS across replicates. This procedure yielded a total of ~44 Mb of total coding sequence for resulting neutral and deleterious SFS, which were then used for downstream demographic and the DFE inference, respectively. To explore the impact of simulation variance, we ran 20 total replicates (each resulting in an SFS for ~44 Mb of coding sequence) for each parameter combination and conducted independent demographic and DFE inference with ∂a∂i (Gutenkunst et al., 2009) and Fit∂a∂i (Kim et al., 2017) on the resulting SFS. A schematic figure of our simulation and inference pipeline is shown in Supplementary Figure S1.

DFE inference

We used the software ∂a∂i (Gutenkunst et al., 2009) and Fit∂a∂i (Kim et al., 2017) to infer the distributions of selection coefficients of new mutations from the simulated data. Fit∂a∂i and ∂a∂i rely on the Poisson random field model of the SFS (Sawyer & Hartl, 1992; Sethupathy & Hannenhalli, 2008). Because both demography and selection change allele frequencies, but we are only interested in quantifying the effects of selection, we accounted for demography by first inferring the demographic parameters (see Supplementary Table S2) using the putatively neutral synonymous sites (the synonymous SFS) with ∂a∂i. We found the demographic parameters that maximized the likelihood (i.e., the maximum likelihood estimates, MLEs) given the data after 30 iterations. Conditioning on resulting demographic parameters, we then inferred selection parameters (DFE) from the nonsynonymous SFS using Fit∂a∂i. Importantly, by default and as run in our study, Fit∂a∂i assumes that all mutations have an additive effect on fitness (h = 0.5). As such, in simulations with recessive lethal mutations, the model that is fit to the data is the incorrect model, allowing us to test the robustness of Fit∂a∂i to model misspecification. We also collected only MLEs of selection parameters after 30 iterations. Detailed information about the methodology used to infer the DFE and demography is provided in Kim et al., (2017) and Gutenkunst et al. (2009).

Fitting the gamma distribution

To assess Fit∂a∂i’s performance on simulated data, we first inferred the DFE under a gamma distribution. We then calculated the proportion of mutations in different categories of selection coefficient (s) by discretizing the gamma distribution into five bins based on the strength of selection coefficients as neutral $(\left|s\right|=[0,{10}^{-5}))$, nearly neutral $(\left|s\right|=[{10}^{-5},{10}^{-4}))$, slightly deleterious $(\left|s\right|=[{10}^{-4},{10}^{-3}))$, moderately deleterious $(\left|s\right|=[{10}^{-3},{10}^{-2}))$, and strongly deleterious $(\left|s\right|=[{10}^{-2},1])$.

Fitting mixture distributions

We also inferred DFEs from the simulated data using Fit∂a∂i assuming distributions other than a gamma distribution. Specifically, we modeled the DFE using a mixture of distributions as described in Kim et al. (2017): (a) Neu+Gamma: a gamma distribution with a proportion of neutral mutations with s uniformly distributed in the range $\left|s\right|=[{10}^{-2},1]$, (b) Gamma+Let: a gamma distribution with a proportion of lethal mutations with s uniformly distributed in the range $\left|s\right|=[0,{10}^{-4}]$; and (c) Neutral+Gamma+Let, a gamma distribution with a proportion of neutral (|s| = [0, 10⁻⁴]) and lethal mutations (|s| = [10⁻², 1]). We assessed whether more complex models provided a better fit to the SFS than the simple gamma distribution using a likelihood ratio test (LRT). The LRT statistic was calculated as $\mathrm{\Lambda }=2(l{l}_{complex}-l{l}_{simple})$, where $l{l}_{complex}$ represents the log-likelihood for the complex DFE and $l{l}_{simple}$ represents the log-likelihood for the gamma distribution in all cases. Because the SNPs in our data set may be correlated with each other due to linkage, we did not rely on the asymptotic theoretical distribution of $\mathrm{\Lambda }$ under the null. Instead, we simulated 40 test data sets under the null (where the true DFE follows a gamma distribution). For each data set, we fit the gamma DFE and the more complex DFEs. We then computed $\mathrm{\Lambda }$ for each data set and used the 95th percentile of the distribution of $\mathrm{\Lambda }$ as the critical value. We then used those critical values to decide whether to reject the gamma model in favor of the more complex model (Table 1). Thus, the LRTs used here account for linkage among SNPs.

Table 1.

Inference of p̂_let and model selection assuming different distributions of fitness effects when simulating varying proportions of lethal mutations.

Dominance of lethals	True lethal Prop. (plet)	Average MLE of p̂let	Proportion of data sets where Gamma+Let fits significantly better than Gammaa	Proportion of data sets where Neu+Gamma fits significantly better than Gammaa	Proportion of data sets where Neu+Gamma+Let fits significantly better than Gammaa
Recessive (h = 0)	0	0.018	0.00	0.00	0.00
	0.01	0.015	0.05	0.00	0.05
	0.05	0.012	0.00	0.35	0.05
	0.1	0.002	0.00	0.90	0.55
Additive (h = 0.5)	0	0.021	0.10	0.00	0.10
	0.01	0.030	0.25	0.00	0.10
	0.05	0.063	0.85	0.00	0.60
	0.1	0.107	1.00	0.00	1.00

Note. Results are reported assuming a nonsynonymous to synonymous sequence length ratio (L_NS/L_S) of 2.31:1, mutation rate (μ) = 1.5 × 10⁻⁸, and 1,000 simulated haploid genomes. For each DFE, 20 replicates were simulated.

^aA likelihood ratio test was used to assess whether the more complex model fits significantly better than the Gamma DFE. The 5% critical values for rejecting the null were found using the empirical distribution from the null simulations (p_let = 0). The critical values were 20 for the Gamma+Let versus Gamma and the Neu+Gamma+Let versus Gamma comparisons. For the Neu+Gamma versus Gamma comparison, the critical value was 5. Note that models with a Let parameter tend to fit better when a large proportion of additive lethals (5% or 10%) are simulated.

Profile log-likelihood of the proportion of lethal mutations

To infer the proportion of lethal mutations using Fit∂a∂i, we performed a composite log-likelihood profile under the Gamma+Let model. To this end, we fixed the proportion of lethal mutations $(p_{let})$ at a given value (ranging from 0 to 0.5) and allowed Fit∂a∂i to infer the other parameters of the DFE (a, β) under the Gamma+Let distribution. For each simulated data set, we then found the value of $p_{let}$ that had the highest log-likelihood, and thus was the MLE. Note that this analysis assumes that mutations are all unlinked. However, in reality and in our simulated data, deleterious variants may be linked. As such, these curves are composite profile likelihoods and cannot be directly used to compute confidence intervals.

Estimating the proportion of lethals through mutation–selection–drift balance

In addition to attempting to infer p_let via Fit∂a∂i using the SFS, we considered a second complementary approach. Specifically, we used mutation–selection–drift balance models coupled with estimates of segregating recessive lethals to estimate the fraction of new mutations that are recessive lethal in humans and in Drosophila melanogaster, following the approach from Amorim et al. (2017). Our aim with this model was to determine what fraction of new nonsynonymous mutations would need to be recessive lethal to explain empirical estimates of the number of segregating recessive lethals per diploid in humans and D. melanogaster. Specifically, this approach leverages the result from Nei (1968) showing the mean stationary distribution of the frequency of a recessive lethal mutation (q) can be related to the mutation rate (µ) and effective population size (N_e):

$${\displaystyle \begin{array}{l}{\displaystyle q\approx \mu \sqrt{2\pi N_e}.}\end{array}}$$ (1)

This formula yields the mean allele frequency in the population at a single locus (q), whereas estimates of segregating recessive lethals for humans and D. melanogaster are genome-wide for a given individual. Assuming that lethal mutations only exist at nonsynonymous sites, no linkage across sites, and that a diploid individual is formed as a random sample of two alleles from the population at each locus, Equation 1 can be extended to model the number of recessive lethal mutations carried per individual (R):

$${\displaystyle \begin{array}{l}{\displaystyle R\approx 2\mu L{P}_n{p}_{let}\sqrt{2\pi N_e}}\end{array}}$$ (2)

where L is the length of the coding sequence for each species, P_n is the proportion of the coding sequence leading to nonsynonymous mutations (Supplementary Table S3), and p_let is the proportion of recessive lethal mutations. We then assessed the proportion of mutations that would need to be recessive lethal (p_let) to explain observed numbers of segregating lethal mutations (R).

To apply this approach for humans, we assumed a mutation rate of 1.5 × 10⁻⁸ per site per generation (Ségurel et al., 2014), coding sequence length of 30 Mb (Keightley, 2012), and NS:SYN ratio of 2.31:1 (Huber et al., 2017; see Supplementary Table S3 for all parameters). As this model assumes equilibrium and the human population size has experienced substantial exponential growth (Duchen et al., 2013; Gravel et al., 2011; Tennessen et al., 2012), we assumed a range of effective population sizes of N_e = {20,000, 30,000, 60,000}. These population sizes were selected based on simulations under a human demographic model suggesting that recessive lethal allele frequencies in modern human populations are approximated by an equilibrium effective population size on the order of 20,000–30,000 (see Results). However, to account for any potential underestimation of recent exponential growth, we also project model results assuming an equilibrium effective population size of 60,000. We compare predictions from all effective population sizes to a range of segregating recessive lethals of 0.6–1.6 lethals per diploid (Gao et al., 2015; Narasimhan et al., 2016). Although Narasimhan et al. (2016) estimated lethal loss-of-function equivalents––and not recessive lethals––we use their estimate as an upper bound, given that the 0.6 estimate from Gao et al. (2015) is likely a slight underestimate because embryonic lethals were not considered in their inference (Gao et al., 2015).

For D. melanogaster, we assumed a mutation rate of 3 × 10⁻⁹ per site per generation (Keightley et al., 2014; Sharp & Li, 1989), coding sequence length of 22 Mb (Kim et al., 2021), and NS:SYN ratio of 2.85:1 (Huber et al., 2017; see Supplementary Table S3 for all parameters). We explored model predictions for several effective population sizes including N_e = {5 × 10⁻⁵, 1 × 10⁻⁶, 5 × 10⁻⁶}, a range that encompasses existing estimates (H. Duchen et al., 2013; Huber et al., 2017; Li & Stephan, 2006; Sheehan & Song, 2016). We compared predictions from this model to an experimentally estimated range of segregating recessive lethals of 1–3 per diploid (Lynch & Walsh, 1998; McCune et al., 2002; Simmons & Crow, 1977).

To test how violations of mutation–selection–drift balance along with varying dominance coefficients affected inference of p_let, we carried out additional simulations under a nonequilibrium demographic model for humans. We focused on humans due to the large effective population size estimates for D. melanogaster (Duchen et al., 2013; Huber et al., 2017; Li & Stephan, 2006; Sheehan & Song, 2016), which are computationally infeasible for forward-in-time simulations. These simulations assumed a demographic model inferred by Kim et al. (2017) inferred based on the 1000G data set for the Europeans. This model assumes an ancestral N_e = 12,378 diploids, followed by a bottleneck to N_e = 1,048 for 248 generations, growth to N_e = 13,625 for 1,744 generations, and finally exponential growth to a final N_e = 657,719. We ran burn-ins at N_e = 12,378 for 1,000 generations, which was sufficient for recessive lethal mutations to reach equilibrium (Supplementary Figure S2). We assumed identical genomic parameters in these simulations as those used for our mutation–selection–drift balance analysis (Supplementary Table S3). To simulate 30 Mb of coding sequence, we modeled 22,500 genes occurring on 22 autosomes, each with a length of 1,340 bp (Keightley 2012). We assumed no recombination within each 1,340 bp gene and a recombination rate of 0.001 crossovers per bp per generation between genes.

Results

Testing the performance of Fit∂a∂i in the presence of recessive lethals

We focus first on the case of recessive lethals, specifically testing whether inferences of the DFE made using Fit∂a∂i are affected by the presence of recessive lethals and whether Fit∂a∂i can estimate the fraction of recessive lethals. In a sample of 1,000 haploid genomes from the population, we found that recessive lethal mutations are segregating in the sample if the proportion of recessive lethals is at least 5% (Supplementary Figure S3). Thus, we wanted to test whether the presence of these mutations affects DFE inference.

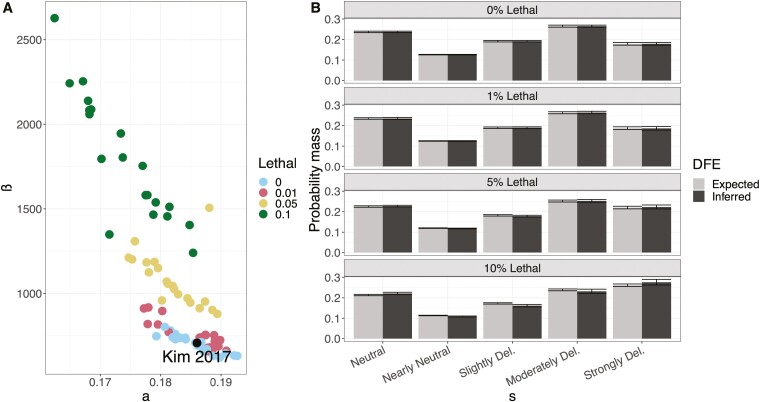
To infer the DFE from these simulated data, we used Fit∂a∂i (Kim et al., 2017). We initially performed inference assuming that the DFE follows a gamma distribution and that all deleterious mutations have an additive effect on fitness (h = 0.5), exploring how varying levels of simulated recessive lethals affect the inference of the shape (a) and scale (β) parameters of this distribution (see Methods, Figure 1A). The presence of recessive lethal mutations shifts the distributions of the estimates of the shape and scale parameters of the DFE (Figure 1A). However, the introduction of recessive lethals has a relatively small impact on the inferred proportions of mutations in each bin of the DFE (Figure 1B), with the largest deviation observed in simulations where 10% of mutations are recessive lethal. Specifically, for a model where 10% of mutations are recessive lethal, we infer a notable deficit of strongly deleterious variation relative to the true proportions (Figure 1B). This deviation is likely due to an excess of segregating variants relative to what is expected under a fully additive model (Supplementary Figure S4). In other words, recessive lethal mutations segregate at higher frequencies than expected under an additive model, and Fit∂a∂i therefore infers these mutations to have selection coefficients that are moderately deleterious, rather than lethal.

Figure 1.

Parameters of the gamma distribution and the inferred distribution of fitness effects (DFE) under different levels of recessive lethal mutations. (A) Inference of the shape (a) and scale (β) parameters under a gamma DFE model from simulated data with different levels of recessive lethals using 1,000 haploid genomes in each simulation. (B) Expected versus inferred DFE for each lethal percentage under a gamma DFE model. Percentages are increments of recessive lethal mutations. Expected and inferred site frequency spectra used to fit the model are presented in Supplementary Figure S4. The DFE categories are defined as neutral $(\left|s\right|=[0,{10}^{-5}))$, nearly neutral $(\left|s\right|=[{10}^{-5},{10}^{-4}))$, slightly deleterious $(\left|s\right|=[{10}^{-4},{10}^{-3}))$, moderately deleterious $(\left|s\right|=[{10}^{-3},{10}^{-2}))$, and strongly deleterious $(\left|s\right|=[{10}^{-2},1])$. Error bars correspond to the range of inferred proportions obtained across 20 simulation replicates.

Because sample size affects the ability to discriminate across different classes of mutations (Kim et al., 2017), we performed the DFE inference under two smaller sample sizes of 10 and 100 haploid genomes (Supplementary Figure S5). As expected, the decrease in sample size increases the observed variance in DFE estimates across simulated data sets (Supplementary Figure S5A). The inferred fraction of moderately and strongly deleterious mutations is especially variable, independent of the proportions of lethals added to the simulation (Supplementary Figure S5B). This result is a consequence of mutations with $\left|s\right|>{10}^{-3}$ being unlikely to segregate in smaller sample sizes, thus impeding inference of the true proportion of moderately and strongly deleterious mutations. Moreover, we observe the counterintuitive result that the inferred DFEs with small sample sizes are closer to the true DFEs in the presence of high levels of recessive lethals, though with higher variance (Supplementary Figure S5A and S5C). This occurs because with smaller sample sizes, recessive lethals do not segregate and affect DFE inference (Supplementary Figure S6), and the tail of the gamma DFE can then be extrapolated from the more weakly deleterious mutations that are segregating and the parametric DFE assumed.

Next, we attempted to fit more complex distributions of fitness effects to determine whether adding a proportion of lethal or neutral mutations may improve inference of the fraction of recessive lethals. For most data sets where 0% or 1% of mutations are recessive lethal, more complex models do not fit the data significantly better than the Gamma model (Table 1). However, when simulating higher fractions of recessive lethals (5% and 10%), the Neu+Gamma model often fits the data significantly better than the Gamma model (Table 1). The reason for the improved fit of the Neu+Gamma model is that recessive lethal mutations segregate at higher frequency under the true recessive model than what is expected under the additive model fit to the data. Thus, Fit∂a∂i infers these mutations to be more neutral than they actually are, and the mixture model with a proportion of neutral mutations ends up fitting the data better than the strict gamma model. Given that adding a proportion of neutral mutations improved fit, we next assessed whether considering a neutral proportion in conjunction with a lethal proportion could further improve inference. Instead, we found this Neu+Gamma+Let model only fits significantly better than the Gamma model in 55% (11/20) of data sets, suggesting that the data still do not consistently support the presence of lethal mutations. Additionally, estimates of p̂_let remain close to zero and often do not correspond to the true parameter values (Table 1). With smaller sample sizes, estimates of p̂_let show an upward bias and have larger confidence intervals (Supplementary Figure S5B).

Finally, to evaluate Fit∂a∂i’s performance under a Gamma+Let model further, we conducted log-likelihood profiling by considering a grid of values for p̂_let. Here, we again find that Fit∂a∂i cannot accurately estimate the true fraction of simulated recessive lethals and performs especially poorly when the DFE contains a high proportion of recessive lethal mutations (5% and 10%; Supplementary Figure S7). Thus, we conclude that Fit∂a∂i has limited power to infer the correct fraction of lethal mutations when lethals are completely recessive. This result demonstrates that misspecification of h in the inference impedes accurate estimation of the proportion of recessive lethals. However, estimates of the nonlethal portion of the DFE from Fit∂a∂i are still remarkably accurate, even when up to 5% of mutations are recessive lethal.

Testing the performance of Fit∂a∂i when lethal mutations are additive

To determine how much our inferences of the proportion of lethal mutations are improved when the data are generated under the dominance model used for inference, we next performed simulations where lethal mutations were additive.

Very few additive lethals segregate in the simulated data sets of sample sizes of 1,000 haploid genomes (Supplementary Figure S8). This is expected given that additive lethals are quickly removed from the population by purifying selection. When estimating the DFE under a gamma model, we find that the inferred DFEs are much closer to the true DFEs when compared with results for recessive lethals (Figure 2). Specifically, the gamma shape (a) parameters estimated under the different increments of additive lethals are less variable than in the recessive case (a ranged between 0.174 and 0.186 for the additive model and between 0.186 and 0.212 for the recessive case). However, the β parameter varied more in the additive scenario (β ranged between 702 and 1814 for the additive case and ranged between 621 and 712 for the recessive case) (Figure 2A, Supplementary Figure S9).

Figure 2.

Parameters of the gamma distribution and the inferred distribution of fitness effects (DFE) under different levels of additive lethals. (A) Inference of the shape (a) and scale (β) parameters under a gamma DFE model from simulated data with different levels of additive lethals in a sample of size 1,000 haploid genomes. (B) Expected versus inferred DFE for each lethal percentage under a gamma DFE, percentages are increments of additive lethal mutations. Expected and inferred site frequency spectra used to fit the model are presented in Supplementary Figure S4. The DFE categories are defined as neutral $(\left|s\right|=[0,{10}^{-5}))$, nearly neutral $(\left|s\right|=[{10}^{-5},{10}^{-4}))$, slightly deleterious $(\left|s\right|=[{10}^{-4},{10}^{-3}))$, moderately deleterious $(\left|s\right|=[{10}^{-3},{10}^{-2}))$, and strongly deleterious $(\left|s\right|=[{10}^{-2},1])$. Error bars correspond to the range of inferred proportions obtained across 20 simulation replicates.

When fitting more complex models of the DFE to this data, we consistently find Gamma+Let to fit the data significantly better than the Gamma model (Table 1). For example, for ≥5% recessive lethals, in at least 85% (17/20) of data sets, the Gamma+Let model had a significantly better fit compared with the Gamma model. Moreover, our estimates of p̂_let are generally close to the true simulation fraction of lethals. Specifically, when assuming lethal levels of 1%, we infer p̂_let = 0.03, and when assuming lethal levels of 10%, we infer p̂_let = 0.107 (Table 1, Supplementary Figure S9B). As previously observed for recessive lethals, the sample size does not affect the inference of the expected nonlethal portion of the DFE (Supplementary Figure S9A), but sample size does improve p̂_let estimation (Supplementary Figure S9B and S9C).

Finally, we again performed log-likelihood profiling to examine Fit∂a∂i’s performance under different levels of simulated additive lethals. Here, we find that estimates of p̂_let are consistently close to the true p_let (Supplementary Figure S10). However, the average p̂_let for 0% and 1% lethals are over-estimates, likely due to the true parameter being near the boundary of the parameter space. In conclusion, these results suggest that Fit∂a∂i performs reasonably well at inferring the proportion of lethal mutations when they are assumed to be additive and when the functional form of the DFE is properly specified.

Using mutation-selection-drift balance to estimate the fraction of recessive lethals to estimate the fraction of new mutations that are recessive lethal, primarily due to violating the assumption of additivity. Although it is possible to extend Fit∂a∂i to infer the proportion of lethal mutations under a recessive model using the SFS, we have extremely limited information on the broader distribution of dominance coefficients in humans, which may confound inferences, particularly in limited sample sizes. Thus, we instead employ a fundamentally different approach for quantifying the fraction of new mutations that are recessive lethal using models of mutation–selection–drift balance.

We first explored predictions of this model using mutation rate and coding sequence length estimates for humans (see Methods; Supplementary Table S3). When evaluating model predictions for a range of effective population sizes of N_e = {20,000, 30,000, 60,000}, we consistently find that empirical estimates of the number of recessive lethals per diploid in humans can be explained by a small proportion of new mutations being recessive lethal (Figure 3). Specifically, available evidence suggests that the average number of segregating recessive lethal mutations in humans is roughly in the range of 0.6 to 1.6 per diploid (Gao et al., 2015; Narasimhan et al., 2016), and analytical predictions with <~0.5% of new nonsynonymous mutations being recessive lethal appear to approximate this range, regardless of the assumed effective population size. By contrast, analytical predictions with ~5% of new mutations being recessive lethal, a value that has recently been proposed (Kardos et al., 2021; Pérez-Pereira et al., 2022), suggest ~10–20 recessive lethal mutations per diploid, well outside of empirical observations (red-shaded region in Figure 3).

Figure 3.

Relationship between the percent of new mutations that are recessive lethal and the predicted number of segregating recessive lethals per diploid under mutation–selection–drift balance for humans and Drosophila melanogaster under varying effective population sizes. X-axis denotes the percent of new nonsynonymous mutations that are recessive lethal and Y-axis denotes the resulting number of segregating recessive lethals per diploid. Red shading indicates the range of empirical estimates of segregating recessive lethals for each species. For humans, these values are derived from Gao et al. (2015) and Narasimhan et al. (2016), and for Drosophila, these values are derived from Simmons and Crow (1977); Lynch and Walsh (1998); and McCune et al. (2002) (see Methods for details). Blue points on the “Humans” panel denote predictions based on simulations under a human demographic model with recent exponential growth and under varying levels of recessiveness. Note that analytical predictions are in good agreement with simulations when h = 0.0 or 0.001.

We next explored predictions of this model using mutation rate and coding sequence length estimates for D. melanogaster (see Methods, Supplementary Table S3). We computed the expected number of recessive lethals per diploid assuming three different effective population sizes N_e = {5 × 10⁵, 1 × 10⁶, 5 × 10⁶}, reflecting the range of estimated effective population sizes in the literature (Duchen et al., 2013; Sheehan & Song, 2016; Huber et al.. 2017; Li & Stephan, 2006). Here, we again find that empirical estimates of segregating recessive lethals can be explained by a small fraction of new mutations being recessive lethal (Figure 3). Specifically, available evidence suggests ~1–3 recessive lethals per diploid in D. melanogaster (Lynch & Walsh, 1998; McCune et al., 2002; Simmons & Crow, 1977), which can be explained in our model by <~1% of new nonsynonymous mutations being recessive lethal, though results are dependent on the assumed effective population size (Figure 3). Importantly, a model where 5% of nonsynonymous mutations are assumed to be recessive lethal predicts ~9–27 recessive lethals per diploid, well beyond the empirical range for D. melanogaster.

Comparing predictions from mutation–selection–drift balance to simulations

The mutation–selection–drift balance model employed above makes a number of assumptions that may not exactly hold. First, these models assume that populations are in demographic equilibrium. As this assumption does not hold for humans or D. melanogaster, we ran forward-in-time simulations using SLiM 3 (Haller & Messer, 2019) under a nonequilibrium demographic model to assess the impact of violations of this model assumption. We restrict this analysis to humans due to computational constraints.

When running simulations under a range of values for p_let, we find that the number of recessive lethals observed at the end of this simulated demography mirrors that seen for an equilibrium population size of ~30,000 (dark blue circles in Figure 3). This is due to the fact that lethal mutations increase only modestly in frequency during recent and rapid exponential growth to N_e = 657,719 (Supplementary Figure S2). Thus, this result demonstrates that our analytical predictions for humans are reasonable despite not including this recent exponential growth. Moreover, these results also suggest that analytical predictions for Drosophila using a wide range of N_e values are also a reasonable approximation for estimating p_let.

Another assumption made by our analytical mutation–selection–drift balance model is that lethal mutations are fully recessive (h = 0). Evidence suggests that some recessive lethal mutations may have some reduction in fitness in heterozygous carriers (Simmons & Crow, 1977). To explore how heterozygous effects could affect the estimates of p̂_let, we again simulated recessive lethal mutations in humans, but where h = 0.001 or h = 0.01. For a given p_let, the number of recessive lethals per diploid decreases as h increases (lighter blue points in Figure 3). This is expected as selection against heterozygotes is stronger with increasing h. When h = 0.001, p̂_let still must be <1% to explain the observed number of recessive lethal mutations in humans. By contrast, results with h = 0.01 suggest p̂_let = ~2% for humans.

In summary, these results for humans and D. melanogaster consistently find that a small fraction (<~1%) of new nonsynonymous mutations are likely to be recessive lethal. Although this model makes a number of simplifying assumptions, results are strikingly consistent across species and appear to be relatively robust to nonequilibrium demography and reduced fitness in heterozygous carriers. Moreover, in both cases, we find that a proposed fraction of 4%–5% of new mutations being recessive lethal (Kardos et al., 2021; Pérez-Pereira et al., 2022) predicts levels of segregating lethal variation that are well outside of empirical estimates. Thus, our results support an upper bound on the recessive lethal portion of the DFE, suggesting that no more than ~1% of new nonsynonymous mutations are recessive lethal.

Discussion

In this study, we have explored different approaches for estimating the proportion of new mutations that are lethal. Our results demonstrate the limitations of SFS-based methods for detecting recessive lethal mutations, while also providing an estimate of the fraction of recessive lethal mutations based on models of mutation–selection–drift balance. Specifically, we show using simulations that a commonly used SFS-based method for DFE inference, Fit∂a∂i (Kim et al., 2017), cannot accurately quantify the proportion of new mutations that are recessive lethal (Table 1, Supplementary Figures S5 and S7). This result is not surprising, given that Fit∂a∂i assumes all mutations are additive by default, whereas our simulations assumed lethal mutations to be fully recessive (h = 0.0) and all other nonlethal deleterious mutations to be additive (h = 0.5). However, despite our inability to correctly infer the fraction of recessive lethals, we demonstrate that the presence of recessive lethals has a relatively minimal impact on inference of the deleterious nonlethal portion of the DFE, especially at low proportions of recessive lethals (Figure 1). The performance of Fit∂a∂i in estimating the nonlethal part of the DFE may be aided by the fact that in our simulated data sets, nonlethal mutations have additive effects on fitness. Thus, to the extent that recessive lethals do comprise a small portion of the DFE (Figure 3) and that the deleterious nonlethal portion of the DFE truly is additive and gamma distributed, our results suggest that existing estimates of this portion of the DFE are robust to the presence of lethals. This conclusion refutes the claim (Kardos et al., 2021) that the proportion of weakly deleterious and nearly neutral mutations has been overestimated in studies of the DFE using fewer than tens of thousands of individuals.

In reality, there is likely to be an inverse relationship between the selection coefficient of a mutation and its dominance coefficient, such that strongly deleterious mutations are highly recessive and nearly neutral mutations are closer to additive (Agrawal & Whitlock, 2011; Huber et al., 2018). Our analysis largely ignores this complexity by assuming mutations to be either fully additive or fully recessive. Future work on refining DFE estimates in humans and other species should incorporate this relationship between h and s, though doing so will require independent information on h and s, something that represents a major challenge (Fuller et al., 2019; Huber et al., 2018). However, recent theoretical work suggests that combining information from the SFS along with linkage disequilibrium may provide sufficient power for obtaining a joint distribution of s and h (Ragsdale, 2022).

In contrast to our results for recessive lethals, we find that Fit∂a∂i can accurately infer the fraction of lethal mutations when they act in an additive manner. This result further emphasizes that the violation of dominance assumptions is the main factor hindering the estimation of recessive lethals. However, the extent to which additive lethals actually exist, and if so, at what abundance, remains unclear. For example, Dukler et al. (2022) attempted to quantify the number of new strongly deleterious mutations by examining sites depleted of variation in ~72,000 human genomes, obtaining an estimate of ∼0.3–0.4 de novo strongly deleterious mutations per potential human zygote. However, the extent to which sites depleted of genetic variation reflects the presence of lethal mutations is not entirely clear. Demonstrating this, Agarwal & Przeworski (2021) used a similar approach by examining invariant methylated CpG sites in a sample of 390,000 human genomes, concluding that an additive mutation with a selection coefficient as small as s = −0.001 is sufficient to result in a lack of variation even in the large sample sizes they used. Thus, approaches for detecting lethal mutations based on genetic variation data may have inherent limitations not only in disentangling s from h, but also in separating lethal mutations from mutations that are strongly deleterious though far from lethal (s on the order of −0.001 to −0.1).

Given the above challenges in quantifying recessive lethals using genetic variation data, we instead sought to obtain an estimate of the recessive lethal portion of the DFE by employing models of mutation–selection–drift balance. This approach leverages direct estimates of segregating recessive lethals in humans and D. melanogaster to provide an estimate of the fraction of new mutations that are recessive lethal. For both humans and Drosophila, we find that the observed number of segregating recessive lethals can be explained by <~1% of new nonsynonymous mutations being recessive lethal (Figure 3). This result implies a de novo mutation rate of ~0.003 recessive lethal mutations per diploid human (assuming a lethal mutation rate of 0.5%) and ~0.001 recessive lethal mutations per diploid fly (assuming a lethal mutation rate of 1%). Notably, when assuming 4%–5% of new nonsynonymous mutations to be recessive lethal, as recently suggested (Kardos et al., 2021; Pérez-Pereira et al., 2022), these models predict levels of segregating recessive lethals that are well above those observed empirically (Figure 3). Thus, our results suggest that we can reject the proposal that the percentage of recessive lethals is as high as 4%–5% (Kardos et al., 2021; Pérez-Pereira et al., 2022).

Our approach based on mutation–selection–drift balance makes a number of simplistic assumptions, which could affect our results. First, mutation–selection–drift balance models assume that populations are at equilibrium, whereas both humans and D. melanogaster are known to have experienced recent exponential growth (Duchen et al., 2013; Gravel et al., 2011; Tennessen et al., 2012). We tested the impact of this assumption using SLiM simulations under a model of human demography. We found the actual increase in recessive lethal mutation frequencies lags somewhat behind the number predicted from the mutation–drift–selection balance in a model with exponential growth. Consequently, the number of recessive lethal mutations in a simulated human population roughly reflects the equilibrium value for a population with N_e on the order of 30,000 (Figure 3), in agreement with results from Amorim et al. (2017). Although we were unable to conduct such simulations for D. melanogaster due to computational limitations, these results suggest that our analytical model may also be a reasonable approximation for estimating p_let in Drosophila.

Second, if recessive lethal mutations confer a fitness effect in the heterozygous state, then they may be found at lower frequency in the population than predicted by mutation–drift–selection balance, which would require a higher p_let to match the observed data. Comparison of our analytical model predictions with those from simulations for humans demonstrates relatively minimal impacts on recessive lethal allele frequencies for h = 0.001, but more substantial effects when h = 0.01 (Figure 3). Although the precise dominance coefficient for lethal mutations in humans and other species remains poorly known, it is notable that a large heterozygous (h = 0.01) effect implies that the deleterious mutations also have a strong additive effect (hs < −0.01) and thus would have been detected in existing SFS-based studies of the DFE. For Drosophila, Huber et al. (2017) found that 0% of nonsynonymous mutations have hs < −0.01, implying that recessive lethal mutations are highly recessive (h << 0.01).

Another important assumption made by our analysis is that recessive lethal mutations can only arise as nonsynonymous mutations. This appears to be a reasonable assumption as a first approximation, especially in light of evidence that recessive lethal load does not appear to be influenced by genome size (McCune et al., 2002). However, it remains possible that lethal mutations can arise in other regions of the genome or as other types of mutations, such as in conserved noncoding regions, loss of function mutations, copy number variants, short tandem repeats, or transposable elements. As with our demographic assumptions, however, relaxing this assumption to include a greater length of sequence or other types of mutations in our analysis would only further decrease the estimated fraction of new nonsynonymous mutations that are recessive lethal. Finally, numerous other factors could contribute to recessive lethals segregating at higher levels than predicted by a simple model of mutation–selection–drift balance, such as epistasis, overdominance, and incomplete penetrance (Amorim et al., 2017; Ballinger & Noor, 2018). Thus, these factors suggest that our estimate of ~0.5% of new mutations being recessive lethal in humans likely represents an upper bound, implying that recessive lethals constitute a very small, though nevertheless important, portion of the nonsynonymous DFE.

In summary, our work investigates two alternative approaches for assessing the proportion of new mutations that are recessive lethal. Although we find that SFS-based approaches may not be well suited for detecting recessive lethal mutations, we find using an alternative approach based in mutation–selection–drift balance that recessive lethals comprise a very small portion of the DFE. These results have implications for understanding the prevalence of lethal mutations across organismal genomes, suggesting that only a small mutation rate of recessive lethals is needed to explain the observed numbers of segregating recessive lethals across diverse taxa. Moreover, this work also has important implications for modeling recessive lethal variation in humans and wild species, given that recessive lethals are an essential determinant of inbreeding depression and genetic load (Hedrick & Garcia-Dorado, 2016; Kyriazis et al., 2022).

Data availability

Scripts for simulations and Fit∂a∂i analysis are available at https://github.com/emmaewade/Lethals_Project. Scripts for mutation–selection–drift balance results are available at https://github.com/ckyriazis/lethals_scripts.

Author contributions

Conceptualization: C.C.K., K.E.L.; Methodology: E.E.W., C.C.K., M.I.A.C., K.E.L.; Formal analysis: E.E.W., C.C.K., M.I.A.C., K.E.L.; Resources: K.E.L.; Data curation: E.E.W., C.C.K., M.I.A.C.; Writing – Original Draft: C.C.K., M.I.A.C., K.E.L.; Writing – Review and Editing: E.E.W., C.C.K., M.I.A.C., K.E.L.; Visualization: E.E.W., C.C.K., M.I.A.C., K.E.L. Supervision: K.E.L.; Project administration: K.E.L.; Funding acquisition: K.E.L.

Conflict of interest:

The authors declare that they have no competing interests. Editorial processing of the manuscript was done independently of K.E.L. who is an associate editor of Evolution.